Refined Leaf Area Index Retrieval in Yellow River Delta Coastal Wetlands: UAV-Borne Hyperspectral and LiDAR Data Fusion and SHAP–Correlation-Integrated Machine Learning
Highlights
- A SHAP–correlation feature selection strategy (aggregated mean absolute SHAP values with Pearson analysis) enhanced robustness and identified critical predictive variables.
- Multi-source feature fusion significantly improved LAI retrieval accuracy across models, and LAI showed a distinct coastal-to-inland spatial gradient.
- Fusing hyperspectral and LiDAR with SHAP–correlation selection provides a robust, generalizable pathway for high-precision LAI mapping in heterogeneous wetlands.
- The mapped coastal–inland LAI gradient offers a quantitative basis for ecological assessment, supporting vegetation succession monitoring, and water–salt regulation practices in the Yellow River Delta.
Abstract
1. Introduction
2. Materials and Methods
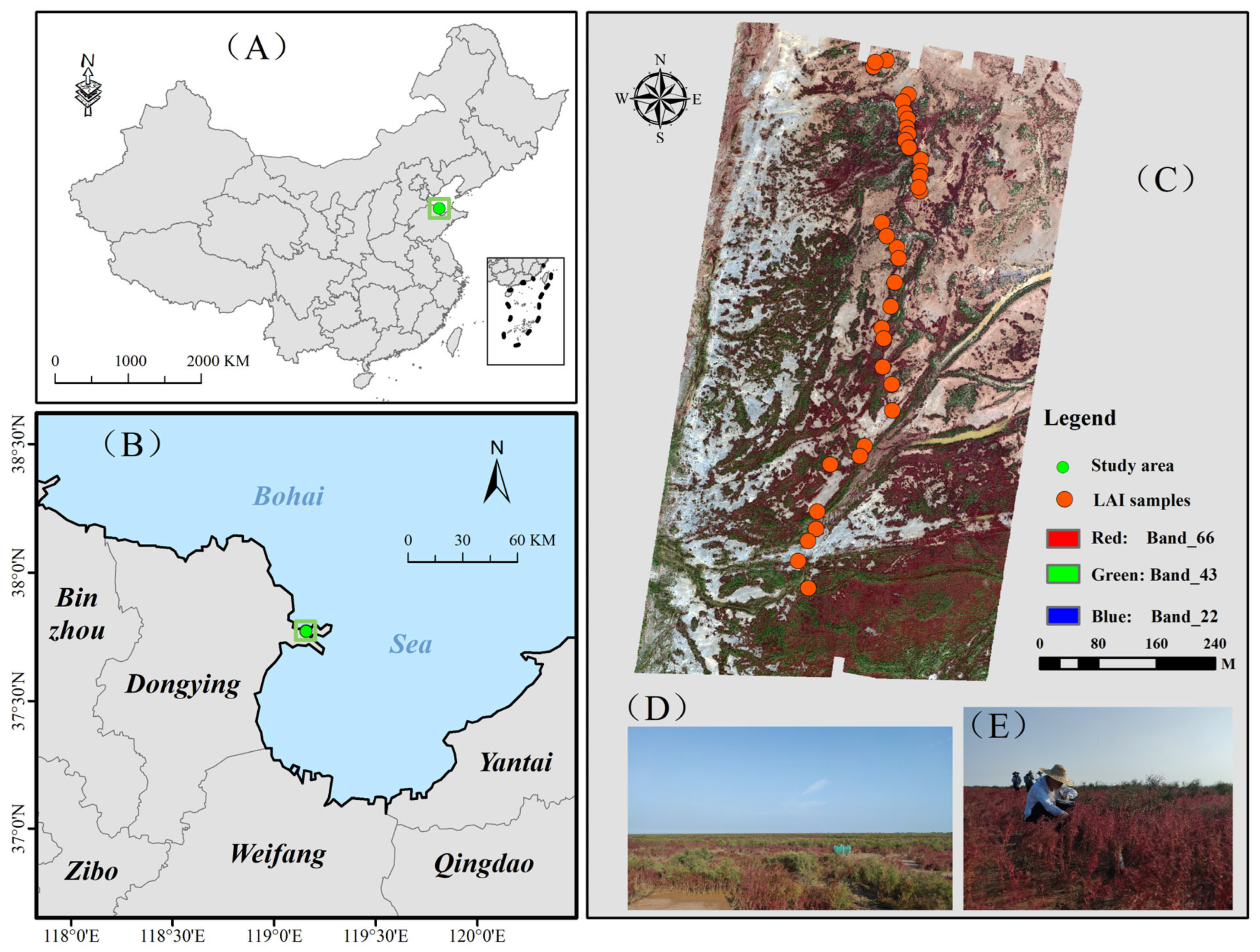
2.1. Study Area
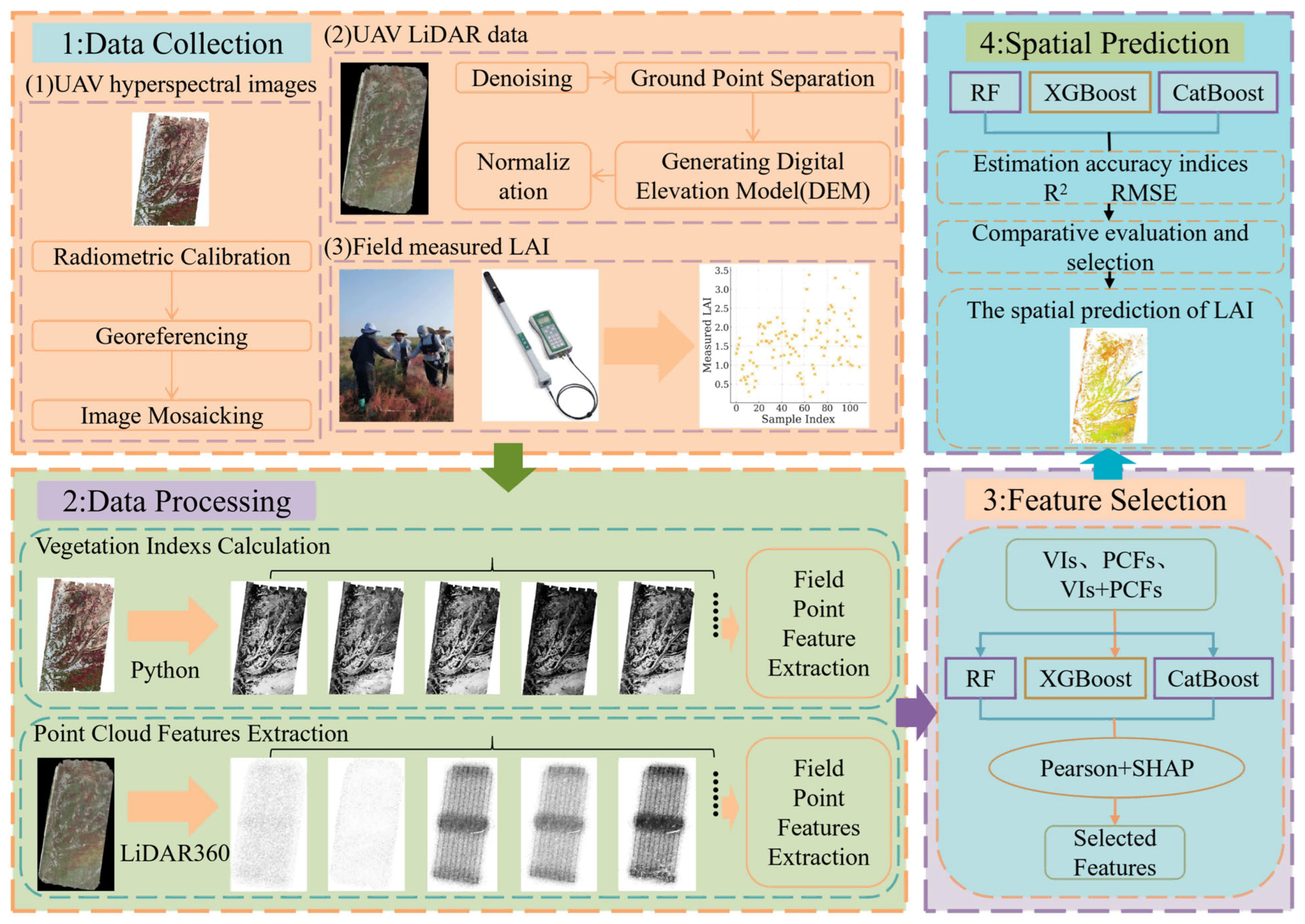
2.2. Data Acquisition and Preprocessing
2.2.1. UAV-Borne Hyperspectral Imagery
2.2.2. UAV-Borne LiDAR Data
2.2.3. In Situ LAI Measurements
2.3. Feature Extraction and Selection
2.3.1. VI Calculation
2.3.2. LiDAR Point Cloud Feature (PCF) Extraction
2.3.3. SHAP–Correlation Feature Selection Strategy
- Pearson correlation analysis was conducted to quantify the strengths of linear relationships among all selected features (VIs and PCFs) and evaluate potential collinearity within the initial feature set.
- Three machine learning models (RF, XGBoost, and CatBoost) were then utilized to calculate the mean absolute SHAP values of all features, which quantified the relative contribution of each feature to model outputs. These features were subsequently selected based on a pre-defined threshold (retaining features with mean SHAP values in the top 50% of all features).
- Finally, for the features retained after importance-based filtering, highly collinear variables (correlation coefficient |r| > 0.95) were identified and removed based on correlation analysis to avoid over-reliance on a single collinearity metric. The resulting optimal feature subset was ultimately used for the construction of wetland vegetation LAI retrieval models.
2.4. Machine Learning Modeling for LAI Retrieval
2.4.1. Model Selection and Parameter Tuning
2.4.2. Performance Evaluation for LAI Retrieval Model
3. Results
3.1. Inter- and Intra-Feature Correlation Patterns
3.1.1. Inter-Feature Correlation Between VIs and PCFs
3.1.2. Intra-Feature Correlation Within VIs and PCFs
3.2. Feature Selection and Optimization-Based SHAP–Correlation Strategy
3.2.1. Key VI Screening with Mean Absolute SHAP Values
3.2.2. Key PCF Selection with Mean Absolute SHAP Values
3.2.3. Fused Feature Screening with Mean Absolute SHAP Values
3.2.4. Final Non-Redundant Feature Subsets
3.3. LAI Retrieval Performance of Different Models
3.3.1. VI-Based Models for LAI Retrieval
3.3.2. PCF-Based Models for LAI Retrieval
3.3.3. Fused Feature-Based Models for LAI Retrieval
3.4. Spatial Distribution of Wetland Vegetation LAI
4. Discussion
4.1. Synergistic Mechanisms of Hyperspectral–LiDAR Fusion for LAI Retrieval
4.2. Role of SHAP–Correlation Selection in Model Accuracy
4.3. Ecological Implication of LAI Spatial Gradients
4.4. Differences in Model Performance
4.5. Limitations and Future Perspectives
5. Conclusions
- Multi-source remote sensing data fusion substantially improves LAI retrieval accuracy. Models dependent on hyperspectral-derived VIs or LiDAR-derived PCFs showed inherent limitations. In contrast, the integration of fused features markedly enhanced model performance and achieved consistently high accuracy results across different algorithms. Notably, the RF model had better performance, attaining R2 = 0.968 and RMSE = 0.125.
- The feature screening strategy exerts a pivotal influence on modeling robustness. The feature selection strategy aggregated the mean absolute SHAP values across the three models, yielding higher and stabler LAI retrieval accuracy. This advantage stems from the aggregated SHAP method to mitigate model-specific biases and retain features with robust informational value, thereby enhancing the ability of LAI retrieval models across different algorithmic frameworks.
- Critical predictive variables for wetland LAI retrieval are identified. Combined Pearson correlation analysis and SHAP value analysis indicated that PCFs (HCV, H50th, H25th, and FG) and VIs (mNDVI, INT, and VCI) significantly contributed to accurate LAI retrieval.
- Wetland LAI exhibits significant fluctuations from the coastal zone to the inland region, with a tendency for increasing values. This spatial trend of LAI in the study area was consistent with the distribution of wetland vegetation and the gradient changes in growth environments. The fused features effectively capture this heterogeneity, validating the fusion model’s capacity to resolve ecologically meaningful spatial patterns in wetland vegetation LAI.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ferreira, C.S.; Kašanin-Grubin, M.; Solomun, M.K.; Sushkova, S.; Minkina, T.; Zhao, W.; Kalantari, Z. Wetlands as nature-based solutions for water management in different environments. Curr. Opin. Environ. Sci. Health 2023, 33, 100476. [Google Scholar] [CrossRef]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An overview of global leaf area index (LAI): Methods, products, validation, and applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Parker, G.G. Tamm review: Leaf Area Index (LAI) is both a determinant and a consequence of important processes in vegetation canopies. For. Ecol. Manag. 2020, 477, 118496. [Google Scholar] [CrossRef]
- Lu, L.; Luo, J.; Xin, Y.; Duan, H.; Sun, Z.; Qiu, Y.; Xiao, Q. How can UAV contribute in satellite-based Phragmites australis aboveground biomass estimating? Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103024. [Google Scholar] [CrossRef]
- Ali, A.M.; Darvishzadeh, R.; Skidmore, A.; Gara, T.W.; O’Connor, B.; Roeoesli, C.; Paganini, M.; Heurich, M.; Paganini, M. Comparing methods for mapping canopy chlorophyll content in a mixed mountain forest using Sentinel-2 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 87, 102037. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, Y.; Ge, Y.; Xie, H.; Tong, X.; Atkinson, P.M. A comprehensive review of spatial-temporal-spectral information reconstruction techniques. Sci. Remote Sens. 2023, 8, 100102. [Google Scholar] [CrossRef]
- Jin, H.; Qiao, Y.; Liu, T.; Xie, X.; Fang, H.; Guo, Q.; Zhao, W. A hierarchical downscaling scheme for generating fine-resolution leaf area index with multisource and multiscale observations via deep learning. Int. J. Appl. Earth Obs. Geoinf. 2024, 133, 104152. [Google Scholar] [CrossRef]
- Li, C.; Zhou, H.; Tang, J.; Wang, C.; Wang, Z.; Qi, J.; Yang, B.; Fang, R. Time-series high spatio-temporal resolution vegetation leaf area index estimation based on NDVI trends. Int. J. Appl. Earth Obs. Geoinf. 2025, 142, 104744. [Google Scholar] [CrossRef]
- Yan, P.; Feng, Y.; Han, Q.; Hu, Z.; Huang, X.; Su, K.; Kang, S. Enhanced cotton chlorophyll content estimation with UAV multispectral and LiDAR constrained SCOPE model. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 104052. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H. Estimation of LAI with the LiDAR technology: A review. Remote Sens. 2020, 12, 3457. [Google Scholar] [CrossRef]
- Shi, Z.; Shi, S.; Gong, W.; Xu, L.; Wang, B.; Sun, J.; Xu, Q. LAI estimation based on physical model combining airborne LiDAR waveform and Sentinel-2 imagery. Front. Plant Sci. 2023, 14, 1237988. [Google Scholar] [CrossRef] [PubMed]
- Du, X.Y.; Wan, L.; Cen, H.Y.; Chen, S.B.; Zhu, J.P.; Wang, H.Y.; He, Y. Multi-temporal monitoring of leaf area index of rice under different nitrogen treatments using UAV images. Int. J. Precis. Agric. Aviat. 2020, 3, 7–12. [Google Scholar] [CrossRef]
- Liu, S.; Jin, X.; Bai, Y.; Wu, W.; Cui, N.; Cheng, M.; Liu, Y.; Meng, L.; Jia, X.; Nie, C.; et al. UAV multispectral images for accurate estimation of the maize LAI considering the effect of soil background. Int. J. Appl. Earth Obs. Geoinf. 2023, 121, 103383. [Google Scholar] [CrossRef]
- Fang, H.; Man, W.; Liu, M.; Zhang, Y.; Chen, X.; Li, X.; Tian, D. Leaf area index inversion of Spartina alterniflora using UAV hyperspectral data based on multiple optimized machine learning algorithms. Remote Sens. 2023, 15, 4465. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Liang, L.; Geng, D.; Yan, J.; Qiu, S.; Di, L.; Wang, S.; Li, L. Estimating crop LAI using spectral feature extraction and the hybrid inversion method. Remote Sens. 2020, 12, 3534. [Google Scholar] [CrossRef]
- Yang, J.; Xing, M.; Tan, Q.; Shang, J.; Song, Y.; Ni, X.; Wang, J.; Xu, M. Estimating effective leaf area index of winter wheat based on UAV point cloud data. Drones 2023, 7, 299. [Google Scholar] [CrossRef]
- Norton, C.L.; Hartfield, K.; Collins, C.D.H.; van Leeuwen, W.J.; Metz, L.J. Multi-temporal LiDAR and hyperspectral data fusion for classification of semi-arid woody cover species. Remote Sens. 2022, 14, 2896. [Google Scholar] [CrossRef]
- Wang, B.; Liu, J.; Li, J.; Li, M. UAV LiDAR and hyperspectral data synergy for tree species classification in the Maoershan Forest Farm region. Remote Sens. 2023, 15, 1000. [Google Scholar] [CrossRef]
- Ma, Y.; Zhao, Y.; Im, J.; Zhao, Y.; Zhen, Z. A deep-learning-based tree species classification for natural secondary forests using unmanned aerial vehicle hyperspectral images and LiDAR. Ecol. Indic. 2024, 159, 111608. [Google Scholar] [CrossRef]
- Xu, Y.; Qin, Y.; Li, B.; Li, J. Estimating vegetation aboveground biomass in Yellow River Delta coastal wetlands using Sentinel-1, Sentinel-2 and Landsat-8 imagery. Ecol. Inform. 2025, 87, 103096. [Google Scholar] [CrossRef]
- Gao, S.; Yan, K.; Liu, J.; Pu, J.; Zou, D.; Qi, J.; Mu, X.; Yan, G. Assessment of remote-sensed vegetation indices for estimating forest chlorophyll concentration. Ecol. Indic. 2024, 162, 112001. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Kaur, N.; Sharma, A.K.; Shellenbarger, H.; Griffin, W.; Serrano, T.; Brym, Z.; Sharma, L.K. Drone and handheld sensors for hemp: Evaluating NDVI and NDRE in relation to nitrogen application and crop yield. Agrosyst. Geosci. Environ. 2025, 8, e70075. [Google Scholar] [CrossRef]
- Bak, H.J.; Kim, E.J.; Lee, J.H.; Chang, S.; Kwon, D.; Im, W.J.; Kim, D.H.; Lee, I.H.; Lee, M.J.; Hwang, W.H.; et al. Canopy-Level Rice Yield and Yield Component Estimation Using NIR-Based Vegetation Indices. Agriculture 2025, 15, 594. [Google Scholar] [CrossRef]
- Yeom, J.; Jung, J.; Chang, A.; Ashapure, A.; Maeda, M.; Maeda, A.; Landivar, J. Comparison of vegetation indices derived from UAV data for differentiation of tillage effects in agriculture. Remote Sens. 2019, 11, 1548. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Zhu, X.; Li, Q.; Guo, C. Evaluation of the monitoring capability of various vegetation indices and mainstream satellite band settings for grassland drought. Ecol. Inform. 2024, 82, 102717. [Google Scholar] [CrossRef]
- Barati, S.; Rayegani, B.; Saati, M.; Sharifi, A.; Nasri, M. Comparison the accuracies of different spectral indices for estimation of vegetation cover fraction in sparse vegetated areas. Egypt. J. Remote Sens. Space Sci. 2011, 14, 49–56. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N.; Chivkunova, O.B. Optical properties and nondestructive estimation of anthocyanin content in plant leaves. Photochem. Photobiol. 2001, 74, 38–45. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Gamon, J.A.; Surfus, J.S. Assessing leaf pigment content and activity with a reflectometer. New Phytol. 1999, 143, 105–117. [Google Scholar] [CrossRef]
- Meng, L.; Yin, D.; Cheng, M.; Liu, S.; Bai, Y.; Liu, Y.; Jin, X. Improved crop biomass algorithm with piecewise function (iCBA-PF) for maize using multi-source UAV data. Drones 2023, 7, 254. [Google Scholar] [CrossRef]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy near-infrared reflectance and terrestrial photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef] [PubMed]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Pu, R.; Gong, P.; Yu, Q. Comparative analysis of EO-1 ALI and Hyperion, and Landsat ETM+ data for mapping forest crown closure and leaf area index. Sensors 2008, 8, 3744–3766. [Google Scholar] [CrossRef]
- Metternicht, G. Vegetation indices derived from high-resolution airborne videography for precision crop management. Int. J. Remote Sens. 2003, 24, 2855–2877. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1998, 25, 295–309. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Kim, Y.; Didan, K. 2-band enhanced vegetation index without a blue band and its application to AVHRR data. In Remote Sensing and Modeling of Ecosystems for Sustainability IV; SPIE: Bellingham, MA, USA, 2007; Volume 6679, pp. 45–53. [Google Scholar]
- Tahir, M.N.; Naqvi, S.Z.A.; Lan, Y.B.; Zhang, Y.L.; Wang, Y.K.; Afzal, M.; Cheema, M.J. Real time estimation of chlorophyll content based on vegetation indices derived from multispectral UAV in the kinnow orchard. Int. J. Precis. Agric. Aviat. 2018, 1, 24–31. [Google Scholar] [CrossRef]
- Hanberry, B.B. Practical guide for retaining correlated climate variables and unthinned samples in species distribution modeling, using random forests. Ecol. Inform. 2024, 79, 102406. [Google Scholar] [CrossRef]
- Bradter, U.; Altringham, J.D.; Kunin, W.E.; Thom, T.J.; O’Connell, J.; Benton, T.G. Variable ranking and selection with random forest for unbalanced data. Environ. Data Sci. 2022, 1, e30. [Google Scholar] [CrossRef]
- Bhattarai, D.; Lucieer, A. Random forest regression exploring contributing factors to artificial night-time lights observed in VIIRS satellite imagery. Int. J. Digit. Earth 2024, 17, 2324941. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, T.; Guo, W.; Xu, X.; Qiao, H.; Xie, Y.; Ma, X. Leaf area index estimation model for UAV image hyperspectral data based on wavelength variable selection and machine learning methods. Plant Methods 2021, 17, 49. [Google Scholar] [CrossRef]
- Mulero, G.; Bonfil, D.J.; Helman, D. Wheat leaf area index retrieval from drone-derived hyperspectral and LiDAR imagery using machine learning algorithms. Agric. For. Meteorol. 2025, 372, 110648. [Google Scholar] [CrossRef]
- Xu, Z.; Li, R.; Dou, W.; Wen, H.; Yu, S.; Wang, P.; Ning, L.; Duan, J.; Wang, J. Plant diversity response to environmental factors in Yellow River delta, China. Land 2024, 13, 264. [Google Scholar] [CrossRef]
- Qiu, M.; Liu, Y.; Chen, P.; He, N.; Wang, S.; Huang, X.; Fu, B. Spatio-temporal changes and hydrological forces of wetland landscape pattern in the Yellow River Delta during 1986–2022. Landsc. Ecol. 2024, 39, 51. [Google Scholar] [CrossRef]
- Chang, D.; Wang, Z.; Ning, X.; Li, Z.; Zhang, L.; Liu, X. Vegetation changes in Yellow River Delta wetlands from 2018 to 2020 using PIE-Engine and short time series Sentinel-2 images. Front. Mar. Sci. 2022, 9, 977050. [Google Scholar] [CrossRef]
- Xu, R.; Fan, Y.; Fan, B.; Feng, G.; Li, R. Classification and Monitoring of Salt Marsh Vegetation in the Yellow River Delta Based on Multi-Source Remote Sensing Data Fusion. Sensors 2025, 25, 529. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Y.; Zong, J.; Wang, Y.; Cao, X.; Wang, Y.; Cheng, X.; Zhang, W. Remote sensing application in ecological restoration monitoring: A systematic review. Remote Sens. 2024, 16, 2204. [Google Scholar] [CrossRef]
- Hawman, P.A.; Mishra, D.R.; O’Connell, J.L. Dynamic emergent leaf area in tidal wetlands: Implications for satellite-derived regional and global blue carbon estimates. Remote Sens. Environ. 2023, 290, 113553. [Google Scholar] [CrossRef]
- Shao, Z.; Ahmad, M.N.; Javed, A. Comparison of random forest and XGBoost classifiers using integrated optical and SAR features for mapping urban impervious surface. Remote Sens. 2024, 16, 665. [Google Scholar] [CrossRef]
- Pawłuszek-Filipiak, K.; Lewandowski, T. The Impact of Feature Selection on XGBoost Performance in Landslide Susceptibility Mapping Using an Extended Set of Features: A Case Study from Southern Poland. Appl. Sci. 2025, 15, 8955. [Google Scholar] [CrossRef]
- Huang, H.; Wu, D.; Fang, L.; Zheng, X. Comparison of multiple machine learning models for estimating the forest growing stock in large-scale forests using multi-source data. Forests 2022, 13, 1471. [Google Scholar] [CrossRef]
- Ding, J.; Du, J.; Wang, H.; Xiao, S. A novel two-stage feature selection method based on random forest and improved genetic algorithm for enhancing classification in machine learning. Sci. Rep. 2025, 15, 16828. [Google Scholar] [CrossRef]
- Luo, Z.; Deng, M.; Tang, M.; Liu, R.; Feng, S.; Zhang, C.; Zheng, Z. Estimating soil profile salinity under vegetation cover based on UAV multi-source remote sensing. Sci. Rep. 2025, 15, 2713. [Google Scholar] [CrossRef] [PubMed]
- Arroyo-Mora, J.P.; Kalacska, M.; Løke, T.; Schläpfer, D.; Coops, N.C.; Lucanus, O.; Leblanc, G. Assessing the impact of illumination on UAV pushbroom hyperspectral imagery collected under various cloud cover conditions. Remote Sens. Environ. 2021, 258, 112396. [Google Scholar] [CrossRef]
- Abdelbaki, A.; Schlerf, M.; Retzlaff, R.; Machwitz, M.; Verrelst, J.; Udelhoven, T. Comparison of Crop Trait Retrieval Strategies Using UAV-Based VNIR Hyperspectral Imaging. Remote Sens. 2021, 13, 1748. [Google Scholar] [CrossRef]
- Jia, W.; Pang, Y.; Tortini, R.; Schläpfer, D.; Li, Z.; Roujean, J.L. A kernel-driven BRDF approach to correct airborne hyperspectral imagery over forested areas with rugged topography. Remote Sens. 2020, 12, 432. [Google Scholar] [CrossRef]
- Lee, K.; Han, X. A study on leveraging unmanned aerial vehicle collaborative driving and aerial photography systems to improve the accuracy of crop phenotyping. Remote Sens. 2023, 15, 3903. [Google Scholar] [CrossRef]
- Zhang, D.; Ni, H. Inversion of forest biomass based on multi-source remote sensing images. Sensors 2023, 23, 9313. [Google Scholar] [CrossRef] [PubMed]
- Queally, N.; Ye, Z.; Zheng, T.; Chlus, A.; Schneider, F.; Pavlick, R.P.; Townsend, P.A. FlexBRDF: A flexible BRDF correction for grouped processing of airborne imaging spectroscopy flightlines. J. Geophys. Res. Biogeosci. 2022, 127, e2021JG006622. [Google Scholar] [CrossRef] [PubMed]
- Brell, M.; Segl, K.; Guanter, L.; Bookhagen, B. Hyperspectral and lidar intensity data fusion: A framework for the rigorous correction of illumination, anisotropic effects, and cross calibration. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2799–2810. [Google Scholar] [CrossRef]









| Subsystem | Parameter | Description/Value |
|---|---|---|
| Hyperspectral system | UAV platform | DJI M300 RTK |
| Hyperspectral imager | PIKA L | |
| Spectral resolution | 2.1 nm | |
| Frame rate | 249 fps | |
| Number of bands | 150 | |
| Spectral range | 400–1000 nm | |
| Flight altitude | 100 m | |
| Flight speed | 2 m/s | |
| Slide overlap ratio | 70% | |
| Spatial resolution | 10 cm | |
| LiDAR system | System parameters | |
| UAV platform | DJI M300 RTK | |
| Flight speed | 10 m/s | |
| LiDAR unit | ||
| Laser sensor | Livox | |
| Scanning mode | Frame scanning | |
| Maximum number of echoes | 3 | |
| Laser wavelength | 905 nm | |
| Maximum measurement range | 450 m | |
| Scanning frequency | 240 K/s | |
| Maximum scanning rate | 480,000 pts./s | |
| Ranging accuracy | 3 cm | |
| Field of view | Repetitive scanning: 70.4° × 4.5° Non-repetitive scanning: 70.4° × 77.2° | |
| Inertial navigation system | ||
| Heading accuracy | 0.15° | |
| Pitch/Roll accuracy | 0.025° | |
| IMU update frequency | 200 Hz |
| Plant Species | Count | Min | Max | Mean | Standard Deviation | Coefficient of Variation |
|---|---|---|---|---|---|---|
| Suaeda salsa | 41 | 0.173 | 2.58 | 1.30 | 0.68 | 52.03% |
| Tamarix chinensis | 47 | 0.925 | 3.3 | 1.70 | 0.46 | 27.23% |
| Phragmites australis | 22 | 0.501 | 3.42 | 1.78 | 0.88 | 49.61% |
| ALL | 110 | 0.173 | 3.42 | 1.57 | 0.67 | 42.93% |
| Abbreviation | Index Name | Formula | Reference |
|---|---|---|---|
| NDVI | Normalized Difference Vegetation Index | [22] | |
| EVI | Enhanced Vegetation Index | [22] | |
| RVI | Ratio Vegetation Index | [23] | |
| NDRE | Normalized Difference Red Edge Index | [24] | |
| GNDVI | Green Normalized Difference Vegetation Index | [22] | |
| LCI | Leaf Chlorophyll Index | [25] | |
| RECI | Red Edge Chlorophyll Index | [26] | |
| CIgreen | Green Chlorophyll Index | [26] | |
| MSR | Modified Simple Ratio Index | [27] | |
| MSAVI | Modified Soil-Adjusted Vegetation Index | [28] | |
| OSAVI | Optimized Soil-Adjusted Vegetation Index | [28] | |
| DVI | Difference Vegetation Index | [29] | |
| NLI | Nonlinear Vegetation Index | [29] | |
| IPVI | Infrared Percentage Vegetation Index | [29] | |
| MTVI | Modified Triangular Vegetation Index | [29] | |
| ARI | Anthocyanin Reflectance Index | [30] | |
| SIPI | Structure Insensitive Pigment Index | [22] | |
| VCI | Vegetation Condition Index | [31] | |
| RGR | NIR-Green Ratio Index | [32] | |
| TVI | Triangular Vegetation Index | [33] | |
| CSI | Composite Spectral Index | [33] | |
| MTCI | MERIS Terrestrial Chlorophyll Index | [22] | |
| MCARI | Modified Chlorophyll Absorption Ratio Index | [33] | |
| TCARI | Transformed Chlorophyll Absorption Ratio Index | [33] | |
| ARVI | Atmospherically Resistant Vegetation Index | [23] | |
| INT | Color Intensity Index | [33] | |
| NIRv | Near-Infrared Reflectance of vegetation | [34] | |
| PSRI | Plant Senescence Reflectance Index | [35] | |
| SR | Simple Ratio | [36] | |
| EXG | Excess Green Index | [34] | |
| NDVIg | Normalized Difference Green Index | [37] | |
| VARI | Visible Atmospherically Resistant Index | [25] | |
| SPVI | Standardized Plant Vegetation Index | [38] | |
| SAVI | Soil-Adjusted Vegetation Index | [39] | |
| SASR | Standardized Absorption Ratio Index | [40] | |
| MVI | Modified Vegetation Index | [41] | |
| mNDVI | Modified Normalized Difference Vegetation Index | [38] | |
| GLI | Green Leaf Index | [33] |
| Sample Set | Plant Species | Count | Min | Max | Mean | Standard Deviation | Coefficient of Variation |
|---|---|---|---|---|---|---|---|
| Full sample set | Suaeda salsa | 41 | 0.173 | 2.58 | 1.30 | 0.68 | 52.03% |
| Tamarix chinensis | 47 | 0.925 | 3.3 | 1.70 | 0.46 | 27.23% | |
| Phragmites australis | 22 | 0.501 | 3.42 | 1.78 | 0.88 | 49.61% | |
| ALL | 110 | 0.173 | 3.42 | 1.57 | 0.67 | 42.93% | |
| Fusion subset | Suaeda salsa | 31 | 0.173 | 2.58 | 1.47 | 0.81 | 55.36% |
| Tamarix chinensis | 44 | 0.925 | 3.3 | 1.71 | 0.47 | 27.46% | |
| Phragmites australis | 22 | 0.501 | 3.42 | 1.78 | 0.88 | 49.61% | |
| ALL | 97 | 0.173 | 3.42 | 1.57 | 0.72 | 44.14% |
| Model | Hyperparameter | Parameter Range | Cross- Validation | Selection Criteria | Optimal Parameters |
|---|---|---|---|---|---|
| RF | n_estimators | [100, 200, 300, …, 1500] | 5-fold cross-validation | R2 | 1200 |
| max_depth | [5, 10, 15, 16, 20] | 16 | |||
| Min_samples_split | [2, 5, 10] | 2 | |||
| Min_samples_leaf | [2, 5, 10] | 2 | |||
| Max_features | [0.6, 0.7, 0.8, 0.9] | 0.8 | |||
| XGBoost | n_estimators | [100, 500, 1000, 1500] | 5-fold cross-validation | R2 | 1500 |
| max_depth | [3, 5, 7, 9] | 7 | |||
| Learning_rate | [0.01, 0.03, 0.05, 0.07] | 0.03 | |||
| subsample | [0.6, 0.7, 0.8, 0.9] | 0.6 | |||
| Colsample_bytree | [0.7, 0.8, 0.9] | 0.9 | |||
| CatBoost | depth | [5, 6, 7, 8] | 5-fold cross-validation | R2 | 5 |
| Learning_rate | [0.01, 0.05, 0.1] | 0.05 | |||
| n_estimators | [200, 400, 600, 800] | 800 | |||
| L2_leaf_reg | [1.0, 3.0, 6.0] | 6.0 | |||
| Min_data_in_leaf | [15, 20, 50] | 50 |
| Feature Type | Retained Features | Number |
|---|---|---|
| VIs | INT, mNDVI, VCI, TVI, NDVIg, NDRE, ARI, GLI, SIPI | 9 |
| PCFs | FG, HCV, RCR, H25th, H50th, H99th | 6 |
| Fused (VIs + PCFs) | HCV, mNDVI, H50th, H25th, INT, FG, VCI | 7 |
| Algorithm | Features | Accuracy | |
|---|---|---|---|
| R2 | RMSE | ||
| RF | VIs | 0.521 | 0.448 |
| PCFs | 0.894 | 0.208 | |
| VIs + PCFs | 0.968 | 0.125 | |
| XGBoost | VIs | 0.735 | 0.333 |
| PCFs | 0.800 | 0.286 | |
| VIs + PCFs | 0.962 | 0.136 | |
| CatBoost | VIs | 0.622 | 0.398 |
| PCFs | 0.782 | 0.299 | |
| VIs + PCFs | 0.949 | 0.159 | |
| Feature Selection Criteria | Retrieval Algorithm | Selected Features | Accuracy | |
|---|---|---|---|---|
| R2 | RMSE | |||
| RF | RF | H50th, H25th, HCV, MSR, mNDVI | 0.952 | 0.153 |
| XGBoost | 0.942 | 0.169 | ||
| CatBoost | 0.894 | 0.227 | ||
| XGBoost | RF | NDVI, HCV, H50th, H25th, FG, INT, VCI, RCR, MCARI, NDRE, GNDVI, EXG | 0.893 | 0.229 |
| XGBoost | 0.895 | 0.226 | ||
| CatBoost | 0.879 | 0.244 | ||
| CatBoost | RF | HCV, H25th, IPVI, INT, FG, RECI | 0.895 | 0.226 |
| XGBoost | 0.918 | 0.200 | ||
| CatBoost | 0.957 | 0.144 | ||
| RF + XGBoost + CatBoost | RF | HCV, mNDVI, H50th, H25th, INT, FG, VCI | 0.968 | 0.125 |
| XGBoost | 0.962 | 0.136 | ||
| CatBoost | 0.949 | 0.159 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Shan, C.; Cai, T.; Wang, J.; Ma, Y.; Du, J.; Jia, X.; Yang, X.; Guo, F.; Li, H.; Qiu, S. Refined Leaf Area Index Retrieval in Yellow River Delta Coastal Wetlands: UAV-Borne Hyperspectral and LiDAR Data Fusion and SHAP–Correlation-Integrated Machine Learning. Remote Sens. 2026, 18, 40. https://doi.org/10.3390/rs18010040
Shan C, Cai T, Wang J, Ma Y, Du J, Jia X, Yang X, Guo F, Li H, Qiu S. Refined Leaf Area Index Retrieval in Yellow River Delta Coastal Wetlands: UAV-Borne Hyperspectral and LiDAR Data Fusion and SHAP–Correlation-Integrated Machine Learning. Remote Sensing. 2026; 18(1):40. https://doi.org/10.3390/rs18010040
Chicago/Turabian StyleShan, Chenqiang, Taiyi Cai, Jingxu Wang, Yufeng Ma, Jun Du, Xiang Jia, Xu Yang, Fangming Guo, Huayu Li, and Shike Qiu. 2026. "Refined Leaf Area Index Retrieval in Yellow River Delta Coastal Wetlands: UAV-Borne Hyperspectral and LiDAR Data Fusion and SHAP–Correlation-Integrated Machine Learning" Remote Sensing 18, no. 1: 40. https://doi.org/10.3390/rs18010040
APA StyleShan, C., Cai, T., Wang, J., Ma, Y., Du, J., Jia, X., Yang, X., Guo, F., Li, H., & Qiu, S. (2026). Refined Leaf Area Index Retrieval in Yellow River Delta Coastal Wetlands: UAV-Borne Hyperspectral and LiDAR Data Fusion and SHAP–Correlation-Integrated Machine Learning. Remote Sensing, 18(1), 40. https://doi.org/10.3390/rs18010040







