Analysis of Image Domain Characteristics of Maritime Rotating Ships for Spaceborne Multichannel SAR

Highlights

What are the main findings?

• For the effect of each rotation motion on the ship’s signal characteristics in image domain, the effect of yaw is minimal and the effect of pitch is the greatest.
• The variations in ATI phase caused by roll and yaw are mainly related to the y′-axis coordinate of the scatterer and are approximately linearly related to $y_{q0}^{\prime }$, while those caused by pitch is mainly related to the y′-axis and z′-axis coordinates of the scatterer and is approximately linearly related to $x_{q0}^{\prime }$ and $z_{q0}^{\prime }$.

What are the implications of the main findings?

• It reveals the scatterer’s azimuth position shift, azimuth defocusing, azimuth sidelobe asymmetry, and ATI phase variation introduced by each rotation motion and their dependence on the scatterer’s position relative to the gravity center of the ship.
• It can lay the foundation for the design of moving target indication methods for rotating ship targets.

Abstract

Ship targets are usually high-value targets, and synthetic aperture radar (SAR) moving ship indication is of great importance in maritime traffic monitoring. However, due to the motion of the ocean, maritime ships may have rotational motion in addition to the conventional translational motion. The rotational motion, including the yaw, pitch, and roll, will cause the signal characteristics of the ship to become very complex, which increases the difficulty of designing moving target indication methods. This paper studies the effect of each rotation motion on the ship’s signal characteristics in image domain for spaceborne multichannel SAR. Firstly, the range equation of an arbitrary scatterer on the ship with both rotational and translational motions is developed. Then, the influences of each rotation motion on the coefficients of the range equation and the scatterer’s along-track interferometric (ATI) phase are revealed. Finally, numerical experiments are conducted to investigate the effect of each rotation motion on the scatterer’s azimuth position shift, azimuth defocusing, azimuth sidelobe symmetry, and ATI phase, which are important parameters for moving target indication.

1. Introduction

Synthetic aperture radar (SAR) has the capability of all-weather, all-day, and long-range imaging and has been widely used in both civil and military fields [1,2,3,4]. Modern SAR systems are usually equipped with the operation mode of ground moving target indication (GMTI) and can indicate ground/maritime moving targets while simultaneously obtaining a high-resolution image of the observed scene. SAR-GMTI systems can play an important role in the fields of ground/maritime traffic monitoring, military reconnaissance, and so on [5,6,7,8,9,10].

Unlike ground moving targets, due to the influence of the ocean’s motion, maritime moving targets may have rotational motion, including the yaw, pitch, and roll, in addition to the conventional translational motion [11,12]. The rotational motion will make maritime moving targets’ range equation and signal characteristics become very complex and, thus, will significantly increase the difficulty of the design of moving target indication methods.

Ship targets are usually high-value targets; thus, SAR moving ship indication has become a research hotspot in recent years. Specifically, the indication of moving ships with only translational motion has been extensively studied [13,14,15,16]. For instance, ref. [13] proposed an efficient maritime moving target detection and imaging method for spaceborne SAR, based on the constant false alarm detection technique and inverse SAR (ISAR) imaging technique. In [14], a maritime moving target detection method based on complex interferometric dissimilarity was proposed for dual-channel SAR. In addition, ref. [15] presented a study on the detection and motion parameter estimation of ships for spaceborne polarimetric SAR-GMTI systems.

For the ships with rotational motion, the existing studies are mainly focused on the analysis of the target defocusing characteristics and the refocusing of rotating ships [17,18,19,20,21,22]. For instance, in [17], the defocusing caused by the rotational motion was intensively investigated through numerical simulations. Ref. [18] further studied the defocusing caused by the six-dimensional oscillations of ships. In [19], the space/time-varying characteristics of the defocusing caused by the rotational motion were analyzed in detail. By combining the range Doppler algorithm with ISAR technique, ref. [20] proposed a rotating ship imaging method for squint SAR. In addition, an imaging method based on the motion state estimation and ISAR technique was proposed for rotating ships in [21]. However, the study on the effect of rotational motion on moving target indication is rare.

SAR moving target indication is usually performed in the image domain. In addition, the azimuth position shift and along-track interferometric (ATI) phase of the target are key parameters for moving target indication. In addition, the azimuth defocusing and sidelobe asymmetry of the target will lead to significant signal-to-noise ratio (SNR) loss and deterioration of the image and, thus, will deteriorate the performance of moving target indication. Therefore, this paper investigates the effect of rotational motion on the ship’s signal characteristics in the SAR image domain, including the azimuth position shift, azimuth defocusing, azimuth sidelobe asymmetry, and ATI phase.

In the paper, firstly, the range equation of an arbitrary scatterer on the ship with both rotational and translational motions is developed for multichannel SAR. Then, the influences of each rotation motion on the coefficients of the range equation and the scatterer’s ATI phase are figured out. Finally, the scatterer’s azimuth position shift, azimuth defocusing, azimuth sidelobe asymmetry, and ATI phase variation introduced by each rotation motion and their dependence on the scatterer’s position relative to the gravity center of the ship are analyzed.

The rest of the paper is organized as follows. In Section 2, the range equation model of the scatterer is developed. In Section 3, the variations in the coefficients of the range equation caused by each rotation motion are figured out. Section 4 presents an analysis on the influence of each rotation on the scatterer’s ATI phase. In Section 5, the effect of rotation motions on the ship’s signal characteristics in the image domain is analyzed via numerical experiments. Finally, Section 6 concludes the paper.

2. Range Equation Modeling

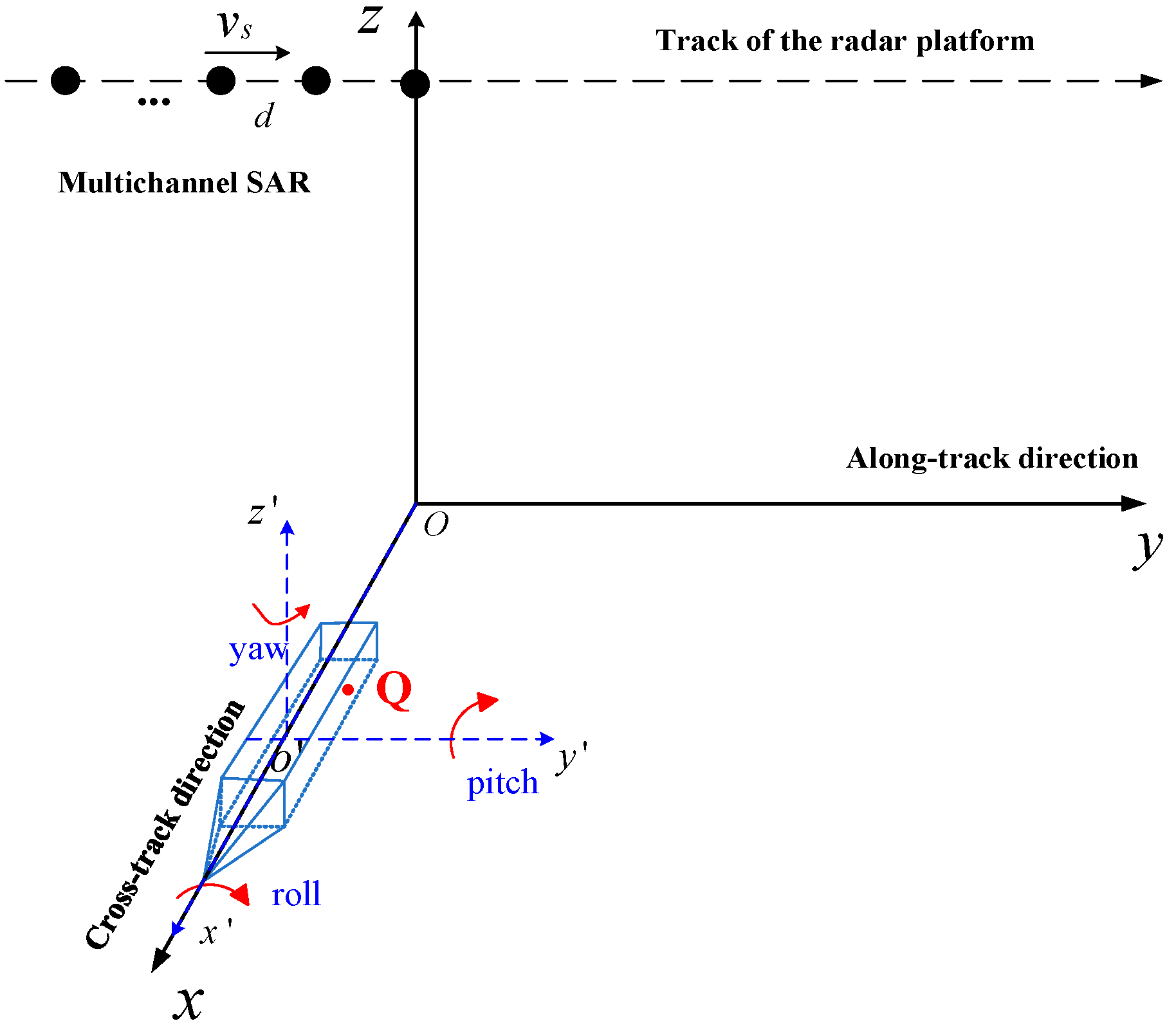
The geometric relationship between the radar and rotating ship is shown in Figure 1. The radar platform moves parallel to the y-axis, with a velocity of v_s and a height of h. The radar has N channels in azimuth, and the distance between the equivalent phase centers of adjacent channels is d. At the azimuth time t_a = 0, the coordinate of the nth channel radar in the o-xyz coordinate system is (0, −(n − 1)d, h), and the coordinate of the ship’s center of gravity in the o-xyz coordinate system is (x₀, 0, 0). In addition, at t_a = 0, the ship’s velocity and acceleration along the x-axis are v_x and a_x, respectively; the velocity and acceleration along the y-axis are v_y and a_y, respectively. o′-x′y′z′ is the ship’s coordinate system with its origin at the ship’s center of gravity. The x′-axis is transverse to the hull, the y′-axis is longitudinal to the hull, and the z′-axis is perpendicular to the hull. Q is an arbitrary scatterer of the ship, and its position at t_a = 0 in the o′-x′y′z′ coordinate system is $(x_{q0}^{\prime },y_{q0}^{\prime },z_{q0}^{\prime })$. The ship rotates under the action of wave thrust, including yaw, pitch, and roll, where the yaw-axis is perpendicular to the hull, the pitch-axis runs longitudinally through the bow and stern of the ship, and the roll-axis runs transversely through the hull. In other words, in the ship’s coordinate system o′-x′y′z′ shown in Figure 1, roll rotates about the x′-axis, pitch rotates about the y′-axis, and yaw rotates about the z′-axis.

According to Figure 1, the position vector of the scatterer Q in the o-xyz coordinate system can be expressed as

$${\mathit{r}}_q(t_a)={\mathit{r}}_c(t_a)+{\mathit{r}}_q^{\prime }(t_a)$$

(1)

with

$${\mathit{r}}_c(t_a)={\left[x_c(t_a) y_c(t_a) 0\right]}^{\mathrm{{\rm T}}}$$

(2)

$$x_c(t_a)=x_0+v_x{t}_a+{\displaystyle \frac{1}{2}}{a}_x{t}_a^2$$

(3)

$$y_c(t_a)=v_y{t}_a+{\displaystyle \frac{1}{2}}{a}_y{t}_a^2$$

(4)

$$\begin{array}{c}{\mathit{r}}_q^{\prime }(t_a)={\left[x_q^{\prime }(t_a) y_q^{\prime }(t_a) z_q^{\prime }(t_a)\right]}^{\mathrm{{\rm T}}}\\ ={\mathit{T}}_{rot}\cdot {\left[x_{q0}^{\prime } y_{q0}^{\prime } z_{q0}^{\prime }\right]}^{\mathrm{{\rm T}}}\end{array}$$

(5)

where r_c(t_a) is the position vector of the ship’s center of gravity in o-xyz, and ${\mathit{r}}_q^{\prime }(t_a)$ is the position vector of the scatterer Q in o′-x′y′z′. x_c(t_a) and y_c(t_a) represent the instantaneous position components of the ship’s center of gravity along the x-axis and y-axis, respectively, in the o-xyz coordinate system. T_rot is the rotation matrix of the ship, and it can be expressed as

$${\mathit{T}}_{rot}=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos {\theta }_r& -\sin {\theta }_r\\ 0& \sin {\theta }_r& \cos {\theta }_r\end{array}\right]\cdot \left[\begin{array}{ccc}\cos {\theta }_p& 0& \sin {\theta }_p\\ 0& 1& 0\\ -\sin {\theta }_p& 0& \cos {\theta }_p\end{array}\right]\cdot \left[\begin{array}{ccc}\cos {\theta }_y& -\sin {\theta }_y& 0\\ \sin {\theta }_y& \cos {\theta }_y& 0\\ 0& 0& 1\end{array}\right]$$

(6)

with

$$\left\{\begin{array}{c}{\theta }_r=A_r\sin ({\omega }_r{t}_a)\\ {\theta }_p=A_p\sin ({\omega }_p{t}_a)\\ {\theta }_y=A_y\sin ({\omega }_y{t}_a)\end{array}\right.$$

(7)

where θ_r, θ_p, and θ_y are the three-dimensional rotation angles, A_r, A_p, and A_y are the three-dimensional rotation amplitudes, and ω_r, ω_p, and ω_y are three-dimensional rotation angle frequencies, with the subscripts r, p, and y representing the parameters corresponding to roll, pitch, and yaw, respectively.

Based on Equation (1), the instantaneous range between the scatterer Q and the nth channel, i.e., the range equation of the scatterer Q, can be expressed as

$$R_n(t_a)=\sqrt{{\left[x_c(t_a)+x_q^{\prime }(t_a)\right]}^2+{\left[z_q^{\prime }(t_a)-h\right]}^2+{\left[y_c(t_a)+y_q^{\prime }(t_a)-v_s{t}_a+(n-1)d\right]}^2}$$

(8)

To facilitate analysis of the effect of rotation on the scatterer’s signal characteristics, the range equation in Equation (8) is expanded using a third-order Taylor series expansion at the time t_a = 0, yielding the following result:

$$R_n(t_a)\approx R_0+\left[l_1+(n-1)d\cdot \alpha \right]t_a+l_2{t}_a^2+l_3{t}_a^3$$

(9)

where

$$R_0=\sqrt{{(x_0+x_{q0}^{\prime })}^2+{(y_{q0}^{\prime })}^2+{(z_{q0}^{\prime }-h)}^2}$$

(10)

$$l_1={\displaystyle \frac{1}{R_0}}\left[\left(x_0+x_{q0}^{\prime }\right)v_x+y_{q0}^{\prime }\left(v_y-v_{\mathrm{s}}\right)-x_0{y}_{q0}^{\prime }{A}_y{\omega }_y+\left(x_0{z}_{q0}^{\prime }+h{x}_{q0}^{\prime }\right)A_p{\omega }_p-h{y}_{q0}^{\prime }{A}_r{\omega }_r\right]$$

(11)

$$\alpha ={\displaystyle \frac{v_y+x_{q0}^{\prime }{A}_y{\omega }_y-z_{q0}^{\prime }{A}_r{\omega }_r-v_s}{R_0}}$$

(12)

$$l_2={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\beta }{R_0}}-{\displaystyle \frac{l_1^2}{R_0}}\right)$$

(13)

$$\begin{array}{cc}\beta =& {\left(v_x+z_{q0}^{\prime }{A}_p{\omega }_p-y_{q0}^{\prime }{A}_y{\omega }_y\right)}^2+{\left(v_y+x_{q0}^{\prime }{A}_y{\omega }_y-z_{q0}^{\prime }{A}_r{\omega }_r-v_s\right)}^2\hfill \\ & +\left(x_0+x_{q0}^{\prime }\right)\left[a_x+x_{q0}^{\prime }\left(-A_p^2{\omega }_p^2-A_y^2{\omega }_y^2\right)\right]+{\left(y_{q0}^{\prime }{A}_r{\omega }_r-x_{q0}^{\prime }{A}_p{\omega }_p\right)}^2\hfill \\ & +y_{q0}^{\prime }\left[a_y-2x_{q0}^{\prime }{A}_r{\omega }_r{A}_p{\omega }_p-y_{q0}^{\prime }\left(A_r^2{\omega }_r^2+A_y^2{\omega }_y^2\right)\right]+\hfill \\ & \left(z_{q0}^{\prime }-h\right)\left[2x_{q0}^{\prime }{A}_r{\omega }_r{A}_y{\omega }_y+2y_{q0}^{\prime }{A}_p{\omega }_p{A}_y{\omega }_y-z_{q0}^{\prime }\left(A_r^2{\omega }_r^2+A_p^2{\omega }_p^2\right)\right]\hfill \end{array}$$

(14)

$$l_3={\left.{\displaystyle \frac{1}{6}}{\displaystyle \frac{d^3{R}_n(t_a)}{d{t}_a^3}}\right|}_{t_a=0}$$

(15)

Note that due to the expression for the cubic coefficient, l₃ is too complex and lengthy which is hence not given in the paper for simplicity of presentation.

3. Influence of Each Rotation Motion on the Coefficients of Range Equation

From Equations (9)–(15), it can be seen that the rotational motion has a significant impact on the coefficients of the range equation. In this section, without loss of generality, the reference channel (the first channel) is taken as an example to investigate the influence of each rotation motion on the coefficients of range equation of the scatterer Q.

According to Equations (11)–(15), when only translational motion exists, the coefficients of range equation can be expressed as follows:

$$l_{1\_t}={\displaystyle \frac{1}{R_0}}\left[\left(x_0+x_{q0}^{\prime }\right)v_x+y_{q0}^{\prime }\left(v_y-v_s\right)\right]$$

(16)

$$l_{2\_t}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{\beta }_t}{R_0}}-{\displaystyle \frac{l_{1\_t}^2}{R_0^3}}\right)$$

(17)

$${\beta }_t=v_x^2+(x_0+x_{q0}^{\prime })a_x+{(v_y-v_s)}^2+y_{q0}^{\prime }{a}_y$$

(18)

$$l_{3\_t}={\left.{\displaystyle \frac{1}{6}}{\displaystyle \frac{d^3{R}_t(t_a)}{d{t}_a^3}}\right|}_{t_a=0}$$

(19)

where R_t(t_a) is the range equation when only translational motion exists, and the subscript t corresponds to the case where only translational motion exists.

By comparing Equations (11) and (16), (13) and (17), and (15) and (19), the changes in the coefficients of range equation caused by the rotational motion are given by

$$\begin{array}{cc}\mathrm{\Delta }{l}_1& =l_1-l_{1\_t}\hfill \\ & ={\displaystyle \frac{1}{R_0}}\left[-x_0{y}_{q0}^{\prime }{A}_y{\omega }_y-h{y}_{q0}^{\prime }{A}_r{\omega }_r+\left(x_0{z}_{q0}^{\prime }+h{x}_{q0}^{\prime }\right)A_p{\omega }_p\right]\hfill \end{array}$$

(20)

$$\begin{array}{cc}\mathrm{\Delta }{l}_2& =l_2-l_{2\_t}\hfill \\ & ={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\beta -{\beta }_t}{R_0}}-{\displaystyle \frac{l_1^2-l_{1\_t}^2}{R_0^3}}\right)\hfill \end{array}$$

(21)

$$\mathrm{\Delta }{l}_3=l_3-l_{3\_t}$$

(22)

The changes in the coefficients of the linear and quadratic terms of the range equation will result in variations in the Doppler center frequency and Doppler chirp rate of a target. The relationships between them are as follows:

$$\mathrm{\Delta }{f}_{dc}=-{\displaystyle \frac{2\mathrm{\Delta }{l}_1}{\lambda }}$$

(23)

$$\mathrm{\Delta }{k}_a=-{\displaystyle \frac{4\mathrm{\Delta }{l}_2}{\lambda }}$$

(24)

where $\mathrm{\Delta }{f}_{dc}$ and $\mathrm{\Delta }{k}_a$ denote the variations in the Doppler center frequency and Doppler chirp rate, respectively, and λ is the wavelength.

According to the principle of SAR imaging, the variation in the Doppler center frequency will result in an azimuth position shift of the target in the SAR image, while the variation in the Doppler chirp rate will cause azimuth defocusing. In addition, variations in the coefficients of the cubic term of the range equation will cause residual azimuth modulation, which leads to azimuth sidelobes asymmetry when it is small and azimuth defocusing when it is large [23].

In the following, the influences of roll, pitch, and yaw on each coefficient of the range equation are analyzed.

3.1. Influence of Roll

When only roll exists, according to Equation (20), the variation in the coefficient of the range equation’s linear term can be expressed as

$$\mathrm{\Delta }{l}_{1\_r}={\displaystyle \frac{1}{R_0}}\left(-h{y}_{q0}^{\prime }{A}_r{\omega }_r\right)$$

(25)

One can see that the variation depends only on the y′-axis coordinate of the scatterer, and it is linearly related to $y_{q0}^{\prime }$, i.e., the farther away from the ship’s center of gravity along the y′-axis (the along-track direction), the greater the variation in the coefficient of linear term.

Similarly, according to Equations (13) and (17), the variation in the coefficient of the range equation’s quadratic term due to roll can be written as

$$\mathrm{\Delta }{l}_{2\_r}={\displaystyle \frac{1}{2R_0}}\left[h{z}_{q0}^{\prime }{A}_r^2{\omega }_r^2-2\left(v_y-v_s\right)z_{q0}^{\prime }{A}_r{\omega }_r\right]$$

(26)

From Equation (26), it can be seen that $\mathrm{\Delta }{l}_{2\_r}$ depends only on the z′-axis (the height direction) coordinate of the scatterer and is linearly related to $z_{q0}^{\prime }$.

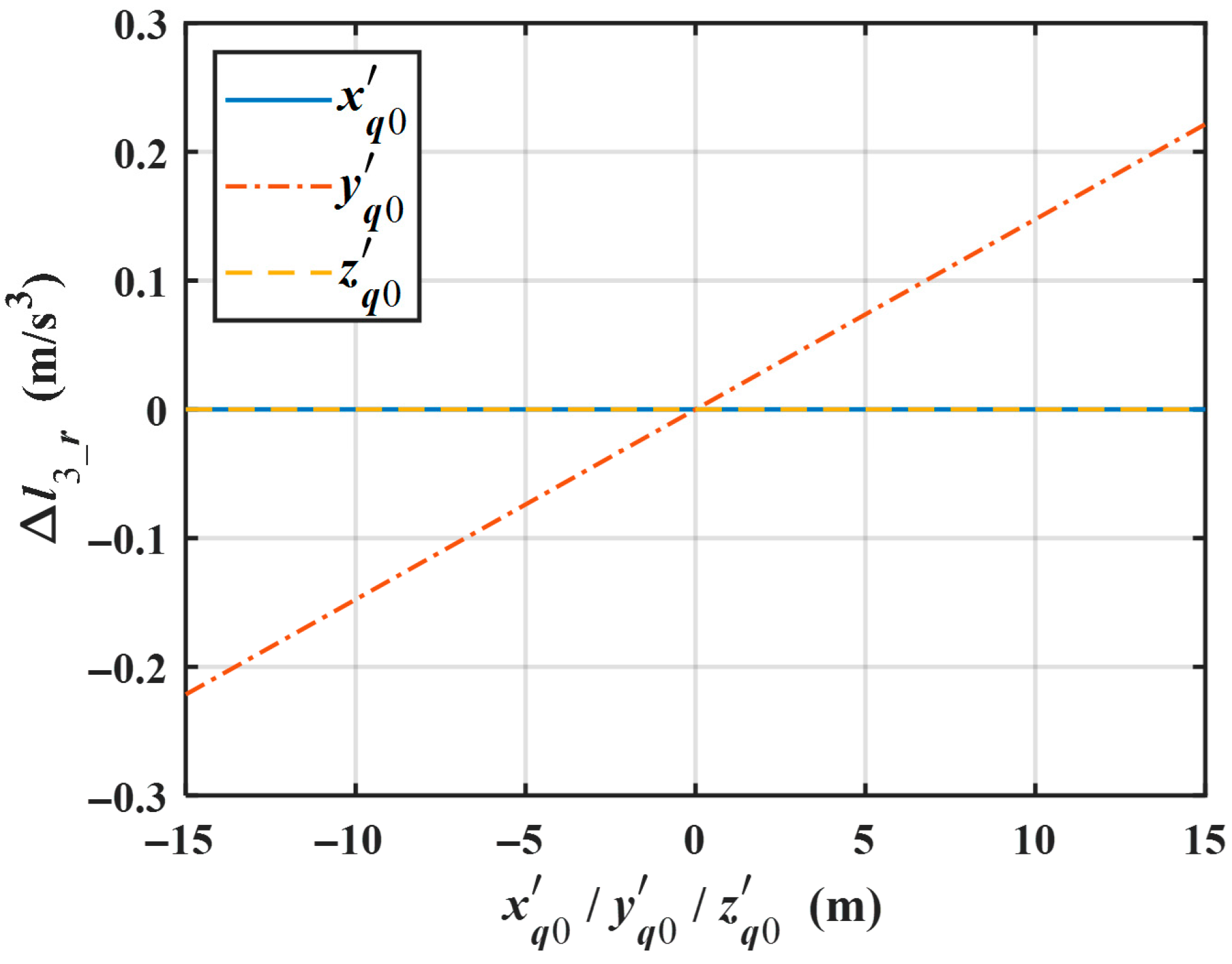
Since the variation in the coefficient of the range equation’s cubic term caused by roll, i.e., $\mathrm{\Delta }{l}_{3\_r}$, is very complex, the numerical analysis is used to clarify its dependence on the coordinates of the scatterer. The parameters for numerical simulations are shown in

Table 1. System parameters of SAR.

System Parameter	Value
Carrier frequency	5.4 GHz
Bandwidth	50 MHz
Pulse repetition frequency	5000 Hz
Radar speed	7352 m/s
Distance from radar to target	1200 km
Synthetic aperture time	2.22 s

and

Table 2. Rotation parameters of the ship.

Rotation Parameter	Value
Roll period	12 s
Roll amplitude	30°
Pitch period	7 s
Pitch amplitude	3.5°
Yaw period	14 s
Yaw amplitude	4°

. The numerical results are shown in Figure 2. One can see that $\mathrm{\Delta }{l}_{3\_r}$ depends only on the y′-axis coordinate of the scatterer and is proportional to $y_{q0}^{\prime }$.

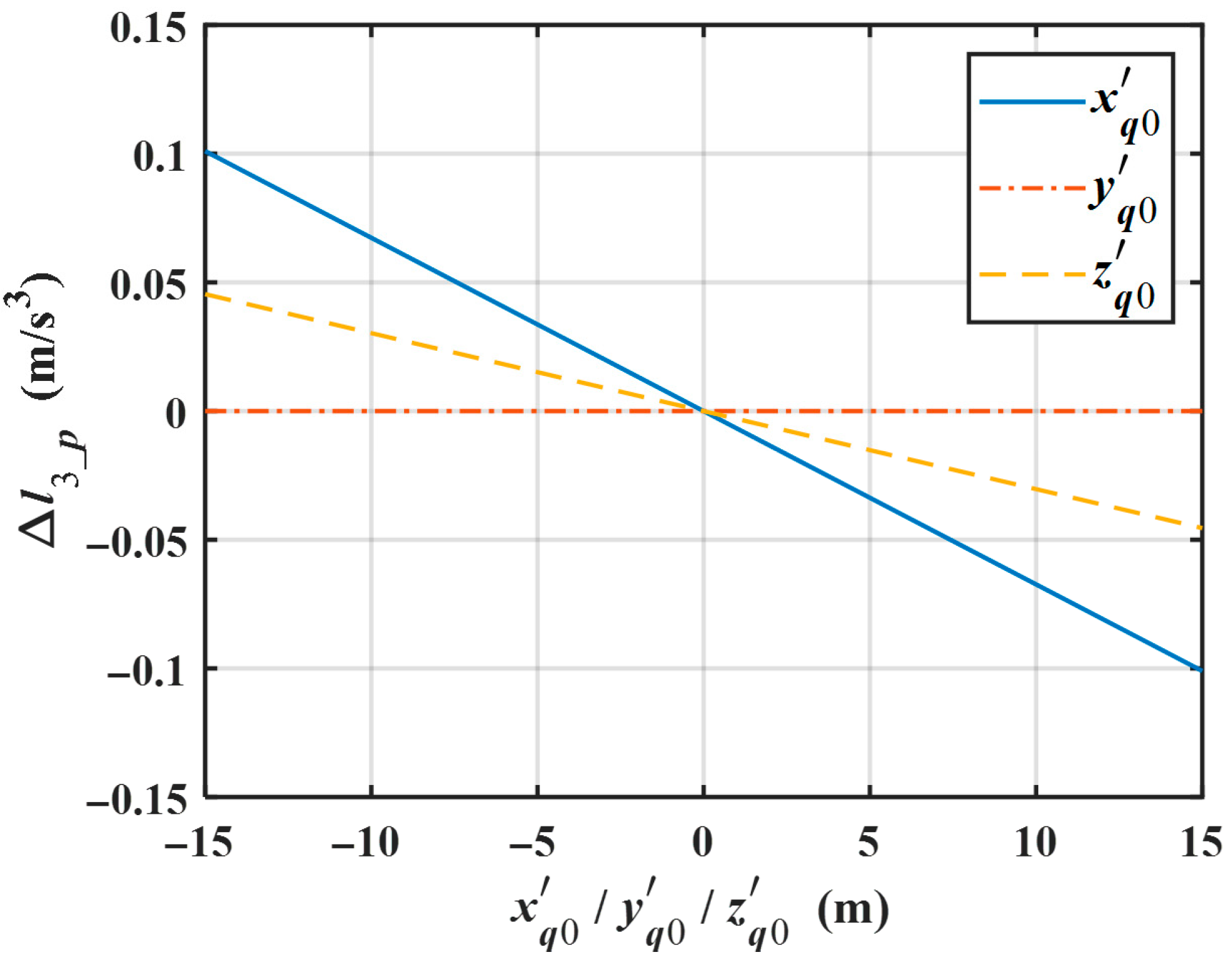
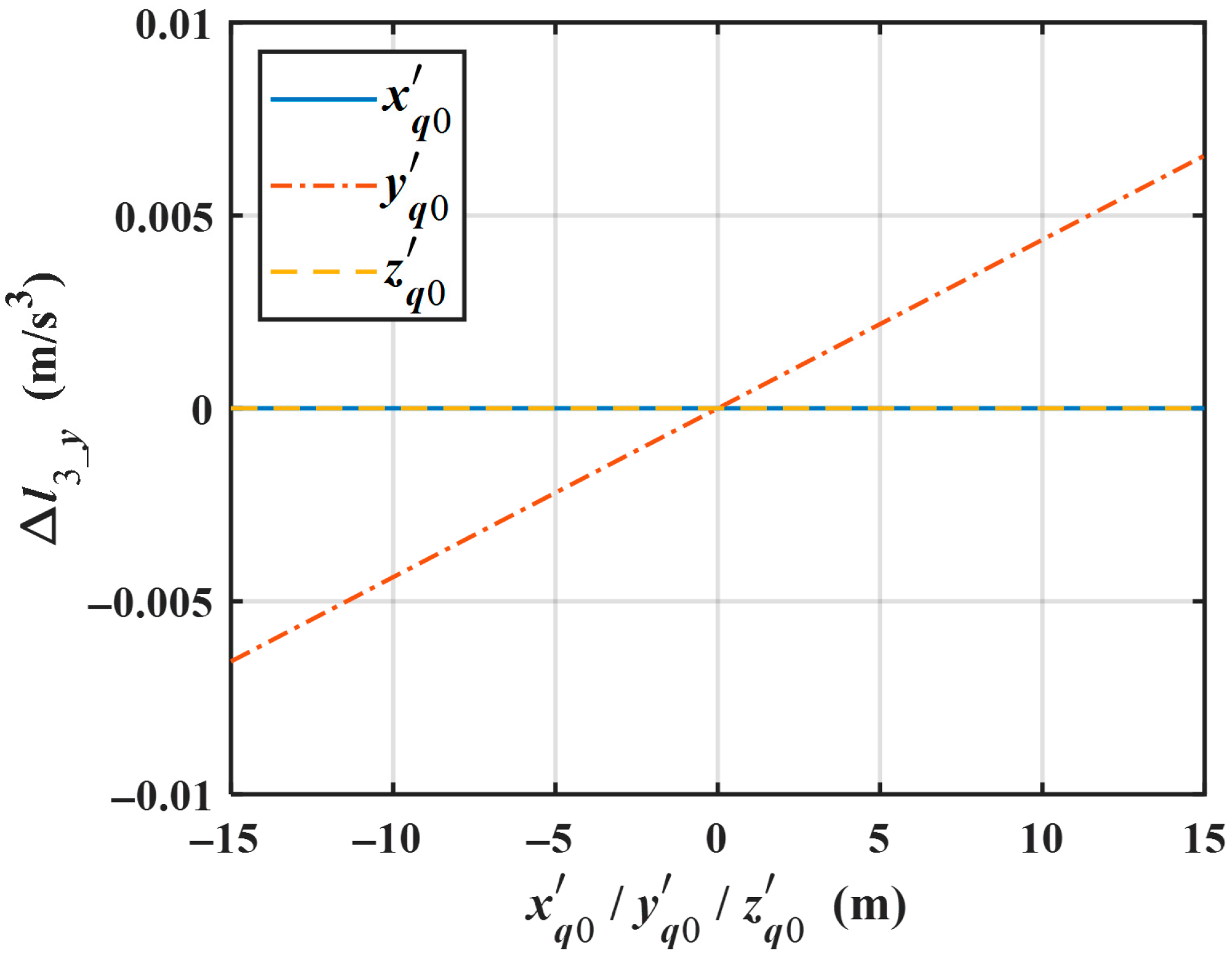
In Figure 2, Figure 3 and Figure 4, “$x_{q0}^{\prime }/y_{q0}^{\prime }/{z^{\prime }}_{q0}(\mathrm{m})$” corresponds to the three lines in the legend, representing the influence of coordinate component $x_{q0}^{\prime }/y_{q0}^{\prime }/z_{q0}^{\prime }$ on the cubic term coefficient when considering roll/pitch/yaw, respectively.

Based on the above analysis and the relationship between the Doppler parameters and the coefficients of range equation, the following conclusions can be obtained: (1) The farther away the scatterer is from the ship’s center of gravity along the along-track direction, the greater the variation in the coefficients of linear and cubic terms;, thus, the greater the azimuth position shift and azimuth sidelobes asymmetry of this scatterer in the SAR image. (2) The farther the scatterer is away from the ship’s center of gravity along the height direction, the greater the variation in the coefficient of the quadratic term, thus resulting in the more severe the azimuth defocusing.

3.2. Influence of Pitch

When only pitch exists, the variation in the coefficient of the range equation’s linear term can be expressed as

$$\mathrm{\Delta }{l}_{1\_p}={\displaystyle \frac{1}{R_0}}\left(h{x}_{q0}^{\prime }{A}_p{\omega }_p+x_0{z}_{q0}^{\prime }{A}_p{\omega }_p\right)$$

(27)

It can be seen that the variation in the coefficient of the linear term due to pitch depends only on the x′-axis (the cross-track direction) and z′-axis coordinates of the scatterer and is linearly related to $x_{q0}^{\prime }$ and $z_{q0}^{\prime }$.

Similarly, according to Equations (13) and (17), the variation in the coefficient of the range equation’s quadratic term caused by pitch is given by

$$\mathrm{\Delta }{l}_{2\_p}={\displaystyle \frac{1}{2R_0}}\left(2v_x{z}_{q0}^{\prime }{A}_p{\omega }_p+h{z}_{q0}^{\prime }{A}_p^2{\omega }_p^2-x_0{x}_{q0}^{\prime }{A}_p^2{\omega }_p^2\right)$$

(28)

From Equation (28) one can see that $\mathrm{\Delta }{l}_{2\_p}$ is also linearly related to $x_{q0}^{\prime }$ and $z_{q0}^{\prime }$.

The variation in the coefficient of the range equation’s cubic term due to pitch (i.e., $\mathrm{\Delta }{l}_{3\_p}$) is figured out via numerical analysis, with results being presented in Figure 3. One can see that $\mathrm{\Delta }{l}_{3\_p}$ depends on the x′-axis and z′-axis coordinate of the scatterer and is linearly related to $x_{q0}^{\prime }$ and $z_{q0}^{\prime }$.

From the above analysis, it can be seen that the variations in the coefficients of the three terms are all linearly to $x_{q0}^{\prime }$ and $z_{q0}^{\prime }$. Therefore, it could be concluded that the farther the scatterer is away from the ship’s center of gravity along the cross-track direction or height direction, the greater the azimuth position shift, azimuth defocusing, and azimuth sidelobes asymmetry of this scatterer in the SAR image.

3.3. Influence of Yaw

When only yaw exists, the variation in the coefficient of the range equation’s linear term can be expressed as

$$\mathrm{\Delta }{l}_{1\_y}={\displaystyle \frac{1}{R_0}}\left(-x_0{y}_{q0}^{\prime }{A}_y{\omega }_y\right)$$

(29)

It can be seen that $\mathrm{\Delta }{l}_{1\_y}$ depends only on the y′-axis coordinate of the scatterer and is linearly related to $y_{q0}^{\prime }$.

Similarly, the variation in the coefficient of the range equation’s quadratic term caused by the yawing motion can be expressed as

$$\begin{array}{cc}\mathrm{\Delta }{l}_{2\_y}& ={\displaystyle \frac{1}{2R_0}}\left[-2y_{q0}^{\prime }{A}_y{\omega }_y{v}_x-x_0{x}_{q0}^{\prime }{A}_y^2{\omega }_y^2+2x_{q0}^{\prime }{A}_y{\omega }_y(v_y-v_s)\right]\hfill \\ & \approx -{\displaystyle \frac{1}{2R_0}}\left[x_0{x}_{q0}^{\prime }{A}_y^2{\omega }_y^2+2x_{q0}^{\prime }{A}_y{\omega }_y{v}_s\right]\hfill \end{array}$$

(30)

It can be seen that $\mathrm{\Delta }{l}_{2\_y}$ mainly depends only on the x′-axis coordinate of the scatterer and is approximately linearly related to $x_{q0}^{\prime }$. Note that the approximation in Equation (30) is due to the fact that v_x and v_y are much less than x₀ and v_s.

The variation in the coefficient of the range equation’s cubic term due to the yaw (i.e., $\mathrm{\Delta }{l}_{3\_y}$) is figured out via numerical analysis, and the results are shown in Figure 4. It can be seen that $\mathrm{\Delta }{l}_{3\_y}$ depends only on the y′-axis coordinate of the scatterer and is proportional to $y_{q0}^{\prime }$.

Based on the above analysis, the following conclusions can be obtained: (1) The farther away the scatterer is from the ship’s center of gravity along the along-track direction, the greater the variation in the coefficient of the linear and cubic terms; thus, the greater the azimuth position shift and the azimuth sidelobe asymmetry of this scatterer in the SAR image. (2) The farther the scatterer is from the ship’s center of gravity along the cross-track direction, the greater the variation in the coefficient of the quadratic term; thus, the more severe the azimuth defocusing.

4. Influence of Each Rotation Motion on ATI Phase

For SAR-GMTI, the ATI phase of a target is a very important parameter because it can be used for target detection and motion parameter estimation. Therefore, in this section, the impact of each rotation motion on the ATI phase is analyzed.

The ATI phase of target between adjacent channels can be expressed as follows [24]:

$${\varphi }_{ATI}={\displaystyle \frac{2\pi d{v}_s}{\lambda R_0}}\cdot {\displaystyle \frac{l_1}{l_2}}$$

(31)

Thus, the variations in ATI phase caused by each rotation motion can be expressed as

$$\begin{array}{cc}\mathrm{\Delta }{\varphi }_{ATI\_r}& ={\displaystyle \frac{2\pi d{v}_s}{\lambda R_0}}\cdot \left({\displaystyle \frac{l_{1\_r}}{l_{2\_r}}}-{\displaystyle \frac{l_{1\_t}}{l_{2\_t}}}\right)\hfill \\ & \approx -{\displaystyle \frac{4\pi d{v}_s}{\lambda R_0}}\cdot {\displaystyle \frac{h{y}_{q0}^{\prime }{A}_r{\omega }_r}{v_x^2+(x_0+x_{q0}^{\prime })a_x+{(v_y-v_s)}^2+y_{q0}^{\prime }{a}_y}}\hfill \end{array}$$

(32)

$$\begin{array}{cc}\mathrm{\Delta }{\varphi }_{ATI\_p}& ={\displaystyle \frac{2\pi d{v}_s}{\lambda R_0}}\cdot \left({\displaystyle \frac{l_{1\_p}}{l_{2\_p}}}-{\displaystyle \frac{l_{1\_t}}{l_{2\_t}}}\right)\hfill \\ & \approx {\displaystyle \frac{4\pi d{v}_s}{\lambda R_0}}\cdot {\displaystyle \frac{(x_0{z}_{q0}^{\prime }+h{x}_{q0}^{\prime })A_p{\omega }_p}{v_x^2+(x_0+x_{q0}^{\prime })a_x+{(v_y-v_s)}^2+y_{q0}^{\prime }{a}_y}}\hfill \end{array}$$

(33)

$$\begin{array}{cc}\mathrm{\Delta }{\varphi }_{ATI\_y}& ={\displaystyle \frac{2\pi d{v}_s}{\lambda R_0}}\cdot \left({\displaystyle \frac{l_{1\_y}}{l_{2\_y}}}-{\displaystyle \frac{l_{1\_t}}{l_{2\_t}}}\right)\hfill \\ & \approx -{\displaystyle \frac{4\pi d{v}_s}{\lambda R_0}}\cdot {\displaystyle \frac{x_0{y}_{q0}^{\prime }{A}_y{\omega }_y}{v_x^2+(x_0+x_{q0}^{\prime })a_x+{(v_y-v_s)}^2+y_{q0}^{\prime }{a}_y}}\hfill \end{array}$$

(34)

where $\mathrm{\Delta }{\varphi }_{ATI\_r}$, $\mathrm{\Delta }{\varphi }_{ATI\_p}$, and $\mathrm{\Delta }{\varphi }_{ATI\_y}$ are the variations introduced by roll, pitch, and yaw, respectively.

From Equations (32)–(34), it can be seen that each rotation motion has an impact on the ATI phase. Moreover, the following points can be noted: (1) The variations in ATI phase caused by roll and yaw are mainly related to the y′-axis coordinate of the scatterer and are approximately linearly related to $y_{q0}^{\prime }$. (2) The variations in ATI phase caused by pitch is mainly related to the y′-axis and z′-axis coordinates of the scatterer and is approximately linearly related to $x_{q0}^{\prime }$ and $z_{q0}^{\prime }$.

5. Experimental Results

In this section, numerical experiments are conducted to analyze the effect of rotation motions on the ship’s characteristics in the SAR image domain, including the azimuth position shift, azimuth defocusing, azimuth sidelobe asymmetry, and ATI phase and their dependences on scatterers’ positions relative to the gravity center of the ship. The parameters of the radar used in the simulations are presented in Table 1. The size of the simulated ship is 135 m in length, 30 m in width, and 30 m in height. The velocity of the ship is 5 m/s. The rotational parameters of the ship are given in Table 2 [25].

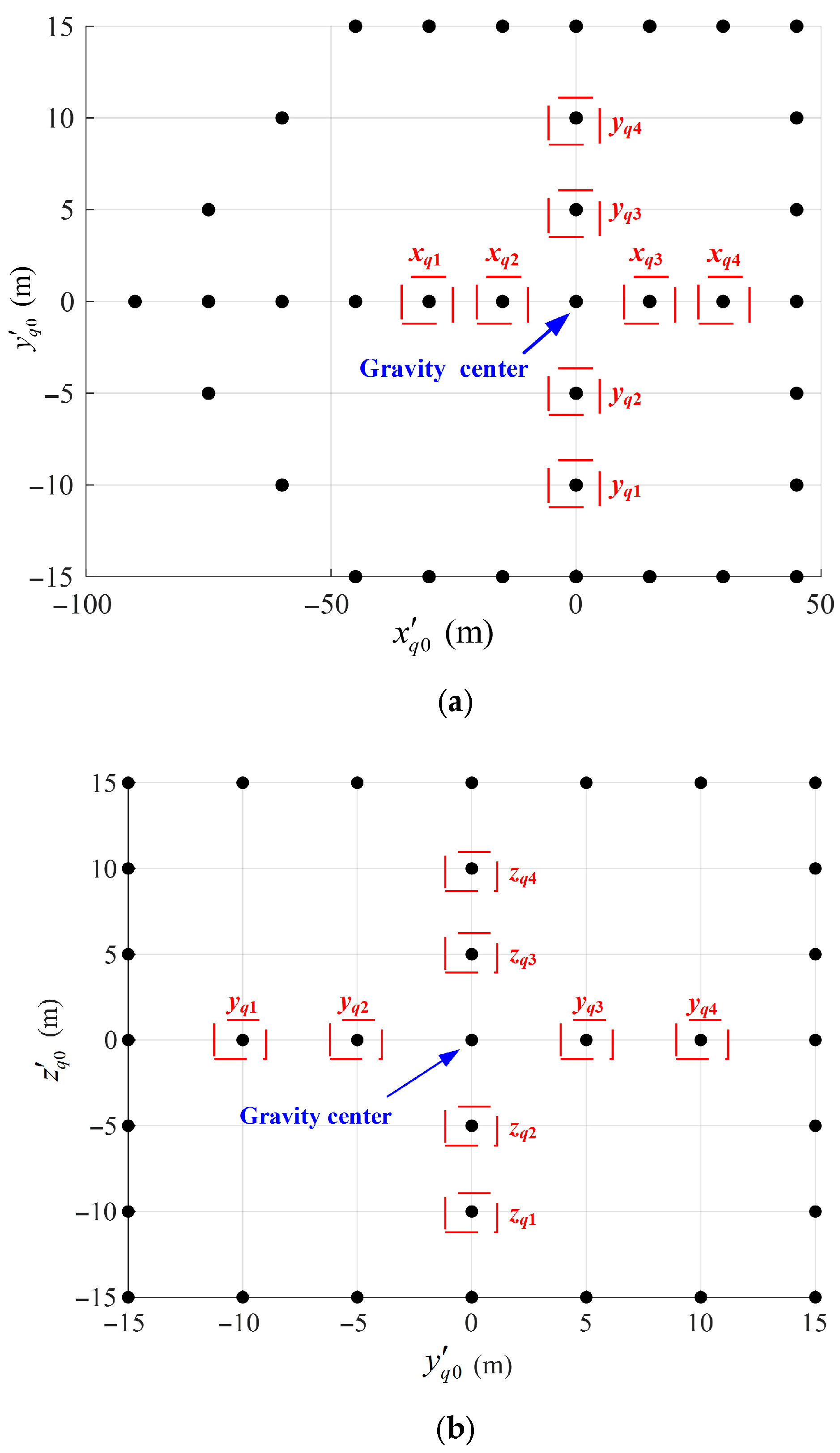
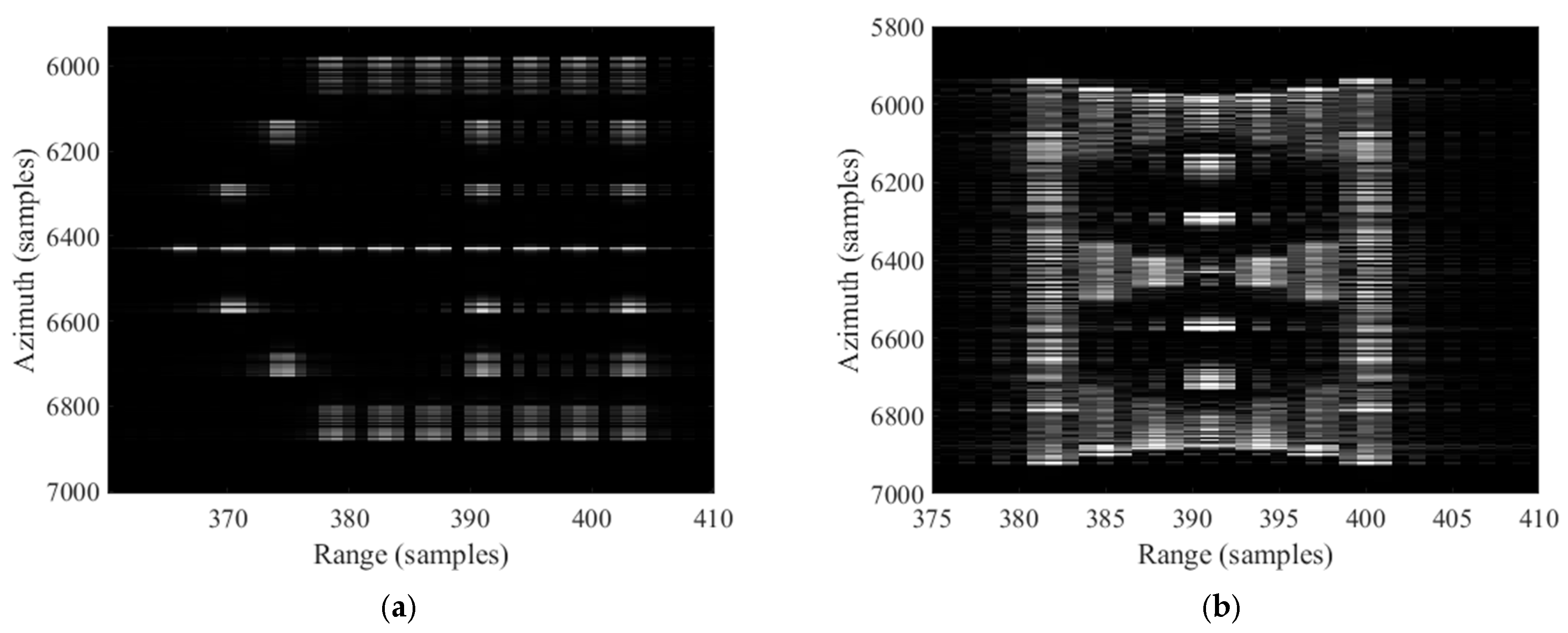
To clearly reveal the dependence of the rotation motions’ effect on the scatterer’s positions, the ship’s horizontal and vertical slices passing through the gravity center are considered in the following analysis, as illustrated in Figure 5. The imaging results of these two slices when only translational motion exists are shown in Figure 6. In addition, the imaging results in the presence of roll, pitch, yaw, and three-dimensional rotation motions are presented in Figure 7, Figure 8, Figure 9 and Figure 10, respectively. Note that the classic range-Doppler algorithm is used in imaging, and only the parameters of the ship’s translational motion are used when performing range migration correction and azimuth compression.

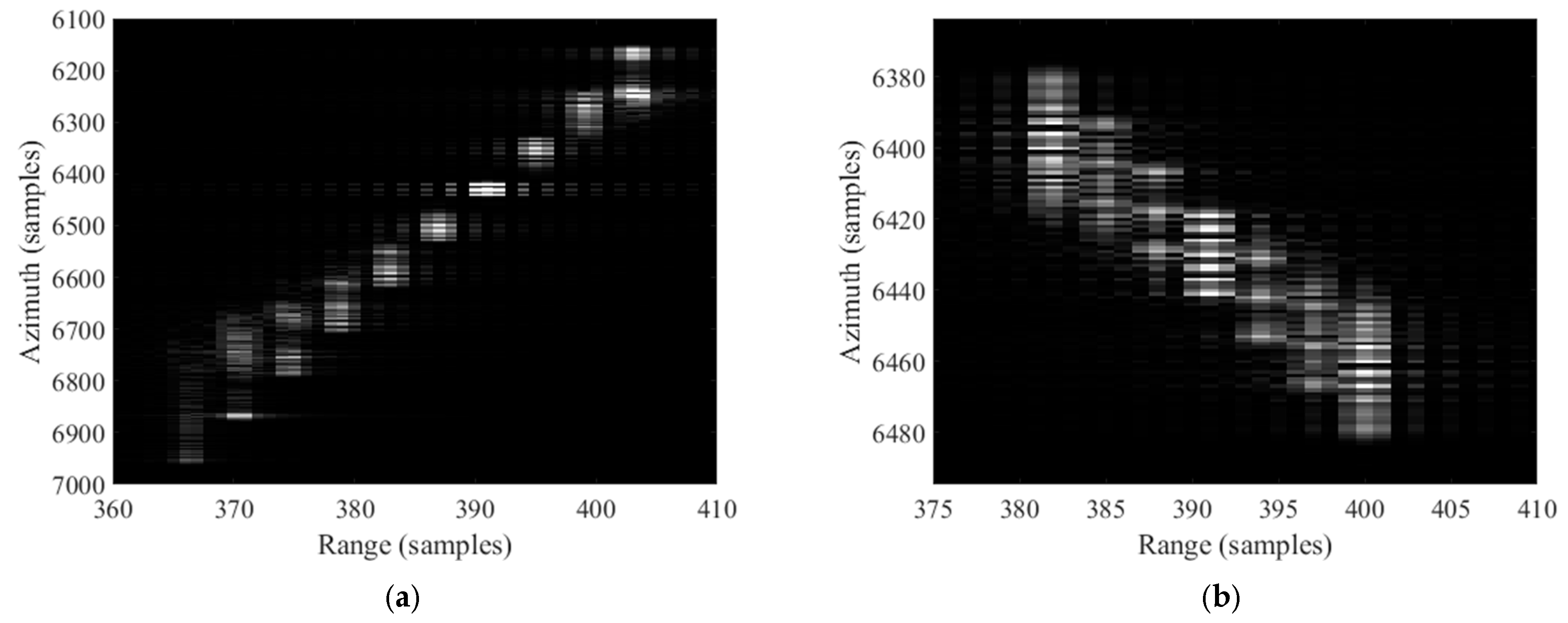
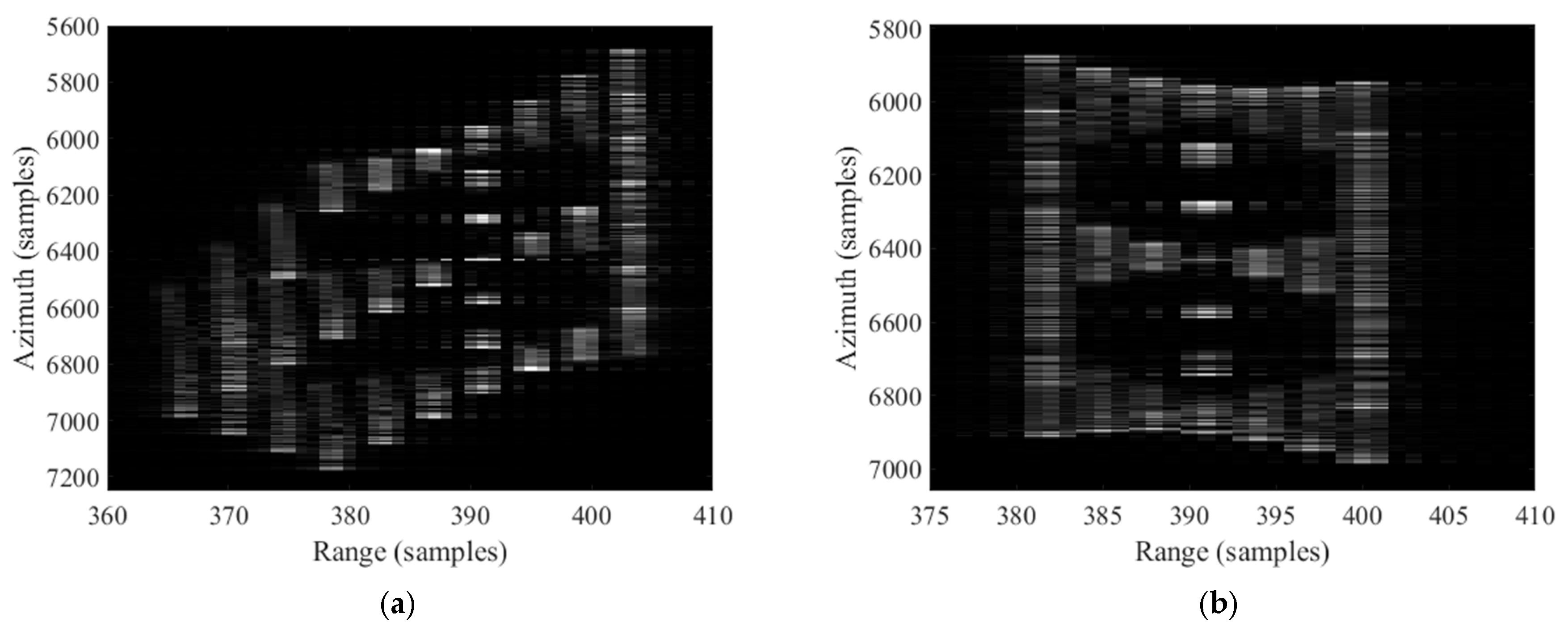
Comparing Figure 6 with Figure 7, Figure 8, Figure 9 and Figure 10, it can be seen that the rotation motions have a significant effect on the imaging results. Specifically, from Figure 7 one can see that in the case of roll, the horizontal slice is significantly stretched and defocused along the azimuth direction, and the vertical slice suffers significant azimuth defocusing. As can be seen from Figure 8, both the horizontal and vertical slices suffer severe deformation when pitch exists, and they look like an oblique ridge. According to Figure 9, in the presence of yaw, the horizontal slice is significantly stretched and defocused along the azimuth direction. In addition, from Figure 10 one can see that when the three types of rotational motion all exist, there is severe stretching, azimuth defocusing, and deformation.

In the following, the twelve scatterers in the red box of Figure 5 are selected to further quantitatively analyze the azimuth position shift (ΔP), azimuth defocusing (ΔD), azimuth sidelobe asymmetry (ΔS), and ATI phase variation (ΔATI) introduced by each rotation motion, as well as their relationship with the coordinates of these scatterers. The measured results are given in

Table 3. Measured position shift, defocusing, sidelobe asymmetry, and ATI phase variation introduced by roll.

	xq1	xq2	xq3	xq4	yq1	yq2	yq3	yq4	zq1	zq2	zq3	zq4
ΔP (m)	0	0	0	0	−397.0	−198.5	198.5	397.0	0	0	0	0
ΔD	0	0	0	0	2.8	2.6	2.6	2.8	106.2	52.4	52.4	106.2
ΔS (dB)	0	0	0	0	25.6	23.0	22.9	26.1	/	/	/	/
ΔATI (rad)	0	0	0	0	0.17	0.08	−0.08	−0.17	0	0	0	0

,

Table 4. Measured position shift, defocusing, sidelobe asymmetry, and ATI phase variation introduced by pitch.

	xq1	xq2	xq3	xq4	yq1	yq2	yq3	yq4	zq1	zq2	zq3	zq4
ΔP (m)	236.8	117.7	−236.8	−117.7	0	0	0	0	34.2	16.4	−16.4	−34.2
ΔD	3.3	2.7	2.7	3.3	0	0	0	0	5.2	1.3	1.3	5.2
ΔS (dB)	31.0	25.3	25.4	31.8	0	0	0	0	20.2	18.1	17.9	20.2
ΔATI (rad)	−0.10	−0.05	0.05	0.10	0	0	0	0	−0.015	−0.007	0.007	0.015

and

Table 5. Measured position shift, defocusing, sidelobe asymmetry, and ATI phase variation introduced by yaw.

	xq1	xq2	xq3	xq4	yq1	yq2	yq3	yq4	zq1	zq2	zq3	zq4
ΔP (m)	0	0	0	0	−20.5	−11.0	9.6	19.2	0	0	0	0
ΔD	3.2	1.1	1.1	3.1	0	0	0	0	0	0	0	0
ΔS (dB)	0	0	0	0	12.2	5.4	5.4	12.2	0	0	0	0
ΔATI (rad)	0	0	0	0	0.009	0.004	−0.004	−0.009	0	0	0	0

. Note that the degree of azimuth defocusing is characterized by the multiple of the broadening of the azimuth impulse response width, and the sidelobe asymmetry is indicated by the difference in peak values of left and right sidelobes.

5.1. Effect of Ship’s Roll Motion

The measured results are given in Table 3, and the following points can be noted.

• Roll has no effect on the scatterers on the x′-axis (i.e., q_x1, q_x2, q_x3, q_x4). This is because the x′-axis is its axis of rotation.
• For the scatterers with non-zero z′-axis coordinates, roll only causes them to suffer severe azimuth defocusing, and the defocusing width increases with the distance between these scatterers and the ship’s gravity center. This is consistent with the analyses presented in Section 3.1, which reveal that only $\mathrm{\Delta }{l}_{2\_r}$ is related to $z_{q0}^{\prime }$ [see Equation (26)]. Note that the measurements of azimuth sidelobe asymmetry are not presented in Table 3 because the azimuth defocusing is too severe to observe the sidelobe.
• Roll has a significant effect on the scatterers with non-zero y′-axis coordinates. It introduces significant azimuth position shift, azimuth defocusing, azimuth sidelobe asymmetry, and ATI phase variation, and they become greater as the distance from these scatterers to the gravity center increases. Moreover, one can see that the azimuth position shift and ATI phase variation are approximately linear to the scatterers’ y′-axis coordinates. This is consistent with the analyses presented in Section 3.1 and Section 4, which reveal that $\mathrm{\Delta }{l}_{1\_r}$ and $\mathrm{\Delta }{\varphi }_{ATI\_r}$ are approximately linear to $y_{q0}^{\prime }$ [see Equations (25) and (32)]. It should be noted that the azimuth defocusing is due to the variation in the coefficient of the range equation’s cubic term which is very large.
• Since the azimuth position shift is directly proportional to the scatterer’s coordinate of the y′-axis (the along-track direction), the ship is significantly stretched along the azimuth direction in the SAR image, which will result in severe SNR loss just like azimuth defocusing.

5.2. Effect of Ship’s Pitch Motion

According to the measured results presented in Table 4, the following points can be noted.

• Pitch has no effect on the scatterers on the y′-axis (i.e., q_y1, q_y2, q_y3, q_y4). This is because the y′-axis is its axis of rotation.
• For the scatterers with non-zero x′-axis or z′-axis coordinates, pitch brings significant effects. It introduces significant azimuth position shift, azimuth defocusing, azimuth sidelobe asymmetry, and ATI phase variation, and they become greater as the distance from these scatterers to the ship’s gravity center increases. Moreover, it can be seen that the azimuth position shift and ATI phase variation are approximately linear to the scatterers’ x′-axis and z′-axis coordinates. This is consistent with the analyses presented in Section 3.1 and Section 4, which reveal that $\mathrm{\Delta }{l}_{1\_p}$ and $\mathrm{\Delta }{\varphi }_{ATI\_p}$ are linearly related to $x_{q0}^{\prime }$ and $z_{q0}^{\prime }$ [see Equations (27) and (33)].
• Since the azimuth position shift is approximately linear to the scatterer’s coordinates of the x′-axis (the cross-track direction) and z′-axis (the height direction), the ship suffers severe deformation and is pulled into a widened oblique line in the SAR image.

5.3. Effect of Ship’s Yaw Motion

The measured results are given in Table 5, and the following points can be noted.

• For the scatterers on the z′-axis (i.e., q_z1, q_z2, q_z3, q_z4), yaw has no effect on them. This is because the z′-axis is its axis of rotation.
• For the scatterers with non-zero x′-axis coordinates, yaw only causes them to suffer azimuth defocusing, and the defocusing width increases with the distance between these scatterers and the ship’s gravity center. This is consistent with the analyses presented in Section 3.3, which reveal that $\mathrm{\Delta }{l}_{2\_y}$ is approximately linearly related to $x_{q0}^{\prime }$ [see Equation (30)].
• For the scatterers with non-zero y′-axis coordinates, yaw introduces significant azimuth position shift and azimuth sidelobe asymmetry and minor ATI phase variation, which become greater as the distance from these scatterers to the center of gravity increases. This is consistent with the analyses presented in Section 3.3 and Section 4 [see Equations (29) and (34)].
• Since the azimuth position shift is directly proportional to the scatterer’s coordinate of the y′-axis (the along-track direction), the ship will be significantly stretched along the azimuth direction after SAR imaging.

5.4. Summary of the Effect of Each Rotation Motion

Based on the measured results and above analyses, the effect of each rotation motion is summarized in

Table 6. Summary of the effect of each rotation motion on the ship’s signal characteristics in the image domain.

	Effect	Azimuth Position Shift	Azimuth Defocusing	Azimuth Sidelobe Asymmetry	ATI Phase Variation
Type of Rotation
Roll		The azimuth position shift is directly proportional to the scatterer’s coordinate of y′-axis (the along-track direction), and the ship is severely stretched along the azimuth direction in the SAR image.	The defocusing width increases rapidly with the distance from the scatterer to the gravity center along the height direction and also increases with the distance from the scatterer to the gravity center along the along-track direction.	The degree of azimuth sidelobe asymmetry increases with the distance from the scatterer to the gravity center along the along-track direction.	The ATI phase variation is approximately linear to the scatterer’s y′-axis coordinate.
Pitch		The azimuth position shift is approximately linear to the scatterer’s coordinates of the x′-axis (the cross-track direction) and z′-axis (the height direction), and the ship suffers severe deformation and is pulled into a widened oblique line in the SAR image.	The defocusing width increases with the distance from the scatterer to the gravity center along the height direction and the cross-track direction.	The degree of azimuth sidelobe asymmetry increases with the distance from the scatterer to the gravity center along the height direction and the cross-track direction.	The ATI phase variation is approximately linear to the scatterer’s x′-axis and z′-axis coordinates.
Yaw		The azimuth position shift is directly proportional to the scatterer’s coordinate of y′-axis (the along-track direction), and the ship is stretched along the azimuth direction in the SAR image.	The defocusing width increases with the distance from the scatterer to the gravity center along the cross-track direction.	The degree of azimuth sidelobe asymmetry increases with the distance from the scatterer to the gravity center along the along-track direction.	Yaw introduces minor ATI phase variation, which is approximately linear to the scatterer’s y′-axis coordinates.

. It could be seen that the effect of yaw is minimal and the effect of pitch is the greatest.

6. Conclusions

From the perspective of SAR moving target indication, an analysis of the effect of each rotation motion on the ship’s signal characteristics in the image domain has been presented in this paper. The range equation model of an arbitrary scatterer on the rotating ship has been established. In addition, the influences of each rotation motion on the coefficients of the range equation and the ATI phase have been analyzed in detail. Moreover, numerical experiments have been conducted to reveal the effect of each rotation motion on the ship’s characteristics in the SAR image domain, including the azimuth position shift, azimuth defocusing, azimuth sidelobe asymmetry, and ATI phase and their dependences on scatterers’ positions relative to the ship’s gravity center.