Heterogeneous Ensemble Landslide Susceptibility Assessment Method Considering Spatial Heterogeneity

Highlights

What are the main findings?

• A partitioning method considering the differences between regions was applied within the study area, effectively addressing the issue of spatial heterogeneity between regions.
• The stacking strategy was used to integrate several single models, and the performance of the heterogeneous ensemble learning model was improved.

What are the implications of the main findings?

• This study provides an idea for solving the problem of less consideration of spatial heterogeneity in landslide susceptibility assessment.
• The proposed method aims to improve landslide prediction accuracy and reliability.

Abstract

Landslide susceptibility mapping (LSM) is an effective means of assessing landslide risk and has been widely applied. However, current landslide susceptibility assessment studies have not fully considered the spatial heterogeneity characteristics between landslide assessment factors. The performance of a single model is limited by the structural characteristics of the model itself, and there is a significant limitation on the space for performance improvement. Based on these issues, this paper proposes a heterogeneous ensemble landslide susceptibility assessment method considering spatial heterogeneity. This method first combines the frequency ratio (FR), geographically weighted regression model (GWR), and clustering to partition the study area. Then, Geodetector is used to select the dominant factors for each subregion. Random forest (RF), support vector machine (SVM), and extreme gradient boosting (XGBoost) are selected as the base models, and logistic regression (LR) is selected as the metamodel. The stacking ensemble strategy is used to construct the model to complete a landslide susceptibility assessment in Fujian Province. The results show that compared with other methods, the GWR-S-Geo model considering spatial heterogeneity proposed in this study performs best in the evaluation effect, and performance is improved by 3.2% compared with the stacking ensemble model. This study provides a certain reference value for exploration of the spatial heterogeneity of landslide susceptibility, and also provides a scientific basis for the prevention and control of landslide disasters in Fujian Province.

1. Introduction

A landslide is a complex geological process triggered by the combined effects of various internal and external forces, including geological structure and rainfall [1]. A frequently occurring geological hazard, landslides are characterized by their sudden occurrence, high level of danger, and difficulty to control [2]. Landslides are a frequent occurrence around the world. Over the last 30 years, landslides have caused economic losses of up to USD 1 billion and claimed the lives of more than 1.6 million people worldwide [3,4]. In order to minimize the economic losses and casualties caused by landslides, it is necessary to assess susceptibility to landslides in advance and formulate relevant prevention and control strategies.

Landslide susceptibility mapping (LSM) uses the spatial distribution of historical landslides and related factors to predict the probability of future landslides [5,6]. LSM is considered an effective means of reducing landslide risk [7,8]. Therefore, the development of a scientifically accurate landslide susceptibility mapping model is of great practical significance and value for early warning of regional landslide disasters and the formulation of disaster prevention and mitigation plans.

Currently, landslide susceptibility assessment models are mainly divided into two categories: qualitative and quantitative. Qualitative methods are mainly empirical, while quantitative methods primarily include mathematical and statistical methods as well as machine learning [9]. Empirical methods primarily rely on the experience and expertise of scholars and experts for judgment and analysis, including models such as fuzzy theory analysis [10] and the analytic hierarchy process [11,12]. The commonly used methods of mathematical statistics are the information quantity method [13] and certainty factor method [14]. However, due to the complex nonlinear relationship between landslide assessment factors, the conventional statistical model has inherent limitations in factor fitting and is not sensitive to the nonlinear relationship between factors [15]. Therefore, more and more scholars are using machine learning models to evaluate landslide susceptibility and promote the development of disaster prevention and control in the direction of intelligence. Machine learning models such as logistic regression model (LR), support vector machine (SVM), random forest (RF), and extreme gradient boosting (XGBoost) have been widely used in this field [1,16,17,18]. However, a single machine learning model is limited by the inherent characteristics of the algorithm, and it is difficult to adapt to multi-scenario requirements in complex geographic environments. In complex scenarios or large study areas, performance may decline [19,20]. Therefore, some scholars have proposed using ensemble learning models for landslide susceptibility modeling to improve the accuracy and effectiveness of prediction results [21,22,23]. Ensemble learning includes homogeneous ensemble and heterogeneous ensemble [24]. The homogeneous ensemble method may further highlight its inherent defects due to the combination of homogeneous classifiers, which may lead to potential overfitting risks. The heterogeneous ensemble method can fuse different types of classifiers and make up for each’s shortcomings by virtue of the advantages of each classifier. This feature helps to improve the robustness and generalization performance of the ensemble classifier and further improve the prediction effect of the ensemble algorithm [9,25]. However, current studies on landslide susceptibility mostly focus on small-scale study areas such as county-level or city-level areas [26,27,28]. Research on heterogeneous ensemble learning models for provincial landslide susceptibility with complex geological environments is still limited. Therefore, it is of great significance to explore an ensemble learning evaluation model for landslide susceptibility that is suitable for a large study area and has good performance.

Spatial heterogeneity affects the change in the dominant factors of landslides in different layers [8,29]. However, current susceptibility assessment models do not fully consider the spatial heterogeneity between landslide assessment factors in local geographic units, which greatly reduces prediction accuracy [30]. The intensity of action and influence of direction of landslide assessment factors often show significant spatial differentiation characteristics [31,32]. From the perspective of the intensity of a single evaluation factor, its impact on landslide disasters shows significant differences with changes in spatial area, and the factors that dominate landslide occurrence in different areas are also different. Most existing studies adopt models that use a unified approach for the entire study area, ignoring the spatial heterogeneity of assessment factors. This makes it difficult for the susceptibility results to reflect the differences in the formation mechanism of local landslides, resulting in local deviations in the evaluation results [33]. This local deviation leads to the lack of pertinence of disaster prevention measures based on the model results, which weakens the application value of the evaluation model in actual disaster reduction work. Therefore, the spatial heterogeneity problem in the study of landslide susceptibility needs to be solved urgently.

Some scholars have realized the importance of spatial heterogeneity to the assessment of landslide susceptibility and carried out relevant research, but existing studies still have significant limitations in the universality, practicability, and rationality of the method [34]. For example, Zhuo et al. [35] divided the whole Loess Plateau into three different regions based on geological background and explored its spatial heterogeneity by modeling the overall region and individual subregions. Similarly, Sun et al. [30] studied the driving factors of landslide susceptibility in the southern and northern parts of the Himalayan transboundary region. However, such zoning division based on specific regional backgrounds has obvious limitations in applicable scenarios, and it is difficult to apply to conventional study areas without special backgrounds. In addition, Chang et al. [36] divided slope units to represent the heterogeneity of influencing factors as the internal variation of these factors within slope units. However, for large-scale study areas, dividing slope units involves high complexity in data processing and is prone to errors. Chen et al. [37] used the clustering method to divide their study into several subregions to solve the problem of spatial heterogeneity. However, the direct clustering of the assessment factors is easily interfered with by a single dominant factor or noise data, which may lead to unreasonable partition structure. These limitations restrict the effective role of spatial heterogeneity in landslide susceptibility assessment and also leave room for improvement in subsequent studies.

In view of the above problems, this study adopted a zoning strategy combining frequency ratio (FR), geographically weighted regression (GWR), and clustering to fully explore the spatial heterogeneity characteristics of landslide assessment factors. At the same time, with the help of Geodetector, the dominant influencing factors of landslide development at different subregions and global scales were revealed, and the explanatory power of a single influencing factor on the spatial differentiation of landslide was quantified. On this basis, an ensemble learning model was constructed to evaluate landslide susceptibility, and the interpretability of the model results was enhanced by the Shapley additive explanations (SHAP) method. Finally, small baseline subset–interferometric synthetic aperture radar (SBAS-InSAR) technology was used to invert the surface deformation characteristics to verify the accuracy of the model prediction results. The purpose of this study was to improve the prediction accuracy and reliability of landslide susceptibility assessment, and to provide scientific support for understanding the spatial differentiation mechanism of regional landslide formation so as to provide a theoretical basis and technical reference for targeted prevention and risk management of regional landslide disasters.

2. Study Area and Data Sources

2.1. Study Area

Fujian Province is located on the southeast coast of China, between 23°30′ and 28°22′ north latitude and 115°50′ and 120°40′ east longitude. Fujian Province covers an area of 124,000 square kilometers, facing the Taiwan Strait in the east. It is a typical mountainous and hilly landform area with complex natural conditions. The area of mountains and hills in the province accounts for about 90% of the total area. The north-central part is dominated by the Wuyi Mountains, and the south is mostly branch hills. The terrain is tilted from northwest to southeast, the landform is undulating, and geological tectonic activities are frequent. These provide a congenital topographic basis for the breeding of geological disasters such as landslides. Annual precipitation in Fujian Province is abundant, especially in the flood season and typhoon period. Short-term heavy rainfall occurs frequently, which becomes the dominant external driving factor of landslide disasters. In this study, Fujian Province was taken as the research area. The geographic location of the research area is shown in Figure 1.

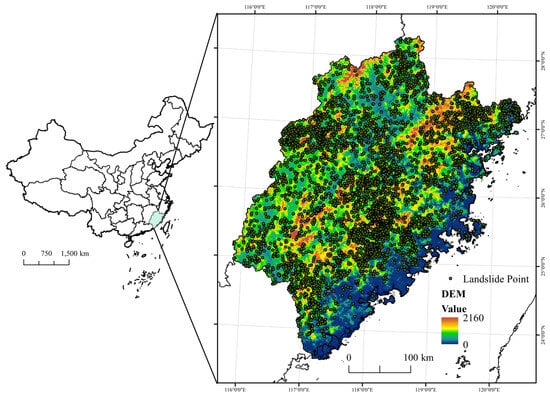
Figure 1. Geographic location and landslide point distribution of the study area.

2.2. Data Sources

2.2.1. Landslide Data

The historical landslide data used in this study were derived from the national spatial distribution dataset of geological hazard points released by the Resource and Environmental Science Data Center of the Chinese Academy of Sciences. The dataset includes information on various geological hazard points such as landslides, debris flows, and collapses. Based on research requirements, we carried out a series of corrections and processing of the original dataset. Finally, 6115 historical landslide points were selected in the study area, and these historical landslide points were used as landslide samples for subsequent model construction. The distribution of historical landslide points in the study area is shown in Figure 1. Considering that there is still a high risk of landslides in areas adjacent to landslides, we established a buffer zone of 1000 m around the known landslide points and randomly selected non-landslide samples at a ratio of 1:1 between landslide point and non-landslide point outside the buffer zone. The dataset was divided into a 70% training set and 30% test set for model training and performance evaluation.

2.2.2. Landslide Assessment Factors

The occurrence of landslides is affected by many complex factors [38]. Based on the existing research and the actual geological environment characteristics of Fujian Province, this study preliminarily screened out 16 landslide assessment factors that are closely related to the triggering of landslides from five aspects (topography, geology, hydrology, land cover, and human activities): elevation (DEM), slope, aspect, plane curvature, profile curvature, topographic relief (relief), topographic surface roughness (roughness), terrain ruggedness index (TRI), lithology, distance from faults (Distance2Fault), soil type (soil), distance from rivers (Distance2River), rain, land use, normalized difference vegetation index (NDVI), and distance from roads (Distance2Road).

The DEM used in this study was obtained from the Geospatial Data Cloud (https://www.gscloud.cn/home, accessed on 16 August 2024). We downloaded a dataset of 30 m resolution provided by the ASTER satellite, and processed the data by splicing, projection, and cropping. Terrain factors such as slope, aspect, plane curvature, profile curvature, topographic relief, topographic surface roughness, and TRI were obtained through a series of operations on the DEM. The lithology data were derived from the ISRIC World Soil Information Database (https://data.isric.org/geonetwork/srv/chi/catalog.search#/home, accessed on 20 August 2024). Based on Engineering Rock Mass Classification Standard GBT50218-2014, the original multi-category lithology data were reclassified based on the hardness of the rock mass. Finally, the lithology was divided into six categories: extremely soft rock, soft rock, relatively soft rock, relatively hard rock, hard rock, and water body. The fault data were sourced from the Chinese GMT community (https://docs.gmt-china.org/6.3/dataset-CN/, accessed on 18 August 2024). The road and water system data were derived from OpenStreetMap (https://download.geofabrik.de/asia/china.html, accessed on 16 August 2024). Through the Euclidean distance rasterization of faults, roads, and water systems, three assessment factors—distance from faults, distance from roads, and distance from rivers, respectively—were generated. The soil type data we obtained was provided by the Chinese Academy of Sciences Resource and Environment Science Data Platform. Vector data were rasterized and reclassified. The Rain factor was based on site observation data provided by the National Centers for Environmental Information (NCEI) of the National Oceanic and Atmospheric Administration (NOAA). We calculated the average precipitation for the 10-year period from 2014 to 2023 and then interpolated it to a resolution of 30 m using the inverse distance weighting method. Land-use data were sourced from Wuhan University China Land-Use Dataset (https://zenodo.org/records/12779975, accessed on 20 August 2024). We used the land-use data from 2023. NDVI data were sourced from the National Qinghai–Tibet Plateau Science Data Centre [39]. The landslide assessment factors we obtained are shown in Figure 2.

Figure 2. Landslide assessment factors. (a) DEM; (b) slope; (c) aspect; (d) plane curvature; (e) profile curvature; (f) relief; (g) roughness; (h) TRI; (i) lithology; (j) Distance2Fault; (k) soil; (l) Distance2River; (m) rain; (n) land use; (o) NDVI; (p) Distance2Road.

3. Methodology

This study consisted of five steps. Firstly, the landslide inventory data and assessment factor data were integrated. Spearman correlation analysis and multicollinearity analysis were used to preliminarily screen the landslide assessment factors, construct the landslide assessment factor database, and establish a buffer zone. The non-landslide samples were screened outside the buffer zone, and the training set and test set data were created. Secondly, spatial division of the study area was carried out using FR, GWR, and clustering, and the spatial heterogeneity of landslide assessment factors was revealed. Then, Geodetector was used to screen the dominant factors of the whole region and each subregion. On this basis, a heterogeneous ensemble landslide susceptibility assessment model was constructed, and the ROC curve was used to evaluate the performance of the model. Then, we used the SHAP method to analyze the interpretability of the model. Finally, SBAS-InSAR technology was used to invert the surface deformation, and the landslide susceptibility assessment results were verified to prove the accuracy and effectiveness of the results. Figure 3 shows the process of this study.

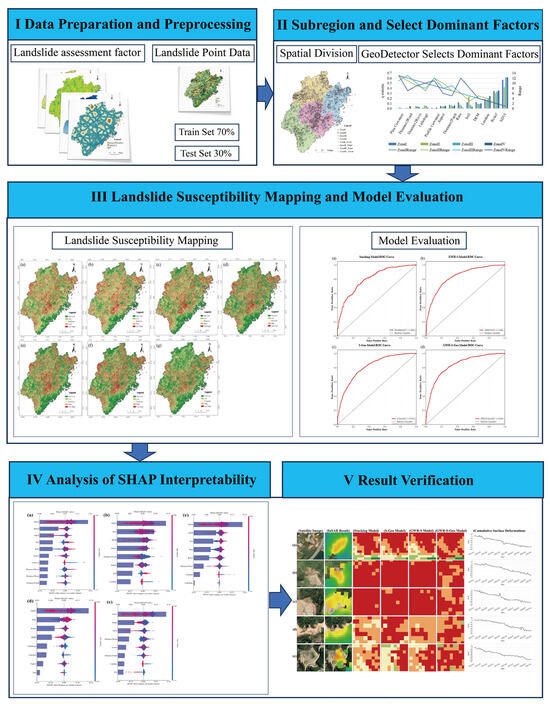
Figure 3. Main workflow framework of this study.

3.1. Frequency Ratio (FR)

FR is used to calculate the probability of landslide occurrence in different classification intervals of landslide assessment factors. This method determines the quantitative relationship between the probability of landslide occurrence and the classification of each assessment factor, and can be used to determine the influence degree of landslide assessment factors on landslide [40]. The calculation formula of FR is as follows:

$${FR}_{ij}={\displaystyle \frac{N_i/N}{A_i/A}}$$

(1)

where $N_i$ represents the number of landslides in the i th classification interval of the assessment factor, $N$ represents the total number of landslides in the whole study area, $A_i$ represents the area of the i th classification interval, and $A$ represents the total area of the study area.

3.2. Geographically Weighted Regression (GWR)

The first law of geography shows that there are often similar associations between the attributes of geographic entities with similar spatial distribution, and the degree of association gradually decreases with increasing spatial distance [19]. By establishing the local regression equation of each spatial unit in the study area, GWR quantifies the influence coefficient of a single driving factor in different spaces so as to reflect the spatial heterogeneity and non-stationary characteristics between the research object and the assessment factor. The equation of the GWR model is as follows:

$$y_i={\beta }_0\left({\mu }_i,v_i\right)+\sum _{k=1}^Q{\beta }_k\left({\mu }_i,v_i\right)x_{ik}+{\epsilon }_i$$

(2)

where $\left({\mu }_i,v_i\right)$ are the spatial coordinates of the ith sample, ${\beta }_k$ is the coefficient of the k th independent variable, $x_{ik}$ is the kth variable of the ith sample, ${\epsilon }_i$ is the random error at the neighborhood i, and Q is the number of variables.

3.3. Geodetector

Geodetector is a statistical method based on the theory of spatial differentiation. This method quantifies the spatial stratification heterogeneity of geographic elements and identifies their driving factors through variance decomposition. The core expression of this method is that if the independent variable landslide assessment factor has an important influence on the occurrence of the dependent landslide variable, the landslide assessment factor should have similar spatial distribution characteristics to the landslide [40]. The q statistic of this method can assess the explanatory power of landslide assessment factors on the spatial distribution of landslides. The closer the q value is to 1, the greater the contribution of this factor to the occurrence of landslides. The formula for calculating the value of q is as follows [41]:

$$\mathrm{q}=1-{\displaystyle \frac{\sum _{m=1}^S{N}_m{\sigma }_m^2}{N{\sigma }^2}}=1-{\displaystyle \frac{WSS}{TSS}}$$

(3)

$$\mathrm{W}\mathrm{S}\mathrm{S}=\sum _{m=1}^S{N}_m{\sigma }_m^2$$

(4)

$$\mathrm{T}\mathrm{S}\mathrm{S}=N{\sigma }^2$$

(5)

where m is the layer of variable Y or factor X, $N_m$ is the number of elements in layer m, and N is the number of elements in the whole region. ${\sigma }_m^2$ is the Y value in the mth layer, and ${\sigma }^2$ is the variance of the Y value in the whole region. $\mathrm{W}\mathrm{S}\mathrm{S}$ is the sum of intra-layer variance, and $\mathrm{T}\mathrm{S}\mathrm{S}$ is the total variance of the whole region.

3.4. Ensemble Learning Model

We used the stacking ensemble strategy to construct a heterogeneous ensemble model, which fully integrates the characteristics of various base models and has better comprehensive performance than a single model [42]. The stacking ensemble strategy uses the output of multiple heterogeneous base models as the training feature of the next-level metamodel, and the final result is obtained by combining the base model with the metamodel [43].

Specifically, this study used RF, SVM, and XGBoost as the base models and LR as the metamodel. The core basis for selecting the abovementioned base model is the complementarity of its algorithmic characteristics. RF can effectively alleviate the problem of imbalanced landslide samples and reduce the risk of overfitting through bootstrap resampling and random feature selection. SVM has a greater ability to describe nonlinear boundaries when dealing with discrete assessment factors such as lithology. XGBoost can effectively capture the complex nonlinear relationships between assessment factors and landslides through a gradient boosting tree structure. The three base models complement each other from the three dimensions of sample equalization processing, discrete feature boundary recognition, and nonlinear relationship modeling, avoiding the inherent limitations of a single algorithm. The selection of the LR metamodel was based on its linear combination features. LR transformed the prediction results $f_1,f_2$, and $f_3$ of the three base models into new features and automatically quantified the relative contribution weights of each base model. We used the landslide assessment factor dataset $X=[x_1,x_2,\dots ,x_p]$ as input, FR, SVM, and XGBoost, respectively, to predict X, and LR performed the optimal combination of the results.

3.4.1. Base Model

• Random Forest (RF)

RF, originally proposed by Breiman [44], is a machine learning algorithm based on ensemble learning. It constructs multiple m decision trees through subsets of different data, votes on the results of multiple decision trees, and finally obtains the output results. The core idea of random forest is bagging and random feature subspace, which aims to reduce the variance of the model and avoid overfitting [45].

$$f_1\left(X\right)={\displaystyle \frac{1}{\mathrm{m}}}{\sum }_{t=1}^m{T}_t\left(X\right)$$

(6)

Here, $f_1\left(X\right)$ is the prediction result of the RF and $T_t\left(X\right)$ is the prediction result of the t-th tree.

2.

Support Vector Machine (SVM)

SVM is a supervised learning algorithm based on statistical learning theory, and is essentially a nonlinear data processing method [46]. This method obtains the effect of nonlinear regression in the original space by mapping the input low-dimensional nonlinear data into a high-dimensional space and performing linear regression in the high-dimensional space [47]. In the modeling process of landslide susceptibility, the radial basis function (RBF) is usually used as the sum function of SVM, which can effectively describe the complex nonlinear relationship between landslide assessment factors and landslides [48].

$$K\left(x,x^{\prime }\right)=\exp (-\gamma {||x-x^{\prime }|\left|\right)}^2$$

(7)

$$f_2\left(X\right)={\sum }_{i=1}^n{\propto }_i{y}_{i}K\left(X,X_i\right)+b$$

(8)

Here, $f_2\left(X\right)$ is the prediction result of the SVM, $K\left(x,x^{’}\right)$ is the RBF, ${\propto }_i$ is the support vector coefficient, and $b$ is the bias term.

3.

Extreme Gradient Boosting (XGBoost)

The XGBoost algorithm is an improvement of gradient boosting decision (GBDT). The algorithm significantly improves the computational efficiency and prediction performance of traditional GBDT through iterative ensemble learning and regularization optimization, and is widely used in classification, regression, and sorting tasks.

$$f_3\left(X\right)={\sum }_{t=1}^k\beta h_t\left(X\right)$$

(9)

Here, $f_3\left(X\right)$ is the prediction result of XGBoost, $\beta$ is the learning rate, and $h_t\left(X\right)$ is the predicted value of the t-th tree.

3.4.2. Metamodel

Logistic regression (LR) is a statistical learning method widely used in classification tasks, especially for binary classification problems. The model maps the linear regression results to (0, 1) through the sigmoid function so as to realize the prediction of landslide probability. The LR function can be expressed as:

$$\mathrm{y}\left(\mathrm{x}\right)={\displaystyle \frac{1}{1+{\mathrm{e}}^{-\mathrm{m}}}},$$

(10)

$$\mathrm{m}={\mathrm{w}}_0+{\mathrm{w}}_1{\mathrm{f}}_1+{\mathrm{w}}_2{\mathrm{f}}_2+{\mathrm{w}}_3{\mathrm{f}}_3$$

(11)

where $\mathrm{y}\left(\mathrm{x}\right)$ represents the probability of a landslide, ${\mathrm{w}}_1$, ${\mathrm{w}}_2$, and ${\mathrm{w}}_3$ represent the relative contributions of RF, SVM and XGBoost, and ${\mathrm{f}}_1$, ${\mathrm{f}}_2$, and ${\mathrm{f}}_3$ are the prediction results of the three base models, respectively.

3.5. Model Assessment

The receiver operating characteristic curve (ROC) and area under the curve (AUC) are used to evaluate the performance of the model. The ROC curve uses false-positive rate (FPR) as the horizontal axis and true-positive rate (TPR) as the vertical axis. By dynamically adjusting the classification threshold, the discriminant ability of the model under different decision boundaries is described, and its geometric shape directly reflects the classification efficiency of the model. TPR and FPR are defined as:

$$\mathrm{T}\mathrm{P}\mathrm{R}={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}},$$

(12)

$$\mathrm{F}\mathrm{P}\mathrm{R}={\displaystyle \frac{\mathrm{F}\mathrm{P}}{\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}}}$$

(13)

TP, FN, TN and FP represent the number of true positives, false negatives, true negatives, and false positives, respectively.

3.6. SBAS-InSAR

SBAS-InSAR technology is a differential interferometry technique based on synthetic aperture radar, which is widely used in landslide monitoring and assessment [49,50]. The processing flow of SBAS-InSAR includes the following key steps. (1) Data preprocessing: the single look complex (SLC) image is registered to a single master image, and precise orbit correction is performed using the Precise Orbit Ephemerides (POD) data released by the ESA. (2) Generate interferogram: in order to reduce the time and space incoherent images, the maximum spatial baseline is set to 5%, and the maximum time baseline is set to 90 days. (3) Interference processing and filtering: in this study, 30 m-resolution Advanced Land Observing Satellite Digital Elevation Model (ALOS DEM) data were used to correct the terrain phase and generate differential interferograms; Goldstein filtering was used to remove noise. (4) Phase unwrapping: a coherence map was generated for each interferogram by phase unwrapping, and the Delaunay MCF algorithm was used for phase unwrapping. (5) Deformation inversion and geocoding: by establishing a linear equation between the interference pairs, singular value decomposition (SVD) was applied to invert the displacement value at each moment. Finally, the SAR coordinate system was encoded into the geographic coordinate system, and the results represent the deformation information in the line of sight (LOS) direction of the radar.

4. Results

4.1. Construction of Landslide Assessment Factor Database

Before the landslide susceptibility assessment, it is necessary to select a suitable landslide assessment unit, which provides a necessary prerequisite for ensuring the accuracy of landslide susceptibility assessment [9]. In the current study of landslide susceptibility assessment, the commonly used assessment units are grid unit and slope unit [51].

The grid unit divides the study area into regular grids, which is convenient for data preprocessing and training models and is suitable for landslide susceptibility assessment in large areas. The study area of this study was the entire Fujian Province, so we took the grid unit as the mapping unit of susceptibility assessment. All the landslide assessment factors were converted into grids with a grid size of 30 × 30 m, and the grids in the whole study area were 17,579 rows and 16,535 columns. In order to eliminate the influence of dimension between factors, the landslide assessment factors were normalized. Because there may be strong correlation and collinearity between landslide assessment factors, which will affect the accuracy of model prediction, correlation analysis and multicollinearity analysis were carried out on all factors, and further screening of landslide assessment factors was carried out. This study calculated the Spearman correlation coefficient between the assessment factors, and the results are shown in Figure 4. When the absolute value of the correlation coefficient is greater than 0.7, it is considered that there is a high correlation between the factors [52].

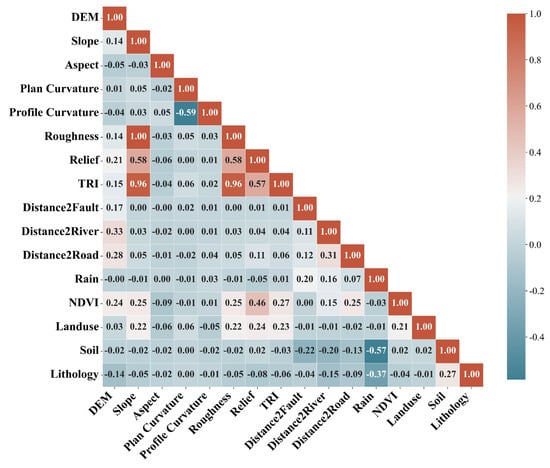
Figure 4. Spearman correlation analysis results.

The variance inflation factor (VIF) and tolerance (TOL) were used to analyze the multicollinearity between factors. In general, when VIF > 10 and TOL < 0.1, it is considered that there is a high collinearity problem between factors [53]. VIF and TOL values are shown in Table 1. As shown in Figure 4, the correlation coefficients of slope, roughness and TRI are all above 0.95 and the correlation degree is very high, and the VIF values of the three factors are all greater than 10. Based on the results of correlation analysis and multicollinearity analysis, we eliminated three assessment factors: slope, roughness and TRI.

Table 1. Multicollinearity analysis results.

Landslide Assessment Factor	TOL	VIF
DEM	0.817	1.224
Slope	0.068	14.750
Aspect	0.989	1.011
Plan Curvature	0.578	1.731
Profile Curvature	0.577	1.732
Roughness	0.094	10.608
Relief	0.554	1.805
TRI	0.055	18.207
Distance2Fault	0.913	1.095
Distance2River	0.898	1.114
Distance2Road	0.855	1.170
Rain	0.628	1.592
NDVI	0.696	1.437
Land Use	0.913	1.095
Soil	0.625	1.601
Lithology	0.856	1.168

4.2. Analysis of Distribution Characteristics of Landslide Assessment Factors

In order to reveal the law of landslide disaster triggering, we analyzed the distribution characteristics of landslide assessment factors in the study area and calculated the proportion of landslide units in different classification intervals and FR values. The larger the FR value, the more prone the area to landslide disasters in the current interval.

4.2.1. Topographic Factors

• DEM

As shown in Figure 5a, on the whole, with the increase in DEM, the proportion of landslide units increases rapidly first, then decreases continuously after reaching the peak. When the DEM of the study area is 143.44–337.5 m, the proportion of landslide units in this interval is the largest and the FR value is also the highest, which is the elevation section with high incidence of landslides. When the DEM is 337.5–885.94 m, the total proportion of landslide units is more than 50% and the FR value is greater than 1, indicating that the probability of a landslide in this interval is also relatively large. However, in the range of too high or too low a DEM, the probability is relatively small. On the whole, it shows the law of medium elevation is a high incidence area of landslide, and there are few landslides at too high or too low an elevation.

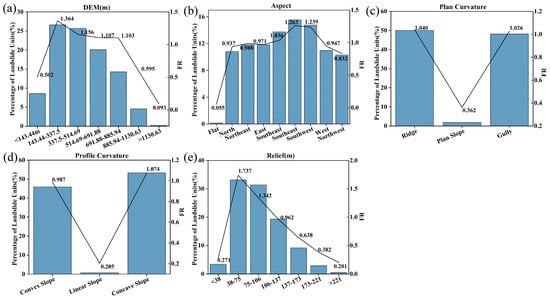
Figure 5. Topographic factors. (a) DEM; (b) aspect; (c) plane curvature; (d) profile curvature; (e) relief.

2.

Aspect

The south and southwest aspects are the high incidence areas of landslides, and the proportions of landslide units and FR values are relatively high. These slope directions are located on the windward slope side of the mountain range in Fujian Province, which experiences abundant precipitation, resulting in a greater probability of landslide occurrence. At the same time, these aspects are affected by external forces such as rainfall, and the weathering degree of rock and soil becomes higher, which is prone to instability and sliding, and is more prone to landslides. There are almost no landslides on the flat. The proportion of landslide units in the north, northeast, east, southeast, west, and northwest aspects is relatively low compared with the south slope and the southwest slope, but there are still some risks. The distribution characteristics of aspect are shown in Figure 5b.

3.

Plan Curvature

The ridge and valley are the plane curvature types with high incidence of landslides. The proportion of landslide units in the two types is high and the FR value is close. There are many mountains in Fujian Province and frequent rainstorms with abundant precipitation. The terrain is high in the ridge area. Rainwater easily results in surface runoff along the slope surface, which scours the rock and soil mass in the ridge area, resulting in a decrease in the stability of the slope. The gully is the area where the surface runoff gathers. During rainfall, a large amount of rainwater quickly gathers in the gully, constantly destroying the stability of the rock and soil mass, so the gully is also a high-incidence area of landslides. The plan slope terrain is relatively flat, the slope body is relatively stable, and the proportion of landslide units is relatively low.

4.

Profile Curvature

There are many mountainous hills in Fujian Province, and the convex slope has a convex trend on the terrain. During rainfall, the rainwater collects quickly and the runoff scours strongly. The rainfall in Fujian Province is abundant, which accelerates the slope instability. The landslide unit accounts for more than 40%, and the frequency ratio is 0.987, which belongs to the landslide-prone form. The concave slope easily converges water flow and accumulates loose materials, which leads to a higher risk of landslides. The landslide unit of the concave slope accounts for more than 50%, and the FR is 1.074, which is a profile curvature type with high incidence of landslide. The linear slope shape is relatively uniform, the slope stability is relatively good, the proportion of landslide units is very low, and landslides occurs less.

5.

Topographic Relief

In Figure 5e, it can be seen that in the range of 38–75 m, the proportion of landslide units is the highest, more than 30%, and the FR is 1.737, which is the range where landslides are prone to occur. The proportion of the 75.106–106.137 m interval is still high, the FR is 1.342, and the landslide susceptibility is also prominent. However, when the relief is too small (221 m), the proportion of landslide units is significantly reduced, the proportion of 221 m is almost 0, and the FR is 0.201.

4.2.2. Geological Factors

• Lithology

As shown in Figure 6a, the hard rock landslide unit accounts for the highest proportion, more than 50%, indicating that in statistical landslide events, the number of hard rock areas is the largest. Relatively hard rock is second, accounting for about 40%. Soft rock accounts for less. The proportion of soft rock and extremely soft rock is very small. The proportion of landslide units corresponding to water bodies is almost 0. The FR of hard rock is 1.188, and the relative possibility of landslides in hard rock area is the largest. Hard rock is widely distributed in the mountainous areas of Fujian Province, so the proportion of landslide units is relatively high, but the FR value does not reach the highest. The FR value of the relatively hard rock is higher, and the lithology type is more susceptible to weathering and structure than the hard rock. The complex geological structure and warm and humid climate in Fujian accelerate the weathering process, so the degree of rock mass fragmentation is relatively high. At the same time, in the environment with abundant precipitation, the slope formed by the relatively hard rock is more likely to reduce the stability due to the infiltration of water, which in turn causes landslides. Soft rock, relatively soft rock, and extremely soft rock have low strength and weak weathering resistance, and their distribution in Fujian is relatively small. In their natural state, they are often in a relatively stable state or have been eroded to form a relatively flat terrain, so the proportion and FR of landslide units are low.

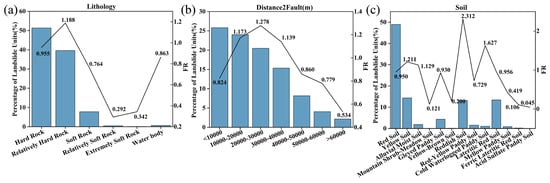
Figure 6. Geological factors. (a) lithology; (b) Distance2Fault; (c) soil.

2.

Distance2Fault

A fault is a structure in which the crustal rock is broken by force and has obvious relative displacement along the fracture surface. The proportion of landslide units is the highest in the interval less than 10,000 m. The rock near the fault is broken, joints and fissures are developed, and the integrity is destroyed. Therefore, landslides are more likely to occur under external forces such as gravity and rainfall. With increasing distance from the fault, the proportion of landslide units gradually decreases. The FR is the highest in the range of 20,000–30,000 m—1.278—indicating that the interval has a greater impact on the occurrence of landslides under the same conditions.

3.

Soil Type

The proportion of landslide units in red soil is more than 50%, and the FR is 0.95. The high proportion of landslide units indicates that the number of landslides in red soil is the largest. The FR of reddish soil is the largest. In some hilly areas of Fujian Province, human activities such as reclamation and road construction have caused great disturbance to the soil type, resulting in the destruction of vegetation in the soil area, and landslides are prone to occur during rainstorms. The FR of cold-waterlogged fields is also relatively high. Cold-waterlogged fields are mostly distributed in low-lying areas in mountainous areas. In some mountainous areas of Fujian Province, cold-waterlogged paddy soil is saturated and soft due to long-term water accumulation. This state is prone to landslides under the action of external forces such as rainfall. However, due to the limitation of its distribution range, the proportion of landslide units has not reached a very high level.

4.2.3. Hydrologic Factors

• Distance2River

As shown in Figure 7a, when the distance from the river is less than 5000 m, the proportion of landslide units is the highest and the FR is 1.074. Fujian Province is rich in precipitation and has a large amount of river flow, resulting in strong erosion ability of the rock and soil of the riverbank. Long-term erosion makes the rock and soil structure of the riverbank loose, the slope steeper, and the stability lower. Therefore, the possibility of landslides in this distance range is relatively large. As the distance from the river increases, the proportion of landslide units and the FR value generally show a downward trend. When the distance is greater than 30,000 m, the FR decreases to 0.242, and the possibility of landslide decreases significantly. When the distance from the river is less than 5000 m, the proportion of landslide units is the highest and the FR is 1.074. Fujian Province is rich in precipitation, the river water is voluminous, and the capacity for erosion of the rock and soil on the riverbank is strong. Long-term erosion makes the structure of the rock and soil on the riverbank loose, the slope steeper, and the stability lower, so the possibility of landslides in this distance range is relatively large. As the distance from the river increases, the proportion of landslide units and the FR generally show a downward trend. When the distance is greater than 30,000 m, the FR decreases to 0.242, and the possibility of landslides decreases significantly.

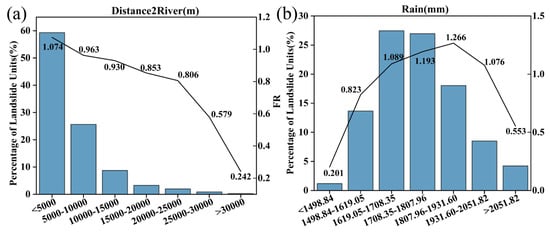
Figure 7. Hydrologic factors. (a) Distance2River; (b) rain.

2.

Rain

Rain is one of the important factors inducing landslide. In the range of 1708.35–1807.96 mm rainfall, the landslide FR is 1.266, the highest in this interval, and the proportion of landslide units is also in the forefront. This may be because the rainfall in this interval makes the rock and soil saturated, the pore water pressure increases, the shear strength decreases, and the slope runoff erosion is strong, which destroys slope stability. In the two intervals of 1619.05–1708.35 mm and 1708.35–1807.96 mm, the proportion of landslide units is the highest, both of which exceed 25%.

4.2.4. Land-Cover Factors

• Land Use

The farmland has a certain proportion and FR of landslide units. In Fujian Province, the mountainous farmland is mostly in the form of terraces and the terrain is undulating. Agricultural activities such as reclamation and irrigation will change soil structure and water content. Unreasonable irrigation and drainage will render the soil in a wet or dry–wet alternate state, reduce soil stability, and cause landslides. Forests are widely distributed in mountainous areas of Fujian Province. Although the proportion of landslide units is high, the FR is not the highest, which is due to the large proportion of forest area, and the understory vegetation and litter layer have a certain soil and water conservation effect. The FR of grassland is the highest because the proportion of grassland area is small, so the calculated FR is the largest.

2.

NDVI

The NDVI is an index reflecting the degree of vegetation coverage. As shown in Figure 8b, the NDVI value in the range of 0.59–0.76 is higher, indicating that the vegetation coverage is better. However, the proportion of landslide units and FR in this interval are high, which may be due to the diversity of vegetation types in mountainous areas of Fujian Province, the shallow roots of some vegetation, and the limited soil consolidation capacity. Although the overall vegetation coverage is acceptable, the soil is still prone to instability under external forces such as heavy rainfall. For example, some slopes dominated by herbaceous plants are prone to landslides in the rainy season.

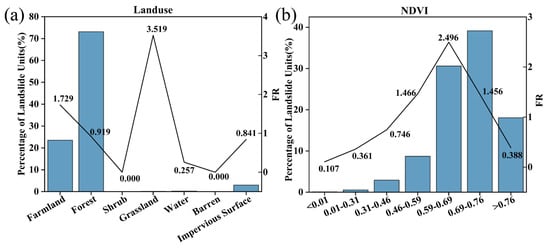
Figure 8. Land-cover factors. (a) land use; (b) NDVI.

4.2.5. Human Activity Factors

• Distance2Road

As shown in Figure 9, in the area less than 2500 m away from the road, the excavation, filling, and other engineering activities in the process of road construction will destroy the original rock and soil structure and stability of the mountain. Under the action of external forces such as rainfall, landslides occur easily, so the proportion of landslide units and the FR is relatively large. In the area far from the road, the interference of human activities is relatively small and the probability of landslides is relatively low.

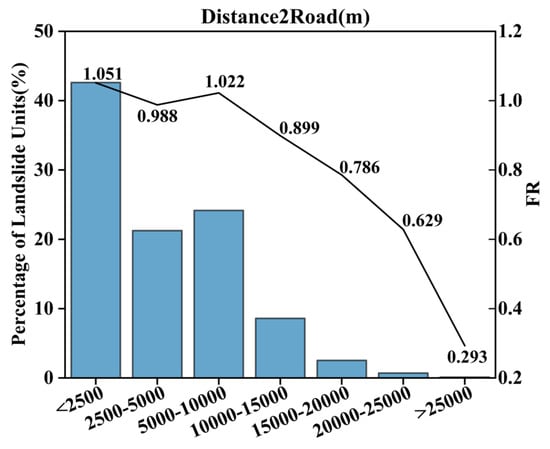
Figure 9. Human activity factors.

4.3. Spatial Heterogeneity Modeling and Regional Division

Landslides have significant spatial heterogeneity. The spatial heterogeneity of landslides is mainly manifested in two respects: the influence of the same assessment factor on landslides in different areas and the difference in dominant factors in different areas. Therefore, it is necessary to identify and quantify the spatial differentiation characteristics of the mechanisms driving landslides. Agglomerative nesting (AGNES) is a classical hierarchical clustering algorithm [54]. It regards each data point as an independent cluster, adopts a bottom-up aggregation strategy, and constructs a tree-like clustering structure by iteratively merging the most similar clusters until the termination condition is satisfied. Based on the combination of FR, GWR, and AGNES, this study modeled the spatial heterogeneity of landslide susceptibility and divided the study area. Firstly, the FR was used to preliminarily evaluate the probability of landslide occurrence, and the calculated FR value was taken as the dependent variable. Then, the local regression coefficients of landslide assessment factors at each landslide point were calculated by the GWR model. GWR establishes local dependence through spatial weight function, and its regression coefficient can reflect the spatial variation characteristics of the influence of independent variables on dependent variables, thus revealing the spatial heterogeneity of landslide assessment factors.

Before clustering partition, we used the Calinski–Harabasz (CH) index [55] to determine the optimal number of clusters based on the similarity within and between clusters. As shown in Figure 10, the results of the CH index show that when the number of clusters is 4, the CH index obtained by the average distance method is the largest. Based on the regression coefficient of each landslide point, the AGNES clustering method was used to cluster the landslide points in Fujian Province. In the process of clustering, the AGNES method classified the landslide points with similar driving mechanisms into the same cluster based on the similarity of regression coefficients, which ensured the geographic rationality of the partition. Then, based on the results of clustering, we constructed a Thiessen polygon based on the landslide points and divided the study area into several homogeneous areas. Each subregion represents a relatively homogeneous area of landslide driving mechanism. If the assessment factors are directly clustered, the accidental similar values of the spatial adjacent units may be classified into one category. GWR establishes a local dependence relationship through the spatial weight function, and the regression coefficient quantifies the spatial non-stationarity of the influence intensity and direction of the independent variables on the dependent variables. Therefore, compared with the direct clustering of assessment factors, this method integrates the correlation information between variables, can more accurately capture the differentiation characteristics of impact factors in geospatial space, and ensure the spatial continuity and geographic rationality of the partition through AGNES clustering.

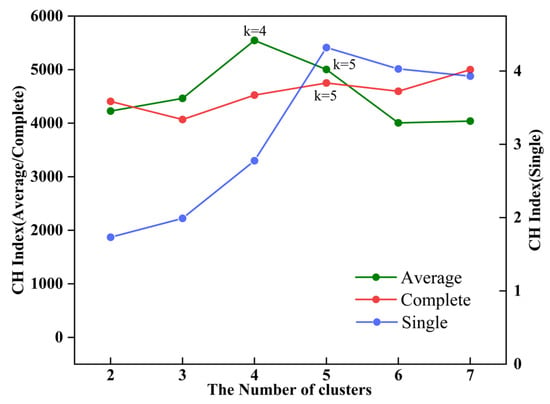
Figure 10. CH index.

Based on the results of clustering, Fujian Province was finally divided into four subregions. The results of area division are shown in Figure 11. Zone I is distributed in the south of Fujian Province, including most of Zhangzhou City, Longyan City, and a small part of Sanming City and Xiamen City. This region is mainly hilly and mountainous, with large terrain and high slope. Zone II is distributed in the central part of Fujian Province, which is located in the mountainous–hilly–coastal plain ecotone of Fujian Province, including Putian City, Quanzhou City, and some areas of Longyan City, Xiamen City, and Sanming City. This region is a typical high-rainfall area with concentrated rainstorms and frequent typhoons. Zone III is distributed in the northeastern part of Fujian Province, including most of Ningde City and Fuzhou City. The region is mixed with hilly and low-mountain areas, with multiple faults and unstable geological conditions. Zone IV is located in the northwest mountainous area, which belongs to the core area of the Wuyi Mountains, including Nanping City and the northwest of Sanming City. The region is dominated by block mountains and alpine hills, and the landforms are complex and changeable.

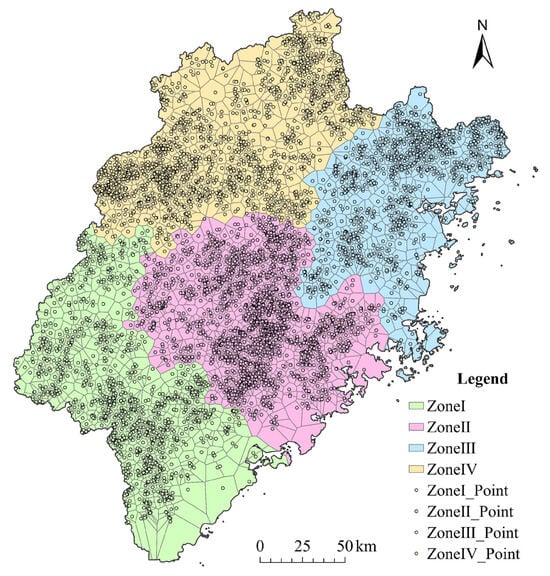
Figure 11. Clustering partition results.

4.4. Geodetector Selects Region Dominant Factor

Geodetector cannot process continuous data, so it is necessary to classify the landslide assessment factors first. Landslide assessment factors are divided into two types: continuous and discrete. We first determined the classification thresholds for distance to roads, distance to rivers, and distance to faults using the natural break method. To facilitate the establishment of standardized safety distance control measures in engineering practice, the values derived from the natural break method were adjusted to nearby integer values for practical application. The distance to roads was classified into seven categories based on intervals of 2500 m, 5000 m, 10,000 m, 15,000 m, 20,000 m, and 25,000 m. Similarly, the distance to rivers was categorized into seven levels using thresholds of 5000 m, 10,000 m, 15,000 m, 20,000 m, 25,000 m, and 30,000 m. The distance to faults was divided into seven grades with intervals of 10,000 m, 20,000 m, 30,000 m, 40,000 m, 50,000 m, and 60,000 m. The aspect was divided into nine grades based on eight slope orientation directions and flat ground. The surface curvature was divided into three categories: >0, =0 and <0. The plane curvature was divided into ridge, plane slope and valley, and the profile curvature was divided into convex slope, linear slope, and concave slope. DEM, slope, rain, NDVI and other continuous assessment factors were divided into seven grades based on the natural break method. The discrete factors were directly divided based on the original categories.

First, we used Geodetector to explore the dominant factors in the entire region of Fujian Province, and Figure 12a shows the results of factor detection. The q statistic values of four factors—plane curvature (0.006), profile curvature (0.010), Distance2River (0.013), and Distance2Road (0.015)—are almost 0, indicating that these assessment factors have poor explanatory power for landslides. The p value > 0.05 did not pass the significance test, so the four factors were eliminated, and the p value for lithology (0.145) did not pass the significance test, so was not included in subsequent model training. Based on the results of factor detection, eight assessment factors, NDVI, relief, soil, land use, DEM, rain, Distance2Fault, and aspect, were selected as the dominant factors affecting landslides in the whole area, among which NDVI had the strongest explanatory power for landslide occurrence.

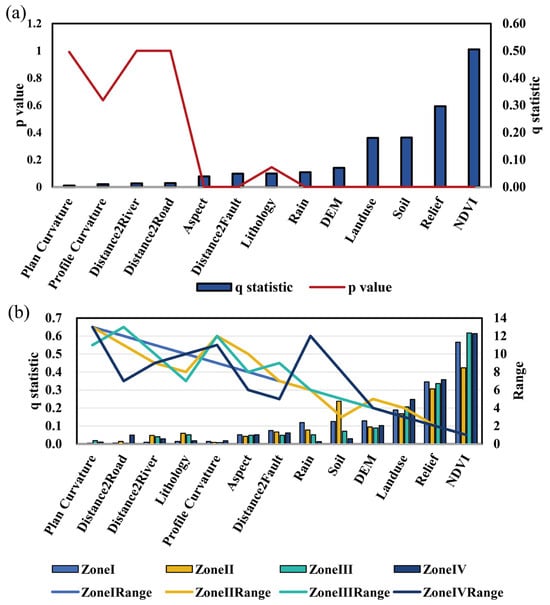
Figure 12. Geodetector results. (a) Geodetector results of the whole region; (b) Geodetector results of four partitions.

In order to reflect the spatial heterogeneity, we carried out factor detection on four different subregions separately using Geodetector, as shown in Figure 12b. Based on the q statistical value and p value, the five factors of plane curvature, Distance2Road, Distance2River, lithology, and profile curvature were finally eliminated in Zone I. In Zone II, the plane curvature, profile curvature, Distance2Road, aspect, and Distance2River were eliminated. In Zone III, five factors—Distance2Road, profile curvature, plane curvature, Distance2River, and Distance2Fault—were eliminated. Five factors—plane curvature, rain, profile curvature, lithology, and Distance2River—were eliminated in Zone IV. The results of factor screening in the four subregions are different, which verifies the heterogeneity of landslide assessment factors across different subregions. Specifically, the impact of the same assessment factor on landslides varies significantly with changes in geographic space. Through the differentiated selection strategy for each subregion, the dominant factors of each subregion were identified. This established a factor input system that accounted for spatial heterogeneity for the subsequent landslide susceptibility assessment model.

4.5. Validation and Comparison of Models

Firstly, in order to verify that the heterogeneous ensemble learning model was able to improve the performance of the model, we used the ROC curve to evaluate the three base models of RF, SVM, and XGBoost and the stacking ensemble learning model. The results showed that the AUC value of the stacking ensemble learning model was 0.806. As shown in Figure 13, the performance of the ensemble learning model was improved compared to the base model. We train the model through fivefold cross-validation and used the grid search method to optimize the hyperparameters of each base model to ensure that each base model achieved the best performance. Table 2 shows the final hyper-parameters set in this study.

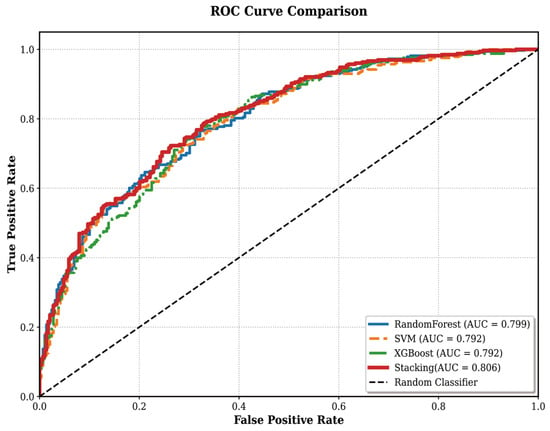
Figure 13. ROC curve of base models and heterogeneous ensemble model.

Table 2. Hyperparameters of the four models.

	RF	SVM	XGBoost	LR
Stacking Model	max_depth: None	C: 1	learning_rate: 0.1	C: 0.1
	max_features: sqrt	gamma: 0.1	max_depth: 6	solver: lbfgs
	min_samples_split: 2	kernel: rbf	n_estimators: 200	penalty:12
			subsample: 0.8	max_iter: 100
				class_weight: None
GWR-S Model	max_depth: None	C: 1	learning_rate: 0.1	C: 1
	max_features: sqrt	gamma: scale	max_depth: 6	solver: liblinear
	min_samples_split: 5	kernel: rbf	n_estimators: 100	penalty:12
	n_estimators: 200		subsample: 0.8	max_iter: 100
				class_weight: balanced
S-Geo Model	max_depth: None	C: 1	learning_rate: 0.1	C: 10
	max_features: sqrt	gamma: scale	max_depth: 3	solver: lbfgs
	min_samples_split: 2	kernel: rbf	n_estimators: 200	penalty:12
	n_estimators: 200		subsample: 1.0	max_iter: 100
				class_weight: None
GWR-S-Geo Model	max_depth: None	C: 1	learning_rate: 0.1	C: 0.1
	max_features: sqrt	gamma: 0.1	max_depth: 6	solver: liblinear
	min_samples_split: 2	kernel: rbf	n_estimators: 200	penalty: l2
	n_estimators: 200		subsample: 0.8	max_iter: 100
				class_weight: None

Then, we constructed the GWR-S, S-Geo, and GWR-S-Geo models. The GWR-S model only partitions the study area. The S-Geo model uses only Geodetector to screen the dominant factors in the entire area. The GWR-S-Geo model not only divides the study area, but also screens the dominant factors in different zones separately. The AUC values of the GWR-S, S-Geo, and GWR-S-Geo models were 0.836, 0.815, and 0.838, respectively, as shown in Figure 14. It can be seen that compared with the stacking model, the performance of the GWR-S-Geo model considering spatial heterogeneity and using Geodetector for factor screening is better than other models. In addition, after removing some factors by Geodetector, the performance of the model did not decrease, indicating that the dominant factors are different in different regions, which further illustrates the spatial heterogeneity between factors. The GWR-S-Geo model proposed in this study not only considers the impact of spatial heterogeneity of assessment factors, but also eliminates some redundant factors when training the model.

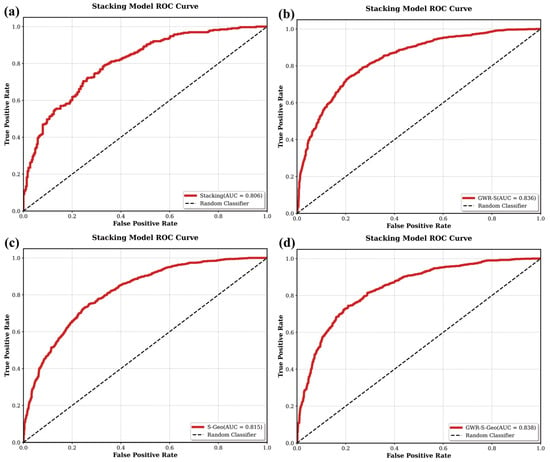
Figure 14. ROC curves of four models. (a) Stacking model; (b) GWR-S model; (c) S-Geo model; (d) GWR-S-Geo model.

4.6. Landslide Susceptibility Mapping

We used the RF, SVM, XGBoost, Stacking, GWR-S, S-Geo, and GWR-S-Geo models to predict the landslide susceptibility in Fujian Province, and calculated the landslide susceptibility index of the grid unit in the study area. The range of the susceptibility index is 0 to 1, and the larger the value, the greater the probability of landslides. The natural breakpoint method was used to reclassify the susceptibility prediction results of different models, which were divided into five susceptibility levels: very high, high, moderate, low, and very low. In general, the distribution of landslides is closely related to the classification of susceptibility. There are more landslide points in the very high- and high-susceptibility zones, while there are fewer landslide points in the moderate- and low-susceptibility zones [45]. The higher the susceptibility level, the greater the density of landslides [56]. As shown in Figure 15, the high-susceptibility zones are distributed in areas with dense landslide points. This shows that the prediction results have a strong correlation with the distribution of historical landslides.

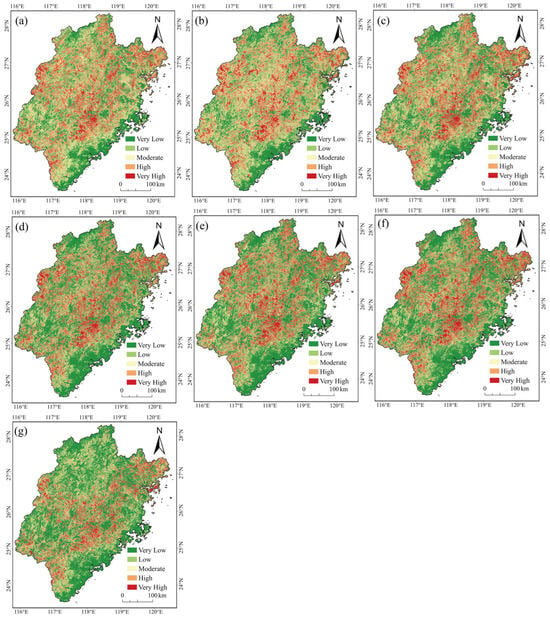
Figure 15. Results of landslide susceptibility mapping. (a) RF model; (b) SVM model; (c) XGBoost model; (d) stacking model; (e) GWR-S model; (f) S-Geo model; (g) GWR-S-Geo model.

To quantify the landslide susceptibility assessment results of different models, we calculated the landslide susceptibility zoning area, the number of landslides, and the density of landslides in different models, as shown in Figure 16a, Figure 16b, and Figure 16c, respectively. Landslide density is the proportion of the number of landslides in a certain susceptibility level to the area of the susceptibility level. As shown in Figure 16c, the landslide density values of all models show a significant increasing trend with the rise in susceptibility levels. The landslide density in low-susceptibility regions generally remains at a low level, while that in very high-susceptibility regions reaches a peak. This pattern is highly consistent with the actual occurrence of landslide disasters, indicating that each model can correctly reflect the spatial distribution of landslide points.

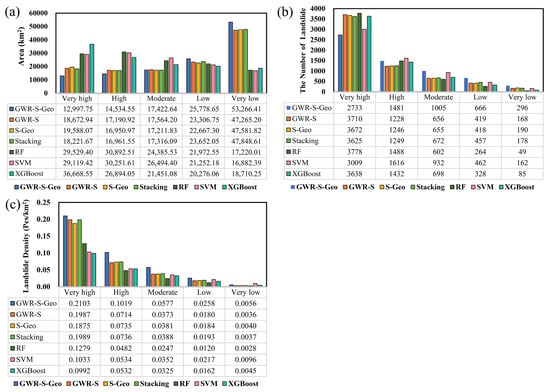
Figure 16. Landslide susceptibility assessment results—classification statistics. (a) Area of each susceptibility classification; (b) number of landslides in each susceptibility classification; (c) landslide density of each susceptibility classification.

The sum of landslide densities in the very high- and high-susceptibility regions derived from the proposed GWR-S-Geo model in this study is 0.311. This value is higher than those of the GWR-S model (0.269), S-Geo model (0.260), and stacking model (0.271), as well as the single machine learning models of RF (0.176), SVM (0.157), and XGBoost (0.152). This indicates that within high-susceptibility regions, the GWR-S-Geo model can more accurately identify regions with high landslide incidence and its prediction results have a higher degree of consistency with the actual distribution of landslides. The GWR-S-Geo model predicts the smallest area for the very high- and high-susceptibility regions. This indicates that the model identifies a relatively large number of landslides within these smaller high-susceptibility regions, leading to more accurate prediction results. In practical geological disaster prevention and control work, smaller high-susceptibility zones mean that prevention and control resources can be more concentrated in key regions. Compared with the GWR-S model, which only accounts for spatial heterogeneity, and the S-Geo model, which only performs factor selection, the GWR-S-Geo model considers both spatial heterogeneity and factor selection. This ensures that the model can select assessment factors for different subregions while eliminating irrelevant assessment factors within subregions, thereby reducing model redundancy. In terms of the number of landslides, the GWR-S-Geo model identified 2733 landslides in the very high-susceptibility zone. Although this number was lower than the 3710 landslides identified by the GWR-S model, the GWR-S-Geo model achieves a higher landslide density when combined with its smaller area. This result further verifies the model’s efficiency in resource concentration and risk identification, providing a more scientific methodological reference for landslide susceptibility assessment in large-scale areas.

5. Discussion

5.1. Interpretability of Models

Shapley additive explanations (SHAP) is a machine learning interpretability method using game theory. Its core advantage is that it can quantitatively reveal the contribution of each input feature to the output of a model, which provides a scientific basis for explaining the decision logic of the landslide susceptibility prediction model [57].

In order to fully analyze the spatial heterogeneity characteristics of the assessment factors in the study area, we modeled the whole region and four subregions and caried out SHAP analysis. Figure 17a shows the SHAP result for the whole region, and the mean value indicates the global contribution strength of the evaluation factor to the model. The positive and negative values of SHAP indicate the direction of influence of the evaluation factor on landslide susceptibility. The positive value indicates that the factor increases landslide susceptibility, and the negative value reduces the result, indicating that it has an inhibitory effect on landslide development. From the global results, the NDVI is the most critical factor affecting the development of landslides in the study area, followed by relief, DEM, soil, and rain. Further analysis shows that there is a negative correlation between the NDVI and landslide probability. In the low-vegetation-coverage area, due to the weak soil fixation ability of vegetation roots, the stability of soil decreases, which provides a strong condition for landslide development. Figure 17b, Figure 17c, Figure 17d, and Figure 17e represent the SHAP analysis results of Zone I, Zone II, Zone III, and Zone IV, respectively. Although the NDVI remained the dominant factor in the whole region and all subregions, the contribution intensity and direction of influence of other assessment factors were significantly different in different subregions. In the whole study area, the influence of relief on landslides is second only to the NDVI, while in Zone I the influence weight of rain is significantly increased. In Zone I, with a larger soil type coding value, the corresponding SHAP value has a promoting effect on landslide development. On the contrary, in Zone III and Zone IV, the increase in soil type coding value is accompanied by a shift in SHAP value to negative, which shows an inhibitory effect on landslide development. The spatial differentiation characteristics of this factor further confirm the spatial heterogeneity of landslide assessment factors. This also shows that in the assessment of landslide susceptibility, it is necessary to consider the dominant influencing factors of different subregions in order to improve the accuracy and reliability of model prediction.

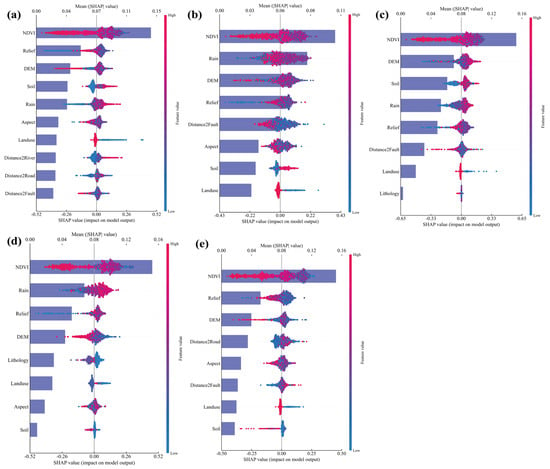
Figure 17. SHAP method results. (a) Global SHAP results; (b) SHAP results for Zone I; (c) SHAP results for Zone II; (d) SHAP results for Zone III; (e) SHAP results for Zone IV.

5.2. SBAS-InSAR

Surface deformation is aggravated under the influence of rain, earthquakes, and human activities, which heightens the risk of landslides. The core purpose of the inversion of surface deformation in this study is to provide support for the landslide susceptibility results. This study selected the ascending orbit data of 91 scenes of the Sentinel-1A C-band SAR SLC from 1 January 2022 to 1 January 2025. These data came from the Alaska Satellite Facility (ASF) Vertex platform (https://search.asf.alaska.edu/, accessed on 20 May 2025). We used ENVI SARscape software 5.6.2 to obtain the surface deformation rate and cumulative variables of Gutian County, Ningde City, and Fujian Province through two inversions based on SBAS-InSAR technology. The surface deformation rate of Gutian County is shown in Figure 18.

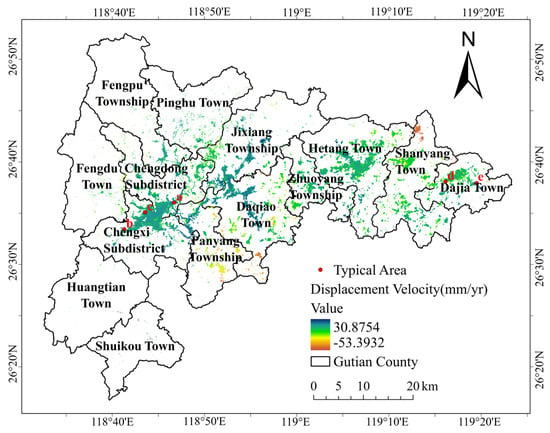
Figure 18. Surface displacement velocity of Gutian County.

We selected several typical regions with relatively large deformation rates for analysis. By comparing the spatial coincidence degree of the high-value region of susceptibility and the region with high deformation rate and large cumulative deformation, we judged whether the results of landslide susceptibility prediction were consistent with the actual unstable region of the slope. If the degree of spatial matching of the two were high, the reliability of the susceptibility prediction results would be proved. Figure 19 shows satellite images of regions a, b, c, d, and e, as well as the corresponding displacement velocity, susceptibility results of the four ensemble models, and cumulative surface deformation variables. Compared with the other three ensemble models, the GWR-S-Geo model predicts a more accurately focused range of very high susceptibility. The a and e regions are located beside the highway. In the process of highway construction, unreasonable excavation and filling operations may destroy the stability of the original mountain, and the influence of human activities will lead to the possibility of landslides. The cumulative surface variables in region b are relatively large, and the rock and soil in this region are exposed. The lack of vegetation leads to the slope being more vulnerable to rain erosion, which in turn increases the possibility of landslides. Region c may aggravate the surface deformation during excavation for construction purposes. Excavation and engineering construction lead to a lack of local vegetation, so the risk of landslides is high. There are residents’ construction and agricultural activities in the d region. The impact of human activities leads to a large cumulative variable in the region and a high level of landslide susceptibility. The surface deformation obtained by SBAS-InSAR technology is mutually confirmed with the results of our landslide susceptibility prediction, which further proves the accuracy of the susceptibility prediction results in this study.

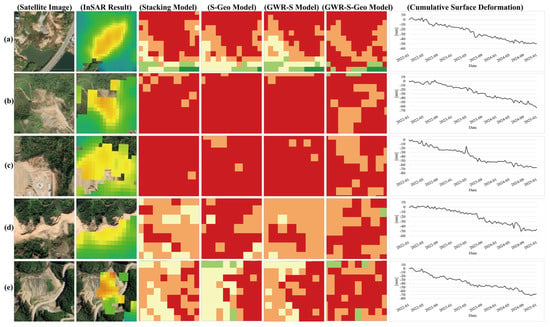
Figure 19. Satellite images of typical regions, deformation velocity, susceptibility results of the four ensemble models, and cumulative surface deformation. (a) region a; (b) region b; (c) region c; (d) region d; (e) region e.

6. Conclusions

This study took Fujian Province as the study area, constructed an ensemble learning model considering spatial heterogeneity, divided the study area, and optimized the factors of each subregion. Finally, the heterogeneous ensemble model GWR-S-Geo was constructed to assess the landslide susceptibility results. SBAS-InSAR technology was used to verify the prediction results, and the interpretability of the model was analyzed. The following conclusions are drawn.

(1)

Through the combination of FR, GWR, and clustering methods, the division of the study area was completed, and the spatial heterogeneity characteristics of landslide assessment factors were effectively explored.

(2)

The dominant factors of each subregion screened by Geodetector did not reduce the performance of the model while reducing the number of assessment factors. Through the screening of factors, the redundancy of data was reduced.

(3)

The heterogeneous ensemble learning model GWR-S-Geo considering spatial heterogeneity proposed in this study is superior to other models in performance, and the results of landslide prediction are more accurate.

However, there are still some limitations of this study. Due to the limitation of landslide data, the historical landslide point data we obtained lacked specific attribute information such as landslide area and affected persons. The lack of attributes of historical data may affect the assessment results. Secondly, this study did not explore whether the classification and quantity of assessment factors would affect the experimental results. Furthermore, Geodetector is influenced by factor classification when conducting factor detection, and this study did not sufficiently consider the impact of differences in assessment factor classification on the results during geographic detection. Therefore, future research will further optimize model performance in these aforementioned respects, providing more scientific methods for the processing of landslide susceptibility assessment factors.