Resource-Constrained 3D Volume Estimation of Lunar Regolith Particles from 2D Imagery for In Situ Dust Characterization in a Lunar Payload

Highlights

What are the main findings?

• Ellipsoid-based models more accurately estimate the 3D volume of lunar regolith particles from 2D images than spherical models.
• Micro-CT scans provide an effective method to validate the accuracy of 2D-based volume estimation techniques.

What is the implication of the main finding?

• This work improves the Lunaris mission’s capacity to accurately analyze lunar regolith adhesion in situ.
• The refined volume estimation directly enhances the reliability of adhesion force calculations, which are fundamentally dependent on particle mass derived from volume.

Abstract

Future lunar exploration will depend on a clearer understanding of regolith behavior, as underscored by adhesion issues observed during Apollo. The Lunaris Payload, a compact instrument developed in Poland, targets in situ assessment of lunar regolith adhesion to engineering materials using a resource-constrained optical approach. Here we introduce and validate six lightweight 2D-to-3D geometric models for estimating particle volume from planar images, benchmarked against the high-resolution micro-computed tomography (micro-CT) ground truth. The tested methods include spherical, cylindrical, fixed-aspect-ratio ellipsoid, adaptive ellipsoid, and Feret-based models and an empirically scaled voxel proxy. Using micro-CT scans of adhered simulant particles, we evaluate accuracy across >8000 particles segmented from 2D projections. Ellipsoid-based models consistently outperform the alternatives, with absolute percentage errors of 30–35%, while fixed-aspect-ratio variants offer strong accuracy–complexity trade-offs suitable for mass- and power-limited payloads. To our knowledge, this is the first comprehensive benchmarking of six 2D-to-3D volume models against micro-CT for bulk-adhered lunar regolith analogs. The results provide a validated, efficient framework for in situ dust characterization and reliable particle mass estimation, advancing Lunaris’ capability to quantify regolith adhesion and supporting broader goals in dust mitigation, ISRU, or habitat construction.

1. Introduction

The Moon, often envisioned as a natural extension of Earth’s space capabilities, is reachable within approximately three days. However, despite this proximity, direct human exploration has been limited to only 12 astronauts, as documented after the Apollo programme by Johnson [1]. Nonetheless, its nearby vicinity and the existing body of knowledge continue to make the Moon an intriguing subject for research and a promising foundation for a space-based economy, as noted by Crawford et al. [2].

More than five decades after the last human lunar landing in 1972 [3], interest in lunar exploration has been reignited. A new era of lunar exploration has emerged with an increasing number of private and governmental missions. This resurgence is largely driven by the pivotal discovery of water ice deposits on the lunar surface. Based on data from the Chandrayaan-1 probe, Pieters et al. [4] published a study detailing these findings, which profoundly altered our understanding of the lunar environment and its potential to support future human habitation and scientific endeavors.

Lunar regolith includes fine particles, characterized by irregular shapes, as described by Isachenkov et al. [5]. The concept of in situ resource utilization (ISRU), as discussed by Meurisse and Carpenter [6], involves harnessing lunar regolith to manufacture structures and other essential commodities directly on the Moon using locally sourced materials. This approach significantly improves the efficiency and sustainability of lunar exploration and resource utilization efforts, as described by Guerrero-Gonzalez and Zabel [7]. ISRU enables the extraction of oxygen, hydrogen, and metals [8], which can support long-term lunar habitation, according to Anand et al. [9]. The entire habitat structure could be built using sintered regolith, which exhibits promising properties for thermal storage and radiation protection according to Percentage Difference Calculation [10,11]. Furthermore, 3D printing technology can facilitate this process, as demonstrated by Taylor et al. [12], and the direct production of solar panels on the Moon using local materials is considered feasible, providing a sustainable energy source, as suggested by Freundlich et al. [13]. As Lin et al. [14] describe, remote observations of the regolith have been conducted using orbiters such as the Lunar Reconnaissance Orbiter [15] and rovers, for instance, the Yutu-2 rover [16], and samples were brought back by the Apollo, Luna, and Chang’e missions. However, in situ observations remain limited. Without direct measurements, neither the formation processes nor the true properties of the lunar regolith can be fully understood, as noted by Plescia [17]. Moreover, the safe human operations that would benefit lunar science the most still rely on robotic missions that provide critical information, as noted by Crawford et al. [18]. Lunar regolith poses a significant threat to human and robotic exploration of the Moon, making it crucial to understand how to mitigate its effects. The fine, abrasive, and adhesive nature of lunar regolith caused significant damage to the equipment during Apollo missions [19,20]. The challenges for ISRU include managing the adhesion and abrasion effects caused by this material, as discussed by Cannon et al. [21]. The thickness of the lunar regolith varies across the Moon, averaging approximately 5 m in the mare regions and 12 m in the highlands, according to Shkuratov [22]. Its unique properties, shaped by distinct erosive processes, make lunar regolith significantly different from terrestrial sand [23].

Many countries are returning to the Moon. China’s Chang’e-6 brought back the first far-side samples in 2024 [24]. India’s Chandrayaan-3 landed near the south pole in 2023 and is already sharing in situ results—for example, thermal profiles of high-latitude regolith [25]. Japan’s SLIM lander was also an example of such programs [26]. In the United States, NASA’s CLPS program opened regular commercial deliveries [27]. Private companies now fly or prepare small payloads alongside national missions. One such initiative that will gather more information on lunar regolith adhesion is the Lunaris payload, a lunar research project developed by a research group from AGH University of Krakow in partnership with Orbital-Space. This payload was selected through a global competition organized by Orbital-Space and is now scheduled to be aboard Astrobotic’s Griffin Mission 3, which is expected to launch no earlier than 2027 [28]. The primary objective of the Lunaris mission is to gather data on how lunar regolith adheres to different materials in situ. Due to strict mass and power constraints, the payload uses a compact optical system to capture 2D images of adherent particles for subsequent analysis. In contrast, three-dimensional imaging methods—such as X-ray computed tomography and LiDAR—are too bulky and resource-intensive (mass, power, and data throughput) to be accommodated within this small platform.

This study introduces techniques for approximating the 3D volumes of lunar regolith particles based on 2D image analysis, addressing a critical requirement for the Lunaris mission. Precise determination of particle volume is particularly significant in experimental methods aimed at measuring particle adhesion forces. Because the mass of individual regolith particles depends directly on their volume, assuming the density is known, accurate volume assessments are fundamental for reliable adhesion force calculations. For instance, in centrifugal adhesion measurement methods commonly employed in regolith particles adhesion research [29,30,31], the maximum adhesion force is calculated based on particle mass, rotational speed, and the radius of rotation. Given that such methods often necessitate rapid estimations of particle volume from 2D imagery due to experimental constraints, the accuracy of 3D volumes significantly influences the reliability of adhesion measurements. While some studies have estimated particle volume using 3D reconstructions, they typically focused on isolated particles, making them less representative of realistic conditions where particles are aggregated or adhered in bulk.

There are many techniques for acquiring 3D information from granular samples. For particles smaller than about $100 \mathsf{\mu }$m, however, practical non-destructive options narrow considerably. X-ray micro-CT remains the only method that retrieves the full internal volume of opaque grains at a relevant resolution and field of view; SEM-based serial sectioning is destructive, while optical methods recover only surface geometry with limited axial accuracy. Recent studies demonstrate that micro-CT yields robust per-particle volumes, shapes, and porosity for genuine lunar soils: Goguen et al. [32] reconstructed thousands of Apollo 11 grains and quantitatively compared their 3D morphologies with several simulants. Related pipelines on the Chang’e-5 collection further automate segmentation and particle-scale volume statistics [33].

This paper is structured as follows: The first section introduces the scientific background and motivations behind this study, highlighting the challenges of lunar exploration and the importance of accurately approximating the volume of lunar regolith particles. An overview of the Lunaris payload follows, detailing the mission design, operational concept, and key components. Subsequently, the materials and methods are described, including the experimental procedures, image acquisition, and post-processing techniques used for regolith analysis. Various volume calculation methods are then presented to estimate particle volumes from 2D images. Finally, the results are discussed in detail, comparing the performance of different methods and evaluating their implications for future lunar exploration and in situ resource utilization.

2. Lunaris Payload Overview

The Lunaris payload is a sub 1U-class, 3D-printed, deployable system for in situ optical sensing under mass (200 g) and power (0.5 W) budgets, illustrating how compact instrumentation can deliver exploration-relevant regolith characterization within smallsat constraints. Its primary structure is made of CRP Windform XT 2.0, a space-qualified material used in CubeSats and deployers [34]. The integrated structure includes a bus and a spring-loaded hatch supporting a camera and a dual-section LED lighting system. These components face a tiltable material sample plate, aligned with the camera using a stepper motor and monitored by Hall effect and optical endstop sensors. A render is shown in Figure 1. The electronics—an onboard computer, power unit, and motor controller—are housed within the bus. The payload operates by deploying the hatch, contacting the lunar surface with the sample plate, illuminating the contact area, capturing images, and transmitting data to Earth. It complies with stringent mission constraints, 200 g total mass, a maximum power consumption of 0.5W, and a compact 1U form factor, as described in [35].

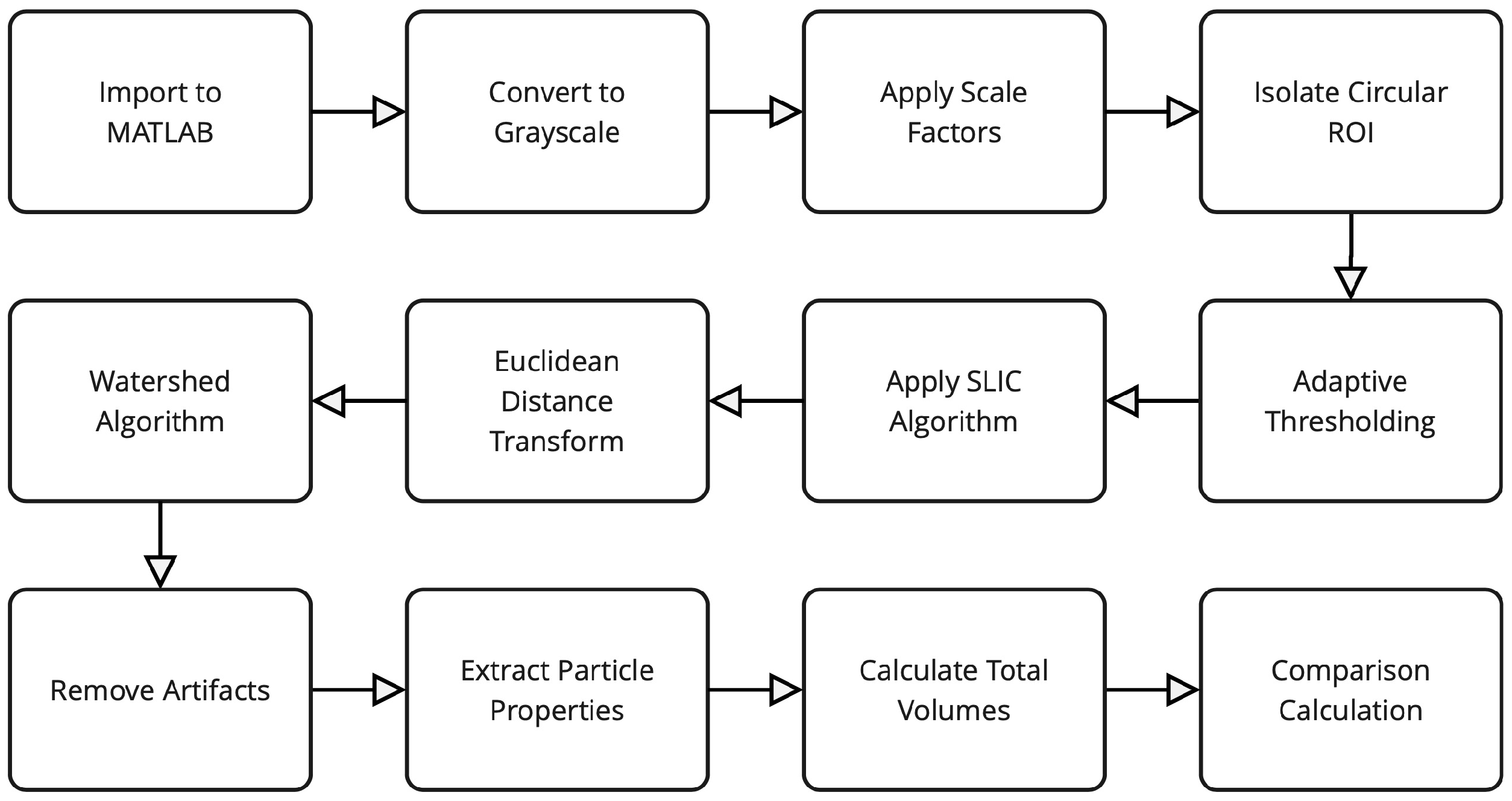
3. Materials and Methods

Due to constraints related to mass, power, and resource limitations, optical methods are employed to analyze the adhesion of lunar regolith particles in situ. The calibration method for the Lunaris payload uses a 3D scanner, specifically a GE phoenix v|tomex|m micro-CT system (Waygate Technologies, Munich, Germany). This approach aims to establish a precise calibration method for quantifying adhered particles of the regolith analog. By determining the 3D volume of particles deposited on PEEK samples, it is possible to estimate the total volume of adhered material. The calibration is performed only once and serves to validate the methodology used to approximate the 3D volume of regolith particles, thereby ensuring the reliability of subsequent optical measurements. Lunex Technology LX-M100 is a mare-type lunar regolith simulant. The mineralogical composition of this simulant is presented in

Table 1. Mineral composition of Lunex technology LX-M100 regolith analog.

Mineral Phase	Volume Fraction [vol%]
Plagioclase feldspar (Labradorite)	38.4
Pyroxene (Augite)	41.9
Olivine (Forsterite)	18.4
Titanomagnetite	1.0
Alkali Feldspar	0.3

.

3.1. Experimental Procedure

The experiment involved the following steps:

• Sieving the regolith to obtain a controlled particle distribution below 100 µm.
• Depositing the regolith onto 2 mm PEEK disk samples, which were then mounted on a glass rod.
• Attaching a piece of low-density foam to the glass rod, to which the sample with regolith was affixed using hot glue.
• Placing the glass rod in a self-centering, rotating holder to ensure stable positioning during scanning.
• Testing two different PEEK samples (B and C), with multiple scans per sample:
  • Sample B: Four scans;
  • Sample C: Three scans.

PEEK was selected due to its compatibility with the measurement technique, specifically its effective X-ray transparency. Scans were performed using a dual-lamp GE Phoenix v|tome|x|m tomograph (Waygate Technologies, Munich, Germany), during which each sample was rotated 360° to ensure comprehensive visualization. The sample was mounted on a glass rod and positioned within a self-centering holder inside the scanner. Centrifugal detachment tests conducted between scans caused a gradual reduction in particle volume, visible across successive images. Differences in the total number of scans between samples B and C are attributable to variations in the visualization approach. Sample C included an initial pre-dusting scan, which was subsequently excluded from comparative analysis. In contrast, scanning of sample B commenced after the dusting procedure, resulting in four scans for sample B and three scans for sample C, all of which were included in the analysis. The reconstructed 3D grayscale model represents the levels of X-ray absorption, which are largely dependent on material density. The voxel size achieved in this study was 2 µm³. Each sample scan took approximately one hour.

3.2. Post-Processing

After export, the scans were initially aligned in VGStudio MAX 3.5.1 and exported as .raw files. Three-dimensional scans can be processed in many ways, including with dedicated commercial software or custom deep learning pipelines; for example, Wu et al. [33] applied neural network-based segmentation to samples from the Chang’e-5 mission. In this study, we used Avizo Thermo Fisher Scientific 2020.3, which enabled segmentation and 3D visualization of the samples.

The workflow began by importing the .raw files and generating an initial rendering to verify data integrity. After validation, a median filter followed by interactive thresholding was applied to segment the regolith, leveraging its distinct X-ray attenuation relative to PEEK. The resulting segmentation is shown in Figure 2.

Due to variations in atmospheric conditions, such as pressure fluctuations that affect scan intensity, each sample was manually analyzed to ensure consistency. Subsequently, the ’separate objects’ function was applied to detach clustered particles. Following segmentation, labeling analysis was conducted, and the 3D volumes of the regolith particles were reconstructed. The overall process is depicted in Figure 3.

To enable quantitative analysis, image stacking was used to create a 2D representation of the segmented volume. The resulting image, shown in Figure 4, illustrates the segmentation results. Each color represents an individual particle. Following segmentation, the processed data—including particle volumes and shape descriptors—were exported for subsequent analysis.

Subsequent processing was performed in MATLAB 2024b, where the images were imported and converted to grayscale. To ensure accurate measurements, the scale was manually determined for each image, enabling the calculation of the pixel-to-micrometre ratio. A circular region of interest was applied to isolate the relevant portions of each image, minimizing the influence of background noise. The process is presented in Figure 5.

The scale factors used for conversion of exported images from Avizo are presented in

Table 2. Scale factors used for pixel-to-micrometer conversion.

Image	Scale Factor (µm/Pixel)
1B	3.8462
2B	3.7031
3B	3.8462
4B	3.8462
1C	3.7736
2C	3.6980
3C	3.7031

.

For particle segmentation, an adaptive thresholding approach was employed to facilitate binarization, followed by the application of the SLIC algorithm (Simple Linear Iterative Clustering) [36], which generated approximately 2300 superpixels per image with a compactness factor of 20. To refine the particle boundaries, the edges between the superpixels were set to zero in the binary image. The described process is presented in Figure 5.

In order to effectively separate touching particles, the Euclidean distance transform of the inverted binary image was computed, followed by the application of the watershed algorithm. A similar approach to that presented by Sun and Luo [37] was used to effectively address the problem of oversegmentation. Extended minima with a height threshold of 0.5 were imposed to identify particle cores, ensuring accurate segmentation. The watershed lines were subsequently set to zero in the binary image to finalize the particle delineation. Finally, any artifacts smaller than one pixel were removed through an area opening to enhance the segmentation accuracy.

Once segmentation was completed, the geometrical properties of the individual particles were extracted using the regionprops function. This allowed for the measurement of key morphological parameters, including particle area, major axis length, and minor axis length, initially in pixel units. These values were then converted to micrometres using the image-specific scale factor. The total particle volume per image was determined by adding the individual particle volumes, allowing for direct comparison with the reference dataset and facilitating an evaluation of the accuracy of the measurement.

4. Volume Calculation Methods

Estimating particle volume from two-dimensional projections is a widely used approach in granular material research, especially when direct three-dimensional measurements are unavailable. Various studies have proposed geometric approximations to infer the volume from segmented 2D images. One common approach models particles as spheres, relating volume to projected area, as described by Fayed and Otten [38]. Ellipsoidal approximations are also common, either with fixed aspect ratios derived from simulant datasheets [39] or based on fitted Feret diameters, as demonstrated in lunar simulant characterization by Zhang et al. [40]. Garboczi et al. conducted full 3D shape analysis of lunar regolith particles using X-ray CT and spherical harmonics, providing a comprehensive database of shapes, surface areas, and volumes for JSC-1A simulant particles [41]. More advanced approaches using principal component analysis on spherical harmonic coefficients have been proposed to statistically reconstruct 3D morphology from 2D observations [42]. Stereological corrections for bias in apparent size distribution have also been rigorously studied for planetary materials [43], and deep learning techniques have emerged as promising alternatives for estimating 3D descriptors from 2D slices [44]. Finally, a recent review emphasizes the strong correlation between 2D perimeter circularity and true 3D sphericity, providing a theoretical and experimental basis for estimating shape descriptors from planar images [39].

To quantify the volume of particles identified in the segmented images, in this study six methods are used, each based on different geometric assumptions about particle shape. Let $A_i$ represent the physical area of the i-th particle (in $\mathsf{\mu }{\mathrm{m}}^2$), derived from the area of the pixel scaled by the square of the scale factor (scale_factor²), where $i=1,2,\dots ,N$ and N are the total number of particles in an image. For methods using Feret diameters or ellipse axes, additional measurements are defined: $d_{\max ,i}$ and $d_{\min ,i}$ are the maximum and minimum Feret diameters, and $l_{\mathrm{major},i}$ and $l_{\mathrm{minor},i}$ are the lengths of the major and minor axes of the fitted ellipse, all in physical units ($\mathsf{\mu }\mathrm{m}$). The total volume for each method is computed as follows:

$$V_{\mathrm{total},\mathrm{method}}=\sum _{i=1}^N{V}_{i,\mathrm{method}},$$

where $V_{i,\mathrm{method}}$ is the volume of the i-th particle according to the specified method. In the following, each method is described and its corresponding volume equation for a single particle is provided.

4.1. Sphere Method

This method follows the principles outlined by [38], where the estimation of particle size approximates particles as spheres whose projected area equals the measured area $A_i$ for simplified calculations. The radius $r_i$ is derived from $A_i=\pi r_i^2$, so $r_i=\sqrt{{\displaystyle \frac{A_i}{\pi }}}$. The volume is then

$$V_{i,\mathrm{sphere}}={\displaystyle \frac{4}{3}}\pi {\left(\sqrt{{\displaystyle \frac{A_i}{\pi }}}\right)}^3$$

(1)

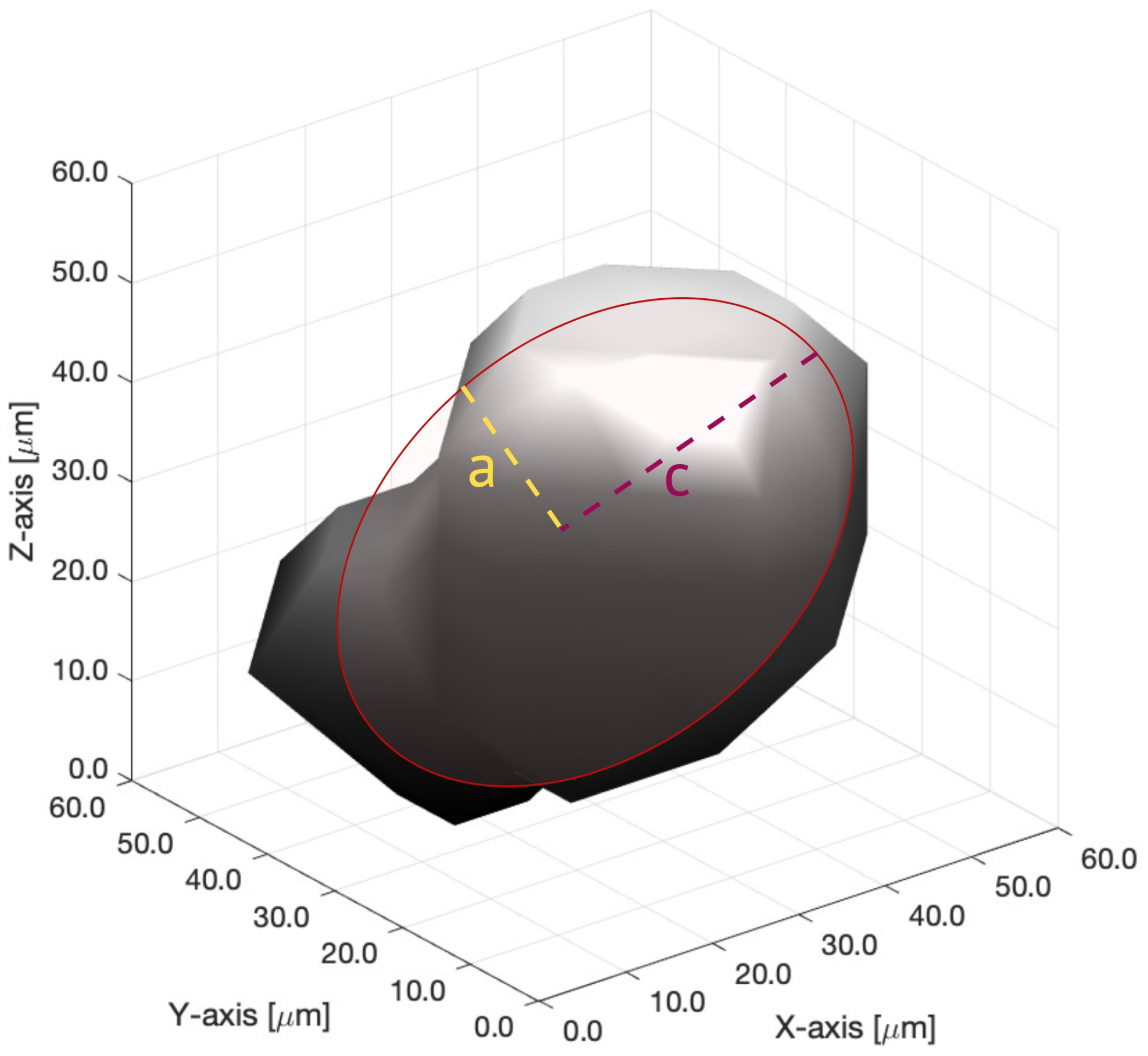
4.2. Ellipsoid with Fixed Aspect Ratio

Here, particles are modeled as ellipsoids [39], with two equal semi-axes and a third axis scaled by a fixed aspect ratio $\mathrm{AR}=0.5$, as specified in the technical datasheet of the employed regolith simulant. Assuming the projected equatorial area is $A_i=\pi a_i^2$ (where $a_i=b_i$), visible in the Figure 6, and the third semi-axis is $c_i=\mathrm{AR}\times a_i$, the volume is derived as follows:

$$V_{i,\mathrm{ellip}1}={\displaystyle \frac{4}{3\sqrt{\pi }}}\times \mathrm{AR}\times A_i^{3/2},\mathrm{where}\mathrm{AR}=0.5$$

(2)

This formulation adjusts the spherical volume by the aspect ratio, reflecting an oblate spheroid when $\mathrm{AR}<1$.

4.3. Feret Method

This approach uses the maximum and minimum Feret diameters to approximate each particle as an ellipsoid [40]. The maximum Feret diameter $d_{\max ,i}$ is the longest distance between two points in the convex hull of the particle, and the minimum Feret diameter $d_{\min ,i}$ is the smallest width perpendicular to this direction, both sized to physical units. The semi-axes are assigned as $a_i={\displaystyle \frac{d_{\max ,i}}{2}}$ and $b_i=c_i={\displaystyle \frac{d_{\min ,i}}{2}}$, yielding

$$V_{i,\mathrm{feret}}={\displaystyle \frac{4}{3}}\pi \left({\displaystyle \frac{d_{\max ,i}}{2}}\right){\left({\displaystyle \frac{d_{\min ,i}}{2}}\right)}^2$$

(3)

4.4. Cylinder Method

Particles are approximated as cylinders with a base area equal to the projected area $A_i$ and a height equal to the diameter of a circle with that area. If $A_i=\pi r_i^2$, then $r_i=\sqrt{{\displaystyle \frac{A_i}{\pi }}}$, and the height is $h_i=2r_i$. The volume is

$$V_{i,\mathrm{cylinder}}=A_i\times 2\sqrt{{\displaystyle \frac{A_i}{\pi }}}$$

(4)

4.5. Voxel Method

This method modifies the cylinder approach by applying an empirical scaling factor of 0.4, possibly to adjust for overestimation or to align with voxel-based measurements. The volume is

$$V_{i,\mathrm{voxel}}=0.4\times A_i\times 2\sqrt{{\displaystyle \frac{A_i}{\pi }}}$$

(5)

4.6. Adaptive Ellipsoid Method

This method models each particle as an ellipsoid with semi-axes derived from the lengths of the major and minor axes of the fitted ellipse ($l_{\mathrm{major},i}$ and $l_{\mathrm{minor},i}$), with the third axis set as half the minor axis. The semi-axes are $a_i={\displaystyle \frac{l_{\mathrm{major},i}}{2}}$, $b_i={\displaystyle \frac{l_{\mathrm{minor},i}}{2}}$, and $c_i={\displaystyle \frac{0.5\times l_{\mathrm{minor},i}}{2}}={\displaystyle \frac{l_{\mathrm{minor},i}}{4}}$, so

$$V_{i,\mathrm{adaptive}}={\displaystyle \frac{\pi }{12}}{l}_{\mathrm{major},i}{l}_{\mathrm{minor},i}^2$$

(6)

4.7. Percentage Difference Calculation

The percentage difference is used to compare the volume estimated by each method with the reference volume for each image. It quantifies the relative error of the estimate as a percentage. The calculation is defined as follows.

For each image i and volume estimation method m, the percentage difference $P_{m,i}$ is calculated using the formula

$$P_{m,i}=\left({\displaystyle \frac{|V_{m,i}-V_{\mathrm{true},i}|}{V_{\mathrm{true},i}}}\right)\times 100$$

(7)

where

• $V_{\mathrm{true},i}$ represents the reference volume of the particles in image i;
• $V_{m,i}$ is the volume estimated by method m for image i;
• $P_{m,i}$ is the percentage difference for method m on image i, expressed as a percentage.

The above methods have been applied for the experimental data processing.

Selection Rationale

(1) Lunar grains are irregular but moderately equant on average; fixed-AR and ellipse-based ellipsoids better reflect 3D priors than spheres [39,45]. (2) All six models compute from $A_i$ or two axes, enabling execution from a 2D image [35]. (3) Feret- and ellipse-based variants test the value of simple shape information obtainable from a single 2D view without bulkier range sensors.

5. Results

The volume estimation results for each image are presented in

Table 3. Comparison of volume estimation methods for each image. Volumes are in $\mathsf{\mu }$${\mathrm{m}}^3$, with the percentage differences from reference volumes indicated below estimated values. The closest estimations (lowest percentage) in each row are underlined. Green-low error, Yellow-moderate error, Red-high error.

Image	Particles	Reference Volume	Sphere	Ellipsoid_AR1	Feret Method	Cylinder	Voxel	Adaptive Ellipsoid
1B	1987	78,390,888	64,477,518 (17.75%)	32,238,759 (58.87%)	102,714,739 (31.03%)	96,716,277 (23.38%)	38,686,511 (50.65%)	32,636,083 (58.37%)
2B	2784	4,790,720	11,204,390 (133.88%)	5,602,195 (16.94%)	17,333,278 (261.81%)	16,806,585 (250.82%)	6,722,634 (40.33%)	5,688,187 (18.73%)
3B	709	836,632	1,665,194 (99.04%)	832,597 (0.48%)	2,600,915 (210.88%)	2,497,791 (198.55%)	999,117 (19.42%)	915,138 (9.38%)
4B	277	195,112	389,406 (99.58%)	194,703 (0.21%)	477,892 (144.93%)	584,109 (199.37%)	233,644 (19.75%)	185,263 (5.05%)
1C	2806	3,395,408	8,843,351 (160.45%)	4,421,675 (30.23%)	14,421,407 (324.73%)	13,265,027 (290.68%)	5,306,011 (56.27%)	4,883,668 (43.83%)
2C	116	20,328	56,541 (178.15%)	28,270 (39.07%)	61,914 (204.58%)	84,812 (317.22%)	33,925 (66.89%)	27,513 (35.35%)
3C	38	31,376	28,921 (7.82%)	14,460 (53.91%)	28,671 (8.62%)	43,382 (38.27%)	17,353 (44.69%)	12,588 (59.88%)

, where the estimated volumes are reported along with the percentage differences from the reference volume. The closest estimation for each sample is underlined.

A heatmap-style coloring scheme has been applied to indicate the accuracy of each method:

• Green (low error, ≤20%): Represents the most accurate estimations.
• Yellow (moderate error, 20–60%): Represents estimations with moderate deviations.
• Red (high error, >60%): Indicates significant deviations from the reference volume.

For images 3B and 4B, the smallest percentage errors were observed, with Ellipsoid_AR1 achieving deviations below 1%. In contrast, images 1B and 1C exhibited greater variations between methods, with errors exceeding 99% for some approaches. The Cylinder and Sphere methods generally produced the highest overestimations, while the Adaptive Ellipsoid and Ellipsoid_AR1 methods provided more accurate results in most cases. The Voxel method demonstrated moderate errors ranging from 19% to 66%, depending on the image. Across all images, Ellipsoid_AR1 achieved the most consistent accuracy, particularly for smaller volumes.

Continuing on from these results, sample 2B showed relatively low errors with Ellipsoid_AR1 ($16.94\%$) and Adaptive Ellipsoid ($18.73\%$), whereas the Sphere method drastically overestimated by $133.88\%$ and the Cylinder method soared to $250.82\%$. Likewise, for sample 2C, the Adaptive Ellipsoid approach produced the smallest error ($35.35\%$), followed closely by Ellipsoid_AR1 ($39.07\%$), while the Cylinder approximation reached $317.22\%$. Conversely, sample 3C offers a rare instance where the Sphere method yielded the lowest error ($7.82\%$). However ellipsoid-based models generally excel—particularly Ellipsoid_AR1.

6. Discussion

Adhesion measurement is a key aspect in the future of lunar exploration. During the Apollo era, numerous problems with regolith greatly impeded moon exploration. Adhesion and its mechanisms differ significantly from those on Earth: the high-vacuum Moon environment eliminates water-related capillary effects, leading to a fundamentally different behavior of lunar regolith particles. To prepare for these challenges, extensive experiments must be performed in simulated environments and then on the Moon.

Many novel techniques have been developed for particle characterization; however, in the context of adhesion studies, the forces typically scale with particle mass, making accurate volume estimation critical.

Among these methods is the Lunaris payload, which uses an onboard camera to visualize the adhered particles. Optical methods are frequently used in such studies because they are simple, fast, and suitable for in situ operations. Nevertheless, 2D-based volume estimation from projected images suffers from stereological biases and shape assumptions, which tend to overestimate the presence of large particles and underestimate true size distributions [43].

In contrast, 3D visualization methods such as X-ray CT offer substantially improved accuracy in determining true volume, shape, and surface area distributions, as demonstrated by Garboczi et al. [41], who analyzed over 130,000 JSC-1A regolith particles and extracted spherical harmonic shape descriptors from CT data.

Several recent studies have relied on simplified geometric assumptions. For instance, Barker et al. [31] estimated particle volumes using Feret diameters under a sphericity assumption, but reported significant deviation from actual mass due to irregular particle shapes. Oudayer et al. [46] and Sun et al. [29] also assumed sphericity in deriving volumes from a single representative diameter, which proved insufficient for accurate volume estimation in non-spherical simulants. Ilse et al. [47] used cross-sectional diameters to define equivalent spherical volumes, but their results indicated high uncertainty in size estimation for angular grains. To improve estimation accuracy, Tripathi et al. [39] conducted a large-scale analysis of granite and limestone particles and found a strong linear correlation between 2D perimeter circularity and true 3D sphericity, suggesting that accurate shape estimation may be achievable from a single 2D image. Ueda et al. [42] developed a spherical harmonic–PCA-based model to convert 2D shape descriptors into 3D volume and surface area estimates, achieving good agreement in DEM simulations of angle of repose. Chou et al. [44] applied deep convolutional neural networks (VGG16 and ACS-VGG19) to predict 3D fabric descriptors from 2D slice images, reaching mean absolute percentage errors (MAPEs) below 5% for key shape and volume metrics—although orientation descriptors were less accurate. In more constrained laboratory setups, a narrower particle size distribution can be achieved through dual-mesh sieving, which enables the use of spherical proxies or particle counter analyzers, as adopted by Wohl et al. [48], who demonstrated improved measurement reproducibility using mesh-sorted samples and optical counters. Ellipsoid_AR1 employs a constant aspect ratio. This method fits our dataset well. However, when the mean value of the aspect ratio is unknown, the adaptive ellipsoid method provides an alternative to calculate volume without a predefined ratio.

In samples 1B and 1C, many particles overlapped, preventing the optical method from capturing regolith grains beneath the top layer. As shown in Figure 7, a side-view micro-CT reconstruction reveals distinct differences in the distribution of regoliths in samples. Sample 1B contains the highest amount of regolith, while sample 4B contains the least. In particular, samples 1B and 2B exhibit substantial particle layering, further emphasizing the limitations of optical methods in densely packed samples.

Regolith grains are highly irregular, and the accuracy of measurement strongly depends on the orientation of the particles. In 2B, more grains were exposed, which yielded better measurements. For 3C, which contains only 38 regolith grains, the error was larger for Ellipsoid_AR1, whereas the spherical approach produced the smallest error.

Limitations and Future Work

This publication reports a first implementation constrained by the Lunaris payload mass and power budgets. These limits affected optics, illumination, and the absence of onboard processing. The current protocol assumes a near-uniform particle layer; however, partial overlap of grains can still occur and may bias area-based descriptors. Ground preparations and preliminary tests indicated a largely uniform surface rather than agglomerates, which reduces but does not eliminate this risk. The present analysis carries measurement uncertainty that we consider acceptable for this study’s comparative aim, namely to rank adhesion under controlled conditions rather than to deliver absolute values. Future work will broaden the operational envelope and reduce uncertainty. Experiments will be extended to vacuum environments with controlled dust loading, and the illumination geometry and spectrum will be varied to mitigate glare and shading effects. We will expand the set of regolith simulants and particle size distributions to probe material dependence. In parallel, advanced data-driven approaches such as machine learning and deep learning will be explored to enhance 2D-to-3D particle volume estimation, providing higher fidelity reconstructions and improved robustness in conditions where optical overlap or irregular geometries introduce errors.

7. Conclusions

This study evaluated six methods for 3D volume approximation of lunar regolith particles, with ellipsoid-based approaches proving most accurate. These findings improve the ability of the Lunaris mission to study regolith adhesion in situ, supporting future lunar exploration and ISRU applications. Unlike prior studies that estimate the volume of individual particles, our approach simultaneously evaluates the total volume of multiple particles identified in a single image, enabling scalable and rapid assessment suitable for adhesion-focused regolith experiments. While most adhesion studies still rely on spherical volume approximations, which often introduce significant errors, our results demonstrate the advantages of more flexible geometric models. These findings underscore the challenge of balancing methodological simplicity with the need for accurate volume estimation. By comparing six geometrically distinct models directly from segmented 2D images, our study offers a validated framework that can be extended with deep learning when higher fidelity is required. Although ellipsoid-based methods can underestimate volume when the particle count is small, they remain the most suitable when the aspect ratio is known. The adaptive ellipsoid method produces similar results and provides an alternative when aspect ratios are uncertain. Certain datasets with few particles or unusual size distributions may favour simpler shapes, but overall, spheres and cylinders tend to significantly overestimate volumes, whereas ellipsoid-based models provide superior and more consistent accuracy across diverse sample sizes.