Highlights
What are the main findings?
- Our algorithm can process airborne radar (AGPR/RES) data to image 2D/3D ice bed interfaces by tracing unobstructed refraction paths and directly calculating travel times.
- Based on Snell’s Law, when the incident angle of an electromagnetic wave exceeds the critical angle, its energy cannot penetrate the air–ice interface to reach the ice–rock interface or return to the receiver, which limits the effectiveness of imaging algorithms.
What is the implication of the main finding?
- By accounting for obstructions in refraction path tracing, the BP-based algorithm discussed here reduces imaging errors in 2D/3D subglacial interface detection.
- Through analytical and numerical analyses of radar signal propagation characteristics under the constraints of Snell’s Law, this research provides a new mechanistic explanation for the weak-focusing phenomenon that may occur in ice rock interface imaging.
Abstract
The deployment of traditional ground-penetrating radar (GPR) systems for ice detection on steep terrain presents substantial safety challenges for ground crews due to inaccessibility and hazardous working conditions. However, airborne GPR (AGPR) and radio echo sounding (RES) provide solutions to these difficulties. Assuming that ice is homogeneous, we introduce a perspective back-projection algorithm designed to process AGPR or RES data that directly searches for unobstructed refracted electromagnetic (EM) wave paths and focuses EM energy below the surface by computing path-specific travel times. The results from the 2D and 3D imaging tests indicate that the perspective back-projection algorithm can accurately image the ice–rock interface. However, Snell’s Law suggests that part of the energy may fail to propagate through the air–ice interface and reach either the ice–rock interface or the receivers in scenarios where the incident angle of an EM wave exceeds a certain threshold. This energy deficit can hinder the perspective back-projection algorithm from accurately imaging such ice–rock interfaces. Despite these limitations, the perspective back-projection algorithm remains a promising tool for imaging sub-ice interfaces in AGPR and RES ice detection.
1. Introduction
Significant transformations in water resources have significantly impacted Earth’s ecosystems [,]. Ice detection [], encompassing the examination of ice thickness, plays a crucial role in freshwater studies [,], along with the monitoring of ice deformation [] and the analysis of the physical and chemical properties of ice [,,,]. Ground-penetrating radar (GPR) [,,] technology has emerged as a highly effective geophysical technique for ice thickness surveying. Meanwhile, airborne ground-penetrating radar (AGPR) [,,] systems, utilizing advanced GPR technology on aerial platforms, significantly expanded operational reach and enabled the surveying of areas that were previously inaccessible. This system has several advantages, including exceptional efficiency, high resolution, and non-intrusiveness, making it highly applicable in various fields. However, complexities that arise from factors such as complex topography [] pose challenges to the effective utilization of AGPR.
In geophysical applications, reverse-time migration (RTM) [] techniques are widely used for the data processing of seismic data to correct imaging distortions of interfaces. RTM is based on the numerical simulations for the propagation of EM waves. In this process, received signals are retrogradely propagated at half the wave speed back into the subsurface medium. In GPR explorations [,,], RTM technology ensures that the EM energy is accurately focused at the underground reflection points, reducing imaging distortions caused by medium heterogeneity and interfacial undulations. However, applying RTM to large-scale airborne or spaceborne GPR glacier detection involves assessing long profiles (extending several kilometers) or extensive areas with significant depths (from tens to hundreds of meters). These large-scale assessments demand substantial computational resources, posing challenges for the practical application of RTM in surveys of solid water resources and related fields.
Radar systems mounted on satellites or aerial platforms play a critical role in ice detection due to their high efficiency and penetrative power [,,,]. The back-projection (BP) algorithm [,], known for its high-precision imaging capabilities in radar data processing, utilizes the time-delay information of radar signals to project scattered signals back to their origins, thus achieving signal focusing. Unlike the RTM algorithm [], which relies on computationally intensive EM wave modeling, the BP algorithm [] achieves imaging by stacking signals based on a pre-computed travel-time table. This travel-time table calculation, typically derived from ray-theoretical approximations of wave propagation. The focusing calculation at each grid node operates independently, the BP algorithm can achieve parallel computation, allowing for it to be used for detection tasks in homogeneous media. In non-homogeneous cases, such as the air–ice–rock model, refraction may occur []. Consequently, because EM waves with relatively low frequencies can penetrate ice to considerable depths, potentially reaching thousands of meters, directly applying the BP algorithm to ice detection data, without accounting for the effects of refraction, may result in inaccuracies in determining the wave travel paths. These inaccuracies may ultimately manifest as false anomalies within the imaging results.
Researchers [,,,] have applied the modified 2D BP algorithm to the processing of AGPR/RES data. However, techniques for calculating refraction paths in these algorithms have been developed based on the geometric assumptions of plain surfaces. For the two-dimensional case, Hélière et al. [] derived a mathematical relationship—a fourth-order equation—linking the spatial coordinates of the transmitter/receiver points, the coordinates of the subglacial scatterer, the coordinates of the refraction point, and the relative permittivity of the ice. This derivation was based on the assumptions of a plain ice surface. Although this equation can analytically calculate the coordinates of the refraction point for any given set of transmitter/receiver coordinates, subglacial scatterer locations, and values of the ice’s relative permittivity, it is fundamentally based on the assumptions that the ice surface is planar. Based on the same assumptions as the algorithm proposed by Hélière et al. [], the algorithm introduced by Kusk and Dall [] processes measured data in a 2D case by treating sections of the ice surface as planar. It then applies a coordinate rotation to each point, ultimately transforming the computational scenario to meet the conditions of a horizontal ice surface. Simultaneously, Kusk and Dall stated that, with a limited aperture and a flat horizontal surface, a small-angle approximation could be applied. Strictly speaking, Kusk and Dall approximated the actual undulating surface as planar and superimposed a small-angle approximation. Thereby, they provided an imaging solution applicable to gently undulating terrains, which is based on multiple approximations. The fundamental concept of Kusk and Dall’s algorithm [] is to reduce the 3D problem to a 2D framework and to approximate the undulating ice surface as planar. It is important to note that a sloped ice surface is not equivalent to an undulating ice surface. Although their algorithm can accurately handle a sloped ice surface, it cannot handle a truly undulating one. Zhang et al. [] proposed a self-correlation back-projection algorithm that can perform 2D imaging with refraction. However, Zhang et al. presumed the solution domain to be planar when calculating refraction point positions. A refraction point estimation method used in the algorithm developed by Qu et al. [] was designed for efficient BP imaging applications with a refractive index greater than or equal to 1, without accounting for total reflection conditions. Similarly to Zhang et al.’s algorithm, this method followed the same fundamental assumption that the surface was a planar.
During RES/AGPR surveys, particularly over mountain glaciers, the radar system may operate at elevated altitudes above an ice surface characterized by complex topography. Generally, typical glacier thicknesses might be several hundred meters. Hence, minor errors in refraction point positioning and surface normal vector estimation can collectively result in substantial inaccuracies in depth retrieval and target localization. Another imaging algorithm [], also based on BP, was developed for synthetic aperture radar (SAR) data to estimate glacier volume. For the same application in AGPR or radio echo sounding (RES) field exploration scenarios, this study proposed a perspective back-projection (PBP) algorithm. This algorithm does not rely on assumptions such as “the ice surface being approximately planar” or “constant flight altitude”. Instead, it mainly employs grid discretization combined with conditional judgments. The PBP framework has two key characteristics: (1) 2D and 3D imaging capability for AGPR and RES data; and (2) systematic detection of propagation path occlusions within the computational workflow. These advancements collectively enabled 2D and 3D subsurface imaging through the comprehensive integration of surface geomorphological constraints. These factors established PBP as a suitable sub-interface imaging methodology for AGPR and RES exploration.
In this study, we first introduce the RTM and BP algorithms and then describe the key steps of our proposed PBP algorithm. Subsequently, we describe several 2D and 3D air–ice–rock models and their corresponding EM forward modeling (FWD) results and compare the imaging profiles generated by the RTM and PBP algorithms. Finally, we discuss the performance of the PBP algorithm using additional numerical experiments and provide conclusions regarding its effectiveness.
2. Materials and Methods
2.1. General Scheme
To address ice–rock interface imaging challenges, in this work, we develop the PBP algorithm by integrating fundamental principles from the reverse-time migration (RTM) method and core strategies from the BP technique. For methodological clarity, we first introduced the essential concepts underlying RTM and BP before detailing the PBP framework.
Various RTM algorithms have been leveraged in seismic exploration to image subsurface interfaces []. Due to the high degree of similarity between the foundational principles of GPR application and seismic exploration, RTM algorithms have also been successfully adapted for use in GPR applications. The fundamental imaging theorem for the RTM in GPR was introduced as follows: Neglecting the effects of complex propagation paths and the influence of multiple scattered waves, the travel time of the emitted EM waves to the scatterer will be approximately equal to that of the scattered signals to the receiving antenna. According to this principle, if the signals received by the receiving antenna are transmitted backward at half of the phase velocity, the EM energy could be accurately concentrated at the scatter and interface locations, thereby achieving imaging.
Compared to the RTM algorithms, the BP algorithm has been widely used in SAR imaging. Grounded in the principles of EM wave propagation in homogeneous media, the core steps of the BP algorithm involve calculating the accurate time delay of scattering and projecting the corresponding echo signals into the imaging plane, which fundamentally aligns with the back-propagating echo signals to the scattering/reflecting points in the RTM algorithms. BP implementation consists of the following: (1) computing time delays for all transmitter–receiver pairs relative to a given node in the mesh grid (i.e., a media interface node); and (2) performing the weighted summation of delay-corresponding echoes to reconstruct an image of the scatter.
The PBP algorithm shared most fundamental steps with the BP algorithm; however, it incorporated some modifications, including refraction calculation and the detection of propagation path occlusion in time-delay computation. The application of the PBP algorithm in ice exploration could be predicated on several key principles: (a) When EM waves traverse different media, their paths will be subjected to refraction. (b) For simplicity, ice could be treated as a homogeneous medium in the air-ice–rock model. (c) Propagation within bedrock could be disregarded, given the limited penetration depth of the signal.
Principle (a) implies that the travel paths found by the PBP algorithm more closely approximate real-world cases than those from the BP algorithm. Meanwhile, principles (b) and (c) enable the simplification of the travel path calculations by confining refraction computations to a homogeneous ice medium.
Considering the aforementioned principle, the principal steps for the PBP algorithm are delineated as follows:
(1) The air–ice interface was discretized and the algorithm searched for the valid refraction point corresponding to each transmitter–receiver pair. The criteria for determining valid refraction points will be provided later.
(2) The coordinates of the refraction points, transmitters, and receivers were used to determine the travel paths for refractions and backscatterings.
(3) The validity of the travel paths (as shown in Figure 1) was determined. If an incident path intersected the air–ice interface at any location(s) except for the refraction point, it was deemed invalid. If a transmitted path intersected the air–ice interface at any location(s) except for the refraction point, only the segment between the refraction point and the nearest intersecting point was considered valid.
(4) The physical parameters of air and ice could be employed to compute the two-way travel time for each travel path.
(5) The travel times could be used to select the appropriate EM field components after pulse-compression processing, and these components could be summed to focus the energy onto the mesh grid.
(6) Steps (1)–(5) can be iteratively executed for every node in the mesh grid.
It should be emphasized that the PBP algorithm does not rely on assumptions such as “the ice surface being approximately planar” or “constant flight altitude” during the search for valid refraction points and travel time calculation. Instead, it employs a grid discretization method combined with conditional judgments to identify valid points, thereby minimizing the use of simplified conditions to maximize the accuracy of coordinate determination for valid refraction points and related parameters.
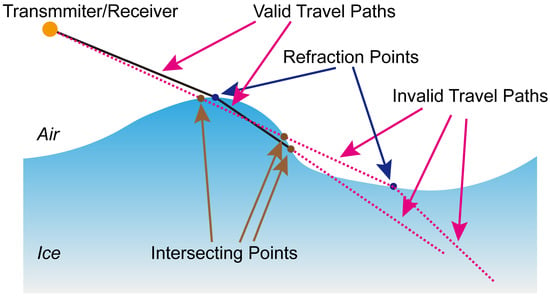
Figure 1.
Illustration of valid and invalid ray paths. The transmitter and receiver are collocated. Legend: Interface intersection points (brown dots), refraction points (blue dots), valid propagation paths (black solid lines), and invalid paths (magenta dashed lines).
2.2. Construction of the Air–Ice Model
Based on principles (b) and (c) mentioned above, the PBP algorithm did not account for rock. Thus, a two-layer model (air–ice model) was used for practical ice surveys. Within this framework, the air and homogeneous ice were separated by the air–ice interface, where refraction occurred. Consequently, travel paths and travel times were calculated within the domains of air and homogeneous ice.
2.3. Identification of Valid Refraction Point
Prior to identification, it was essential to define the concept of a valid refraction point. In this study, a valid refraction point refers to a point that, along with the transmitter and receiver, determines the reasonable incident, refracted, and reflected paths that are consistent with the classical electrodynamics. The validity of a refraction point was maintained by following fundamental principles derived from electrodynamics. Assuming that the refractive index of ice was n, the following inequalities and conditions had to be satisfied:
(a) cos(θi) > 0 and cos(θr) > 0, where θi and θr denote the incidence and refraction angles (Figure 2), respectively.
(b) In general, the incidence and refraction path had to be separated by a line, which coincided with the normal vector at the refraction point on the air–ice interface.
(c) The sine values of the angles, determined using Snell’s Law, had to be less than or equal to one.
(d) Specifically, if the incidence and refraction paths determined by the current refraction point were both collinear with the normal vector at the refraction point, then the current refraction point was also deemed valid.
(e) Except for the intersection at the refraction point, no other intersections could be present between the paths and the air–ice interface. Otherwise, the refraction point would be deemed invalid.
(f) In general cases, it could be possible to encounter multiple valid refraction points for a specific transmitter, receiver, and scattering node combination. Consequently, the PBP algorithm often handled instances of multiple refractions.
(g) A refraction point associated with an invalid incident path was considered invalid.
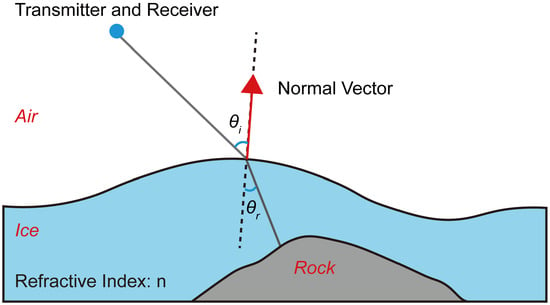
Figure 2.
Illustration of refraction.
2.4. Detection of Propagation Path Occlusions
The problem of detecting obstruction in an electromagnetic wave propagation path by undulating terrain can be reduced to determining if the path’s line-of-sight is intersected by the terrain. The proposed methodology involves the following steps: First, the propagation path is defined. This path is then discretized along its direction. Using known terrain elevation data, the ground height at each discrete point is interpolated. By comparing the vertical coordinate (height) of each path point to the interpolated terrain elevation at the corresponding horizontal position, we can determine if the point lies above or below the ground’s surface. Ultimately, an obstruction is detected if the relative spatial relationship—whether the path point is above or below the terrain—changes along the path.
2.5. Determination of the Travel Path
Once refraction points were determined, the spatial coordinates of the associated transmitters, receivers, and scattering points could be combined to derive the travel paths. Based on the known or assumed electrical properties of the media, the travel times for each path could be subsequently determined.
To simplify the analysis in this study, two further simplifications were introduced. First, we assumed that, for any given transmission-reception event, the transmitter and receiver shared the same antenna. Second, we hypothesized that the forward and reverse propagation signals followed identical travel paths.
2.6. Mesh Grid for Imaging
The PBP algorithm differs from the RTM algorithm in how it handles the imaging mesh grid. Theoretically, the PBP algorithm can perform computations on uniformly partitioned or non-uniformly partitioned grids of any density. According to the computation steps mentioned above, the PBP algorithm is insensitive to the mesh grid density, allowing for it to handle both sparse and dense grids without compromising computational stability. This flexibility was especially advantageous for long-distance profiling tasks spanning from tens to hundreds of kilometers or 3D imaging tasks for large areas.
3. Results
In this section, we conduct the FWDs of synthetic air–ice–rock 2D and 3D models to provide input data for the RTM and PBP algorithms. Then, the resulting imaging profiles from these algorithms are depicted and compared. The FWD algorithm is based on the finite-difference time-domain (FDTD) method [] and the convolutional perfectly matched layer (CPML) technique [].
The EM properties of the air, ice, and rock used in this study for the synthetic tests are detailed in Table 1. To maintain numerical stability and make sure that the signal was sampled accurately in space, the time step had to satisfy the Courant–Friedrichs–Lewy (CFL) condition [], where the grid step was not larger than a fraction of the highest-frequency wavelength. For a reasonable FDTD simulation, setting the highest-frequency wavelength to be larger than 20 cells size was sufficient []. The central frequency of the electromagnetic wave signal used in the simulation experiments of this study was 900 MHz (the signal is shown in the next section). To sufficiently suppress numerical dispersion and minimize the impact of computational errors on the imaging results, the time step and grid step were set as 4.1461 × 10−12 s and 2−9 m, respectively, for all 2D computations, while for the 3D simulations, the values were 3.3853 × 10−12 s and 2−9 m.

Table 1.
The electromagnetic properties of air, ice, and rock used in this study.
3.1. Signal
The Blackman–Harris window, a versatile windowing function, has been widely used for signal processing and spectral analysis [,]. In this study, the derivative of the Blackman–Harris window function (the central frequency was 900 MHz, as shown in Figure 3) served as the electric current source in the forward modeling of AGPR exploration. Notably, our decision to use this function as the current source was not driven by any specific theoretical or empirical justification. In addition, a single antenna was used for both transmission and reception.
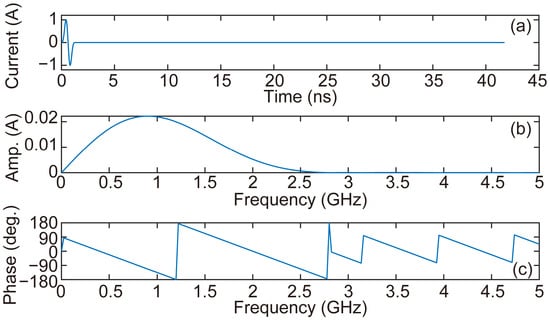
Figure 3.
Derivative of the Blackman–Harris window function in time domain and frequency domain. (a) Current signal and (b,c) current signal amplitude and phase, respectively.
3.2. Two-Dimensional Model Tests
In this work, we performed four 2D imaging tests. First, as shown in Figure 4a, we constructed a 2D model, designated as Model-2D-HAI-SIG, characterized by a horizontal air–ice interface and an approximately stepped ice–rock interface. The model dimensions were 6 m in the x-direction and 3 m in the z-direction, yielding 3072 cells along the x-direction and 1536 cells along the z-direction. The curve to determine the ice–rock interface takes the following form:
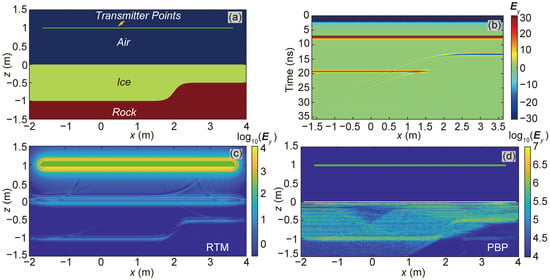
Figure 4.
The test of Model-2D-HAI-SIG. (a) Model-2D-HAI-SIG model; (b) FWD results of AGPR survey for the Model-2D-HAI-SIG model; (c,d) imaging results obtained using the RTM and PBP algorithms, respectively.
The transmitters were positioned on the green line in Figure 4a, each 1.0 m above the air–ice interface. We established 337 transmitter points in total, performing 337 2D FWD computations to construct the received signal profile, as shown in Figure 4b. The imaging results of RTM and PBP are shown in Figure 4c and Figure 4d, respectively. Both algorithms successfully reconstructed the ice–rock interface, though with lower energy focus at the steeply inclined part of the interface compared to the horizontal ones.
As shown in Figure 5a, we constructed a 2D model, designated as Model-2D-SAI-HIG, characterized by an approximately stepped air–ice interface and a horizontal ice–rock interface. The model dimensions were 4 m in the x-direction and the z-direction, yielding 2048 cells along both the x-direction and the z-direction. The curve to determine the ice–rock interface takes the following form:
where h is the vertical coordinate of the air–ice interface and x is the horizontal coordinate. The transmitters are positioned on the green line in Figure 5a, one meter above the peak elevation of the air–ice interface. We set up 225 transmitter points for this test, resulting in 225 two-dimensional FWD computations to construct the received signal (Ey) profile, as shown in Figure 5b.
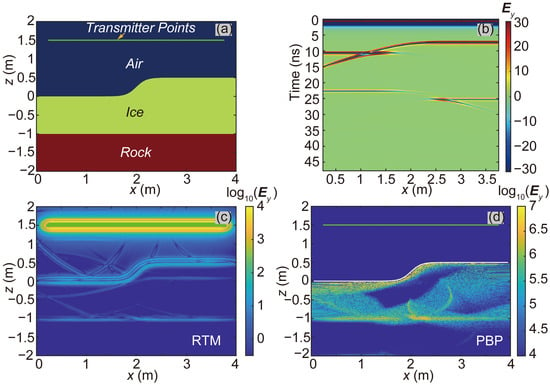
Figure 5.
The test of Model-2D-SAI-HIG. (a) Model-2D-SAI-HIG model; (b) FWD results of AGPR survey for the Model-2D-SAI-HIG model; (c,d) imaging results obtained using the RTM and PBP algorithms, respectively.
The imaging results of the RTM and PBP algorithms are shown in Figure 5c,d. The RTM and PBP algorithm successfully identified the undulating air–ice interface. The results from the RTM and PBP algorithms show obvious energy focusing on the interface between ice and rock. Notably, the rapid undulation of the air–ice interface in the central region of the model, similar to the effects of convex and concave lenses, can potentially diverge or focus the electromagnetic field and eventually affect the energy focus. However, this effect may have contributed to the analogous low-energy-focusing phenomena observed in the regions immediately beneath the rapidly undulating air–ice interface region in Figure 5c,d; the results support the effectiveness of the PBP algorithm in models such as Model-2D-SAI-HIG, which are characterized by undulating air–ice interfaces and horizontal ice–rock interfaces.
To validate the PBP algorithm in a more complex scenario, we subsequently constructed another 2D synthetic model, designated as Model-2D-SAI-SIG (Figure 6a), which featured approximately stepped ice–rock and air–ice interfaces. The model dimensions were 4 m in the x-direction and 3.5 m in the z-direction. Consequently, we achieved 2048 cells along the x-direction and 1792 cells along the z-direction. The equation for the air–ice interface and ice–rock interface is as follows:
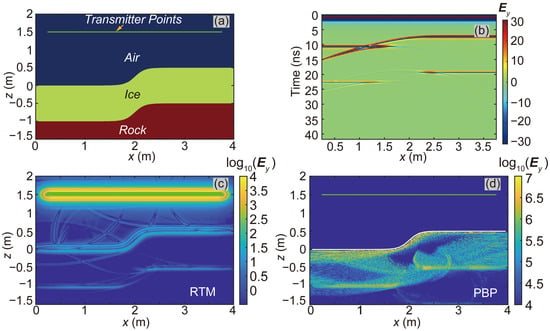
Figure 6.
Model-2D-SAI-SIG test. (a) model geometry (transmitter array on the green line); (b) AGPR forward modeling results; (c,d) results of the RTM and PBP algorithms, respectively.
The transmitters were positioned along the green line in Figure 6a and were placed 1.0 m above the peak elevation of the air–ice interface. We also established 225 transmitter points. The received signal (Ey) profile is depicted in Figure 6b.
Figure 5d and Figure 6c present the imaging results obtained from the RTM and PBP algorithms. Both algorithms achieved energy focusing on the ice–rock interface, but exhibited a limited resolution on the steeply inclined interface segments in this test.
Ice fractures are a common occurrence. To evaluate the performance of the PBP algorithm in detecting such fractures, we created a synthetic model, as shown in Figure 7a, named Model-2D-HAI-HIG-F. This model was designed with horizontal air–ice and ice–rock interfaces, and it incorporated ice fractures within the ice layer, providing a controlled scenario to test the algorithm’s fracture detection capabilities. The model dimensions were 4 m in the x-direction and 3 m in the z-direction. Accordingly, the model comprised 2048 cells along the x-direction and 1536 cells along the z-direction. There were three fractures in this model. The horizontal fracture is named F1, the tilted fracture F2, and the vertical fracture F3. F1 was set using the equation below:
F2 took the following form:
F3 took the following form:
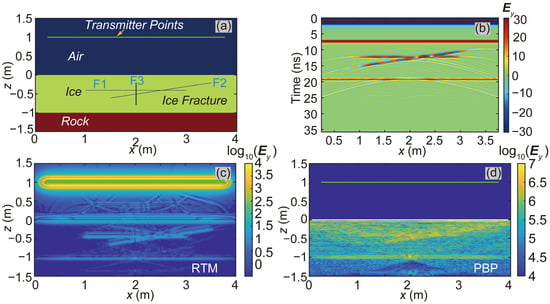
Figure 7.
The test of Model-2D-HAI-HIG-F. (a) Model-2D-HAI-HIG-F model; (b) FWD results of AGPR survey for the Model-2D-HAI-HIG-F model; (c,d) imaging results obtained using the RTM and PBP algorithms, respectively. The horizontal fracture is named F1, the tilted fracture is named F2, and the vertical fracture is named F3.
The transmitters were located along the green line in Figure 7a, one meter above the air–ice interface. We set up 225 transmitter points and illustrate the profile of the received signals (Ey) in Figure 7b.
Figure 7c,d shows the imaging results from the RTM and PBP algorithms. Both the RTM and PBP algorithms could accurately recover the ice–rock interface and the gently inclined fractures. However, when it comes to the vertical fracture, neither the RTM nor the PBP algorithm could provide obvious imaging results in this test.
3.3. Three-Dimensional Model Test
We also constructed a 3D synthetic model, designated as Model-3D-HAI-SIG (Figure 8a), to validate our algorithm’s performance under the 3D condition. To achieve balance among the validation requirements of the PBP algorithm, computational costs, and numerical stability of FWD, this 3D model featured a slightly depressed ice–rock interface, a horizontal air–ice interface, and a compact size in all dimensions. The model dimensions were 0.6 m in the x-direction, 0.4 m in the y-direction, and 1 m in the z-direction. The model was discretized into 308 cells along the x-direction, 205 cells along the y-direction, and 513 cells along the z-direction. The ice–rock interface geometry can be defined by the following equation:
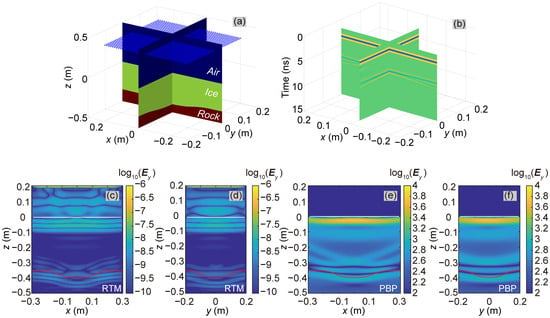
Figure 8.
Model-3D-HAI-SIG test. (a) Model geometry (transmitters are indicated by the blue dots); (b) AGPR forward modeling results; (c,d) results of the RTM algorithm (slices at y = 0, x = 0); (e,f) results of the PBP algorithm (slices at y = 0, x = 0).
We established 1763 transmitter points 0.4 m above the air–ice interface. These points are marked by blue dots in Figure 8a. The received Ey-component signal slices are shown in Figure 8b.
The imaging results obtained from the RTM and PBP algorithms are presented in Figure 6d and Figure 8c, respectively. Both algorithms successfully revealed the ice–rock interface. In this experiment, the geoelectric model used for the RTM calculations is the same as the one employed for the forward modeling. Under this premise, when the time series of the electromagnetic signal is reversed and input into the RTM process, the end of each EM sequence in the forward time series arrives at the interface positions earlier than the onset of each sequence. This leads to reflection and transmission phenomena, which can be observed in the RTM results in the vicinity above and below each interface position (the air–ice interface and the ice–rock interface). Additionally, it should be noted that the basic energy focusing strategy of the PBP algorithm can be considered a reduced version of the RTM algorithm’s. Therefore, the results obtained using the PBP algorithm are expected to be similar to, but not better than, those of the RTM algorithm.
4. Discussion
Backscattering refers to a phenomenon where waves, such as EM or sound waves, encounter obstacles or medium inhomogeneities during propagation, causing some of the energy to be reflected or scattered back toward the wave source. The PBP algorithm proposed in this work is an imaging algorithm that solely utilizes backscattering signals to achieve EM wave energy focusing. Previous studies [,] found that (1) the energy intensity of backscattered signals varied with the incident angle and that (2) a strong backscattered signal was generated when EM waves were incident perpendicular to a material interface. The 2D imaging results on the synthetic model demonstrate degraded performance at steeply inclined ice–rock interfaces. This limitation stems from the combined influence of interface geometries (both air–ice and ice–rock) and the physical properties of the icy medium, which, together, prevent the EM waves from achieving normal incidence at steeply inclined ice–rock interfaces. As a result, strong vertically backscattered signals could not be acquired from the steeply inclined interface, leading to the PBP algorithm’s impaired imaging capability. To validate the above hypothesis, this study employed Snell’s Law and geometric analysis to analytically determine the specific locations along the ice–rock interface in the electrical model of the Model-2D-HAI-SIG capable of producing strong backscattering, as well as the corresponding time instances in the B-SCAN profile exhibiting intense backscattering signals. Figure 9 shows the basic strategy for determining the specific locations along the ice–rock interface that is capable of producing strong backscattering. TR represents the transmitting/receiving antenna; gai denotes the arbitrary discrete grid nodes on the air–ice interface; vai represents the normal vector of the air–ice interface at point gai; and ptr-ai denotes the vector pointing from gai to TR. Assuming that the refractive index of ice is known, the transmission direction pai-ig, corresponding to all discrete nodes on the air–ice interface, can be calculated using Snell’s Law, excluding all cases of total reflection.
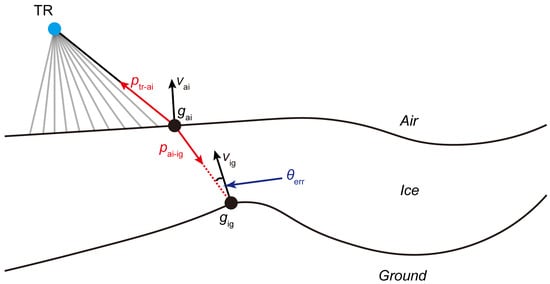
Figure 9.
Schematic diagram of the geometric strategy for identifying strong backscattering nodes at the subglacial interface. TR represent the transmitting/receiving antenna; gai denotes arbitrary discrete grid nodes on the air–ice interface; vai represents the normal vector of the air–ice interface at point gai; ptr-ai denotes the vector pointing from gai to TR; vig represents the normal vector of the ice–ground interface at point gig; pai-ig denotes the vector pointing from gai to gig; and θerr denotes the angle between the vectors of (−pai-ig) and vig.
Then, we could determine the position where pai-ig (the electromagnetic wave propagation path) intersects with the ice–ground interface, denoted as gig. At this point, the interface normal vector vig at position gig was compared with the propagation path pai-ig. If the angle θerr between them is smaller than a predefined threshold, the grid node on the ice–ground interface capable of producing strong backscattering is identified.
Considering that the identified grid node gig on the ice–ground interface capable of producing strong backscattering, along with the spatial coordinates of the corresponding gai and TR, the travel times of the electromagnetic wave propagation paths pai-ig and ptr-ai can be calculated.
These predicted positions and timings are explicitly marked by triangles in Figure 10. The analytical results demonstrate that, in this configuration, steeply inclined ice–rock interfaces could not generate significant backscattering due to the constraints imposed by Snell’s Law. Conversely, echoes from gently inclined or horizontal ice–rock interfaces dominated the B-SCAN profile.
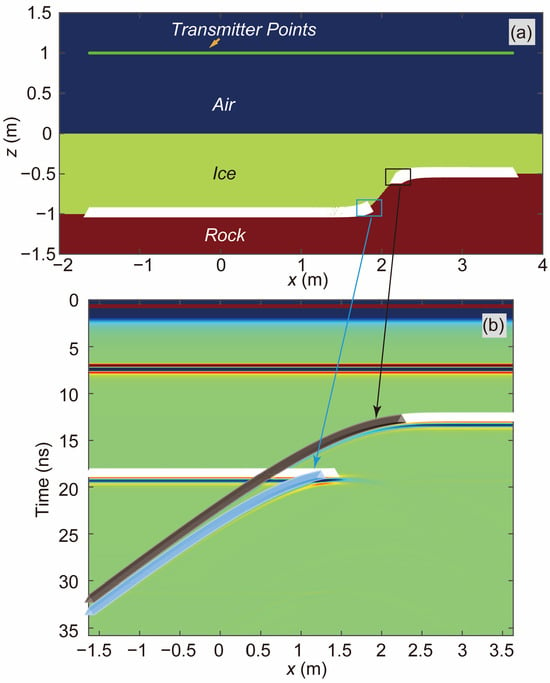
Figure 10.
Analysis of strong backscattering mechanisms. (a) Triangles indicate the analytically predicted locations along the ice–rock interface in Model-2D-HAI-SIG that satisfy the geometric conditions for strong backscattering; (b) triangles mark the corresponding time positions in the radar profile (B-SCAN) that were theoretically predicted to exhibit strong backscattering signals, matching the interface locations shown in (a); black triangles in (b) correspond to the white triangles inside the black box in (a); blue triangles in (b) correspond to the white triangles inside the blue box in (a).
Additionally, the normal vectors of all grid nodes on the ice–ground interface are provided in Figure 11b. Given the normal vector at any point on this interface, a straightforward calculation based on Snell’s Law can determine whether electromagnetic waves propagating along the normal vector direction at any nodal location can penetrate the air–ice interface and transmit into the air. The nodes corresponding to cases where such electromagnetic waves fail to penetrate are designated as IG. In Figure 11b, the curve segments associated with IG nodes are colored red. The horizontal coordinate ranges corresponding to these red-colored curve segments are bounded by two blue dashed lines in Figure 11a,b. It could be observed that the horizontal coordinate ranges of these red-colored curve segments corresponded to those of the grid nodes that were not marked by white triangles in Figure 10a. This phenomenon implied that some parts of the grid nodes on the ice–ground interface could not generate strong backscattered signals.
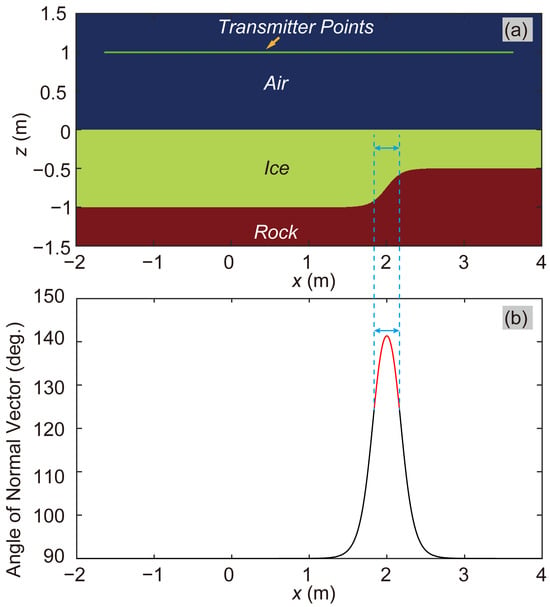
Figure 11.
Assessment of backscattering effectiveness and spatial distribution characteristics at the ice–rock interface. Segments of the ice–ground interface that could not generate strong backscattered signals are colored red. (a) The Model-2D-HAI-SIG and (b) the angle of normal vectors on the ice-rock interface.
To further verify that steeply inclined ice–rock interfaces in this case could not generate strong backscattering signals, we conducted an equivalent simulation experiment. In Model-2D-HAI-SIG, we densely arranged 337 radar signal transmission points along the steeply inclined ice–rock interface. This experimental design enabled the transmission of a quasi-planar EM wave approximately parallel to the steeply inclined ice–rock interface near its central region, with the propagation direction perpendicular to the interface. The inability of this plane wave to penetrate the air–ice interface constituted definitive proof that strong backscattering could not originate from the steeply inclined ice–rock interface. Six time-slices are shown in Figure 12. The results demonstrate that the quasi-planar wave emitting from the central region of the steeply inclined ice–rock interface failed to penetrate the air–ice interface. Notably, the simulation results reveal that certain EM waves successfully propagated through the air–ice interface into the air. Notably, as these waves originated from transmitter locations at both marginal zones of the steeply inclined ice–rock interface, the EM fields out of these edge locations could not be treated as components of the plane waves, but the EM fields from two-dimensional line sources. Thus, these phenomena did not weaken the conclusion that steeply inclined ice–rock interfaces in this case could not generate strong backscattering signals. In summary, the absence of strong backscattering from steeply inclined ice–rock interfaces likely constituted a key factor limiting the imaging performance of both RTM and PBP methods for these interfacial structures.
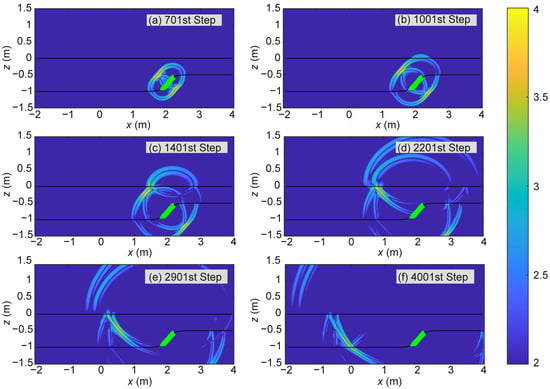
Figure 12.
Time-domain slices from the forward modeling computations of Model-2D-HAI-SIG, with transmitters arrayed on the steeply inclined interface. (a) 701st time step, (b) 1001st time step, (c) 1401st time step, (d) 2201st time step, (e) 2901st time step, and (f) 4001st time step, where green triangles indicate radar transmitter positions.
5. Conclusions
Firstly, the results of the imaging tests suggest that the PBP algorithm is capable of accurately determining the positions of 2D and 3D ice–rock interfaces below undulating surfaces.
Secondly, a critical divergence between the algorithms lies in their computational demands. The RTM algorithm, based on the FDTD method, is constrained by the CFL condition, requiring very small time and spatial steps to avoid instability and numerical dispersion. This inherently limits its practicality for large-scale problems. The PBP algorithm, however, is free from such constraints. By inheriting the flexibility of BP imaging, it can employ a spatially sparse mesh tailored to the application’s resolution needs, resulting in high computational feasibility and making it a practical choice for extensive 3D surveys.
Thirdly, the PBP algorithm could handle some combinations of air–ice and ice–rock interfaces, but not all. This was due to the refraction introduced by the AGPR or RES detection itself. Notably, when imaging the ice–rock interface, it was not essential to examine whether the ice–rock was steeply inclined, but it was necessary to determine whether the strong backscattering signal could propagate through the air–ice interface on the basis of Snell’s Law and ultimately be detected by the receivers.
Fourthly, compared to other BP algorithms, the PBP algorithm also detects obstruction in an electromagnetic wave propagation path by undulating terrain to reduce errors in imaging.
In summary, the PBP algorithm demonstrated its reliability and effectiveness as an interface imaging tool, not only for ice detection using AGPR or RES, but also for various penetrating detection scenarios that utilize the penetration capabilities of EM signals. In the future, we will consider incorporating denoising to enhance performance.
Author Contributions
Y.W.: Conceptualization, methodology, software, validation, writing—original draft. J.Z.: Conceptualization, formal analysis, supervision. J.P.: Investigation, funding acquisition. Y.L.: Conceptualization, supervision, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (grant number: No. 2022YFB3902602).
Data Availability Statement
Several 2D models and forward modeling results associated with this research are available and can be accessed via the following URL: https://1drv.ms/f/c/a48d583f70de6d0d/Em__VNGISK5CmDpMFi81MqcBkMc7zEpGqNNf4T7ivYiZSw?e=W8i6A5, accessed on 10 August 2025.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| GPR | Ground-penetrating radar |
| AGPR | Airborne ground-penetrating radar |
| RES | Radio echo sounding |
| EM | Electromagnetic |
| RTM | Reverse-time migration |
| BP | Back-projection |
| SAR | Synthetic aperture radar |
| PBP | Perspective back-projection |
| FWD | Forward modeling |
| FDTD | Finite-difference time-domain |
| CPML | Convolutional perfectly matched layer |
| CFL | Courant-Friedrichs-Lewy |
References
- Feng, X.; Fu, B.; Piao, S.; Wang, S.; Ciais, P.; Zeng, Z.; Lü, Y.; Zeng, Y.; Li, Y.; Jiang, X.; et al. Revegetation in China’s Loess Plateau is approaching sustainable water resource limits. Nat. Clim. Chang. 2016, 6, 1019–1022. [Google Scholar] [CrossRef]
- Peng, S.; Terrer, C.; Smith, B.; Ciais, P.; Han, Q.; Nan, J.; Fisher, J.B.; Chen, L.; Deng, L.; Yu, K. Carbon restoration potential on global land under water resource constraints. Nat. Water 2024, 2, 1071–1081. [Google Scholar] [CrossRef]
- Zakharov, I.; Puestow, T.; Khan, A.A.; Briggs, R.; Barrette, P. Review of River Ice Observation and Data Analysis Technologies. Hydrology 2024, 11, 126. [Google Scholar] [CrossRef]
- Farinotti, D.; Huss, M.; Fürst, J.J.; Landmann, J.; Machguth, H.; Maussion, F.; Pandit, A. A consensus estimate for the ice thickness distribution of all glaciers on Earth. Nat. Geosci. 2019, 12, 168–173. [Google Scholar] [CrossRef]
- Millan, R.; Mouginot, J.; Rabatel, A.; Morlighem, M. Ice velocity and thickness of the world’s glaciers. Nat. Geosci. 2022, 15, 124–129. [Google Scholar] [CrossRef]
- Yang, Z.; Xi, W.; Yang, Z.; Shi, Z.; Qian, T. Monitoring and Prediction of Glacier Deformation in the Meili Snow Mountain Based on InSAR Technology and GA-BP Neural Network Algorithm. Sensors 2022, 22, 8350. [Google Scholar] [CrossRef]
- Du, Z.; Cui, H.; Wang, L.; Yan, F.; Liu, Y.; Xu, Q.; Xie, S.; Dou, T.; Li, Y.; Liu, P.; et al. Characteristics of methane and carbon dioxide in ice caves at a high-mountain glacier of China. Sci. Total Environ. 2024, 946, 174074. [Google Scholar] [CrossRef]
- Huber, C.J.; Eichler, A.; Mattea, E.; Brütsch, S.; Jenk, T.M.; Gabrieli, J.; Barbante, C.; Schwikowski, M. High-altitude glacier archives lost due to climate change-related melting. Nat. Geosci. 2024, 17, 110–113. [Google Scholar] [CrossRef]
- Radić, V.; Hock, R. Regionally differentiated contribution of mountain glaciers and ice caps to future sea-level rise. Nat. Geosci. 2011, 4, 91–94. [Google Scholar] [CrossRef]
- Zamora, R.; Uribe, J.; Oberreuter, J.; Rivera, A. Ice thickness surveys of the Southern Patagonian Ice Field using a low frequency ice penetrating radar system. In Proceedings of the 2017 First IEEE International Symposium of Geoscience and Remote Sensing (GRSS-CHILE), Valdivia, Chile, 15–16 June 2017. [Google Scholar]
- Church, G.; Bauder, A.; Grab, M.; Maurer, H. Ground-penetrating radar imaging reveals glacier’s drainage network in 3D. Cryosphere 2021, 15, 3975–3988. [Google Scholar] [CrossRef]
- Grab, M.; Mattea, E.; Bauder, A.; Huss, M.; Rabenstein, L.; Hodel, E.; Linsbauer, A.; Langhammer, L.; Schmid, L.; Church, G.; et al. Ice thickness distribution of all Swiss glaciers based on extended ground-penetrating radar data and glaciological modeling. J. Glaciol. 2021, 67, 1074–1092. [Google Scholar] [CrossRef]
- Letamendia, U.; Navarro, F.; Benjumea, B. Ground-penetrating radar as a tool for determining the interface between temperate and cold ice, and snow depth: A case study for Hurd-Johnsons glaciers, Livingston Island, Antarctica. Ann. Glaciol. 2023, 64, 343–351. [Google Scholar] [CrossRef]
- Fu, L.; Liu, S.; Liu, L.; Lei, L. Development of an Airborne Ground Penetrating Radar System: Antenna Design, Laboratory Experiment, and Numerical Simulation. IEEE J-STARS 2014, 7, 761–766. [Google Scholar] [CrossRef]
- Rutishauser, A.; Maurer, H.; Bauder, A. Helicopter-borne ground-penetrating radar investigations on temperate alpine glaciers: A comparison of different systems and their abilities for bedrock mapping. Geophysics 2016, 81, WA119–WA129. [Google Scholar] [CrossRef]
- Tjoelker, A.R.; Baraër, M.; Valence, E.; Charonnat, B.; Masse-Dufresne, J.; Mark, B.G.; McKenzie, J.M. Drone-Based Ground-Penetrating Radar with Manual Transects for Improved Field Surveys of Buried Ice. Remote Sens. 2024, 16, 2461. [Google Scholar] [CrossRef]
- Chi, Y.; Mao, L.; Wang, X.; Pang, S.; Yang, Y. Three-dimensional numerical simulation and experimental validation of airborne ground-penetrating radar based on CNCS-FDTD method under undulating terrain conditions. Sci. Rep. 2024, 14, 22156. [Google Scholar] [CrossRef]
- Zhou, H.-W.; Hu, H.; Zou, Z.; Wo, Y.; Youn, O. Reverse time migration: A prospect of seismic imaging methodology. Earth-Sci Rev. 2018, 179, 207–227. [Google Scholar] [CrossRef]
- Delf, R.; Bingham, R.G.; Curtis, A.; Singh, S.; Giannopoulos, A.; Schwarz, B.; Borstad, C.P. Reanalysis of Polythermal Glacier Thermal Structure Using Radar Diffraction Focusing. J. Geophys. Res-Earth 2022, 127, e2021JF006382. [Google Scholar] [CrossRef]
- Liu, H.; Long, Z.; Tian, B.; Han, F.; Fang, G.; Liu, Q.H. Two-Dimensional Reverse-Time Migration Applied to GPR With a 3-D-to-2-D Data Conversion. IEEE J-STARS 2017, 10, 4313–4320. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, Z.; Lu, X.; Qin, S.; Wang, H.; Wang, X. Imaging of the Internal Structure of Permafrost in the Tibetan Plateau Using Ground Penetrating Radar. Electronics 2019, 9, 56. [Google Scholar] [CrossRef]
- Blankenship, D.D.; Moussessian, A.; Chapin, E.; Young, D.A.; Wesley Patterson, G.; Plaut, J.J.; Freedman, A.P.; Schroeder, D.M.; Grima, C.; Steinbrügge, G.; et al. Radar for Europa Assessment and Sounding: Ocean to Near-Surface (REASON). Space Sci. Rev. 2024, 220, 51. [Google Scholar] [CrossRef]
- Paolo, F.D.; Lauro, S.E.; Castelletti, D.; Mitri, G.; Bovolo, F.; Cosciotti, B.; Mattei, E.; Orosei, R.; Notarnicola, C.; Bruzzone, L.; et al. Radar Signal Penetration and Horizons Detection on Europa Through Numerical Simulations. IEEE J-STARS 2017, 10, 118–129. [Google Scholar] [CrossRef]
- Rémy, F.; Parouty, S. Antarctic Ice Sheet and Radar Altimetry: A Review. Remote Sens. 2009, 1, 1212–1239. [Google Scholar] [CrossRef]
- Tang, X.; Dong, S.; Luo, K.; Guo, J.; Li, L.; Sun, B. Noise Removal and Feature Extraction in Airborne Radar Sounding Data of Ice Sheets. Remote Sens. 2022, 14, 399. [Google Scholar] [CrossRef]
- Ulander, L.M.H.; Hellsten, H.; Stenstrom, G. Synthetic-aperture radar processing using fast factorized back-projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef]
- Zhang, H.; Shan, O.; Wang, G.; Li, J.; Wu, S.; Zhang, F. Back-projection algorithm based on self-correlation for ground-penetrating radar imaging. J. Appl. Remote Sens. 2015, 9, 095059. [Google Scholar] [CrossRef]
- Yegulalp, A.F. Fast backprojection algorithm for synthetic aperture radar. In Proceedings of the 1999 IEEE Radar Conference. Radar into the Next Millennium (Cat. No.99CH36249), Waltham, MA, USA, 22 April 1999. [Google Scholar]
- Hélière, F.; Lin, C.; Corr, H.; Vaughan, D. Radio Echo Sounding of Pine Island Glacier, West Antarctica: Aperture Synthesis Processing and Analysis of Feasibility from Space. TGRS Trans. Geosci. Remote Sens. 2007, 45, 2573–2582. [Google Scholar] [CrossRef]
- Kusk, A.; Dall, J. SAR focusing of P-band ice sounding data using back-projection. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar] [CrossRef]
- Qu, L.; Yin, Y.; Sun, Y.; Zhang, L. Efficient back projection imaging approach for airborne GPR using NUFFT technique. In Proceedings of the 2016 16th International Conference on Ground Penetrating Radar (GPR), Hong Kong, China, 13–16 June 2016. [Google Scholar]
- Wang, K.; Wu, Y.; Qiu, X.; Zhu, J.; Zheng, D.; Shangguan, S.; Pan, J.; Liu, Y.; Jiang, L.; Li, X. A novel airborne TomoSAR 3-D focusing method for accurate ice thickness and glacier volume estimation. ISPRS J. Photogramm. 2025, 220, 593–607. [Google Scholar] [CrossRef]
- Atef, E.; Demir, V. The Finite Difference Time Domain Method for Electromagnetics: With Matlab Simulations, 2nd ed.; SciTech Publishing, Inc.: Raleigh, NC, USA, 2015. [Google Scholar]
- Roden, J.A.; Gedney, S.D. Convolution PML (CPML): An efficient FDTD implementation of the CFS–PML for arbitrary media. Microw. Opt. Techn Let. 2000, 27, 334–339. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. On the Partial Difference Equations of Mathematical Physics. Ibm J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Chen, Y.; Tong, M.-S.; Mittra, R. Efficient and accurate finite-difference time-domain analysis of resonant structures using the Blackman–Harris window function. Microw. Opt. Techn Let. 1997, 15, 389–392. [Google Scholar] [CrossRef]
- Kivinukk, A.; Tamberg, G. On Blackman-Harris Windows for Shannon Sampling Series. STSIP Sampl. Theory Signal Image Process. 2007, 6, 87–108. [Google Scholar] [CrossRef]
- Champion, I. Simple modelling of radar backscattering coefficient over a bare soil: Variation with incidence angle, frequency and polarization. Int. J. Remote Sens. 1996, 17, 783–800. [Google Scholar] [CrossRef]
- O’Grady, D.; Leblanc, M.; Gillieson, D. Relationship of local incidence angle with satellite radar backscatter for different surface conditions. Int. J. Appl. Earth Obs. 2013, 24, 42–53. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).