Highlights
What are the main findings?
- Based on real BDS-3 ground tracking data in China, it is demonstrated that regional ground stations alone cannot achieve high-precision orbit determination (OD) for BDS-3 IGSO and MEO satellites. Incorporating onboard BDS-3 data from LEO enables high-precision OD for both types, with IGSO satellites showing significant improvement, reaching the same orbit determination accuracy as MEO satellites.
- A LEO ISL-assisted rapid joint orbit determination method for GNSS and LEO is proposed. Taking advantage of the reduced number of parameters required by LEO ISL data, the method uses a subset of LEO onboard GNSS data, together with regional ground GNSS data and LEO ISLs, to achieve fast full-network orbit determination of large LEO constellations and GNSS. Results show that this method significantly reduces estimation time without sacrificing orbit accuracy of GNSS or LEO.
What is the implication of the main finding?
- Integrating LEO onboard BDS-3 data allows GNSS operators to achieve high-precision orbit determination for both IGSO and MEO satellites, enabling more autonomous and reliable constellation maintenance without relying solely on ground stations.
- The LEO ISL-assisted rapid joint orbit determination method offers a practical solution for fast, full-network OD of large GNSS and LEO constellations, improving operational efficiency while maintaining orbit accuracy.
Abstract
BDS-3 faces challenges in achieving precision orbit determination (POD) due to the difficulty of establishing a globally uniform distribution of independently operated ground tracking stations. The use of onboard BDS-3 observations collected by low Earth orbit (LEO) satellites can partially mitigate this limitation. However, these observations introduce additional parameters, such as receiver clock offsets and carrier-phase ambiguities, which substantially increase the computational burden. Therefore, the capability of achieving real-time (RT) joint POD for BDS-3 and LEO satellites, relying solely on independently operated tracking stations, is greatly constrained. Currently, the inter-satellite links (ISLs) of BDS-3 have been successfully demonstrated to be effective for POD of BDS-3 satellites. In the future, ISLs of LEO satellites will also be incorporated as a measurement technique. Compared to traditional BDS-3 onboard observations, POD using ISLs involves almost no additional parameters other than the orbital states. Therefore, this paper proposes a method that combines onboard BDS-3 receivers on a subset of LEO satellites with LEO ISL observations to achieve rapid high-precision joint POD for BDS-3 and the full LEO constellation. To validate the proposed approach, measured BDS-3 data from regional ground stations in China are employed, together with simulated onboard BDS-3 data and simulated LEO ISL observations. All datasets were obtained over a three-day period, corresponding to days 131–133 of the year 2025. Firstly, it is demonstrated that, when relying solely on regional ground stations, the 24 MEO and 3 IGSO satellites of BDS-3 cannot achieve high-precision POD, with 1D RMS orbit accuracies of only 11.6 cm and 26.9 cm, respectively. Incorporating onboard BDS-3 data from LEO satellites significantly improves orbit determination accuracy, with 1D RMS accuracies reaching 4.9 cm for MEO and 6.4 cm for IGSO satellites, while LEO satellites themselves achieve orbit accuracy better than 5 cm. Subsequently, the computational burden introduced by onboard BDS-3 data from LEO satellites in joint POD is further assessed. On average, incorporating onboard BDS-3 data from 10 LEO satellites adds approximately 6780 parameters to be estimated, substantially increasing computation time. When onboard BDS-3 data from 20 LEO satellites are included, the achieved BDS-3 orbit accuracy shows negligible degradation compared to using data from all LEO satellites, with 1D RMS accuracies of 4.9 cm and 6.7 cm for MEO and IGSO, respectively. Meanwhile, the processing time for a single batch least squares (BLSQ) solution decreases dramatically from 27.0 min to 5.7 min. Increasing the number of LEO satellites to 30 further improves BDS-3 orbit accuracy, mainly due to the enhanced orbit precision of the LEO satellites. After incorporating LEO ISLs, LEO satellites achieve orbit accuracy in the 1D direction of approximately 1 cm, regardless of whether their onboard BDS-3 data are used. In summary, the proposed approach significantly reduces computational burden while ensuring orbit determination accuracy for both BDS-3 and LEO satellites. This approach is more likely to realize real-time joint POD of BDS-3 and LEO satellites based on large-scale LEO constellations.
1. Introduction
Currently, the concept of using LEO constellations to achieve global internet communication, navigation, and other services is attracting increasing attention, with large-scale LEO constellation projects such as Iridium [1], SpaceX [2], and CentiSpace [3] being proposed. LEO constellations are expected to enhance the overall performance of Global Navigation Satellite System (GNSS) services by broadcasting navigation signals. The higher velocity of LEO satellites can reduce the convergence time of Precise Point Positioning (PPP) [4,5,6,7,8]. Meanwhile, due to lower orbital altitude, LEO satellites provide stronger downland signals, which can overcome the weak or absent Global Navigation Satellite System (GNSS) signals in complex urban environments [9]. Many researchers have conducted extensive studies on LEO-enhanced GNSS (LeGNSS) positioning [10,11,12,13]. Precise orbit determination (POD) of LEO satellites is essential for the above applications. It is usually achieved either by joint POD of GNSS and LEO (the one-step method) [14] or by determining LEO orbits separately using existing GNSS precise products (the two-step method) [15]. Rim et al. [16] compared POD results of the T/P satellite using both methods and found the one-step method achieved better orbit accuracy. Therefore, this study mainly focuses on one-step POD of BDS-3 and LEO.
Huang et al. [17] performed joint POD using GPS satellites and seven LEO satellites (including GRACE-A/B, Jason-2/3, and Swarm-A/B/C). The results showed that introducing LEO satellites improved GPS orbit accuracy by 34% based on data from 26 global stations. Li et al. [18] conducted a joint POD of LEO-GPS-BDS using FY-3C/D satellites. The results indicated that adding two LEO satellites reduced GPS and BDS orbit errors by 25%, while the 1D orbit overlap error of the FY-3C/D satellites was better than 5 cm. Due to the current lack of measured LEO constellation data, most LeGNSS research based on LEO constellations relies on simulations. Li et al. [19] designed six different LEO constellations based on simulated GNSS observations. The results showed that introducing LEO constellations significantly improved the POD accuracy for all GNSS satellites by over 70%. Li et al. [20] simulated a 66-satellite Iridium constellation to explore real-time LeGNSS applications. This showed that using a subset of LEO satellites for LeGNSS is the optimal operation mode for real-time PPP. She et al. [21] proposed a simplified joint POD method that greatly reduced processing time without significant loss of GPS orbit accuracy. Lai et al. [22] and Zheng et al. [23] further investigated the performance of joint POD in filter-based real-time orbit determination. Their results showed that LEO satellites can significantly shorten GPS orbit convergence time and complement ground stations in achieving highly accurate GPS orbit solutions. In summary, current joint POD schemes based on onboard GNSS observations and ground GNSS observations can achieve centimeter-level accuracy for both GNSS and LEO orbits. However, computation time remains one of the major limitations for practical real-time applications.
Currently, inter-satellite links (ISLs) have recently been introduced into GNSS satellite POD as a high-precision measurement technique. This application effectively reduces reliance on ground tracking stations and enhances the overall performance of the system. By the end of 2016, all 31 GPS satellites were equipped with autonomous navigation capability. Without support from ground control systems, they can provide autonomous navigation services for up to 180 days [24]. In addition to GPS, Galileo and GLONASS have also actively developed inter-satellite link programs [25,26]. BDS-3 is also equipped with inter-satellite link terminals [27]. In terms of autonomous orbit determination, Tang et al. [28] studied centralized autonomous orbit determination of four BDS-3 experimental satellites with anchored stations. The results showed that the radial overlap arc accuracy was better than 15 cm for Inclined Geosynchronous Orbit (IGSO) satellites and better than 10 cm for Medium Earth Orbit (MEO) satellites. Ren et al. [29] studied the case without anchored stations and demonstrated that using a priori orbit constraints can resolve the rank deficiency problem in orbit determination relying solely on inter-satellite links. When the a priori orbit accuracy is 10 m, the satellite position accuracy is better than 2 m. In joint orbit determination, Zhao et al. [30] enhanced regional ground station POD using inter-satellite links. Satellite laser ranging (SLR) residuals indicated radial accuracy better than 10 cm. Orbit overlap comparisons showed radial accuracy of 1.6 cm, along-track accuracy of 8.8 cm, cross-track accuracy of 8.7 cm, and standard deviation (STD) of clock offset error of approximately 0.10 ns. Feng et al. [31] proposed a POD method for BDS-3 that jointly utilizes ground stations, LEO onboard data, and inter-satellite link data. Incorporating inter-satellite link data on top of ground stations and LEO satellites can further improve orbit determination accuracy. Yang et al. [32] pointed out that the currently under-construction LEO constellations have a strong demand for autonomous orbit determination, requiring ISL equipment for independent orbit and clock offset estimation. As a result, preliminary studies on the application of ISLs for LEO orbit determination have been conducted. Li et al. [33] employed a kinematic orbit determination method to verify the independent orbit determination capability using LEO ISL data. The results showed that higher ranging accuracy and a greater number of links lead to improved orbit precision. For a constellation of 120 LEO satellites, the average 3D orbit error was 0.010 m, while for 192 satellites, the error was 0.006 m. He et al. [34] investigated the performance of joint POD using observations from ground tracking networks of varying scales combined with ISLs. The results demonstrated that with ISL observations, even a small regional ground network can achieve orbit determination accuracy comparable to a global network of 60 stations. Li et al. [35] further confirmed that the combined use of onboard, ground LEO observations, and LEO ISL data provides significant advantages in LEO POD, improving orbit accuracy by approximately 64.9% compared to using onboard GNSS observations alone.
In summary, LEO constellations, as a current focus of aerospace development, will in the future be equipped with ISL payloads to supplement data from onboard receivers and ground tracking stations. However, current research on POD for LEO satellites mainly concentrates on processing onboard GNSS data. Due to the high velocity of LEO satellites, GNSS signals frequently experience loss of lock and reacquisition on the onboard receivers. This leads to a large number of ambiguity parameters that need to be estimated. The joint POD based on onboard GNSS data faces substantial computational burdens, making real-time applications difficult to achieve. In contrast, ISL data require estimating only one set of constant delay parameters. Therefore, this paper proposes a method that uses onboard GNSS data from a subset of LEO satellites within a large-scale constellation to establish fixed spatial references; this is then combined with LEO ISL data to achieve rapid joint POD for both GNSS and all LEO satellites. This approach provides a valuable reference for future real-time joint POD models of BDS-3 and LEO constellations.
In this paper, a comprehensive evaluation of the joint POD performance of BDS-3 and LEO satellites enhanced by LEO ISLs is conducted. First, the simulation strategies for the BDS-3 and LEO constellations used in this study are introduced, followed by the simulation models for onboard BDS-3 and ISL observations. Then, the relevant models and strategies for joint POD are presented. In Section 4, the joint POD results combining measured regional ground BDS-3 data and simulated onboard BDS-3 data are first derived, further demonstrating the performance of the proposed rapid joint POD method. Section 5 provides a discussion of the results, and Section 6 concludes the paper.
2. Simulation and Method
2.1. BDS-3 and LEO Constellation Design
To evaluate the performance of BDS and LEO joint POD enhanced by LEO ISLs, a constellation consisting of 24 BDS-3 MEO satellites, 3 IGSO satellites, and a Walker 60/10/1 LEO constellation was designed.
Based on the nominal parameters of the BDS-3 constellation, the entire BDS constellation consists of 3 Geostationary Earth Orbit (GEO), 3 IGSO, and 24 MEO satellites [36]. This study simulates the BDS-3 constellation using the final orbit and clock products from the Wuhan University Multi-GNSS Experiment (MGEX) Analysis Center [37]. This approach ensures that the simulated BDS constellation closely matches the actual situation. It also allows for the incorporation of more realistic dynamic model errors, thereby making the POD results more reliable. Additionally, since measured BDS-3 ground data are used in this study, it is necessary to employ the final orbit and clock products in the simulation. It is worth noting that BDS-3 GEO satellites were not considered in this study and, therefore, were not simulated.
Previous studies have shown that a number of 60 LEO satellites enable LeGNSS POD to reach optimal accuracy, with sun-synchronous orbits providing better augmentation effects than polar orbits [19]. To evaluate the contribution of LEO ISLs observations to joint POD, a Walker 60/10/1 LEO constellation was designed with an orbital altitude of 1500 km and an inclination of 97°. The detailed nominal parameters for BDS-3 and the LEO constellation are listed in Table 1. Table 2 presents the orbital plane distribution of satellites in the Walker-Delta (60/10/1) constellation at the initial epoch. The complex dynamic models used for the LEO constellation configuration are summarized in Table 3. The 3D and 2D views of the designed LEO constellation are shown in Figure 1.

Table 1.
Nominal parameters of the BDS-3 and LEO constellation configurations.

Table 2.
Orbital plane distribution of satellites in the Walker-Delta (60/10/1) constellation at the initial epoch.

Table 3.
The dynamic models applied in the LEO constellation configurations.

Figure 1.
Three-dimensional and two-dimensional views of the Walker 60/10/1 constellation (left: 3D view; right: 2D view).
2.2. Onboard BDS-3 Observation Simulation
Since the onboard BDS-3 receivers have not yet been applied to large-scale LEO constellations, to evaluate the performance of BDS and LEO joint POD enhanced by LEO ISLs, the onboard BDS-3 observation data were simulated. The simulation model for the onboard BDS-3 observation data is described as follows:
In the above equations, the superscripts and subscript and denote the BDS-3 satellite, the LEO satellite, and the signal frequency, respectively. and represent the pseudorange and carrier phase observations. is the distance between the antenna phase centers of the BDS-3 satellite and the onboard receiver. Therefore, it was necessary to apply corrections for the phase center offset (PCO) and phase center variation (PCV) of the BDS-3 satellite antennas to the satellite coordinates. The BDS-3 satellite PCO and PCV corrections were taken from the values in the igs20.atx file (https://files.igs.org/pub/station/general/igs20.atx accessed on 6 August 2025), while the PCO and PCV for the LEO satellites were set to zero. is the speed of light in vacuum. and are the clock offsets of the BDS-3 satellite and the onboard receiver, respectively. The BDS-3 satellite clock offsets were obtained from the Wuhan University MGEX Analysis Center’s final clock products [37]. The LEO satellite receiver clock offset was simulated as white noise. It is worth noting that since the LEO satellites are located above the troposphere, the onboard BDS-3 observations are not affected by the tropospheric delay. represents the ionospheric delay on the propagation path for frequency of the LEO satellite. It affects both the pseudorange and carrier phase measurements with the same magnitude but opposite signs. The first-order ionospheric delay was calculated using the ionospheric grid files published by CODE [38] through temporal and spatial interpolation. For onboard observations, it was assumed that charged particles are uniformly distributed across different altitudes, and the delay was scaled according to the propagation height relative to the total ionospheric height. is the carrier phase integer ambiguity corresponding to the wavelength . and denote the measurement noise of the pseudorange and carrier phase observations at frequency for the onboard BDS-3 data, which were set to 2 m and 8 mm, respectively, in this study. Additionally, relativistic corrections, phase cycle slips, and tidal offsets were considered in the simulation.
2.3. ISL Observation Simulation
Due to the lack of available real ISL observation data from LEO constellations, we simulated the ISL observation data based on the LEO constellation design described in Section 2.1. Generally, ISLs can be categorized into four-link and full-link configurations. The four-link configuration means that each LEO satellite is connected only with the two adjacent satellites in the same orbital plane and the two nearest satellites in the adjacent orbital planes. The full-link configuration means that each satellite establishes inter-satellite ranging measurements with all visible LEO satellites [33]. This study adopted the full-link configuration due to its superior enhancement capabilities. Before simulating the inter-satellite link (ISL) data, the visibility between each pair of LEO satellites needs to be calculated and evaluated. An ISL can be established only when the visibility condition is satisfied. The visibility calculation formula is given as follows.
In the equation, the subscripts and represent different LEO satellites. The vector denotes the position vector from the Earth’s center to the LEO satellite, and represents the Earth’s average radius. This formula calculates the distance between the midpoint of the two satellites and the Earth [33]. Obviously, if this distance is greater than the Earth’s radius, it indicates that the two satellites are mutually visible. If a pair of LEO satellites satisfies the above condition at the current epoch, it is considered that an ISL can be established between them at that time. The ISL observation data were then simulated, which can be described by the following formula.
In the equation, represents the ISL observations. denotes the sum of the receiving and transmitting delays of the inter-satellite equipment. This term is used in the orbit determination equations for BDS-3 ISL observations and is known to have high stability. According to Pan et al. [39], this parameter can be treated as a constant and calibrated out prior to data processing;, thus, it is not estimated during data processing. Therefore, this error was not considered in the ISL simulation. represents the measurement noise of the inter-satellite link data. According to the study by Li et al., when the precision of LEO ISLs reaches 1 cm, the improvement in LEO orbit determination accuracy is close to optimal [35]. Meanwhile, 1 cm precision maintains a high level of improvement while requiring less demanding equipment and offering better cost efficiency, thus making it more suitable for deployment in large-scale LEO constellations. Therefore, in this study, the measurement noise of LEO ISL data was set to 1 cm.
It should be noted that ISL observation data consist of two one-way ranging measurements, which are generated at different times. Therefore, it is necessary to epoch-normalize these measurements to obtain two one-way observations at the same epoch. Since our work is simulation-based, and to simplify the data preprocessing, we directly simulated the inter-satellite distances with measurement noise included, rather than simulating the two one-way observations separately.
3. Joint POD Methods and Strategy
3.1. Joint POD Methods
Based on the traditional LeGNSS joint POD model, the LeGNSS joint POD model with LEO ISLs can be easily derived. In BDS-3 data processing, the ionospheric delay is eliminated by using the ionospheric-free (IF) combination of dual-frequency codes and phase observations, and in LEO ISLs data processing, the ionospheric delay is not considered. For simplicity, the joint POD model with LEO ISLs is expressed as follows:
where the subscripts and denote different LEO satellites. , , and denote the ground BDS-3, onboard BDS-3 receiver, and inter-satellite link observation, respectively. , , and represent their corresponding measurement errors, respectively. refers to the epoch time. and contain the position, velocity, dynamics, and empirical force parameters of the BDS-3 and LEO satellites at the initial epoch, respectively. indicates station-related parameters, such as station coordinates, tropospheric delay parameters, etc. denotes observation-related parameters, such as carrier phase ambiguity and clock offset for BDS-3 observations, or equipment delays in ISL data. G, F, and K respectively represent the BDS-3 ground observation equation, the LEO onboard observation equation, and the LEO inter-satellite observation equation, which were formulated based on satellite parameters, station parameters, and measurement-related parameters.
The observation equation above is linearized and expressed in matrix form as follows.
with
where denotes the estimated corrections of the parameter, and denotes the initial value of the parameter. For simplicity, the left part of Equation (5) is called the matrix, and the right part of the equation consists of the , , and matrices, respectively. Then, according to principle of the whole network adjustment, the joint POD is performed by the following equation.
where , , and are the weights of the ground BDS-3, onboard BDS-3, and ISLs observations, respectively. In this study, we adopted an a priori variance stochastic model to determine the weights of multi-source data, which can be described as , where is the corresponding measurement noise.
3.2. Joint POD Processing Strategy
To avoid uncertainties in the framework of joint POD, 12 stations distributed across China were selected from the Huace self-built GNSS monitoring network (as shown in Figure 2). The time span covers days 131–133 in 2025, totaling three days of observation data. Additionally, based on the BDS-3 and LEO constellation described in Section 2.1, we simulated the corresponding onboard BDS-3 observation data and LEO ISL data for the same period. The sampling interval for all three types of data was set to 30 s. Table 4 details the processing strategy for joint POD. Since the observation arcs of regional stations for MEO satellites within a single day are often insufficient, a 72 h arc length was chosen for POD based solely on regional stations. For non-regional station cases, a 24 h arc length was selected, with a processing interval of 300 s for both cases. The elevation cut-off angle refers to the lower limit of elevation below which observations were excluded during data processing, typically used to mitigate observation errors caused by atmospheric delays, multipath effects, and other factors. Based on previous studies [21,35], the elevation cut-off angle for both ground stations and LEO satellites was set to 7°. In the force models, BDS-3 and LEO satellites experience different perturbations, mainly due to non-conservative forces. For BDS-3 satellites, atmospheric drag was neglected in BDS-3 POD processing due to the thin atmosphere at GNSS altitudes. In contrast, LEO satellite orbits are affected by both solar radiation pressure and atmospheric drag, necessitating the inclusion of atmospheric drag in LEO POD processing. It is noteworthy that all current atmospheric models exhibit significant limitations. Therefore, periodic empirical force parameters in the along-track and cross-track components were estimated for each orbital period [22].
Figure 2.
The distribution of ground tracking stations.

Table 4.
Description of data processing strategies and related models.
4. Results and Analyses
In this section, to evaluate the rapid BDS-3 and LEO joint POD method proposed in this paper, we first assessed the enhancement effect of LEO onboard BDS-3 observations on the POD of measured regional BDS-3 ground data in China as a reference. Secondly, we investigated the use of onboard BDS-3 data from a subset of LEO satellites, combined with LEO ISLs observations, to achieve rapid joint POD for the entire BDS-3 and LEO constellation network.
4.1. Analysis of POD Performance for Regional Ground Observations Enhanced by LEO Onboard Observations
The regional monitoring network often provides insufficient observation arc for MEO satellites within a single day, resulting in inadequate orbital accuracy. Typically, three days of accumulated observation arcs are required to achieve decimeter-level POD accuracy. This requirement increases the difficulty of independently operating and maintaining the BDS-3 system. Fortunately, LEO satellites can address this deficiency by enabling sufficient tracking of MEO satellite observation arcs within a single day, effectively improving BDS-3 POD accuracy. Based on the strategy described in Section 3.2, BDS-3 POD results were derived using only regional monitoring stations. Joint POD results were also obtained after incorporating LEO onboard BDS-3 observations, and their average accuracies were compared.
Figure 3 presents the average orbital accuracy results for two schemes: using only regional monitoring stations and incorporating LEO satellites. From the top left to the bottom right, the figure shows the results for the along-track, cross-track, radial, and 1D RMS components for both schemes. The shaded areas represent the results for IGSO satellites, while the unshaded areas represent MEO satellites. The bar chart represents the orbit determination results, while the line chart represents the improvement ratios. The figure shows that incorporating LEO satellites most significantly enhances the along-track orbital accuracy, followed by cross-track, with the least improvement in the radial direction. The enhancement is more pronounced for IGSO satellites, with substantial improvements in the radial direction as well. This is related to the geometric configurations of the MEO, IGSO, and LEO satellites. SPDOP (Satellite Position Dilution of Precision) is an important indicator for evaluating the geometric strength between satellites and visible stations. It is derived from the weight coefficient matrix, with smaller values indicating better geometric configurations. To further analyze the geometric characteristics of BDS-3 satellites, we calculated the average SPDOP values under two scenarios: (1) relying solely on ground stations, and (2) incorporating LEO satellites. Figure 4 presents the comparison results. When relying only on ground stations, both MEO and IGSO satellites exhibited relatively high SPDOP values, indicating poor overall geometric configurations, with IGSO generally worse than MEO, which corresponds to their inferior orbit determination accuracy. After introducing LEO satellites, the geometries of both MEO and IGSO were significantly improved, with SPDOP values reduced to about 2. Although the SPDOP of IGSO satellites remained slightly higher than that of MEO, the gap narrowed considerably, and the corresponding orbit determination accuracy neared that of MEO, with both achieving centimeter-level precision overall. Overall, with the inclusion of LEO satellites, both BDS-3 MEO and IGSO satellites achieved centimeter-level orbit determination accuracy. Table 5 provides further detailed results. For MEO satellites, after incorporating LEO, the orbital accuracy in the along-track, cross-track, radial, and 1D RMS components improved from 15.3, 10.5, 6.7, and 11.6 cm to 4.6, 5.2, 4.5, and 4.9 cm, respectively, with improvement rates of 69.6%, 51.3%, 32.5%, and 57.8%. For IGSO satellites, the accuracy improved from 35.2, 21.6, 18.3, and 26.9 cm to 6.8, 7.3, 4.1, and 6.4 cm, with improvement rates of 80.1%, 66.2%, 77.8%, and 76.0%. The improvement was notably greater for IGSO satellites. Although regional stations in China can track all arc segments of IGSO satellites, the weak geometric strength between IGSO satellites and ground stations is significantly mitigated by the inclusion of LEO satellites. This leads to more substantial accuracy improvements.
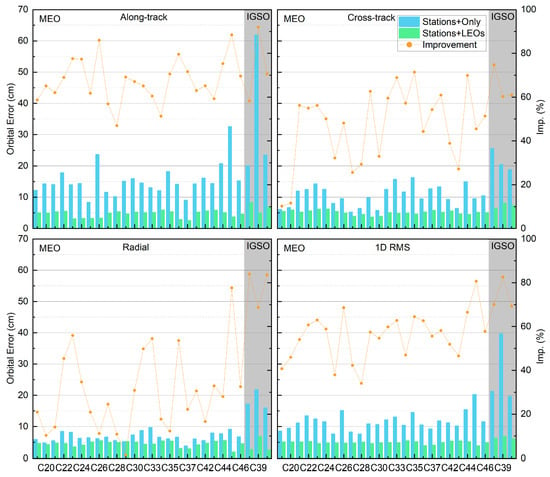
Figure 3.
BDS-3 POD orbital accuracy for regional monitoring stations and after incorporating LEO satellites.
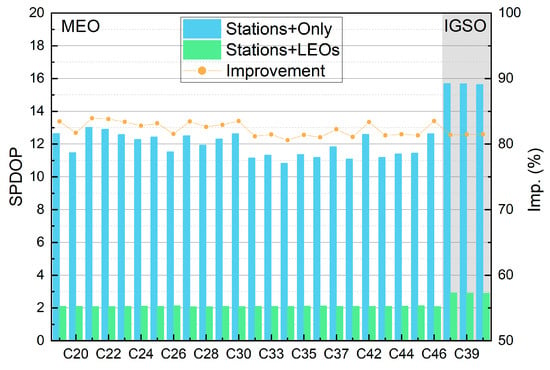
Figure 4.
BDS-3 MEO/IGSO average SPDOP.

Table 5.
BDS-3 POD orbital accuracy for regional monitoring stations and after incorporating LEO satellites (unit: cm).
Since LEO satellites are expected to provide navigation services in the future, their orbital accuracy is also critical. Figure 5 shows the average orbital accuracy of the LEO satellites in the along-track, cross-track, and radial directions. As shown, the along-track component exhibited the largest orbital error, with an average of 4.1 cm. This is likely due to the along-track components aligning with the satellite’s motion, where the largest non-conservative perturbing force, atmospheric drag, fully impacts this component, resulting in the greatest acceleration error. The cross-track and radial components were smaller and relatively close, with average errors of 2.5 cm and 2.1 cm, respectively.
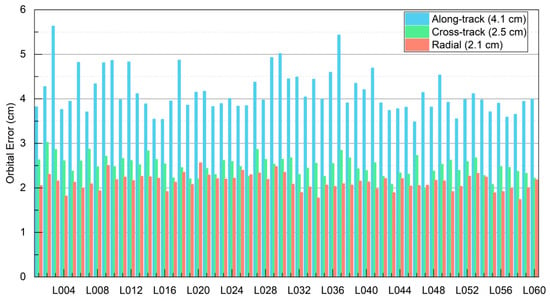
Figure 5.
LEO POD orbital accuracy.
In summary, this section demonstrates that high-precision BDS-3 POD cannot be achieved using only regional ground station data. This limitation makes independent maintenance of BDS-3 orbits challenging. The incorporation of LEO satellites can overcome this issue, enabling high-precision independent orbit maintenance. However, the computational burden of joint POD limits its practical real-time application. These results also provide a reference for the accuracy of the rapid entire BDS-3 and LEO POD proposed in the next section.
4.2. Assessment of POD Performance for Partial Onboard BDS-3 Observations Incorporating Inter-Satellite Links
As in previous studies, incorporating LEO satellites into GNSS and LEO joint POD significantly increased the computation time. One important reason is the introduction of a large number of carrier phase ambiguity parameters (parameters related to onboard GNSS observations). Rapid BDS-3 and LEO POD can be achieved by using only a small number of LEO satellites with onboard BDS-3 observations (LEO-BDS3), together with LEO satellites without BDS-3 observations (LEO-nonBDS3) and LEO ISL data. If the loss in orbit accuracy remains small, this achievement would be highly significant. Such an approach would enable independent, high-precision maintenance of both BDS-3 and LEO systems. It would also have considerable implications for controlling the construction costs of LEO constellations. Therefore, in this section, POD tasks were performed with 10, 20, 30, 40, 50, and 60 LEO-BDS3 satellites for comparison. The selection of LEO-BDS3 satellites was made to cover each orbital plane as much as possible and to ensure an even distribution within each plane. In addition, all POD tasks in this section were executed on the same hardware: a dual-CPU system, each with 6 cores and 12 threads, a base clock frequency of 2.60 GHz (boost frequency of 3.10 GHz), and 124 GB of RAM.
Figure 6 shows the number of estimated parameters (NEP) and the computation time of a single BLSQ (CT-BLSQ) for different numbers of LEO-BDS3 satellites. It can be observed that as the number of LEO-BDS3 satellites increases, the NEP grows linearly. This is because each additional LEO-BDS3 satellite introduces a substantial number of parameters. It can also be seen that due to the linear increase in NEP, the CT-LSQ shows a dramatic rise. Table 6 provides details of the NEP and CT-BLSQ, showing that for every additional 10 LEO-BDS3 satellites, the NEP increases by an average of 6780 parameters. Among these, 2880 parameters are LEO receiver clock offsets (which are not required for POD using ISL data), while the rest are ambiguity parameters. This results in a sharp increase in computation time, rising from only 3.6 min with 10 LEO-BDS3 satellites to 27 min with 60 LEO-BDS3 satellites, corresponding to a 650% increase.
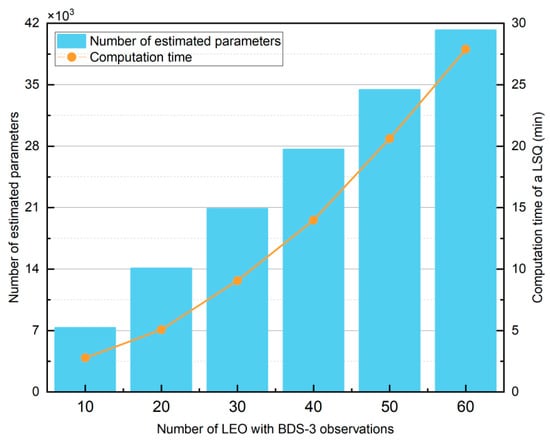
Figure 6.
Number of estimated parameters and computation time of a single BLSQ (blue bar: number of estimated parameters; orange line: computation time of a single BLSQ).

Table 6.
Number of estimated parameters (NEP) and computation time of a single BLSQ (CT-LSQ) for different numbers of LEO-BDS3 satellites.
Figure 7 shows the POD accuracy of BDS-3 MEO and IGSO satellites for different numbers of LEO-BDS3 satellites. Only the onboard BDS-3 observations from LEO-BDS3 satellites were used in the solution. The LEO-nonBDS3 satellites contribute solely through ISL data. Therefore, varying the number of LEO-BDS3 satellites leads to different BDS-3 orbit accuracies. For MEO satellites, it can be seen that when the number of LEO-BDS3 satellites reaches 20, the orbit accuracy in all components shows almost no further improvement. For IGSO satellites, the along-track and cross-track accuracies also plateau at around 30 LEO-BDS3 satellites, whereas the radial accuracy continues to improve until about 50 LEO-BDS3 satellites. This behavior may be related to the geometric configuration of the LEO constellation. Overall, using 20 LEO-BDS3 satellites already achieves satisfactory orbit accuracy for both BDS-3 MEO and IGSO satellites. According to Table 6, 20 LEO-BDS3 satellites require only 5.7 min to complete a single BLSQ, which is about 21% of the computation time in the 60 LEO-BDS3 case. Table 7 presents detailed orbit accuracies, showing that with 20 LEO-BDS3 satellites, the 1D RMS orbit accuracies for MEO and IGSO satellites were 4.9 cm and 6.7 cm, respectively. From Table 5 in Section 4.1, without LEO ISLs, the solution with 60 LEO-BDS3 satellites and BDS-3 achieved accuracies of 4.9 cm and 6.4 cm, respectively. This indicates that with the addition of LEO ISLs, using 20 LEO-BDS3 satellites can achieve BDS-3 orbit accuracy with almost no degradation. When the number of LEO-BDS3 satellites was 30 or more, the accuracy is even slightly better, likely due to improved LEO orbit accuracy. Overall, these results further demonstrate the superiority of the rapid BDS-3 and LEO joint POD method proposed in this section.
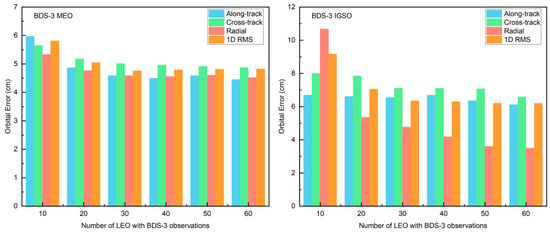
Figure 7.
Orbital accuracy of BDS-3 MEO and IGSO satellites under different numbers of LEO-BDS3 satellites (note the different y-axis scales).

Table 7.
Orbital accuracy of BDS-3 MEO and IGSO satellites under different numbers of LEO-BDS3 satellites (unit: cm).
In addition to the orbit accuracy of BDS-3 satellites, the orbit accuracy of LEO satellites is equally important. Figure 8 shows the orbit accuracy of both LEO-BDS3 and LEO-nonBDS3 satellites under different numbers of LEO-BDS3 satellites. Benefiting from the assistance of LEO ISLs, the orbit accuracies of both types of LEO satellites remain nearly consistent across varying numbers of LEO-BDS3 satellites, with 1D RMS values around 1 cm. Table 8 provides the detailed results. The 1D RMS orbit accuracy difference between the two types of LEO satellites under different LEO-BDS3 satellite counts is within 3 mm, showing essentially no difference. Compared with Figure 5 in Section 4.1, the inclusion of LEO ISLs leads to a substantial improvement in LEO orbit accuracy. These results demonstrate that the proposed BDS-3 and LEO joint POD method can rapidly provide high-precision orbit products for both BDS-3 and LEO satellites simultaneously.
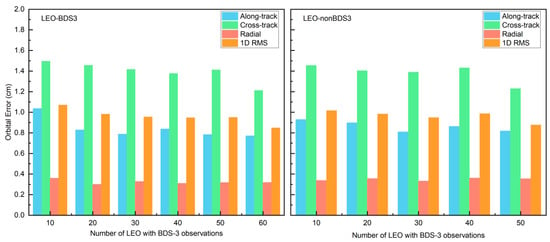
Figure 8.
Orbital accuracy of LEO-BDS3 and LEO-nonBDS3 satellites under different numbers of LEO-BDS3 satellites.

Table 8.
Orbital accuracy of LEO-BDS3 and LEO-nonBDS3 satellites under different numbers of LEO-BDS3 satellites (unit: cm).
In summary, this section demonstrates the superiority of the new BDS-3 and LEO joint POD method proposed in this paper. Benefiting from the ISL payloads to be deployed on future LEO constellations, this method can achieve joint POD products for the entire BDS-3 and LEO network with a relatively low computational burden. It provides important reference value for the independent and high-precision real-time maintenance of both BDS-3 and LEO systems.
5. Discussion
ISLs have already been successfully applied to BDS-3, with plans to include other GNSS systems in their next-generation systems. ISLs can be applied to autonomous POD of the satellite constellation, or to joint POD with traditional GNSS observations. Previous studies have mainly reported the capability of ISLs for autonomous and joint POD in GNSS, and some studies have also reported the POD performance of ISLs applied to LEO constellations. The use of LEO onboard BDS-3 data was first validated for enabling high-precision, independent POD based on ground stations in China. More importantly, high-precision real-time independent orbit maintenance of BDS-3 and LEO was investigated for the first time. A novel joint POD method based on LEO ISLs is also proposed. With this method, the computational burden in joint POD of BDS-3 and LEO can be greatly reduced without degrading orbital accuracy. This provides valuable insights for real-time POD of both systems.
However, due to the lack of real LEO ISL data, all work in this study was carried out based on simulations. In the simulation process, ISL data were generated considering only the inter-satellite distance and measurement noise, without including various corrections that would be needed in practice. For simplicity, the inter-satellite distance with measurement noise was simulated directly instead of dual one-way ranging values, so that epoch synchronization could be avoided. In addition, the measurement principles of ISL and BDS-3 observations are different, and the associated equipment delays are not consistent. These differences may introduce systematic errors into the joint POD results, so the weighting of different types of observations should be carefully considered. In addition, this study employed the batch least-squares method primarily to verify the feasibility of the joint BDS-3 and LEO orbit determination scheme within a unified framework. However, for practical real-time high-precision orbit maintenance applications, recursive filtering methods (such as the extended Kalman filter and the square-root information filter, SRIF) are more advantageous. These methods can update the state vector epoch by epoch, thereby alleviating the computational burden caused by large-scale parameter estimation. In future work, we plan to extend the proposed rapid joint orbit determination scheme to a real-time filtering framework to further enhance its applicability in real-time scenarios. In this study, a simple prior-variance weighting was used, which may lead to unexpected errors during data processing. In practical applications, more sophisticated stochastic models, such as elevation-dependent or SNR-based weighting schemes, can more accurately reflect the quality of observations. It should be emphasized that the core conclusion of this study is that the inclusion of LEO satellites and ISL can significantly reduce the computational burden of real-time BDS-3 and LEO orbit maintenance without compromising accuracy. This improvement primarily relies on constellation geometry and observation quality, and even a simplified prior-variance-based model is sufficient to demonstrate this advantage. More complex weighting strategies may further improve the solution accuracy to some extent, but the improvement will not alter the overall order of magnitude and thus does not affect the validity of the conclusion. Finally, to avoid inconsistencies between LEO downlink navigation data and its orbit and clock offsets, the downlink navigation data should also be included in LEO orbit determination. However, in this study, such data have not yet been considered. For these reasons, further refinement of the POD results is still required.
6. Conclusions
This study is the first to investigate the real-time issue in joint POD of BDS-3 and LEO. Considering the large number of carrier-phase ambiguity parameters in onboard BDS-3 data, a method is proposed. In this method, onboard BDS-3 data from a subset of LEO satellites are combined with LEO ISL data. This enables rapid joint POD for the entire BDS-3 and LEO constellation network. To validate this approach, joint POD experiments for BDS-3 and LEO were conducted. The data used included (1) BDS-3 data from a regional ground network established by Huace in China; (2) simulated onboard BDS-3 observations; and (3) simulated LEO ISL data. All data correspond to the period from day of year (DOY) 131 to 133 in 2025.
First, the results are based on China regional ground BDS-3 data and simulations of the Walker 60/10/1 LEO constellation. With only regional ground stations, the MEO orbit accuracies in the along-track, cross-track, radial, and 1D RMS components were 15.3, 10.5, 6.7, and 11.6 cm. The IGSO orbit accuracies were 35.2, 21.6, 18.3, and 26.9 cm. These results verify that high-precision POD of BDS-3 MEO and IGSO cannot be achieved using regional ground stations alone. After the inclusion of LEO satellites, the MEO orbit accuracy improved to 4.6, 5.2, 4.5, and 4.9 cm, corresponding to improvement rates of 69.6%, 51.3%, 32.5%, and 57.8%, respectively. The IGSO orbit accuracy improved to 6.8, 7.3, 4.1, and 6.4 cm, with improvement rates of 80.1%, 66.2%, 77.8%, and 76.0%. Meanwhile, the LEO orbit accuracy in the along-track, cross-track, and radial components were 4.1, 2.5, and 2.1 cm, respectively. These results demonstrate that the inclusion of LEO satellites enables independently high-precision orbit maintenance for both BDS-3 and LEO. However, this POD method has been shown to impose a significant computational burden, making real-time high-precision maintenance of BDS-3 and LEO challenging to achieve.
Therefore, the proposed rapid joint POD of BDS-3 and LEO was further validated in this study. The results show that incorporating onboard BDS-3 data from an additional 10 LEO satellites into the data processing increases the number of receiver clock offset parameters by 2880 and ambiguity parameters by approximately 3900, totaling 6780 parameters. This leads to a substantial increase in computation time. When onboard BDS-3 data from only 10 LEO satellites are included, a single BLSQ requires 3.6 min to estimate all orbit parameters of BDS-3 and LEO satellites. However, when the number increases to 60 satellites, the required time rises to 27.0 min. Regarding orbit accuracy, for BDS-3 MEO and IGSO, the 1D RMS accuracy values are 5.7, 4.9, 4.7, 4.7, 4.7, and 4.6 cm, and 8.6, 6.7, 6.2, 6.1, 5.9, and 5.6 cm, respectively, corresponding to LEO-BDS3 satellite counts of 10, 20, 30, 40, 50, and 60. In comparison, when LEO ISL data are not included, the 1D RMS orbit accuracies of MEO and IGSO in the joint POD with 60 LEO and BDS-3 satellites are 4.9 and 6.4 cm, respectively. When the number of LEO-BDS3 satellites reaches 20, negligible loss of BDS-3 orbit accuracy is observed, while the computation time of a single BLSQ reduces to only 5.7 min. Moreover, the orbital accuracy of LEO-BDS3 and LEO-nonBDS3 satellites shows minimal differences across varying numbers of LEO-BDS3 satellites, with the 1D RMS orbit accuracy remaining around 1 cm. These results demonstrate that the proposed rapid joint POD method successfully maintains the orbit accuracy for both constellations while simultaneously greatly reducing the computational burden.
In summary, the proposed rapid joint POD method for BDS-3 and LEO shows greater potential for achieving real-time joint POD of BDS-3 and LEO. It is suggested that if the highest precision is not required, incorporating onboard BDS-3 data from 20 LEO satellites into the joint POD is sufficient. This achieves centimeter-level orbit accuracy for both BDS-3 and LEO. Using 30 satellites represents a more balanced choice.
Author Contributions
Conceptualization, L.W.; Methodology, L.W., W.L. and G.H.; Software, L.W., D.S. and W.L.; Writing—original draft, L.W., D.S. and W.L.; Writing—review & editing, L.W., W.L. and B.C.; supervision: L.W.; project administration: L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (42374025), Programs of the Fundamental Research Funds for the Central Universities (CHD 300102265503, 300102261301, 300102264105), Key Research and Development Program of Shaanxi (2021LLRH-06), and Shaanxi Post-doctoral Scientific Research Funding (2024BSHSDZZ217).
Data Availability Statement
The WUM MGEX final products during the current study are available from ftp://igs.gnsswhu.cn/pub/gps/products/ (accessed on 10 July 2025). The IGS antenna file is available from https://files.igs.org/pub/station/general/igs20.atx (accessed on 10 July 2025). The CODE final product file is available from www.aiub.unibe.ch/download/CODE/ (accessed on 10 July 2025). All websites have been checked and confirmed accessible.
Acknowledgments
We are thankful for the data support of IGS, MEGX.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Keller, H.; Salzwedel, H. Link strategy for the mobile satellite system Iridium. In Proceedings of the Vehicular Technology Conference—VTC, Atlanta, GA, USA, 28 April–1 May 1996; Volume 2, pp. 1220–1224. [Google Scholar] [CrossRef]
- Reid, T.; Neish, A.; Walter, T.; Walter, T.F.; Enge, P.K. Leveraging Commercial Broadband LEO Constellations for Navigation. In Proceedings of the 29th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016. [Google Scholar] [CrossRef]
- Xiaohong, Z.; Fujian, M.A. Review of the development of LEO navigation-augmented GNSS. Acta Geod. Cartogr. Sin. 2019, 48, 1073–1087. [Google Scholar]
- Joerger, M.; Gratton, L.; Pervan, B.; Cohen, C.E. Analysis of Iridium-Augmented GPS for Floating Carrier Phase Positioning. Navigation 2010, 57, 137–160. [Google Scholar] [CrossRef]
- Li, X.; Ma, F.; Li, X.; Lv, H.; Bian, L.; Jiang, Z.; Zhang, X. LEO constellation-augmented multi-GNSS for rapid PPP convergence. J. Geod. 2019, 93, 749–764. [Google Scholar] [CrossRef]
- Ge, H.; Li, B.; Ge, M.; Zang, N.; Nie, L.; Shen, Y.; Schuh, H. Initial Assessment of Precise Point Positioning with LEO Enhanced Global Navigation Satellite Systems (LeGNSS). Remote Sens. 2018, 10, 984. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, P.; Tu, R.; Xu, X.; Zhang, K.; Tao, L. Performance analysis of GNSS carrier phase time transfer based on LEO enhancement. Navig. Position. Timing 2025, 12, 131–143. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Zhang, K.; Deng, Z.; Yang, J.; Li, M. Performance analysis of LEO satellite augmented BeiDou precise point positioning. Navig. Position. Timing 2025, 12, 51–63. (In Chinese) [Google Scholar] [CrossRef]
- Reid, T.G.R.; Neish, A.M.; Walter, T.; Enge, P.K. Broadband LEO Constellations for Navigation. Navigation 2018, 65, 205–220. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, X.; Li, X.; Cheng, J.; Guo, F.; Hu, J.; Pan, L. Hybrid constellation design using a genetic algorithm for a LEO-based navigation augmentation system. GPS Solut. 2020, 24, 62. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, X.; Hu, J.; Li, P.; Pan, L.; Yu, S.; Zhang, Z. Frequency design of LEO-based navigation augmentation signals for dual-band ionospheric-free ambiguity resolution. GPS Solut. 2022, 26, 53. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Ma, F.; Li, P.; Pan, L.; Yu, S.; Zhang, Z. Improved PPP Ambiguity Resolution with the Assistance of Multiple LEO Constellations and Signals. Remote Sens. 2019, 11, 408. [Google Scholar] [CrossRef]
- Li, X.; Lv, H.; Ma, F.; Li, X.; Liu, J.; Jiang, Z. GNSS RTK Positioning Augmented with Large LEO Constellation. Remote Sens. 2019, 11, 228. [Google Scholar] [CrossRef]
- König, R.; Reigber, C.; Zhu, S.Y. Dynamic model orbits and Earth system parameters from combined GPS and LEO data. Adv. Space Res. 2005, 36, 431–437. [Google Scholar] [CrossRef]
- Zhu, S.; Reigber, C.; König, R. Integrated adjustment of CHAMP, GRACE, and GPS data. J. Geod. 2004, 78, 103–108. [Google Scholar] [CrossRef]
- Rim, H.; Schutz, B.; Abusali, P.; Tapley, B.D. Effect of GPS Orbit Accuracy on GPS-determined Topex/Poseidon Orbit. In Proceedings of the 8th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1995), Palm Springs, CA, USA, 12–15 September 1995. [Google Scholar]
- Huang, W.; Männel, B.; Sakic, P.; Ge, M.; Schuh, H. Integrated processing of ground- and space-based GPS observations: Improving GPS satellite orbits observed with sparse ground networks. J. Geod. 2020, 94, 96. [Google Scholar] [CrossRef]
- Li, X.; Zhang, K.; Meng, X.; Zhang, Q.; Zhang, W.; Li, X.; Yuan, Y. LEO–BDS–GPS integrated precise orbit modeling using FengYun-3D, FengYun-3C onboard and ground observations. GPS Solut. 2020, 24, 48. [Google Scholar] [CrossRef]
- Li, X.; Zhang, K.; Ma, F.; Zhang, W.; Zhang, Q.; Qin, Y.; Zhang, H.; Meng, Y.; Bian, L. Integrated Precise Orbit Determination of Multi-GNSS and Large LEO Constellations. Remote Sens. 2019, 11, 2514. [Google Scholar] [CrossRef]
- Li, B.; Ge, H.; Ge, M.; Nie, L.; Shen, Y.; Schuh, H. LEO enhanced Global Navigation Satellite System (LeGNSS) for real-time precise positioning services. Adv. Space Res. 2019, 63, 73–93. [Google Scholar] [CrossRef]
- She, H.; Huang, G.; Wang, L.; Qin, Z.; Xie, S.; Lai, W.; Tian, J. A simplified GNSS/LEO joint orbit determination method. Measurement 2024, 236, 115029. [Google Scholar] [CrossRef]
- Lai, W.; Huang, G.; Wang, L.; She, H.; Xie, S.; Xie, W.; Wang, Q. Real-time high-precision joint orbit determination of GPS and LEO using SRIF. Meas. Sci. Technol. 2025, 36, 056310. [Google Scholar] [CrossRef]
- Zheng, H.; Yuan, Y.; Li, X.; Zhang, K. Improving real-time GNSS orbits and clocks by filtered integrated processing multiple LEO onboard and ground observations. GPS Solut. 2025, 29, 102. [Google Scholar] [CrossRef]
- Ananda, M.P.; Bernstein, H.; Cunningham, K.E.; Feess, W.; Stroud, E. Global Positioning System (GPS) autonomous navigation. In Proceedings of the IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences, Las Vegas, NV, USA, 20–20 March 1990; pp. 497–508. [Google Scholar] [CrossRef]
- Fernández, F.A. Inter-satellite ranging and inter-satellite communication links for enhancing GNSS satellite broadcast navigation data. Adv. Space Res. 2011, 47, 786–801. [Google Scholar] [CrossRef]
- D’Angelo, P.; Fernández, A.; Guardabrazo, T.; Amarillo, F. Enhancement of GNSS navigation function by the use of Inter-Satellite Links. In Proceedings of the 2012 6th ESA Workshop on Satellite Navigation Technologies (Navitec 2012) & European Workshop on GNSS Signals and Signal Processing, Noordwijk, The Netherlands, 5–7 December 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, D.; Yang, J.; Li, G.; Zhou, Y.; Tang, C. Globalization highlight: Orbit determination using BeiDou inter-satellite ranging measurements. GPS Solut. 2017, 21, 1395–1404. [Google Scholar] [CrossRef]
- Tang, C.; Hu, X.; Zhou, S.; Liu, L.; Pan, J.; Chen, L.; Guo, R.; Zhu, L.; Hu, G.; Li, X.; et al. Initial results of centralized autonomous orbit determination of the new-generation BDS satellites with inter-satellite link measurements. J. Geod. 2018, 92, 1155–1169. [Google Scholar] [CrossRef]
- Ren, X.; Yang, Y.; Zhu, J.; Xu, T. Orbit determination of the Next-Generation Beidou satellites with Intersatellite link measurements and a priori orbit constraints. Adv. Space Res. 2017, 60, 2155–2165. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, X.; Tang, C.; Zhou, S.; Cao, Y.; Wang, Q.; Su, R. Inter-satellite link augmented BeiDou-3 orbit determination for precise point positioning. Chin. J. Aeronaut. 2022, 35, 332–343. [Google Scholar] [CrossRef]
- Feng, L.; Mao, Y.; Song, X.; Sun, B. Analysis of the Accuracy of Beidou Combined Orbit Determination Enhanced by LEO and ISL. Acta Geod. Cartogr. Sin. 2017, 45, 109–115. [Google Scholar]
- Yang, Y.; Mao, Y.; Ren, X.; Jia, X.; Sun, B. Demand and key technology for a LEO constellation as augmentation of satellite navigation systems. Satell. Navig. 2024, 5, 11. [Google Scholar] [CrossRef]
- Li, X.; Jiang, Z.; Ma, F.; Lv, H.; Yuan, Y.; Li, X. LEO Precise Orbit Determination with Inter-satellite Links. Remote Sens. 2019, 11, 2117. [Google Scholar] [CrossRef]
- He, X.; Hugentobler, U.; Schlicht, A.; Nie, Y.; Duan, B. Precise orbit determination for a large LEO constellation with inter-satellite links and the measurements from different ground networks: A simulation study. Satell. Navig. 2022, 3, 22. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Zhang, K.; Fu, Y.; Zhang, W.; Zheng, H. Precise orbit determination for LEO constellation based on onboard GNSS observations, inter-satellite links and ground tracking data. GPS Solut. 2025, 29, 107. [Google Scholar] [CrossRef]
- Gao, W.; Zhou, W.; Tang, C.; Li, X.; Yuan, Y.; Hu, X. High-precision services of BeiDou navigation satellite system (BDS): Current state, achievements, and future directions. Satell. Navig. 2024, 5, 20. [Google Scholar] [CrossRef]
- Guo, J.; Wang, C.; Chen, G.; Xu, X.; Zhao, Q. BDS-3 precise orbit and clock solution at Wuhan University: Status and improvement. J. Geod. 2023, 97, 15. [Google Scholar] [CrossRef]
- Jee, G.; Lee, H.-B.; Kim, Y.H.; Chung, J.-K.; Cho, J. Assessment of GPS global ionosphere maps (GIM) by comparison between CODE GIM and TOPEX/Jason TEC data: Ionospheric perspective. J. Geophys. Res. Space Phys. 2010, 115, 1–11. [Google Scholar] [CrossRef]
- Pan, J.; Hu, X.; Zhou, S.; Tang, C.; Guo, R.; Zhu, L.; Tang, G.; Hu, G. Time synchronization of new-generation BDS satellites using inter-satellite link measurements. Adv. Space Res. 2018, 61, 145–153. [Google Scholar] [CrossRef]
- Yan, X.; Liu, C.; Huang, G.; Zhang, Q.; Wang, L.; Qin, Z.; Xie, S. A Priori Solar Radiation Pressure Model for BeiDou-3 MEO Satellites. Remote Sens. 2019, 11, 1605. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).