Abstract
This paper presents a near real-time implementation of the Karhunen–Loève Transform (KLT) for Radio Frequency Interference (RFI) mitigation in microwave radiometry. KLT is a powerful, data-adaptive technique capable of adjusting to various signal types by estimating the covariance matrix of the incoming signal and segmenting its eigenvectors to form an effective RFI basis. In this paper, the KLT is evaluated with real signals in laboratory conditions, aiming to characterize its performance in realistic conditions. To that effect, the dual Rx/Tx capability of a Pluto SDR is used to generate and capture RFI. The main mitigation metrics are computed for the KLT and other commonly used mitigation methods. In addition, while previous studies have shown the effectiveness of offline processing of recorded I/Q data, real-time mitigation is often necessary. Given the computational cost of eigendecomposition, this work introduces a low-complexity solution using the “economy covariance” approach alongside asynchronous covariance decomposition. The proposed implementation, realized within the GNU Radio framework, demonstrates the practical feasibility of real-time KLT-based mitigation and underscores its potential for improving signal integrity in digital radiometers operating under dynamic RFI conditions.
1. Introduction
1.1. Radio Frequency Interference
Microwave radiometers are increasingly exposed to Radio Frequency Interference (RFI), which corrupts the natural radiometric signal and impairs the retrieval of geophysical parameters, despite existing protections established by ITU Radio Regulations. The persistent growth of anthropogenic radio emissions has driven the development of many RFI detection and mitigation techniques. Statistical metrics, notably Kurtosis-based methods [1,2,3] and Anderson–Darling tests [4,5,6], analyze deviations from the expected Gaussian noise distribution to detect interference. Spectral Kurtosis performs a similar function in the frequency domain [7,8,9,10]. More recently, the use of “whiteness metrics” based on autocorrelation has also been proposed as an RFI detection method [11]. Polarimetric signatures have likewise been employed to identify RFI [12,13,14]. Mitigation techniques often rely on analysis in transformed time-frequency domains, including the use of spectrograms [15,16,17], wavelet transforms [18,19], multifourier transform [20], and nonlinear techniques [21]. Other approaches involve spatial filtering using adaptive antennas and beamforming or image processing [22,23]. Recently, machine learning methods, including neural networks and support vector machines, have shown promising results for RFI detection and classification [24,25,26,27].
Most mitigation techniques share a common structure: signal decomposition followed by RFI detection. In the decomposition step, the signal is transformed to concentrate RFI energy into a reduced number of components. These coefficients are then binned and tested for RFI. Any RFI-affected bin is then selectively removed (blanked) to reconstruct a cleaner signal.
A fundamental limitation in many of these approaches lies in their use of fixed transformation bases, such as Digital Fourier Transform (DFT), Short-Term Fourier Transform (STFT), etc. These are tailored to specific types of RFI and may perform suboptimally when the interfering signal deviates from the assumed structure. For example, DFT excels at narrowband RFI but fails in wideband scenarios. To address this lack of adaptability, this paper proposes the use of the Karhunen–Loève Transform (KLT), which offers a data-driven basis derived from the signal’s covariance structure. This makes KLT inherently adaptable to a wide range of RFI waveforms. The focus of this work is the design and demonstration of a computationally efficient, real-time implementation of KLT using an asynchronous strategy within the GNU Radio framework, enabling its application in systems with limited processing resources and high dynamic RFI variability.
This paper is organized as follows: First, Section 1.2–Section 1.4 describe how to use KLT for RFI mitigation. Then, Section 2 presents the experimental setup and methodology used to characterize mitigation performance under laboratory conditions. Finally, Section 3 presents the mitigation performance, along with an example demonstrating the real-time operation of such a system.
1.2. The Karhunen–Loève Transform
The KLT was independently introduced in 1946 by Kari Karhunen [28] and Michel Loève [29]. It is a signal processing technique that decomposes a stochastic process into a sum of random variables weighted by deterministic functions. It is closely connected to Principal Component Analysis (PCA) [30], and mathematically equivalent when finite sequences are considered.
The KLT is the projection of a stochastic process into the eigenvectors of its covariance matrix. Given the complex random vector of N random variables , with ⊤ denoting its transpose, its covariance matrix () is defined by the following:
with H denoting the conjugate transpose. The eigenvectors and eigenvalues of the covariance matrix are obtained through the eigendecomposition of . Specially, since is positive definite, it can be decomposed as follows:
where denotes the matrix whose columns are the eigenvectors , and is a diagonal matrix containing the associated eigenvalues . The eigenvectors and eigenvalues fulfill the following:
Then, the KLT is the projection of the random vector into the eigenvector orthogonal basis:
Exploiting the unitary property of , the inverse transform is given by the following:
which achieves its intended purpose of decomposing into a sum of random variables () multiplying a deterministic basis (). The unbiased estimator of the covariance matrix can be calculated using the following matrix multiplication ([31] (Eqs. 5.2-4)):
where is an matrix of observations, with each column representing a realization of the process after subtracting the sample mean. However, if the number of samples N is large, this eigendecomposition can be computationally costly. The “economy covariance” can be estimated with the alternative derivation
In this case, is , with M being the number of observations of the process, . Using the definition of the eigenvector and eigenvalue given by Equation (3):
The normalizing factors in Equations (6) and (7) have been omitted here for clarity. It is evident that and share the same non-zero eigenvalues (). Moreover, their corresponding eigenvectors are connected through multiplication by :
Therefore, the “economy covariance” can be used instead of the full covariance to compute the first M eigenvectors. This is one of the strategies used to reduce the complexity of the problem in pursuit of a real-time implementation.
1.3. Using KLT Decomposition for RFI Mitigation
The use of KLT for RFI mitigation has been described in detail in [32]. In the absence of RFI, the discrete stochastic process of N samples received by a radiometer corresponds exclusively to a complex Gaussian noise process :
In this case, and provided that the frequency response of the filters has been properly equalized, the covariance matrix will approximate the identity, and the eigenvalues will all be of similar values. In the presence of RFI, the random Gaussian process has been contaminated by an unknown arbitrary interfering signal , which should also be considered stochastic:
Provided that the interfering signal is statistically independent of the noise, the covariance of the combined process will now be the sum of the covariances of the two processes:
The covariance of the combined process can be estimated using Equations (6) or (7), and eigendecomposed. Once the column-eigenvector matrix is obtained, this enables computing the KLT transformation by using Equation (4). This can be used as an adaptive signal decomposition, as the eigenvectors are the optimum representation of the process, including the interference component. The coefficients in the “KLT space” can then be tested for RFI using a detection algorithm, excising the interference-affected coefficients. For example, a suitable detection algorithm would be one that evaluates the instantaneous variance in the transformed coefficients. This method is often used with other transformations, such as DFT or STFT. The combination of a given decomposition/transformation technique and an instantaneous univariate power detector is often termed “blanking” in some publications, e.g., “frequency blanking” for the combination of DFT and instantaneous power detection [33,34]. It should be noted, however, that the use of other types of detectors is also possible (e.g., Kurtosis). Therefore, to avoid confusion, the detection method has been made explicit in this paper. The filtered signal can then be transformed back into the temporal domain using Equation (5), leading to a “cleaned” signal. In contrast to other signal transformations, such as the DFT or the STFT, KLT has the great advantage that the basis is not fixed, but adaptive to the process. As such, if the covariance estimation is accurate and the dimensionality of the RFI signals is low, it will be able to concentrate the RFI regardless of the RFI type, approximating the ideal “matched filter”. A good concentration of the RFI energy facilitates further detection and an efficient separation of RFI and noise.
1.4. KLT Direct Excision
An alternative method, that does not require a detection stage (then termed “direct excision”), was also proposed in [32]. Examining the eigenvalues can reveal some with significantly higher power than others. Their associated eigenvectors (called the "principal components") capture the largest portion of the process covariance, primarily due to RFI. In contrast, eigenvalues from the Gaussian noise process tend to be similar and lower in power. Thus, it may be possible to distinguish a subset of eigenvalue/eigenvectors linked mainly to RFI contamination (“eigen-RFI”) from those dominated by radiometric noise. A strategy to determine the subset of “eigen-RFI” is described in ([32] (II.B)), based on the statistical distribution of the eigenvalues in the absence of interference. By removing the portion of the signal being projected into the “eigen-RFI”, and recovering the rest, it is possible to bypass the detection stage altogether.
The two methods proposed, KLT and power detection and KLT “direct excision”, were evaluated in ([32] (IV)) with the help of simulated signals, demonstrating that KLT is adaptive and potentially able to mitigate any type of waveform efficiently, provided that the covariance is properly estimated and the dimensionality is low. However, the simulated scenarios considered in that study are not particularly realistic, primarily due to simplifying assumptions about process dimensionality and its statistical properties. To address these limitations, this work extends the analysis by evaluating mitigation performance using real, non-simulated signals.
2. Materials and Methods
This section describes the laboratory setup used to evaluate the performance of the KLT algorithm with real-world signals. In addition, a real-time implementation of KLT has been developed to demonstrate its feasibility as a practical mitigation solution.
2.1. Experimental Set-Up Description
The main device used in this experiment has been the ADALM-PLUTO SDR Rev. C. It is a versatile, low-cost SDR (Software-Defined Radio) platform developed by Analog Devices [35]. It features a fully integrated RF transceiver, the AD9363, enabling both transmit and receive functionalities. In its COTS form, the PlutoSDR offers one receive channel and one transmit channel which can be operated in full duplex, being capable of generating or measuring RF IQ signals from 325 to 3800 MHz, at up to 61.44 MSPS, and up to 20 MHz bandwidth (limited by the RF front-end, and not by the sampling rate).
The AD9363 RF front-ends are based on the homodyne (or direct conversion) architecture [36]. Each Rx chain integrates an independent AGC, DC offset correction, quadrature correction, and digital filtering. The I/Q components are then digitized using a pair of 12-bit ADCs per channel. The operation of PlutoSDR is enabled by the Libiio library [37], which interfaces between the Linux kernel in the Xilinx Zynq and the AD9363. In this work, the RadioGNU and Matlab frontends of Libiio are used.
In order to evaluate the mitigation performance of KLT, it is necessary to be able to control the received signal power and waveform accurately. To that effect, instead of acquiring samples from free space, the capability of the PlutoSDR to transmit and receive at the same time was used. The Tx and Rx ports have been directly connected using an SMA pigtail. To avoid damaging the receiver, the transmission gain has been fixed to −10 dB, following the recommendations of the manufacturer. For further reassurance, a generic 6 dB attenuator (0–6 GHz) has been added between the Rx and Tx.
2.2. Mitigation Performance Evaluation
Mitigation performance can be evaluated using the Rx/Tx capabilities of PlutoSDR and the experimental setup described, connecting the Rx and Tx ports of the PlutoSDR, and continuously transmitting through the Tx port.
As a first step, the channel has been equalized. The spectral response of the PlutoSDR presents a very noticeable roll-off in the combined filter for frequencies above . With a decimation factor of 2, this is greatly reduced, but requires some compensation anyway. The resulting channel response has been estimated by transmitting a white noise signal for observations, computing the frequency magnitude, and averaging them together. Then, the equalization function is computed by inverting this response and applying it to any received signal. This method, which is also known in communications as zero-forcing (due to its capability to remove inter-symbol interference), is not very stable when the channel response approximates 0, and it has no finite response, but it works well enough with the channel response after decimation obtained here.
Computing the mitigation performance is only possible if the RFI signal is known in the absence of noise. Therefore, only the RFI waveform was transmitted, using the RFI waveforms types used in ([32] (Fig. 2)). In particular, the following types of RFI have been tested:
- A Delta function: An instantaneous signal where all the RFI power is concentrated in a single, randomly chosen temporal bin.
- A train of pulses with a 10% duty cycle: a train of rectangular pulses with a Pulse Repetition Time (PRT) of samples, a pulse width of samples, and a central frequency of .
- A train of pulses with a 50% duty cycle: a sequence of rectangular pulses sharing the same PRT and frequency, each with a pulse width of samples.
- A continuous wave (CW): A single tone signal (sinusoidal), simulating a narrowband modulation, of of frequency.
- An amplitude-modulated continuous wave (CW): A single-tone sinusoidal signal centered at frequency , representing narrowband modulation, and modulated by a slowly varying signal formed by the sum of two Gaussian envelopes to introduce non-stationarity.
- A narrowband chirp signal centred at : A linearly swept chirp with a bandwidth of and a pulse repetition time of samples. Such chirp patterns are typical of RADAR signals and jamming sources.
- A wideband chirp signal: A linearly swept chirp covering a bandwidth of , with a pulse repetition time of samples.
- The combination of a CW and a narrowband chirp signal, as defined above.
After receiving the RFI (plus instrumental noise), it was equalized and added to a complex white noise signal (of the appropriate power to guarantee a given INR), simulating the radiometric noise. Reception has been performed in packets of samples and with an RF gain of 10 dB.
As a reference to compare with, the received RFI and noise have been transformed using common mitigation techniques: Temporal (no transformation), DFT, Spectrogram/STFT, and Wavelet Digital Transform (DWT), using the definitions found in ([38] (pp. 125–126)). The transformed coefficients’ instantaneous power has been tested for RFI using the following threshold ([38] (Eq. 7.48)) (univariate power detector):
with being the standard deviation of the noise, and the Probability of False Alarm. Once the detection of the RFI-free components has been performed, the residual power can be computed as the variance in the RFI components not excised.
As described in [32], the main performance metrics are the mitigation performance (MP) and the resolution loss (RL). MP and RL are computed using the following:
with being the original RFI power, and the number of excised samples. MP is the ratio between the residuals and the original RFI power, and the RL is the percentage of lost resolution due to the removal of radiometric samples. The excision of radiometric components decreases the radiometric accuracy, with , and and being the original and post-mitigation radiometric accuracies, and the resolution loss metric.).
Monte Carlo observations were considered, with the mitigation conducted independently for each one, and the performance metrics MP and RL were averaged. The sequences have also been used as the observation matrix to estimate the covariance and derive the KLT basis. It should be noted that the observation matrix will be composed of different acquisitions of the same Tx RFI “type” but with different phases. In addition to the instantaneous power detection, the case of direct excision has also been considered for the KLT. As explained in section ([32] (II.B)), this entails identifying the subset of eigen-RFI and rejecting them directly, without a separate detection stage. It should be noted that, in this latter case, is directly the number of identified eigen-RFI.
2.3. Real-Time Asynchronous Mitigator Description
The scenario described in Section 2.2 is based on the offline processing of a previously captured batch of data. Although the post-processing of IQ samples can be useful, real-time mitigation is often the preferable approach, as downloading I/Q samples from a satellite is challenging due to downlink limitations. The eigendecomposition of a matrix is often considered a computationally intensive procedure, as no efficient and fast algorithm is currently known. In this section, a first attempt to implement a real-time architecture is presented and evaluated, which is based on asynchronous covariance decomposition.
This RFI mitigator has been implemented using the GNURadio framework, with the PlutoSDR acting as the front-end. The block diagram of the mitigator is presented in Figure 1, and it is described hereafter. The PlutoSDR has been configured to provide samples per frame at a kHz sampling rate. independent observations will be considered to compute the KLT. After a DC-block of 256 samples to remove the signal bias, the signal is divided into two streams: the upper is the actual data stream where the mitigation will take place, while the lower will serve to compute the decomposition basis.
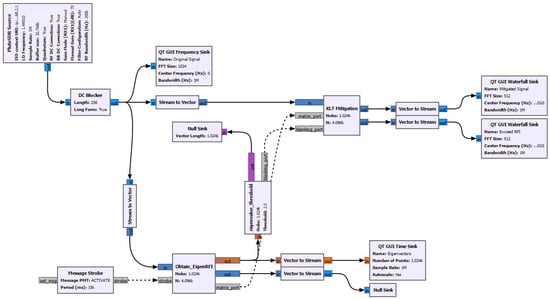
Figure 1.
GNU-Radio block diagram for a KLT-based asynchronous real-time mitigator. Solid lines are for synchronized communications, while dashed lines are for asynchronous message passing.
The KLT involves two computational steps: first, the estimation of the covariance matrix, which is achieved through the multiplication of two matrices, and second, the eigendecomposition of the resulting matrix. The covariance estimation step requires approximately floating-point operations (FLOPs) ([39] (p. 12)), while the eigendecomposition of a symmetrical matrix requires around FLOPs ([39] (p. 462)). Consequently, the total computational complexity of the KLT process is .
If , the economy-sized covariance matrix can be employed to reduce complexity. In this case, the complexity of the eigendecomposition is FLOPs, but an additional matrix multiplication is required to recover the original eigenvectors (Equation (9)), totalling FLOPs. Despite this optimization, the computational burden remains significant when compared with more efficient algorithms such as the Fast Fourier Transform (FFT), which requires FLOPs.
Under the above configuration ( kHz, , ), the PlutoSDR will acquire a full complex observation matrix every s. Updating the KLT basis using the economy trick requires 287.3 GFLOPs. Assuming a CPU that performs one operation every 5 clock cycles and operates at 2.5GHz (2 ns per operation), the computation time for the KLT would be approximately 2.44 s, making its real-time use challenging without parallelization or hardware acceleration. It is worth noting that this estimation does not account for additional constant overheads that can significantly influence practical performance, and other implementation-specific details.
In order to overcome this limitation, the fact that it is not required to update the decomposition basis for all the received data is leveraged. At the lower stream, a buffer (the first “stream to vector”) is used to accumulate observations. This is then passed to a custom Python 3.11.9 block, obtain_EigenRFI, that performs the “economy” covariance eigen-decomposition and the extraction of eigenvectors and eigenvalues. This block is only triggered when indicated by a configurable strobe signal, which can be tailored to the computational power of the target system. In this example, an arbitrary time of 10 seconds is used. In between strobes, obtain_EigenRFI provides the previously computed eigenvectors and eigenvalues to the following blocks. The eigenvectors are arranged in columns and asynchronously passed (via GNU-Radio message) to the main mitigation block, KLT_Mitigation. The eigenvalues are also provided to a thresholding block, eigenvalue_threshold, which compares the eigenvalues with a configurable threshold, and outputs a boolean blanking vector to KLT_Mitigation.
As mentioned, the main mitigation takes place at KLT_Mitigation. There, the last available decomposition basis is used to transform the signal into the KLT-space, and the blanking vector excises those directions believed to be affected by RFI. The signal is reconstructed in the time domain by subtracting the excised RFI from the original signal, after inverse transformation. The outputs are then passed to the visualization sinks. For comparison, the original signal is also passed to the visualization sinks (e.g., spectrogram waterfall).
It should be noted that this asynchronous approach is possible because once the decomposition basis has been derived with M sequences, it can be applied to any other sequence, even if not included in the training dataset. This will be applicable as long as the RFI can be spanned by the eigen-RFI. If the RFI waveform changes, the mitigation performance will decrease. A spaceborne instrument will face this limitation, as the RFI environment is expected to change rapidly due to the movement of the antenna footprint. Hence, it is necessary to tailor the update rate to the specific observation geometry being considered.
3. Results
In this Section, the mitigation performance results are included and discussed, highlighting the advantages of KLT over other mitigation methods. Then, the near real-time operation of the GNURadio implementation is showcased.
3.1. Mitigation Performance
Mitigation results (both mitigation performance and resolution loss ) are depicted in Figure 2. The following conclusions were drawn from a previous intercomparison of mitigation methods, such as in [34]. In this work, the KLT is added into the comparison and can be extracted:
- Temporal is ideal for delta functions and pulsed signals, and less for the modulated CW. It reaches good mitigations (<−25 dB) for moderate resolution loss (<8%), particularly in the case of low duty cycles. However, it does not work for narrowband signals.
- DFT offers very good performance for narrowband RFI, particularly for CW signals, achieving performances of <−30 dB with low resolution loss (<2%). However, it does not work for wideband signals.
- STFT is able to mitigate all types of waveform, but achieving lower performances for selected types than the above. For example, it is able to mitigate both delta functions and CW, but temporal and DFT offer a better performance for these types, respectively. In addition, the resulting resolution loss is quite high (reaching (>20%) for INR > 10.
- DWT is qualitatively similar. It offers better results for delta functions, but its performance is below STFT for the rest of the types.
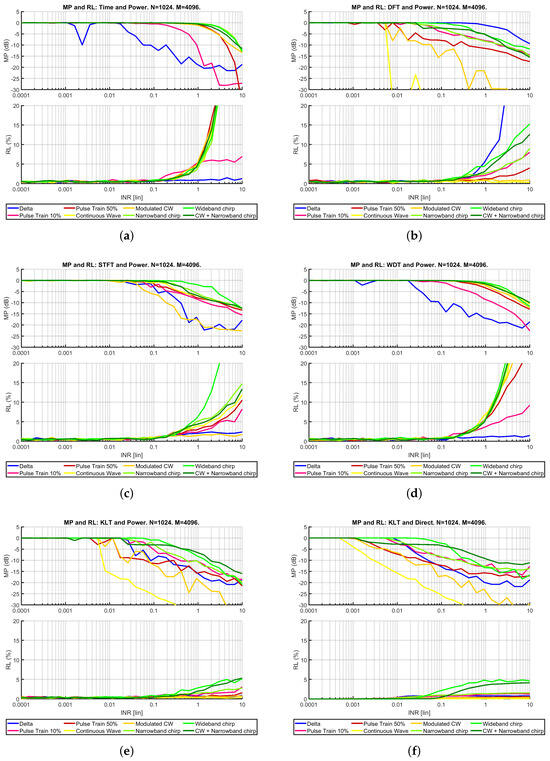
Figure 2.
Mitigation Performance (MP) and Resolution Loss (RL) for the different mitigation algorithms: (a) Temporal and power detection, (b) DFT and power detection, (c) STFT and power detection, (d) DWT and power detection, (e) KLT and power detection, (f) KLT and direct excision.
In addition, Temporal, DFT, STFT and DWT have the common property that their RL “explodes” for some types of high-power RFI, i.e., . This is because these decompositions are unable to fully concentrate the RFI power in a few components, and eventually, all the coefficients will trigger the detection algorithm. When all the components are flagged as RFI, no radiometric signal remains.
In comparison, the KLT is able to mitigate all types of waveforms, being qualitatively similar to DWT or STFT. For the studied cases, however, it offers better mitigation performance, and with lower RL (<5%), even for high mitigation performances (up to −20 dB). Waveforms such as wideband and narrowband chirps exhibit poorer performance due to the higher RFI space dimensionality, but, anyway, a certain degree of mitigation is always possible without increasing the RL above 5%. Its capability of mitigating all types while preserving a low RL is a strong argument in favor of KLT as a mitigation tool.
It is worth remarking that the direct excision strategy (that is, rejecting any eigenvalue identified as eigen-RFI, without an additional detection stage) works better than KLT and power detection, especially for the case of low INR, and with a marginal increase in resolution loss. This should be expected: as there is a strategy to separate the signal space (without a “classical” detection involved), then this enables bypassing some of the challenges of the detection (i.e., detection for low INR). This is especially relevant for low-power RFI (“insidious RFI”), prone to introducing biases in the data. It should be noted that for a noise power of 200 K, an RFI with an INR = 0.01 is of 2 K, above the radiometric sensitivity for salinity retrieval, e.g., see [40]. Achieving mitigations of −5–10 dB can be key to reducing the impact of these types of low-power RFI.
To further illustrate the ability of KLT to extract the RFI signal, Figure 3 presents an example of this mitigation technique, compared with the results obtained using STFT, for a 10% pulsed RFI with an interference-to-noise ratio (INR) of . Additionally, the corresponding eigenvalue distribution is shown in Figure 4. It can be appreciated how the excised RFI with KLT has better fidelity to the original than with STFT.
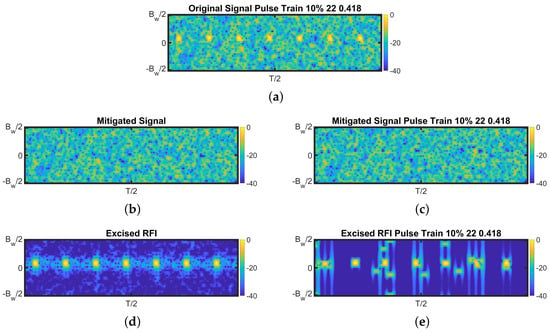
Figure 3.
Spectrograms of a single observation of RFI-contaminated data: (a) original signal; after mitigation using KLT-direct excision (b) and STFT and power detection (c) and the corresponding differences (d,e). The example corresponds to a 10% pulsed RFI with .
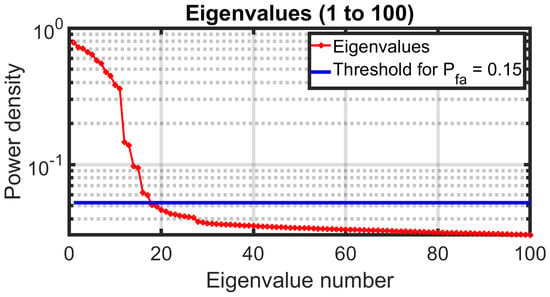
Figure 4.
Eigenvalue distribution of the estimated covariance, for a 10% Pulsed RFI with INR = 0.418.
3.2. Operation in Real Time
The real-time implementation has been demonstrated by executing the GNU-Radio block diagram described in Figure 1 for different input signals and analyzing the output spectrograms.
First, a basic CW RFI has been tested by combining two CW tones (with amplitudes of 1 and 2) and a white noise signal (with an amplitude of 0.5) in GNU Radio. The resulting signal was transmitted through the output port of the Pluto SDR. The output waterfall diagrams are depicted in Figure 5 for the first 30 s of acquisition. During the first seconds, no mitigation takes place, as demonstrated by the “Excised RFI” set to 0. When the first strobe message is received and the decomposition basis is computed, then the mitigation starts. As can be appreciated, it is quite effective in removing the CW tones. As can be seen in the eigenvalue distribution, only a few eigen-RFIs are enough to represent most of the RFI power. In each strobe message, the decomposition matrix will be recalculated with the latest 256 sequences. In terms of performance, there is some staggering of the waterfall diagrams when computing the decomposition, and some overflows are reported in the GNU-Radio console. Otherwise, the simulation runs smoothly, especially if the graphical sinks are deactivated.
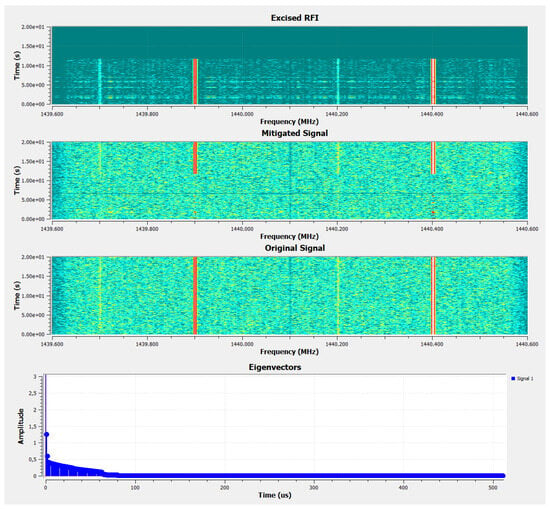
Figure 5.
2 CW Tones mitigated by KLT in real time. The range of the waterfall diagrams is [−20 dB, −60 dB].
The same exercise has been performed with a more complex RFI, modeling an interference caused by a Frequency Modulated CW Radar (FMCW). This type of transmitter can be modeled by a saw-tooth or triangular chirp. GNU-Radio conveniently provides a signal source block to generate these types of signals. It has been configured to generate a triangular chirp of 128 samples of period, sweeping 30% of the bandwidth, and with an amplitude of 0.8 (with a noise signal of 0.5 of amplitude).
In this case, to improve the estimation, 512 sequences have been used to compute the decomposition matrix. The waterfall spectrograms have been represented in Figure 6. As can be seen in the eigenvalue distribution, this time the interference is less concentrated, reflecting the greater complexity (dimensionality) of this RFI.
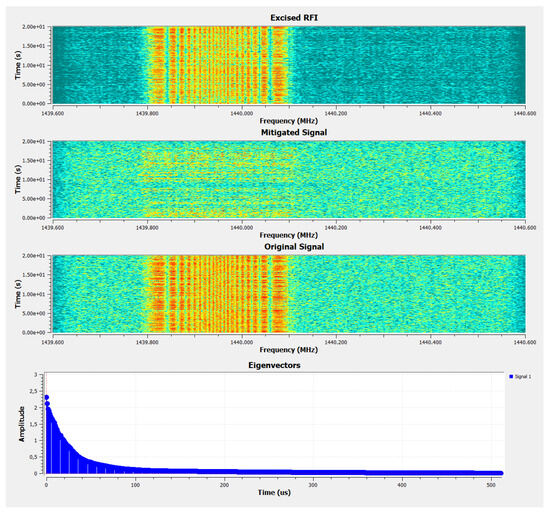
Figure 6.
FMCW Radar signal mitigated by KLT in real time. The range of the waterfall diagrams is [−20 dB, −60 dB].
Nevertheless, once the matrix is computed, the mitigation is quite effective, successfully removing the majority of the RFI energy. However, as shown in the figure, some dynamic residuals remain. Refining the threshold selection or increasing the number of training acquisitions could enhance excision performance. Nonetheless, being dynamic, these residuals may also stem from variations in the RFI waveform that were not adequately captured by the eigen-RFI basis. In such cases, more frequent recomputation of the basis could improve the mitigation process, at the cost of processing power.
4. Conclusions
This paper demonstrates the practicality of KLT-based mitigation and evaluates its performance using real signals with an ADALM-Pluto SDR. Both mitigation effectiveness and resolution loss metrics were assessed using the PlutoSDR’s Tx/Rx capabilities and compared with other common mitigation methods, including temporal, DFT, STFT, and DWT. The results confirm several initial hypotheses about the effectiveness of KLT for RFI mitigation in practical scenarios. Unlike classical transformations with fixed bases, the KLT transformation basis is adaptive to the process under mitigation. As such, it can approximate the ideal matched filter, effectively concentrating RFI power. This confirms its adaptability to various signal types and its good mitigation performance, while maintaining a low resolution loss. KLT is based on the eigendecomposition of the covariance matrix, a computationally demanding task for which no fast algorithm currently exists. Additionally, its performance depends on the dimensionality of the interference signal space and the ability to estimate the covariance matrix accurately with a limited number of observations.
Finally, to demonstrate that a practical KLT mitigator is feasible even under these constraints, a near real-time implementation using GNU Radio is presented. It is based on the asynchronous update of the transformation at regular intervals. The results confirm that it is possible to implement KLT for online mitigation, but significant trade-offs exist among processing power, the number of samples used, frequency of update, and the mitigation performance achieved.
Author Contributions
Conceptualization, R.D.-G. and A.C.; methodology, R.D.-G. and A.C.; software, R.D.-G.; writing—original draft preparation, R.D.-G.; writing—review and editing, A.C.; funding acquisition, A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by ESA, grant number ITT AO9359, by project “GENESIS: GNSS Environmental and Societal Missions—Subproject UPC”, Grant PID2021-126436OB-C21, sponsored by MCIN/AEI/10.13039/501100011033/ and EU ERDF “A way to do Europe”, and grant for recruitment of early stage research staff of Agència Gestió d’Ajuts Universitaris i de Recerca (AGAUR) Generalitat de Catalunya, Spain (FISDUR2020/105).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RFI | Radio Frequency Interference |
| KLT | Karhunen–Loève Transform |
| PCA | Principal Component Analysis |
| SVD | Singular Value Decomposition |
| SDR | Software Defined Radio |
| COTS | Commercial Off-The-Shelf |
| ADC | Analog-to-Digital Converter |
| AGC | Automatic Gain Control |
| I/Q | In-phase/Quadrature |
| INR | Interference-to-Noise Ratio |
| CW | Continuous Wave |
| FMCW | Frequency-Modulated Continuous Wave |
| RL | Resolution Loss |
| MP | Mitigation Performance |
| ITU | International Telecommunication Union |
References
- Ruf, C.; Misra, S.; Gross, S.; De Roo, R. Detection of RFI by Its Amplitude Probability Distribution. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; IEEE: New York, NY, USA, 2006; pp. 2289–2291. [Google Scholar]
- De Roo, R.D.; Misra, S.; Ruf, C.S. Sensitivity of the Kurtosis Statistic as a Detector of Pulsed Sinusoidal RFI. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1938–1946. [Google Scholar] [CrossRef]
- De Roo, R.D. A Simplified Calculation of the Kurtosis for RFI Detection. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3755–3760. [Google Scholar] [CrossRef]
- Tarongi, J.M.; Camps, A. Normality Analysis for RFI Detection in Microwave Radiometry. Remote Sens. 2009, 2, 191–210. [Google Scholar] [CrossRef]
- Tarongí Bauzá, J.M. Radio Frequency Interference in Microwave Radiometry: Statistical Analysis and Study of Techniques for Detection and Mitigation. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2013. [Google Scholar]
- Forte, G.F.; Bauza, J.M.T.; Depau, V.; Vall-llosera, M.; Camps, A. Experimental Study on the Performance of RFI Detection Algorithms in Microwave Radiometry: Toward an Optimum Combined Test. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4936–4944. [Google Scholar] [CrossRef]
- Vrabie, V.; Granjon, P.; Serviere, C. Spectral Kurtosis: From Definition to Application. In Proceedings of the 6th IEEE International Workshop on Nonlinear Signal and Image Processing (NSIP 2003), Grado, Italy, 8–11 June 2003. [Google Scholar]
- Antoni, J. The Spectral Kurtosis: A Useful Tool for Characterising Non-Stationary Signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Søbjærg, S.S.; Svoboda, J.; Balling, J.E.; Skou, N. Detection of Radio-Frequency Interference in Microwave Radiometers Using Spectral Kurtosis. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; IEEE: New York, NY, USA, 2012; pp. 7141–7144. [Google Scholar]
- Taylor, J.; Denman, N.; Bandura, K.; Berger, P.; Masui, K.; Renard, A.; Tretyakov, I.; Vanderlinde, K. Spectral Kurtosis-Based RFI Mitigation for CHIME. J. Astron. Instrum. 2019, 8, 1940004. [Google Scholar] [CrossRef]
- Díez-García, R.; Camps, A. A Novel RFI Detection Method for Microwave Radiometers Using Multilag Correlators. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Lahtinen, J.; Kovanen, A.; Lehtinen, K.; Kristensen, S.S.; Søbjærg, S.S.; Skou, N.; D’Addio, S. Real-Time RFI Processor for the Next Generation Satellite Radiometers. In Proceedings of the 2018 IEEE 15th Specialist Meeting on Microwave Radiometry and Remote Sensing of the Environment (MicroRad), Cambridge, MA, USA, 27–30 March 2018; IEEE: New York, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Kainulainen, J.; Kristensen, S.S.; Saarinen, T.; Uusitalo, J.; Søbjærg, S.S.; Martín-Neira, M. Demonstration of the Polarimetric Cross-Frequency Algorithm for RFI Detection and Filtering. In Proceedings of the IGARSS 2023-2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; IEEE: New York, NY, USA, 2023; pp. 5475–5478. [Google Scholar]
- Kristensen, S.S.; Balling, J.; Skou, N.; Søbjœrg, S.S. RFI in SMOS Data Detected by Polarimetry. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; IEEE: New York, NY, USA, 2012; pp. 3320–3323. [Google Scholar]
- Tarongi, J.M.; Camps, A. Radio Frequency Interference Detection and Mitigation Algorithms Based on Spectrogram Analysis. Algorithms 2011, 4, 239–261. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, Y.; Yang, L.; Dong, Z.; Liang, D. The RFI Suppression Method Based on STFT Applied to SAR. Prog. Electromagn. Res. M 2013, 31, 171–188. [Google Scholar] [CrossRef]
- Mohammed, P.N.; Aksoy, M.; Piepmeier, J.R.; Johnson, J.T.; Bringer, A. SMAP L-band Microwave Radiometer: RFI Mitigation Prelaunch Analysis and First Year On-orbit Observations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6035–6047. [Google Scholar] [CrossRef]
- Camps, A.; Tarongí, J.M. RFI Mitigation in Microwave Radiometry Using Wavelets. Algorithms 2009, 2, 1248–1262. [Google Scholar] [CrossRef]
- Querol, J.; Alonso-Arroyo, A.; Onrubia, R.; Pascual, D.; Camps, A. Assessment of Back-End RFI Mitigation Techniques in Passive Remote Sensing. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), 2015 IEEE International, Milan, Italy, 13–18 July 2015; IEEE: New York, NY, USA, 2015; pp. 4746–4749. [Google Scholar]
- Querol, J. Radio Frequency Interference Detection and Mitigation Techniques for Navigation and Earth Observation. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2018. Available online: https://www.tdx.cat/handle/10803/663905 (accessed on 23 December 2022).
- Díez-García, R.; Camps, A.; Park, H. On the Potential of Empirical Mode Decomposition for RFI Mitigation in Microwave Radiometry. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5304810. [Google Scholar] [CrossRef]
- González-Gambau, V.; Turiel, A.; Olmedo, E.; Martinez, J.; Corbella, I.; Camps, A. Nodal Sampling: A New Image Reconstruction Algorithm for SMOS. IEEE Trans. Geosci. Remote Sens. 2015, 54, 2314–2328. [Google Scholar] [CrossRef]
- Faucheron, R.; Anterrieu, E.; Yu, L.; Khazaal, A.; Rodríguez-Fernández, N.J. Deep Learning Based Approach in Imaging Radiometry by Aperture Synthesis: An Alias-Free Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 6693–6711. [Google Scholar] [CrossRef]
- Kerrigan, J.; Plante, P.L.; Kohn, S.; Pober, J.C.; Aguirre, J.; Abdurashidova, Z.; Alexander, P.; Ali, Z.S.; Balfour, Y.; Beardsley, A.P.; et al. Optimizing Sparse RFI Prediction Using Deep Learning. Mon. Not. R. Astron. Soc. 2019, 488, 2605–2615. [Google Scholar] [CrossRef]
- Sun, H.; Deng, H.; Wang, F.; Mei, Y.; Xu, T.; Smirnov, O.; Deng, L.; Wei, S. A Robust RFI Identification for Radio Interferometry Based on a Convolutional Neural Network. Mon. Not. R. Astron. Soc. 2022, 512, 2025–2033. [Google Scholar] [CrossRef]
- Mohammed, P.N.; Piepmeier, J.R. Microwave Radiometer RFI Detection Using Deep Learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6398–6405. [Google Scholar] [CrossRef]
- Nazar, I.M.; Aksoy, M. Radio Frequency Interference Detection in Microwave Radiometry Using Support Vector Machines. Radio Sci. Lett. 2020, 2, 20–34. [Google Scholar]
- Karhunen, K. Ueber Lineare Methoden in der Wahrscheinlichkeitsrechnung; Annales Academiae Scientiarum Fennicae, Series A, 1, Mathematica-Physica; Universitat Helsinki: Helsinki, Finland, 1947. [Google Scholar]
- Loeve, M. Probability Theory: Foundations, Random Sequences; Van Nostrand: New York, NY, USA, 1955. [Google Scholar]
- Gerbrands, J.J. On the Relationships Between SVD, KLT and PCA. Pattern Recognit. 1981, 14, 375–381. [Google Scholar] [CrossRef]
- Stark, H.; Woods, J.W. Probability, Random Processes, and Estimation Theory for Engineers; Prentice-Hall, Inc.: Saddle River, NJ, USA, 1986. [Google Scholar]
- Díez-García, R.; Camps, A.; Park, H. RFI Mitigation in Microwave Radiometry Using the Karhunen–Loève Transform. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5302513. [Google Scholar] [CrossRef]
- Guner, B.; Johnson, J.T.; Niamsuwan, N. Time and Frequency Blanking for Radio-Frequency Interference Mitigation in Microwave Radiometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3672–3679. [Google Scholar] [CrossRef]
- Querol, J.; Onrubia, R.; Alonso-Arroyo, A.; Pascual, D.; Park, H.; Camps, A. Performance Assessment of Time–Frequency RFI Mitigation Techniques in Microwave Radiometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3096–3106. [Google Scholar] [CrossRef]
- Analog Devices. ADALM-PLUTO Overview. 2024. Available online: https://wiki.analog.com/university/tools/pluto (accessed on 28 November 2024).
- Analog Devices. AD9363 Datasheet. 2024. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/AD9363.pdf (accessed on 28 November 2024).
- Analog Devices. What Is libiio? 2024. Available online: https://wiki.analog.com/resources/tools-software/linux-software/libiio (accessed on 28 November 2024).
- Díez-García, R. New Methods for Radio Frequency Interference in Microwave Radiometry. Ph.D Thesis; Universitat Politècnica de Catalunya: Barcelona, Spain, 2025. Available online: http://hdl.handle.net/10803/694933 (accessed on 23 July 2025).
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Le Vine, D.M.; Dinnat, E.P. Sensitivity of Wide Bandwidth Radiometer for Remote Sensing of Ocean Salinity. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5301517. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).