A Cost-Sensitive Small Vessel Detection Method for Maritime Remote Sensing Imagery

Abstract

Vessel detection technology based on marine remote sensing imagery is of great importance. However, it often faces challenges, such as small vessel targets, cloud occlusion, insufficient data volume, and severely imbalanced class distribution in datasets. These issues result in conventional models failing to meet the accuracy requirements for practical applications. In this paper, we first construct a novel remote sensing vessel image dataset that includes various complex scenarios and enhance the data volume and diversity through data augmentation techniques. Secondly, we address the class imbalance between foreground (small vessels) and background in remote sensing imagery from two perspectives: the sensitivity of IoU metrics to small object localization errors and the innovative design of a cost-sensitive loss function. Specifically, at the dataset level, we select vessel targets appearing in the original dataset as templates and randomly copy–paste several instances onto arbitrary positions. This enriches the diversity of target samples per image and mitigates the impact of data imbalance on the detection task. At the algorithm level, we introduce the Normalized Wasserstein Distance (NWD) to compute the similarity between bounding boxes. This enhances the importance of small target information during training and strengthens the model’s cost-sensitive learning capabilities. Ablation studies reveal that detection performance is optimal when the weight assigned to the NWD metric in the model’s loss function matches the overall proportion of small objects in the dataset. Comparative experiments show that the proposed NWD-YOLO achieves Precision, Recall, and ${\mathrm{AP}}_{50}$ scores of 0.967, 0.958, and 0.971, respectively, meeting the accuracy requirements of real-world applications.

1. Introduction

Maritime vessel target detection is a critical technology in marine environmental monitoring, with extensive applications in both military and civilian domains, including vessel tracking and navigation safety management. With the rapid development of remote sensing imaging technology, utilizing remote sensing for vessel target detection has become an effective strategy. Its advantages include high data availability, high temporal responsiveness, and a broad observation range, making it an ideal choice for monitoring vessel activities across large oceanic areas. In recent years, with the continuous advancement of high-performance computing, deep learning techniques based on neural networks have gradually dominated the field of artificial intelligence. Compared to traditional clustering and classification methods that rely on manually set category features, deep learning technology can automatically learn category features from training data, demonstrating significant performance advantages in classification or regression tasks, thereby also promoting the development of fields such as computer vision [1]. However, in offshore remote sensing images, buildings, docks, and other structures may exhibit spectral characteristics similar to those of vessels. This means that the background in offshore remote sensing images has a complex and diverse feature distribution compared to vessel targets, which can affect the judgment of target detection models [2,3,4,5].

From the perspective of small vessel target detection in offshore remote sensing imagery, we explore a deep learning method focused on small target detection, aiming to address the issue of low detection accuracy caused by the imbalance in feature complexity between small targets and the background during the learning process of deep artificial neural networks. This method can be applied to the learning of the bounding box classification task in vessel detection models for offshore remote sensing images, thereby improving the detection performance of the vessel detection model, enabling precise and rapid identification and localization of vessels in offshore remote sensing images, and counting the number of vessels within port areas. This provides technical support for maritime control and traffic management planning. The specific contributions are as follows:

(1) Addressing the issue of limited high-resolution satellite remote sensing vessel data, we constructed a dataset of remote sensing vessel images under various complex backgrounds. Through data augmentation, the dataset was expanded to include 3831 remote sensing images.

(2) We analyzed the sensitivity of the IoU metric in current mainstream detectors to positional deviations of small objects and introduced NWD as an indicator to measure the similarity between predicted and ground-truth bounding boxes.

(3) To address the imbalance between vessel target and background classes, we propose to replace the IoU component in the confidence loss and bounding box regression loss of YOLOv7 with the NWD metric and provide the optimal replacement ratio. Experimental results indicate that the model’s metrics are significantly higher than the baseline and are as higher than those of the Gold-YOLO and YOLOv8/10/11 models. Additionally, it is demonstrated that the optimal performance is achieved when the proportion of NWD in the model’s loss function matches the overall proportion of small targets in the dataset.

The remainder of our content is organized as follows: Section 2 provides a brief introduction to key technologies related to target detection, outlining some of the current challenges from the perspectives of small targets and imbalanced learning. Section 3 introduces and analyzes the sensitivity of the IoU metric in mainstream detectors to positional deviations of small targets, as well as solutions proposed for class imbalance issues. Section 4 presents experimental validation. Section 5 discusses potential problems. Section 6 concludes the paper with a summary and future outlooks.

2. Related Works

2.1. Object Detection

Deep learning-based object detection primarily focuses on identifying and classifying object instances in digital images, such as humans, landmarks, and vehicles [6]. Object detection algorithms can be categorized based on their implementation methodologies into two-stage detectors and one-stage detectors. Two-stage object detection algorithms mainly consist of two phases: candidate box generation and classification discrimination. During the candidate box generation phase, various strategies are employed, such as selective search, edge boxes, and region proposal networks, to generate region proposals that may contain objects. In the classification discrimination phase, convolutional neural networks (CNNs) are utilized for classification to determine whether an object is present within the candidate box. Traditional algorithms include R-CNN [7] and SPPNet [8], while Fast R-CNN [9] has the capability to jointly train the detector and bounding box regressor. Building upon this, S. Ren et al. proposed Faster R-CNN [10], a deep learning detector that enables near real-time detection with an almost cost-free region proposal generation. T.-Y. Lin et al. [11] introduced Feature Pyramid Networks (FPNs), which employ a top–down architecture with lateral connections to produce multi-scale, high-level semantic feature maps for improved object detection. While two-stage methods offer higher accuracy in discrimination, they are more time-consuming and not conducive to real-time applications.

Single-stage detectors can retrieve all objects in a single inference step. Due to their real-time and easy-to-deploy characteristics, they are widely used in mobile devices. However, their performance is easily affected when detecting densely populated and small objects. You Look Only Once (YOLO) is the first single-stage object detection algorithm widely applied in the field of deep learning [12]. It demonstrated fast speed on the Pascal VOC 2007 dataset, with the fast version achieving an mAP of 52.7% and a processing speed of up to 155 FPS. YOLO utilizes a single neural network to divide the input image into multiple regions and predict bounding boxes and probabilities for each region, which shortens the required detection time but is highly unfavorable for the localization of small objects. YOLO has continuously improved in enhancing the localization accuracy. Recently, YOLOv7, through the introduction of dynamic label assignment and reparameterization of the model structure, has achieved a superior performance in terms of speed and accuracy (ranging from 5 FPS to 160 FPS) compared to most existing object detectors [13]. The Single Shot MultiBox Detector (SSD) is a single-stage object detection algorithm proposed by W. Liu et al. [14], which introduces multi-reference and multi-resolution detection techniques to improve the model’s detection performance. It also has multi-scale detection capabilities, allowing for the detection of objects of different scales at different network levels. N. Carion et al. [15] proposed the Detection Transformer (DETR), which views object detection as a set prediction problem and employs an end-to-end detection network. The introduction of DETR marks a new era in object detection, eliminating the need for anchor boxes or points to detect objects.

In computer vision, small object detection refers to the detection of objects with a limited number of pixels. It has many application scenarios, including video surveillance, remote sensing image processing, and interpretation of unmanned aerial vehicle (UAV) aerial survey data. The term “small” is typically defined in two ways. The first is absolute size: for example, in the COCO dataset, objects with 1024 pixels or less are considered small objects [16]. The second is relative size: according to the definition of the International Society for Optics and Photonics, small objects are those whose size is less than 0.12% of the original image [17,18]. The ships in Figure 1a are examples of small objects, while the ships in Figure 1b are of conventional size.

While the advancements in deep learning have led to significant breakthroughs in object detection, the majority of objects in these tasks are of normal size [19,20]. Due to the limited number of effective pixels occupied by small objects in images, the limited feature information they contain makes it difficult for models to learn target features, resulting in unsatisfactory detection performance. In addition to common issues in general object detection, such as intra-class variation, inaccurate localization, and occluded object detection, there are also some other typical problems in the small object detection task, mainly including missing target features, noisy representation, sensitivity to location bias, and insufficient training samples [21].

(1) Information loss: General feature extractors typically use subsampling, filtering, and noisy activation, which automatically leads to the loss of object. Since the final features still retain most of the information of normal-sized objects, the loss of some information hardly reduces the detection accuracy. However, such operations almost eliminate the weak signals of small objects, making it difficult for the detection module to achieve accurate predictions.

(2) Noise characterization: In object detection, feature representation constitutes the foundational prerequisite for successful object identification. Due to the limited number of pixels occupied by small objects and their susceptibility to interference from background factors and other noise, detectors find it difficult to effectively identify features [4,22,23].

(3) Sensitivity to location bias: Compared with normal-sized objects, locating small objects is more challenging. As shown in Figure 2, the same location offset for objects of different sizes can result in significant differences in IoU changes. In the diagram, we illustrate the sensitivity of the IoU metric to positional deviations in bounding boxes of different sizes. Box A represents the ground truth bounding box. Box B represents a predicted bounding box with a small positional deviation. Box C represents a predicted bounding box with a larger deviation. For an object with only a few pixels, if the pixel deviation between the predicted box and the real box changes from 1 to 3, the IoU value drops from 0.53 to 0.14, which in turn affects the allocation of target labels. However, for a normal-sized object with more pixels, the same deviation only causes the IoU to drop from 0.85 to 0.63. This indicates that in the detection of small objects, IoU is difficult to deal with the perturbation of its bounding box, is extremely sensitive to location bias, which is not conducive to label assignment, and requires higher learning requirements for the regression branch [24].

(4) Insufficient training samples: Selecting positive and negative samples is a necessary operation to achieve high-performance detection, but small objects occupy a relatively small area and have limited overlap with priors (anchor boxes or points). This greatly challenges traditional label assignment strategies, which collect positive and negative samples based on the overlap of bounding boxes or central regions, leading to an insufficient number of positive samples assigned to small objects during the training process.

2.2. Ship Target Detection

The comparison of common ship detection methods in remote sensing images is shown in Table 1. Due to the characteristics of high-resolution satellite remote sensing images, such as scale diversity, density, redundancy, and background complexity, deep learning-based methods primarily enhance detection accuracy through four aspects: (1) improving the effectiveness of feature extraction; (2) enhancing the model’s scalability to scale variations; (3) increasing the stability of bounding box regression; and (4) improving the model’s robustness in different environments.

To capture ultra-scale features and improve the model’s adaptability to scale changes, Zheng et al. [25] proposed a multi-receptive field convolutional group representation aggregation module. This module effectively aggregates features of different scales and enables information sharing and interaction between different scales, thereby improving the model’s detection performance. Wang et al. [26] proposed a unified framework called Feature Merge Single Shot Multibox Detector (FMSSD), which utilizes an Atrous Spatial Feature Pyramid (ASFP) module to fuse contextual information from multi-scale features using feature pyramids and multiple atrous rates. Zhang et al. propose a novel early feature fusion network, named FasterSal, which uses a single-stream structure to receive RGB images and depth maps, extracting features based on the 3D geometric relationships in the depth map while fully leveraging the pretrained RGB encoder [19]. The key to improving the object detection performance in these methods is to construct an optimal feature fusion architecture.

Due to the diverse aspect ratios of ship targets and severe interference with the background, using general horizontal annotation boxes can lead to a large amount of background appearing in the target area, resulting in deviations in regression positions. Zhang et al. [27] addressed the problem of exacerbated offsets in detection box regression by introducing a dynamic feature discrimination module, which improves the model’s discriminative ability through bidirectional spatial aggregation and multi-scale mechanisms. Dong et al. [28] statistically analyzed the scale range of objects in high-resolution remote sensing images to determine appropriate scales for regions of interest in object detection and applied these to the CNN framework for object detection. The results showed a good detection performance. Zhang et al. [29] implemented a recall priority branch function based on the output part of the CenterNet object detector to accurately predict the center points of bounding boxes, thereby reducing the model’s false alarm rate.

The aforementioned methods enhance the detection performance by improving target region alignment, but they struggle to address the issue of imbalanced distribution of target scales. Yu et al. [30] first accurately extracted candidate regions of ships, then performed center cropping on these candidate regions to obtain images of different scales, and finally used these as inputs to the network model. Wang et al. [31] detected objects using detection blocks of different sizes and calculated the average accuracy of detection results from different blocks. They then selected the image scale corresponding to the optimal average accuracy to perform adaptive ship detection, improving the model’s detection accuracy. Sun et al. [32] enhanced feature representation using multi-scale large kernel convolutions, effectively improving the model’s ability to process ships under noisy conditions.

Currently, some scholars are dedicated to addressing the issue of imbalanced data by integrating cost-sensitive concepts with deep learning. This approach aims to enhance the model’s robustness by minimizing the total cost while maintaining accuracy, thereby strengthening deep learning’s capacity to handle imbalanced data [33]. Zhang et al. [34] employed a cost-sensitive ensemble learning method to train speech data, assigning new weights to the basic loss function to improve the performance of separating low signal-to-noise ratio (SNR) audio signals. To distinguish various ocular diseases, Jiang et al. [35] proposed a deep cost-sensitive residual convolutional neural network, utilizing an improved cross-entropy (CE) loss function for classifying ophthalmic images. However, these methods do not specifically address the imbalance in complexity between background features and target features within images.

Related methods are summarized in Table 1.

Table 1. Summary of remote sensing methods for detecting ship targets.

Categories	Feature Extraction Enhancement	Multi-Scale	Improved Bounding Box Regression	Robustness Enhancement	Imbalanced Learning
Related Works	[25,27]	[25,26,30,31,32]	[27,29]	[28,32]	[34,35]
Our Methods	–	–	Adopt NWD Loss for Regression Optimization	Oversampling for Robustness in Complex Scenes	Cost-sensitive Function + Oversampling

Table 1. Summary of remote sensing methods for detecting ship targets.

Categories	Feature Extraction Enhancement	Multi-Scale	Improved Bounding Box Regression	Robustness Enhancement	Imbalanced Learning
Related Works	[25,27]	[25,26,30,31,32]	[27,29]	[28,32]	[34,35]
Our Methods	–	–	Adopt NWD Loss for Regression Optimization	Oversampling for Robustness in Complex Scenes	Cost-sensitive Function + Oversampling

2.3. Imbalanced Learning in Object Detection

Data imbalance is a pervasive challenge in classification problems, often leading to classifiers lacking the ability to recognize minority class samples during training, which in turn impacts the classifier’s performance. To address this imbalance, existing solutions primarily involve data preprocessing and model algorithmic approaches [36].

Data preprocessing involves performing certain operations on the dataset to achieve a balance among various classes. Oversampling and undersampling are the two most commonly used methods in data preprocessing. Oversampling methods primarily aim to balance the number of samples in each class within the dataset by increasing the number of minority class samples. Techniques such as SMOTE (Synthetic Minority Over-sampling Technique) have been widely used for synthetic sample generation [37]. In contrast, undersampling methods achieve dataset balance by reducing the number of majority class samples while ensuring that the classifier’s performance is not significantly affected [38,39]. Data-level methods (oversampling and undersampling) are intuitive and easy to implement, as they operate directly on the dataset without modifying the model architecture, making them compatible with most detection algorithms. Oversampling effectively increases the representation of minority classes, but it may introduce overfitting risks due to repeated use of limited minority samples. Undersampling reduces the size of majority classes to balance the dataset, but it can discard valuable information from the majority class, especially when the majority class contains diverse subcategories or rare but important patterns.

Besides data-level approaches, algorithmic approaches are also crucial for handling imbalance. Cost-sensitive algorithms, ensemble learning, and one-class classification are commonly used methods. Among these, cost-sensitive algorithms are one of the primary methods for addressing data imbalance. They solve the problem by assigning different costs to misclassifications of different samples, thereby better balancing the importance of various classes. For example, in medical diagnosis, accurately identifying a patient’s disease state is crucial, so different penalties are applied to misclassifications to improve the classifier’s performance [40]. In contrast, algorithm-level methods (e.g., cost-sensitive algorithms) adjust the model’s learning process by dynamically emphasizing minority classes through cost assignment, avoiding data distortion issues in data-level methods. They are more adaptive to complex data distributions, as they directly guide the model to focus on hard-to-learn minority samples during training. However, these methods require domain knowledge to set reasonable cost parameters, and their performance heavily depends on the rationality of cost design, which increases the complexity of model tuning. Additionally, algorithm-level methods are often tightly coupled with specific model architectures (e.g., loss function design), limiting their generalizability across different detection frameworks compared to data-level methods.

Due to the advantages of high-resolution satellite remote sensing images, such as high clarity, convenient acquisition methods, and low data costs, researchers can employ mature computer vision object detection methods to conduct validation and evaluation experiments on large-scale data [41]. Therefore, ship target detection based on high-resolution remote sensing images has garnered significant attention from scholars both domestically and internationally, with a surge in related research papers. From a developmental perspective, ship target detection methods based on high-resolution remote sensing images can be categorized into two main types: those based on traditional manual feature modeling and those based on deep learning. Detection methods based on manual feature modeling require human intervention to remove interference factors and generally involve the following steps: extracting similar target candidate regions, acquiring target regions, performing target detection and localization, and ensuring precise target localization. These methods include those based on statistics, voting, and feature learning. Most of these methods require human involvement, heavily rely on human experience, and result in a low detection efficiency and accuracy that do not meet the standards of practical applications. In contrast, deep learning-based methods have become dominant in recent years due to their powerful feature-learning capabilities and end-to-end training. Methods based on convolutional neural networks (CNNs), such as Faster R-CNN, YOLO, and SSD, have been widely adopted for ship detection tasks. Improvements such as Feature Pyramid Networks (FPNs) allow for better multi-scale feature representation, which is crucial for detecting small or densely packed ships. These deep learning models have demonstrated superior accuracy and robustness across various complex maritime scenarios, making them the mainstream approach in modern ship detection research.

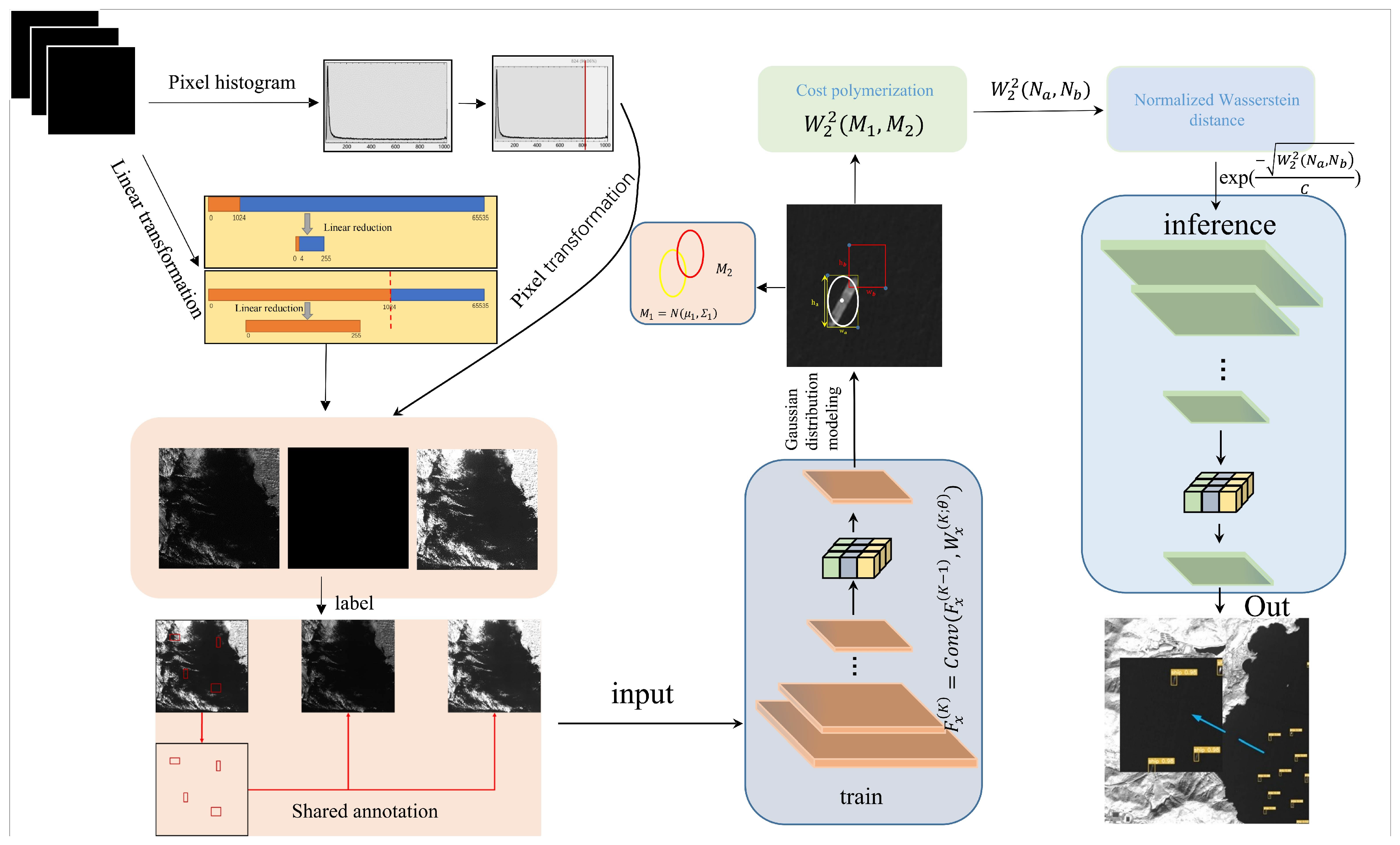
3. Proposed Method

In the task of small object detection in remote sensing images, the conventional IoU metric of standard detectors struggles to handle bounding box perturbations. It exhibits excessive sensitivity to positional deviations, which adversely affects final label assignment. To address this, we aim to minimize the number of erroneous predictions and reduce the impact of skewed class distributions on the cost function. Based on the YOLOv7 model, we introduce a novel metric NWD for small object detection [42]. The NWD replaces the IoU in both the confidence loss and bounding box regression loss within YOLOv7. It calculates the similarity between predicted and ground-truth bounding boxes by modeling their corresponding Gaussian distributions. This approach enables the detector to focus more effectively on small objects characterized by fewer pixels. Furthermore, we employ an oversampling strategy on the remote sensing dataset. Specifically, we duplicate ship targets present in the original dataset as copies. Instances of these copied ships are then randomly selected and copy-pasted onto arbitrary locations within images. This mitigates class imbalance issues from the perspective of dataset augmentation. The pixel pre-process method referenced [43]. The overall data flow diagram of the proposed method is illustrated in Figure 3. It mainly contains three stages; from left to right, they are data preprocessing, training, and inference. In the data preprocessing stage, input remote sensing images undergo pixel transformation and histogram processing to enhance the contrast and suppress the noise, followed by cost polymerization to weight foreground (vessel) and background regions based on class importance. In the training stage, preprocessed images are fed into the model, with vessel bounding boxes in both ground-truth labels and model predictions modeled as 2D Gaussian distributions M1 and M2. The Normalized Wasserstein Distance (NWD) between these distributions is computed to measure their similarity, replacing the traditional IoU metric in both confidence loss and bounding box regression loss. In the inference stage, the trained model processes new input images to output vessel detection results, including bounding box coordinates and confidence scores, enabling precise localization and identification of small vessels under complex maritime conditions.

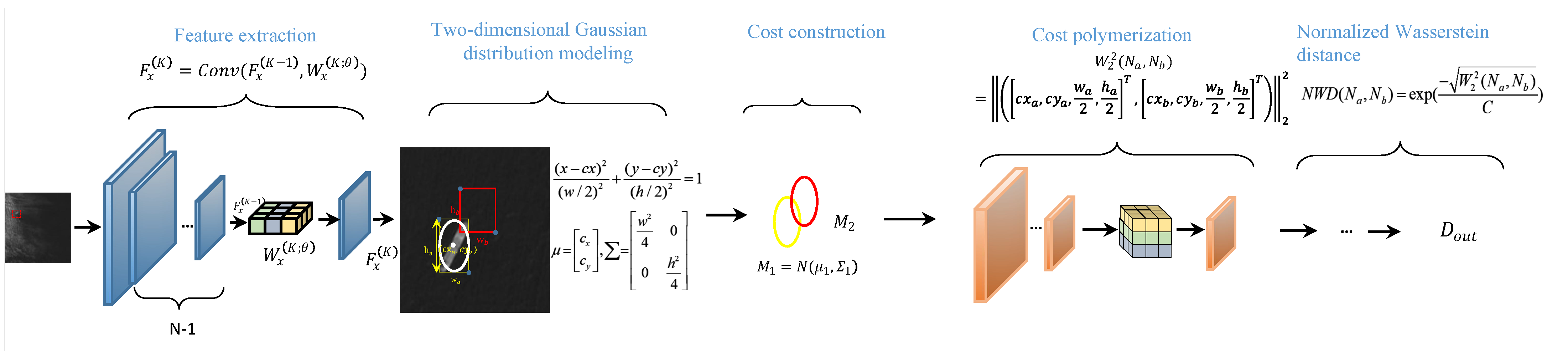
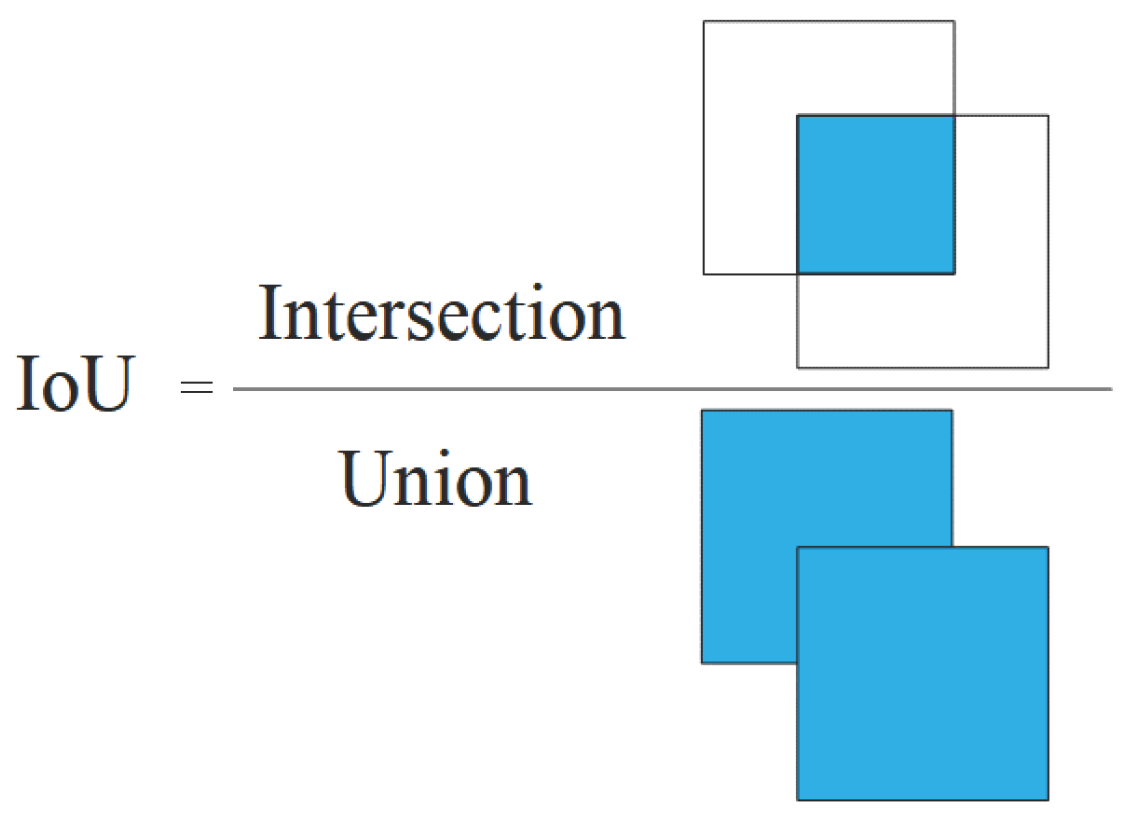
3.1. IoU-Based Cost-Sensitive Improvements

The localization accuracy of an object detection model is primarily determined by its regression branch. To enhance the effectiveness of this module, a loss function is required to optimize the prediction of bounding boxes. The IoU loss is a commonly adopted solution, aiming to align predicted boxes more closely with ground-truth boxes to improve localization performance [44]. However, it fails to provide meaningful gradients when predicted and ground-truth boxes exhibit no overlap. To address this limitation, GIoU introduces the smallest enclosing rectangle covering both boxes. It evaluates the regression box by considering the proportional relationship between the predicted box and the ground-truth box within this enclosed area [45]. Since GIoU degenerates to standard IoU when both boxes are axis-aligned, DIoU incorporates an additional parameter: the normalized distance between their centroids. This accelerates the convergence speed of the loss function [46].

To further enhance the precision of the predicted box, CIoU introduces an additional aspect ratio consistency term, accounting for the discrepancy in width-to-height ratios [47]. The network architecture diagram of the proposed method is illustrated in Figure 4.

The loss function of YOLOv7 comprises classification loss, bounding box regression loss, and confidence loss, as shown in Equation (1). Both the confidence loss and classification loss are computed using the Binary Cross Entropy loss function, while the regression loss employs CIoU.

$$Loss=L_{\mathrm{box}}+L_{\mathrm{obj}}+L_{\mathrm{cls}}$$

(1)

GIoU, DIoU, and CIoU are primarily applied in Non-Maximum Suppression (NMS) and loss functions to replace IoU, thereby enhancing general object detection performance. However, their application in label assignment is seldom discussed. NWD is mainly employed to reduce IoU’s sensitivity to positional deviations in small objects and can substitute for IoU in anchor-based object detectors. We adopt NWD to replace IoU in the computation of both regression loss and confidence loss.

Since the bounding boxes of small objects often contain background pixels, with the target and background predominantly concentrated at the center and boundaries of the box, respectively, the bounding box can be modeled as a 2D Gaussian distribution. In this model, the central region of the bounding box is assigned the highest weight, with weights gradually decreasing from the center towards the boundaries. For a horizontal bounding box $R=(cx,cy,w,h)$, where $cx,cy$ represent the center coordinates, and w and h denote the width and height, respectively; its inscribed ellipse equation can be expressed as Equation (2), and it can be modeled as a two-dimensional Gaussian distribution $N(\mu ,\Sigma )$, as shown in Equation (3).

$${\displaystyle \frac{{(x-cx)}^2}{{(w/2)}^2}}+{\displaystyle \frac{{(y-cy)}^2}{{(h/2)}^2}}=1$$

(2)

$$\begin{array}{c}\hfill \mu =\left[\begin{array}{c}{c}_x\\ c_y\end{array}\right],\Sigma =\left[\begin{array}{cc}{\displaystyle \frac{w^2}{4}}& 0\\ 0& {\displaystyle \frac{h^2}{4}}\end{array}\right]\end{array}$$

(3)

First, the similarity between the predicted box and the ground truth box can be transformed into the distributional distance between two Gaussian distributions. Then, the Wasserstein distance, based on optimal transport theory, is used for computation. For two 2D Gaussian distributions $M_1=({\mu }_1,{\Sigma }_1)$ and $M_2=({\mu }_2,{\Sigma }_2)$, the second-order Wasserstein distance between them is defined as shown in Equation (4), where ${∥·∥}_F$ denotes the Frobenius norm. For bounding boxes $A=(c{x}_a,c{y}_a,w_a,h_a)$ and $B=(c{x}_b,c{y}_b,w_b,h_b)$, Equation (4) can be simplified to Equation (5).

$$W_2^2(M_1,M_2)={\parallel {\mu }_1-{\mu }_2\parallel }_2^2+{∥{\Sigma }_1^{1/2}-{\Sigma }_2^{1/2}∥}_F^2$$

(4)

$$W_2^2(N_a,N_b)={∥\left({\left[c{x}_a,c{y}_a,{\displaystyle \frac{w_a}{2}},{\displaystyle \frac{h_a}{2}}\right]}^T,{\left[c{x}_b,c{y}_b,{\displaystyle \frac{w_b}{2}},{\displaystyle \frac{h_b}{2}}\right]}^T\right)∥}_2^2$$

(5)

However, since $W_2^2(N_a,N_b)$ in Equation (4) represents a distance, whereas a similarity measure must range between 0 and 1, we apply an exponential normalization to obtain what we call the Normalized Wasserstein Distance (NWD), as shown in Equation (6).

$$NWD(N_a,N_b)=exp\left({\displaystyle \frac{-\sqrt{W_2^2(N_a,N_b)}}{C}}\right)$$

(6)

where C is a constant tightly coupled to the characteristics of the experimental dataset; in practice, one usually sets C to the dataset’s mean object size in order to achieve an optimal performance [42].

Under small perturbations of a detection box’s center coordinates and dimensions, the NWD exhibits an approximately linear response with a small slope. This means that for tiny shifts, the NWD-based loss function changes smoothly, and its gradient remains more stable than that of CIoU, still yielding a meaningful penalty even when the boxes do not overlap; moreover, across boxes of different scales, the NWD’s reaction is both stronger and more consistent. The detailed derivation is as follows:

Equation (4) is equivalent to the following:

$$W_2^2(M_1,M_2)={\parallel {\mu }_1-{\mu }_2\parallel }_2^2+\mathrm{Tr}\left({\Sigma }_1+{\Sigma }_2-2\sqrt{{\Sigma }_1{\Sigma }_2}\right)$$

(7)

If a perturbation vector is present, it will introduce small disturbances to both the mean vectors and the covariance matrices. Specifically, the mean vectors change to ${\mu }_1+\Delta \mu$ and ${\mu }_2+\Delta \mu$, and the covariance matrices change to ${\Sigma }_1+\Delta \Sigma$ and ${\Sigma }_2+\Delta \Sigma$, where $\Delta \mu$ and $\Delta \Sigma$ denote small perturbation terms. The variation of the expression is as shown in Equation (8).

$$\begin{array}{cc}\hfill W_2^2(M_1^{\prime },M_2^{\prime })& ={∥({\mu }_1+\Delta \mu )-({\mu }_2+\Delta \mu )∥}_2^2\hfill \\ \hfill & +\mathrm{Tr}\left[({\Sigma }_1+\Delta \Sigma )+({\Sigma }_2+\Delta \Sigma )-2\sqrt{({\Sigma }_1+\Delta \Sigma )({\Sigma }_2+\Delta \Sigma )}\right]\hfill \end{array}$$

(8)

To further calculate the variation in the second-order Wasserstein distance, we subtract Equation (8) from Equation (7):

$$\begin{array}{cc}\hfill \Delta W_2^2& =W_2^2(M_1^{\prime },M_2^{\prime })-W_2^2(M_1,M_2)\hfill \\ \hfill & \approx 2{({\mu }_1-{\mu }_2)}^{\mathrm{T}}\Delta \mu +\mathrm{Tr}\left[2\left({\Sigma }_1{\Sigma }_2-\sqrt{{\Sigma }_1{\Sigma }_2}\right)\Delta \Sigma \right]\hfill \end{array}$$

(9)

From Equation (9), we see that the change in the second-order Wasserstein distance is linearly related to the perturbation, and the proportionality coefficients are quite small. Because $f\left(x\right)=exp\left(-{\displaystyle \frac{\sqrt{x}}{C}}\right)$ is monotonically decreasing, the behavior of the NWD (as defined in Equation (6)) will follow the same trend with respect to the perturbation.

As for how to weight the NWD loss within the overall loss, by Equation (1) the total loss of our system can be written as follows:

$$Loss={\lambda }_1(1-NWD)+{\lambda }_2{L}_{cls}$$

(10)

where $0<{\lambda }_1<1$, $0<{\lambda }_2<1$ and ${\lambda }_1+{\lambda }_2=1$.

The overall model loss is therefore a linear combination of the NWD loss and the original regression loss. Considering that the system focuses on small target objects and the corresponding relationship between the change trend of NWD and input data, the replacement ratio ${\lambda }_1$ should be consistent with the overall proportion of small targets in the dataset.

3.2. Design of a Cost-Sensitive Function Based on Imbalanced Learning

For object detection on the remote-sensing ship dataset, the task can be viewed as a binary classification problem involving ship targets and background categories. In this context, ship targets are positive samples, while the background is the negative sample. In remote sensing datasets, ship categories are sparsely distributed, and the majority of pixels in the images belong to the background category. This results in an imbalance between the ship target category and the background category, meaning that the number of ship target samples is significantly smaller than that of the background category. Under this imbalanced data distribution, general deep learning algorithms tend to favor predicting the category with more samples while performing poorly in the category with fewer samples, which can lead to missed detections or even false positives. As introduced in Section 2.3, the imbalanced learning problem can be addressed from both the algorithmic and data perspectives.

3.2.1. Cost Sensitivity Based on Binary Cross-Entropy Loss

Using BCEWithLogitsLoss as the loss function can evaluate the model’s performance in binary classification problems. This loss function is based on binary cross-entropy and the sigmoid function, used to compare the model’s output with the true labels. The output of the sigmoid function serves as the model’s probability distribution, ranging from 0 to 1; 0 or 1 typically encodes the true labels. As the model output approaches the true label, the value of binary cross-entropy decreases. BCEWithLogitsLoss is an improvement over binary cross-entropy loss (BCELoss), as it allows the model output to be directly passed to the function without first being processed through the sigmoid function. The advantage of this approach is that it improves the numerical stability and reduces the likelihood of gradient vanishing, especially when the absolute values of the model outputs are large. Specifically, the calculation of this loss function is as shown in Equation (11):

$$Loss=-{\displaystyle \frac{1}{N}}\sum _{n=1}^N\left[y_n·log\left(\sigma \left(x_n\right)\right)+(1-y_n)·log(1-\sigma \left(x_n\right))\right]$$

(11)

where $\sigma \left(x\right)={\displaystyle \frac{1}{1+exp(-x)}}$ represents the model output corresponding to the n-th sample, and $y_n$ represents the label category corresponding to the n-th sample. In addition, this loss function can be used in conjunction with cost sensitivity by adding the “pose_weight” parameter to give positive samples a higher weight, thereby placing greater emphasis on the misclassification of positive samples.

As described above in the loss function of YOLOv7, both the confidence loss and classification loss are calculated using BCEWithLogitsLoss. The description of the cost-sensitive object detection algorithm is shown in Algorithm 1.

Algorithm 1 Cost-sensitive YOLOv7 object detection algorithm
Require: High-resolution satellite remote sensing ship images
Ensure: Ship detection result map
	Preprocessing: Data augmentation operations such as Mosaic and random cropping
	Initialisation: Initialise YOLOv7 and weights
	Training:
	for each training iteration do
	1. The YOLOv7 extracts image features and performs classification predictions
	2. Use the ground truth and predictions to the cost-sensitive function to calculate the loss value
	3. Backpropagate the loss and optimise the parameters using the SGD optimiser
	4. After each iteration, evaluate performance using validation set and calculate metrics
	5. Based on the validation set performance, update the weight file, compare the current parameters with the previous iteration’s parameters, and retain the better parameters
	end for
	Testing:
	Input the remote sensing ship test set images and use the trained model for testing to obtain the final detection result image

3.2.2. Oversampling

We employ oversampling methods to address the imbalance issue in data preprocessing, specifically by applying oversampling to remote sensing ship images through repeated copying and pasting [48], as detailed below. There are three different methods for copying and pasting targets. First, select an object in the image, randomly copy it multiple times, and paste it into different positions; second, perform multiple copies and pastes on all objects in the image, again randomly selecting regions; third, select ship targets from the original dataset as copies and randomly choose a few of them to copy and paste into any position. To enhance the diversity of target samples in each image, we choose the third approach. Finally, to avoid conflicts, the pasted samples do not overlap with existing targets in the image during the pasting process. The pasting results are shown in Figure 5.

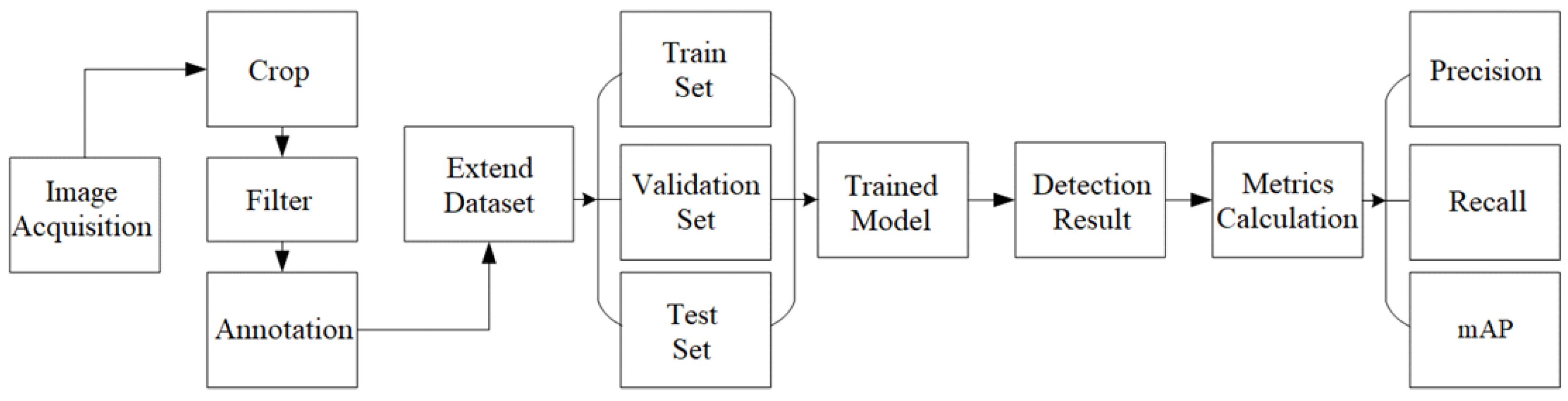
4. Experiments and Analysis

4.1. Implementation Details

The experiment is conducted using YOLOv7 as the base network, with the experimental setup shown in Figure 6. First, the acquired satellite remote sensing images are cropped without overlap. Then, the portions containing ships are selected from the cropped image patches, and these selected image portions are annotated using LabelMe V5.5.0. To enhance the model’s ability to detect targets, traditional data augmentation methods are employed to expand the dataset, which is subsequently divided into training, validation, and test sets. After obtaining a trained model, the test set is input to generate the final detection results and model evaluation metrics.

The experimental environment consists of the Ubuntu 18.04 operating system, an RTX 3080Ti GPU(which was manufactured by NVIDIA Corporation, headquartered in Santa Clara, CA, USA), the PyTorch framework, CUDA 11.3, and Python 3.8. During model training, to ensure sufficient training, the key parameters are set as follows: the number of training epochs is set to 300, the batch size is adjusted to 8, the optimisation function used is SGD, the momentum parameter is 0.937, and the weight decay parameter is 0.0005. In this experiment, to better fit the target, the kmeans algorithm provided in the script is used to calculate the target bounding box, instead of the default bounding box in the ‘yolov7.yaml’ configuration file. In a binary classification problem, if one category is called a positive example, the other category is called a negative example. When the classifier makes a prediction on a sample, if it is correct, it is judged as true (True), otherwise as false (False). Based on these four basic combinations, a confusion matrix can be constructed, which includes four basic elements.

AP (Average Precision), Precision, and Recall are three fundamental evaluation metrics. Precision measures the probability of accurately detecting positive classes. It quantifies the probability that a classifier correctly predicts true examples, as shown in Equation (12). Recall is used to assess a classifier’s ability to identify positive classes. Specifically, Recall refers to the ratio of correctly detected positive samples to the total number of positive samples when the classifier classifies samples, as shown in Equation (13).

$$\mathrm{Precision}={\displaystyle \frac{TP}{TP+FP}}$$

(12)

$$\mathrm{Recall}={\displaystyle \frac{TP}{TP+FN}}$$

(13)

The PR curve uses Recall and Precision as the x and y axes, respectively, representing the balance between the classifier’s ability to identify positive samples and its ability to identify all positive samples. AP is typically calculated as the area enclosed by the PR curve. mAP denotes the average AP across all categories, as shown in Equation (14).

$$\mathrm{mAP}={\displaystyle \frac{{\sum }_{i=1}^{C}A{P}_i}{C}}$$

(14)

where $A{P}_i$ represents the accuracy rate of different categories, C represents the total number of categories. mAP@0.5 denotes the mean Average Precision at an IoU threshold of 0.5. mAP@0.5:0.95 denotes the mean of the AP values computed at IoU thresholds from 0.5 to 0.95 in 0.05 increments, where IoU is the ratio of the area of overlap between a predicted box and the ground-truth box to the area of their union, as shown in Figure 7.

4.2. Datasets

A total of 70 high-resolution satellite remote sensing images with a resolution of approximately $\mathrm{28,000}\times \mathrm{28,000}$ are used in the experiment. We set the resolution of the cropped images to $1024\times 1024$ (for areas less than 1024 pixels at the edges, the original image was retained without filling). After screening, a total of 1275 images containing ships are obtained. Finally, using traditional data augmentation methods, such as contrast adjustment and brightness adjustment, 3825 images are generated, with some examples shown in Figure 8. The enhancement technique applied to the first enhanced image in Figure 8 makes the image as a whole brighter, enhancing the details in the dark part but losing some details in the bright part. The ship is more obvious when it is not occluded, but the effect is worse when it is occluded by clouds and fog. The second enhanced image is slightly darker after processing, and the details of the bright and dark parts are more balanced. Although the ship feature is not prominent enough, it is less affected in the case of cloud and fog occlusion. The brightness and contrast of the third enhanced image are more balanced, and the natural color distribution is more in line with human visual habits while retaining more detailed information. The ship is clearer, and the influence of clouds and fog is weaker. Through the three image enhancement methods, it not only expands the scale of the dataset but also enables the model to learn more diverse visual features, which makes the performance more stable under different lighting, environment, and occlusion conditions and enhances the generalization ability of the model.The dataset is then divided into training, validation, and test sets in a 7:2:1 ratio.

Through a statistical analysis of ship targets in the dataset, it was found that most ship targets have lengths or widths concentrated between 8 and 24 pixels, accounting for approximately 78%, as shown in Figure 9. Calculating the average values of the length and width data for ship targets yields an average of approximately 18 pixels, so the constant C in the NWD is set to 18.

4.3. Experimental Results and Analysis of IoU-Based Cost-Sensitive Improvements

To validate the effectiveness of the NWD metric, the experiment uses YOLOv7 as the base network and compares it with YOLOv5 [49] and YOLOv8 [50] networks. In the loss function of YOLOv7, two components utilize IoU for calculation: the confidence loss and the bounding box regression loss. In the experiments, we completely replace the IoU components in the confidence loss and bounding box regression loss with NWD and compare the results with the original model. We primarily evaluate the model’s performance using the aforementioned metrics. To ensure the validity of the comparisons, all methods are conducted under the same configuration environment. The experimental results are presented in

Table 2. Comparison between NWD and IoU.

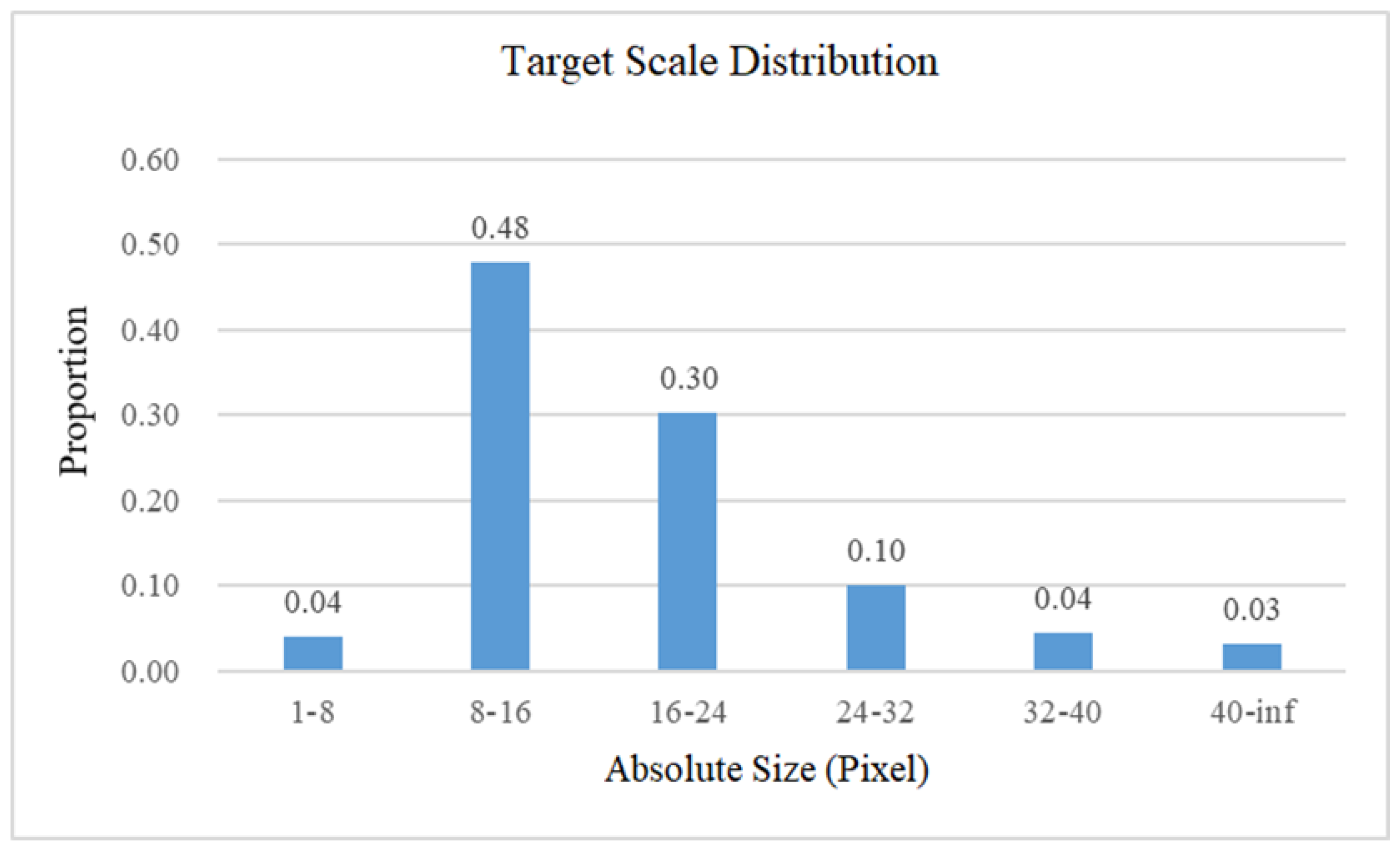
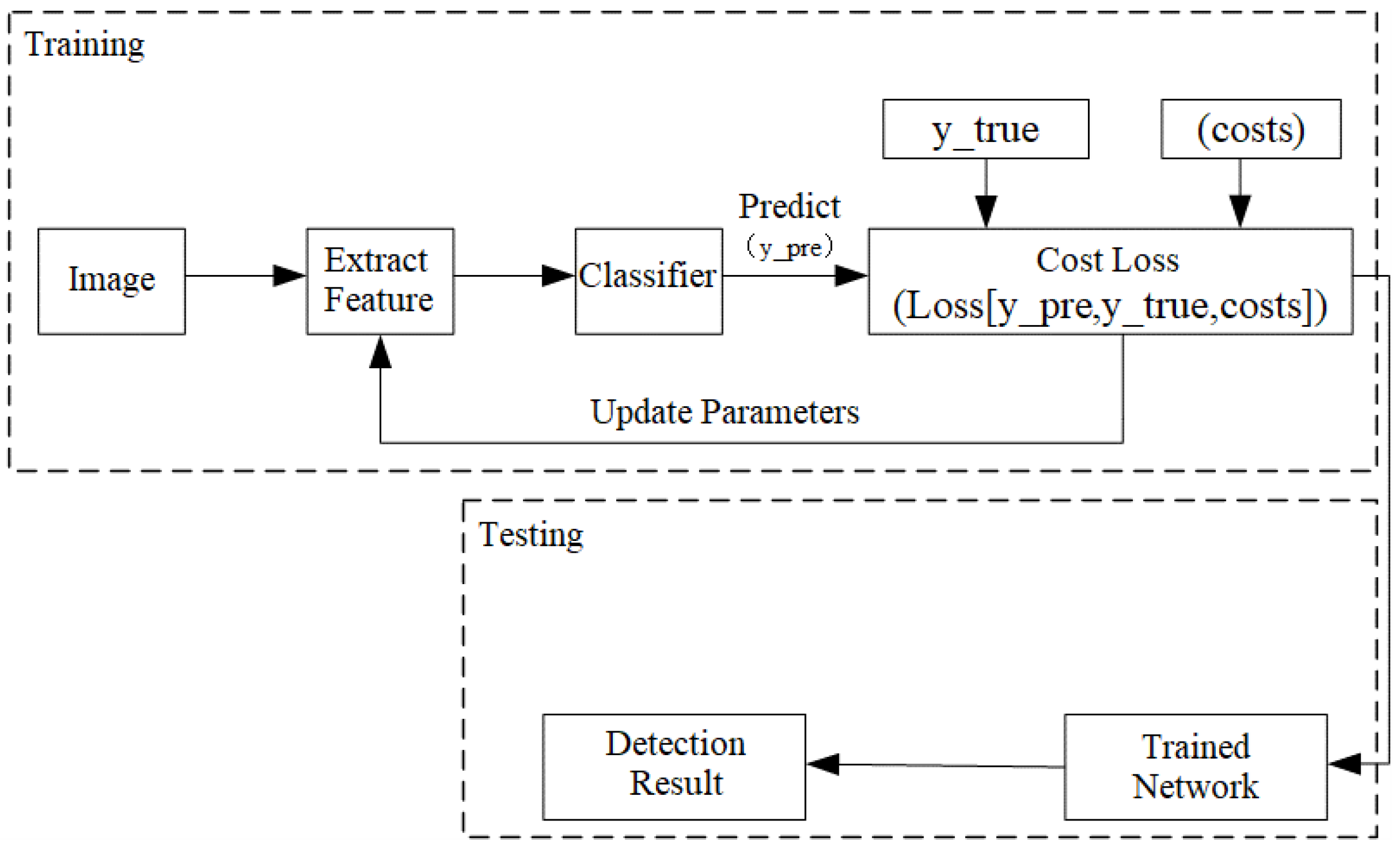
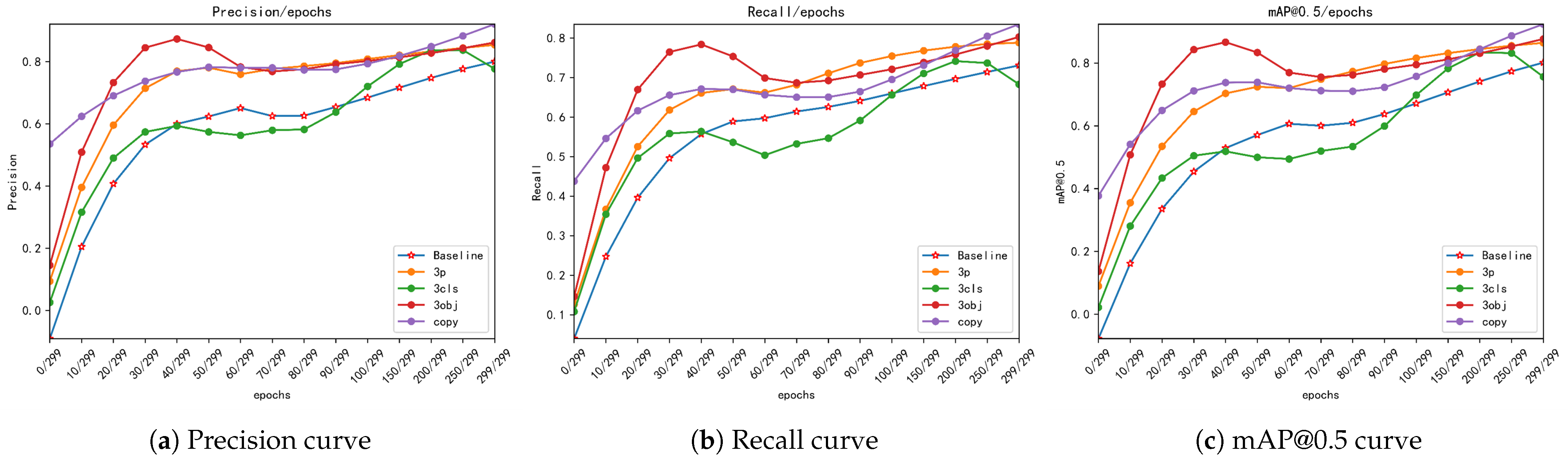
Method	Precision	Recall	${\mathbf{AP}}_{50}$	mAP@0.5:0.95
YOLOv5s [49]	0.859	0.851	0.892	0.448
CBAM-YOLOv7 [51]	0.841	0.811	0.862	0.414
YOLOv7x [13]	0.848	0.782	0.857	0.398
YOLOv7 [13]	0.864	0.766	0.841	0.405
YOLOv8 [50]	0.910	0.904	0.944	0.569
GOLD-YOLO [52]	0.897	0.890	0.930	0.527
RT-Detr [53]	0.959	0.928	0.958	0.594
YOLOv10 [54]	0.927	0.940	0.964	0.617
YOLOv11 [55]	0.927	0.938	0.966	0.605
YOLOv10 (NWD)	0.950	0.917	0.963	0.601
YOLOv11 (NWD)	0.911	0.910	0.952	0.570
YOLOv7 (NWD)	0.967	0.958	0.971	0.588

.

As shown in Table 2, the YOLOv7 model using the NWD to calculate loss outperforms not only the YOLOv7 baseline model but also SOTA models, such as YOLOv8, GOLD-YOLO, RT-Detr, YOLOv10, and YOLOv11, across almost all metrics. Specifically, the improved YOLOv7 model’s Precision metric increases from 0.864 to 0.967, with mAP@0.5 improving from 0.841 to 0.971. Notably, the Recall improves from 0.766 to 0.958, representing a 25% increase. The experimental results indicate that, for small object detection, the NWD is more effective than IoU, improving both the accuracy and Recall. When comparing the experimental results of introducing NWD into YOLOv10/11, it can be observed that the introduction of NWD may even have a negative impact on accuracy. This may be because the multi-scale feature fusion capability of YOLOv7 complements the distribution matching characteristics of NWD. The shallow feature maps of YOLOv7 retain more geometric details of small objects, and NWD can more effectively utilize these details for loss calculation, avoiding information loss caused by downsampling. Conversely, if the backbone network of a model such as YOLOv10/11 is weak in shallow feature extraction, even with the introduction of NWD, it is difficult to fully exploit the potential information of small objects, leading to limited performance improvements.

As shown in Figure 10, the test results more intuitively reflect the differences between the two metrics. In each group of images, the left side represents the original model, while the right side represents the improved model based on the NWD. Therefore, from a qualitative analysis, it can be concluded that in the context of remote sensing small object detection for ships, the NWD-based model outperforms the IoU-based model in both accuracy and Recall. Overall, whether from the quantitative analysis (which comprehensively reflects the performance of the two models on all 3825 images through metrics like Precision and Recall) or the qualitative analysis (which intuitively displays the advantages of the NWD-based model in challenging cases via the six representative images), the results consistently indicate that the NWD-based model performs better than the IoU-based model.

We select three representative remote sensing images: dense ships (a), small ships (b), and cloud cover (c). Compared to the first type, models based on both metrics can detect ships, but the model based on IoU has lower confidence, only around 0.8, while the model based on NWD can reach 0.98. Compared to the second type, the model based on NWD measurement achieves higher Precision while maintaining accuracy, enabling more complete detection of small ships in the image; for the third scenario of cloud cover, the model based on IoU measurement cannot even detect the specific location of ships or provide bounding boxes, while the model based on NWD measurement accurately locates ship targets with a confidence level of 0.98. Therefore, from a qualitative analysis, it can be concluded that in the context of remote sensing small object detection for ships, the NWD-based model outperforms the IoU-based model in both accuracy and Recall. In the aforementioned experiments, the YOLOv7 neural network is used as the base model, with the IoU in both the confidence loss and bounding box regression loss replaced with NWD. To verify the specific impact of NWD on small target detection, we conduct the following ablation experiments: starting from 0, we gradually increased the proportion of NWD in the confidence loss and bounding box regression loss in increments of 0.1.

As shown in

Table 3. Experimental results for different NWD ratios. The optimal NWD ratio is between 0.8 and 0.9.

Ratio	Precision	Recall	mAP@0.5	mAP@0.5:0.95
0.0	0.864	0.766	0.841	0.405
0.1	0.824	0.842	0.875	0.410
0.2	0.854	0.802	0.861	0.401
0.3	0.885	0.848	0.899	0.438
0.4	0.882	0.861	0.897	0.446
0.5	0.922	0.895	0.937	0.501
0.6	0.944	0.949	0.962	0.572
0.7	0.958	0.963	0.976	0.601
0.8	0.974	0.969	0.979	0.646
0.9	0.977	0.963	0.977	0.640
1.0	0.967	0.958	0.971	0.588

, as the proportion of NWD increases, the overall trend in the model’s performance metrics (Precision, Recall, and mAP) first increases and then begins to decline after exceeding 0.8. As shown in the second small object definition method presented in Section 2.2, for images of a certain size, the total size of small objects is approximately 1258 pixels. Based on the analysis of the experimental dataset in Figure 9, the proportion of small objects in the dataset is also around 80–90%. Therefore, this further validates the usefulness of the NWD for small object detection.

4.4. Experimental Validation of Cost-Sensitive Function Design Based on Imbalanced Learning

For ship target detection in remote sensing images, a YOLOv7 target detection algorithm based on a cost-sensitive function is adopted. The specific experimental flowchart is shown in Figure 11. First, the model’s input is the remote sensing ship training set image. The YOLOv7 neural network performs feature extraction and classification prediction on it. Then, using the ground truth information and the cost-sensitive function we set, the current prediction loss value is calculated. The loss value is backpropagated to the network to update the model parameters, and SGD is used to optimise the network parameters. When updating the weight file, the current parameters are compared with the previous round’s parameters, and the better parameters are retained. When the predefined number of rounds is reached, training is no longer performed. After the model is trained, the remote sensing ship test set images are input, and the best weight file is used for testing to obtain the final detection result image.

This experiment validates cost-sensitive methods based on oversampling and binary cross-entropy loss. When validating the oversampling method, to verify its effectiveness and reliability, oversampling is only performed on the original training and validation sets, while the test set remains unchanged. When validating the cost-sensitive method based on binary cross-entropy loss, the following experiments were conducted: assigning higher weights to positive samples in the confidence loss, assigning higher weights to positive samples in the classification loss, and simultaneously assigning higher weights to positive samples in both losses. To provide a more intuitive analysis of the experimental process, this experiment plotted line charts for various metrics to illustrate the training processes of different methods, as shown in Figure 12.

In Figure 12, “Baseline” refers to the baseline model, “3p” represents assigning higher weights to positive samples in both loss functions, “3cls” refers to assigning higher weights to positive samples in the classification loss, “3obj” refers to assigning higher weights to positive samples in the confidence loss, and “copy” represents the results of the oversampling method for few-instance data. The results in Figure 12 show that, for different improvement methods, the model’s performance metrics during training are as follows: Using oversampling, up-weighting positive samples in the confidence-loss term, and up-weighting positive samples in both the confidence and classification losses all yield performance curves above the baseline. However, the method of assigning higher weights to positive samples in the classification loss only outperforms the baseline for a short period and finally becomes worse than the baseline, as shown in Figure 12, curve “3cls”.

As shown in

Table 4. Results of experimental testing.

Method	Precision	Recall	mAP@0.5	mAP@0.5:0.95
Baseline(1,1)	0.837	0.682	0.764	0.364
copy	0.834	0.831	0.861	0.376
3,3	0.861	0.771	0.847	0.407
3,1	0.814	0.705	0.783	0.366
1,3	0.855	0.770	0.856	0.410

, the test results for different experimental methods are presented. In “Baseline (1,1),” the first “1” denotes the initial weight for positive samples in the classification loss, and the second “1” denotes the initial weight for positive samples in the confidence loss; the remaining entries follow the same convention. Compared with the baseline, the oversampling method (note as “copy” in the table) achieves a 22% increase in Recall and an improvement in mAP while barely affecting the Precision. When comparing the baseline with the method of increasing the weights of positive samples in both the confidence loss and classification loss (note as “3,3” in the table), it can be seen that the latter boosts all metrics: Precision rises to 86.1%, and mAP@0.5 reaches 84.7%. However, when applying weights to positive samples in both the confidence loss and classification loss separately(note as “3,1” and “1,3” in the table), it is found that simply weighting positive samples in the classification loss does not significantly improve the model’s metrics and even led to a decrease in accuracy, whereas assigning higher weights to positive samples in the confidence loss alone resulted in metrics similar to those achieved by weighting both simultaneously. The experimental results indicate that when addressing the imbalance between ship target classes and background classes, it is more important to focus on the sample weights in the confidence loss, emphasizing the presence of the target rather than the classification loss issue.

5. Discussions

5.1. Comparison with Prior Research

We further elaborate on the rationale behind adopting YOLOv7 instead of YOLOv10 or YOLOv11. One of the core innovations of YOLOv7 is the E-ELAN (Extended Efficient Layer Aggregation Network), which enhances feature diversity and expressive capacity through group convolutions and feature reorganization (shuffle-merge). This design allows the model to retain more detailed information in shallow layers, which is particularly crucial for small object detection. In contrast, YOLOv10/11 may prioritize global optimization or efficiency in large object detection, and their backbone networks may lose more small object information due to increased depth or larger downsampling factors. Some community-improved versions of YOLOv7 dynamically enhance the weight of small object regions by introducing BRA (Bottleneck Residual Attention) or regional attention modules, whereas the multi-head attention mechanism of YOLOv10/11 may have disadvantages in small object feature extraction. YOLOv7’s dynamic label assignment and gradient flow optimization (such as R-ELAN) ensure that small objects receive sufficient gradient updates during training, improving the training efficiency for small objects, and the lightweight YOLOv7-tiny performs better under limited computational resources. YOLOv10/11 may rely on more traditional training methods, resulting in poorer convergence effects in complex scenarios. Overall, YOLOv10/11 may have limited performance improvement, even with the introduction of NWD, due to architectural designs that are more biased towards general scenarios without an equivalent optimization for small objects.

5.2. Significance of Research Findings

The introduction of the NWD metric not only enhances the performance of small object detection but also provides a new perspective for remote sensing image analysis. By adjusting the weights of classification loss and confidence loss and employing oversampling data augmentation methods, the detection model’s ability to recognize minority classes in imbalanced datasets is effectively improved. Our research underscores the importance of considering metric methods when designing deep learning models, offering valuable references for future research in related fields. These findings will contribute to the development of more accurate remote sensing image recognition systems, especially in application scenarios with small target sizes or high scene complexity [56].

5.3. Limitations of the Study

We analyzed the possible reasons why YOLOv10/11 performs worse than YOLOv7 but did not provide countermeasures. We only provided the empirical value of the constant C in the NWD without giving a specific derivation process.

5.4. Future Research Directions

Future works can explore two main directions. First, combining the inherent shape characteristics of ships, rotation bounding box detection methods can be used instead of horizontal bounding box methods to reduce the impact of background factors on ship target detection [57]. Second, to address the issue of poor imaging quality in satellite remote sensing images, algorithms for removing rain and fog can be integrated into the target detection to further improve the detection performance [58].

6. Conclusions

We constructed a remote sensing image dataset for ship detection, including complex scenarios such as cloud and fog occlusion, ships in close proximity, and entering or exiting ports. Through data augmentation, the dataset comprised a total of 3881 remote sensing images. Additionally, we conducted a detailed analysis of the issue of pixel offset sensitivity when generating prediction boxes for small objects using IoU in current detectors. Our findings indicated that small objects were highly sensitive to pixel offsets in general detectors, resulting in insufficient positive sample allocation. Consequently, the remote sensing dataset contained limited information on small object samples, while background samples constituted a larger proportion. To address the class imbalance issue in remote sensing data, we mitigated its impact on the detection task from both data and algorithmic perspectives. At the dataset level, we employed oversampling techniques, selecting ship targets from the original dataset as duplicates and randomly copying and pasting them to various positions. This approach enriched the target sample information in each image, thereby reducing the impact of foreground and background class imbalance on model detection performance. In terms of cost-sensitive learning, we modified the CIoU loss function of the original YOLOv7 detector by introducing a novel metric—the Normalized Wasserstein Distance (NWD)—as the cost function. By modeling bounding boxes as two-dimensional Gaussian distributions and calculating the similarity between their corresponding Gaussian distributions, the detector increased its emphasis on the foreground (small ships) in remote sensing images during training. By completely replacing the confidence loss and regression loss in the YOLOv7 cost function with NWD, our experiments demonstrated superior performance in detecting small objects, achieving Precision, Recall, and ${\mathrm{AP}}_{50}$ scores of 0.967, 0.958, and 0.971, respectively, surpassing state-of-the-art models like YOLOv10/11 and GOLD-YOLO. Finally, ablation studies revealed that when the proportion of NWD as the cost function aligned with the proportion of small objects in the overall dataset, the model achieved optimal performance, with Precision, Recall, and ${\mathrm{AP}}_{50}$ scores reaching 0.974, 0.969, and 0.979, respectively.

Future works may consider adopting rotated detection boxes instead of horizontal detection boxes to mitigate the impact of the background, as well as integrating de-rain and de-fog algorithms to further enhance target detection performance.