Abstract
Rock hardness significantly impacts comminution efficiency, one of mining’s most energy-intensive processes. Accurate, rapid, and non-invasive hardness characterization can enhance mine-to-mill optimization and energy management. This study investigates sensor-based technologies, hyperspectral imaging, and portable X-ray fluorescence (pXRF) integrated with machine learning (ML) algorithms for characterizing rock hardness in open-pit gold mining contexts. A total of 159 rock samples from two Canadian open-pit gold mines were analyzed through Leeb rebound hardness (LRH), short-wave infrared (SWIR) hyperspectral imaging, and a pXRF analyzer for chemical characterization. The most critical spectral features of SWIR images were extracted using a novel and automated feature extraction approach and further refined by applying a recursive feature elimination (RFE) algorithm to reduce the dimensionality of the spectral feature space. Three ML algorithms, including Random Forest Regressor (RFR), Adaptive Boosting (AdaBoost), and Multivariate Linear Regression (MLR), were applied to develop predictive hardness models considering three scenarios: using chemical features, using refined spectral features, and their combination. The findings underscore the potential of advanced sensor integration and analytics in remotely characterizing rock hardness, which could contribute to enhancing efficiency and sustainability in modern mining operations.
1. Introduction
Comminution, a processing stage to facilitate the liberation of valuable minerals from gangue through particle size reduction, directly influences the efficiency of subsequent mineral processing stages such as flotation [1]. It accounts for a significant portion of the capital and operational costs as well as the highest energy consumption in mine-to-mill operations. According to the U.S. Department of Energy, comminution accounts for around 44 percent of the total consumed energy in the mining sector [2]. Understanding and optimizing these processes play a vital role in improving the economic and environmental sustainability of mine-to-mill operations [3].
Over the past couple of decades, a notable decline in the grade of processed ore has been reported, which could be attributed not only to the depletion of ore reserves but also to advancements in ore extraction and processing technologies [4,5]. At the same time, the high demand of modern society for goods has led to a drastic increase in material extraction. For instance, a 170 percent increase in world material extraction was reported for primary commodities from 1998 to 2014 [4,6]. These changes have resulted in a significant increase in energy consumption in the comminution process, primarily for two reasons. First, processing low-grade materials typically demands greater effort and energy input for crushing and grinding in order to achieve the finer particle sizes necessary for effective liberation and recovery compared to high-grade ores. This increased energy requirement could be primarily attributed to the finer dispersion of the target commodity within low-grade ores, necessitating more intensive comminution to achieve adequate liberation. Second, more low-grade material must be processed to produce the same amount of a commodity as the high-grade material [7]. Considering these effects together highlights the need for a greater focus on optimizing the comminution process. It is important to note that the magnitude of the increase in energy consumption, as a function of a decrease in grade, varies across different commodities, as thoroughly discussed by Calvo et al. [4].
Several factors influence the efficiency of the comminution process in terms of energy consumption and the quality of the final product, with rock hardness being one of the most important [8,9]. Feeding hard rock material into grinders for an extended period results in lower mill throughput and a higher rate of energy consumption. It also increases wear on liners and ball consumption in ball mills and the frequency of downtime for maintenance. The accurate prediction of rock hardness and its variability within ore deposits provides engineers with valuable information, enabling them to make informed decisions regarding prioritization and blending strategies, the optimization of processing parameters, and better maintenance planning [10,11].
From a geomechanical point of view, hardness can be defined as the ability of rocks to resist scratching, penetration, or permanent deformation [12]. It depends on various factors such as mineral type, the bond strength between minerals, grain size, and shape, each having different degrees of importance [13]. Various testing methods have been proposed to measure the hardness of rocks. These testing methods can be categorized into four main groups based on the utilized mechanism: indentation, rebound, scratch, and grinding [14,15]. Among these categories, rebound testing methods, such as the Leeb rebound hardness (LRH) test, have found their way into a broad range of different geomechanical projects because of their flexibility, practicality, and non-destructivity [8,14,16,17,18,19,20,21,22,23].
Measuring rock hardness requires extensive sample collection, preparation, and manual testing procedures, making the process inherently time- and cost-intensive and reducing its practicality. The situation could even be exacerbated when measuring the rock hardness and spatial variability in a newly blasted rock pile. In such a situation, the engineer must collect rock samples from various parts of the newly blasted rock pile. This task can disrupt mining activities and place the engineer in an unsafe location. Therefore, various researchers have attempted to predict rock hardness using other available rock properties, such as geochemical and mineralogical information, to eliminate the mine process interruption and potential safety risks when collecting rock samples from rock piles.
Li et al. [24] established rock hardness predictive models through mineral composition and particle size data obtained from X-ray diffraction (XRD) and thin-section analyses. Houshmand et al. [25] developed machine learning-based models using geochemistry and P- and S-wave velocity data to predict rock hardness measured along core samples. The results showed that geochemistry data could effectively estimate rock hardness. Ghadernejad and Esmaeili [26] employed geochemical data to predict the hardness of rock samples collected from different blasted rock piles within a gold mine. The results implied that raw geochemical data could be used to predict rock hardness. Although these studies have provided a link between geochemical data, rock hardness, and abrasivity, the proposed models still require samples to be taken, prepared, and tested to obtain the required information as input parameters.
Both and Dimitrakopoulos [27] employed Measure While Drilling (MWD) data as a proxy for rock hardness to predict ore throughput by indirectly relating rock hardness to how quickly or slowly the drill bit penetrated the rock. However, MWD techniques often rely on indirect measurements, such as weight on bit, torque, or rate of penetration, which are affected by several factors beyond rock hardness, including the type of drilling equipment used as well as factors like temperature, rock heterogeneity, pressure, vibration, and noise from the drilling process, which can each affect the data quality and accuracy differently. The condition of the drill bit—whether it is new or significantly worn—also plays a crucial role in the observed penetration rates. Moreover, the resolution of MWD data is typically coarse, posing challenges in accurately filling the gaps between drill holes to create a consistent model of rock hardness throughout the mining area, which is of great importance when the behavior of rocks changes significantly within a small area, such as a contact zone between two different geological units.
To overcome the need for extensive sample preparation and testing, hyperspectral imaging techniques provide a non-invasive and rapid alternative, allowing for the collection of mineralogical data directly from rock surfaces. This imaging technique utilizes an imaging spectrometer, commonly referred to as a hyperspectral camera, to capture spectral information. By breaking down the light reflected from a scene into individual wavelengths, the hyperspectral camera generates a two-dimensional image while simultaneously recording the spectral data of each pixel within the image. The detailed spectral profiles obtained facilitate the differentiation of minerals based on their unique spectral characteristics, such as transmission, emission, absorption, and reflectance patterns [28]. This capability enhances geological interpretations and resource assessments. Hyperspectral imaging, as a rapid, non-destructive, and simultaneous multi-range spectral technique, finds application in remote regions to rapidly collect a considerable amount of data.
In mining activities, hyperspectral remote sensing has been primarily utilized for mineral mapping and surface compositional analysis in mineral exploration. It is also used for the lithologic mapping and monitoring of mine tailings, with a particular focus on acid-generating minerals [29,30,31,32,33,34]. Moreover, hyperspectral remote sensing has recently found its way into other geoengineering applications, such as characterizing the physical, geochemical, and mechanical properties of rocks [35,36,37,38,39,40,41,42,43,44].
As one of the initial attempts, Ghadernejad and Esmaeili [45] employed hyperspectral imaging data to develop a non-intrusive, remote, and real-time approach for rock hardness characterization. By relating the spectral features extracted from the reflectance spectrum of visible and near-infrared (VNIR) and short-wave infrared (SWIR) regions to rock hardness, the approach provides engineers and decision-makers at a mine site with both the hardness value and the spatial variability of hardness for the scanned, blasted rock piles. The proposed approach has some drawbacks, such as the feature extraction approach, which involves manually inspecting the results of the K-means clustering analysis performed on the training dataset, which raises two issues. Firstly, performing K-means clustering on the training dataset is inefficient in terms of both time and computational resources. This makes it challenging to adopt the approach for new projects or retrain the model with additional data in the future. The second issue is related to the subjectivity of the proposed approach when manually inspecting observed spectra.
This research has two primary objectives. First, it aims to propose an automated, robust, non-subjective feature extraction approach for hyperspectral data. The goal is to use the extracted features to develop predictive models for rock hardness, addressing the challenges of manual inspection and the subjectivity in feature extraction encountered in the previous work. The focus on the SWIR region is based on previous findings, which identified that the most critical spectral features influencing rock hardness are located in this region. Second, as one of the initial attempts, this study aims to compare the performance and explore the potential benefits of integrating geochemical data with hyperspectral data in predicting rock hardness, which is essential for two reasons. First, to determine whether integrating geochemical and hyperspectral data can enhance the performance of the predictive models. Second, since hyperspectral imaging requires specific environmental conditions, such as adequate lighting, geochemical data serves as an alternative means to provide engineers and decision-makers with the essential information about rock hardness when conducting hyperspectral imaging is not feasible.
The novelty of this study lies not only in the methodology employed for hyperspectral data analysis—specifically, the fast, lightweight, and dimensionality-reduced approach that still preserves predictive power—but also in its contribution to the field by being one of the first studies to use and compare the application of pXRF and hyperspectral data for rock characterization. This comparative approach offers significant practical value, particularly for decision-makers in the mining industry, by guiding the selection of the most suitable tools for effective and efficient rock characterization.
2. Materials and Methods
This section outlines the step-by-step methodology used for collecting and analyzing rock samples, which leads to the development of predictive models for rock hardness. Section 2.1 details the rock sampling protocol and the geology of the study area. In Section 2.2, the discussion focuses on the train–test split, highlighting how the dataset was partitioned to prevent data leakage and address potential class imbalance. Section 2.3 explores the pre-processing and feature engineering techniques applied, as well as the extraction of the absorption peak features; a subsequent feature elimination process is described in Section 2.4. Then, Section 2.5 presents an exploratory data analysis aimed at identifying relationships among geochemical, spectral, and hardness variables. Finally, Section 2.6 details the development of the predictive models, including the algorithms used, hyperparameter tuning, and cross-validation procedures.
2.1. Data Collection
Rock samples were collected from two adjacent open-pit gold mines in Quebec, Canada (Figure 1). The geological setting of the studied open-pit mines features rocks from two main groups: the Pontiac and Piché groups. The Pontiac group consists of sedimentary rocks such as turbiditic greywacke, mudstone, minor siltstone, and thin horizons of ultramafic volcanic rocks. The Piché group includes typically bluish-grey, pervasively foliated rocks with numerous talc–carbonate veinlets and less altered variants that occur as massive, aphanitic to fine-grained serpentinized ultramafic rocks. The results of XRD analyses indicated that the main minerals identified in the collected rock samples included quartz, biotite, muscovite, chlorite, dolomite, calcite, pyrite, talc, magnetite, hornblende, albite, potassium feldspar, and fluorapatite.

Figure 1.
The relative location of the studied open-pit mines and examples of rock samples collected from each pit.
Seventy rock samples were collected from two blasted rock piles in pit 1, mainly comprising sedimentary and meta-sedimentary rocks. For the second pit, eighty-nine rock samples were taken from four blasted rock piles to cover all the rock types in the deposit, including mafic, ultramafic, and intrusive rocks. A total of 159 handpicked rock samples were collected, with a slightly higher number of rock samples for pit 2 due to the complex local geology. Field conditions, such as site accessibility, logistical issues, and costs associated with sampling, transporting, and testing, constrained the number of samples. Nevertheless, the sample size remained within the acceptable range for rock engineering applications. Following the sampling, three rock characterization tests were performed on the collected rock samples, as described in what follows.
The first stage involved measuring the surface concentration of chemical elements using a Portable X-ray Fluorescence (pXRF) device. To do so, a 3-Beam Olympus Vanta Max specialized for mining and geological engineering applications (Figure 2a) was used, which can determine the surface concentration in part per million (ppm) for the following chemical elements: Ag, Al, As, Ba, Ca, Cd, Ce, Co, Cr, Cu, Fe, Hg, K, LE, La, Mg, Mn, Mo, Nb, Nd, Ni, P, Pb, Pr, Rb, S, Sb, Si, Sn, Sr, Th, Ti, U, V, W, Y, Zn, and Zr. The employed pXRF device had a measurement spot with a diameter of approximately 10 mm when the device made full contact with the rock. The representative surface concentration of chemical elements for each rock sample was obtained by taking five measurements on the surface of the samples. Care was taken to place the measurement points on the surface of the rock samples in a way that covered all parts of the testing surface. Furthermore, each beam’s maximum allowable measuring time was used to ensure the utmost reliability and resilience in outcomes. To uphold measurement accuracy, the Certified Reference Material (CRM) SRM2711a [46] and Silica-Blank were employed at the onset of each testing session. A comprehensive set of 18 measurements for both SRM2711a and Silica-Blank were taken to assess instrument precision and bias.

Figure 2.
Workflow of rock characterization tests: (a) pXRF for measuring bulk geochemical concentrations, (b) LRH test for measuring rock hardness, and (c) hyperspectral imaging system.
The LRH test was applied to characterize the rock hardness value for all rock samples in the second stage. LRH is a fast and non-intrusive dynamic impact-and-rebound test initially devised for evaluating the hardness of metallic materials [47]. Recently, the LRH test has been extensively employed for rock hardness characterization in a wide range of geomechanical and geometallurgical projects [8,20,48,49,50,51,52]. The LRH test relies on the concept of energy consumption. During this test, the hardness measurement is determined by comparing the rebound velocity of a solid tungsten carbide sphere upon impact to its initial velocity. Although the impact velocity remains constant, the physical and mechanical characteristics of the rock being tested, like surface elasticity and strength, serve as resistance factors, causing a decrease in the rebound velocity [53]. In this study, LRH tests were performed using an Equotip 550 Leeb D device (Proceq, Zurich, Switzerland) (Figure 2b), following recommendations by the American Society for Testing and Materials (ASTM) and the manufacturer’s testing guidelines [53,54]. Throughout this paper, the term “HLD” will be consistently used to denote the hardness value obtained via a D-type Leeb rebound device.
An integrated approach based on the Small Sample Theory and confidence interval was employed to measure the representative mean HLD value for each sample. This methodology allowed us to determine the minimum number of LRH measurements necessary to derive the representative mean HLD value for each rock sample, considering an error level and a given confidence interval rather than conducting a fixed number of measurements. The key idea behind this approach was that rock samples with different levels of heterogeneity require different numbers of LRH measurements to yield the representative mean HLD value. A detailed description of the utilized approach can be found in [14]. It must also be noted that the device underwent constant calibration, either after every ten consecutive sample tests or at the commencement of each testing day.
In the last data collection stage, hyperspectral imaging was conducted on the gathered rock samples. For this study, the collected rock samples underwent scanning utilizing the HySpex Mjolnir VS-620 (HySpex, Oslo, Norway). The VS-620 operates within the VNIR to the SWIR, covering wavelengths ranging from 400 to 2500 nm. The VNIR region features 1240 spatial pixels, with 200 spectral channels per pixel, in a 3 nm interval. In comparison, the SWIR region offers 620 spatial pixels and 300 spectral channels per pixel in a 5.1 nm interval (Table 1) [55]. The VS-620 was mounted on a custom-built lab rack specifically designed for hyperspectral scanning. Figure 2c details the various components of the hyperspectral imaging system.

Table 1.
The technical specification of the HySpex VS-620 [55].
Variations in rock types and mineral compositions among the collected rock samples could lead to observing diverse albedo during lab scanning. Two distinct diffuse reference panels with predetermined spectral curves were utilized to ensure accurate scanning. It is important to note that each rock sample was individually scanned. This study used only data from the SWIR region to develop the predictive models, minimizing the pre- and post-processing time, reducing the complexity of the models, and increasing the practicality of the proposed approach.
2.2. Train and Test Split
One of the essential steps in developing machine learning (ML) models is to use a proper data partitioning approach, which enables the performance assessment of developed models using testing datasets as unseen data. To ensure that the testing dataset accurately reflects unseen data, no information must be leaked into the model development process. Data leakage commonly arises during data preparation and exploratory data analysis. A typical example of data leakage could be when a model gains information about parameter ranges from the testing dataset [26,45]. Therefore, it is crucial to partition the dataset before proceeding to prevent unintentional data leaks.
Different data necessitate different approaches to partitioning. One commonly used method is the random split approach, which divides the dataset by a random shuffle. However, employing the random split method presents potential issues [8]. It is essential to evaluate the split bias, especially given that 159 rock samples were gathered from six distinct locations during the experimental phase. Random shuffle bias may occur when one data point is allocated to the training set and its neighbouring point to the testing set. This issue is particularly pertinent when dealing with geospatially correlated data, such as core log data. Table 2 represents the statistical summary of the collected rock samples for each sampling location. Observed variation within the collected samples at each sampling location suggested no geospatial correlation.

Table 2.
Statistical summary of measured HLD values for the collected rock samples with respect to the sampling location.
Furthermore, imbalanced data, where the distribution across a target parameter’s range is uneven, can significantly impact predictive model performance. Typically, this results in a concentration of data within a specific range, leaving other segments with fewer data points. Such an uneven distribution can adversely affect model efficacy since increased data volume introduced to the model correlates with enhanced performance. As a result, inadequate data representation within specific parameter ranges hinders a model’s ability to perform optimally. Figure 3 illustrates the uneven distribution of the measured HLD values for all collected rock samples.
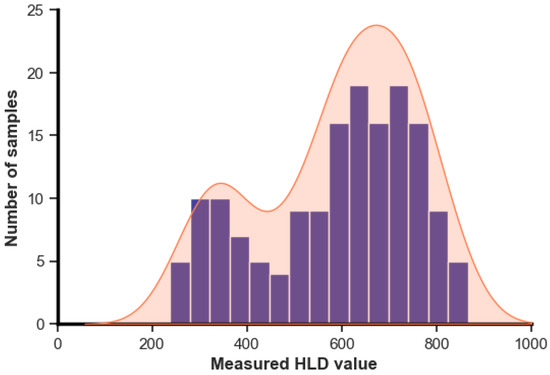
Figure 3.
The distribution of measured HLD values for all collected rock samples.
This study employed a class weighting method to balance the ratio among different classes within the training and testing datasets. This process entailed establishing two auxiliary thresholds for mean HLD values and categorizing distributions into Low, Medium, and High hardness classes. HLD thresholds of 450 and 650 were utilized to categorize the collected rock samples into three classes. Samples with HLD values below 450 were classified as Low, those with HLD values ranging from 450 to 650 were categorized as Medium, and samples with HLD values exceeding 650 were designated High. It is worth mentioning that these class divisions were only used during the train–test split. Eighty percent of the collected rock samples (127 rock samples) were considered for the training and the remaining 20 percent (32 rock samples) were used only for performance assessment, as unseen data. In addition, an attempt was made to keep the same ratio of 80 to 20 percent for the collected rocks in each pit. Moreover, a five-fold cross-validation approach was used in the process of developing the predictive models. The outcomes of the random split, addressing class imbalance for both HLD values, and preserving the same ratio for the collected rocks in each pit are depicted in Figure 4.
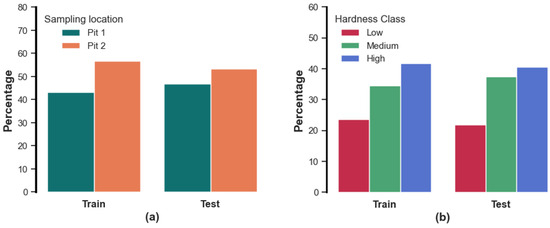
Figure 4.
The outcome of the used train–test split: (a) the ratio of collected rock samples from each pit in the training and testing dataset and (b) the ratio of HLD classes used in the training and testing dataset.
2.3. Preprocessing and Feature Engineering
This section outlines the necessary steps for pre-processing, feature extraction, and feature selection to obtain the most robust and reliable chemical and spectral features for further analyses.
2.3.1. Portable X-Ray Fluorescence Data
Five pXRF measurements were taken for each rock sample to measure the representative surface concentrations of chemical elements. The following steps were taken to determine the most reliable chemical elements. In the first step, the lower detection limit (LDL) of the measured chemical elements was statistically calculated using the reported pXRF measurement concentrations and errors of the collected pXRF data across all training samples [56,57]. For this study, a threshold of 50 percent was considered, implying that 50 percent of the measurements for a particular chemical element were above its LDL.
In the second step, the precision and bias of the pXRF data were checked using the results of 18 replicate pXRF measurements of SRM2711a, which were taken at the beginning of each testing day. This process was essential for assessing the accuracy and consistency of the chemical data before proceeding to further analysis. The precision of each chemical element was evaluated by calculating the percent relative standard deviation (RSD) of all replicate pXRF measurements of the SRM2711a sample. Bias was also determined by calculating the percent difference of the mean concentration of SRM2711a resulting from all replicate measurements to the best value (BV) recommended by the CRM certificate. From the 38 chemical elements analyzed by the pXRF device, those exhibiting over 50% of values surpassing the LDL and less than 20% of RSD were kept for subsequent analyses, as outlined in Table 3.

Table 3.
Detection limit information for pXRF instruments and analytical summary of CRM SRM2711a (n/a = not available).
In the third step, the variance inflation factor (VIF) test was utilized to detect potential collinearity between chemical elements [58]. The findings revealed strong interdependence among Ni, Mg, and Zr. Consequently, Ni and Zr were excluded from the dataset. After considering all the steps, the following chemical elements were selected for the subsequent analysis: Al, Ca, Cr, Fe, K, Mg, Mn, Pb, Rb, Sr, Si, Ti, and Zn.
The statistical summary of the selected geochemical variables is listed in Table 4.

Table 4.
Statistical summary of the measured geochemical variables for the training dataset.
2.3.2. Hyperspectral Imaging Data
Each SWIR image contained the raw spectral information, including the intensity of the electromagnetic radiation reflected from the scanned objects. Each scene comprised the scanned rock sample, the diffuse reference panel, and the tray (Figure 5). The diffuse reference panels—materials with known spectral characteristics—were used to convert the raw spectral values of the SWIR image into reflectance. Two distinct diffuse reference panels, manufactured by SphereOptics under ISO/TS 16949 [59], with predetermined spectral reflectance vectors were utilized to ensure the accurate post-processing of scanned data. These reference panels were Lambertian reflectors at 20 and 50 percent reflectance across the panel’s surface and all collected wavelengths. This process aided in compensating for differences in lighting conditions and sensor reactions, ensuring accurate and reliable data production. The process was completed using the software provided by the manufacturer, following the instructions provided. A comprehensive guide to the use of diffuse reference panels and albedo matching in hyperspectral scanning can be found in [60]. The outcome of radiometric correction using a diffuse reference panel of 50 percent for a spectrum taken from a randomly chosen pixel on the surface of a rock sample is illustrated in Figure 5. Afterward, cropping was performed to reduce image dimensions, retaining only the sample areas while discarding unwanted regions. This aided in streamlining subsequent analyses by removing unnecessary data. The final step focused on masking the background, the area outside the rock sample in the spatial domain, which was essential for accurately defining the samples’ spectral characteristics.
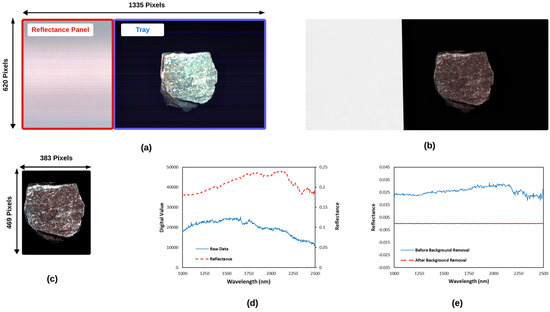
Figure 5.
Pre-processing steps of hyperspectral data: (a) raw SWIR image, (b) radiometric corrected SWIR image (false color at R: 1650 nm, G: 1072 nm, B: 1026 nm), (c) cropped SWIR image, (d) comparison between raw data and reflectance for the same spot before and after radiometric correction, and (e) comparison between the background spectrum for the same spot before and after masking unwanted area.
SWIR images included three-dimensional data with different shapes, depending on the size of the scanned rock samples, that needed to be translated into the tabular form of the same shape to be compatible with the structure of the ML algorithms. This study proposes an absorption peak-based approach to identify and extract the most important spectral features. An absorption peak refers to a characteristic feature in the spectral curve where a significant drop in the reflected electromagnetic radiation occurs at a specific wavelength. The proposed approach calculates the frequency of the absorption peak occurring for a given wavelength over all pixels of a rock sample. It measures the ratio of 0 to 100 percent of how often an absorption peak at a particular wavelength occurs for a rock sample. Instead of feeding the hyperspectral images directly into the ML algorithms, a representative vector that contains information about the frequency of absorption peaks at different wavelengths is provided to the ML.
Figure 6 demonstrates the step-by-step absorption peak extraction process. The continuum removal function is first applied for each pixel by fitting a convex hull over the spectrum using straight-line segments that connect local spectral maxima [61]. It is important to highlight that the first and last data points on the spectrum are specifically constrained to align with the hull, yielding a value of 1.0 for these points in the final continuum-removed spectrum. Then, the approach investigates the spectrum for absorption peaks by detecting changes in the derivative sign of the spectrum at each wavelength. An absorption peak is identified when the sign of the spectral slope changes from negative to positive. The process is repeated for all pixels and the results are saved as tabular data suitable for developing ML predictive models. Combining the absorption peaks extracted from all training samples resulted in a new feature space comprising 289 spectral features. It should be noted that no thresholds (depth and width of absorption peaks) were applied for filtering insignificant spectral features.
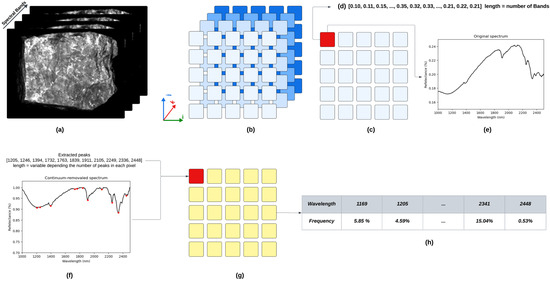
Figure 6.
The utilized absorption peak-based feature extraction approach: (a) the graphical representation of the hyperspectral image, (b) a 3D matrix representation of the hyperspectral image in which each pixel represented a reflectance value, (c) a 2D matrix representation of the hyperspectral image in which each pixel represented the reflectance spectrum, (d) 1D numerical representation of a pixel value, (e) a graphical representation of a pixel of the hyperspectral matrix stored in a 2D matrix, (f) the graphical representation of the feature extraction approach for the continuum removal spectrum of the given reflectance spectrum, (g) applying the peak extraction approach for all pixels and retrieving the extracted absorption peaks for each pixel as a 1D array, and (h) calculating the frequency of absorption peaks at different wavelengths per sample.
2.4. Recursive Feature Elimination
Unlike the final pXRF data, which comprised a limited number of chemical features, 13 in total, the utilized absorption peak extraction approach resulted in 289 spectral features. A significant portion of these spectral features could be related to the noise spectra within the rock samples, usually observed when a major difference in albedo existed on the rock surface. In fact, only a small portion of the remaining spectral features could be found for each rock sample. In addition, the possible presence of highly correlated predictors within the remaining spectral features could inversely impact the ability of the predictive models to identify strong predictors [62]. Although there is a considerable number of studies highlighting the effectiveness of tree-based ML techniques in handling the higher dimensionality of a feature space, even when the number of features is higher by an order of 10 to 100 times than the instances [63,64,65], it is essential to eliminate insignificant features and develop predictive models using the most reliable spectral features. This can eventually reduce the complexity of predictive models and pre-processing times. Hence, this study employed a recursive feature elimination (RFE) approach to exclude the insignificant and highly intercorrelated spectral features from the dataset, as illustrated in Figure 7.

Figure 7.
Workflow of the utilized recursive feature elimination approach.
The RFE approach starts with shuffling the training dataset and applying 5-fold cross-validation. A class-weighting method was used to preserve the same ratio of different hardness classes within each fold. Next, a Random Forest Regressor (RFR) was trained on four folds and validated using the remaining fold. This process was repeated five times, considering one of the folds as validation data each time, and the model’s performance on the validation data was recorded each time. Afterward, the importance of spectral features in the developed model was calculated and the ten least important spectral features were excluded from the dataset. The procedure continued until either (I) a significant drop in model performance was observed or (II) the number of spectral features in the training dataset reached ten. The decision to exclude the ten least important spectral features, which initially represented 3 percent of the spectral feature space, was made after considering the trade-off between high computational demands and the required accuracy and resolution of the RFE approach. This process resulted in 29 runs of the RFR algorithm. The only exception was the first iteration, excluding the nine least important features. The RFE approach is discussed well by [62].
2.5. Exploratory Data Analysis
Hierarchical clustering analysis (HCA) and principal component analysis (PCA) were employed to investigate and understand the relationship between the selected chemical and spectral features with respect to the HLD value as the target parameter. This research represents the first known instance of integrating spectral and geochemical features for rock hardness characterization. In particular, it aimed to explore the potential relationships between geochemical and spectral features and the HLD value, with an emphasis on absorption-based spectral attributes, which had not yet been thoroughly investigated. To do so, the chemical and spectral data obtained for the entire training dataset (127 rock samples) were merged, normalized, and then fed into HCA and PCA algorithms.
HCA is an unsupervised ML technique that groups features based on their similarities. It creates a hierarchy of clusters by merging or splitting existing clusters. This method does not require a predefined number of clusters and provides valuable insights into the natural structure of data [66]. In this study, the agglomerative strategy, also called bottom-up, was used to build up the clusters, in which each data point started in its cluster, and pairs of clusters were merged toward the top of the hierarchy. PCA is another unsupervised ML technique, initially developed for dimensionality reduction while preserving most of the variability present in a dataset. By transforming the original variables into a new set of uncorrelated variables called principal components, PCA allows for a more simplified and interpretable representation of data [67]. This method can be applied to identify the underlying structure of data, highlighting patterns and visualizing differences among groups without requiring any prior knowledge or labelling of data points.
2.6. Developing Predictive Models
Three supervised ML algorithms, including RFR, Adaptive Boosting (AdaBoost), and Multivariate Linear Regression (MLR), were employed to develop predictive models for HLD values based on chemical features, spectral features, and their combination. It must be noted that this study employed an RFE based on the RFR algorithm for feature elimination and the development of predictive models. It also used the other two algorithms, AdaBoost and MLR, to assess the results of feature elimination rather than aiming to compare the performance of the mentioned ML algorithms in predicting HLD values. A brief description of the mentioned ML algorithms is provided below.
RFR is an ensemble learning algorithm that combines predictions from multiple trees, called base learners, to produce more accurate predictions [68]. Numerous trees are trained on different bootstrapped subsets of a given dataset to yield estimations of higher precision. The main reason for using multiple trees is to overcome the instability and substantial variability associated with individual trees, which could lead to varying generalization behaviour, even with insignificant changes in the dataset [69]. By forming an ensemble model from trees, one could expect more accurate predictions, especially when the individual trees are independent. For each tree within the RFR algorithm, the data is recursively divided into more homogeneous groups, called nodes, aiming to enhance the predictability of the response variable [70]. The splits are determined based on the values of predictor features, which hold significant explanatory factors. The mean of the fitted responses obtained from all the individual trees generated by each bootstrapped sample is reported as the final predicted value.
AdaBoost is another ensemble learning technique that improves the performance of weak base learners by focusing on the training instances that previous models predicted poorly. AdaBoost sequentially applies a weak base learner, typically a tree with a single split (decision stump), to the training data, adjusting the weights of misclassified instances to emphasize their importance in subsequent rounds. This process continues for a specified number of iterations or until the model’s accuracy reaches a predefined value. The final prediction is a weighted sum of the predictions from all the weak base learners, allowing AdaBoost to produce a robust predictive model by combining the strengths of multiple weak models [71].
MLR is a fundamental statistical technique to model the linear relationship between a dependent variable and multiple independent variables. In MLR, the model assumes that the target variable is a linear combination of the input features, with coefficients representing the contribution of each feature. The primary goal of MLR is to estimate these coefficients by minimizing the sum of squared differences between the observed and predicted values of the target variable. Despite its simplicity, MLR provides a baseline for comparison and helps in understanding the linear dependencies among the features [72]. The foundational principles and formulations underlying RFR can be found in [68], those for AdaBoost are discussed in [71], and those for MLR are elaborated upon in [72].
The learning process involved applying 5-fold cross-validation on the training dataset to train the mentioned ML algorithms. The employed cross-validation approach systematically split the data into five folds. In each iteration, four folds were used for model training, while the remaining fold served as validation. This cross-validation process was repeated five times, with each fold serving exactly once as the validation set. Hyperparameter tuning was conducted using Bayesian Optimization, an informed approach to hyperparameter tuning. This optimization method uses prior information about the unknown objective function and sample information to determine the posterior distribution of the function. Based on the posterior information, the objective function can be optimized [73]. A complete guide on how Bayesian Optimization was used in this study for hyperparameter tuning can be found in [74]. Finally, the testing dataset was used to assess the performance of the developed predictive models.
3. Results
Figure 8 shows the results of the RFE approach in terms of the lower limit, upper limit, and mean on cross-validation. As can be seen, reducing the number of used spectral features did not significantly affect the performance of the developed model, and the mean fluctuated around 0.71. The highest performance was observed when 40 spectral features were used in developing the models, and further feature elimination slightly decreased the model performance, which was not significant. In addition, Figure 8 reveals that the lower the number of used spectral features, the smaller the difference between the upper and the lower limit, indicating a more robust model. Therefore, it was decided to choose the results of the last iteration as the final spectral feature for further analysis. It is worth noting that the feature elimination process was carried out on the training dataset, and the testing dataset was not yet revealed. The following ten wavelengths, where the most important absorption peaks occurred, were selected for the subsequent analysis: 1082, 1087, 1159, 1174, 1404, 2331, 2336, 2341, 2346, and 2438 nm.
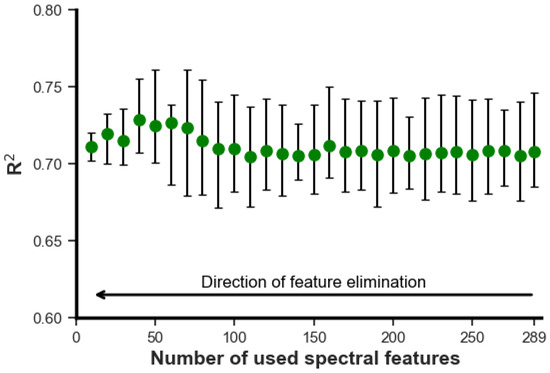
Figure 8.
Results obtained from the recursive feature elimination process.
Figure 9 depicts the results of HCA through a dendrogram diagram. The dendrogram effectively highlights the hierarchical relationships among the features, allowing us to see which features were more closely related to each other and how they progressively grouped into larger clusters. Each leaf of the dendrogram—elements on the horizontal axis—represents a single feature, while branches indicate clusters formed by combining these features based on their similarities. The vertical axis represents the distance or dissimilarity between clusters. The obtained results revealed that there were two general clusters, showing that HLD correlated with the following features: Cr, Fe, Mg, Pb, Sr, 1082, 1087, 1159, 1174, 2336, and 2341.
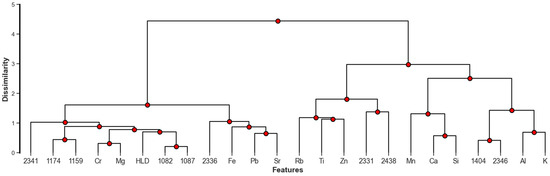
Figure 9.
The results of hierarchical clustering analysis using the dendrogram diagram on the training dataset (127 rock samples).
PCA was also used to study the relationship between chemical and spectral features and the HLD value.
Figure 10 presents the PCA biplot, illustrating the projection of data points onto the first two principal components. Each point in the biplot corresponds to a rock sample within the training dataset, with colours distinguishing the two data sources, Pit 1 and Pit 2. Arrows represent the original features, with their direction and length indicating the contribution and importance of each feature to the principal components. Regarding the relationship between features, features pointing in the same direction were positively correlated. In contrast, features pointing in opposite directions were negatively correlated, and features with arrows perpendicular to each other were uncorrelated. The results show that features such as Mg, Cr, Ni, Fe, Mn, Pb, 1082, 1087, 1159, 1174, 2336, and 2341 were closely related to HLD as they clustered together and pointed in either the same or opposite directions in the biplot. The first two PCAs accounted for 57% of the explained variance since we integrated two different feature spaces: spectral and chemical. Additionally, we did not use PCA to assist in discriminating the rocks; it was used solely to study the relationship between the features and HLD.
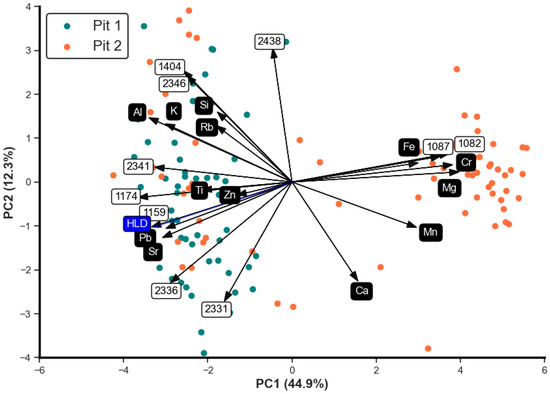
Figure 10.
PCA biplot of chemical features, spectral features, and HLD on the training dataset (127 rock samples).
To better understand how the chemical and spectral features could affect the HLD value, the relationship between the measured HLD value and six of the chemical and spectral features that showed the highest correlation with the target parameter resulting from HCA and PCA was explored. Figure 11 reveals that elements like Mg, Fe, and Cr were negatively correlated with HLD. Similarly, some spectral features (1087 nm) were correlated negatively with HLD, whereas spectral features like 1174 nm and 2336 nm demonstrated a positive correlation.
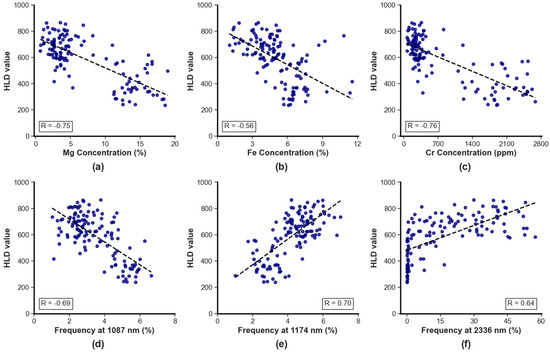
Figure 11.
The correlations between measured HLD and (a) Mg concentration, (b) Fe concentration, (c) Cr concentration, (d) frequency of peaks at 1087 nm, (e) frequency of peaks at 1174 nm, and (f) frequency of peaks at 2336 nm.
In this study, the possibility of three different scenarios, including developing models using (1) chemical features, (2) spectral features, and (3) their combination, was explored in predicting the rock hardness (HLD) value of handpicked rock samples taken from two different open pits. This section presents the obtained results for the developed model using the RFR, AdaBoost, and MLR algorithms.
Several statistical evaluation indices, including the coefficient of determination (), adjusted coefficient of determination (), variance account for (), root mean square error (), and mean absolute error () between the actual and predicted values, were employed to evaluate the accuracy of the predictive models. While the measured the proportion of the variance for the dependent variable explained by the independent variables, the considered the number of independent variables. This is particularly important when comparing the performance of predictive models with different numbers of independent variables. Table 5 presents the performance evaluation results for the RFR model on the testing dataset.

Table 5.
Performance evaluation for the RFR model.
4. Discussion
As shown in Table 5, the performances of the developed RFR models using chemical and spectral features were similar. To further compare the performance of the developed RFR models based on chemical, spectral, and integrated features, a series of statistical tests were conducted to determine whether the observed differences in model accuracy were statistically significant. The comparison focused on the distribution of values obtained from 30 repeated evaluations per model, corresponding to six independent data splits, each with five-fold cross-validation.
An analysis of variance (ANOVA) was first performed using the F-test, which assesses whether there are significant differences among group means, in this case, the mean values across the three model types. The resulting F-statistic was 1.46 with 2 and 58 degrees of freedom, yielding a p-value of 0.24. This suggested that the variability in predictive accuracy between the three model types was not statistically greater than the variability within each group. To investigate potential differences, three paired t-tests were performed on the distributions obtained from the same 30 splits, with an unadjusted significance level of . For the chemical versus spectral models, a value of was observed. A value of was obtained for the chemical versus integration models. Finally, the spectral versus integration comparison yielded . In all cases, p-values exceeded 0.05, indicating that no pairwise differences in mean achieved statistical significance. The 95% confidence intervals around the mean further underscored this overlap—chemical: 0.713 to 0.743; spectral: 0.727 to 0.760; integration: 0.733 to 0.754—indicating that any apparent differences fell within model variability. Together, these results demonstrate that, in the case of this study, neither the chemical nor the integration dataset yielded a statistically significant improvement in predictive accuracy over the spectral model.
This similarity arose because both pXRF and SWIR sensors provided information about the geochemical characteristics of the rock samples in different ways. Although SWIR data did offer insight into the mineralogical composition of the scanned rock, the spectral feature extraction method employed here primarily targeted local spectral features (absorption peaks) that could represent geochemical rather than mineralogical information. On the other hand, this similarity in the performance of the predictive models based on chemical and spectral features is of great importance. As mentioned earlier, while pXRF measurements are local, time-consuming, and interruptive, the hyperspectral imaging system can provide information for a large part of a mine without interrupting mining activities. However, considering that the hyperspectral imaging system requires specific environmental and operational conditions, such as illumination, to yield reliable results, one can use the pXRF device as an alternative approach for characterizing rock hardness when performing hyperspectral imaging is not feasible at a mine site. In addition, the results showed that integrating the chemical and spectral features would not lead to a superior predictive model for predicting HLD values compared to developing models based on either chemical or spectral data.
The robustness of the RFE approach was assessed by repeating the procedure with five additional different train–test splits. This approach ensured that the model’s performance was not biased or dependent on a specific data split, reducing the risk of overfitting. The consistent R2 values across various splits, as depicted in Figure 12, demonstrated the stability and reliability of the model. The method reduced bias, ensured balanced performance evaluation, and confirmed the model’s robustness, with consistent performance across different data subsets. The results showed that the coefficient of variation of the obtained R2 value for all three scenarios was less than 5 percent, ensuring the robustness of the employed RFE.
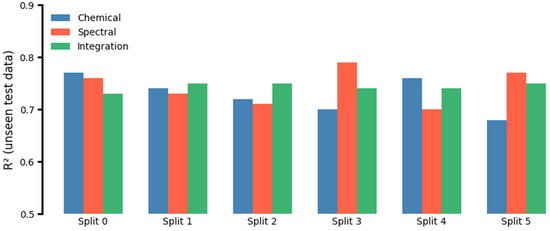
Figure 12.
The performance of the RFR models across different train–test splits.
The other important aspect to investigate was the general effectiveness of the selected spectral features. To do so, the final 10-feature subset obtained through the RFE approach was subsequently used to train an additional ML algorithm, such as AdaBoost and MLR. By evaluating the performance of these alternative algorithms on the reduced feature set, it became possible to determine whether the feature selection process was genuinely robust. In other words, if comparable predictive accuracy was achieved across different modelling techniques using the same compact set of features, this provided strong evidence that the RFE procedure successfully identified features of high predictive value. It must be noted that this procedure was followed only for the main train–test split (split 0 in Figure 12).
Table 6 shows that the AdaBoost algorithm performed similarly to the models developed based on the RFR algorithm, confirming that the proposed feature extraction and RFE resulted in the most robust and critical spectral features. Table 6 also presents the performance evaluation for the MLR models. Although the performance of the MLR models was lower than that of the other algorithms, this outcome was consistent with the previous results since their performance remained relatively stable across different data sources.

Table 6.
Performance evaluation for the AdaBoost and MLR models.
Figure 13 illustrates the performance evaluation for the developed models through a 1:1 plot between the actual and predicted HLD values, providing a concise and straightforward way to evaluate the performance of predictive models. The closer the data is to the 1:1 line, the better the model’s performance. The blue dashed line represents the 1:1 line and the red line represents the trend line between the true and predicted hardness values.
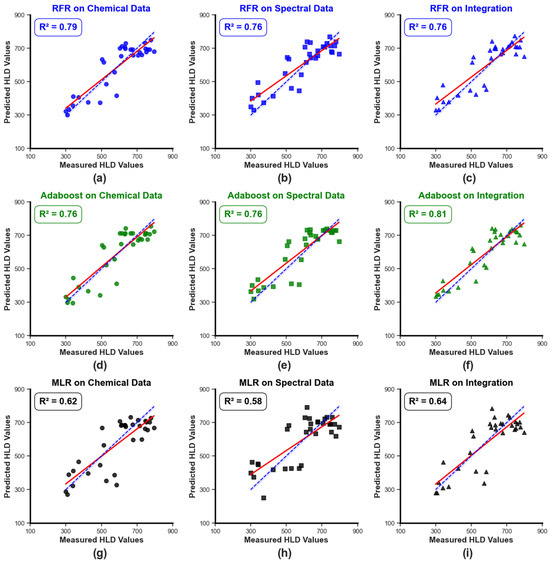
Figure 13.
The 1:1 plots between actual and predicted rock hardness values using the (a) RFR algorithm on chemical data, (b) RFR algorithm on spectral data, (c) RFR algorithm on the integration of chemical and spectral data, (d) AdaBoost algorithm on chemical data, (e) AdaBoost algorithm on spectral data, (f) AdaBoost algorithm on the integration of chemical and spectral data, (g) MLR algorithm on chemical data, (h) MLR algorithm on spectral data, and (i) MLR algorithm on the integration of chemical and spectral data (the blue dashed line represents the 1:1 line and the red line represents the trend line between the true and predicted HLD).
The developed predictive HLD models in this study offer a potentially transformative approach to characterizing rock hardness at mine sites. Traditionally, rock hardness is inferred indirectly through time-consuming and labor-intensive laboratory-based mechanical tests or estimated qualitatively by experienced geologists during blast monitoring and sampling. In many operating mines, including the studied site, there is no formal, real-time system in place for characterizing rock hardness prior to comminution. This lack of timely feedback can lead to suboptimal decisions in blast design, crusher throughput, and mill energy consumption.
The proposed predictive HLD models provide a quantitative and automated method for characterizing rock hardness using a non-destructive, indirect, remote method, enabling early-stage hardness classification and material routing decisions. For example, integrating the spectral-based model with the real-time scanning of rock piles could enable engineers to separate soft and hard materials during the loading and hauling stages, especially before they reach the crusher. This would allow decision-makers and mine engineers to make informed decisions regarding the prioritization of the feed to the mill to optimize the process. Moreover, the proposed models significantly reduce the time, labour, and cost associated with traditional mechanical testing. Even a modest improvement in ore-stream classification could translate into measurable reductions in mill wear, grinding energy, and maintenance downtime, which are key drivers of operational cost in comminution circuits. Future studies will aim to validate the models under actual field conditions and quantify the direct cost–benefit trade-offs of implementation. Nonetheless, the current results represent a promising step toward integrating data-driven rock hardness characterization into practical mine-to-mill workflows.
5. Conclusions
This study aimed to develop ML models to characterize rock hardness, a crucial property of rocks that can significantly impact the comminution process, by utilizing geochemical and hyperspectral data and their integration. The experimental procedure consisted of three stages, including scanning rock samples using the hyperspectral SWIR sensor, conducting pXRF measurements to assess the geochemical data, and performing the LRH test to quantify the hardness of rock samples. Additionally, it aimed to develop a rapid and objective spectral feature extraction method based on the absorption peak concept, converting the 3-dimensional form of hyperspectral data into a tabular format that was more compatible with the structure of the ML algorithms.
In this study, an REF approach was employed on the training dataset to systematically evaluate the feasibility of omitting unrelated spectral features associated with HLD. This process successfully reduced the number of spectral features from 289 to 10, without significantly degrading the performance of the predictive models. Subsequently, HCA and PCA were applied to the final spectral and chemical feature spaces obtained from the training dataset—127 rock samples—to investigate the relationship between these features and HLD. Both methods yielded consistent results, identifying Mg, Cr, Ni, Fe, Mn, Pb, 1082, 1087, 1159, 1174, 2336, and 2341 as being closely related to HLD.
In the next step, three different scenarios, including developing predictive HLD models using the RFR algorithm on chemical features, the top ten selected spectral features, and their combination, were explored. The obtained results showed that the developed models could effectively predict rock hardness. The results also showed that the performance of the developed models, based on both geochemical and hyperspectral data, was comparable and closely aligned. It also revealed that the integration of chemical and spectral features did not enhance the predictive models’ performance. To evaluate the differences in model performance, statistical comparisons using ANOVA and paired t-tests were conducted on repeated R2 values. The results showed no statistically significant differences among the chemical, spectral, and integration models, indicating comparable predictive accuracy across all three data sources. This was primarily because the employed spectral feature extraction in this study primarily focused on local spectral features, which may have been related to geochemical information rather than mineralogical composition.
To test the robustness and practicality of the proposed feature extraction and RFE approach, the process of developing predictive models for the mentioned three scenarios—using chemical features, spectral features, and their combination—was first repeated with five different train–test splits. Across all models, the coefficient of variation remained below 5%, confirming that the models’ performance did not depend on any single train–test split. Furthermore, to assess the overall effectiveness of the selected spectral features, the final ten-feature subset obtained through the RFE approach was subsequently used to train additional ML algorithms, including AdaBoost and MLR. The minimal performance fluctuations observed using various data sources for each ML algorithm further demonstrated the robustness of the selected features.
Despite these technical advances, several constraints remain. First, the number of rock samples used, while sufficient for initial model development, may not capture the full geological variability encountered across the entire ore body. It is worth noting that the purpose of this study was not to develop a hardness model that could be directly applied to all parts of the mine from which we collected samples but, rather, to present a novel approach for predicting ore hardness using chemical and spectral data. If a mine decides to adopt the developed model, it must be regularly updated based on new samples and tests. Second, all hyperspectral data were acquired under controlled laboratory conditions—constant illumination, zero moisture, and fixed sensor distance—which did not reflect the heterogeneity of open-pit environments (e.g., variable sunlight, dust, moisture, and atmospheric scattering). Third, practical implementation will demand portable SWIR sensor platforms, on-site calibration protocols, and real-time data-processing pipelines. Finally, industry adoption will depend on demonstrating clear cost–benefit advantages, seamless integration with existing operational workflows, and user-friendly decision-support interfaces.
Author Contributions
Conceptualization, S.G., K.E., and M.P.C.; methodology, S.G. and K.E.; software, S.G.; validation, S.G., K.E., and M.P.C.; formal analysis, S.G.; investigation, S.G.; resources, K.E.; data curation, S.G.; writing—original draft preparation, S.G.; writing—review and editing, K.E. and M.P.C.; visualization, S.G.; supervision, K.E.; project administration, K.E.; funding acquisition, K.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science and Engineering Research Council of Canada (NSERC), grant number ALLRP 561062–20.
Data Availability Statement
Some or all data, models, or codes that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors would like to acknowledge the Weir Group and the Natural Science and Engineering Research Council of Canada (NSERC) for their financial support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Napier-Munn, T.J.; Morrell, S.; Morrison, R.D.; Kojovic, T. Mineral Comminution Circuits Their Operation and Optimization; Julius Kruttschnitt Mineral Research Centre, University of Queensland: Indooroopilly, Australia, 1996; ISBN 064628861X. [Google Scholar]
- Abdelhaffez, G.S. Estimation of the Wear Rate Associated with Ball Mill of Mahd Ad Dahab Gold Mine, Saudi Arabia (Ksa). Min. Miner. Depos. 2018, 12, 36–44. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Wang, E.; Liu, X.; Geng, J.; Chen, J. Comminution Energy Based on Particle Size Distribution and Crushing Mechanism During Coal and Gas Outburst. Nat. Resour. Res. 2024, 34, 1147–1167. [Google Scholar] [CrossRef]
- Calvo, G.; Mudd, G.; Valero, A.; Valero, A. Decreasing Ore Grades in Global Metallic Mining: A Theoretical Issue or a Global Reality? Resources 2016, 5, 36. [Google Scholar] [CrossRef]
- Runge, K.C.; Frausto, J.J.; Lisso, M.M.; Jokovic, V.; Yahyaei, M. Importance of Considering Classification and Liberation When Optimising Comminution and Flotation. Miner. Eng. 2024, 209, 108612. [Google Scholar] [CrossRef]
- U.S. Geological Survey Water Resources Division. Mineral Commodity Summaries 2015; U.S. Geological Survey Water Resources Division: Reston, VA, USA, 2015.
- Merrill-Cifuentes, J.; Cracknell, M.J.; Escolme, A. Rock Hardness and Copper Recovery Prediction Using Textural Clustering. Miner. Eng. 2023, 193, 108005. [Google Scholar] [CrossRef]
- Houshmand, N.; Esmaeili, K.; Goodfellow, S.; Carlos Ordóñez-Calderón, J. Predicting Rock Hardness Using Gaussian Weighted Moving Average Filter on Borehole Data and Machine Learning. Miner. Eng. 2023, 204, 108448. [Google Scholar] [CrossRef]
- Carrasco, C.; Keeney, L.; Napier-Munn, T.J.; Bode, P. Unlocking Additional Value by Optimising Comminution Strategies to Process Grade Engineering® Streams. Miner. Eng. 2017, 103, 2–10. [Google Scholar] [CrossRef]
- Bye, A.R. Case Studies Demonstrating Value from Geometallurgy Initiatives. In Proceedings of the First AusIMM International Geometallurgy Conference, Brisbane, Australia, 5–7 September 2011; Australasian Institute of Mining and Metallurgy: Carlton, Australia, 2011; pp. 9–30. [Google Scholar]
- Nwaila, G.T.; Ghorbani, Y.; Becker, M.; Frimmel, H.E.; Petersen, J.; Zhang, S. Geometallurgical Approach for Implications of Ore Blending on Cyanide Leaching and Adsorption Behavior of Witwatersrand Gold Ores, South Africa. Nat. Resour. Res. 2020, 29, 1007–1030. [Google Scholar] [CrossRef]
- Demirdag, S.; Yavuz, H.; Altindag, R. The Effect of Sample Size on Schmidt Rebound Hardness Value of Rocks. Int. J. Rock Mech. Min. Sci. 2009, 46, 725–730. [Google Scholar] [CrossRef]
- Atkinson, R.H. Hardness Tests for Rock Characterization. In Comprehensive Rock Engineering; Hudson, J.A., Ed.; Pergamon: Oxford, UK, 1993; pp. 105–117. [Google Scholar]
- Ghadernejad, S.; Esmaeili, K. The Application of Small Sample Theory and Confidence Interval Method to Determine the Representative Mean Leeb Rebound Hardness Value. Bull. Eng. Geol. Environ. 2024, 83, 25. [Google Scholar] [CrossRef]
- Ghorbani, S.; Hoseinie, S.H.; Ghasemi, E.; Sherizadeh, T. A Review on Rock Hardness Testing Methods and Their Applications in Rock Engineering. Arab. J. Geosci. 2022, 15, 1067. [Google Scholar] [CrossRef]
- Garrido, M.E.; Petnga, F.B.; Martínez-Ibáñez, V.; Serón, J.B.; Hidalgo-Signes, C.; Tomás, R. Predicting the Uniaxial Compressive Strength of a Limestone Exposed to High Temperatures by Point Load and Leeb Rebound Hardness Testing. Rock Mech. Rock Eng. 2022, 55, 1–17. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Z.; Shi, Z.; Xu, P.; Chang, Z. Influence Mechanism of High Temperature on Drilling Rate and Hardness of Sandstone. Nat. Resour. Res. 2022, 31, 2589–2601. [Google Scholar] [CrossRef]
- Akbay, D.; Ekincioğlu, G. Estimating the Brittleness Values of Carbonated Rocks with Shore, Schmidt, and Leeb Hardness Values. Environ. Earth Sci. 2022, 81, 206. [Google Scholar] [CrossRef]
- Ghorbani, S.; Hoseinie, S.H.; Ghasemi, E.; Sherizadeh, T. Application of Leeb Hardness Test in Prediction of Dynamic Elastic Constants of Sedimentary and Igneous Rocks. Geotech. Geol. Eng. 2022, 40, 3125–3145. [Google Scholar] [CrossRef]
- Benavente, D.; Fort, R.; Gomez-Heras, M. Improving Uniaxial Compressive Strength Estimation of Carbonate Sedimentary Rocks by Combining Minimally Invasive and Non-Destructive Techniques. Int. J. Rock Mech. Min. Sci. 2021, 147, 104915. [Google Scholar] [CrossRef]
- Ince, I.; Bozdag, A. An Investigation on Sample Size in Leeb Hardness Test and Prediction of Some Index Properties of Magmatic Rocks. Arab. J. Geosci. 2021, 14, 182. [Google Scholar] [CrossRef]
- Gomez-Heras, M.; Benavente, D.; Pla, C.; Martinez-Martinez, J.; Fort, R.; Brotons, V. Ultrasonic Pulse Velocity as a Way of Improving Uniaxial Compressive Strength Estimations from Leeb Hardness Measurements. Constr. Build Mater. 2020, 261, 119996. [Google Scholar] [CrossRef]
- Dong, S.; Zhang, W.; Chang, Z.; Wang, Z.; Shi, Z.; Qiao, W. Influence Mechanism of Temperature Paths on Hardness of Sandstone. Nat. Resour. Res. 2023, 32, 2927–2944. [Google Scholar] [CrossRef]
- Li, Q.; Li, J.; Duan, L.; Tan, S. Prediction of Rock Abrasivity and Hardness from Mineral Composition. Int. J. Rock Mech. Min. Sci. 2021, 140, 104658. [Google Scholar] [CrossRef]
- Houshmand, N.; GoodFellow, S.; Esmaeili, K.; Ordóñez Calderón, J.C. Rock Type Classification Based on Petrophysical, Geochemical, and Core Imaging Data Using Machine and Deep Learning Techniques. Appl. Comput. Geosci. 2022, 16, 100104. [Google Scholar] [CrossRef]
- Ghadernejad, S.; Esmaeili, K. Investigating the Relationship Between Geochemistry, Leeb Rebound Hardness, and Cerchar Abrasivity Index. Int. J. Geomech. 2024, 24, 04024280. [Google Scholar] [CrossRef]
- Both, C.; Dimitrakopoulos, R. Integrating Geometallurgical Ball Mill Throughput Predictions into Short-Term Stochastic Production Scheduling in Mining Complexes. Int. J. Min. Sci. Technol. 2023, 33, 185–199. [Google Scholar] [CrossRef]
- Yang, B.; Wang, S.; Li, S.; Zhou, B.; Zhao, F.; Ali, F.; He, H. Research and Application of UAV-Based Hyperspectral Remote Sensing for Smart City Construction. Cogn. Robot. 2022, 2, 255–266. [Google Scholar] [CrossRef]
- Akbar, S.; Abdolmaleki, M.; Ghadernejad, S.; Esmaeili, K. Applying Knowledge-Based and Data-Driven Methods to Improve Ore Grade Control of Blast Hole Drill Cuttings Using Hyperspectral Imaging. Remote Sens. 2024, 16, 2823. [Google Scholar] [CrossRef]
- Gaillard, N.; Williams-Jones, A.E.; Clark, J.R.; Lypaczewski, P.; Salvi, S.; Perrouty, S.; Piette-Lauzière, N.; Guilmette, C.; Linnen, R.L. Mica Composition as a Vector to Gold Mineralization: Deciphering Hydrothermal and Metamorphic Effects in the Malartic District, Quebec. Ore Geol. Rev. 2018, 95, 789–820. [Google Scholar] [CrossRef]
- Lypaczewski, P.; Rivard, B.; Gaillard, N.; Perrouty, S.; Piette-Lauzière, N.; Bérubé, C.L.; Linnen, R.L. Using Hyperspectral Imaging to Vector towards Mineralization at the Canadian Malartic Gold Deposit, Québec, Canada. Ore Geol. Rev. 2019, 111, 102945. [Google Scholar] [CrossRef]
- Tuşa, L.; Kern, M.; Khodadadzadeh, M.; Blannin, R.; Gloaguen, R.; Gutzmer, J. Evaluating the Performance of Hyperspectral Short-Wave Infrared Sensors for the Pre-Sorting of Complex Ores Using Machine Learning Methods. Miner. Eng. 2020, 146, 106150. [Google Scholar] [CrossRef]
- Luo, H.; Guo, N.; Li, C.; Jiang, H. Prediction of Lithium Mineralization Potential in the Jiulong Area, Western Sichuan (China), Using Spectral Residual Attention Convolutional Neural Network. Nat. Resour. Res. 2025, 34, 1331–1350. [Google Scholar] [CrossRef]
- Wu, D.; Jia, K.; Zhang, X.; Zhang, J.; Abd El-Hamid, H.T. Remote Sensing Inversion for Simulation of Soil Salinization Based on Hyperspectral Data and Ground Analysis in Yinchuan, China. Nat. Resour. Res. 2021, 30, 4641–4656. [Google Scholar] [CrossRef]
- Schaefer, L.N.; Kereszturi, G.; Villeneuve, M.; Kennedy, B. Determining Physical and Mechanical Volcanic Rock Properties via Reflectance Spectroscopy. J. Volcanol. Geotherm. Res. 2021, 420, 107393. [Google Scholar] [CrossRef]
- Schaefer, L.N.; Kereszturi, G.; Ben, K.; Kennedy, M.; Villeneuve, M. Characterizing Lithological, Weathering, and Hydrothermal Alteration Influences on Volcanic Rock Properties via Spectroscopy and Laboratory Testing: A Case Study of Mount Ruapehu Volcano, New Zealand. Bull. Volcanol. 2023, 85, 43. [Google Scholar] [CrossRef]
- Kereszturi, G.; Heap, M.; Schaefer, L.N.; Darmawan, H.; Deegan, F.M.; Kennedy, B.; Komorowski, J.C.; Mead, S.; Rosas-Carbajal, M.; Ryan, A.; et al. Porosity, Strength, and Alteration—Towards a New Volcano Stability Assessment Tool Using VNIR-SWIR Reflectance Spectroscopy. Earth Planet Sci. Lett. 2023, 602, 117929. [Google Scholar] [CrossRef]
- Lee, S.J.; Jeong, G.C.; Kim, J.T. Analysis and Comparison of Rock Spectroscopic Information Using Drone-Based Hyperspectral Sensor. J. Eng. Geol. 2021, 31, 479–492. [Google Scholar] [CrossRef]
- Bakun-Mazor, D.; Ben-Ari, Y.; Notesko, G.; Marco, S.; Ben-Dor, E. Measuring Carbonate Rock Strength Using Spectroscopy across the Optical and Thermal Region. IOP Conf. Ser. Earth Environ. Sci. 2021, 833, 012025. [Google Scholar] [CrossRef]
- Okada, N.; Maekawa, Y.; Owada, N.; Haga, K.; Shibayama, A.; Kawamura, Y. Automated Identification of Mineral Types and Grain Size Using Hyperspectral Imaging and Deep Learning for Mineral Processing. Minerals 2020, 10, 809. [Google Scholar] [CrossRef]
- van Duijvenbode, J.R.; Cloete, L.M.; Shishvan, M.S.; Buxton, M.W.N. Material Fingerprinting as a Tool to Investigate between and within Material Type Variability with a Focus on Material Hardness. Miner. Eng. 2022, 189, 107885. [Google Scholar] [CrossRef]
- Maras, E.E.; Caniberk, M.; Odabas, M.S.; Degerli, B.; Maras, S.S.; Maras, H.H. An Evaluation of the Relationship between Physical/Mechanical Properties and Mineralogy of Landscape Rocks as Determined by Hyperspectral Reflectance. Arab. J. Geosci. 2016, 9, 164. [Google Scholar] [CrossRef]
- Bakun-Mazor, D.; Ben-Ari, Y.; Marco, S.; Ben-Dor, E. Predicting Mechanical Properties of Carbonate Rocks Using Spectroscopy Across 0.4–12 Μm. Rock Mech. Rock Eng. 2024, 57, 8951–8968. [Google Scholar] [CrossRef]
- Del Rio-Salas, R.; Ayala-Ramírez, Y.; Loredo-Portales, R.; Romero, F.; Molina-Freaner, F.; Minjarez-Osorio, C.; Pi-Puig, T.; Ochoa–Landín, L.; Moreno-Rodríguez, V. Mineralogy and Geochemistry of Rural Road Dust and Nearby Mine Tailings: A Case of Ignored Pollution Hazard from an Abandoned Mining Site in Semi-Arid Zone. Nat. Resour. Res. 2019, 28, 1485–1503. [Google Scholar] [CrossRef]
- Ghadernejad, S.; Esmaeili, K. Predicting Rock Hardness and Abrasivity Using Hyperspectral Imaging Data and Random Forest Regressor Model. Remote Sens. 2024, 16, 3778. [Google Scholar] [CrossRef]
- Mackey, E.A.; Johnson, C.S.; Lindstrom, R.M.; Long, S.E.; Marlow, A.F.; Murphy, K.E.; Paul, R.L.; Popelka-Filcoff, R.S.; Rabb, S.A.; Sieber, J.R.; et al. Certification of Three NIST Renewal Soil Standard Reference Materials® for Element Content: SRM 2709a San Joaquin Soil, SRM 2710a Montana Soil I, and SRM 2711a Montana Soil II. NIST Spec. Publ. 2010, 260, 1–39. [Google Scholar] [CrossRef]
- Leeb, D. Dynamic Hardness Testing of Metallic Materials. NDT Int. 1979, 12, 274–278. [Google Scholar] [CrossRef]
- Aoki, H.; Matsukura, Y. Estimating the Unconfined Compressive Strength of Intact Rocks from Equotip Hardness. Bull. Eng. Geol. Environ. 2008, 67, 23–29. [Google Scholar] [CrossRef]
- Aoki, H.; Matsukura, Y. A New Technique for Non-Destructive Field Measurement of Rock-Surface Strength: An Application of the Equotip Hardness Tester to Weathering Studies. Earth Surf. Process Landf. 2007, 32, 1759–1769. [Google Scholar] [CrossRef]
- Bhuiyan, M.; Esmaieli, K.; Ordóñez-Calderón, J.C. Application of Data Analytics Techniques to Establish Geometallurgical Relationships to Bond Work Index at the Paracutu Mine, Minas Gerais, Brazil. Minerals 2019, 9, 302. [Google Scholar] [CrossRef]
- Bhuiyan, M.; Esmaeili, K.; Ordóñez-Calderón, J.C. Evaluation of Rock Characterization Tests as Geometallurgical Predictors of Bond Work Index at the Tasiast Mine, Mauritania. Miner. Eng. 2022, 175, 107293. [Google Scholar] [CrossRef]
- Desarnaud, J.; Kiriyama, K.; Bicer Simsir, B.; Wilhelm, K.; Viles, H. A Laboratory Study of Equotip Surface Hardness Measurements on a Range of Sandstones: What Influences the Values and What Do They Mean? Earth Surf. Process Landf. 2019, 44, 1419–1429. [Google Scholar] [CrossRef]
- ASTM A956; Standard Test Method for Leeb Hardness Testing of Steel Products. ASTM International: West Conshohocken, PA, USA, 2017. [CrossRef]
- Proceq, S.A. Equotip 3 Portable Hardness Tester, Operating Instructions; Proceq SA: Schwerzenbach, Switzerland, 2007. [Google Scholar]
- HySpex HySpex Mjolnir VS-620 Configuration. Available online: https://www.hyspex.com/hyspex-products/hyspex-mjolnir/hyspex-mjolnir-vs-620/ (accessed on 19 May 2024).
- Kadachi, A.N.; Al-Eshaikh, M.A. Limits of Detection in XRF Spectroscopy. X-Ray Spectrom. 2012, 41, 350–354. [Google Scholar] [CrossRef]
- EPA SW-846 Test Method 6200: Field Portable X-Ray Fluorescence Spectrometry for the Determination of Elemental Concentrations in Soil and Sediment; SW-846; EPA: Washington, DC, USA, 2007; pp. 1–32.
- Alin, A. Multicollinearity. Wiley Interdiscip Rev. Comput. Stat. 2010, 2, 370–374. [Google Scholar] [CrossRef]
- ISO/TS 16949; Quality Management Systems—Particular Requirements for the Application of ISO 9001 for Automotive Production and Relevant Service Part Organizations. International Organization for Standardization: Geneva, Switzerland, 2009.
- Clark, R.N.; Swayze, G.A.; Livo, K.E.; Kokaly, R.F.; Sutley, S.J.; Dalton, J.B.; McDougal, R.R.; Gent, C.A. Imaging Spectroscopy: Earth and Planetary Remote Sensing with the USGS Tetracorder and Expert Systems. J. Geophys. Res. Planets 2003, 108, 5131. [Google Scholar] [CrossRef]
- Clark, R.N.; Roush, T.L. Reflectance Spectroscopy: Quantitative Analysis Techniques for Remote Sensing Applications. J. Geophys. Res. 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Darst, B.F.; Malecki, K.C.; Engelman, C.D. Using Recursive Feature Elimination in Random Forest to Account for Correlated Variables in High Dimensional Data. BMC Genet. 2018, 19, 1–6. [Google Scholar] [CrossRef]
- Moorthy, K.; Mohamad, M.S. Random Forest for Gene Selection and Microarray Data Classification. Bioinformation 2011, 7, 142–146. [Google Scholar] [CrossRef]
- Kursa, M.B. Robustness of Random Forest-Based Gene Selection Methods. BMC Bioinform. 2014, 15, 1–8. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; Alvarez de Andrés, S. Gene Selection and Classification of Microarray Data Using Random Forest. BMC Bioinform. 2006, 7, 1–13. [Google Scholar] [CrossRef]
- Zhang, Z.; Murtagh, F.; Van Poucke, S.; Lin, S.; Lan, P. Hierarchical Cluster Analysis in Clinical Research with Heterogeneous Study Population: Highlighting Its Visualization with R. Ann. Transl. Med. 2017, 5, 75. [Google Scholar] [CrossRef]
- Jollife, I.T.; Cadima, J. Principal Component Analysis: A Review and Recent Developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Brown, G. Ensemble Learning. In Encyclopedia of Machine Learning; Springer: Boston, MA, USA, 2011; pp. 312–320. [Google Scholar]
- Berhane, T.M.; Lane, C.R.; Wu, Q.; Autrey, B.C.; Anenkhonov, O.A.; Chepinoga, V.V.; Liu, H. Decision-Tree, Rule-Based, and Random Forest Classification of High-Resolution Multispectral Imagery for Wetland Mapping and Inventory. Remote Sens. 2018, 10, 580. [Google Scholar] [CrossRef]
- Wang, R. AdaBoost for Feature Selection, Classification and Its Relation with SVM, A Review. Phys. Procedia 2012, 25, 800–807. [Google Scholar] [CrossRef]
- Matthews, D.E. Multiple Linear Regression. In Wiley StatsRef: Statistics Reference Online; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Jones, D.R. A Taxonomy of Global Optimization Methods Based on Response Surfaces. J. Glob. Optim. 2001, 21, 345–383. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter Optimization for Machine Learning Models Based on Bayesian Optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).