Abstract
Spinach, leafy vegetables with growing demand and high nutritional value, has a heightened focus on nitrate content. An open-field experiment evaluated the potential of vis-NIR-SWIR hyperspectral data for classifying spinach nitrate content. Shallow artificial neural networks (ANN) and ensemble techniques—majority voting (MV) and stacked generalization (stacked)—were applied. The competitive adaptive reweighted sampling (CARS), its stability version (SCARS), Elastic Net, and modified boosted versions of each (CARSplus, SCARSplus, and ENplus) were used as feature selection methods. ANNs were optimized for hidden layer size. The resulting models were further used in ensemble techniques by grouping them into two sets: one with all models and another with models trained using the three boosted feature selection subsets (fifty-three wavelengths). The best-performing ANNs were based on the SCARS, SCARSplus, and full datasets, achieving an accuracy (Acc) of 0.83. While the majority voting approach did not improve performance (Acc 0.82), the stacked ensemble models reached Acc 0.88. Notably, stacked performed well also with models trained on 53 wavelengths, demonstrating strong potential for transferability as the required sensors would be less complex than those used in this study. Furthermore, a simulation of the practical application was conducted using Italian Ministry of Health official data with the scope of showing a potential use case in improving nitrate management and for advancing efficient farming practices in agriculture. The stacked models demonstrated their utility in doubling the monitoring capacity for internal quality assurance in spinach farming within a regulated framework.
1. Introduction
Global vegetable consumption remains below the recommended intake of 240 g per day [1], and various strategies have been proposed to address this issue [2]. Cultivation trends pair with projections of global agricultural production increasing by 2050 [3].
Vegetables (especially leafy ones) contain phytochemicals offering health benefits beyond basic nutrition [4]. Alongside beneficial bioactives, leafy vegetables may contain varying amounts of nitrates that, non-toxic per se, can be converted into nitrite, which correlates with detrimental effects on human health, especially on infants [5]. The International Agency for Research on Cancer categorizes nitrate under group 2A [6] and provides important contextualization as vegetables’ nitrates come with other compounds (i.e., vitamin C and polyphenols) that could inhibit nitrosation [7]. In addition to being converted into nitrite, dietary nitrate—particularly derived from vegetables—can also be metabolized into nitric oxide, with a demonstrated protective role against cardiovascular diseases [8,9].
Such a dual role of dietary nitrate, encompassing both detrimental and beneficial effects, necessitates careful consideration when establishing Acceptable Daily Intakes (ADI) and regulatory measures. To date, the World Health Organization has set a nitrate ADI [10], and the European Commission has fixed a limit for nitrate concentration on certain food products [11]. Global spinach production has registered an overall upward trend, increasing by 13% between 2019 and 2023 [12]; meanwhile, European production share declined from 2.3% to 1.6%. Among vegetables subject to EU regulation, spinach provides a relevant example for the challenge of meeting increased demands within regulated conditions, which might go beyond the common management of fertilization, irrigation, sowing density, and cultivar selection [13], or innovative techniques such as soil inoculum, genetic intervention, or protein hydrolysates application [14,15]. Relevant factors remain beyond the farmer’s control, such as geographical location, cropping season, and meteorological conditions [16].
Within the framework of the ongoing digital agriculture revolution, farmers could benefit from mapping procedures capable of non-destructive monitoring of nitrate content [17]. Such systems rely on sensors in the circulating solution and are commonly applied in soilless farming [18]. Further, there is a lack of similar procedures for soil-grown crops since those currently available, i.e., nitrate selective electrodes or sensitive test strips, are time-consuming, difficult to scale-up, and lack precision [19], while the non-destructive, scalable real-time methods have been proposed only in recent years. Despite their great potential, it is important to highlight that the economic accessibility of the sensors involved can represent a barrier, and research is actively engaged in developing low-cost portable solutions to overcome this limitation [20,21]. These methods leverage the convergence of two enabling technologies: optical sensors and machine learning algorithms [22,23,24]. The latter are indispensable not only for interpreting these complex datasets and mitigating spectral interferences, but also for enabling the indirect estimation of compounds such as nitrates, which often lack a strong, direct spectral signature in the utilized optical range [25]. In this context, while approaches based on portable FTIR spectroscopy require sample grinding [26], other research using vis-NIR reflectance on just-harvested samples reported commendable results [27].
The present work aims to expand upon such promising findings by exploring the potential of in situ, pre-harvest vis-NIR-SWIR reflectance for determining nitrates in spinach under real farming conditions to unveil potentialities for homogeneous mapping based on nitrate content to drive farmer operations well before post-harvest controls. A key aspect of our approach, which seeks to enhance practical applicability and transferability—to achieve significant improvements in operational efficiency—hinted at in previous studies, is a strong emphasis on feature reduction. A research activity aimed at finding spectral reflectance wavebands in the vis-NIR and short-wave-infrared (SWIR) regions informative for nitrate content at a canopy level in spinach at open-field level, with some findings published by Stagnari et al. [28]. During the batch-level sampling and recording, data at a finer scale (leaves) were also collected. Such data were explored through the development of various classification models, emphasizing feature reduction to improve transferability by minimizing required sensor complexity. In addition, we adopted two ensemble techniques, known for prediction amelioration [29]. The presented classifiers were implemented in a simulation procedure demonstrating the potential for significant improvement on self-monitoring efficiency for regulatory compliance and/or quality assurance.
2. Materials and Methods
2.1. Field Experiment
The experiment was conducted in an open-field farming site in the Sant’Omero municipality, Italy (42°47′50″N; 13°47′02″E), within a farm that, experienced in managing spinach for the deep-freezing chain, collaborated operatively. Spinacia oleracea L. var. Bufflehead RZ F1 (Rijk Zwaan Zaadteelt en Zaadhandel B.V., Bologna, Italy) was cultivated in the whole field, where an area of 60 m × 30 m was delimited for experimental use only. Within, a randomized block with 3 replications and 6 Nitrogen (N) fertilization (Urea) treatments at 0, 50, 100, 150, 200, and 250 kg N ha−1, in order to explore a significant range of nitrate, as well as of biomass, content in spinach leaves (ranging from 932 to 4885 mg kg−1 DW of NO3-N and from 14.67 to 35.55 t ha−2 of biomass yield, on average; see [28]). A total of 18 experimental units (6.0 m × 7.0 m), each comprising 40 spinach rows, was considered. The experiment itself—corresponding to experiment A—was described in Stagnari et al. [28], which we recommend reading for further details.
2.2. Reflectance Measurements
At harvest, 15 leaves for each experimental unit were collected—by dividing the experimental units in a 6 × 7 grid and from the center of 1 m2 grid cells, following an alternating pattern by skipping every other cell—for analytical determination and their reflectance signature was recorded using a portable spectroradiometer (FieldSpec® 4 Hi-Res, ASD Inc., Boulder, CO, USA) equipped with a direct optical fiber contact probe (ASD Plant Probe; ASD Inc., Boulder, CO, USA) and its integrated halogen reflector lamp to gather leaf reflectance spectra in active mode. The instrument was warmed up before measurements. For each scan, 20 spectra were averaged, and for each leaf, 3 to 5 scans (depending on leaf size) were replicated along the lamina avoiding the petiole and the central vein. Collected spectra cover vis, NIR, SWIR (from 350 to 2500 nm) with three different resolutions (3, 5, and 8 nm) depending on the specific band ([350 nm:1000 nm], [1000 nm:1800 nm], and [1800 nm:2500 nm]). Raw data were treated only with splice correction; no other preprocessing was applied.
2.3. Nitrate Content Determination
Due to the inability to accurately measure the fresh weight of the small-sized leaves, all the samples were immediately stored in refrigerated bags and transferred to the laboratory to perform analytical determinations. Nitrate nitrogen (NO3-N) on a dry weight basis (DW) was determined following the procedure described by Cataldo et al. [30]. European regulations indicate nitrate content on a fresh weight basis (FW); consequently, the obtained data were then reported on a fresh weight basis. Hence, while the dry matter (DM) content of the samples remained unknown, the DM content of all the experimental units was accurately determined from randomly sampled plant material collected in sub-plots within the experimental units, as described in Stagnari et al. [28].
The nitrate value fresh weight (NO3 FW) was expressed as a confidence interval where the extremes were calculated as follows:
where NO3 is the sample nitrate concentration (mg kg−1), NO3-N is the sample nitric nitrogen concentration (mg kg−1), μDM and σDM are the mean and standard deviation for the dry matter content of the experimental unit.
NO3 Upper limit = 4.427 × NO3-N × (μDM + σDM)
NO3 Lower limit = 4.427 × NO3-N × (μDM − σDM)
This approach enabled the establishment of a threshold value for dividing the data into three subcategories: Positive (i.e., entirely above the threshold), Negative (i.e., entirely below the threshold), and Undecidable (i.e., threshold included within the interval). We chose a threshold value of 800 mg kg−1 that align with the scope of the paper: (i) the dataset was well balanced, with 124 positive and 126 negative samples; and (ii) there were only 8 Undecidable samples—to be added to the 12 outliers excluded in a prior step (described below).
Outliers were identified and excluded based on their registered NO3 content values. Specifically, the mean NO3 content (calculated using μDM) of each sample was compared to the average value of the samples within the same N fertilization group. Samples with NO3 values, deviating by two standard deviations from their N-fertilization group’s μDM mean, were considered outliers.
2.4. Data Modelling and Statistics
2.4.1. Feature Selection Methods
For selecting the most important features, we evaluated three different techniques: the competitive adaptive reweighted sampling (CARS), its stability version (SCARS), and the Elastic Net (EN). In addition, we adopted a further selection method for each one of them (secondary selection) to reduce the number to around 20 features only (CARSplus, SCARSplus, and ENplus, respectively). All methods were also compared with a no-feature selection dataset (FULL).
The core principle of CARS lies in the absolute values of the coefficients of a partial least squares regression (PLSR), which serve as proxies for feature importance. The method involves both enforced wavelength selection via an exponentially decreasing function and an adaptive reweighted sampling to refine the selection of key wavelengths, iteratively and competitively performed through a Monte Carlo process, mimicking the “survival of the fittest” principle, using RMSE for comparison [31].
SCARS introduces a stability index for each feature, calculated by normalizing the absolute value of the feature’s coefficient on its own standard deviation, favoring features that consistently provide valuable information across various subsets. This approach offers certain protection against noise and tends to produce robust selections [32].
Elastic Net (EN), first introduced by Zou and Hastie [33], still relies on coefficients. EN combines Ridge Regression (RR) and the Least Absolute Shrinkage and Selection Operator (LASSO). Both methods aim to minimize a loss function that incorporates the residual sum of squares along with a penalty on the feature coefficients. LASSO enforces sparsity by shrinking some coefficients exactly to zero; in contrast, RR applies a more gradual shrinkage, making it effective in handling multicollinearity but less aggressive as a selector. EN bridges these two techniques by introducing the α parameter (0.4 in our case) for balancing.
All adopted methods are linear and coefficient-based; this allows a common secondary selection step by clustering wavelengths based on their correlation matrix and selecting two representative features from each cluster. This approach was intended to further reduce multicollinearity while preserving features deemed valuable by the initial methods, fostering the simulation and comparison of a customized sensor with reduced complexity, an aspect required by the applicative context that framed our research. For each feature selection dataset, we generated 10 clusters, balancing expected reduction (99%) and information retention, and selected the wavelengths with the highest positive and lowest negative beta coefficients from each cluster.
2.4.2. Classification Models
As a base classifier, we used a shallow ANN architecture, all the procedures were conducted using R software (version 4.4.2) [34] and the “keras3” package (version 1.2.0) [35]. The ADAM algorithm was implemented with the initial learning rate controlled via a custom cycle within a range determined through the “LR range test” described by Smith [36]. Various models were explored via grid search, focusing on the number of neurons in the single hidden layer (HL) ranges based on the dimensionality of the input layer’s features.
To support the validation required for subsequent ensemble techniques, ANNs were trained and validated using only a fixed working set comprising 80% of the data [37,38]; the remaining 20% (Test set) was reserved for meta-model validation. The working set was further randomly split into 80:20 for each base ANN model training:validation (Figure 1).
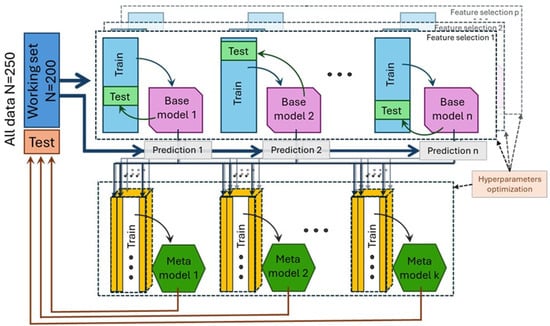
Figure 1.
Schematization of data flow. The working set, composed of 80% of the data, was used for base models training and testing with a secondary 80:20 random split. Base models’ predictions on the working set were used for meta-model training.
Moreover, the training process included z-score calculation, validation_split, shuffle, dropout, and early stopping with weight restoration. These measures reverted the model to the best-performing state and prevented weight co-adaptation, ensuring more robust and generalized models by limiting the occurrence of overfitting [39]. To enhance performance, two parallel ensemble methods were tested: the majority of votes (MV), known for simplicity and speed, and stacked generalization (Stacked), which uses meta-models trained on the predictions of multiple base models [40]. In our case, classifiers produced while optimizing ANNs were used as base models. These parallel strategies were preferred over other ensemble paradigms discussed in the literature. For example, bagging, while also a parallel method, typically aims to reduce variance by training homogeneous base learners on different data samples while sequential methods such as boosting, conversely, operate by iteratively correcting the errors of preceding models, often simpler or ‘weaker’ base learners, to reduce overall bias and variance [41]. This iterative refinement approach differs from our objective of integrating predictions from a set of already specialized and proficient ANN classifiers. The Stacked meta-model training process followed the same hyperparameter optimization steps as for the base models. Both ensemble methods were built using predictions from all base models at first and then with predictions that came exclusively from models built on the secondary selection dataset (Figure 2), resulting in four ensembles: MV_all, MV_plus, Stacked_all, and Stacked_plus.
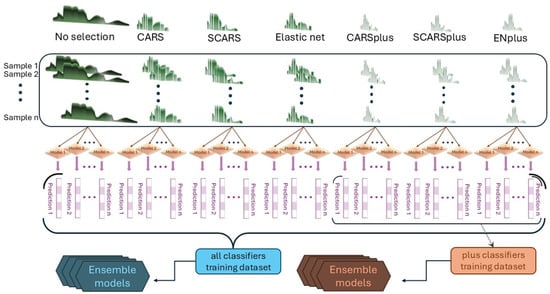
Figure 2.
Schematization of data elaboration, base model, and meta-model construction through different feature selection techniques to obtain ensemble models relying on the entire spectrum (350–2500 nm) or only on a few selected wavelengths.
2.4.3. Models’ Evaluation
Classification models’ predictions were compared using accuracy (Acc), Cohen’s kappa (K), positive and negative likelihood ratios (LR+ and LR−), and diagnostic odds ratio (DOR). DOR is a well-established metric for comparing binary classifiers in practical applications [42]. LR+ and LR− metrics were chosen to estimate post-test odds. In addition, and for illustration purposes only, reference data from the Italian Ministry of Health [43] were incorporated to demonstrate the calculation of these odds. These data were used solely as a hypothetical example and do not reflect actual values because: (i) Ministry’s tables differentiate samples’ categories for non-compliances not for the total sample size, therefore, for estimating the probability of a sample resulting in non-compliance before any test (P-pre) we divided total sample size for the number of categories; (ii) we assumed the same nitrate content distribution for our dataset and Ministry’s dataset, and made use of the fact that the value of 800 ppm was very close to the median value implying that any positive sample would have a probability of exceeding regulatory limits approximately 2 P-pre. All metrics were calculated using the equations reported in Table 1.

Table 1.
Equation for metrics employed in classifier evaluation and applicability demonstration. Acc: Accuracy; K: Cohen’s kappa; TP: true positive; TN: true negative; FP: false positive; FN: false negative; LR+: positive likelihood ratio; LR−: negative likelihood ratio; DOR: diagnostic odds ratio. Odds and P represent the odds for an event to occur and probability of such an event; pre and postbetween brackets refer to P and odds of a sample before and after being tested for such an event. Positive and negative symbols (+ and −) after Odds(post) and P(post) refer to the odds of being positive calculated for a sample tested as positive (+) or negative (−). P(reg)+ is the posttest probability for a sample tested as positive of exceeding regulatory limits, and P(reg)− is the posttest probability for a sample tested as negative of not exceeding regulatory limits.
3. Results
3.1. Nitrate Distribution
NO3 content in leaves was influenced by N fertilization, increasing for dosages stronger than N_50. The binary dataset showed the occurrence of positive samples (i.e., NO3 FW ≥ 800 mg kg⁻1) growing from N_50 (7%) to N_250 (90%) (Figure 3). The dataset cleaning process, through the outlier detection based on nitrate content and the exclusion of undecidable cases, resulted in sample removal being evenly distributed across the 6 N treatments (Figure 3).
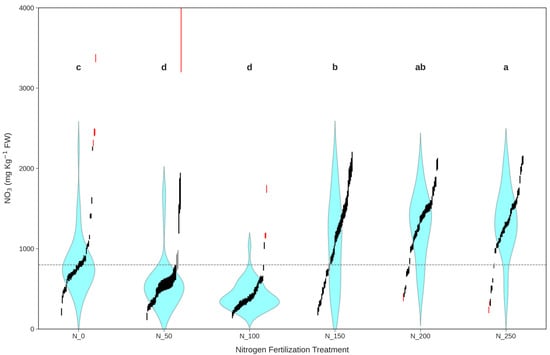
Figure 3.
All samples nitrate (NO3) content on a fresh weight (FW) basis data (mg kg−1, vertical axis), reconstructed as confidence intervals (vertical segments), are distinguished into 3 categories: outliers, undecidable, and allowed for further analysis (red, grey, and black, respectively). Letters referring to Tuckey’s HSD post hoc test output and violin plots (cyan shapes) are performed across the varying nitrogen fertilization treatments (horizontal axis), considering only allowed samples. The horizontal grey dashed line represents the threshold to determine the sample’s actual classes (positive above).
3.2. Selection of Important Features
The feature selection techniques impacted the dataset at different levels. EN resulted in the least reduction, selecting 663 wavelengths out of 2150 (~70% reduction). In contrast, CARS and SCARS both reduced the dataset to 262 wavelengths (~90% reduction); the latter two methods shared only 55% (145 wavelengths) of the selected features. Figure 4A–C shows the distribution of the important features individuated by the three non-custom feature selection methods. In addition, it also displays the clustering of the selected wavelengths used to identify the 10 most collinear groups of features from which the groups’ representatives are extracted for the secondary, and more aggressive, selection. These methods were preconfigured to achieve approximately a 99% reduction and performed as expected. Interestingly, the secondary reduction methods shared only six features out of the total 59 selected wavelengths, resulting in a combined dataset of 53 wavelengths. It could be concluded that all feature selection methods identified important bands distributed across the entire spectrum, rather than concentrating on specific regions (Figure 4). Nonetheless, a closer examination of the occurrences of features selected with secondary methods, performed by dividing the spectrum into 50 nm-wide intervals (Figure 5), reveals a preference for bands near the early NIR region (750–800 nm) and the blue-cyan region (400–500 nm).
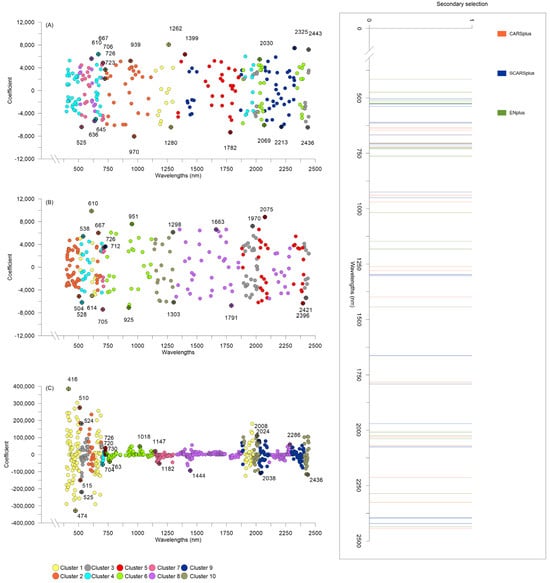
Figure 4.
Features selected by (A) CARS, (B) SCARS, and (C) Elastic Net, EN techniques are represented by colored dots with the horizontal axis following wavelength (nm) and the vertical axis the recorded b coefficient. Features selected by secondary selection methods CARSplus, SCARSplus, and ENplus (in (A), (B), and (C), respectively) are identified/highlighted by the ⛒ symbol and labeled with the corresponding wavelength. Colors represent the clusters identified during the secondary selection procedures. In the box, the distribution of the combined secondary selection features across the entire recorded spectrum for CARSplus, SCARSplus, and ENplus (labeled/identified with different colors).
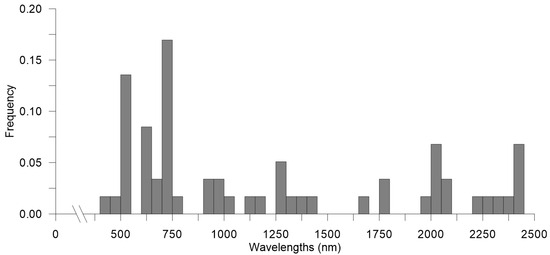
Figure 5.
Frequency histogram of all features (wavelengths, nm) selected by secondary selection methods (CARSplus, SCARSplus, and ENplus), across the entire spectrum, within 50 nm wide intervals (horizontal axis).
3.3. Base Models
The optimization of ANNs for HL size, conducted on the same working set with seven different feature sets, resulted in 69 different neural networks. Each model presented a distinct profile of performance metrics. Table 2 reports the best value for each metric across all feature selections, along with the corresponding HL size. Among the feature selection strategies, FULL, SCARS, and SCARSplus achieved the best overall performances in terms of accuracy (Acc) and Cohen’s kappa (K), all reaching identical values. Notably, SCARS yielded the highest diagnostic odds ratio (DOR), with a top value of 34.3 obtained using 35 neurons.

Table 2.
Best values for selected metrics, divided by feature selection method. Models providing the best value are identified by indicating the number of neurons (Neurons) in the hidden layer. For selected metrics definitions, please refer to Table 1.
However, the SCARS model that performed best in Acc and K (30 neurons) reported a lower DOR. For comparison, the best models from FULL and SCARSplus (based on Acc) also outperformed this SCARS model in terms of DOR. Differences among models were also evident in terms of likelihood ratios. The FULL model showed LR+ of 4.06 and LR− of 0.150, while SCARSplus reported LR+ of 6.33 and LR− of 0.238. This pattern of divergent strengths was observed not only between different feature selections, but also within models derived from the same feature set but with varying HL sizes: in four out of seven feature selections, the best-performing models for LR+ and LR− were different.
3.4. Ensemble Techniques
The application of ensemble techniques to the base models aimed to enhance classification performance by combining their distinct decision boundaries. Table 3 reports the outcomes of both the MV and Stacked approaches. The MV ensemble did not yield any performance improvement in our case. This indicates that the base models may have produced similar and evenly distributed classification errors. In contrast, the Stacked technique led to performance gains. Two stacked models, Stacked_all (16 neurons) and Stacked_plus (10 neurons), achieved an Acc of 0.88 and a K of 0.76. These models exhibited different values for LR+ and DOR. Notably, Stacked_plus achieved zero false positives on the test set (Table 3). Furthermore, Stacked_plus operated using only 53 wavelengths, in contrast to the broader spectral inputs used by Stacked_all.

Table 3.
Recorded values for selected metrics, obtained with ensemble techniques, divided by base model predictions (Predictors). Models providing the best value are identified by indicating the number of neurons (Neurons) in the hidden layer. For selected metrics definitions, please refer to Table 1.
3.5. Use Case Demonstration
The meta-models developed in this study were tested for their practical applicability in real farming contexts, particularly in screening samples with very low nitrate content. Table 3 presents the post-test probabilities for a sample predicted as positive to exceed the regulatory nitrate limit [P(reg)+], as computed from the MV approach and both Stacked meta-models. These post-test probabilities were derived using an estimated pre-test probability (P-pre) of 2.30%, based on data from the Italian official control plan for agricultural contaminants (2020–2022) [43]. All models demonstrated a notable increase from the P-pre baseline. However, because the classifiers tend to discriminate around the median nitrate content, P(reg)+ values remained below 4.60%, limiting the models’ utility for identifying non-compliant samples. Conversely, the post-test probability for a sample predicted as negative to not exceed the regulatory threshold [P(reg)−] was remarkably high, peaking at 99.4% for Stacked_all and 99.3% for Stacked_plus. These values correspond to false negative rates lower than 0.6% and 0.7%, respectively. Such performance suggests the potential for doubling the amount of sampled material, increasing the incidence of true positives, and enhancing the spatial resolution of monitoring, all without additional chemical analyses.
4. Discussion
The size of the confidence intervals for NO3 content on an FW basis, shown as vertical segments in Figure 3, was not uniform, as it depended on the DM variance observed at the experimental unit level, nonetheless, the binarization threshold set at 800 ppm allowed a clear distinction between samples. Single samples are also distinct with color codes—showing outliers, undecidable, and allowed for further analysis in red, grey, and black, respectively—allowing the visualization of the even distribution, among treatments, of the excluded samples with outliers displaying higher NO3 concentrating in low N treatments and lower NO3 in high N ones demonstrating expected behavior. Figure 3 also displays a distinctive, J-shaped, NO3 response to N dosage, with N_0 being higher than expected. This may be attributable to several factors, including reduced plant vigor, that are beyond the scope of this work. However, this also ensures that any attempt to predict NO3 content must account for complex relations and cannot rely solely on the determination of the N fertilization dosage.
The similarity between the CARS and SCARS dataset absolute reduction is unsurprising given that the two algorithms differ only in minor details. By contrast, the low number of common features selected by the two methods was less anticipated and might be attributed to two main factors: (i) the presence of groups of strongly correlated features where the resampling procedure led to the randomized emergence of only few representatives; and (ii) noisy patterns shared by small groups of samples incidentally resampled together enough times to be selected by CARS but not by SCARS which reduces this occurrence by design. The second hypothesis is supported by the stronger predictive performance of SCARS-based ANNs compared to CARS-based ones.
A remarkable finding obtained during the feature selection with the secondary methods (CARSplus, SCARSplus, and ENplus) is the high occurrence of features selected in the close vicinity and inside two bands that were shown by Stagnari et al. [28] to consistently correlate with NO3-N content across varying genotypes and environments (blue cyan and early NIR). This parallel is particularly noteworthy, even if the samples in this study were drawn from one of the experimental fields used in Stagnari et al. [28]. In fact, they were collected and treated with significantly different sampling and measurement procedures. Specifically, this study used single leaves and a contact probe in active mode, while the previous work relied on batches of plant material and passive canopy-level measurements. These methodological differences have strong implications for generalization and transferability. The contact probe employed in this study bypasses the noise caused by atmospheric gas absorption bands in the regions between 1350–1410 nm and 1800–1950 nm [44], potentially enabling the detection of significant but less transferable features. Moreover, canopy-level reflectance, as used in the earlier study, integrates data from a circular field of view (FOV) with a radius of 40 cm, encompassing reflectance from all elements within, including the crop canopy, weeds, and soil. Meanwhile, the contact probe collects reflectance from a 1 cm FOV, isolating a single leaf blade. These distinctions, coupled with the uneven distribution of NO3 within leaf tissues—i.e., veins, petioles, and leaf blades [45]—highlight the relevance of any observed parallels between the two experiments’ results. In this case, the identification of very close critical spectral bands strongly reinforces the significance of the findings. In addition to that, results from Mahanti et al. [27], who conducted a similar investigation—but collecting reflectance after harvest, in active mode and not using a contact probe—found a very small number of important wavelengths (i.e., 558, 706, 780, 1000, and 1420 nm), most of which fall in the same region previously highlighted.
It is worth mentioning the same study from Mahanti et al. [27], also considering the promising regression results obtained with a PLS approach. Nitrates are not heavily active in the observed spectrum (i.e., vis, NIR, SWIR), as their light interaction peaks in the UV [46], so estimates can rely on underlying relations between NO3 and other observable compounds and/or metabolic activities. Therefore, measurements taken before (as in our study) or after (as in [27]) a wounding event such as leaf cut might differ substantially for both metabolic changes [47,48] and spectral properties modifications [49,50]. So, even without changing NO3 leaf content, the transferability to a pre-harvest condition of a method developed using fresh-cut spinach can be challenging, highlighting the significance of a study focused on field measurements taken in real farming conditions.
The models’ evaluation results suggest that SCARS may be the most effective feature selection method in reducing noise and redundancy, as indicated by its superior DOR. This could reflect a broader strength of the SCARS technique. That could be valid for the technique as a whole, because it is also true that, albeit among the SCARS models, there was one resulting in the best DOR. The SCARS model that provided the best Acc and K had a much lower DOR, lower in particular of both DOR values from FULL and SCARSplus best models, which now result as the best performing pair. However, these two models are very different from each other. Their LR+ and LR− are reversed, resulting in the FULL model being much more sensitive and the SCARSplus more specific. This increases the difficulty of selecting the best model, as it depends heavily on the specific use case in question. Deeper consideration about the reasons behind the higher performance obtained by SCARS and SCARSplus feature selection methods in contrast to the other tested ones should start by confronting CARS and SCARS with the EN. The latter directly fits a linear model and minimizes error + penalties [33], while both CARS and SCARS starts by building a latent space in which the covariance between the features (i.e., spectral wavelengths) and the response variable (i.e., NO3) is maximized, this passage possibly better captured their underlying relationships. Furthermore, the observed outperformance of SCARS-based methods over their CARS counterparts (SCARS slightly surpassing CARS, and SCARSplus significantly outperforming CARSplus) likely stems from SCARS’s distinctive stability criterion: normalizing PLS beta coefficients by their standard deviation, rather than relying on absolute values. This strategy mitigates the selection of features whose apparent importance is merely an artifact of specific, transient co-feature subsets. Such normalization also inherently improves robustness to collinearity, ultimately fostering models with more interpretable, stable relationships and enhanced generalization capabilities [32].
The performance variability across models with different HL sizes—particularly within the same feature selection—underscores the sensitivity of ANN outcomes to architectural hyperparameters. This is consistent with the principle that altering model complexity shifts the underlying class boundary [51]. The observed trade-offs across metrics, especially between LR+ and LR−, reveal that no single model consistently dominates across all performance dimensions. Rather, the choice of the “best” model should be contingent on the specific application and its priorities—e.g., favoring sensitivity over specificity or vice versa. This is further emphasized by the divergence in performance profiles between FULL and SCARSplus, despite both achieving top results in Acc and K. Additionally, the choice to employ a randomized train/test split instead of full k-fold cross-validation influenced the outcome. While this approach reduced data exploitation efficiency, it allowed for the exploration of a broader architectural variance space. With just one training repetition per model, this increased the heterogeneity of base learners—albeit slightly—thereby creating favorable conditions for ensemble learning techniques such as majority voting (MV) and stacked generalization [52,53]. This method, although unconventional, provided a diverse yet coherent pool of base models that support robust ensemble strategies.
The limited improvement observed with the MV ensemble supports the notion that base models, despite being trained under varying conditions and feature subsets, shared similar classification error profiles. This redundancy limits the added value of a voting-based strategy. Conversely, stacked generalization was more effective, likely due to its capacity to exploit disagreement patterns among base learners [54,55]. This aligns with previous findings using hyperspectral data in crop studies, where Stacked ensembles showed notable advantages [56,57]. The performance of Stacked_plus, which reached high accuracy using only 53 wavelengths, suggests strong potential for model transferability and practical deployment. Reducing spectral input requirements theoretically enables the use of simpler and more cost-effective sensors. However, the selected bands are still distributed across the visible (22), NIR (12), and SWIR (19) regions, requiring multispectral instrumentation. This requirement for SWIR sensors poses a transferability challenge due to their current market conditions: they are more difficult to produce and, consequently, more expensive. Nonetheless, ongoing advancements in manufacturing techniques suggest potential for future cost reduction [21]. Moreover, the inclusion of the 1399 nm wavelength—falling within an atmospheric absorption band—poses a critical constraint, as it necessitates a contact probe for accurate measurement. These technical requirements partially offset the anticipated gains in simplicity and affordability and may influence the applicability of the models in less-controlled environments or mobile platforms. Additionally, the dataset used for training was limited to a single field, growing season, and genotype. While this constraint is further addressed below, it already calls attention to a key challenge in translating these results to broader agronomic contexts.
The high performance in identifying samples unlikely to exceed regulatory nitrate limits highlights the potential of these models in practical settings, particularly for farms subject to compliance requirements under EU Regulation 2023/915 [11]. Effective implementation would require access to real-world data on the occurrence rate of non-compliant samples and the distribution of nitrate content to estimate pre-test probabilities. Fortunately, such information is often available in farms with existing control systems, where regulatory record-keeping is mandatory [58]. Despite their practical relevance, the models face important limitations. Firstly, they were originally trained to optimize accuracy rather than sensitivity, which creates a mismatch when repurposed for non-compliance screening. This can be addressed by retraining with a loss function specifically penalizing false negatives. Secondly, although the reduction in the number of required wavelengths facilitates implementation, constraints previously discussed—such as the presence of the 1399 nm band—remain critical, especially in scenarios where non-contact sensing is preferred. Finally, the generalizability of the results is inherently limited by the dataset’s scope. The models were trained and tested within a specific agronomic and environmental context, restricting their immediate applicability across different seasons, genotypes, or geographic conditions. Nonetheless, the study demonstrated that compliant, real-world data can effectively support the development of robust classifiers. Adjusting classification thresholds may also allow for adaptation under alternative regulatory frameworks or market demands, confirming the potential of agronomic data to transcend its original collection purpose when properly leveraged.
5. Conclusions
This study presents a robust framework for utilizing spectral reflectance to assess nitrate content in spinach leaves under varying nitrogen fertilization regimes. Advanced feature selection techniques—Elastic Net, CARS, SCARS, and a customized enhancement based on autocorrelation clustering of the selected wavelengths—successfully reduced hyperspectral data to key wavelengths, enhancing model efficiency and interpretability. Particularly, selected features matched previous findings, reinforcing the relevance of blue cyan and early NIR spectra regions for nitrate determination.
ANN models, further optimized through ensemble learning, achieved high classification performance, with stacked models reaching up to 0.88 accuracy and perfect specificity in select configurations. This demonstrates strong potential for real-world applications, such as identifying low-nitrate produce to support regulatory compliance and minimizing chemical testing costs.
By enabling precise, non-destructive nitrate monitoring in open-field conditions, this research contributes to more informed fertilization strategies and improved production efficiency, offering tangible benefits for sustainable agricultural management.
Author Contributions
Conceptualization, W.P. and A.G.; Methodology, W.P.; Software, W.P.; Validation, W.P. and A.G.; Formal analysis, W.P.; Investigation, W.P. and A.G.; Resources, A.G. and F.S.; Data curation, W.P. and A.G.; Writing—original draft, W.P. and A.G.; Writing—review & editing, W.P., A.G. and F.S.; Visualization, A.G. and F.S.; Supervision, F.S. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by “Ministero dell’Agricoltura, della Sovranità Alimentare e delle Foreste (MASAF)”, within the project “AgriDigit”, “Tecnologie digitali integrate per il rafforzamento sostenibile di produzioni e trasformazioni agroalimentari (AgroFiliere)” [DM 36503.7305.2018 of 20 December 2018].
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We would also like to thank Cristiano Platani, Maria Assunta Dattoli, Gabriele Campanelli, and Flaviano Trasmundi for their support in data collection and analysis.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kalmpourtzidou, A.; Eilander, A.; Talsma, E.F. Global vegetable intake and supply compared to recommendations: A systematic review. Nutrients 2020, 12, 1558. [Google Scholar] [CrossRef] [PubMed]
- Mandracchia, F.; Llauradó, E.; Tarro, L.; del Bas, J.M.; Valls, R.M.; Pedret, A.; Radeva, P.; Arola, L.; Solà, R.; Boqué, N. Potential use of mobile phone applications for self-monitoring and increasing daily fruit and vegetable consumption: A systematized review. Nutrients 2019, 11, 686. [Google Scholar] [CrossRef] [PubMed]
- FAO (Food and Agriculture Organization). The Future of Food and Agriculture—Trends and Challenges; Food and Agriculture Organization: Rome, Italy, 2017; ISBN 978-92-5-109551-5. [Google Scholar]
- Li, N.; Wu, X.; Zhuang, W.; Xia, L.; Chen, Y.; Wang, Y.; Wu, C.; Rao, Z.; Du, L.; Zhao, R.; et al. Green leafy vegetable and lutein intake and multiple health outcomes. Food Chem. 2021, 360, 130145. [Google Scholar] [CrossRef]
- Gorenjak, H.A.; Cencič, A. Nitrate in vegetables and their impact on human health. A review. Acta Aliment. 2013, 42, 158–172. [Google Scholar] [CrossRef]
- IARC (International Agency for Research on Cancer). Ingested nitrate and nitrite, and cyanobacterial peptide toxins. In IARC Monographs on the Evaluation of Carcinogenic Risks to Humans; International Agency for Research on Cancer: Lyon, France, 2010; Volume 94. Available online: https://www.ncbi.nlm.nih.gov/books/NBK326544/ (accessed on 16 January 2025).
- Bondonno, C.P.; Zhong, L.; Bondonno, N.P.; Sim, M.; Blekkenhorst, L.C.; Liu, A.; Rajendra, A.; Pokharel, P.; Erichsen, D.W.; Neubauer, O.; et al. Nitrate: The Dr. Jekyll and Mr. Hyde of human health? Trends Food Sci. Technol. 2023, 135, 57–73. [Google Scholar] [CrossRef]
- Apte, M.; Nadavade, N.; Sheikh, S.S. A review on nitrates’ health benefits and disease prevention. Nitric Oxide 2024, 142, 1–15. [Google Scholar] [CrossRef]
- Tan, L.; Stagg, L.; Hanlon, E.; Li, T.; Fairley, A.M.; Siervo, M.; Matu, J.; Griffiths, A.; Shannon, O.M. Associations between Vegetable Nitrate Intake and Cardiovascular Disease Risk and Mortality: A Systematic Review. Nutrients 2024, 16, 1511. [Google Scholar] [CrossRef]
- Hambrige, T. Nitrate and Nitrite. In WHO Food Additives Series 50; World Health Organization: Geneva, Switzerland, 2003; Volume 50. [Google Scholar]
- EU (European Union). Commission Regulation (EC) No 2023/915 of 25 April 2023 on Maximum Levels for Certain Contaminants in Food and Repealing Regulation (EC) No 1881/2006 (Text with EEA Relevance). The Official Journal of the European Union. 2023. Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=CELEX:32023R0915 (accessed on 25 May 2025).
- FAO (Food and Agriculture Organization). Online Statistical Database. Available online: https://www.fao.org/faostat/en/#data/QCL (accessed on 11 January 2025).
- Luetic, S.; Knezovic, Z.; Jurcic, K.; Majic, Z.; Tripkovic, K.; Sutlovic, D. Leafy vegetable nitrite and nitrate content: Potential health effects. Foods 2023, 12, 1655. [Google Scholar] [CrossRef]
- Ciriello, M.; Campana, E.; De Pascale, S.; Rouphael, Y. Implications of Vegetal Protein Hydrolysates for Improving Nitrogen Use Efficiency in Leafy Vegetables. Horticulturae 2024, 10, 132. [Google Scholar] [CrossRef]
- Wang, M.; Liu, Y.; Cai, Y.; Song, Y.; Yin, Y.; Gong, L. Inhibition of nitrate accumulation in vegetable by Chroococcus sp. and related mechanisms. Rhizosphere 2024, 31, 100934. [Google Scholar] [CrossRef]
- Agusta, H.; Kartika, J.G.; Sari, K.R. Nitrate concentration and accumulation on vegetables related to altitude and sunlight intensity. IOP Conf. Ser. Earth Environ. Sci. 2021, 896, 012052. [Google Scholar] [CrossRef]
- van Es, H.; Woodard, J. Innovation in Agriculture and Food Systems in the Digital Age. In The Global Innovation Index; Dutta, S., Lanvin, B., Wunsch-Vincent, S., Eds.; World Intellectual Property Organization: Geneva, Switzerland, 2017; pp. 97–104. [Google Scholar]
- Hong, Y.; Lee, J.; Park, S.; Kim, J.; Jang, K.J. Next-Generation Nitrate, Ammonium, Phosphate, and Potassium Ion Monitoring System in Closed Hydroponics: Review on State-of-the-Art Sensors and Their Applications. Agric. Eng. 2024, 6, 4786–4811. [Google Scholar] [CrossRef]
- Parks, S.E.; Irving, D.E.; Milham, P.J. A critical evaluation of on-farm rapid tests for measuring nitrate in leafy vegetables. Sci. Hortic. 2012, 134, 1–6. [Google Scholar] [CrossRef]
- Chowdhury, M.; Khura, T.K.; Parray, R.A.; Kushwaha, H.L.; Upadhyay, P.K.; Jha, A.; Patra, K.; Kushwah, A.; Prajapati, V.K. The use of destructive and nondestructive techniques in concrete nitrogen assessment in plants. J. Plant Nutr. 2024, 47, 2271–2294. [Google Scholar] [CrossRef]
- Zhu, B.; Jonathan, H. A Review of Image Sensors Used in Near-Infrared and Shortwave Infrared Fluorescence Imaging. Sensors 2024, 24, 3539. [Google Scholar] [CrossRef]
- Sabzi, S.; Pourdarbani, R.; Rohban, M.H.; Fuentes-Penna, A.; Hernández-Hernández, J.L.; Hernández-Hernández, M. Classification of cucumber leaves based on nitrogen content using the hyperspectral imaging technique and majority voting. Plants 2021, 10, 898. [Google Scholar] [CrossRef]
- Jamshidi, B.; Yazdanfar, N. Development of a spectroscopic approach for non-destructive and rapid screening of cucumbers based on maximum limit of nitrate accumulation. J. Food Compos. Anal. 2022, 110, 104513. [Google Scholar] [CrossRef]
- Matteini, P.; Distefano, C.; de Angelis, M.; Agati, G. Assessment of Nitrate Levels in Greenhouse-Grown Spinaches by Raman Spectroscopy: A Tool for Sustainable Agriculture and Food Security. Pre-Print Article. 2024. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5002503 (accessed on 11 January 2025).
- Boros, I.F.; Sipos, L.; Kappel, N.; Csambalik, L.; Fodor, M. Quantification of nitrate content with FT-NIR technique in lettuce (Lactuca sativa L.) variety types: A statistical approach. J. Food Sci. Technol. 2020, 57, 4084–4091. [Google Scholar] [CrossRef]
- Ma, F.; Du, C.; Zheng, S.; Du, Y. In Situ Monitoring of Nitrate Content in Leafy Vegetables Using Attenuated Total Reflectance—Fourier-Transform Mid-infrared Spectroscopy Coupled with Machine Learning Algorithm. Food Anal. Methods 2021, 14, 2237–2248. [Google Scholar] [CrossRef]
- Mahanti, N.K.; Chakraborty, S.K.; Kotwaliwale, N.; Vishwakarma, A.K. Chemometric strategies for nondestructive and rapid assessment of nitrate content in harvested spinach using Vis-NIR spectroscopy. J. Food Sci. 2020, 85, 3653–3662. [Google Scholar] [CrossRef]
- Stagnari, F.; Polilli, W.; Campanelli, G.; Platani, C.; Trasmundi, F.; Scortichini, G.; Galieni, A. Nitrate content assessment in spinach: Exploring the potential of spectral reflectance in open field experiments. Agronomy 2023, 13, 193. [Google Scholar] [CrossRef]
- Mahajan, P.; Uddin, S.; Hajati, F.; Moni, M.A. Ensemble learning for disease prediction: A review. Healthcare 2023, 11, 12. [Google Scholar] [CrossRef] [PubMed]
- Cataldo, D.A.; Maroon, M.; Schrader, L.E.; Youngs, V.L. Rapid colorimetric determination of nitrate in plant tissue by nitration of salicylic acid. Commun. Soil Sci. Plant Anal. 1975, 6, 71–80. [Google Scholar] [CrossRef]
- Li, H.; Liang, Y.; Xu, Q.; Cao, D. Key wavelengths screening using competitive adaptive reweighted sampling method for multivariate calibration. Anal. Chim. Acta 2009, 648, 77–84. [Google Scholar] [CrossRef]
- Zheng, K.; Li, Q.; Wang, J.; Geng, J.; Cao, P.; Sui, T.; Wang, X.; Du, Y. Stability competitive adaptive reweighted sampling (SCARS) and its applications to multivariate calibration of NIR spectra. Chemom. Intell. Lab. Syst. 2012, 112, 48–54. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- R Core Team, R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. 2022. Available online: https://www.R-project.org/ (accessed on 8 July 2024).
- Kalinowski, T.; Allaire, J.; Chollet, F. _keras3: R Interface to ‘Keras’_. R Package Version 1.2.0. 2024. Available online: https://CRAN.R-project.org/package=keras3 (accessed on 18 November 2024).
- Smith, L.N. Cyclical learning rates for training neural networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 464–472. [Google Scholar]
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine learning algorithm validation with a limited sample size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef]
- Sasse, L.; Nicolaisen-Sobesky, E.; Dukart, J.; Eickhoff, S.B.; Götz, M.; Hamdan, S.; Komeyer, V.; Kulkarni, A.; Lahnakoski, J.; Love, B.C.; et al. On Leakage in Machine Learning Pipelines. arXiv 2023, arXiv:2311.04179. [Google Scholar]
- Ying, X. An overview of overfitting and its solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Naimi, A.I.; Balzer, L.B. Stacked generalization: An introduction to super learning. Eur. J. Epidemiol. 2018, 33, 459–464. [Google Scholar] [CrossRef]
- Mohammed, A.; Kora, R. A comprehensive review on ensemble deep learning: Opportunities and challenges. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 757–774. [Google Scholar] [CrossRef]
- Glas, A.S.; Lijmer, J.G.; Prins, M.H.; Bonsel, G.J.; Bossuyt, P.M. The diagnostic odds ratio: A single indicator of test performance. J. Clin. Epidemiol. 2003, 56, 1129–1135. [Google Scholar] [CrossRef] [PubMed]
- Ministero della Salute. Informativa sul Controllo Ufficiale dei Contaminanti Agricoli e delle Tossine Vegetali Negli Alimenti Oggetto di Campionamento nell’anno 2022; Piano Nazionale di Controllo Ufficiale dei Contaminanti Agricoli e Tossine Vegetali negli Alimenti. Available online: https://www.salute.gov.it/imgs/C_17_pubblicazioni_3444_allegato.pdf (accessed on 10 December 2024).
- Lin, C.; Tsogt, K.; Chang, C.I. An empirical model-based method for signal restoration of SWIR in ASD field spectroradiometry. Photogramm. Eng. Remote Sens. 2012, 78, 119–127. [Google Scholar] [CrossRef]
- Yang, H.Y.; Inagaki, T.; Ma, T.; Tsuchikawa, S. High-resolution and non-destructive evaluation of the spatial distribution of nitrate and its dynamics in spinach (Spinacia oleracea L.) leaves by near-infrared hyperspectral imaging. Front. Plant Sci. 2017, 8, 1937. [Google Scholar] [CrossRef]
- Kröckel, L.; Schwotzer, G.; Lehmann, H.; Wieduwilt, T. Spectral optical monitoring of nitrate in inland and seawater with miniaturized optical components. Water Res. 2011, 45, 1423–1431. [Google Scholar] [CrossRef]
- Prasad, A.; Kumar, A.; Matsuoka, R.; Takahashi, A.; Fujii, R.; Sugiura, Y.; Kikuchi, H.; Aoyagi, S.; Aikawa, T.; Kondo, T.; et al. Real-time monitoring of superoxide anion radical generation in response to wounding: Electrochemical study. Peer J. 2017, 5, e3050. [Google Scholar] [CrossRef]
- Clark, B.J.; Prioul, J.L.; Couderc, H. The physiological response to cutting in Italian ryegrass. Grass Forage Sci. 1977, 32, 1–5. [Google Scholar] [CrossRef]
- Kuleshova, T.E.; Seredin, I.S.; Cheglov, S.A.; Blashenkov, M.N.; Chumachenko, A.V.; Feofanov, S.V.; Kiradiev, V.K.; Odnoblyudov, M.A. Spectrometric method for measuring light absorption by plant leaves. J. Phys. Conf. Ser. 2018, 1135, 012013. [Google Scholar] [CrossRef]
- Lee, M.; Huang, Y.; Yao, H.; Thomson, S.J.; Bruce, L.M. Effects of sample storage on spectral reflectance changes in corn leaves excised from the field. J. Agric. Sci. 2014, 6, 214. [Google Scholar] [CrossRef][Green Version]
- Bejani, M.M.; Ghatee, M. A systematic review on overfitting control in shallow and deep neural networks. Artif. Intell. Rev. 2021, 54, 6391–6438. [Google Scholar] [CrossRef]
- Varoquaux, G.; Raamana, P.R.; Engemann, D.A.; Hoyos-Idrobo, A.; Schwartz, Y.; Thirion, B. Assessing and tuning brain decoders: Cross-validation, caveats, and guidelines. NeuroImage 2017, 145, 166–179. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.; Giraud-Carrier, C. Diversity, accuracy and efficiency in ensemble learning: An unexpected result. Intell. Data Anal. 2019, 23, 297–311. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Chen, S.; Hu, T.; Luo, L.; He, Q.; Zhang, S.; Lu, J. Prediction of nitrogen, phosphorus, and potassium contents in apple tree leaves based on in-situ canopy hyperspectral reflectance using stacked ensemble extreme learning machine model. J. Soil Sci. Plant Nutr. 2021, 22, 10–24. [Google Scholar] [CrossRef]
- Huang, X.; Guan, H.; Bo, L.; Xu, Z.; Mao, X. Hyperspectral proximal sensing of leaf chlorophyll content of spring maize based on a hybrid of physically based modelling and ensemble stacking. Comput. Electron. Agric. 2023, 208, 107745. [Google Scholar] [CrossRef]
- EU (European Union). Commission Regulation (EC) No 852/2004 of 25 April 2023 on the hygiene of foodstuffs. Off. J. Eur. Union 2004, L139, 82004. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).