Displacement Estimation Performance of a Cost-Effective 2D-LiDAR-Based Retaining Wall Displacement Monitoring System

Abstract

Monitoring the displacement of retaining walls is essential for maintaining their stability. Traditional displacement monitoring by inclinometer is costly and time-consuming, owing to the need for manual measurements. A recently developed 2D-LiDAR-based retaining wall displacement monitoring system offers advantages over traditional methods, such as easy installation and dismantling, as well as the cost-effective monitoring of three-dimensional displacement compared to terrestrial laser scanners (TLSs). However, a previous study did not account for the actual deformation of the retaining wall, potentially compromising the reliability of the displacement estimation. This study aims to assess the displacement estimation performance of the system by using a retaining wall that simulates real-world deformations, considering key parameters related to the displacement estimation algorithm and the quality of point cloud data. Using the multiple model-to-model cloud comparison algorithm and a developed algorithm for filtering duplicate point cloud data, the system’s average performance across various deformation types yielded mean absolute error (MAE), ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$, and compound error values of 1.7, 2.2, and 2.0 mm, respectively. The results demonstrate that even a 2D-LiDAR, which has lower precision than a TLS, can effectively monitor retaining wall displacement through the post-processing of point cloud data.

1. Introduction

In urban construction sites, a retaining wall is a temporary structure installed beside the excavation face during underground excavation to prevent the collapse of surrounding soil, and it is one of the essential structures that should be built to construct the underground space of a building. It is difficult to predict the stability of retaining walls in advance, owing to factors such as lack of data on ground conditions, the use of degraded recycled materials, and construction errors [1,2]. Thus, it is important to continuously verify the stability of retaining walls. Among the methods for verifying the stability of retaining walls, structural health monitoring (SHM) is applied to a variety of structures, including bridges, tunnels, and buildings [3,4,5,6,7]. The SHM of retaining walls involves using various sensors to monitor factors such as the displacement of the retaining wall, soil pressure at the construction site, groundwater levels, and cracks in adjacent buildings. This monitoring is performed in real time or at regular intervals, and preventive measures are taken based on predetermined management criteria to prevent disasters, such as the collapse of the retaining wall [8]. Hence, in South Korea, it is mandatory to comprehensively assess the stability of retaining walls on construction sites where the excavation depth exceeds 10 m [9]. This assessment is conducted using various measuring instruments, such as inclinometers, piezometers, and strain gauges, to monitor the displacement of retaining walls, groundwater levels, and soil settlements [9].

Among the measurement items for the SHM of retaining walls, the displacement of the retaining wall is a crucial factor in monitoring retaining wall behavior. Therefore, various countries, such as the United States [10], China [11], and South Korea [12], have set displacement thresholds to effectively manage the displacement of retaining walls, as shown in Table 1. The displacement of a retaining wall is typically measured using an inclinometer. However, inclinometers have high costs and significant manpower requirements because (1) it is difficult to install and dismantle inclinometers [13,14,15], (2) the measurement method relies on manpower [16,17], and (3) the displacement measurements are limited to one dimension [2,18,19,20]. Furthermore, these methods have the drawback of taking approximately one week for measurement experts to compile multiple sets of inclinometer displacement data and report the stability of retaining walls to construction site managers [15,21]. Consequently, various cutting-edge technologies, such as the Internet of Things (IoT) [1,19,22,23,24], vision sensor technology [2,20,25], and LiDAR sensor technology [15,18,26,27,28,29,30,31,32], are being used to address the limitations of traditional measurement methods.

Table 1. Displacement thresholds of retaining walls.

Category		Maximum Displacement
KCS 11 10 15 [12]	Rigid retaining wall	0.002 H	H (mm): Excavation depth
	Standard retaining wall	0.0025 H
	Soft retaining wall	0.003 H
Geotechnical design manual [10]	MSE (Mechanically stabilized earth)	50 mm
GB 50497-2019 [11]	SMW (Soil mixing wall)	50 mm

Regarding IoT technology, a sensor node is used to collect measurement data from existing measuring devices, and various communication technologies, such as 5G, LTE, and LoRA, enable the real-time monitoring of the displacement data of retaining walls. This resolves the issues associated with the labor-intensive measurement method of inclinometers used in the traditional displacement monitoring of retaining walls. Despite these advancements, the use of IoT-based inclinometers still involves challenges in terms of installation and dismantling, as well as limitations in measuring displacement within a restricted range of one dimension. In contrast, technologies employing vision and LiDAR sensors offer easy installation and dismantling compared with IoT technologies, and enable the three-dimensional displacement measurement of retaining walls. However, within LiDAR sensor technology, TLSs are costly and require measurement operators to manually collect 3D point cloud data at specific intervals, followed by alignment using specialized software. Although vision sensors are more affordable than TLSs, they have limitations in their application on construction sites, where they may be exposed to rain, snow, and other elements, as markers are required to increase the accuracy of displacement estimation.

A cost-effective 2D-LiDAR-based retaining wall displacement monitoring system has recently been developed [33]. This system supports remote measurements with continuous outdoor installation, offering superior waterproofing, dustproofing, and vibration resistance, and an extended operating temperature range compared to TLSs. However, in a previous study [33], the actual deformation of the retaining wall was not considered, and the discontinuous deformation of the retaining wall was artificially created to evaluate the performance of the system, making it difficult to trust the displacement estimation performance. Additionally, because the 2D-LiDAR sensor has lower precision than the TLS commonly used in previous studies, it is necessary to analyze the impact of parameter variations on widely used displacement analysis algorithms. Therefore, this study aims to construct simulated retaining walls that resemble actual retaining wall deformations and analyze the displacement estimation performance of a 2D-LiDAR-based retaining wall displacement monitoring system according to different deformation types and key parameters related to displacement estimation algorithms and the quality of point cloud data. The findings of this study are expected to increase the reliability of the displacement estimation results of the 2D-LiDAR-based retaining wall displacement monitoring system, as they enable the determination of the appropriate parameter values for the system.

2. Related Works

2.1. Previous Research on LiDAR-Based Monitoring Systems for Retaining Wall Displacement

LiDAR sensors are one of the key technologies for non-contact measurement that can determine the three-dimensional displacement of a retaining wall without attaching sensors directly to the wall, such as inclinometers and tiltmeters that estimate displacement by calculating the angle of the attached part. Oskouie et al. [31] developed an algorithm that uses a terrestrial laser scanner (TLS) to collect point cloud data and extract horizontal features by employing plane estimation and cluster analysis. The algorithm focuses on mechanically stabilized earth (MSE), which is primarily used in American bridges. It estimates displacement by analyzing the difference in distances between the centroids of horizontal features. McGuire et al. [29,30] used a TLS to collect baseline and comparison point cloud data for MSE and segmental retaining walls. They derived line-fitting functions from the collected data and estimated the displacement of the retaining wall by measuring the difference between the two line-fitting functions. Lin et al. [28] developed a semi-automated algorithm that estimates displacements in a defined region of interest using a TLS and collects images. They used segmentation techniques and normal vectors to estimate the displacements in the defined region. Seo [32] used a TLS to collect point cloud data on retaining walls in tunnels. They also assessed the extent to which variables such as displacement estimation algorithms, the distance between the scanner and the retaining wall, scanning angle, and point cloud data density affect the displacement estimation results. Zhao et al. [18] and Seo et al. [27] utilized a TLS to collect point cloud data on sheet piles used in construction excavation sites. They directly defined the region of interest for the displacement estimation and removed noisy data using azimuth and elevation angles. The point cloud data with noise removed were used along with the cloud-to-mesh (C2M) algorithm to estimate the final displacement. Aldosari et al. [26] developed a mobile LiDAR mapping system (MMS) equipped with a global navigation satellite system (GNSS)/inertial navigation system (INS), two LiDAR sensors, and cameras to monitor the displacement of retaining walls installed on highways. Kalenjuk et al. [15] developed an MMS system equipped with GNSS/inertial measurement unit/distance measurement information and two LiDAR sensors to collect point cloud data from retaining walls installed on highways. They developed a system that can automatically extract and analyze retaining walls and their displacement from the collected point cloud data. Techniques that analyze the displacement of retaining walls using LiDAR sensors require measurement personnel to directly collect the point cloud data of the retaining wall at regular intervals. The collected point cloud data are then used to estimate the displacement of the retaining wall. Depending on the LiDAR sensor and displacement estimation algorithm, the estimation error of displacement may vary. However, in general, the estimation error of displacement is typically in the order of millimeters, which is sufficient to determine the magnitude of change in the displacement of a retaining wall. However, TLSs and MMSs have been shown to possess the drawbacks of high initial costs and the need for measurement workers to visit the construction site and perform measurement tasks according to the measurement cycle.

Kim et al. [33] developed a 2D-LiDAR-based retaining wall displacement monitoring system that is more cost-effective compared to TLSs and conventional inclinometers and allows for remote measurement. They evaluated the performance of the system using a discontinuous deformation simulation model. However, their study has limitations in that it fails to simulate the actual deformation of continuous retaining walls. Furthermore, the lack of analysis on the displacement estimation performance based on the main parameters of the system makes it difficult to determine the optimal values of these parameters.

2.2. Retaining Wall Displacement Monitoring System Based on 2D-LiDAR

The 2D-LiDAR-based retaining wall displacement monitoring system, which can measure displacements cost-effectively, is divided into two components: the hardware for measuring the displacement of the retaining wall and the software for analyzing and managing the displacements and their history. Figure 1 illustrates these two components. The hardware for measuring the displacement of the retaining wall is installed on the corner strut of the wall. With the constant rotation of the 2D-LiDAR sensor, it is possible to collect and transmit point cloud data of the construction site, including the retaining wall. The specifications of the hardware are shown in Table 2. The software for analyzing and managing the displacement of retaining walls can be installed on a construction site manager’s personal computer or laptop. The construction site manager can then remotely control the hardware to measure the displacement of the retaining walls and collect point cloud data from the construction site using LTE communication technology. Subsequently, the collected point cloud data are used to estimate three-dimensional displacements and visually display the displacement estimation results to construction site managers. This allows for the direct recording and monitoring of reinforcement measures and photographic evidence in the event of displacements exceeding a certain threshold.

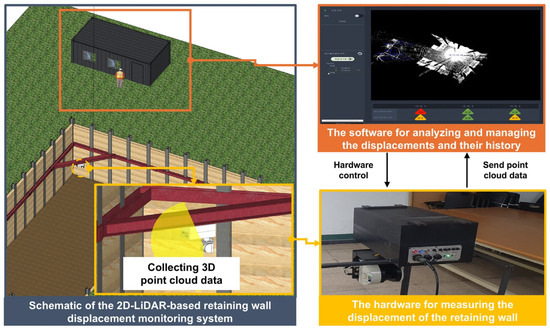
Figure 1. Configuration diagram of the 2D-LiDAR-based retaining wall displacement monitoring system.

Table 2. Key specifications of the hardware for measuring the displacement of the retaining wall.

Category		Value
Servo motor	Rotation speed	2°/s
	Horizontal resolution	0.08°
2D-LiDAR (LMS511-10100 PRO)	Scan frequency	25 Hz
	Scan range	0.2–80 m
	Scan angle	190°
	Accuracy	±25 mm (at 10 m), ±35 mm (at 10–20 m), ±50 mm (at 20–30 m)
	Precision	6 mm (at 10 m), 8 mm (at 10–20 m), 14 mm (at 20–30 m)
	Vertical resolution	0.1667°

Figure 2 illustrates the measurement process of the 2D-LiDAR-based retaining wall displacement monitoring system. The process is as follows.

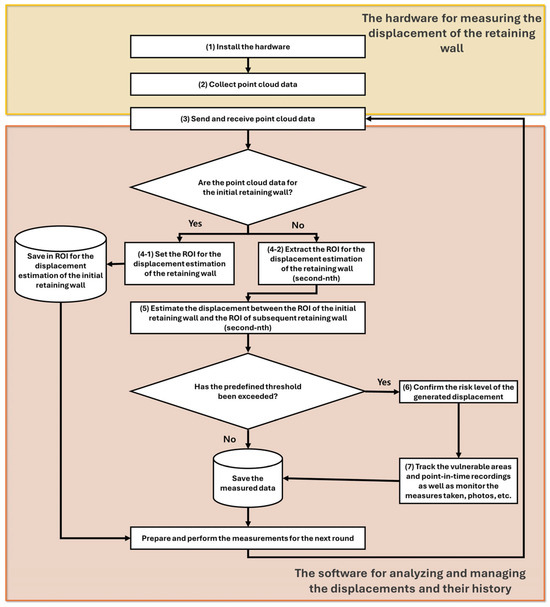
Figure 2. Measurement process of 2D-LiDAR-based retaining wall displacement monitoring system.

(1)

Hardware installation: The hardware for measuring the displacement of the retaining wall is installed on the corner strut.

(2)

Data collection: Point cloud data are collected as the hardware rotates at a constant speed.

(3)

Data transmission: The collected point cloud data are transmitted to the software for analyzing and managing the displacement of retaining walls using LTE communication technology.

(4)

Region of interest (ROI) setting: The ROI for the displacement estimation of the retaining wall is set for each measurement cycle.

(5)

Displacement estimation: Steps 2 through 4 are repeated at regular intervals. The software estimates the displacement between the ROI of the initial (first) retaining wall and that of subsequent retaining walls (second-nth).

(6)

Threshold exceedance confirmation: The locations of the ROI where the displacement exceeds a predefined threshold are confirmed.

(7)

Vulnerability tracking: Vulnerable areas exceeding the threshold are tracked, with the system supporting the recording and monitoring of any identified vulnerable areas.

To enhance the reliability of the estimated displacement of the retaining wall, high-quality point cloud data should be collected. Furthermore, it is necessary to estimate the displacement of the retaining wall using high-quality point cloud data and appropriate displacement estimation algorithms. The quality of the point cloud data collected using LiDAR sensors varies, depending on the distance between measurement surfaces, angles, the reflectivity of the surfaces, and density. These factors have been analyzed in various previous studies [32,34,35,36,37,38,39] that employed TLSs. However, the hardware of the 2D-LiDAR-based retaining wall displacement monitoring system can collect point cloud data by rotating the 2D-LiDAR sensor multiple times, which has a significant impact on the quality of the point cloud data. Therefore, it is necessary to analyze the displacement estimation performance based on changes in the number of rotations.

2.3. Related Algorithm for Displacement Estimation Based on Point Cloud Data

The 2D-LiDAR-based retaining wall displacement monitoring system requires the selection of an appropriate displacement estimation algorithm to enhance the reliability of the estimated results, considering that three-dimensional point cloud data are collected. An investigation and analysis were conducted on displacement estimation algorithms based on point cloud data. Point cloud data-based displacement estimation algorithms can be classified into three types: cloud-to-cloud (C2C), C2M, and multiple model-to-model cloud comparison (M3C2).

A C2C algorithm analyzes displacement, typically by calculating the distance of a point in one of the comparison point cloud datasets to the nearest point in the baseline point cloud dataset (Figure 3a) [40]. In C2C, displacement analysis is performed on the entire point cloud dataset used for comparison. The C2C algorithm is dependent on the direction and magnitude of the displacement in the point cloud data, which means that errors in LiDAR sensor measurements or a high amount of noise in the point cloud data can lead to increased errors in the estimated displacement results.

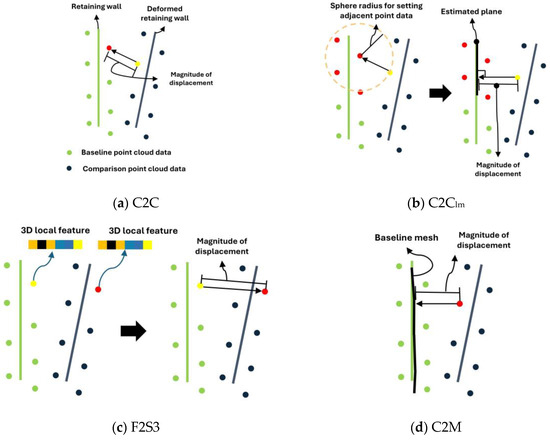
Figure 3. Estimation of displacement using algorithms from the C2C series and the C2M algorithm.

Subsequently, to address the shortcomings of the C2C algorithm, algorithms such as cloud-to-cloud based on local modeling (C2C_lm) and feature-to-feature supervoxel-based spatial smoothing (F2S3) were developed. The C2C_lm algorithm (Figure 3b) aims to reduce displacement estimation errors caused by sensor errors. It follows the same approach as the C2C method by selecting the closest data point from the baseline point cloud data. The selected data are then used to estimate local models, such as planes, curves, and cylinders, within a certain radius. The displacement is derived by calculating the perpendicular distance between the local model and the data points within the radius [40]. This algorithm has the ability to reduce sensor errors in the baseline point cloud data; however, it has the disadvantage of being sensitive to sensor errors in the direction and comparison point cloud data. The F2S3 algorithm (Figure 3c) uses deep learning to extract 3D local features from the baseline and comparison point cloud data. It then matches the baseline point cloud data with similar 3D local features in the comparison point cloud data and calculates the distance between the two datasets to derive displacement [41]. The algorithm in question employs deep learning algorithms to accurately determine the displacement direction, compared with the C2C_lm algorithm. However, it relies on C2C analysis to calculate the distance between two points of data, which leads to an increase in the displacement estimation error as the LiDAR sensor error increases.

The C2M algorithm (Figure 3d) uses the baseline point cloud data to generate mesh data and then calculates the vertical distance between the comparison point cloud data and mesh data to derive the displacement [42]. The C2M algorithm exhibits similar performance to that of C2C_lm, and it can estimate displacements, even in the presence of missing values in the baseline point cloud data. However, certain parameter settings are required for mesh generation, and if outliers occur in the baseline point cloud data, the mesh quality deteriorates, and the displacement estimation errors increase. Furthermore, the C2M algorithm is sensitive to sensor noise in the comparison point cloud data.

The M3C2 algorithm (Figure 4) selects core points from the baseline point cloud data as targets for displacement estimation. It then generates normal vectors that represent the displacement direction using adjacent point data within a certain diameter (D) for each core point [43]. After creating a cylinder with a fixed diameter (d) and height (H) based on the direction of the normal vector, the displacement is analyzed by calculating the difference in average position between the baseline point cloud data and the comparison point cloud data projected onto the normal vector within the cylinder. Compared with other algorithms, the M3C2 algorithm confers the advantage of reducing sensor errors by analyzing the displacement through the average positions of adjacent data. However, it is necessary to configure parameters related to the number of adjacent point data, and the algorithm has the disadvantage of being unable to estimate displacement in areas where missing values occur. Given the existence of advantages and disadvantages for each analyzed displacement estimation algorithm (Table 3), it is necessary to select a displacement estimation algorithm to be applied in the 2D-LiDAR-based retaining wall displacement monitoring system. Three types of displacement analysis algorithms—C2C, C2M, and M3C2—were individually applied to evaluate displacement estimation performance.

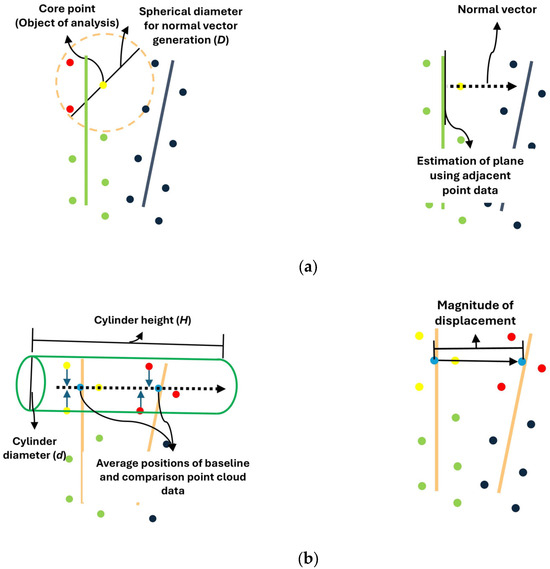
Figure 4. Estimation of displacement using the M3C2 algorithm. (a) Generating normal vectors for each core point. (b) Estimation of the displacement of the baseline and comparison point data using cylinders.

Table 3. Characteristics of displacement estimation algorithms based on point cloud data.

Category		Displacement Analysis Method		Characteristics
		Magnitude	Direction
C2C Series	Basic	Point to point		- Faster displacement analysis than other algorithms as it does not require estimation of planes, meshes, or normal vectors. - High variability in displacement analysis results due to errors in LiDAR measurements.
	C2Clm	Point to plane		- Higher displacement analysis accuracy than the C2C algorithm through plane estimation. - Greater variability in displacement analysis results due to errors in comparison point cloud compared to the M3C2 algorithm.
	F2S3	Point to point	3D local feature	- More accurate estimation of displacement direction than other algorithms using deep learning. - Similar to the C2C algorithm, displacement magnitude is analyzed, leading to high variability in displacement analysis results due to errors in LiDAR measurements.
C2M		Point to mesh		- Performs similarly to the C2Clm algorithm and can still analyze displacement if there are missing values in the baseline point cloud data. - Slower displacement analysis than other algorithms as it requires mesh data. - There is a risk of degraded mesh data quality if outliers occur in the point cloud data.
M3C2		Average location of neighboring points	Normal vector	- Lower variability in displacement analysis results due to errors in LiDAR measurements. - Requires parameter setting for displacement analysis and cannot analyze displacement if there are missing data.

3. Methodology for Evaluating the Displacement Estimation Performance of the 2D-LiDAR-Based Retaining Wall Displacement Monitoring System

To evaluate the displacement estimation performance of the 2D-LiDAR-based retaining wall displacement monitoring system, parameters for the displacement estimation performance were defined based on the analytical results presented in Section 2.2 and Section 2.3. Various simulated retaining walls were constructed using actual displacement data from retaining walls, and performance evaluations were conducted based on parameter variations (Figure 5).

Figure 5. Overall evaluation methodology for the displacement estimation performance of the 2D-LiDAR-based retaining wall displacement monitoring system.

3.1. Definition of Parameters for Estimating Displacement Performance and the Development of an Algorithm for Filtering Duplicate Point Cloud Data

The parameters for displacement estimation were divided into two main categories. First, in Section 2.2, parameters were selected based on the quality of point cloud data in relation to rotation frequency. Second, Section 2.3 examined various displacement estimation algorithms, with the robust C2C_lm, C2M, and M3C2 algorithms—chosen for their resilience to sensor errors—selected for this experiment. However, for the rotation frequency established in Section 2.2, an algorithm was required to filter out duplicate point cloud data accumulating at the same position as the rotation count increases, as illustrated in Figure 6.

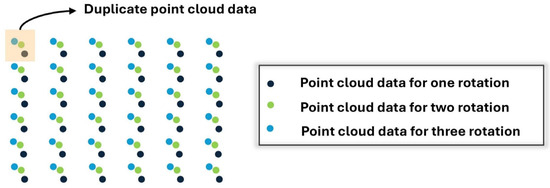
Figure 6. Example of duplicate point cloud data, according to the number of rotations.

The voxel grid downsampling technique is commonly used to filter duplicate point cloud data. It extends the pixels in two-dimensional image data into a three-dimensional (x, y, z) space by setting a voxel size and determining the central position of the point cloud data within each voxel. This method reduces the number of point cloud data by downsampling them (Figure 7a). However, voxel grid downsampling has the drawback of not being able to determine the positions of points that are collected redundantly (Figure 7b). This results in the formation of a voxel grid with non-redundant data. In addition, determining the appropriate voxel size is challenging, owing to variations in voxel size depending on the distance between the LiDAR sensor and the obstructing wall. Hence, it is difficult to remove noise data when moving objects occur and are treated as different voxels (Figure 7c).

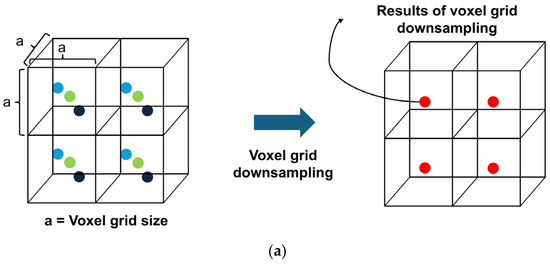
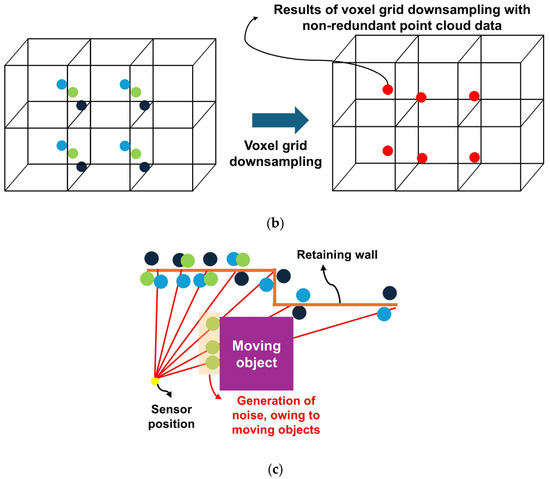
Figure 7. Method and problems of filtering duplicate point cloud data based on voxel grid downsampling. (a) Results of voxel grid downsampling. (b) Problems of voxel grid downsampling caused by voxel positioning. (c) Problems of voxel grid downsampling caused by moving objects.

The aforementioned voxel grid downsampling technique suffers from the issue of not being able to set the initial voxel position, owing to the Cartesian coordinate system (x, y, z) that is used to define the voxel size. Thus, an algorithm has been developed to filter duplicate point cloud data by converting them from Cartesian coordinates (x, y, z) to spherical coordinates (r, φ, θ), as shown in Figure 8.

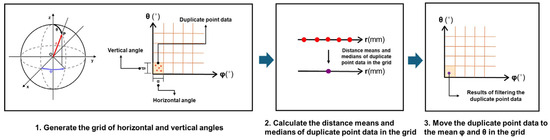
Figure 8. Algorithm for filtering duplicate point cloud data based on a spherical coordinate system.

This algorithm generates a fixed grid of horizontal (φ) and vertical (θ) angles through the resolution of the LiDAR sensor and hardware rotation speed. The mean and median positions of the distance (r) data within the grid are then calculated. Next, the calculated distance value is used to transform duplicate point data into a single point, based on the mean horizontal and vertical angles within the grid. Two methods for filtering the distance (r) data within the grid are the mean-based method and median-based method. The median-based method allows for the elimination of noisy point cloud data generated by moving objects. Contrarily, the mean-based method possesses a susceptibility to noise. In this method, the mean value is calculated after applying the z-score method to eliminate noisy data points. The standard scores are calculated for each data point based on the distance from duplicate data, and any data points with standard scores exceeding a certain threshold are eliminated. The standard score is then calculated, as shown in Equation (1). The parameters for estimating the displacement performance were selected comprehensively, as summarized in Table 4.

$$\begin{array}{c}z-score\left(r_i\right)={\displaystyle \frac{r_i-\overline{R}}{{\sigma }_R}}\\ R=(r_1,r_2,\cdots r_n),\overline{R}={\displaystyle \frac{\sum _{i=1}^n{r}_i}{n}},{\sigma }_R=\sqrt{{\displaystyle \frac{\sum _{i=1}^n{\left(r_i-\overline{R}\right)}^2}{n}}}\end{array}$$

(1)

Table 4. Selected parameters for estimating the displacement performance.

Parameter			Value
Point cloud data quality	Number of rotations (counts)		1, 2, 3, 4, 5
	Algorithm for filtering duplicate point cloud data	Median-based method	-
		Mean-based method (z-score threshold)	1, 2
Displacement estimation algorithm	C2Clm	Local modeling	Least squares plane
		Radius (mm)	100, 200, 300
	C2M	Mesh generation	Poisson surface reconstruction
		Resolution (mm)	100, 200, 300
	M3C2	Normal vector diameter (mm)	100, 200, 300
		Cylinder diameter (mm)	50, 100, 150, 200, 250, 300
		Cylinder height (mm)	100

3.2. Definition and Construction of Simulated Retaining Walls by Deformation Type

A simulated retaining wall was constructed to evaluate the displacement estimation performance of the 2D-LiDAR-based retaining wall displacement monitoring system, based on the collapse type of the retaining wall. The collapse of a retaining wall can occur in three manners [44,45]. The first occurs when the supporting structure is destroyed. This results in the maximum displacement of the retaining wall occurring at the location of the support (upper, middle, or lower). The second occurs when the excavation foundation is weak or the backfill material is insufficient, which causes either the lower part of the retaining wall to move or the entire retaining wall to be within the active zone. This results in maximum displacement and collapse at the lower part of the retaining wall. The third occurs when a bending moment generated in the retaining wall exceeds the capacity of its components. This results in maximum displacement and collapse in the middle part of the retaining wall. For the simulated retaining wall, the deformation types are defined as upper deformation, middle deformation, lower deformation, and a compound type in which upper, middle, and lower deformations occur simultaneously, considering the aforementioned collapse types (Figure 9). The displacement data of retaining walls for the four defined types of deformation were obtained from field data collected using inclinometers in previous studies [46,47,48,49].

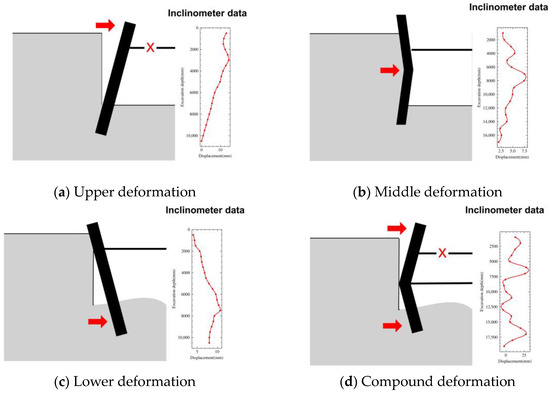
Figure 9. Definitions of retaining wall deformation types and inclinometer data.

First, a baseline simulated retaining wall with no deformation was fabricated using a wood computer numerical control. The retaining wall was 950 mm wide, 2400 mm high, and 50 mm thick, as shown in Figure 10a. The baseline simulated retaining wall is secured to a fixed stand at the back. In addition, retaining walls of different types (upper, middle, lower, and compound) were simulated based on the data defined in Figure 9, using the same dimensions as those of the baseline simulated retaining wall (Figure 10). Here, the height of the simulated retaining wall and the data height of the inclinometer were different. Therefore, while maintaining the displacement data of the inclinometer, the spacing between the displacement data was reduced to match the height of the simulated retaining wall. In addition, the design ensured that the same displacement would occur in the horizontal direction of the simulated retaining wall. The deformation simulated retaining walls were also secured to the same stand as the baseline simulated retaining wall.

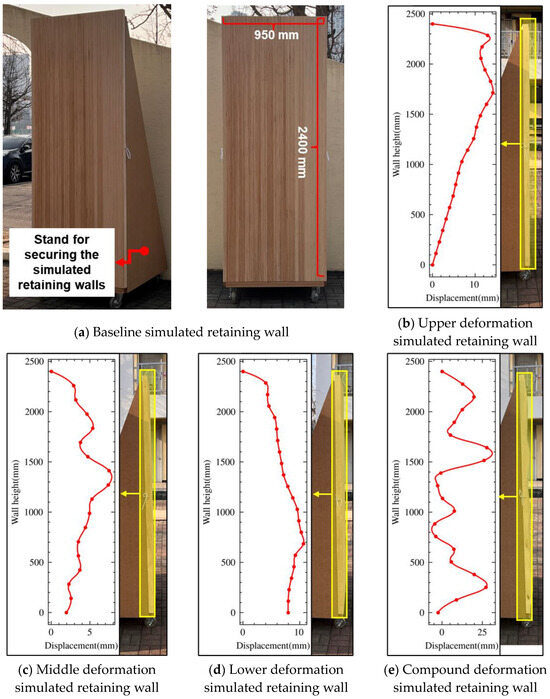
Figure 10. Results of the construction of the baseline and deformation simulated retaining walls.

3.3. Definition of the Process for Evaluating Displacement Estimation Performance

The process for evaluating displacement estimation performance was defined based on the parameters and simulated retaining walls, as shown in Figure 11. The process took place as follows.

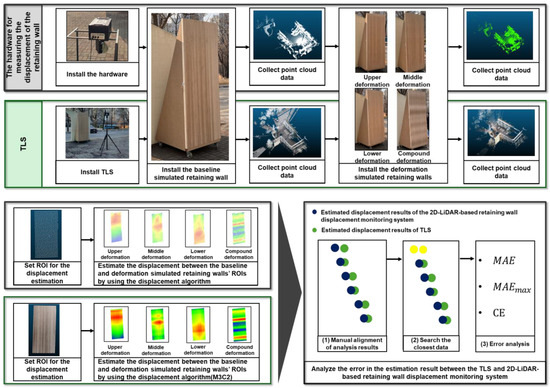
Figure 11. Process for evaluating the displacement estimation performance using TLS and simulated retaining walls.

(1)

Hardware and TLS installation: The hardware for measuring the displacement of the retaining wall and TLS were installed.

(2)

Baseline simulated retaining wall installation: The baseline simulated retaining wall was installed.

(3)

Data collection of baseline simulated retaining wall: The point cloud data of the baseline simulated retaining wall were collected using the hardware and TLS.

(4)

Deformation simulated retaining wall installation: The deformation simulated retaining walls were installed.

(5)

Data collection of the deformation simulated retaining walls: The point cloud data of the deformation simulated retaining walls were collected using the hardware and TLS.

(6)

ROI setting: The ROI for the displacement estimation was set.

(7)

Displacement estimation: The displacement estimation algorithms (C2C_lm, C2M, M3C2) were applied separately to estimate the displacement between the ROI of the baseline simulated retaining wall and the ROI of the deformation simulated retaining walls.

(8)

Error analysis: The error was analyzed between the estimated displacement results of the TLS and the estimated displacement results of the 2D-LiDAR-based retaining wall displacement monitoring system.

Ground truth values were measured using a TLS, as the displacement of the retaining wall varied with temperature, owing to the simulated retaining wall being constructed using wood. Here, the Faro S350 scanner was used as the TLS, and the M3C2 algorithm was used for displacement estimation. The specifications of the Faro S350 scanner are provided in Table 5.

Table 5. Key specifications of the Faro S350 scanner.

Category	Value
Scan range	0.6–350 m
Accuracy	±1 mm(at 10–25 m)

To minimize the utilization of the surrounding data, the normal vector and cylinder diameter were restricted to 10 mm. The error in estimating the displacement of the TLS and the 2D-LiDAR-based retaining wall displacement monitoring system was analyzed by manually aligning the displacement estimation results of the TLS with the displacement estimation results of the 2D-LiDAR-based retaining wall displacement monitoring system. The analysis was then performed by searching for the closest point to the TLS in the monitoring system’s analysis results and comparing the displacement estimation results obtained from the two points. The performance evaluation metrics used were the mean absolute error (MAE), which represents the average error in displacement estimation; ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$, which represents the error near the maximum displacement; and compound error (CE), which evaluates the combined error between the average error and the error near the maximum displacement. The formulas for each metric are given in Equations (2) to (4):

$$\begin{array}{c}MAE\left(MeanAbsoluteError\right)={\displaystyle \frac{\sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|}{n}};\\ y=Groundtruth\left(\mathrm{TLS}\right);\widehat{y}=\mathrm{S}ystemdisplacementresult;\end{array}$$

(2)

$$\begin{array}{c}{MAE}_{D_{max}}={\displaystyle \frac{\sum _{i\in D_{max}}^M\left|y_i-{\widehat{y}}_i\right|}{M}};\\ D_{max}=\left\{\left(y_i,{\widehat{y}}_i\right)|y_i\in \left[y_{max}-1mm,y_{max}\right]\right\};\\ M=Thenumberofdatabelongingto{D}_{max};\end{array}$$

(3)

$$\mathrm{C}\mathrm{E}\left(\mathrm{C}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}\right)={\displaystyle \frac{MAE+{MAE}_{D_{max}}}{2}}.$$

(4)

4. Evaluation of the Displacement Estimation Performance of the 2D-LiDAR-Based Retaining Wall Displacement Monitoring System

The hardware for measuring the displacement of the retaining wall was positioned approximately 20 m from the simulated retaining wall. The ground truth value was obtained from a TLS that was installed approximately 3 m from the simulated retaining wall. Point cloud data were collected, as shown in Figure 12. The ROIs for the displacement estimation were manually set from the collected point cloud data, and the ROIs from the TLS were manually aligned with the ROIs from the 2D-LiDAR-based retaining wall displacement monitoring system. Additionally, the TLS data used as ground truth were downsampled to a voxel size of 10mm. The details of data collection are presented in Table 6. A performance evaluation was then conducted.

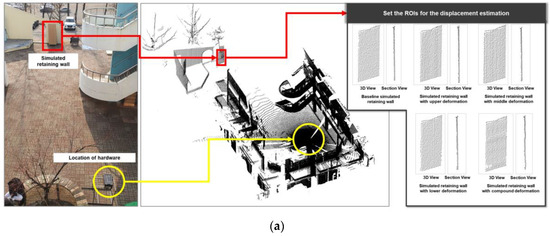
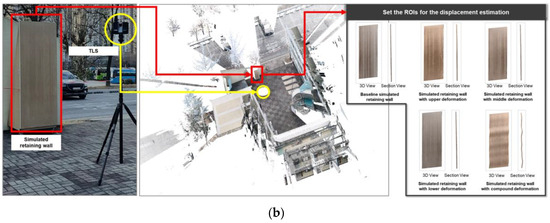
Figure 12. Results of the point cloud data collection by the 2D-LiDAR-based retaining wall displacement monitoring system and the TLS. (a) Results of point cloud data collection and ROIs for displacement estimation by the 2D-LiDAR-based retaining wall displacement monitoring system. (b) Results of point cloud data collection and ROIs for displacement estimation by TLS.

Table 6. Details of data collection.

Category	Measurement Distance	Measurement Angles of Incidence	Point Interval
TLS	Approximately 3 m	Approximately perpendicular	Vertical interval: 10 mm Horizontal interval: 10 mm
2D-LiDAR-based retaining wall displacement monitoring system	Approximately 20 m	Approximately 78.5°	Vertical interval: 63.1 mm Horizontal interval: 30.8 mm

4.1. Evaluation of the Displacement Estimation Performance of Different Displacement Estimation Algorithms

The performance evaluation of the C2C_lm, C2M, and M3C2 algorithms was conducted by fixing the rotation count and speed at 1 count and 2°/s, respectively. The displacement analysis was performed using CloudCompare software (version 2.13.1). The overall performance evaluation results are presented in Appendix A. The parameter with the lowest CE for each displacement estimation algorithm was selected as the representative parameter for that algorithm (Figure 13). Descriptive statistics for each displacement estimation algorithm are presented in Table 7 below. The histograms for each displacement estimation algorithm are shown in Figure 14, and the width of the bins in the histograms was determined by the Freedman–Diaconis rule. In addition, kernel density estimation (KDE) was applied to compare the displacement estimation algorithms. Excluding the simulated retaining wall with lower deformations, the MAE (blue bar graph in Figure 13) of the M3C2 analysis algorithm was the lowest for the simulated retaining wall with upper deformation at 1.4 mm, middle deformation at 0.8 mm, and compound deformation at 4.5 mm. However, in the case of the simulated retaining wall with lower deformation, the MAE of the C2C_lm algorithm was the lowest at 4.6 mm. However, upon examining the results of the M3C2 analysis (MAE: 4.9 mm), it was determined that an offset of approximately 5 mm occurred owing to external factors, as indicated by the blue line graph (KDE of M3C2) in Figure 14c. Moreover, the simulated retaining wall with compound deformation, which exhibited a significant change in the displacement rate according to the height of the retaining wall, had a high MAE of 4.5 mm compared with those of the other deformation types, as shown in Figure 13. This is because the rate of change of the displacement was high, which resulted in a lower cylinder diameter parameter in the M3C2 algorithm, compared with the other deformation types, thereby leading to a decrease in the number of surrounding data used. Based on the evaluation results of the displacement estimation performance for the simulated retaining wall with lower compound deformation, it is not possible to guarantee displacement estimation performance with a single scan. Therefore, it is necessary to increase the number of rotations to eliminate the sensor noise and improve the precision of the point cloud data. The ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$ (red bar graph in Figure 13) had the lowest values for the simulated retaining wall with upper deformation at 0.7 mm, middle deformation at 1.4 mm, lower deformation at 5.7 mm, and compound deformation at 5.7 mm. Overall, excluding the simulated retaining wall with lower deformation, the M3C2 algorithm, which showed the lowest CE (green bar graph in Figure 13) values, had the best performance compared with other displacement estimation algorithms. According to the analysis of the displacement estimation algorithms in Section 2.3, the C2C_lm and C2M algorithms demonstrated similar performance levels (Figure 14). The M3C2 algorithm, however, exhibited lower variability in the displacement analysis results because it uses averaged data for the comparison point cloud data. As a result, except for the simulated retaining wall with lower deformation, the M3C2 algorithm produced results that closely matched the ground truth (Figure 14).

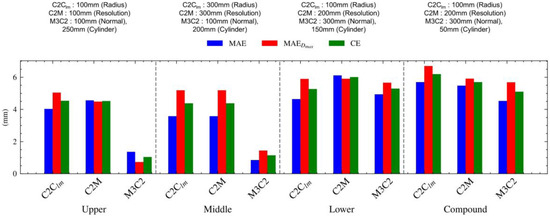
Figure 13. Displacement estimation performance results by displacement estimation algorithm for different types of deformation.

Table 7. Descriptive statistics results for the displacement estimation algorithms and deformation types.

Deformation Types	Displacement Estimation Algorithms	Descriptive Statistics
		Count	MAE (mm)	Std Dev (mm)	Min (mm)	Q1 (mm)	Q2 (mm)	Q3 (mm)	Max (mm)
Upper	C2Clm	1218	4.0	3.3	2.2 × 10−2	1.5	3.2	5.7	26.5
	C2M	1218	4.6	3.7	2.2 × 10−3	1.8	3.7	6.4	25.9
	M3C2	1134	1.4	1.7	3.3 × 10−3	0.4	0.9	1.6	11.1
Middle	C2Clm	1213	3.6	2.9	2.0 × 10−3	1.4	3.0	5.0	24.9
	C2M	1213	4.5	3.8	9.5 × 10−3	1.7	3.7	6.3	24.6
	M3C2	1134	0.8	0.7	3.6 × 10−4	0.3	0.7	1.2	5.5
Lower	C2Clm	1135	4.6	3.0	6.2 × 10−3	2.2	4.4	6.6	24.3
	C2M	1135	6.1	4.7	2.5 × 10−3	2.8	5.5	8.3	35.3
	M3C2	1134	4.9	1.3	2.4 × 10−1	4.2	5.0	5.8	10.9
Compound	C2Clm	1155	5.7	4.4	7.5 × 10−3	2.4	4.8	8.0	25.7
	C2M	1155	5.5	4.0	9.2 × 10−4	2.3	4.7	7.8	25.4
	M3C2	1132	4.5	3.2	7.7 × 10−3	2.0	4.0	6.3	22.1

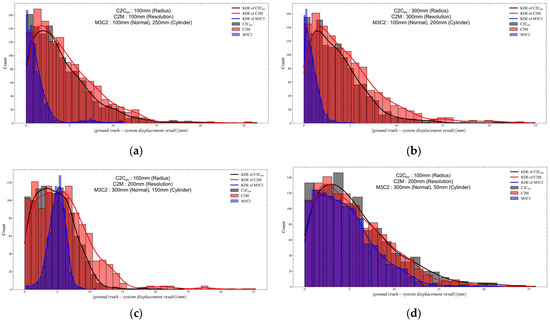
Figure 14. Histogram results for the displacement estimation algorithms and deformation types. (a) Simulated retaining wall with upper deformation. (b) Simulated retaining wall with middle deformation. (c) Simulated retaining wall with lower deformation. (d) Simulated retaining wall with compound deformation.

The results of the performance evaluation analysis of the M3C2 algorithm, based on the variations in the parameters of the normal vector diameter and cylinder diameter, revealed that as the normal vector diameter increased, a negligible variation in the displacement estimation performance appeared (Figure 15). Conversely, the cylinder diameter significantly impacted displacement estimation performance. It was observed that for the simulated retaining walls with upper, middle, and lower deformations, the MAE gradually decreased and converged to a certain level as the cylinder diameter increased (Figure 16). In the case of the simulated retaining wall with compound deformation, the MAE gradually increased as the cylinder diameter increased, owing to the significant displacement difference in the surrounding data of the compound deformation. However, the simulated retaining walls with upper, middle, and lower deformations were characterized by errors caused by sensor noise rather than errors resulting from displacement differences in the surrounding data. Consequently, the MAE gradually decreased. However, as the cylinder diameter increased, two problems occurred: the displacement at the maximum displacement point was underestimated, as shown in Figure 17, and the displacement at the minimum displacement point was overestimated. The underestimation was problematic; although the actual displacement level of the retaining wall was a concern, the estimation algorithm considered it safe. Therefore, when performing displacement estimation using the M3C2 algorithm, careful attention should be paid to the CE, which comprehensively considers both the average error (MAE) of the entire dataset and the error at the maximum displacement (${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$)

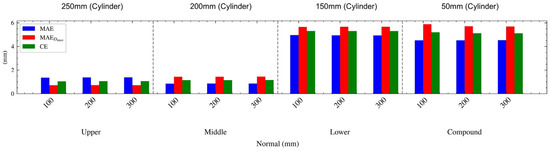
Figure 15. Analytical results of the displacement performance for different types of deformation, according to changes in the normal vector diameter.

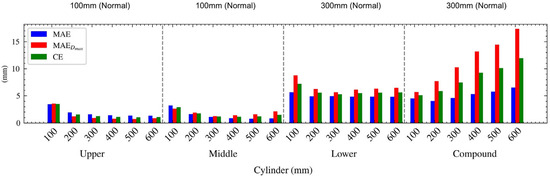
Figure 16. Analytical results of the displacement performance, according to variations in the cylinder diameter and deformation type.

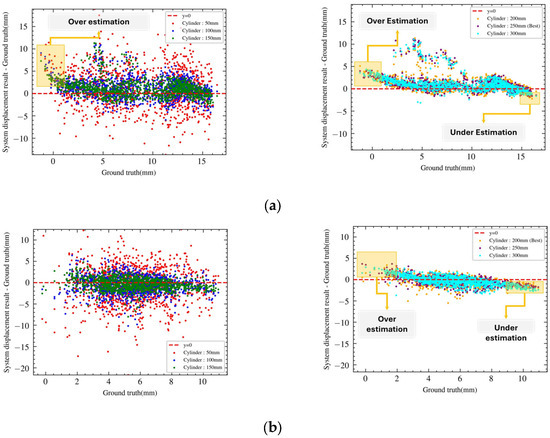
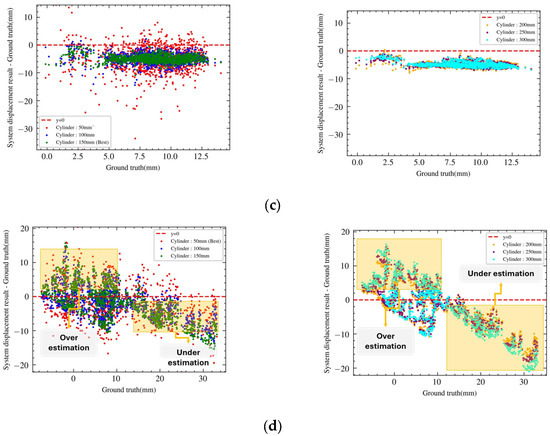
Figure 17. Analytical results of the differences between the ground truth and system displacement results for different types of deformation, according to changes in the cylinder diameter. (a) Simulated retaining wall with upper deformation. (b) Simulated retaining wall with middle deformation. (c) Simulated retaining wall with lower deformation. (d) Simulated retaining wall with compound deformation.

4.2. Evaluation of Displacement Estimation Performance Based on Rotation Counts and Algorithms for Filtering Duplicate Point Cloud Data

According to the performance analysis of the simulated retaining walls with lower and compound deformations discussed in Section 4.1, it is difficult to address the sensor noise caused by external factors. Moreover, the precision of the point cloud data is low when only a single rotation is taken. Therefore, to improve the quality of the point cloud data, it is necessary to increase the rotation count. Filtering the duplicate point cloud data was carried out with the median-based method and the mean-based method with the standard score (z-score). The parameters of the M3C2 algorithm for each deformation type were used based on the optimal parameters derived in Section 4.1. The displacement estimation performance was analyzed by rotation count (Appendix B, Figure 18). The descriptive statistics of each deformation type for the first rotation and five rotations (median-based and mean-based methods) are presented in Table 8. The histograms and scatter plots for each deformation type are shown in Figure 19, with the bin width and KDE applied in the same manner as described in Section 4.1. The simulated retaining walls with upper (Figure 18a and Figure 19A) and middle deformations (Figure 18b and Figure 19B) yielded MAE, ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$, and CE values of approximately 1 mm, owing to the excellent quality of the point cloud data in the first iteration. However, there was a difference of approximately 5 mm between the actual displacement and the deformation in the simulated retaining wall with lower deformation. As the number of rotations increased, the MAE, ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$, and CE values gradually decreased (Figure 18c). For example, compared with the results obtained using one rotation (CE: 4.9 mm, ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$: 5.7 mm, CE: 5.3 mm), the MAE, ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$, and CE for five rotations (median-based method) decreased by 71.4% (1.4 mm), 70.2% (1.7 mm), and 71.7% (1.5 mm), respectively. These results indicate that, similar to the simulated retaining walls with upper and middle deformations, the CE was approximately 1 mm. Accordingly, the sensor’s noise-filtering effect improved significantly as the number of rotations increased (Figure 19C). In the case of the simulated retaining wall with compound deformation, the ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$ remained constant (${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$ for one rotation: 5.7 mm; ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$ for five rotations: 5.3 mm). However, at five rotations (median-based method) in comparison to one rotation (MAE: 4.5 mm, CE: 5.1 mm), the MAE and CE decreased by 37.8% (MAE: 2.8 mm) and 19.6% (CE: 4.1 mm), respectively. These results suggest that the quality of the point cloud data improved with an increase in the number of rotations (Figure 19D). Among the algorithms for filtering duplicate point cloud data, the average performance by different types of deformation based on five rotations had a slight but higher difference in the following order: median-based method (CE: 2.0 mm), mean-based method with a z-score threshold of one (CE: 2.0 mm), and mean-based method with a z-score threshold of two (CE: 2.1 mm).

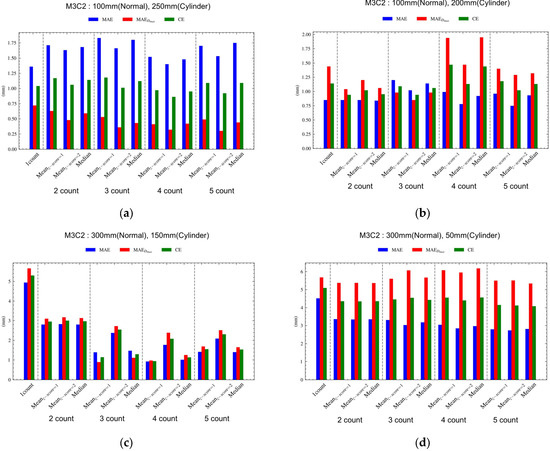
Figure 18. Analytical results of the displacement performance by different types of deformation, based on the rotation count and algorithm for filtering duplicate point cloud data. (a) Simulated retaining wall with upper deformation. (b) Simulated retaining wall with middle deformation. (c) Simulated retaining wall with lower deformation. (d) Simulated retaining wall with compound deformation.

Table 8. Descriptive statistics results of each deformation type for the first rotation and five rotations.

Deformation Types	Number of Rotations	Descriptive Statistics
		Count	MAE (mm)	Std Dev (mm)	Min (mm)	Q1 (mm)	Q2 (mm)	Q3 (mm)	Max (mm)
Upper	1	1134	1.4	1.7	3.3 × 10−3	0.4	0.9	1.6	11.1
	5 (Meanz-score=1)	1111	1.7	1.7	2.2 × 10−3	0.6	1.2	2.1	10.8
	5 (Meanz-score=2)	1112	1.5	1.7	1.6 × 10−3	0.5	1.0	1.9	10.6
	5 (Median)	1112	1.7	1.8	8.9 × 10−4	0.7	1.3	2.1	11.1
Middle	1	1134	0.8	0.7	3.6 × 10−4	0.3	0.7	1.2	5.5
	5 (Meanz-score=1)	1111	1.0	0.8	1.5 × 10−3	0.3	0.7	1.4	4.6
	5 (Meanz-score=2)	1112	0.8	0.6	4.4 × 10−3	0.3	0.6	1.1	3.4
	5 (Median)	1112	0.9	0.7	1.2 × 10−3	0.4	0.8	1.3	3.6
Lower	1	1134	4.9	1.3	2.4 × 10−1	4.2	5.0	5.8	10.9
	5 (Meanz-score=1)	1111	1.4	1.0	7.2 × 10−4	0.7	1.3	2.0	6.4
	5 (Meanz-score=2)	1112	2.1	1.0	1.2 × 10−2	1.3	2.0	2.8	6.6
	5 (Median)	1112	1.4	1.0	2.0 × 10−3	0.6	1.3	2.0	6.3
Compound	1	1132	4.5	3.2	7.7 × 10−3	2.0	4.0	6.3	22.1
	5 (Meanz-score=1)	1098	2.8	2.3	1.6 × 10−2	1.0	2.3	4.0	16.3
	5 (Meanz-score=2)	1097	2.7	2.1	3.8 × 10−6	1.1	2.2	4.0	15.4
	5 (Median)	1099	2.8	2.3	5.9 × 10−3	1.0	2.3	4.1	20.4

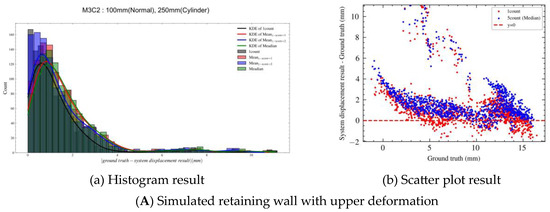
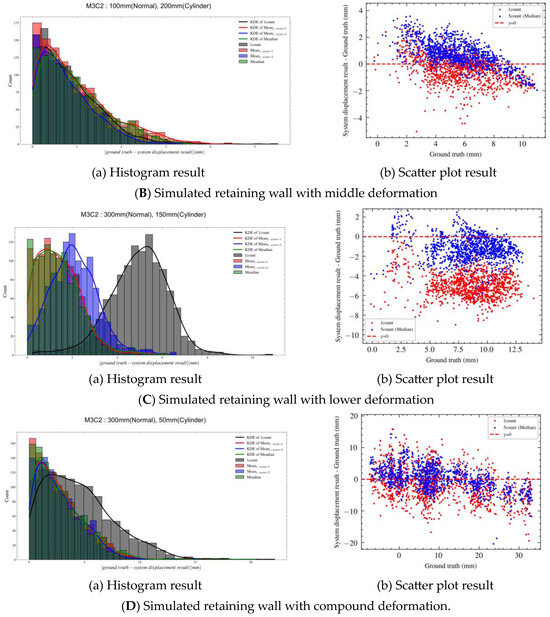
Figure 19. Histogram and scatter plot results of each deformation type for the first rotation and five rotations.

4.3. Discussion

Overall, the average displacement estimation performance across different types of deformation based on five rotations (using the median-based method) and a rotation speed of 2°/s was 1.7, 2.2, and 2.0 mm for MAE, ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$, and CE, respectively. Therefore, the retaining wall displacement monitoring system exhibits an average error of approximately 2 mm when compared to a high-precision TLS. This level of error suggests that the system is capable of detecting a minimum displacement threshold of 4–6 mm, which is applicable to retaining walls in South Korea with a typical excavation depth of 2–3 m. Figure 20 shows that the estimated displacement results of the 2D-LiDAR-based retaining wall displacement monitoring system with five rotations (using the median-based method) and a rotation speed of 2°/s are similar to the estimated displacement results (ground truth) of the TLS.

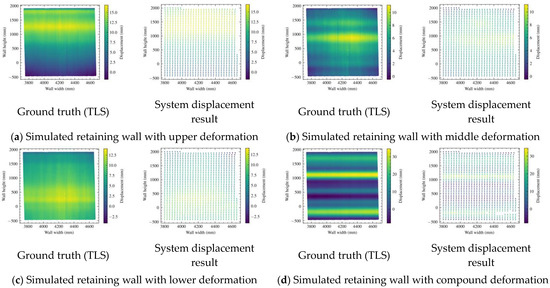
Figure 20. Comparison of the displacement results of 2D-LiDAR-based retaining wall displacement monitoring system and estimated displacement results of the TLS (ground truth).

By utilizing the M3C2 algorithm along with an algorithm for filtering duplicate point cloud data, it was found that even a 2D-LiDAR sensor, which has lower precision than a TLS, can adequately monitor the displacement of retaining walls. This suggests that, despite its lower measurement precision, a cost-effective LiDAR sensor can effectively measure displacement through the post-processing of point cloud data. However, as demonstrated in the performance analysis of a simulated retaining wall with combined deformation, the error in the 2D-LiDAR-based retaining wall displacement monitoring system increases when the rate of deformation changes significantly. To reduce the system’s error, it is necessary to develop a method to optimize the cylinder for each point while considering the density of neighboring points. Additionally, this experiment has limitations as it considered only wood as the material and did not include other materials, such as those used in the steel and wood h-pile and timber method, steel-based sheet piles, or concrete-based cast-in-place methods. Future research should focus on monitoring the displacement of various types of retaining walls over extended periods at actual construction sites to further validate the effectiveness of these algorithms.

5. Conclusions

The evaluation of the displacement estimation of the 2D-LiDAR-based retaining wall displacement monitoring system was conducted from three perspectives: (1) deformation type (upper, middle, lower, compound), (2) displacement estimation algorithm, and (3) quality of point cloud data (rotation count, filtering of duplicate point cloud data). The conclusions of this study are as follows.

(1)

The results of the displacement estimation performance using the constructed simulated retaining walls show that the M3C2 algorithm performed the best (CE_upper: 1.0 mm; CE_middle: 1.1 mm; CE_compound: 5.1 mm) for the simulated retaining walls with upper, middle, and compound deformations. However, in the case of the simulated retaining wall with lower deformation, owing to sensor noise, an offset problem of approximately 5 mm occurred. This offset made it impossible to guarantee displacement estimation performance with only one rotation. Furthermore, when the rate of displacement change was high (the simulated retaining wall with compound deformation), it became difficult to use the surrounding point data, which resulted in a decrease in the displacement estimation performance.

(2)

The analysis of the displacement estimation performance based on the parameter variations in the M3C2 algorithm revealed that the sensitivity of the displacement estimation performance was significant regarding changes in cylinder diameter. Moreover, as the cylinder diameter increased, a problem of displacement underestimation at the maximum displacement point occurred. Therefore, it is necessary to determine the appropriate cylinder diameter value based on the magnitude and variation of displacement in the retaining wall.

(3)

The analysis of the displacement estimation performance according to the variation in rotation counts revealed that for the simulated retaining wall with lower deformation, where sensor noise was present, the MAE, ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$, and CE for five rotations (using the median-based method) were reduced by 71.4% (1.4 mm), 70.2% (1.7 mm), 71.7% (1.5 mm), respectively, compared to a single rotation. This indicates that the noise-filtering performance of the algorithm for filtering duplicate point cloud data is superior. Furthermore, for the simulated retaining wall with combined deformation, the MAE, ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$, and CE for five rotations (using the median-based method) decreased by 37.8% (2.8 mm), 7.0% (5.34 mm), and 19.6% (4.1 mm), respectively, compared to a single rotation. This suggests that the precision of the point cloud data improves with an increased number of rotations. Finally, the MAE, ${\mathrm{M}\mathrm{A}\mathrm{E}}_{D_{max}}$, and CE of the average displacement estimation performance across different types of deformation obtained using five rotations and a rotation speed of 2°/s were 1.7, 2.2, and 2.0 mm, respectively.

The contributions of this study are as follows. First, the developed algorithm for filtering duplicate point cloud data based on a spherical coordinate system significantly reduced noise, improving the quality of the point cloud data. Second, it was demonstrated that by applying a displacement estimation algorithm like the M3C2, which utilizes surrounding data, a 2D-LiDAR sensor with greater error than a TLS can still effectively and cost-efficiently monitor the displacement of retaining walls. Reliable displacement estimation is expected to be achieved using the parameter values obtained from this research, provided that the distance between the system and the retaining wall is within 20 m. Future research should focus on developing various algorithms for monitoring the displacement of retaining walls on construction sites, including (1) an ROI-setting algorithm for displacement estimation; (2) a stability evaluation algorithm based on displacement analysis results; and (3) an algorithm for tracking vulnerable sections of the retaining wall. Additionally, the effectiveness of the 2D-LiDAR-based retaining wall displacement monitoring system should be verified through field experiments.