Abstract
Atmospheric turbulence characteristics are essential in determining the quality of astronomical images and implementing adaptive optics systems. In this study, the vertical distributions of optical turbulence at the Peak Terskol observatory (43.27472°N 42.50083°E, 3127 m a.s.l.) using the Era-5 reanalysis and scintillation measurements are investigated. For the closest reanalysis grid node to the observatory, vertical profiles of the structural constant of the air refractive index turbulent fluctuations were obtained. The calculated vertical profiles are compared with the vertical distribution of turbulence intensity obtained from tomographic measurements with a Shack–Hartmann sensor. The atmospheric coherence length at the location of Terskol Peak was estimated. Using a combination of atmospheric models and paramaterization schemes of turbulence, profiles at Mt. Kurapdag were obtained. The values of atmospheric coherence length at Peak Terskol are compared with estimated values of this length at the ten astronomical sites, including Ali, Lenghu and Daocheng.
1. Introduction
Adaptive optics systems that correct optical distortions in a wide field of view require information about the vertical profiles of optical turbulence and wind speed. The key characteristics of optical turbulence are the structural constant of the air refractive index turbulent fluctuations () and the atmospheric coherence length, which are often associated with the Fried parameter () and seeing [1,2]. These quantities determine the potential for achieving high angular resolution in astronomical observations.
There are several techniques for measuring the vertical profiles of optical turbulence. In astronomical observations, the vertical profiles above a telescope can be determined using a multidirectional Shack–Hartmann wavefront sensor [3]. Specifically, the vertical profiles of are calculated using the Solar Differential Image Motion Monitor (S-DIMM+) or Slope Detection and Ranging (SLODAR) techniques [4,5,6,7,8,9,10,11,12]. A comprehensive review of methods for measuring optical turbulence vertical profiles is provided in a recent paper [13]. Griffiths R. et al., present the results of an intercomparison of turbulence profiling instruments, including Stereo Scintillation Detection and Ranging (S-SCIDAR), DIMM, 24-hour Shack–Hartmann Image Motion Monitor (24hSHIMM), Ring-Image Next Generation Scintillation Sensor (RINGSS), and Multi-Aperture Scintillation Sensor-Differential Image Motion Monitor (MASS-DIMM) [13]. It is important to note that the comparison of these turbulence profiling instruments revealed that the largest deviations correspond to estimates of the isoplanatic angle (), the values of which are highly sensitive to turbulence in the upper atmospheric layers. These deviations, shown as scattered points, are due to limited accuracy in determining the strength of optical turbulence at different atmospheric levels and, presumably, differences in radiation propagation paths during measurements.
Measurement of optical turbulence vertical profiles is a difficult procedure [14]. Most often, the profile measurements are carried out only for a limited number of nights or days. In order to estimate the optical turbulence characteristics over long time intervals or, in other words, for a statistical ensemble, special atmospheric models are widely used [15,16,17,18,19,20]. The atmospheric models are applied to estimate the characteristics of mesoscale, micrometeorological and optical turbulence, on spatial scales comparable to the aperture diameters of ground-based telescopes. Below, a few recent papers demonstrating interesting results in this direction are discussed. A very interesting approach to predict optical turbulence was demonstrated by Cuevas et al. [21], who applied a combination of models to improve the forecasts of profiles and seeing at Paranal using the Weather Research and Forecasting model. Also, Macatangay et al. [22] utilized advanced numerical simulations with the Weather Research and Forecasting model to predict astronomical seeing. The meteorological model used by the authors reproduced variations very well, especially in comparison with smoothed DIMM data. Using the 21-yr European Centre for Medium-Range Weather Forecasts’ fifth set of reanalysis (Era-5) data, the optical turbulence and the wind speed characteristics were simulated at the Lenghu site [23]. Analysis of the optical turbulence statistics shows that the calculated median value of seeing is slightly lower than measured seeing. In particular, the Era-5 derived value is and the measured seeing is . Also, in our opinion, significant fundamental results in the optical turbulence diagnostics and forecasting with atmospheric models were achieved by English scientific teams, resulting in the development of new methods and tools for studying optical turbulence [24,25].
When estimating optical turbulence characteristics using atmospheric models, a crucial step is the selection of a small-scale turbulence parameterization scheme [26]. The correct selection and adjustment of the parameterization scheme to the atmospheric conditions of a particular site are necessary to obtain representative estimates of the key characteristics of optical turbulence. In mountainous regions like Tibet and the Caucasus, turbulence behavior is complex. The choice of parameterization scheme for mountain regions should be based on an analysis of preliminary measurement data. It is important to note that further research is needed to understand the dependencies in turbulence evolution and determine the extent to which these dependencies, specific to a given mountainous region, can be applied to other regions.
The present study focuses on the simulation of optical turbulence above the Peak Terskol Observatory (43.27472°N 42.50083°E, 3127 m a.s.l.) and Mt. Kurapdag (41.79609°N, 47.37428°E, 3553 m a.s.l.). These sites were chosen as reference locations due to the availability of special atmospheric measurements data [27]. Figure 1 illustrates the locations of the Terskol Peak Observatory, known for its high astroclimatic characteristics, Mount Kurapdag, characterized by low water vapor content [28], and the Big Telescope Alt-Azimuthal Telescope (BTA), the largest optical telescope with a non-segmented mirror in Eurasia [29]. Recent studies show that new suitable locations for ground-based telescopes include mountain regions of Dagestan. In this regard, the figure shows the location of the mountain village of Gunib as a place with potentially high characteristics.
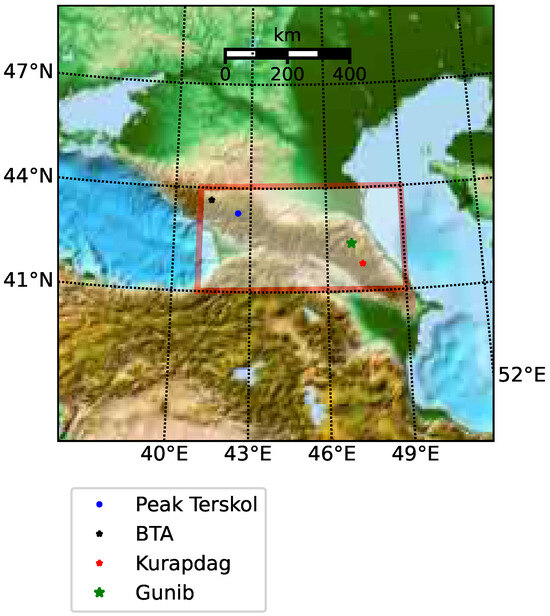
Figure 1.
Sites of the Terskol Peak Observatory, Big Telescope Alt-Azimuthal Telescope (BTA), Gunib with high astroclimatic indicators and Mount Kurapdag with low water vapor content. Red rectangle shows the BTA region.
In March 2023, the special experiments at the Peak Terskol Observatory were carried out to characterize the optical turbulence. Together with the measurements of optical turbulence profiles and meteorological characteristics in the surface layer, variations of were simulated using a gradient method. Below, we discuss the results of estimating optical turbulence profiles using vertical shears of wind speed, mast meteorological measurements and measured height distributions of optical turbulence.
2. Data
This study aims to estimate the image quality at nighttime at the Terskol Peak Observatory, where optical turbulence monitoring is carried out, and at a new location, on the slope of Mt. Kurapdag, which is considered one of the reference sites for methodological tests. In this study, we solved a number of tasks. Firstly, using remote telescopic measurements, we determined vertical distributions of the optical turbulence intensity over the Peak Terskol observatory. Vertical distributions of turbulence intensity were obtained under conditions of good and mediocre image quality. Secondly, in order to estimate the vertical profiles of the structural constant of air refractive index turbulent fluctuations , we used a gradient method, the foundations of which have been created by Tatarsky. Using the gradient method, the vertical profiles of optical turbulence over the Terskol Peak Observatory and Mt. Kurapdag were determined.
For the simulation of vertical profiles, we used the European Centre for Medium-Range Weather Forecasts’ fifth set of reanalysis (Era-5) data [30]. The Era-5 reanalysis contains observational data from around the world from 1940 to the present. Compared to previous databases, Era-5 demonstrates significant improvements in both spatial resolution and accuracy of atmospheric characteristics [31,32]. The reanalysis contains assimilated meteorological characteristics, including air temperature and wind speed components at various pressure levels. The meteorological characteristics are available with a flat horizontal resolution of about 30 km and a continuous 1-hour temporal resolution. In particular, for the grid node closest to the observatory, hourly values of air temperature and horizontal components of wind speed at various pressure surfaces were used.
3. Results
3.1. Vertical Distributions of Optical Turbulence from Shack–Hartmann Sensor Measurements at the Peak Terskol Observatory
In solar astronomy, Shack–Hartmann wavefront sensors with different fields of views are typically employed for estimated wavefront distortions [33]. The parameters of standard sensor depend on the optical turbulence characteristics. In this paper, we present the results of an observing campaign of the Shack–Hartmann sensor at the Peak Terskol Observatory in March 2023. We used the Shack–Hartmann sensor placed in the focal plane of a MEADE LX200 Telescope (Meade Instruments Corporation, Guangdong, China), which is installed inside the Schmidt–Cassegrain Telescope (Figure 2). The sensor is equipped with a high frame-rate camera. The subaperture size of the Shack–Hartmann sensor is 6 × 6 mm. The exposure time is 5 ms. The sampling is 65 frame/s. In the experiments, we analyzed 20 full time series and 10,000 hartmannograms were obtained during the night of 19 March 2023. Analysis of these measurement data made it possible to estimate and analyze the character of optical turbulence above the telescope.

Figure 2.
The dome of the Schmidt–Cassegrain Telescope at the Peak Terskol Observatory.
Obtained data sets correspond to average seeing conditions suitable for astronomical observations and thus were selected for processing. Assuming that the turbulence structure obeys the Kolmogorov model, we can estimate the height distribution of optical turbulence strength. For these calculations, we used an expansion of the spatial spectrum of amplitude perturbations into modes. The model spectrum of the scintillation is related to the height distribution of optical turbulence strength:
where is the weight function, which depends on the turbulent layer height and subaperture geometry, is the turbulent layer thickness, is the number of turbulent layers. Details of the method are described in the paper [34].
By solving this equation in terms of , we obtain the vertical distributions of optical turbulence strength above the Peak Terskol Observatory. Night-time vertical distributions of optical turbulence strength at the Peak Terskol Observatory for different image qualities are shown in Figure 3 and Figure 4. Image quality is estimated through the parameter:
where variance of the differential displacements of the solar subimages is related to the Fried parameter by the following equation:
where is the numerical constant, is the light wavelength and D is the telescope diameter.
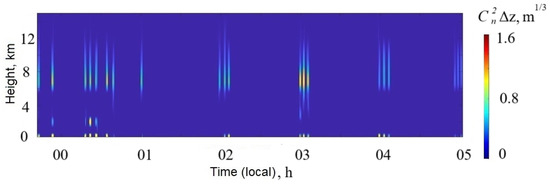
Figure 3.
Night-time vertical distributions of optical turbulence strength at the Peak Terskol Observatory for the average image quality, 19 March 2023. In the figure, we used a local time.
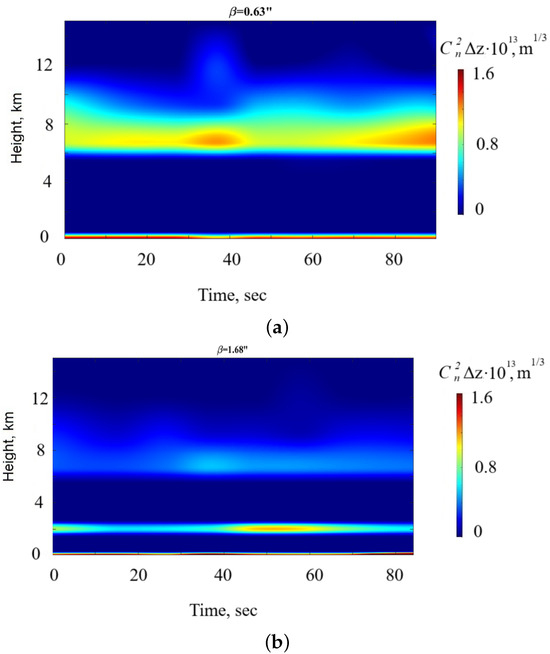
Figure 4.
Night-time vertical distributions of optical turbulence strength at the Peak Terskol Observatory for (a) the best ( = ) and (b) the worst atmospheric conditions ( = ), 19 March 2023. In the figure, we used a local time.
Analyzing these figures, we can see that pronounced turbulent layers are formed at heights of 7–8 km and 2–2.5 km above the ground. The turbulent layer at these heights leads to a significant decrease in image quality. For example, the parameter determined by the integral over height increases from 0.63 to . These changes are mainly due to generation of intensive turbulent fluctuations of air refractive index within these layers.
It is necessary to emphasize that, conditionally, we consider three different cases, including good seeing ( ranges from 0.5 to ), average seeing ( ∼ ) and bad seeing ( ranges from 1.5 to ). Good seeing is associated with a thin lower turbulent layer (∼50–100 m) and the absence of a layer at heights of 2–2.5 km. With a thickness of the night boundary layer of 150–250 m, the seeing increases to ∼. Values higher than are often associated with the development of optical turbulence within the surface layer and an additional turbulent layer at heights of 2–2.5 km.
3.2. Analysis of Sonic Measurements within the Atmospheric Surface Layer–Estimation of Optical Turbulence Strength
The lower part of the atmospheric boundary layer is known to make a major contribution to the formation of integral optical turbulence (along line of sight) and, as a consequence, to the resolving power of ground-based telescope [35,36]. Within this layer, variations in the intensity of optical turbulence are most poorly described, both in time and in height. At the very least, the accuracy of estimating and forecasting optical turbulence based on standard atmospheric models or limited optical remote measurement data is insufficient for planning observation times. In order to obtain the correct shape of optical turbulence profiles within the lowest atmospheric layers under the different atmospheric conditions, we analyzed measurement data carried out with a sonic anemometer. The sonic anemometer “Meteo-2” was placed on a 7-m meteorological mast at the Peak Terskol Observatory site (Figure 5). The observatory is located in the vicinity of the Elbrus, on a flat platform at an altitude of 3100 m above sea level.


Figure 5.
(a) The dome of Schmidt–Cassegrain Telescope and (b) Meteo-2 sonic anemometer.
Below, for calculations of atmospheric turbulence characteristics, we used long-period quasi-continuous measurement data of the sonic anemometer (from January 2023 to December 2023). Thanks to the high frequency measurements (10 Hz) of the wind field and the sonic temperature, we calculated a number of the turbulence characteristics, including surface values of .
Based on the 1-year measurements with the sonic anemometer, the 3-min average values of were obtained [37]. In Figure 6, we present the number of nights of sonic measurements for each month. The fewest number of nights analyzed occurs in February–April. The largest number corresponds to January as well as the warm period of observations.
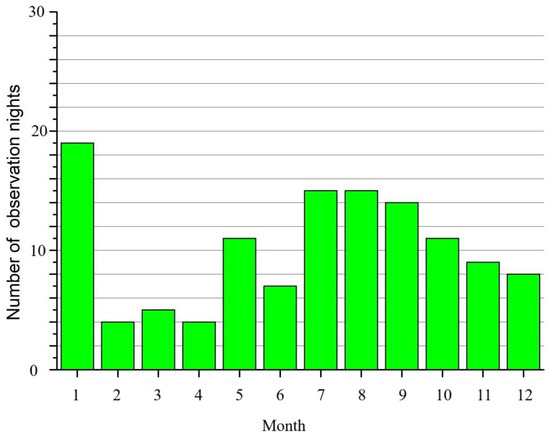
Figure 6.
The number of nights of sonic measurements by month, 2023.
Distributions of measured values of within the surface layer of the atmosphere for different seasons at the Peak Terskol Observatory site are depicted in Figure 7 and Figure 8.
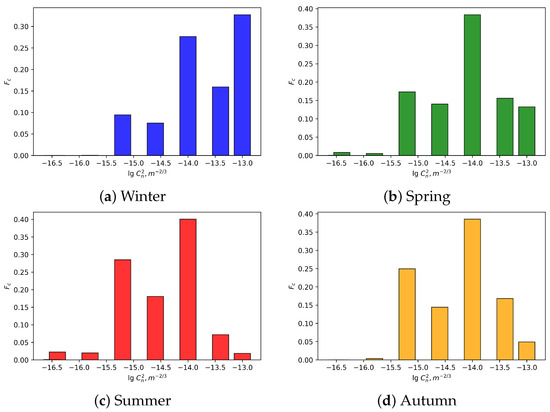
Figure 7.
Distributions of measured values of within the surface layer of the atmosphere at the Peak Terskol Observatory site under average atmospheric conditions, 2023.
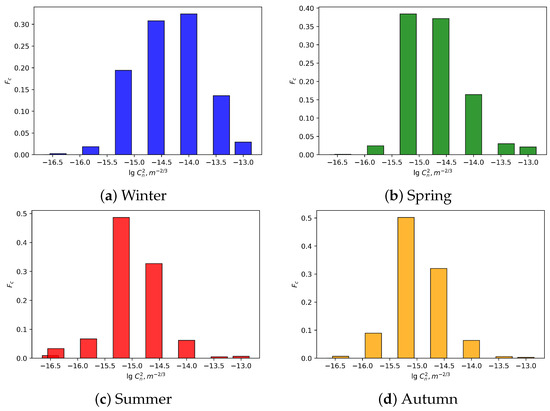
Figure 8.
Distributions of measured values of within the surface layer of the atmosphere at the Peak Terskol Observatory site under clear sky and low intensity of optical turbulence, 2023.
Table 1 contains the calculated percentiles of in the surface layer of the atmosphere. Calculated values of obtained from the results of processing sonic measurement data are higher in comparison with estimations derived from optical measurement data under clear sky conditions. This fact is confirmed by previous studies [38]. Higher amplitudes of are largely determined by the influence of dynamic processes on the formation of small-scale turbulence in the surface layer of the atmosphere. Due to the fact that astronomical observations are carried out under good astro-optical conditions, when the intensity of optical turbulence along the line of sight is minimal, calculated values in the upper part of Table 1 differ from the statistics corresponding only to clear sky conditions. In this regard, we evaluated the statistics of surface turbulence for medium atmospheric conditions and low intensity of optical turbulence.

Table 1.
Percentiles of in the surface layer of the atmosphere at the Peak Terskol Observatory, 2023.
Analysis of estimations shows that the intensity of turbulent fluctuations of the air refractive index has a pronounced seasonal dependence. The highest intensity of optical turbulence in the surface layer of the atmosphere is observed in winter. During this period, the median values of , estimated for nighttime (from 0:00 to 6:00 local time), are equal to 8.6 · and 2.6 · for average atmospheric condition and under clear sky, respectively. In spring, we observe an increase in the non-dimensional number of atmospheric situations with low intensity optical turbulence. At this time, during periods of high image quality, the median of is about 8.0 · .
In comparison with winter and spring, in summer and autumn, turbulence in the surface layer is significantly suppressed: the number of atmospheric situations with strong turbulence does not exceed 7%. We should emphasize that the largest number of cases with the best atmospheric conditions ( ), occurs in summer and autumn. In this period, about 7–10% of the observing time corresponds to weak optical turbulence.
3.3. Vertical Distribution of Optical Turbulence Strength Estimated from Era-5 Reanalysis
For the simulation of the vertical profiles of optical turbulence, the gradient method was used. Correction of the vertical profiles was performed using sonic measurements and optical observations of image scintillation. The calculations were based on the following equation:
where is the numerical constant, which is equal to 2.8. The parameter is the vertical gradient of the air refractive index, and is the outer scale of turbulence.
The calculation of the air refractive index gradients at different heights in the atmosphere is performed using the vertical gradients of the natural logarithm of the air potential temperature :
where P is the atmospheric pressure, T is the air temperature, is the potential air temperature. The potential air temperature is related to the air temperature by the following formula:
The key parameter is the outer scale of atmospheric turbulence [39]. In general, vertical changes of the outer scale can be determined through vertical gradients of the horizontal component of the wind velocity S:
where
u and v are the horizontal components of wind velocity. Under conditions of weak turbulence, the coefficient a = 1.64, b = 42, c = 0.506 and d = 50.
Use of standard coefficients a = 1.64, b = 42, c = 0.506 and d = 50 gives mediocre results. In particular, we calculated a vertical profile for 18–19 March 2023 (Figure 9a). By integrating this profile using Formula (9), we obtained the average estimation of the parameter:
where H is the height of the optically active atmosphere, is the zenith angle, and is the wavelength of light. On average, the model value of is higher than the measured and the estimated in the upper atmospheric layers are higher than the expected values. In order to correct the vertical profile of , we calculated new parameterization coefficients and by finding the best-fitting model linking measured and model near-surface values of .
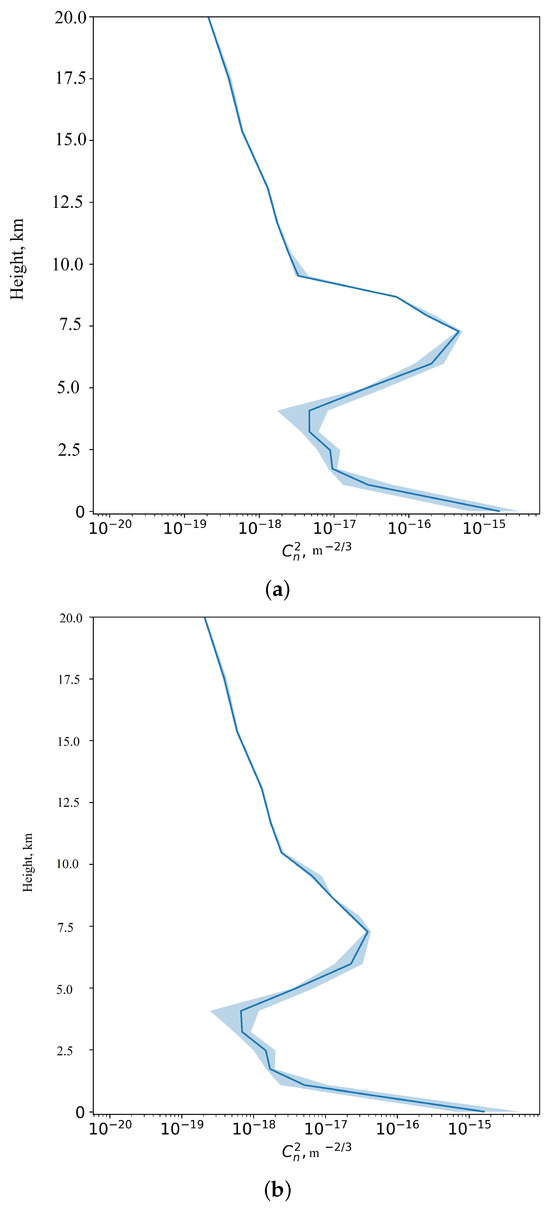
Figure 9.
Calculated vertical profile of optical turbulence at the Peak Terskol Observatory, 18–19 March 2023. Shading corresponds to the interval between the first and the third quartiles estimated for all nights in March 2023. (a) a = 1.64, b = 42, = 5.66 cm, = 1.79 arc sec; (b) = 0.95, = 10, = 8.20 cm, = 1.23 arc sec.
Specifically, new coefficients were calculated by minimizing the standard deviation between the model values and the measured, sonic, values of :
where is the measured value of in the surface layer, is the model (calculated) value of . Summation is performed over the entire time implementation, the length of which is . Using this minimization condition, the weight coefficients and are estimated. New parametrization coefficients at the Terskol Peak Observatory differ significantly from standard values: = 0.95 and = 10. Figure 9b shows the corrected vertical profile of with the new parametrization coefficients. This profile corresponds to 19 March 2023.
One of the most important characteristics of optical turbulence is the height of the atmospheric boundary layer (ABL). In order to determine the ABL height, we used a well-known method based on the profile of the bulk Richardson number. The ABL height is defined as the height where the bulk Richardson number exceeds a critical threshold. From Figure 9, we can see that the new coefficients used to parameterize the night variations of made it possible to reduce the height of ABL. Obtained night-time heights of the atmospheric boundary layer range from 100 to 300 m. As a result, the estimated strength of optical turbulent fluctuations decreases more rapidly with height at night above Terskol Peak. We associate this decrease of turbulent fluctuations strength within the lower atmospheric layer above the Terskol Peak with the low heights of the atmospheric boundary layer at night.
Considering a large region, the minimum height of the atmospheric boundary layer is observed above Terskol Peak not only on individual nights, but also on average, over a long time period (Figure 10). The high quality of astronomical images at Terskol Peak is related to the low height of the atmospheric boundary layer. On some nights, its height is limited by 50–100 m. Mt Kurapdag and Big Telescope Alt-Azimuthal are located in worse atmospheric conditions, the mean night-time heights of the atmospheric boundary layer are ∼250–300 m and 250–350 m, respectively (Figure 10a). We believe that the observed character of vertical changes is in good agreement with theoretical and experimental data on the evolution of the atmospheric boundary layer.
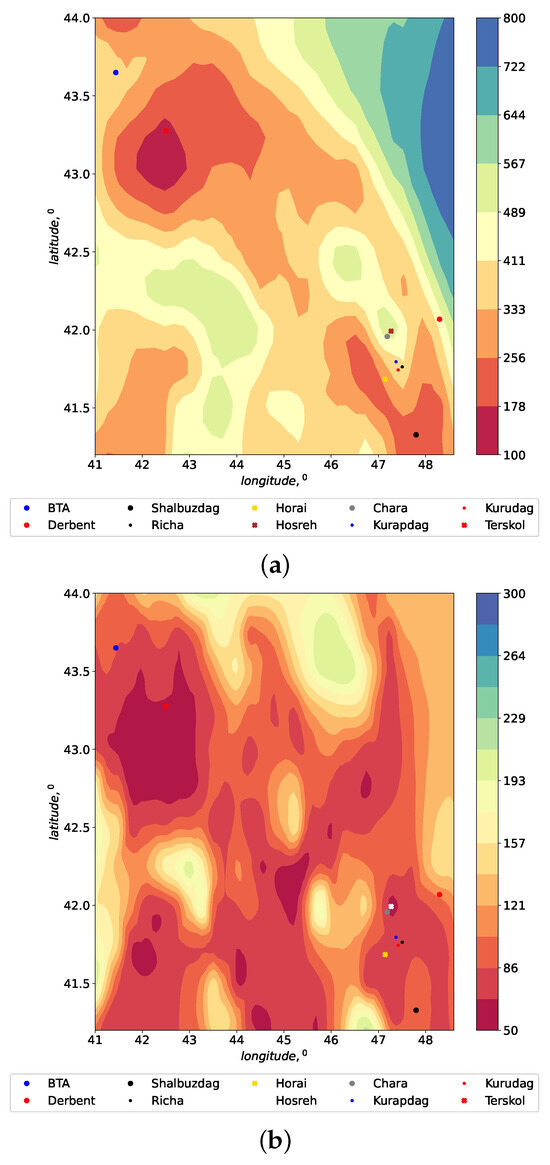
Figure 10.
Distributions of atmospheric boundary layer height (in meters) within the Peak Terskol Observatory region. (a) Average atmospheric conditions, 2013–2023; (b) 19 March 2023.
The data of optical and meteorological measurements as well as the fields of wind speed and air temperature extracted from the reanalysis Era-5, served as the basis for calculation of the average profiles of optical turbulence above the observatory and Mt. Kurapdag. In Figure 11a we demonstrate calculated vertical profiles of optical turbulence above the Peak Terskol Observatory averaged over January 2023 and June 2023.
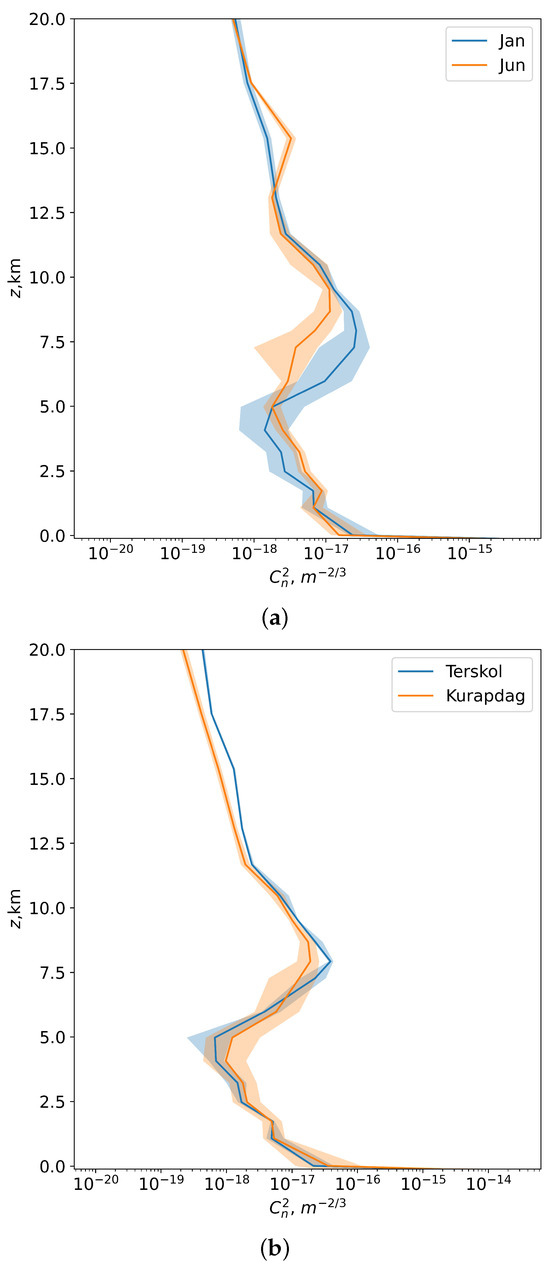
Figure 11.
Night-time vertical profiles of optical turbulence above the Peak Terskol Observatory and Mt. Kurapdag. (a) Peak Terskol Observatory, 2023. The blue line corresponds to January. The orange line corresponds to June. The shading corresponds to the interval between the first and the third quartiles; (b) Mt. Kurapdag, 2013–2023. The blue line corresponds to the Peak Terskol Observatory. The orange line corresponds to Mt. Kurapdag. The shading corresponds to the interval between the first and the third quartiles.
Analyzing these profiles, it can be noted that the structure of turbulence in the upper atmospheric layers changes significantly in summer. This fact is indicated by deformations of the vertical profiles of optical turbulence. On the one hand, these deformations manifest in a greater vertical uniformity of optical turbulence and suppression of turbulent fluctuations in the surface layer of the atmosphere. On the other hand, the turbulence strength in the upper atmospheric layers decreases in summer.
Also, using Era-5 reanalysis data and identified patterns in optical turbulence behaviour at the Peak Terskol Observatory site, we calculated averaged vertical profiles of above the Mt. Kurapdag. For comparison, Figure 11b shows vertical profiles above Terskol Peak and Kurapdag Mountain over the period of 2013–2023.
Analysis of these vertical profiles indicates the presence of an intense lower turbulence layer. It should be noted that within the surface layer, the intensity of turbulence, in terms of , at the Mt. Kurapdag site exceeds by more than an order of magnitude the values of observed at the Peak Terskol Observatory. Moreover, at the Mt. Kurapdag site, turbulence in this atmospheric layer is characterized by high intensity regardless of the parameterization coefficients. The nature of the turbulence is largely due to strong vertical wind speed shears near the ground.
4. Estimation of the Fried Parameter at the Sites with Good Astroclimatic Conditions
Figure 12 displays the monthly averaged Fried parameter estimated using Era-5 reanalysis data at the ten astronomical sites. European Southern Observatory, Tibetan Plateau, and the Ethiopian Plateau are some of the most favorable sites. In contrast to the Fried parameter of the European Southern Observatory and Tibetan Plateau (TP) sites, the Ethiopian Plateau has a different pattern, possibly owing to different climate patterns. Throughout the year, the Ethiopian Plateau atmospheric coherence length is high in winter and low in summer. In winter, atmospheric coherence length at the Ethiopian Plateau is better than that at the ESO and TP sites, indicating that the Ethiopian Plateau has high potential conditions that are comparable to some of the best astronomical observatories in the world.
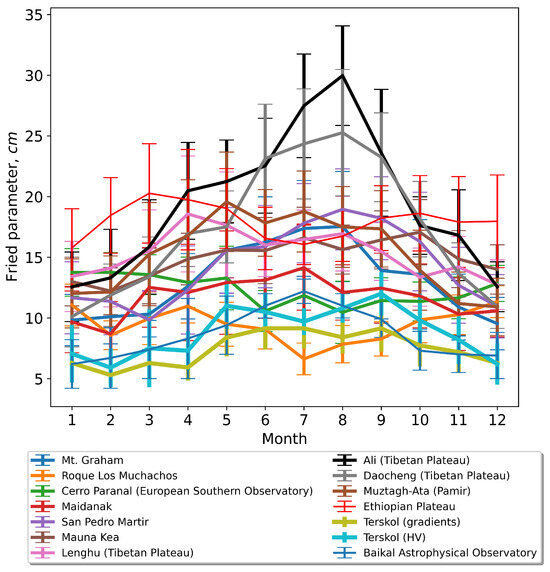
Figure 12.
Variations of the Fried parameter = calculated for the period 2018–2022.
The Estimated Fried parameter at the Ali site located in western China and the Tibetan plateau, one of the best astronomical sites, is about 20 cm in the best months. These sites are presently under study for astronomy [5]. The Era-5 derived values of the Fried parameter corresponding to spatial coherence length are consistent with measured values at the Maidanak Observatory [40].
We also compare the variation of the Fried parameter at the site of Peak Terskol Observatory. The figure also shows variations of the Fried parameter at the Terskol Peak Observatory. As demonstrated in the figure, the site of Terskol Peak has a high image quality, close to that of the best places in the world. In particular, in summer, is about 1.0–. In terms of , these values correspond to 8.3–10.0 cm. In addition to the average monthly values of the Fried parameter obtained using the gradient method, the figure shows the results of applying the Hufnagel–Vally (HV) climate model to describe vertical changes in [41]. The HV model is based on the processing of experimental data and, on average, describes the structure of optical turbulence well. Nevertheless, detailed information about the vertical distribution of optical turbulence cannot be reflected using this model. Analysis of the figure shows that the gradient model and the model give similar results in terms of .
5. Discussion
In this paper, we present the results of studies on optical turbulence in the atmospheric boundary layer and free atmosphere, up to a height of 20 km. To determine the structural constant of turbulent fluctuations of the air refractive index, we refined the parameterization scheme for calculating this quantity. In the region of interest, this turbulent parameter was calculated by comparing reanalysis data, mast meteorological measurements, and observations of image scintillation.
Specifically, the processing of mast measurement data allowed us to estimate not only the statistics of in the atmospheric surface layer but also to select optimal parameterization coefficients that determine the contribution of wind speed shear instability to turbulence formation. By using these coefficients, we obtained more accurate estimates of values at different heights in the atmospheric boundary layer, enabling us to refine the shapes of the vertical profiles of optical turbulence. The validity of our approach, which utilizes constant parameterization coefficients within the atmospheric boundary layer, is supported by the fact that the structure of turbulence in this layer is primarily influenced by processes in the surface layer of the atmosphere, at least for long time periods.
The accuracy of our calculations is further confirmed by the results of estimating the height of the atmospheric boundary layer. Figure 10 shows the distributions of the atmospheric boundary layer height (in meters) within the Peak Terskol Observatory region. Analysis of these distributions reveals the formation of a relatively thin boundary layer above the Observatory, indicating that turbulence predominantly develops near the ground. During the measurements, the thickness of the atmospheric boundary layer was minimal compared to average atmospheric conditions (Figure 10a).
It can be noted that the gradient method outputs are in good agreement with the data of optical measurements of turbulence at different height levels in the atmosphere, at least for the Terskol Peak Observatory. Based on the selected profile calculation scheme for the Terskol Peak Observatory, we estimated the optical turbulence characteristics for other sites as well. Analysis of spatial distribution of the atmospheric boundary layer height, as well as calculated profiles of optical turbulence, can serve as the basis for choosing optimal site for a ground-based astronomical telescope. Taking into account the recent data on the spatial distribution of astroclimatic characteristics within this macroregion, the following areas suitable for optical telescopes are located: in mountain Dagestan, including Gunib, as well as Shalbuzdag and Peak Terskol Observatory. The location of Mt. Kurapdag is not good due to strong surface winds and strong surface optical turbulence, which is the main reason of high values of (2–).
6. Conclusions
In this work we demonstrated that, using the gradient method and additional measurement data, we can estimate the vertical profiles of optical turbulence more accurately. The increase of accuracy of optical turbulence profiles within the lower atmosphere is due to using both measured values of and applying new parametrization coefficients between vertical shears of wind speed and model values of . Moreover, the gradient method takes into account variations in the height of the atmospheric boundary layer estimated from reanalysis data. Estimations of the atmospheric boundary layer height and the vertical profiles of wind shears are important for obtaining smooth vertical profiles of and . Above the atmospheric boundary layer, vertical profiles of optical turbulence are reconstructed only on the basis of vertical profiles of wind speed shears with parameterization coefficients a = 1.64 and b = 42, that describe variations well for weak turbulence. Thus, we can conclude that the hypotheses of optical turbulence embedded in the gradient method are valid as, in average, used atmospheric models converge to the measurements: the measured and model values of are practically identical.
For the first time, by linking simulation outputs to measurement data, we have obtained representative optical turbulence vertical profiles for the sites of Peak Terskol Observatory and the Mt. Kurapdag. We have shown that the Kurapdag mountain should not be considered as a potential site for a new optical telescope.
Author Contributions
A.Y.S. and P.G.K. developed the methodology and performed the investigation; E.A.K. conducted the formal analysis; C.Q. and S.A.P. were engaged in measurements and data analysis. All authors have read and agreed to the published version of the manuscript.
Funding
Section 3 was supported by the Ministry of Science and Higher Education of the Russian Federation. The optical turbulence profiling was funded by RSF grant No. 23-72-00041.
Data Availability Statement
Data used are available on request from the corresponding author.
Acknowledgments
Measurements were verified using the Unique Research Facility Large Solar Vacuum Telescope http://ckp-rf.ru/usu/200615/ accessed on 1 February 2024.
Conflicts of Interest
The author declares no conflict of interest.
References
- Coulman, C.E. Fundamental and applied aspects of astronomical “seeing”. Annu. Rev. Astron. Astrophys. 1985, 23, 19–57. [Google Scholar] [CrossRef]
- Tokovinin, A. The Elusive Nature of “Seeing”. Atmosphere 2023, 14, 1694. [Google Scholar] [CrossRef]
- Ran, X.; Zhang, L.; Rao, C. The AC-SLODAR: Measuring daytime normalized optical turbulence intensity distribution based on slope autocorrelation. Mon. Not. R. Astron. Soc. 2024, 528, 3981–3991. [Google Scholar] [CrossRef]
- Hickson, P.; Ma, B.; Shang, Z.; Xue, S. Multistar turbulence monitor: A new technique to measure optical turbulence profiles. Mon. Not. R. Astron. Soc. 2019, 485, 2532–2545. [Google Scholar] [CrossRef]
- Hickson, P.; Feng, L.; Hellemeier, J.A.; Shen, Z.; Xue, S.; Yao, Y.; Ma, B.; Chen, H.; Yang, R. Optical turbulence at Ali, China—Results from the first year of lunar scintillometer observation. Mon. Not. R. Astron. Soc. 2020, 494, 5992–6000. [Google Scholar] [CrossRef]
- Wilson, R. SLODAR: Measuring optical turbulence altitude with a Shack–Hartmann wavefront sensor. Mon. Not. R. Astron. Soc. 2002, 337, 103–108. [Google Scholar] [CrossRef]
- Deng, J.; Song, T.-F.; Liu, Y. A Review of Daytime Atmospheric Optical Turbulence Profile Detection Technology. Chin. Astron. Astrophys. 2023, 47, 257–284. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L.; Kong, L.; Bao, H.; Guo, Y.; Rao, X.; Zhong, L.; Zhu, L.; Rao, C. A modified S-DIMM+: Applying additional height grids for characterizing daytime seeing profiles. Mon. Not. R. Astron. Soc. 2018, 478, 1459–1467. [Google Scholar] [CrossRef]
- Subramanian, S.K.; Rengaswamy, S. Forward modelling of turbulence strength profile estimation using S-DIMM+. Proc. SPIE 2023, 12638, 1263812. [Google Scholar] [CrossRef]
- Shikhovtsev, A.Y. A Method of Determining Optical Turbulence Characteristics by the Line of Sight of an Astronomical Telescope. Atmos. Ocean. Opt. 2022, 35, 303–309. [Google Scholar] [CrossRef]
- Joo, J.Y.; Ha, H.S.; Lee, J.H.; Kim, Y.S.; Butterley, T. SLODAR System Development for Vertical Atmospheric Disturbance Profiling at Geochang Observatory. Curr. Opt. Photonics 2024, 8, 30–37. [Google Scholar] [CrossRef]
- Bennoui, F.; Bahloul, D. Estimation of the Atmospheric Turbulence Parameters Using the Angle-of-Arrival Covariance Function. Atmos. Ocean. Opt. 2023, 36, 569–577. [Google Scholar] [CrossRef]
- Griffiths, R.; Bardou, L.; Butterley, T.; Osborn, J.; Wilson, R.; Bustos, E.; Tokovinin, A.; Le Louarn, M.; Otarola, A. A comparison of next-generation turbulence profiling instruments at Paranal. Mon. Not. R. Astron. Soc. 2024, 529, 320–330. [Google Scholar] [CrossRef]
- Zhang, K.; Luo, T.; Wang, F.-F.; Sun, G.; Liu, Q.; Qing, C.; Li, X.-B.; Weng, N.-Q.; Zhu, W.-Y. Influence of low clouds on atmospheric refractive index structure constant based on radiosonde data. Acta Phys. Sin. 2022, 71, 089202. [Google Scholar] [CrossRef]
- Bolbasova, L.A.; Shikhovtsev, A.Y.; Kopylov, E.A.; Selin, A.A.; Lukin, V.P.; Kovadlo, P.G. Daytime optical turbulence and wind speed distributions at the Baikal Astrophysical Observatory. Mon. Not. R. Astron. Soc. 2019, 482, 2619–2626. [Google Scholar] [CrossRef]
- Qing, C.; Wu, X.; Li, X.; Luo, T.; Su, C.; Zhu, W. Mesoscale optical turbulence simulations above Tibetan Plateau: First attempt. Opt. Express 2020, 28, 4571–4586. [Google Scholar] [CrossRef]
- Bi, C.; Qing, C.; Qian, X.; Luo, T.; Zhu, W.; Weng, N. Investigation of the Global Spatio-Temporal Characteristics of Astronomical Seeing. Remote Sens. 2023, 15, 2225. [Google Scholar] [CrossRef]
- Yang, Q.; Wu, X.; Han, Y.; Chun, Q.; Wu, S.; Su, C.; Wu, P.; Luo, T.; Zhang, S. Estimating the astronomical seeing above Dome A using Polar WRF based on the Tatarskii equation. Opt. Express 2021, 29, 44000–44011. [Google Scholar] [CrossRef]
- Quatresooz, F.; Griffiths, R.; Bardou, L.; Wilson, R.; Osborn, J.; Vanhoenacker-Janvier, D.; Claude, O. Continuous daytime and nighttime forecast of atmospheric optical turbulence from numerical weather prediction models. Opt. Express 2023, 31, 33850–33872. [Google Scholar] [CrossRef]
- Wu, X.-Q.; Xiao, C.-Y.; Esamdin, A.; Xu, J.; Wang, Z.-W.; Xiao, L. Quantitative Analysis of Seeing with Height and Time at Muztagh-Ata Site Based on ERA5 Database. Res. Astron. Astrophys. 2024, 24, 015006. [Google Scholar] [CrossRef]
- Cuevas, O.; Marin, J.C.; Blazquez, J.; Meyer, C. Combining models to forecast the optical turbulence at Paranal. Mon. Not. R. Astron. Soc. 2024, 529, 2208–2219. [Google Scholar] [CrossRef]
- Macatangay, R.; Rattanasoon, S.; Butterley, T.; Bran, S.H.; Sonkaew, T.; Sukaum, B.; Sookjai, D.; Panya, M.; Supasri, T. Seeing and turbulence profile simulations over complex terrain at the Thai National Observatory using a chemistry-coupled regional forecasting model. Mon. Not. R. Astron. Soc. 2024, 530, 1414–1423. [Google Scholar] [CrossRef]
- Bi, C.; Qing, C.; Qian, X.; Zhu, W.; Luo, T.; Li, X.; Cui, S.; Weng, N. Astroclimatic parameters characterization at lenghu site with ERA5 products. Mon. Not. R. Astron. Soc. 2024, 527, 4616–4631. [Google Scholar] [CrossRef]
- Masciadri, E.; Jabouille, P. Improvements in the optical turbulence parameterization for 3D simulations in a region around a telescope. Astron. Astrophys. 2001, 376, 727–734. [Google Scholar] [CrossRef][Green Version]
- Turchi, A.; Masciadri, E.; Fini, L. Forecasting surface-layer atmospheric parameters at the Large Binocular Telescope site. Mon. Not. R. Astron. Soc. 2017, 466, 1925–1943. [Google Scholar] [CrossRef]
- Shikhovtsev, A. Reference optical turbulence characteristics at the Large Solar Vacuum Telescope site. Publ. Astron. Soc. Jpn. 2024, psae031. [Google Scholar] [CrossRef]
- Bolbasova, L.A.; Kopylov, E.A. Long-Term Trends of Astroclimatic Parameters above the Terskol Observatory. Atmosphere 2023, 14, 1264. [Google Scholar] [CrossRef]
- Khaikin, V.B.; Shikhovtsev, A.Y.; Shmagin, V.E.; Lebedev, M.K.; Kopylov, E.A.; Lukin, V.P.; Kovadlo, P.G. Eurasian Submillimeter Telescopes (ESMT) project. Possibility of submm image quality improvement using adaptive optics. Zhurnal Radioelektroniki [J. Radio Electron.] 2022, 7. (In Russian) [Google Scholar] [CrossRef]
- Shikhovtsev, A.Y.; Kovadlo, P.G. Statistical estimations of the vapor content and optical thickness of the atmosphere using reanalysis and radiosonding data as applied to millimeter telescopes. Optika Atmosfery i Okeana 2024, 37, 169–175. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Huang, J.; Yin, J.; Wang, M.; He, Q.; Guo, J.; Zhang, J.; Liang, X.; Xie, Y. Evaluation of Five Reanalysis Products with Radiosonde Observations Over the Central Taklimakan Desert During Summer. Earth Space Sci. 2021, 8, 2021EA001707. [Google Scholar] [CrossRef]
- Rao, P.; Wang, F.; Yuah, X.; Liu, Y.; Jiao, Y. Evaluation and comparison of 11 sets of gridded precipitation products over the Qinghai-Tibet Plateau. Atmos. Res. 2024, 302, 107315. [Google Scholar] [CrossRef]
- Townson, M.J.; Kellerer, A.; Saunter, C.D. Improved shift estimates on extended Shack–Hartmann wavefront sensor images. Mon. Not. R. Astron. Soc. 2015, 452, 4022–4028. [Google Scholar] [CrossRef][Green Version]
- Potanin, S.A.; Kornilov, M.-V.; Savvin, A.D.; Safonov, B.S.; Ibragimov, M.A.; Kopylov, E.A.; Nalivkin, M.A.; Shmagin, V.E.; Huy, L.X.; Thao, N.T. A Facility for the Study of Atmospheric Parameters Based on the Shack–Hartmann Sensor. Astrophys. Bull. 2022, 77, 214–221. [Google Scholar] [CrossRef]
- Kornilov, V.; Safonov, B.; Kornilov, M.; Shatsky, N.; Voziakova, O.; Potanin, S.; Gorbunov, I.; Senik, V.; Cheryasov, D. Study on atmospheric optical turbulence above mount Shatdzhatmaz in 2007–2013. Publ. Astron. Soc. Pac. 2014, 126, 482–495. [Google Scholar] [CrossRef][Green Version]
- Panchuk, V.E.; Afanas’ev, V.L. Astroclimate of Northern Caucasus-myths and reality. Astrophys. Bull. 2011, 66, 233–254. [Google Scholar] [CrossRef]
- Odintsov, S.L.; Gladkikh, V.A.; Kamardin, A.P.; Nevzorova, I.V. Determination of the Structural Characteristic of the Refractive Index of Optical Waves in the Atmospheric Boundary Layer with Remote Acoustic Sounding Facilities. Atmosphere 2019, 10, 711. [Google Scholar] [CrossRef]
- Lukin, V.P.; Botygina, N.N.; Gladkikh, V.A.; Emaleev, O.N.; Konyaev, P.A.; Odintsov, S.L.; Torgaev, A.V. Joint measurements of atmospheric turbulence level with optical and acoustic meters. Atmos. Ocean. Opt. 2015, 28, 254–257. [Google Scholar] [CrossRef]
- Rao, R. Effect of Outer Scale of Atmospheric Turbulence on Imaging Resolution of Large Telescopes. Guangxue Xuebao/Acta Opt. Sin. 2023, 43, 2400001. [Google Scholar]
- Tillayev, Y.; Azimov, A.; Ehgamberdiev, S.; Ilyasov, S. Astronomical Seeing and Meteorological Parameters at Maidanak Observatory. Atmosphere 2023, 14, 199. [Google Scholar] [CrossRef]
- Mahmood, D.A.; Naif, S.S.; Al-Jiboori, M.H.; Al-Rbayee, T. Improving Hufnagel-Andrews-Phillips model for prediction using empirical wind speed profiles. J. Atmos. Sol. Terr. Phys. 2022, 240, 105952. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).