Abstract
The noise-like behavior of geomagnetic anomalies observed in Tlamacas station (the Popocatepetl volcano, Mexico), linked to the ionization produced by intensive radon release, is presented in the experimental part of the study. The magnetic-field perturbations produced by electrical currents due to micro-discharges on the terrain irregularities are considered in a theoretical model. The simulations demonstrated that the discharge mechanism can generate perturbations with magnitudes of up to 1–10 nT in the ultra-low frequency (ULF)) range of 10−3–10−1 Hz. ULF Magnetic-field perturbations can be higher within storm-weather conditions under an accumulation of electric charges in clouds in the mountainous regions.
1. Introduction
Earth has three main shells (spheres)—the geosphere, the hydrosphere, and the atmosphere. Each of the spheres is characterized by a different aggregate state of matter, size, and dynamics. The interaction of these spheres among themselves, as well as with the sun, the moon, and the planets of the solar system, determines the geodynamics of Earth as a planet [1,2,3]. Between the individual elements of this geodynamic system there are connections that are clearly traceable in time and space, the study of which is an important element in the knowledge of our planet [4,5]. Obviously, the huge size of this geodynamic system does not allow the carrying out of area-based direct observation of its physical fields, so the role of remote-sensing methods, which have been widely developed in recent decades, is increasing [6,7,8,9,10]. Our work is devoted to the analysis of geomagnetic anomalies associated with volcanic and seismological sources.
In general terms, geodynamic processes are subject to the theory of lithospheric plate tectonics [1], which explains the origin of seismicity and volcanism due to predominantly horizontal movements of the plates of the lithosphere. The main manifestations of seismicity are observed at plate boundaries. Only a relatively small number of epicenters are located inside the lithospheric plates; these are so-called intraplate earthquakes [11,12]. Their nature is still not quite clear, although many of them represent large centers of seismicity and modern volcanism.
Numerous studies show that seismic events can be frequently used as precursors to volcanic processes [13,14,15]. Boulesteix et al. [16] noted that volcanoes very often erupt, i.e., change from a passive phase to an active phase, soon after strong earthquakes. Many authors refer to catastrophic earthquakes as a seismic trigger for volcanism [15,16,17].
In our paper, we consider issues related to the mechanism of ultra-low frequency (ULF)-generation of electric currents and perturbations of the earth’s magnetic field against the background of seismological and volcanic processes. This article is a logical continuation of the works of our team of authors. In previous papers [18,19], we considered the electrode effect of the discharge mechanism. In the present work, we present the results of micro-discharge modeling. The practical example for modeling is the region of the active Popocatepetl volcano (Mexico).
The Popocatépetl volcano (latitude: 19.023 N, longitude: −98.622 E, elevation: 5465 m), located in the platform part of Mexico and one of the most active volcanoes in North America, was chosen as an object for studying these processes. A number of researchers [16] have suggested that the activity of Popocatepetl is influenced by tectonic activity. These authors introduced an index based on the near-field concept to assess the influence of seismicity on volcanic activity [16]. In that case, the time series of strong earthquakes was compared with the intensity of volcanic activity, characterized by the number and energy of volcano-tectonic earthquakes, the number of dome extrusions, the intensity of thermal and degassing flows, and ash formation. By comparing seismo-tectonic processes with the intensity of volcanic activity at Popocatepetl between 1994 and 2022, those authors concluded that Popocatepetl is intensely active, with significant tectonic processes. Enhanced extrusion appears to quickly follow significant earthquakes—pulses of dome extrusion that peak after 1.3 ± 0.3 years. Conversely, extrusive activity disappears when significant seismicity disappears, as was the case in the period 2003–2011, which coincided with a 12-year period of no significant seismicity [16].
As a natural development of our own experimental and theoretical studies, we have already presented models of generation of geomagnetic anomalies caused by the convective movement of magma [18], radon emanation, and current flow [19,20].
In this paper, we like to present the discharge mechanism of generation of the noise component due to the separation of electric charges, which is also caused by the intense ionization of the air due to the exceptional high emanation of radon in the area of Tlamacas station. It is this component that we see as the most intense in power and prevailing over all other signal components.
In addition to the model presented, we emphasize once again the importance of Tlamacas Mountain as a unique natural geophysical laboratory, in which a number of physical phenomena are observed that are not observed in less-aggressive environments.
Earthquake forecasting is the prediction of the occurrence of an earthquake of a particular magnitude at a particular location at a particular time [21,22]. Despite considerable efforts by seismologists, scientifically reproducible predictions for a specific day or month cannot be made [23]. However, in the case of seismic hazard-assessment maps of studied faults, it is possible to estimate the probability that an earthquake of a given magnitude will occur at a given location within a given number of years. In general, the ability to predict earthquakes, either individually or on a statistical basis, remains unlikely. It should also be noted that the statistical approach of probabilistic seismic hazard analysis (PSHA) has been put in doubt by recent publications that try to suggest different approaches that are more deterministic [24].
If an earthquake has already started, early warning devices can alert observers seconds before strong tremors reach a given location. This technology takes advantage of the different propagation velocities of different types of vibrations. Aftershocks are also possible after a major earthquake, and they are usually included in disaster-management protocols [25,26].
In the effort to predict earthquakes, attempts have been made to associate an impending earthquake with phenomena as varied as seismicity patterns, electromagnetic fields, ground motions, unusual weather conditions and clouds, radon or hydrogen gas content of soil or groundwater, animal behavior, and the phases of the moon [27,28,29]. In [27], the authors pointed out the importance of atmospheric physical and chemical parameters, such as Earth’s surface temperature (sometimes microwave bright temperature), CO, SO2 gas release, the concentration of aerosol, and high outgoing longwave radiation [27].
Many pseudoscientific theories and predictions have been produced. The natural randomness of earthquakes and frequent seismic activity in certain areas can be used to make “predictions” that can generate unwarranted credibility. Generally, such predictions leave certain details unspecified, which increases the likelihood that vague prediction criteria will be met and unforeseen earthquakes will be ignored.
1.1. Radon
Radon concentration in soil has been used experimentally to locate near-surface geologic faults, since the concentration is generally higher above faults. It is a tracer of natural phenomena associated with radiation from the soil along faults, fractures, and discontinuities in the earth’s crust [19,20,30,31,32].
Recent studies have shown the effectiveness of analyzing and monitoring radon concentration in soil and groundwater as an important parameter in studying active faults in the earth’s crust [33]. This information is used as a precursor of volcanic events [34,35,36,37].
In other words, the studies show that elevated radon concentrations in soil or rapid changes in radon concentrations in soil or groundwater can be used to predict earthquakes [31].
Although most radon studies and measurements are confined to soil or aquifers, it should be kept in mind that radon is the most abundant naturally occurring radionuclide in the atmosphere. Radon 222Rn has a half-life of t1/2 ≈ 3.8 days and thoron (radon 220Rn) has a half-life of t1/2 ≈ 55 s. Radon is a radioactive noble gas that emanates from terrestrial regions and diffuses into the lower troposphere by advection and diffusion [38]. After its radioactive decay, radon daughter products (mainly radionuclides Po, Pb, Bi, and Tl) are formed. The presence of aerosols leads to the attachment of radon daughter products to them, forming radioactive aerosols. In this form, they participate in the formation of cloud droplets and raindrops and, thus, return to the earth’s surface.
In Section 3, we consider the atmospheric chemical potential and its relation to radon activity confined to volcanic regions.
1.2. Pre-Earthquake ULF Electromagnetic Perturbations
Among the methods that are used as earthquake precursors, the ULF electromagnetic perturbations have been studied as a result of inductive seismomagnetic phenomena during microfracturing [39,40,41]. These authors have stated that magnetic and electric perturbations must be of the order of 1–10 nT and 1–10 µV/m, respectively, at the distance 10–50 km from the epicenter.
Ultra-low frequency (ULF) electromagnetic waves (frequency 1–10 mHz) carry important information about electron propagation and diffusion in the Earth’s radiation belts [42]; this leads, ultimately, to changes in the dynamics of the magnetosphere [43,44,45,46,47]. ULF waves are strongly driven by coupling of the magnetosphere to the solar wind, giving rise to disturbances of the magnetopause [44,48].
Chao-Song Huang [49] analyzed global ionospheric disturbance current systems, which, in his opinion, are caused by many processes of solar and magnetospheric origin. Apparently, these processes can lead to reorientations of the interplanetary magnetic field, changes in the dynamics of the solar wind, magnetospheric storms, and variations in the parameters of ultra-low frequency waves. Thus, Zhang et al. [50] argued that ultra-low frequency (ULF, 0.001–1 Hz) perturbations are responsible for radial transport (diffusion) of high-energy electrons and for energizing the ionosphere with field-aligned currents.
2. Description of the Site
Popocatepetl is a volcano located in Central Mexico on the border of the states of Mexico City and Puebla (Figure 1). In Nahuatl, Popocatépetl means “Smoking Volcano”.
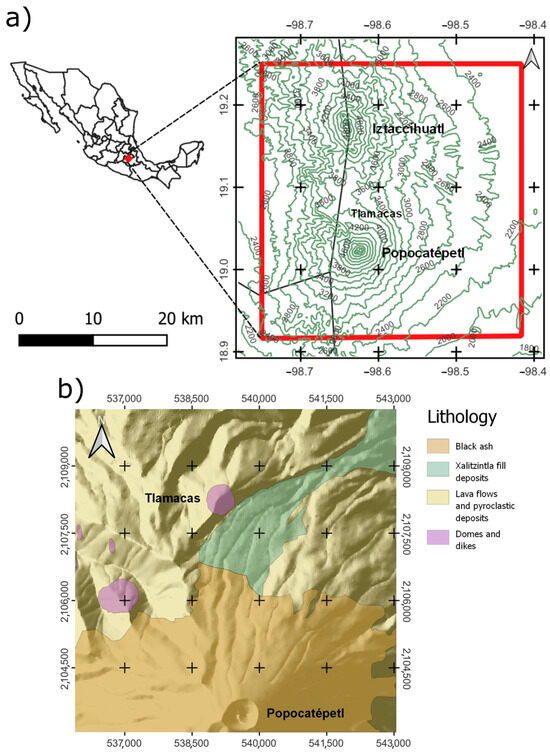
Figure 1.
(a) Location map of study area and (b) geologic map of the Popocatepetl volcano.
2.1. Geological and Geophysical Setting
Morphologically, Popocatépetl is located along the Mexican Neovolcanic Cordillera on the southern edge of the Mexican highlands, 16 km south of the Itztachihuatl volcano, and 72 km southeast of Ciudad Mexico. Popocatepetl’s perpetually snow-covered symmetrical cone rises to an altitude of 5465 m, second only to Mexico’s highest volcano, Pico de Orizaba (5610 m).
The geology, structural position, and dynamics of the volcanic structures of the Mexican Neovolcanic Belt have been described in many papers. The main points can be found in [51,52,53,54,55] and other publications. The focus of our paper is on the Popocatepetl volcano and adjacent areas [56,57]. The geologic map shown in Figure 1 [58,59] schematically depicts the major volcanic-sedimentologic complexes of Popocatepetl, which include domes and dikes, lava flows and pyroclastic sediments at the periphery of the volcanic edifice, and black ash. As well as the crater of the main volcano, the map also shows the Tlamacas dome on the northern slope of the volcano and the Yoloxochitl dome located to the northeast of the crater. Popocatepetl is an active stratovolcano with an altitude of 5400 m above sea level. The vertical elevation of the volcanic cone above the surrounding terrain reaches 3000 m [56]. Together with the Iztaccihuatl volcano, it forms a single sub-meridional geomorphologic system of volcanic rises (Figure 2a,b).
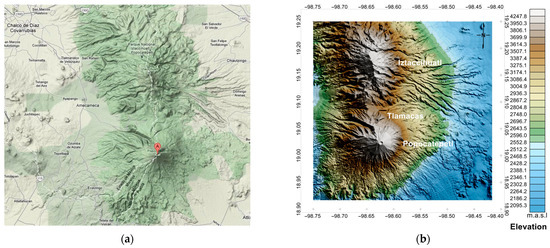
Figure 2.
(a,b) Geomorphology of Popocatepetl and adjacent areas (Model ETOPO1, a 1 arc-minute global digital elevation model (DEM) of Earth’s surface) [60].
The history of the formation of the modern appearance of the volcano is quite complex. According to [61,62,63], the present-day cone formed in the last 23,500 years as a result of a major collapse. At the same time, numerous large avalanche flows were formed and propagated southward [62,63,64]. The present-day cone was built up in the last ~23,500 14C y BP after an older volcano collapsed, producing a huge debris avalanche to the south [58,63,65]. The upper part of the volcanic cone is covered with a thick layer of black ash, which represents remnants of recent eruptions (Figure 3). The northeastern region of the volcano is represented mainly by lahars [58].

Figure 3.
The upper part of the volcanic cone Popocatepetl (https://gbank.gsj.jp/vsidb/image/Popocatepetl/bestvnir.html). Accessed on 15 October 2023.
Tlamacas Mountain is located to the north of the main volcanic cone of Popocatepetl (Figure 1, Figure 2 and Figure 3). It is of great scientific and practical interest, as it is characterized by many geophysical characteristics similar to those of the main volcano. At the same time, it is an area of relatively low seismicity and is not subject to lava eruptions. Thus, Tlamacas represents a natural geophysical laboratory for the study of the active Popocatepetl volcano.
2.2. Geophysical Remote Sensing and Land Information
As mentioned, modern geophysical data on the difficult-to-access areas of Earth, which include high-mountain areas of the Popocatepetl–Iztaccíhuatl volcanic system, are obtained mainly through remote-sensing methods. For gravimetric data, these are mainly satellite altimetry and terrestrial gravimetry; for magnetic data, the main method is aeromagnetometry. In this article, the methodology of surveying and data processing is not significant. We only provide the basic characteristics of geophysical fields, which are important for the discussion of the topic of the paper.
The gravity data used for the maps (Figure 4a,b and Figure 5b) were obtained by combining free-access satellite data [66] with a global gravity model (GGMplus2013) [62]. The data were computed with gravity forward modeling from 7.5 arc-second (~200 m) SRTM topography by assuming a constant density of 2670 kg·m−3 [67]. Free-air gravity data can be accessed via the GGMplus [62]. The International Gravimetric Bureau’s WGM2012 global model database, which includes 2881 ground gravity survey points, was used in preparing the GGMplus model [68]. Data reduction and anomaly calculations were performed in accordance with the recommendations of [69].
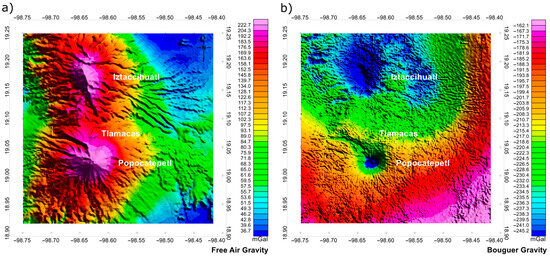
Figure 4.
Gravity anomalies: (a) free-air gravity; (b) complete Bouguer anomaly.
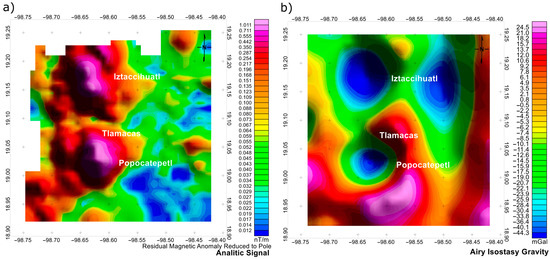
Figure 5.
Geophysical anomalies: (a) analytic signal of reduced-to-pole residual magnetic field; (b) Airy isostatic gravity anomaly.
The free-air anomaly (Figure 4a) shows intense gravity-positive values associated with the central areas (craters) of the Popocatépetl and Iztaccíhuatl volcanoes. The shape of the anomalies corresponds to the relief (Figure 2b), the maximum values exceed 220 milligal (mGal), and the amplitude reaches 187–180 mGal, in comparison with the eastward located regions. The structure of the gravity field has a sub-meridional orientation. Two predominant trends are clearly distinguished—N–S and W–E—and the latter is obviously related to the fault separating these two volcanic structures.
To calculate the complete Bouguer anomaly (Figure 4b), which represents the most comprehensive information about the deep structure of the region, we used a digital elevation model (DEM) with a resolution of 15–30 m. The resulting complete Bouguer anomaly thus reflects the disturbance between the observed gravity and that computed for a given reference Earth model at a same point [68].
The Bouguer anomaly varies between −160 and −250 mGal, which corresponds to the continental-type crust and the intraplate position of the region. The central parts of the craters are characterized by the most intense negative values of the gravitational field. The general configuration of the gravitational field has a close-to-isometric structure. The presence of a relative gravitational minimum in the area of a volcanic cone indicates the presence of less-dense material, compared to that of the surrounding rocks. This can obviously be explained by the presence of a magma chamber (or several magma chambers) in the interior of the volcano. The chambers are filled with molten material of relatively lower density.
The data used to construct the magnetic-field maps were obtained from the geomagnetic database of North America (magnetic anomaly map of North America) [70]. The map of magnetic-field anomalies was constructed by taking into account the International Geomagnetic Reference Field (IGRF). Subsequently, the separation of the anomalous magnetic field into regional and residual components was realized and the reduction to the pole was applied.
To better correlate the magnetic field thus obtained with the geologic structure of the Popocatepetl volcanic area, we constructed a map of the analytical signal of the magnetic field (Figure 5a). The analytic signal is the square root of the sum of the squares of the data derivatives in the x, y, and z directions. The analytic signal is useful in locating the edges of magnetic source bodies, particularly where remanence and/or low magnetic latitudes complicate interpretation. As expected, the highest analytical signal values of more than 1 nT per meter are confined to the central parts of both volcanoes. The magnetic-field structure shows the same trend as the gravity-field structure: a sub meridional trend of volcanoes and a sub-latitudinal zone of lowered values. Both of these lineaments indicate the presence of deep crustal faults.
Figure 5b shows complete spherical isostatic gravity anomaly (Airy–Heiskanen, Tc = 30 km). The spherical harmonic gravity coefficients were derived for the compensation of all relief components for the Airy–Heiskanen isostatic model with a constant compensation depth of Tc = 30 km [71,72,73]. Analysis of isostatic anomalies shows that the Popocatepetl volcano and the areas surrounding it are in isostatic disequilibrium.
The central parts of Popocatepetl and Iztaccihuatl are characterized by negative anomalies of −30 −40 mGal. At the same time, Tlamacas Mountain is obviously isostatically compensated. In general, multidirectional trends of vertical movements are observed in the area. This factor explains the presence of seismic events and associated faults and volcanism.
3. Atmospheric Chemical Potential
It was established that the atmospheric chemical potential (ACP), which can be derived from meteorological parameters (air temperature and relative humidity), is the proxy of the radon activity [74]. It provides us with an instrument for determining the operative radon activity-monitoring in large areas, including the areas of seismic and volcanic activity, especially during periods of preparation for strong earthquakes or volcano eruption. Examples of ACP variations before eruption of volcanoes at Kamchatka peninsula and Hawai’i were presented in [75]. It was established that the area of increased ACP signal occupies several hundred square kilometers, and time dynamics demonstrated the sharp increase in ACP a few days before eruption.
We checked the ACP behavior around the time of several cases of Popocatepetl volcano eruptions and registered similar patterns: an increase in ACP values before an eruption of more than 100%, and then a return to the values registered before anomaly development started. The top panels of Figure 6 and Figure 7 show the temporal behavior of ACP and the bottom panels show their spatial distribution for the period of ACP maximum registered in temporal curves (0.045 eV in the first case and 0.035 eV in the second one).
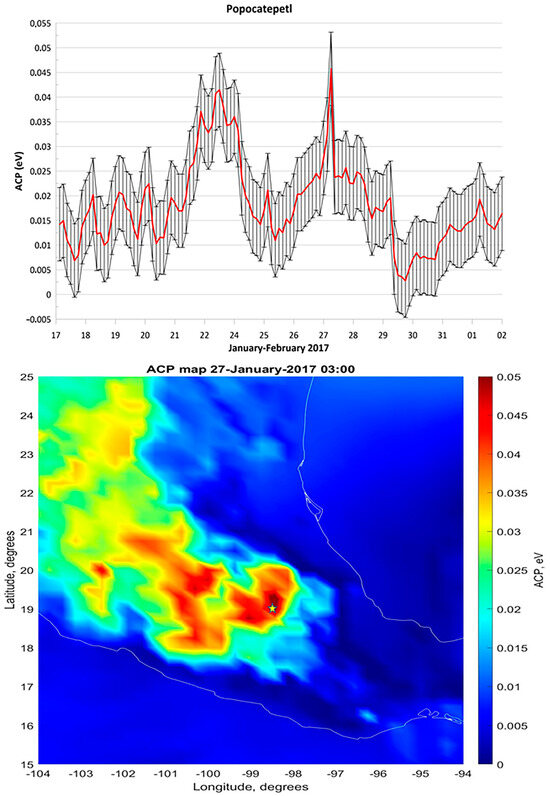
Figure 6.
Top panel—ACP variations over the Popocatepetl volcano caldera around the time of volcano eruption at the end of January 2017. Bottom panel—the spatial ACP distribution registered on 27 January 2017.
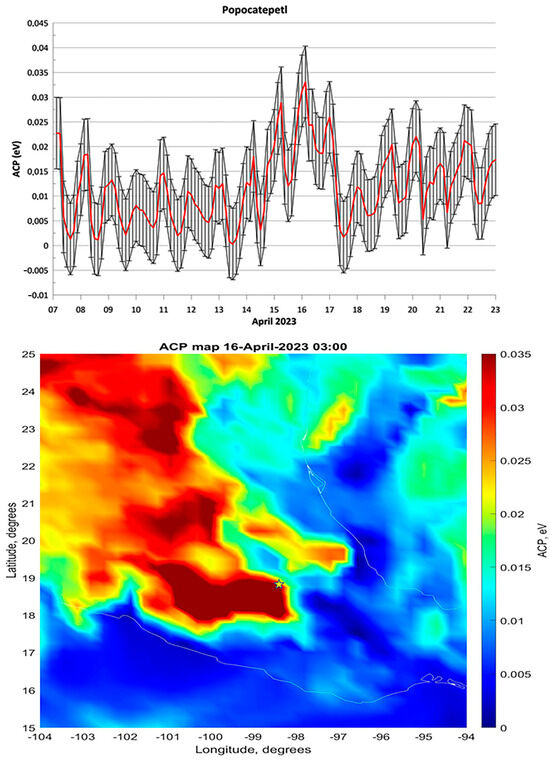
Figure 7.
Top panel—ACP variations over the Popocatepetl volcano caldera around the time of volcano eruption in the middle of April 2023. Bottom panel—the spatial ACP distribution registered on 16 April 2023. The location of the Popocatepetl volcano is marked by the yellow star.
It is interesting to note that during the period of volcano-eruption preparation, both the increase in the ACP level around the volcano caldera and the sharp decrease in it are observed. Such examples are shown in Figure 8 for the period of Klyuchevskoi volcano activity at the Kamchatka peninsula [76]. These effects are probably due to the periodic volcano chamber and surrounding crust expanding and compressing, which leads to opening and closing the cracks that serve as ways of radon migration to the surface. Such changes were confirmed by the lineament analysis of the ground surface of the volcano and the surrounding area [77].
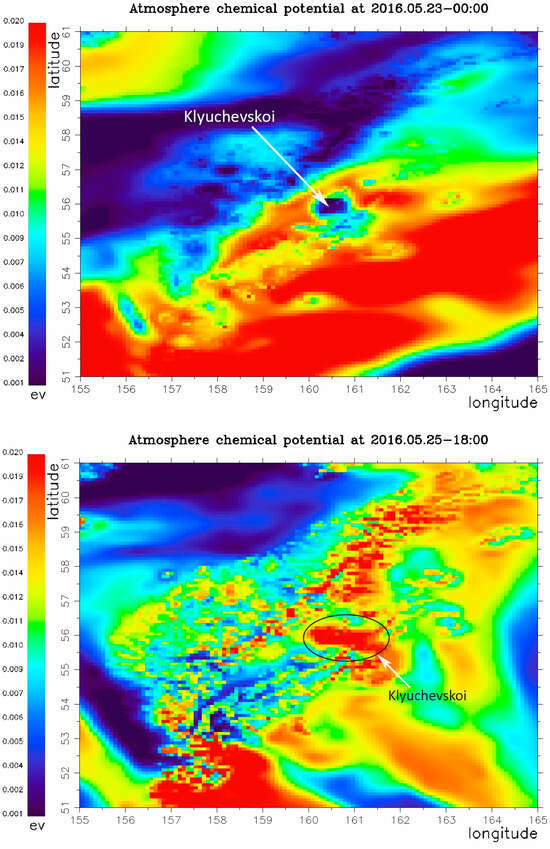
Figure 8.
Top panel—Spatial distribution of ACP at Kamchatka peninsula on 23 May 2016, Bottom panel—spatial distribution of ACP at Kamchatka peninsula on 25 May 2016.
4. The Data of Observations
Geomagnetic observations were carried out at the Tlamacas measurement site (98°37′41″W, 19°04′01″N) using a UCLA-designed Fluxgate-type magnetometer (3 orthogonal components, 1 Hz sampling frequency), purposely designed to study magnetospheric phenomena in a number of meridional networks such as the Mid-continent Magneto-Seismic Chain (McMac) [78,79]. An identical instrument as a reference in an area devoid of seismic or volcanic activity was installed at Juriquilla.
The study included the analysis of dynamic spectra as part of a traditional analysis for the continuous component of the magnetic field and the analysis of geomagnetic micropulsations for the pulse component. Temporal intervals with a high geomagnetic activity (estimated by the equatorial Dst index) are normally discarded from the analysis. In order to distinguish the local character of the observed phenomena from the global ones, we compared our results with those calculated from the closest Mexican station at Juriquilla (JU2, (100°26′48.81″E, 20°42′14.87″N, elevation 1946 m.a.s.l.), which is integrated to the Mid-continent Magneto-Seismic Chain [78,79] network with the same equipment
The anomalously elevated electromagnetic (EM) noise in the volcano station was a topic of our study.
As we have previously noted, the location of Juriquilla is in a busy urban area, neighboring a number of technological industries. However, the EM noise at Tlamacas station, which is located in an area away from any human-made influence, is significantly higher in power than that observed at Juriquilla.
The background noise can increase for a period from 2 h up to several days of continuous operation (Figure 9 and Figure 10).
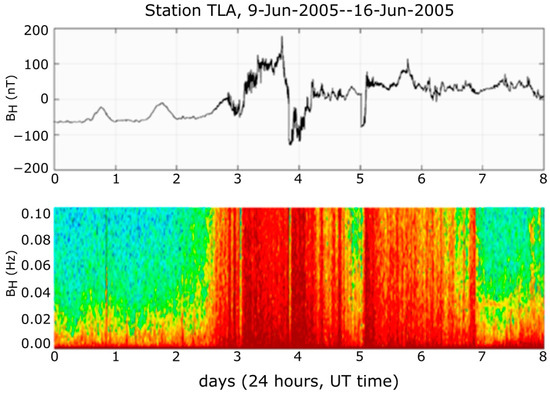
Figure 9.
Top panel: H—component signal, Tlamacas station. Bottom panel: its dynamic spectra.
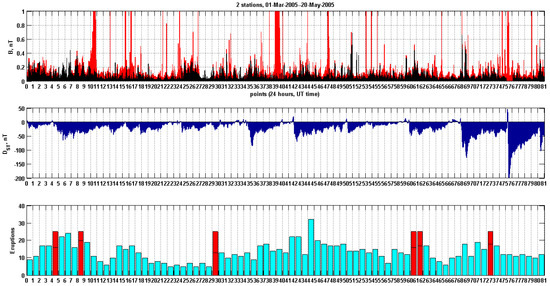
Figure 10.
The excess EM background at Tlamacas can vary from 3 to 15 times in power, compared to a more “quiet” EM measurement period at the same location.
At a minimum, the average cumulative distribution of noise-signal amplitudes at Tlamacas during a 24 h period was more than twice as large as that in Juriquilla (Figure 11).
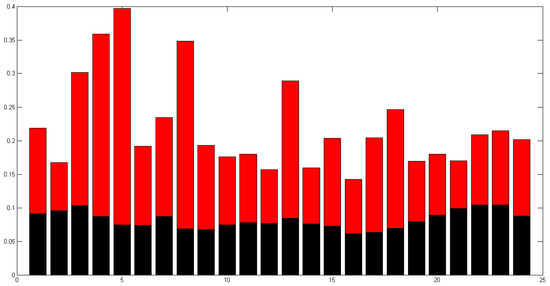
Figure 11.
Comparison of the cumulative distribution of noise-signal amplitudes at Tlamacas (red) and Juriquilla (black) stations during 24 h.
Previously, the above-mentioned reason for such a phenomenon was proposed to be the anomalous increased release of the main isotope radon-222 from the near-surface soil layer (about 10,000.00 Bq/m3 [20]) and the associated release of alpha-particles, capable of intensive ionization of air in the atmosphere, leading to the formation of charges of different signs. The interaction of secondary ionization products with initially electrically neutral water molecules and finely dispersed dust particles leads to the formation of a whole family of charged complexes of different masses, resulting in spatial charge separation by height, mobility, and stratification [73].
As a new interpretation of the scheme of their formation and interaction in the form of micro-discharges, we created the present model on the basis of computer modeling.
5. Simulations of Discharging of Atmospheric Electricity and ULF Magnetic Perturbations
There are several possible mechanisms of generation of ULF electric currents that can produce ULF magnetic-field perturbations. They are (1) telluric currents within the lithosphere [41,80,81] due to volcanic and seismic activity; (2) currents in the near-Earth atmosphere due to the classic electrode effect in the presence of the fair-weather electric field and the air ionization due to radon emanation [19,82]; and (3) the electric currents produced by the local electric discharges of charges accumulated in the clouds to Earth’s surface, stimulated by the radon emanation [83,84,85,86,87,88].
The telluric currents and the radon release are due to the same phenomenon—namely, the motions in the lithosphere (for instance, the motion of magma with the volcanic chambers). These currents may be quite large, but they are not determined by the radon release. Therefore, the presence of radon is only an indicator of the generation of electric currents due to motions within the solid earth in that mechanism.
The classic electrode effect seems too weak under realistic conditions [19] when the fair-weather bias electric field is of about E = 100–1000 V/m and the light ion concentration is ≤ 1012 m−3. There, the generated magnetic field perturbations are δB ~ 0.01–0.1 nT. The efficiency can be enhanced by the increase in the ionization and by the increase in the static electric field. Such an increase can take place when the electrically charged clouds approach Earth’s surface. If the electric field exceeds the values of 5–10 kV/m, then spreading electric currents result in magnetic-field perturbations up to 1 nT, as our simulations demonstrated. However, within large electric fields, the processes of the impact ionization and the corona discharges near the sharp spikes occur [89,90], and the last mechanism takes place.
This section is devoted to the last mechanism of generation of electric currents where the radon release plays an active role in the generation of electric currents. Our measurements were realized at the end of June, when the rainy season takes place at the site, together with increased electric atmospheric phenomena. Thus, the following scenario may be proposed. In the period of preparation of electric thunderstorms, the separation and accumulation of charges within the clouds occurs. Because of the mountainous site, the charged clouds can approach the slope of Tlamacas Mountain; see Figure 12a. The radon emanation results not only in the ionization of the near-Earth air, but also in the impact ionization with the strong electric field and the initiation of the corona discharge at the projecting parts of the mountain slope. As a result, the short circuiting of the charge of the cloud to Earth’s surface due to the region of a lower resistance takes place. Finally, the partial discharging of the accumulated charge of the cloud occurs. This process is equivalent to the discharging of the capacitance through the resistance series; see Figure 12b. The resistances Rj in the series of each part of the air between the mountain slope and the charged cloud are discussed below.
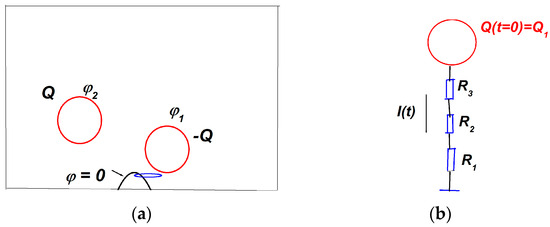
Figure 12.
The geometry of the problem. Part (a) is the mountain area with two oppositely charged clouds Q, −Q. The mountain is marked by a black arrow. The region of air ionization is marked by a blue line. Part (b) is the equivalent circuit for discharging through the resistance series.
The simulations of the discharging problem include the following steps: the electrostatic problem, the stationary currents, and the partial quasi-stationary discharge. The direct simulations were performed with COMSOL Multiphysics 3.5 software. Nevertheless, for simple estimations, using the equivalent circuits is also suitable.
5.1. The Electrostatic Problem
The goal of this subsection was to estimate the possible total charges of clouds near the Tlamacas site, as well as the capacitances of charged clouds under realistic conditions. The typical distances were 0.3–3 km. The sizes of the charged clouds were 0.3–1 km. The basic equation was the Poisson equation for the electric potential φ created by the charge distributions within the clouds ρ(r) [82,83,89,91]:
The relative permittivity of the air is 1; ε0 is the electric constant, SI units. In Equation (1), the ground boundary condition is applied at Earth’s surface SE and at the surface of the box SB. The electric fields is .
The density of charge is due to ions:
Here, n+, n− are the concentrations of positive and negative ions, which are assumed as single-charged.
The sizes of the simulation boxes should be quite large to provide for independence of results from the sizes of the box. In our simulations, they were Lx = Ly = 4–5 km in the horizontal plane and Lz = 2–3 km along the vertical axis OZ. Two spherical clouds of equal sizes but with opposite charges were considered, to connect the electric field lines between the charges and, thus, to avoid an influence of external boundaries; see Figure 13. In Figure 13, the parameters are as follows: the radii of the clouds are A1 = A2 = 400 m and the charge densities are within them, ρ1 = −ρ2 = 10−8 C/m3. Thus, the total charges are Q1 = −Q2 ≡ (4/3) πA13 ρ1≈ 3 C. These charges are typical for charged clouds under pre-thunderstorm periods [36,79,80,81,82,83,87,92], considering that thunderstorm lightning discharges values that are significantly larger, as Q ≥ 10 C. The values of charges Q1, Q2 are limited by the breakdown electric fields in the air, which are of about 106–3 × 106 V/m [84,87]. In our simulations, the electric fields in the air were < 2 × 105 V/m but were sharply increased at Earth’s surface with the radon release. The region of the air ionization had a shape of ellipsoid. The shape of the mountain was approximated by the cone of the altitude 300 m and the radius of the base 300 m. More complicated approximations of the shape of the mountain, like a superposition of several ellipsoids, did not change the principal results.
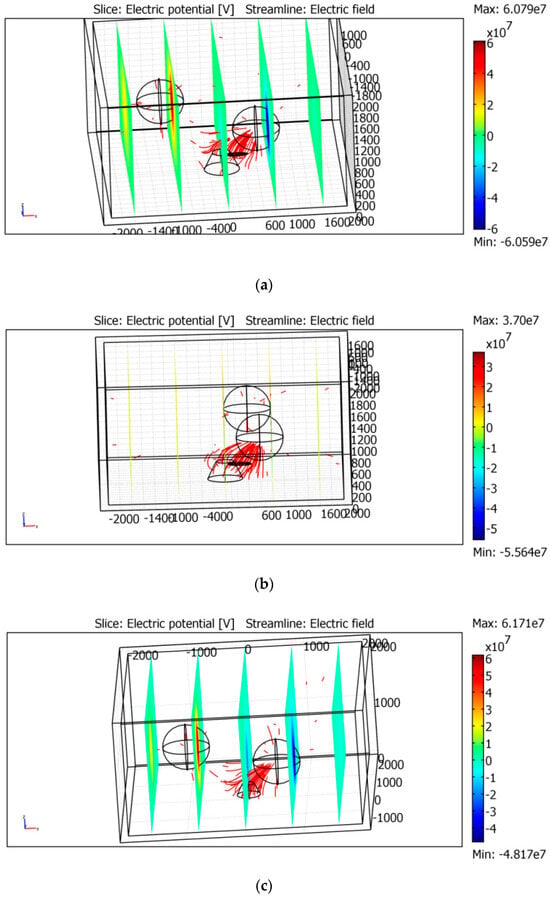
Figure 13.
Clouds and the site in the electrostatic simulations. There are 2 different configurations here. The lines of the electric field are presented in red.
The results of the simulations demonstrated that the electric field at Earth’s surface is determined by the distance between the mountain site and the nearest electric cloud and the sharpness of the ionization region at Earth’s surface. An influence of another charged cloud is not essential for the distribution of the electric field near the ionized region, as seen in Figure 13a,b and Figure 14a,b. Figure 13c and Figure 14c correspond to the mountain without the ionized region. They show that the electric field near Earth’s surface is 1 order smaller than in the cases with the ionization. Moreover, the electric field is greater at Earth’s surface below the cloud, not near at the surface of the mountain.
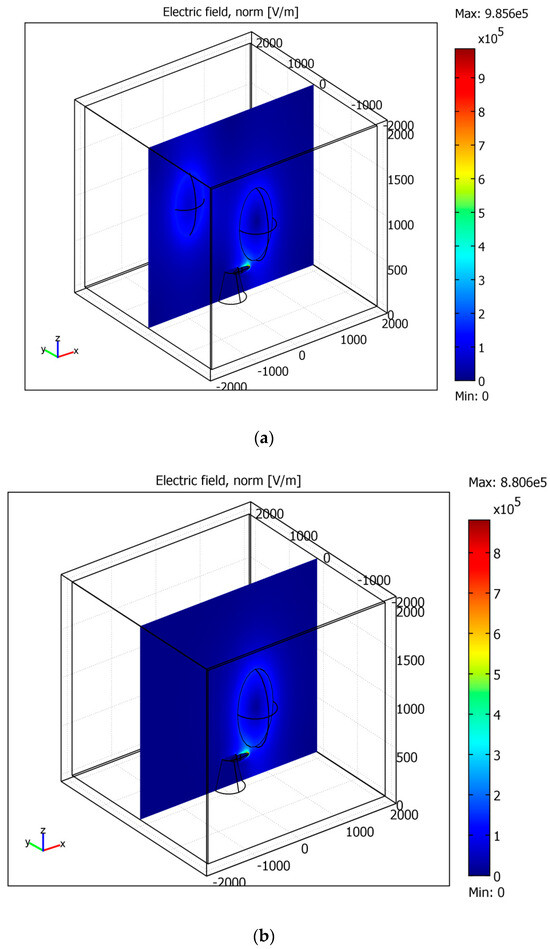
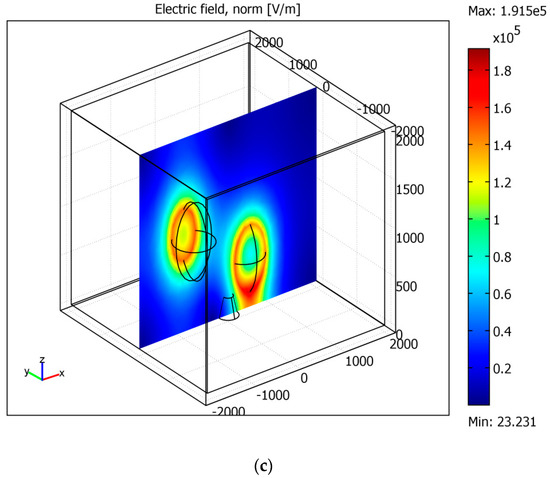
Figure 14.
The enhancement of the electric field near the ionization region. The cross-sections cut the mountain, the region of the ionized air, and the charged cloud. Parts (a–c) correspond to the mountain without the ionized region.
The electric field normal to Earth’s surface is essentially increased under the ionization, reaching the values of E ≈ 106 V/m. The ionization region plays the role of a sharp edge. These values of the electric field are sufficiently large for the initiation of the corona discharge. In turn, the role of the corona discharge is to increase the ion concentration in the air near the mountain.
5.2. The Stationary and Quasi-Stationary Currents Problems
The quasi-stationary problem includes the solving of the equations for the electric potential (1) and (2) jointly with the equations for the ion concentrations. In the presence of the impact ionization, the simplified equations for ion concentrations are as follows [82,83,89]:
Here, q is the ionization rate, α is the recombination coefficient, and β+,− are the coefficients of the impact ionization. These coefficients depend on the molecular and ion concentrations and on the value of the electric field E. Note that the turbulent diffusion is neglected here, as well as the equation for the temperature. Despite the simplifications, the solving of the joint set of equations for the electric field potential φ (Equation (1)) and for the ion concentrations is a very complicated problem. Therefore, in solving the equation for the electric field, the ion concentrations are assumed as estimated; then, the conductivities in each region, as well as and the resistances in series, can be calculated.
The simplified single equation for the electric potential within the conducting media is as follows [93]:
Here, σ is the air conductivity and ε0 is the electric constant. In the stationary case, δφ/δt = 0, it is assumed that the potential of the nearest cloud takes the value obtained from the electrostatic problem considered above: φ|S1 = φ1.
The conductivity of the air is as follows:
Here, e is the electron charge; the positive and negative on concentrations are n+, n-; and b+, b- are the ion mobilities. Due to the corona discharge, the ion concentrations are increased in the near-Earth discharge region, n01 ≈ n+ ≈ n- ≈ 1013 m−3. The light ion mobilities are approximately b+ ≈ 0.01 m2/V·s [82,83] at the heights z = 4–5 km.
5.3. The Discharging Problem
The discharging problem can be considered by the equivalent circuit problem. The circuit includes the total resistance R in series, as shown in Figure 15b, and the capacitance C. The capacitance can be estimated as C = Q0/φ1, where Q0 is the initial total charge of the approaching cloud and φ1 is its potential. The discharge time of the circuit is τ = RC. Therefore, the following equations and the initial condition are approximately valid [85]:
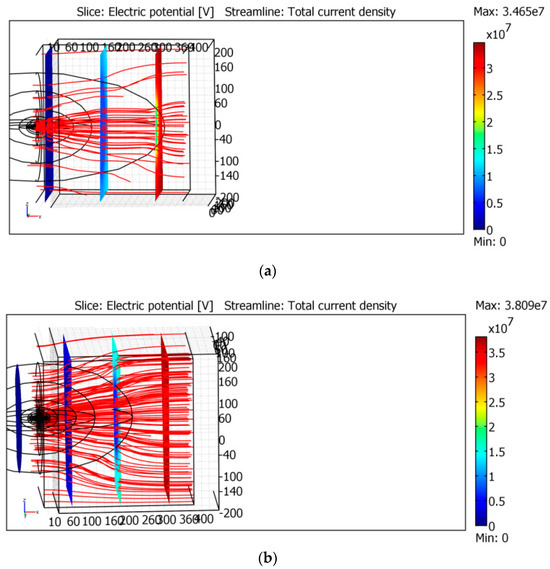
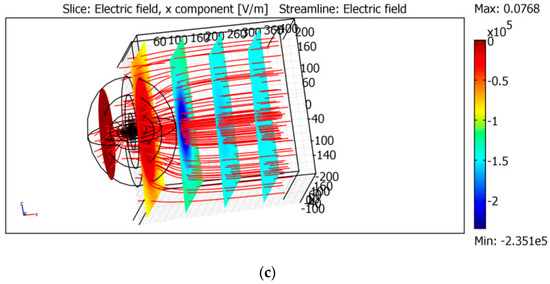
Figure 15.
Simulations of DC problem. The concentration of the electric current at the corona region. The lines of the current are presented in red. Parts (a–c) correspond to different longitudinal sizes of the ionization regions.
In the electrostatic simulations we used Q0 = 2–5 C, and the potential of the cloud is φ1 = 107–6 × 107 V. Thus, the equivalent capacitance is C = 10−8–10−7 F, R ≡ R1 + R2 + R3 = 109–1011 Ω. Therefore, the discharge time is τ = 10–1000 s and, thus, I(0) = 10−3–10−1 A. Note that only a part Q1 < Q0 of the total charge can be discharged, due to a low conductivity of the inner cloud [85,86]. It is assumed below that Q1 = 1 C.
The resistances in series R1,2,3 are determined by different physical processes. R1 ≤ 108 Ω is relatively low due to the corona discharge, where there is an enhanced ion concentration due to the impact ionization.
The simple expression for a resistance is
The resistance regions are assumed to be cylindrical.
The length of the corona region is L1 ≈ 10 m; a1 ≈ 3 m is its radius; and the ion concentration is n01 ≈ 1013 m−3. This yields the magnitudes σ1 ≈ 10−8 S/m and R1 ≈ 3 × 107 Ω.
The resistance R2 is for the region out of the corona discharge but with the ionization due to radon. The length of this region is L2 ≈ 100 m, a2 ≈ 10 m and the ion concentration is n02 ≈ 1012 m−3. Thus, σ2 ≈ 10−9 S/m and R2 ≈ 3 × 108 Ω.
The last resistance R3 is for the air near the cloud. The fair-weather air conductivity depends on the altitude [91,94,95]. At the height z = 4 km, it is approximately σ3 = 10−13 S/m. However, there are several factors that can increase the conductivity up to σ3 = 10−12 S/m. They are the presence of volcanic ashes in the air and the transferring of the ions at some distances from Earth’s surface [86], due to air turbulence. It was demonstrated that light ions can transfer up to distances of 2–4 km from the corona discharge region [91]. When the length of this region is L3 ≈ 200 m, a3 ≈ 300 m, σ3 ≈ 10−12 S/m, and the value is R3 ≈ 2 × 109 Ω. Thus, the total resistance is approximately R ≈ R3 ≈ 2 × 109 Ω for the parameters mentioned above.
An influence of air ionization on the discharge current is illustrated by Figure 15 and Figure 16. The simplest plane geometry is considered. Namely, there are two planes, and the distance between them is Lx = 400 m. The sizes of the simulation boxes are Ly = Lz = 400 m, 0 ≤ x ≤ Lx, −Ly/2 ≤ y ≤ Ly/2, Lz/2 ≤ z ≤ Lz/2. The difference in the potentials between the planes is φ(x = Lx) − φ(x = 0) = 5 × 107 V. The plane x = 0 corresponds to the surface of the mountain, whereas x = Lx corresponds to the surface of the cloud with charge. Near the central axis, y = z = 0, there is the ionization region. The simulations have been done within the framework of stationary Equation (4), i.e., they correspond to the initial stage of the discharge. The dependence of the air conductivity on x and ρ ≡ (y2 + z2)1/2 are provided in Figure 17.
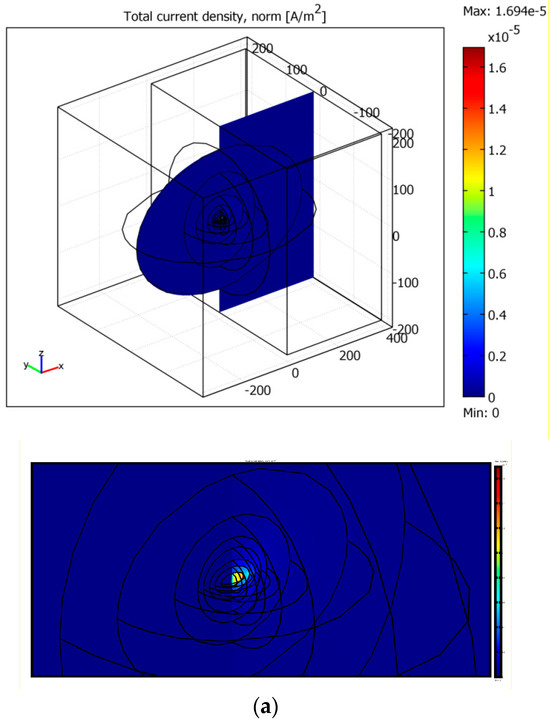
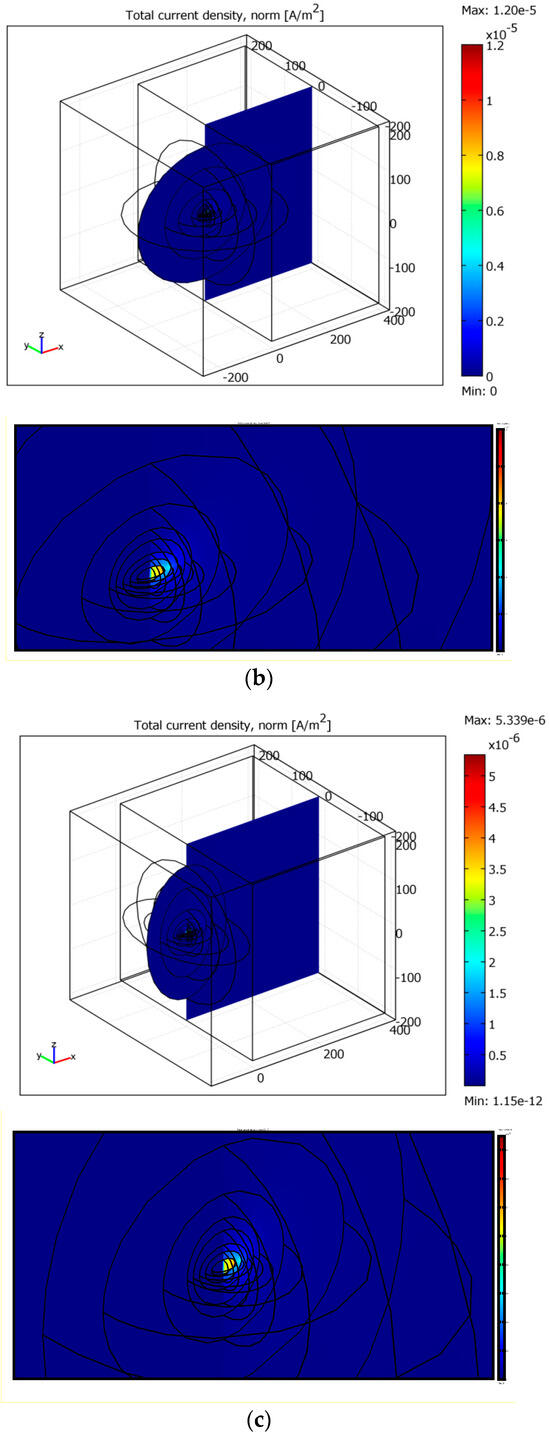
Figure 16.
The concentration of the electric current in the region of the air ionization. The parts (a–c) correspond to the proper parts in Figure 15. The lower panels are the detailed views.
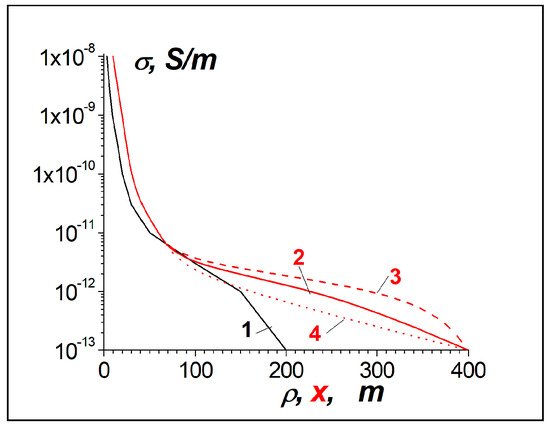
It is seen the electric current lines are concentrated into the regions with the increased conductivity near x = 0. When the ionization region becomes closer to the plane x = Lx, this concentration becomes more essential, as shown in Figure 15a and Figure 16a. The total electric current was calculated within the cross-section a = 10 m near x = 0; it is 6 × 10−3 A in Figure 15a and Figure 16a. In Figure 15b,c and Figure 16b,c, the currents are 1.5 and 3.5 times smaller. In Figure 16, both general views of each cross-section and the detailed ones are presented.
5.4. Estimations of the Magnetic-Field Perturbations
Near Earth’s surface, the magnetic-field perturbation excited by the discharge electric current I(t) is
Here, a is the distance from the center of the corona discharge to the sensor and I is the current within that crosses the circle with the radius a. The coefficient κ = 0.5 is due to the fact that the electric current leaks into the soil and occupies the finite distance that is bigger than a. It is assumed that near Earth’s surface, the current lines are almost parallel, as our simulations demonstrated. For the values of the current I = 0.1 A and a = 3 m, it is possible to estimate δB ≈ 5 nT. Fourier spectra of the magnetic-field bursts are in the ULF range f ~ 1/τ–0.01–0.1 Hz, as shown in Figure 18.
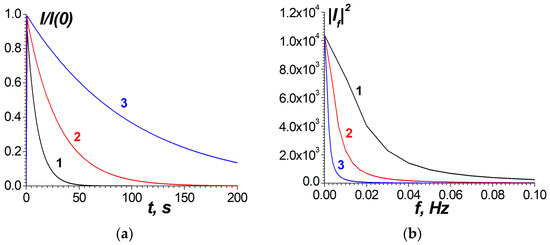
Figure 18.
(a) I(t) and (b) the frequency spectra of I. The curves 1, 2, and 3 correspond to the discharge times τ = 10 s, 30 s, 100 s, respectively.
As possible current sources for ULF magnetic perturbations in the volcano and the seismic regions, the telluric electric currents should also be mentioned. Their origin may be either by a magmatic motion or by the electrokinetic effect [96]. Electrokinetic magnetic fields result from fluid flows and, thus, from the transfer of ions through the crust in the presence of the ionic electric double layers at the solid–liquid interfaces. There were estimations of the telllutic currents that were necessary for measured magnetic perturbations [97]. The detailed investigation of the telluric currents in the vicinity of the Popocateptl volcano is a subject for future work.
6. Discussion
It should be noted that a full-fledged experimental analysis of the noise component, observed to be anomalously overestimated at the Tlamacas observation site, is not possible, due to the insufficient exposure rate (sampling rate) of the magnetometer. The most important criterion in the essence of the observed phenomenon was, for us, the possibility of temporal separation of the signal from micro-discharges, which can occur at a characteristic time. This is also important for the statistical evaluation of the characteristic time of individual discharges, amplitude, and frequency of their succession.
For future improvements, we suggest the use of more cost-efficient devices (such as a loop coil in the form of an induction antenna) in the direction of observations. In this case, the measurement of the field itself was of secondary importance, and the main interest was the registration of electric discharge pulses in situ, with good temporal resolution. This was especially concerned with the distinction of signals of any physical nature when studying possible precursors of natural cataclysms (earthquakes, volcanic activity, or atmospheric phenomena such as hurricanes or cyclones). The main method of their mathematical processing was signal processing. In this study, we had to accept that in the modern methodology of setting up the experiment, we are still very far from the desired method.
Based on the results of the simulations presented in Section 5, it is possible to state that the mechanism of generation of electric currents is suitable, which is due to the corona discharge in the air at the place of the radon emanation. As a result, the partial discharge of the charged clouds can be realized through the decreased resistance of the ionized air between the clouds and Earth’s surface. Note that, in the simulations, we used the realistic, not enhanced, parameters of the ionized air.
The Tlamacas site combines the following features that make possible this mecha-nism:
- (1)
- The vicinity of the volcano, which elevates 1400 m over the site. The volcano activity is not only the source of the radon emanation, but it is also the source of the volcanic dust and, thus, the additional electric charging of the clouds. The measured values of the electric field in the air are at least one order higher than they are in lower places. Thus, the ignition of the corona discharge near Earth’s surface can be simplified.
- (2)
- Enhanced formation and the charging of the clouds occur during the tropical rainy season in the mountainous site.
- (3)
- There is an essential elevation of the site over the mountain saddle point Paso de Cortes of about 500 m. This makes possible the spreading of the radon and the ionized air along the mountain slope and, therefore, the ionized air can decrease the total resistance between the partially charged clouds and Earth’s surface. Thus, the essential leakage currents from the partially electrized clouds to the site can be realized.
- (4)
- Due to the high altitude of the site, 4 km above sea level, the conductivity of the air is essentially higher than it is at lower places; this is also due to the vicinity of the volcano, as mentioned above.
- (5)
- Due to the mountainous relief, the clouds can approach to within 200–300 m of the site. This simplifies the partial discharge of the clouds and the ignition of the corona discharge at Earth’s surface.
The specific features of the site have also been confirmed by the gravimetrical measurements and the maps of the chemical potential of the air. As mentioned above, ACP is a proxy of radon activity [74]. The process of ion induced nucleation leads to formation of aerosol-size cluster ions which, due to their low mobility, may form in quadrupole structures near the ground layer of the atmosphere [98]. Reconnection of electric field lines of the formed quadrupoles create the surface coronal discharge, which can be a source of ELF electromagnetic emission. Contraction and expansion of the volcano chamber before eruption lead to closing and opening the cracks—which are ways of radon migration to the ground surface. This process is reflected in the dynamics of ACP distribution around caldera, as shown in Figure 8: the dark blue spot around the Klyuchevskoi volcano caldera (upper panel), and the bright red spot in the bottom panel.
Analysis of the gravity field suggests tectonic instability of the Popocatepetl volcano region and its vicinity. The intense negative Bouguer residual anomaly indicates the presence of decompacted matter in the crustal structure, which apparently corresponds to a magma chamber. At the same time, the negative gravity isostasy indicates a tendency to upward vertical movements, which generate faults in contrasting zones, providing magma pathways to the surface.
In addition, simultaneous measurement of different physical parameters—such as magnetic field, registration of electric impulses by contour antenna, near-surface radon emanation, measurement of atmospheric electric field and air conductivity—would be the most informative. Also, measurements of the chemical content of the air, as well as the ion species, are necessary. Integrated measurements in the form of long-time monitoring are seen as the best way to conduct geophysical research, as they provide the opportunity to link them together to build a complete picture of the observed anomalies. Future authors should discuss the results and how they can be interpreted from the perspective of previous studies and on the basis of the working hypotheses. The findings and their implications should be discussed in the broadest context possible.
7. Conclusions
This paper presents a discharge mechanism of the generation of the noise component due to the separation of electric charges. This study is a follow-up and development of the authors’ previous models of generation of geomagnetic anomalies caused by convective movement of magma, radon emanation, and current flow.
A complex analysis of natural geophysical fields, in combination with geological, meteorological, and other information, allows for a significant increase in the efficiency of seismic and volcanic manifestation forecasting.
An important component of such analysis is the monitoring of the concentration of radioactive radon gas in the near-surface soil layer and in the atmosphere, analysis of atmospheric chemical potential, monitoring of ultra-low frequency (ULF) electromagnetic waves, and analysis of the dynamics of the magnetosphere.
It was established that telluric currents within the lithosphere due to the volcanic and seismic activity, currents in the near-Earth atmosphere due to the classic electrode effect, and the electric currents produced by the local electric discharges of charges accumulated in the clouds to Earth’s surface, stimulated by the radon emanation, may be responsible for the possible generation of ULF electric currents that can produce ULF magnetic-field perturbations.
Simulations of the discharging of atmospheric electricity and magnetic perturbations were realized, including the electrostatic problem, the stationary- and quasi-stationary-currents problems, and the discharging problem.
Author Contributions
Conceptualization, V.G., A.K. and V.Y.; methodology, V.G., A.K. and V.Y.; software, V.G.; validation, V.G. and V.Y.; formal analysis, V.G.; investigation, V.G., A.K., V.Y. and S.P.; resources, V.Y.; data curation, A.K.; writing—original draft preparation, V.G., V.Y., A.K. and S.P.; writing—review and editing, V.Y. and A.D.R.G.; visualization, V.G., A.D.R.G., V.Y., S.P. and A.K.; supervision, V.G. and V.Y.; project administration, V.Y.; funding acquisition, V.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The APC was partially funded by the Potosino Research and Technology Institute to Vsevolod Yutsis.
Data Availability Statement
Gravity data are available through http://ddfe.curtin.edu.au/gravitymodels/GGMplus/ (accessed on 15 October 2023). Magnetic data are available through https://www.usgs.gov/maps/magnetic-anomaly-map-north-america (accessed on 15 October 2023).
Acknowledgments
The authors acknowledge the Potosino Research and Technology Institute (IPICYT) and the Universidad Autónoma del Estado de Morelos (UAEM) for their technical and administrative support. The authors are grateful to three anonymous reviewers, whose valuable observations and comments allowed us to significantly improve the work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Burke, K. Plate Tectonics, the Wilson Cycle, and Mantle Plumes: Geodynamics from the Top. Annu. Rev. Earth Planet. Sci. 2011, 39, 1–29. [Google Scholar] [CrossRef]
- Brune, S.; Williams, S.E.; Müller, R.D. Potential Links between Continental Rifting, CO2 Degassing and Climate Change through Time. Nat. Geosci. 2017, 10, 941–946. [Google Scholar] [CrossRef]
- Cawood, P.A.; Hawkesworth, C.J.; Pisarevsky, S.A.; Dhuime, B.; Capitanio, F.A.; Nebel, O. Geological Archive of the Onset of Plate Tectonics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170405. [Google Scholar] [CrossRef] [PubMed]
- Campbell, I.H.; Squire, R.J. The Mountains that Triggered the Late Neoproterozoic Increase in Oxygen: The Second Great Oxidation Event. Geochim. Et Cosmochim. Acta 2010, 74, 4187–4206. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Zong, K.; Kusky, T.M.; Wang, Y. Plate Tectonics: The Stabilizer of Earth’s Habitability. J. Earth Sci. 2023, 34, 1645–1662. [Google Scholar] [CrossRef]
- Chen, G.X.; Cheng, Q.M.; Lyons, T.W.; Shen, J.; Agterberg, F.; Huang, N.; Zhao, M. Reconstructing Earth’s Atmospheric Oxygenation History Using Machine Learning. Nat. Commun. 2022, 13, 5862. [Google Scholar] [CrossRef] [PubMed]
- Zaher, M.A.; Saibi, H.; Mansour, K.; Khalil, A.; Soliman, M. Geothermal exploration using airborne gravity and magnetic data at Siwa Oasis, Western Desert, Egypt. Renew. Sustain. Energy Rev. 2018, 82, 3824–3832. [Google Scholar] [CrossRef]
- Van der Werff, H.; Van der Meer, F. Sentinel-2 for Mapping Iron Absorption Feature Parameters. Remote Sens. 2015, 7, 12635–12653. [Google Scholar] [CrossRef]
- Saibi, H.; Bersi, M.; Mia, M.B.; Saadi, N.M.; Al Bloushi, K.M.S.; Avakian, R.W. Applications of Remote Sensing in Geoscience. In Recent Advances and Applications in Remote Sensing; InTech: London, UK, 2018. [Google Scholar] [CrossRef]
- Surajit, P.; Krishnendu, B. Remote sensing for geology-geophysics. In Basics of Computational Geophysics; Elsevier: Amsterdam, The Netherlands, 2021; pp. 223–269. [Google Scholar] [CrossRef]
- U.S. Geological Survey. Advanced National Seismic System (ANSS) Comprehensive Catalog. 2021. Available online: https://earthquake.usgs.gov/earthquakes/search/ (accessed on 15 October 2023).
- Ryan, W.B.F.; Carbotte, S.M.; Coplan, J.; O’Hara, S.; Melkonian, A.; Arko, R.; Weissel, R.A.; Ferrini, V.; Goodwillie, A.; Nitsche, F.; et al. Global Multi-Resolution Topography (GMRT) synthesis data set. Geochem. Geophys. Geosyst. 2009, 10, Q03014. [Google Scholar] [CrossRef]
- Eldholm, O.; Coffin, M. Large Igneous Provinces and Plate Tectonics. Geophys. Monogr. 2000, 121, 309–326. [Google Scholar] [CrossRef]
- Fuentes, J.J.; Crowley, J.W.; Dasgupta, R.; Mitrovica, J.X. The Influence of Plate Tectonic Style on Melt Production and CO2 Outgassing Flux at Mid-Ocean Ridges. Earth Planet. Sci. Lett. 2019, 511, 154–163. [Google Scholar] [CrossRef]
- Murphy, K.R.; Inglis, A.R.; Sibeck, D.G.; Watt, C.E.J.; Rae, I.J. Inner magnetospheric ULF waves: The occurrence and distribution of broadband and discrete wave activity. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027887. [Google Scholar] [CrossRef]
- Boulesteix, T.; Legrand, D.; Taquet, N.; Coppola, D.; Laiolo, M.; Valade, S.; Massimetti, F.; Caballero-Jiménez, G.; Campion, R. Modulation of Popocatépetl’s activity by regional and worldwide earthquakes. Bull Volcanol. 2022, 84, 80. [Google Scholar] [CrossRef]
- Walter, T.R.; Wang, R.; Zimmer, M.; Grosser, H.; Lühr, B.; Ratdomopurbo, A. Volcanic activity influenced by tectonic earthquakes: Static and dynamic stress triggering at Mt. Merapi. Geophys. Res. Lett. 2007, 34, L05304. [Google Scholar] [CrossRef]
- Kotsarenko, A.; Yutsis, V.; Grimalsky, V.; Koshevaya, S.; Kotsarenko, Y. Geophysical anomalies in the area of volcano Popocatepetl area, Mexico. Geofísica Int. 2019, 58, 101–111. [Google Scholar] [CrossRef]
- Yutsis, V.; Kotsarenko, A.; Grimalsky, V.; Pulinets, S. On the Radon-Related Mechanism of the Seismo- and Volcanogenic Geomagnetic Anomalies: Experiments in Tlamacas Mountain (Volcano Popocatepetl Area) and Electrode Effect Model. Atmosphere 2023, 14, 705. [Google Scholar] [CrossRef]
- Kotsarenko, A.; Yutsis, V.; Grimalsky, V.; Koshevaya, S. Detailed study of Radon spatial anomaly in Tlamacas Mountain area, volcano Popocatepetl, Mexico. Open J. Geol. 2016, 6, 158–164. [Google Scholar] [CrossRef]
- Beroza, G.C.; Segou, M.; Mostafa Mousavi, S. Machine learning and earthquake forecasting—Next steps. Nat. Commun. 2021, 12, 4761. [Google Scholar] [CrossRef]
- Herrmann, M.; Piegari, E.; Marzocchi, W. Revealing the spatiotemporal complexity of the magnitude distribution and b-value during an earthquake sequence. Nat. Commun. 2022, 13, 5087. [Google Scholar] [CrossRef]
- Jordan, T.H.; Chen, Y.-T.; Gasparini, P.; Madariaga, R.; Main, I.; Marzocchi, W.; Papadopoulos, G.; Sobolev, G.; Yamaoka, K.; Zschau, J. Operational Earthquake Forecasting. State of Knowledge and Guidelines for Utilization. Ann. Geophys. 2011, 54, 315–391. [Google Scholar] [CrossRef]
- Panza, G.F.; Bela, J. NDSHA: A new paradigm for reliable seismic hazard assessment. Eng. Geol. 2020, 275, 105403. [Google Scholar] [CrossRef]
- Chung, A.I.; Meier, M.A.; Andrews, J.; Böse, M.; Crowell, B.W.; McGuire, J.J.; Smith, D.E. Shake Alert Earthquake Early Warning System Performance during the 2019 Ridgecrest Earthquake Sequence. Bull. Seismol. Soc. Am. 2020, 110, 1904–1923. [Google Scholar] [CrossRef]
- Peng, C.; Jiang, P.; Ma, Q.; Su, J.; Cai, Y.; Zheng, Y. Chinese Nationwide Earthquake Early Warning System and Its Performance in the 2022 Lushan M6.1 Earthquake. Remote Sens. 2022, 14, 4269. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D.; Karelin, A.; Boyarchuk, K. Earthquake Precursors in the Atmosphere and Ionosphere: New Concepts; Springer: Dordrecht, The Netherlands, 2022; ISBN 978-94-024-2170-5. [Google Scholar]
- Segou, M.; Parsons, T. A new technique to calculate earthquake stress transfer and to probe the physics of aftershocks. Bull. Seismol. Soc. Am. 2020, 110, 863–873. [Google Scholar] [CrossRef]
- Shcherbakov, R.; Zhuang, J.; Zöller, G.; Ogata, Y. Forecasting the magnitude of the largest expected earthquake. Nat. Commun. 2019, 10, 4051. [Google Scholar] [CrossRef] [PubMed]
- King, C.-H.; King, B.-S.; Evans, W.C. Spatial Radon anomalies on active faults in California. Appl. Geochem. 1996, 11, 497–510. [Google Scholar] [CrossRef]
- Neri, M.; Ferrera, E.; Giammanco, S.; Currenti, G.; Cirrincione, R.; Patanè, G.; Zanon, V. Soil radon measurements as a potential tracer of tectonic and volcanic activity. Sci. Rep. 2016, 6, 24581. [Google Scholar] [CrossRef]
- Cigolini, C.; Laiolo, M.; Ulivieri, G.; Coppola, D.; Ripepe, M. Radon mapping, automatic measurements and extremely high 222Rn emissions during the 2002–2007 eruptive scenarios at Stromboli volcano. J. Volcanol. Geotherm. Res. 2013, 256, 49–65. [Google Scholar] [CrossRef]
- Taquet, N.; Stremme, W.; Grutter, M.; Baylón, J.; Bezanilla, A.; Schiavo, B.; Rivera, C.; Campion, R.; Boulesteix, T.; Nieto-Torres, A.; et al. Variability in the gas composition of the Popocatépetl volcanic plume. Front. Earth Sci. 2019, 7, 114. [Google Scholar] [CrossRef]
- Immè, G.; La Delfa, S.; Lo Nigro, S.; Morelli, D.; Patane, G. Gas Radon emission related to geodynamic activity of Mt. Etna. Ann. Geophys. 2005, 48, 65–71. [Google Scholar] [CrossRef]
- Bonforte, A.; Federico, C.; Giammanco, S.; Guglielmino, F.; Liuzzo, M.; Neri, M. Soil gases and SAR data reveal hidden faults on the sliding flank of Mt. Etna (Italy). J. Volcanol. Geotherm. Res. 2013, 251, 27–40. [Google Scholar] [CrossRef]
- Richon, P.; Klinger, Y.; Tapponnier, P.; Li, C.-X.; Van Der Woerd, J.; Perrier, F. Measuring radon flux across active faults: Relevance of excavating and possibility of satellite discharges. Radiat. Meas. 2010, 45, 211–218. [Google Scholar] [CrossRef]
- Richon, P.; Sabroux, J.-C.; Halbwachs, M.; Vandemeulebrouck, J.; Poussielgue, N.; Tabbagh, J.; Punongbayan, R. Radon anomaly in the soil of Taal volcano, the Philippines: A likely precursor of the M 7.1 Mindoro earthquake (1994). Geophys. Res. Lett. 2003, 30, 1–4. [Google Scholar] [CrossRef]
- Patiris, D.; Tsabaris, C.; Livanou, K.; Roumelioti, S.K.; Alexakis, S. Atmospheric in situ gamma-ray spectrometry for precipitation investigation. Acta Geophys. 2023, 71, 2517–2533. [Google Scholar] [CrossRef]
- Surkov, V.V.; Molchanov, O.A.; Hayakawa, M. Pre-earthquake ULF electromagnetic perturbations as a result of inductive seismomagnetic phenomena during microfracturing. J. Atmos. Sol. -Terr. Phys. 2003, 65, 31–46. [Google Scholar] [CrossRef]
- Surkov, V.V.; Hayakawa, M. ULF geomagnetic perturbations due to seismic noise produced by rock fracture and crack formation treated as a stochastic process. Phys. Chem. Earth Parts A/B/C 2006, 31, 273–280. [Google Scholar] [CrossRef]
- Surkov, V.V.; Hayakawa, M. Ultra and Extremely Low Frequency Electromagnetic Fields; Springer: Tokyo, Japan; Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2014; p. 495. ISBN 978-4-431-54367-1. (eBook). [Google Scholar] [CrossRef]
- Elkington, S.R. A review of ULF interactions with radiation belt electrons. In Magnetospheric ULF Waves: Synthesis and New Directions; Takahashi, K., Chi, P.J., Denton, R., Lysak, R.L., Eds.; American Geophysical Union: Washington, DC, USA, 2013; pp. 177–193. [Google Scholar] [CrossRef]
- Mann, I.R.; Murphy, K.R.; Ozeke, L.G.; Rae, I.J.; Milling, D.K.; Kale, A.A.; Honary, F.F. The role of ultralow frequency wave in radiation belt dynamics. In Dynamics of the Earth’s Radiation Belts and Inner Magnetosphere; Summers, D., Mann, I.R., Baker, D.N., Schulz, M., Eds.; American Geophysical Union: Washington, DC, USA, 2013; pp. 69–92. [Google Scholar] [CrossRef]
- McPherron, R.L. Magnetic pulsations: Their sources and relation to solar wind and geomagnetic activity. Surv. Geophys. 2005, 26, 545–592. [Google Scholar] [CrossRef]
- Menk, F.W. Magnetospheric ULF waves: A review. In The Dynamic Magnetosphere; IAGA Special Sopron Book Series; Liu, W., Fujimoto, M., Eds.; Springer: Dordrecht, The Netherlands, 2011; Volume 3, pp. 223–256. [Google Scholar] [CrossRef]
- Takahashi, K. ULF waves in the inner magnetosphere. In Low-Frequency Waves in Space Plasmas; Keiling, A., Lee, D.-H., Nakariakov, V., Eds.; John Wiley: Hoboken, NJ, USA, 2016; pp. 51–63. [Google Scholar] [CrossRef]
- Ozeke, L.G.; Mann, I.R.; Murphy, K.R.; Rae, I.J.; Milling, D.K. Analytic expressions for ULF wave radiation belt radial diffusion coefficients. J. Geophys. Res. Space Phys. 2014, 119, 1587–1605. [Google Scholar] [CrossRef]
- Bentley, S.N.; Watt CE, J.; Owens, M.J.; Rae, I.J. ULF wave activity in the magnetosphere: Resolving solar wind interdependencies to identify driving mechanisms. J. Geophys. Res. Space Phys. 2018, 123, 2745–2771. [Google Scholar] [CrossRef]
- Huang, C.-S. Systematical analyses of global ionospheric disturbance current systems caused by multiple processes: Penetration electric fields, solar wind pressure impulses, magnetospheric substorms, and ULF waves. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027942. [Google Scholar] [CrossRef]
- Zhang, X.-J.; Angelopoulos, V.; Artemyev, A.V.; Hartinger, M.D.; Bortnik, J. Modulation of whistler waves by ultra-low-frequency perturbations: The importance of magnetopause location. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028334. [Google Scholar] [CrossRef]
- Aranda-Gómez, J.J.; Carranza Castañeda, O.; Wang, X.; Tseng, Z.J.; Pacheco-Castro, A. Notes on the origin of extensive endorheic regions in central and northern Mexico, and some implications for paleozoogeography. J. South Am. Earth Sci. 2018, 83, 55–67. [Google Scholar] [CrossRef]
- Aranda-Gómez, J.J.; Luhr, J.F.; Housh, T.; Valdez-Moreno, G.; Chávez-Cabello, G. Late-Cenozoic intraplate-type volcanism in central and northern México: A review. In Geology of Mexico: Celebrating the Centenary of the Geological Society of Mexico; Alaniz-Álvarez, S.A., Nieto-Samaniego, A.F., Eds.; Geological Society of America Special Paper: Boulder, CO, USA, 2007; Volume 422, pp. 93–128. [Google Scholar] [CrossRef]
- Ferrari, L.; Orozco-Esquivel, T.; Manea, V.; Manea, M. The dynamic history of the Trans-Mexican Volcanic Belt and the Mexico subduction zone. Tectonophysics 2012, 522–523, 122–149. [Google Scholar] [CrossRef]
- Alanís-Álvarez, S.A.; Nieto-Samaniego, A.F.; Ferrari, L. Effects of strain rate in the distribution of monogenetic and polygenetic volcanism in the Trans-Mexican Volcanic Belt. Geology 1998, 26, 591–594. [Google Scholar] [CrossRef]
- Gómez-Tuena, A.; Orozco-Esquivel, T.; Ferrari, L. Igneous petrogenesis of the trans-Mexican volcanic belt. In Geology of Mexico: Celebrating the Centenary of the Geological Society of México; Alaniz-Alvarez, S.A., Nieto-Samaniego, A.F., Eds.; Geological Society of America Special Paper: Boulder, CO, USA, 2007; Volume 422, pp. 1–53. [Google Scholar] [CrossRef]
- Martin-Del Pozzo, A.L. Precursors to eruptions of Popocatépetl Volcano, Mexico. Geofis. Intl. 2012, 51, 87–107. [Google Scholar] [CrossRef]
- Martin Del Pozzo, A.L.; Alatorre Ibargüengoitia, M.; Arana Salinas, L.; Bonasia, R.; Capra Pedol, L.; Cassata, W.; Córdoba, G.; Cortés Ramos, J.; Delgado Granados, H.; Ferrés López, M.D.; et al. Estudios geológicos y actualización del mapa de peligros del volcán Popocatépetl. In Memoria Técnica del Mapa de Peligros del Volcán Popocatépetl; Jaime, Y.V., Ed.; Universidad Nacional Autónoma de México, Instituto de Geofísica: Mexico City, Mexico, 2018; p. 167. ISBN 978-607-02-9782-3. [Google Scholar]
- Espinasa-Pereña, R.; Martin-Del Pozzo, A.L. Morphostratigraphic Evolution of Popocatépetl Volcano, México; Special Paper of the Geological Society of America: Boulder, CO, USA, 2006; Volume 402, pp. 115–137. [Google Scholar] [CrossRef]
- Arango-Galván, C.; Martin-Del Pozzo, A.L.; Flores-Márquez, E.L.; González-Morán, T.; Vidal-Amaro, M.; Ruiz-Aguilar, D. Unraveling the complex structure of Popocatepetl volcano (Central Mexico): New evidence for collapse features and active faulting inferred from geophysical data. J. Volcanol. Geotherm. Res. 2020, 407, 107091. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis. NOAA Technical Memorandum NESDIS NGDC-24; National Geophysical Data Center: Boulder, CO, USA, 2009; p. 19. Available online: http://www.ngdc.noaa.gov/mgg/global/global.html (accessed on 15 October 2023).
- Macías, J.L. Geology and eruptive history of some active volcanoes of México. Boletín De La Soc. Geológica Mex. 2005, 57, 379–424. [Google Scholar] [CrossRef]
- Siebe, C.; Salinas, S.; Arana-Salinas, L.; Macías, J.L.; Gardnerd, L.; Bonasia, R. The ~23,500 y14C BP White Pumice Plinian eruption and associated debris avalanche and Tochimilco lava flow of Popocatépetl volcano, México. J. Volcanol. Geotherm. Res. 2017, 333–334, 66–95. [Google Scholar] [CrossRef]
- Siebe, C.; Abrams, M.; Macías, J.L.; Obenholzner, J. Repeated volcanic disasters in Prehispanic time at Popocatépetl, Central Mexico: Past key to the future? Geology 1996, 24, 399–402. [Google Scholar] [CrossRef]
- Macías-Vázquez, J.L.; Carrasco-Núñez, G.; Delgado-Granados, H.; Martin-del Pozzo, A.L.; Siebe-Grabach, C.; Hoblitt, R.P.; Sheridan, M.F.; Tilling, R.I.; Bonifaz, R.; Cabrera, A.L.; et al. Mapa de Peligros del Volcán Popocatépetl, Escala 1:250,000: México, D.F.; Universidad Nacional Autónoma de México, Instituto de Geofísica: México City, Mexico, 1995. [Google Scholar]
- Boudal, C.; Robin, C. Volcan Popocatepetl: Recent Eruptive History, and Potential Hazards and Risks in Future Eruptions. In Volcanic Hazards (IAVCEI Proceedings in Volcanology 1); Latter, J.H., Ed.; Springer: Berlin/Heidelberg, Germany, 1989; Available online: https://link.springer.com/content/pdf/10.1007/978-3-642-73759-6_6.pdf (accessed on 15 October 2023).
- GOCE Global Gravity Field Models and Grids. Available online: www.esa.int/Applications/Observing_the_Earth/FutureEO/GOCE (accessed on 15 October 2023).
- Hirt, C.; Claessens, S.J.; Fecher, T.; Kuhn, M.; Pail, R.; Rexer, M. New ultrahigh-resolution picture of Earth’s gravity field. Geophys. Res. Lett. 2013, 40, 4279–4283. [Google Scholar] [CrossRef]
- Bonvalot, S.; Balmino, G.; Briais, A.; Kuhn, M.; Peyrefitte, A.; Vales, N.; Biancale, R.; Gabalda, G.; Reinquin, F.; Sarrailh, M. World Gravity Map; Commission for the Geological Map of the World, Ed.; BGI-CGMW-CNES-IRD: Paris, France, 2012. [Google Scholar]
- Hinze, W.J.; Aiken, C.; Brozena, J.; Coakley, B.; Dater, D.; Flanagan, G.; Forsberg, R.; Hildebrand, T.; Keller, G.R.; Kellogg, J. New standards for reducing gravity data: The North American gravity database. Geophysics 2005, 70, J25–J32. [Google Scholar] [CrossRef]
- Magnetic Anomaly Map of North America. Available online: https://www.usgs.gov/maps/magnetic-anomaly-map-north-america (accessed on 15 October 2023).
- Balmino, G.; Vales, N.; Bonvalot, S.; Briais, A. Spherical harmonic modeling to ultra-high degree of Bouguer and isostatic anomalies. J. Geod. 2012, 86, 499–520. [Google Scholar] [CrossRef]
- McNutt, M. Gravity and isostasy. In Geophysics. Encyclopedia of Earth Science; Springer: Boston, MA, USA, 1989. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) Model—An Unified Concept for Earthquake Precursors Validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Pulinets, S.; Budnikov, P.; Karelin, A.; Žalohar, J. Thermodynamic instability of the atmospheric boundary layer stimulated by tectonic and seismic activity. J. Atmos. Sol. -Terr. Phys. 2023, 246, 106050. [Google Scholar] [CrossRef]
- Pulinets, S.; Budnikov, P. Atmosphere Critical Processes Sensing with ACP. Atmosphere 2022, 13, 1920. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D.; Davidenko, D.; Petrukhin, A. Multiparameter monitoring of short-term earthquake precursors and its physical basis. Implement. Kamchatka Reg. E3S Web Conf. 2016, 11, 00019. [Google Scholar] [CrossRef]
- Khrenov, A.P.; Pieri, D.; Blinkov, A.N.; Zaitsev, A.N.; Shkarin, V.E. Aerospace studies of the active volcanoes of Kamchatka in 1993–1996. Mod. Probl. Remote Sens. Earth Space 1999, 6, 70–82. (In Russian) [Google Scholar]
- Chi, P.J.; Engebretson, M.J.; Moldwin, M.B.; Russell, C.T.; Mann, I.R.; Samson, J.C.; López Cruz-Abeyro, J.A.; Yumoto, K.; Lee, D.H. Mid-Continent Magnetoseismic Chain (McMAC): A Meridional Magnetometer Chain for Magnetospheric Sounding. In Proceedings of the Enviroment Modeling Workshop, Snowmass, CO, USA, 17–22 June 2005. [Google Scholar]
- Kotsarenko, A.; Pérez Enríquez, R.; López Cruz-Abeyro, J.A.; Koshevaya, S.; Grimalsky, V.; Yutsis, V.; Kremenetsky, I. ULF geomagnetic anomalies of possible seismogenic origin observed at Teoloyucan station, México, in 1999–2001: Intermediate and short-time analysis. Tectonophysics 2007, 431, 249–262. [Google Scholar] [CrossRef]
- Helman, D.S. Earth Electricity: A Review of Mechanisms Which Cause Telluric Currents in the Lithosphere. Ann. Geophys. 2013, 56, G0564. [Google Scholar] [CrossRef]
- Guglielmi, A.V.; Pokhotelov, O.A. Geoelectromagnetic Waves; IOP Publishing: Bristol, UK, 1996. [Google Scholar]
- Sedunov, Y.S. (Ed.) Atmosphere. In Handbook; Gidrometeoizdat: Leningrad, Russia, 1991. (In Russian) [Google Scholar]
- Trakhtengerts, V.Y.; Iudin, D.I. Actual Problems of Thundercloud Electrodynamics. In Sprites, Elves and Intense Lightning Discharges; Füllekrug, M., Mareev, E.A., Rycroft, M.J., Eds.; NATO Science Series, II; Mathematics, Physics and Chemistry; Springer: Dordrecht, The Netherlands, 2006; Volume 225, pp. 341–376. [Google Scholar]
- Dwyer, J.R.; Uman, M.A. The physics of lightning. Phys. Rep. 2014, 534, 147–241. [Google Scholar] [CrossRef]
- Rakov, V.A.; Uman, M.A. Lightning: Physics and Effects; Cambridge University Press: Cambridge, UK, 2003; p. 687. [Google Scholar] [CrossRef]
- Wilson, L.; Lane, S.J.; Gilbert, J.S.; Mather, T.A.; Harrison, R.G.; Martin, R.S.; James, M.R. Electrical Charging of Volcanic Plumes. In Planetary Atmospheric Electricity; Leblanc, F., Aplin, K.L., Yair, Y., Harrison, R.G., Lebreton, J.P., Blanc, M., Eds.; Springer: Berlin, Germany, 2008; pp. 399–418. [Google Scholar]
- Smirnov, B.M. Global Atmospheric Phenomena Involving Water. Water Circulation, Atmospheric Electricity, and the Greenhouse Effect; Springer Atmospheric Sciences: Berlin, Germany, 2020; p. 313. ISSN 2194-5225. (electronic); Available online: https://link.springer.com/book/10.1007/978–3–030-58039-1 (accessed on 15 October 2023).
- Rycroft, M.J. Introduction to the Physics of Sprites, Elves and Intense Lightning Discharges. In Sprites, Elves and Intense Lightning Discharges; Füllekrug, M., Mareev, E.A., Rycroft, M.J., Eds.; NATO Science Series, II; Mathematics, Physics and Chemistry; Springer: Dordrecht, The Netherlands, 2006; Volume 225, pp. 1–18. [Google Scholar]
- Bazelyan, E.M.; Raizer, Y.P. Spark Discharge; CRC Press: Boca Raton, CA, USA, 1998. [Google Scholar]
- Raizer, Y.P. Physics of the Gas Discharge; Intellect Publishing: Dolgoprydnyi, Russia, 2009. (In Russian) [Google Scholar]
- Chalmers, J.A. Atmospheric Electricity; Pergamon Press: New York, NY, USA, 1967. [Google Scholar]
- Rycroft, M.J.; Odzimek, A. Effects of lightning and sprites on the ionospheric potential, and threshold effects on sprite initiation, obtained using an analog model of the global atmospheric electric circuit. J. Geophys. Res. 2010, 115, A00E37. [Google Scholar] [CrossRef]
- Rapoport, Y.; Grimalsky, V.; Krankowski, A.; Pulinets, S.; Fedorenko, A.; Petrishchevskii, S. Algorithm for modeling electromagnetic channel of seismo-ionospheric coupling (SIC) and the variations in the electron concentration. Acta Geophys. 2020, 68, 253–278. [Google Scholar] [CrossRef]
- Cole, R.K., Jr.; Pierce, E.T. Electrification in the Earth’s Atmosphere for Altitudes between 0 and 100 Kilometers. J. Geophys. Res. 1965, 70, 2735–2749. [Google Scholar] [CrossRef]
- Rycroft, M.J.; Harrison, R.G.; Nicoll, K.A.; Mareev, E.A. An Overview of Earth’s Global Electric Circuit and Atmospheric Conductivity. In Planetary Atmospheric Electricity; Leblanc, F., Aplin, K.L., Yair, Y., Harrison, R.G., Lebreton, J.P., Blanc, M., Eds.; Springer: Berlin, Germany, 2008; pp. 83–106. [Google Scholar]
- Johnston, M.J.S. Review of electric and magnetic fields accompanying seismic and volcanic activity. Surv. Geophys. 1997, 18, 441–476. [Google Scholar] [CrossRef]
- Fidani, C.; Orsini, M.; Iezzi, G.; Vicentini, N.; Stoppa, F. Electric and Magnetic Recordings by Chieti CIEN Station During the Intense 2016–2017 Seismic Swarms in Central Italy. Front. Earth Sci. 2020, 8, 536332. [Google Scholar] [CrossRef]
- Kachurin, L.G. Physical Bases of Influence on Atmospheric Processes; Hidrometeoizdat: Leningrad, Russia, 1990; (In Russian). Available online: www.tnu.in.ua/study/books/entry-2699640.html (accessed on 15 October 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).