UAV Network Path Planning and Optimization Using a Vehicle Routing Model
Abstract
1. Introduction
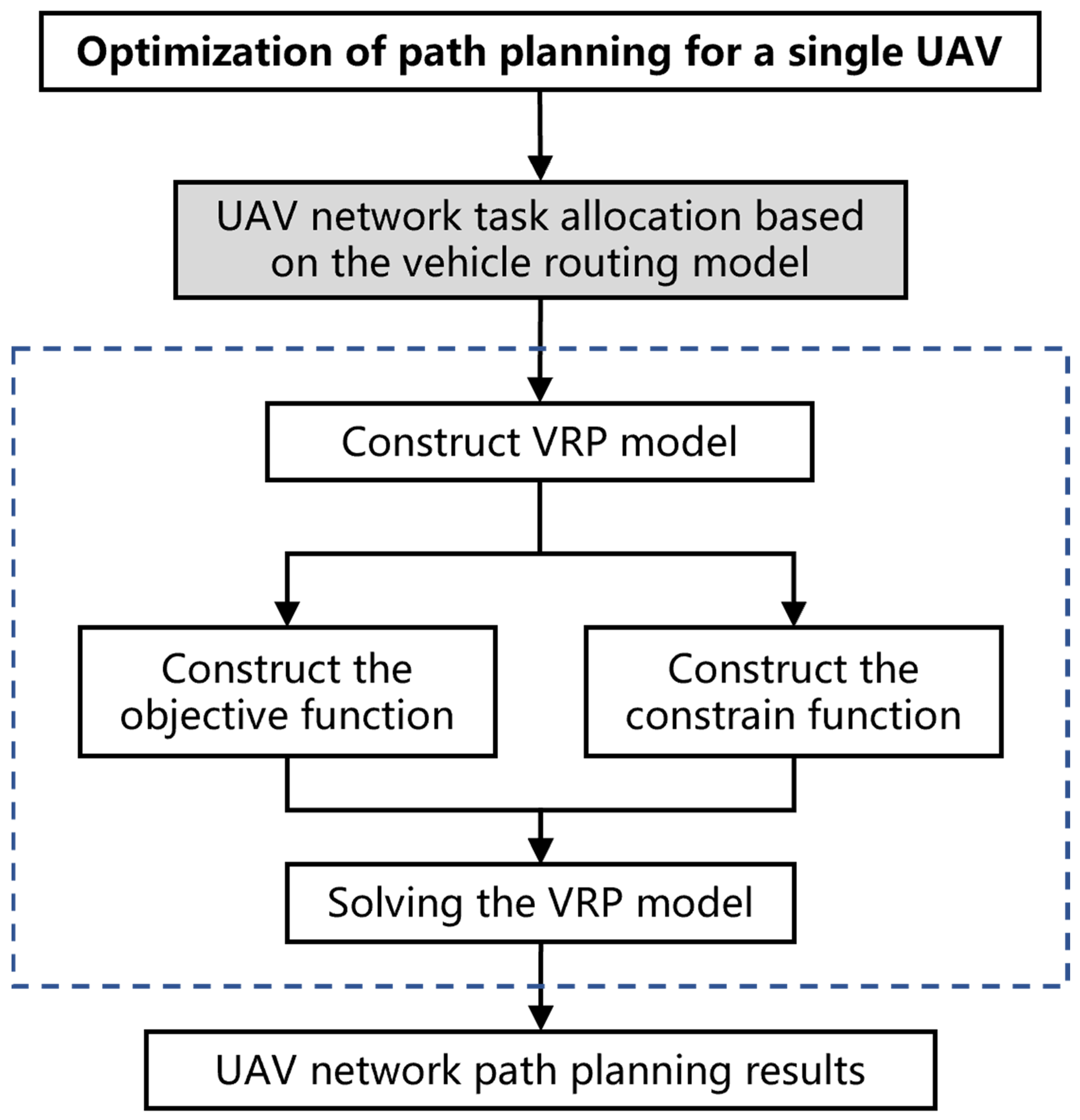
2. Methods
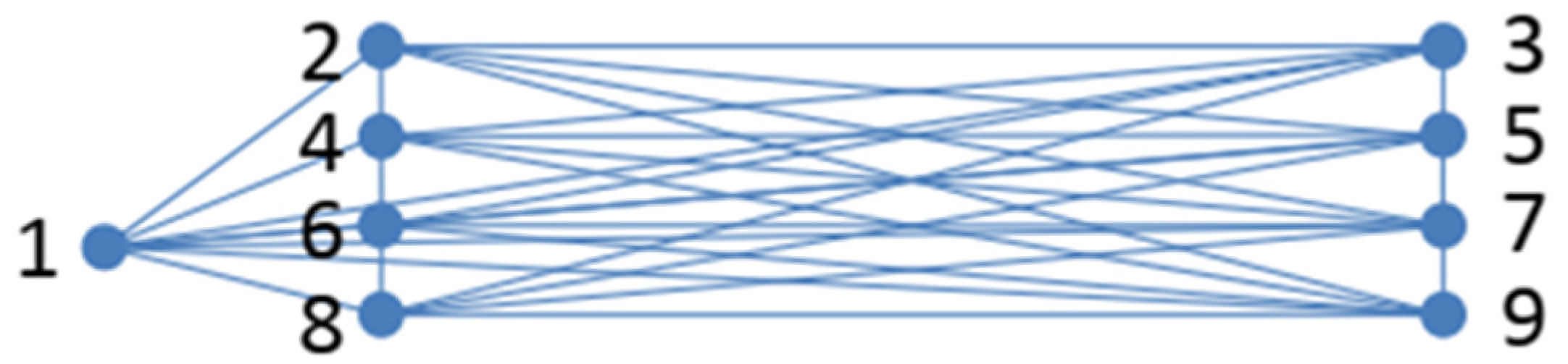
2.1. Problem Definition
2.2. Model Establishment
3. Simulations
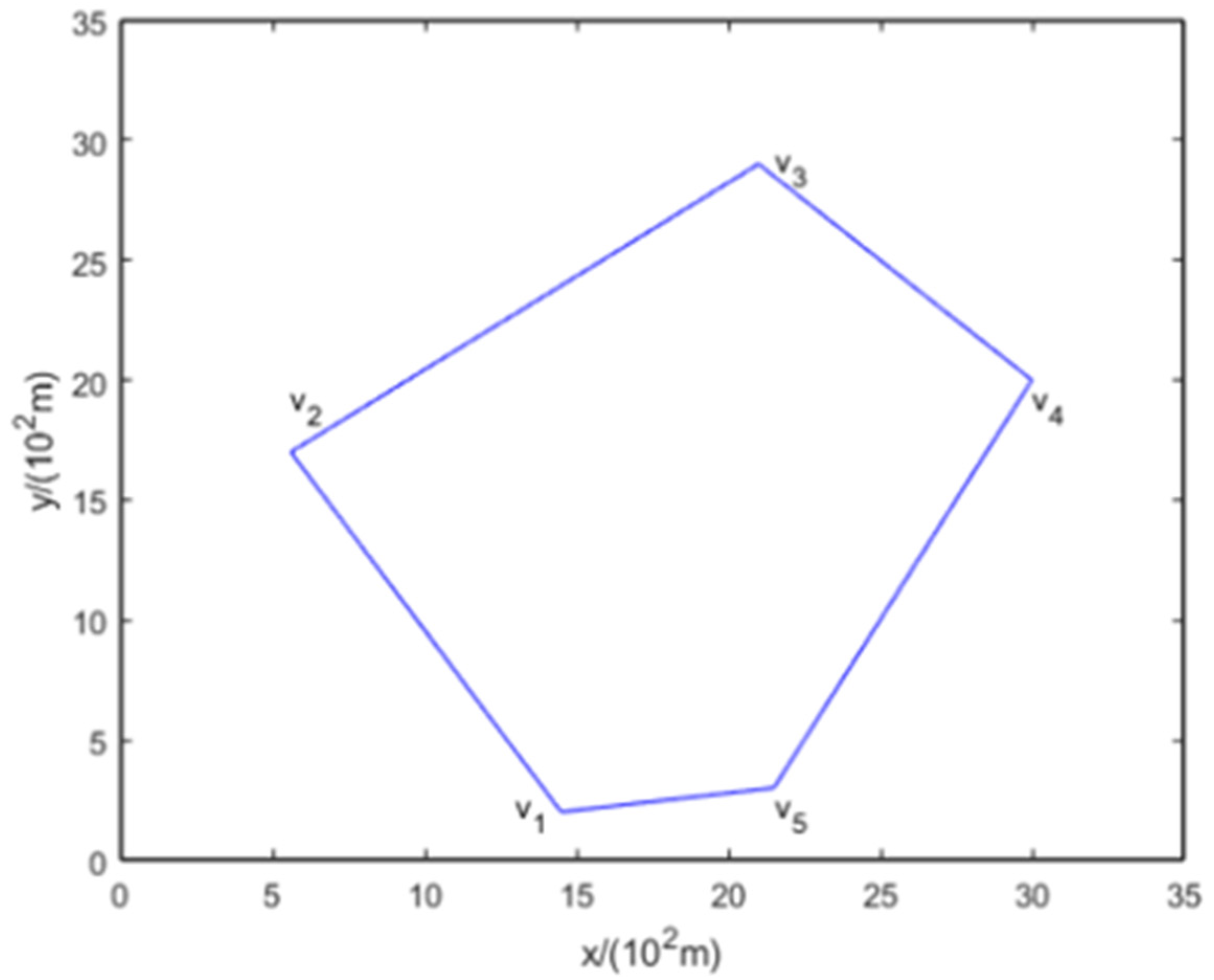
3.1. Observation Area
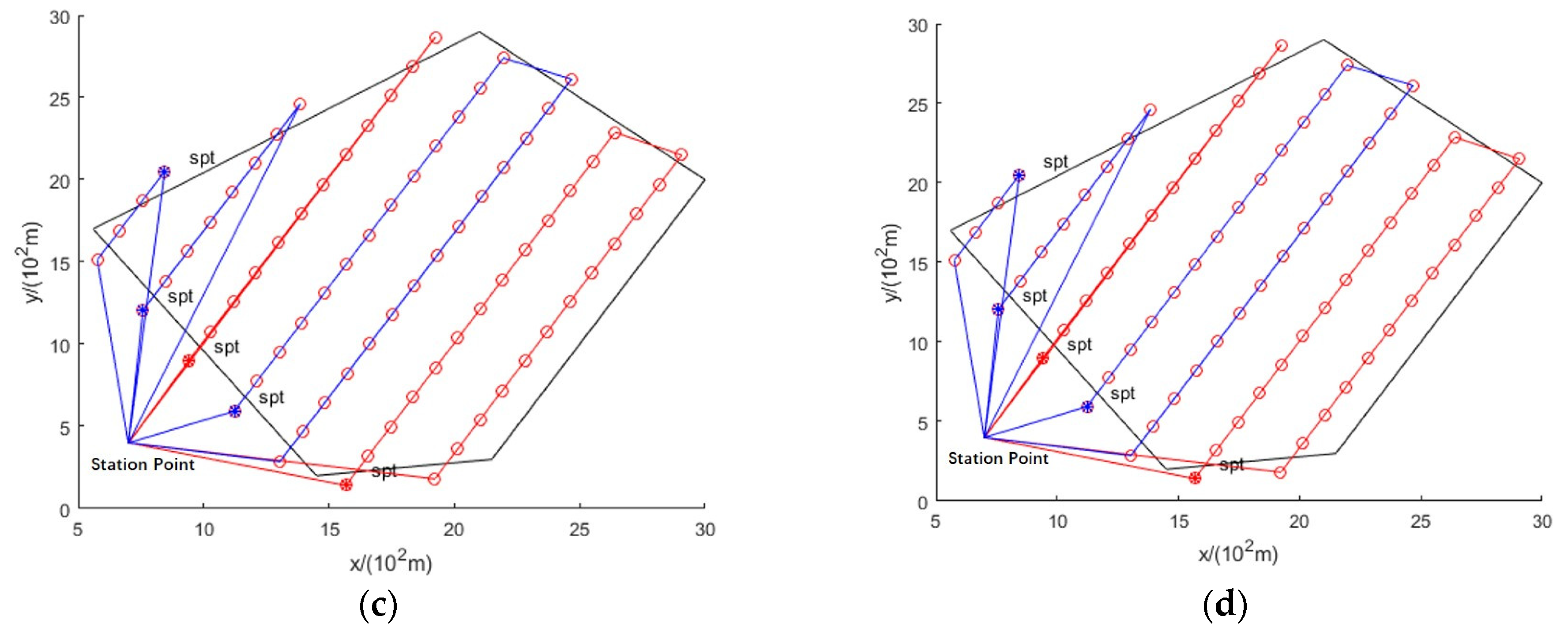
3.2. Simulation Results
- The VRP model-based UAV network path planning algorithm can perform task assignments after optimizing the coverage path of a single UAV, substantially reducing the time for UAV network observations.
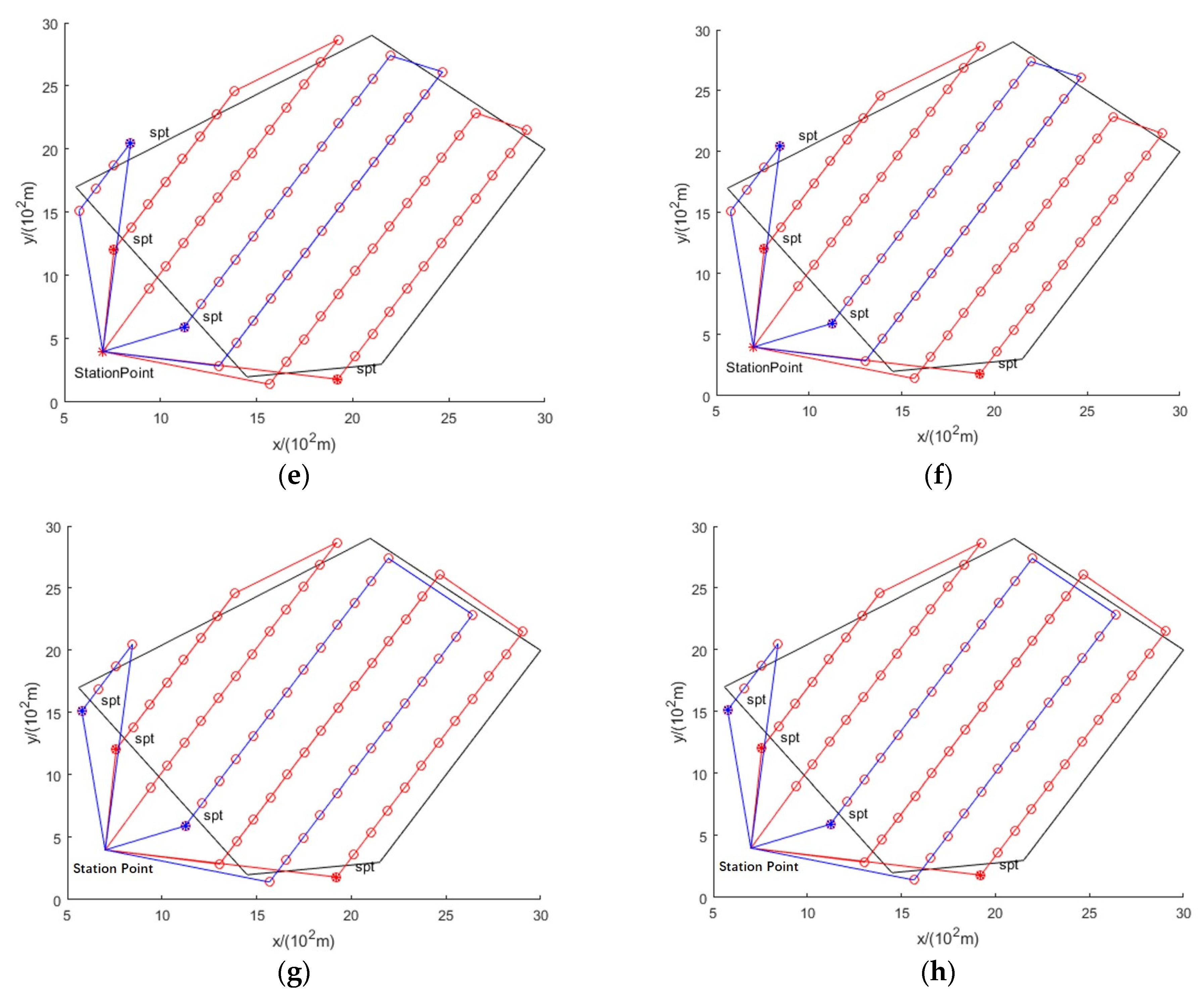
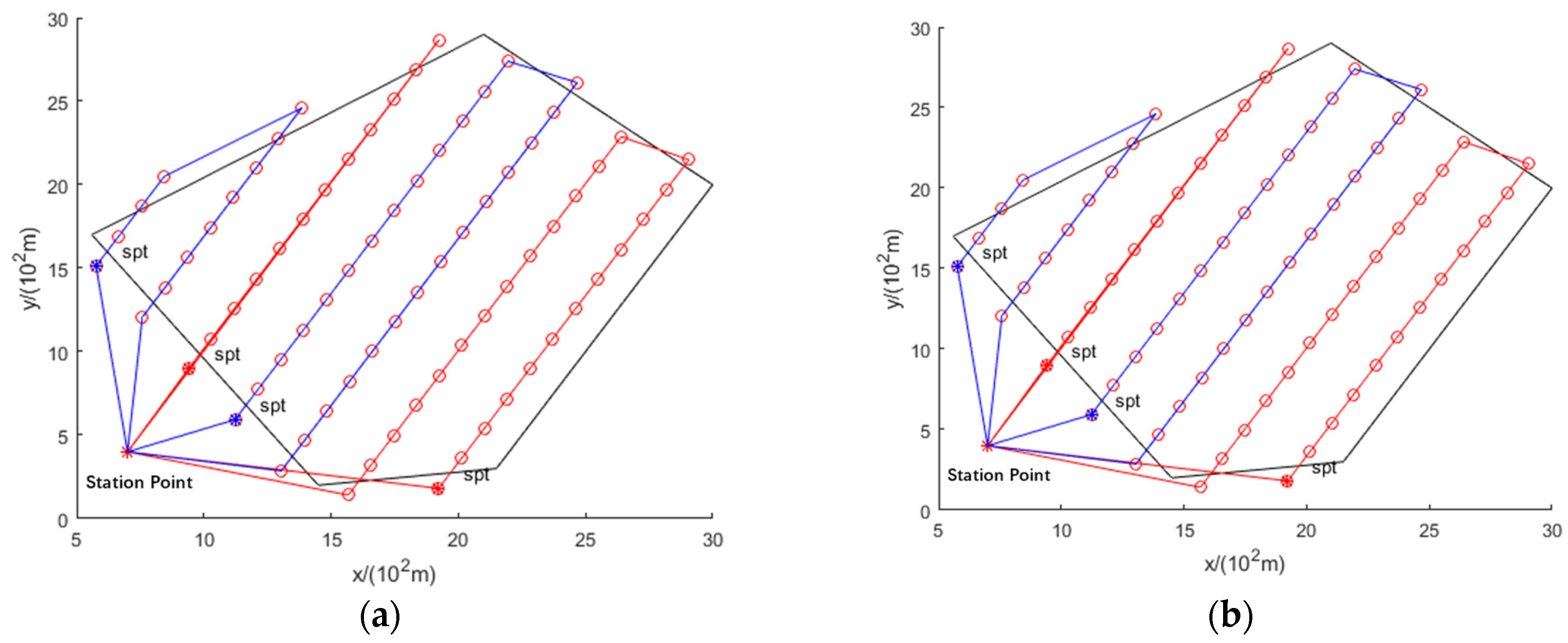
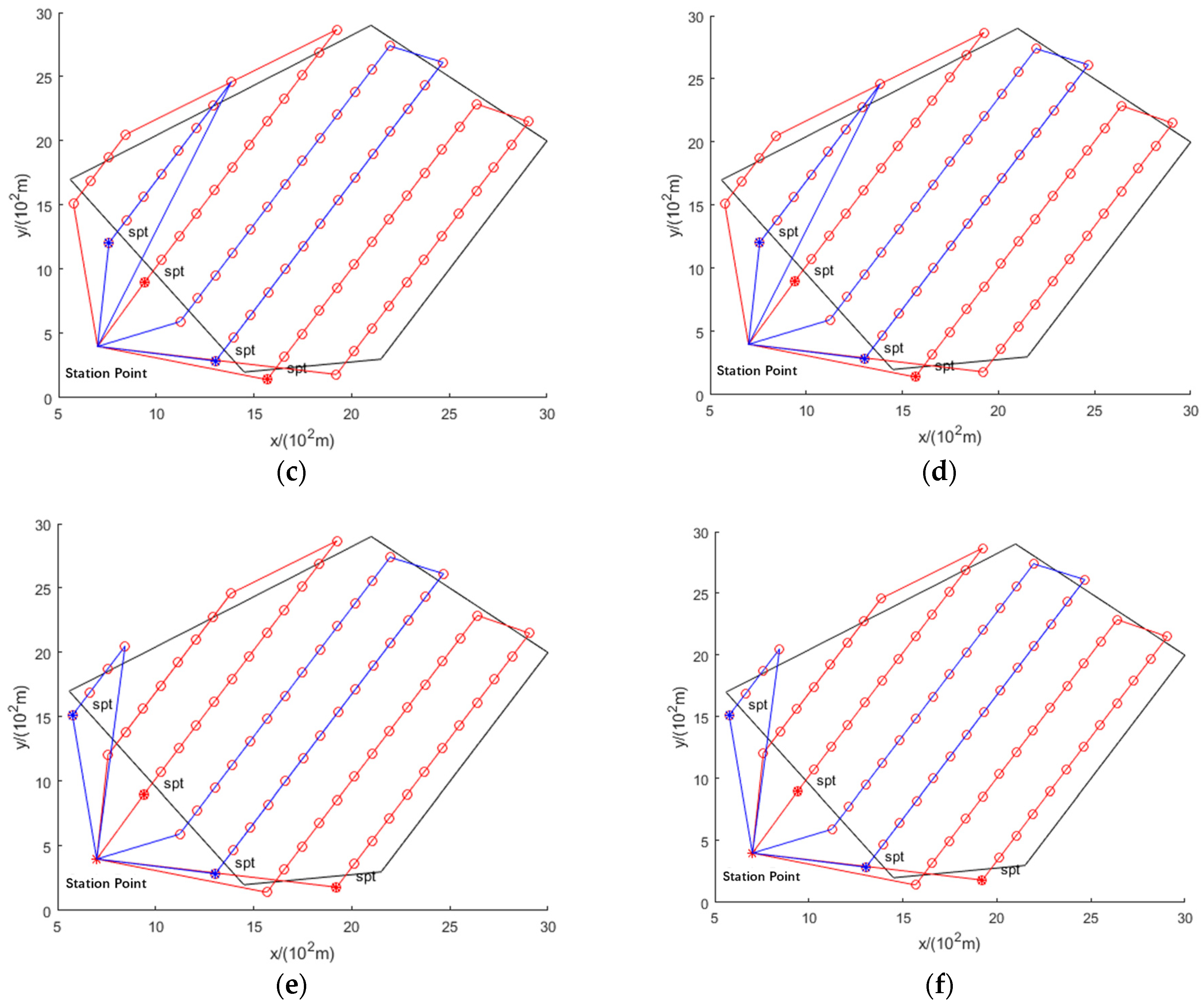
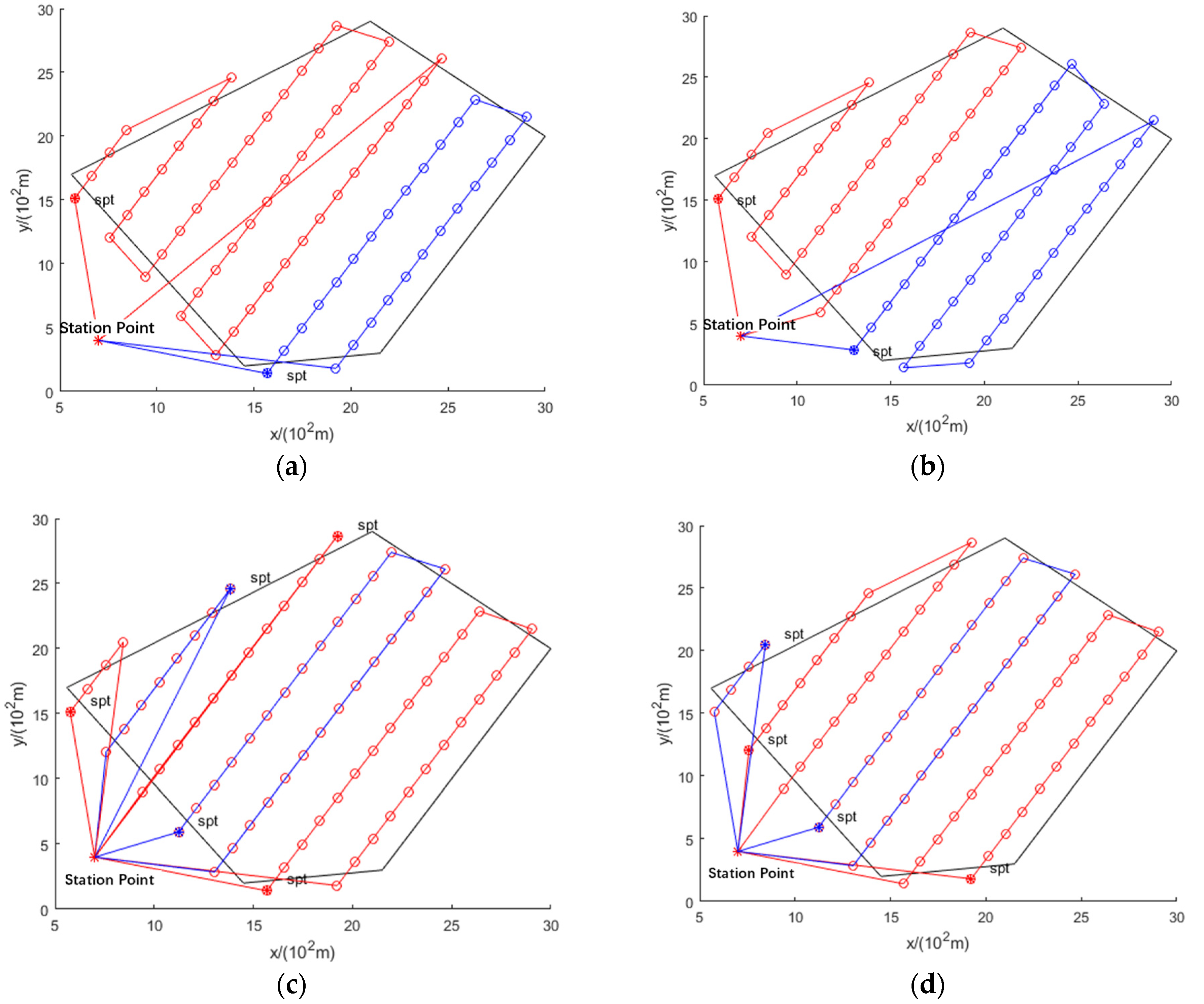
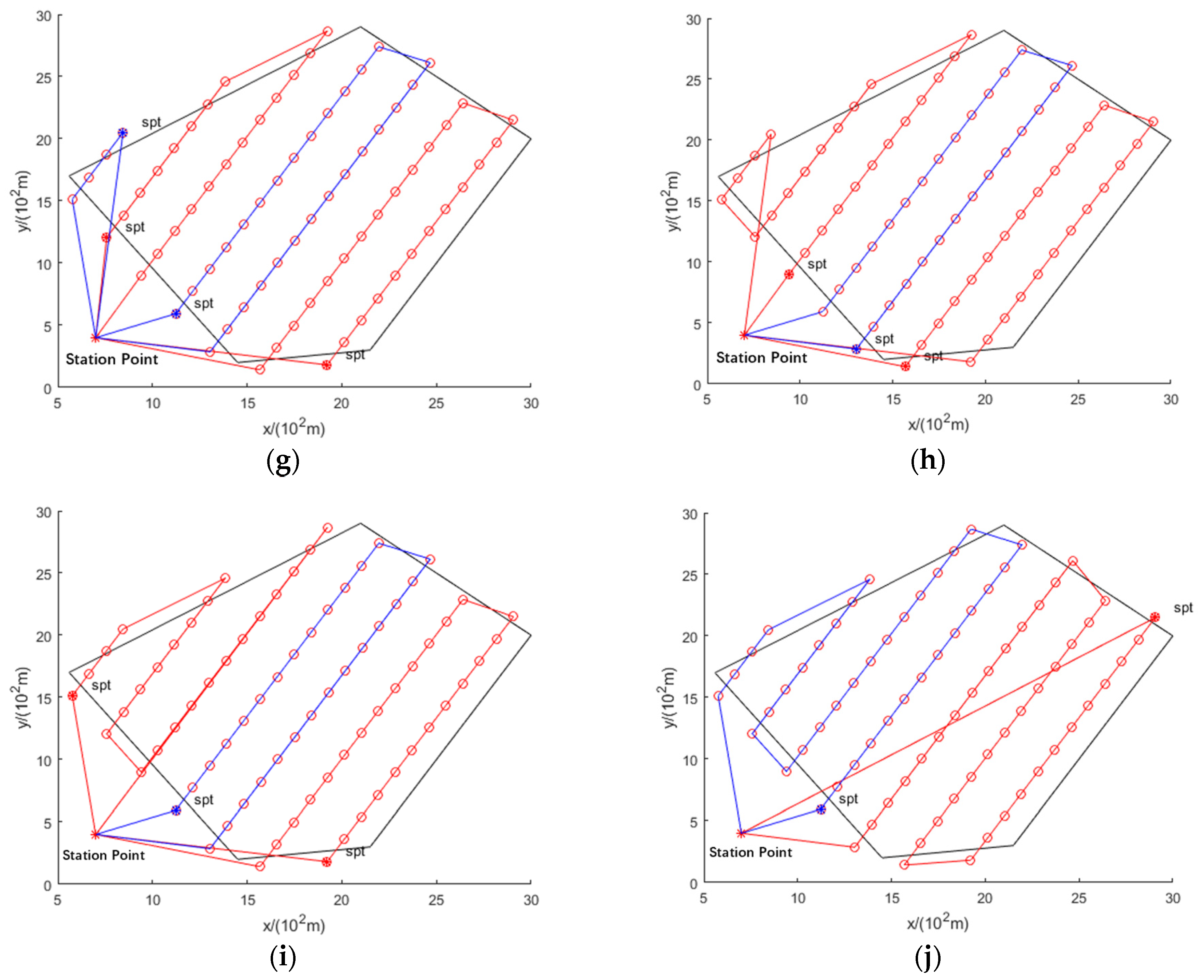
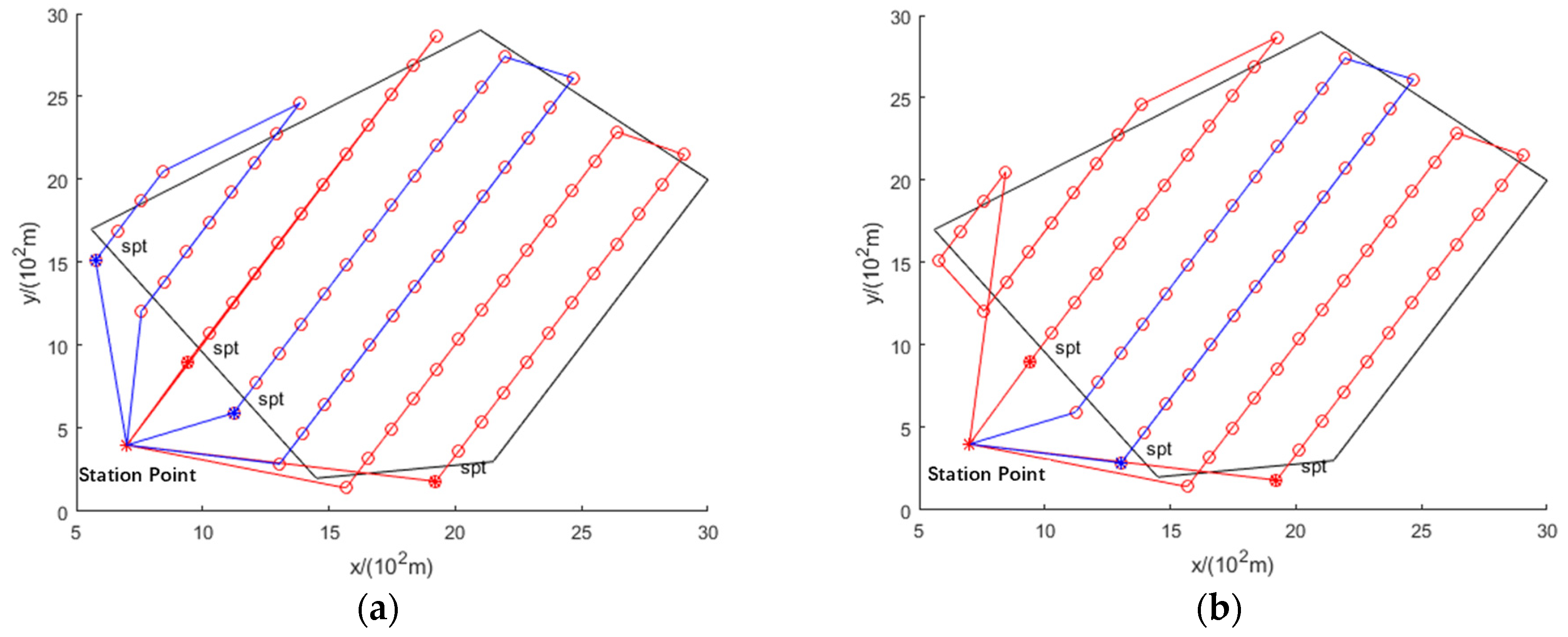
- The proposed method effectively solves the UAV route crossing problem and is superior to the original method. The path planning results of the original method show a route crossing (Figure 4g,h and Figure 5c,d). By adding the constraint function, the optimized path planning results of the proposed method are shown in Figure 5a,b,e,f. The data in Table 1 indicate that the number of UAVs and the observation time are the same for the proposed and original methods, i.e., the proposed method solves the route-crossing problem without increasing the time.
- The preparation time of the UAV affects the result of the network task assignment. As shown in Table 1, the smaller the , the larger the number of UAVs. For instance, at a UAV flight speed of 7.5 km/h, the number of UAVs increased from 4 to 5 when the decreased from 0.2 h to 0.1 h. However, when the flight duration of the UAV was short, did not affect the number of required UAVs significantly. For example, at a flight speed of 6 km/h, the number of required UAVs remained at 4 whether the was 0.1 h or 0.2 h.
- The number of UAVs and the total observation time obtained from the solvers CPLEX and Gurobi are the same using the same method with the same parameters.
4. Discussion
4.1. Comparison of Path Planning Results for Two Task Allocation Goals
4.2. Modification of Objective Function
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bejiga, M.B.; Zeggada, A.; Nouffidj, A.; Melgani, F. A Convolutional Neural Network Approach for Assisting Avalanche Search and Rescue Operations with UAV Imagery. Remote Sens. 2017, 9, 100. [Google Scholar] [CrossRef]
- Chen, Q.J.; He, Y.R.; He, T.; Fu, W. The typhoon disaster analysis emergency response system based on UAV remote sensing technology. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 42, 959–965. [Google Scholar] [CrossRef]
- Hu, J.B.; Zhang, J. Unmanned Aerial Vehicle remote sensing in ecology: Advances and prospects. Acta Ecol. Sin. 2018, 38, 20–30. [Google Scholar]
- Ouamri, M.A.; Oteşteanu, M.-E.; Barb, G.; Gueguen, C. Coverage Analysis and Efficient Placement of Drone-BSs in 5G Networks. Eng. Proc. 2022, 14, 18. [Google Scholar]
- Stacy, N.J.S.; Craig, D.W.; Staromlynska, J.; Smith, R.B. The Global Hawk UAV Australian deployment: Imaging radar sensor modifications and employment for maritime surveillance. Int. Geosci. Remote Sens. Symp. (IGARSS) 2002, 2, 699–701. [Google Scholar]
- Zhu, H.L.; Huang, Y.W.; Li, Y.C.; Yu, F.; Tu, T.S.; Wang, W.; Zhang, Y.P.; Li, J.L.; Luo, Y.Z. Diversity of Plant Community in Flood Land of Henan Section of the Lower Yellow River based on Unmanned Aerial Vehicle Remote Sensing. Wetl. Sci. 2021, 19, 17–26. [Google Scholar]
- Rao, X.F.; Zhou, L.Y.; Yang, C.L.; Liao, S.P.; Li, X.K.; Liu, S.S. Counting Cigar Tobacco Plants from UAV Multispectral Images via Key Points Detection Approach. Trans. Chin. Soc. Agric. Mach. 2023, 54, 266–273. [Google Scholar]
- Kuai, Y.; Wang, B.; Wu, Y.L.; Chen, B.T.; Chen, X.D.; Xue, W.B. Urban Vegetation Classification based on Multi-scale Feature Perception Network for UAV Images. J. Geo-Inf. Sci. 2022, 24, 962–980. [Google Scholar]
- Wang, K.; Yang, P.; Lv, W.S.; Zhu, L.Y.; Yu, G.M. Current status and development trend of UAV remote sensing applications in the mining industry. Chin. J. Eng. 2020, 42, 1085–1095. [Google Scholar]
- Zheng, L.; Dong, W.Y.; Yuan, B.C. Application of UAV Remote Sensing in Overseas Highway Reconnaissance. Bull. Surv. Mapp. 2017, 7, 81–84. [Google Scholar]
- Wang, E.L.; Hu, S.B.; Han, H.W.; Liu, C.Q. Research on ice concentration in Heilong River based on the UAV low-altitude remote sensing and OTSU algorithm. J. Hydraul. Eng. 2022, 53, 68–77. [Google Scholar]
- Levenson, E.S.; Fonstad, M.A. Characterizing coarse sediment grain size variability along the upper Sandy River, Oregon, via UAV remote sensing. Geomorphology 2022, 417, 108447. [Google Scholar] [CrossRef]
- Yang, Z.; Yu, X.; Dedman, S.; Rosso, M.; Zhu, J.; Yang, J.; Xia, Y.; Tian, Y.; Zhang, G.; Wang, J. UAV remote sensing applications in marine monitoring: Knowledge visualization and review. Sci. Total Environ. 2022, 838, 155939. [Google Scholar] [CrossRef] [PubMed]
- Miura, N.; Saito, H.; Hada, T. Drone Remote Sensing for the Controlled Capture of Sika Deer (cervus Nippon): Case Study in Village of Yamanakako. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2022, XLIII-B3-2022, 927–932. [Google Scholar] [CrossRef]
- Aristizábal-Botero, Á.; Páez-Pérez, D.; Realpe, E.; Vanschoenwinkel, B. Mapping microhabitat structure and connectivity on a tropical inselberg using UAV remote sensing. Prog. Phys. Geogr. Earth Environ. 2021, 45, 427–445. [Google Scholar] [CrossRef]
- Wang, M.; Yang, L.; Sun, D.; Zhao, H.; Wu, Y. Design and Implementation of Flight Path Planning for Low-altitude Photogrammetry UAV. Geomat. Spat. Inf. Technol. 2016, 39, 110–113. [Google Scholar]
- Wang, Z.L.; Luo, D.L.; Wu, S.X. A method of UAV track planning for the concave polygon area covering. Aero Weapon. 2019, 26, 95–100. [Google Scholar]
- Coombes, M.; Fletcher, T.P.; Chen, W.; Liu, C. Optimal polygon decomposition for UAV survey coverage path planning in wind. Sensors 2018, 18, 2132. [Google Scholar] [CrossRef]
- Shen, F.Q. Automatic UAV Route Planning Method Based on Three Dimention Surface Mode; Southwest Jiaotong University: Chengdu, China, 2015. [Google Scholar]
- Yan, L.; Liao, X.H.; Zhou, C.H.; Fan, B.K.; Gong, J.Y.; Cui, P.; Zheng, Y.Q.; Tan, X. The impact of UAV remote sensing technology on the industrial development of China: A review. J. Geo-Inf. Sci. 2019, 21, 476–495. [Google Scholar]
- Peng, H.; Shen, L.C.; Huo, X.H. Research on Multiple UAV Cooperation Area Coverage Searching. J. Syst. Simul. 2007, 19, 2472–2476. [Google Scholar]
- Chen, H.; He, K.F.; Qian, W.Q. Cooperative coverage path planning for multiple UAVS. Acta Aeronaut. Astronaut. Sin. 2016, 37, 928–935. [Google Scholar]
- Agarwal, A.; Hiot, L.M.; Nghia, N.T.; Joo, M.E. Parallel Region Coverage Using Multiple UAVs. In Proceedings of the 2006 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2006; pp. 1–8. [Google Scholar]
- Guastella, D.C.; Cantelli, L.; Giammello, G.; Melita, C.D.; Spatino, G.; Muscato, G. Complete coverage path planning for aerial vehicle flocks deployed in outdoor environments. Comput. Electr. Eng. 2019, 75, 189–201. [Google Scholar] [CrossRef]
- Araujo, J.F.; Sujit, P.B.; Sousa, J.B. Multiple UAV area decomposition and coverage. In Proceedings of the 2013 IEEE Symposium on Computational Intelligence for Security and Defense Applications (CISDA), Singapore, 16–19 April 2013; pp. 30–37. [Google Scholar]
- Schuldt, D.W.; Kurucar, J.A. Efficient partitioning of space for multiple UAS search in an unobstructed environment. Int. J. Intell. Robot. Appl. 2018, 2, 98–109. [Google Scholar] [CrossRef]
- Huang, H.Y. Research on Multi-UAV Cooperative Tracking Ground Moving Target System. Master’s Thesis, Jilin University, Changchun, China, 2020. [Google Scholar]
- Gustavo, S.C.A.; Guilherme, A.S.P.; Luciano, C.A. Multi-UAV Routing for Area Coverage and Remote Sensing with Minimum Time. Sensors 2015, 15, 27783–27803. [Google Scholar]
- Li, Q.; Liu, X.L.; Li, R.H.; Feng, Z.H.; Li, Z.J.; Zhao, H.Y. UAV Networking Remote Sensing Simulation Track Planning based on Field Station. J. Geo-Inf. Sci. 2021, 23, 948–957. [Google Scholar]
- Toth, P.; Vigo, D. The Vehicle Routing Problem; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Christofides, N.; Mingozzi, A.; Toth, P. Exact algorithms for the vehicle routing problem, based on spanning tree and shortest path relaxations. Math. Program. 1981, 20, 255–282. [Google Scholar] [CrossRef]
- Löfberg, J. A toolbox for modeling and optimization in MATLAB. In Proceedings of the CACSD Conference. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Chen, H.; Wang, X.M.; Jiao, Y.S.; Li, Y. An algorithm of coverage flight path planning for UAVs in convex polygon areas. Acta Aeronaut. Astronaut. Sin. 2010, 31, 1802–1808. [Google Scholar]





| Flight Speed/km/h | Preparation Time/h | Solver | Method | Number of UAVs | Observation Time of the k-th UAV/h | Network Observation Time/h | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 7.5 | 0.1 | CPLEX | Optimization | 5 | 0.94 | 0.95 | 0.93 | 0.88 | 0.85 | 0.95 |
| Original | 5 | 0.94 | 0.95 | 0.93 | 0.88 | 0.85 | 0.95 | |||
| Gurobi | Optimization | 5 | 0.94 | 0.95 | 0.93 | 0.88 | 0.85 | 0.95 | ||
| Original | 5 | 0.94 | 0.95 | 0.93 | 0.88 | 0.85 | 0.95 | |||
| 0.2 | CPLEX | Optimization | 4 | 0.94 | 1.05 | 1.15 | 1.05 | \ | 1.15 | |
| Original | 4 | 0.97 | 1.11 | 115 | 1.0 | \ | 1.15 | |||
| Gurobi | Optimization | 4 | 0.94 | 1.05 | 1.15 | 1.05 | \ | 1.15 | ||
| Original | 4 | 0.97 | 1.11 | 115 | 1.0 | \ | 1.15 | |||
| 6 | 0.1 | CPLEX | Optimization | 4 | 1.17 | 1.16 | 1.12 | 1.07 | \ | 1.17 |
| Original | 4 | 1.17 | 1.16 | 1.17 | 1.03 | \ | 1.17 | |||
| Gurobi | Optimization | 4 | 1.17 | 1.16 | 1.12 | 1.07 | \ | 1.17 | ||
| Original | 4 | 1.17 | 1.16 | 1.17 | 1.03 | \ | 1.17 | |||
| 0.2 | CPLEX | Optimization | 4 | 1.17 | 1.26 | 1.34 | 1.16 | \ | 1.34 | |
| Original | 4 | 1.17 | 1.26 | 1.34 | 1.16 | \ | 1.34 | |||
| Gurobi | Optimization | 4 | 1.17 | 1.26 | 1.34 | 1.16 | \ | 1.34 | ||
| Original | 4 | 1.17 | 1.26 | 1.34 | 1.16 | \ | 1.34 | |||
| Endurance Distance/km | Task Allocation Goal | Preparation Time/h | Number of UAVs | Network Observation Time/h |
|---|---|---|---|---|
| 16.7 | Minimum observation time | 0.1 | 5 | 0.95 |
| 0.2 | 4 | 1.15 | ||
| Minimum number of UAVs | 0.1 | 2 | 1.98 | |
| 0.2 | 2 | 1.98 | ||
| 13.3 | Minimum observation time | 0.1 | 4 | 1.17 |
| 0.2 | 4 | 1.34 | ||
| Minimum number of UAVs | 0.1 | 2 | 1.89 | |
| 0.2 | 2 | 1.89 |
| Flight Distance/km | Coefficient | Preparation Time/h | Number of UAVs | Network Observation Time/h | |
| a | b | ||||
| 16.7 | 1 | 0 | 0.1 | 5 | 0.95 |
| 0.9 | 0.1 | 3 | 1.05 | ||
| 0.8 | 0.2 | 3 | 1.05 | ||
| 0.7 | 0.3 | 3 | 1.05 | ||
| 0.6 | 0.4 | 2 | 1.51 | ||
| 0.5 | 0.5 | 2 | 1.51 | ||
| 0 | 1 | 2 | 1.98 | ||
| 1 | 0 | 0.2 | 4 | 1.15 | |
| 0.9 | 0.1 | 3 | 1.25 | ||
| 0.8 | 0.2 | 3 | 1.25 | ||
| 0.7 | 0.3 | 2 | 1.51 | ||
| 0.6 | 0.4 | 2 | 1.51 | ||
| 0.5 | 0.5 | 2 | 1.51 | ||
| 0 | 1 | 2 | 1.98 | ||
| 13.3 | 1 | 0 | 0.1 | 4 | 1.17 |
| 0.9 | 0.1 | 3 | 1.27 | ||
| 0.8 | 0.2 | 3 | 1.27 | ||
| 0.7 | 0.3 | 3 | 1.27 | ||
| 0.6 | 0.4 | 2 | 1.89 | ||
| 0.5 | 0.5 | 2 | 1.89 | ||
| 0 | 1 | 2 | 1.89 | ||
| 1 | 0 | 0.2 | 4 | 1.34 | |
| 0.9 | 0.1 | 4 | 1.34 | ||
| 0.8 | 0.2 | 3 | 1.46 | ||
| 0.7 | 0.3 | 3 | 1.46 | ||
| 0.6 | 0.4 | 2 | 1.89 | ||
| 0.5 | 0.5 | 2 | 1.89 | ||
| 0 | 1 | 2 | 1.89 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Li, Q.; Li, R.; Cai, X.; Wei, J.; Zhao, H. UAV Network Path Planning and Optimization Using a Vehicle Routing Model. Remote Sens. 2023, 15, 2227. https://doi.org/10.3390/rs15092227
Chen X, Li Q, Li R, Cai X, Wei J, Zhao H. UAV Network Path Planning and Optimization Using a Vehicle Routing Model. Remote Sensing. 2023; 15(9):2227. https://doi.org/10.3390/rs15092227
Chicago/Turabian StyleChen, Xiaotong, Qin Li, Ronghao Li, Xiangyuan Cai, Jiangnan Wei, and Hongying Zhao. 2023. "UAV Network Path Planning and Optimization Using a Vehicle Routing Model" Remote Sensing 15, no. 9: 2227. https://doi.org/10.3390/rs15092227
APA StyleChen, X., Li, Q., Li, R., Cai, X., Wei, J., & Zhao, H. (2023). UAV Network Path Planning and Optimization Using a Vehicle Routing Model. Remote Sensing, 15(9), 2227. https://doi.org/10.3390/rs15092227





