Abstract
Aphids cause severe damage to agricultural crops, resulting in significant economic losses, and an increased use of pesticides with decreased efficiency. Monitoring aphid infestations through regular field surveys is time-consuming and does not always provide an accurate spatiotemporal representation of the distribution of pests. Therefore, an automated, non-destructive method to detect and evaluate aphid infestation would be beneficial for targeted treatments. In this study, we present a machine learning model to identify and quantify aphids, localizing their spatial distribution over leaves, using a One-Class Support Vector Machine and Laplacian of Gaussians blob detection. To train this model, we built the first large database of aphids’ hyperspectral images, which were captured in a controlled laboratory environment. This database contains more than 160 images of three aphid lines, distinctive in color, shape, and developmental stages, and are displayed laying on leaves or neutral backgrounds. This system exhibits high-quality validation scores, with a of 0.97, a of 0.91, an score of 0.94, and an score of 0.98. Moreover, when assessing this method on new and challenging images, we did not observe any false negatives (and only a few false positives). Our results suggest that a machine learning model of this caliber could be a promising tool to detect aphids for targeted treatments in the field.
1. Introduction
Aphids cause severe damage to agricultural crops and can lead to significant economic losses. As they feed on plant sap, they can affect plant growth and could act as vectors for pathogens such as viruses or saprophytic fungi [1,2,3,4,5]. Aphid population control is, therefore, a priority for farmers, who are required to take regular scouting reports from random points in the field to assess the severity of the infestation and treat the pests accordingly [2]. However, these time-consuming surveys do not provide accurate information on the spatiotemporal distribution of aphids, and farmers generally miss the appropriate time-frame to efficiently protect their crops from aphid infestation [3]. They generally resort to using pesticides at a high frequency but with low efficiency, knowing that only 0.3% of pesticides applied through aerial application comes in contact with the targeted pest [6]. This method is unreliable as it is costly, threatens human health and the environment, and can even increase insect resistance [3]. Several international and national institutions have supported the reduction of the use of agrochemicals, such as the United Nations FAO (Food and Agriculture Organization) with the International Code of Conduct on Pesticide Management [7], and the French government with the Ecophyto II+ plan, which is supported by Europe and aims to reduce the use of agrochemicals by 50% by 2025 [8]. To achieve this ambitious goal, many alternative solutions are being developed, and combining different approaches to enhance the efficiency of pest control is a promising strategy, as established by the reputable integrated pest management (IPM) [2] methodology. One crucial step in this strategy is the accurate detection of pests in time and space. Therefore, an automated non-destructive method to detect and evaluate aphid infestation would be beneficial for targeted treatments.
Several optical sensors are being tested in the field and under laboratory conditions to detect pests and diseases on crops. These sensors can measure the light reflectance spectra of objects in the visible (400–700 nm), near-infrared (NIR, 700–1000 nm), and short-wave infrared (SWIR, 1000–2500 nm) ranges. Depending on their spectral resolution, sensors are categorized into two families, namely multispectral and hyperspectral sensors. The former usually focuses on several relatively broad wave bands (red–green–blue, NIR), whereas the latter covers a broader range of wavelengths, providing a higher spectral resolution [9,10]. Moreover, depending on their output, the sensors have been classified as imaging if they output the spectra for each pixel of the captured image, or non-imaging if they only output the average reflectance over an area [10]. Finally, optical datasets can be acquired at different spatial scales by satellite-borne, unmanned airborne vehicles (UAVs) and handheld sensors [11,12]. Depending on their distance from the target, these sensors can be classified as large-scale distal devices or proximal devices.
Large-scale remote sensing often uses non-imaging multi- and hyperspectral sensors to rapidly analyze large plots of land. These sensors detect major crop symptoms and, thus, can indirectly detect the presence of pests. There are currently only a few studies that explore the use of imaging methods for mapping infested areas with low-resolution [13]. In this process, vegetation indices are usually computed from the reflection of specific wavelengths. For instance, the normalized difference vegetation index (NDVI) [14], as well as other similar indicators [15,16,17,18,19], have been used to assess plant health and, therefore, indirectly asses crop infestation, since symptoms such as leaf yellowness caused by sap-sucking insects are known to impact photosynthesis. Following this, a recent study used a hyperspectral radiometer to detect soybean aphid-induced stress and introduce treated/non-treated classes based on the economic threshold [19]. Nevertheless, the effectiveness of detection is variable and the interpretations that can be extracted from these measures are limited. Indeed, plants responses are complex (e.g., chlorophyll dynamics [20]) and it can be difficult to distinguish spectral changes induced by pests from confounding factors, such as diseases, nutritional deficiencies [21], and water stress. Moreover, large-scale sensors tend to have lower spatial resolution than proximal sensors, which reduces the specificity and sensitivity of the detection [22].
Proximal remote sensing enables high-resolution monitoring of diseases and pest infestations down to the scale of individual plants and leaves [23]. It also allows for the identification, quantification, and localization of the pest itself and its specific symptoms. To achieve this, most studies use digital image analysis and machine learning classifiers to detect and count pests on both sticky traps [24,25] and in the field [26,27], and can even localize them on plants regardless of their density or color (with high accuracy) [28,29]. The classification of digital images of insects with complex backgrounds relied on the following various methods: multi-level learning features [27]; a combination of support vector machines (SVMs), maximally stable extremal regions (MSER), and the histogram of oriented gradients (HOG) [28]; and convolutional neural networks (CNNs) [26,29]. Digital color imaging is easy to use and provides copious amounts of information regarding pests, symptoms, and spatial distributions. Nevertheless, this technique has its limits as colors and shapes can become mixed up; its efficiency strongly depends on the image quality and the distance and orientation of the device [11,30]. One solution would be to couple spatial and spectral resolutions with spectral sensors such as hyperspectral imaging (HSI) systems [30,31,32]. A hyperspectral image is a hypercube composed of two spatial axes and one spectral axis at high resolution, providing a light spectrum with full wavelength information for each pixel of the image. Thus, hyperspectral images contain a large amount of information (≈1 Gb) making it possible to analyze a complex environment with minor components using machine learning approaches suitable for this type of data [30]. In this context, previous studies successfully used HSI analysis to classify leaves and plants as non-infected or infected by various diseases [33,34] or aphids [32,35]. These studies, respectively, used SVM [33] and 3D–2D hybrid CNN (Y-Net) [34] models on leaf patches, as well as CNN, achieving results similar to SVM [32], and least-squares SVM (LS-SVM) [35] for hyperspectral image classification. Other methods aim at detecting the pests themselves as well as their symptoms on crops, such as larvae [36,37] or leaf miners over time and across different fertilizer regimes [38]. Back-propagation neural network (BPNN) and partial least squares discriminant analysis (PLS-DA) models were developed based on full wavelengths or a selection of effective wavelengths to classify leaves and Pieris rapae larvae [36]. Although all models showed high accuracy, the BPNN models worked slightly better (but with considerably long computation times), and the models based on a selection of wavelengths had slightly weaker performances. Detecting insects on host plants can be challenging because background data can vary depending on the plants organs and their health. Thus, another study used LS-SVM and PLS-DA with full wavelengths or simply the most significant ones to detect infections on mulberry leaves based on five classes of samples: leaf vein, healthy mesophyll, slight damage, serious damage, and Diaphania pyloalis larva [37]. The LS-SVM model showed better results while using full wavelengths or specific selections displayed similar results to distinguish the five classes. Finally, a recent study considered the interaction between crop infestation and agricultural practices using SVM algorithms and detailed hyperspectral profiles to accurately diagnose leaf miner infestation over time and across fertilizer regimes [38]. The conclusions highlight the limitations of using a selection of specific wavelengths for detecting pest infestation in complex environments. However, no previous work has addressed the localization and counting of aphids on hyperspectral images.
The aim of this study is to introduce an automated, non-destructive machine learning-based method to detect, localize, and quantify aphid infestation on hyperspectral images. To train the machine learning model, we built a large aphid HSI database since no such dataset was readily available. The database developed in this work contains over 160 images captured in a controlled environment. These images feature three distinct aphid lines that vary in color, shape, and developmental stage and are shown either on leaves or on white backgrounds. Previous works have mainly framed the pest detection problem as a binary or multi-class classification task [36,37,38]. Nevertheless, this formalism requires representative examples for all classes in the training dataset. Consequently, when binary or multi-class classifiers are applied to datasets suffering from ill-defined classes (such as under-sampled, absent, or imbalanced), they tend to misclassify testing samples and exhibit poor generalization capabilities. The aforementioned database contains representative examples of the positive class (i.e., aphids), but the background images captured under controlled conditions are not likely to be representative of negative examples (i.e., not aphids) in real-world conditions. Therefore, in this study, the aphid detection task was framed as a one-class classification problem, which aims to learn how to identify aphids from positive examples only. One-class classification is an important research domain in the fields of data mining and pattern recognition. Among the one-class techniques proposed so far, One-Class SVM has been successfully applied in various domains, including disease diagnosis, anomaly detection, and novelty detection [39]. In addition, SVMs have been used successfully to classify hyperspectral spectra in agricultural data [32,33,38]. In this work, we trained a One-Class SVM to classify each pixel’s spectrum as arising from an aphid or not, then we used a Laplacian of Gaussian (LoG) blob detection to localize aphids in a given space and quantify them. The model proposed in this article exhibits high-quality evaluation scores on validation and test data, which suggests that this system could be a promising tool for aphid detection in the field.
2. Materials and Methods
2.1. Data Acquisition
2.1.1. Insects and Plants
The aphids used in this study are from parthenogenetic females from field-originated lines. The three aphid lines have different colors and sizes. This diversity provides a broad spectral database to develop an automated aphid detection program (Figure 1). Acyrthosiphon pisum lines LL01 (green) and YR2 (pink) were maintained on young broad bean plants (Vicia faba, L. cv. Aquadulce) and Rhopalosiphum padi line LR01 (black, two to three times smaller than A. pisum) on wheat seedlings (Triticum aestivum [L.] cv. Orvantis). Aphids and their host plants have been reared in controlled conditions in a phytotron at 20 °C ± 1 °C and 60% RH ± 5% with a 16 h photoperiod.
Organic seeds of V. faba and T. aestivum were supplied by Graines-Voltz® (Loire-Authion, France) and Nature et Progrès® (Alès, France), respectively. The seeds were germinated in a commercial peat substrate Florentaise® TRH400 (Saint-Mars-du-Désert, France). The collection of plant material in this manuscript complies with relevant institutional, national, and international guidelines and can be obtained from various seed companies worldwide.
The sampling of synchronized aphids was performed as described previously [40,41,42] to create a spectral signature database of the three aphid lines at 9 developmental stages: nymphs N1, N2, N3, N4 (1, 2, 5, 7 days old, respectively); wingless adults A9, A13, A15 (9, 13, 15 days old, respectively) during the reproductive period and A23 (23 days old) during the senescent period, and winged adults, AW (Figure 1). Finally, in order to test the detection program under challenging conditions, a group of A. pisum LL01 (green) nymphs N1 (first instar) were placed on a V. faba leaf.
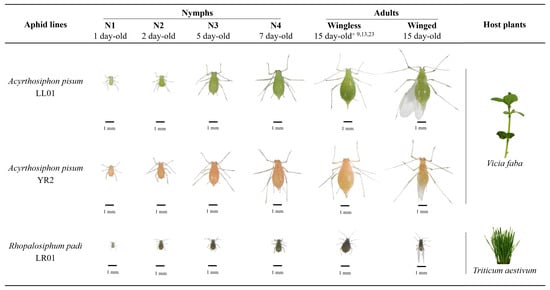
Figure 1.
Developmental stages of the three aphid lines used in this work. These aphid lines have different colors and sizes. The database consists of images of living aphids from the three lines at nine developmental stages with three biological replicates under two different conditions (aphids on a neutral background or their host plant leaf), providing over 160 hyperspectral images. Adapted from Gaetani et al. [43].
2.1.2. Image Acquisition
Hyperspectral images of the three aphid lines at the nine developmental stages previously mentioned (three biological replicates each) were taken under two different conditions: aphids on a white neutral background or on their host plant leaf, providing over 160 images in total. All the images produced in this work are publicly available at Peignier et al. [44]. The images were acquired using a pushbroom HSI system (Figure 2a) consisting of an HSI camera Specim FX10 and a halogen lighting mounted on a Specim LabScanner 40 × 20 cm (Specim, Spectral Imaging, Ltd., Oulu, Finland). Specim’s LUMO Scanner Software controls the HSI system on a computer. The camera has a visible NIR (VNIR) spectral range of 400–1000 nm and a mean spectral resolution of 5.5 nm (224 bands). Thus, it is possible to place an aphid on the moving plate of the Labscanner, and record a hyperspectral image with a camera line of 1024 spatial pixels and a spectral data acquisition along this line with a maximum frame rate of 327 frames per second (fps) full-frame (Figure 2b). During hyperspectral measurements, the HSI system was placed in a controlled environment, in a black room with only LabScanner halogen lamps as the light source. It is possible to apply filters to reduce high levels of stochastic noise in hyperspectral images [38]. However, it was not necessary for these images and, therefore, we kept all spectral data for further analysis. Each hyperspectral image was taken with two extra images for reflectance calibration, where the dark current reference was recorded by closing an internal camera shutter, and the white reference was recorded on a Teflon white calibration bar with standard reflectance of 99%. Then, we normalized the raw data using dark and white references to display light reflectance spectra between 0 (minimum reflectance) and 1 (maximum reflectance). Since we knew that the reduction of spectral information can limit pest detection in complex environments [36,38], we relied on full wavelengths light reflectance spectra to develop the automated detection program based on three aphid lines with varying colors and sizes.
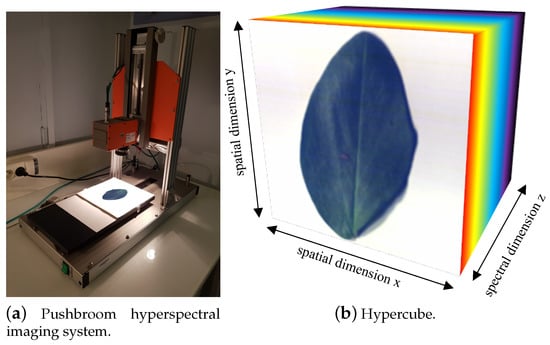
Figure 2.
Pushbroom HSI (a) for hyperspectral image acquisition, combining the spatial and spectral dimensions (b). The spatial X and Y axes and the spectral Z axis form a hypercube.
2.2. Training Dataset Annotation
The detection of aphids in hyperspectral images could have been framed as a binary classification task. However, since the images were captured under controlled conditions, examples corresponding to the negative class would not be representative of negative examples in real conditions. Therefore, we decided to frame the problem as a one-class classification task, which learns to identify aphids only from positive examples. To train such a classifier, we elaborated a one-class training dataset using principal component analysis (PCA) [45] and the K-means clustering algorithm [46]. These techniques are traditionally known to perform reliably for labeling and classification of hyperspectral images [30,33,36,47]. Thus, in order to capture each aphid’s spectrum, given its small size with respect to the entire image, we focused on the aphid’s surrounding area. Then, we applied a PCA on the zoomed image pixel spectra, computed the percentage of variance carried by each principal component (PC), and visualized the zoomed images projected on the most important PCs. These steps allowed us to select the number of PCs to be kept for the remaining steps. Afterward, we applied the K-means clustering algorithm to the pixels of the zoomed image, projected into the first PCs space, to capture a single cluster that gathered the aphid’s pixels. The number of clusters was adjusted for each image. Finally, we computed the average spectrum of the pixels corresponding to the aphid’s cluster and stored it in a positive examples dataset. To evaluate the method, we also collected negative examples from our controlled experiment. To do so, we removed the aphid’s pixels from the entire image and ran a K-means clustering on the full image to extract 50 clusters that summarize the given image. Then, the mean spectra of each cluster were stored in a negative example dataset. For further analysis, we also stored, for each aphid’s spectrum, its corresponding line and stage. For the negative examples, we labeled the aphid’s surrounding area cluster spectrum as either a leaf or a background.
This computer-assisted hyperspectral image-training set annotation was achieved using a Jupyter Notebook script [48], relying on scikit-learn [49], Pandas [50], Numpy [51], Matplotlib [52], Seaborn [53], and Spectral [54] Python libraries. The notebook script for the training dataset annotation is available online in a dedicated GitLab repository https://gitlab.com/bf2i/ocsvm-hyperaphidvision (last updated on 22 March 2023).
2.3. One-Class SVM Aphid Classifier
The One-Class SVM algorithm is an extension of the well-known Support Vector Machine method designed for outlier detection [55]. The One-Class SVM only receives samples from one class and learns a decision function that returns a positive value for instances lying in a small region of the feature space that captures most training samples, and a negative value elsewhere. To do so, One-Class SVM maps the data points into a new feature space defined by a corresponding kernel and then learns a maximum margin hyperplane that separates the training instances from the origin in the kernel feature space. Once the One-Class SVM is trained, each new point is classified depending on the side of the hyperplane where it falls. A point falling on the side where most training examples lay is classified as a normal or positive sample, while a point falling on the other side of the hyperplane is classified as an outlier or a negative sample.
More formally, let be a dataset with N samples from a set . In this article, each represents a reflection spectrum measured along D different wavelengths, and then ; the training set X is composed of the average reflection spectrum of an aphid’s pixels that were standardized to have zero mean and unit standard deviation. Let be a function that maps the input space to a possibly infinite, feature space, such that for any pair of samples , the dot product in space can be computed using a kernel function as . Then, as stated by Schölkopf et al. [55], the algorithm aims to learn a maximum margin hyperplane to separate the positive examples dataset from the origin, by minimizing the objective function formalized in Equation (1).
where is a parameter that controls the trade-off between the maximization of the margin (i.e., minimization of ), and the minimization of the sum of nonzero-slack variables, denotes a positive slack variable associated with sample , w is the normal vector to the separating hyperplane, and is the intercept. As aforementioned, One-Class SVM classifies each new data point as positive or negative depending on the side of the hyperplane where it lays. More formally, let be the decision function, such that is positive if x lays on the same side as most training examples, and negative otherwise. In practice, the previous objective is derived in the dual problem formalized in Equation (2).
The aforementioned decision function is also modified according to the dual problem, as stated in Equation (3).
Based on this equation, it is useful to derive a simple score function , which assigns a high output to normal data points and a low output to outliers, as formalized in Equation (4).
Given the dual problem and the derived decision function, the separating hyperplane is never computed explicitly, and the data samples are never mapped into feature space . Instead, the problem is addressed using the kernel function K and the nonzero Lagrange multiplier coefficients assigned to the training samples denoted as support vectors. In this work, we used the well-known radial basis function (RBF) kernel [55] , with being a parameter of the RBF kernel. To tune the two major parameters of the algorithm, namely the trade-off parameter and the kernel parameter , we explored a large grid of pairs of parameters, as detailed in the dedicated section below. In practice, we used the One-Class SVM implementation available in the scikit-learn Python library [49]. For the sake of reproducibility, the method’s implementations, the training dataset, and the pre-trained model are available online in a dedicated GitLab repository https://gitlab.com/bf2i/ocsvm-hyperaphidvision (last updated on 22 March 2023).
2.3.1. Evaluation Procedure
We assessed the performance of the One-Class SVM using a binary classification task evaluation protocol. Even though only positive examples, i.e., aphid spectra, were used to train the algorithm, we used the negative samples collected from the hyperspectral images to evaluate the performance of the algorithm, as described above. Since 99% of the data samples belong to the negative class and only 1% to the positive aphid class, our learning task is under imbalanced conditions. Therefore, we chose standard evaluation measures for binary classification that are suitable under unbalanced conditions, namely the score, , , and the area under the – curve (), as formally defined in the appendix (Appendix A). Finally, we used a 10-fold stratified cross-validation procedure to compute such evaluation measures for different validation sets.
2.3.2. One-Class SVM Hyperparameters Exploration
To select the best parameters for the One-Class SVM algorithm, and simultaneously assess the sensitivity of the algorithm with respect to its main parameters, we applied the assessment procedure, as defined in the section below, for different parameter values. As aforementioned, the One-Class SVM algorithm has two major hyperparameters, namely (the kernel coefficient) and (the trade-off coefficient). Interestingly, according to [55], simultaneously defines an upper bound for the fraction of training errors (i.e., a fraction of outliers within the training set), and a lower bound for the fraction of support vectors.
Parameter determines the inverse of the radius of influence of each training instance selected as a support vector, on the classification of other samples. In general, SVMs are sensitive to parameter : large values of imply a very small region of influence of each support vector, while small values of imply that all support vectors influence the classification of any other sample. Therefore, high may lead to overfitting, while low will likely lead to highly constrained and under-fitted models.
To define a rather large parameter exploration grid, we tested the possible combinations between , and .
2.3.3. Blobs Detection
In order to detect aphids in a new image, we simply applied the One-Class SVM score function, defined in Equation (4), to each standardized hyperspectral pixel spectrum of the image, obtaining a matrix of scores with the same 2D shape as the hyperspectral image. This score matrix, once normalized between 0 and 1, can be seen as a grayscale image, where light pixels represent high One-Class SVM scores and dark pixels represent low One-Class SVM scores. To detect individual aphids in each One-Class SVM score’s image and then estimate their frequencies, we applied an algorithm to detect image blobs, i.e., regions sharing properties that differ from surrounding areas, e.g., bright spots on a dark background. According to Han and Uyyanonvara [56], different blob detection methods have been proposed so far in the literature, but three techniques stand out in terms of usefulness, namely Laplacian of Gaussian (LoG), difference of Gaussian (DoG), and determinant of Hessian (DoH). Among these techniques, LoG [57] is recognized as more accurate than DoG and DoH. Given an input image, this method applies a Gaussian kernel convolution with a standard deviation . Then, it applies the Laplacian operator on the convolved image, which results in strong positive (respectively, negative) outputs for dark (respectively, bright) blobs of radius ; consequently, the coordinates of local optima in the LoG-transformed image are output as blob locations.
In practice, we used the skimage.feature.blob_log function from the scikit-image Python library [58]. This function applies the LoG method for a number num_sigma of successively increasing values for the Gaussian kernel standard deviation , between a minimal (min_sigma) and a maximal (max_sigma), in order to detect blobs with different sizes. The function outputs local optima with a LoG output higher than a given threshold, and such that its area does not overlap by a fraction greater than a threshold overlap with a larger blob.
Basically, we set min_sigma=3, max_sigma=20, and num_sigma=10, to search blobs with different diameters between 5 and more than 12 pixels, which corresponds to the size of aphids on the hyperspectral images that were captured in this work. Notice that modifications in the image resolution would require adapting this parameter accordingly. Moreover, we used a high overlapping threshold of overlap=0.9 to detect agglomerated aphids, removing small blobs only when more than 90% of their area overlaps with a larger blob. Finally, we set a rather low threshold=0.01 to detect as many blobs as possible and reduce the risk of false negatives. Nevertheless, depending on the application, it may be necessary to increase the threshold to decrease the risk of false positives instead.
2.3.4. Comparisons with Alternative Schemes
In order to assess the scheme proposed in this article, we compared its performance with respect to alternative schemes that rely on random forest (RF) [59] or a multilayer perceptron neural network (NN) [60], to classify each pixel spectrum as arising from an aphid or not, following a binary classification formalism. The main parameter for the RF classifier is the number of trees. In this study, we set a large number of decision trees equal to 500 to ensure better performance for the method. Regarding the architecture of the NN, we included two hidden layers, so the NN would be able to represent an arbitrary decision boundary [61]. We set the number of neurons in the first hidden layer to 224 neurons (i.e., ) and the number of neurons in the second hidden layer to 112 neurons (i.e., ), i.e., between their respective input and output layers, as suggested in [61]. In both layers, the ReLU activation function was used. In practice, the scikit-learn [49] implementations were used for both methods. Since the training dataset (for each hyperspectral image) contains 1 aphid spectrum and 50 background spectra, the training dataset is strongly imbalanced. Then, in order to cope with this problem, we also applied two imbalance correction techniques from the imbalanced-learn Python library [62], namely the synthetic minority over-sampling technique (SMOTE) [63] and ClusterCentroids (CC), a prototype generation under-sampling technique based on K-means [46]. In total, six alternative schemes were tested, combining RF and NN with SMOTE, CC, or no imbalance correction. All computations were executed on a 2.9 GHz Intel Core i9 CPU running macOS BigSur 11.2.3, using only one CPU core.
3. Results
3.1. HSI Database and Dataset Analysis
We first analyzed the spectral signatures of the different developmental stages within each aphid line, lying on a leaf or a white background (Figure 3a–c). For each aphid line, the shape of spectral signatures of different developmental stages is rather similar, but some differences were observed in the overall level of light reflectance. The nymphal stages reflect more light than the adult stages. Moreover, winged adults tend to reflect more light than wingless ones.
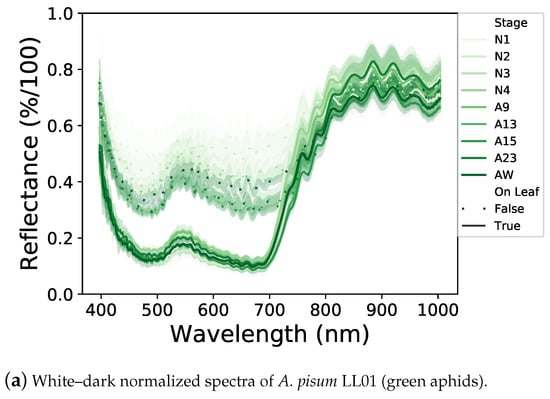
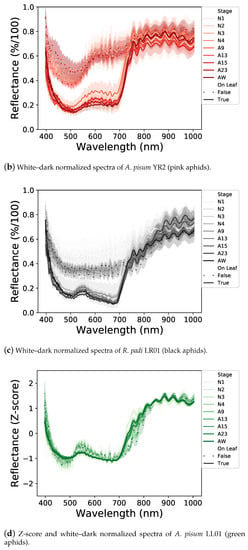
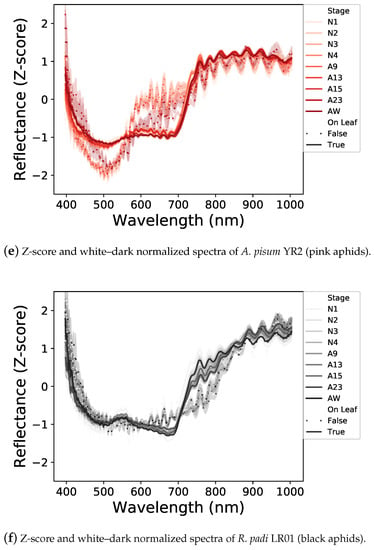
Figure 3.
Normalized light reflectance spectra of the three aphid lines before (a–c) and after (d–f) Z-score standardization. All aphid stages, on a white background or a leaf, are represented. Spectral signatures differ between aphid lines and neutral and leaf backgrounds. Differences in light reflectance between nymphal and adult stages are reduced by the Z-score application.
Between the two backgrounds, aphids reflect much more of the visible part of the light (400–700 nm) on a white background than on a leaf, with the latter potentially absorbing a part of the light transmitted by the aphid (Figure 3a–c). In addition, the shapes of the spectral signatures of aphids laying on a white background or on a leaf are different, probably due to an interaction between aphids and leaves.
Concerning differences between aphid lines (Figure 3a–c), on a white background, aphids reflect some specific ranges differently. A. pisum LL01 aphids reflect the green light area (500–570 nm) while the A. pisum YR2 ones reflect the red-light area (600–700 nm) and R. padi reflects the visible parts of the light equally, which could be explained by their different colors. These specific reflectances are less obvious on a leaf background, but they are still visible, especially with the YR2 line, which reflects the red light area. Finally, the three aphid lines strongly reflect NIR, each in a different way, notably with a higher reflectance between 700 and 800 nm for the YR2 line.
These different spectral signatures can, therefore, be used to potentially detect aphids on leaves with a One-Class SVM classifier. To this end, we applied a Z-score standardization of the spectral dataset (Figure 3d–f), which allowed to reduce the light reflectance differences between the different developmental stages and have a synthesis of the spectral signatures of aphids according to their lines and backgrounds used for the following One-Class SVM classification.
3.2. One-Class SVM Assessment and Sensitivity Analysis
Figure 4 depicts the average validation performance scores of the One-Class SVM method in terms of , , , and , for a 10-fold cross-validation procedure, over different combinations of parameters and . This figure allows assessing the sensitivity of the methods proposed in this article on the main parameters, as well as justifying the parameter setting.
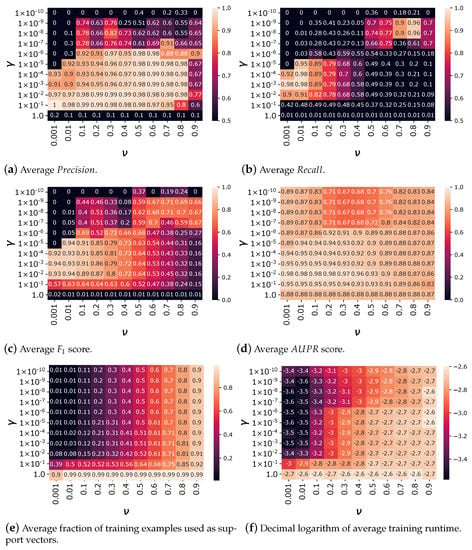
Figure 4.
Average , , , , relative number of support vectors, and training runtime for 10-fold cross-validation scores over different combinations of parameters and . Better results are obtained for and .
In general, the performance of the algorithm tends to increase when increases since the model is more flexible and less prone to underfitting. Nevertheless, when is too high (i.e., ), the performance of the model in the validation set abruptly drops, which is likely due to overfitting. Moreover, for suitable ranges of between and , the parameter tends to increase the of the algorithm while reducing its . This is because controls the fraction of training instances that can be considered as errors, enabling the location of a more conservative hyperplane with a larger margin, which tends to reduce the risk of false positives, improving its , while increasing the risk of false negatives, degrading its .
Both parameters also control the fraction of training examples used as support vectors by the algorithm, as shown in Figure 4e. The number of support vectors is mainly controlled by for values of . In this case, the fraction of examples taken as support vectors is almost equal to . When , the fraction of examples used as support vectors is significantly higher, and almost all of the 143 objects for each cross-validation training set are taken as support vectors for . A higher number of support vectors retained also leads to higher runtimes, as reported in Figure 4f.
The different evaluation measures are higher than 0.9 for low values of between and , and large enough values of , between and . Considering the different evaluation measures, suitable results were obtained for and , namely to a , , , and . Moreover, with this parameter setting, only 8% of the training samples were taken as support vectors, which controls the complexity of the model, limiting the risks of overfitting, and reducing both fit and prediction runtimes. In the following, we present the results obtained by a model trained with and parameters.
3.3. Model Inspection
To deepen our understanding of the One-Class SVM model’s decision function, we compared, for each spectrum, its One-Class SVM score and its provenance class. The score histogram depicted in Figure 5a shows that the score distribution forms three clearly distinguishable clusters. The cluster with the highest scores above 0.495 corresponds to aphids spectra, the intermediate cluster with scores between 0.4 and 0.49 corresponds to leaf spectra, and finally, the cluster with the lowest scores, mostly below 0.1, corresponds to other spectra such as the background or other objects. Only two spectra from other objects and one leaf spectrum have a score higher than the One-Class SVM offset threshold (i.e., 0.495), while twelve aphid spectra were selected as support vectors to define the decision boundary.
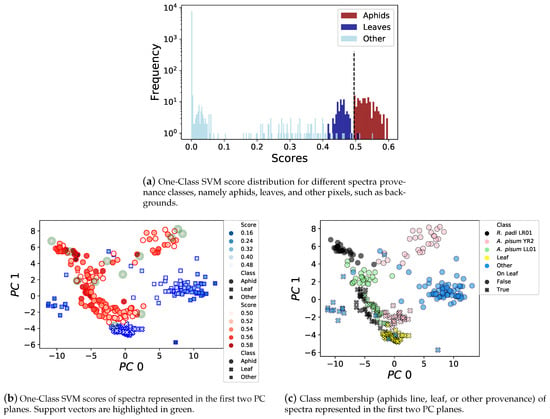
Figure 5.
One-Class SVM score distribution for aphids, leaves, and other kinds of spectra, with a clear separation between aphids and others for the threshold set at 0.495. PCA representation of highly-scored spectra, different aphid lines on different backgrounds forming distinct clusters, and a few support vectors are needed to discriminate aphid spectra.
Figure 5b,c depicts spectra having scores higher than 0.1 in the two first PCA component planes, which capture 77.48% of the dataset variance. Figure 5b represents the scores assigned by the One-Class SVM, as well as the aphid spectra selected as support vectors. Figure 5c represents a fine-grained provenance class for each spectrum, including leaves, other pixels such as the background, and the aphid type, whether it was on a leaf or a white background. In addition, Figure 6a,b, represents the standardized average top-scored spectra for each one of the previous classes, surrounded by a 68% confidence interval, respectively, on a white background or on a leaf. These results show that the background of the aphid has an important influence on the measures, as already suggested by the dataset analysis made in Figure 3. Indeed, the aphid spectra captured on leaves (Figure 6b) have more similarities between them, and are more similar to the spectra of a leaf than the aphid spectra measured on a white background (Figure 6a). Moreover, in the first two principal component planes (Figure 5c), the separation between other kinds of pixels and aphid ones is better than the separation between aphids and leaves. However, despite the similarity between aphid and leaf spectra, the One-Class SVM algorithm successfully learned to distinguish aphids from such other classes as shown in Figure 5b.
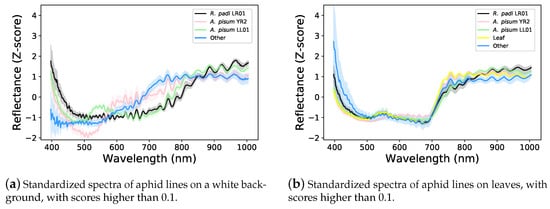
Figure 6.
Z-score standardized average light reflectance spectra of the three aphid lines, including all aphid stages. Aphid spectral signatures are different between lines and seem to overlap with leaf spectral signatures.
3.4. Full Detection System Assessment
To assess the aphid detection system based on One-Class SVM and LoG blob detection, we ran the method on three new challenging images. Two images contained a variable number of A. pisum LL01 aphids at stage N1 on a white background and a broad bean leaf, respectively, and a third image contained a single R. padi LR01 aphid at stage A9 on a wheat leaf with other objects in the background. The scores assigned by the One-Class SVM to each pixel of the aforementioned images are represented in Figure 7.
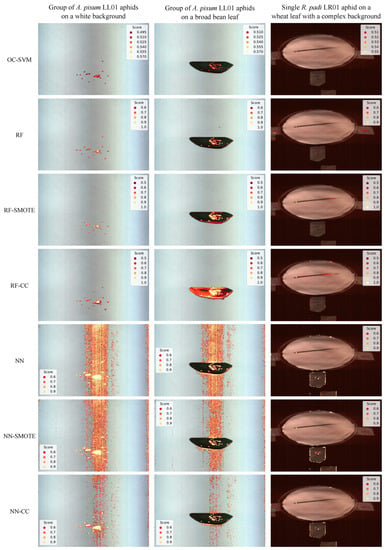
Figure 7.
Aphid score for all pixels classified as arising from aphids, assigned by each scheme (represented in each row), on three challenging images. The two first images represent a group of A. pisum LL01 aphids at stage N1 on a white background (column 1) or on a broad bean leaf (column 2), and the third image represents a single R. padi LR01 aphid on a wheat leaf with a complex background (column 3).
On a white background, the only pixels that have a nonzero score are those associated with aphids, while on a leaf, given the spectrum similarity between aphids and leaves, the One-Class SVM also assigns a relatively high score to leaf pixels. Nevertheless, the scores assigned to leaf pixels remain lower than those assigned to aphids on the leaf, and the decision function of the One-Class SVM only retains aphid pixels as belonging to the positive class.
Regarding the LoG application on the One-Class SVM score image, Figure 8 represents an RGB reconstruction of the hyperspectral images; aphids that could be detected by the LoG method are localized using red bounding boxes of 35 pixels, centered around each detected blob, using the Matplotlib library [52]. The LoG blob detector caught the presence of 26 aphid blobs on the image with a group of aphids on a white background, 33 on the image with a group of aphids on a leaf background, and 1 on the image with a single aphid on a complex background.
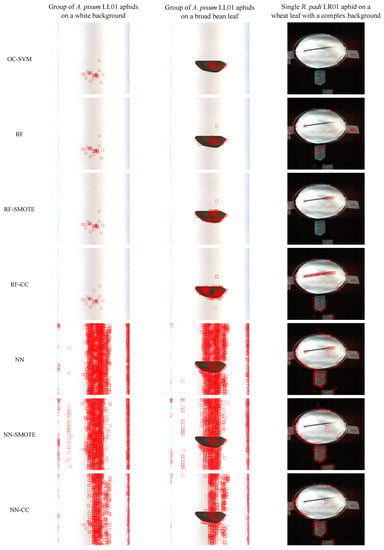
Figure 8.
Aphids detected by the LoG method (red bounding boxes), on score images obtained using each scheme (represented in each row), on three challenging images. The first two images represent a group of A. pisum LL01 aphids at stage N1 on a white background (column 1) or on a broad bean leaf (column 2), and the third image represents a single R. padi LR01 aphid on a wheat leaf with a complex background (column 3).
The system did not output false negatives in the three cases, and only a few false positives were output from the right border of the broad bean leaf. This border, unlike the others, presents some irregularities since it was lacerated. Therefore, depending on the application, the requirements, and the conditions, it could be necessary to incorporate solutions to reduce the risk of possible false positives.
Regarding runtimes, the scoring of a hyperspectral image with 448 wavelengths and 950,272 pixels took on average 2.57 ± 0.016 s, which corresponds to an average of 2.7 microseconds per hyperspectral pixel. The execution of the LoG blob detection took, on average, 1.85 ± 0.018 s.
3.5. Comparison with Alternative Schemes
The One-Class SVM system presented in this article was compared to six alternative schemes relying on RF or NN classifiers, and possibly incorporating an imbalance correction technique (i.e., SMOTE, CC, or no correction) as described in Section 2.3.4. The average , , , and scores, as well as the training runtimes obtained by each scheme under 10-fold cross-validation, are reported in Table 1. In general, the different pipelines tend to present rather similar and high-quality results. In terms of , the only two methods that exhibit lower results are RF•CC and NN•CC (equal to 0.727 for RF and 0.846 for NN, respectively); thus, these methods are more prone to detecting false positives. In terms of , all methods exhibit rather good quality results, but the One-Class SVM depicts the lowest , and is, thus, prone to making more false negative detections. However, its is sufficient to detect most of the positive examples in the dataset. In terms of scores, the different methods exhibit rather comparable results, only the RF•CC scheme depicts clearly lower results (i.e., 0.839). In terms of , all methods exhibit comparable and high-quality results. Finally, the One-Class SVM system clearly outperforms the other methods in terms of runtimes, as it is more than 100 times faster than the second fastest method, RF•CC. Despite the aforementioned differences, in terms of test quality scores, most schemes exhibit rather similar performances, which suggests that the training pipeline is underspecified [64]. Underspecification is a common problem in machine learning pipelines [64]; models have similar results on the training/validation dataset but behave differently once deployed, often exhibiting instability and poor performance. Therefore, it was particularly important to assess the system under the challenging scenarios described in Section 3.4. The aphid scores obtained by the six other alternative schemes are represented in Figure 7 and the LoG blob predictions on such score images are represented in Figure 8. Both results clearly show that the other six alternative schemes predict a very high number of false positives and, thus, exhibit poor generalization capabilities, while the One-Class SVM method exhibits suitable generalization capabilities.

Table 1.
Average 10-fold cross-validation of , , , and scores and the training time obtained by the One-Class SVM (OC-SVM), the random forest classifier with no imbalance correction (RF), with SMOTE imbalance correction (RF•SMOTE), and with CC imbalance correction (RF•CC), the multilayer perceptron with no imbalance correction (NN), with SMOTE imbalance correction (NN•SMOTE), and with CC imbalance correction (NN•CC).
4. Discussion
In this study, we provided a method to detect aphids on hyperspectral images based on a One-Class SVM. To do so, an essential step was the production of a large database composed of 160 hyperspectral images, including the three aphid lines, A. pisum LL01 (green), A. pisum YR2 (pink), and R. padi LR01 (black, 2 to 3 times smaller) at nine developmental stages with three biological replicates, in two different conditions: aphids on a neutral white background or on their host plant leaf.
The dataset analysis first revealed that aphids at different developmental stages have overall the same spectral profile, but the nymphal stages reflected more light than adults, and winged adults reflected more light than wingless ones. Our hypothesis is that developing embryos and higher fat body content in the adult wingless morphs densify the aphids’ body and increase their light absorption compared to nymphs, which have not yet developed embryos, or adult winged aphids, which contain very few embryos [65]. These differences have been reduced with Z-score standardization to obtain aphid’s average spectral signatures according to their line and background.
The three aphid lines exhibit different responses to specific ranges of visible light. A. pisum LL01 reflects the green light area, A. pisum YR2 reflects the red light area, and R. padi reflects all visible light equally. These particular reflectances explain why A. pisum LL01 appears green, A. pisum YR2 appears pink, and R. padi appears dark (a mix of all colors equally reflected) to human eyes. All lines strongly reflect NIR in different ways, with the YR2 line exhibiting higher reflectance between 700 and 800 nm. The literature on insect infrared properties is limited, but it has been observed that high levels of NIR reflectance are widespread among insects living on leaves [66], likely for adaptive camouflage, with the latter also reflecting NIR strongly [67]. Furthermore, reflectance between 700 and 800 nm is particularly prominent in red insects such as the pink A. pisum line (YR2), compared to the green (A. pisum LL01) or dark (R. padi) lines [66]. According to the literature, the basis of infrared reflectance is not yet well understood, but some approaches suggest that NIR reflectance may be due to structural properties, including the organization and pigmentation of cuticles and internal tissues [66,67].
We also discovered that the aphid background has a significant influence on aphid spectral signatures. By comparing the spectral signatures of aphids on a white background versus a leaf, we observed that the presence of the leaf reduces aphid light reflectance and results in a reflectance peak in the green light area. On one hand, light not absorbed by the aphid and transmitted through its body is likely to be reflected by the white background and transmitted again through the aphid to be finally captured by HSI. On the other hand, light transmitted through the aphid body is probably partially absorbed by the leaf, mainly the blue and red lights used for photosynthesis by chlorophyll a and b, while the remaining light, especially the green light, is reflected by the leaf and transmitted through the aphid [67].
These different spectral signatures have, thus, been used to detect aphids with success on a challenging background, such as leaves, with a One-Class SVM classifier. A joint best parameter selection and sensitivity analysis was conducted for the One-Class SVM algorithm with respect to its main parameters, namely (the kernel coefficient) and (the trade-off coefficient). Under controlled conditions, this system allows detecting aphids with a of 0.98, a of 0.91, an score of 0.94, and an of 0.98. Moreover, the One-Class SVM manages to distinguish diverse aphid spectra, from background leaf spectra, despite the similarities between such spectra, which suggests that it could be applied to more realistic conditions, such as in the field, and could be coupled with other innovative strategies, such as laser-based technologies [43], to detect and neutralize crop pest insects.
In addition, applying a simple blob detection system such as LoG to the One-Class SVM scores was sufficient to locate and count aphids on a leaf or neutral background, even when they were densely packed together, which is considered a particularly challenging configuration [28,29]. This simple procedure results in only a few false positives when applied to lacerated leaves, while alternative methods based on random forest and multilayer perceptron binary classifiers reveal a higher number of false positive detections. Future research aimed at deploying such a system in the fields could include: (i) applying more sophisticated shape recognition to the One-Class SVM score image to count aphids in real conditions and (ii) acquiring a more complex training database that includes beneficial insects to avoid false positive detections.
Here, we focused on optimizing the detection of various aphids on different backgrounds using full wavelength information. Our detection system displayed high accuracy and good speed. The speed of our detection system is fast enough to run periodic monitoring of fixed areas, such as identifying and counting insects on sticky traps [24,25]. However, to analyze a video stream on a robotic engine, further studies should be conducted in order to reduce runtimes [68]. Future works could evaluate the possibility of reducing the selection of wavelengths to increase the detection speed [36] while maintaining high accuracy and good sensitivity in complex environments.
5. Conclusions
In summary, this work collected the first aphid hyperspectral signature database in controlled conditions and used this information to develop an efficient automatic system for identifying, quantifying, and localizing the spatial distribution of aphids on leaf surfaces. Further studies to extend the database, improve shape recognition, and manage runtimes on moving robots could enhance the system’s capabilities, making it beneficial for IPM and targeted treatments in the field.
Author Contributions
S.P., V.L., M.-G.D., F.C., A.H. and P.d.S. conceived and designed the study. J.-C.S. provided biological materials. S.P. and V.L. set up the experiment hardware and carried out the experiments. P.B.-P. participated in the data curation and made the hyperspectral images database available online. S.P., V.L. and P.d.S. analyzed the data and wrote the manuscript. All authors reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by INSA Lyon, INRAE, and the French ANR-17-CE34-0012-03 (GREENSHIELD) program grant, which awarded V.L. an engineering contract.
Data Availability Statement
All hyperspectral images produced in this work are publicly available at Peignier et al. [44] https://doi.org/10.15454/IS11ZH (last updated on 22 March 2023). For the sake of reproducibility, the method implementations, training dataset, and pre-trained model are available online in a dedicated GitLab repository https://gitlab.com/bf2i/ocsvm-hyperaphidvision (last updated on 22 March 2023).
Acknowledgments
The authors are very grateful to Loa Mun for the careful editing of the manuscript. The authors are also grateful to GreenShield Technology for the discussion.
Conflicts of Interest
The authors declare that they have no competing interest, either financial or non-financial.
Appendix A
Metrics Definitions
In the context of binary classification, samples belong to two categories, i.e., positive and negative. In this article, the positive class corresponds to aphids, and the negative class corresponds to any other source. Depending on the outcome of a classifier, four possible scenarios exist for each sample: (i) true positive (): the classifier correctly predicts a positive sample; (ii) false negative (): the method fails to retrieve a positive sample; (iii) false positive (): the method predicts a negative sample as a positive; and (iv) true negative (): the method correctly predicts a negative sample.
In this context, the of a classifier is simply the fraction of positive samples retrieved by the classifiers, i.e., . The of a classifier is the fraction of true positive samples among the samples predicted as positive by the classifier, i.e., .
A model exhibiting high and low tends to predict many samples as positive, including truly positive samples, but most of its predictions tend to be incorrect. Conversely, a model exhibiting high and low predicts few positive samples, but most of them are correctly predicted. Ideally, a model should exhibit both high and high , and both measures should be considered while evaluating a model.
In order to consider both measures simultaneously, two important techniques have been proposed so far, namely the score and the area under the – curve (), as defined hereafter. The score of a classifier is the harmonic mean of its and its , i.e., . The so-called - curve aims to represent the obtained by a model, as a function of its , for different decision thresholds for the binary classification task. This curve represents the trade-off between both metrics. Computing the area under the curve aims to assess both measures simultaneously, as high scores for both metrics result in a high score. These four measures are particularly useful when the dataset exhibits a strong class imbalance, as portrayed in this article.
References
- Calevro, F.; Tagu, D.; Callaerts, P. Acyrthosiphon pisum. Trends Genet. 2019, 35, 781–782. [Google Scholar] [CrossRef] [PubMed]
- Olson, K.D.; Badibanga, T.M.; DiFonzo, C. Farmers’ Awareness and Use of IPM for Soybean Aphid Control: Report of Survey Results for the 2004, 2005, 2006, and 2007 Crop Years. Technical Report. 2008. Available online: https://ageconsearch.umn.edu/record/7355 (accessed on 22 March 2023).
- Ragsdale, D.W.; McCornack, B.; Venette, R.; Potter, B.D.; MacRae, I.V.; Hodgson, E.W.; O’Neal, M.E.; Johnson, K.D.; O’neil, R.; DiFonzo, C.; et al. Economic threshold for soybean aphid (Hemiptera: Aphididae). J. Econ. Entomol. 2007, 100, 1258–1267. [Google Scholar] [CrossRef]
- Simon, J.C.; Peccoud, J. Rapid evolution of aphid pests in agricultural environments. Curr. Opin. Insect Sci. 2018, 26, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Consortium, I.A.G. Genome sequence of the pea aphid Acyrthosiphon pisum. PLoS Biol. 2010, 8, e1000313. [Google Scholar]
- van der Werf, H.M. Assessing the impact of pesticides on the environment. Agric. Ecosyst. Environ. 1996, 60, 81–96. [Google Scholar] [CrossRef]
- Office, F.M.R. FAO—News Article: Q&A on Pests and Pesticide Management. 2021. Available online: https://www.fao.org/news/story/en/item/1398779/icode/ (accessed on 22 March 2023).
- French Government. Ecophyto II+: Reduire et Améliorer l’Utilisation des Phytos. Technical Report. 2019. Available online: https://agriculture.gouv.fr/le-plan-ecophyto-quest-ce-que-cest (accessed on 22 March 2023).
- Žibrat, U.; Knapič, M.; Urek, G. Plant pests and disease detection using optical sensors/Daljinsko zaznavanje rastlinskih bolezni in škodljivcev. Folia Biol. Geol. 2019, 60, 41–52. [Google Scholar] [CrossRef]
- Mahlein, A.K.; Kuska, M.T.; Behmann, J.; Polder, G.; Walter, A. Hyperspectral sensors and imaging technologies in phytopathology: State of the art. Annu. Rev. Phytopathol. 2018, 56, 535–558. [Google Scholar] [CrossRef]
- Mahlein, A.K. Plant disease detection by imaging sensors–parallels and specific demands for precision agriculture and plant phenotyping. Plant Dis. 2016, 100, 241–251. [Google Scholar] [CrossRef]
- Bansod, B.; Singh, R.; Thakur, R.; Singhal, G. A comparision between satellite based and drone based remote sensing technology to achieve sustainable development: A review. J. Agric. Environ. Int. Dev. (JAEID) 2017, 111, 383–407. [Google Scholar]
- Mirik, M.; Ansley, R.J.; Steddom, K.; Rush, C.M.; Michels, G.J.; Workneh, F.; Cui, S.; Elliott, N.C. High spectral and spatial resolution hyperspectral imagery for quantifying Russian wheat aphid infestation in wheat using the constrained energy minimization classifier. J. Appl. Remote Sens. 2014, 8, 083661. [Google Scholar] [CrossRef]
- Elliott, N.; Mirik, M.; Yang, Z.; Jones, D.; Phoofolo, M.; Catana, V.; Giles, K.; Michels, G., Jr. Airborne Remote Sensing to Detect Greenbug1 Stress to Wheat. Southwest. Entomol. 2009, 34, 205–211. [Google Scholar] [CrossRef]
- Kumar, J.; Vashisth, A.; Sehgal, V.; Gupta, V. Assessment of aphid infestation in mustard by hyperspectral remote sensing. J. Indian Soc. Remote Sens. 2013, 41, 83–90. [Google Scholar]
- Luo, J.; Wang, D.; Dong, Y.; Huang, W.; Wang, J. Developing an aphid damage hyperspectral index for detecting aphid (Hemiptera: Aphididae) damage levels in winter wheat. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1744–1747. [Google Scholar]
- Shi, Y.; Huang, W.; Luo, J.; Huang, L.; Zhou, X. Detection and discrimination of pests and diseases in winter wheat based on spectral indices and kernel discriminant analysis. Comput. Electron. Agric. 2017, 141, 171–180. [Google Scholar]
- Prabhakar, M.; Prasad, Y.G.; Vennila, S.; Thirupathi, M.; Sreedevi, G.; Rao, G.R.; Venkateswarlu, B. Hyperspectral indices for assessing damage by the solenopsis mealybug (Hemiptera: Pseudococcidae) in cotton. Comput. Electron. Agric. 2013, 97, 61–70. [Google Scholar]
- Marston, Z.P.; Cira, T.M.; Knight, J.F.; Mulla, D.; Alves, T.M.; Hodgson, E.W.; Ribeiro, A.V.; MacRae, I.V.; Koch, R.L. Linear Support Vector Machine Classification of Plant Stress from Soybean Aphid (Hemiptera: Aphididae) Using Hyperspectral Reflectance. J. Econ. Entomol. 2022, 115, 1557–1563. [Google Scholar] [PubMed]
- Alves, T.M.; Macrae, I.V.; Koch, R.L. Soybean aphid (Hemiptera: Aphididae) affects soybean spectral reflectance. J. Econ. Entomol. 2015, 108, 2655–2664. [Google Scholar] [CrossRef]
- Reisig, D.D.; Godfrey, L.D. Remotely sensing arthropod and nutrient stressed plants: A case study with nitrogen and cotton aphid (Hemiptera: Aphididae). Environ. Entomol. 2010, 39, 1255–1263. [Google Scholar] [CrossRef]
- Mahlein, A.; Kuska, M.; Thomas, S.; Bohnenkamp, D.; Alisaac, E.; Behmann, J.; Wahabzada, M.; Kersting, K. Plant disease detection by hyperspectral imaging: From the lab to the field. Adv. Anim. Biosci. 2017, 8, 238–243. [Google Scholar] [CrossRef]
- Liu, L.; Ma, H.; Guo, A.; Ruan, C.; Huang, W.; Geng, Y. Imaging Hyperspectral Remote Sensing Monitoring of Crop Pest and Disease. In Crop Pest and Disease Remote Sensing Monitoring and Forecasting; EDP Sciences: Les Ulis, France, 2022; pp. 189–220. [Google Scholar]
- Cho, J.; Choi, J.; Qiao, M.; Ji, C.; Kim, H.; Uhm, K.; Chon, T. Automatic identification of whiteflies, aphids and thrips in greenhouse based on image analysis. Red 2007, 346, 244. [Google Scholar]
- Xia, C.; Chon, T.S.; Ren, Z.; Lee, J.M. Automatic identification and counting of small size pests in greenhouse conditions with low computational cost. Ecol. Inform. 2015, 29, 139–146. [Google Scholar]
- Cheng, X.; Zhang, Y.; Chen, Y.; Wu, Y.; Yue, Y. Pest identification via deep residual learning in complex background. Comput. Electron. Agric. 2017, 141, 351–356. [Google Scholar] [CrossRef]
- Xie, C.; Wang, R.; Zhang, J.; Chen, P.; Dong, W.; Li, R.; Chen, T.; Chen, H. Multi-level learning features for automatic classification of field crop pests. Comput. Electron. Agric. 2018, 152, 233–241. [Google Scholar] [CrossRef]
- Liu, T.; Chen, W.; Wu, W.; Sun, C.; Guo, W.; Zhu, X. Detection of aphids in wheat fields using a computer vision technique. Biosyst. Eng. 2016, 141, 82–93. [Google Scholar] [CrossRef]
- Li, R.; Wang, R.; Xie, C.; Liu, L.; Zhang, J.; Wang, F.; Liu, W. A coarse-to-fine network for aphid recognition and detection in the field. Biosyst. Eng. 2019, 187, 39–52. [Google Scholar]
- Lacotte, V.; Dell’Aglio, E.; Peignier, S.; Benzaoui, F.; Heddi, A.; Rebollo, R.; Da Silva, P. A comparative study revealed hyperspectral imaging as a potential standardized tool for the analysis of cuticle tanning over insect development. Heliyon 2023, 9, e13962. [Google Scholar]
- Jin-Ling, Z.; Dong-Yan, Z.; Ju-Hua, L.; Yang, H.; Lin-Sheng, H.; Wen-Jiang, H. A comparative study on monitoring leaf-scale wheat aphids using pushbroom imaging and non-imaging ASD field spectrometers. Int. J. Agric. Biol. 2012, 14, 136–140. [Google Scholar]
- Yan, T.; Xu, W.; Lin, J.; Duan, L.; Gao, P.; Zhang, C.; Lv, X. Combining Multi-Dimensional Convolutional Neural Network (CNN) with Visualization Method for Detection of Aphis gossypii Glover Infection in Cotton Leaves Using Hyperspectral Imaging. Front. Plant Sci. 2021, 12, 74. [Google Scholar]
- Lacotte, V.; Peignier, S.; Raynal, M.; Demeaux, I.; Delmotte, F.; da Silva, P. Spatial–Spectral Analysis of Hyperspectral Images Reveals Early Detection of Downy Mildew on Grapevine Leaves. Int. J. Mol. Sci. 2022, 23, 10012. [Google Scholar] [CrossRef]
- Jia, Y.; Shi, Y.; Luo, J.; Sun, H. Y–Net: Identification of Typical Diseases of Corn Leaves Using a 3D–2D Hybrid CNN Model Combined with a Hyperspectral Image Band Selection Module. Sensors 2023, 23, 1494. [Google Scholar]
- Zhao, Y.; Yu, K.; Feng, C.; Cen, H.; He, Y. Early detection of aphid (Myzus persicae) infestation on Chinese cabbage by hyperspectral imaging and feature extraction. Trans. ASABE 2017, 60, 1045–1051. [Google Scholar]
- Wu, X.; Zhang, W.; Qiu, Z.; Cen, H.; He, Y. A novel method for detection of pieris rapae larvae on cabbage leaves using nir hyperspectral imaging. Appl. Eng. Agric. 2016, 32, 311–316. [Google Scholar]
- Huang, L.; Yang, L.; Meng, L.; Wang, J.; Li, S.; Fu, X.; Du, X.; Wu, D. Potential of visible and near-infrared hyperspectral imaging for detection of Diaphania pyloalis larvae and damage on mulberry leaves. Sensors 2018, 18, 2077. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Nansen, C. Hyperspectral remote sensing to detect leafminer-induced stress in bok choy and spinach according to fertilizer regime and timing. Pest Manag. Sci. 2020, 76, 2208–2216. [Google Scholar] [CrossRef]
- Alam, S.; Sonbhadra, S.K.; Agarwal, S.; Nagabhushan, P. One-class support vector classifiers: A survey. Knowl.-Based Syst. 2020, 196, 105754. [Google Scholar]
- Simonet, P.; Duport, G.; Gaget, K.; Weiss-Gayet, M.; Colella, S.; Febvay, G.; Charles, H.; Vi nuelas, J.; Heddi, A.; Calevro, F. Direct flow cytometry measurements reveal a fine-tuning of symbiotic cell dynamics according to the host developmental needs in aphid symbiosis. Sci. Rep. 2016, 6, 19967. [Google Scholar] [CrossRef]
- Simonet, P.; Gaget, K.; Balmand, S.; Ribeiro Lopes, M.; Parisot, N.; Buhler, K.; Duport, G.; Vulsteke, V.; Febvay, G.; Heddi, A.; et al. Bacteriocyte cell death in the pea aphid/Buchnera symbiotic system. Proc. Natl. Acad. Sci. USA 2018, 115, E1819–E1828. [Google Scholar] [CrossRef]
- Vi nuelas, J.; Febvay, G.; Duport, G.; Colella, S.; Fayard, J.M.; Charles, H.; Rahbé, Y.; Calevro, F. Multimodal dynamic response of the Buchnera aphidicola pLeu plasmid to variations in leucine demand of its host, the pea aphid Acyrthosiphon pisum. Mol. Microbiol. 2011, 81, 1271–1285. [Google Scholar] [CrossRef] [PubMed]
- Gaetani, R.; Lacotte, V.; Dufour, V.; Clavel, A.; Duport, G.; Gaget, K.; Calevro, F.; Da Silva, P.; Heddi, A.; Vincent, D.; et al. Sustainable laser-based technology for insect pest control. Sci. Rep. 2021, 11, 11068. [Google Scholar]
- Peignier, S.; Lacotte, V.; Duport, M.G.; Calevro, F.; Heddi, A.; Da Silva, P. Aphids Hyperspectral Images. 2022. Available online: https://entrepot.recherche.data.gouv.fr/dataset.xhtml?persistentId=doi:10.15454/IS11ZH (accessed on 4 January 2023).
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Manian, V.; Alfaro-Mejía, E.; Tokars, R.P. Hyperspectral image labeling and classification using an ensemble semi-supervised machine learning approach. Sensors 2022, 22, 1623. [Google Scholar] [CrossRef]
- Kluyver, T.; Ragan-Kelley, B.; Pérez, F.; Granger, B.E.; Bussonnier, M.; Frederic, J.; Kelley, K.; Hamrick, J.B.; Grout, J.; Corlay, S.; et al. Jupyter Notebooks—A Publishing Format for Reproducible Computational Workflows. In Proceedings of the 20th International Conference on Electronic Publishing, Göttingen, Germany, 7–9 June 2016; Volume 2016. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- McKinney, W. Pandas: A foundational Python library for data analysis and statistics. Python High Perform. Sci. Comput. 2011, 14, 1–9. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Waskom, M.L. Seaborn: Statistical data visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Boggs, T. Spectral Python (SPy)—Spectral Python 0.14 Documentation. 2014. Available online: http://www.spectralpython.net (accessed on 4 January 2023).
- Schölkopf, B.; Williamson, R.C.; Smola, A.J.; Shawe-Taylor, J.; Platt, J.C. Support vector method for novelty detection. In Proceedings of the Advances in Neural Information Processing Systems 12 (NIPS 1999), Denver, CO, USA, 29 November–4 December 1999; Volume 12, pp. 582–588. [Google Scholar]
- Han, K.T.M.; Uyyanonvara, B. A survey of blob detection algorithms for biomedical images. In Proceedings of the 2016 IEEE 7th International Conference of Information and Communication Technology for Embedded Systems (IC-ICTES), Bangkok, Thailand, 20–22 March 2016; pp. 57–60. [Google Scholar]
- Marr, D.; Hildreth, E. Theory of edge detection. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1980, 207, 187–217. [Google Scholar]
- Van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Hoboken, NJ, USA, 1994. [Google Scholar]
- Heaton, J. Introduction to Neural Networks with Java; Heaton Research, Inc.: St. Louis, MO, USA, 2008. [Google Scholar]
- Lemaître, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- D’Amour, A.; Heller, K.; Moldovan, D.; Adlam, B.; Alipanahi, B.; Beutel, A.; Chen, C.; Deaton, J.; Eisenstein, J.; Hoffman, M.D.; et al. Underspecification presents challenges for credibility in modern machine learning. J. Mach. Learn. Res. 2020, 23, 10237–10297. [Google Scholar]
- Lopes, M.R.; Gaget, K.; Renoz, F.; Duport, G.; Balmand, S.; Charles, H.; Callaerts, P.; Calevro, F. Bacteriocyte plasticity in pea aphids facing amino acid stress or starvation during development. Front. Physiol. 2022, 13, 982920. [Google Scholar] [CrossRef] [PubMed]
- Mielewczik, M.; Liebisch, F.; Walter, A.; Greven, H. Near-infrared (NIR)-reflectance in insects–Phenetic studies of 181 species. Entomol. Heute 2012, 24, 183–215. [Google Scholar]
- Jacquemoud, S.; Ustin, S. Leaf Optical Properties; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Cubero, S.; Marco-Noales, E.; Aleixos, N.; Barbé, S.; Blasco, J. Robhortic: A field robot to detect pests and diseases in horticultural crops by proximal sensing. Agriculture 2020, 10, 276. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).