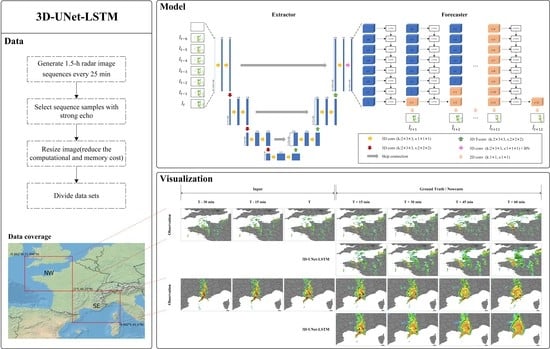
3D-UNet-LSTM: A Deep Learning-Based Radar Echo Extrapolation Model for Convective Nowcasting
Abstract
1. Introduction
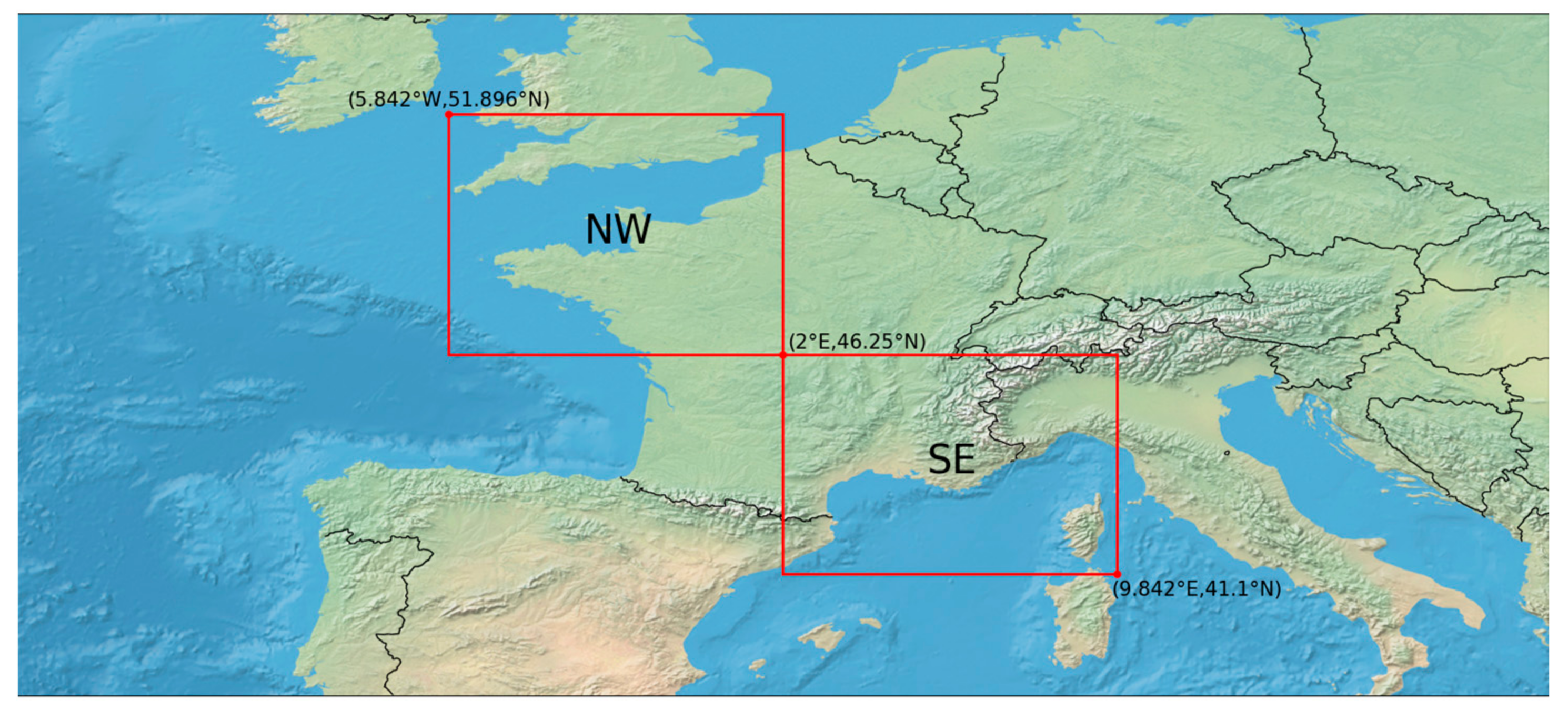
2. Data
3. Methodology
3.1. 3D-UNet-LSTM
3.2. Loss Function
3.3. Evaluation Metrics
4. Experiments and Results
4.1. Implementation Details for Training
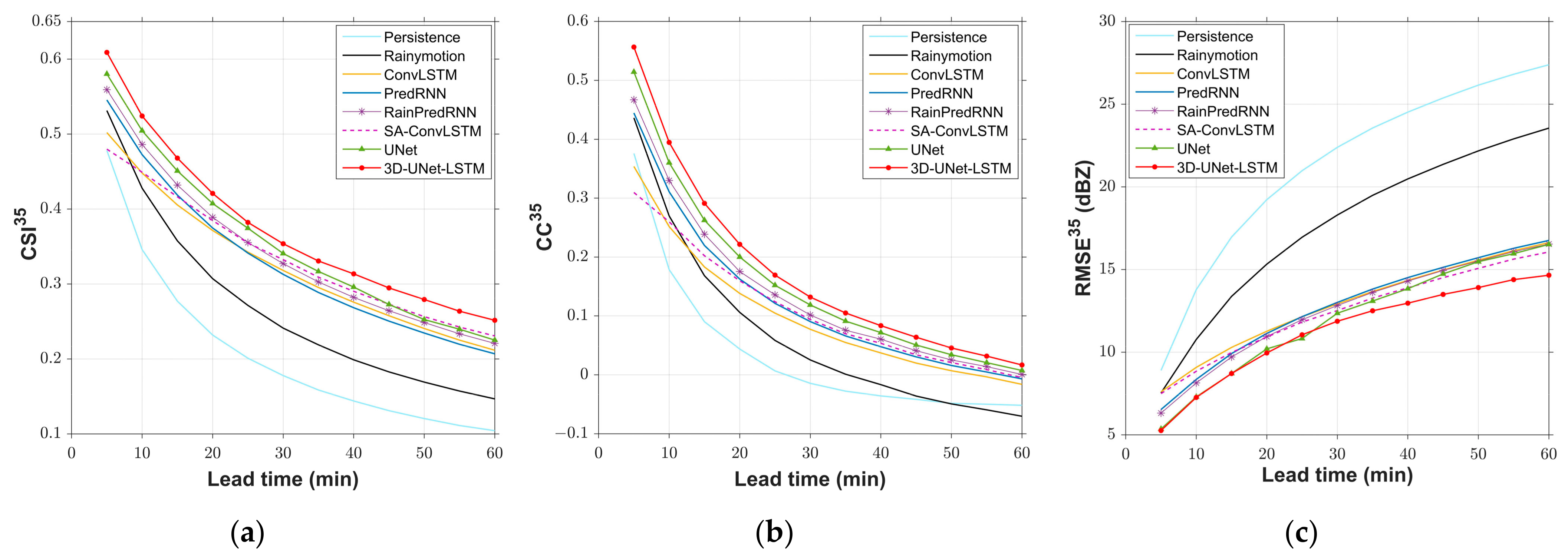
4.2. Quantitative Evaluation of Eight Models on the Test Set
4.3. Evaluation of the Model Design
4.4. Evaluation of Different Loss Functions
4.5. Representative Case Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. ConvLSTM Unit
Appendix A.2. Structure
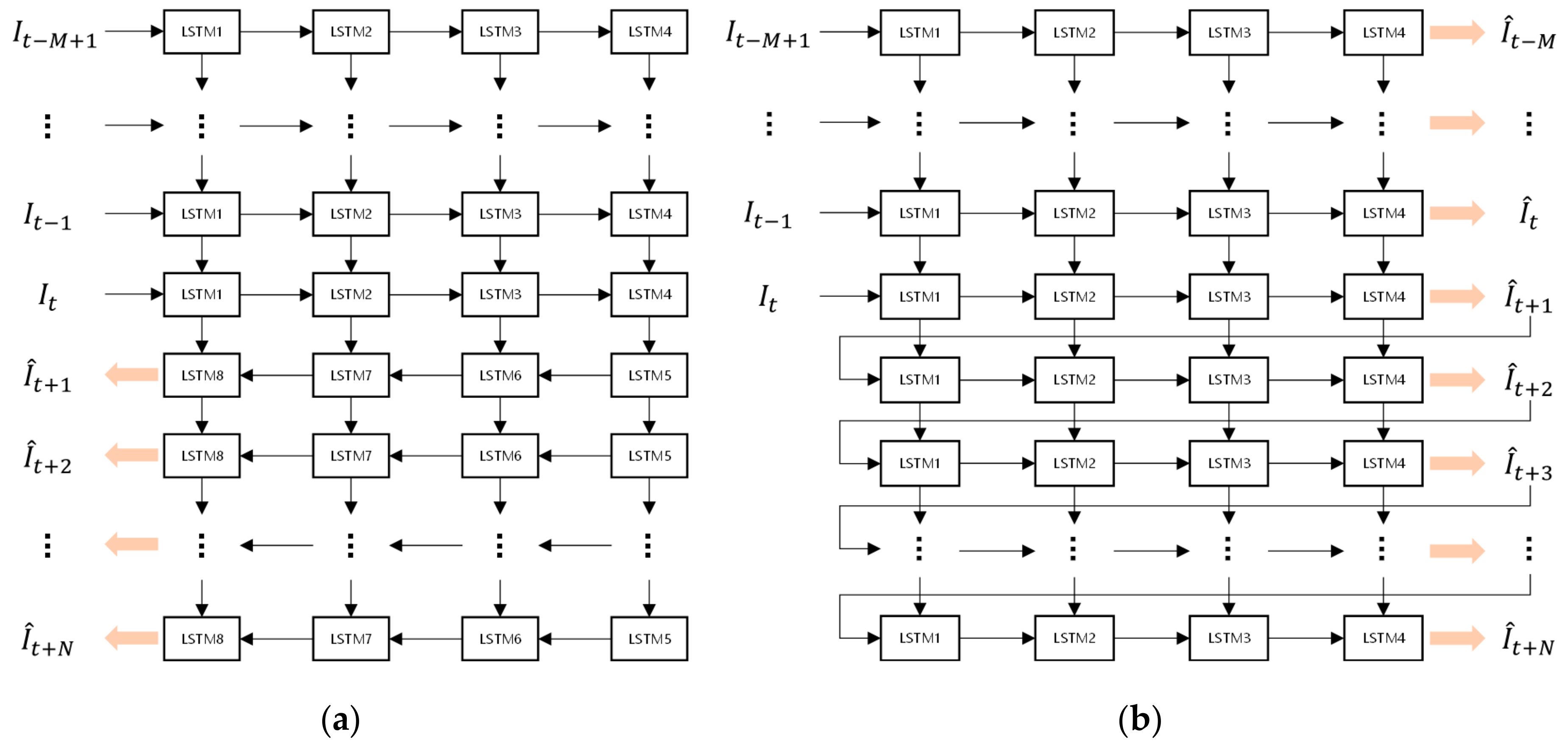
Appendix A.3. Adversial Loss Function
References
- Sun, J.; Xue, M.; Wilson, J.W.; Zawadzki, I.; Ballard, S.P.; Onvlee-Hooimeyer, J.; Joe, P.; Barker, D.M.; Li, P.-W.; Golding, B.; et al. Use of NWP for Nowcasting Convective Precipitation: Recent Progress and Challenges. Bull. Am. Meteorol. Soc. 2014, 95, 409–426; [Google Scholar] [CrossRef]
- Wilson, J.W.; Feng, Y.; Chen, M.; Roberts, R.D. Nowcasting Challenges during the Beijing Olympics: Successes, Failures, and Implications for Future Nowcasting Systems. Weather Forecast. 2010, 25, 1691–1714. [Google Scholar] [CrossRef]
- Li, P.-W.; Wong, W.-K.; Cheung, P.; Yeung, H.-Y. An overview of nowcasting development, applications, and services in the Hong Kong Observatory. J. Meteorol. Res. 2014, 28, 859–876. [Google Scholar] [CrossRef]
- Mecikalski, J.R.; Bedka, K.M. Forecasting Convective Initiation by Monitoring the Evolution of Moving Cumulus in Daytime GOES Imagery. Mon. Weather Rev. 2006, 134, 49–78. [Google Scholar] [CrossRef]
- Cancelada, M.; Salio, P.; Vila, D.; Nesbitt, S.W.; Vidal, L. Backward Adaptive Brightness Temperature Threshold Technique (BAB3T): A Methodology to Determine Extreme Convective Initiation Regions Using Satellite Infrared Imagery. Remote Sens. 2020, 12, 337. [Google Scholar] [CrossRef]
- Marshall, J.S.; Langille, R.C.; Palmer, W.M.K. Measurement of rainfall by radar. J. Atmos. Sci. 1947, 4, 186–192. [Google Scholar] [CrossRef]
- Peng, X.; Li, Q.; Jing, J. CNGAT: A Graph Neural Network Model for Radar Quantitative Precipitation Estimation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Akbari Asanjan, A.; Yang, T.; Hsu, K.; Sorooshian, S.; Lin, J.; Peng, Q. Short-Term Precipitation Forecast Based on the PERSIANN System and LSTM Recurrent Neural Networks. J. Geophys. Res. Atmos. 2018, 123, 12543–12563. [Google Scholar] [CrossRef]
- Germann, U.; Zawadzki, I. Scale-Dependence of the Predictability of Precipitation from Continental Radar Images. Part I: Description of the Methodology. Mon. Weather Rev. 2002, 130, 2859–2873. [Google Scholar] [CrossRef]
- Dixon, M.; Wiener, G. TITAN: Thunderstorm Identification, Tracking, Analysis, and Nowcasting—A Radar-based Methodology. J. Atmos. Ocean. Technol. 1993, 10, 785–797. [Google Scholar] [CrossRef]
- Johnson, J.T.; MacKeen, P.L.; Witt, A.; Mitchell, E.D.W.; Stumpf, G.J.; Eilts, M.D.; Thomas, K.W. The Storm Cell Identification and Tracking Algorithm: An Enhanced WSR-88D Algorithm. Weather Forecast. 1998, 13, 263–276. [Google Scholar] [CrossRef]
- Walker, J.R.; MacKenzie, W.M.; Mecikalski, J.R.; Jewett, C.P. An Enhanced Geostationary Satellite–Based Convective Initiation Algorithm for 0–2-h Nowcasting with Object Tracking. J. Appl. Meteorol. Climatol. 2012, 51, 1931–1949. [Google Scholar] [CrossRef]
- Rinehart, R.E.; Garvey, E.T. Three-dimensional storm motion detection by conventional weather radar. Nature 1978, 273, 287–289. [Google Scholar] [CrossRef]
- Ayzel, G.; Heistermann, M.; Winterrath, T. Optical flow models as an open benchmark for radar-based precipitation nowcasting (rainymotion v0.1). Geosci. Model Dev. 2019, 12, 1387–1402. [Google Scholar] [CrossRef]
- Pulkkinen, S.; Nerini, D.; Pérez Hortal, A.A.; Velasco-Forero, C.; Seed, A.; Germann, U.; Foresti, L. Pysteps: An open-source Python library for probabilistic precipitation nowcasting (v1.0). Geosci. Model Dev. 2019, 12, 4185–4219. [Google Scholar] [CrossRef]
- Hwang, Y.; Clark, A.J.; Lakshmanan, V.; Koch, S.E. Improved Nowcasts by Blending Extrapolation and Model Forecasts. Weather Forecast. 2015, 30, 1201–1217. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-c. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Agrawal, S.; Barrington, L.; Bromberg, C.; Burge, J.; Gazen, C.; Hickey, J. Machine learning for precipitation nowcasting from radar images. arXiv 2019, arXiv:1912.12132. [Google Scholar] [CrossRef]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S.; et al. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Liang, H.; Chen, H.; Zhang, W.; Ge, Y. Convective Precipitation Nowcasting Using U-Net Model. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–8. [Google Scholar] [CrossRef]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Deep learning for precipitation nowcasting: A benchmark and a new model. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5618–5628. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 879–888. [Google Scholar]
- Tuyen, D.N.; Tuan, T.M.; Le, X.-H.; Tung, N.T.; Chau, T.K.; Van Hai, P.; Gerogiannis, V.C.; Son, L.H. RainPredRNN: A New Approach for Precipitation Nowcasting with Weather Radar Echo Images Based on Deep Learning. Axioms 2022, 11, 107. [Google Scholar] [CrossRef]
- Jing, J.; Li, Q.; Peng, X. MLC-LSTM: Exploiting the Spatiotemporal Correlation between Multi-Level Weather Radar Echoes for Echo Sequence Extrapolation. Sensors 2019, 19, 3988. [Google Scholar] [CrossRef] [PubMed]
- Villegas, R.; Yang, J.; Hong, S.; Lin, X.; Lee, H. Decomposing motion and content for natural video sequence prediction. arXiv 2017, arXiv:1706.08033. [Google Scholar] [CrossRef]
- Lin, Z.; Li, M.; Zheng, Z.; Cheng, Y.; Yuan, C. Self-attention convlstm for spatiotemporal prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 11531–11538. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Chafik Bakkay, M.; Serrurier, M.; Kivachuk Burda, V.; Dupuy, F.; Citlali Cabrera-Gutierrez, N.; Zamo, M.; Mader, M.-A.; Mestre, O.; Oller, G.; Jouhaud, J.-C.; et al. Precipitaion Nowcasting using Deep Neural Network. arXiv 2022, arXiv:2203.13263. [Google Scholar] [CrossRef]
- Prudden, R.; Adams, S.; Kangin, D.; Robinson, N.; Ravuri, S.; Mohamed, S.; Arribas, A. A review of radar-based nowcasting of precipitation and applicable machine learning techniques. arXiv 2020, arXiv:2005.04988. [Google Scholar] [CrossRef]
- Klein, B.; Wolf, L.; Afek, Y. A Dynamic Convolutional Layer for short rangeweather prediction. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4840–4848. [Google Scholar]
- Ayzel, G.; Heistermann, M.; Sorokin, A.; Nikitin, O.; Lukyanova, O. All convolutional neural networks for radar-based precipitation nowcasting. Procedia Comput. Sci. 2019, 150, 186–192. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Ayzel, G.; Scheffer, T.; Heistermann, M. RainNet v1.0: A convolutional neural network for radar-based precipitation nowcasting. Geosci. Model Develop. 2020, 13, 2631–2644. [Google Scholar] [CrossRef]
- Trebing, K.; Staǹczyk, T.; Mehrkanoon, S. SmaAt-UNet: Precipitation nowcasting using a small attention-UNet architecture. Pattern Recognit. Lett. 2021, 145, 178–186. [Google Scholar] [CrossRef]
- Pan, X.; Lu, Y.; Zhao, K.; Huang, H.; Wang, M.; Chen, H. Improving Nowcasting of Convective Development by Incorporating Polarimetric Radar Variables Into a Deep-Learning Model. Geophys. Res. Lett. 2021, 48, e2021GL095302. [Google Scholar] [CrossRef]
- Che, H.; Niu, D.; Zang, Z.; Cao, Y.; Chen, X. ED-DRAP: Encoder–Decoder Deep Residual Attention Prediction Network for Radar Echoes. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Larvor, G.; Berthomier, L.; Chabot, V.; Le Pape, B.; Pradel, B.; Perez, L. MeteoNet, An Open Reference Weather Dataset by Meteo-France. 2020. Available online: https://meteonet.umr-cnrm.fr/ (accessed on 6 April 2022).
- Wang, C.; Wang, P.; Wang, P.; Xue, B.; Wang, D. Using Conditional Generative Adversarial 3-D Convolutional Neural Network for Precise Radar Extrapolation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5735–5749. [Google Scholar] [CrossRef]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning dense volumetric segmentation from sparse annotation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2016; pp. 424–432. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Niu, D.; Huang, J.; Zang, Z.; Xu, L.; Che, H.; Tang, Y. Two-Stage Spatiotemporal Context Refinement Network for Precipitation Nowcasting. Remote Sens. 2021, 13, 4285. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467. [Google Scholar] [CrossRef]
- Liu, H.B.; Lee, I. MPL-GAN: Toward Realistic Meteorological Predictive Learning Using Conditional GAN. IEEE Access 2020, 8, 93179–93186. [Google Scholar] [CrossRef]
- Oprea, S.; Martinez-Gonzalez, P.; Garcia-Garcia, A.; Castro-Vargas, J.A.; Orts-Escolano, S.; Garcia-Rodriguez, J.; Argyros, A. A Review on Deep Learning Techniques for Video Prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 2806–2826. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Tian, L.; Li, X.; Ye, Y.; Xie, P.; Li, Y. A Generative Adversarial Gated Recurrent Unit Model for Precipitation Nowcasting. IEEE Geosci. Remote Sens. Lett. 2020, 17, 601–605. [Google Scholar] [CrossRef]
- Veillette, M.; Samsi, S.; Mattioli, C. Sevir: A storm event imagery dataset for deep learning applications in radar and satellite meteorology. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–12 December 2020; pp. 22009–22019. [Google Scholar]


| Period | Sample Number | Total | ||
|---|---|---|---|---|
| NW | SE | |||
| Training | 2016.1–2018.5 | 5504 | 4865 | 10,369 |
| Validation | 2018.6–2018.7 | 480 | 517 | 997 |
| Test | 2018.8–2018.10 | 308 | 829 | 1137 |
| Method | CSI↑ | twaCSI↑ | CC↑ | RMSE↓ | ||||
|---|---|---|---|---|---|---|---|---|
| 18 dBZ | 35 dBZ | 18 dBZ | 35 dBZ | 18 dBZ | 35 dBZ | 18 dBZ | 35 dBZ | |
| Persistence | 0.4181 | 0.2068 | 0.3591 | 0.1554 | 0.2644 | 0.0355 | 16.92 | 21.34 |
| Rainymotion | 0.5149 | 0.2675 | 0.4581 | 0.2107 | 0.3616 | 0.0694 | 14.01 | 17.69 |
| ConvLSTM | 0.5814 | 0.3244 | 0.5421 | 0.2786 | 0.4350 | 0.1007 | 10.70 | 12.89 |
| PredRNN | 0.5898 | 0.3278 | 0.5468 | 0.2755 | 0.4500 | 0.1256 | 10.58 | 12.78 |
| RainPredRNN | 0.5906 | 0.3314 | 0.5483 | 0.2868 | 0.4624 | 0.1363 | 10.45 | 12.63 |
| SA-ConvLSTM | 0.5811 | 0.3349 | 0.5444 | 0.2933 | 0.4422 | 0.1110 | 10.47 | 12.50 |
| UNet | 0.5938 | 0.3550 | 0.5497 | 0.2998 | 0.4707 | 0.1570 | 10.41 | 12.03 |
| 3D-UNet-LSTM | 0.5990 | 0.3742 | 0.5512 | 0.3201 | 0.4853 | 0.1760 | 9.72 | 11.34 |
| Method | POD↑ | FAR↓ | BIAS | |||
|---|---|---|---|---|---|---|
| 18 dBZ | 35 dBZ | 18 dBZ | 35 dBZ | 18 dBZ | 35 dBZ | |
| Persistence | 0.5664 | 0.3202 | 0.4205 | 0.6727 | 0.9845 | 1.0220 |
| Rainymotion | 0.6525 | 0.3585 | 0.3170 | 0.5315 | 0.9546 | 0.7718 |
| ConvLSTM | 0.7887 | 0.4776 | 0.3230 | 0.5085 | 1.1795 | 0.9820 |
| PredRNN | 0.7888 | 0.4651 | 0.3129 | 0.4923 | 1.1622 | 0.9072 |
| RainPredRNN | 0.7953 | 0.4836 | 0.3206 | 0.5049 | 1.1584 | 1.0659 |
| SA-ConvLSTM | 0.8012 | 0.5021 | 0.3319 | 0.5133 | 1.2178 | 1.0384 |
| UNet | 0.8005 | 0.5480 | 0.3145 | 0.5136 | 1.1863 | 1.1500 |
| 3D-UNet-LSTM | 0.8238 | 0.5610 | 0.3235 | 0.4844 | 1.2462 | 1.1489 |
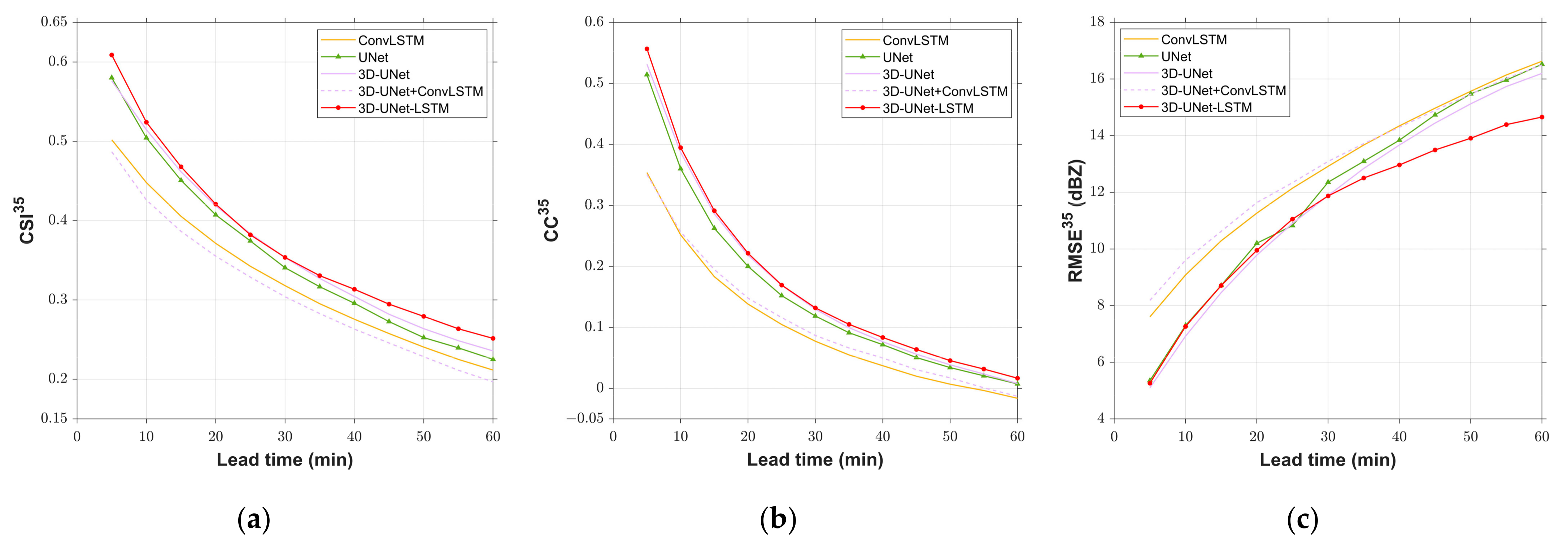
| Method | CSI↑ | twaCSI↑ | CC↑ | RMSE↓ | ||||
|---|---|---|---|---|---|---|---|---|
| 18 dBZ | 35 dBZ | 18 dBZ | 35 dBZ | 18 dBZ | 35 dBZ | 18 dBZ | 35 dBZ | |
| ConvLSTM | 0.5814 | 0.3244 | 0.5421 | 0.2786 | 0.4350 | 0.1007 | 10.70 | 12.89 |
| UNet | 0.5938 | 0.3550 | 0.5497 | 0.2998 | 0.4707 | 0.1570 | 10.41 | 12.03 |
| 3D-UNet | 0.5897 | 0.3642 | 0.5439 | 0.3099 | 0.4735 | 0.1687 | 10.27 | 11.76 |
| 3D-UNet + ConvLSTM | 0.5567 | 0.3097 | 0.5197 | 0.2648 | 0.4208 | 0.1087 | 10.96 | 13.03 |
| 3D-UNet-LSTM | 0.5990 | 0.3742 | 0.5512 | 0.3201 | 0.4853 | 0.1760 | 9.72 | 11.34 |
| Loss Function | CSI↑ | twaCSI↑ | CC↑ | RMSE↓ | ||||
|---|---|---|---|---|---|---|---|---|
| 18 dBZ | 35 dBZ | 18 dBZ | 35 dBZ | 18 dBZ | 35 dBZ | 18 dBZ | 35 dBZ | |
| 0.6045 | 0.3302 | 0.5575 | 0.2636 | 0.4460 | 0.1114 | 11.26 | 13.86 | |
| 0.5950 | 0.3392 | 0.5463 | 0.2794 | 0.4535 | 0.1433 | 11.08 | 13.37 | |
| 0.5990 | 0.3742 | 0.5512 | 0.3201 | 0.4853 | 0.1760 | 9.72 | 11.34 | |
| 0.5978 | 0.3716 | 0.5520 | 0.3161 | 0.4760 | 0.1622 | 10.12 | 11.57 | |
| 0.5884 | 0.3639 | 0.5385 | 0.3058 | 0.4635 | 0.1529 | 10.76 | 12.37 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Sun, N.; Pei, Y.; Li, Q. 3D-UNet-LSTM: A Deep Learning-Based Radar Echo Extrapolation Model for Convective Nowcasting. Remote Sens. 2023, 15, 1529. https://doi.org/10.3390/rs15061529
Guo S, Sun N, Pei Y, Li Q. 3D-UNet-LSTM: A Deep Learning-Based Radar Echo Extrapolation Model for Convective Nowcasting. Remote Sensing. 2023; 15(6):1529. https://doi.org/10.3390/rs15061529
Chicago/Turabian StyleGuo, Shiqing, Nengli Sun, Yanle Pei, and Qian Li. 2023. "3D-UNet-LSTM: A Deep Learning-Based Radar Echo Extrapolation Model for Convective Nowcasting" Remote Sensing 15, no. 6: 1529. https://doi.org/10.3390/rs15061529
APA StyleGuo, S., Sun, N., Pei, Y., & Li, Q. (2023). 3D-UNet-LSTM: A Deep Learning-Based Radar Echo Extrapolation Model for Convective Nowcasting. Remote Sensing, 15(6), 1529. https://doi.org/10.3390/rs15061529