Evaluation and Analysis of Remotely Sensed Water Vapor from the NASA VIIRS/SNPP Product in Mainland China Using GPS Data

Abstract

Precipitable water vapor (PWV) is a vitally important factor in atmospheric circulation. PWV is significant for forecasting extreme weather and understanding the dynamics of climate change. Comprehensively evaluating the performance of newly proposed remotely sensed water vapor products is crucial for guaranteeing their suitability for futural PWV applications. In this study, the accuracy of the recently established remotely sensed water vapor product from the Visible Infrared Imaging Radiometer Suite (VIIRS) satellite sensor on the Suomi National Polar-orbiting Partnership (SNPP) (VIIRS-PWV) platform within various regions of mainland China was evaluated via the PWV from Global Positioning System (GPS) observations. The GPS-derived PWV from 231 stations of the Crustal Movement Observation Network of China (CMONOC) from 2012 to 2018 was obtained through precise point positioning (PPP) techniques. The results showed that the mean value of the correlation coefficient (CC), the mean bias (MB), and the root-mean-square error (RMSE) between the VIIRS-PWV and the GPS-PWV were 0.92, −1.6 mm, and 4.7 mm, respectively. These values were comparable with the results of the PWV data derived from the Atmospheric Infrared Sounder (AIRS) and Moderate Resolution Imaging Spectroradiometer (MODIS) products. This indicates that the VIIRS product could provide PWV data with satisfactory accuracy for large-area scientific applications. Moreover, the MB and RMSE of the differences between the GPS-PWV and VIIRS-PWV showed obvious seasonal variations. The VIIRS-PWV generally performed better in winter (with the MB and RMSE values of 0.1 mm and 2.3 mm) than in summer (with the MB and RMSE values of −4.4 and 7.0 mm). Analysis among different regions revealed that the Central South (CS) region of China attained the largest mean RMSE value of 6.3 mm, and the North West (NW) region attained the smallest mean RMSE value of 3.8 mm. In addition, the southern region of China obtained a mean RMSE value of 5.6 mm, while that for the northern region of China was 3.9 mm. This indicates that the VIIRS-PWV has better accuracy within the northern region of China than within the southern region.

1. Introduction

Precipitable water vapor (PWV), one of the expressions of the atmospheric water vapor amount, is the linkage of the land–atmosphere water cycle [1]. The variation of PWV significantly influences the occurrence of extreme weather around the globe [2,3]. In addition, as the most important greenhouse gas [4], PWV has a feedback relationship with climate change [5]. Accurately measuring the PWV within the atmosphere is significant for forecasting extreme weather and understanding the dynamics of climate change [6,7].

Traditionally, PWV is detected through a radiosonde carried on a sounding balloon or a ground-based microwave radiometer. However, the traditional techniques have low temporal resolution and spatial coverage due to high operating costs [8]. Profiting from the rapid development of remote sensing techniques, a more economical large-scale PWV detection method based on satellite-based microwave radiometers was proposed. However, the performance of satellite passive remote sensing water vapor products is susceptible to the influences of cloud coverage, dark surfaces, and hazy conditions [9]. Therefore, evaluating the performance of remotely sensed water vapor products is a prerequisite before extensive applications. GNSS-based PWV estimation, another remote sensing technique [10], has advantages in high temporal resolution, strong continuity, and consistent precision and accuracy compared with traditional methods [11,12,13]. Thus, it is extensively utilized to evaluate the performance of PWV derived from remotely sensed water vapor products [14,15,16].

During the past years, numerous studies have been carried out to evaluate the accuracy of remotely sensed water vapor products via GNSS techniques. It is generally found that the PWV data derived from the remotely sensed water vapor products share different performances among different regions. Take the Moderate Resolution Imaging Spectroradiometer (MODIS) water vapor products as an example; the accuracy of MODIS-derived PWV was 0.8~1.4 mm in Germany [17], 13.9 mm in Hong Kong [18], 3~7 mm in Turkey [19], 1~9 mm in the Indian subcontinent [20], etc. In addition, the error characteristics of remotely sensed water vapor products within different regions are also different. For example, Prasad and Singh validated the MODIS Terra water vapor product using ground-based GPS receivers in India [21]. Results showed that PWV from both near-infrared and infrared channels of MODIS overestimated the water vapor in all seasons over India than PWV derived from GPS; this caused a root-mean-square error (RMSE) of 5.4 mm between two kinds of PWV. However, for the north Tibetan Plateau, Wang et al. found that the MODIS infrared product was shown to underestimate water vapor levels by more than 20% compared with GPS estimation, while the MODIS near-infrared product overestimates them by over 40% [22]. Bai et al. assessed the accuracy of PWV from the MODIS near-infrared product with GPS observations in mainland China [23]. They found that MODIS overestimates PWV in temperate continental climates while underestimating water vapor in other climate regions. It is evident that different accuracy and error characteristics will influence the application of remotely sensed water vapor products. Thus, comprehensively evaluating the performance of a newly proposed remotely sensed water vapor product is required.

Recently, a new remotely sensed water vapor product from the Visible Infrared Imaging Radiometer Suite (VIIRS) satellite sensor on the National Aeronautics and Space Administration (NASA) Suomi National Polar-orbiting Partnership (SNPP) and Atmospheric Administration-20 (NOAA-20) platform was established [24]. The water vapor data is retrieved through a statistical regression algorithm with selected infrared measurements over land and ocean for both day and night. Borbas et al. recently assessed its accuracy via a comparison with MODIS products and found R² values greater than 0.95 over land and ocean for both day and night [25]. However, the VIIRS algorithms were adapted from the MODIS MOD07 algorithm [24]; comparing with MODIS products was reasonably regarded as an internal evaluation. Thus, a more independent, external evaluation using GPS was considered to be carried out. This paper aims to evaluate the performance of PWV derived from the VIIRS/SNPP product generated by NASA (hereafter called the VIIRS product) using GPS observations from 231 GNSS stations in various regions of mainland China. For comparison purpose, two other kinds of commonly used remotely sensed water vapor products (i.e., the Atmospheric Infrared Sounder (AIRS) and MODIS) are also assessed by GPS in this study [26,27].

The structure of this paper is organized as follows: Section 2 describes data utilization and pre-processing strategies, including the GNSS precise point positioning (PPP) method. Section 3 illustrates the analysis methods for the water vapor derivation, the height correction procedure, and the evaluation metrics. Section 4 gives a result analysis and discussions, and Section 5 contains the conclusions.

2. Data Description

In order to comprehensively assess the performance of the PWV data from the VIIRS water vapor product, the GNSS data, radiosonde-based PWV data, and PWV data derived from AIRS and MODIS products were utilized in this study. This section describes the data information in detail.

2.1. GPS Data

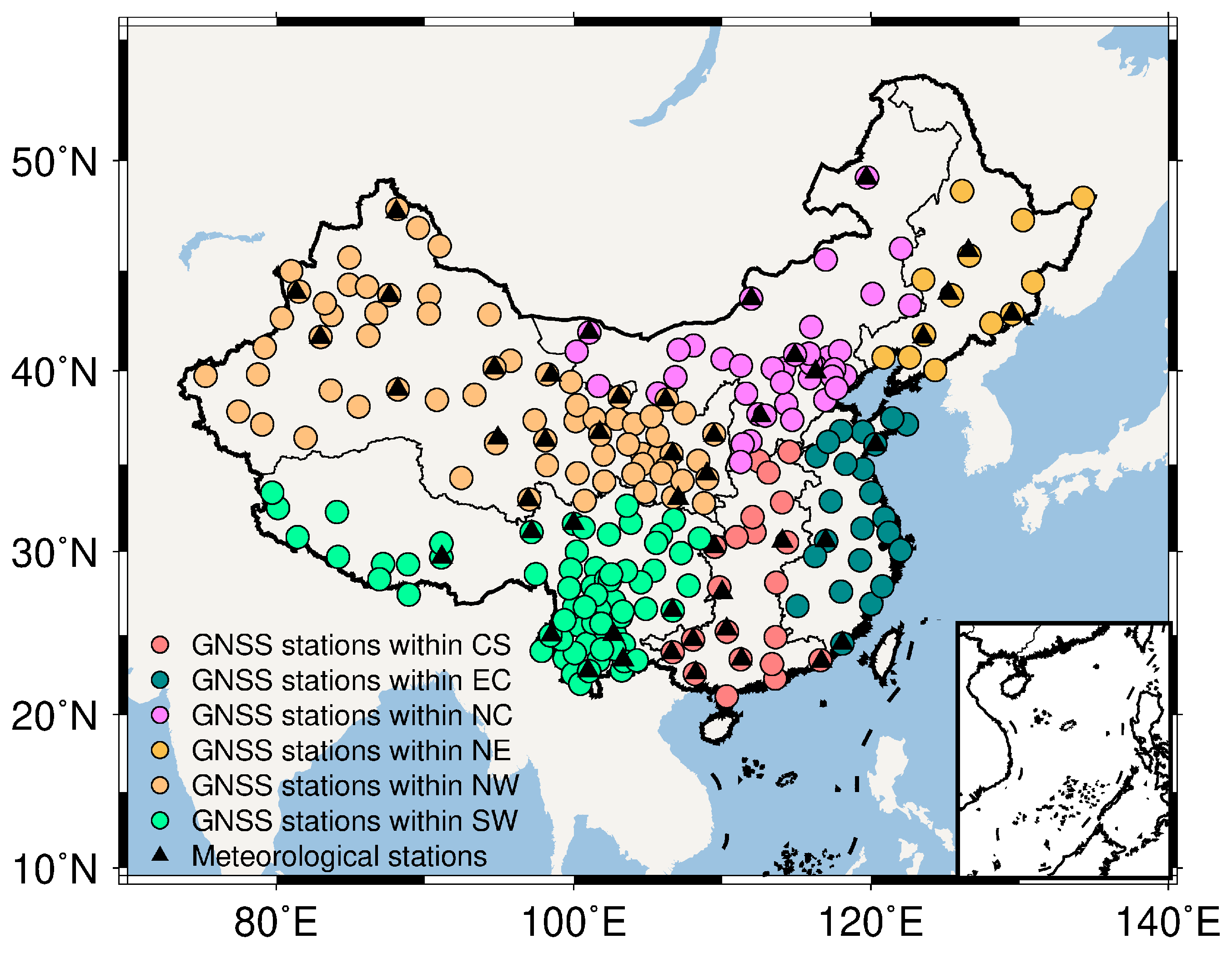
A total of 231 GNSS stations subordinated to the Crustal Movement Observation Network of China (CMONOC) managed by the China Earthquake Administration (CMA) were utilized in this study, as the dots shown in Figure 1. In order to comprehensively assess the accuracy of PWV derived from the VIIRS products within different regions of mainland China, all GNSS stations were divided into six geographical regions of China (represented by different colors in Figure 1). These six regions include the Central South (CS) of China, East China (EC), North China (NC), the North East (NE) of China, the North West (NW) of China, and the South West (SW) of China. This division was based on the criteria from the Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences (https://www.resdc.cn/data.aspx?DATAID=276, accessed on 7 January 2023).

Continuous GPS observations from 1 January 2012 to 31 December 2018 were obtained from these GNSS stations. It should be noted that although these GNSS stations can receive two types of observations (i.e., the GPS and GLONASS), only GPS observations were utilized for ZTD estimation in this study, which is the same as the routine International GNSS Service (IGS) ZTD product [28]. The precise point positioning (PPP) process [29] was applied daily to all stations with the same strategies as shown in

Table 1. GPS data descriptions and PPP processing strategies.

Observation data	Observation combination	Carrier-phase: L1 and L2 Pseudo-range: C1 and P2
	Processing interval	300 s
	Weighted strategy	$p=1, e>30°; p={\sin }^{2}e, e\le 30°$  1
	Cut off angle	7°
Error correction model	Satellite ephemeris	ESA repro3 (ES3)
	Phase wind up	Corrected [33]
	Tidal loading	Earth tide, polar tide and ocean tide correction [34]
	Relativistic effect	Corrected [34]
	Ionosphere delay	Ionosphere-free combination is adopted to eliminate the first-order of ionospheric delay
	ZTD priori model	GPT2 and Saastamoinen
	ZTD mapping function	VMF1
	Differential code bias (DCB)	DCB products from the CODE (Center for Orbit Determination in Europe)
Estimated parameters	ZTD stochastic model	Estimated as piece wise constant (1 h) and random walk between pieces (20 mm$/\sqrt{\mathrm{hour}}$)
	Horizontal tropospheric gradients	Estimated as daily constant parameters
	Station coordinates	Estimated as daily constant parameters
	Receiver clock offset	Estimated as white noises
	Ambiguity parameter	Estimated as float constants for each arc

¹ Note that $p$ represents the weight of observation and $e$ denotes the satellite elevation.

. In order to eliminate the first-order ionospheric delay, the ionosphere-free combination of GPS dual-frequency observation was used. The third-generation reprocessing satellite orbit and clock products provided by the European Space Agency (ESA) (i.e., ESA repro3, ES3) were adopted to reduce the impacts brought by reference frame updating. Additionally, the Saastamoinen model [30], input with the empirical meteorological parameters obtained from Global Pressure and Temperature 2 (GPT2) [31], were utilized to serve as the prior correction for the tropospheric delay, and the Vienna Mapping Function (VMF1) was adopted [32]. The tropospheric Zenith Total Delay (ZTD) was estimated as a piece-wise constant parameter every 1 h, and the horizontal tropospheric gradients were estimated as a daily constant parameter. Thus, the ZTD products with a sampling interval of 1 h at each GNSS station could be obtained through PPP processing, which was subsequently converted into PWV data.

2.2. Radiosonde Data

A total of 47 meteorological stations adjacent to GNSS stations in mainland China were utilized in this study, as the black triangles show in Figure 1. All meteorological stations satisfy the two following criteria [35], i.e., (a) the horizontal distances between the GNSS stations and their adjacent meteorological stations are less than 30 km, and (b) the height difference between the GNSS stations and their adjacent meteorological stations is less than 100 m. All meteorological stations could provide water vapor observations from radiosondes from 1 January 2012 to 31 December 2018. These data were obtained every 12 h at 00:00 and 12:00 UTC every day, which could be used as the independent assessment for GPS-derived PWV.

2.3. Water Vapor Data Derived from Remotely Sensed Water Vapor Products

2.3.1. VIIRS-Derived Water Vapor Data

Some infrared windows (at 8.6, 10.8, and 12 µm) of VIIRS sensors are useful to give some indication of low-level moisture which constitutes much of the total column water vapor amount. However, owing to the absence of some other infrared water vapor absorption bands, it is difficult to retrieve the atmospheric water vapor by VIIRS sensors alone. Fortunately, this project was realized with the assistance of two kinds of water vapor soundings, i.e., the CrIS (Cross-track Infrared Sounder) and the ATMS (Advanced Technology Microwave Sounder).

The NASA VIIRS/SNPP water vapor product provides total column water vapor properties from merged VIIRS infrared measurements, and the sounding data retrieved from the CrIS and ATMS which were calculated from the NOAA Unique Combined Atmospheric Processing System (NUCAPS). First, a statistical regression based on the split-window radiances was utilized to retrieve water vapor values from VIIRS observations. Then, the NUCAPS water vapor soundings data was calculated from a global training radiosonde-based profile dataset. Afterwards, a clear sky regression relationship was established between water vapor and the infrared window brightness temperatures of VIIRS and the sounding data from the NUCAPS. The NUCAPS water vapor data was added in clear and partly cloudy regions to enhance the water vapor depiction and to extend the coverage. Ultimately, the combined VIIRS water vapor product was accomplished.

In this study, the NASA VIIRS/SNPP Level-3 Daily Mean Water Vapor Products were utilized, which were generated with a gridding software called Yori developed by the University of Wisconsin-Madison Space Science Engineering Center [36]. The VIIRS product provides the global daily mean PWV value with a spatial resolution of 0.5° × 0.5°. The time span of the VIIRS product was from 1 April 2012 to 30 June 2018 on a daily resolution. It should be noted that the VIIRS product provided PWV data over daytime and nighttime, which is defined by the solar zenith angle of 85°. These data can be downloaded from the website of the Level-1 Atmosphere Archive and Distribution System Distributed Active Archive Center (LAADS DAAC) managed by NASA (https://ladsweb.modaps.eosdis.nasa.gov/archive/allData/5110/WATVP_D3_VIIRS_SNPP/, accessed on 7 January 2023).

2.3.2. AIRS-Derived Water Vapor Data

The AIRS is a hyperspectral infrared grating spectrometer carried on the polar-orbiting Aqua spacecraft platform, with a spectral resolution ($\lambda /\mathsf{\Delta }\lambda$) of 1200 [37]. As it scans, the AIRS collects radiances in 2378 inferred channels with wavelengths ranging from 3.7 to 15.4 µm, and 4 visible channels with wavelengths ranging from 0.4 to 0.94 µm [38]. Some channels among them can be utilized in water vapor retrieval due to their response to the concentration of water vapor at various heights.

The cloud-cleared radiances in the water vapor absorption channels were utilized to determine the amount of radiation absorbed by the water vapor within the atmosphere. Afterwards, the column integrated water vapor value could be generated through the combination of some channels with differing sensitivity to the water vapor, with the help of additional temperature-measured channels. Note that a first-guess profile, in which the atmospheric state variables are assumed to be known, were used to drive the retrieval algorithm. Moreover, the first-guess water vapor profile was corrected via the differences between the measured and computed radiances for all used channels after comparison.

In this study, the AIRS Level 3 Daily Gridded Product (Version 7) was adopted. It provides the daily averaged PWV values which have been averaged and binned into 1° × 1° on a global scale since 8 August 2002. To be consistent with PWV derived from the VIIRS product, AIRS data from 1 April 2012 to 30 June 2018 were extracted, which can be freely accessed from NASA’s Goddard Earth Sciences Data and Information Services Center (GES DISC) (https://disc.gsfc.nasa.gov/datasets/AIRS3STD_7.0/summary?keywords=Aqua%20AIRS, accessed on 7 January 2023).

2.3.3. MODIS-Derived Water Vapor Data

The MODIS is an earth observing system (EOS) instrument aboard the Terra and Aqua spacecrafts, which is used for global monitoring of atmospheric properties from space [9]. Relying on the absorption of water vapor from near-infrared solar radiation reflected by the bottom surface, five near-infrared bands around the 0.94 µm within MODIS were utilized for water vapor retrieval.

The ratios of three water vapor absorbing bands (0.905, 0.936, and 0.930 µm) and two atmospheric window bands (0.86 and 1.24 µm) were employed to quantify the column water vapor amount with the help of the transmittance from a table lookup. King et al. pointed out that the water vapor values from MODIS near-infrared observations can be determined with errors of about 7% compared with water vapor measurements using ground-based microwave radiometers [39].

The Level-3 atmosphere daily global product (MOD08_D3) was selected in this study to provide intercomparison with the accuracy of the VIIRS product. The MOD08_D3 product contains daily 1° × 1° grid average values of atmospheric water vapor since February 2000. As for the AIRS, MODIS-derived PWV data from 1 April 2012 to 30 June 2018 were utilized. The data could be obtained from the LAADS DAAC through the following link: https://ladsweb.modaps.eosdis.nasa.gov/archive/allData/61/MOD08_D3, accessed on 7 January 2023.

3. Methodology

In this section, the approach to PWV data derived from GPS observations and three remotely sensed water vapor products (i.e., VIIRS, AIRS, and MODIS) are first presented. Furthermore, the method of the height correction for remotely sensed water vapor products is then introduced, followed by the performance evaluation metrics for the comparisons between PWV data from GPS and radiosonde, and between PWV data from GPS and three remotely sensed water vapor products.

3.1. PWV Derivations from GPS Observation

Based on the PPP method, the GPS-ZTD time series of each GNSS station was obtained. Two parts of the zenith delay are contained within the ZTD derived from GPS observations, i.e., the zenith hydrostatic delay (ZHD) and the zenith wet delay (ZWD). To convert ZTD to PWV, ZHD must be firstly calculated and removed from ZTD. The ZHD for each GNSS station was calculated through the Saastamoinen model [30] with the pressure data from the fifth-generation meteorological reanalysis data products (ERA5) from the ECMWF [40]. Afterward, the ZWD was obtained by removing ZHD from ZTD. Consequently, the PWV derived from GPS observations (GPS-PWV) was calculated with the following equations:

$${\mathrm{PWV}}_{\mathrm{GPS}}=\Pi \times \left(\mathrm{ZTD}-\mathrm{ZHD}\right)$$

(1)

$$\Pi =\frac{{10}^6}{{\rho }_w{R}_w\left(\frac{k_3}{T_m}+k_2^{\prime }\right)}$$

(2)

where $\Pi$ represents the conversion factor [41], which is the key factor in converting ZWD into PWV [42]. $k_2^{\prime }$ ($=17\pm 10 \mathrm{K}/\mathrm{hPa}$) and $k_3$ ($=3.776\pm 0.004\times {10}^5 {\mathrm{K}}^2/\mathrm{hPa}$) represent atmospheric refraction coefficients; $R_w$ ($=461.51 \mathrm{J}/\left(\mathrm{K}\times \mathrm{kg}\right)$) is the water vapor gas constant; ${\rho }_w$ ($=1000 \mathrm{kg}/{\mathrm{m}}^3$) is the density of liquid water. $T_m$ is the weighted mean temperature, which is calculated with temperature and partial pressure of water vapor from ERA5 [43].

It should be noted that the meteorological data (e.g., the pressure and temperature) were derived from gridded-based ERA5 pressure level products. However, the GNSS stations are generally not located in the center of grids and the antenna heights of each station are not consistent. As a result, the horizontally bilinear interpolation to the locations of GNSS stations and the vertical elevation compensation for the antenna height (i.e., the exponential interpolation for pressure and the linear interpolation for temperature) were conducted to obtain meteorological data at each GNSS station. The abovementioned procedures were accomplished with the help of the GNSS Meteorological Ensemble Tools (GMET) developed by the GNSS Research Center, Wuhan University [44]. Considering that PWV data from remotely sensed water vapor products share the temporal resolution of 1 day, the 1 h GPS-PWV was averaged into a daily resolution for the following comparison.

3.2. PWV Derivations from Remotely Sensed Water Vapor Products

It should be noted that PWV data provided by three kinds of remotely sensed water vapor products are gridded-based, and the GNSS stations are generally not located in the center of the grid. Thus, the nearest neighbor method, which was extensively used in extracting remotely sensed products at a specific spatial location [45,46], was applied to obtain the PWV value of each GNSS station. Furthermore, the VIIRS product provides PWV data for both day- and night-time. As a result, the VIIRS-derived PWV obtained for one day is based on the mean value of day- and night-time, and those days when the day- or night-time value was missing would be eliminated.

Furthermore, the PWV derived from the remotely sensed water vapor products usually represent the mean value of the satellite footprint within a specific grid, but the mean elevation of a grid point and the included GNSS stations are not generally consistent [22]. This will cause a bias between the GPW-PWV and the remotely sensed PWV due to the exponential variation of PWV with the height [47]. Hence, a height correction procedure was required before conducting the performance evaluation [48,49]. In this study, PWV data derived from remotely sensed water vapor products were modified to GNSS station heights. The height correction procedure was conducted according to Kouba et al. as the following equation [50]

$${\mathrm{PWV}}_{mod}={\mathrm{PWV}}_{ori}·\exp \left(-\frac{H_1-H_0}{2000}\right)$$

(3)

where ${\mathrm{PWV}}_{ori}$ and $H_0$ represent the original remotely sensed PWV value and the mean surface elevation of a specific grid point, and ${\mathrm{PWV}}_{mod}$ and $H_1$ are the modified remotely sensed PWV value and the target height of the GNSS station included within the grid point. Note that the mean surface elevations of grid points were derived from the Terra Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global Digital Elevation Model (GDEM) Version 3 (ASTGTM) provided by the Land Processes Distributed Active Archive Center (LP DAAC) (https://lpdaac.usgs.gov/products/astgtmv003/, accessed on 7 January 2023).

3.3. Evaluation Metrics

To evaluate the performance of PWV data, three different metrics were applied in this study, i.e., the correlation coefficient (CC), the mean bias (MB), and the root-mean-square error (RMSE).

The correlation coefficient (CC) represents the linear relationship between two groups of PWV data, which is defined as shown:

$$\mathrm{CC}=\frac{{{\displaystyle \sum }}_{i=1}^N\left({\mathrm{PWV}}_{test}^i-\overline{{\mathrm{PWV}}_{test}}\right)\left({\mathrm{PWV}}_{ref}^i-\overline{{\mathrm{PWV}}_{ref}}\right)}{\sqrt{{{\displaystyle \sum }}_{i=1}^N{\left({\mathrm{PWV}}_{test}^i-\overline{{\mathrm{PWV}}_{test}}\right)}^2}\sqrt{{{\displaystyle \sum }}_{i=1}^N{\left({\mathrm{PWV}}_{ref}^i-\overline{{\mathrm{PWV}}_{ref}}\right)}^2}}$$

(4)

where the ${\mathrm{PWV}}_{test}$ and ${\mathrm{PWV}}_{ref}$ represent PWV value from the tested and the referred data sources, e.g., the VIIRS-derived PWV compared with the GPS-derived PWV. $\overline{{\mathrm{PWV}}_{test}}$ and $\overline{{\mathrm{PWV}}_{ref}}$ are the mean values of ${\mathrm{PWV}}_{test}$ and ${\mathrm{PWV}}_{ref}$, respectively.

The MB represents the derivation between two groups of PWV, which is defined as

$$\mathrm{MB}=\frac{{{\displaystyle \sum }}_{i=1}^N\left({\mathrm{PWV}}_{test}^i-{\mathrm{PWV}}_{ref}^i\right)}{N}$$

(5)

where ${\mathrm{PWV}}_{test}$ and ${\mathrm{PWV}}_{ref}$ represent the PWV value being tested and being referred. Thus, when MB is higher than 0, it means the VIIRS-PWV overestimates the water vapor compared to the GPS-PWV.

The RMSE, which is an accuracy indicator representing the overall performance, is calculated as

$$\mathrm{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^N{\left({\mathrm{PWV}}_{test}^i-{\mathrm{PWV}}_{ref}^i\right)}^2}{N}}$$

(6)

4. Result and Discussion

In this section, the accuracy of the GPS-derived PWV (GPS-PWV) is firstly verified with the radiosonde observation (Radio-PWV) from 47 adjacent meteorological stations. Subsequently, the PWV derived from the VIIRS and two other kinds of remotely sensed water vapor products (i.e., the AIRS and MODIS) at each GNSS station are evaluated and analyzed within different seasons and various regions of mainland China via the GPS-PWV after the height correction procedure was applied.

4.1. Comparison between GPS-PWV and Radio-PWV

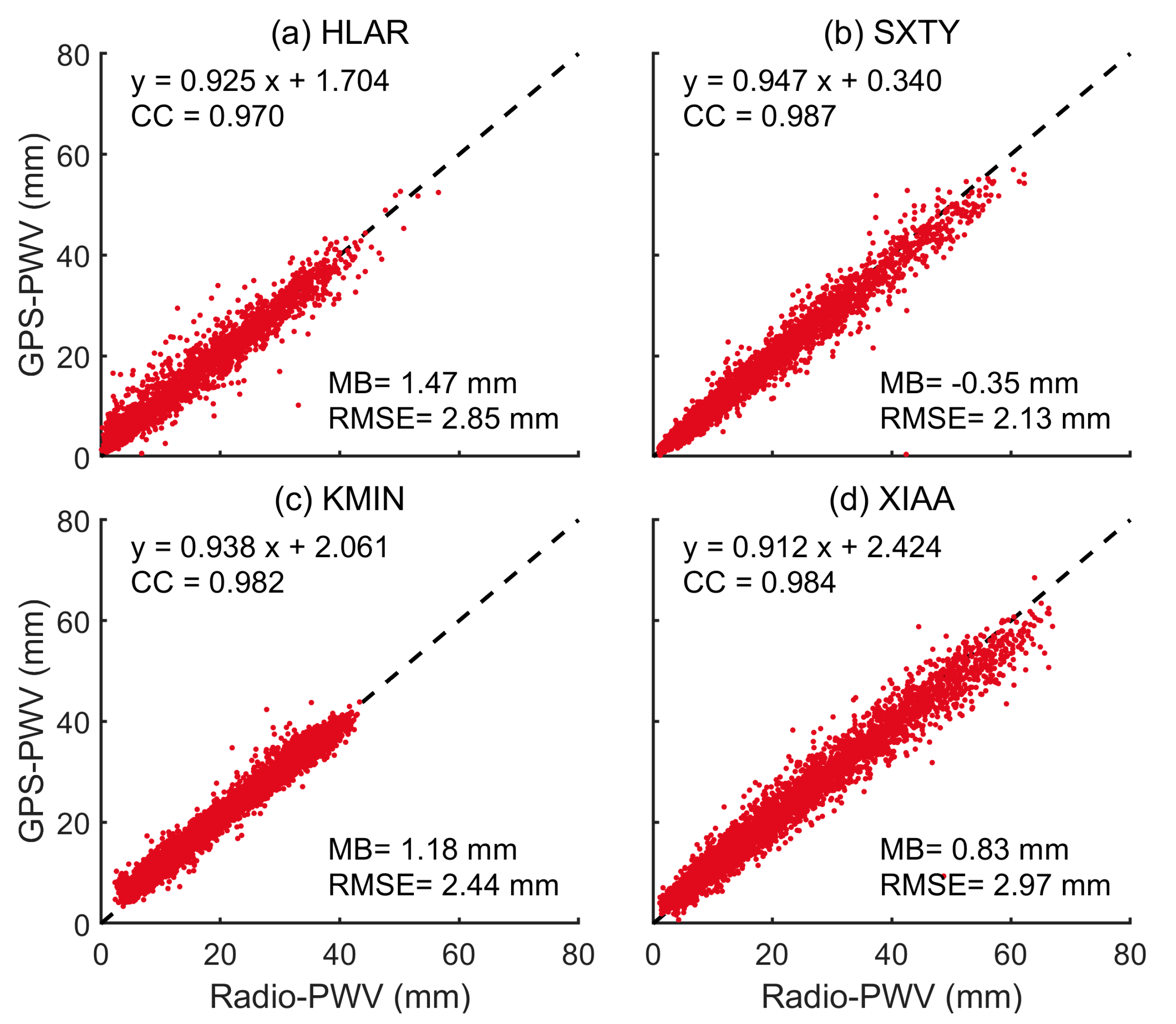
GPS-derived PWV (GPS-PWV) can be effectively evaluated with radiosonde-based PWV (Radio-PWV) [51]. In this study, a total of 47 radiosonde-equipped meteorological stations adjacent to the GNSS stations from 1 January 2012 to 31 December 2018 were utilized to guarantee the accuracy of the GPS-PWV. Figure 2 gives the scatter plots of the GPS-PWV from four selected GNSS stations (i.e., HLAR (a), SXTY (b), KMIN (c), and XIAA (d)) versus the corresponding Radio-PWV from adjacent meteorological stations. It revealed that the correlation coefficients (CC) were all larger than 0.97 for these four stations. The MB values of four stations varied from −0.35 to 1.47 mm, and the corresponding RMSE varied from 2.13 to 2.97 mm. This indicated that the GPS-PWV was consistent and unbiased with reference to the Radio-PWV.

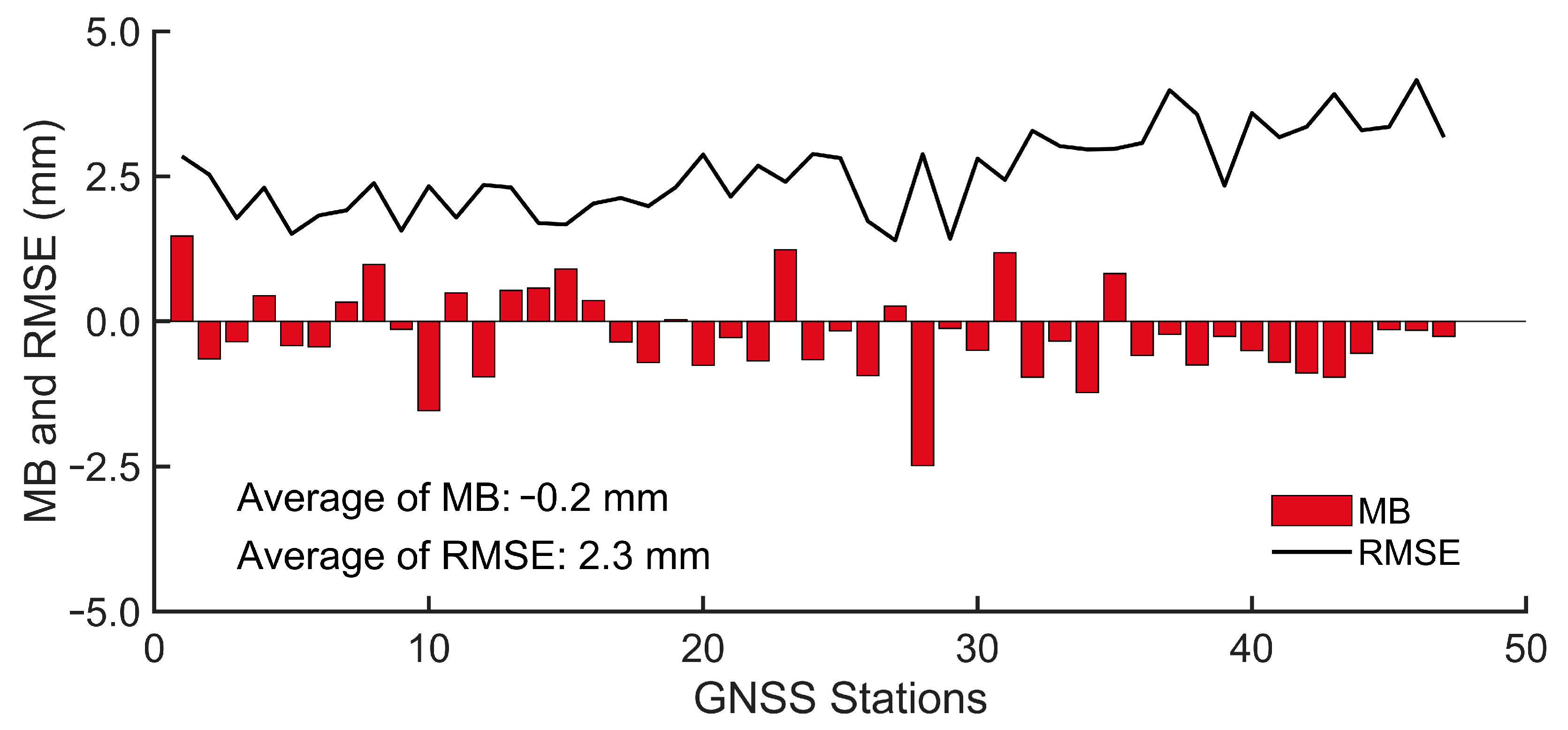
For all 47 GNSS stations assessed by radiosonde results, all stations showed a correlation coefficient higher than 0.94 with an average value of 0.98. Figure 3 gives the statistical results of the assessment from all 47 GNSS stations. It showed that the MB values of all stations varied from −2.49 mm to 1.47 mm with an average value of −0.2 mm. This revealed that there are no systematic biases between the GPS-PWV and the Radio-PWV. The corresponding RMSE varied from 1.40 mm to 4.16 mm with an average value of 2.3 mm. These results coincided with previous studies [52,53], which indicated that the PWV can be effectively derived from GPS observations with satisfactory accuracy in this study. As a result, GPS-derived PWV served as the reference for evaluating PWV performance from VIIRS and two other remotely sensed water vapor sources.

4.2. Assessment of PWV Derived from Different Remotely Sensed Water Vapor Products

The PWV data retrieved from the VIIRS, AIRS, and MODIS products (i.e., the VIIRS-PWV, AIRS-PWV, and MODIS-PWV) from 1 April 2012 to 30 June 2018 at 231 GNSS stations were assessed with the GPS-PWV via three evaluation metrics (i.e., the CC, MB, and RMSE). The statistical results (i.e., the maximum, minimum, and mean values) of the CC, MB, and RMSE for each product are exhibited in

Table 2. The statistical results (i.e., the maximum, minimum, and mean values) of three evaluation metrics of the PWV data derived from the remotely sensed water vapor products compared with the GPS-PWV in mainland China.

Evaluation Metrics	PWV Source	Min	Max	Mean
	VIIRS	0.572	0.980	0.92
CC	AIRS	0.756	0.980	0.96
	MODIS	0.566	0.961	0.92
	VIIRS	−7.20	4.03	−1.6
MB (mm)	AIRS	−5.83	8.50	−0.2
	MODIS	−9.80	6.96	−1.6
	VIIRS	2.06	9.44	4.7
RMSE (mm)	AIRS	1.16	9.88	4.0
	MODIS	1.73	12.76	5.5

, and the histograms of the statistical results are given in Figure 4.

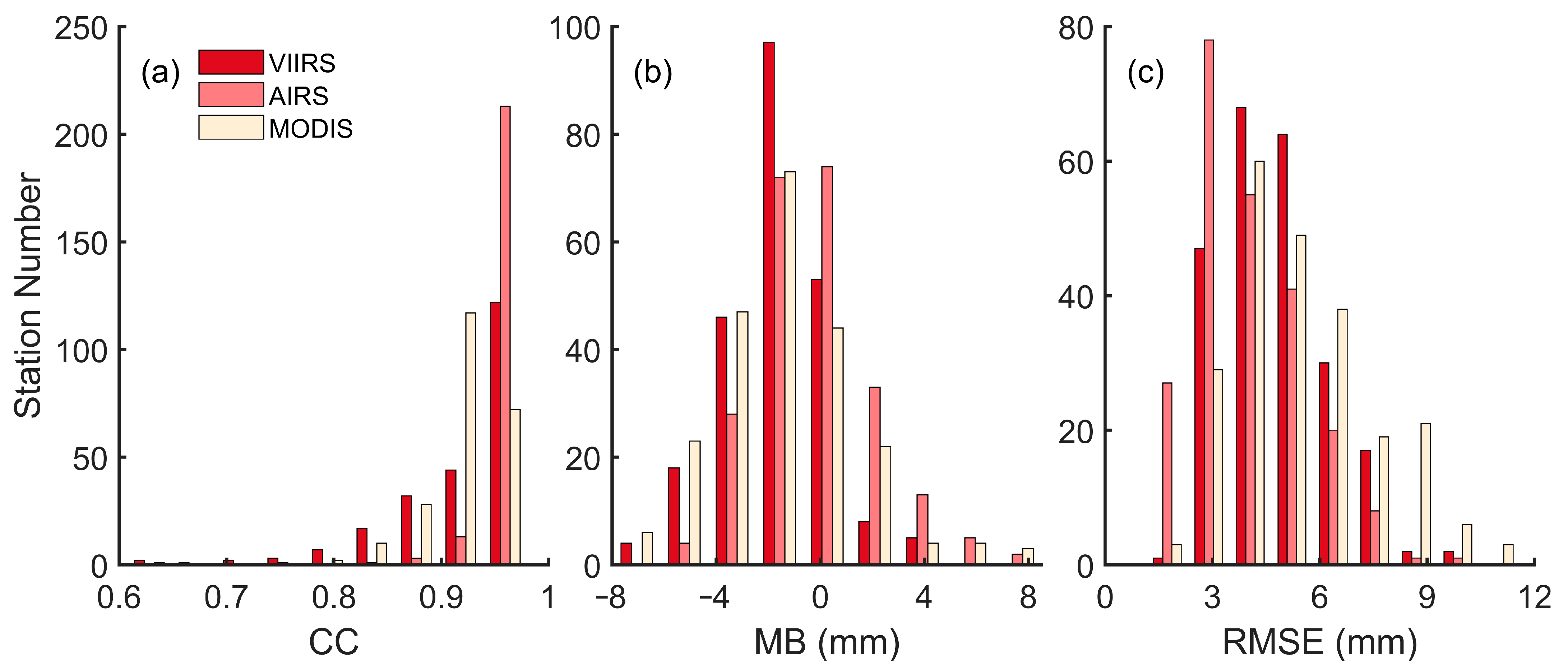
Results showed that the PWV data from the VIIRS attained CC values varying from 0.572 to 0.980, and most stations attained a CC value higher than 0.9 (Figure 4a). The mean value of the CC for all 231 stations was 0.92, which indicated that the VIIRS-PWV was generally highly correlated with the GPS-PWV in mainland China. Furthermore, the AIRS-PWV and MODIS-PWV attained the mean CC values of 0.96 and 0.92, respectively. Compared with the AIRS-PWV and MODIS-PWV, the mean CC value of the VIIRS-PWV was consistent with the MODIS-PWV, but it was smaller than that of the AIRS-PWV. Moreover, the minimum CC values of the VIIRS-PWV and MODIS-PWV were both smaller than 0.6, while the minimum CC value of the AIRS-PWV was larger than 0.75. This manifested that the VIIRS-PWV shared similar results with the MODIS-PWV, but they both performed slightly poorer than the AIRS-PWV.

For the MB results, results from the histograms showed that the MB of three remotely sensed water vapor products all followed an approximate normal distribution (Figure 5b). Statistical results revealed that the MB value of the VIIRS-PWV showed the range from −7.20 to 4.03 mm, with a mean value of −1.6 mm. This indicated that the VIIRS-PWV generally underestimated the PWV value in mainland China. In addition, the mean MB values of the AIRS-PWV and MODIS-PWV were −0.2 and −1.6 mm, respectively. Compared with the results of the AIRS-PWV and MODIS-PWV, the mean MB value of VIIRS-PWV coincided with the MODIS-PWV, but its absolute value was larger than the AIRS-PWV. This showed that the VIIRS-PWV generally had a larger deviation than the AIRS-PWV in mainland China.

The RMSE of the VIIRS-PWV was in a range from 2.06 to 9.44 mm, with a mean value of 4.7 mm. This indicated that the VIIRS-PWV had good accuracy within mainland China. For the two other kinds of water vapor products, the AIRS-PWV and MODIS-PWV showed the mean RMSE values of 4.0 and 5.5 mm, respectively. These results were close to that of the VIIRS-PWV, which indicated that the PWV data derived from the VIIRS product have similar accuracy to those from the AIRS and MODIS products. In general, the VIIRS product provided PWV data of comparable accuracy with those from the AIRS and MODIS products, which showed that the VIIRS-PWV could be applied in large-area research with satisfactory accuracy.

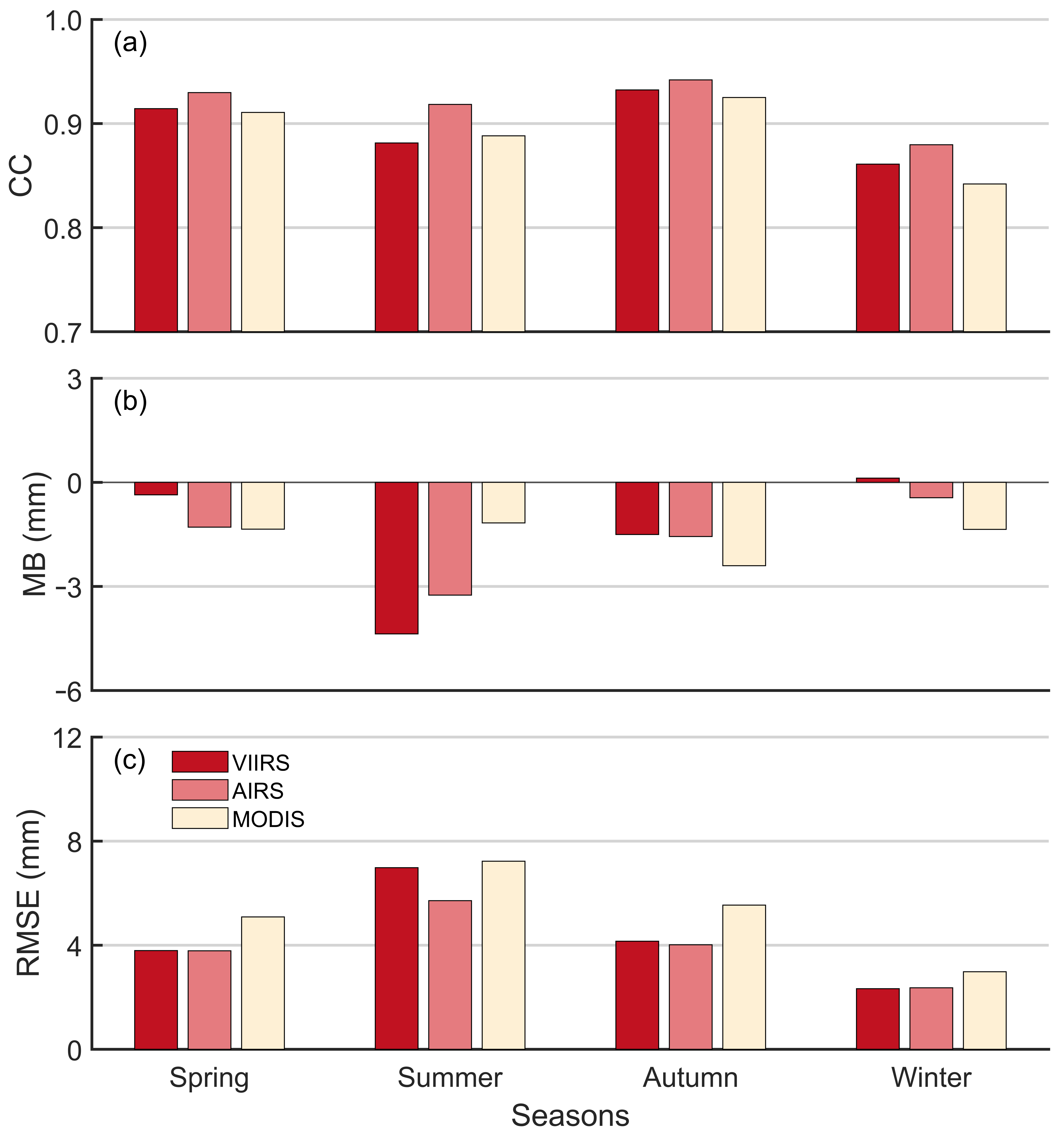
4.3. PWV Performance Evaluation of Different Remotely Sensed Water Vapor Products within Various Seasons in Mainland China

To further analyze the differences of the inter-seasonal performance of the PWV data from the VIIRS, AIRS, and MODIS in mainland China, assessments were carried out at all GNSS stations for four different seasons within the research time span. To be specific, the PWV data derived from the remotely sensed water vapor products were grouped into four seasons in the north hemisphere, i.e., spring (March, April, and May), summer (June, July, and August), autumn (September, October, and November), and winter (December, January, and February). 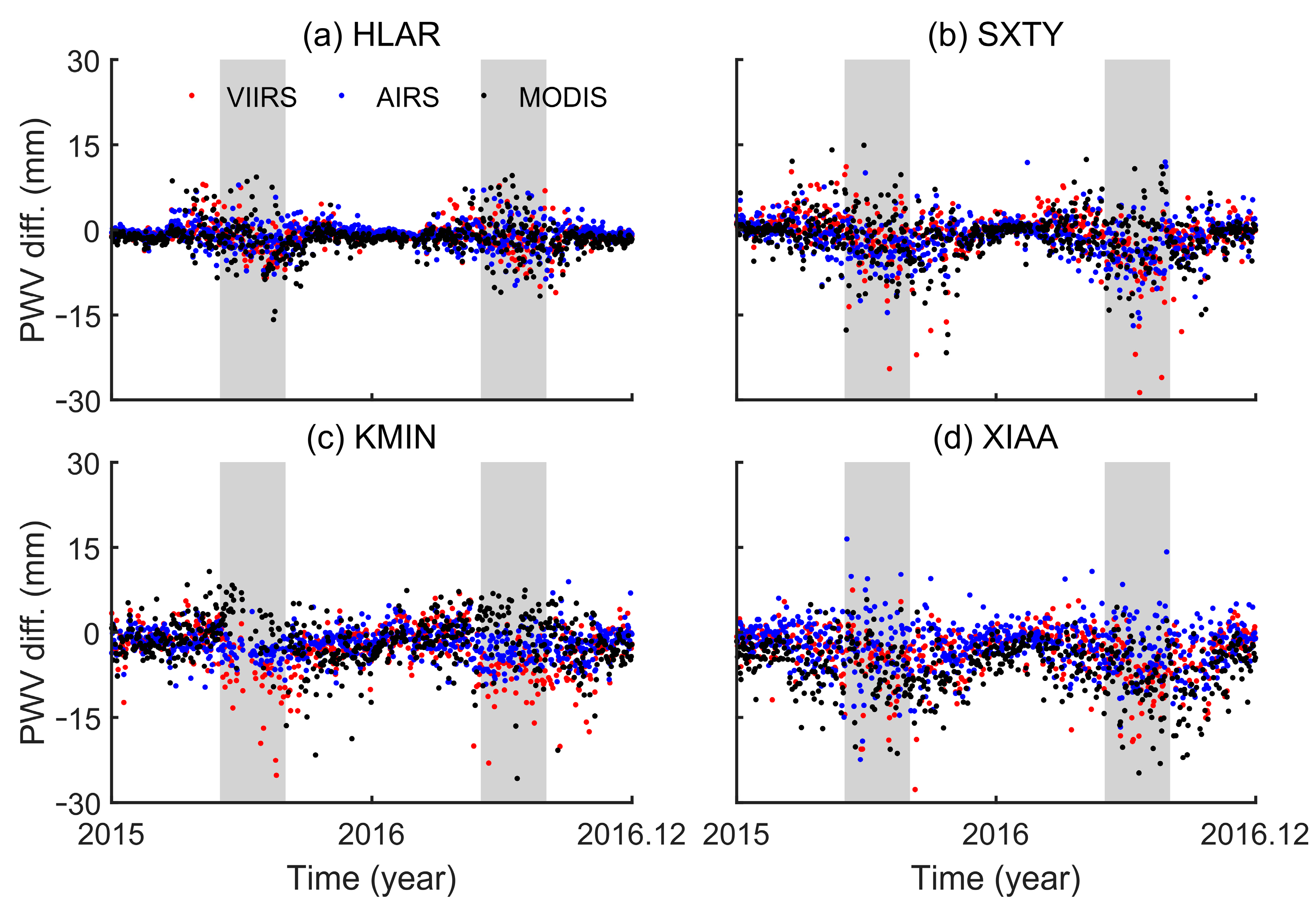Three evaluation metrics (i.e., the CC, MB, and RMSE) for different regions were summarized in Figure 5. The time series of the PWV differences between the data derived from the remotely sensed water vapor products and the GPS observations at four selected stations are given in Figure 6. For the convenience of observation, Figure 6 only gives the time series from 2015 to 2016. In addition, the grey areas in Figure 6 represent the periods of summer for each year.

In general, the PWV data derived from three kinds of water vapor products highly correlated with the GPS-PWV for all seasons. The mean CC values for different products within different seasons were all higher than 0.85. Among different products, the AIRS product performed the best with higher CC values than the VIIRS and MODIS products, which coincides with the previous analysis in Section 4.2. However, the MB and RMSE of the differences between the PWV data derived from the remotely sensed water vapor products and GPS generally revealed seasonal variations. For the results of the MB, the VIIRS products revealed the greatest bias in summer (−4.4 mm) and the smallest bias in winter (0.1 mm). This phenomenon was also observed for the AIRS product but was not significant for the MODIS product. This indicated that the seasonal bias of the PWV differences between remotely sensed water vapor products and GPS observations might be sensor-dependent. On the other hand, all three products revealed higher RMSE values in summer and lower values in winter when the PWV is generally the lowest in mainland China. The RMSE of the VIIRS products were 7.0 mm in summer and 2.3 mm in winter. The time series at four selected stations also demonstrated the phenomenon of the PWV differences fluctuating more severely in summer (i.e., the grey area) than other seasons with in a year (Figure 6). The seasonal variations of the PWV differences between the remotely sensed water vapor products and GPS observations in mainland China were also reported in previous studies, e.g., [23,54].

4.4. PWV Performance Evaluation of Different Remotely Sensed Water Vapor Products within Various Regions in Mainland China

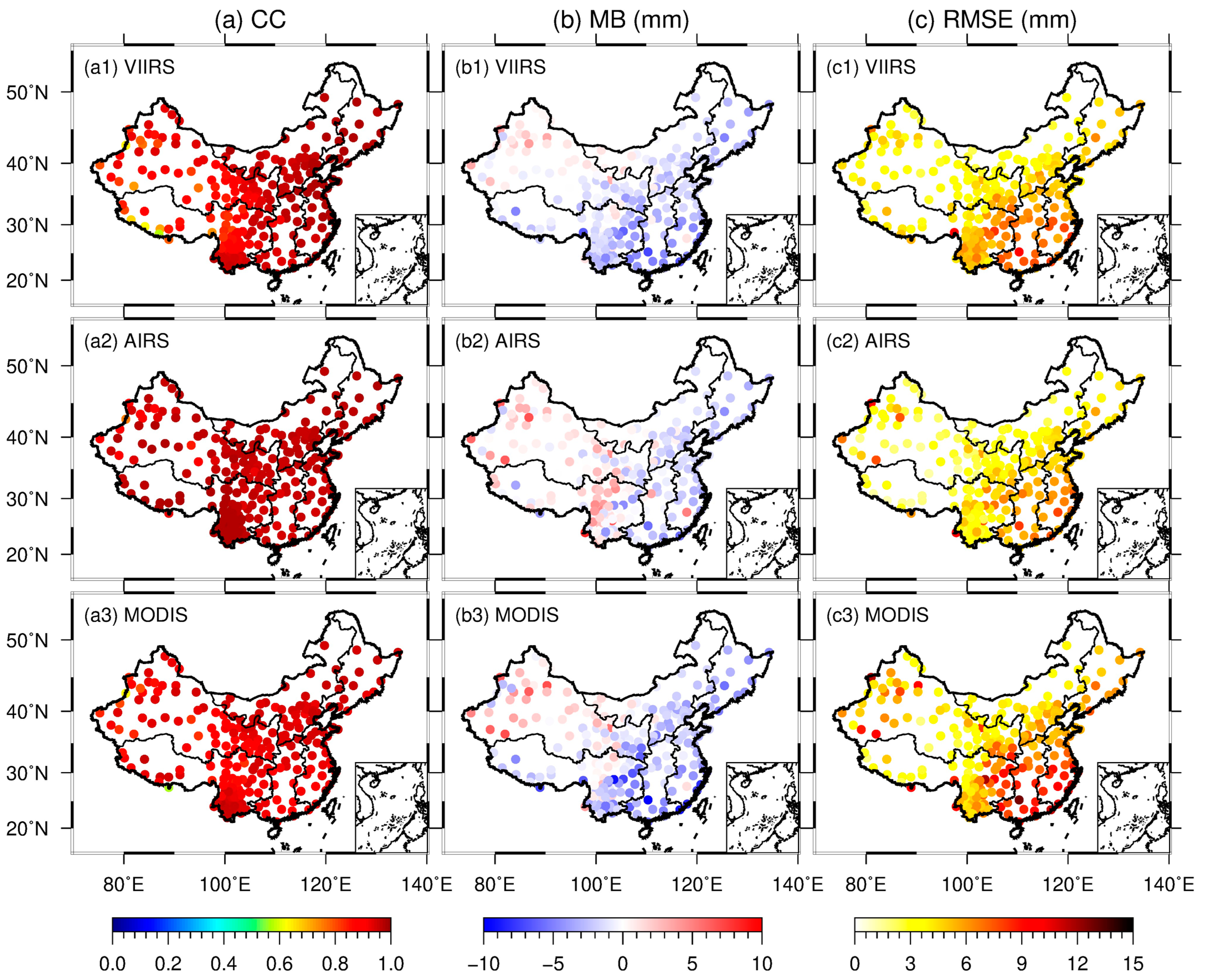
To further analyze the performance of the PWV data from the VIIRS, AIRS, and MODIS products among various regions of mainland China, all GNSS stations were divided into six geographical regions according to their station locations. Three evaluation metrics (i.e., the CC, MB, and RMSE) of the VIIRS-PWV, AIRS-PWV, and MODIS-PWV compared with the GPS-PWV at all GNSS stations within various regions in mainland China are shown in Figure 7. The mean values and standard deviations of the evaluation metrics within various regions are presented in Figure 8. Note that the six regions were grouped by the northern region (i.e., the NW, NC, and NE regions) and the southern region (i.e., the SW, CS, and EC regions) of China, which is shown as the two parts separated by the dashed line in Figure 8.

From the CC results, it can be observed that the VIIRS-PWV was generally correlated with the GPS-PWV in mainland China (see Figure 7(a1)). Among various regions, the SW region attained the lowest mean CC value of 0.88, while the NE region achieved the highest mean CC value of 0.97 (Figure 8a). However, the results of the VIIRS-PWV at some stations within the western region of China displayed low CC values, especially in the Himalayas and the mountainous region of Xinjiang. Statistical results also illustrated that the mean CC values of the NW and SW regions were 0.89 and 0.88, respectively. These values were relatively lower than those of other regions in mainland China. This indicated that the PWV data derived from the VIIRS product are less consistent with the GPS-PWV in western China. Similarly, the MODIS-PWV exhibited the mean CC values of 0.90 and 0.91 in the NW and SW regions, respectively. However, this situation was not significant for the AIRS-PWV, which attained mean CC values of 0.95 and 0.97 within these two regions. This is why the VIIRS-PWV and MODIS-PWV performed slightly poorer than the AIRS-PWV assessed by the CC, as illustrated in Section 4.2.

For the MB results, we can see that the VIIRS-PWV generally underestimated the PWV value in most regions in mainland China (see Figure 7(b1)). Among various regions, the NW region displayed the smallest deviation of −0.2 mm, while the CS region displayed the largest deviation of −3.4 mm. In general, the VIIRS-PWV exhibited a similar regional characteristic to those of the AIRS-PWV and MODIS-PWV. Compared with the GPS-PWV, the PWV data derived from the different remotely sensed water vapor products overestimated the PWV value at some stations in the western region of China and underestimated the PWV value in other regions (Figure 7b). This phenomenon was also consistent with previous studies [23,55]. In addition, the VIIRS-PWV exhibited smaller deviation than the AIRS-PWV and MODIS-PWV within the NW region. This is because fewer stations revealed overestimation for the VIIRS-PWV in the NW region than those for the AIRS-PWV and MODIS-PWV (see Figure 7b).

For the RMSE results, the VIIRS-PWV generally revealed an obviously larger RMSE in southeastern China than the northwestern China (Figure 7(c1)). Among various regions, statistical results showed that the maximum RMSE was obtained from the CS region with a mean RMSE value of 6.3 mm, while the minimum RMSE was obtained from the NW region with a mean RMSE value of 3.8 mm (Figure 8c). This coincided with the regional characteristics of the MB. In addition, the mean RMSE values of the southern region of China for the VIIRS-PWV, AIRS-PWV, and MODIS PWV were 5.6, 4.5, and 6.3 mm, respectively. Comparatively speaking, the mean RMSE values of the northern region of China for VIIRS-PWV, AIRS-PWV, and MODIS PWV were 3.9, 3.5, and 4.8 mm, respectively. This indicated that these remotely sensed water vapor products have better accuracy within the northern region of China than in the southern region.

5. Conclusions

PWV is a vitally important factor in atmospheric circulation. Accurately measuring the PWV within the atmosphere is significant for forecasting extreme weather and understanding the dynamics of climate change. The remote sensing techniques make wide-range PWV acquisition possible, while comprehensively evaluating the performance of a newly proposed remotely sensed water vapor product is a prerequisite before its extensive application. In this study, the accuracy of the newly established remotely sensed water vapor product from the NASA VIIRS/SNPP platform (VIIRS-PWV) within various regions of mainland China was evaluated via the PWV data derived from GPS observations to verify its suitability for future utilization.

Specifically, GPS-derived PWV data (GPS-PWV) from 231 stations subscribed to the CMONOC were firstly calculated through the PPP technique and meteorological reanalysis data from the ERA5. Then, the GPS-PWV was compared with the PWV data from the radiosonde records (Radio-PWV) at 47 meteorological stations adjacent to the GNSS stations. Results showed that all stations revealed a CC value of 0.98, an MB value of −0.2 mm, and an RMSE value of 2.3 mm on average, which verified the suitability of the GPS-PWV for accuracy assessment.

Subsequently, the performance of the VIIRS-PWV was evaluated via the GPS-PWV from 2012 to 2018 in mainland China. Furthermore, the performance of two other kinds of remotely sensed water vapor products (i.e., the AIRS and MODIS) were also assessed by the GPS-PWV to serve as the intercomparison. Results of the VIIRS-PWV showed that the mean values of the CC, MB, and RMSE were 0.92, −1.6 mm, and 4.7 mm, respectively. These values were similar to the results of the AIRS-PWV and MODIS-PWV, which manifested that the VIIRS product could provide PWV data of comparable accuracy with those from other kinds of remotely sensed water vapor products.

Furthermore, the performance of the VIIRS-PWV within different seasons and various regions in mainland China was analyzed. The results of temporal analysis revealed that the CC of the PWV derived from three remotely sensed water vapor products and GPS observations did not exhibit significant differences, while the MB and RMSE of the differences between the PWV data derived from the remotely sensed water vapor products and GPS generally revealed seasonal variations. The VIIRS products generally performed better in winter (with the MB and RMSE value of 0.1 mm and 2.3 mm) than in summer (with the MB and RMSE value of −4.4 and 7.0 mm). The results of temporal analysis revealed that the VIIRS-PWV attained the lowest accuracy within the CS region, which had a mean MB value of −3.4 mm and a mean RMSE value of 6.3 mm. The highest accuracy appeared within the NW region, which exhibited a mean MB value of −0.2 mm and a mean RMSE value of 3.8 mm. In addition, the southern region of China (i.e., the SW, CS, and EC regions) obtained a mean RMSE value of 5.6 mm, while the northern region of China (i.e., the NW, NC, and NE regions) obtained a mean RMSE value of 3.9 mm. This indicated that the VIIRS-PWV products have better accuracy within the northern region of China than within the southern region. In general, the VIIRS product could provide PWV data with satisfactory accuracy for large-area scientific applications.