Screening Image Features of Collapsed Buildings for Operational and Rapid Remote Sensing Identification
Abstract
:1. Introduction
2. Data and Methodology
2.1. Data
2.1.1. Building Sample Set
2.1.2. Application Test Image Set
2.2. Methodology
2.2.1. Ability Evaluation of Features
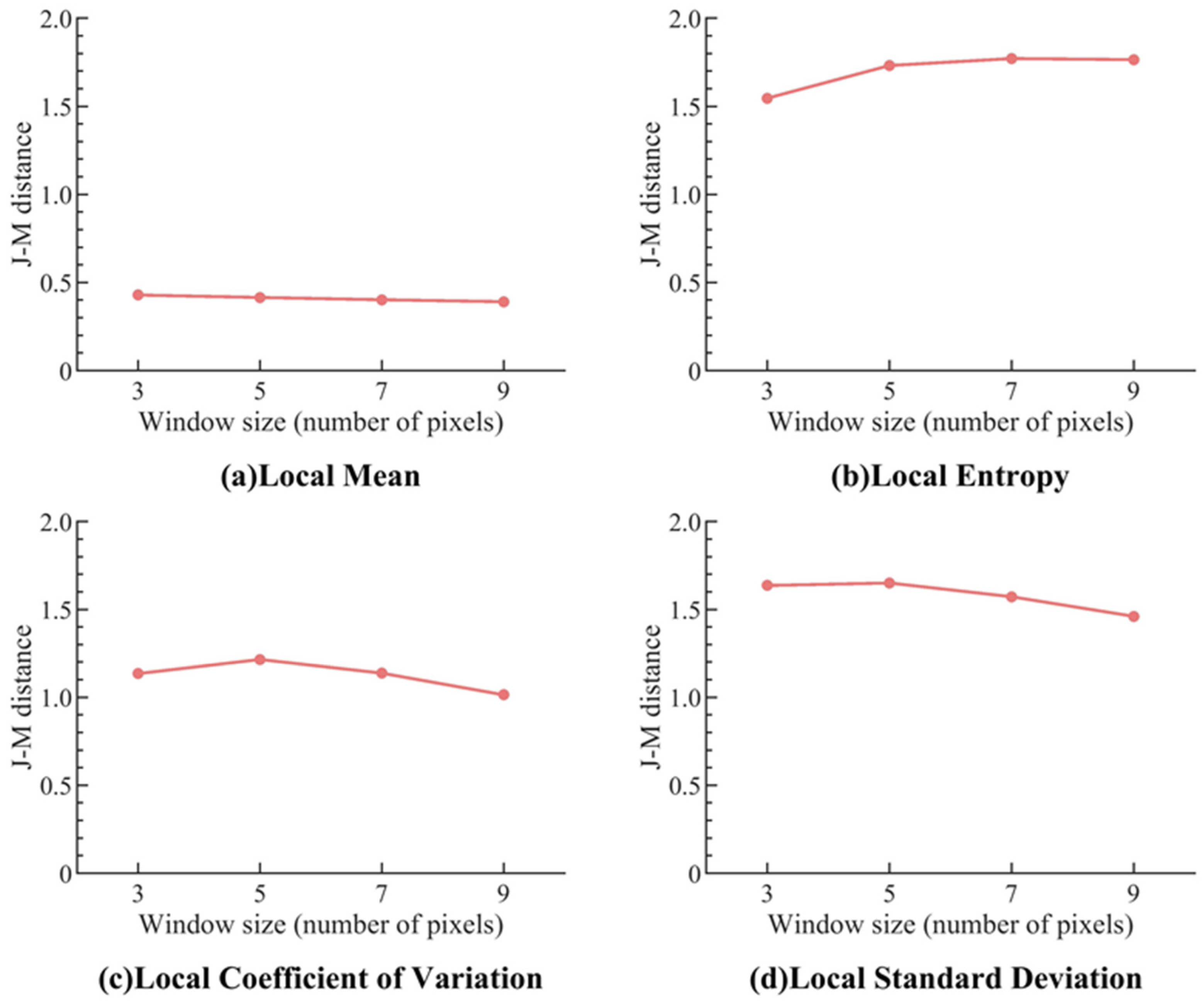
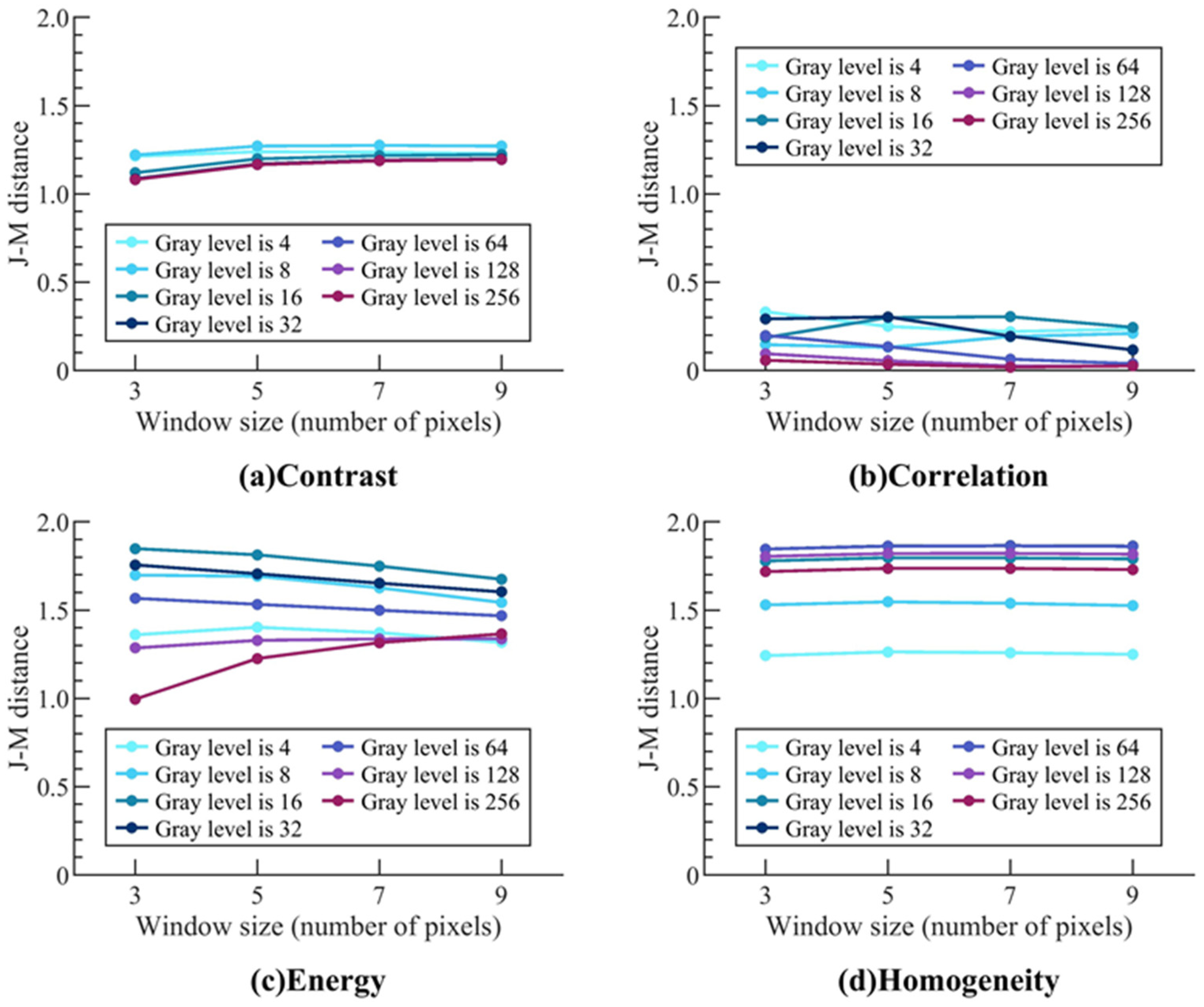
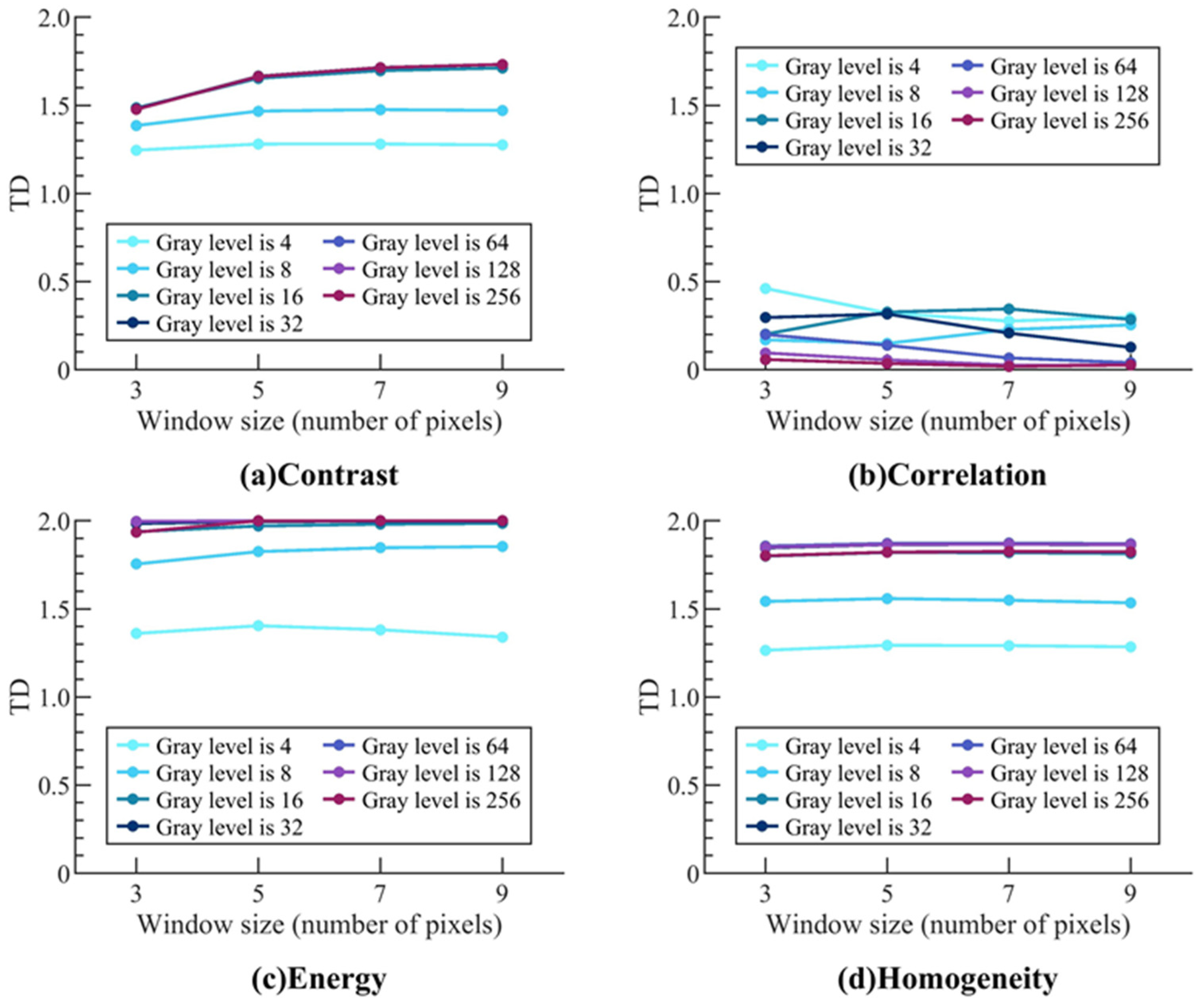
2.2.2. Optimization of Parameters in Feature Extraction
2.2.3. Assessment of the Application Effects of Selected Features
- (1)
- Collapsed building identification
- (2)
- Accuracy evaluation
3. Results
3.1. Ability of 25 Features to Distinguish Collapsed Buildings from Non-Collapsed Buildings
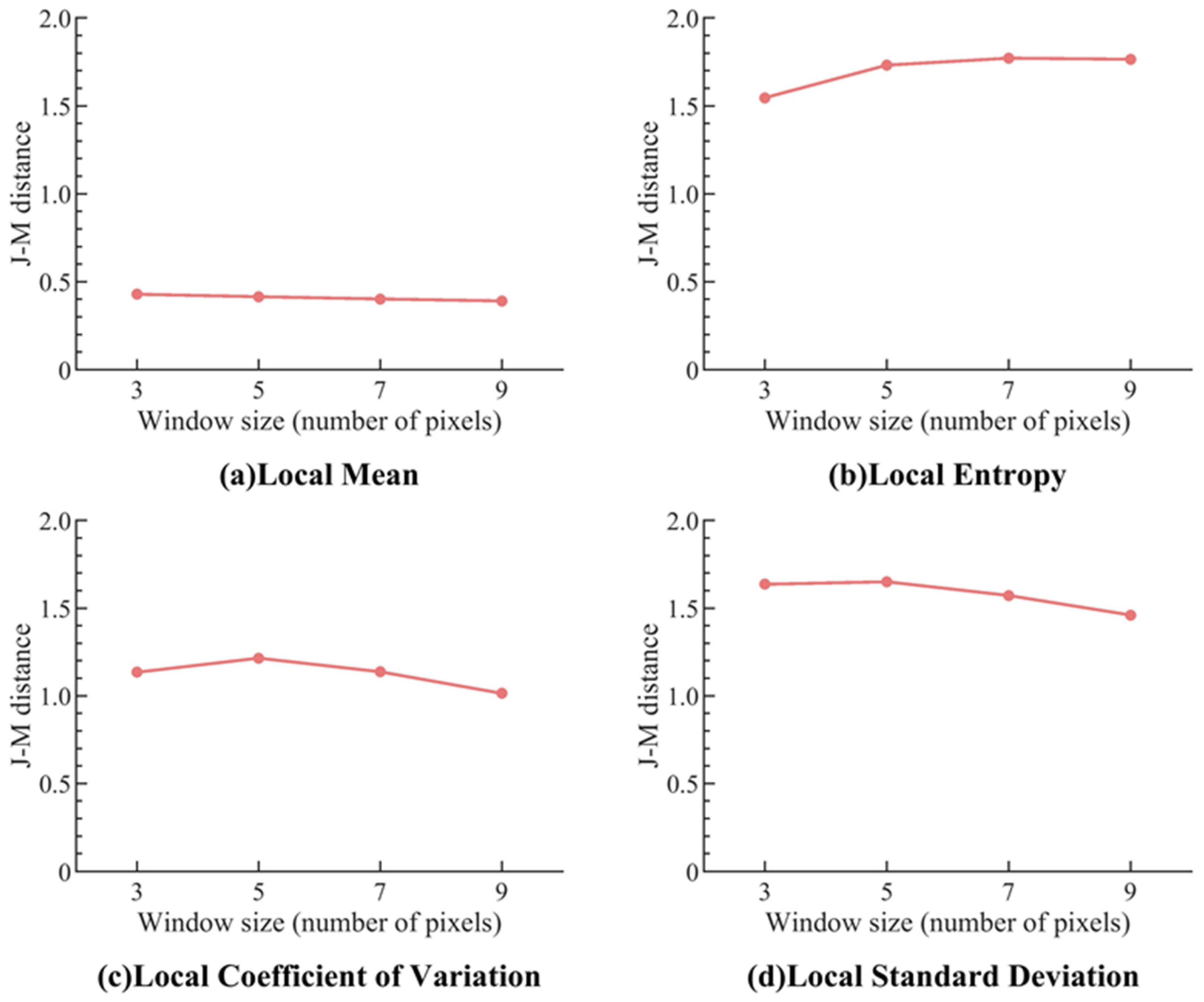
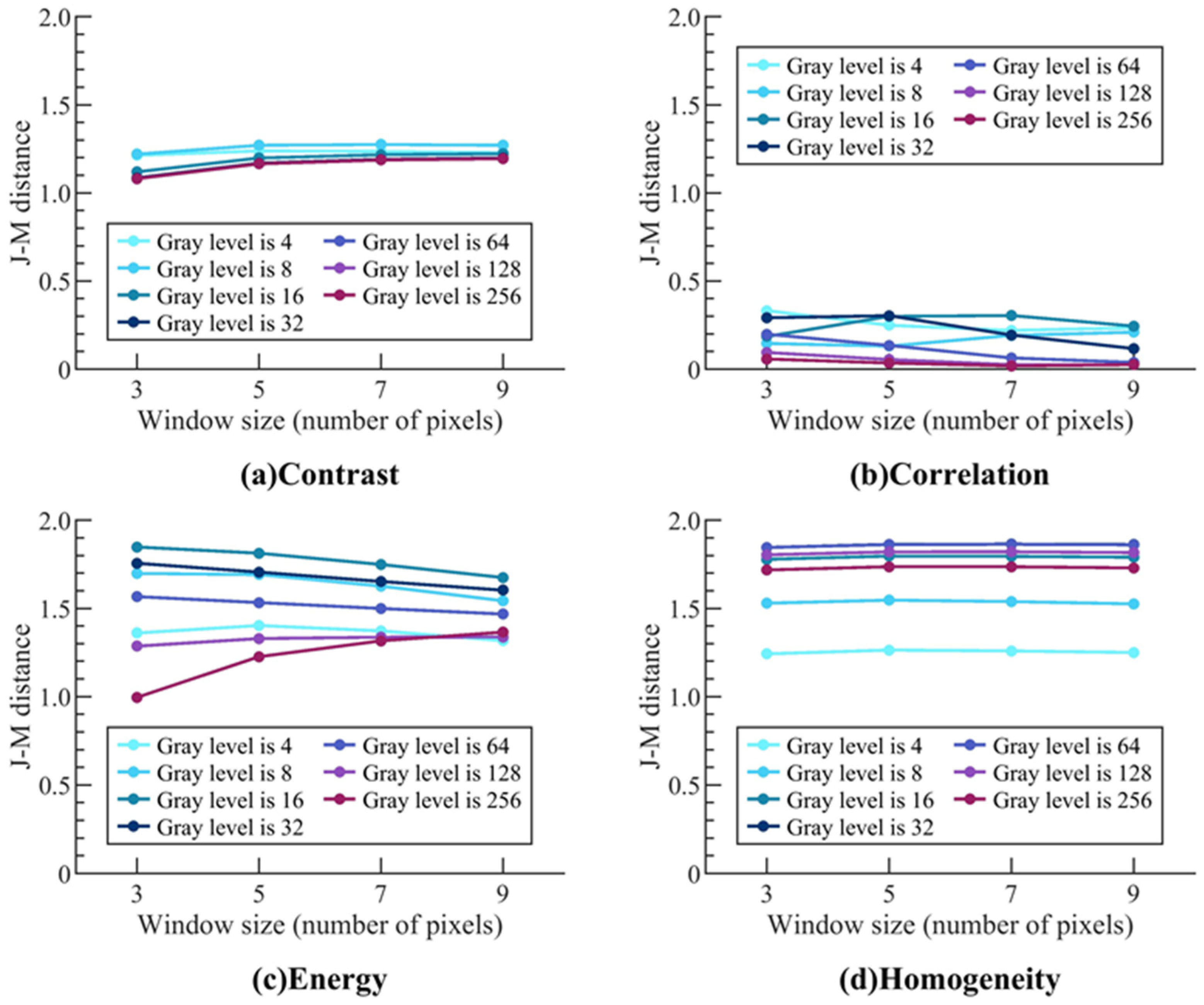
3.2. Optimal Parameters for Feature Extraction
3.3. Application Ability of Selected Features
4. Discussion
4.1. The Best Features Selected for Rapid Remote Sensing Identification of Collapsed Buildings and Their Influencing Factors
4.2. Operational Implementation Process and Application Prospects of Applying Selected Features to Rapid Identification of Collapsed Buildings
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B

References
- Wu, J.; Chen, P.; Liu, Y.; Wang, J. Method of earthquake collapsed building information extraction based on high-resolution remote sensing. Geo. Spat. Inf. Sci. 2013, 29, 35–38+47+2. [Google Scholar]
- Lei, L.; Liu, L.; Zhang, L.; Bi, J.; Wu, Y.; Jiao, Q.; Zhang, W. Assessment and analysis of collapsing houses by aerial images in the Wenchuan earthquake. J. Remote Sens. 2010, 14, 333–344. [Google Scholar]
- Dong, L.G.; Shan, J. A comprehensive review of earthquake-induced building damage detection with remote sensing techniques. ISPRS J. Photogramm. Remote Sens. 2013, 84, 85–99. [Google Scholar] [CrossRef]
- Deng, L.; Wang, Y. Post-disaster building damage assessment based on improved U-Net. Sci. Rep. 2022, 12, 15862. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Ji, L.; Shi, F.; Li, J.; Wang, J.; Enan, I.H.; Wu, T.; Yang, J. Collapsed building detection in high-resolution remote sensing images based on mutual attention and cost sensitive loss. IEEE Geosci. Remote Sens. Lett. 2023, 20, 8000605. [Google Scholar] [CrossRef]
- Xia, Z.; Li, Z.; Bai, Y.; Yu, J.; Adriano, B. Self-supervised learning for building damage assessment from large-scale xBD satellite imagery benchmark datasets. In Proceedings of the Database and Expert Systems Applications, Cham, Switzerland, 22–24 August 2022; pp. 373–386. [Google Scholar]
- Zhou, Y.; Zhang, Y.; Chen, S.; Zhou, Z.; Zhu, Y.; Zhao, R. Disaster damage detection in building areas based on DCNN features. Remote Sens. Nat. Resour. 2019, 31, 44–50. [Google Scholar]
- Yang, W.; Zhang, X.; Luo, P. Transferability of convolutional neural network models for identifying damaged buildings due to earthquake. Remote Sens. 2021, 13, 504. [Google Scholar] [CrossRef]
- Ma, H.; Liu, Y.; Ren, Y.; Yu, J. Detection of Collapsed Buildings in Post-Earthquake Remote Sensing Images Based on the Improved YOLOv3. Remote Sens. 2020, 12, 44. [Google Scholar] [CrossRef]
- Wu, F.; Wang, C.; Zhang, B.; Zhang, H.; Gong, L. Discrimination of collapsed buildings from remote sensing imagery using deep neural networks. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 2646–2649. [Google Scholar]
- Duan, P.; Kang, X.; Ghamisi, P.; Li, S. Hyperspectral Remote Sensing Benchmark Database for Oil Spill Detection With an Isolation Forest-Guided Unsupervised Detector. IEEE Trans. Geosci. Electron. 2023, 61, 5509711. [Google Scholar] [CrossRef]
- Ye, X.; Wang, J.; Qin, Q. Damaged building detection based on GF-1satellite remote sensing image: A case study for Nepal M_S8.1 earthquake. Acta Seismol. Sin. 2016, 38, 477–485+509. [Google Scholar]
- Zeng, Z.; Li, L.; Wang, Z.; Lei, L. Fast extraction of collapsed buildings in post-earthquake high-resolution images using supervised classification. Remote Sens. Inf. 2011, 5, 76–80. [Google Scholar]
- Ye, X.; Qin, Q.M.; Liu, M.C.; Wang, J.; Wang, J.H. Building damage detection from post-quake remote sensing image based on fuzzy reasoning. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 529–532. [Google Scholar]
- Sumer, E.; Turker, M. An integrated earthquake damage detection system. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 6. [Google Scholar]
- Du, H.; Zhang, F.; Lu, Y.; Lin, X.; Deng, S.; Cao, Y. Recognition of the earthquake damage to buildings in the 2021 Yangbi, Yunnan MS_6.4 earthquake area based on multi-source remote sensing images. J. Seismol. Res. 2021, 44, 490–498. [Google Scholar]
- Li, X.; Yang, W.; Ao, T.; Li, H.; Chen, W. An improved approach of information extraction for earthquake-damaged buildings using high-resolution imagery. J. Earthq. Tsunami 2011, 5, 389–399. [Google Scholar] [CrossRef]
- Ye, X.; Qin, Q.; Wang, J.; Wang, J.; Yang, X.; Qin, X. Detecting damaged buildings caused by earthquake using local gradient orientation entropy statistics method. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 3568–3571. [Google Scholar]
- Rathje, E.M.; Crawford, M.; Woo, K.; Neuenschwander, A. Damage patterns from satellite images of the 2003 Bam, Iran, Earthquake. Earthq. Spectra 2005, 21, S295–S307. [Google Scholar] [CrossRef]
- Li, J.; Zhao, S.; Jin, H.; Li, Y.; Guo, Y. A method of combined texture features and morphology for building seismic damage information extraction based on GF remote sensing images. Acta Seismol. Sin. 2019, 41, 658–670+681. [Google Scholar]
- Samadzadegan, F.; Rastiveis, H.; Viii, W.G. Automatic detection and classification of damaged buildings, using high resolution satellite imagery and vector data. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 415–420. [Google Scholar]
- Gupta, R.; Goodman, B.; Patel, N.; Hosfelt, R.; Sajeev, S.; Heim, E.; Doshi, J.; Lucas, K.; Choset, H.; Gaston, M. Creating xBD: A dataset for assessing building damage from satellite imagery. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 15–20 June 2019; pp. 10–17. [Google Scholar]
- Abdullah, W.M.; Yaakob, S.N. Modified excess green vegetation index for uneven illumination. Int. J. Curr. Res. 2017, 9, 48656–48661. [Google Scholar]
- Liu, J.; Li, P. Extraction of Earthquake-Induced Collapsed Buildings from Bi-Temporal VHR Images Using Object-Level Homogeneity Index and Histogram. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2755–2770. [Google Scholar] [CrossRef]
- Song, J.; Wang, X.; Li, P. Urban building damage detection from VHR imagery by including temporal and spatial texture features. J. Remote Sens. 2012, 16, 1233–1245. [Google Scholar]
- Pesaresi, M.; Gerhardinger, A.; Haag, F. Rapid damage assessment of built-up structures using VHR satellite data in tsunami-affected areas. Int. J. Remote Sens. 2007, 28, 3013–3036. [Google Scholar] [CrossRef]
- Ye, X.; Qin, Q.; Wang, J.; Zheng, X.; Wang, J. Detecting damaged buildings caused by earthquake from remote sensing image using local spatial statistics method. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 125–131. [Google Scholar]
- Zhang, R.; Zhou, Y.; Wang, S.; Wang, F.; Zhang, T.; He, Y.; You, S. Construction and application of a post-quake house damage model based on multiscale self-adaptive fusion of spectral textures images. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Waikoloa, HI, USA, 26 September–2 October 2020; pp. 6631–6634. [Google Scholar]

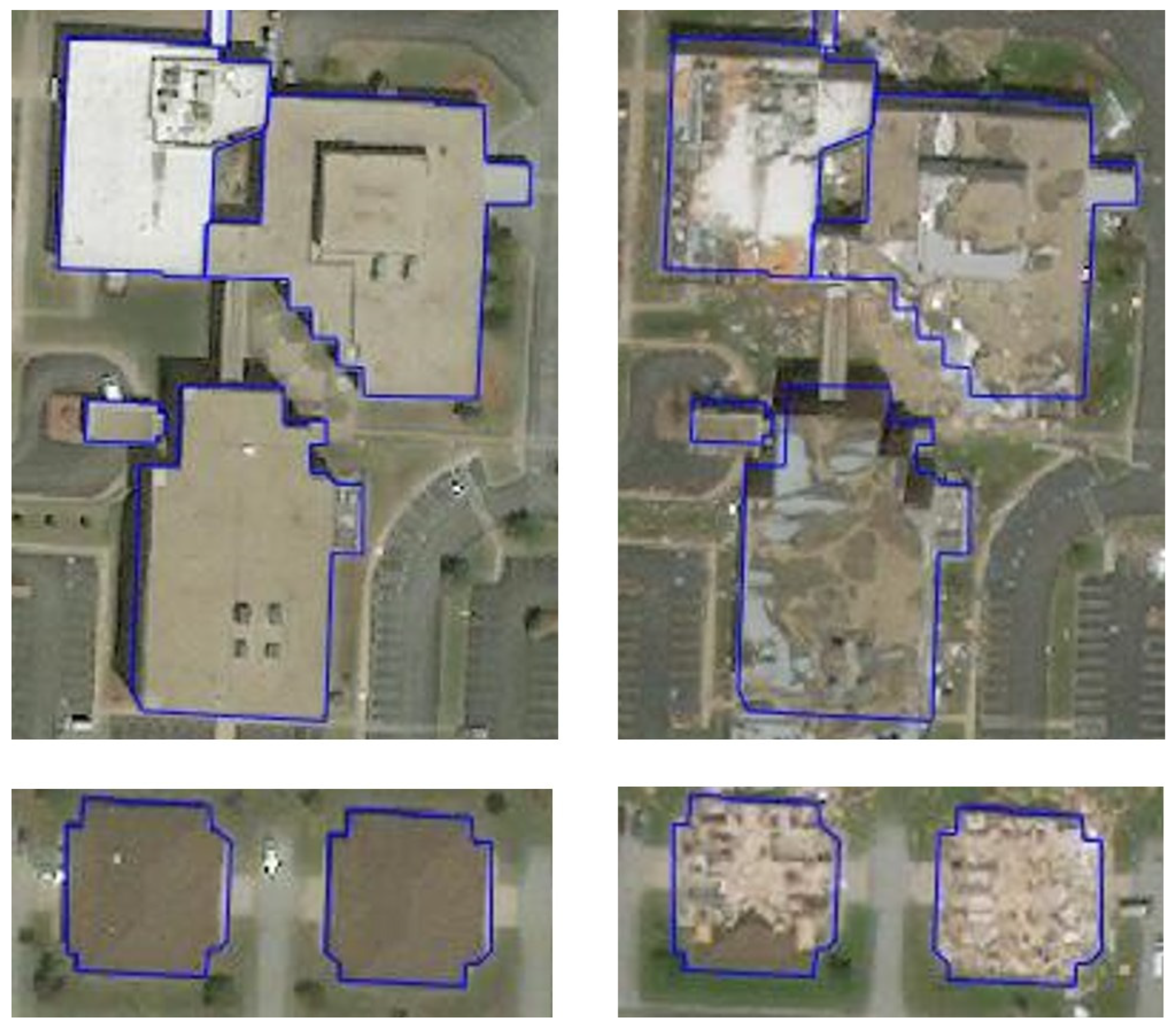


| Image Shooting Location | Reasons and Timing of Building Collapse | Image Shooting Time | Number of Samples for Building Pairs |
|---|---|---|---|
| Bata (Equatorial Guinea—Litoral, 1.87°N, 9.77°E) | explosion (7 March 2021) | image before collapse: 7 August 2020 image after collapse: 9 March 2021 | 92 |
| Beirut (Lebanon—Beirut, 33.87°N, 35.70°E) | explosion (4 August 2020) | image before collapse: 31 July 2020 image after collapse: 5 August 2020 | 30 |
| Joplin (USA—Missouri, 37.10°N, 94.58°W) | tornado (22 March 2011) | image before collapse: 8 August 2009 image after collapse: 29 May 2011 | 1558 |
| Moore (USA—Oklahoma, 35.33°N, 97.50°W) | tornado (20 May 2013) | image before collapse: 17 February 2013 image after collapse: 22 May 2013 | 594 |
| Tuscaloosa (USA—Alabama, 33.2°N, 87.51°W) | tornado (27 April 2011) | image before collapse: 21 June 2006 image after collapse: 19 May 2011 | 277 |
| Woolsey (USA—California, 34.06°N, 118.76°W) | wild fire (8 November 2018) | image before collapse: 23 October 2018 image after collapse: 18 November 2018 | 79 |
| Features | Calculation Methods |
|---|---|
| Red/Green/Blue | Calculate the mean of the red/green/blue band values of all pixels as the Red/Green/Blue feature of the building sample |
| Hue/Saturation/Intensity | Calculate the mean of hue/saturation/intensity values of the color space transformed sample image of all pixels as the Hue/Saturation/Intensity feature of the building sample |
| Global Entropy | Calculate the entropy of grayscale values of all pixels as the Global Entropy feature of the building sample |
| Global Coefficient of Variation | Calculate the coefficient of variation of grayscale values of all pixels as the Global Coefficient of Variation feature of the building sample |
| Local Mean | Using a specific-sized sliding window, calculate the mean/the standard deviation/the entropy/the coefficient of variation of the grayscale values in the window as the mean/the standard deviation/the entropy/the coefficient of variation value of the central pixel, and take the mean of the calculated values of all pixels as the Local Mean/the Local Standard Deviation/the Local Entropy/the Local Coefficient of Variation feature of the building sample |
| Local Standard Deviation | |
| Local Entropy | |
| Local Coefficient of Variation | |
| Local Moran’I | Calculate the local Moran’I of each pixel, and take the mean of the local Moran’I values of all pixels as the Local Moran’I feature of the building sample |
| Gradient | Calculate the gradient value for every pixel by the Sobel operator, and take the mean of the gradient values of all pixels as the gradient feature of the building sample |
| Gradient Orientation Entropy | Calculate the gradient orientation for every pixel by the Sobel operator, and take the entropy for the gradient orientation values of all pixels as the Gradient Orientation Entropy feature of the building sample |
| Gradient Orientation Standard Deviation | Calculate the gradient orientation for every pixel by the Sobel operator, and take the standard deviation for the gradient orientation values of all pixels as the Gradient Orientation Standard Deviation feature of the building sample |
| Edge | Perform a convolution operation using the Laplacian operator, and take the mean value as the edge feature of the building sample |
| Edge Density | Perform a convolution operation using the Laplacian operator and apply thresholding segmentation to obtain edges. Calculate the density of edges in each pixel’s neighborhood, pixel by pixel. Afterwards, take the mean of the edge density values of all pixels as the edge density feature of the building sample |
| Contrast | Based on GLCM, calculate the contrast/correlation/energy/homogeneity value at each pixel and take the mean of the contrast/correlation/energy/homogeneity values of all pixels as the Contrast/Correlation/Energy/Homogeneity feature of the building sample |
| Correlation | |
| Energy | |
| Homogeneity | |
| Local Binary Patterns (LBP) | Calculate LBP for every pixel with a certain radius, and take the mean of the LBP values of all pixels as the LBP feature of the building sample |
| Gabor Feature | Calculate the Gabor value for every pixel by Gabor filtering, and take the mean of the Gabor values of all pixels as the Gabor feature of the building sample |
| Fractal Dimension | Calculate the fractal dimension using the Box Counting Method as the Fractal Dimension feature of the building sample |
| Features | Joplin | Tuscaloosa | Moore | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Precision (%) | Recall (%) | F1-Score | Precision (%) | Recall (%) | F1-Score | Precision (%) | Recall (%) | F1-Score | |
| Local Entropy | 94.50 | 93.20 | 0.94 | 70.10 | 96.29 | 0.81 | 84.00 | 97.45 | 0.90 |
| Homogeneity | 92.10 | 92.28 | 0.92 | 63.20 | 96.78 | 0.76 | 77.20 | 96.74 | 0.86 |
| Energy | 84.00 | 94.59 | 0.89 | 56.20 | 95.74 | 0.71 | 69.90 | 97.63 | 0.81 |
| Local Standard Deviation | 91.10 | 94.50 | 0.93 | 62.20 | 93.82 | 0.75 | 75.00 | 97.40 | 0.85 |
| Gradient | 79.80 | 91.30 | 0.85 | 59.80 | 94.77 | 0.73 | 62.30 | 97.04 | 0.76 |
| Feature | Parameter | Optimum Parameter | Parameter Setting Principle |
|---|---|---|---|
| Local Entropy | Window size | The window size is about 3.5 m | The optimal window size is influenced by the size of the roof area of a non-collapsed building, the size of fragments from collapsed buildings, and the spatial resolution of the image. Theoretically, the optimal window should be able to contain different fragments of collapsed buildings and should not be larger than the roof area of a non-collapsed building. |
| Local Standard Deviation | The window size is about 2.5 m | ||
| Local Coefficient of Variation | The window size is about 2.5 m | ||
| Contrast | Window size and gray level | The window size is about 3.5 m and the gray level is 8 | The optimal window setting principle is the same as above. The optimal gray level is influenced by the complexity of the image. In terms of the identification of collapsed buildings, the more complex the roof structure is, the larger the optimal gray level should be. |
| Energy | The window size is about 2.5 m and the gray level is 16 | ||
| Homogeneity | The window size is about 3.5 m and the gray level is 64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Zhu, W.; Yang, X. Screening Image Features of Collapsed Buildings for Operational and Rapid Remote Sensing Identification. Remote Sens. 2023, 15, 5747. https://doi.org/10.3390/rs15245747
Liu R, Zhu W, Yang X. Screening Image Features of Collapsed Buildings for Operational and Rapid Remote Sensing Identification. Remote Sensing. 2023; 15(24):5747. https://doi.org/10.3390/rs15245747
Chicago/Turabian StyleLiu, Ruoyang, Wenquan Zhu, and Xinyi Yang. 2023. "Screening Image Features of Collapsed Buildings for Operational and Rapid Remote Sensing Identification" Remote Sensing 15, no. 24: 5747. https://doi.org/10.3390/rs15245747
APA StyleLiu, R., Zhu, W., & Yang, X. (2023). Screening Image Features of Collapsed Buildings for Operational and Rapid Remote Sensing Identification. Remote Sensing, 15(24), 5747. https://doi.org/10.3390/rs15245747








