Abstract
Rockfall presents a significant risk to the safety and economy of communities and infrastructure in mountainous regions. The recently-developed Rockfall Activity Index (RAI) utilizes high-resolution terrestrial lidar-derived digital elevation models (DEMs) of rock slopes to categorize a slope face into seven distinct morphological units, or “RAI classes”. This paper focuses on a comprehensive study conducted at four sites in Alaska, USA, where a robust lidar-based five-year inventory of 4381 rockfall events was analyzed. The primary objective was to investigate variations in failure characteristics, such as cumulative magnitude–frequency distributions, non-cumulative power–law parameters, average annual failure rates, and average failure depths, among the different RAI classes. The findings demonstrate that the seven RAI classes effectively differentiate the rock slope based on unique mass-wasting characteristics. Furthermore, the research explores spatial and temporal variations in these failure characteristics. Based on the study’s outcomes, recommendations are provided for modifying the RAI parameters for each RAI class, specifically the annual failure rate and average failure depth. These modifications aim to enhance the accuracy and effectiveness of rockfall hazard assessments.
1. Introduction
1.1. State of Practice in Rock Slope Stability Assessment
Rockfall, which refers to the detachment, fall, rolling, and bouncing of individual rock fragments that have limited interaction [1], presents a substantial risk to the economy and the safety of communities and infrastructure in mountainous regions. Among the various infrastructure systems, linearly-distributed networks such as transportation corridors, pipelines, and powerlines are especially susceptible to economic and life-safety hazards caused by rockfall [2]. This vulnerability arises from extensive exposure to rock slopes and the practical challenges and costs associated with conducting comprehensive rock slope stability assessments across large areas [3].
Relatively high-quality rock masses (i.e., rock masses with widely-spaced discontinuities separating relatively strong rock blocks) are often assessed using discontinuum (e.g., distinct-element) modeling by mapping discontinuities and performing kinematic and limit-equilibrium analyses to evaluate the stability of individual rock blocks [4]. As rock-mass quality decreases or evaluation area increases, discontinuum modeling becomes impractical. Relatively low-quality rock masses (with closely-spaced discontinuities and/or weaker rock) are instead traditionally assessed using rock-mass classification systems, which rely on visual inspections and/or the collection of generic data from the rock mass [5]. These data are then input into a classification scheme, such as the Rockfall Hazard Rating System (RHRS) [6], the Rock Mass Rating system (RMR) [7], the Slope Mass Rating system (SMR) [8], the Geological Strength Index (GSI) [9], the Rockslope Deterioration Assessment (RDA) [10], or the Q-Slope Rating System [11]. The output of such systems can be used to analyze the behavior of the rock mass physically or empirically [3], including rockfall hazard.
1.2. Development of the Rockfall Activity Index (RAI)
Recent advancements in lidar technology have enabled the development of centimeter-scale-resolution topographic models of the surface of rock slopes from a safe distance [12]. To take advantage of these new technological developments, Dunham et al. [13] developed the Rockfall Activity Index (RAI), a framework for assessing relative rockfall hazards using these high-resolution topographic models. Based on field observations, Dunham et al. [13] created seven unique classifications (RAI classes) for the rock slope surface to capture different topographic and morphologic expressions, which are expected to exhibit unique erosion and mass-wasting characteristics. The RAI framework uses surface slope inclination and roughness (at different scales) to delineate areas of the slope face quantitatively and repeatably into the seven RAI classes shown in Table 1.

Table 1.
Original definitions of the 7 RAI classes and their preliminary estimated annual failure rates and average failure depths (after Dunham et al. [13]).
To quantify the rockfall hazard associated with each RAI class, Dunham et al. [13] present a framework to estimate the annual delivery of kinetic energy from the rock slope to the roadway at the base of the slope. For this computation, preliminary annual failure rates (referred to in Dunham et al. [13] as the “Instability Rate”, which represents the probability that a location may be involved in a rockfall during a given year) and average failure depths (depth of failure, on average, given a failure occurs) were assigned to each RAI class on a 5 cm × 5 cm grid (each grid space is referred to as a “cell” in this paper) on the rock slope surface. Initially, the annual failure rate and average failure depth were estimated based on coarse lidar-based change detection data collected over one year at two sites in Alaska, USA [13]. The preliminary estimated annual failure rates and average failure depths assumed by Dunham et al. [13] for each RAI class are shown in Table 1. Then, the annual failure rate, average failure depth, and location on the rock slope (height above the base) are combined to compute the estimated average annual kinetic energy delivered to the base of the slope [13]. An example output of the RAI framework is shown in Figure 1. Olsen et al. [14,15] recently implemented the RAI framework in the software package RAMBO, a commercially available software package used for lidar processing, change analysis, and rock-slope stability analysis.

Figure 1.
Example output of the RAI framework: (a) Lidar-based colorized point cloud; (b) RAI classes assigned to the rock slope face; (c) Estimated annual kinetic energy delivery from each 5 cm by 5 cm cell in joules (data visualized using CloudCompare v2.11.3 [16]).
1.3. Lidar-Based Rockfall Inventory Development and Utilization
The statistical analysis of an inventory of past mass-wasting events is a rigorous method to inform models that project the future likelihood of mass-wasting [17]. Mass-wasting events, such as landslides and rockfalls, have been shown to self-organize into a power–law magnitude–frequency distribution [18,19,20,21,22,23,24]. Researchers have recently compiled lidar-based inventories of hundreds to thousands of rockfall events over multi-year periods [20,21,22,23,24,25,26] that have demonstrated power–law magnitude–frequency relationships over several orders of magnitude. Some authors have recommended frameworks for informing hazard assessment methodologies using their lidar-based rockfall inventories [26].
In this paper, we significantly expand the Dunham et al. [13] database by developing a robust and comprehensive lidar-based inventory of 4381 rockfall events occurring over five years (2012 to 2017) at four study sites (Site A, Site B, Site C, and Site D) located in Alaska, USA. This database is openly accessible through a Designsafe-CI data repository. With this inventory, we evaluate the geomorphic evolution of rock slopes by investigating the magnitude–frequency distributions of rockfall events and the variation of these distributions spatially, temporally, and with RAI class. Importantly, we use this inventory to calculate a revised set of annual failure rates and average failure depths for each cell within each RAI class, and thus recommend the modification of the preliminary parameters used for the original RAI framework presented in Dunham et al. [13].
1.4. Study Site Locations
The data used to develop the RAI framework and for this current work were obtained along the Glenn Highway (AK-1), about 110 km northeast of Anchorage, Alaska, at specific sites along an approximately 25 km segment of the highway within the Matanuska Valley. Dunham et al. [13] selected this area to develop the RAI framework because of its proximity to a major roadway providing access for laser scanning survey instrumentation, the absence of vegetation on the rock slopes, and their high rates of slope activity (based on the maintenance records from the Alaska Department of Transportation and Public Facilities). Figure 2 presents the approximate locations of the study sites.
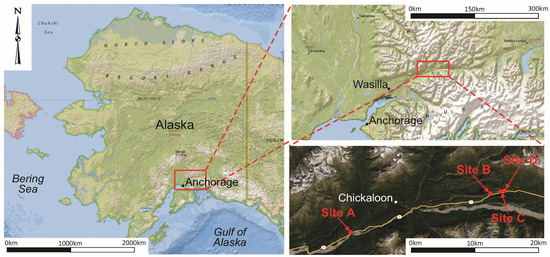
Figure 2.
Locations of the study sites. Site A is located at 61.7530, −148.6270; Site B is located at 61.8060, −148.2285; Site C is located at 61.8096, −148.1960; Site D is located at 61.8099, −148.1927. (Maps obtained from Esri ArcGIS, National Geographic Maps layer; aerial photograph obtained from Google Earth, dated 30 May 2017).
1.5. Geologic Setting and Rock Mass Characteristics
This area of the Matanuska Valley consists of a complex assortment of tilted and folded sedimentary units [27]. Site A is underlain by dark gray carbonaceous mudstone (grain size ranges 1/8–1/4 mm) from the Cretaceous Matanuska Formation [28]. The mudstone bedding is nearly vertical, with dip and dip directions of 80° and 140°, respectively. The road cut stands up to 47 m high sloped at approximately 79°, facing about 130°, which roughly parallels the bedding dip. Other structural features include four sets of faults and/or joints. We observed slickensides along some high-angle fault contacts, which suggested normal faulting as the sense of displacement.
Site B consists of a 6-m-high road cut sloped at approximately 56°, facing about 140°. The rock is an Eocene gabbro sill, consisting of orthopyroxene, clinopyroxene phenocrysts up to 3 mm, and plagioclase. We made 94 measurements of joints exposed in the gabbro road cut, which group into three main joint sets.
At Sites C and D, the Glenn Highway traverses the side of a steep slope, forming an approximately 760-m-long road cut into the late Paleocene to early Eocene Chickaloon Formation [28]. This road cut is up to about 37 m high and is sloped at approximately 60°, facing about 170°. Above the road, a gabbroic sill forms a prominent cliff, contributing this rock type to the talus and colluvium stratigraphically above the sedimentary bedrock in the area. The road cut consists of interlayered mudstone and poorly cemented sandstone, with some minor conglomerate as basal layers in the sandstone. Some of these basal layers contain cobbles of carbonaceous mudstone. The lithic sandstone is fine-grained (1/8–1/2 mm), containing quartz, plagioclase, and mica grains, and exhibits cross-bedding. These sites demonstrate predominant bedding oriented with dip and dip direction of 42° and 20°, respectively, and a conjugate fault set. Figure 3 contains representative photographs of the four sites, and Figure 4 presents stereographic projections of the major fault and joint sets, and the cut slope faces.

Figure 3.
Photographs of the study sites: (a) Carbonaceous mudstone with steeply-dipping bedding at Site A; (b) Road cut in gabbro at Site B; (c) Example of a normal fault at Sites C and D, indicating sense and amount of displacement; The blue lines also coincide with a contact between sandstone (above) and mudstone (below).
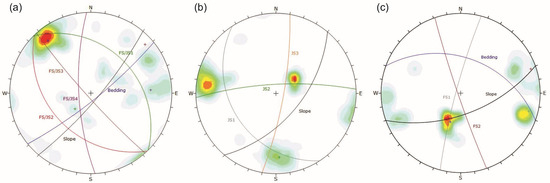
Figure 4.
Stereonets for (a) Site A mudstone (95 measurements), (b) Site B gabbro (94 measurements), and (c) Sites C and D sedimentary rocks (27 measurements). For great circles, slope angle is black, bedding is blue, and joint and/or fault sets are various colors. The color gradient scales with fault/joint set pole density, with green being lower concentration, and red being higher concentration.
1.6. Potential Failure Mechanisms at the Study Sites
Kinematic analyses can be completed using the stereonet projections shown in Figure 4 in order to evaluate the potential failure mechanisms at the study sites [29]. At Site A, toppling along the bedding plane and wedge failures on Fault Set/Joint Set (FS/JS) 2 and FS/JS 4 are kinematically viable. At Site B, wedge failures on Joint Set (JS) 1 and JS 3 are kinematically viable. The discontinuities at Sites C and D do not form obvious failure mechanisms based on their geometry. It should also be noted that these observations of possible failure mechanisms do not consider friction angle. Although this information is useful as background information regarding rock mass characteristics at the study sites, it should be noted that the RAI framework is not intended to characterize the susceptibility to large-scale structural failures often captured in a kinematic analysis.
2. Materials and Methods
2.1. Data Collection and Processing
For this study, four Terrestrial Laser Scanner (TLS) surveys were completed at Sites A, B, C, and D (2013, 2014, 2015 and 2017), and a fifth TLS survey was conducted at Sites B, C, and D (2012). The 2012 surveys were conducted using a TITAN Mobile TLS (David Evans and Associates, Inc., Portland, OR, USA). The 2013, 2014, and 2015 surveys were completed using a Riegl VZ-400 TLS (Riegl USA, Inc., Winter Garden, FL, USA). The 2017 surveys were completed using a Leica ScanStation P40 TLS (Leica Geosystems, St. Gallen, Swizerland). A digital SLR camera was mounted on the scanner in 2013, 2014, and 2015 to colorize the scans; the scanner used in 2017 had a built-in camera that automatically colorized the scans. In addition, a survey-grade GPS receiver was mounted above the scanners for georeferencing the point clouds using the methodology described in Olsen et al. [30,31] for the 2013 and 2014 datasets. Targets and additional ground control points with total station and GNSS observations were added to the 2015 and 2017 surveys. Figure 5 shows the colorized point clouds acquired in 2017 for all sites. The images have been cropped to focus on the study area.

Figure 5.
Colorized point clouds of each site obtained in 2017. (a) Site A; (b) Site B; (c) Site C; (d) Site D (data visualized using CloudCompare v2.11.3 [16]).
Data processing was completed following the procedure of Olsen et al. [15]. First, scan data were manually cropped to include only the exposed rock slope face areas, which involved the removal of unwanted data points such as heavily vegetated areas, the highway surface, individual shrubs on the slope face, and other features, using Maptek I-Site Studio v7.0 [32].
A best-fit plane was then determined (such that the z-axis of the plane was perpendicular to the rock slope), and the data were transformed into this plane to simplify further calculations and ensure computations were consistent across all change periods (referred to as “epochs” in this paper) [15]. An automated vegetation filtering algorithm was implemented to remove the data points likely associated with shrubbery on the slope face. A hole-filling operation was then implemented to interpolate points in areas with insufficient data [15]. Finally, a triangulation scheme generated a representative surface for the point-cloud data [33].
2.2. Change Detection Methodology and Rockfall Inventory
Surface models generated from point clouds of the same slope face, taken at different points in time, were differenced (subtracted) at each cell, producing a grid of 1-dimensional change magnitudes for each cell of the surface model, following the procedures in Olsen et al. [15]. To reduce the effects of georeferencing biases between the two data sets, the point clouds were co-registered using the Maptek I-Site Studio v7.0 [32] cloud-to-cloud registration tool before implementing the change detection algorithm; however, errors related to georeferencing, hole-filling, vegetation filtering, surface generation, and the geometrically complex nature of some study rock slopes can still lead to falsely-identified change. To reduce the occurrence of falsely-identified change, a significant change threshold was applied to the change grid, such that a difference less than that threshold was disregarded as noise. Based on extensive trial and error and a visual inspection of the scan data and change grids, an optimized significant change threshold of 0.05 m was found to minimize falsely identified change while capturing the greatest number of real failures.
Cells indicating change adjacent to other changed cells were assumed to be involved in the same failure event. This assumption generates a source of error, as multiple smaller failures in the same area may be attributed to only one large failure. Using a connected components algorithm [15], these associated changed cells were identified, and each failure cluster was assigned a unique identification number and a calculated total change volume.
To reduce the influence of falsely identified change clusters, each negative change (failure) cluster identified by the change detection algorithm was visually/manually inspected using Maptek I-Site Studio v7.0 [32] to affirm its accuracy as part of this study. When evidence for an actual failure was not observed for an identified failure cluster, the event was removed from the failure inventory, and the change grid was adjusted accordingly.
Another possible source of error in change event clustering is derived from the temporal resolution of the survey periods, especially at highly active sites. For example, two discrete events occurring between two survey periods (one epoch) may overlap spatially, resulting in the identification of one single larger event rather than two smaller events. Surveys must be completed at a higher temporal resolution to reduce this source of error [15,34].
Using the change detection methodology described above, we collected a robust inventory of 4381 rockfall events at the four study sites over the five years of survey data, ranging in volume from small (less than 1 × 10−5 m3) to large (up to 28.1 m3). Each event was assigned a predominant RAI class based on the RAI class of the plurality of the cells comprising the failure cluster. Using this inventory, we investigate the morphological evolution of rock slopes and how rockfall event magnitudes and frequencies vary spatially, temporally, and by RAI class. Figure 6 shows the detected failures at each site for the 2015 to 2017 epoch. It should be noted that scales among the four sites differ substantially, which can be visually misleading regarding the size and distribution of events when comparing the sites.
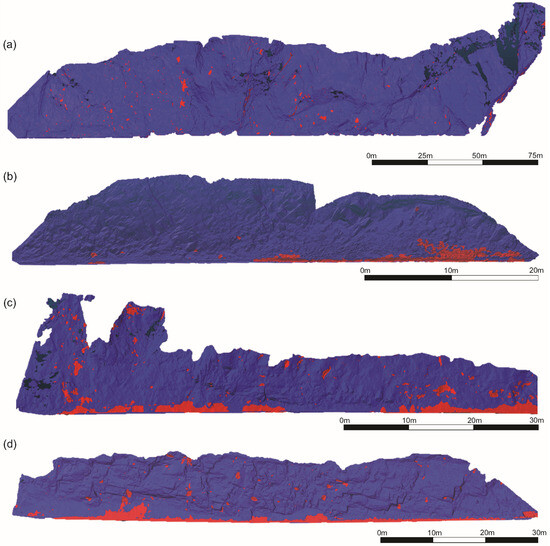
Figure 6.
Failures at each site for the 2015 to 2017 epoch. Failed cells are colored red, while non-failed cells are colored blue; (a) Site A; (b) Site B; (c) Site C; (d) Site D (data visualized using MapTek I-Site Studio v7.0 [31]).
We also use the rockfall inventory to calculate annual failure rate and average failure depth for cells associated with each RAI class. This is accomplished by dividing failed cells from the inventory by total cells associated with each RAI class and averaging the failure depth for each failed cell. These calculated values are used to recommend the modification of annual failure rates and average failure depths used in the RAI framework.
2.3. Magnitude–Frequency Relationships of Rockfall
Mass-wasting events, such as landslides and rockfalls, have been shown to self-organize into power–law magnitude–frequency distributions [18,19,20,21,22,23,24] with a lower-end roll-off related to sampling resolution for rockfall [35,36], and an upper-end roll-off related to slope morphology, vertical relief, and the temporal extent of the surveys [34,35]. For this study, we use the negative power–law scaling relationship between the cumulative frequency of events (F) and the event magnitude (V), given by the following equation:
F(V) = BV−A
The non-cumulative frequency of events (f) scales with the event magnitude (V) using the following equation:
f(V) = βV−α
The non-cumulative power–law parameters (Activity Parameter, β, and Scaling Parameter, α) are related to the cumulative power–law parameters (B and A) as follows:
β = B × A
α = A + 1
3. Results
3.1. Spatial Variation in Magnitude–Frequency Distributions
Figure 7 and Table 2 show the cumulative magnitude–frequency distributions and their respective non-cumulative power–law parameters for the four study sites over four or five years (2013 to 2017 for Site A, and 2012 to 2017 for Sites B, C, and D).
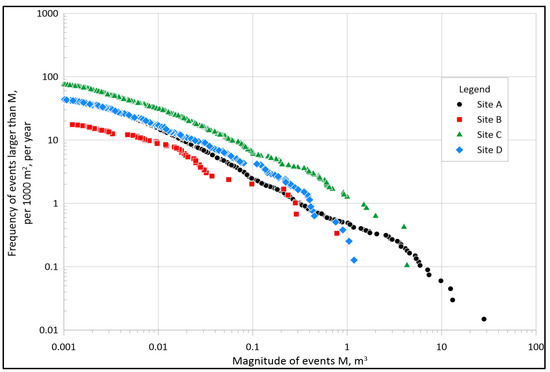
Figure 7.
Cumulative magnitude–frequency distributions for the four study sites over four or five years, per 1000 m2 of slope area, per year (2013 to 2017 for Site A; 2012 to 2017 for Sites B, C and D).

Table 2.
Non-cumulative Activity Parameters (β) and Scaling Parameters (α) for each site across four or five years, per 1000 m2 of slope area, per year (2013 to 2017 for Site A; 2012 to 2017 for Sites B, C, and D).
3.2. Temporal Variation in Magnitude–Frequency Distributions
Power–law parameters have also been shown to vary considerably through time, perhaps based on variations in the weather at the same sites [37]. Figure 8 shows the cumulative magnitude–frequency distributions for each epoch (2012 to 2013, 2013 to 2014, 2014 to 2015, and 2015 to 2017) for each of the four sites. Table 3 shows each site’s Activity Parameters and Scaling Parameters for each epoch, and Figure 9 shows the variation of power–law parameters through time at each site.
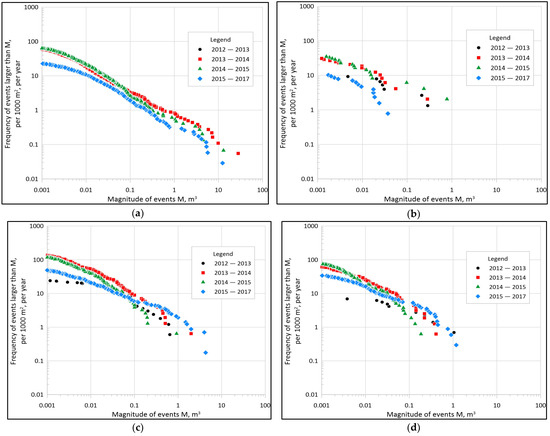
Figure 8.
Cumulative magnitude–frequency distributions at each site for each epoch: (a) Site A; (b) Site B; (c) Site C; (d) Site D.

Table 3.
Non-cumulative Activity Parameters (β) and Scaling Parameters (α) for each epoch, for each site, per 1000 m2 of slope area (per year event frequency for the 2015–2017 epoch was halved). 1 N/A indicates data not available; an initial 2012 scan was not completed at Site A.
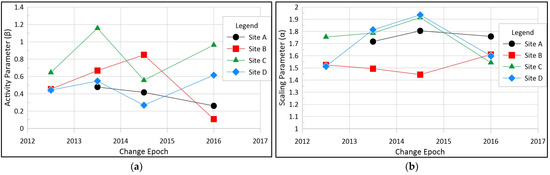
Figure 9.
Temporal variation in non-cumulative power–law parameters at each site: (a); Activity Parameter (β); (b) Scaling Parameter (α), per 1000 m2 of slope area (per year event frequency for the 2015–2017 epoch was divided by two).
3.3. RAI Class Variation in Magnitude–Frequency Distributions
We hypothesize that areas of rock slopes with different morphologic indicators (roughness and slope inclination, which are correlated to RAI class) will be described by different cumulative magnitude–frequency distributions and non-cumulative power–law parameters. Figure 10 shows cumulative magnitude–frequency distributions for all sites, separated by RAI class for all four/five years of data collection. Table 4 shows the average non-cumulative Activity Parameter and Scaling Parameter for all years of rockfall data for all sites, separated by RAI class. Table 5 shows the standard deviations and coefficients of the variation of these parameters among the sites.
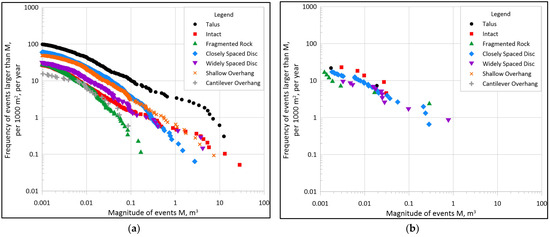
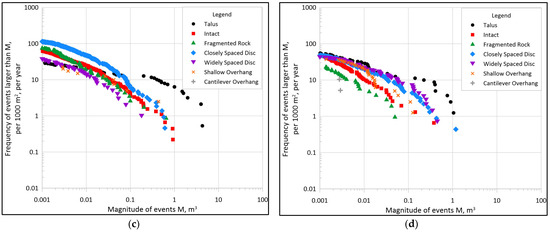
Figure 10.
Cumulative magnitude–frequency distributions at each site for each RAI class: (a) Site A; (b) Site B; (c) Site C; (d) Site D.

Table 4.
Non-cumulative Activity Parameters (β) and Scaling Parameters (α) for each RAI class at each site, averaged across the years of evaluation, per 1000 m2 of slope area. 1 N/A indicates too few rockfall events occurred within this RAI class to deduce power–law parameters.

Table 5.
Average, Standard Deviation, and Coefficient of Variation (CoV) of non-cumulative Activity Parameter (β) and Scaling Parameter (α) for each RAI class.
3.4. Estimating Annual Failure Rates and Average Failure Depths
As previously described, the RAI framework utilizes an annual failure rate and average failure depth for each cell on the slope face to estimate hazard ratings (RAI Score) along the rock slope. The annual failure rate represents the probability that a cell may be involved in a rockfall during a given year. The average failure depth represents the depth, on average, of change in cells that may be involved in a failure event. Using our robust rockfall event inventory gathered as part of this study, we calculated the average annual failure rates and average failure depths for the four study sites over the latter four years of rockfall event data, as shown in Table 6; the 2012 to 2013 data were omitted because the 2012 scans had relatively low resolution, reducing confidence in the accuracy of the calculated rates and depths. Table 7 shows the averages, standard deviations, and coefficients of variation of the annual failure rate and average failure depth data. Table 8 shows the weighted average annual failure rate and average failure depth data, weighted by approximate site area (Site A: 16,882 m2; Site C: 2197 m2; Site D: 1647 m2; Site B: 563 m2). The 2015 to 2017 data were weighted twice as heavily in calculating the weighted averages because they covered two years of change. Figure 11 and Figure 12 show the temporal variation of annual failure rates (Figure 11) and average failures depths (Figure 12) for each of the four sites, separated by RAI class. Annual failure rate and average failure depth data were lost for the Site D 2014 to 2015 epoch, precluding its use to calculate averages.

Table 6.
Annual failure rate (r) and average failure depth (D) for each RAI class, averaged across all epochs; 2012 to 2013 data omitted for all sites, and 2014 to 2015 data omitted for Site D.

Table 7.
Average, Standard Deviation, and Coefficient of Variation (CoV) of annual failure rate (r) and average failure depth (D, in meters) for each RAI class.

Table 8.
Average of annual failure rates and average failure depths, averaged across all sites and epochs; 2012 to 2013 data omitted for all sites, and 2014 to 2015 data omitted for Site D; weighted by site area.
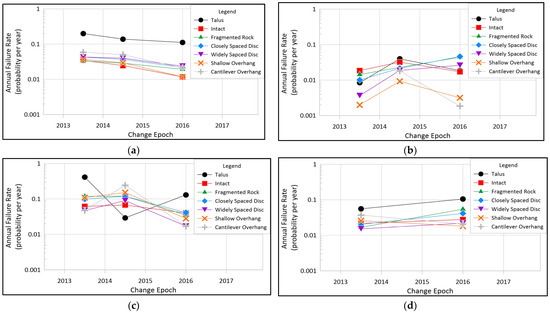
Figure 11.
Temporal variation of annual failure rate by RAI class (2012 to 2013 data omitted for all sites; 2014 to 2015 data omitted for Site D, described above): (a) Site A; (b) Site B; (c) Site C; (d) Site D.
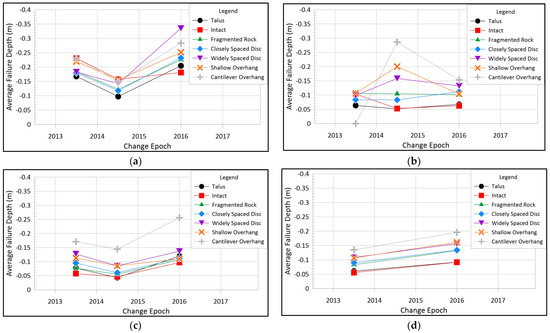
Figure 12.
Temporal variation of average failure depth by RAI class (2012 to 2013 data omitted for all sites; 2014 to 2015 data omitted for Site D, described above): (a) Site A; (b) Site B; (c) Site C; (d) Site D.
3.5. Measuring Talus Slope Angle
Dunham et al. [13] used a maximum talus slope angle of 35 degrees to assign the Talus (T) RAI class. As part of this study, we measured talus slope angles using the Maptek I-Site Studio v7.0 [32] Strike and Dip Query Tool on the 2015 point clouds at Sites A, C, and D. The 2015 point cloud was arbitrarily selected to obtain the measurements; the scan year used should not affect the results as, based on our rockfall failure inventory, talus tends to fail due to planar adjustments rather than deep-seated failures, resulting in a similar slope angle through time. Site B did not contain significant talus and was omitted from this study. A probability density histogram of talus slopes is presented in Figure 13.
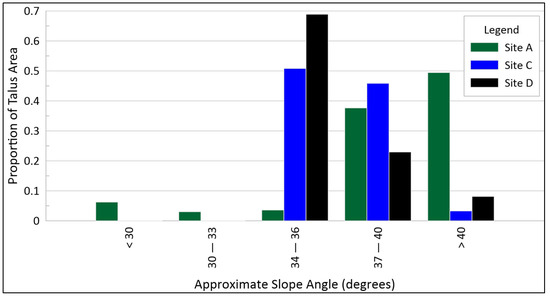
Figure 13.
Histogram of talus slope angle for Sites A, C, and D.
4. Discussion
Based on an extensive inventory consisting of 4381 rockfall events observed at the four study sites over five years, we observe that cumulative magnitude–frequency distributions and their associated power–law parameters are appreciably different: among the four sites, through time, and when sites are discretized by RAI class. This result indicates that site-specific geomorphologic, hydrogeologic, and geologic conditions (characterized by spatial variability) are important components of rockfall activity, along with weather and climate (characterized by temporal variability), and fracture spacing and slope inclination (characterized by RAI class). We discuss these components in Section 4.2 through Section 4.4. In Section 4.5, we discuss the variation in the RAI annual failure rate and average failure depth parameters, and recommend modifying these default parameters for the RAI framework, along with the threshold slope angle for delineating the Talus (T) RAI class. Section 4.6 discusses the sources of error and uncertainty in our current study.
4.1. General Inferences from the Rockfall Inventory
As shown in Figure 7, cumulative rockfall magnitude–frequency plots relatively linearly on a log-log graph over three (Sites B and D), four (Site C), or five (Site A) orders of magnitude, an effect that is similarly observed in rockfall inventories collected by other researchers [20,21,22,23,24,25,34,36]. This observation indicates that rockfall at the study sites follows a power–law magnitude–frequency distribution, as observed frequently in nature.
The data indicate that Site A experienced the most significant rockfall events (up to 28.1 m3), followed by Site C (up to 4.3 m3), Site D (up to 1.2 m3), and then Site B (up to 0.8 m3). These maximum failure volumes are roughly proportional to site surface area (Site A: 16,882 m2; Site C: 2197 m2; Site D: 1647 m2; Site B: 563 m2). Other researchers have found that the upper-end magnitude roll-off (maximum failure size) is typically correlated to slope morphology, vertical relief, and the temporal extent of the surveys [35,36], the latter two factors perhaps being analogous to site surface area due to increased sample size.
The low-end roll-offs of the cumulative magnitude–frequency distributions appear to be generally consistent among the sites, at an event volume between 0.001 m3 and 0.01 m3. This low-end roll-off is equal to or lower than many other rockfall inventories [20,21,22,23,24,25,34,36], indicating that the change detection methodologies used for this study, developed by Olsen et al. [15] and described in Section 2.2, are capturing relatively small rockfall events, comparable to the change detection methodologies developed by others. As observed in Figure 8, the low-end roll-off appears to occur at a higher magnitude in the 2012 to 2013 magnitude–frequency distributions than for the other epochs. As previously described, the 2012 lidar scans were relatively low-resolution (average point spacing of about 5 cm) compared to the subsequent lidar scans (average point spacing of about 1 cm), inhibiting our ability to detect rockfall on the scale of 0.001 m3 to 0.01 m3.
4.2. Spatial (Site-to-Site) Variation in Magnitude–Frequency Distributions
Figure 7 and Table 2 show that the cumulative magnitude–frequency distributions and associated non-cumulative power–law parameters vary significantly among the four sites. In the literature, the power–law parameters for rockfall have been shown to depend considerably on site-specific geology, morphology, and hydrology [37]. As described in Section 1.5, Sites A, B, and C are characterized by distinct geologic settings, each with different rock types, and different bedding, jointing, faulting, and cut-slope orientation. Sites C and D are relatively similar in rock mass characteristics and cut-slope orientation.
The sites are fairly close to one another (within about 25 km), suggesting that weather, climate, and seismic history were similar among the sites for a given epoch. Therefore, the differences between magnitude–frequency distributions and the associated power–law parameters between each site shown in Figure 7 and Table 2 are likely attributed to the differences mentioned above in structural geology, along with differences in site size, groundwater regimes, vegetation, and roadway maintenance/construction history, rather than weather and climate forcing. For example, at Site A, the kinematically viable planar failures (bedding planes approximately parallel to the cut slope), the fractured nature of the mudstone, and the large surface area of exposed rock contribute to this site’s largest rockfall events. In contrast, at Site B, stronger intact rock with distinct perpendicular joint sets, coupled with the smallest exposed surface area, contributes to the lowest activity rate (β) but flattest magnitude–frequency slope (lowest scaling parameter, α, resulting in the greatest large-failure-to-small-failure ratio) of the four sites.
4.3. Temporal Variation in Magnitude–Frequency Distributions
As shown in Figure 8 and Figure 9 and Table 3, the cumulative magnitude–frequency distributions and associated non-cumulative power–law parameters vary significantly at the same site temporally (from year to year), indicating that weather and climate forcing are other important components of rockfall characteristics. We also show that the temporal variation in power–law parameters differs between sites, suggesting that weather and climate forcing have different effects depending on site-specific geology, morphology, and hydrology. The data also indicate that power–law parameters at Sites C and D followed similar trends, as observed by their approximately parallel trendlines shown in Figure 9. This result indicates that similar rock mass characteristics at Sites C and D respond similarly to weather and climate forcing, while other sites with different rock mass characteristics demonstrate different responses.
4.4. RAI Class Variation in Magnitude–Frequency Distributions
As shown in Figure 10 and Table 4 and Table 5, the cumulative magnitude–frequency distributions and associated non-cumulative power–law parameters vary significantly for different parts of the rock slope described by different RAI classes, indicating that the RAI framework is effectively identifying unique erosion and mass-wasting processes on a rock slope. Some trends in the data can be inferred, such as the Intact (I) RAI class typically having a relatively low Activity Parameter (indicating infrequent failures) and a high Scaling Parameter (indicating small failures). Another trend that can be inferred is that the Fragmented Discontinuous Rock (Df), Closely Spaced Discontinuous Rock (Dc), and Widely Spaced Discontinuous Rock (Dw) RAI classes have similar Scaling Parameters (indicating similar size failures) to one another at the same site, but significantly different Activity Parameters (indicating different frequencies). Another inference is that the Shallow Overhang (Os) and Cantilever Overhang (Oc) RAI classes often have relatively low Scaling parameters (indicating relatively large failures).
Another trend that can be inferred is that the Talus (T) RAI class typically has a high Activity Parameter (indicating frequent failures) and a low Scaling Parameter (indicating large failures). We expect that many failures in the talus slope are related to the planar shifting of loose material as the talus slopes are overloaded with rockfall deposits from above. These effects represent the naturally occurring geomorphic evolution of rock slopes; however, we also expect that some of the talus slope toes are actively undercut by highway maintenance activities (for example, clearing ditches and debris catchments with heavy equipment). Although data processing (see Section 2.1) included cropping of the slope toe adjacent to the highway, undercutting the toe also may result in planar shifting higher on the talus slope, which would concentrate detected rockfall events in the talus at the slope base.
As shown in Figure 6, rockfall events in the inventory were observed to “group” together on the slope faces, which is more apparent at the larger sites (Site A and Site C). Researchers have attributed this effect at other sites to strain accumulation preceding and succeeding failures [36], propagation of rockfall events [38], or as a reflection of structural geology [38]. Because our results show that magnitude–frequency distributions and associated power–law parameters vary significantly among RAI classes, we expect that the RAI framework will be moderately effective in capturing this “grouping” effect, though we acknowledge that other effects may also be influential.
Although significant differences between cumulative magnitude–frequency distributions and associated non—cumulative power–law parameters discretized by the RAI class are observed, these differences are not uniform among sites. This indicates that site-specific geology, morphology, and hydrology, such as the differences in rock mass characteristics described in Section 1.5, continue to be influential even when areas of the rock slope are discretized into RAI class.
4.5. Evaluation and Modification of the RAI
4.5.1. Evaluation of the RAI
As shown in Table 6 and Figure 11 and Figure 12, annual failure rate, r, and average failure depth, D, differ significantly between RAI classes for each site (similar to the magnitude–frequency); however, there are notable variations in these parameters for each RAI class among sites and through time, as evidenced by the relatively high standard deviations and coefficients of variation shown in Table 7. The spatial (site-to-site) variation of annual failure rate and average failure depth is significant; however, as with magnitude–frequency distributions and power–law parameters, trends can be observed among the sites, such as very high rates and low depths in Talus (T), low rates and low depths in Intact (I), moderate rates and moderate depths in Fragmented Discontinuous Rock (Df), Closely Spaced Discontinuous Rock (Dc), and Widely Spaced Discontinuous Rock (Dw), and moderate rates and high depths in Shallow Overhang (Os) and Cantilever Overhang (Oc). Significant temporal (through time) variation in the annual failure rate and average failure depth was observed, but these parameters tend to scale proportionally with the other RAI classes at a specific site over time.
Based on these observations, the RAI framework provides a useful relative hazard map for a specific rock slope through time. The observed trends in annual failure rates and average failure depths among sites also indicate that a set of default RAI parameters can provide a useful relative hazard map for different sites with varying geology, morphology, and hydrology. That said, we expect that RAI parameters are affected by site-specific climatic, and geologic and geotechnical domains, so site-specific RAI parameters (annual failure rates and average failure depths) informed by change detection at the evaluated location would increase the efficacy of the RAI.
4.5.2. Modification of the Average Annual Failure Rate, r, and Average Failure Depth, D
Based on the results of this study, we use the robust rockfall inventory to recommend modifications to the default RAI annual failure rates and average failure depths for each RAI class, as shown in Table 9.

Table 9.
Recommended Annual Failure Rates and Average Failure Depths for use in the RAI framework.
4.5.3. Modification of the Talus (T) Slope Angle Threshold
As shown in Figure 12, a significant portion of the talus-surfaced slope area at Sites A, C, and D exceeds an angle of 35°. The preliminary slope inclination threshold for the Talus (T) RAI class of 35° is generally too low to classify talus-surfaced slopes accurately. While the talus slope inclination varies from site to site, we observed it to exceed 40° in some locations. To classify talus areas accurately, we recommend one of two solutions: increasing the slope inclination threshold for Talus (T) classification to 42°; or, preferably, creating a variable Talus (T) slope inclination threshold that can be adjusted on a site-specific basis when implementing the RAI. The variable Talus (T) slope inclination threshold has been incorporated into the RAMBO software as an input parameter in the user interface, with the default threshold set to 42°.
It is worth noting that the measured talus slope angles at Sites A, C, and D are generally steeper than the average natural talus slope angles reported in the literature. Some authors report typical well-drained talus slope angles of about 35° [39,40,41], which is notably lower than the typical effective friction angles of fragmented rock [42]. It also has been shown that talus slopes experiencing toe erosion by river or wave action stand systematically steeper than slopes without erosion at the toe [42]. We hypothesize that talus slopes at Sites A, C, and D emulate toe-eroded talus slope angles because highway maintenance activities periodically remove material at the slope toe as it encroaches on the highway, over-steepening the talus slopes.
4.6. Sources of Error and Uncertainty in this Study
The change detection methodology and the process of identifying rockfall events presents avenues for potential errors in our rockfall inventory. These errors primarily stem from georeferencing inaccuracies [15], data gaps (including cross-referencing data with voids occurring in distinct locations) [15], shifts and expansion of slope vegetation, and the intricate translation of complex three-dimensional geometry transposed into “2.5-dimensional space”. As described in Section 2.2, we manually verified each of the 4381 failure events included in the rockfall inventory to establish a high accuracy level, dramatically reducing the significance of these error sources.
Another potential source of error in the rockfall inventory is related to the temporal resolution of the TLS surveys. Researchers have shown that the temporal resolution of scan surveys can affect the frequency of rockfalls (by decreasing number) and rockfall magnitude (by increasing size) [34]. As previously described, TLS surveys were completed every one to two years (2012, 2013, 2014, 2015, and 2017). Multiple failures that overlapped spatially during one epoch were calculated as one failure in this study, skewing magnitude–frequency and power–law parameters toward a higher distribution of larger failures and lower distribution of smaller failures. For example, the 2015 to 2017 epoch covers two years instead of one, potentially skewing the annual failure rate down and average failure depth up if failures overlap. The RAI output will not be affected by this source of error because the RAI output is quantified as the annual estimated kinetic energy release from each cell on the slope face (actual discrete failure size is irrelevant).
In Section 4.4, it was discussed that some failures in the Talus (T) RAI class could potentially result from the undermining of the talus slope toe due to road maintenance activities, leading to the artificial inflation of the average failure rates. However, we believe that most Talus (T) failures are linked to shallow, infinite-slope-type failure caused by the accretion of rockfall debris from the higher elevation regions of the slope. Hence, the influence of road maintenance activities on the calculation of failure parameters is negligible. For perched talus slopes, these events pose a similar debris fall hazard to infrastructure as traditional rockfalls. Therefore, we recommend assigning RAI parameters to the Talus (T) RAI class as calculated. Other Talus (T) slopes typically occur at the base of the slope, so the RAI scoring will be minimal. A soil slope stability analysis may be warranted for larger talus slopes extending high up the hillside.
The rockfall inventory compiled within this study is limited to four study sites, all situated within one climatic, geological, and tectonic setting. The RAI was developed to support the analysis of large-scale rock slopes over broad regions. As such, further expanding of the rockfall inventory to include other sites with different characteristics would allow the RAI parameters to be further refined. It is worth noting that the current RAI framework does not explicitly address site-specific factors such as climate, seismicity, and geology. However, some of these factors are inherently addressed by the RAI morphological categorizations (e.g., the identification of slope details such as overhanging rock).
5. Conclusions
Based on our robust inventory of 4381 rockfall events at the four study sites over four/five years, we observe that cumulative magnitude–frequency distributions, associated non-cumulative power–law parameters, annual failure rates, and average failure depths are appreciably different among the four sites, indicating that site-specific geology, morphology, and hydrology are important components of rockfall activity. Also significant, however, are the differences in cumulative magnitude–frequency distributions, associated non-cumulative power–law parameters, annual failure rates, and average failure depths at the same site from year to year, indicating that weather and climate forcing are further critical components. We also show the temporal variation in cumulative magnitude–frequency distributions, associated non-cumulative power–law parameters, annual failure rates, and average failure depths differs among sites, indicating that weather and climate forcing have different effects depending on site-specific geology, morphology, and hydrology.
Notably, the cumulative magnitude–frequency distributions, associated non-cumulative power–law parameters, annual failure rates, and average failure depths are significantly different when discretized by RAI class, indicating that the RAI is a useful tool to identify unique erosion and active mass-wasting processes on a rock slope. There are also notable variations in cumulative magnitude–frequency distributions, associated non-cumulative power–law parameters, annual failure rates, and average failure depths separated by RAI class among sites and through time, indicating that site-specific geology, morphology, and hydrology, along with weather and climate forcing, continue to be influential even when areas of the rock slope are discretized into RAI class. These parameters, however, tend to scale proportionally with the parameters from other RAI classes at a specific site through time and between sites; therefore, the default annual failure rate and average failure depth assigned to each RAI class should provide a useful relative hazard map of rock slopes, regardless of significant spatial (site-to-site) and temporal (year-to-year) variation. Site-specific RAI parameters (annual failure rates and average failure depths), informed by change detection at the location where the evaluation is to be completed, would increase the efficacy of the RAI.
We recommend the modification of the annual failure rates and average failure depths for each RAI class based on the results of this study. We also recommend creating a variable Talus (T) RAI class slope angle threshold, as the original threshold of 35° misclassifies some areas of Talus (T) as other RAI classes. Lastly, we recommend increasing the default Talus (T) slope angle threshold to 42°.
Author Contributions
Conceptualization, S.J.M., J.W. and M.O.; methodology, S.J.M. and J.W.; software, M.O.; validation, S.J.M. and M.O.; formal analysis, S.J.M.; investigation, S.J.M., J.W., M.O. and M.M.D.; resources, J.W. and M.O.; data curation, S.J.M., J.W. and M.O.; writing—original draft preparation, S.J.M.; writing—review and editing, J.W., M.O. and M.M.D.; visualization, S.J.M. and M.O.; supervision, J.W.; project administration, J.W. and M.O.; funding acquisition, J.W. and M.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Pacific Northwest Transportation Consortium (PACTRANS), grant numbers DTRT13-G-UTC40 and UWSC10217.
Data Availability Statement
The raw DTM TLS data used for this study are available upon request due to file size. The rockfall inventory and failure characteristics data are openly available on Design Safe at https://doi.org/10.17603/ds2-zv25-jt06, reference number PRJ-4018.
Conflicts of Interest
Co-author Michael Olsen has financial interests in EzDataMD LLC, a technology transfer company that develops software for point cloud analysis, such as the Rambo software used in this research. The outcomes and reporting of this research could potentially benefit EzDataMD LLC and Olsen.
References
- Hungr, O.; Leroueil, S.; Luciano, P. The Varnes classification of landside types, an update. Landslides 2013, 11, 167–194. [Google Scholar] [CrossRef]
- Turner, A.K.; Jayaprakash, G.P. Rockfall Characterization and Control. TR News 2013, 284, 39–41. [Google Scholar]
- Hoek, E. Practical Rock Engineering; Association of Environmental & Engineering Geologists: Vancouver, BC, Canada, 2007. [Google Scholar]
- Stead, D.; Eberhardt, E.; Coggan, J.; Benko, B. Advanced Numerical Techniques in Rock Slope Stability Analysis—Applications and Limitations. In Proceedings of the UEF International Conference on Landslides—Causes, Impacts and Countermeasures, Davos, Switzerland, 17 June 2001; pp. 615–624. [Google Scholar]
- Hoek, E. Strength of Rock and Rock Masses. Int. Soc. Rock Mech. News J. 1994, 2, 4–16. [Google Scholar]
- Piersen, L.A. The Rockfall Hazard Rating System; Oregon State Highway Division, Engineering Geology Group: Salem, OR, USA, 1991. [Google Scholar]
- Bieniawski, Z.T. Engineering Rock Mass Classifications, A Complete Manual for Engineers and Geologists in Mining, Civil and Petroleum Engineering; John Wiley & Sons, Inc.: New York, NY, USA, 1989. [Google Scholar]
- Romana, M. New adjustment ratings for application of Bieniawski classification to slopes. In Proceedings of the International Symposium on the Role of Rock Mechanics, International Society of Rock Mechanics, Zacatecas, Mexico, 2 September 1985; pp. 49–53. [Google Scholar]
- Heok, E.; Brown, E.T. The Hoek-Brown failure criterion and GSI—2018. J. Rock Mech. Geotech. Eng. 2019, 11, 445–463. [Google Scholar] [CrossRef]
- Nicholson, D.T. Hazard assessment for progressive, weathering-related breakdown of excavated rockslopes. Q. J. Eng. Geol. Hydrogeol. 2004, 37, 327–346. [Google Scholar]
- Bar, N.; Barton, N. The Q-Slope Method for Rock Slope Engineering. Rock Mech. Rock Eng. 2017, 50, 3307–3322. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Oppikofer, T.; Abellan, A.; Derron, M.; Loye, A.; Metzger, R.; Pedrazzini, A. Use of LIDAR in landslide investigations: A review. Nat. Hazards 2012, 61, 5–28. [Google Scholar]
- Dunham, L.; Wartman, J.; Olsen, M.J.; O’Banion, M.; Cunningham, K. Rockfall Activity Index (RAI): A lidar-derived, morphology-based method for hazard assessment. Eng. Geol. 2017, 221, 184–192. [Google Scholar] [CrossRef]
- Olsen, M.J.; Massey, C.; Leschinsky, B.; Senogles, A.; Wartman, J. Predicting Seismically Induced Rockfall Hazard for Targeted Site Mitigation; Oregon Department of Transportation Research: Salem, OR, USA, 2020. [Google Scholar]
- Olsen, M.J.; Wartman, J.; McAlister, M.; Mahmoudabadi, H.; O’banion, M.S.; Dunham, L.; Cunningham, K. To Fill or Not to Fill: Sensitivity Analysis of the Influence of Resolution and Hole Filling on Point Cloud Surface Modeling and Individual Rockfall Event Detection. Remote Sens. 2015, 7, 12103–12134. [Google Scholar] [CrossRef]
- CloudCompare (Version 2.11.3). Available online: https://www.cloudcompare.org/ (accessed on 8 March 2016).
- Corominas, J.; Moya, J. A review of assessing landslide frequency for hazard zoning purposes. Eng. Geol. 2008, 102, 193–213. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Guzetti, F.; Rossi, M. Probability distributions of landslide volumes. Nonlinear Process. Geophys. 2009, 16, 179–188. [Google Scholar] [CrossRef]
- Hergarten, S. Landslides, sandpiles and self-organized criticality. Nat. Hazards Earth Syst. Sci. 2003, 3, 505–514. [Google Scholar] [CrossRef]
- Janeras, M.; Lantada, N.; Núñez-Andrés, M.A.; Hantz, D.; Pedraza, O.; Cornejo, R.; Guinau, M.; García-Sellés, D.; Blanco, L.; Gili, J.A.; et al. Rockfall Magnitude-Frequency Relationship Based on Multi-Source Data from Monitoring and Inventory. Remote Sens. 2023, 15, 1981. [Google Scholar] [CrossRef]
- Guerin, A.; Stock, G.M.; Radue, M.J.; Jaboyedoff, M.; Collins, B.D.; Matasci, B.; Avdievitch, N.; Derron, M.H. Quantifying 40 years of rockfall activity in Yosemite Valley with historical Structure-from-Motion photogrammetry and terrestrial laser scanning. Geomorphology 2020, 356, 107069. [Google Scholar] [CrossRef]
- DiFrancesco, P.M.; Bonneau, D.A.; Hutchinson, D.J. Computational Geometry-Based Surface Reconstruction for Volume Estimation: A Case Study on Magnitude-Frequency Relations for a LiDAR-Derived Rockfall Inventory. Int. J. Geo-Inf. 2021, 10, 157. [Google Scholar] [CrossRef]
- Giacomini, A.; Thoeni, K.; Santise, M.; Diotri, F.; Booth, S.; Fityus, S.; Roncella, R. Temporal-Spatial Frequency Rockfall Data from Open-Pit Highwalls Using a Low-Cost Monitoring System. Remote Sens. 2020, 12, 2459. [Google Scholar] [CrossRef]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J.; Afana, A.A. Optimising 4-D surface change detection: An approach for capturing rockfall magnitude-frequency. Earth Surf. Dyn. 2018, 6, 101–119. [Google Scholar] [CrossRef]
- Hartmeyer, I.; Keuschnig, M.; Delleske, R.; Krautblatter, M.; Lang, A.; Schrott, L.; Gunther, P.; Otto, J. A 6-year lidar survey reveals enhanced rockwall retreat and modified rockfall magnitudes/frequencies in deglaciating cirques. Earth Surf. Dyn. 2020, 3, 753–768. [Google Scholar] [CrossRef]
- Veen, M.V.; Hutchinson, D.J.; Bonneau, D.A.; Sala, Z.; Ondercin, M.; Lato, M. Combining temporal 3-D remote sensing data with spatial rockfall simulations for improved understanding of hazardous slopes within rail corridors. Nat. Hazards Earth Syst. Sci. 2018, 18, 2295–2308. [Google Scholar] [CrossRef]
- Connor, C. Roadside Geology of Alaska, 2nd ed.; Mountain Press: Missoula, MT, USA, 2014. [Google Scholar]
- Trop, J.M.; Cole, R.B.; Sunderlin, D.; Hults, C.; Todd, E. Bedrock Geology of the Glenn Highway from Anchorage to Sheep Mountain, Alaska—Field Trip Guide; Geological Society of America and Alaska Geological Society: Boulder, CO, USA, 2015. [Google Scholar]
- Wyllie, D.C.; Mah, C.W. Rock Slope Engineering, Civil and Mining, 4th ed.; Hoek, E., Bray, J.W., Eds.; The Institute of Mining and Metallurgy: Oxon, UK, 2004. [Google Scholar]
- Olsen, M.J.; Johnstone, E.; Driscoll, N.; Ashford, S.A.; Kuester, F. Terrestrial laser scanning of extended cliff sections in dynamic environments: A parameter analysis. J. Surv. Eng. 2009, 135, 161–169. [Google Scholar] [CrossRef]
- Olsen, M.J.; Johstone, E.; Kuester, F.; Ashford, A.A.; Driscoll, N. New automated point-cloud alignment for ground based lidar data of long coastal sections. J. Surv. Eng. 2011, 137, 14–25. [Google Scholar] [CrossRef]
- Maptek. I-Site Studio; (Version 7.0); Maptek: Adelaide, Australia, 2017. [Google Scholar]
- Olsen, M.J.; Kuester, F.; Johnstone, E. Hinged, Pseudo-Grid Triangulation Method for Long, Near-Linear Cliff Analyses. J. Surv. Eng. 2013, 139, 105–109. [Google Scholar] [CrossRef]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J. The Importance of Monitoring Interval for Rockfall Magnitude-Frequency Estimation. J. Geophys. Res. Earth Surf. 2019, 124, 2841–2853. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L.; Guzetti, F.; Reichenback, P. Landslide inventories and their statistical properties. Earth Surf. Process. Landf. 2004, 29, 687–711. [Google Scholar] [CrossRef]
- Barlow, J.; Lim, M.; Rosser, N.; Petley, D.; Brain, M.; Norman, E.; Geer, M. Modeling cliff erosion using negative power law scaling of rockfalls. Geomorphology 2012, 139–140, 416–424. [Google Scholar] [CrossRef]
- Hantz, D. Quantitative assessment of diffuse rock fall hazard along a cliff foot. Nat. Hazards Earth Syst. Sci. 2011, 11, 1303–1309. [Google Scholar] [CrossRef]
- Whadcoat, S.K.; Rosser, N.J.; Brain, M.J.; Hadry, R.J. Spatial and Temporal Patterns of Rockfalls in Hard Rock Coastal Cliffs, North Yorkshire, UK. In Proceedings of the 3rd North American Symposium on Landslides, Roanoke, VA, USA, 4–8 June 2017. [Google Scholar]
- Carson, M.A. Angles of repose, angles of shearing resistance and angles of talus slopes. Earth Surf. Process. 1977, 2, 363–380. [Google Scholar] [CrossRef]
- Sæter, M.B. Dynamics of Talus Formation. Master’s Thesis, University of Oslo, Oslo, Norway, 2008. [Google Scholar]
- Katsube, K.; Oguchi, T. Altitudinal Changes in Slope Angle and Profile Curvature in the Japan Alps: A Hypothesis Regarding a Characteristic Slope Angle. Geogr. Rev. Jpn. 1999, 72, 63–72. [Google Scholar] [CrossRef]
- Chandler, R.J. The Inclination of Talus, Arctic Talus Terraces, and Other Slopes Composed of Granular Materials. J. Geol. 1973, 81, 1–14. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).