1. Introduction
Moving target detection has been studied in radar signal processing for many years. Accordingly, many state-of-the-art works for moving target detection have been proposed [
1,
2,
3,
4]. However, detecting a moving target is a challenging task due to the presence of multipath signals. These multipath signals arise from interactions between electromagnetic waves and rough or glistening surfaces, resulting in reflections and scattering [
5]. Therefore, studying radar target detection in multipath signal environments has become a research hotspot in the past few decades [
6,
7,
8,
9]. While multipath signals are commonly perceived as unfavorable influences, many processing methods have focused on distinguishing or eliminating them [
10,
11]. However, it is essential to acknowledge that multipath signals also carry valuable target information, thereby augmenting the spatial diversity of radar systems.
For target detection in dense multipath environments, various methods have been proposed [
12,
13,
14,
15,
16]. In addition to the above methods, time-reversal (TR) technology [
17], which matches the propagation channel and utilizes space–time focusing to transform the influence of multipath signals into favorable factors, is also an effective method for mining multipath signals without prior environmental knowledge. TR technology can be understood as a radar waveform adaptive transmission scheme. By the TR technique, the transmission waveform can be obtained, which is adaptive to the propagation medium and the scattering characteristics of the target. The TR technique can combine various advantages, such as using multipath signals to build virtual sensors to expand the virtual radar aperture and adapting easily to other waveform design methods to improve target detection performance. Subsequently, TR technology is applied to target detection, leading to the development of various TR detectors that effectively enhance the detection performance for different radar systems [
18,
19,
20,
21,
22].
Most of the previous studies [
18,
19,
20,
21] on TR detection have primarily focused on ideal environments where no clutter is present or the target is assumed to be static. This continuous presence of clutter [
23] and the dynamic nature of targets [
24] significantly degrade the performance of radar detection systems. Precisely for this reason, radar waveform design methods that fully exploit transmission freedom have been considered to improve target detection performance [
9,
25,
26]. Moving targets are detected through the orthogonal frequency division multiplexing (OFDM) waveform in multipath environments where the clutter is nonexistent [
9]. It is worth noting that the Doppler shift of moving targets plays a crucial role in distinguishing them from the clutter background due to the difference between the target velocity and the motion of the clutter scatters. To this end, Naghsh considers the radar coding design problem of moving target detection in a cluttered environment in reference [
27] and proposes a novel waveform optimization method, which improves the probability of moving target detection in a cluttered environment under the reparameterization framework. In addition, under the constraint of a low peak-to-average power ratio, De Maio studies the worst-case coding design problem [
28]. As highlighted earlier, in the context of moving target detection, most waveform design methods do not take into account the challenges that arise in environments where multipath signals and clutter coexist. Then, the existing detection algorithms are unable to achieve satisfactory target detection performance for a moving target in this environment. Therefore, based on this observation, it is valuable to investigate and explore moving target detection in practical cluttered environments.
This paper proposes a detection method for moving targets with an unknown Doppler with the simultaneous presence of clutter and multipath signals. To achieve this, we utilize time-reversal (TR) technology and the waveform optimization (WO) method to address the moving target detection problem. By leveraging these techniques, we propose the TR-WO algorithm to solve the unknown Doppler target detection problem in environments where clutter and multipath signals exist. We first outline the detection problem using a binary hypothesis test framework. Secondly, we derive a TR average likelihood ratio test (TR-ALRT) as a comparison benchmark. Finally, we incorporate waveform optimization (WO) to design the TR-ALRT-WO detector. A conventional likelihood ratio test (C-LRT) detector is also derived as a comparison benchmark. We evaluate the performance of several other detectors that utilize multipath signals to provide a comprehensive comparison and demonstrate the superiority of the proposed TR-ALRT-WO detector.
The significant contributions of our article can be summarized as follows. 1. We investigate the problem of moving target detection under the environment where clutter and multipath signals are. 2. We specifically focus on leveraging TR technology as the basis for our study and develop a comprehensive TR signal model that accurately captures the characteristics of the complex environment. 3. We propose the TR-ALRT-WO detector, which exploits multipath signals, mitigates clutter interference and adapts to moving targets with unknown Doppler information.
The rest of this paper is organized as follows.
Section 2 provides a detailed description of the detection problem and introduces the channel response.
Section 3 describes the detection algorithm, proposes the TR-ALRT-WO detector, and introduces the parameter estimation method. In
Section 4, the C-LRT detector is derived, and the flowchart of the proposed detection algorithm is summarized. A series of numerical examples are analyzed in
Section 5. Finally,
Section 6 concludes the article.
Notations: In this paper, conjugate, transpose and Hermite transpose are represented by the symbols , and , respectively. The symbol denotes the vector formed by collecting the diagonal entries of the matrix argument, whereas denotes the diagonal matrix formed by the entries of the vector argument. is the N-dimensional identity matrix. We use the symbol ⊙ to denote the Hadamard product of two matrices of the same dimension. We denote matrices and vectors with uppercase and lowercase bold letters, respectively. denotes the expectation operator. The uniform distribution from a to b is denoted by . The trace of a square matrix argument is denoted by . and are the determinant and inverse, respectively, of the matrix . The symbol represents the logarithm. The ∼ denotes a statistical distribution.
2. Problem Formulation
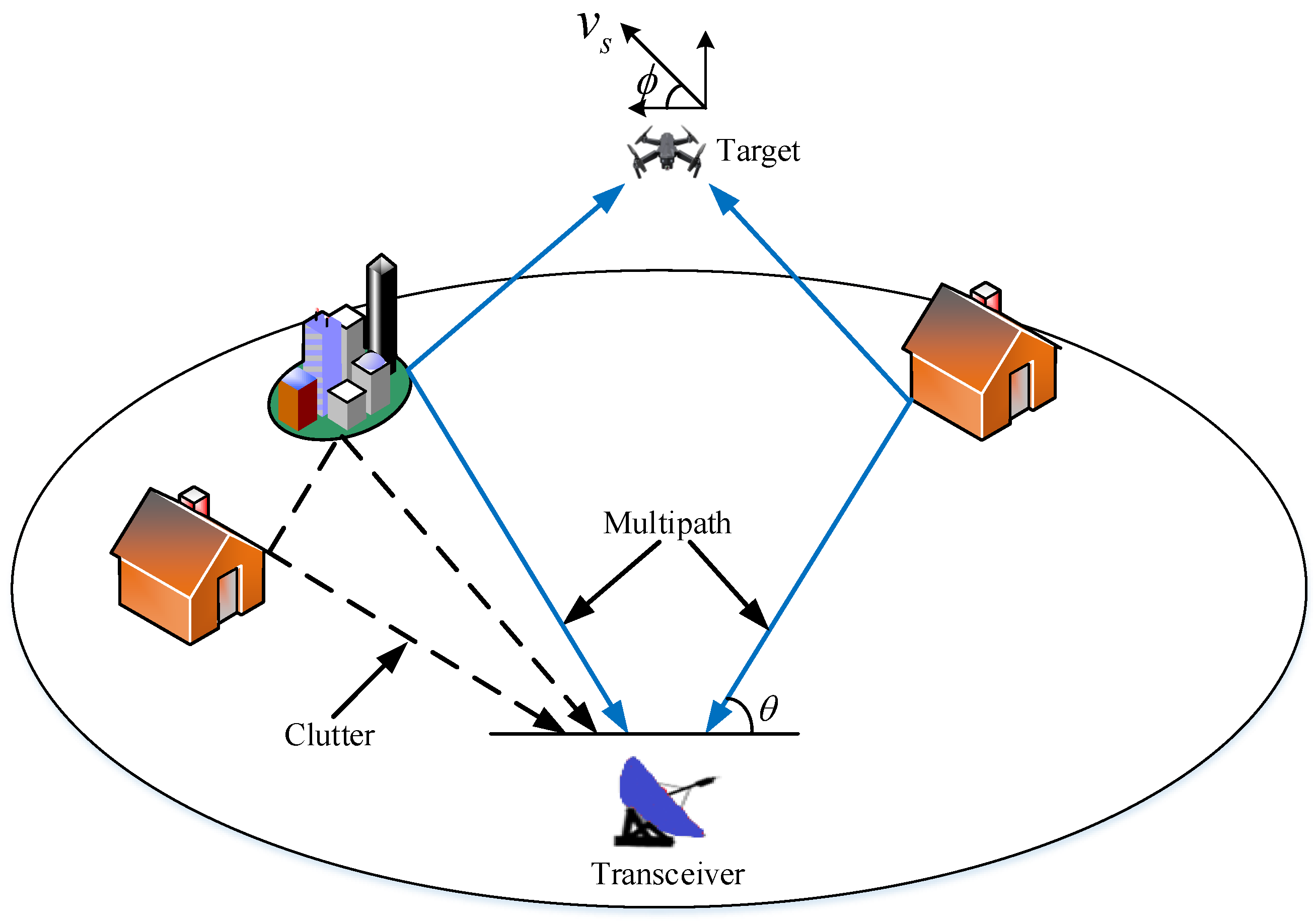
The detection problem of a moving target with an unknown Doppler is considered in an environment where clutter and multipath coexist, as shown in
Figure 1. The target may experience occlusion in specific environments due to excessive reflection surfaces; so, it is assumed that there is no direct path for the target [
24]. Therefore, we define the multipath signals as the scattered target signal that propagates to other objects or reflective surfaces and are finally eventually received by radar.
Moreover, the clutter refers to the signal echoes generated by numerous individual points scattered and distributed across the delay domains. We consider a narrowband radar system that utilizes an omnidirectional antenna. The initial transmitted signal is denoted as
at time instant
t with a total of
T; then, the energy
can be modeled as
The number of propagation paths between the radar and the target is estimated precisely as the prior knowledge [
9]. Thus, the scattering environment contains
L paths associated with the target. And the radar received the
L path signals coming from different distinct directions
. Note that the radar antenna receives abundant diffuse multipath signals at random angles in the environment. Thus,
is considered to follow the uniform distribution from 0 to
. Relative to the radar, the target moves at a constant speed
, and its motion is characterized by an angle
. Based on
and
, we define the Doppler factor in frequency domain as [
29]
Next, the Doppler shift of the target can be obtained as follows
where
is used to represent the radar carrier frequency.
The clutter response consists of
M independent response scatterers in the time-delay domain, which can be represented as
where
M represents the number of clutter scatterers under time delay, and
represents Dirac delta function;
is the specific amplitude of clutter scattering at time delay, satisfying a complex Gaussian random distribution with zero mean and
variance, described as
Similarly, the target multipath response
can be expressed as
where
is the
lth propagation path’s target response, expressed by
where
denotes the
lth path’s time delay. Only overlapping echoes are considered, ignoring the multipath signals whose delay time is greater than the signal duration
T. As a result, we know that the multipath signal’s Delay gratification is
.
is the
lth path’s attenuation coefficient. Since the coherence time of the target channel is much longer than the pulse duration, we use
to represent
[
30,
31].
Since the propagation paths are independent, similarly to the
,
also satisfies a complex Gaussian distribution, which is expressed by
The clutter and target responses are superimposed to form the channel response
, as follows
A two-hypothesis test is considered. In the null hypothesis,
, there are only clutter responses in the channel. In contrast, in the alternative hypothesis,
, there is a moving target in the environment. Here, the binary hypothesis testing problem regarding the channel is
3. TR-WO Detection Algorithm
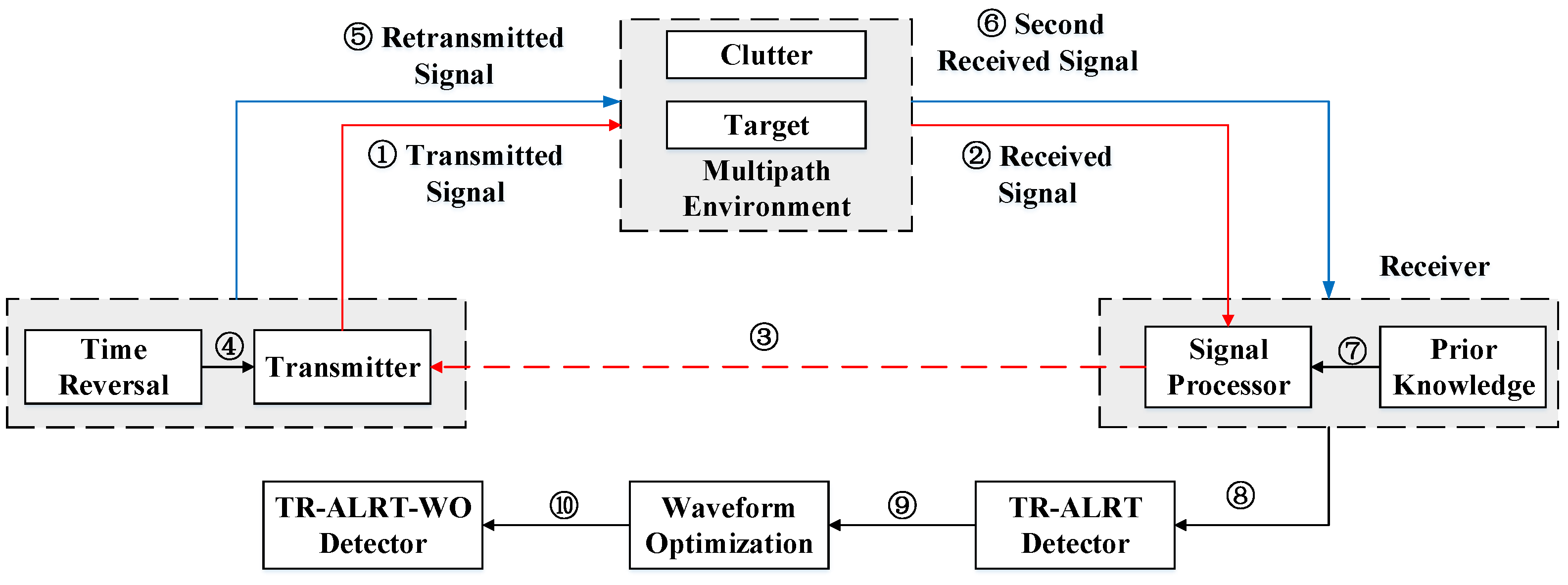
This section discusses the TR-WO detection algorithm, divided into four steps, as shown in
Figure 2. In
Section 3.1, we stack the time-reversed echoes into the vector form and describe a new binary hypothesis test. In
Section 3.2, we simplify the binary hypothesis test problem and derive the TR-ALRT detector.
Section 3.3 introduces the waveform optimization method, and we derive the TR-ALRT-WO detector. In
Section 3.4, we introduce the parameter estimation method for the required prior knowledge.
3.1. TR Received Echoes and TR Binary Hypothesis Test
In this subsection, we first summarize the entire signal processing procedure, composed of the
learning period,
forward transmission period and
backward transmission period, as expressed in
Figure 3.
Learning Period: In this period, we assume the moving target does not yet exist; through repeated transmissions, the noise and the clutter can be estimated accurately.
Forward Transmission Period: The target is moving at Doppler frequency
in the mixed background. By convolving the transmitted signal
with the clutter and target response, a received signal
is formed
where
.
Backward Transmission Stage: We perform the TR procedure in this period using the received signal
obtained from the last period. Firstly, we perform a reversal operation on
in the time domain. Secondly, to ensure that the energy between
of the forward period and
of the backward period is equal, the energy normalization term is calculated. Finally, through the processing procedure of time-reversal processing and energy normalization processing, the retransmitted signal is emitted into the mixed environment and can be described as
where
k is the energy normalization term and is expressed as follows
Then, the TR received signal
can be calculated and written as
where
satisfies
We substitute (12) into (14) and obtain the
as follows:
The clutter and the target are independent according to the assumption of [
18]. Therefore, the second and fourth terms at the right-hand side (RHS) of (16) have a much smaller amplitude and can be ignored. Hence, the TR received signal can be further described as
where
In a dense multipath signal environment, the amplitude of the second term at the RHS of (18) is very small compared with that of the first term [
29]. Therefore, we can ignore the second term’s influence on the
while only retaining the first term. Hence, the
can be reduced to
where
D highlights the multipath signals focusing effect
when
varies by
radian, the phase term changes
, and
is a minimum value so that the phase term will change rapidly in the range
, even for small target motions. In a practical scattering environment, many propagation paths of the radar antenna received from different directions always exist so that
D can be regarded as a random process. Based on the central limit theorem [
32], when the number of multipath signals is large,
D satisfies the complex Gaussian distribution as follows
is obtained by convolving the transmitted signal with the clutter response and is described as
The third and sixth terms at the RHS of (16) are classified as noise term
After the above analysis, therefore, the simplified expression for
is
where
is a big value, and
cannot be ignored. We define the normalized Doppler shift as
; for convenience, we assume that the normalized Doppler shifts of different paths are almost same, i.e.,
; so, the expression of
is as follows
where,
, and
.
Finally, the discrete-time TR target signal model is given by
where
is the focusing factor of the multipath signals,
is the waveform vector and
N is the sample number.
, where the vectors
and
represent the noise and clutter, respectively.
The TR signal model is constructed, and the TR received signal is obtained. Thus, we can describe a new binary hypothesis test problem for TR detection, shown as
3.2. TR-ALRT Detector
For the binary hypothesis testing problem, it is difficult to derive the detector directly. To this end, we consider a mathematical means of simplification: the whitening process. So, we whiten the vector
as follows:
where
, and
and
are the covariance matrix forms of
and
, respectively.
After whitening, (27) can be further simplified, and the expression is described as
where
, with
and
.
Next, we perform a likelihood ratio test on
and obtain
where
is the detection threshold, and
and
are the probability density functions (pdfs) of the alternative hypothesis
and the null hypothesis
, respectively. The pdf of
is as follows
and the pdf of
is expressed as
Next, we take the logarithm of
and remove the constant term to obtain the reduced form of
as follows
However, when the target Doppler is unknown, the vector does not satisfy the Gaussian distribution, and the TR detector is no longer a closed expression, making it unsuitable for detecting a target with the unknown Doppler.
To detect the target of an unknown Doppler, we consider using the pdf
of
p and the average likelihood ratio test to obtain the corresponding TR detector. Then, we derive the TR average likelihood ratio test (TR-ALRT) detector for an unknown Doppler shift, which is expressed as
where
is the interval of
p.
stands for the signal-to-clutter-noise ratio (SCNR), which significantly impacts the performance of the detector. The expression for
is
3.3. TR-ALRT-WO Detector
We introduce a waveform optimization method to maximize SCNR and improve the probability of detecting an unknown Doppler shift moving target in multipath clutter environments. However, clutter is present, and the moving target’s Doppler is unknown; the TR-ALRT detector cannot adapt to the environment and Doppler information. Therefore, based on the mathematical background in [
33], we use a transition criterion, namely the average performance criterion, to optimize
to adapt to the environment and Doppler information. This average performance standard is as follows
where
.
Appendix A analyzes the reasons for choosing such a criterion.
Then, based on the average performance criterion, the improvement of detection performance can be obtained by maximizing the average performance criterion. Thus, under the energy constraint, the optimization problem is described as
where
is the maximum energy available for transmission. If
is the solution of
, it is feasible for some
(
) to lead to
; so, the energy constraint is effective. In the following, we utilize a framework in [
27] to tackle the waveform optimization problem.
According to the framework, we introduce two auxiliary variables,
and
, and the energy constraint can be expressed as
where
is a diagonal matrix expressed as
and
The variable to be solved is converted from
to
. The optimization problem can be boiled down to a semidefinite programming problem (SDP), and the optimal variable
can be obtained using the CVX toolbox [
34].
Using an efficient cyclic iterative algorithm, the optimal
can be synthesized by the optimum
obtained by SDP. An auxiliary variable,
, is essential during the process of the efficient cyclic algorithm. The auxiliary matrix
is given by
where the
and
are obtained by solving the singular value decomposition (SVD) of
. Finally, the optimal
is given by
By substituting the optimal
into (34), the performance of the TR-ALRT detector can be further enhanced. We define the detector using the optimal
as the TR-ALRT-waveform optimization (TR-ALRT-WO) detector, which is expressed as
where
and
3.4. Parameter Estimation
In real scenarios, the time-delay and attenuation coefficient of each propagation path, the target’s Doppler shift and the clutter and noise of the environment are unknown. However, in the target detection problem, these parameters seriously affect the performance of algorithms. These parameters must be estimated through some methods in advance.
(1)
Time-Delay Estimation: At present, there are many estimation algorithms for time delay. We can first make a rough estimation, such as using the adaptive matched filter (AMF) method [
12], and secondly, for the multipath signal environment, the Kumaresan–Tufts (KT) algorithm can be utilized [
35].
(2)
Clutter and Noise Estimation: By utilizing geographic, meteorological or prescan information, it can be assumed that the
and
are known prior [
36,
37].
(3)
Doppler Estimation: First, we can use prior knowledge about the target type, such as whether the target is an aircraft, a ship or a missile. Secondly, we can use the prescan procedures to obtain rough estimates. Finally, these values can be obtained by some cognitive methods, such as those in the literature [
33,
38,
39].
(4)
Amplitude Estimation: According to the obtained time delay and Doppler shift, we can utilize the method in [
24] to determine the propagation paths’ attenuation coefficient.
5. Numerical Simulation Analysis
To illustrate the performance of our proposed TR-WO detection algorithm, we conduct numerical analyses in this section. In this paper, the CVX package solves the convex problem [
34]. The CVX package is a MatLAB-based convex optimization modeling system. CVX translates Matlab into a modeling language, allowing constraints and goals to be specified using standard Matlab expression syntax. CVX supports many standard problem types, including linear and quadratic programs, second-order cones and semidefinite programs. We use the Monte Carlo simulation experiment to obtain the receiver operating characteristic (ROC) curves.
In this paper, the signal-to-noise ratio (SNR) is defined as
and we define the signal-to-clutter ratio (SCR) as
Table 1 enumerates the prior information on the clutter and noise covariance matrices the proposed detection algorithm requires.
In this section, we set , , and . For the case where the target Doppler frequency shift is unknown, we assume that p follows a uniform distribution on . The accuracy of prior information estimation plays a significant role in determining the detection performance of the algorithm proposed in this paper. To make the algorithm we proposed perform better, we need to estimate the prior information as accurately as possible.
5.1. Detection Performance Compared with Other Algorithms
In this subsection, we assess the detection performance of the proposed algorithm compared with other algorithms. Under the same conditions, we compare some algorithms utilizing multipath signals with our proposed detection algorithm, including the TR-LRT detector and TR-GLRT detector, as well as some non-TR technology algorithms, such as the T-AMF algorithm in [
8], the multipath AMF (MP-AMF) detection algorithm in [
15], and the GLRT detection algorithm in [
16]. A snapshot process of TR includes two transmissions, i.e., forward transmission and backward transmission, whereas each snapshot of the conventional detection process includes only one transmission. Therefore, in order to ensure fairness, the number of snapshots of the conventional detection is twice that of the TR detection. We set
,
dB, and the normalized Doppler shift follows a uniform
.
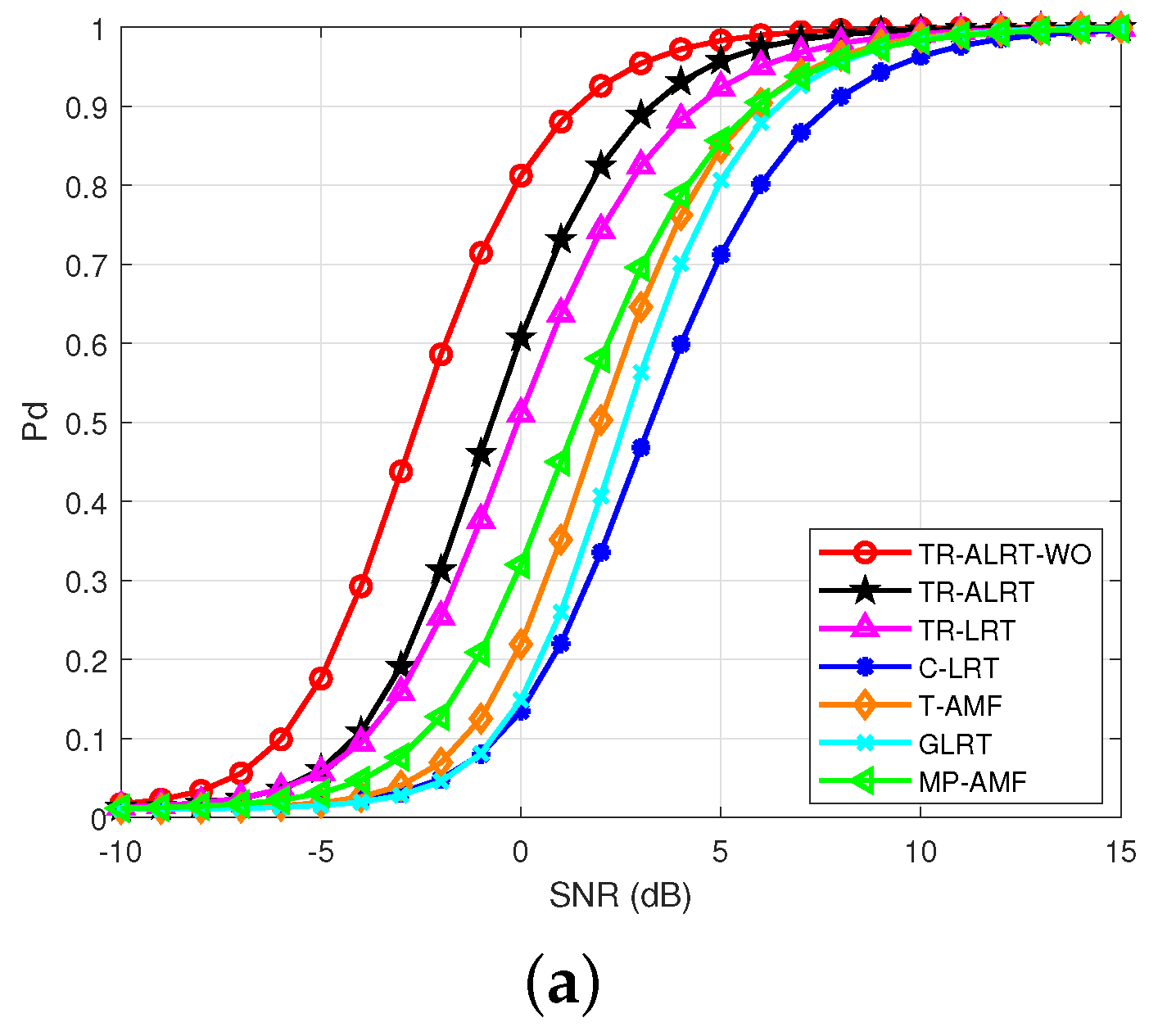
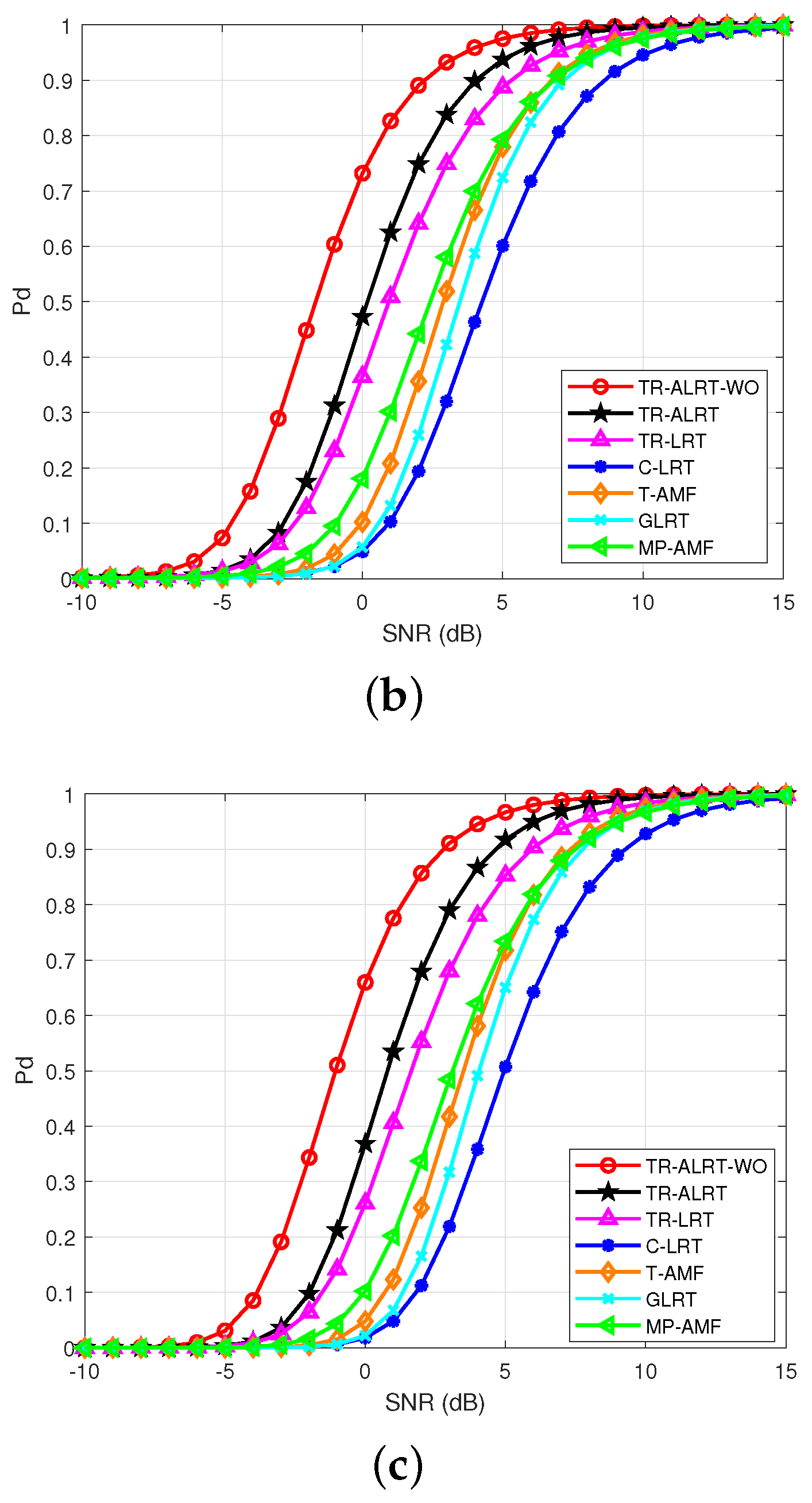
Figure 4 shows the detection probabilities
of different detection algorithms versus the SNR.
Figure 4 consists of three subgraphs with false-alarm probabilities (a)
, (b)
, and (c)
, respectively.
From
Figure 4, it is obvious that the proposed TR-ALRT-WO detector has the best detection performance under different false-alarm probabilities, and the detection probability of the TR detector is higher than that of the non-TR detectors. This is because the TR-ALRT-WO detector can adapt to the Doppler information and can suppress clutter, while the TR-ALRT detector can only average unknown Doppler information; the TR-LRT detector cannot deal with the existence of clutter and an unknown Doppler. It shows that our proposed detection algorithm is the most suitable for moving target detection in a mixed environment.
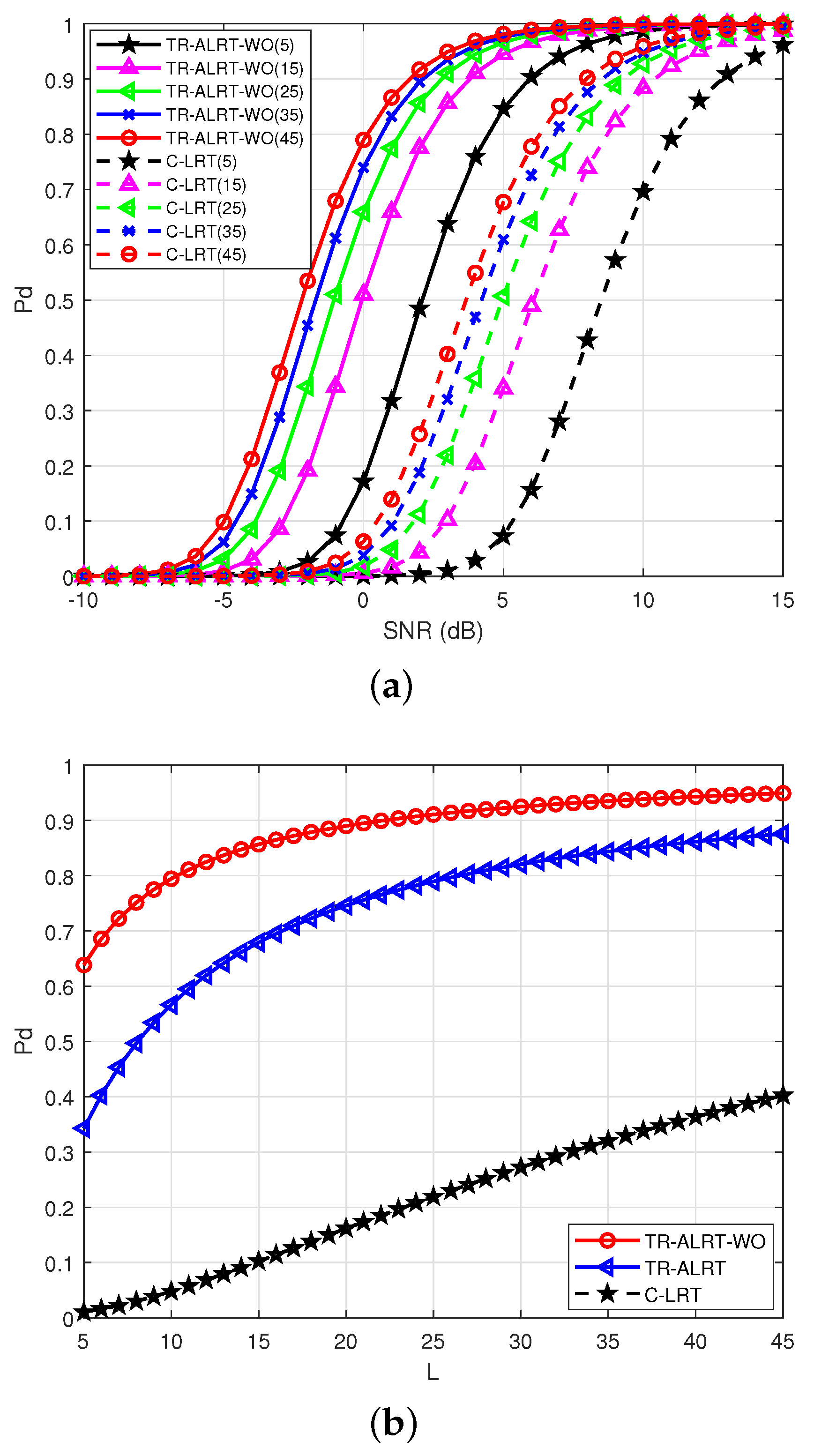
5.2. Detection Performance versus the Propagation Paths
In this subsection, we study the effect of propagation path number on the proposed algorithms’ detection performance. We set
,
dB and
. The connection between the detection probability and the propagation paths is shown in
Figure 5.
The variation curve of detection probability with SNR under different path numbers is shown in
Figure 5a. The detection probabilities versus the propagation path number are shown in
Figure 5b under
dB and
dB. The numeric values in the legend’s parentheses indicate the number of propagation paths. The simulation results show that as the number of paths increases, the detection probabilities of different detectors increase. This result indicates that our proposed detection algorithm can increase energy through the focusing effect and effectively utilize multipath signals. The TR-ALRT-WO detector utilizes the multipath signals and uses the waveform design method to suppress clutter while adapting to target Doppler information to improve detection performance. Therefore, its detection performance is superior to TR-ALRT and C-LRT detectors. In contrast, the TR-ALRT detector can utilize multipath signals through TR technology; however, for unknown Doppler and clutter information, the TR-ALRT detector is helpless. The C-LRT detector does not consider the multipath signals, clutter or Doppler information; therefore, it cannot adapt to the environment.
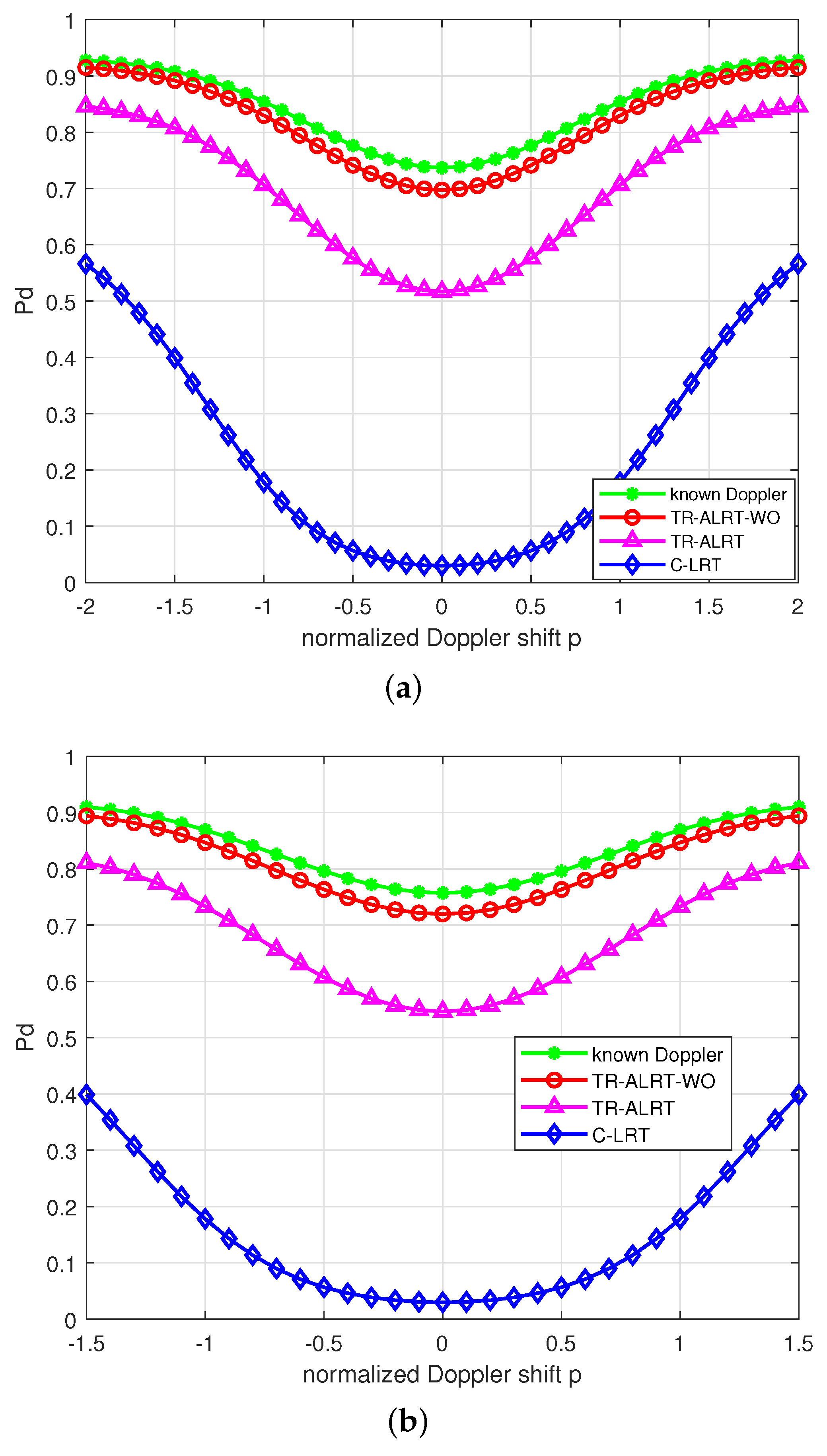
5.3. Detection Performance versus the Target Doppler Shift
Here, we consider the detection performance versus the normalized target Doppler shift
p. We set
dB,
dB,
,
and two different Doppler shift intervals,
and
. We also study the corresponding
when the normalized target Doppler shift is known. We obtain the optimal
by maximizing (35) of each normalized Doppler; therefore, different normalized target Doppler shifts result in different detection probabilities. The simulations of the case are shown in
Figure 6.
From the two subgraphs in
Figure 6, it can be seen that the PD of the TR-ALRT-WO detector is slightly lower than that under known Doppler conditions. Due to the frequency domain overlap between the target and clutter signals, all curves with
exhibit poor values. The TR-ALRT detector only utilizes multipath signals and averages unknown Doppler information, and the C-LRT detector cannot adapt to a moving target and the mixed environment. Therefore, the detection probabilities of these two detectors are relatively low. The TR-ALRT-WO detector outperforms the TR-ALRT and C-LRT detectors significantly, demonstrating the good ability of our proposed detector to adapt to the environment information and detect a moving target with an unknown Doppler shift.
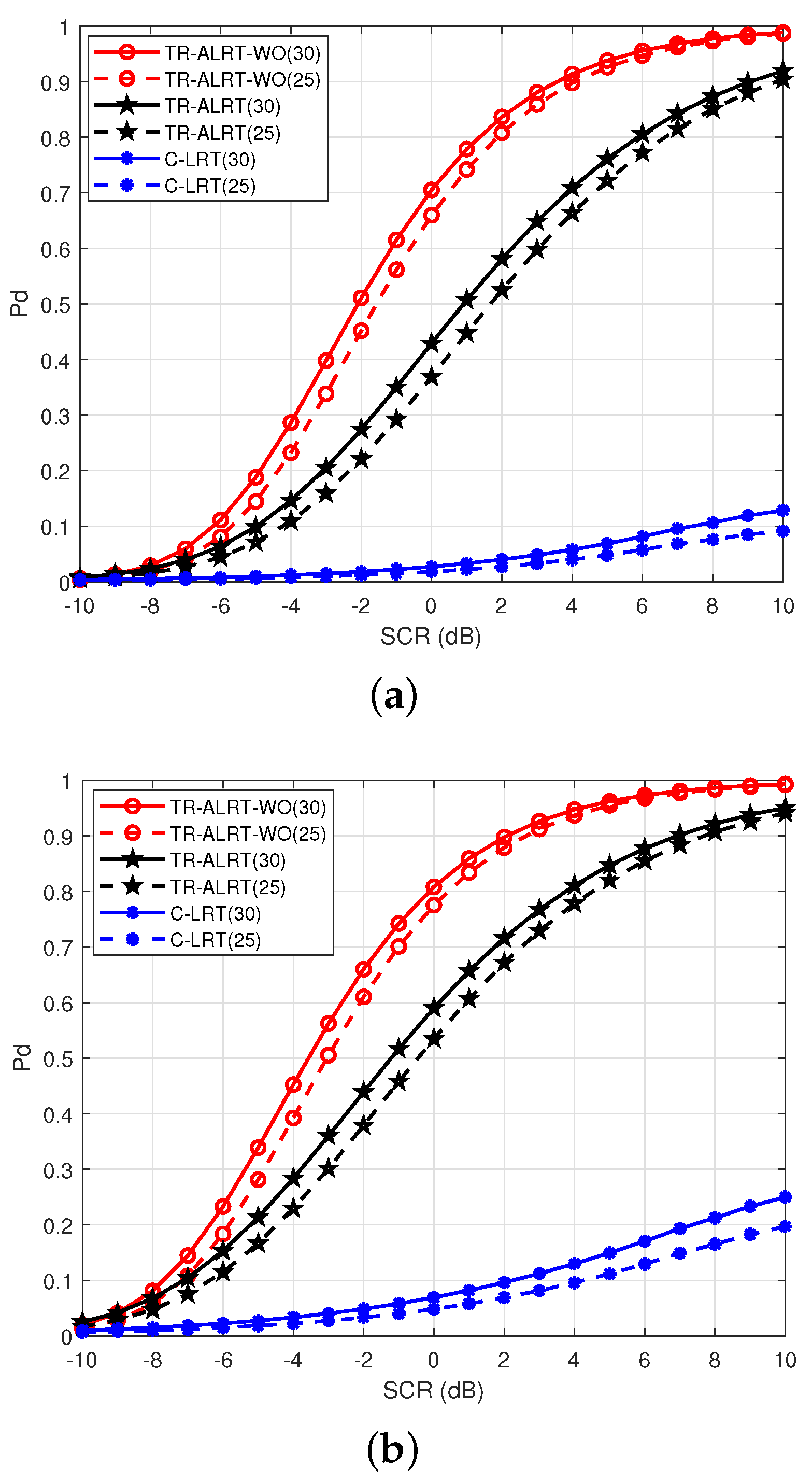
5.4. Detection Performance versus the SCR
Here, we investigate the detection performance versus SCR. We set the Doppler shift interval
, two propagation paths
and
,
. The trend of detection probability versus the SCR corresponding to different conditions of
dB and
dB is shown in
Figure 7a,b.
In
Figure 7a, the SNR is set to 0 dB. When the detection probability of the TR-ALRT-WO detector is greater than 0.9, SCR is only 4dB, while the TR-ALRT detector needs to satisfy
dB to achieve the detection probability. Even worse, the detection probability of the C-LRT detector, which does not utilize the TR technology, is always lower than 0.12. The results of
Figure 7a show that the TR-ALRT-WO detector exploits multipath signals, mitigating clutter, adapting to a moving target with unknown Doppler information and improving the target detection probability.
We set the SNR as 1 dB in
Figure 7b. In the case that SNR is different from that of
Figure 7a, the phenomenon of
Figure 7b is consistent with that of
Figure 7a. Even if the SCR is low, the detection probability of our proposed TR-ALRT-WO detector is still high. However, unlike the TR-ALRT-WO detector, the C-LRT detector‘s detection probability remains very low, while slowly increasing with the increase in the SCR and tending to saturation.
Figure 7b further indicates that the TR-ALRT-WO detector can adapt to the mixed clutter and multipath signals environment and the target Doppler information, as well as improve detection probability.