Abstract
The interest in bistatic SAR systems for soil moisture monitoring has grown over recent years, since theoretical studies suggest that the impact of surface roughness on the retrieval of soil moisture decreases when multistatic, i.e., simultaneous mono- and bistatic, radar measurements are used. This paper presents a semi-empirical method to retrieve soil moisture over bare agricultural fields, based on effective roughness modeling, and applies it to a series of L-band fully-polarized SAR backscatter and bistatic scattering observations. The main advantage of using effective roughness parameters is that surface roughness no longer needs to be measured in the field, what is known to be the main source of error in soil moisture retrieval applications. By means of cross-validation, it is shown that the proposed method results in accurate soil moisture retrieval with an RMSE well below 0.05 m3/m3, with the best performance observed for the cross-polarized backscatter signal. In addition, different experimental SAR monostatic and bistatic configurations are evaluated in this study using the proposed retrieval technique. Results illustrate that the soil moisture retrieval performance increases by using backscatter data in multiple polarizations simultaneously, compared to the case where backscatter observations in only one polarization mode are used. Furthermore, the retrieval performance of a multistatic system has been evaluated and compared to that of a traditional monostatic system. The recent BELSAR campaign (in 2018) provides time-series of experimental airborne SAR measurements in two bistatic geometries, i.e., the across-track (XTI) and along-track (ATI) flight configuration. For both configurations, bistatic observations are available in the backward region. The results show that the simultaneous use of backscatter and bistatic scattering data does not result in a profound increase in retrieval performance for the bistatic configuration flown during BELSAR 2018. As theoretical studies demonstrate a strong improvement in retrieval performance when using backscatter and bistatic scattering coefficients in the forward region simultaneously, the introduction of additional bistatic airborne campaigns with more promising multistatic SAR configurations is highly recommended.
1. Introduction
Soil moisture (Mv) is an essential variable in the hydrological cycle both at the global and local scale, since it plays a critical role in the water and energy balance, affecting crop development, and controlling runoff processes. Acquiring ground measurements of soil moisture is labor intensive. Therefore, ground measurements are often limited in spatial coverage and to few snapshots in time. Remote sensing provides a means of monitoring soil moisture over a range of spatial and temporal scales [1]. It is well known that Synthetic Aperture Radar (SAR) systems are capable of observing soil moisture, with relatively high spatial resolution, typically about 5–20 m [2]. Studies by Schmugge [3] and Ulaby et al. [4,5] illustrated a relationship between the radar backscatter signal and the soil moisture content. Several models have been developed and evaluated over the last decades to retrieve soil moisture from the SAR backscattering coefficient (see [6,7] for an overview). The Integral Equation Model (IEM) is one of the most frequently used scattering models that performs well for bare or sparsely vegetated land surfaces [8].
The backscattered microwave energy not only depends on the soil moisture content, but also on other surface parameters such as surface roughness and vegetation cover. Decoupling the contributions of soil moisture and surface roughness on radar backscatter is difficult when relying on a measurement from a monostatic SAR system, making the retrieval of soil moisture challenging. Therefore, the interest in bistatic remote sensing systems for soil moisture retrieval has grown over recent years. Thereby, one aims to evaluate the improvement in estimation accuracy from the simultaneous use of the monostatic backscattering and bistatic scattering signal, the so-called multistatic system, compared to the standard monostatic system (e.g., [9,10,11,12,13,14,15]).
A bistatic radar system is defined when a transmitter is placed at one site and a receiver at another site, separated by a considerable distance. The receiver detects and processes the echoes scattered by the Earth’s surface, which is illuminated by the transmitter [16]. The bistatic scatter can be regarded as an independent observation of the target, as different scattering mechanisms affect the bistatic observation. The bistatic geometry is depicted in Figure 1, with the zenith incidence angle and and the scattering zenith and azimuth angle, respectively. Scattering in the plane of incidence is observed when = 0° or 180°. The backscattering and specular directions are in this case ( = and = 180°) and ( = and = 0°), respectively. The zenith angles can range from 0° to 90° and the azimuth scattering angle can range from −180° to 180°.
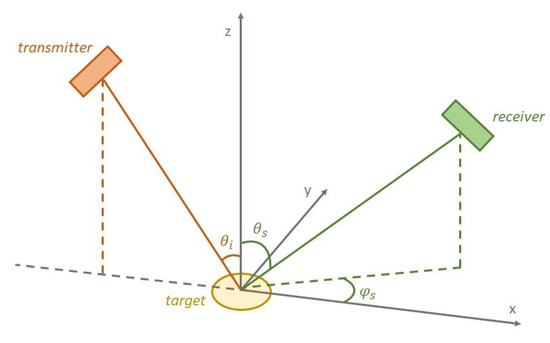
Figure 1.
Geometry of the bistatic active-passive SAR system.
Global navigation satellite signal reflectometry (GNSS-R) is a bistatic soil moisture detection technique that has been studied intensively over recent years. Both modeling and experimental GNSS-R studies are available evaluating the potential and effectiveness of bistatic SAR systems for soil moisture sensing, e.g., [17,18,19]. The GNSS-R studies mostly focus on bistatic scattering in the specular region because of received power considerations. However, studies evaluating the various bistatic SAR geometries for soil moisture detection are to-date only limited to theoretical model simulations, e.g., [10,12,20]. These theoretical studies make use of the Advanced Integral Equation Model (AIEM) [21,22] to simulate various geometric SAR configurations and to show the potential of the combined use of monostatic backscatter and bistatic scattering signals for bare soil moisture retrieval. In these studies, it is hypothesized that the impact of surface roughness on the retrieval decreases due to the two simultaneous observations. Especially, for bistatic observations in the forward region, an increase in sensitivity towards soil moisture is expected [10,20]. A recent study by Pierdicca et al. [15] investigated the best possible bistatic SAR configurations for soil moisture sensing using the small slope approximation up to the second-order model (SSA2). It was found that the following set of polarizations is very interesting: VV bistatic with VV and HH monostatic, with most promising region of scattering angles: 30° < < 60° and 60° < < 80°. Furthermore, it was pointed that all bistatic measurements performed in the forward region could improve the soil moisture retrieval accuracy.
In order to validate these theoretical model results and to further assess the feasibility of a bistatic active-passive satellite configuration for soil moisture retrieval, an airborne campaign for fully-polarized bistatic SAR measurements in the L-band has been carried out over an agricultural test site in Belgium, i.e., the BELSAR campaign. The campaign provided time series of airborne monostatic and bistatic measurements in the L-band, recorded during the crop growing season in 2018 including bare soil conditions. In addition, in situ measurements of soil moisture and surface roughness were acquired concurrently with the airborne flights. As stated by Ulaby et al. [23], the surface correlation length (l) and standard deviation of the surface height variation, also called root-mean-square height (s), are two geophysical parameters that are commonly used to characterize surface roughness. The autocorrelation function (ACF) is also an important factor in characterizing the surface roughness. According to Davidson et al. [24] and Callens et al. [25], the exponential ACF is capable of characterizing a relative smooth agricultural soil surface, particularly in the L-band.
By inverting radar scattering models, one is able to retrieve soil moisture from SAR observations. Yet, these soil moisture retrieval results are prone to errors, which are found to be mainly caused by inadequate surface roughness parameterization from field measurements [26,27]. Here, we present a method which relies on calibrated or effective surface roughness, in which SAR observations are first used to calibrate roughness parameters that can then be used in an inversion scheme to retrieve soil moisture with higher accuracy. These effective roughness parameters no longer have a physical meaning, but must rather be seen as tuning parameters of the scattering models improving the retrieval accuracy. The main advantage of using effective roughness parameters is that surface roughness no longer needs to be measured in the field. Lievens et al. [28] proposed a method in which a statistical model is developed that allows for the estimation of effective surface roughness parameters from SAR backscatter observations in the L- and C-band over bare agricultural soils. These effective roughness parameters are updated for every acquisition, resulting in more accurate soil moisture retrieval results compared to more traditional techniques in which a fixed effective roughness parameter is used, e.g., Su et al. [29]. In this paper, the method proposed by Lievens et al. [28] is further developed in order to improve the accuracy and to allow the modeling of effective surface roughness parameters from bistatic SAR observations.
In this article, we evaluate the potential of monostatic and bistatic SAR data to estimate soil moisture over bare agricultural fields, whereby the soil moisture retrieval performance obtained from monostatic SAR data is compared with those obtained using a multistatic configuration. This work has been accomplished in the frame of the Belgian Science Policy Office (BELSPO) funded project BELSAR-Science and provides the opportunity to evaluate the performances of L-band SAR monostatic and multistatic imagery for soil moisture retrieval based on experimental SAR observations.
In Section 2, a description of the study site, the experimental SAR data and in situ ground measurements is given and the developed technique for effective roughness modeling is proposed. Section 3 analyzes and validates the soil moisture retrieval results from L-band mono- and bistatic scattering observations, and furthermore, identifies the SAR configurations that provide the best retrieval performances. Finally, the concluding remarks are summarized in Section 4.
2. Materials and Methods
2.1. Study Site
The BELSAR airborne and field campaign took place during the 2018 crop growth season (May–September), including bare soil conditions, in the BELAIR Hesbania test site near Gembloux, Belgium. Belgium is characterized by a temperate, maritime climate with an average cumulative precipitation amount of 910 mm/year with a peak occurring in winter and a mean annual temperature of 10.2 °C, with highest temperatures occurring in July (after: https://www.meteo.be, 25 January 2022). A total of 20 reference plots (10 winter wheat and 10 maize fields) were selected in the area to perform the BELSAR-Science study. The fields are relatively large, about 1–19 ha, and have a uniform topsoil texture of silt loam. Ground measurements campaigns were performed concurrently with the SAR acquisitions, to acquire in situ measurements of soil moisture and soil surface roughness in the reference plots. The location of the Hesbania test site and reference plots within the site are depicted in Figure 2.
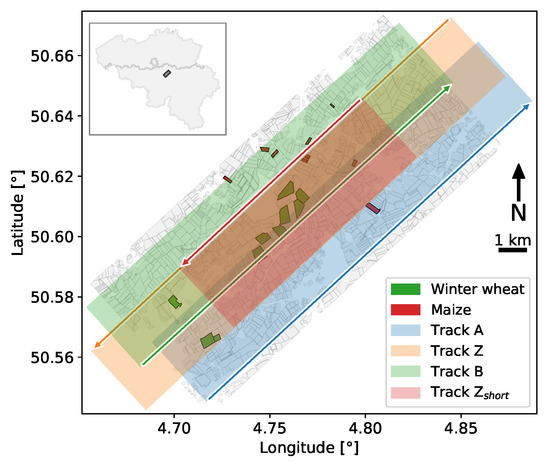
Figure 2.
The BELAIR Hesbania test site, with the winter wheat and maize fields in green and red, respectively, and all the other agricultural fields inventoried on the anonymous cadastral map for agricultural land provided in Wallonia’s land-parcel identification system (Système Intégré de Gestion et Contôle (SIGeC)) in grey. The four parallel flight tracks are represented by colored arrows.
2.2. Airborne SAR Data
The BELSAR project intended to carry out an airborne campaign over a Belgian test site in order to acquire bistatic and interferometric SAR measurements in the L-band (1.375 GHz) in full-polarization (HH, VV, HV and VH) [30]. Five flights were conducted over the test site during the vegetation growth period in 2018. The first flight took place on 30 May, the second on 20 June, the third on 30 July, the fourth on 28 August and the final flight on 10 September. Since this study focuses on the application potential of multistatic SAR images for soil moisture retrieval over predominantly bare soil surfaces, only harvested winter wheat and maize fields are taken into account here, further referred to as bare-wheat and bare-maize. Winter wheat fields measured in July, August and September missions are classified as bare-wheat. Wheat stubble was still present on the winter wheat fields during the July flight. Scattering data acquired during this flight are taken into account in the analysis. Some maize fields measured in August and all maize fields measured in September are classified as bare-maize.
During each flight-day, the HESBANIA site was imaged in four overlapping parallel tracks, i.e., Alpha (A), Bravo (B), Zulu (Z) and a short data sample of Zulu (Zs), once in across-track (XTI) and once in along-track (ATI) formation. Tracks A and B are oriented from south to north and are therefore referred to as ascending tracks. Tracks Z and Zs are oriented from north to south and defined as descending tracks (see Figure 2). The baseline between the transmitting antenna (SAR) and receiving antenna (BISAR) in across-track formation is set at 25 m, while in along-track, the baseline equals 400 m, for a flight altitude of 2500 m. Furthermore, both sensors are left-looking. The main characteristics of the BELSAR bistatic active-passive radar system configuration are listed in Table 1.

Table 1.
The main characteristics of the Active-Passive Radar System.
The acquisition and processing of the BELSAR data have been performed with MetaSensing’s airborne SAR system and software [31]. The radiometric and polarimetric calibration were performed according to the procedure described in [32]. The processing delivered Single-Look Complex (SLC) monostatic and bistatic SAR focused data with a 1 m spatial ground resolution. For each reference plot, the field-average monostatic and bistatic scattering coefficient () in linear scale was calculated from each calibrated SAR image, in order to reduce uncertainty.
Given the limited dynamic range of the soil moisture measurements during the BELSAR campaign (see below in Section 2.3), additional SAR data have been added to the BELSAR dataset to test the retrieval approach over a wider range of conditions. To do so, full-polarized ALOS/Palsar backscatter observations in the L-band over the bare Orgeval study site have been added. Coincident with the SAR acquisition on 8 April 2009, measurements of soil moisture and surface roughness were conducted. Fields with surface roughness conditions similar to the bare-wheat fields of the BELSAR campaign were selected for further analysis (four fields in total). For a detailed description of the dataset, we refer to the assessment paper of Baghdadi et al. [33].
It is well known that the radar backscatter not only depends on target properties, but is also influenced by the radar system configuration, i.e., incidence angle, polarization and frequency. To account for the impact of the incidence angle over bare soils, a radiometric normalization is performed, whereby the backscatter and bistatic scattering coefficient () are normalized to a reference incidence angle of 40°. Several normalization techniques have been described and compared by Abdel-Messeh and Quegan [34] and Mladenova et al. [35]. A cosine normalization is applied here, because of its simple and fast implementation as no parameter has to be fitted. The normalization approach is based on Lambert’s law for optics and was initially applied in Ulaby et al. [4]. The normalization of the backscatter coefficient is defined as
where is the backscattering coefficient (m2/m2) at the original incidence angle , and is the backscattering coefficient (m2/m2) at the reference incidence angle , in this case 40°.
In addition, the normalization of the bistatic scattering coefficient is defined as
where is the bistatic scattering coefficient (m2/m2) at the zenith scattering angle, and is the bistatic scattering coefficient (m2/m2) at the reference zenith scattering angle, in this case 40°.
It should be noted that the BELSAR data used for this study are limited to very short baselines and corresponding small bistatic angles between the transmitting and receiving antennas (0.6° and 9° for the XTI and ATI configuration, respectively), with very small differences in zenith incidence () and scattering () angles and azimuth scattering angles () that are very close to −180°, especially in XTI configuration. This implies that bistatic observations are only available in the backward region and not in the theoretically more promising forward region [10,15,20]. Therefore, one might conclude that the bistatic configurations of the BELSAR campaign may likely not be optimal for soil moisture retrieval applications over bare agricultural fields. The baseline was kept low to keep the coherence between monostatic and bistatic signals for change detection, which was also an objective of the BELSAR-Science study. This issue limits the study of the full potential of multistatic radar data to account for the impact of surface roughness in soil moisture retrieval. A flight configuration in specular or orthogonal direction was desired based on theoretical model results [10,15].
2.3. Ground Measurements
Coincident with each SAR acquisition, volumetric soil moisture content was measured using Time Domain Reflectometry (TDR) sensors with 11 cm rods. At least 10 locations per reference plot were monitored with 3 repetitions per location. All soil moisture measurements within each plot were averaged to provide field average soil moisture values. Within-field soil moisture variations are low, which could be expected given the flat topography and homogeneous soil texture. The range of soil moisture values is 0.030–0.189 m3/m3, which corresponds to very dry conditions. The average soil moisture content for bare-wheat soils is 0.05, 0.134 and 0.127 m3/m3, with a standard deviation of 0.008, 0.033 and 0.029 m3/m3, respectively, on 30 July, 28 August and 10 September. Especially during the July flight campaign, soil moisture values were found to be low. Furthermore, it should be stressed that the dynamic range of soil moisture is limited, which is not ideal for developing and testing soil moisture retrieval techniques. Therefore, soil moisture observations over the bare Orgeval study site have been added in order to test the retrieval approach over a wider range of soil moisture conditions (0.030–0.22 m3/m3).
Soil surface roughness was determined using a pin profilometer of 1 m length, with a spacing of 1 cm. Roughness profiles along and across the direction of tillage were acquired to allow determination of correlation length (l) and root-mean-square height (s). At least five profiles per reference plot were taken in both orientations on each acquisition date and field averages were calculated to reduce uncertainty. Correlation length l and root-mean-square height s range from 1.44 to 6.25 cm and from 0.49 to 2.05 cm, respectively, in this study.
In addition, the bulk density of the soil in the reference plots was sampled using Kopecky rings. During the first flight campaign, five samples per reference plot were taken to derive the field average bulk density and within-field standard deviation. If the bulk density changed due to tillage operations in later flight campaigns, additional samples were taken. The average bulk density in the study area over the entire investigation period is 1.205 g/cm3.
2.4. Effective Roughness Modeling as a Tool for Soil Moisture Retrieval
Soil moisture can be retrieved by inverting radar scattering models, using measured SAR backscatter and bistatic scattering as input. The scattering models used in this study are the semi-empirical Oh model [36] and the physically-based Advanced Integral Equation Model (AIEM) [8,21,22]. These models require input information on the surface roughness state in terms of the root-mean-square height (s), and for the AIEM also the correlation length (l), and type of autocorrelation function (ACF). Both Gaussian and exponential ACFs have been evaluated in this study (not shown here) and best results were obtained with the exponential ACF. Therefore, the exponential ACF will be adopted in all simulations in this study. The surface roughness parameterization from field measurements is found to be problematic [26,27] and is therefore often reported as the main source of error in soil moisture retrieval. To circumvent these issues, a method is proposed here which relies on calibrated or effective surface roughness parameters, in which SAR observations are used to calibrate roughness parameters that can then be used in an inversion scheme in order to retrieve soil moisture.
Lievens et al. [28] proposed a method for effective roughness modeling as a tool for soil moisture retrieval from SAR. In the study of Lievens et al. [28], effective roughness parameters were defined by propagating a range of s- and l-values through the IEM and calculating the absolute soil moisture retrieval error for every combination of roughness parameters. The s- and l-values for which the absolute soil moisture retrieval error is minimal, were defined as the effective roughness parameters. By analyzing the behavior of these effective roughness parameters, Lievens et al. [28] have found that a linear relationship exists between normalized SAR backscatter observations and effective roughness parameters. Based on this analysis, a simple linear regression model has been developed in their study that allows for the estimation of effective roughness parameters from HH polarized L-band backscatter observations
with being the modeled effective roughness parameter (here the correlation length l), a and b being regression parameters and the normalized backscatter signal (dB) [28]. The method implies that surface roughness no longer needs to be measured in the field for soil moisture retrieval from SAR. The model parameters a and b have been calibrated for L-band HH polarized backscatter for the IEM, based on a range of (, Mv)-observations for agricultural fields with a smooth to medium smooth roughness state. In the study of Lievens et al. [28], the best soil moisture retrieval results were obtained when s was fixed at a predefined value of 2 cm, and l was estimated using regression model parameters a = −8.833 and b = −102.7 for L-band HH SAR backscatter observations. The modeled effective correlation lengths have then propagated through an iterative inversion scheme of the IEM [8] for the retrieval of the soil dielectric constant, which may then be converted to volumetric soil moisture using the four-component dielectric mixing model [37]. The performance of the linear model has been assessed through cross-validation. The observed and retrieved soil moisture showed good agreement with RMSE close to 4 vol% and R values of approximately 0.87. For a detailed description of the developed technique, we refer to [28].
In this paper, the technique of Lievens et al. [28] has been further developed in order to improve accuracy and to make it applicable for fully-polarized SAR backscatter and bistatic scattering signals. To do so, a range of linear models () have been evaluated for every polarization which allow for the estimation of s and l based on normalized backscatter and bistatic scattering data, by considering a range of values for slope a and intercept b in Equation (3). These modeled effective roughness parameters are then propagated through an iterative inversion scheme of the Oh model [36] and the AIEM [21,22] for the retrieval of the soil dielectric constant, which may then be converted to volumetric soil moisture using the four-component dielectric mixing model [37]. This scheme can be regarded as an iterative optimization procedure. Thereby, a range of soil moisture values (0.001–0.45 m3/m3) are inserted in the dielectric mixing model to compute corresponding soil dielectric constants. Subsequently, these dielectric constants are used as input to the Oh model and AIEM, together with the modeled s- and l-values, and associated backscatter coefficients (HH, VV and HV) are simulated. The retrieved soil moisture value is then reported as the one for which the difference in simulated and observed backscatter is minimal. Once all linear regression models are propagated through the iterative inversion scheme, an optimal linear regression model can be determined. This best linear regression is defined, as the one resulting in the best soil moisture retrieval results, evaluated by the Kling–Gupta Efficiency [38]. The modeled surface roughness parameters corresponding with this best linear regression are defined as the effective roughness parameters (). The Kling–Gupta Efficiency (KGE) is a goodness-of-fit measure between observed and simulated soil moisture and is defined as
where R is the linear correlation between observations and simulations, the standard deviation in observations, the standard deviation in simulations, the observation mean and the simulation mean. Negative KGE values are considered as bad model performance and good model performance is obtained for positive values. The closer to 1, the more accurate the model is. A graphical overview of the developed technique for effective roughness modeling is given in Figure 3.
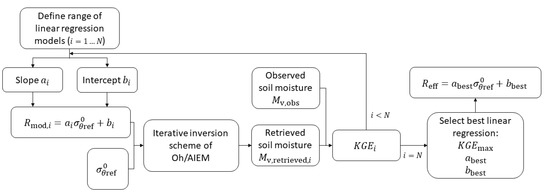
Figure 3.
Graphical overview of the effective roughness modeling algorithm.
Optimal linear regression models are defined for both the Oh model and AIEM separately, what implies that different effective roughness parameters are found for each model. The Oh model only needs the root-mean-square-height s as roughness input parameter. An optimal linear regression for modeling s-values for the Oh model will thus be defined. The AIEM needs both root-mean-square height s and correlation length l as input parameters. We choose to set s at a fixed predefined value, as this parameter can be better measured in the field, and evaluate linear regression models for the estimation of l.
Because of the limited amount of data available, the accuracy of the soil moisture retrieval method has been assessed through cross-validation [39]. The validation of the developed retrieval models is performed based on two strategies. In the first strategy, the data are trained on all data points and subsequently validated on these data points. It should be noted that there are no independent data for validation in this strategy, yet, the validation results of this strategy can be used as a reference. For the second strategy, a leave-one-out cross-validation is carried out. This implies that the linear regression model is trained on all but one data point, and subsequently evaluated on that data point. This procedure is repeated for every data point until a soil moisture value is retrieved for all data points. All these retrieved soil moisture values are then pooled together and plotted and compared against the observed soil moisture values.
2.5. Experimental Set-Up
The BELSAR-Science study is the first experimental study that makes use of fully-polarized L-band airborne backscatter and bistatic scattering observations in two geometric configurations in order to evaluate different SAR configurations for soil moisture sensing. Here, we compare different soil moisture retrieval approaches over bare agricultural soils and we select the most promising one, resulting in accurate retrieval performance. To do so, three cases are studied. In the first one, a comparison is made between two scattering models that can be used for retrieving soil moisture from single co-polarized and cross-polarized backscatter data, i.e., the semi-empirical Oh model and the physically-based AIEM. The second case compares the soil moisture retrieval performance based on single-polarized backscatter data with that based on multi-polarized backscatter data. In the final case, we analyze whether more accurate soil moisture retrieval performance can be obtained when using both co-polarized backscatter and bistatic scattering observations simultaneously in the retrieval process, i.e., the multistatic configuration, compared to monostatic backscatter data. The correlation coefficient (R2) and Root-Mean-Square Error (RMSE) are used to evaluate the retrieval performance of the different SAR configurations.
For the first two cases, only monostatic backscatter data are considered. Normalized backscatter data of the BELSAR campaign are used [30], accompanied by normalized SAR backscatter observations in the L-band over another bare agricultural study site, i.e., Orgeval, France [33], in order to increase the dynamic range of soil moisture. For the third case, normalized backscatter and bistatic scattering data in ATI and XTI flight configuration of the BELSAR campaign are used [30]. It should be noted that the angular separation between transmitter and receiver is limited in both geometric configurations, especially in XTI flight configuration, making the active-passive SAR system rather quasi-bistatic instead of true bistatic.
Two scattering models are evaluated in this study, i.e., the semi-empirical Oh model [36] and the physically-based AIEM [21,22]. The Oh model allows SAR backscatter simulations in co-polarization modes HH and VV and in cross-polarization mode HV. A second scattering model that is evaluated in this study is the physically-based AIEM [21,22]. The single scattering AIEM is an updated version of the widely used IEM model and is capable of simulating bistatic scattering coefficients over bare soil surfaces for a wide range of scattering directions and roughness parameters [40,41]. This way, the AIEM would allow a comparison between the soil moisture retrieval performance using backscatter and bistatic scattering data simultaneously, i.e., multistatic, with that using only backscatter data. The main drawback of the single scattering AIEM is the fact that the model is a first-order model, implying that no cross-polarized backscatter can be simulated due to the lack of the multiple scattering contribution in the model [41]. In addition, it cannot accurately simulate cross-polarized bistatic scattering close to the incidence plane and co-polarized bistatic scattering close to the orthogonal plane. Given the fact that the geometric configuration of the BELSAR campaign corresponds to bistatic scattering coefficients close to the incidence plane, both in XTI and ATI configurations, it is not possible to include cross-polarized bistatic scattering observations in the analysis.
Case 1. In the first experimental case, a comparison is made between soil moisture retrieval performance obtained with the semi-empirical Oh model and the physically-based AIEM using single-polarized backscatter data of the BELSAR and Orgeval campaign. In order to allow a comparison in both co-polarization and cross-polarization modes, a hybrid version of the AIEM is evaluated, whereby the cross-polarized backscatter signal HV is estimated by multiplying the VV signal with an empirical factor q, as is done in the Oh model [36]. This factor represents the cross-polarized ratio and is empirically determined. We refer to Oh et al. [36] for a detailed description. It should be noted that this is a very simple approach to simulate cross-polarized backscatter coefficients and that it not necessarily represents the physical processes that contribute to the depolarization of the radar signal. The Oh model only has one roughness parameter, i.e., root-mean-square height s. For the first experimental case, effective s-values are modeled for the Oh model for HH, VV and HV backscatter based on linear regressions, as described in Section 2.4. Linear regression models are evaluated for each polarization. For the AIEM, the s-value is fixed at 1.75 cm and effective l-values are modeled based on a similar technique. This fixed s-value is determined after iterative optimization (not shown here). These effective s- and l-values are then propagated through an iterative inversion scheme of the Oh model and AIEM, and the four-component dielectric mixing model [37] for the retrieval of soil moisture. To do so, a range of soil moisture values (0.001–0.45 m3/m3) are inserted in the Oh model and AIEM together with the modeled s- and l-values, and associated backscatter coefficients (HH, VV and HV) are calculated. When single-polarized backscatter data are considered, the following cost function can then be evaluated
where is the simulated backscatter in HH, VV or HV polarization and the observed backscatter in HH, VV or HV polarization. The soil moisture value corresponding with the minimal cost, is reported as the retrieved soil moisture value.
Case 2. The second case study analyzes whether more accurate retrieval performance can be obtained when the information of all three polarization modes (HH, VV and HV) is evaluated together. Therefore, one can consider to integrate all backscatter observations in one cost function to take into account all the information. Since the BELSAR and Orgeval dataset comprises fully-polarized backscatter data, it was possible to perform the soil moisture retrieval approach using the information of three polarization modes simultaneously (HH, VV and HV). To do so, we used the modeled effective s- and l-values that were found in the first case. These effective s- and l-values are then propagated through an iterative inversion scheme of the Oh model and AIEM, and the four-component dielectric mixing model [37] for the retrieval of soil moisture. To do so, a range of soil moisture values (0.001–0.45 m3/m3) are inserted in the Oh model and AIEM, together with the modeled s- and l-values, and associated backscatter coefficients (HH, VV and HV) are calculated. For multi-polarized data, the following cost function has been introduced
whereby all backscatter observations in all three polarization modes are taken into account. The soil moisture value corresponding with the minimal cost, can then be defined as the retrieved soil moisture value. This way, the soil moisture retrieval performance based on single-polarized and multi-polarized backscatter data can then be compared for both the Oh model and AIEM. This way, the second experimental case studies whether more accurate retrieval results can be obtained when using the information of three polarization modes simultaneously (HH, VV and HV) in the retrieval process.
Case 3. The third experimental case evaluates whether more accurate retrieval results can be obtained by using backscatter and bistatic scattering data simultaneously, i.e., multistatic, in the retrieval process. Since the AIEM cannot simulate bistatic cross-polarization coefficients close to the incidence plane, this case is focused on the co-polarization mode. A second-order model, e.g., the small slope approximation up to second order (SSA2) [42], could be evaluated in further research to include the depolarization effects originating from multiple scattering. For this experimental case, field average backscatter and bistatic scattering observations in ATI and XTI flight configuration of the BELSAR campaign over bare-wheat soils are used. The s-value is fixed at 1.75 cm and effective l-values are modeled for both the normalized backscatter and bistatic scattering observations in HH and VV polarization, based on a linear regression as described in Section 2.4. These effective roughness parameters are then propagated through an iterative inversion scheme of the AIEM and the four-component dielectric mixing model for the retrieval of soil moisture. To do so, a range of soil moisture values (0.001–0.45 m3/m3) are inserted in the AIEM, together with the modeled l-values, and associated backscatter and bistatic scattering coefficients are calculated. The following cost function is then evaluated to retrieve soil moisture from backscatter observations
with the simulated backscatter in HH or VV polarization and the observed backscatter in HH or VV polarization.
For retrieving soil moisture using backscatter and bistatic observations simultaneously, the following cost function is considered
with the simulated backscatter in HH or VV polarization, the observed backscatter in HH or VV polarization, and with the simulated bistatic scattering in HH or VV polarization and the observed bistatic scattering in HH or VV polarization. The soil moisture value corresponding to the minimal cost is reported as the retrieved soil moisture value.
3. Results and Discussion
3.1. Backscatter Simulations and Soil Moisture Retrieval Using In Situ Measured Surface Roughness Parameters
In order to illustrate the usefulness of effective surface roughness modeling as a tool for soil moisture retrieval, we first illustrate forward backscatter simulations and soil moisture retrievals performed using in situ measured surface roughness parameters and in situ measured soil moisture. To do so, the BELSAR airborne backscatter data are used accompanied by SAR backscatter observations in the L-band over another bare agricultural study site, i.e., Orgeval, France. The field-average SAR backscatter coefficients are normalized to a reference incidence angle of 40° based on Lambert’s law for optics as illustrated in Section 2.2 and, afterwards, the field averaged normalized scatter signals of the four tracks of the BELSAR campaign are averaged, so that for every field average soil moisture value one field average backscatter observation is available, i.e., (, Mv). We found that the field average scattering signal of bare-maize soils is generally higher than that of bare-wheat soils, especially in cross-polarization mode (not shown here). Since soil moisture content and surface roughness are similar for bare-wheat and bare-maize soils, the strong scattering signal of bare-maize soils could result from large crop residues of maize that were still present on the soil surface after harvest. Due to the fact that no information is available regarding crop residue cover in the BELSAR dataset, the data of maize fields are not taken into account in this study.
Next, the SAR observations are confronted with backscatter simulations, obtained through forward backscatter modeling with the Oh model [36], whereby the in situ measured soil moisture and in situ measured root-mean-square height s are used as input parameters for the model. Figure 4 shows the simulated versus observed SAR backscatter coefficients for HH, VV and HV polarization. The simulations are in good agreement with the SAR observations, especially for VV polarization. The Oh model slightly underestimates the backscatter in HH and VV polarization, with a bias of 2.5 dB in HH and 0.6 dB in VV. For the cross-polarization mode HV, a larger bias (5.7 dB) is observed, with the simulated backscatter coefficients being lower than the observed ones. Especially for soil moisture values lower than 0.10 m3/m3, the Oh model tends to underestimate the cross-polarized backscatter coefficient. The origin of this discrepancy might be in the calibration or normalization process of SAR data, in the parameterization of surface roughness or in the model itself, which does not simulate all physical interactions for the cross-polarization. This strong underestimation might also be due to the fact that the radar response is below the noise equivalent sigma zero (NESZ = −31 dB). Therefore, the results presented here related to cross-polarization should be interpreted with caution.
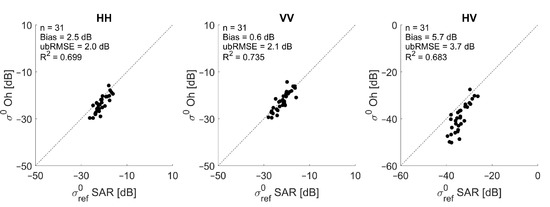
Figure 4.
Simulated versus observed field average bare soil SAR backscatter for HH (left), VV (middle) and HV (right) polarization. Backscatter simulations are performed with the semi-empirical Oh model and in situ measured root-mean-square heights.
Figure 5 illustrates the retrieved versus observed soil moisture values when in situ measured root-mean-square heights s are used in the retrieval process. These in situ measured s-values are inserted in the Oh model together with the backscatter coefficient in order to estimate the associated soil moisture. In order to account for the discrepancy between simulated and observed SAR signals, illustrated in Figure 4, a bias correction has been applied to the SAR backscatter observations prior to the retrieval. This implies that the backscatter observations are corrected by subtracting the biases that were found in Figure 4, i.e., subtracting 2.6 dB for HH, 0.6 dB for VV and 5.7 dB for HV. This way, the SAR observations are in closer agreement with the SAR simulations. Next, we define the retrieved soil moisture values by evaluating the cost function defined in Equation (5). These results indicate that classical measurement techniques for surface roughness parameters in remote sensing campaigns are not accurate enough for retrieving soil moisture using theoretical models, with errors larger than 0.05 m3/m3. Instead, calibrated or effective roughness parameters can be used in the retrieval process.
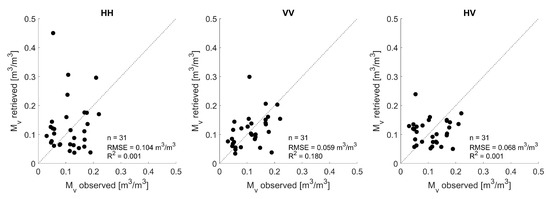
Figure 5.
Retrieved field-average soil moisture values using in situ measured root-mean-square heights in the retrieval process with the Oh model against observed field-average soil moisture values, using single-polarized backscatter data.
3.2. Modeling Effective Root-Mean-Square Height s from SAR Backscatter
Here, we propose a technique for calibrating effective s-values from fully-polarized SAR backscatter observations for the semi-empirical Oh model. The BELSAR airborne backscatter data are used accompanied by SAR backscatter observations in the L-band over another bare agricultural study site, i.e., Orgeval, France, to model effective s-values.
A technique is developed that allows for calibrating effective s-values from fully-polarized SAR backscatter observations. In order to account for the discrepancy between simulated and observed SAR signals, illustrated in Figure 4 and which may result from the calibration or normalization process of SAR data, a bias correction has been applied first to the SAR backscatter observations, similar to the one applied in Section 3.1. Next, different linear regression models are designed and evaluated which allow for the estimation of s from normalized, bias-corrected backscatter coefficients. The slope a of the selected linear regressions for simulating s for the Oh model ranges from 0.001 to 0.20, with a = 0.001, and intercept b ranges from 0 to 8, with b = 0.01 (as optimal KGE values were found within this range). These modeled effective roughness parameters can then be propagated through an iterative inversion scheme of the Oh model [36]. Next, the best linear regression is defined as the one resulting in the best soil moisture retrieval results, evaluated by the Kling–Gupta Efficiency [38], as illustrated in Section 2.4. A visual representation of the KGE for the range of linear regression models (the slope a ranging from 0.001 to 0.20 and intercept b ranging from 0 to 8) that allow for the estimation of effective s-values from HH (left) VV (middle) and HV (right) polarized SAR backscatter, is illustrated in Figure 6. The slope and intercept corresponding with the highest KGE are selected as optimal calibration parameters of the linear model for that particular polarization. The modeled surface roughness parameters corresponding with this best linear regression are defined as the effective roughness parameters.
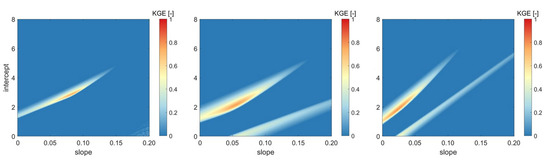
Figure 6.
Kling–Gupta Efficiency (KGE) values for a range of linear regression models (slope a ranging from 0.001 to 0.20 and intercept b ranging from 0 to 8), obtained by inverting the Oh model for HH (left) VV (middle) and HV (right) normalized bias-corrected backscatter coefficients.
As such, an optimal linear model has been developed for HH, VV and HV normalized SAR backscatter observations. An overview of the regression coefficients of these simple linear models and corresponding KGE values is given in Table 2. The corresponding modeled effective s-values range from 0.49 to 1.34 cm for HH, 0.56 to 1.33 cm for VV and 0.74 to 1.11 cm for HV, which is within the validity condition of the Oh model (0.13 < ks < 6.98 with k the wave number, for the L-band k = 0.288 cm) and within the range of in situ measured root-mean-square heights. Yet, the link between observed and effective roughness parameters is not of importance for this study and is therefore not investigated here, but could be subject of further research. Furthermore, the selection of the optimal linear model may be further optimized in future research by including additional data, spanning a wider range of soil moisture values.

Table 2.
Regression model parameters for estimating the effective s-values for the Oh model from normalized backscatter observations.
3.3. Modeling Effective Correlation Length l from SAR Backscatter and Bistatic Scattering
A similar technique has been developed for modeling effective correlation lengths l for the physically-based AIEM [21,22]. As already illustrated in Section 2.5, the AIEM cannot simulate the cross-polarized bistatic scattering coefficient given the geometric flight configuration of the BELSAR campaign. Therefore, linear regression models will only be set up for co-polarized bistatic scattering coefficients. A second-order model, e.g., the small slope approximation up to second order (SSA2) [42], could be evaluated in further research to include the depolarization effects. For the backscatter signal, a hybrid version of the AIEM is evaluated, as described in Section 2.5. As already noted before, this is a very simple approach, which does not necessarily represent the physical processes that contribute to the depolarization of the radar signal.
Data of the BELSAR campaign are used for modeling effective l-values from SAR backscatter and bistatic scattering data. First, backscatter and bistatic scattering observations have been normalized to a reference incidence and zenith scattering angle of 40° as illustrated in Section 2.2 and averages of scattering coefficients of the four flight tracks are calculated. Next, the backscatter and bistatic scattering observations of the XTI and ATI flight configuration are confronted with backscatter and bistatic scattering simulations from the single scattering AIEM. For this purpose, we perform forward backscatter and bistatic scattering modeling with the AIEM. The AIEM requires following input: surface roughness parameters (i.e., root-mean-square height s, correlation length l and the type of autocorrelation function), the soil dielectric constant, radar frequency and geometric information of the SAR configuration (incidence angle , zenith and azimuth scattering angle). In situ measured soil moisture and in situ measured surface roughness are used for the forward backscatter and bistatic scattering modeling, along with an exponential autocorrelation function. The SAR simulations are plotted against normalized SAR observations in Figure 7 for backscatter and, in Figure 8 and Figure 9, for bistatic scattering in XTI and ATI flight configuration, respectively.
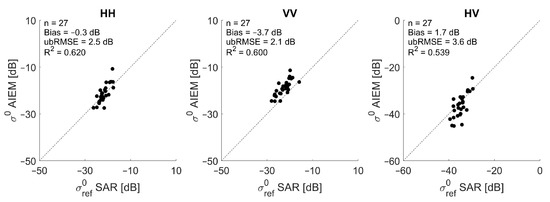
Figure 7.
Simulated versus observed field average bare soil SAR backscatter for HH (left), VV (middle) and HV (right) polarization. Backscatter simulations are performed with the physically-based AIEM and in situ measured roughness parameters.
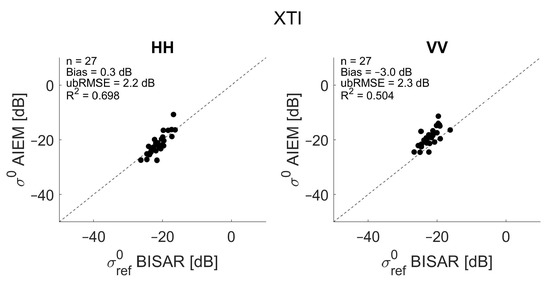
Figure 8.
Simulated versus observed field average bare soil SAR bistatic scattering in XTI flight configuration for HH (left) and VV (right) polarization. Bistatic scattering simulations are performed with the physically-based AIEM and in situ measured roughness parameters.
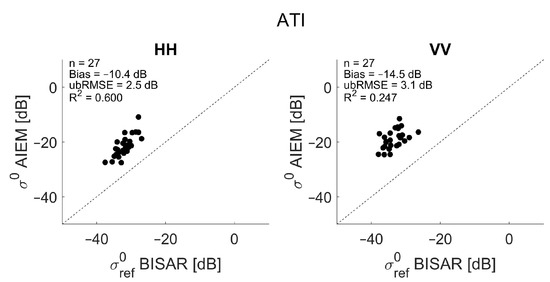
Figure 9.
Simulated versus observed field average bare soil SAR bistatic scattering in ATI flight configuration for HH (left) and VV (right) polarization. Bistatic scattering simulations are performed with the physically-based AIEM and in situ measured roughness parameters.
Good agreement is observed for backscatter and XTI bistatic scattering, especially for HH polarization. A slight underestimation is observed for low signals in HV polarization. As already mentioned, this discrepancy might be due the model description itself, where an empirical factor is used to simulate the cross-polarized signal or it may also be due to the fact that the radar response is below the noise equivalent sigma zero (NESZ = −31 dB). Therefore, the results presented here related to cross-polarization should be interpreted with caution, as was also the case for the Oh model. For the VV signal, a bias is visible between simulated and observed backscatter and bistatic scattering with the simulations being slightly higher than the observations. This might be caused by the calibration or normalization process of the airborne SAR data or by parameterization errors of the surface roughness measurements. If these in situ measured surface roughness parameters would be propagated through an inversion scheme of the AIEM for soil moisture retrieval, inaccurate soil moisture retrieval results would be obtained, as was illustrated for the Oh model in Figure 5. For the ATI flight configuration, the simulated bistatic scattering coefficients are not in agreement with the observed coefficients, with the airborne measurements being approximately 10.4 dB (HH) to 14.5 dB (VV) lower than what was simulated with the AIEM. This discrepancy is found to be related to the calibration process of the airborne SAR data.
In order to correct for these inconsistencies, a bias correction is applied first to the BELSAR backscatter and bistatic scattering observations. To do so, biases that were found in Figure 7, Figure 8 and Figure 9 were subtracted from the SAR observations in order to obtain a closer agreement between simulations and observations, i.e., subtracting −0.3 dB for HH, −3.7 dB for VV and 1.7 dB for HV from the backscatter observations, and for the bistatic observations subtracting 0.3 dB for HH and −3.0 dB for VV in XTI mode, and −10.4 dB for HH and −14.5 dB for VV in ATI mode. Next, effective roughness parameters are modeled for the AIEM which can then be used for soil moisture retrieval. The model needs both root-mean-square height s and correlation length l as input parameters. For effective roughness modeling, we set the s parameter at a predefined value of 1.75 cm, and we define and evaluate a range of linear regression models which allow the estimation of l-values from normalized, bias-corrected backscatter and bistatic scattering data. The slope a of the selected linear regressions for simulating l for the AIEM ranges from −20 to 1, with a = 0.1, and intercept b ranges from −100 to 30 for co-polarized and from −250 to −150 for cross-polarized data, with b = 0.1 (as optimal KGE values were found within this range). These simple linear models have been evaluated by the KGE, as described in Section 2.4, and best linear regressions have been identified for each polarization, corresponding with modeled effective l-values that result in accurate soil moisture retrieval results. An overview of the regression coefficients of these optimal linear models and corresponding KGE values for HH, VV and HV backscatter and HH and VV bistatic scattering for the XTI and ATI flight configuration is given in Table 3 and Table 4, respectively. Modeled effective l-values for backscatter range from 23.6 to 38.4 cm for HH, from 8.3 to 93.2 cm for VV, and from 61.4 to 146.7 cm for HV. For bistatic scattering in ATI mode, the modeled effective l-values range from 22.2 to 34.9 cm for HH and from 4.2 to 96.8 cm for VV and in XTI mode they range from 22.5 to 35.5 cm for HH and from 13.3 to 95.9 cm for VV. These values are much larger than in situ measured correlation lengths, which typically range from 2 to 8 cm, e.g., [43]. It is not clear whether there exists a link between in situ measured and effective correlation length. This could be subject of further research.

Table 3.
Regression model parameters for estimating the effective l-values for the AIEM from normalized backscatter observations, whereby s is set at 1.75 cm.

Table 4.
Regression model parameters for estimating the effective l-values for the AIEM from normalized bistatic scattering observations, whereby s is set at 1.75 cm.
3.4. Soil Moisture Retrieval Based on Effective Roughness Modeling
In the previous section, a technique has been developed in which we search for an optimal linear regression model which allows for the estimation of effective roughness parameters from normalized backscatter and bistatic scattering data. As already illustrated before, these modeled effective roughness parameters can be propagated through an iterative inversion scheme of a scattering model for the retrieval of soil moisture. Optimal linear regression models have been developed for HH, VV and HV backscatter observations in the L-band (for modeling effective s-values for the Oh model and effective l-values for the AIEM) and for HH and VV bistatic scattering observations in the L-band for the ATI and XTI flight configuration of the BELSAR campaign (for modeling effective l-values for the AIEM), see Section 3.2 and Section 3.3.
Because of the limited amount of data available (n = 32), the accuracy of the soil moisture retrieval method has been assessed through cross-validation [39]. Figure 10 shows the retrieved field-average soil moisture values against the observed values and this for fully-polarized backscatter data (BELSAR and Orgeval study site), whereby we made use of the inverse of the Oh model. The top line represents the first strategy in which the data are trained on all data points and subsequently validated on these data points. The bottom line represents the second strategy, where a leave-one-out cross-validation is performed. The scatterplots demonstrate a close agreement with the retrieved and observed soil moisture values, with RMSE values well below 0.05 m3/m3. These retrieval results are much better compared to what we found when using in situ measured surface roughness parameters in the retrieval process (see Figure 5). Furthermore, in Figure 10, similar results are obtained for the two strategies, illustrating the robustness of the developed retrieval technique. The best results are obtained for the cross-polarization mode HV, with errors below 0.04 m3/m3 and a maximum R value of 0.626. The co-polarization mode VV also yields accurate soil moisture retrieval results. For the co-polarization mode HH, the retrieval results are slightly worse with R values lower than 0.55 and errors equal to or slightly larger than 0.04 m3/m3.
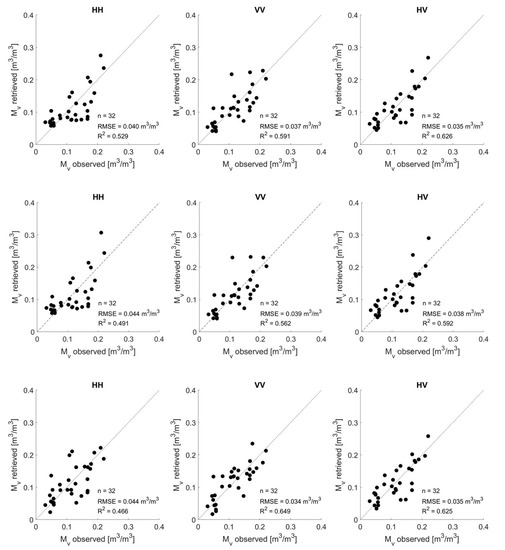
Figure 10.
Simulated field-average soil moisture values based on effective roughness modeling for the Oh model and AIEM against observed field-average soil moisture values for HH (left), VV (middle) and HV (right) polarization. The top line represents the first validation technique performed with the Oh model. The middle line represents the second validation technique, i.e., leave-one-out cross-validation, performed with the Oh model. The bottom line represents the first validation technique performed with the AIEM.
Because of the intensive computation time, the leave-one-out cross-validation of the linear regression model has not been investigated for the AIEM. Nevertheless, the accuracy of the soil moisture retrieval results obtained with the modeled effective l-values for the AIEM (bottom line in Figure 10) is similar to that with the Oh model. Therefore, we can assume a good performance of the developed technique for the AIEM.
3.5. Evaluating Different Soil Moisture Retrieval Approaches
In this section, we compare different soil moisture retrieval approaches over bare agricultural soils, using experimental L-band SAR backscatter and bistatic scattering data, and we detect the most promising one, resulting in accurate retrieval performance. To do so, three experimental cases are studied, which were described in Section 2.5.
Case 1. The first case focuses on the comparison between soil moisture retrieval performance obtained with the semi-empirical Oh model and the physically-based AIEM using single-polarized backscatter data. A hybrid version of the AIEM is evaluated here in order to evaluate both co- and cross-polarization modes. Effective s-values have been simulated for the Oh model, based on the linear regression model described in Section 3.2. For the AIEM, the s-value is fixed at 1.75 cm and effective l-values have been simulated. Based on the method described in Section 3.3, optimal linear regression models were defined for the simulation of l-values based on normalized bare-soil backscatter observations from the BELSAR campaign [30] and one additional field campaign, i.e., Orgeval [33]. The optimal regression coefficients for modeling these effective l-values are: a = −0.1 and b = 23.8 for HH polarization, a = −7.9 and b = −91.2 for VV polarization and a = −8.6 and b = −213.3 for HV polarization. These effective s- and l-values have been propagated through the Oh model and AIEM, and retrieved soil moisture values are defined by evaluating Equation (5).
The top line and bottom line in Figure 10 represent plots of the retrieved field-average soil moisture values obtained with the semi-empirical Oh model and the physically-based AIEM, respectively, against the observed field-average soil moisture values. It is found that for HH polarization, the Oh predictions are closer to the 1:1 line compared to the AIEM, suggesting that the Oh model performs slightly better for retrieving soil moisture from HH polarized backscatter observations. For VV polarization, a slightly lower retrieval error and higher correlation is found for the AIEM. Very similar retrieval performance is found for the cross-polarization mode HV, which can be explained by the fact that the HV signal in the hybrid AIEM is simulated by multiplying the VV signal with an empirical factor, which is also used in the semi-empirical Oh model.
Case 2. In the second experimental case, we study and compare the soil moisture retrieval performance based on single-polarized backscatter data with that based on multi-polarized backscatter data, both for the Oh model and AIEM, by evaluating Equation (6). The modeled effective s- and l-values for HH, VV and HV backscatter that were found in the first experimental case are used.
Intuitively, we would expect that more accurate soil moisture retrieval results can be obtained when multi-polarized backscatter data are used in the retrieval approach because more information is taken into account in the retrieval process compared to the case where only single-polarized backscatter data are used. Figure 10 (top line) and Figure 11 (left) represent plots of the retrieved field-average soil moisture values against the observed values, based on single-polarized backscatter data and multi-polarized backscatter data respectively using the semi-empirical Oh model. Slightly better soil moisture retrieval performance is observed when multi-polarized data are considered, with an error of 0.032 m3/m3 and a correlation coefficient of 0.665. This is in line with what we expect and could be linked to the BELSAR sensitivity study of Bouchat et al. [44], whereby a higher sensitivity to soil moisture and a lower sensitivity to surface roughness was observed when the combination of dual-polarized backscatter was evaluated. For the AIEM, the retrieved versus observed soil moisture based on single-polarized data is represented in Figure 10 (bottom line) and the retrieved versus observed soil moisture based on multi-polarized data is represented in Figure 11 (right). For the AIEM, using multi-polarized data in the retrieval process does not result in a profound increase in retrieval performance, the retrieval performance is rather similar to the one obtained with single-polarized SAR data in VV and HV polarization.
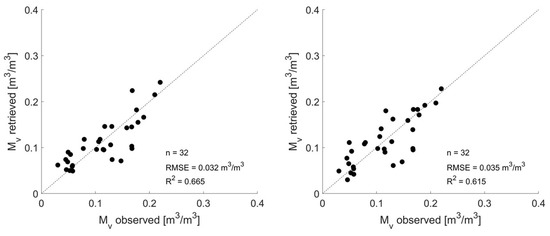
Figure 11.
Simulated field-average soil moisture values based on effective roughness modeling for the Oh model (left) and AIEM (right) against observed field-average soil moisture values, using multi-polarized backscatter data.
Case 3. The third case analyzes whether more accurate soil moisture retrieval results can be obtained when using backscatter and bistatic scattering observations simultaneously, the so-called multistatic case. For this purpose, field-average co-polarized backscatter and bistatic scattering observations in ATI and XTI flight configuration of the BELSAR campaign over bare-wheat soils are used. The effective l-values are modeled based on the optimal linear regression models described in Section 3.3 for both the normalized backscatter and bistatic scattering observations. These effective roughness parameters are then propagated through the AIEM. First, soil moisture is retrieved using only co-polarized backscatter data, as defined in Equation (7). For retrieving soil moisture using co-polarized backscatter and bistatic observations simultaneously, Equation (8) is evaluated.
The left plot in Figure 12 represents the retrieved field-average soil moisture values as a function of the observed values when co-polarized backscatter data were used in the retrieval process and both HH and VV polarizations are considered in the cost function (see Equation (7)). The retrieved field-average soil moisture values when using both backscatter and bistatic scattering observations simultaneously, as illustrated in Equation (8), is reported in the middle and left plot of Figure 12 for the XTI and ATI flight configuration, respectively. We can observe that slightly better soil moisture retrieval results are obtained when using backscatter and bistatic scattering observations simultaneously, and most accurate results are obtained for the ATI flight configuration. Yet, the increase in accuracy is very limited, i.e., RMSE = −0.001 m3/m3 and R2 = +0.028 for XTI flight configuration and RMSE = −0.002 m3/m3 and R2 = +0.066 for ATI flight configuration. This limited increase in retrieval performance was expected given the flight configuration of the BELSAR campaign with short along-track and especially short across-track baseline, and corresponding small bistatic angles. Because of this, the scattering mechanisms involved in the monostatic and bistatic geometry are similar, resulting in the fact that the bistatic scattering coefficients do not give substantial added value to the backscattering. The model-based theoretical study of Pierdicca et al. [15] highlights that the scattering mechanism of the monostatic and bistatic system should be sufficiently different in order to increase the retrieval performance if both scattering coefficients are used simultaneously in the retrieval process. Bistatic scattering in the forward region was therefore desired, with a special focus on the specular and orthogonal direction. These findings are in agreement with the BELSAR sensitivity study of Bouchat et al. [44] where no increase in sensitivity to soil moisture was observed when considering backscatter and bistatic scattering coefficients simultaneously. Given this, the introduction of additional bistatic airborne campaigns with more promising active-passive SAR configurations is highly recommended in order to further verify the improvement in soil moisture retrieval performance.
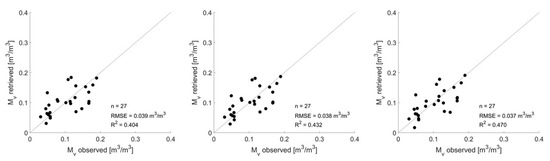
Figure 12.
Simulated field-average soil moisture values based on effective roughness modeling for the AIEM against observed field-average soil moisture values. Left: using HH- and VV-polarized backscatter data of the BELSAR campaign. Middle: using HH- and VV-polarized backscatter and XTI bistatic scattering data of the BELSAR campaign. Right: using HH- and VV-polarized backscatter and ATI bistatic scattering data of the BELSAR campaign.
4. Conclusions
This paper presents a semi-empirical method to retrieve soil moisture over bare agricultural fields, based on effective roughness modeling, and applies it to a series of L-band fully-polarized SAR backscatter and bistatic scattering observations over the Hesbania site and Orgeval site. The technique relies on estimating effective surface roughness parameters for each new SAR acquisition based on simple linear regression modeling. The results of this study illustrate that the developed technique is a promising tool for soil moisture retrieval over bare agricultural soils, especially since it removes the need of surface roughness field measurements, which are known to be the main source of error in soil moisture retrieval applications. Given the limited dynamic range of soil moisture values in this study, it is recommended to evaluate additional linear regression models using a broader range of scattering coefficients and compare these with the regressions that were found in this study. This way, the applicability of the developed linear regression models to other SAR databases can be evaluated. In addition, further research can be carried out in which the developed technique is used as a basis for soil moisture retrieval under a vegetation layer, as is done in the study of Lievens et al. [45].
In addition, different airborne SAR monostatic and bistatic configurations are evaluated in this study for soil moisture retrieval over bare soils, making use of the developed technique and the semi-empirical Oh [36] and physically-based AIEM [21,22] scattering models. Based on the results, we can conclude that using multi-polarized backscatter observations in the retrieval process is recommended to increase soil moisture retrieval performance from L-band SAR backscatter, especially when using the semi-empirical Oh model. Furthermore, the physically-based AIEM shows good potential for simulating backscatter and bistatic scattering coefficients. Yet, some model refinements are recommended, with a special focus on the simulation of cross-polarized backscatter and bistatic scattering close to the incidence plane, in order to evaluate soil moisture prediction accuracy of a fully-polarized bistatic SAR configuration. An attempt has been made by Yang et al. [46] to include a multiple scattering term for the simulation of cross-polarized scattering coefficients.
The retrieval performance of a multistatic system has been evaluated in this study and compared to that of a traditional monostatic system. Airborne SAR data were available for two bistatic geometries, i.e., the XTI and ATI flight configuration. For both configurations, bistatic scattering observations were only available in the backward region close to the incidence plane, which limited the scope of this study to co-polarized multistatic data. Experimental results of this study show that using backscatter and bistatic scattering data simultaneously does not result in a profound increase in retrieval performance. As theoretical studies demonstrate a strong improvement in retrieval performance when using backscatter and bistatic scattering coefficients in the orthogonal direction simultaneously [15], the introduction of additional bistatic airborne campaigns with more promising active-passive SAR configurations (i.e., bistatic scattering in the forward region with a special focus on the orthogonal and specular direction) is highly recommended.
We can conclude that a more optimal active-passive radar system, with bistatic scattering observations in the forward region, in combination with the developed technique for surface roughness modeling, might result in a promising soil moisture detection tool over bare agricultural fields, whereby the need for measuring surface roughness on the field disappears. Especially, in the light of future satellite missions that are foreseen to operate in the L-band, i.e., SAOCOM [47], NISAR [48] and ROSE-L [49], this work is of relevance as it proposes a promising tool for soil moisture retrieval from L-band SAR.
Author Contributions
Conceptualization, E.T., H.L. and N.E.C.V.; methodology, E.T., H.L. and N.E.C.V.; software, E.T.; validation, E.T., H.L., N.B. and N.E.C.V.; formal analysis, E.T.; investigation, E.T.; resources, E.T.; H.L., N.B. and N.E.C.V.; data curation, E.T., J.B.; writing—original draft preparation, E.T.; writing—review and editing, E.T., H.L., J.B., P.D., N.B. and N.E.C.V.; visualization, E.T., H.L. and N.E.C.V.; supervision, H.L. and N.E.C.V.; project administration, P.D. and N.E.C.V.; funding acquisition, P.D. and N.E.C.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the STEREO III program of the Belgian Federal Science Policy Office (BELSPO) grant number SR/00/371, and the PRODEX program of the European Space Agency (ESA) under contract 4000130683.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Restrictions apply to the availability of the data presented in this study. The European Space Agency (ESA) will make the data available after a certain period of time.
Acknowledgments
The authors would like to thank all BELSAR and BELSAR-Science team members for the collection, processing and distribution of the data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kornelsen, K.C.; Coulibaly, P. Advances in soil moisture retrieval from synthetic aperture radar and hydrological applications. J. Hydrol. 2013, 476, 460–489. [Google Scholar] [CrossRef]
- Meyer, F. Spaceborne Synthetic Aperture Radar: Principles, data access, and basic processing techniques. In Synthetic Aperture Radar (SAR) Handbook: Comprehensive Methodologies for Forest Monitoring and Biomass Estimation; SERVIR Global Science Coordination Office: Huntsville, AL, USA, 2019; pp. 21–64. [Google Scholar]
- Schmugge, T. Remote sensing of surface soil moisture. J. Appl. Meteorol. 1978, 17, 1549–1557. [Google Scholar]
- Ulaby, F.; Moore, R.; Fung, A. Rader remote sensing and surface scattering and emission theory. In Microwave Remote Sensing Active and Passive; Artech House Publishers: Norwood, MA, USA, 1982; Volume 2. [Google Scholar]
- Ulaby, F.; Moore, R.; Fung, A. From theory to applications. In Microwave Remote Sensing Active and Passive; Artech House Publishers: Norwood, MA, USA, 1986; Volume 3. [Google Scholar]
- Karthikeyan, L.; Pan, M.; Wanders, N.; Kumar, D.N.; Wood, E.F. Four decades of microwave satellite soil moisture observations: Part 1. A review of retrieval algorithms. Adv. Water Resour. 2017, 109, 106–120. [Google Scholar] [CrossRef]
- Choker, M.; Baghdadi, N.; Zribi, M.; El Hajj, M.; Paloscia, S.; Verhoest, N.E.; Lievens, H.; Mattia, F. Evaluation of the Oh, Dubois and IEM backscatter models using a large dataset of SAR data and experimental soil measurements. Water 2017, 9, 38. [Google Scholar] [CrossRef]
- Fung, A.K.; Li, Z.; Chen, K.S. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Ferrazzoli, P.; Guerriero, L.; Del Monaco, C.I.; Solimini, D. A further insight into the potential of bistatic SAR in monitoring the earth surface. In Proceedings of the IGARSS 2003, 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No. 03CH37477), Toulouse, France, 21–25 July 2003; Volume 2, pp. 776–777. [Google Scholar]
- Pierdicca, N.; Pulvirenti, L.; Ticconi, F.; Brogioni, M. Radar bistatic configurations for soil moisture retrieval: A simulation study. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3252–3264. [Google Scholar] [CrossRef]
- Pierdicca, N.; De Titta, L.; Pulvirenti, L.; Della Pietra, G. Bistatic radar configuration for soil moisture retrieval: Analysis of the spatial coverage. Sensors 2009, 9, 7250–7265. [Google Scholar] [CrossRef]
- Brogioni, M.; Pettinato, S.; Macelloni, G.; Paloscia, S.; Pampaloni, P.; Pierdicca, N.; Ticconi, F. Sensitivity of bistatic scattering to soil moisture and surface roughness of bare soils. Int. J. Remote Sens. 2010, 31, 4227–4255. [Google Scholar]
- Johnson, J.T.; Ouellette, J.D. Polarization features in bistatic scattering from rough surfaces. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1616–1626. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, K.S. Theoretical study of global sensitivity analysis of L-band radar bistatic scattering for soil moisture retrieval. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1710–1714. [Google Scholar] [CrossRef]
- Pierdicca, N.; Brogioni, M.; Fascetti, F.; Ouellette, J.D.; Guerriero, L. Retrieval of biogeophysical parameters from bistatic observations of land at L-band: A theoretical study. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–17. [Google Scholar] [CrossRef]
- Willis, N.J. Bistatic Radar; SciTech Publishing: Raleigh, NC, USA, 2005; Volume 2. [Google Scholar]
- Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Camps, A.; Vall-Llossera, M.; Valencia, E.; Marchan-Hernandez, J.F.; Ramos-Perez, I. Soil moisture retrieval using GNSS-R techniques: Experimental results over a bare soil field. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3616–3624. [Google Scholar] [CrossRef]
- Egido, A.; Caparrini, M.; Ruffini, G.; Paloscia, S.; Santi, E.; Guerriero, L.; Pierdicca, N.; Floury, N. Global navigation satellite systems reflectometry as a remote sensing tool for agriculture. Remote Sens. 2012, 4, 2356–2372. [Google Scholar] [CrossRef] [Green Version]
- Zribi, M.; Motte, E.; Baghdadi, N.; Baup, F.; Dayau, S.; Fanise, P.; Guyon, D.; Huc, M.; Wigneron, J.P. Potential Applications of GNSS-R observations over agricultural areas: Results from the GLORI airborne campaign. Remote Sens. 2018, 10, 1245. [Google Scholar] [CrossRef] [Green Version]
- Zeng, J.; Chen, K.S.; Bi, H.; Chen, Q.; Yang, X. Radar response of off-specular bistatic scattering to soil moisture and surface roughness at L-band. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1945–1949. [Google Scholar] [CrossRef]
- Chen, K.S.; Wu, T.D.; Tsang, L.; Li, Q.; Shi, J.; Fung, A.K. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar]
- Wu, T.D.; Chen, K.S. A reappraisal of the validity of the IEM model for backscattering from rough surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 743–753. [Google Scholar]
- Ulaby, F.T.; Kouyate, F.; Fung, A.K.; Sieber, A.J. A backscatter model for a randomly perturbed periodic surface. IEEE Trans. Geosci. Remote Sens. 1982, GE-20, 518–528. [Google Scholar] [CrossRef]
- Davidson, M.W.; Le Toan, T.; Mattia, F.; Satalino, G.; Manninen, T.; Borgeaud, M. On the characterization of agricultural soil roughness for radar remote sensing studies. IEEE Trans. Geosci. Remote Sens. 2000, 38, 630–640. [Google Scholar] [CrossRef] [Green Version]
- Callens, M.; Verhoest, N.E.; Davidson, M.W. Parameterization of tillage-induced single-scale soil roughness from 4-m profiles. IEEE Trans. Geosci. Remote Sens. 2006, 44, 878–888. [Google Scholar] [CrossRef]
- Verhoest, N.E.; Lievens, H.; Wagner, W.; Álvarez-Mozos, J.; Moran, M.S.; Mattia, F. On the soil roughness parameterization problem in soil moisture retrieval of bare surfaces from synthetic aperture radar. Sensors 2008, 8, 4213–4248. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lievens, H.; Vernieuwe, H.; Alvarez-Mozos, J.; De Baets, B.; Verhoest, N.E. Error in radar-derived soil moisture due to roughness parameterization: An analysis based on synthetical surface profiles. Sensors 2009, 9, 1067–1093. [Google Scholar] [CrossRef] [Green Version]
- Lievens, H.; Verhoest, N.E.; Keyser, E.D.; Vernieuwe, H.; Matgen, P.; Álvarez-Mozos, J.; De Baets, B. Effective roughness modelling as a tool for soil moisture retrieval from C-and L-band SAR. Hydrol. Earth Syst. Sci. 2011, 15, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Su, Z.; Troch, P.; De Troch, F. Remote sensing of soil moisture using EMAC/ESAR data. In Proceedings of the IGARSS’96, 1996 International Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 31 May 1996; Volume 2, pp. 1303–1305. [Google Scholar]
- Meta, A.; Trampuz, C.; Coccia, A.; Ortolani, M.; Turtolo, R. First results of the BelSAR L band airborne bistatic fully polarimetric Synthetic aperture radar campaign. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1040–1042. [Google Scholar]
- de Macedo, K.A.C.; Placidi, S.; Meta, A. Bistatic and monostatic insar results with the metasensing airborne sar system. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; pp. 1–5. [Google Scholar]
- Fore, A.G.; Chapman, B.D.; Hawkins, B.P.; Hensley, S.; Jones, C.E.; Michel, T.R.; Muellerschoen, R.J. UAVSAR polarimetric calibration. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3481–3491. [Google Scholar] [CrossRef]
- Baghdadi, N.; Dubois-Fernandez, P.; Dupuis, X.; Zribi, M. Sensitivity of main polarimetric parameters of multifrequency polarimetric SAR data to soil moisture and surface roughness over bare agricultural soils. IEEE Geosci. Remote Sens. Lett. 2012, 10, 731–735. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Messeh, M.; Quegan, S. Variability in ERS scatterometer measurements over land. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1767–1776. [Google Scholar] [CrossRef]
- Mladenova, I.E.; Jackson, T.J.; Bindlish, R.; Hensley, S. Incidence angle normalization of radar backscatter data. IEEE Trans. Geosci. Remote Sens. 2012, 51, 1791–1804. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-Rayes, M.A. Microwave dielectric behavior of wet soil-Part II: Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 35–46. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; Volume 2. [Google Scholar]
- Wu, T.D.; Chen, K.S.; Shi, J.; Lee, H.W.; Fung, A.K. A study of an AIEM model for bistatic scattering from randomly rough surfaces. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2584–2598. [Google Scholar]
- Zeng, J.; Chen, K.S.; Bi, H.; Zhao, T.; Yang, X. A comprehensive analysis of rough soil surface scattering and emission predicted by AIEM with comparison to numerical simulations and experimental measurements. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1696–1708. [Google Scholar] [CrossRef]
- Voronovich, A.G.; Zavorotny, V.U. Full-polarization modeling of monostatic and bistatic radar scattering from a rough sea surface. IEEE Trans. Antennas Propag. 2013, 62, 1362–1371. [Google Scholar] [CrossRef]
- Álvarez-Mozos, J.; Casalí, J.; González-Audícana, M.; Verhoest, N.E. Assessment of the operational applicability of RADARSAT-1 data for surface soil moisture estimation. IEEE Trans. Geosci. Remote Sens. 2006, 44, 913–924. [Google Scholar] [CrossRef]
- Bouchat, J.; Tronquo, E.; Lievens, H.; Verhoest, N.; Defourny, P. Assessing the potential of fully-polarimetric simultaneous mono-and bistatic airborne SAR acquisitions in L-band for applications in agriculture and hydrology. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2703–2706. [Google Scholar]
- Lievens, H.; Verhoest, N.E. On the retrieval of soil moisture in wheat fields from L-band SAR based on water cloud modeling, the IEM, and effective roughness parameters. IEEE Geosci. Remote Sens. Lett. 2011, 8, 740–744. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, K.S.; Xu, P.; Liu, Y. An update of AIEM model with multiple scattering of rough surface. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 4459–4462. [Google Scholar]
- Giraldez, A.E. Saocom-1 Argentina L band SAR mission overview. In Proceedings of the Coastal and Marine Applications of SAR Symp, Svalbard, Norway, 8–12 September 2003. [Google Scholar]
- Kellogg, K.; Hoffman, P.; Standley, S.; Shaffer, S.; Rosen, P.; Edelstein, W.; Dunn, C.; Baker, C.; Barela, P.; Shen, Y.; et al. NASA-ISRO synthetic aperture radar (NISAR) mission. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–21. [Google Scholar]
- Davidson, M.W.; Furnell, R. ROSE-L: Copernicus L-Band Sar Mission. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Online, 29 March–1 April 2021; pp. 872–873. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).