Abstract
In radio occultation (RO) data processing and data assimilation, the forward model (FM) is used to calculate bending angle (BA) from refractivity (N). The accuracy and precision of forward modeled BA are affected by refractivity profiles and FM methods, including Abel integral algorithms (direct, exp, exp_T, linear) and methods of interpolating refractivity during integral (log-cubic spline and log-linear). Experiment 1 compares these forward model methods by comparing the difference and relative difference (RD) of the experimental value (forward modeled ECMWF analysis) and the true value (BA of FY3D RO data). Results suggested that the exp with log-cubic spline (log-cubic) interpolation is the most accurate FM because it has better integral accuracy (less than 2%) to inputs, especially when the input is lower than an order of magnitude of 1 × 10−2 (that is, above 60 km). By contrast, the direct induced a 10% error, and the improvement of exp T to exp is limited. Experiment 2 simulated the exact errors of an FM (exp) based on inputs on different vertical resolutions. The inputs are refractivity profiles on model levels of three widely used analyses, including ECMWF 4Dvar analysis, final operational global analysis data (FNL), and ERA5. Results demonstrated that based on exp and log-cubic interpolation, BA on model level of ECMWF 4Dvar has the highest accuracy, whose RD is 0.5% between 0–35 km, 4% between 35–58 km, and 1.8% between 58–80 km. By contrast, the other two analyses have low accuracy. This paper paves the way to better understanding the FM, and simulation errors on model levels of three analyses can be a helpful FM error reference.
1. Introduction
The global navigation satellite system (GNSS) radio occultation (RO) technique has many advantages: high vertical resolution, global coverage, and long-term steady data. It has been proven that RO can significantly improve the accuracy of numerical weather prediction (NWP) after being assimilated into the NWP assimilation system. According to [1], RO observation ranked fourth among data that affected NWP. With the rapid development of the RO technique, numerous missions have been planned, launched, and run steadily to serve the operational NWP, such as Constellation Observing System for Meteorology, Ionosphere, and Climate (COSMIC/COSMIC-2), the Meteorological Operational satellite Programme-A/B (MetOpA/B), FengYun-3C/D (FY-3C/D) [2], GRACE/GRACE-FO, Scientific Application Satellite-C/D (SAC-C/D), Korea Multi-Purpose Satellite-5 (KOMPSAT-5), and Spanish PAZ (‘peace’ in Spanish) [3,4,5]. By 2027, these missions will provide approximately 18,400 observations per day which theoretically is the number threshold of the positive effect that RO could bring to NWP [6,7]. It will reduce error in prediction by 25% if all these observations are assimilated into the NWP assimilation system [8]. However, the actual situation does not coincide with theoretical expectations because almost half of the RO data either cannot be received or cannot pass quality control before assimilation [9]. There are two strategies to increase the RO observation available. The first one focus on increasing the soundings received per day via more missions, more receivers on the cube satellite, e.g., the cube satellite constellation of Spire company [10], and more multi-system-compatible RO receiver such as GNSS Radio Occultation Sonder (GNOS) onboard FY3 [2,11,12,13]. The second strategy is to improve the RO data processing technique. The current RO data processing center includes the Danish Meteorological Institute (DMI), German Research Centre for Geosciences (GFZ), Jet Propulsion Laboratory (JPL), University Corporation for Atmospheric Research (UCAR), the National Oceanic and Atmospheric Administration (NOAA) ’s National Environmental Satellite, Data, and Information Service (NESDIS), and Wegener Center/the University of Graz (WEGC). Each center developed different schemes to process RO data. The quality of their RO data is accessed by the international RO working group (IROWG) every other year [14]. The consistency and structural uncertainty of their RO data records are promising to step up to another level. Thus, improvements are expected in the RO data processing and RO data assimilation techniques. The forward model (FM) plays a critical role during these two processes. Firstly, the more accurate the FM, the more accurate these two processes. Secondly, the error of FM should be quantified, so that the other errors during these two processings can be accurately evaluated. The FM mainly consists of Abel integral algorithm and interpolation methods before Abel integral.
1.1. FM Algorithm in Data Assimilation and RO Data Processing
(1) FM in RO data assimilation. In terms of the RO data assimilation, two options, the bending angle (BA) or refractivity, are used for variational assimilation [15,16]. The option of forward modeled BA is convenient and concise. During assimilation, atmospheric parameters are firstly transformed to refractivity (N)
where T is temperature, e is water vapor partial pressure, and p is pressure. Then the refractivity is inverted to BA () by the Abel integral, a core part of FM
where a is impact parameter, refractive index n = 10−6N + 1. Hence, the accuracy of BA is strongly affected by n and the FM. This BA is then assimilated into the NWP data assimilation system. Therefore, the FM is critical for RO data assimilation.
(2) FM in RO data processing. The FM is employed to correct the ionospheric error to BA during RO data processing by the method of statistical optimization. The ionosphere frequently interferes with GPS signals [17]. There are several approaches for ionospheric calibration: the linear combination of two frequencies corrects the first order; the K-correction corrects the higher-order [18]; the statistical optimization corrects all the ionospheric error [19]. The last one is based on background climatological models such as MSIS-90 (mass spectrometer and incoherent scatter radar in 1990) [20], BAROCLIM (the bending angle radio occultation climatology) based on Formosat-3/COSMIC data [21], and CIRA (the 1986 COSPAR International Reference Atmosphere) [21]. Most data in these background climatological models are stored as refractivity. Therefore, we need to invert them to BA via FM. Therefore, the accuracy of the FM is important.
In another aspect, the RO data are also used in commercial companies or civilian industries, wherein they might consider using some analysis data sets to assimilate RO data in their assimilation systems or develop their own RO data processing program. Generally, widely used and free analysis data sets are considered. However, some of those data sets have limited vertical and horizontal resolution. Therefore, how many biases the forward modeling results contain is open to debate. The biases are generated by not only forward models but also the level resolution of the analysis data. Therefore, the level resolution of the original data should also be under consideration for evaluating the error of FMs.
1.2. FM Algorithm
The core of an FM is the Abel integral, whose original form is given by Equation (2), in which two singularities exist: and . To solve such problem, [22] used hyperbolic transformation and an algorithm that closely resembles the Abel integral was obtained, which we call the direct algorithm in this study.
To further improve the approximation accuracy, the interpolation and numerical approximation methods were employed. For example, based on the physical assumption of isothermal atmosphere and temperature exponential approximation with height, refractivity was assumed to decrease exponentially with impact parameters. Methods of exponential extrapolation and interpolation of refractivity were summarized by the European Center for Medium-Range Weather Forecasts (ECMWF) [23,24,25]. In such a method, numerical approximation, such as the error function (erf), was also employed. This method is called the exp algorithm in this paper. Subsequently, the linear assumption of the BA was considered in the Abel integral inversion, called the linear algorithm in this paper. Both exp and linear algorithms are incorporated in the radio occultation processing package (ROPP) software developed by the Radio Occultation Meteorology Satellite Application Facility [24,26]. Later, it was found that oscillations occur between levels (vertical grids) of the forward modeled BA using the exp algorithm. In order to correct this oscillation, [24] revised the exp algorithm by adopting more temperature operators in the refractivity operator; the modified algorithm is called the exp_T algorithm in this paper. For more details on these four algorithms, refer to Appendix A: Abel Integral Algorithms. In addition to the four methods, the NOAA National Centers for Environmental Prediction (NCEP) used quadratic Lagrangian polynomials [27], which avoided the exponential decay of refractivity with height.
The FM is the integral algorithm as shown in Equation (2), in which the refractivity was firstly interpolated along a denser grid of impact parameter to improve integration accuracy. Therefore, the accuracy of an FM is closely associated with the interpolation method and numerical integral method. In terms of interpolation methods, authors of [28] found that the log-cubic spline (hereafter, log-cubic) is the most accurate one. Log-cubic interpolation projects refractivity into the log space and then interpolates it by the log-cubic method. In addition to this interpolation method, log-linear interpolation is tested in this paper. To the best of our limited knowledge, most studies either focus on the numerical integration method or only on the interpolation methods.
Thus far, a systematic discussion on the combination of interpolation and integration methods has not been reported. In addition, to the best of our knowledge, only a few results have been reported on the estimation of the error of the FM occurring on a fixed model level, for example 137 EC. The present study aims to discuss both of these aspects.
In this study, first, we compare three Abel integral algorithms, namely direct, exp, and exp_T algorithms, and two interpolation methods, namely log-cubic and log-linear. Second, we evaluate errors of FMs on the model levels of three analyses. To achieve these two aims, we set two experiments. In experiment 1, we compare FMs and interpolation methods. In experiment 2, the most accurate FM is employed to calculate the BA on model levels of three widely used analysis datasets, namely ECMWF 4Dvar analysis with 137 levels, ECMWF ERA5 analysis with 37 levels, and final operational global analysis data (FNL) with 31 levels. Furthermore, the errors of FMs are simulated, providing an error reference for FMs under the analyzed model levels. The simulation also demonstrates to what extent a low-resolution model level can be used for conducting comparative research of RO products. Our research provides a better understanding of the error of FMs in RO data processing and assimilation. In the experiments conducted in this study, a point-to-point comparison is made horizontally. It should be noted that we ignore the tangent point drift (that is the practical RO profiles are slanting rather than being vertical to the ground, which may result in the refractivity gradient bias [27]), since the interval of each level is less than 10 km [28].
This paper is organized as follows. The principles of the four algorithms in the forward model are described in Section 1. In Section 2, the progress of experiments 1 and 2 are introduced, together with data selection and low-pass filter strategies. Results are presented in Section 3. Finally, we discuss and present the discussion and conclusion in Section 4.
2. Experiments
In this study, two experiments were conducted. The first experiment compared the algorithms together with interpolation methods. Subsequently, the most accurate integral and interpolation method was used in the second experiment, in which the refractivity profiles on levels of widely used analyses—FNL, EC4Dvar, and ERA5—were calculated to the BA by FMs. Then, the bias of results was evaluated.
2.1. Data, Collocation, and Quality Control
2.1.1. Data
We used the FY3D observation in September 2019 as the ‘true value’ which is available for download at http://www.nsmc.org.cn (accessed on 8 June 2021). The daily number of occultation soundings is approximately 500, and the vertical resolution is approximately 150–300 m. The quality control of the FY3D data is assessed by the China Meteorological Administration [29], and the result has been qualified by ECMWF [5]. The qualiy control result is displayed in near real-time (NRT) monitoring at the ROM SAF website (Available at: https://www.romsaf.org/monitoring/index.php (accessed on 8 June 2021)). As shown in Figure A2 in Appendix B, the quality of FY3D (The mean relative difference (RD) between ECMWF forecast and FY3D is less than 2%) in September 2019 established a good condition for experiment 1.
We also used ECMWF operational analyses in experiment 1, which can be accessed at https://www.ecmwf.int/en/forecasts/dataset/operational-archive (accessed on 8 June 2021). Such data are produced daily by ECMWF’s direct 4Dvar atmospheric model. Hereafter we call this data EC4Dvar. These data are in 128 × 64 grids; hence, the resolution is approximately 2.8° × 2.8°; They have 137 levels and are output daily at four hours: 00, 06, 12, and 18 UTC. Since the resolution of EC4Dvar is very coarse, we used strict collocation and quality control.
In experiment 1, the refractivity profiles were the experimental values; Therefore, we first calculated refractivity from temperature, water vapor partial pressure, and pressure of EC4Dvar via Equation (1) according to their own level grids.
In experiment 2, we used FY3D to simulate analyses such as ECMWF, ERA5, and FNL. The level of them are 137, 37, and 31 respectively. The height and levels interval can be found Figure A3 in Appendix B.
2.1.2. Spatial and Temporal Collocation
Experiment 1 aims to compare the BA from FY3D retrievals and calculated using Equation (2) from EC4Dvar atmospheric profiles. To improve the accuracy of the comparison, we must ensure that the refractivity profiles of EC4Dvar and FY3D are collocated.
In terms of temporal collocation, we only selected the occultation soundings whose time is less than one hour to EC4Dvar’s four main synoptic hours, namely 00, 06, 12, and 18 UTC; that is, h. 5914 out of 17791 FY3D GNOS soundings in September 2019 satisfied the temporal collocation.
In terms of spatial collocation, we used the tangent point of occultation profiles as its location to search its nearest EC4Dvar profile. The profile with 137 levels on grids nearest to the tangent point was selected. In such a way, we assume the EC4Dvar and the FY3D profiles are collocated. However, because a grid resolution of 2.8° × 2.8° is too large, the collocated profiles of EC4Dvar may be far be far FY3D. We fixed it in quality control as explained in the next subsection. Figure A7 in Appendix C shows that FY3D soundings in experiment 1 generally have an evenly spatial and temporal distribution, which makes the mean (statistical values) feasible in the subsequent analysis.
2.1.3. Quality Control
Since we used coarse resolution EC4Dvar to collocate with FY3D data, some FY3D’s collocated profile may be far from it. To ensure that the refractivity of FY3D is close to that of ECMWF and to make sure the results have statistical representativeness, we set four steps of quality control (hereafter 4QC). These four steps were initially a scheme for quality control used by [30] to compare MetOp RO data from two different RO data processing centers, which is concise and effective [31]. The details of 4QC can be found in Appendix C. After 4QC, 368 out of 5914 FY3D soundings remained for experiment 1. The high rate of discard is attributed to the low resolution (2.8° × 2.8°) EC4Dvar.
In experiment 1, EC4Dvar’s refractivity was transformed to BA. The forward-modeled BA contained not only the bias introduced by FMs and interpolations but also the inherent bias of the inputs when they were refractivity. Experiment 2 was a simulation experiment, in which only FY3D was used. Therefore, the data quality was not taken into consideration.
2.2. Experiment 1: Algorithm Comparison
Experiment 1 aims to determine the most accurate FM by comparing FM algorithms that considered interpolation methods.
There are three types of bias in RO data processing: observation errors, ionospheric errors, and errors incurred within the data processing. We focused on the third error in experiment 1, mainly the bias from the Abel numerical integral and interpolation methods. The Abel integral methods considered in this experiment were the direct, exp, and exp_T algorithms. The interpolation methods were log-cubic and log-linear, indicated in the subsequent figures by no label and “lin”, respectively. The log-cubic maps refractivity into the log space and then interpolates it by the cubic spline method; the log-linear also projects refractivity into the log space, but interpolates it in a linear fashion.
In this experiment, 368 FY3D BA profiles in September 2019 were regarded as the true value (T). The collocated refractivity profiles of EC4Dvar were the experimental value (E), which were calculated via Equation (1) on the data’s inherent 137 levels. The temporal and spatial collocation of both sets of data is described in Section 2.1., as well as the further 4QCs for collocation. From the statistical perspective, we used the mean to analyze the results, which would not be affected by outliers s. Two statistics were selected for the analysis: the difference of the BA, i.e., (E − T); and the relative difference (RD) of the BA, i.e., ((E − T)/T × 100%). Based on these statistics, we determine how close an FM’s result is to the true value; Another form of RD, which is the difference between two experimental values, i.e., ((E1 − E2)/E2 × 100%), can avoid introducing the bias of true value and provide the difference between the two experimental values. Subsequently, the relatively better FM can be obtained.
Figure 1 shows the process of experiment 1. (1) FY3D profiles collocated with the EC4Dvar atmospheric profiles with respect to time, longitude, and latitude. Subsequently, the EC4Dvar profiles of atmospheric parameters were transformed to refractivity profiles. Then, the 4QC was performed for FY3D and EC4Dvar. We regarded the 4QC-passed FY3D BA as the true value (T). (2) The EC4Dvar refractivity profiles on 137 levels were interpolated into a resolution of 100 m by the log-cubic space and log-linear methods. (3) The interpolated refractivity was then transformed into the BA by three different integral methods. (4) The forward-modeled EC4Dvar BA was regarded as the experimental value (E) and was compared with the FY3D BA in terms of the difference (E − T) and RD (E − T)/T 100%. Note that the log-cubic interpolation was applied to the impact parameter instead of the mean sea level (MSL) height, since impact parameter x equals refractivity(n) multiple position vector (r). Because dn/dr is extremely large near a high-water-vapor region, which cannot satisfy the condition of applying cubic spline interpolation: the value to be interpolated should be continuously incremented.
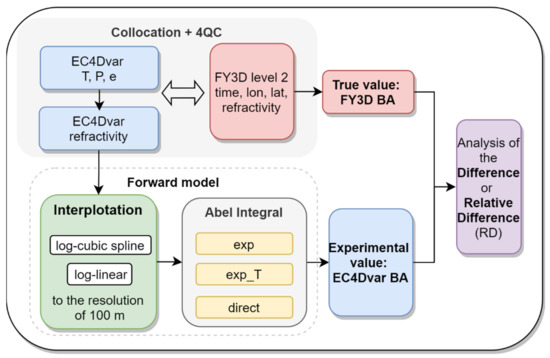
Figure 1.
Flow chart for experiment 1, the algorithm comparison.
It is noteworthy that the true value and experimental value are only an estimated value to their actual values. Therefore, the difference between any FM and FY3D, (EFMx − T), is just an estimate showing which algorithm is closer to the truth. By contrast, the difference between any two FMs (EFM1 − EFM2) is the absolute difference value. Experiment one shows which FM is better, instead of expressing how much error is incurred from the FM. Through experiment 1, although we can determine which FM is better, how much error exactly is incurred from the FM cannot be expressed. Such a question can refer to experiment 2.
2.3. Experiment 2: Evaluation of Errors of FMs on the Fixed Model Level
Experiment 2 explores how much bias was introduced from transforming the analyses’ refractivity to the BA. As shown in Figure 2, FY3D refractivity profiles were first linearly interpolated into a resolution of 20 m and then transformed to the BA as the true value. These interpolated refractivity profiles were then filtered to remove the small-scale chaos less than the model grid interval of analyses such as 137 levels of ECMWF 4dvar, 31 levels of FNL, and 37 levels of ERA5 via the low pass filter. Their intervals are shown in Figure A3 source not found. in Appendix B. Subsequently, the refractivity profiles were linearly interpolated onto model grids and then transformed to the BA as the experimental value. Finally, obeying the nearest principle, the nearest true value level to the experimental value was selected to evaluate the experimental value. Note that the FM used in this experiment was the most accurate one with its experimental value being the nearest to the true value. In addition, considering computation efficiency [28], we chose two interpolation methods, namely log-spine cubic and log-linear.
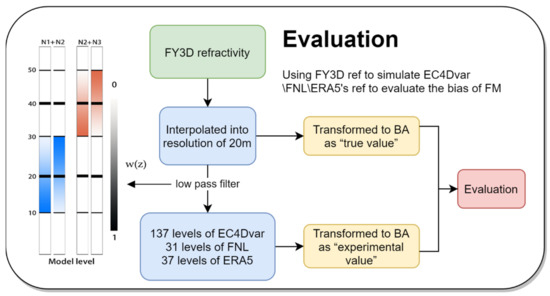
Figure 2.
Flow chart of experiment two, evaluation of forward modeled analysis.
Finally, the low pass filter must be mentioned here. Interpolation from a high resolution (20 m) to a low resolution (model levels) requires a filter, or it will induce representativeness errors [32]. For this purpose, we applied the Savitzky-Golay low-pass filter [33]. In general, the data are filtered with a window of or ( typically results in instability [34]). In this study, is set. The next problem we encountered was that intervals of model levels increasing with height. To fix it, on the basis of [28], we divided the intervals into three groups: below the height of 0–20 km, 20–40 km, and above the height of 40–60 km. A window of twice the average interval of each group, 2, was applied to filter the whole profile; thus, we had three filtered refractivity profiles, N1, N2, and N3. To merge them smoothly at the transition point (20 km and 40 km), we used a transition function, w(z), which is changed linearly from 1 to 0, as shown in the left subfigure in Figure 2. The refractivity profiles at the transition point are expressed as
where is the transition function to (i = 1, 2, 3), and z is the height. and were filtered by the filter window themselves. The combination of those slices by height was the terminal profiles.
Furthermore, the following details were considered in this experiment. First, to improve simulation accuracy and reduce the interpolation error, we selected 20 m, instead of 100 m, as the resolution for FY3D to simulate the analysis. Second, the analysis model level was simulated, and those levels were transformed into MSL height for convenience. Third, the true value was refractivity instead of BA. The true value also passed the same Abel transform as the forward-modeled BA in the analysis.
3. Results
In this section, the results of experiment 1 are presented, which demonstrate the most accurate FM. Subsequently, two simulated errors of the most accurate FM are obtained on the basis of three widely used analyses: EC4Dvar, FNL, and ERA5.
3.1. Experiment 1: Algorithm Comparison
In this experiment, we compared three Abel integral algorithms and two interpolation methods. The BA of FY3D was the true value, while the forward-modeled EC4Dvar BA was the experimental value. The FY3D observation data were filtered by the strict collocation and 4QC strategies. Subsequently, 368 FY3D profiles in September 2019 remained, which were regarded as the true value (T). EC4Dvar refractivity data collocated with the true values were the experimental values (E). We used two statistics in this experiment: the difference (A B) and relative difference (A B)/B × 100%, where A and B can be either E and T or E and E, respectively. The obtained statistics were all mean values. Note that we compared the exp algorithm with the direct and exp_T algorithms independently because the exp_T algorithm is too close to the exp algorithm. If the exp_T algorithm was drawn in the same figure with the direct algorithm, it would coincide with the graph of the exp algorithm.
3.1.1. Difference Analysis for Direct and Exp
First, we compared the difference (E T), in which E is the BA integrated by the exp and direct Abel integral algorithms, together with two interpolation methods. The altitude starts from 5 km because the signal-to-noise ratio below it is low, and some RO observations are unavailable. As shown in Figure 3a,b, differences of both algorithms are in the same order of magnitude; 1 × 10−5 is within 5–30 km, and 1 × 10−6 is within 30–60 km. However, the exp is more accurate than the direct because it is closer to the true value except at heights of 12.5–17.5 km, which reflects the errors passed by refractivity. Figure 3c,d shows the difference between the two algorithms. The result of the direct is larger than that of the exp until at a height of 50 km. Figure 3e,f shows the difference due to interpolation. In the height range of 5–30 km, the error induced by log-linear is less than ±1 × 10−6, and above 30 km, it is less than ±0.5 × 10−7. Interestingly, log-linear interpolation causes more undulation compared with log-cubic interpolation. The undulation due to interpolation is larger for the exp algorithm. To verify this result, we repeated this experiment using MetOp as the true value, and the same conclusion was drawn (see Figure A4 in Appendix B).
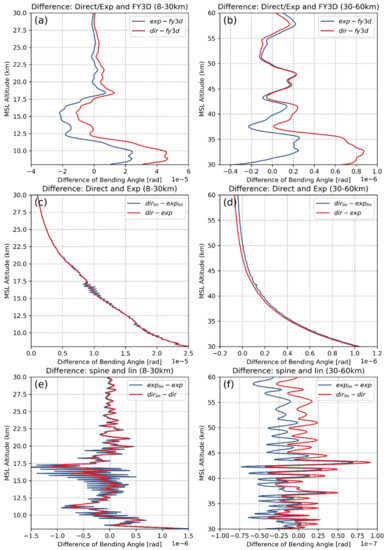
Figure 3.
Difference between the BA of FY3D (T) and EC4Dvar BA (E) using the direct and exp Abel integral algorithms, together with log-linear and log-cubic interpolation methods. (a,b) (Eexp/dir − T) using the log-cubic interpolation; (c,d) difference of the Abel integral algorithms (Edir − Eexp) based on the log-linear and log-cubic interpolation, respectively; (e,f) difference of interpolation methods (Elin − E) based on exp and direct Abel integral algorithms, respectively.
3.1.2. Relative Difference Analysis of Direct and Exp Algorithms
Next, we analyzed the RD, (E T)/T × 100%, of the FY3D BA (T) and the forward modeled EC4Dvar BA (E) in different FMs and show the results in Figure 4a–c. The orders of magnitude of the differences in the ranges of 5–55 km, 55–70 km, and 70–80 km are within 1–1.5%, 4–−10%, and 10–80%, respectively. This result is consistent with those of the previous studies [28,35,36]. The results shown in Figure 4a–c are divided into three aspects for clarity. (i) The RD of the exp is near to zero than that of the direct, indicating the BA of the exp algorithm is closer to the true value. In other words, the exp algorithm is more accurate than the direct algorithm. The result of the direct algorithm is larger than the true value below 60 km (approximately 0.3% larger than exp) and considerably less than the true value above 60 km. (ii) Since these two algorithms have the same input and same vertical-level setting, this gap is probably due to the integral accuracy of the algorithm. The integral accuracy depends on the order of magnitude of refractivity (input), which is shown in Figure A5 in Appendix B. Intriguingly, when the order of magnitude is 1 × 10−2 above (below) a height of 60 km, the direct algorithm’s result is less (larger) than the true value. (iii) Note that at heights of 18, 48, and 58 km, larger errors are incurred by refractivity rather than the errors of the FM. Unexpectedly, the errors of the exp algorithm at these heights are larger than those of the direct algorithm. This difference can be attributed to the fact that refractivity of the exp algorithm exponentially decays faster than that of the direct algorithm.
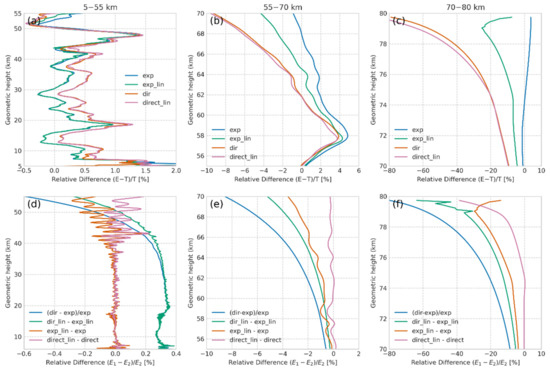
Figure 4.
RD of the BAs of FY3D (T) and EC4Dvar (E) based on the direct and exp Abel integral algorithms, with log-linear and log-cubic interpolation methods. (a–c) (E − T)/T, where E can be calculated by either the exp or direct algorithm, with both interpolation methods; (d–f) (E1 − E2)/E2, where 1, 2 indicate two different FMs.
The green and blue lines in Figure 4d–f illustrate the RD between the direct and exp algorithms. Below 60 km, their difference is less than ±2%, whereas above 60 km, it is considerably large. The RDs between the two algorithms based on the two interpolation methods are indicated by the orange and pink lines; the RD is even larger when the algorithms are based on log-cubic interpolation. In general, the errors due to log-linear interpolation of the FM with the exp algorithm are larger than those with the direct algorithm. The RD of two interpolations with the exp algorithm is less than 0.2%, −2%, and −20% for heights of 5–50, 55–65, and 70–80 km, respectively. Specifically, because these errors are almost equal to the monthly errors of FY3D to ECMWF recorded in the ROM website (see Figure A2) the log-linear interpolation can be considered to be not sufficiently accurate. However, if such an error is acceptable, the exp algorithm with log-linear interpolation will be a timely and effective FM, since the log_linear interpolation is more cost-efficient than the log-cubic interpolation.
3.1.3. Analysis to exp_T
Herein, we discuss the RD and difference between the exp and the revised exp algorithm (exp_T). The RD is two orders of magnitude lower than the difference between exp and direct. Hence, the RD and difference are plotted in separate graphs as shown in Figure 5, the BA of the exp_T algorithm is slightly larger than that of the exp algorithm. According to [24], this difference is due to the temperature term in the new polynomial, which corrects the error of the exp algorithm. However, the corrected amount is limited. Since the exp_T algorithm introduced temperature operator, it requires considerably more computation and time resources. Thus, the exp algorithm is superior operationally.
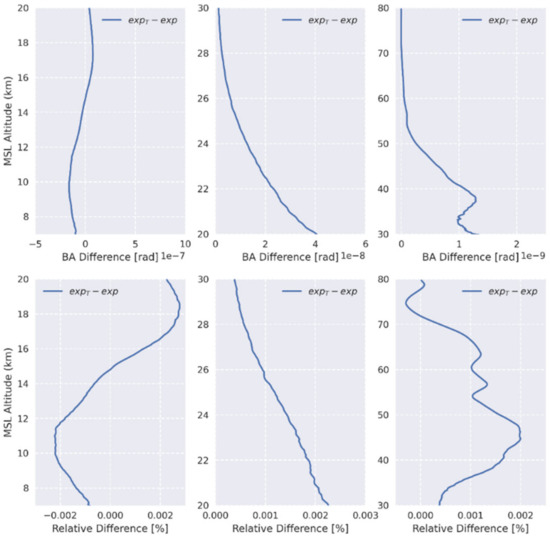
Figure 5.
Difference (first row) and RD (second row) between the exp_T and exp algorithms.
Finally, we list the RD between the true value and all experimental values in Table 1. The above analysis identified that the exp algorithm with log-cubic is the most accurate FM; therefore, the quantity of each FM’error is written as exp’s RD plus the left error of the FM for clarity. First, the RD of the exp_lin algorithm is the same as that of the exp algorithm below a height of 55 km; however, it becomes 3% and 20% larger than that of the exp algorithm within 55–60 km and 70–80 km, respectively. Second, the RD of the direct algorithm is approximately 0.3% larger than that of the exp algorithm within 8–45 km, which becomes −10% and −80% less than that of the exp algorithm within 60–70 km and 70–80 km, respectively. Third, the improvement of the exp_T algorithm is limited (approximately 0.002%) compared to that of the exp algorithm. It should be noted within heights of 55–60 km, the error of the exp_lin algorithm is less than that of the exp algorithm, which is due to errors contributed by refractivity.

Table 1.
Relative difference, (E−T)/T × 100%, between the FY3D BA (T) and the forward-modeled BA (E), in which E can be the exp and direct algorithm, and each algorithm has two interpolation methods: log linear (denoted by lin) and cubic spline (no label).
The exp algorithm with log-cubic is the most accurate FM; therefore, the quantity of each FM’error is written as exp’s RD plus the left error of the FM for clarity.
It is important to note that when E was refractivity, there are already been errors in Eref (ref is refractivity). This error was then passed to BA’s (E−T)/T. Therefore, what we got in experimentone is the which FM is better, rather than how much error exactly one FM causes. This issue will be tested in experiment two. Since analysis above identified that the exp algorithm with log-cubic interpolation is the most accurate FM, in next experiment we will figure out how much exactly the error of exp algorithm is on three fixed model levels.
It is important to note that when E is refractivity, errors exist in Eref (where ref denotes refractivity), which are then passed to the (E−T)/T value of the BA. Therefore, experiment 1 demonstrates which FM is better, rather than how much error exactly an FM causes, which will be tested in experiment 2. The above analysis indicated that the exp algorithm with log-cubic interpolation is the most accurate FM; therefore, in experiment 2, we determined the extent of error of the exp algorithm on three fixed model levels.
3.2. Experiment 2: Evaluation of the Error of the FM on the Fixed Model Level
Experiment 1 identified the exp algorithm with the log-cubic interpolation as the ideal FM owing to its high accuracy. Therefore, when computation efficiency is the primary focus, the exp algorithm with the log-linear interpolation is also considered. This experiment tested the extent of errors of the FMs. Another factor that introduced error to the FM is the model level (resolution of vertical levels). Thus, in this experiment, we chose three widely used analyses with different levels: 137 levels EC4Dvar, 31 levels FNL, and 37 levels of ERA5. The refractivity profiles of these analyses were all simulated by FY3D level 2 refractivity products. During this simulation, FY3D data were first interpolated into a resolution of 20 m and then extracted according to the model level. Subsequently, each simulated analysis was transformed to the BA via the FMs. Next, the results were compared with the FM true value, providing FY3D level 2 product refractivity profiles. Their RDs and differences are listed at the end, which can provide an error reference for the FM under the model levels considered here.
Figure 6 shows how the level interval, indicated by the rainbow colors, affects the RD ((EBA − TBA)/TBA × 100%). In general, the less the interval, the less is the RD. EC4Dvar’s RD is less than the RDs for others because of the higher resolution of its levels. For example, EC4Dvar’s resolution is less than 1 km below 35 km, and its RD is less than ±0.5%. By contrast, the errors for FNL and ERA5 are less than ±1% for heights of 0–30 km owing to their low resolution. Interestingly, ERA5 and FNL show similar vertical resolution. However, the RD for ERA5 below 10 km is mostly less than that for FNL. This is because the Abel integral integrates values from lower levels to higher levels, and ERA5 owns the other six levels (i.e., 875, 825, 775, 225, 175, and 125 hPa), which ensures more accurate interpolation results for ERA5. Figure 6 also shows the comparison of the log-cubic interpolation (a–c) with log-linear interpolation (d–f). The errors of the latter are 1–2% larger than those of the former owing to the lower interpolation accuracy of log-linear.
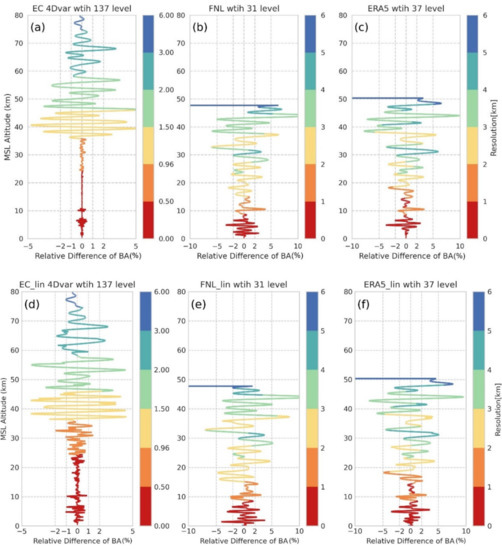
Figure 6.
Effects of various model level intervals (km) on the FM error. The x-axis represents the RD, ((E − T)/T × 100%), of the BA between true value (T) and three simulated analyses (E): (a,d) 137 levels of EC4Dvar; (b,e) 31 levels of FNL; (c,f) 37 levels of ERA5. The FM is the exp algorithm, together with (a–c) log-cubic or (d–f) log-linear.
Figure 7 compares the results of the RD (a–c) and difference (d–f) of the exp algorithm with log-cubic interpolation on the model levels of the three analyses.
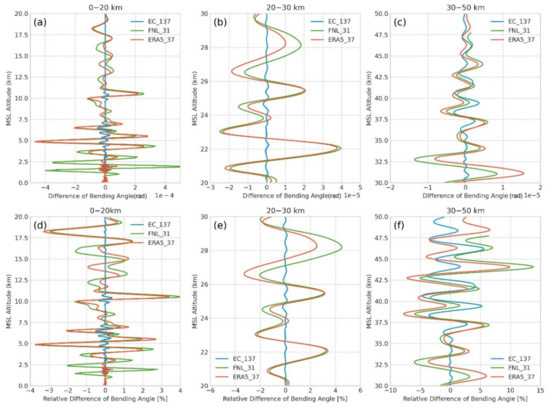
Figure 7.
Under various model levels, the difference (a–c) and RD (d–f) of FM based on the exp algorithm and log-cubic interpolation. The RD for EC4Dvar below 35 km is less than 0.5%, whereas RDs for FNL and ERA5 below 35 km are less than 5%. Above 35 km, the RD for EC4Dvar is less than 5%, while RDs for FNL and ERA5 are up to 10%.
Below 35 km, the RD and difference for EC4Dvar are less than ±0.5% and ±0.5 × 10−5, respectively, while those for FNL and ERA5 frequently oscillate in the range of ±2% to ±4%. Above 35 km, the RD and difference for EC4Dvar are similar to those for FNL and ERA5. The large bias for FNL and ERA5 resulted from two aspects: (i) the low resolution of the level interval; (ii) the rapid change in the atmospheric condition below 10 km. In such conditions, if the vertical grid density of refractivity profiles is insufficient, a larger oscillation of BA profiles will occur. The same comparison as Figure 7 but for log-linear interpolation is shown in Figure A6 in Appendix B.
Figure 8a–f concludes the detailed errors, the difference (grey), and RD (red) for forward-modeled three analyses, which are listed in Table 2. Figure 8g–i concludes the difference in the RD between two interpolation methods based on each analysis. Below 30 km, the RD of log-cubic interpolation is 0.5–1% lower than that of log-linear interpolation, 2% lower for 30–50 km, and back to 1% lower for a height above 50 km. For FNL, the log-cubic results are 2% lower than the results of log-linear. For ERA5, the log-cubic results are 1.8% lower than the results of log-linear.
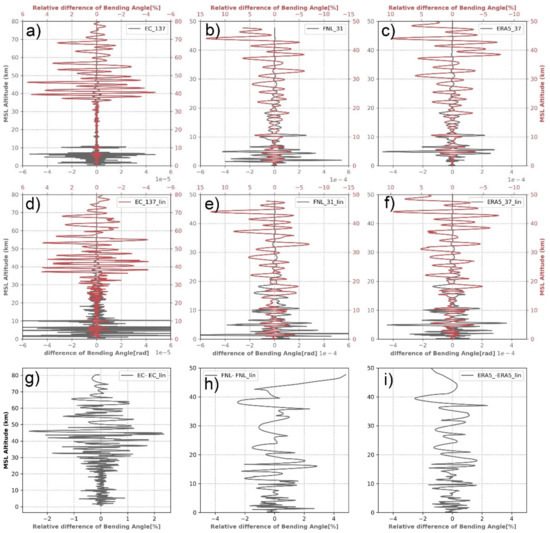
Figure 8.
BA difference (, in gray) and RD (, in red) for EC4Dvar, FNL, ERA5, and FY3D based on the exp algorithm and log-cubic interpolation (a–c) and log-linear interpolation (d–f). (g–i) The difference between the RD of log-cubic interpolation and that of log-linear interpolation.

Table 2.
RD and difference for forward modeled analyses in MLS (mean sea level, km).
4. Discussion
An FM plays an important role during GNSS RO data processing and assimilation. The more accurate the FM, the more accurate are the two processes. Although the Abel algorithm and interpolation methods separately are sufficiently discussed, to the best of our knowledge, there has been no systematic discussion on the combination of interpolation and integration methods. In addition, no results on estimating the error of an FM on a fixed model level, for example 137 EC, have been reported.
In this study, we first reviewed the principles of four Abel integral methods. Subsequently, we conducted experiment 1 to compare three Abel integral algorithms (i.e., direct, exp, and exp_T) and two interpolation methods (i.e., log-cubic and log-linear) via the mean value analysis of the difference and relative difference between the experimental value (forward-modeled EC4Dvar) and true value (FY3D BA). The results suggested that (1) the exp algorithm with log-cubic interpolation is the most accurate one in every level because it has better integral accuracy (errors approximately 2%) to inputs, especially when the input is lower than an order of magnitude of 1 × 10−2 (that is, above a height of 60 km). Above this height, the direct algorithm induced a 10% error. (2) When errors exist in inputs, the exp algorithm tends to amplify the error compared with the direct algorithm. (3) The exp algorithm with log-linear interpolation is often feasible for its computation efficiency. Its errors were 0.2%, −2%, and −20% larger than those of log-cubic for the heights of 5–50, 55–65, and 70–80 km, respectively. (4) The improvement of exp_T algorithm to the exp algorithm is limited. Our results are consistent with results of [35,36].
Subsequently, we conducted experiment 2 to determine the exact errors caused by the exp algorithm, which would be affected by the level interval of inputs. Therefore, we selected refractivity profiles on model levels of three widely used analyses (i.e., 137 levels of EC4Dvar, 31 FNL, and 37 ERA5) as the inputs. Results demonstrated that the forward-modeled BA of denser resolution analysis EC4Dvar was closer to the true value FY3D. The errors of the exp algorithm with log-cubic and log-linear were less than 1% and 0.5% below 38 km, less than 4% within 38–50 km, and less than 1.8% and 2% above 58 km, respectively. By contrast, the other two analyses had low accuracy. Our results are in good agreement with the results of [28].
This study paves a way to better understand the errors of the FM in RO data assimilation and processing. Simulation errors on model levels of three analyses can be a helpful FM error reference. This experiment only compared direct, exp, and exp_T algorithms, while excluding the fourth Abel integral: the linear algorithm. Such an algorithm is not feasible for data assimilation but can be used in RO data processing. In the future, linear algorithm and other integral algorithms can be addressed to compare the FM. Regarding the interpolation method, we only considered log-linear and log-cubic interpolation methods, which might have inferior representativeness above 60 km, where the interval is too large. Machine learning methods might be resorted to solve this problem.
Author Contributions
Conceptualization, N.D. and W.B.; Methodology, N.D.; Software, J.X., X.W., Y.C. and X.M.; Validation, N.D., W.B., C.L., C.Y., F.H., G.T. and P.H.; Formal analysis, N.D. and X.L.; Investigation, N.D.; Resources, Y.S. and Q.D.; Data curation, N.D.; Writing—original draft preparation, N.D.; Writing—review and editing, W.B.; Visualization, N.D.; Supervision, W.B. and Y.S.; Project administration, Y.S. and Q.D.; Funding acquisition, Q.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported jointly by the Youth Cross Team Scientific Research Project of the Chinese Academy of Sciences (JCTD-2021-10), the National Natural Science Foundation of China under Grant no. 42074042 and 41775034, the Feng Yun 3 (FY-3) Global Navigation Satellite System Occultation Sounder (GNOS and GNOS II) Development and Manufacture Project led by the National Space Science Center, Chinese Academy of Sciences (NSSC/CAS), and Strategic Priority Research Program of Chinese Academy of Sciences, Grant no. XDA15007501.
Data Availability Statement
FY3D datasets were analyzed in this study, which can be found here: http://www.nsmc.org.cn (accessed on 9 January 2022). We also used ECMWF operational analyses in experiment 1, which are available at: https://www.ecmwf.int/en/forecasts/dataset/operational-archive (accessed on 9 January 2022), with the permission of ECMWF. The FNL datasets can be found here: https://rda.ucar.edu/datasets/ds083.2/#access. The ERA5 datesets are available at: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5 (accessed on 9 January 2022).
Acknowledgments
We acknowledge the support and funding from the National Space Science Center, Chinese Academy of Sciences (NSSC/CAS). We appreciate the valuable and constructive suggestions from reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Abel Integral Algorithms
The forward model (FM) consists of the Abel integral methods and interpolation methods. Before we explain the principles of the four Abel integral algorithms, it is necessary to understand how the Abel integral is formed and its important assumption of a spherically symmetric atmosphere.
Appendix A.1. Spherically Symmetric Assumption
The spherically symmetric assumption is the prerequisite of the Abel integral. The bending angle (BA) α is defined as the accumulated direction change of a signal from being transmitted by the GPS to being received by a low earth satellite (Figure A1). The BA α is twice the size of θ based on the spherically symmetric atmosphere assumption. We assume the earth below the bent ray is symmetric about OC (rt). If the right triangles AOC and BOC are the same, and the right triangles MOB and MAP are similar; then, ∠α is twice the size of ∠θ since they have the shared angle ∠AMP. According to Bouquer’s law, the impact parameter a = nrsin90° [37,38,39]. The direction vector r is the same as the direction of the refractive index n’s gradient. The BA is expressed as
where nr is replaced with x, then we have Equation (2) [23,25,39].
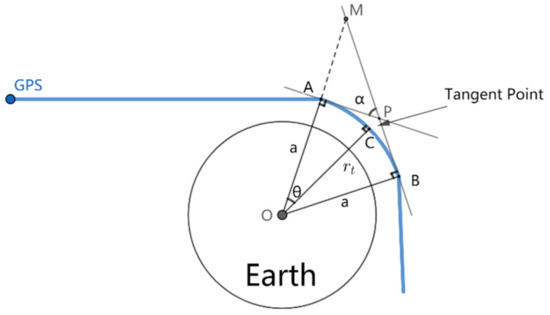
Figure A1.
Schematic of radio occultation geometry based on the spherically symmetric atmosphere assumption. That is, if triangles of ΔAOC and ΔBOC are symmetric (equal), then α = 2θ. OA(a), OB(a), and OC(rt) on the ray path are the position vectors of a transmitter, receiver, and tangent point, respectively. The ray is over bent for the clarity of the geometry relationship.
There are two singularities in Equation (2): x = a and x→∞. The finite upper limit is set as 120 km or 150 km (for Beidou FY3C/D) in a real-world application. The singularity of x = a can be eliminated by different analytical methods, called the Abel integral methods.
A.2. Abel Integral
Abel integral methods include the numerically mapped direct algorithm [22], exponentially interpolated refractivity in the exp algorithm [23,40], the linear assumption of bending angle in the lin-algorithm [35], the temperature-revised exp algorithm (hereafter exp_T) by authors of [24].
A.2.1. Direct Algorithm
To solve the singularity of x = a in Equation (2), [22] used hyperbolic transformation, and this formula is called the direct Abel integral method (hereafter direct). First, dln(n) in Equation (2) is replaced with the Abel integral inversion (Details have been given in Appendix B in [37])
Then the Equation (A1) becomes
in which hyperbolic transformation can solve the singularity.
This method is the most accurate solution among all other pure mathematics to the Abel integral [41]. However, pure mathematics relies on high-quality input, whose order of magnitude should be larger, or it will become less representative. We test the exact number in experiment 1.
It is also the algorithm of the early version of the End-to-End GNSS Occultation Performance Simulation and Processing System (EGOPS) software developed by the Wegener Center/the University of Graz (WEGC) [42]. This Abel integral method closely resembles the Abel integral and is widely used in all fields concerning the Abel integral. For example, it maps three dimensional images into its two dimensional objection [41]. Hicksterin also developed an open-access project named Pyabel in GitHub (Available online at https://github.com/luli/hedp/blob/master/hedp/math/abel.py, accessed on 8 June 2021), which was also used in our experiment.
A.2.2. Exp Algorithm
This method was proposed by the EUMETSAT GRAS-SAF and was summarized and applied in numerical assimilation by [23,40]. The refractivity is assumed to exponentially decrease with height since it has a relationship with temperature according to Equation (1). At a height of over 12 km, where water vapor is sparse, we can assume e equals zero. Based on the isothermal atmosphere assumption, , and Equation (1), the refractivity is exponentially decreased with height [26,43,44]. Therefore, the refractivity N as the jth level can be expressed as [35]:
where kj = ln(Nj/Nj+1)/(xj+1 − xj), and the value is positive with a minimum of 10−6. In addition, the term lnn = ln(10−6N + 1) in Equation (2) is equivalent to 10−6N based on infinitesimal assumption. Moreover, at the tangent point, we have when we assume the impact parameter x is equivalent to the impact parameter a because a and x of air in the higher magnitude of order (6000 km) and their difference are less (<80 km).
Therefore, the differential at the jth level is expressed as [35]
To improve the integral accuracy and compute it economically, [45] used the error function (erf) by writing .
Notably, the algorithm is not feasible under the condition of super refraction (often in the troposphere, below 12 km) because the gradient of N is large (resulting in a large kj) such that the BA is overestimated [35]. In such circumstances, the second line of Equation (7) is written as:
This formula is still under the exponential decay assumption; However, it is acceptable because the interval is relatively small in the troposphere.
The error of the exp algorithm comes from its advantage. When the input refractivity is smaller in high levels, the exponential decay is faster than linear decay, making it closer to the actual refractivity. However, when an abnormally larger (less) refractivity exist at some level, the results of the exp algorithm will be considerably larger (less) than the results of the direct algorithm, as shown in Equation (A6).
The exp algorithm is widely used in the FM for NWP data assimilation since the interpolation of Equation (A5) is a reliable approximation between levels. However, this interpolation can yield oscillations when the interval is too large, specifically between 25 km and 45 km [36]. Furthermore, the desirable interval for avoiding this phenomenon is less than 100 m. Focused on this problem, [36] improved this algorithm with a physical association between refractivity and temperature. Thus, it is called the temperature revised exp algorithm.
A.2.3. Exp_T Algorithm
Ref. [24] extended the Equation (1) physically by introducing three new parameters in the jth level, which are [26]:
where the temperature gradient , the subscript m is the middle point of two successive levels, i.e., and . When , we have , which is exactly the exp algorithm. The terminal differential at jth level is expressed as [26]:
This method alleviated the oscillation. The error of this algorithm is the same as that of the exp algorithm, that is, its exponential decay of refractivity with increasing height. A larger abnormal refractivity has a more significant impact on its value than other algorithms.
This paper mainly compared two algorithms: direct and exp. We dismissed the lin algorithm because it required the interval to be less than 100 m. Most observations input to FM cannot satisfy this condition. In addition, we only compared the exp_T algorithm with the exp algorithm because their difference is too small to be noticeable if the direct algorithm is combined. In another aspect, we also considered the difference incurred from the interpolation method, including the log-spine cubic interpolation and the log-linear interpolation. Furthermore, the algorithms were compared in experiment 1.
Appendix B. Figures
Figure A2 shows the monthly O-B/B statistics of FY3D used in experiment one, the relative difference between ECMWF forecast and FY3D is less than 2%. Since the RO sounding occurs randomly on the earth’s surface, the standard deviation is relatively huge, less than 10%, which is an acceptable range. The FY3D in September with such quality established a good condition for experiment one.
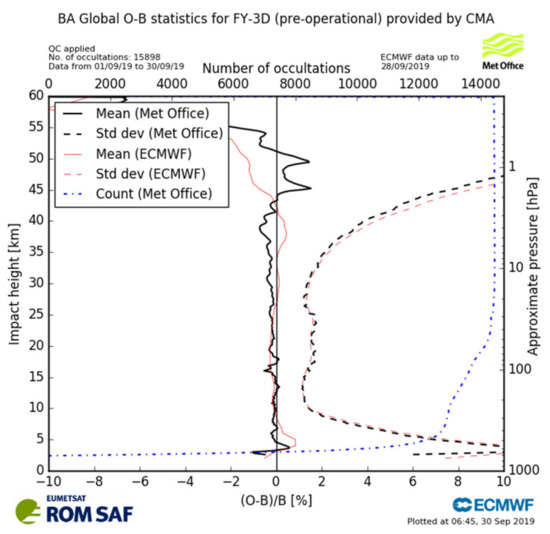
Figure A2.
Monthly O-B statistics of FY3D, September 2019. The mean relative difference (RD) between ECMWF forecast and FY3D is less than 2%. Copyright © 2022 EUMETSAT.
Figure A3 shows level intervals of 137 ECMWF 4dvar, 31 levels of FNL, and 37 levels of ERA5. Their interval generally increases as the altitude increases. EC4Dvar has the smallest intervals, which are less than 500 m below the height of 25 km. The level intervals of FNL and ERA5 are similar, but between 2–4 km, 12–15 km, ERA5 has a smaller interval than FNL.
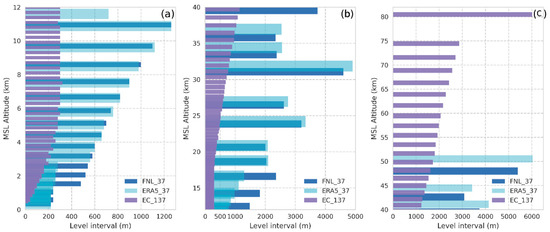
Figure A3.
Level interval of FNL, ERA5, and EC4Dvar. Interval decreases with increasing height. (a) 0–12 km, (b) 12–40 km, (c) 40–80km.
To ensure the reliability of experiment one, we also did the comparison using 541 MetOp RO profiles on 1 March 2018. The results were shown in Figure A4, and FY3D’s results are in Figure 3. These two figure were set with the same coordinate, axes, and ticks. The results of MetOp are consistent with that of FY3D. Firstly, the difference (E T) of both direct and exp algorithm are in the same order of magnitude, which is 1 × 10−5 in the range of 5–30 km and 1 × 10−6 in the range of 30–60 km, as shown in Figure A4a,b and Figure 3a,b. The results of FY3D have less error because it has passed 4QC. The experiment based on MetOp used the same collocation method as experiment 1. But we did not use 4QC. Secondly, they have the same conclusion on which algorithm is more accurate, that if the exp. Thirdly, the log-linear interpolation also causes more undulation to () than which is caused by log-cubic interpolation. Moreover, the error induced by interpolation for exp is larger than that for direct. Therefore, the results of experiment one are reliable.
The integral accuracy is subject to the order of magnitude of refractivity (input), which is shown in Figure A5. Intriguingly, when the order of magnitude is 1 × 10−2 above (below) the height of 60 km, the direct algorithm’s result is less (larger) than the true value.
Figure A4.
Mean difference from MetOp and experimental value calculated from direct and exp. (a,b) Difference (E − T) of BA based on the log-cubic interpolation; (c,d) difference of BA between exp and direct based on the log-linear and log-cubic interpolation; (e,f) difference of BA between log-linear and log-cubic interpolation based on exp and direct. (a,c,e) 10–30 km; (b,d,f) 30–60 km; Results from MetOp are the same as the results using FY3D.
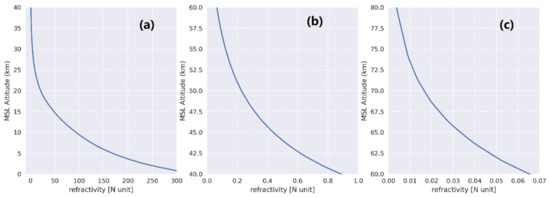
Figure A5.
Mean refractivity in 0–40 km, 40–60 km, and 60–80 km, and their order of magnitude are 1 × 10−0, 1 × 10−1, 1 × 10−2, respectively. (a) 0–40 km, (b) 40–60 km, (c) 60–80km.
Figure A6 is the same as Figure 7 but based on the log-linear interpolation. Below the height of 35 km, the RD and difference of EC4Dvar become 1%, 1 × 10−5 from 0.5% and 0.5× 10−5 in Figure 7. Between 35 to 50 km, those values are the same, less than 5%. In terms of FNL and ERA5, more RD values reach 4% below 35 km, and more of those are over 5% above 35 km. There is more undulation for results based on linear interpolation.
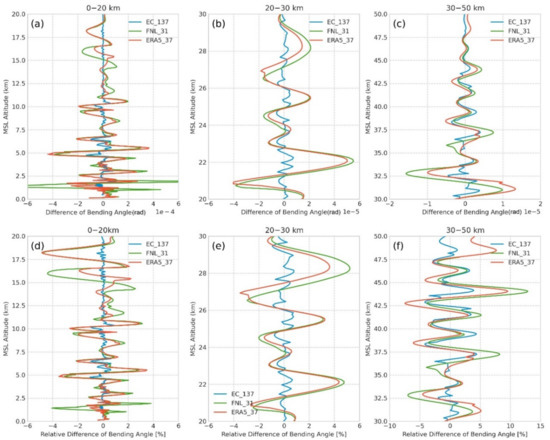
Figure A6.
The same as Figure 7 but in log-linear interpolation, the difference (a–c) and RD (d–f) of FM based on the exp algorithm and log-linear interpolation. The BA RD of EC4Dvar below 35 km is less than ±1%, whereas it of FNL and ERA5 below 35 km is less than ±5%. Above 35 km, the RD EC4Dvar is less than ±5%, while it of FNL and ERA5 is up to 10%.
Appendix C. 4QC
This four QCs processing is used in [30]. In this method, reliability was calculated using critical parameter Z. (usually about Z > 2–4, the smaller Z is stricter) excludes outliers [30]. In this study, mean value is used to discuss all the results. If the sample is obey Gaussian distribution, the mean value has representativeness. The 4QCs discard outliers, making the sample similar to Gaussian distribution. Each level will be checked by QC. If a level cannot pass the QC, the whole profile will be discarded.
(1) Ensure soundings were between 60 °S and 60 °N horizontally, and between 5–80 km vertically; The RO data at high altitude may easily be affected by the ionosphere, and some sounding may lack observation in the lower level below 5 km. After this QC1, 2824 (out of 5914) were left.
(2) Eliminate outliers horizontally on each level: use the bi-weight method proposed by [45] to FY3D’s refractivity on each level, and set the Z > 3, which is the crucial parameter for the bi-weight method. After this QC2, 1655 (out of 2824) were left.
(3) Ensure the FY3D’s BA is closer to EC4Dvar’s BA: use bi-weight method to the difference of the refractivity between FY3D and EC4Dvar with Z as 3. It is noticed that this QC solved the drift tangent point phenomenon partly because we only made comparisons horizontally at every level, the slant profile will be discarded. Drift tangent point phenomenon is that the actual RO profile is slanted, which results in a bias of the difference between the slanted FY3D and EC4Dvar. As long as FY3D and EC4Dvar are closer in each level horizontally, the drift tangent point phenomenon will be ignored, and collocation spatially will prove to be reasonable. Furthermore, experiment one used statistics, the average bending angle, which can effectively eliminate the anomalies. Accordingly, the bias question left after spatial collocation is fixed too. After this QC3, 1436 (out of 1665) were left.
(4) Eliminate the anomaly interval via the Bi-weight method. A similar interval among each profile effectively can reduce the bias introduced by interpolation. After QC4, 368 (out of 1436) were left.
The 4 QC help eliminate bias from the spatial collocation and drift tangent point phenomenon, ensuring the forward modelled bias mainly resulted from integral and interpolation methods. These soundings are evenly distributed spatially and temporally (Figure A7), making the mean (statistical values) feasible in the following analysis. Figure A7 shows FY3D soundings in experiment one are generally distributed evenly spatially and temporally, which makes the mean (statistical values) feasible in the following analysis.
To test the quality of refractivity profiles after 4QC, we used statistics, the mean relative difference of refractivity between FY3D profiles and EC4Dvar in each level. Their original profiles are interpolated into fixed levels with an interval of 100 m. As shown in Figure A8, although the standard deviation of those profiles is large than 2%, the mean hovers around zero. Unfortunately, there is a large difference at the heights of 18 (errors about 0.3%), 48 (errors about 1.3%), 58 (errors about 3.1%), 78 (errors about 10%) km, which passed our 4QC. This error will be propagated to the following experiments.”
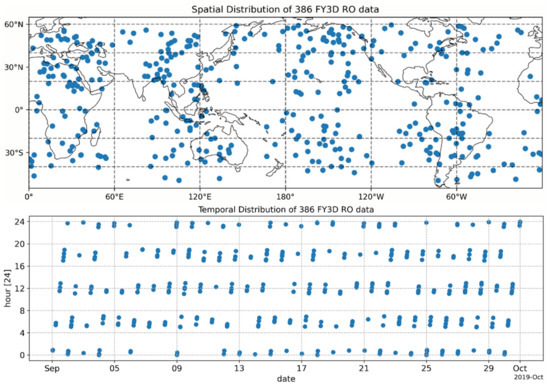
Figure A7.
Spatial (upper) and temporal (lower) distribution of 386 samples after collocation and 4QC. In general, these samples are evenly distributed in longitude and latitude, and are evenly distributed in different hours on each day in September.
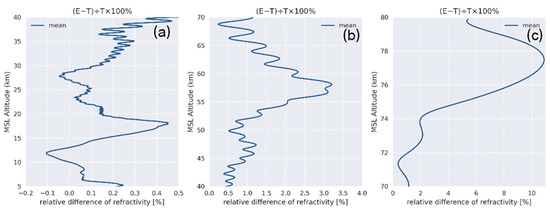
Figure A8.
Mean value of refractivity profiles’ relative difference (RD), , between FY3D (True value, T) and EC4Dvar (Experimental value, E). There are large differences at the heights of 18 (0.3%), 48 (1.3%), 58 (3.1%), 78 (10%) km. (a–c) shows the mean value of it.
References
- Cardinali, C.; Healy, S. Impact of Gps Radio Occultation Measurements in the Ecmwf System Using Adjoint-Based Diagnostics. Q. J. R. Meteorol. Soc. 2014, 140, 2315–2320. [Google Scholar] [CrossRef]
- Sun, Y.; Bai, W.; Liu, C.; Yan, L.; Du, Q.; Wang, X.; Yang, G.; Mi, L.; Yang, Z.; Zhang, X. The Fengyun-3c Radio Occultation Sounder Gnos: A Review of the Mission and Its Early Results and Science Applications. Atmos. Meas. Tech. 2018, 11, 5797–5811. [Google Scholar] [CrossRef]
- Schreiner, W.S.; Weiss, J.P.; Anthes, R.A.; Braun, J.; Chu, V.; Fong, J.; Hunt, D.; Kuo, Y.; Meehan, T.; Serafino, W.; et al. Cosmic-2 Radio Occultation Constellation: First Results. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Bai, W.; Tan, G.; Sun, Y.; Xia, J.; Cheng, C.; Du, Q.; Wang, X.; Yang, G.; Liao, M.; Liu, Y.; et al. Comparison and Validation of the Ionospheric Climatological Morphology of Fy3c/Gnos with Cosmic During the Recent Low Solar Activity Period. Remote Sens. 2019, 11, 2686. [Google Scholar] [CrossRef]
- Liao, M.; Healy, S.; Zhang, P. Processing and Quality Control of Fy-3c gnos Data Used in Numerical Weather Prediction Applications. Atmos. Meas. Tech. 2019, 12, 2679–2692. [Google Scholar] [CrossRef]
- Oscar. Available online: https://www.wmo-sat.info/oscar/gapanalyses?mission=9 (accessed on 15 August 2021).
- Bai, W.; Deng, N.; Sun, Y.; Du, Q.; Xia, J.; Wang, X.; Meng, X.; Zhao, D.; Liu, C.; Tan, G.; et al. Applications of Gnss-Ro to Numerical Weather Prediction and Tropical Cyclone Forecast. Atmosphere 2020, 11, 1204. [Google Scholar] [CrossRef]
- Harnisch, F. Scaling of Gnss Radio Occultation Impact with Observation Number Using an Ensemble of Data Assimilations. Mon. Weather. Rev. 2013, 141, 4395–4413. [Google Scholar] [CrossRef]
- ECMWF Observation Monitoring. Available online: https://www.ecmwf.int/en/forecasts/charts/obstat/gpsro_gpsro__count_0001_plot_o_count_gpsro_gpsro?facets=Parameter,Bending%20angles&time=2021062100&Phase=Setting (accessed on 22 June 2021).
- Bowler, N.E. An Assessment of Gnss Radio Occultation Data Produced by Spire. Q. J. R. Meteorol. Soc. 2020, 146, 3772–3788. [Google Scholar] [CrossRef]
- Bai, W.; Sun, Y.; Du, Q.; Yang, G.; Yang, Z.; Zhang, P.; Bi, Y.; Wang, X.; Wang, D.; Meng, X. An Introduction to FY3 GNOS in-Orbit Performance and Preliminary Validation Results. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 27 April–2 May 2014. [Google Scholar]
- Bai, W. An Introduction to the Fy3 Gnos Instrument and Mountain-Top Tests. Atmos. Meas. Tech. 2014, 7, 1817–1823. [Google Scholar] [CrossRef]
- Liao, M. Preliminary Validation of the Refractivity from the New Radio Occultation Sounder Gnos/Fy-3c. Atmos. Meas. Tech. 2016, 9, 781–792. [Google Scholar] [CrossRef]
- Steiner, A.K.; Ladstädter, F.; Ao, C.O.; Gleisner, H.; Ho, S.; Hunt, D.; Schmidt, T.; Foelsche, U.; Kirchengast, G.; Kuo, Y.; et al. Consistency and Structural Uncertainty of Multi-Mission Gps Radio Occultation Records. Atmos. Meas. Tech. 2020, 13, 2547–2575. [Google Scholar] [CrossRef]
- Bi, Y.; Yuan, B.; Wang, Y.; Ma, G.; Zhang, P. Assimilation experiment of GPS bending angle using WRF model — analysis of impact on Typhoon “SinLaku”. J. Tropical Meteorol. 2013, 29, 149–154. [Google Scholar]
- Gorbunov, M.; Stefanescu, R.; Irisov, V.; Zupanski, D. Variational Assimilation of Radio Occultation Observations into Numerical Weather Prediction Models: Equations, Strategies, and Algorithms. Remote Sens. 2019, 11, 2886. [Google Scholar] [CrossRef]
- Bai, W.; Tan, G.; Sun, Y.; Xia, J.; Du, Q.; Yang, G.; Meng, X.; Zhao, D.; Liu, C.; Cai, Y.; et al. Global Comparison of F2-Layer Peak Parameters Estimated by Iri-2016 with Ionospheric Radio Occultation Data During Solar Minimum. IEEE Access 2021, 9, 8920–8934. [Google Scholar] [CrossRef]
- Liu, C.; Kirchengast, G.; Syndergaard, S.; Schwaerz, M.; Danzer, J.; Sun, Y. New higher-order correction of GNSS RO bending angles accounting for ionospheric asymmetry: Evaluation of performance and added value. Remote Sens. 2020, 12, 3637. [Google Scholar]
- Gorbunov, M.E. Ionospheric Correction and Statistical Optimization of Radio Occultation Data. Radio Sci. 2002, 37, 1–9. [Google Scholar] [CrossRef]
- Hedin, A.E. Extension of the Msis Thermosphere Model into the Middle and Lower Atmosphere. J. Geophys. Res. Space Phys. 1991, 96, 1159–1172. [Google Scholar] [CrossRef]
- Scherllin-Pirscher, B.; Syndergaard, S.; Foelsche, U.; Lauritsen, K.B. Generation of a Bending Angle Radio Occultation Climatology (Baroclim) and Its Use in Radio Occultation Retrievals. Atmos. Meas. Tech. 2015, 8, 109–124. [Google Scholar] [CrossRef][Green Version]
- Hocke, K. Inversion of Gps Meteorology Data. In Paper presented at the Annales Geophysicae 1997. In Proceedings of the Annales Geophysicae, Vienna, Austria, 30 April 1997. [Google Scholar]
- Healy, S.B.; Thépaut, J.N. Assimilation Experiments with Champ Gps Radio Occultation Measurements. Q. J. R. Meteorol. Soc. 2006, 132, 605–623. [Google Scholar] [CrossRef]
- Burrows, C.; Healy, S.; Culverwell, I. Improvements to the Ropp Refractivity and Bending Angle Operators. 2013. Available online: https://www.romsaf.org/general-documents/rsr/rsr_15.pdf (accessed on 22 June 2021).
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s Atmosphere with Radio Occultation Measurements Using the Global Positioning System. J. Geophys. Res. Atmos. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- The ROM SAF Consortium, some. The Radio Occultation Processing Package (Ropp) Forward Model Module User Guide. 2019.
- Cucurull, L.; Derber, J.C.; Purser, R.J. A Bending Angle Forward Operator for Global Positioning System Radio Occultation Measurements. J. Geophys. Res. Atmos. 2013, 118, 14–28. [Google Scholar] [CrossRef]
- Gilpin, S.; Anthes, R.; Sokolovskiy, S. Sensitivity of Forward-Modeled Bending Angles to Vertical Interpolation of Refractivity for Radio Occultation Data Assimilation. Mon. Weather Rev. 2019, 147, 269–289. [Google Scholar] [CrossRef]
- Brenot, H.; Rohm, W.; Kačmařík, M.; Möller, G.; Sá, A.; Tondaś, D.; Rapant, L.; Biondi, R.; Manning, T.; Champollion, C. Cross-Comparison and Methodological Improvement in Gps Tomography. Remote. Sens. 2019, 12, 30. [Google Scholar] [CrossRef]
- Xu, X.; Zou, X. Comparison of Metop-A/-B GRAS Radio Occultation Data Processed by CDAAC and ROM. GPS Solut. 2020, 24, 1–16. [Google Scholar] [CrossRef]
- Zou, X.; Zeng, Z. A Quality Control Procedure for Gps Radio Occultation Data. J. Geophys. Res. 2006, 111, 111. [Google Scholar] [CrossRef]
- Lohmann, M.S. Analysis of Global Positioning System (Gps) Radio Occultation Measurement Errors Based on Satellite De Aplicaciones Cientificas-C (Sac-C) Gps Radio Occultation Data Recorded in Open-Loop and Phase-Locked-Loop Mode. J. Geophys. Res. 2007, 112, 112. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Orszag, S.A. On the Elimination of Aliasing in Finite-Difference Schemes by Filtering High-Wavenumber Components. J. Atmos. Sci. 1971, 28, 1074. [Google Scholar] [CrossRef]
- Lewis, H. Abel Integral Calculations in Ropp. 2008. Available online: https://www.romsaf.org/general-documents/gsr/gsr_04.pdf (accessed on 22 June 2021).
- Burrows, C.P.; Healy, S.B.; Culverwell, I.D. Improving the Bias Characteristics of the Ropp Refractivity and Bending Angle Operators. Atmos. Meas. Tech. 2014, 7, 3445–3458. [Google Scholar] [CrossRef][Green Version]
- Fjeldbo, G.; Kliore, G.; Eshleman, V. The Neutral Atmosphere of Venus as Studied with the Mariner V Radio Occultation Experiments. Astron. J. 1970, 76, 123. [Google Scholar] [CrossRef]
- Yan, H.; Fu, Y.; Hong, Z. Spaceborne Gps Meteorology and Retrieval Technique (Chinese Version); Science and technology of China Press: Beijing, China, 2007. [Google Scholar]
- Jin, S.; Cardellach, E.; Xie, F. Gnss Remote Sensing; Springer: Berlin/Heidelberg, Germany, 2014; Volume 16. [Google Scholar]
- Marquardt, C.; Healy, S.; Luntama, J.; McKernan, E. GRAS Level 1 B Product Validation with 1d-Var Retrieval. EUMETSAT: Darmstadt, Germany, 2004. [Google Scholar]
- Hickstein, D.D.; Gibson, S.T.; Yurchak, R.; Das, D.D.; Ryazanov, M. A Direct Comparison of High-Speed Methods for the Numerical Abel Transform. Rev. Sci. Instrum. 2019, 90, 065115. [Google Scholar] [CrossRef]
- Schweitzer, S.; Pirscher, B.; Pock, M.; Ladstädter, F.; Borsche, M.; Foelsche, U.; Fritzer, J.; Kirchengast, G. End-to-End Generic Occultation Performance Simulation and Processing System Egops: Enhancement of Gps Ro Data Processing and Ir Laser Occultation Capabilities. University of Graz, Graz, Austria: Wegener Center for Climate and Global Change (WegCenter). 2008. Available online: http://wegcwww.uni-graz.at/publ/wegcpubl/arsclisys/2008/igam7www_sschweitzeretal-wegctechrepfffg-alr-no1-2008.pdf (accessed on 22 June 2021).
- Sheng, F.X. Atmospheric Physics; Peking University Press: Beijing, China, 2013. [Google Scholar]
- Lewis, H. Error Function Calculation in Ropp. 2007. Available online: https://www.romsaf.org/general-documents/gsr/gsr_04.pdf (accessed on 22 June 2021).
- Lanzante, J.R.R. Robust and Non-Parametric Techniques for the Analysis of Climate Data: Theory and Examples, Including Applications to Historical Radiosonde Station Data. Int. J. Climatol. A J. R. Meteorol. Soc. 1996, 16, 1197–1226. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).