Fast Line Segment Detection and Large Scene Airport Detection for PolSAR

Abstract

In this paper, we propose a fast Line Segment Detection algorithm for Polarimetric synthetic aperture radar (PolSAR) data (PLSD). We introduce the Constant False Alarm Rate (CFAR) edge detector to obtain the gradient map of the PolSAR image, which tests the equality of the covariance matrix using the test statistic in the complex Wishart distribution. A new filter configuration is applied here to save time. Then, the Statistical Region Merging (SRM) framework is utilized for the generation of line-support regions. As one of our main contributions, we propose a new Statistical Region Merging algorithm based on gradient Strength and Direction (SRMSD). It determines the merging predicate with consideration of both gradient strength and gradient direction. For the merging order, we set it by bucket sort based on the gradient strength. Furthermore, the pixels are restricted to belong to a unique region, making the algorithm linear in time cost. Finally, based on Markov chains and a contrario approach, the false alarm control of line segments is implemented. Moreover, a large scene airport detection method is designed based on the proposed line segment detection algorithm and scattering characteristics. The effectiveness and applicability of the two methods are demonstrated with PolSAR data provided by UAVSAR.

1. Introduction

Detection of line segments in images, as a basic processing function, plays a crucial role in various applications. Line segments can describe a variety of objects, such as roads, rivers, airports, and more [1]. More importantly, when the quality of the image decreases, line segments are more stable and clear than edge features [2]. Therefore, line segment detection has been successfully applied to image registration [3,4], target detection [5,6], target recognition [7], change detection [8,9], etc.

The polarimetric synthetic aperture radar (PolSAR) is an advanced imaging radar system which measures the reflectivity of targets using four polarizations [10]. The additional information in PolSAR can be utilized by target detection algorithms to improve performance; for instance, Li et al. [11] implemented marine oil slick detection using polarimetric decomposition components and descriptors, and He et al. [12] used multi-channel scattering information for ship detection of PolSAR data. Hence, image interpretation by PolSAR data has received increasing attention. This paper aims to design an algorithm for detecting line segments of PolSAR images, providing basic characteristics for advanced image interpretation tasks.

Recently, many approaches have been developed for line segment detection. One of the well-known methods is Hough Transform (HT), proposed by Duda and Hart [13], which has attracted much attention. This method constructs the parameter space using edge pixels and performs peak detection within the parameter space to determine the position of line segments. Based on the concept of HT, a large number of line segment detection algorithms have been proposed [14,15,16]. However, such methods perform line segment detection using binary edge mapping, discarding the strength and direction information of the gradient, which makes it more susceptible to interference from noise. To enable such methods to be applied to SAR images with strong speckle [17,18], Wei et al. [19] proposed the Image Edge Field Accumulation (IEFA) straight-line detection method, utilizing both edge strength and direction information for peak detection to detect line segments. Subsequently, Wei et al. [2] used the Fourier transform and the central slice theorem to transform the image from the space domain to the frequency domain, which accelerates the straight-line extraction process. In addition, Xiong et al. [20] proposed to decompose the edge information in parameter space into horizontal and vertical components, stripping off part of the random edge information, which reduces the interference of pseudo-peaks with the line segment detection results.

Other typical line segment detection methods are referred to as non-HT methods. Non-HT methods use local information to detect line segments. The Line Segment Detector (LSD) [21] and Edge Drawing Line Segments Detection (EDLines) [22] methods are representative algorithms. They group the pixels by the gradient direction and validate each group of pixels by the Helmholtz principle [23] and a contrario approach. By introducing the knowledge of undirected graphs, Cho et al. [24] designed a Linelet-based line segment detection (Linelet-LSD) method. Linelets are defined as horizontally or vertically connected pixels. Linelets and the relationships between them form an undirected graph, which can help to achieve line segment detection. Moreover, with the development of deep learning [25,26], Li et al. [27] implemented the detection of line segments using a deep learning-based model. For the characteristics of SAR images, Liu et al. [28] modified the LSD, obtaining Line Segment Detector for SAR images (LSDSAR).

Line segment detection for optical and SAR images has been thoroughly studied. However, due to the multiplicative noise and multi-polarization information of PolSAR data, the gradient calculation methods used for optical and SAR data cannot obtain accurate gradient results from PolSAR data. Furthermore, there are fewer studies on line segment detection for PolSAR data. An important contribution was made by D. Borghys [29], who proposed a scheme for detecting linear features in PolSAR images using the Hotellings test. Based on this, Jin [30] proposed a linear feature detection method for PolSAR images by replacing the Hotellings test with the Wilks test. In [31], a fuzzy linear feature detector was constructed from the Wishart likelihood ratio test statistic. Nevertheless, all the above algorithms detect many curves in PolSAR data along with the line segments. Moreover, the width of the obtained linear region is large, which leads to difficulty in describing the line segments accurately. To address the above problems, we propose a PolSAR image Line Segment Detection method (PLSD) which concentrates on detecting the line segments in PolSAR images. PLSD can be divided into three stages. In the first stage, the gradient map of the PolSAR image is acquired by the improved Constant False Alarm Rate (CFAR) edge detector [32]. Then, Statistical Region Merging based on gradient Strength and Direction (SRMSD) is applied to obtain line-support regions. Finally, to validate the line-support regions, an extension of the a contrario approach is utilized, which is based on the Helmholtz principle [23] and Markov chains. In addition, based on PLSD, we propose a large scene airport detection method for PolSAR images. The experimental results validate the effectiveness of the two methods and demonstrate the potential of line segments for application in PolSAR images.

In all, the main contributions of this paper are as follows:

• The literature on line segment detection is surveyed and the importance of line segments in the image interpretation task is determined. Then, we propose a new fast line segment detection algorithm, PLSD, to detect line segments in PolSAR images. It can detect line segments in linear time.
• Based on PLSD and the scattering characteristics of airports, we propose an airport detection method for large scenes.
• The results of the above two detection methods and the state-of-the-art (SOTA) method are compared on several PolSAR images. The superiority of the two models is demonstrated.

The rest of this paper is organized as follows. Section 2 describes the design details of the PLSD and the airport detection method. Experimental results are presented and analyzed in Section 3. Section 4 discusses the parameter settings and algorithm complexity of the line segment detector. Finally, Section 5 draws conclusions.

2. Method

This section introduces our proposed methods, including the line segment detector and the airport detection method. First, the line segment detector is described. Specifically, the edge detector with the covariance matrix is described first, followed by SRMSD, then the line segment validation method is presented. Finally, the complete PLSD algorithm is provided and the airport detection algorithm based on the line segment detector is introduced.

2.1. Line Segment Detection for PolSAR (PLSD)

To obtain line segments from PolSAR images, PLSD is divided into three steps: (1) obtaining the gradient strength and gradient direction of each point in PolSAR images by improved edge detector with covariance matrix; (2) performing SRMSD to acquire line-support regions; and (3) utilizing the Helmholtz principle [23] and Markov chains, the line-support region is validated, removing the false alarms. The flowchart of the PLSD is illustrated in Figure 1.

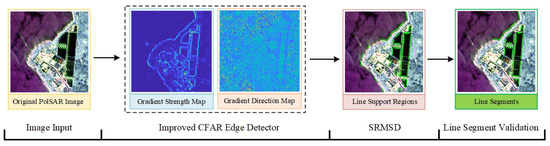
Figure 1. Flowchart of the PLSD.

2.1.1. Edge Detector with Covariance Matrix

PolSAR measures the backscattering coefficient of the target using multiple combinations of transmitting and receiving antenna polarizations. In the case of a full PolSAR, each resolution unit is described by a 2 × 2 complex scattering matrix S, as shown in Equation (1):

$$S=\left[\begin{array}{cc}{S}_{hh}& S_{hv}\\ S_{vh}& S_{vv}\end{array}\right]$$

(1)

where the elements $S_{ij}$ in the scattering matrix represent the complex scattering coefficient, with i denoting the transmitting polarization and j denoting the receiving polarization.

Under the monostatic backscattering case, there exists a reciprocity theorem, i.e., $S_{hv}$ = $S_{vh}$; the scattering matrix becomes symmetric, and can be reduced to a three-dimensional single-look scattering vector $\Omega ={\left[S_{hh}\sqrt{2}{S}_{hv}{S}_{vv}\right]}^T$, with T being transpose. We discuss this backscattering case in the following part of this paper.

For the purpose of speckle reduction, multi-look processing is usually performed on PolSAR data. For multi-look PolSAR data, each pixel can be represented by a covariance matrix C, which is defined as

$$C=\frac{1}{L}\sum _{i=1}^L{\Omega }_i\times {\Omega }_i^{\ast T}$$

(2)

where the superscript $\ast T$ denotes the conjugate transpose, L represents the number of looks, and ${\Omega }_i$ is the scattering vector to be averaged. The covariance matrix C follows a complex Wishart distribution, i.e., $C\in W_C\left(q,L,\sum \right)$, with $\sum =E\left(\Omega \times {\Omega }^{\ast T}\right)$ and with q representing the dimension of the scattering vector. For a fully polarimetric SAR under the monostatic backscattering case reciprocity, q = 3. This can be described by the following probability density function:

$$P\left(C|\sum \right)=\frac{L^{q\times L}\times |C{|}^{L-q}\times exp\left(-L\times Tr\left({\sum }^{-1}C\right)\right)}{K\left(L,q\right)\times |\sum {|}^L}$$

(3)

$$K\left(L,q\right)={\pi }^{q\left(q-1\right)/2}\prod _{j=1}^q\Gamma \left(L-j+1\right)$$

(4)

where $\Gamma \left(\dots \right)$ is the Gamma function, while $Tr\left(\dots \right)$ and $|\dots |$ denote the trace and determinant, respectively.

Suppose $C_x$ and $C_y$ are independent and both follow a complex Wishart distribution, i.e., $C_x\in W_C\left(q,L,{\sum }_x\right)$ and $C_y\in W_C\left(q,L,{\sum }_y\right)$. Then, their equality can be tested by the Wishart likelihood ratio test (LRT) statistic, Q [33], and Q becomes

$$Q=\frac{{\left(2\times L\right)}^{2\times q\times L}}{L^{2\times q\times L}}\times \frac{|C_x{|}^L\times |C_y{|}^L}{|C_x+C_y{|}^{2\times L}}$$

(5)

To simplify the calculation, the ln operation is applied to Q according to [33]:

$$lnQ=L\times \left(2\times q\times ln2+ln|C_x|+ln|C_y|-2ln|C_x+C_y|\right)$$

(6)

The term $lnQ$ is limited by [$-\infty$, 0], with $lnQ$ = 0 for $C_x$ = $C_y$.

Based on Equation (6), the polarimetric CFAR Edge Detector [32] is proposed. It visits each pixel in the image continuously, applying a set of filters with different orientations for each pixel. The filter estimates the average covariance matrix on both sides of the center pixel and then calculates the Wishart likelihood ratio test statistic as a measure of the probability of edge pixels. Usually, to achieve better edge detection, eight sets of filters with different orientations are provided at each pixel in the image. This increases the computational complexity of edge detection. We designed the filter setup as shown in Figure 2 according to the approach in [21], which reduces computational complexity and maintains good accuracy. To be specific, with the LRT statistic $lnQ$ calculated as shown in Equation (6) for the left and right filter configurations shown in Figure 2a, we can find the horizontal gradient intensity of the center pixel. The size of the filter window is set by a speckle suppression parameter $\rho$, i.e., $w_f=⌈log\left(10\right)\times \rho ⌉$, ${\mathrm{l}}_f=2\times w_f+1$. The gradient $G^v\left(x,y\right)$ along the vertical direction can be computed in the same way, as shown in Figure 2b. The strength $|GR\left(x,y\right)|$ and direction $ang\left(GR\left(x,y\right)\right)$ at a position $(x,y)$ are defined as

$$|GR\left(x,y\right)|=\sqrt{G^h{\left(x,y\right)}^2+G^v{\left(x,y\right)}^2}$$

(7)

$$ang\left(GR\left(x,y\right)\right)=arctan\frac{G^v\left(x,y\right)}{G^h\left(x,y\right)}$$

(8)

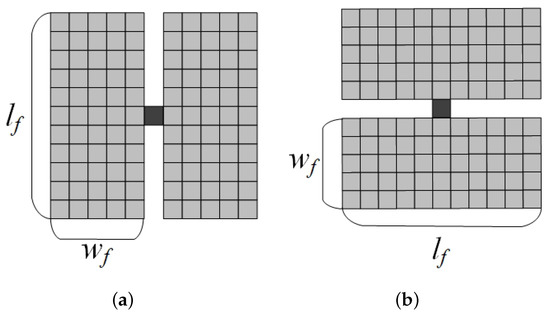
Figure 2. Edge detection filter configuration, $l_f$: length of the filter, $w_f$: width of the filterfileter, $l_f$ = 2 ×$w_f$+ 1. (a) Filter setting for the horizontal gradient calculation. (b) Filter setting for the vertical gradient calculation.

2.1.2. Statistical Region Merging Based on Gradient Strength and Direction

In optical images, the gradient map is obtained by performing a difference operation on adjacent pixels. To ensure that the gradient of each point is only affected by the adjacent pixels, the region affected by the pixel mutation is small, i.e., the width of the region having the same gradient direction is small. Therefore, grouping the adjacent pixels with similar gradient directions provides accurate line-support regions.

Nevertheless, this method is not applicable to PolSAR images. In [28], LSDSAR was used to replace the finite-differences method with the ratio-based calculation method in order to obtain a more accurate gradient map. However, LSDSAR does not consider the problem that the gradient maps obtained by the ratio-based calculation method have a large width at the pixel mutations. The same problem appears in the gradient maps obtained by the CFAR edge detector. Therefore, a line-support region generation algorithm based on the gradient direction alone increases the width of the line-support region and even change its direction, decreasing the detection accuracy of the line segment. In the proposed method, we consider both gradient strength and gradient direction to diminish the damage. As shown in Figure 3c, when the the pixel mutation is closer, the gradient strength is higher. Hence, the utilization of gradient strength can effectively distinguish edge points from interference points. In addition, the average attributes of the regions are more representative compared to the attributes of the pixels at the edges of the regions,; thus, the Statistical Region Merging (SRM) algorithm is used. Overall, we propose a line-support region generation algorithm called SRMSD that is more suitable for PolSAR data.

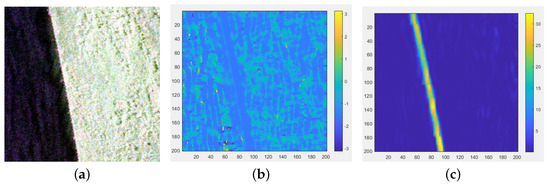
Figure 3. Gradient map. (a) PauliRGB map. (b) Gradient direction map. (c) Gradient strength map.

Meanwhile, the seed pixel selection of statistical region merging has an important influence on the final result. Pixels with higher gradient strength are selected as seed pixels first, as they are more likely to belong to line segments. In addition, the gradient direction of the seed pixels is considered to be similar to the line segment direction. Therefore, the gradient direction of each tested pixel is compared with the gradient direction of the seed pixel, preventing the appearance of line segments in the region with slow gradient direction change, i.e., the scene shown in Figure 4a. The effectiveness of this measure is demonstrated in Figure 4b,c.

Figure 4. Effect of the seed pixel direction. (a) Scenes with slow directional changes. (b) With seed pixel direction information. (c) Without seed pixel direction information.

Figure 5 illustrates the process of SRMSD. Specifically, a pixel is first selected as the seed pixel, as shown in Figure 5a. The gradient direction of the seed pixel is ${\alpha }_0$, and the initial region angle is set to ${\alpha }_0$ as well. Then, the pixels adjacent to the line-support region are tested and added it to the region if it satisfies the following conditions:

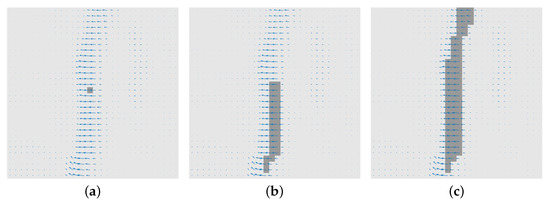
Figure 5. Process of SRMSD. The arrow represents the gradient direction and the length represents the gradient strength. (a) Selection of the seed pixel. (b) Iterative process of SRMSD. (c) Results of SRMSD.

(1)

Gradient strength equals the average region strength up to a strength tolerance $\mu$;

(2)

Gradient direction equals the region angle up to an angle tolerance $\eta$;

(3)

Gradient direction equals the initial region angle ${\alpha }_0$ up to an angle tolerance $\eta$.

At each iteration, the region angle $\alpha$ is updated to

$$\alpha =arctan\left(\frac{{\displaystyle \sum _{i=1}^n}sin\left(an{g}_i\right)}{{\displaystyle \sum _{i=1}^n}cos\left(an{g}_i\right)}\right)$$

(9)

where n is the number of pixels in the line-support region. The process is repeated until none of the adjacent pixels satisfies the join condition. The final result of the SRMSD is obtained as shown in Figure 5c.

Moreover, Algorithm 1 provides the implementation details of SRMSD according to [28]. It is worth noting that we specify that a pixel can only be added to a unique line-support region, making the SRMSD greedy and linear in time.

Algorithm 1 SRMSD

Require:  A gradient strength image $G_s$; a gradient direction image $G_d$; a starting pixel (x, y); an angle threshold $\mu$; a strength threshold $\eta$; An image Status that records whether pixels have been added to a region. Ensure:  Line-support Region: region. 1: region ← (x, y) 2: ${\alpha }_{region}$←$G_d(x,y)$ 3: $S_x$← cos(${\alpha }_{region}$) 4: $S_y$← sin(${\alpha }_{region}$) 5: for pixel $P(x_r,y_r)$ in region do 6:   for $P_a(x_a,y_a)$ adjacent to P and $Status(x_a,y_a)$ = Not Used do 7:    if Diff($G_d(x_a,y_a)$, ${\alpha }_{region}$) < $\mu$ and Diff($G_d(x_a,y_a)$, $G_d(x,y)$) < $\mu$ and Diff($G_s(x_a,y_a)$,    $G_s(x_r,y_r)$) < $\eta$ then 8:    Add $P_a$ to region. 9:    $Status(x_a,y_a)$← Used. 10:    $S_x$←$S_x$ + cos($G_d(x_a,y_a)$). 11:    $S_y$←$S_y$ + sin($G_d(x_a,y_a)$). 12:    ${\alpha }_{region}$← arctan($S_y/S_x$). 13:    end if 14:   end for 15: end for 16: return region;

2.1.3. Line Segment Validation

Following the SRMSD, further validation is required for each line-support region. The line-support region is composed of a set of pixels, while the line segment is represented by a rectangle [34]. To unify them, a rectangle is used to approximate each line-support region. The rectangle with four parameters, i.e., length, width, angle, and center of the rectangle, is shown in Figure 6. The length and width of the rectangle are defined as the length and width of the minimum bounding rectangle for the line-support region. With the gradient strength as the mass of the pixel, the center of the rectangle is defined as the center of mass [35], and the first inertia axis to select the rectangle’s angle.

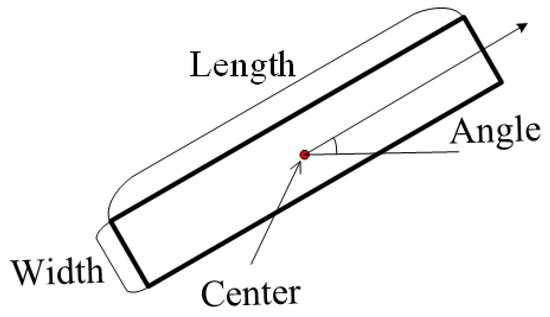
Figure 6. Rectangular description of the line-support region.

The validation of line segments using the a contrario approach is already present in several methods, such as LSD, EDLines, etc. In the a contrario approach, the detection of line segments is treated as a simplified hypothesis testing problem. It is based on the Helmholtz principle [23], i.e., no meaningful structure should happen by chance in a random configuration. A line segment, as a structure with perceptual significance, has obvious anisotropy; thus, it should not appear in the background model. The background model, as Desolneux et al. [36] state, is simply one in which all gradient directions are independent and uniformly distributed. Such a background model has good isotropy; therefore, line segments can be judged as outliers in the background model.

However, the filter-based gradient calculation method requires local averaging, resulting in gradient directions that do not satisfy the assumption of independent distribution. Fortunately, Myaskouvskey et al. [37] extended the a contrario approach by introducing Markov chains, allowing the modelling of the background model with the presence of low-order dependent events. Here, we say that the extended background model is $H_0$. For a random image $I_0$ (defined on the grid $\Psi =\left[1,N\right]\times \left[1,M\right]$) obeying the $H_0$ model, $I_0$ should satisfy the following:

(1)

$\forall m\in \Psi$, $Angle\left(\nabla I_0\left(m\right)\right)$ is uniformly distributed over $\left[0,2\pi \right]$;

(2)

The family ${\left\{Angle\left(\nabla I_0\left(m\right)\right)\right\}}_{m\in \Psi }$ follows a Markov chain of order one.

Prior to validation by a contrario approach, the aligned pixels within the rectangle, i.e., where the gradient direction of the pixel is approximately orthogonal to the rectangle’s direction, need to be counted. A rectangle is considered a valid line-support region if the percentage of aligned pixels in the rectangle exceeds the density threshold D. Otherwise, we let $\mu$ = $\mu /2$ and perform SRMSD again.

For a rectangle r with m $(X_1,\dots ,X_m)$ pixels, the joint distribution of the pixels is described by a Markov chain of order one; that is, we specify that for all $1<i\le m$,

$$\begin{array}{c}\hfill P\left(X_i=x_i|X_{i-1},\dots ,X_1=x_1\right)=P\left(X_i=x_i|X_{i-1}=x_{i-1}\right)\hfill \end{array}$$

(10)

Therefore, the distribution of aligned pixels is characterized by $\mathrm{P}\left(X_1=x_1|X_0=x_0\right)$ for $x_1,x_0\in \left\{0,1\right\}$.

Suppose that r contains n(r) pixels and k aligned pixels, and that the number of aligned pixels of rectangle r in $I_0$ is $k_0$. The Number of False Alarms (NFA) [37] of r is denoted as

$$\begin{array}{c}\hfill NFA\left(r\right)=N_R\times P_{H_0}\left(k_0\ge k\right)\hfill \end{array}$$

(11)

where $N_R$ denotes the number of rectangles in I, which can be approximated as $5\times {\left(M\times N\right)}^{5/2}$ in an image of size M × N [28]. As $I_0$ follows the Markov chain assumption, $P_{H_0}\left(k_0\ge k\right)$ can be found by

$$\begin{array}{c}\begin{array}{c}{P}_{H_0}\left(k_0\ge k\right)\hfill \\ ={\displaystyle \sum _{x_1+\dots +x_{n\left(r\right)}\ge k}}P\left(X_1=x_1\right)\times {\displaystyle \prod _{t=1}^{n\left(r\right)}}P\left(X_t=x_t|X_{t-1}=x_{t-1}\right)\hfill \end{array}\hfill \end{array}$$

(12)

A heavy computational burden results from the straightforward computation of Equation (12). Therefore, a dynamic programming algorithm [38] is employed to achieve more efficient computation. Letting $Y_t={\displaystyle \sum _{j=t}^n}{X}_j$, it can be observed that for $t<n-1$ we have

$$\begin{array}{c}P\left(Y_t\ge k\right)=\hfill \\ P\left(Y_{t+1}\ge k|X_t=0\right)\times P\left(X_t=0\right)\\ +P\left(Y_{t+1}\ge k-1|X_t=1\right)\times P\left(X_t=1\right)\hfill \end{array}$$

(13)

In addition, for $x\in \left\{0,1\right\}$ and $k^{{}^{\prime }}\ge 1$,

$$\begin{array}{c}P\left(Y_{t+1}\ge k^{{}^{\prime }}|X_t=x\right)\hfill \\ ={\displaystyle \sum _{y\in \left\{0,1\right\}}}P\left(Y_{t+2}\ge k^{{}^{\prime }}-y,X_{t+1}=y|X_t=x\right)\hfill \\ =P\left(Y_{t+2}\ge k^{{}^{\prime }}|X_{t+1}=0\right)\times P\left(X_{t+1}=0|X_t=x\right)\hfill \\ +P\left(Y_{t+2}\ge k^{{}^{\prime }}-1|X_{t+1}=1\right)\times P\left(X_{t+1}=1|X_t=x\right)\hfill \end{array}$$

(14)

and $P\left(Y_n\ge k^{{}^{\prime }}|X_{n-1}=x\right)$ is provided by

$$\begin{array}{c}\hfill P\left(Y_n\ge k^{{}^{\prime }}|X_{n-1}=x\right)=\left\{\begin{array}{c}1\\ P\left(1|x\right)\\ 0\end{array}\right.\begin{array}{c}{k}^{{}^{\prime }}=0,\\ k^{{}^{\prime }}=1,\\ otherwise.\end{array}\hfill \end{array}$$

(15)

2.1.4. The Complete PLSD Algorithm

The complete PLSD algorithm is shown in Algorithm 2 with reference to [21,28]. Status determines that pixels are assigned to one unique line-support region within SRMSD, which is the key to ensuring that the algorithm completes in linear time.

Algorithm 2 PLSD

Require:  An image I; Speckle suppression parameter $\rho$; the angle tolerance $\mu$; the strength tolerance $\eta$; the NFA threshold $ϵ$ and the density threshold D. Ensure:  A list of line segment L. 1: Initialization: Apply the CFAR edge detector with parameter $\rho$ on the input image to obtain the gradient strength map $G_s$ and the gradient direction map $G_d$. Compute $OrderedList$, sorting the pixels of I in descending order according to gradient strength. Define $Status$, All($Status$) ← Not Used. 2: for pixel P (x, y) in OrderedList do 3:    region ← SRMSD(P (x, y), $G_s$, $G_d$, $\mu$, $\eta$, Status); 4:    rect ← Rectangle(region); 5:    while AlignedPixelDensity(rect, $\mu$) < D do 6:      region ← Refine(region); 7:      rect ← Rectangle(region); 8:    end while 9:    nfa ← NFA(rect); 10:    if nfa<$ϵ$ then 11:      ADD rect to L; 12:      Status(region) ← Used; 13:    else 14:      region ← Not Used; 15:    end if 16: end for 17: return L;

2.2. PLSD-Based Airport Detection on PolSAR Images

One possible application of line segment detection is airport detection, because the edges of runways appear as line segments on the image. It is extensively used for pre-processing of aircraft detection [39,40]. In addition to the ability to form line segments, a priori knowledge that surface scattering is the dominant scattering mechanism in the airport region can help to detect the airport. Based on the line segment detector and scattering characteristics, we design a new large scene airport detection method.

The airport detection method is divided into two steps. In the first stage, Yamaguchi four-component-based Fuzzy C-Means (Y-FCM) is utilized to acquire the airport Region Of Interest (ROI). In the second stage, the precise airport region is obtained by PLSD to validate the airport ROI. Figure 7 shows the flowchart of the airport detection method.

Figure 7. Flowchart of the airport detection method. ⊕ means take the intersection. Red rectangles mark the airport region.

(1) Y-FCM: We apply the Yamaguchi four-component decomposition [41] to the PolSAR data. Four scattering components are obtained, i.e., the surface scattering component ($P_S$), the double-bounce scattering component ($P_D$), the volume scattering component ($P_V$), and the helix scattering component ($P_H$). Different terrains have different polarization scattering properties. The main scattering mechanism of the runway is surface scattering, as it has a moderately rough surface. Fuzzy C-Means (FCM) [42], as a soft clustering algorithm, allows each sample to belong to multiple classes with varying degrees of membership. Moreover, as FCM is more robust to the selection of initial clustering centers, excellent clustering results can be obtained. With $\left[P_S,P_D,P_V,P_H\right]$ as the characteristic of each pixel, FCM is utilized to classify the pixels with different scattering. The Y-FCM is implemented as described below.

Set the number of class m and the initial cluster centers $\overrightarrow{c_j}\left(j=1,2,3\dots ,m\right)$. To reduce the subsequent computational complexity, m can be set to a larger value. In our experiments, m is set to 15. The initial clustering centers are obtained by taking a random choice.

Then, the degree of membership $u_{ij}$ of pixel $x_i$ and the j-th class is calculated based on $\left[P_S,P_D,P_V,P_H\right]$:

$$u_{ij}=\frac{\frac{1}{\left|\right|x_i-c_j{\left|\right|}_2^2}}{{\displaystyle \sum _{j=1}^m}\frac{1}{\left|\right|x_i-c_j{\left|\right|}_2^2}}$$

(16)

After each iteration, the cluster centers need to be updated, as follows:

$$\overrightarrow{c_j}=\frac{{\displaystyle \sum _{i=1}^N}{u}_{ij}^2\times \overrightarrow{x_i}}{{\displaystyle \sum _{i=1}^N}{u}_{ij}^2}$$

(17)

Considering the small sum of $P_D$, $P_V$, and $P_H$ in the runway, we take the class with the smallest sum of $P_D$, $P_V$, and $P_H$ as the ROI for subsequent detection. It is worth noting that Y-FCM performs only one iteration to obtain the accurate ROI.

(2) PLSD: Next, PLSD is performed to acquire line segments in the PolSAR images. To test the parallelism of the line segments, we define the rule for parallel lines according to [43]. Suppose the line segments L and S consist of the point sets $\left\{L_x,x=1,\dots ,N_L\right\}$ and $\left\{S_x,x=1,\dots ,N_S\right\}$, respectively, with $D_L$ and $D_S$ being their angles. If L and S are parallel, they must first satisfy the angle similarity condition, i.e., $⟨D_L,D_S⟩<An{g}_{thred}$. Furthermore, for each point $L_i$ on the line segment L, we must find the line P that passes through $L_i$ and is perpendicular to L. If P intersects S at $S_i$, we find the Euclidean distance $di{s}_i$ between $L_i$ and $S_i$ and obtain the average value dis of the distance set $\left\{di{s}_x,x=1,\dots ,N_L\right\}$. The percentage of points in the set $\left\{di{s}_x,x=1,\dots ,N_L\right\}$ smaller than dis$di{s}_x$ is $Pe{r}_L$. The proportion $Pe{r}_S$ can be obtained in the same way. If both $Pe{r}_L$ and $Pe{r}_S$ are smaller than the threshold $Pe{r}_{thred}$, the line segments L and S are considered parallel. In our experiments, we set $An{g}_{thred}$ = 3° and $Pe{r}_{thred}$ = 0.7.

Finally, the ROI is validated by line segments. A region is considered an airport region if there are parallel line segments within the ROI.

3. Result

In this section, the results of our proposed algorithms and other comparative methods are reported for PolSAR images. First, the PolSAR datasets are presented, followed by the performance comparison of different methods and in-depth analysis of SRMSD. Finally, the applicability of the line segment detection method is demonstrated based on airport detection.

3.1. Datasets

Here, we choose three pieces of PolSAR data to demonstrate the effectiveness of our proposed algorithm, consisting of a river, a road, and an airport, as shown in Figure 8. The PolSAR data were provided by the UAVSAR project. They are acquired in L-band with an azimuth resolution of 4.9 m and a range resolution of 7.2 m, and are based on a four-look GRD product. More detailed information on the data is listed in Table 1.

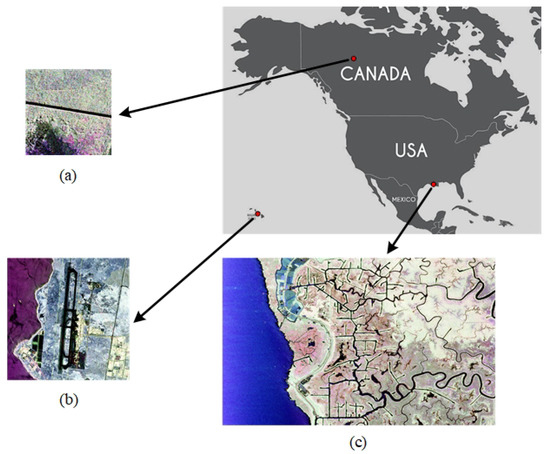
Figure 8. PauliRGB images of the three PolSAR data. (a) Simple road area. (b) Kona airport. (c) Complex river area.

Table 1. Descriptions of three PolSAR data items for line detection.

Image	Size (Pixel)	Acquisition Date	Location
Figure 8a	$300\times 300$	September 2017	Fort Smith, Canada
Figure 8b	$700\times 700$	January 2012	Hawaii Island, America
Figure 8c	$2281\times 1400$	May 2015	Calumet, Louisiana, America

Figure 8a is of a short road in Fort Smith, Canada with a simple background. Figure 8b shows the Kona airport, located on Hawaii Island, America. The difference between the runway of the airport and the surrounding environment forms the line segment. Figure 8c is an area located in Calumet, Louisiana, America, containing a river with a well-defined edge. The complexity of its scenarios poses a considerable challenge to the line segment detector.

3.2. Comparison of Line Segment Detection Algorithms

In this subsection, we compare the line segment detection results of six methods, i.e., LSD [21], EDLines [22], Linelet-LSD [23], LSDSAR [28], HT [15], and our proposed method. The parameter settings of comparison methods are set as optimal values according to independently experiments with ten times for each image. Note that all the methods are implemented using the MATLAB language on a PC with a 2.6-GHz i5 CPU.

Figure 9 presents the line segment detection results of different methods for Figure 8a,b. The first and third rows show the detection results on the PauliRGB image, and the results on the solid color background are shown in the second and fourth rows. Figure 9a shows the results of LSD, where we can see that most of the detected line segments are locate in the region of gradient variation. Nevertheless, there are errors of miss detection, such as parts of roads and runways. Figure 9b,e suffers from the same errors of line segment miss detection. In addition, they over-cut the line segments into small line segments. The results in Figure 9c demonstrate that the Linelet-LSD method can effectively detect more line segments. However, it generates more false alarms as well, and appears to engage in serious over-cutting of the line segments. The results of LSDSAR depicted in Figure 9d seem better than all of the former methods, with most of the line segments detected well and with fewer over-cutting errors. Nevertheless, the most serious false alarms appear in these results, and line segments even appear in the ocean. Figure 9f shows the results of our proposed method; it can be observed that it finds a better tradeoff between accurate detection of line segments and removal of false alarms.

Figure 9. Line segment detection results of different methods for PolSAR image. (a) LSD. (b) EDLines. (c) Linelet-LSD. (d) LSDSAR. (e) HT. (f) PLSD.

In addition, the number of line segments and the time cost of the different methods are provided in Table 2. It can be seen that our line segment detector has the best detection performance, and the detection time is lower than most of the others.

Table 2. Line segment detection results.

Method	Image	Number of Line Segments	Times (s)
LSD	Figure 8c Figure 8b Figure 8a	319 26 1	4145.76 60.12 0.85
EDLines	Figure 8c Figure 8b Figure 8a	728 152 9	46.29 8.54 2.12
Linelet-LSD	Figure 8c Figure 8b Figure 8a	4782 580 33	15,007.67 211.27 8.31
LSDSAR	Figure 8c Figure 8b Figure 8a	2663 442 52	8.84 1.74 0.28
HT	Figure 8c Figure 8b Figure 8a	62 69 6	0.11 0.05 0.04
PLSD	Figure 8c Figure 8b Figure 8a	538 49 2	6.69 1.52 0.27

The detection performance of LSD, Linelet-LSD, LSDSAR, and PLSD in complex scenarios is discussed below. Figure 10 shows the line segment detection results of the four methods in a complex scenario. From Figure 10a,b, it can be seen that when using the LSD, there are many obvious line segment regions missed in the results, although most of the detected line segments are correct (for example, the regions marked by red circles in Figure 10a,b). This indicates that the edge detection method of LSD, i.e., the difference method, is not well adapted to PolSAR images. The results of Linelet-LSD in Figure 10c,d seem to detect more line segments. Nevertheless, the over-cutting of line segments is very serious, as Linelet-LSD detects Linelets (short line segments) in horizontal or vertical directions and forms line segments by aggregating them. Figure 10e,f shows the result of the LSDSAR method, where it can be seen that most of the line segments can be correctly discriminated with fewer over-cutting results than LSD and Linelet-LSD. However, in the homogeneous region the detection result is not very satisfactory, as there exist a large number of false alarms. In addition, line segments are detected in curved regions. The detection results of our proposed approach are shown in Figure 10g,h, where it can be seen that both false alarms and over-cutting are well controlled. The reason for this is that our proposed method both considers the statistical model of the distribution in PolSAR images and utilizes the a contrario approach to validate the line-support region. More importantly, we incorporate both the direction and strength information of the gradient into the SRM, resulting in more accurate detection of line-support regions with less over-cutting than other methods. Therefore, it can be demonstrated that our method outperforms the other three methods in terms of the ability to the preservation of complete line segments and elimination of false alarms.

Figure 10. Line segment detection results of different methods in complex scenarios. (a,b) LSD. (c,d) Linelet-LSD. (e,f) LSDSAR. (g,h) PLSD. Red circle: obvious line areas missed in the results.

3.3. In-Depth Analysis of the SRMSD

In this subsection, we focus on the performance improvement introduced by the addition of gradient strength. Figure 11a,b shows the results of line segment detection with and without strength information, respectively. Figure 11c,e shows the enlarged results of the two selected areas marked with red rectangles in Figure 11a,b. What we can observe from Figure 11a,b is that the addition of strength information removes false alarms. Most of the removed line segments exist in the interior of the river, as shown in Figure 11e,f. Due to the fact that the gradient calculation with filter-based methods generates interference points at the pixel mutations, they have similar gradient directions to the edge points, making SRM by the gradient direction alone unable to distinguish the edge points from the interference points. A large number of line segments appear in between the rivers that are expected to not appear, as shown in Figure 11e. In comparison, our method considers the gradient strength, separating the edge points from the interference points. Therefore, the line segment in the middle of the river is removed, as shown in Figure 11c.

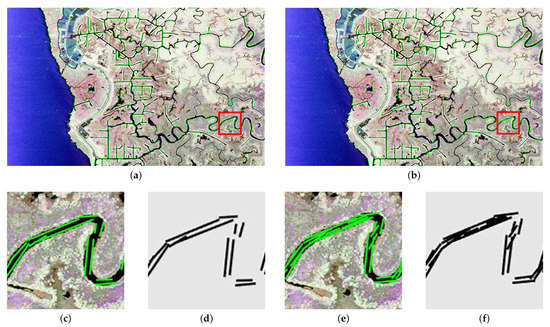
Figure 11. Enhancement of gradient strength. (a) With gradient strength. (b) Without gradient strength. (c,d) Enlarged results of the red rectangular areas in (a). (e,f) Enlarged results of the red rectangular areas in (b).

To further evaluate the effect of gradient strength addition, Table 3 displays the statistics on the detection results for both cases. It can be seen that the difference in detection time between the two cases is not significant. Therefore, the incorporation of gradient strength imposes almost no additional time burden on the algorithm. Meanwhile, the addition of strength information reduces the number of incorrect line segments. Furthermore, the line segments in Figure 11a have a smaller average width than thoes in Figure 11b, demonstrating the superiority of our new SRMSD algorithm.

Table 3. Comparison of results with and without gradient strength.

	Number of Line Segments	Average Width of Line Segments (Pixel)	Time (s)
With strength	538	4.8753	6.48
Without strength	575	5.7394	6.41

The histograms of the line-width obtained by the line segment detector with and without strength information are shown in Figure 12a,b, respectively. It can be seen that the width of the line segment is concentrated between four and five after the incorporation of the strength information. In comparison, the width of the line segment without strength information is more apparent in [5,6]. Furthermore, the number of line segments in Figure 12a is lower than in Figure 12b when the width of the line segments exceeds 5, demonstrating the effectiveness of the incorporated strength information.

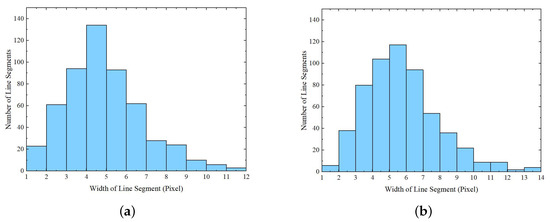
Figure 12. Statistics on line segment width. (a) With strength information. (b) Without strength information.

3.4. Comparison of Airport Detection Methods

Four PolSAR images were used to demonstrate the effectiveness of our airport detection method. The images are L-band GRD products provided by the UAVSAR project. Details are shown in Table 4. The airports are located in mountainous, seaside, and urban areas.

Table 4. Description of the data for airport detection.

Name	Image Size (Pixel)	Airport Size (Pixel)	Acquisition Data	Location
Coldfoot Airport	4297 × 2697	249 × 214	10/2015	Coldfoot, America
Perales Airport	4164 × 2878	136 × 427	04/2014	Ibague, Colombia
Kona Airport	3195 × 2141	658 × 177	01/2012	Hawaii Island, America
Changuinola Airport	3086 × 2162	55 × 187	02/2010	Changuinola, Panama

In order to demonstrate the effectiveness of our method, we compared it with CSA-SOACM [44]. CSA-SOACM utilizes local contrast to obtain the airport ROI; then, the ROI is examined by line segments. Finally, the airport contour is refined in the airport area with Active Contour Model (ACM). Furthermore, we replaced PLSD with other line segment detectors. However, LSD and Linelet-LSD are difficult to apply to airport detection in large scenarios due to heavy time consumption. Meanwhile, owing to the poor results of EDLines and HT for line segment detection, all airport targets were lost. Only LSDSAR-based airport detection (LSDSAR-AD) was able to achieve promising detection results.

Figure 13 presents the results of airport detection. The airport areas are marked with a red rectangle. It can be seen that our method accurately detects the airports. CSA-SOACM shows false alarms and incomplete detection. This because of the CSA-SOACM not utilizing the polarization information of PolSAR data as well as due to for its inaccurate line segment detection. Although two airports are detected by LSDSAR-AD, a large number of false alarms occur. This can be attributed to the result of line segment detection by LSDSAR. LSDSAR detects a large number of line segments in homogeneous regions, leading to the false alarms.

Figure 13. Comparison of airport detection results. (a) Ours. (b) CSA-SOACM. (c) LSDSAR-AD.

The results of airport detection prove the superiority of PLSD and demonstrate the applicability of line segment detection.

4. Discussion

This section discusses the parameter settings and algorithmic complexity of PLSD. First, the effects of different free parameter settings are analyzed and the optimal parameters determined on our dataset are provided, followed by analysis of the algorithm’s complexity.

4.1. Parameter Settings

There are five parameters in PLSD: the speckle suppression parameter $\rho$, angle tolerance $\mu$, strength tolerance $\eta$, NFA threshold $ϵ$, and density threshold D; $\rho$ is used to control the size of the filter for the gradient calculation. Increasing the value of $\rho$ helps to suppress the speckle, providing more accurate gradient calculation results; in turn, however, it increases the number of interference points. According to our experiments, we find that setting $\rho$ to 4 provides the best performance in most scenarios. However, it may not be able to distinguish line segments that are very close to each other, such as the river branches in Figure 8c. Setting $\rho$ to a smaller value, e.g., 2, can solve this problem. Here, $\mu$ and $\eta$ are the angle tolerance and strength tolerance used in the search for line-support regions, respectively. A small value is more restrictive, leading to over-cutting of line segments. A large value leads to the merging of unrelated pixels, resulting in large regions. We set $\mu$ to 22.5 according to [45], and obtained good results. For the selection of $\eta$, we analyzed the gradient strength obtained by $\rho$ at different values, as shown in Figure 14. We chose two rows of the PauliRGB image; the strength profiles are displayed in Figure 14a. Although the value of $\rho$ is different, the gradient strength always shows a large drop somewhere, owing to the filter deviating from the pixel mutation. The points are marked in Figure 14b–f with green dotted lines, with the gradient strength showing a large decrease. With $\eta$ set to 3, the edge points (points inside the dotted line) and interference points (points outside the dotted line) are well distinguished. Similar to other contrario approaches, the NFA threshold $ϵ$ represents an upper bound on the average number of detections that we allow in a pure noise image. Usually, setting it to 1 yields good performance. The density threshold D is used to control the density of aligned pixels in the line-support region. During SRMSD, the angle tolerance $\mu$ decreases until the density of aligned pixels in the line-support region is greater than D. The presence of speckles leads to inaccurate gradient direction detection; thus, too large values of D have the effect of over-cutting the line segments into small subsegments, as shown in Figure 15. Therefore, we suggest a value of 0.4 for D, and confirm its validity is in the experiments.

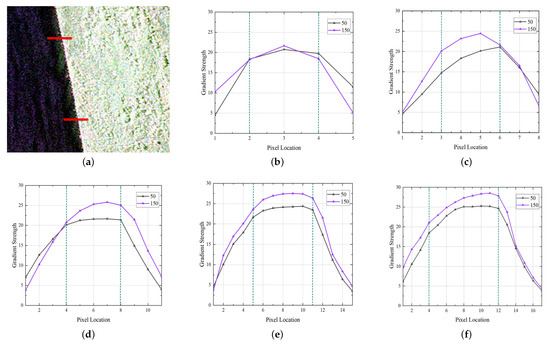
Figure 14. Analytical results for $\mu$ with different $\rho$. (a) PauliRGB Image (red lines represent the pixel locations, which are the 50th and 150th rows, respectively). (b) $\rho$ = 1. (c) $\rho$ = 2. (d) $\rho$ = 3. (e) $\rho$ = 4. (f) $\rho$ = 5.

Figure 15. Line segment detection results for different values of D. (a) D = 0.4. (b) D = 0.8.

Unless explicitly mentioned, we use the default setting $\rho$ = 4, $\mu$ = 22.5°, $\eta$ = 3, $ϵ$ = 1, and D = 0.4 in our proposed algorithm.

4.2. Complexity of the PLSD Algorithm

For our proposed algorithm, the computational costs mainly consist of gradient strength and direction acquisition, line-support region generation, and line segment validation. The computation of the gradient strength and direction is proportional to the number of pixels and the size of the filter. Pixel sorting is achieved by bucket sorting, an operation that can be performed in linear time. The computational time of the line-support region generation algorithm is proportional to the number of visited pixels. It is worth noting that no overlap exists between the regions. Thus, the number of visited pixels is proportional to the total number of pixels in the image. The line segment validation can be divided into two tasks, i.e., counting aligned pixels in the line-support region and calculation of NFA. The former is proportional to the total number of pixels involved in all regions. The latter needs to be computed for each region to ensure that it is proportional to the number of regions. Both the number of line-support regions and the total number of pixels involved in the line-support regions are at most equal to the number of pixels. All in all, the execution time of PLSD is proportional to the number of pixels in the image.

5. Conclusions

This paper proposes a fast line segment detection algorithm for PolSAR images. To reduce the time consumption of the CFAR edge detector, a new filter setup is designed. Then, the SRM framework is utilized to quickly find the line-support region. Considering both gradient strength and gradient direction, we design a new similarity measure that effectively suppresses the interference gradient points and makes the line-support region narrower. Finally, according to the Helmholtz principle and a contrario approach, the line-support regions are validated to remove false alarms. Meanwhile, we analyze the free parameters of PLSD and provide a default setting, which achieves satisfactory results in all our experiments. Furthermore, we propose a large scene airport detection method based on PLSD and scattering characteristics. The experimental results demonstrate that PLSD is able to detect line segments more accurately than other line segment detectors while effectively controlling time consumption in large scenes.

To a certain extent, the quality of the edge detector determines the accuracy of subsequent line segment detection. In future research, we plan to modify the filter shape and distribution probability model of the edge detection algorithm to achieve more accurate line segment detection in heterogeneous regions. Moreover, we intend to reduce the computational complexity with the adaptive removal of regions with weak gradient strength before acquiring line segment support regions.