Coherence of Eddy Kinetic Energy Variation during Eddy Life Span to Low-Frequency Ageostrophic Energy
Abstract
1. Introduction
2. Data and Methods
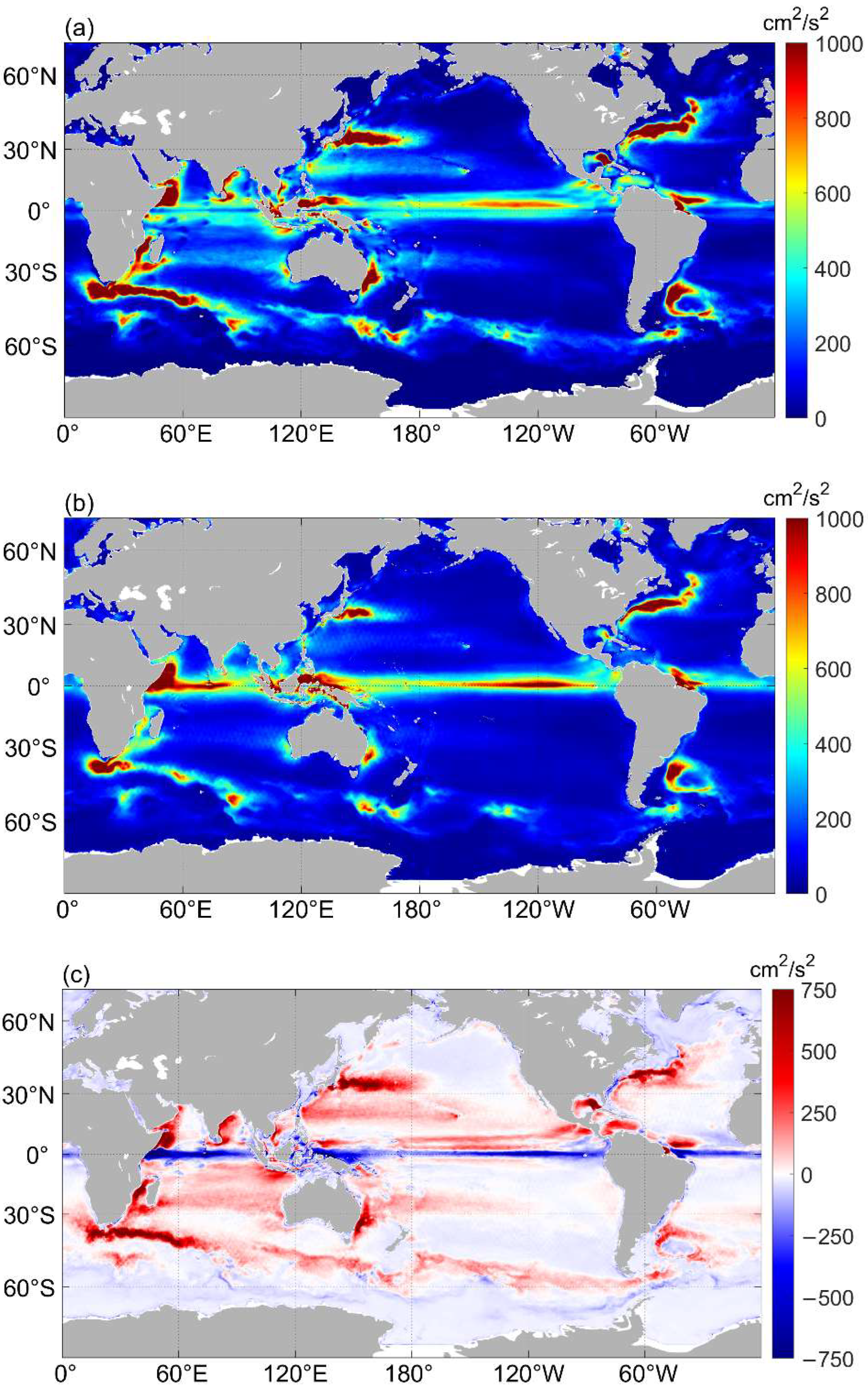
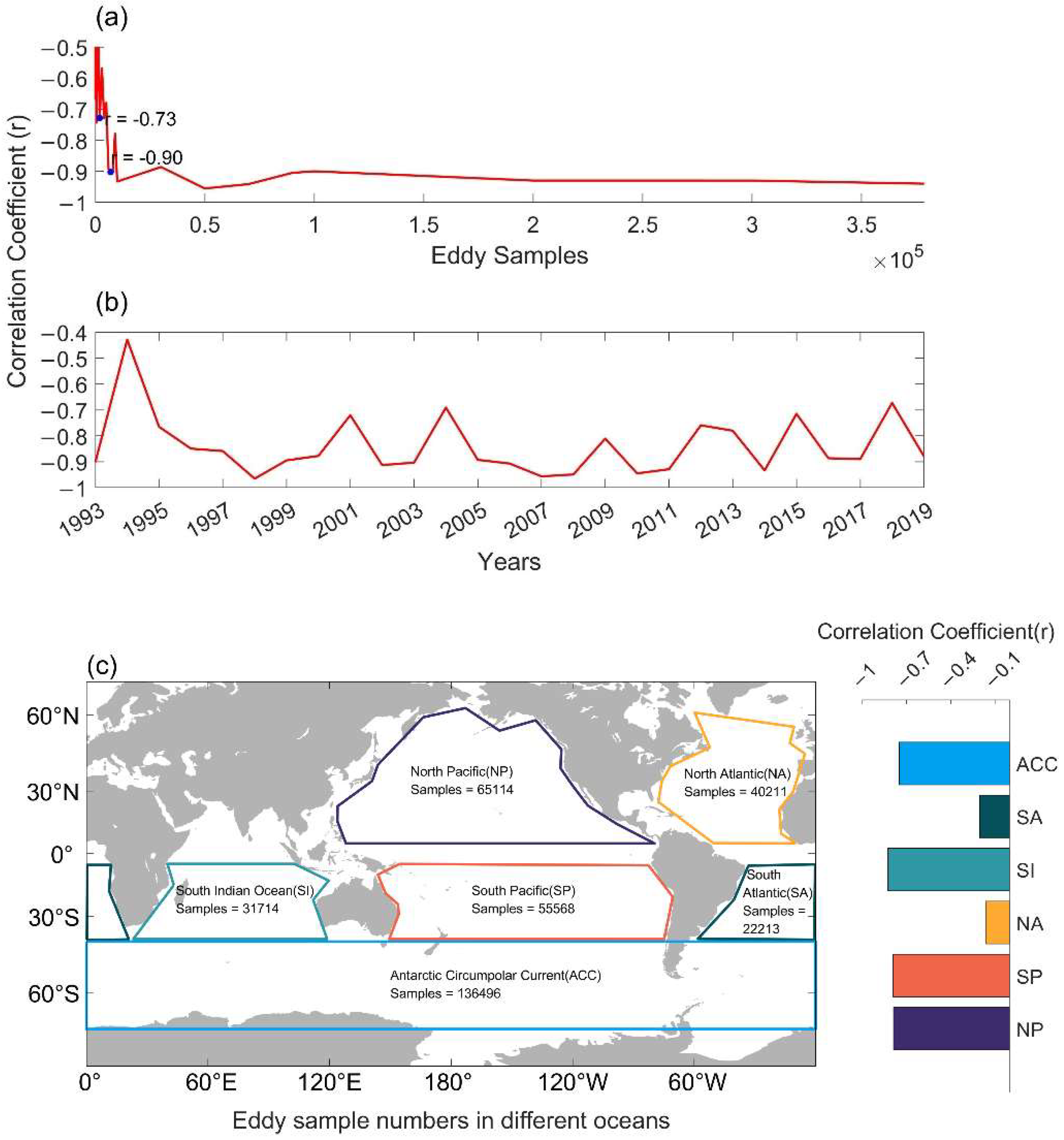
2.1. Satellite Altimetry Data and Eddy Tracking Dataset
2.2. Reanalysis Dataset of Total Current Velocity
2.3. Calculation of Geostrophic and Ageostrophic Kinetic Energy
2.4. Matching Gridded Data and Normalization
3. Results
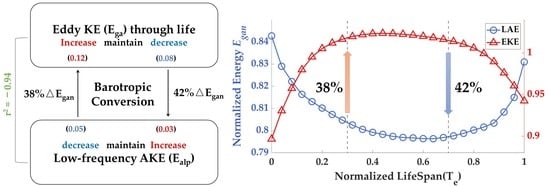
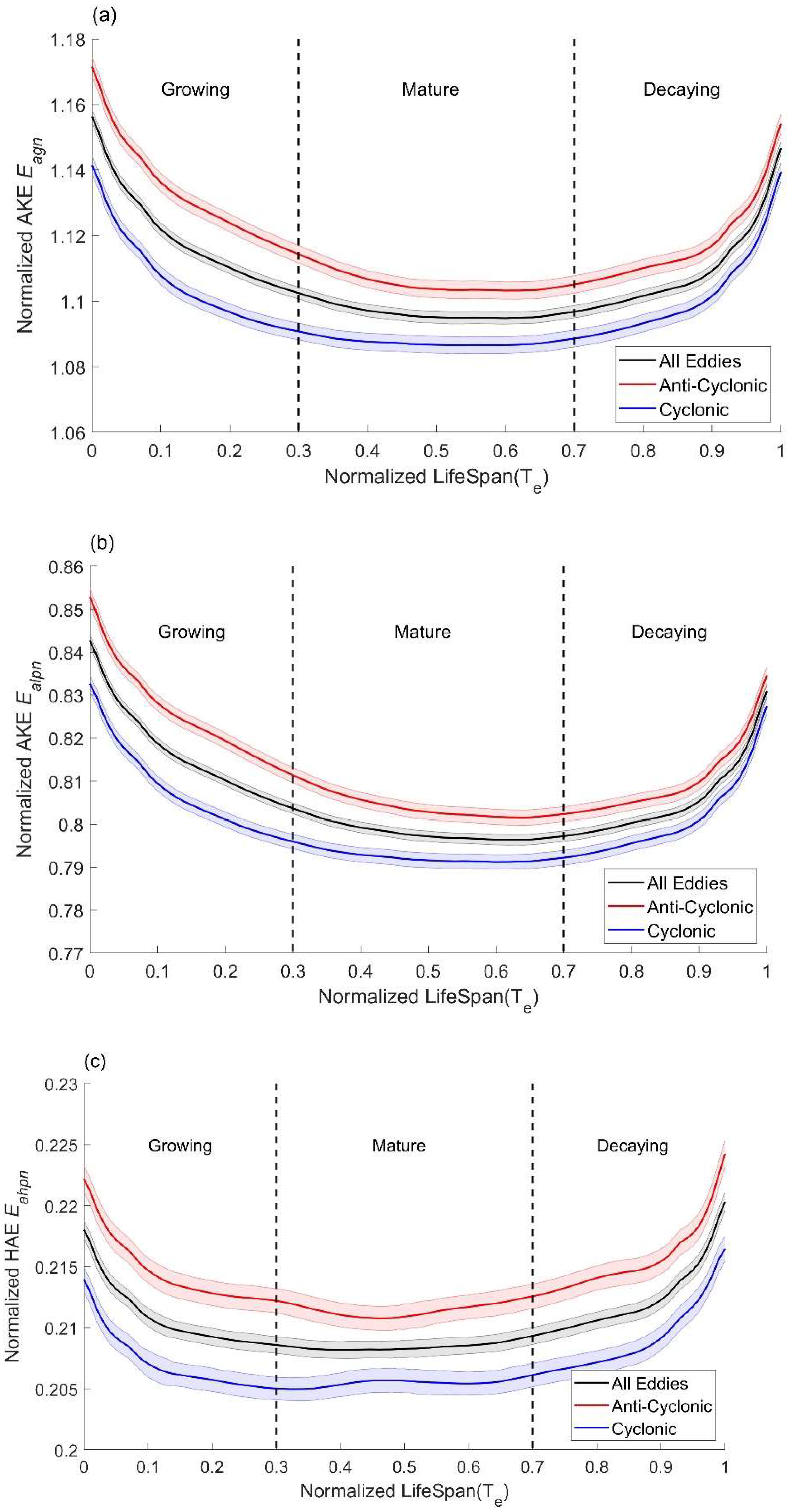
3.1. Eddy Kinetic Energy Variation during Eddy Life Span
3.2. Ageostrophic Kinetic Energy Variation during Eddy Life Span
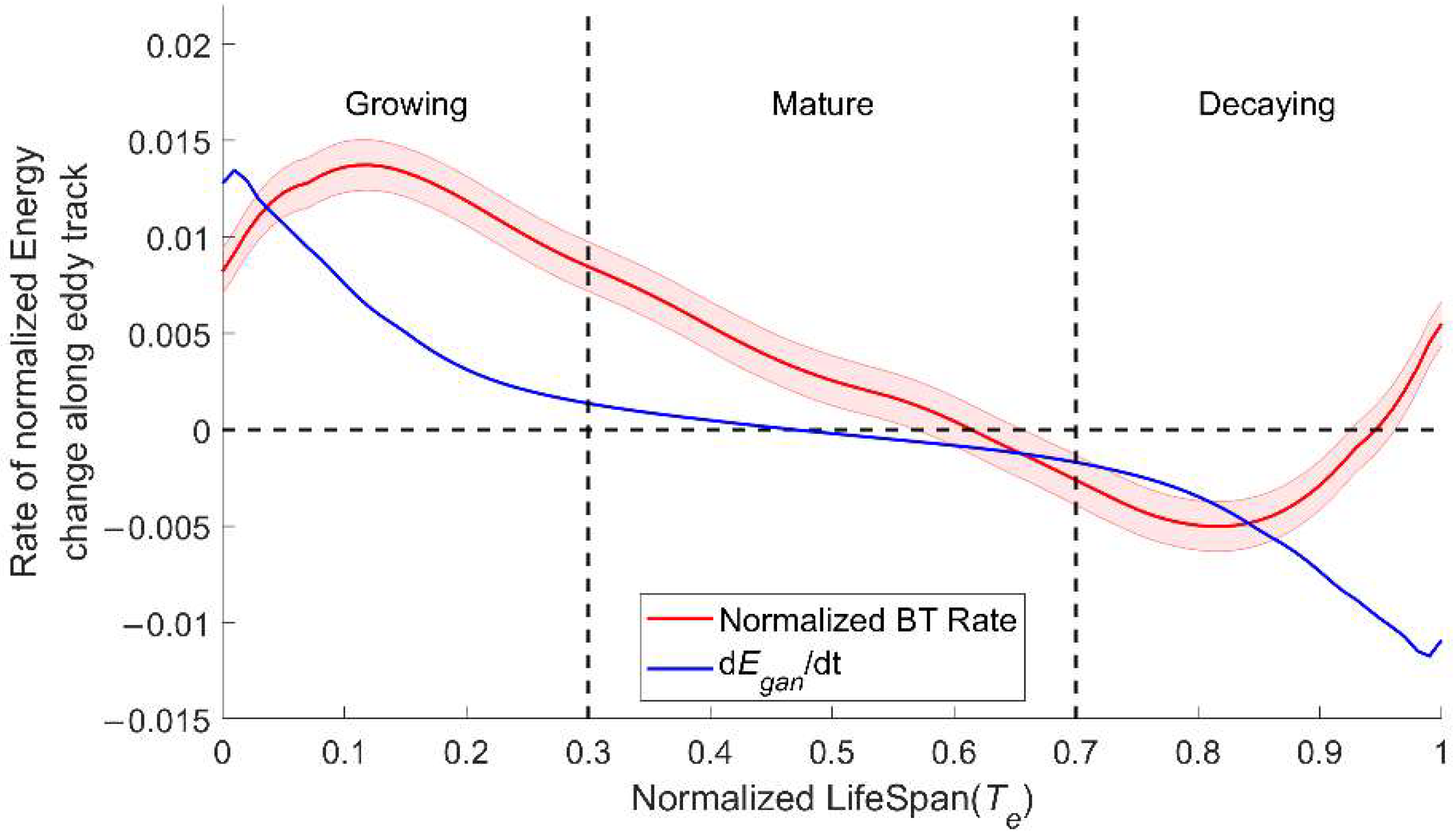
3.3. Analysis of Coherence of EKE Variation to Low-Frequency Ageostrophic Motions
3.4. Barotropic Conversion Rate
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roemmich, D.; Gilson, J. Eddy Transport of Heat and Thermocline Waters in the North Pacific: A Key to Interannual/Decadal Climate Variability? J. Phys. Oceanogr. 2001, 31, 675–687. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global heat and salt transports by eddy movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, W.; Qiu, B. Oceanic mass transport by mesoscale eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Qiu, B.; Klein, P.; Travis, S. The influence of geostrophic strain on oceanic ageostrophic motion and surface chlorophyll. Nat. Commun. 2019, 10, 2838. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.K.; McGillicuddy, D.J., Jr.; Zamudio, L.; Thurnherr, A.M.; Liang, X.; Rouxel, O.; German, C.R.; Mullineaux, L.S. Surface-generated mesoscale eddies transport deep-sea products from hydrothermal vents. Science 2011, 332, 580–583. [Google Scholar] [CrossRef]
- Hausmann, U.; Czaja, A. The observed signature of mesoscale eddies in sea surface temperature and the associated heat transport. Deep Sea Res. Part I Oceanogr. Res. Pap. 2012, 70, 60–72. [Google Scholar] [CrossRef]
- Kamenkovich, I.; Berloff, P.; Haigh, M.; Sun, L.; Lu, Y. Complexity of Mesoscale Eddy Diffusivity in the Ocean. Geophys. Res. Lett. 2021, 48, e2020GL091719. [Google Scholar] [CrossRef]
- Ferrari, R.; Wunsch, C. Ocean Circulation Kinetic Energy: Reservoirs, Sources, and Sinks. Annu. Rev. Fluid Mech. 2009, 41, 253–282. [Google Scholar] [CrossRef]
- Huang, R.X. Ocean Circulation: Wind-Driven and Thermohaline Processes; Cambridge University Press: Cambridge, UK, 2010; p. 195. [Google Scholar]
- Chen, R.; Flierl, G.R.; Wunsch, C. A Description of Local and Nonlocal Eddy–Mean Flow Interaction in a Global Eddy-Permitting State Estimate. J. Phys. Oceanogr. 2014, 44, 2336–2352. [Google Scholar] [CrossRef]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Kang, D.; Curchitser, E.N. Energetics of Eddy–Mean Flow Interactions in the Gulf Stream Region. J. Phys. Oceanogr. 2015, 45, 1103–1120. [Google Scholar] [CrossRef]
- Zhang, Z.; Qiu, B. Evolution of Submesoscale Ageostrophic Motions Through the Life Cycle of Oceanic Mesoscale Eddies. Geophys. Res. Lett. 2018, 45, 11847–11855. [Google Scholar] [CrossRef]
- McWilliams, J.C. Submesoscale currents in the ocean. Proc. Math. Phys. Eng. Sci. 2016, 472, 20160117. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Shang, X.-D.; Huang, R.X. Estimate of eddy energy generation/dissipation rate in the world ocean from altimetry data. Ocean Dyn. 2011, 61, 525–541. [Google Scholar] [CrossRef]
- Yang, Z.; Zhai, X.; Marshall, D.P.; Wang, G. An Idealized Model Study of Eddy Energetics in the Western Boundary “Graveyard”. J. Phys. Oceanogr. 2021, 51, 1265–1282. [Google Scholar] [CrossRef]
- Xu, C.; Zhai, X.; Shang, X.-D. Work done by atmospheric winds on mesoscale ocean eddies. Geophys. Res. Lett. 2016, 43, 12174–112180. [Google Scholar] [CrossRef]
- Chelton, D.B.; Gaube, P.; Schlax, M.G.; Early, J.J.; Samelson, R.M. The influence of nonlinear mesoscale eddies on near-surface oceanic chlorophyll. Science 2011, 334, 328–332. [Google Scholar] [CrossRef]
- Chen, G.; Wang, D.; Hou, Y. The features and interannual variability mechanism of mesoscale eddies in the Bay of Bengal. Cont. Shelf Res. 2012, 47, 178–185. [Google Scholar] [CrossRef]
- Zhai, X.; Marshall, D.P. Vertical Eddy Energy Fluxes in the North Atlantic Subtropical and Subpolar Gyres. J. Phys. Oceanogr. 2013, 43, 95–103. [Google Scholar] [CrossRef]
- Trott, C.B.; Subrahmanyam, B.; Chaigneau, A.; Delcroix, T. Eddy Tracking in the Northwestern Indian Ocean During Southwest Monsoon Regimes. Geophys. Res. Lett. 2018, 45, 6594–6603. [Google Scholar] [CrossRef]
- Zheng, S.; Feng, M.; Du, Y.; Meng, X.; Yu, W. Interannual Variability of Eddy Kinetic Energy in the Subtropical Southeast Indian Ocean Associated With the El Niño-Southern Oscillation. J. Geophys. Res. Ocean. 2018, 123, 1048–1061. [Google Scholar] [CrossRef]
- Li, J.; Roughan, M.; Kerry, C. Dynamics of Interannual Eddy Kinetic Energy Modulations in a Western Boundary Current. Geophys. Res. Lett. 2021, 48, e2021GL094115. [Google Scholar] [CrossRef]
- Chen, S.; Qiu, B. Variability of the Kuroshio Extension Jet, Recirculation Gyre, and Mesoscale Eddies on Decadal Time Scales. J. Phys. Oceanogr. 2005, 35, 2090–2103. [Google Scholar]
- Liu, Y.; Dong, C.; Guan, Y.; Chen, D.; McWilliams, J.; Nencioli, F. Eddy analysis in the subtropical zonal band of the North Pacific Ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 2012, 68, 54–67. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Randomness, Symmetry, and Scaling of Mesoscale Eddy Life Cycles. J. Phys. Oceanogr. 2014, 44, 1012–1029. [Google Scholar]
- Ji, J.; Dong, C.; Zhang, B.; Liu, Y.; Zou, B.; King, G.P.; Xu, G.; Chen, D. Oceanic Eddy Characteristics and Generation Mechanisms in the Kuroshio Extension Region. J. Geophys. Res. Ocean. 2018, 123, 8548–8567. [Google Scholar] [CrossRef]
- Chen, G.; Han, G. Contrasting Short-Lived With Long-Lived Mesoscale Eddies in the Global Ocean. J. Geophys. Res. Ocean. 2019, 124, 3149–3167. [Google Scholar] [CrossRef]
- Huang, R.; Xie, L.; Zheng, Q.; Li, M.; Bai, P.; Tan, K. Statistical analysis of mesoscale eddy propagation velocity in the South China Sea deep basin. Acta Oceanol. Sin. 2021, 39, 91–102. [Google Scholar] [CrossRef]
- Zhai, X.; Johnson, H.L.; Marshall, D.P. Significant sink of ocean-eddy energy near western boundaries. Nat. Geosci. 2010, 3, 608–612. [Google Scholar] [CrossRef]
- Kang, D.; Curchitser, E.N.; Rosati, A. Seasonal Variability of the Gulf Stream Kinetic Energy. J. Phys. Oceanogr. 2016, 46, 1189–1207. [Google Scholar] [CrossRef]
- Macdonald, H.S.; Roughan, M.; Baird, M.E.; Wilkin, J. The formation of a cold-core eddy in the East Australian Current. Cont. Shelf Res. 2016, 114, 72–84. [Google Scholar] [CrossRef]
- Geng, W.; Xie, Q.; Chen, G.; Zu, T.; Wang, D. Numerical study on the eddy–mean flow interaction between a cyclonic eddy and Kuroshio. J. Oceanogr. 2016, 72, 727–745. [Google Scholar] [CrossRef]
- Yang, H.; Wu, L.; Liu, H.; Yu, Y. Eddy energy sources and sinks in the South China Sea. J. Geophys. Res. Ocean. 2013, 118, 4716–4726. [Google Scholar] [CrossRef]
- Pujol, M.-I.; Faugère, Y.; Taburet, G.; Dupuy, S.; Pelloquin, C.; Ablain, M.; Picot, N. DUACS DT2014: The new multi-mission altimeter data set reprocessed over 20 years. Ocean Sci. 2016, 12, 1067–1090. [Google Scholar] [CrossRef]
- Schlax, M.G.; Chelton, D.B. The “Growing Method” of Eddy Identification and Tracking in Two and Three Dimensions; College of Earth, Ocean and Atmospheric Sciences, Oregon State University: Corvallis, OR, USA, 2016; pp. 1–8. Available online: https://www.aviso.altimetry.fr/fileadmin/documents/data/products/value-added/Schlax_Chelton_2016.pdf (accessed on 14 December 2021).
- Thomas, L.N.; Tandon, A.; Mahadevan, A. Submesoscale processes and dynamics. In Ocean Modeling in an Eddying Regime; Geophysical Monograph Series; Wiley-Blackwell Publishing: Hoboken, NJ, USA, 2008; pp. 17–38. [Google Scholar]
- Lévy, M.; Ferrari, R.; Franks, P.J.S.; Martin, A.P.; Rivière, P. Bringing physics to life at the submesoscale. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Colas, F.; Capet, X.; McWilliams, J.C.; Li, Z. Mesoscale Eddy Buoyancy Flux and Eddy-Induced Circulation in Eastern Boundary Currents. J. Phys. Oceanogr. 2013, 43, 1073–1095. [Google Scholar] [CrossRef]
- Stammer, D.; Böning, C.; Dieterich, C. The role of variable wind forcing in generating eddy energy in the North Atlantic. Prog. Oceanogr. 2001, 48, 289–311. [Google Scholar] [CrossRef][Green Version]
- Hogg, A.M.; Meredith, M.P.; Chambers, D.P.; Abrahamsen, E.P.; Hughes, C.W.; Morrison, A.K. Recent trends in the Southern Ocean eddy field. J. Geophys. Res. Ocean. 2015, 120, 257–267. [Google Scholar] [CrossRef]
- Semtner, A.J.; Mintz, Y. Numerical Simulation of the Gulf Stream and Mid-Ocean Eddies. J. Phys. Oceanogr. 1977, 7, 208–230. [Google Scholar] [CrossRef]
- Kundu, P.K.; Cohen, I.M. Fluid Mechanics; Elsevier Science: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Rai, S.; Hecht, M.; Maltrud, M.; Aluie, H. Scale of oceanic eddy killing by wind from global satellite observations. Sci. Adv. 2021, 7, eabf4920. [Google Scholar] [CrossRef]
- Yang, Q.; Nikurashin, M.; Sasaki, H.; Sun, H.; Tian, J. Dissipation of mesoscale eddies and its contribution to mixing in the northern South China Sea. Sci. Rep. 2019, 9, 556. [Google Scholar] [CrossRef] [PubMed]
- Jan, S.; Mensah, V.; Andres, M.; Chang, M.H.; Yang, Y.J. Eddy-Kuroshio Interactions: Local and Remote Effects. J. Geophys. Res. Ocean. 2017, 122, 9744–9764. [Google Scholar] [CrossRef]
- Chern, C.-S.; Wang, J. Interactions of Mesoscale Eddy and Western Boundary Current: A Reduced-Gravity Numerical Model Study. J. Oceanogr. 2005, 61, 271–282. [Google Scholar] [CrossRef]
- Kuo, Y.-C.; Tseng, Y.-H. Influence of anomalous low-level circulation on the Kuroshio in the Luzon Strait during ENSO. Ocean Model. 2021, 159, 101759. [Google Scholar] [CrossRef]
- Langlais, C.E.; Rintoul, S.R.; Zika, J.D. Sensitivity of Antarctic Circumpolar Current Transport and Eddy Activity to Wind Patterns in the Southern Ocean. J. Phys. Oceanogr. 2015, 45, 1051–1067. [Google Scholar] [CrossRef]
- Zhang, N.; Liu, G.; Liu, Q.; Zheng, S.; Perrie, W. Spatiotemporal Variations of Mesoscale Eddies in the Southeast Indian Ocean. J. Geophys. Res. Ocean. 2020, 125, e2019JC015712. [Google Scholar] [CrossRef]
- Ayouche, A.; De Marez, C.; Morvan, M.; L’Hegaret, P.; Carton, X.; Le Vu, B.; Stegner, A. Structure and Dynamics of the Ras al Hadd Oceanic Dipole in the Arabian Sea. Oceans 2021, 2, 105–125. [Google Scholar] [CrossRef]
- Gnevyshev, V.G.; Malysheva, A.A.; Belonenko, T.V.; Koldunov, A.V. On Agulhas eddies and Rossby waves travelling by forcing effects. Russ. J. Earth Sci. 2021, 21, 3. [Google Scholar] [CrossRef]
- Laxenaire, R.; Speich, S.; Blanke, B.; Chaigneau, A.; Pegliasco, C.; Stegner, A. Anticyclonic Eddies Connecting the Western Boundaries of Indian and Atlantic Oceans. J. Geophys. Res. Ocean. 2018, 123, 7651–7677. [Google Scholar] [CrossRef]
- Keppler, L.; Cravatte, S.; Chaigneau, A.; Pegliasco, C.; Gourdeau, L.; Singh, A. Observed Characteristics and Vertical Structure of Mesoscale Eddies in the Southwest Tropical Pacific. J. Geophys. Res. Ocean. 2018, 123, 2731–2756. [Google Scholar] [CrossRef]
- Errico, R.M. The Strong Effects of Non-Quasigeostrophic Dynamic Processes on Atmospheric Energy Spectra. J. Atmos. Sci. 1982, 39, 961–968. [Google Scholar]
- Straub, D.N.; Bartello, P.; Ngan, K. Dissipation of Synoptic-Scale Flow by Small-Scale Turbulence. J. Atmos. Sci. 2008, 65, 766–791. [Google Scholar]


| All | AEs | CEs | |
|---|---|---|---|
| Eddy number | 378,513 | 185,937 | 192,577 |
| Eddy radius (km) median (mean ± std) | 74.20 (82.33 ± 35.93) | 74.95 (83.13 ± 36.23) | 73.45 (81.53 ± 35.60) |
| Eddy lifespan (day) median (mean ± std) | 51.00 (73.38 ± 66.40) | 51.00 (74.43 ± 69.62) | 51.00 (72.60 ± 63.33) |
| Egn | Ean | Ealpn | Eahpn | |
|---|---|---|---|---|
| Growing stage | 0.12 (100%) | −0.07 (57%) | −0.05 (38%) | −0.01 (8%) |
| Decaying stage | −0.08 (100%) | 0.06 (75%) | 0.03 (42%) | 0.01 (15%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Xie, L.; Zheng, Q.; Li, M.; Li, J.; Li, M. Coherence of Eddy Kinetic Energy Variation during Eddy Life Span to Low-Frequency Ageostrophic Energy. Remote Sens. 2022, 14, 3793. https://doi.org/10.3390/rs14153793
Zhang Z, Xie L, Zheng Q, Li M, Li J, Li M. Coherence of Eddy Kinetic Energy Variation during Eddy Life Span to Low-Frequency Ageostrophic Energy. Remote Sensing. 2022; 14(15):3793. https://doi.org/10.3390/rs14153793
Chicago/Turabian StyleZhang, Zhisheng, Lingling Xie, Quanan Zheng, Mingming Li, Junyi Li, and Min Li. 2022. "Coherence of Eddy Kinetic Energy Variation during Eddy Life Span to Low-Frequency Ageostrophic Energy" Remote Sensing 14, no. 15: 3793. https://doi.org/10.3390/rs14153793
APA StyleZhang, Z., Xie, L., Zheng, Q., Li, M., Li, J., & Li, M. (2022). Coherence of Eddy Kinetic Energy Variation during Eddy Life Span to Low-Frequency Ageostrophic Energy. Remote Sensing, 14(15), 3793. https://doi.org/10.3390/rs14153793