Direction of Arrival Estimation of Acoustic Sources with Unmanned Underwater Vehicle Swarm via Matrix Completion
Abstract
:1. Introduction
1.1. Direction of Arrival Estimation of Acoustic Sources
1.2. Underwater Unmanned Vehicle Swarm (UUVS)
1.3. Challenges of UUVS DOA Estimation
1.4. Contributions of This Work
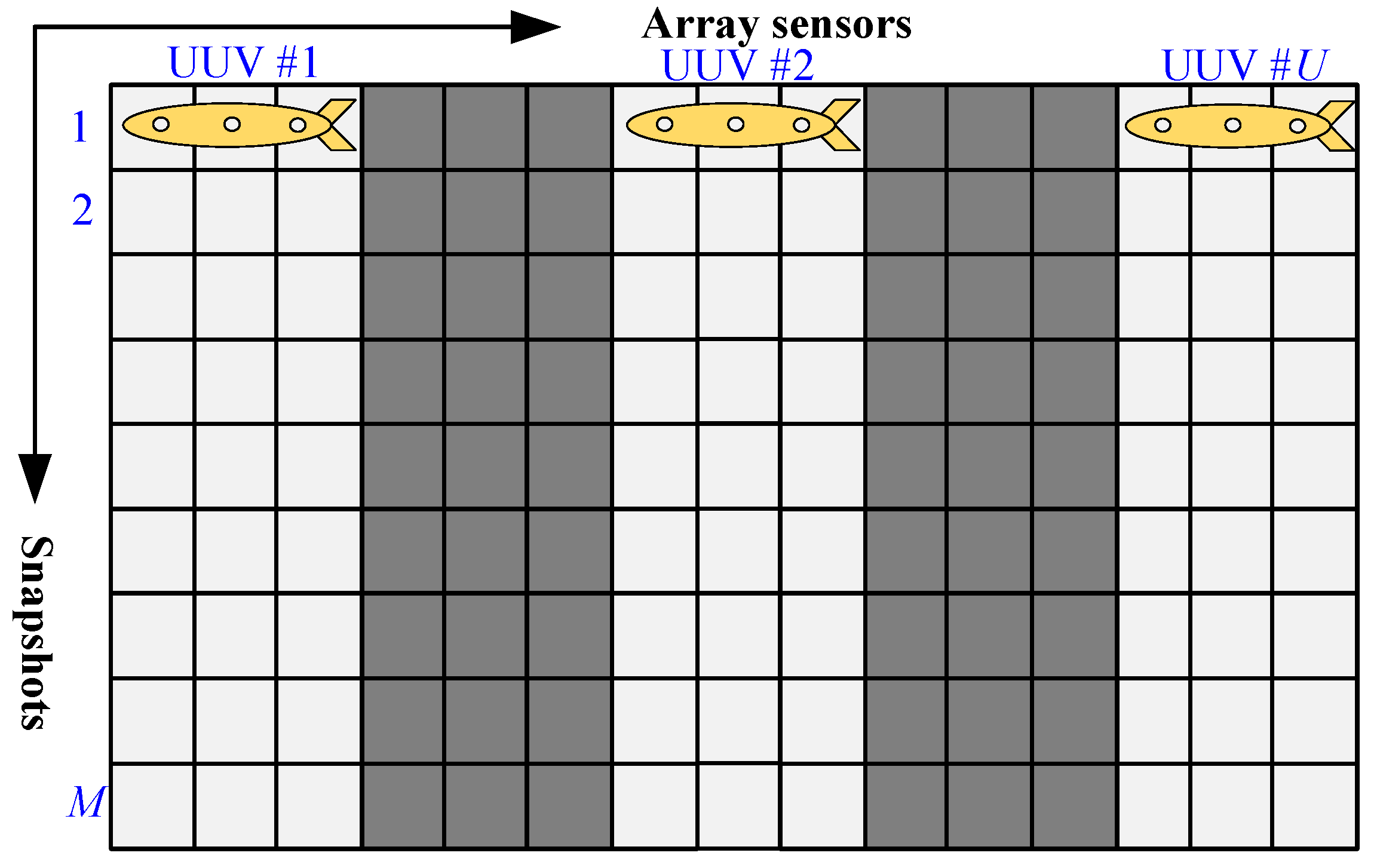
2. UUVS DOA Estimation via Structured MC
2.1. UUVS Array Signal Model
2.2. UUVS Array Data Recovery via MC
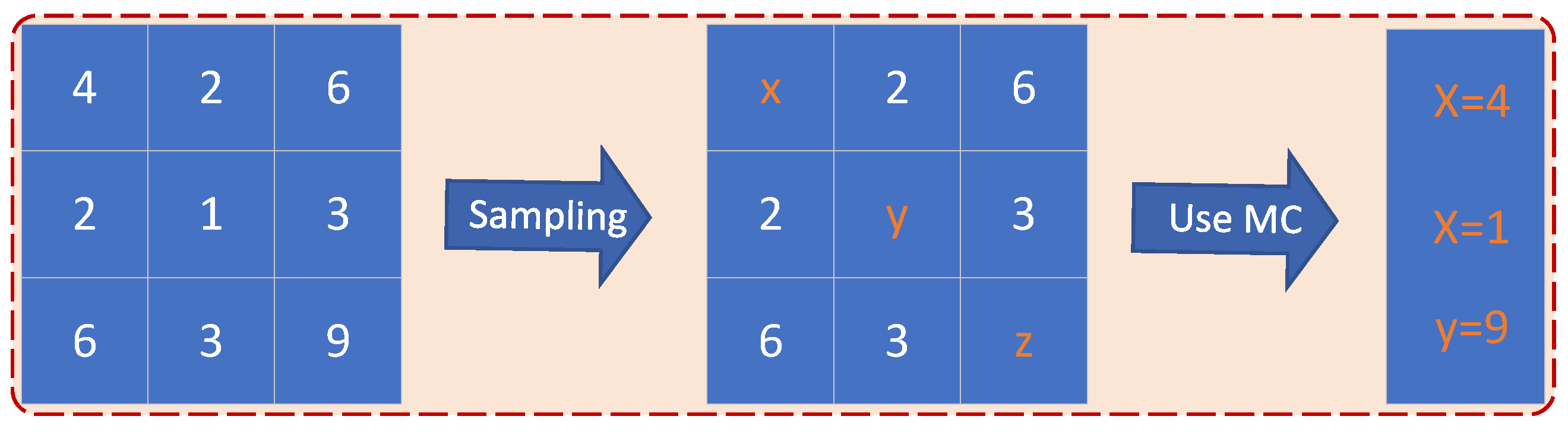
2.2.1. Preliminaries of MC
2.2.2. UUVS Array Data Pre-Processing
2.2.3. UUVS Array Data Recovery via Structured MC
2.3. DOA Estimation Based on Recovered Data Matrix
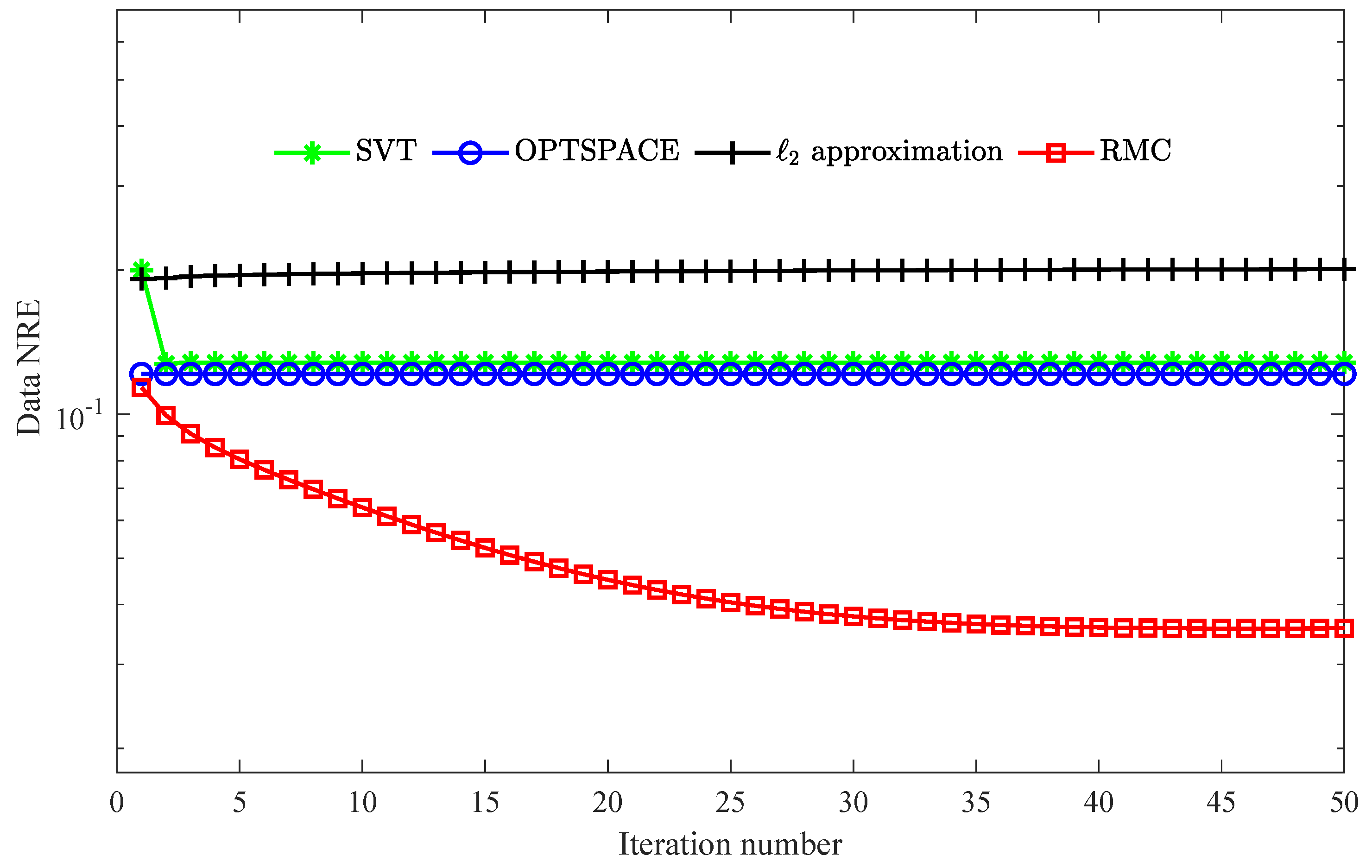
3. Numerical Results
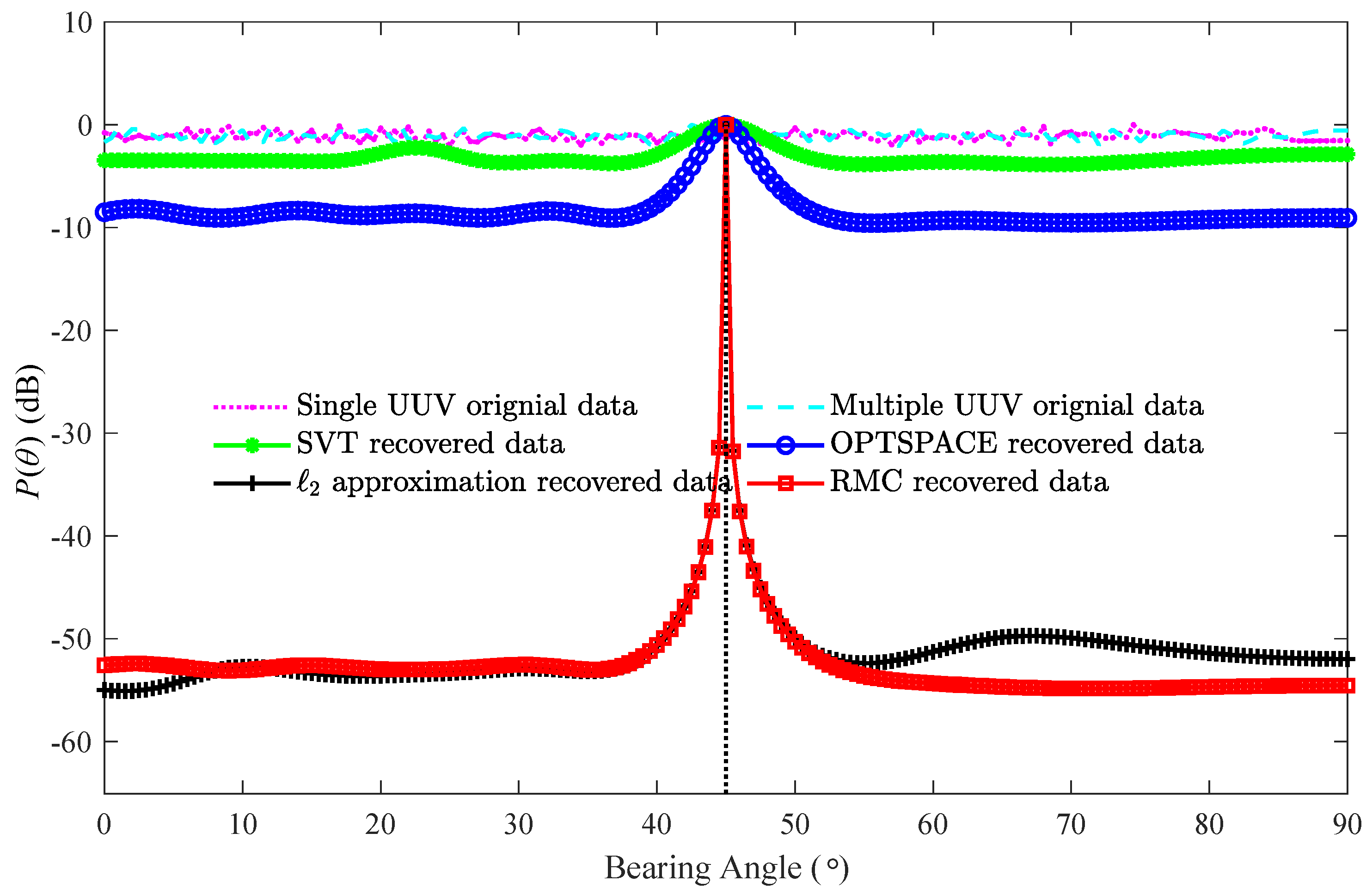
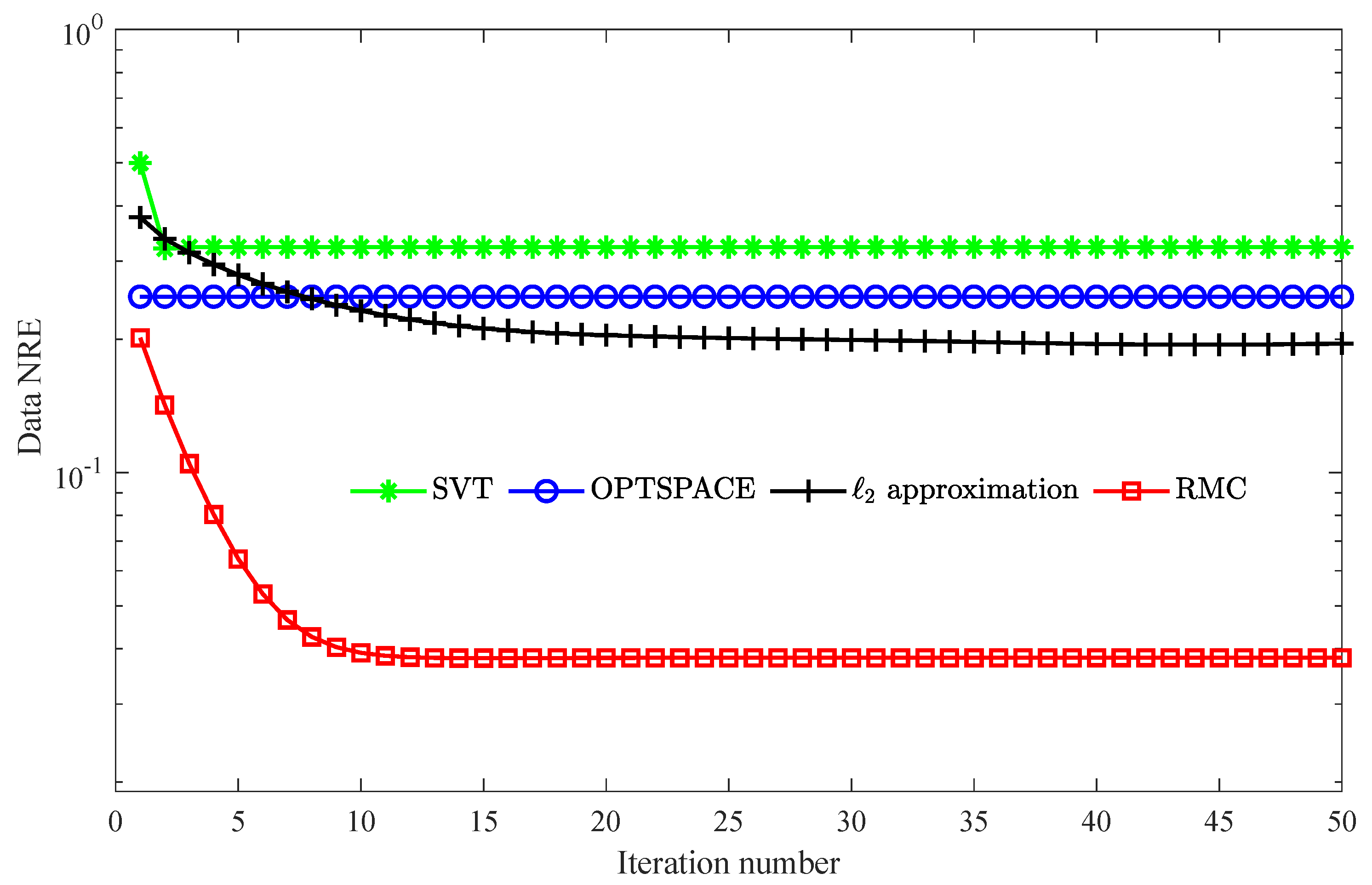
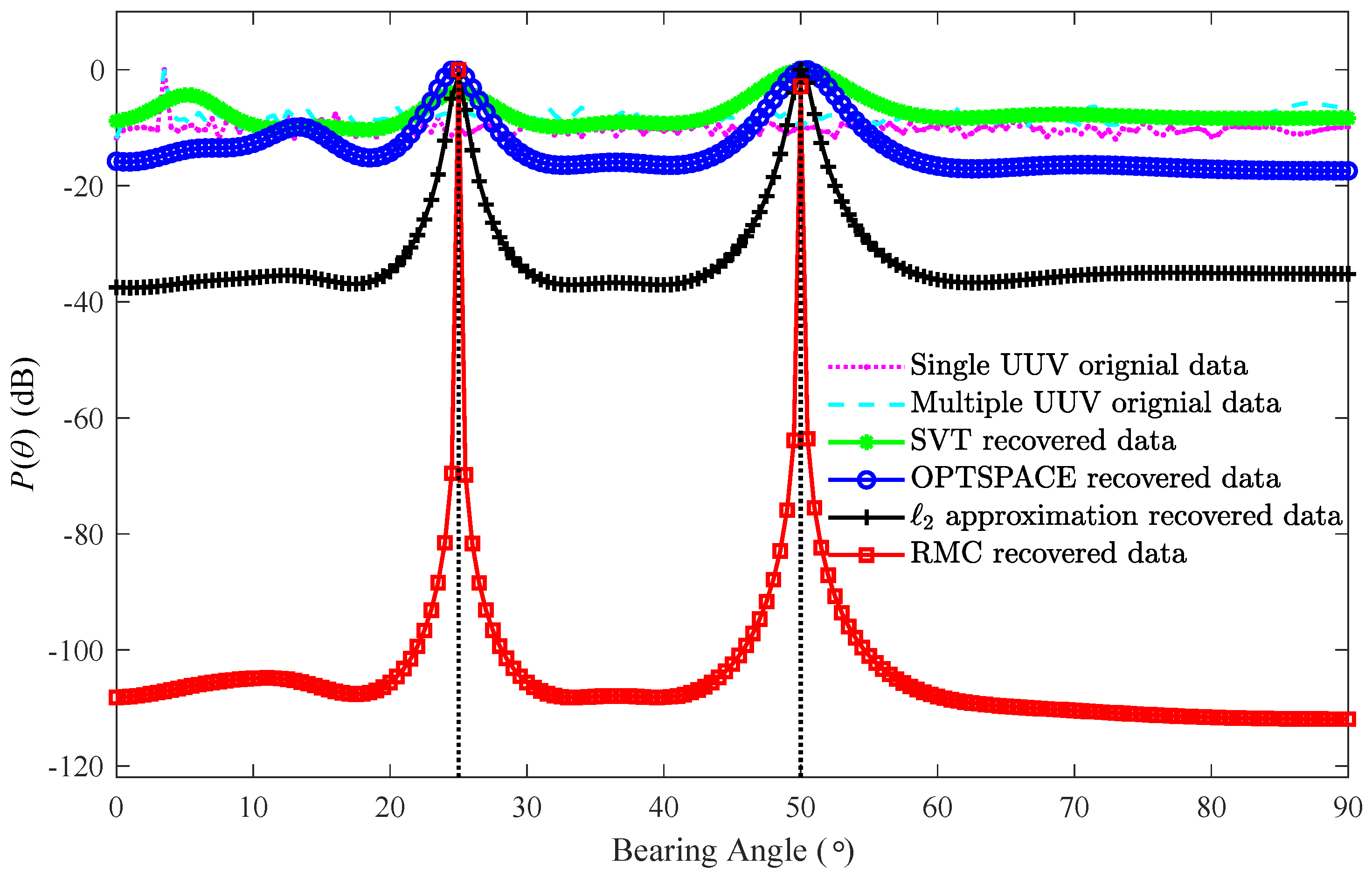
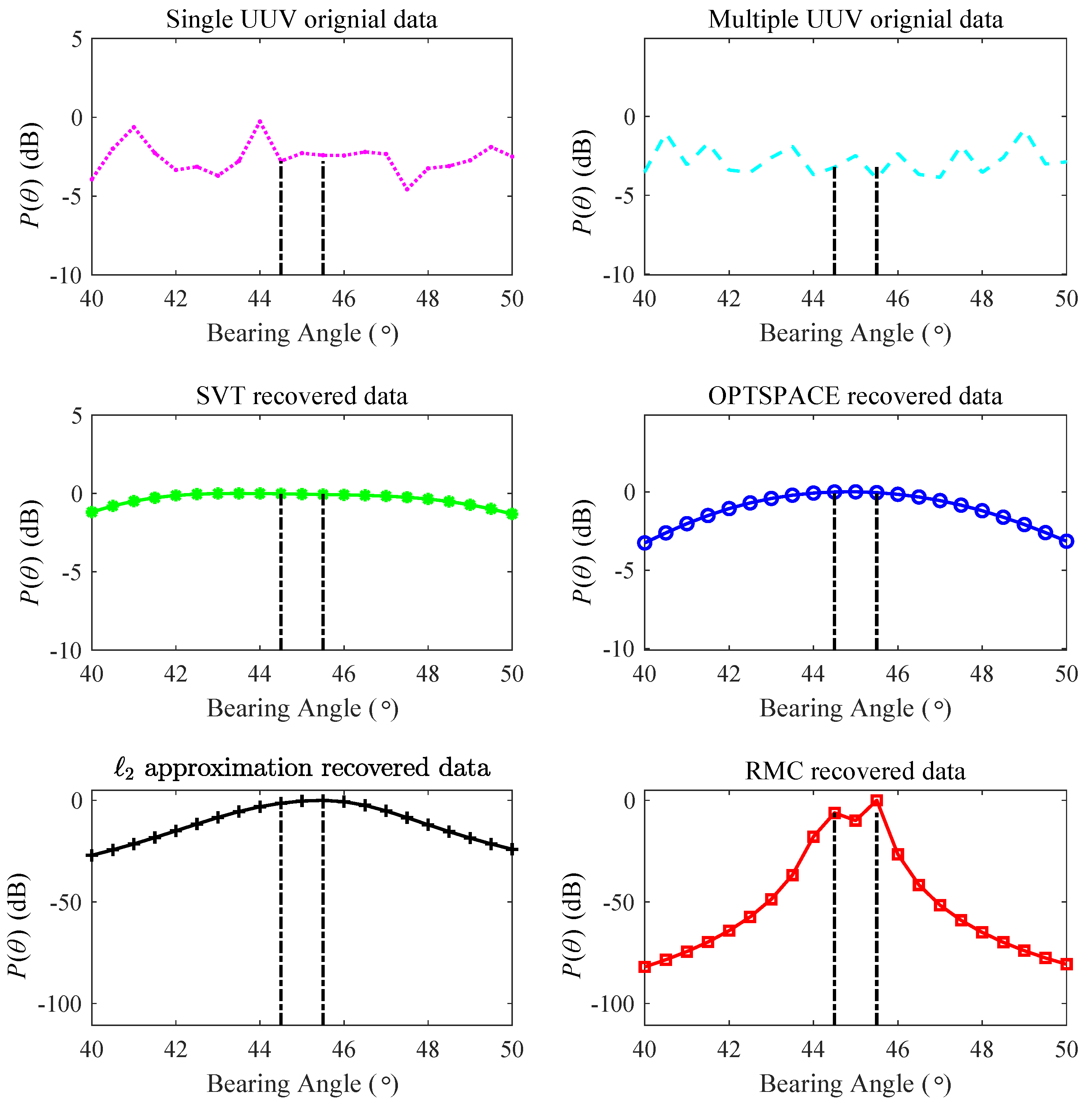
3.1. Single Target
3.2. Two Targets
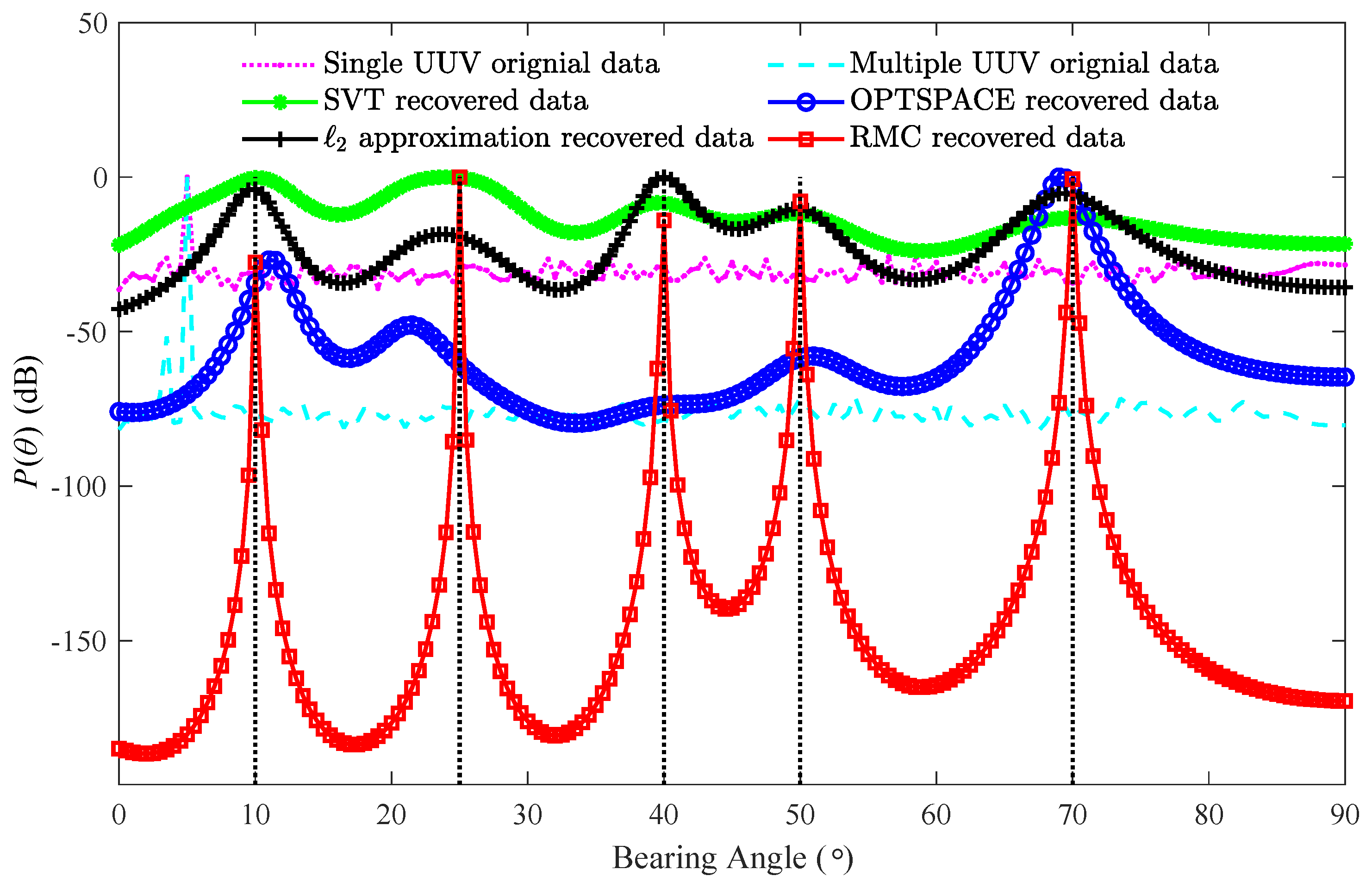
3.3. Large Number of Targets
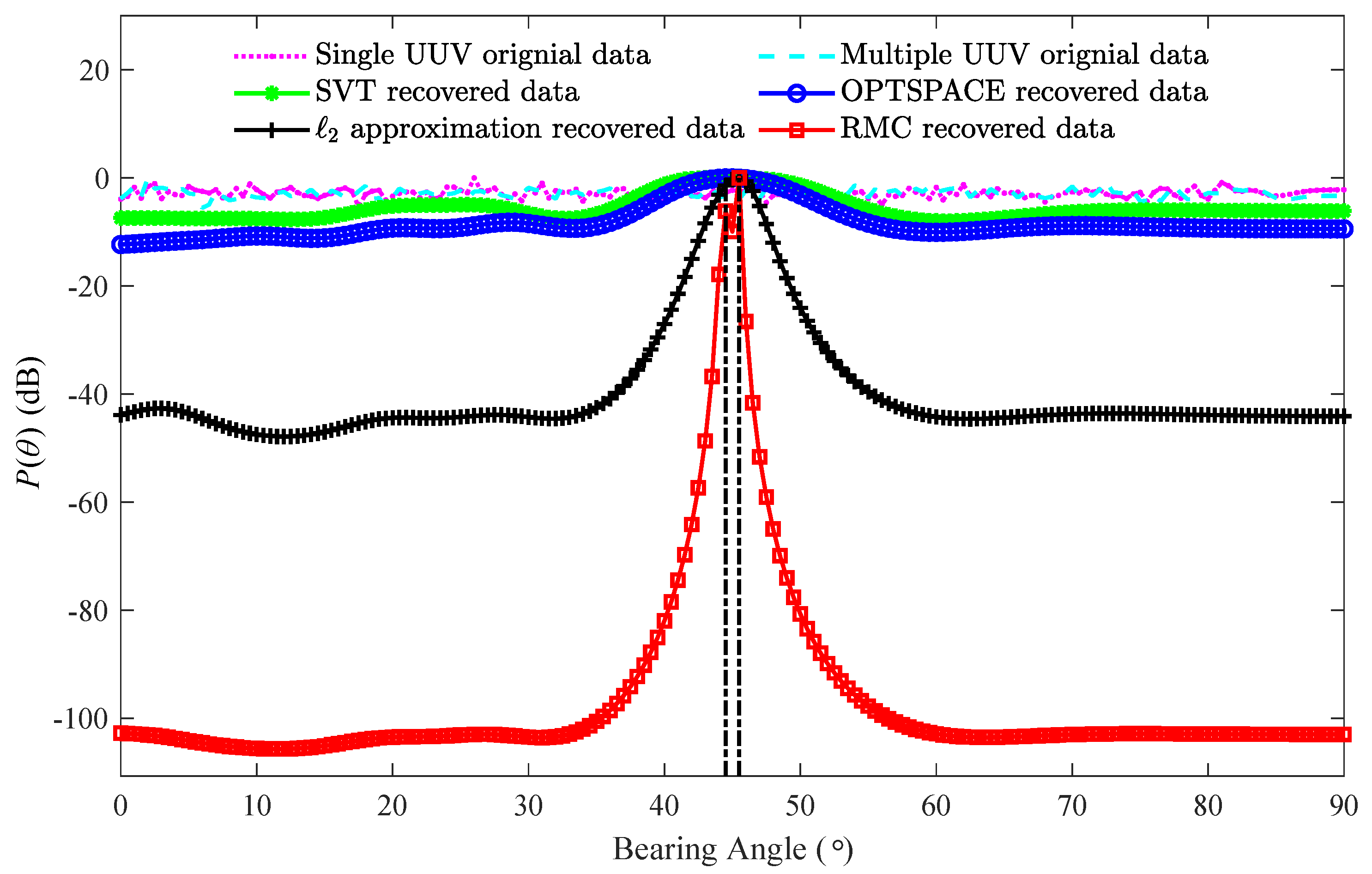
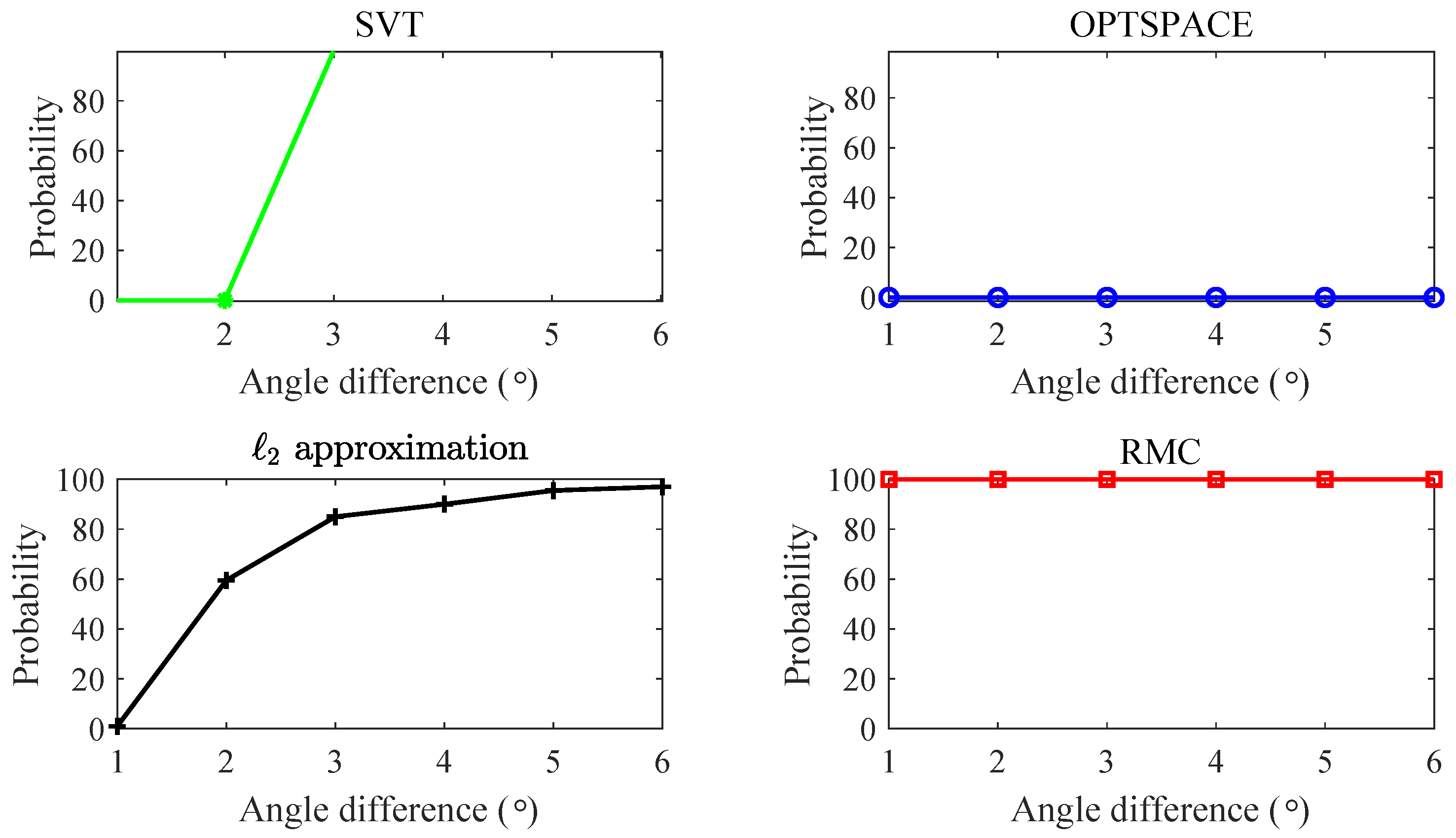
3.4. Angular Resolution
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Lim, H.S.; Ng, B.P.; Reddy, V.V. Generalized MUSIC-Like array processing for underwater environments. IEEE J. Ocean. Eng. 2017, 42, 124–134. [Google Scholar] [CrossRef]
- Xu, Z.; Li, H.; Yang, K. A modified differential beamforming and its application for DOA estimation of low frequency underwater signal. IEEE Sens. J. 2020, 20, 8890–8902. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H.; Tolstoy, A. Computational Ocean Acoustics; Springer: New York, NY, USA, 2011. [Google Scholar]
- Wang, F.; Chen, Y.; Wan, J. In-depth exploration of signal self-cancellation phenomenon to achieve DOA estimation of underwater acoustic sources. Appl. Sci. 2019, 9, 570. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Nehorai, A. Maximum likelihood direction-of-arrival estimation of underwater acoustic signals containing sinusoidal and random components. IEEE Trans. Signal Process. 2011, 59, 5302–5314. [Google Scholar]
- Han, X.; Liu, M.; Zhang, S.; Zheng, R.; Lan, J. A passive DOA estimation algorithm of underwater multipath signals via spatial time-frequency distributions. IEEE Trans. Veh. Technol. 2021, 70, 3439–3455. [Google Scholar] [CrossRef]
- Petillot, Y.R.; Antonelli, G.; Casalino, G.; Ferreira, F. Underwater robots: From remotely operated vehicles to intervention-autonomous underwater vehicles. IEEE Robot. Autom. Mag. 2019, 26, 94–101. [Google Scholar] [CrossRef]
- Jiang, W.; Yang, X.; Tong, F.; Yang, Y.; Zhou, T. A low-complexity underwater acoustic coherent communication system for small AUV. Remote Sens. 2022, 14, 3405. [Google Scholar] [CrossRef]
- Abtahi, S.F.; Alishahi, M.M.; Yazdi, E.A. Identification of pitch dynamics of an autonomous underwater vehicle using sensor fusion. China Ocean. Eng. 2019, 33, 563–572. [Google Scholar] [CrossRef]
- Yokota, Y.; Matsuda, T. Underwater communication using UAVs to realize high-speed AUV deployment. Remote Sens. 2021, 13, 4173. [Google Scholar] [CrossRef]
- Verdun, J.; Roussel, C.; Cali, J.; Maia, M.; D’Eu, J.-F.; Kharbou, O.; Poitou, C.; Ammann, J.; Durand, F.; Bouhier, M.-É. Development of a Lightweight Inertial Gravimeter for Use on Board an Autonomous Underwater Vehicle: Measurement Principle, System Design and Sea Trial Mission. Remote Sens. 2022, 14, 2513. [Google Scholar] [CrossRef]
- Button, R.W.; Kamp, J.; Curtin, T.B.; Dryden, J. A Survey of Missions for Unmanned Undersea Vehicles; RAND Corporation: Santa Monica, CA, USA, 2009. [Google Scholar]
- Guo, H.; Sun, Z.; Wang, P. Joint design of communication, wireless energy transfer, and control for swarm autonomous underwater vehicles. IEEE Trans. Veh. Technol. 2021, 70, 1821–1835. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, X. Research on the application of unmanned system cluster in marine combat applications. Ship Electron. Eng. 2019, 39, 21–25. [Google Scholar]
- Jin, W.; Ge, H.L.; Du, H.Q.; Xu, X.J. A review on unmanned aerial vehicle remote sensing and its application. Remote Sens. Inf. 2009, 1, 88–92. [Google Scholar]
- Zhu, J.N.; Yu, M.L.; Yang, Y.X. Overview of development of unmanned-surface-vehicle sensing technology. J. Harbin Eng. Univ. 2020, 41, 1492–1686. [Google Scholar]
- Liu, Y.; Chen, L.; Su, Q.; Liu, C.J.; Lai, M. Research on the development and combat application of foreign underwater unmanned vehicle. Ship Sci. Technol. 2020, 42, 1–7. [Google Scholar]
- Yan, Z.P.; Wu, Y.; Liu, Y.B.; Ren, H.L.; Du, X. Multiple unmanned underwater vehicles consensus control with unmeasurable velocity information and environmental disturbances under switching directed topologies. China Ocean. Eng. 2020, 34, 631–640. [Google Scholar] [CrossRef]
- Nichols, R.K.; Ryan, J.J.; Mumm, H.C.M.; Lonstein, W.D.; Carter, C.M.; Shay, J.; Mai, R.; Hood, J.P.; Jackson, M. Unmanned Vehicle Systems & Operations on Air, Sea, Land; New Prairie Press: Manhattan, KN, USA, 2021. [Google Scholar]
- Trees, H.L.V. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; John Wiley & Sons, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Ince, L.; Sezen, B.; Saridogan, E.; Ince, H. An evolutionary computing approach for the target motion analysis (TMA) problem for underwater tracks. Exp. Syst. Appl. 2009, 36, 3866–3879. [Google Scholar] [CrossRef]
- Dogan, M.C.; Mendel, J.M. Applications of cumulants to array processing. I. aperture extension and array calibration. IEEE Trans. Signal Process. 1995, 43, 1200–1216. [Google Scholar] [CrossRef] [Green Version]
- Balzano, L.; Recht, B.; Nowak, R. High-dimensional matched subspace detection when data are missing. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010; pp. 1638–1642. [Google Scholar]
- Kim, Y.G.; Kim, Y.; Lee, S.H.; Moon, S.T.; Jeon, M.; Kim, H.K. Underwater acoustic sensor fault detection for passive sonar systems. In Proceedings of the 2016 First International Workshop on Sensing, Processing and Learning for Intelligent Machines (SPLINE), Aalborg, Denmark, 6–8 July 2016; pp. 1–4. [Google Scholar]
- Liu, C.L.; Vaidyanathan, P.P. Robustness of difference coarrays of sparse arrays to sensor failures—Part I: A theory motivated by coarray MUSIC. IEEE Trans. Signal Process. 2019, 67, 3213–3226. [Google Scholar] [CrossRef]
- Donoho, D.; Elad, M.; Temlyakov, V. Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Trans. Inf. Theory 2006, 52, 6–18. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, M. Correction of corrupted columns through fast robust Hankel matrix completion. IEEE Trans. Signal Process. 2019, 67, 2580–2594. [Google Scholar] [CrossRef]
- Candes, E.J.; Plan, Y. Matrix completion with noise. Proc. IEEE 2010, 98, 925–936. [Google Scholar] [CrossRef] [Green Version]
- Candes, E.J.; Recht, B. Exact matrix completion via convex optimization. Commun. ACM 2012, 55, 111–119. [Google Scholar] [CrossRef] [Green Version]
- Recht, B. A simpler approach to matrix completion. J. Mach. Learn. Res. 2011, 12, 3413–3430. [Google Scholar]
- Candès, E.J.; Tao, T. The power of convex relaxation: Near-optimal matrix completion. IEEE Trans. Inf. Theory 2010, 56, 2053–2080. [Google Scholar] [CrossRef] [Green Version]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef] [Green Version]
- Candes, E.J.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Wu, F.Y.; Yang, K.; Duan, R. Compressed sensing of underwater acoustic signals via structured approximation l0-norm. IEEE Trans. Veh. Technol. 2018, 67, 8504–8513. [Google Scholar] [CrossRef]
- Keshavan, R.H.; Montanari, A.; Oh, S. Matrix completion from a few entries. IEEE Trans. Inf. Theory 2010, 56, 2980–2998. [Google Scholar] [CrossRef]
- Darsena, D.; Verde, F. Anti-jamming beam alignment in millimeter-wave MIMO systems. IEEE Trans. Commun. 2022. Early Access. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Weimer, M. Quantile Matrix Factorization for Collaborative Filtering. In Proceedings of the International Conference on Electronic Commerce and Web Technologies, Bilbao, Spain, 1–3 September 2010; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 210–227. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.S.; Lam, J.; Zheng, W.X. Control design for fuzzy systems based on relaxed nonquadratic stability and performance conditions. IEEE Trans. Fuzzy Syst. 2007, 15, 188–199. [Google Scholar] [CrossRef]
- Meng, J.J.; Yin, W.t.; Li, H.S.; Hossain, E.; Han, Z. Collaborative spectrum sensing from sparse observations in cognitive radio networks. IEEE J. Sel. Areas Commun. 2011, 29, 327–337. [Google Scholar] [CrossRef] [Green Version]
- Tachwali, Y.; Barnes, W.J.; Basma, F.; Refai, H. The feasibility of a fast fourier sampling technique for wireless microphone detection in IEEE 802.22 air interface. In Proceedings of the 2010 Infocom IEEE Conference on Computer Communications Workshops, San Diego, CA, USA, 15–19 March 2010. [Google Scholar]
- Taubock, G.; Hlawatsch, F.; Eiwen, D.; Rauhut, H. Compressive estimation of doubly selective channels in multicarrier systems: Leakage effects and sparsity-enhancing processing. IEEE J. Sel. Top. Signal Process. 2010, 4, 255–271. [Google Scholar] [CrossRef] [Green Version]
- HesamMohseni, A.; Babaie Zadeh, M.; Jutten, C. Inflating compressed samples: A joint source-channel coding approach for noise-resistant compressed sensing. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009. [Google Scholar]
- Chen, Y.; Lei, C.; Wu, Y.C. Bayesian low-rank matrix completion with dual-graph embedding: Prior analysis and tuning-free inference. arXiv 2022, arXiv:2203.10044v1. [Google Scholar] [CrossRef]
- Liao, B.; Guo, C.; Huang, L.; Wen, J. Matrix completion based direction-of-arrival estimation in nonuniform noise. In Proceedings of the 2016 IEEE International Conference on Digital Signal Processing (DSP), Beijing, China, 16–18 October 2016; pp. 66–69. [Google Scholar]
- Ji, H.; Liu, C.Q.; Shen, Z.W.; Xu, Y.H. Robust video denoising using low rank matrix completion. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 5 August 2010. [Google Scholar]
- Wang, M.; Wang, W. DOA estimation of array radar via random interval sub-Nyquist-sampling. In Proceedings of the 2013 IEEE International Conference on Signal Processing, Communication and Computing (ICSPCC 2013), Kunming, China, 5–8 August 2013. [Google Scholar]
- Cheng, L.; Xing, C.; Wu, Y.C. Irregular array manifold aided channel estimation in massive MIMO communications. IEEE J. Sel. Top. Signal Process. 2019, 13, 974–988. [Google Scholar] [CrossRef]
- Cherapanamjeri, Y.; Gupta, K.; Jain, P. Nearly-optimal robust matrix completion. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar] [CrossRef]
- Cai, J.F.; Candès, E.J.; Shen, Z.W. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Keshavan, R.H.; Oh, S. A gradient descent algorithm on the grassman manifold for matrix completion. arXiv 2009, arXiv:0910.5260. [Google Scholar]
- Zeng, W.J.; Thus, H.C. Outlier-robust matrix completion via ℓp-minimization. IEEE Trans. Signal Process. 2017, 66, 1125–1140. [Google Scholar] [CrossRef]
- Zhang, Q.T. Probability of resolution of the MUSIC algorithm. IEEE Trans. Signal Process. 1995, 43, 978–987. [Google Scholar] [CrossRef]
- Lee, H.B.; Wengrovitz, M.S. Statistical characterization of the MUSIC null spectrum. IEEE Trans. Signal Process. 1991, 39, 1333–1347. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Huang, J.; Zhang, H.; Liao, B. Direction of Arrival Estimation of Acoustic Sources with Unmanned Underwater Vehicle Swarm via Matrix Completion. Remote Sens. 2022, 14, 3790. https://doi.org/10.3390/rs14153790
Xu L, Huang J, Zhang H, Liao B. Direction of Arrival Estimation of Acoustic Sources with Unmanned Underwater Vehicle Swarm via Matrix Completion. Remote Sensing. 2022; 14(15):3790. https://doi.org/10.3390/rs14153790
Chicago/Turabian StyleXu, Liya, Jianjun Huang, Hao Zhang, and Bin Liao. 2022. "Direction of Arrival Estimation of Acoustic Sources with Unmanned Underwater Vehicle Swarm via Matrix Completion" Remote Sensing 14, no. 15: 3790. https://doi.org/10.3390/rs14153790
APA StyleXu, L., Huang, J., Zhang, H., & Liao, B. (2022). Direction of Arrival Estimation of Acoustic Sources with Unmanned Underwater Vehicle Swarm via Matrix Completion. Remote Sensing, 14(15), 3790. https://doi.org/10.3390/rs14153790





