Abstract
Polarization calibration without artificial calibrators has been one of the focuses of research and discussion for PolSAR communities. However, there is limited research on the treatment of dual-polarization systems and the calibration methods for getting rid of distributed targets. In this paper, we contribute to proposing a new and convenient method for estimating the polarimetric channel imbalance phase at the transmitter and receiver, which can be used for both quad-pol and dual-pol SAR systems. We found a brand-new reference object in the urban area scene, namely the effective dihedrals. A statistical calculation method was proposed correspondingly, which obtained an effective estimation of the channel imbalance phases. The theoretical explanation of the proposed method was consistent with the statistical phenomena presented in the experiments. The technique was illustrated and verified through C-band SAR images, including GaoFen-3 (GF-3) data and Sentinel-1 data. The technique was also validated and successfully applied in airborne SAR data of P, L, S, C, and X bands. The estimation error could be within 7° when crosstalk items were less than −30 dB. The method realizes a fast and low-cost dual-polarization phase imbalance estimation and provides a new technical approach to supplement the traditional tropical-rainforest-based quad-pol system calibration. The method can be conveniently applied to the monitoring of polarization distortion parameters, ensuring good polarization SAR data quality.
1. Introduction
The polarimetric synthetic aperture radar (PolSAR) plays an important role in a variety of quantitative applications with the incremental information of target properties from the performance under polarized radar waves. However, polarization distortions always exist in the raw single-look complex (SLC) data [1], such as energy leakage and amplitude and phase inconsistency when transmitting and receiving different polarized waves. Polarization calibration is a key step to correct these distortions so that the data can truly reflect the polarimetric backscattering performance of ground objects, which is the basis of various subsequent quantitative applications of PolSAR data.
The polarization calibration technique by using artificial calibrators is mature, such as corner reflectors (CRs) and polarimetric active radar calibrators (PARCs). Because of its controllable high precision, it has been widely used in the initial calibration of various space-borne SAR systems [1,2,3]. However, the calibrators’ arrangement and maintenance in the calibration field are costly, and the measurement range and calibration frequency provided by these calibrators are limited. With the development of polarimetric SAR technology, the calibration of the multi-beam, multi-band, and multi-working-mode polarimetric SAR system has become a huge burden to the traditional calibration methods. Therefore, it is of great scientific significance and application value to study ground objects with special properties in usual SAR scenes for polarization calibration.
For the quad-pol calibration methods, there has been a lot of outstanding research published. Van Zyl et al. first used only image parameters and one trihedral corner reflector to achieve calibration for Jet Propulsion Laboratory (JPL) airborne SAR (AIRSAR) data [4]. Furthermore, Quegan et al. [5] and Ainsworth et al. [6] utilized natural targets to solve crosstalk and cross-polarization channel imbalance elements. To further reduce the cost of assembling and deploying calibrators, researchers have focused on methods that do not require any external calibrators to be deployed before imaging. Shimada et al. [7] utilized the three-component Freeman–Durden decomposition method to estimate the distortion elements. Lei Shi proposed the co-polarization channel imbalance determination methods by the use of bare soil and corner-reflector-like targets [8,9]. By combining the information of the distributed target and a corner reflector, using a numerical optimizer for polarimetric calibration was researched [10]. Jiang Sha et al. proposed a fast polarization distortion estimation method for GF-3 data only based on volume scattering targets [11]. Based on this method [11], S. Shangguan et al. realized the normalized monitoring of the polarimetric distortions of GF-3 quad-pol data [12].
A quad-polarized system is limited by some systematic constraints. As a compromise, in the case of providing cross-polarization information, a dual-polarized system can be applied to a higher imaging resolution mode or a larger swath width mode. Dual-polarization SAR data has a wide range of applications, such as marine monitoring [13,14] and biomass retrieval [15,16]. These precise quantization applications require good polarization data quality for dual-polarization data. Chen Lin et al. discussed a general calibration method of the dual-pol SAR system based on three ideal artificial calibrators, namely, a trihedron, a 0° dihedral reflector, and a 45° dihedral reflector [17]. M. Lavalle et al. proposed a calibration approach of dual polarimetric C-band data using two gridded trihedrons and an oriented dihedron for Sentinel-1 [18]. As far as we know, the known dual-polarization calibration methods are all mainly based on artificial calibrators. Differently from quad-pol SAR data, some assumptions of volume-scattering targets are no longer available for dual-pol SAR data, such as the reciprocity, which limits the feasibility of the distributed targets of volume scattering for polarization calibration of dual-polarization systems.
Achieving an effective estimation of the phase imbalance of dual-pol or full-pol data without relying on a calibrator has been a difficult problem. In this paper, we contribute to proposing an effective estimation of the channel imbalance phase at both transmitter and receiver of the polarimetric SAR system based on the discovered novel ground reference objects and the proposed corresponding statistical estimation method.
For this technique, we innovatively utilized the statistical information of the cross-pol phase difference (XPD) of the double-bounce backscatter targets from urban areas. Atwood and Thirion-Lefevre et al. introduce the concept of the effective dihedral [19], with one plate coincident with the building wall and one plate associated with some ground facet, oriented to support double bounces of radar waves. In this paper, we develop a technique based on this concept to achieve the estimation of the phase imbalance. First, the effective dihedrals with specific rotation angles, namely rotated double-bounce backscatters (RDBs), were extracted from complex reflections in urban areas through a series of extraction operations. Then, we used the distribution statistics information of XPD values of the RDBs to achieve the estimation of the phase imbalance. Finally, for the 180-degree phase ambiguity problem that arises in the method, we temporarily adopted the method of inverting its orientation for a specific ground building to make the whole estimation technique complete.
We used a variety of SAR data and multiple approaches to verify the validity and accuracy of the estimation method. The feasibility of the method in normally monitoring dual-pol phase imbalance was verified by calibrated Sentinel-1 dual-pol data. The validity and accuracy of the method were verified by comparing it with other polarimetric calibration methods based on GF-3 full-pol data. The universality of the method for P, L, S, C, X-band SAR data was verified by running on the airborne multi-band full-pol SAR data.
This paper is organized as follows: Section 2 expounds on the principle, derivation, implementation details, properties, and theoretical estimation errors of the method. Section 3 presents the experiments, the operation results, and verification comparison results of the method on GF-3 and other data. The entire estimation method is discussed in Section 4. Section 5 gives the conclusion.
2. Method
2.1. The Polarimetric Distortion Model of the PolSAR System
The observed polarized SAR data should reflect the real polarimetric reflection signal of the observed targets, but it is distorted by multi error factors. The distortion model for the whole link is given in the literature [20] and can be expressed as follows:
where the matrix is the true scattering matrix. is the absolute amplitude factor, and is the absolute phase. The measurement matrix is distorted by the transmitted and received distortion matrices, which results from non-ideal polarized transmitting and receiving channels and antennas, and is the polarization orientation angle aroused by the platform’s attitude. is the ionosphere-induced Faraday rotation matrix. is the additive noise, which can be roughly estimated out by the coherence relationship between HV and VH data [21]. In general, for polarization calibration, people focus on the distortion matrix R/T of the system, while other factors are not the concerns of this article. Then, Equation (1) can be rewritten as [11]:
where the subscript means the horizontal/vertical transmit/receive channel. is the channel imbalance, which represents the differences between H and V channels. The crosstalk items , , , and , respectively, represent the other leaked polarized signal when the system receives or transmits one polarized signal.
The dual-pol SAR system transmits one polarized wave and receives both co- and cross-polarization signals. For the case of H-transmission, the measured scattering matrix can be written as follows:
The V-transmission case is similar to E, only the crosstalk item should change. As a dual-pol system is used, it is not possible to correct for the transmit crosstalk distortion . However, it will affect the phase imbalance estimation.
The proposed method can solve the phase of , namely the phase imbalance of the receiver, based only on HH and HV observations in urban areas. For full-pol data, the phase imbalance of the transmitter can be obtained only by using the HH and VH observations. The following mainly introduces the whole method in the case of HH and HV to solve the phase imbalance of the receiver.
2.2. The Phase Imbalance Estimation Method Based on the Rotated Dihedral Corner Reflector
For the dihedral corner reflector, in the case of a perfect electrical conductor and incidence along the dihedral bore site, the scattering matrix of the dihedral is [22]:
where angle is the rotation of the perfect dihedral about the SAR look direction. The positive values correspond to clockwise (CW) rotation, and negative values correspond to counterclockwise (CCW) rotation [19]. and are the objects of this study. They are plotted together in Figure 1a, where the variation range of angle is set from −90° to 90°.
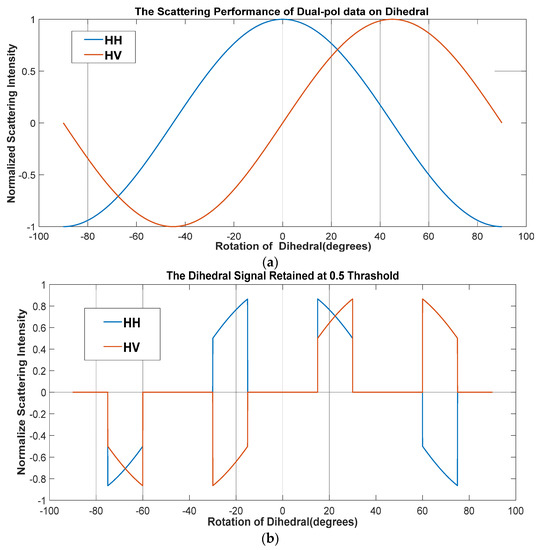
Figure 1.
Simulation schematic diagram of dual-pol data on a perfect dihedral: (a) The perfect dihedral scattering responses of the HH and HV polarization channels; (b) 0.5 is set as a threshold, the part where absolute amplitudes of both HH and HV are above the threshold is retained.
From Equation (4), we can see that since both signals are real numbers, from the perspective of complex numbers, the phase of both is only 0 degrees and 180 degrees. One sees that there are only two cases of the phase relationship between the HH and HV channels:
For the H-transmission dual-pol SAR system, Equation (3) can be rewritten as:
Considering that the values of cross-talk items are small, the measured phase of and is mainly determined by the corresponding and :
For a dihedral with a specific rotation angle, which conforms to Equation (5a), the phase imbalance can be estimated from Equation (7) using the cross-pol phase difference (XPD) of and :
where is the estimated phase of channel imbalance. We can see from Equation (6) that the crosstalk items are the major source of error in estimating the phase of .
For this phase estimation error, we consider the phase error caused by small disturbances of cross-talks that are not considered in the above calculation. Due to the amplitude characteristics of the point targets extracted by the subsequent method, this analysis is simplified by setting the signal strength of each polarization channel to 1. Thereby, the estimation error can be approximately expressed as:
when the vector sum of the interference terms is orthogonal to the reference signal and the direction of each interference term is consistent, the extreme worst-case estimation error can be approximately expressed as:
where means an amplitude level of the equivalent crosstalk. For example, a −30 dB crosstalk level may lead to an estimation error of up to about 7 degrees in this extreme case. It can be seen that the accuracy of the method is severely affected by the channel isolation of the system. Notice that the magnitude of crosstalk is small and can easily reach −30 dB for today’s space-borne SAR sensors. As the above-mentioned extreme case should be very rare, the error of the actual phase estimation should be much smaller than this value in most cases.
2.3. The Phase Imbalance Estimation Method Based on the Urban Rotated Double-Bounce Backscatters (RDBs)
The phase imbalance estimation method expressed in Section 2.2 is based on the polarimetric scattering properties of the dihedral corner reflector. Instead of studying the traditional calibration method that relies on the precisely deployed calibrators, this paper utilizes the widespread double-bounce backscatters in urban areas to achieve the phase imbalance estimation. The technique uses a statistical method on a wide range of extracted targets rather than precisely extracting some specific objects and treating them as dihedral-like targets.
Atwood and Thirion-Lefevre researched the phase behavior of the double-bounce backscatters of urban areas [19]. The concept of the effective dihedral is introduced, with one plate coincident with the building wall and one plate associated with some ground facet. They also derived the relationship of the rotation angle of the effective dihedral and the rotation angle of the building wall [19]:
where is the SAR local incidence angle and is the rotation angle of the building wall around the vertical axis. The literature describes the urban scenario as the result of a forest of dihedrals; the XPD information of all pixels in the scenario is counted for the classification of urban areas [19].
In this method, we first perform a series of filtering operations on urban targets to obtain those valid double-bounce backscattering structures with specific rotation angles.
Specifically, the first filtering operation can be expressed as:
where is an expression that calculates the average amplitude of the corresponding polarized channel ( stands for or ) of the scene. The symbol is logical.
The symbol K here is a multiplying coefficient. The K value relates to the content of the scene’s features. Generally, the appropriate range of K values may be between 1 and 10. When the K value is chosen too small, too many point targets are obtained, and even some points lose the function of phase imbalance calculation, but it is a way to barely cope with the scenario of insufficient building targets. Too large K values may cause an insufficient number of extracted points, it can cause statistical bias in the subsequent statistical histogram calculation of peak positions. Empirically, K can be set to about 3 for general scenarios. In practice, the principle is to appropriately increase the K value under the premise of ensuring sufficient obtained point targets.
The function of this filtering process (Equation (12)) can be seen visually in Figure 1b. It reserves the parts with two polarization channels greater than a threshold of 0.5, while the other parts are discarded.
The polarimetric strong scattering points’ filtering is to remove interference from other scattering mechanisms in urban areas, such as the trihedral reflection structure that also exists. Meanwhile, it can ensure the reliability of the target phase. If the scattering intensity of one polarization channel of the target is small, its phase is susceptible to noise and other clutter signals, which is not conducive to the statistics of phase information.
In addition, for the extracted strong scattering points, we perform coherence filtering on the local regions of HH and HV of these points, reserving target points whose coherence coefficient is greater than a threshold. It can be expressed as:
where the symbol represents the data of a certain size of a square area centered on the th target point. In the experiment, the side length size of the local area was set as 7 pixels. The coherence coefficient threshold was set at 0.8. The filtering operation of Equation (13) can ensure the validity of polarization information of target points and avoid the multiple scattering mixed invalid signals in urban areas and some strong scattering volume scattering target signals in the scene.
Next, we use Equation (8) to estimate the phase imbalance estimation value of each extracted RDB target. For the numerous estimates obtained from the set of point targets, we count the cluster centers of these values as the final estimates for this whole scene. There are various kinds of processing methods, and this paper uses the method of statistical distribution histogram. The peak position of the statistical histogram is the estimation result of phase imbalance of the whole scene. To accurately obtain the peak position from the distribution histogram, we use the approach of normal distribution fitting to estimate the fitted peak position as the estimated phase imbalance. The estimated phase imbalance can be expressed as:
For a scene with enough buildings, the target obtained should preferably exceed 30,000, and the normal curve fitting approach is to fit the midpoint position of the frequency of each interval within plus or minus 40 degrees around the peak as each fitting point. Technical details will be given in conjunction with specific experiments in Section 3.
2.4. The 180-Degree Phase Ambiguity Problem
From Figure 1b, one can see that the phase relationship of HH and HV has two cases listed as Equations (5a) and (5b). The above estimation method is based on Equation (5a). However, with complete randomness for an urban area, the situation of Equation (5b) will occur with equal probability, which will result in another solution with a phase difference of 180 degrees. We name this problem the 180-degree phase ambiguity problem. The specific manifestation of this problem is that the RDBs’ XPD distribution histogram will have two statistical peaks, which is also observed by Atwood and Thirion-Lefevre with one peak centered at zero and one peak centered at [19].
The estimated phase imbalance corresponds to one of the two peaks, namely the target peak. For the calibrated PolSAR product, the phase imbalance should be zero, so the peak centered at zero or close to zero is the target peak, which means that the method does not need to consider the 180-degree phase ambiguity problem in the PolSAR data quality monitoring task.
However, for the uncalibrated SAR data, the phase imbalance is unknown, so the determination of the target peak in the twin peaks is a problem to be solved. A wrong peak selection will result in a phase difference of 180 degrees in estimating phase imbalance.
There is currently no convenient and simple way to solve this problem. We adopt the most straightforward approach in implementation, which is to reverse the rotation angle of the effective dihedral according to the orientation of the specific building wall relative to the line of sight of the satellite (according to Equation (11)) and then judge whether the statistical peak is the target peak according to the position of the rotation angle in Figure 1b. For example, when the rotation angle is about 22.5 degrees, it is determined as the target peak.
There are two key points, one is to identify such a building target. We combined optical images from Google Maps and RDBs from SAR images to find such a building target. The target building structure should be as simple as possible, with a flat wall structure and a simple top structure. Such architectural targets should be dominated by only one dihedral scattering pattern, i.e., the RDBs all correspond to the same peak.
After identifying the specific building wall, the next key point is to calculate the rotation angle of the wall along the vertical axis. For intuitive expression, a schematic diagram is shown in Figure 2. Where is the line of sight of the SAR sensor, V is the direction of the building wall (V0 when it is directly facing the sensor), and is the rotation angle of the building wall, where a positive value corresponds to CCW rotation around Z (the vertical axis). We calculate the value of using the following approach.
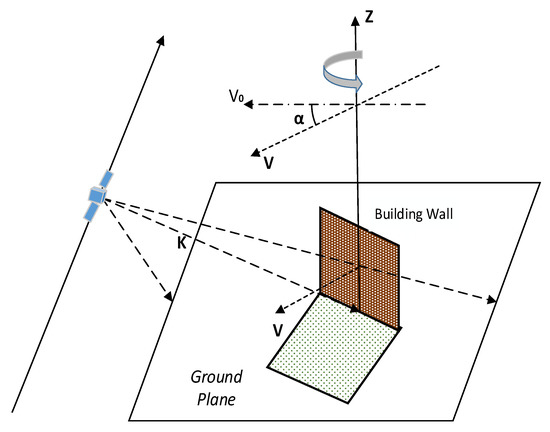
Figure 2.
A schematic diagram of a simple geometric model of double-bounce scatters formed between a horizontal ground plane and a rotating building wall.
If we calculate the rotation angle by relative geometric relations using the L1A image, it is considered that the direction of V0 is the range direction, which is from left to right in the L1A image. When calculating the rotation angle of the building, it is necessary to consider the different pixel spacing sizes in the azimuth direction and range direction of the pixels. Meanwhile, it is necessary to consider the need to invert the image up and down when the scene is ascending.
If we calculate the rotation angle by absolute geometric relations, first, we use the imaging trajectory of the SAR image or the geometrically corrected image to determine the azimuth direction. The line of sight of the radar in strip mode is vertical to the azimuth direction, and we can get the direction of V0 for this scene. Then, we need to determine the orientation V of the corresponding building wall in Google optical maps or the geometrically corrected SAR images. Finally, we can obtain the rotation angle as shown in Figure 2.
Naturally, the rotation angle calculated by the method above has a certain deviation, which comes from the error of human judgment of the rotation angle , nonhorizontal ground, or even nonvertical reflective walls, etc. However, the filtering of Equation (12) produces the effect that only the RDBs of a specific rotation angle interval can be selected. From Figure 1b it can be seen that there is a difference of the rotation angle of more than 20 degrees between different peaks, which provides redundancy for the inversion calculation of the rotation angle in this section. It assures the validity and feasibility of this 180-degree phase ambiguity determination approach.
2.5. The Framework of the Imbalance Estimation Method
From Section 2.2, Section 2.3, Section 2.4, the whole implementation approach and principle of the method are given, which is based only on HH and HV data. It can be used for the corresponding dual-pol and full-pol SAR data estimation to obtain the phase imbalance of the receiver. As seen in Equation (4), the and have the same expression on the dihedral reflector. Therefore, using HH and VH polarization data of full-polarization data, we can estimate the phase imbalance of the transmitter without changing the implementation details of the method.
In addition, the proposed method does not need to consider the screening for urban areas, but only requires the existence of urban areas or a certain number of man-made buildings of villages and towns in the scene, because the two filtering operations in the method make the RDBs be efficiently extracted. A key factor is that the more RDBs extracted from the scene, the more reliable the statistical distribution obtained, therefore, there is still a certain demand for the scene.
The proposed phase imbalance estimation process chain is shown in Figure 3.
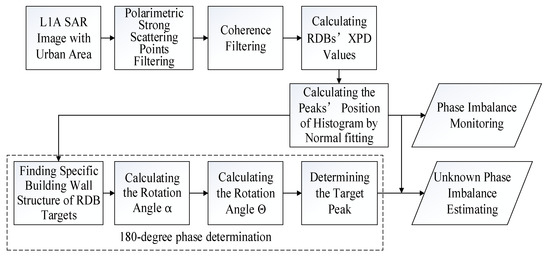
Figure 3.
The flowchart of the phase imbalance estimation algorithm.
3. Result
In this paper, the effectiveness and feasibility of the proposed method were verified through the following series of experiments. The robustness of the proposed method was verified by applying it to various data sources, especially on P/L/S/C/X multi-band data of airborne data. For the 180-degree phase ambiguity problem, two implementation examples realized by specific ground buildings are given in Section 3.2 and Section 3.3. Through these two complete solution examples, the correctness of the method’s principle was verified, and a deeper understanding of the double-bounce reflections of the ground surface was obtained. Since the method can be applied to estimate the phase imbalance of full-polarization data, we used other polarization calibration algorithms to verify the accuracy of the estimated phase imbalances.
In Section 3.1, the feasibility of the proposed method for phase imbalance monitoring on calibrated polarimetric SAR data is verified by using Sentinel-1 dual-polarization data. In Section 3.2 and Section 3.3, the phase imbalance estimation performance is studied using the uncalibrated GF-3 full-polarization data and GF-3 dual-polarization data. Finally, the performance of the proposed method in different bands is given under the multi-band full-polarization airborne data in Section 3.4.
3.1. Phase Imbalance Monitoring Using Sentinel-1 Dual-Pol Data
As seen in the flow chart of Figure 3, the 180-degree phase ambiguity determination operation can be omitted to obtain a fast phase imbalance monitoring for the calibrated SAR images. Because the residual phase imbalance is unlikely to reach or exceed 90°, the peak close to 0° should be the target peak of the two estimated phase-imbalance peaks. The experiment used Sentinel-1 calibrated dual-polarization single look complex (SLC) data of the Stripmap mode. The Stripmap mode acquires data with an 80 km swath and 5 m by 5 m spatial resolution. The characteristics of the Stripmap products are a phase error within 5°, radiometric accuracy with 1 dB (3σ), and maximum NESZ with −22 dB [23]. The operation of the experiment data is the same as shown in Figure 3, that is, first, extract the RDBs through polarimetric strong scattering points filtering and coherence filtering, then, calculate each RDB’s phase imbalance. Finally, the histogram statistics of the results are performed. In the specific parameters in the experiment, K was 2, and the threshold was set to 0.8 for local 7-by-7 pixel areas. The results based on Sentinel-1 data are shown in Figure 4.
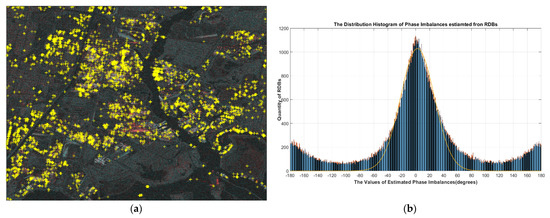
Figure 4.
The phase imbalance estimation results of Sentinel-1 dual-pol SAR data: (a) The extracted RDBs are displayed in a local area of the Houston urban area (Scene: S1A_S3_SLC__1SDH_20160922T001818_20160922T001841_013158_014E8E_7926). The color assignment is red for the HH channel, green for the HV channel, and blue for the HV channel divided by the HH channel; (b): The distribution histogram of the estimated phase imbalances.
This scene locates in the city of Houston and contains the entire urban area. One local area is shown in Figure 4a, where the yellow crosses mark the extracted RDB targets. There are a total of 186,474 RDBs extracted in this scenario. The histogram statistical results are shown in Figure 4b. As can be seen, the peak of the distribution histogram occurs at the position of about 0°, which is in line with expectation, and the other peak that locates around 180° can be ignored. Meanwhile, Figure 4b shows the normal fitting curve of the data within the range of plus or minus 40° centered at 0°, and the corresponding peak position can be obtained as 2.55° according to the normal fitting results. Therefore, the phase imbalance of this scene is estimated to be 2.55°.
As seen from the experimental results, there were enough RDB targets extracted in such an urban located scene, and its statistical distribution presented an obvious characteristic similar to the normal distribution, which can ensure that the final results obtained are accurate enough in the statistical sense. The results obtained in the experiments prove an excellent polarization phase performance of the Sentinel-1 data, which is consistent with its technical index that phase error within 5°. At the same time, the experimental results also prove the effectiveness of the proposed method for phase imbalance monitoring applications. Although the quantity of RDBs is large, the processing algorithm of individual RDB is not complicated, so the method can realize the phase imbalance monitoring mission quickly.
3.2. Phase Imbalance Estimation Using Uncalibrated GF-3 Quad-Pol Data
In this part, we use GAOFEN-3 (GF-3) quad-pol data for the estimation of the unknown polarimetric phase imbalances at the transmitter and receiver. GF-3 is the first full polarization SAR satellite of China launched in August 2016. It is designed so that the channel isolation is better than −35 dB, and the channel imbalance is within 0.5 dB/10°. It provides full-polarized data with swaths of at least 20 km with a resolution of about 8 m (QPSI mode), and a 35 km swath with a resolution of about 25 m (QPSII mode).
GF-3 has been polarimetric-calibrated using polarimetric active radar calibrators’ methods. The calibration of GF-3 quad-pol data was implemented in July 2017 [2]. However, to validate the method for the estimation of unknown and possibly large phase imbalances, in this experiment, we specifically chose the SAR data that was imaged earlier than July 2017. It means that the used quad-pol SAR data was not calibrated.
In the case of full-polarization data, the comparison object of experimental results is a full-polarization distortion parameters’ estimation method based on common distributed targets [11], which utilizes the forest area of volume scattering to effectively obtain the channel imbalances with an accuracy of about 0.3 dB/4°. To facilitate the comparison of the two methods, the experimental scene was selected to be located in Jiangmen, Guangdong Province, imaged on 30 December 2016. This scene has both the urban area and forest area. Meanwhile, the quantization between polarization channels should be considered when processing the SLC data of GF3, the details of which can be found in the literature [12]. The Pauli polarization pseudo-color image of this scene and the phase imbalance estimation results of the two methods are shown in Figure 5.
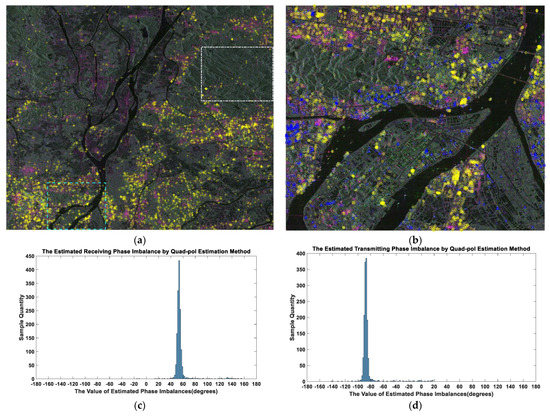
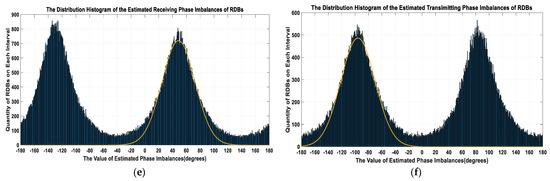
Figure 5.
The phase imbalance estimation results of the two estimation methods in a typical scene of GF-3 quad-pol data (Product ID: GF3_MYN_QPSI_002054_E113.3_N22.5_20161230_L1A_AHV_L10002080826). (a) The Pauli polarization pseudo-color image of this scene. The yellow cross marks represent the extracted RDB targets, while the white box represents the forest areas used for the quad-pol estimation method, and the blue box corresponds to the areas in image (b). (b) The distribution of RDBs in the local urban area of this scene, where the yellow circle marks correspond to the peak on the right in figure (e), and the blue triangle marks correspond to the peak on the left in figure (e). (c) The results of the receiving phase imbalance estimation obtained by the quad-pol method based on the forest area in figure (a). (d) The results of the transmitting phase imbalance estimation obtained by the quad-pol method based on the forest area in figure (a). (e) The distribution histogram of the receiving phase imbalances obtained from the extracted RDBs from the whole scene. (f) The distribution histogram of the transmitting phase imbalances obtained from the extracted RDBs from the whole scene.
As shown in Figure 5a,b, there were a lot of factories and residential areas in this complex scene. In addition, the area marked by the white dashed box in the upper right corner of Figure 5a was a densely forested mountainous area, which satisfied the requirements of the quad-pol estimation method for distribution targets. The extraction details of RDBs were the same as in the previous experiment, and the RDB targets obtained are marked as yellow crosses in Figure 5a. It can be seen that they were densely distributed in areas of buildings, and a small number of sporadic targets in areas such as farmland and mountain forests could be considered discrete values, which had little effect on the final statistical results.
Figure 5c,d shows the results obtained by the distributed-target-based method, for which the transmitting phase imbalance was −91.1°and the receiving phase imbalance was 52.3°. Figure 5e,f shows the estimation results that come from RDBs. HH and VH were used to obtain the transmitting phase imbalance, from Figure 5f, the peak position of the normal fitting of the left peak was −94.5°. Similarly, it can be seen in Figure 5e that the receiving phase imbalance at the right peak was 49.3°.
As seen in Figure 5e,f, there were two peaks in one distribution histogram. It was the representation of the 180-degree phase ambiguity problem, which was caused by the fact that the phase relations of Equations (5a) and (5b) are not distinguished in the RDBs extraction. The difference of about 180° between the two peaks was consistent with the analysis in Section 2. For the case of estimating the receiving phase imbalance, we marked these RDB targets of the two peaks separately in the SAR scene, as shown in Figure 5b. The yellow rings correspond to the right peak, and the blue triangles correspond to the left peak in Figure 5e. As the orientations of the buildings in the same residential area tend to be consistent, the rotation angles of these effective dihedrals were likely to be consistent, which caused the RDB of the same peak to cluster according to geographic location.
Next, the 180-degree phase ambiguity determination needed to be executed to determine the final phase imbalance estimation result. The experiment was based on the case of receiving phase imbalance estimation, which is shown in Figure 6. Some RDBs corresponding to the left peak in Figure 5e appeared on the factory circled in Figure 6a. It is an L1-level image, where the radar illuminates from the left to the right on the image. Figure 6b is a Google optical image of the corresponding area, where the circled building is the research target. It can be seen that the effective dihedral of the factory building should be composed of protruding bars on the roof and the roof plane. Further, the orientations of the walls of the buildings in this area were all the same, facing the direction perpendicular to the road. From the SAR image, we could obtain about 96 m in the direction of (the direction is shown in Figure 2) and about 42 m in the azimuth direction. Then, was estimated to be about 23.6°. The incidence angle of this scene was 26.17°. Assuming that the scene had no obvious slope, the local incidence angle was considered to be 26.17°. Using Equation (11), we could obtain the rotation angle of these effective dihedrals, which was about −25.9 degrees. From Figure 1b, we can see that the phase relationship between HH and HV of these effective dihedrals was opposite, which was not the assumed case in the method (Equation (5a)). Therefore, the corresponding peak (left peak in Figure 5e) was not the target peak. The receiving phase imbalance of the scene finally obtained with the proposed method was 49.3°, which was consistent with the result of the distributed-targets-based method.
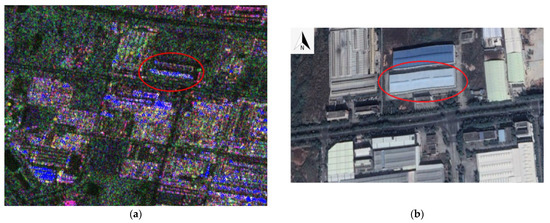
Figure 6.
The 180-degree phase ambiguity determination process based on a specific building of this scene: (a) The local area of Figure 5b in the Jiangmen scene, the RDBs marked in blue triangles correspond to the left peak in Figure 5e, and the building circled in red is the target. (b) The optical image of the corresponding building on a Google image.
It can also be proved that the left peak was the target peak in the estimation of transmitting phase imbalance; the similar derivation process was not repeated here. From the experimental results, the phase imbalance estimation differences between the two methods turned out to be 3.4 degrees and 3.0 degrees. Considering both methods’ estimation errors, the experimental results were reasonable and in line with expectations. This experiment fully verified the correctness, accuracy, and completeness of the proposed method.
3.3. The Receive Phase Imbalance Estimation Using Uncalibrated GF-3 Dual-Pol Data
In this part, we apply the proposed phase imbalance estimation method to the uncalibrated GF-3 dual-polarization data. The scene was imaged in the urban area of Beijing, which was the FSI mode, ascending, and with an incidence angle of 30.77°. The operation of the experiment was the same as in the previous two experiments. The result is shown in Figure 7.
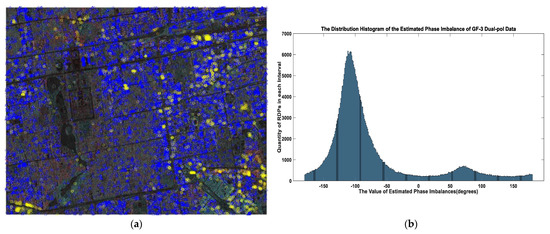
Figure 7.
The phase imbalance estimation results of GF-3 uncalibrated dual-pol SAR data: (a) The extracted RDBs are displayed locally in the Beijing urban area (Product ID: 2931251). The color assignment is red for the HH channel, green for the HV channel, and blue for the HV channel divided by the HH channel; (b) the distribution histogram of the estimated phase imbalances of the extracted RDBs of the whole scene.
Figure 7a shows the polarization pseudo-color image of a local area in the Beijing scene, where the RDB targets marked in blue triangles correspond to the left peak in Figure 7b, and the RDBs marked in yellow circles correspond to the right peak. Figure 7b shows the statistical results of the phase imbalance estimation of the extracted total of 528,819 RDB targets from the entire scene. It can be seen that the peak on the left was dominant, and its phase imbalance was estimated to be −108.1°. The peak on the right was relatively weak, it corresponded to an estimated phase imbalance of about 70°.
The phenomenon that one peak was much stronger than the other peak was seen in this experiment. When a large number of buildings in an urban area have the same orientation (i.e., most buildings in Beijing have a north-south orientation), the orientation of the walls corresponding to the effective dihedrals is the same. Then, the extracted RDBs correspond to the same type mostly, resulting in a strong peak.
However, since the data was not calibrated, we cannot judge whether the dominant peak was the target peak. The 180-degree phase ambiguity determination still needed to be performed.
The experiment is shown in Figure 8. It was a local area of this scene, in which there were a large number of RDBs marked in blue and a small number of RDBs marked in yellow, which corresponds to the two peaks, respectively, in Figure 7b. Two typical architectural targets were selected as the research objects. One was the building cluster corresponding to the circled blue RDBs, which was the Beijing West Railway Station and nearby buildings, almost facing due south, as shown in Figure 8c. The other was the building corresponding to the yellow RDBs, which was the Beijing Electric Power Hospital, as shown in Figure 8d.
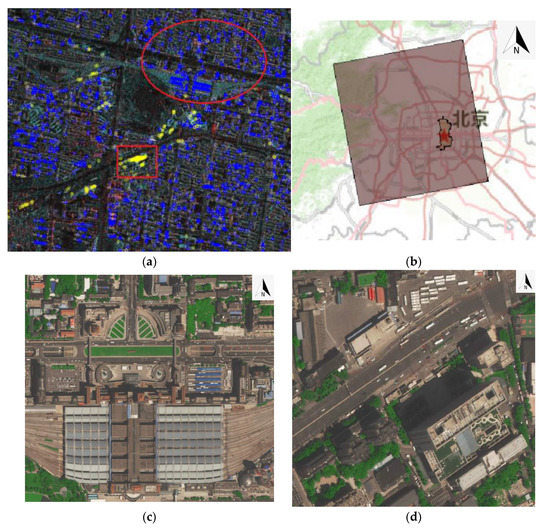
Figure 8.
(a): The local area in the Beijing scene. (b) The geographic location projection of the scene on the map (text in the picture is Beijing); (c) a Google optical image of the Beijing West Railway Station and the nearby buildings, corresponding to the area circled in figure (a). (d) A Google optical image of the Beijing Electric Power Hospital building, corresponding to the yellow-marked targets framed in figure (a).
The imaging range of the entire scene is displayed in Figure 8b, the latitude and longitude of the upper-left corner were (40.150°N, 115.912°E), and the lower-left corner was (39.669°N, 116.031°E). After conversion, the difference between the two points was 53 km in the north-south direction and 10 km in the east-west direction. The angle about the north-south direction was about 10.7°.
For the wall of the buildings facing south, the angle was equivalent to about 79.3°. Meanwhile, the incidence angle of this scene was 30.77°. Assuming that the scene had no obvious slope, the local incidence angle should be about 30.77°. Using Equation (11), we could obtain the rotation angle of these effective dihedrals was about −80.78 degrees. However, note that the only meaningful range for is between −45°and 45° [24]. Since urban blocks are usually rectangular, rotations exceeding ±45° begin to present the orthogonal sides as the stronger backscatter target [19]. Therefore, the value of should be about –10.7°, for which the western wall should be the main backscatter target. Then, the rotation angle of these effective dihedrals should be about 12.4°.
From Figure 1b, it can be seen that these RDBs should belong to the type of phase relationship of Equation (5a), which was exactly the condition used in the method. Therefore, the left peak in Figure 7b should be the target peak. The phase imbalance of this scene was eventually estimated to be −108.1°.
While the building shown in Figure 8d was located along the road, the wall of the main building facing the road was the structure corresponding to the strong scatter targets, whose orientation was not the north-south direction. It can be seen that it was rotated about 45 degrees from the north-south direction, then, the phase characteristic of HH and HV changed. For the corresponding RDBs, the yellow marks in the figure indicate that they belonged to the right peak in Figure 7b, which was not the target peak.
In general, the estimated rotation angle of the effective dihedral may not have been a completely accurate value, because the estimation of was affected by image parameters, geometric accuracy, etc., and the local incidence angle was also based on the assumption that the ground was flat. However, the phase difference of from one peak to another peak in Figure 1b was 45 degrees, which provided enough redundancy and insurance for the estimation errors of the rotation angle . Therefore, the judgment of the 180-degree phase ambiguity determination of the two experiments should have been correct and valid.
Since GF-3 dual-polarization data were not calibrated, the result could not be verified temporarily, but a meaningful reference value has been obtained for the first time.
3.4. The Phase Imbalance Estimation Experiments on Multiple Band Airborne SAR Data
The experiments in this subsection apply the method to airborne SAR data of different bands to verify the universality and robustness of the method.
The Aerospace Information Research Institute, Chinese Academy of Sciences (AIRCAS) led a development of an airborne multidimensional space joint-observation (SARMSJosSAR) system and carried out data acquisition experiments [25]. The airborne multidimensional SAR system includes six bands in total, among which the Ka-band has some problems, and here, a total of five bands of P, L S, C, and X data were used accordingly in this experiment. The system parameters of this airborne multi-band data are shown in the Table 1. “Br” is bandwidth, “Fsr” is the sampling rate, “Xbin” is the pixel interval in the azimuth direction, and “Rbin” is the pixel interval in the range direction.

Table 1.
Basic parameters of each band’s SAR data.
The data set used in the experiment was imaged in the Houhai area, east of Wanning, Hainan Province, on 25 December 2020. This data set has not undergone a calibration operation, the distortion parameters of each band are unknown. We chose a scene that contained a village and a forest area, as seen in Figure 9. The airborne SAR image range was small, encompassing only a few towns and villages. As can be seen from the figure, the color of some ground surface changed significantly with the change of radar wavelength.
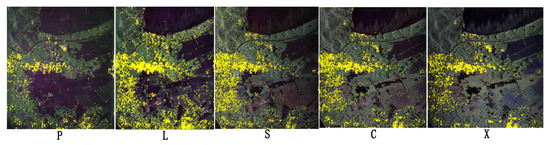
Figure 9.
The RDB targets extracted from airborne data of different bands in the same scene. The corresponding P/L/S/C/X band information is given at the bottom of each figure. The Pauli pseudo-color map is shown in the figure, and the RDB targets extracted from the scene are shown as yellow markers on each band image.
The experiment was conducted in the same way as in Section 3.2. The reference values were obtained by the distributed-targets-based polarimetric distortion estimation method. In the experiment, we chose the mountain forest region on the upper right of this scene as the object. The method proposed in the paper estimated the phase imbalance parameters using a limited number of village buildings in the scene. Meanwhile, the points marked in yellow in Figure 9 are the extracted RDB targets, for which we appropriately relaxed the K value to 2 or 1.5 to ensure that enough point targets were extracted. With the results of a forest-based quad-pol calibration method as a reference, we skipped the determination for 180-degree phase ambiguity. The results are shown in Table 2.

Table 2.
The phase imbalances estimation results of each band’s SAR data.
From Table 2, it can be seen that the estimation differences between the two methods in most cases were within the range of about 5 degrees. The S-band transmitting result that reached a level of 10 degrees was regarded as a discrete value, which may have been a statistical error caused by insufficient target points, for which we think it had no significant representative significance. Interestingly, the phase imbalance results estimated by RDBs were generally larger than those estimated by the distributed targets in this experiment. The systematic difference may have come from the unknown crosstalk of the airborne polarimetric system.
As for the reasons why the results were not ideal, firstly, the SAR data quality of the airborne data was not very good, including the poor radiation quality and unsatisfactory polarization isolation. In addition, due to the small image scene of the airborne data, the quantity of the RDBs obtained in this experiment was small (about 20,000, and even less for some bands’ data), which reduced the accuracy of the estimation results.
Nevertheless, the estimation differences were still within an allowable range in such complex multi-band scenes with poor data quality. From the results, the estimated errors did not show a clear correlation with the band, and it was seen that the method worked effectively in these bands. Therefore, it was shown that the method could be used for a rough estimation in complex airborne SAR data conditions. The method had a significant contribution to the quality assurance of full-polarization data and dual-polarization data.
4. Discussion
This method achieved an efficient and fast estimation of the phase imbalance of the full-polarization system and the phase imbalance of the receiver side of the dual-polarization system without relying on any calibrators.
It is necessary to fully discuss the considerations and limitations of this method. Firstly, the proposed method is suitable for SAR systems with high polarization isolation. The theoretical estimation error range is directly affected by the system cross-talks. Although there is an amplitude imbalance term in Equation (10), it is generally close to 1. As for the crosstalk, its magnitude directly affects the uncertainty of the estimation results. Fortunately, with the improvement of antenna technology, nowadays the SAR systems can generally achieve a high level of polarization isolation. Therefore, the method applies to most cases, and this can be proved in the experiment of airborne multi-band data.
In addition, the method requires the presence of a certain number of building targets in the scene, and there is no doubt that data imaged in urban areas are the ideal targets. Otherwise, a small number of RDBs will cause unknown bias in the statistical estimates. The impact of this error on the estimation results may be serious and cannot be quantified. Empirically, it is desirable to have more than 50,000 statistical samples in one scenario.
Processing parameters such as K-values and coherence thresholds are empirical, and changes in their values can have an impact on the number of extracted RDB targets. However, with a sufficient number, the results obtained from histogram statistics should be stable. If the scene is mostly urban, these parameters can be appropriately strict, and if the scene has limited buildings, these parameters can be appropriately relaxed. When the relaxed parameters still do not yield enough RDBs, the scenario may not be suitable.
The extracted RDB targets may also appear in small amounts in ridge regions, exposed rock areas, and so on. These targets most likely do not correspond to dihedral reflection structures and may be invalid. However, because we used the statistical method, the method itself has a strong tolerance to invalid values. As long as the point set is mostly extracted from an urban area, it will not affect the statistical results. For simplicity, we extracted the RDBs from the whole scene in the experiment. Future improvements for refinement and automation could add to the operation of identifying urban areas, but this was not the focus of this article.
Another limitation is the problem of 180-degree phase ambiguity determination, which can only be executed based on the double-bounce backscatters of a specific building structure at present. This operation requires human intervention and is kind of cumbersome as seen in the experiments. Fortunately, as the system is generally stable without jumps in distortion parameters, only one-time 180-degree phase ambiguity determination processing is needed for one system. In addition, there is enough error redundancy of inversion calculation to ensure the accuracy of the determination result. Of course, an automated and convenient 180-degree phase ambiguity determination approach will be an important advance for this RDBs-based phase imbalance estimation method.
5. Conclusions
In this paper, the extraction of numerous dihedral reflector clusters at specific rotation angles in urban areas was achieved by taking advantage of the existence of the secondary reflection structure of SAR radar waves widely present in urban areas. Innovatively, the calculated XPD values of these RDBs were used to obtain the estimation of the polarimetric phase imbalance by using the statistical big data approach with the help of the dihedral reflector characteristics. Finally, the proposed method achieved the effective estimation of the phase imbalance at the receiver side and transmitter side without relying on any artificial calibrators, of which the accuracy can be within 7 degrees. The method can be conveniently applied to dual-polarization data and full-polarization data in common wavebands with convenient, universal, and robust features.
The article gives a detailed theoretical derivation and principle explanation and gives detailed operational steps, especially the estimation error analysis of the method. It can be seen that although the method needs to deal with a large number of point targets, the method itself is relatively simple and intuitive, which reduces the application limitations and application threshold of the method, and the computation burden is not severe and can be performed in parallel. The universality, robustness, and high estimation accuracy of the proposed method were fully verified by a series of experiments. In practical application, the estimation error was generally within 5 degrees.
The method can be applied to assist in the calibration of dual-polarization systems or to the long-term monitoring of the key parameter of dual-polarization systems. Especially, this novel method can estimate the transmitting and receiving phase imbalances of the quad-polarization SAR data based on the urban areas, which means it can be an important supplement to the traditional distributed-targets-based quad-pol polarization calibration methods, such as the Quegan method [5] and the Ainsworth method [6]. Undoubtedly, the method presented in this paper has important reference and supplementary significance to the traditional polarization distortions’ calibration algorithms independent of calibrators.
Differently from the discrete point requirements emphasized in Lei Shi’s research about corner-reflector-like targets [9], because of the statistics of massive point targets, there is no need to carry out fine processing on individual points, which means the proposed method has a strong tolerance to complex SAR data performance. Therefore, the method has the advantages of strong robustness and low complexity.
As mentioned in the discussion, there are also some limitations to the proposed approach. The calibration of artificial calibrators cannot be replaced by the proposed method. Regarding the 180-degree phase ambiguity problem, an automatic and convenient solution approach is the focus of our future work. In addition, the method for achieving adaptive and automated extraction of RDBs in an unknown scene can continue to be researched and developed. At last, there are still two key distortion parameters of the polarimetric system, i.e., amplitude imbalance and crosstalk, which deserve more innovative work to be implemented, especially the estimation of amplitude imbalance at the receiver of the dual-polarization system, which is of great importance to realize the initial correction of the dual-polarization system.
6. Patents
The work reported in this article has applied for a national invention patent of China (Application Number: 202210527642.1).
Author Contributions
Conceptualization, S.S., X.Q., B.H. and K.F.; methodology, S.S. and K.F.; software, S.S.; validation, S.S., X.Q., K.F. and W.L.; formal analysis, S.S. and W.L.; investigation, S.S. and K.F.; resources, B.H. and K.F.; data curation, B.H.; writing—original draft preparation, S.S.; writing—review and editing, S.S. and X.Q.; visualization, S.S., B.H. and W.L.; supervision, K.F. and B.H.; project administration, X.Q. and K.F.; funding acquisition, W.L. and K.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation, China, grant number 62022082 and grant number 61725105.
Data Availability Statement
Not applicable.
Acknowledgments
GF-3 data were obtained from https://osdds.nsoas.org.cn (accessed on 15 December 2020). The authors would like to thank National Satellite Oceanic Application Center (NSOAS) for providing the data free of charge. The authors would like to thank to European Space Agency for providing Sentinel-1 data.
Conflicts of Interest
The authors declare no conflict of interests.
References
- Freeman, A. SAR calibration: An overview. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1107–1121. [Google Scholar] [CrossRef]
- Liang, W.; Jia, Z.; Qiu, X.; Hong, J.; Zhang, Q.; Lei, B.; Zhang, F.; Deng, Z.; Wang, A. Polarimetric Calibration of the GaoFen-3 Mission Using Active Radar Calibrators and the Applicable Conditions of System Model for Radar Polarimeters. Remote Sens. 2019, 11, 176. [Google Scholar] [CrossRef] [Green Version]
- Fore, A.G.; Chapman, B.D.; Hawkins, B.P.; Hensley, S.; Jones, C.E.; Michel, T.R.; Muellerschoen, R.J. Uavsar polarimetric calibration. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3481–3491. [Google Scholar] [CrossRef]
- Van Zyl, J. Calibration of polarimetric radar images using only image parameters and trihedral corner reflector responses. IEEE Trans. Geosci. Remote Sens. 1990, 28, 337–348. [Google Scholar] [CrossRef]
- Quegan, S. A unified algorithm for phase and cross-talk calibration of polarimetric data-theory and observations. IEEE Trans. Geosci. Remote Sens. 1994, 32, 89–99. [Google Scholar] [CrossRef]
- Ainsworth, T.; Ferro-Famil, L.; Lee, J.-S. Orientation angle preserving a posteriori polarimetric SAR calibration. IEEE Trans. Geosci. Remote Sens. 2006, 44, 994–1003. [Google Scholar] [CrossRef]
- Shimada, M. Model-based polarimetric sar calibration method using forest and surface-scattering targets. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1712–1733. [Google Scholar] [CrossRef]
- Shi, L.; Yang, J.; Li, P. Co-polarization channel imbalance determination by the use of bare soil. ISPRS J. Photogramm. Remote Sens. 2014, 95, 53–67. [Google Scholar] [CrossRef]
- Shi, L.; Li, P.; Yang, J.; Zhang, L.; Ding, X.; Zhao, L. Co-polarization channel imbalance phase estimation by corner-reflector-like targets. ISPRS J. Photogramm. Remote Sens. 2019, 147, 255–266. [Google Scholar] [CrossRef]
- Villa, A.; Iannini, L.; Giudici, D.; Monti-Guarnieri, A.V.; Tebaldini, S. Calibration of SAR Polarimetric Images by Means of a Covariance Matching Approach. IEEE Trans. Geosci. Remote Sens. 2015, 53, 674–686. [Google Scholar] [CrossRef]
- Jiang, S.; Qiu, X.; Han, B.; Hu, W. A Quality Assessment Method Based on Common Distributed Targets for GF-3 Polarimetric SAR Data. Sensors 2018, 18, 807. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shangguan, S.; Qiu, X.; Fu, K.; Lei, B.; Hong, W. GF-3 Polarimetric Data Quality Assessment Based on Automatic Extraction of Distributed Targets. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4282–4294. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W.; Zhang, J.; Uhlhorn, E.W.; He, Y. High-Resolution Hurricane Vector Winds from C-Band Dual-Polarization SAR Observations. J. Atmos. Ocean. Technol. 2014, 31, 272–286. [Google Scholar] [CrossRef]
- Schuler, D.; Lee, J.; Kasilingam, D.; Pottier, E. Measurement of ocean surface slopes and wave spectra using polarimetric SAR image data. Remote Sens. Environ. 2004, 91, 198–211. [Google Scholar] [CrossRef]
- Cartus, O.; Santoro, M.; Kellndorfer, J. Mapping forest aboveground biomass in the Northeastern United States with ALOS PALSAR dual-polarization L-band. Remote Sens. Environ. 2012, 124, 466–478. [Google Scholar] [CrossRef]
- Bouvet, A.; Le Toan, T.; Dao, N.L. Estimation of agricultural and biophysical parameters of rice fields in Vietnam using X-band dual-polarization SAR. In Proceedings of the IGARSS 2014—2014 IEEE International Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 1504–1507. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, J.-J.; Li, Y.; Hong, W. General Calibration Algorithm for Single-transmitting-dual-receiving Polarimetric SAR System. J. RADARS 2012, 1, 323–328. [Google Scholar] [CrossRef]
- Lavalle, M.; Pottier, E.; Ainsworth, T.; Solimini, D.; Rosich, B. Calibration of dual polarimetric c-band sar data: A possible approach for sentinel-1. In Proceedings of the Fourth International Workshop on Science & Applications of Sar Polar, Frascati, Italy, 22 January 2009. [Google Scholar]
- Atwood, D.K.; Thirion-Lefevre, L. Polarimetric Phase and Implications for Urban Classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1278–1289. [Google Scholar] [CrossRef]
- Jiang, S.; Qiu, X.; Han, B.; Sun, J.; Ding, C. Error Source Analysis and Correction of GF-3 Polarimetric Data. Remote Sens. 2018, 10, 1685. [Google Scholar] [CrossRef] [Green Version]
- Reigber, A.; Jager, M.; Pinheiro, M.; Scheiber, R.; Prats, P.; Fischer, J.; Horn, R.; Nottensteiner, A. Performance of the P-band subsystem and the X-band interferometer of the F-SAR airborne SAR instrument. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5037–5040. [Google Scholar]
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Geudtner, D.; Torres, R.; Snoeij, P.; Ostergaard, A.; Navas-Traver, I. Sentinel-1 mission capabilities and SAR system calibration. In Proceedings of the 2013 IEEE Radar Conference (RadarCon13), Ottawa, ON, Canada, 29 April–3 May 2013. [Google Scholar]
- Lee, J.-S.; Ainsworth, T.L.; Wang, Y. Investigating slanted double bounce scattering mechanisms based on scattering models. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]
- Wen, H. Research progresss on multidimensional space joint- observation SAR. In Proceedings of the Conference Proceedings of 2013 Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Tsukuba, Japan, 23–27 September 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).