A Fixed-Threshold Method for Estimating Fractional Vegetation Cover of Maize under Different Levels of Water Stress

Abstract

Accurate estimation of fractional vegetation cover (FVC) from digital images taken by commercially available cameras is of great significance in order to monitor the vegetation growth status, especially when plants are under water stress. Two classic threshold-based methods, namely, the intersection method (T₁ method) and the equal misclassification probability method (T₂ method), have been widely applied to Red-Green-Blue (RGB) images. However, the high coverage and severe water stress of crops in the field make it difficult to extract FVC stably and accurately. To solve this problem, this paper proposes a fixed-threshold method based on the statistical analysis of thresholds obtained from the two classic threshold approaches. Firstly, a Gaussian mixture model (GMM), including the distributions of green vegetation and backgrounds, was fitted on four color features: excessive green index, H channel of the Hue-Saturation-Value (HSV) color space, a* channel of the CIE L*a*b* color space, and the brightness-enhanced a* channel (denoted as a*_I). Secondly, thresholds were calculated by applying the T₁ and T₂ methods to the GMM of each color feature. Thirdly, based on the statistical analysis of the thresholds with better performance between T₁ and T₂, the fixed-threshold method was proposed. Finally, the fixed-threshold method was applied to the optimal color feature a*_I to estimate FVC, and was compared with the two classic approaches. Results showed that, for some images with high reference FVC, FVC was seriously underestimated by 0.128 and 0.141 when using the T₁ and T₂ methods, respectively, but this problem was eliminated by the proposed fixed-threshold method. Compared with the T₁ and T₂ methods, for images taken in plots under severe water stress, the mean absolute error of FVC obtained by the fixed-threshold method was decreased by 0.043 and 0.193, respectively. Overall, the FVC estimation using the proposed fixed-threshold method has the advantages of robustness, accuracy, and high efficiency, with a coefficient of determination (R²) of 0.99 and root mean squared error (RMSE) of 0.02.

1. Introduction

Under climate change, water stress has become a great challenge to maize products globally. In research on crop yield, non-destructive monitoring of crop structural traits is of great significance. As one of the most widely used structural traits, fractional vegetation cover (FVC), defined as the proportion of ground surface occupied by green vegetation [1], plays an important role in monitoring vegetation growth status and estimating crop yields (e.g., evapotranspiration and above-ground biomass) [2,3,4]. In addition, FVC is also a key parameter in the AquaCrop model, which is widely used to simulate crop yield response to water under different irrigation and field management practices [5,6]. Therefore, it is important to estimate FVC rapidly and accurately for annual crops under different irrigation treatments during crop growing seasons.

Visual estimation, direct sampling, and digital photography have been developed to measure FVC for agricultural applications [7,8]. With the development of sensor technology, many researchers have used Red-Green-Blue (RGB) digital cameras [9,10,11] or near infrared (NIR) spectral sensors [12] in the field of agriculture. However, RGB digital imagery has been used more widely than NIR spectral sensors in image segmentation, with the advantages of low cost and higher spatial resolution. With the availability of inexpensive high-quality digital cameras in agriculture applications, estimating FVC by image segmentation is becoming more common. In general, image-based FVC estimation can be grouped into two categories: (1) machine learning methods (e.g., K-means, Decision Tree, Artificial Neural Networks, and Random Forest) [13,14,15] and (2) threshold-based methods [16,17]. Machine learning methods need a large amount of training data sets for the purposes of calibration. The generation of training data, affected by human intervention, has a great influence on model accuracy. Threshold-based methods, with their advantages of simplicity, high efficiency, and accuracy, play an important role in precision agriculture [18], and have been successfully used for crops such as wheat, maize, cotton, and sugar beet [12,19,20,21].

Selecting an appropriate color feature for crop segmentation is a key step to obtain FVC estimations using threshold-based methods [17,22]. Excessive green index (ExG) [23,24], H channel of the Hue-Saturation-Value (HSV) color space [25], and a* channel of the CIE L*a*b* color space [26] are the three widely used color features. The visible spectral index, ExG, can be calculated directly from digital numbers in three components of RGB images, and represents the contrast of the green spectrum against red and blue [24]. The H channel from the HSV color space uses an angle from 0° to 360° to represent different colors [27]. The a* channel from the CIE L*a*b* color space is relative to the green-red opponent colors [26]. In addition, to deal with the shadow effect in classification, the Shadow-Resistant LABFVC (SHAR-LABFVC) method was proposed [28]. In the SHAR-LABFVC method, the CIE L*a*b* color space, from which the a* color feature was extracted, was transformed from the brightness-enhanced RGB. To distinguish it from the a* color space in other research [26], the a* color feature in the SHAR-LABFVC method is denoted as the a*_I color feature in this study.

Another key step to obtain FVC estimations using threshold-based methods is searching for the appropriate classification threshold. Otsu’s method is one of the most widely used threshold techniques [29], and has been used in many applications of image segmentation and plant detection [30,31,32]. However, this method can produce under-segmentation in some circumstances [18]. Another widely used threshold method was proposed by [16] based on a Gaussian mixture model (GMM) of color features derived from images. Specifically, a Gaussian mixture model is a parametric probability density function represented as a weighted sum of Gaussian component densities. Classification thresholds for discriminating vegetation and backgrounds can be calculated from a GMM fitted on different color features. Fitting a GMM on an appropriate color feature contributes to accurate threshold calculation.

To evaluate the separability of two Gaussian distributions on different color features, the separability distance index (SDI) [26] and the instability index (ISI), which is the reciprocal of SDI [33], were proposed. SDI (Equation (1)) describes the separability of the distributions between vegetation and backgrounds,

$$\mathrm{SDI}=\frac{\left|{\mu }_v-{\mu }_b\right|}{{\sigma }_v+{\sigma }_b}$$

(1)

where ${\mu }_v$ and ${\mu }_b$ are mean values of green vegetation and backgrounds, respectively; and ${\sigma }_v$ and ${\sigma }_v$ are standard deviations of green vegetation and backgrounds, respectively. The larger the SDI is, the easier it is to fit these two Gaussian distributions. However, whether the SDI is an appropriate criterion for selecting the right color feature to produce the best performance of GMM fitting is still uncertain and has not been explored in previous research. It is necessary to further study the applicability of SDI in selecting color features.

With GMM fitted on an appropriate color feature, applying an optimal approach to obtain the classification threshold is essential for calculating FVC. Once the parameters for both Gaussian distributions of vegetation and backgrounds have been estimated, classification thresholds can be calculated by two classic methods, namely, the intersection method, and the equal misclassification probability method. In the intersection method, the intersection of the two Gaussian distributions is used as the classification threshold (hereinafter referred to as T₁). In the equal misclassification probability method (hereinafter referred to as T₂), the threshold makes the green vegetation and backgrounds have an equal misclassification probability [26]. Both two classic methods derive thresholds based on the Gaussian distributions of green vegetation and backgrounds in each image.

However, both the two abovementioned threshold methods have limitations. Firstly, both perform well when the bimodality is clearly seen in the distributions of images on a color feature; however, when FVC is extremely low or the canopy is nearly closed, the thresholds obtained by these methods may be inaccurate. Secondly, in semi-arid and arid areas, where climate is characterized by long periods of drought with decreasing projected rainfall, the high possibility of crops suffering from water stress may raise a new challenge for FVC estimation caused by spectral changes. To cope with water stress, crops usually exhibit adaptive mechanisms at the leaf level to reduce light absorption and dissipate excess absorbed energy, such as the decrease in chlorophyll concentration and down-regulation of photosynthesis, and increase in the concentration of deep oxidized xanthophyll cycle components [34,35,36,37]. The spectral changes of crops caused by the pigment changes at the leaf level may have a great influence on the accuracy of threshold calculation using the two methods. Therefore, RGB images collected across the entire crop growing season with a wider FVC range and different levels of water stress conditions need to be further studied regarding the performance of FVC estimation using threshold methods based on GMM. In addition, in our previous research for cotton FVC estimation [21], an interesting phenomenon was found: a fixed classification threshold exists in the a* channel. Therefore, further study is needed to determine if there is a fixed classification threshold for maize.

In this study, there were two main objectives: (1) to determine if a fixed-threshold method exists and is applicable for images covering the full range of FVC from open to nearly closed; (2) to explore if the fixed-threshold method outperforms the two classic threshold-based methods (T₁ and T₂ methods) in estimating FVC for images with high reference FVC or captured from deficit irrigation plots. This research could provide a more practical, efficient, and accurate way to estimate the FVC of field maize under water stress based on RGB imagery.

2. Materials

2.1. Study Site and Management

Field experiments were conducted during 2013, 2015, and 2016 growing seasons at the USDA-ARS Limited Irrigation Research Farm, in Greeley, Colorado, USA (40°26′57″N, 104°38′12″W, elevation 1427 m). The maize (Zea mays L.) was planted with 0.76 m row spacing on May 14 (day of year, DOY 134), June 3 (DOY 154), and May 5 (DOY 126) in 2013, 2015, and 2016, respectively. Twelve irrigation treatments (TRTs) (Table 1), each 9 m wide by 43 m long, were randomly arranged with four replications (Figure 1a). Deficit irrigation was applied during the late vegetative and maturation growth stages. The dates when maize reached the late vegetative stage (V8), beginning of reproductive stage (R1), and beginning of maturation stage (R4) were July 1 (DOY 182), July 29 (DOY 210), and August 19 (DOY 231) for the 2013 growing season, respectively. In 2015, these dates were July 6 (DOY 187), August 3 (DOY 215), and August 24 (DOY 236), respectively. In 2016, these dates were June 27 (DOY 179), July 25 (DOY 207), and August 9 (DOY 222), respectively. Each treatment targeted a percent of maximum non-stressed crop evapotranspiration (ET) during late vegetative and maturation growth stages, respectively. Table 1 shows the sum of actual net irrigation amounts and precipitation for each treatment. Details can be found in [38] for the calculation of maximum ET.

Table 1. Irrigation treatment and total irrigation and precipitation amount (mm) in different growing stages. In 2015 and 2016, irrigation treatment 5 (TRT5) (80/50) was replaced by TRT13 (40/80).

Treatment	Late Vegetative Stage			Reproductive Stage			Maturation Stage			Total
	2013	2015	2016	2013	2015	2016	2013	2015	2016	2013	2015	2016
TRT1(100/100)	228	176	164	127	139	177	254	264	198	609	579	539
TRT2(100/50)	228	176	165	122	113	169	165	98	74	515	387	408
TRT3(80/80)	180	136	141	128	131	169	217	211	155	525	478	465
TRT4(80/65)	181	136	141	128	121	179	196	152	96	505	409	416
TRT5(80/50)	180	/	/	128	/	/	165	/	/	473	/	/
TRT6(80/40)	180	136	141	128	133	195	137	65	56	445	334	392
TRT7(65/80)	136	94	99	149	134	185	217	224	155	502	452	439
TRT8(65/65)	136	94	97	149	135	189	196	134	96	481	363	382
TRT9(65/50)	136	95	98	150	135	189	165	89	73	451	319	360
TRT10(65/40)	136	95	93	150	137	195	138	65	56	424	297	344
TRT11(50/50)	101	64	97	158	136	200	165	89	73	424	289	370
TRT12(40/40)	83	50	76	158	136	211	137	65	56	378	251	343
TRT13(40/80)	/	50	76	/	134	194	/	214	155	/	398	425

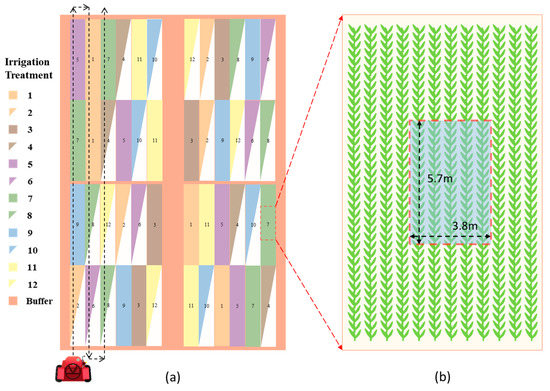
Figure 1. Schematic diagram of the experimental field indicating layout of irrigation treatments and image capturing route (a), and location and target view of Red-Green-Blue (RGB) image acquisition (b). In 2015 and 2016, irrigation treatment 5 (TRT5) was replaced by TRT13 (Table 1).

2.2. Canopy Temperature and Meteorological Data Measurements

Infrared thermometers (IRT, model: SI-121, Apogee Instruments, Inc., Logan, UT, USA) were used to continuously monitor maize canopy temperature. The view angle and accuracy were 36° and ±0.2 °C, with a temperature range of −10 °C to 65 °C. To ensure the maize canopy was primarily included in the field of view, the IRTs were attached to telescoping posts and angled 23° below horizon and 45° from north (looking northeast). The IRTs were kept at a height of 0.8 m above the top of canopy with the viewing area of 13.35 m² and adjusted twice per week during the vegetative stage. In 2013, IRT sensors were installed in six of the twelve treatments: TRT1 (100/100), TRT2 (100/50), TRT3 (80/80), TRT6 (80/40), TRT8 (65/65), and TRT12 (40/40). In 2015 and 2016, IRT sensors were installed for all treatments except for: TRT4 (80/65) and TRT6 (80/40).

Meteorological data were taken by the on-site Colorado Agricultural Meteorological Network station GLY04 (CoAgMet), including daily precipitation, air temperature, relative humidity (and subsequent vapor pressure deficit), solar radiation, and wind speed taken at 2 m above a grass reference surface. The canopy temperature and meteorological data were used to calculate the crop water stress index (CWSI), which is one of the most frequently adopted indicators of crop water stress [39].

2.3. Crop Water Stress Index (CWSI)

The empirical CWSI method defined by [40] was adopted in this study. It is calculated as in Equation (2):

$$\mathrm{CWSI}=\frac{{\mathrm{dT}}_{\mathrm{m}}-{\mathrm{dT}}_{\mathrm{LL}}}{{\mathrm{dT}}_{\mathrm{UL}}-{\mathrm{dT}}_{\mathrm{LL}}}$$

(2)

where dT_m is the difference between measured canopy and air temperature; dT_LL and dT_UL are the lower and upper limits of canopy-air temperature differential. CWSI values of 0 indicate no stress and values of 1 indicate maximum stress. In this study, 5 °C was used as the upper baseline. The actual CWSI could be slightly greater than 1, due to the fact that measured dT_m values could be occasionally greater than the upper baseline [41]. The lower baseline for 2013, 2015, and 2016 can be found in Equations (3)–(5), respectively:

$${\mathrm{dT}}_{\mathrm{LL}}=-1.79\times \mathrm{VPD}+2.34$$

(3)

$${\mathrm{dT}}_{\mathrm{LL}}=-1.97\times \mathrm{VPD}+3.43$$

(4)

$${\mathrm{dT}}_{\mathrm{LL}}=-2.76\times \mathrm{VPD}+4.98$$

(5)

where VPD is the vapor pressure deficit of the atmosphere with the unit of kPa. VPD is related to air temperature and relative humidity, and can be calculated by Equation (6) [42]:

$$\mathrm{VPD}=0.6108\times \exp \left(\frac{17.27{\mathrm{T}}_{\mathrm{a}}}{{\mathrm{T}}_{\mathrm{a}}+237.3}\right)\times (\frac{100-\mathrm{RH}}{100})$$

(6)

where T_a is air temperature with the unit of °C, and RH is relative humidity.

2.4. RGB Image Acquisition

A Canon EOS 50D DSLR camera (Canon Inc., Tokyo, Japan) was attached to a boom that was mounted on a high clearance tractor and then elevated about 7 m above the ground. The sensor size and resolution were 22.3 mm × 14.9 mm and 4752 × 3168 pixels. The target view of the ground was about 5.7 m × 3.8 m at the center row of each plot (encompassing 5 rows, Figure 1b), and due to the adoption of the small resolution mode (2352 pixels × 1568 pixels), the pixel size of images was about 0.24 cm. Nadir view RGB images were taken near solar noon from each treatment plot. Figure 1a shows the capturing route of RGB images. Detailed RGB image collection dates are shown in Table 2.

Table 2. Red-Green-Blue (RGB) images and crop water stress index (CWSI) data measurements with respect to the day of year (DOY). ”√” represents that there are corresponding CWSI data.

Growing Stages	2013		2015		2016 *
	DOY	CWSI	DOY	CWSI	DOY	CWSI
Other vegetative stage	169		174		/
	176		181		175
Late vegetative stage	183		195	√	180	√
	192		198	√	188
	197		204	√	194	√
	206	√	209	√	202	√
Reproductive stage	211	√	218	√	207	√
	227	√	233	√	215	√
Maturation stage	232	√	237	√	228	√
	247	√	244	√	/
	/		253		/

* Severe hail damage occurred on 19 August 2016 (DOY 232).

2.5. Image Selection

To better evaluate the adaptability of the proposed method in this study to different FVC levels and water stress levels, a total of 102 RGB images were selected from 2013, 2015, and 2016 growing seasons. These images cover the full range of FVC from open to nearly closed. Of these images, 54 were taken from fully irrigated plots (TRT1) to test the adaptability of the new method to different FVC levels, and 48 were taken from plots under different irrigation treatments to test the adaptability of the new method to different water stress levels. Specifically, water stress levels were defined using CWSI: no water stress (NWS) when CWSI was less than 0.20; intermediate water stress (MWS) when CWSI was between 0.20 and 0.60; and severe water stress (SWS) when CWSI was greater than 0.60. The 54 images taken from TRT1 were divided into the test image group (hereinafter referred to as Test_full) and the validation image group (hereinafter referred to as Val_full) with a ratio of 2:1. In the same way, the 48 images with different levels of water stress were divided into Test_ws and Val_ws groups. Deficit irrigation started from the late vegetative stage when FVC_ref reached about 0.50 for maize from fully irrigated plots, and images from Test_ws and Val_ws sets were captured after the late vegetative stage. Therefore, compared with the Test_full and Val_full image sets, the lower limits of FVC_ref of Test_ws and Val_ws image sets were higher. The details of all these 102 images are listed in Table 3.

Table 3. A total of 102 RGB images were selected, with 54 images from fully irrigated plots and 48 images from plots under different levels of water stress. FVC_ref represents the reference fractional vegetation cover (FVC) of the image. NWS, MWS, and SWS represent no water stress, intermediate water stress, and severe water stress, respectively.

Image Details	Images Taken from Fully Irrigated Plots		Images Taken from Plots with Different Irrigation Treatments
	Test_Full	Val_Full	Test_ws	Val_ws
Number of images	36	18	32	16
Range of FVCref	0.07~0.90	0.03~0.87	0.29~0.75	0.25~0.69
Water stress level	NWS	NWS	NWS	NWS
			MWS	MWS
			SWS	SWS

3. Methodology

Three main steps were taken to estimate maize FVC based on RGB images: (1) extraction of four color features, namely, a*_I, a*, ExG, and H; (2) classification threshold computation and analysis; and (3) removal of background scatters based on the morphological differences between maize plant and background scatters. Details can be found hereafter for these three steps. Figure 2 shows the procedure of maize FVC estimation using three different threshold-based methods. In this study, proximally sensed RGB images were processed and analyzed by using custom-written scripts programmed in R language (R-3.5.3, https://www.r-project.org/ (accessed on 1 June 2020)).

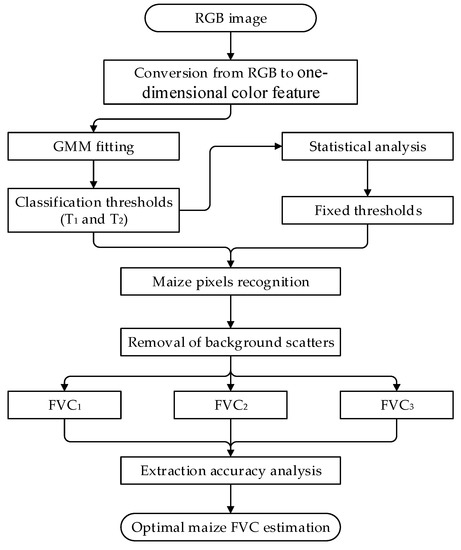
Figure 2. The procedure to estimate maize fractional vegetation cover (FVC) using three different threshold-based methods based on RGB images.

3.1. Aquisition of Four Color Features

The selection of an appropriate color feature contributes to a better performance in image segmentation. In this study, four color features, a*_I, a*, ExG, and H, were extracted from CIE L*a*b*, RGB, and HIS color spaces. The calculation process is shown in Figure 3, and the four color features are highlighted using rectangles covered with orange lines.

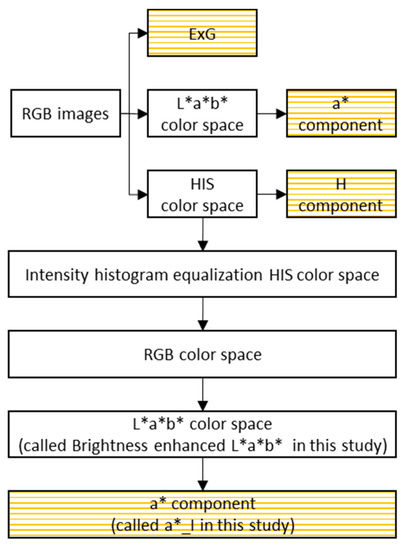
Figure 3. The process of extracting four color features (a*_I, a*, ExG, and H) from RGB images directly and indirectly.

3.2. Approaches to Calculating the Thresholds for Image Segmentation

In proximally sensed images, the distributions of vegetation and backgrounds were assumed to follow GMM on one color feature. With the assumption of only two classes in these images [20], the GMM function can be given by:

$$F(x)={\omega }_v\times N({\mu }_v,{\sigma }_v^2)+{\omega }_b\times N({\mu }_b,{\sigma }_b^2)$$

(7)

where $\omega$, $\mu$, $\sigma$ and are weight, mean value, and standard deviation, respectively; subscript $v$ and $b$ represent vegetation and backgrounds, respectively; $N(\mu ,{\sigma }^2)$ represents the Gaussian distribution function; and x is the value of image on the color feature. The GMM function was fitted using the “mixtools” package in R [43].

Two classic threshold methods: the two Gaussian distribution curves of GMM shown in Figure 4 represent the distributions of green vegetation and backgrounds, respectively. Based on the GMM fitted on one color feature, T₁ can be calculated by solving Equation (8).

$${\omega }_v\times N({\mu }_v,{\sigma }_v^2)={\omega }_b\times N({\mu }_b,{\sigma }_b^2)$$

(8)

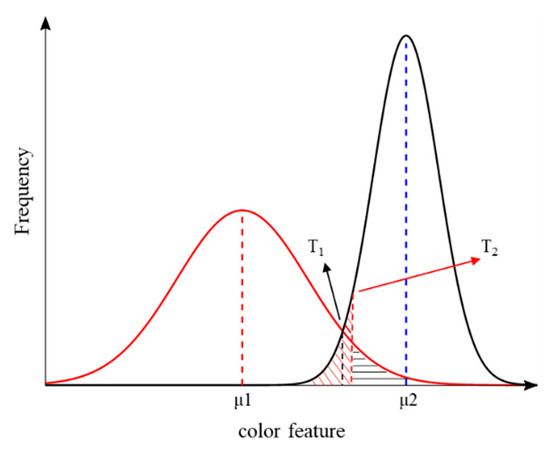
Figure 4. An example of a Gaussian mixture model (GMM) fitted on one color feature with two distinct peaks representing vegetation and backgrounds. The T₁ and T₂ are classification thresholds of vegetation and backgrounds: T₁ represents the intersection of the two Gaussian distributions; T₂ represents the point at which the misclassification probability for vegetation (zone covered with red lines) and backgrounds (zone covered with black lines) is equal.

Secondly, the threshold obtained using the T₂ method made the misclassification probabilities of green vegetation and backgrounds equal. As shown in Figure 4, T₂ can be calculated by solving a complementary error function as in Equation (9):

$${\omega }_v\times erfc({\mu }_v,{\sigma }_v^2)={\omega }_b\times erfc({\mu }_b,{\sigma }_b^2)$$

(9)

where $erfc$ is the complementary Gaussian error function. Classification thresholds and FVC estimation were obtained using these two approaches. To distinguish different combinations of two threshold calculation methods and four color features, they are denoted using the color feature name and threshold calculation name with an underscore between them. For example, a*_I_T₁ is used to represent the combination of the T₁ method and the a*_I color feature.

The fixed-threshold method was proposed based on the statistical analysis of one of the classic methods which performs better in FVC estimation. If a real threshold which generates the reference FVC (FVC_ref) of maize exists, the smaller the absolute estimation error, the closer the thresholds calculated from the T₁/T₂ method are to the real threshold. In this study, we set the upper limit of absolute estimation error at 0.025 to get a more accurate threshold. Therefore, in the statistical analysis, only the thresholds which made the absolute estimation error of FVC less than 0.025 were used. The thresholds calculated from RGB images with FVC_ref less than 0.5 were averaged. Then, the average value was referred to as the initial threshold of the fixed-threshold method. On the other hand, the average of thresholds obtained from the images with FVC_ref greater than 0.5 was used as the adjusted threshold of the fixed-threshold method.

3.3. Removal of Scatters and Spurs Using Morphological Method

Considering that the GMM model is fitted based on the distribution of color features of each pixel, there are two main drawbacks when estimating FVC using this method: it may generate misclassified scatters with a high probability, and the edge of the extracted vegetation may not be well preserved [22]. In this study, to remove misclassified scatters and to trim the edge of extracted vegetation, the morphological algorithm was adopted. After vegetation pixels were recognized, all extracted pixel clusters (including misclassified scatters) could be treated as regions with different numbers of pixels. In general, misclassified scatters were regions with small numbers of pixels. Therefore, the size of the pixel cluster area was used as the criterion to decide whether it was a misclassified scatter. The optimal threshold used to remove the scatters was determined by comparing the differences between the FVC estimations and FVC_ref. The smallest difference was obtained when the threshold of 500 was used. It is worth noting that similar differences were obtained around the optimal threshold of 500. Thus, in this study, if the area of the pixel cluster was less than 500 pixels, it was treated as a misclassified scatter and was removed. As for trimming the edge of extracted vegetation, maize leaves should be closed regions with smooth edges. However, after vegetation pixels were recognized, small spurs often appeared on the edge. If the area of the pixel cluster on the edge of extracted vegetation was less than 500 pixels, it was treated as a spur and was removed.

3.4. Assessment of FVC Extraction Accuracy

The FVC_ref of all test images was obtained by supervised classification via Environment for Visualizing Images (ENVI; Exelis, Inc., Boulder, CO, USA). Due to the high resolution of proximal RGB images, the FVC_ref values obtained from this method are reliable [18,44]. Specifically, to get the accurate FVC_ref, training samples of about 12,000 pixels including pure green vegetation and pure backgrounds were selected for each image using the tool of New Region of Interest in ENVI. Then, a supervised classification using support vector machine algorithm [45] was performed based on these training samples. Finally, a classified image was obtained, and the proportion of green vegetation was calculated as the FVC_ref. In addition, a set of test samples of about 8000 pixels was selected for each test image using the tool of New Region of Interest in ENVI, and was used to evaluate the accuracy of the classified image. For all classified images, the average of kappa coefficient was 0.983, and the average of overall accuracy was 99.1%. The results demonstrated that the FVC_ref values calculated from the classified images were accurate enough to assess the performance of FVC estimations of other methods. In this study, the performance of FVC estimations was assessed using the estimation error (EE) and mean absolute error (MAE), which were defined as:

$$\mathrm{EE}=\mathrm{FVC}-{\mathrm{FVC}}_{\mathrm{ref}}$$

(10)

$$\mathrm{MAE}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{\mathrm{EE}}_i}$$

(11)

where FVC_ref and FVC are reference FVC and FVC estimations derived from three threshold methods. N and i represent the total number of images and image index, respectively. In addition, the root mean squared error (RMSE) and the coefficient of determination (R²) were used to assess the correlation between FVC_ref and FVC obtained using different methods.

4. Results

4.1. Deficit Irrigation Results Evaluated by CWSI

The sensitivity of the CWSI empirical method for maize water stress has been verified within the same research field in previous studies [46,47]. Significant correlations were found between CWSI and classical water stress indicators (soil water deficit and sap flow). Figure 5 shows the seasonal trends of CWSI for TRT1(100/100), TRT3(80/80), TRT8(65/65), and TRT12(40/40). Clear differences among TRT1, 3, 8, and 12 were found for the 2015 growing season during the late vegetative stage when deficit irrigation was applied. The corresponding mean CWSI values for TRT1, 3, 8, and 12 were 0.06, 0.23, 0.69, and 0.90, respectively. With the release of deficit irrigation during the reproductive stage, all deficit irrigation treatments (TRT3, 8, and 12) had clear deceases, with mean CWSI values decreased to 0.02, 0.15, and 0.18, respectively. When deficit irrigation was re-imposed during the maturation stage, clear differences among TRT1, 3, 8, 11, and 12 showed again, with average CWSI values of 0.09, 0.26, 0.47, and 0.51. At the same time, it could be observed that the differences in CWSI became more obvious as deficit irrigation progressed, with values of 0.15, 0.32, 0.57, and 0.69 for TRT1, 3, 8, and 12 on DOY 253. Similar patterns were also observed for the 2013 and 2016 growing seasons. Overall, different levels of water stress were observed for all three maize growing seasons.

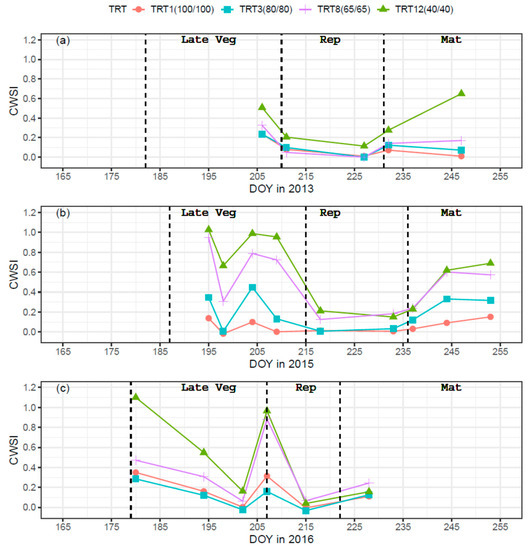
Figure 5. Time series of crop water stress index (CWSI) for TRT1(100/100), TRT3(80/80), TRT8(65/65), and TRT12(40/40) in the 2013 (a), 2015 (b), and 2016 (c) growing seasons. The black dotted lines are boundaries between different growing stages. Late Veg, Rep, and Mat are the abbreviations for late vegetative, reproductive, and maturation stages, respectively.

4.2. Comparison of Two Classic Methods on Four Color Features

The mean absolute error (MAE) of maize FVC estimations was calculated based on Test_full and Test_ws image sets (Table 4). Compared with the T₂ method, the T₁ method performed better with lower MAEs for all four color features. When the T₁ method was used, the a*_I color feature performed best for both Test_full and Test_ws image sets with an MAE of 0.021 and 0.047, respectively. The H color feature resulted in the greatest MAE for Test_full (0.122) and Test_ws (0.150) among the four color features. The a* color feature generated greater MAEs than the ExG color feature for both Test_full and Test_ws image sets. All these results showed that the T₁ method was better than the T₂ method, and the a*_I color feature had the best robustness for images with the wide range of FVC_ref and with different water stress levels.

Table 4. Mean absolute error (MAE) of T₁ and T₂ methods on four color features.

Image Sets	Color Features	Threshold Methods	MAE
Test_full	a*_I	T1	0.021
		T2	0.073
	a*	T1	0.093
		T2	0.169
	ExG	T1	0.032
		T2	0.06
	H	T1	0.122
		T2	0.146
Test_ws	a*_I	T1	0.047
		T2	0.168
	a*	T1	0.099
		T2	0.2
	ExG	T1	0.047
		T2	0.114
	H	T1	0.15
		T2	0.189

4.3. Calculation Results of Two Threholds in the Fixed-Threshold Method

Considering that a*_I_T₁ outperformed all other methods used above, statistical analysis of thresholds was implemented based on the results of the a*_I_T₁ method. The classification thresholds with absolute estimation error less than 0.025 obtained by the a*_I_T₁ method are shown in Figure 6. For images with FVC_ref less than 0.5, the classification thresholds showed a small variation with a mean value of −2.72 and standard deviation of 0.39. Thus, the mean value of −2.72 was used as the initial threshold of the fixed-threshold method. On the other hand, there is a decreasing trend for classification thresholds when FVC_ref is greater than 0.5. To make the second fixed threshold applicable to most images with FVC_ref greater than 0.5, the average value of −4.60 was used as the adjusted threshold of the fixed-threshold method.

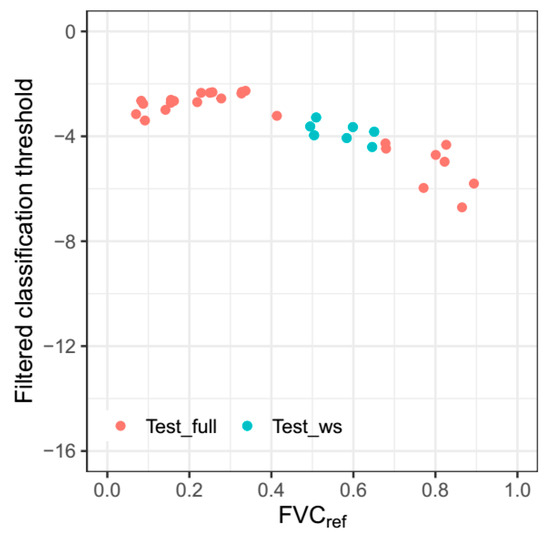
Figure 6. The classification thresholds obtained by a*_I_T₁ with absolute estimation error less than 0.025, varying with reference fractional vegetation cover (FVC_ref).

4.4. Results of FVC Estimations of Different Methods

4.4.1. Comparison based on Test Image Groups

Considering that a*_I outperformed all other color features, the following comparison was based on the a*_I color feature. The performance of FVC estimation using the T₁ method, T₂ method, and fixed-threshold method on the a*_I color feature is shown in Table 5. For both of the Test_full and Test_ws image groups, the fixed-threshold method performed best with smallest MAE and RMSE, and greatest R², followed by the T₁ method and then the T₂ method. Compared with the T₁ method, the MAE obtained by using the fixed-threshold method was decreased by 0.06 and 0.033 for Test_full and Test_ws, respectively. Compared with the T₂ method, the MAE obtained by the fixed-threshold method was decreased by 0.058 and 0.154 for Test_full and Test_ws, respectively.

Table 5. Performance of FVC estimation using three methods on a*_I color feature.

Image Set	Method	MAE	R2	RMSE
Test_full	T1	0.021	0.99	0.03
	T2	0.073	0.97	0.05
	Fixed-threshold	0.015	1	0.02
Test_ws	T1	0.047	0.89	0.03
	T2	0.168	0.5	0.05
	Fixed-threshold	0.014	0.99	0.01

The correlation between FVC_ref and FVC estimations obtained by using three methods based on the test group images (Test_full and Test_ws) is shown in Figure 7. On one hand, for the images with high FVC_ref, captured from fully irrigated plots, the T₁ and T₂ methods performed unstably with some FVC estimations being underestimated, as shown in Figure 7a,b. However, it can be observed from Figure 7c that the fixed-threshold method worked well on all these images. Figure 8 shows the comparison of FVC maps obtained by applying three different methods to an image with high FVC_ref. It could be observed that the result of the fixed-threshold method was closer to the RGB image and the FVC_ref map.

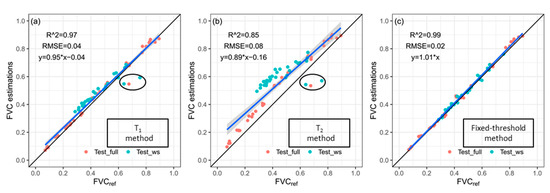
Figure 7. FVC estimation results obtained using (a) T₁ method, (b) T₂ method, and (c) fixed-threshold method on the a*_I color feature of the test image group (Test_full and Test_ws).

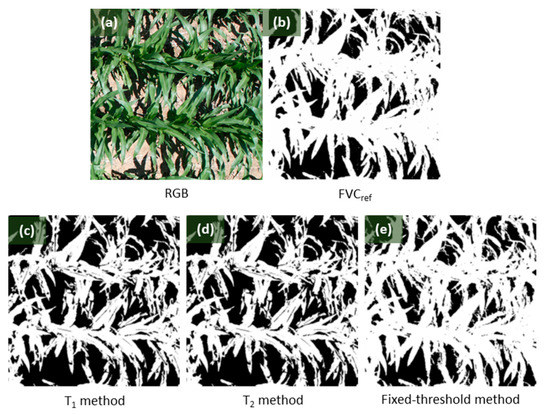
Figure 8. Part of the (a) RGB image captured from fully irrigated plots, with FVC_ref of 0.67; (b) the FVC_ref obtained by supervised classification via Environment for Visualizing Images (ENVI); and comparison of FVC maps obtained by using (c) T₁ method, (d) T₂ method, and (e) the fixed-threshold method proposed in this study.

On the other hand, for the images with different levels of water stress, the FVC results of T₁ and T₂ methods were overestimated as shown in Figure 7a,b, especially the FVC estimations by the T₂ method. However, Figure 7c shows that the fixed-threshold method improved the FVC estimation accuracy of those images with different levels of water stress. In addition, for the T₁ and T₂ methods, the more severe the water stress, the more overestimated the FVC estimations. To provide a better explanation of this phenomenon, EEs of all test group images with FVC_ref ranging from 0.3 to 0.6 are shown in Figure 9. The limit condition of FVC_ref used to select an image can ensure that the effect only comes from different levels of water stress. As shown in Figure 9a,b, compared with the images taken in NWS and MWS plots, the EEs of images taken in SWS plots were higher when the T₁ or T₂ method was used. When the fixed-threshold method was used, the EEs of these images showed no big differences among the images regardless of water stress level, as shown in Figure 9c.

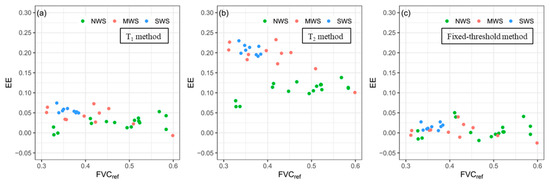
Figure 9. Estimation errors (EEs) of all test group images with FVC_ref ranging from 0.3 to 0.6, obtained by (a) T₁ method, (b) T₂ method, and (c) fixed-threshold method. NWS, MWS, and SWS represent no water stress, intermediate water stress, and severe water stress, respectively.

4.4.2. Validation of the Fixed-Threshold Method

To validate the performance of the fixed-threshold method, the initial threshold (−2.72) and the adjusted threshold (−4.60) were applied to the validation image groups (Val_full and Val_ws). The Val_full image group includes 18 images captured in fully irrigated plots. The Val_ws image group includes 16 images captured in plots suffering different levels of water stress. A high correlation (R² = 0.99, RMSE = 0.02) between FVC estimations obtained by the fixed-threshold method and FVC_ref can be observed in Figure 10a. The EEs shown in Figure 10b were concentrated near 0, with a mean value of 0.012 and standard deviation of 0.018.

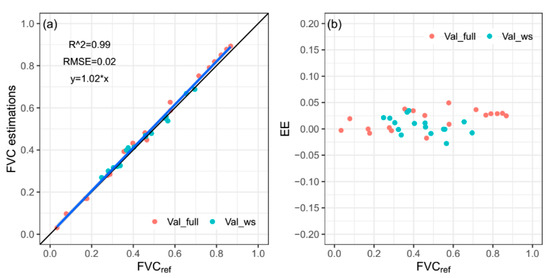
Figure 10. FVC estimation results (a) obtained using fixed-threshold method on a*_I color feature of validation image group (Val_full and Val_ws), and corresponding EEs (b).

5. Discussion

5.1. Selecting the Appropriate Color Feature for a GMM-Based Threshold Method

The first key step to estimate crop FVC using a GMM-based threshold method is the selection of the appropriate color feature. In previous studies [25,26], the separability distance index (SDI) was proposed as the criterion to select the color feature. A larger SDI means that it should be easier to separate vegetation from non-vegetated backgrounds. However, in this study, the H channel had the largest SDI with mean values of 1.50 and 1.45 for Test_full and Test_ws image sets (Figure 11). At the same time, the greatest MAE was observed for the H channel among the four color features when the T₁ method was used. The a*_I color feature outperformed other color features, with MAEs of 0.021 and 0.047 for Test_full and Test_ws image sets using the T₁ method. These results indicate that the color feature with the largest SDI may not always result in a low FVC EE, and the SDI cannot be used as the sole criterion to choose an appropriate color feature. Once the Gaussian distributions of green vegetation and backgrounds can be successfully fitted within all the color features, the ability of each color feature to identify green vegetation may be the key to influence the FVC estimation accuracy [21]. Future studies are needed to quantify the ability of SDI to separate green vegetation from backgrounds within a color feature, and to find the threshold where the Gaussian distributions of vegetation and backgrounds can be accurately fitted.

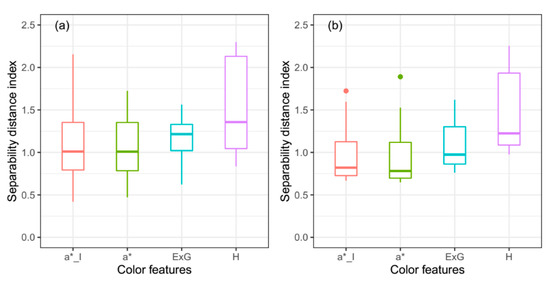
Figure 11. The distribution of separability distance index for a*_I, a*, ExG, and H: (a) is based on the Test_full data set; (b) is based on the Test_ws data set.

5.2. The Fixed-Threshold Method Provides the Most Accurate FVC Estimations

Threshold-based approaches have been widely applied to RGB images with high spatial resolution. Some threshold methods are based on a GMM, which is fitted on one color feature derived from RGB images, representing the distribution of green vegetation and backgrounds [26]. However, these methods perform unstably when the canopy is nearly closed [9,48] and show an obvious overestimation when crops suffer from severe water stress. Firstly, to investigate the performance of GMM fitting of images with different levels of FVC, a sequence that fits the GMM was simulated and white noise was added to it. To make the sequence more practical, mean values and standard deviations similar to those from green vegetation and backgrounds on the a*_I color feature were used. Different levels of FVC were simulated by changing the weight of the distribution of backgrounds. All sequences representing different levels of FVC were processed to fit the GMM, and R² was calculated based on the real GMM and the GMM fitted from the sequence. The change of R² with the weight of the distribution of backgrounds is shown in Figure 12. The R² was not stable and was less than 0.90 when the weight of the distribution of backgrounds is less than 0.2, which means that the GMM fitting and threshold results are not accurate when FVC is high.

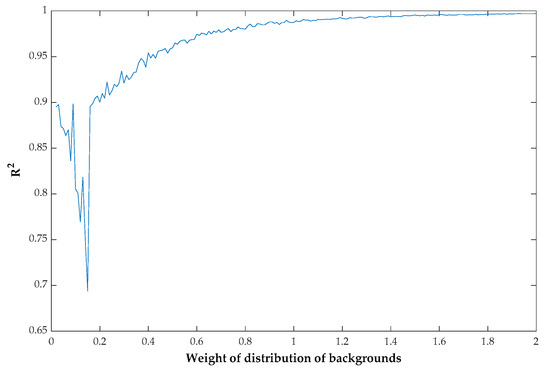
Figure 12. The coefficient of determination (R²) curve changes with the weight of the distribution of backgrounds.

Second, the FVC of crops under water stress was overestimated by these threshold methods based on GMM. More severe water stress led to higher MAE (Table 6). When the T₁ method was used, the MAEs obtained from MWS and SWS plots were increased by 0.016 (61.5%) and 0.031 (119%), respectively, compared with those from NWS plots. A similar phenomenon was observed for the T₂ method. This may result from the spectral changes of crops caused by pigment changes at the leaf level. Water stress can affect the leaf pigment content, such as chlorophyll content [36]. The leaf chlorophyll content decreases as crop water stress increases, resulting in a minimal reflectance in the green spectrum. The T₁ and T₂ methods were applied on the a*_I color feature, which is relative to the green-red opponent colors, with negative values toward green and positive values toward red. Therefore, green vegetation with lower chlorophyll content has a higher a*_I value, which makes it more difficult to distinguish green vegetation from the background. Further study is needed to explain this specifically.

Table 6. The mean absolute errors (MAEs) obtained from plots with no water stress (NWS), intermediate water stress (MWS), and severe water stress (SWS) using different methods.

Method	Water Stress Level	MAE
T1	NWS	0.026
	MWS	0.042
	SWS	0.057
T2	NWS	0.082
	MWS	0.189
	SWS	0.207
Fixed-threshold	NWS	0.014
	MWS	0.013
	SWS	0.014

In this study, the proposed fixed-threshold method addressed the problems mentioned above. Compared with the T₁ and T₂ methods, the new method exhibits stronger robustness, especially when the canopy is nearly closed (Table 5) and provides similar accuracy for images with different levels of water stress (Table 6). The new method is highly accurate and robust to different vegetation cover levels and water stress levels, with an overall RMSE of 0.02 and R² of 0.99 for both test group images (Figure 7c) and validation group images (Figure 10a). Similar results were observed in [12], which showed that the optimal threshold of VARI images for sugar beet segmentation tends to be around a constant value of 0.14.

In the fixed-threshold method, the initial threshold was −2.72 for maize with FVC_ref less than 0.5, and the adjusted threshold was −4.60 for maize with FVC_ref equal to or greater than 0.5. The adjusted threshold is smaller than the initial threshold, which may be due to the changes in spectral reflectance at different FVC levels. In the visible spectrum, the reflectance of blue and red bands is negatively correlated with the FVC of maize [49]. However, there was no obvious correlation between the reflectance of the green band and the FVC of maize [49]. With the increase in maize FVC, the decrease in the reflectance of red and blue bands leads to a decrease in the a*_I color feature. Hence, for the maize with greater FVC_ref, the threshold is slightly lower than that of maize with smaller FVC_ref. The critical point was set at the FVC of 0.5 because there was an obvious change in threshold before and after 0.5 (Figure 6). The reason why the threshold changes a lot around an FVC 0.5 still needs to be studied in the future.

In addition to having higher FVC estimation accuracy and robustness, the proposed fixed-threshold method is simpler and more efficient. Once the initial threshold and the adjusted threshold have been obtained, the time to extract FVC of maize using the fixed-threshold method is less than the time using the T₁ or T₂ method. Taking the test group image as an example, the time to extract FVC using the fixed-threshold method is 43.63 and 56.05 s/per image faster than T₁ and T₂, respectively (Table 7).

Table 7. The time to estimate FVC of maize using three different threshold methods in R with a 2.4 GHz computer processor.

Method	Time (s/per Image)
T1	48.01
T2	60.43
Fixed-threshold	4.38

6. Conclusions

This study proposed a fixed-threshold method based on the statistical analysis of the thresholds obtained using the T₁ method. In this method, some images were selected and processed to obtain the initial threshold and the adjusted threshold, which can be applied to all images collected from plots with different levels of FVC and water stress. As such, the proposed method addressed the problems of robustness and accuracy that occur when the canopy is nearly closed, or when crops are subjected to water stress. Compared with the two threshold methods (T₁ and T₂ methods), the fixed-threshold method generated more accurate and robust FVC estimations, especially for maize with high FVC or under severe water stress. The performance of the fixed-threshold method was assessed based on FVC_ref with an RMSE of 0.02 and R² of 0.99 for both test group images and validation group images. The results strongly suggest that the fixed-threshold method could provide an efficient and accurate way to obtain reference FVC used for validating FVC estimations obtained from UAV or satellite remote sensing platforms.