Abstract
Urban forests are part of the global forest network, providing important benefits to human societies. Advances in remote-sensing technology can create detailed 3D images of trees, giving novel insights into tree structure and function. We used terrestrial laser scanning and quantitative structural models to provide comprehensive characterizations of the woody surface area allometry of urban trees and relate them to urban tree anatomy, physiology, and structural complexity. Fifty-six trees of three species (Gleditsia triacanthos L., Quercus macrocarpa Michx., Metasequoia glyptostroboides Hu & W.C. Cheng) were sampled on the Michigan State University campus. Variations in surface area allocation to non-photosynthesizing components (main stem, branches) are related to the fractal dimension of tree architecture, in terms of structural complexity (box-dimension metric) and the distribution of “path” lengths from the tree base to every branch tip. The total woody surface area increased with the box-dimension metric, but it was most strongly correlated with the 25th percentile of path lengths. These urban trees mainly allocated the woody surface area to branches, which changed with branch order, branch-base diameter, and branch-base height. The branch-to-stem area ratio differed among species and increased with the box-dimension metric. Finally, the woody surface area increased with the crown surface area of the study trees across all species combined and within each species. The results of this study provide novel data and new insights into the surface area properties of urban tree species and the links with structural complexity and constraints on tree morphology.
1. Introduction
Urban trees provide a wide range of important ecosystem services, including temperature regulation, carbon storage, water purification, air pollutants uptake, biodiversity, etc. [1,2,3,4,5,6,7,8]. Trees in urban areas are growing under very different conditions than forest-grown counterparts and it is important to study their architecture and their physiological performance [9] to increase our understanding of their adaptability to urban environments [10].
The fundamental physiological processes of trees, including urban ones, include rates of respiration and photosynthesis, production efficiency, water balance, energy and gaseous exchange with the atmosphere, and leaching of nutrients from bark and leaves [11,12]; all of these have long been hypothesized to relate to tree surface area [13]. The roles of leaf area and crown surface area in tree carbon balance, through photosynthesis and respiration, is well known, e.g., [11,12,14,15,16] and tree respiration rates, in particular, are closely related to their woody surface area [17,18,19,20,21]. Furthermore, the woody surface area of trees and their bark structure create a rich web of bark-using organisms [22]. Therefore, the detailed quantification of the surface area of the woody components of trees is necessary for understanding their physiological ecology.
Whitaker and Woodwell [13] published one of the earliest studies focused on tree surface area and highlighted the need to consider its relationship to tree structural complexity. Urban trees can have a very distinct above-ground architecture which can inform us about the growth and functional limits of different tree species [23]. Since competition for light [24] significantly reduces the structural complexity (i.e., inherent fractal character) of trees that grow in closed-forest conditions [25,26,27,28], we expect that urban trees should better express their fractal character, due to the typically lower number or complete absence of neighboring trees in cities. Of course, the highly heterogeneous growing environment of urban trees can affect the structural complexity of their crowns [10], but, in general, more open-grown, urban trees should have more evident fractal complexity compared to trees growing in forest stands. Therefore, focusing on open-grown urban trees gives us the opportunity to study important aspects of tree allometry, such as the above-ground woody surface area, considering their distinct structural complexity.
Woody surface areas, and particularly branch areas, have long proved difficult to measure [29]. Branch area has often been studied secondarily to leaf area estimation, e.g., as a source of noise when trying to estimate leaf area index, e.g., [30]. Direct methods of woody surface area quantification are highly laborious, requiring destructive sampling, where trees are cut up into components and the surface areas of various parts are measured, e.g., [29]. This has led to the necessity of developing allometric equations to generalize from destructive sampling data, e.g., [29,31,32,33], to be applied to standing trees via easily measured allometric variables (e.g., diameter at breast height, crown length, crown ratio). However, allometric equations have been previously found to significantly underestimate the total woody surface area of trees [34,35]. Moreover, destructive sampling, which is required to build allometric equations, can be highly problematic in urban areas, due to the additional challenges and costs of safely removing urban trees.
Many indirect methods of woody surface area estimation have been advanced. More specifically, different studies have utilized geometric approximations of stem, branch, and crown shapes, have estimated branch surface area from vertical photographs and multispectral canopy imaging, and derived woody surface area from principles of the pipe model theory and branch divarication theory, along with combinations of the previous methods [13,19,29,36,37,38,39]. A major challenge for any of these methods is dealing with the structural complexity of trees [13], which exhibits a fractal-like pattern [27] that is very common in ecology [40].
According to the pipe model theory [41] and the WBE model [42], trees have a fractal-like branching architecture which consists of a network of self-similar branching shoots beginning at a central trunk and terminating in leaves at the ends of small twigs [43,44]. Therefore, simple geometric representations of stem and branches to estimate woody surface areas are likely inadequate and inaccurate since they do not explicitly account for the structural (fractal) complexity of the woody skeleton of trees. However, recent advances in terrestrial laser scanning (TLS) provide new, non-destructive ways for quantifying the structural complexity of trees, including the prospect of directly measuring the total tree surface area [35]. TLS instruments belong to active remote sensing and they emit laser pulses and capture “point clouds” of the surrounding environment by analyzing the returned energy as a function of either time (time-of-flight systems) or shift in the phase of the light wave of the emitted laser beam (phase-shift technology), as well as using precise angular measurements through optical beam deflection mechanisms [45,46].
The above-ground structural complexity of trees can be directly quantified from TLS data using the “box-dimension” (Db) metric, also known as Minkowski-Bouligand dimension [27]. The box-dimension metric is derived from fractal geometry principles [47], and it is a measure of plant material density and distribution [48]. The estimation of the total woody surface area of trees from TLS data does not rely on biological assumptions and it is relatively new [35], for example, Ma et al. [49] used terrestrial laser scanning data to compute the woody to total surface area ratio of trees, to estimate their leaf area index. In general, TLS data have been previously used to mainly study other important aspects of tree allometry and ecology, e.g., stem density, stem profiles, and timber volume [50,51,52,53,54], leaf and canopy properties [55,56,57,58,59,60,61,62,63,64,65,66], above-ground tree biomass and carbon stocks [45,53,67,68,69].
In this study, we used TLS technology to produce novel woody surface area data for urban trees. The objectives of the study are the following: (i) to measure the total above-ground woody surface area of urban trees of different species; (ii) to examine the above-ground woody surface area allocation into stems and branches of different sizes and positions in tree crowns (branch orders, branch-base diameter, and branch-base height classes); (iii) to quantify the relationship between tree woody surface area and tree fractal-structural complexity (i.e., the box-dimension metric) and different Euclidean measures of tree architecture (i.e., metrics that account for the length of all paths from the tree base to each branch tip, and crown surface area).
2. Materials and Methods
2.1. Urban Tree Data
We chose open-grown urban trees as our object of study, since we expected to get better TLS-based measurements of tree attributes, without occlusion from neighboring trees, but also since we expected that the low or complete absence of competition from tree neighbors in cities should allow trees to better express their inherent fractal character in terms of structural complexity [25,26,27,28].
Fifty-six trees, of three species, that represent different tree functional types were sampled on the Michigan State University campus: 18 Gleditsia triacanthos L. trees (compound-leaved, deciduous angiosperms), 15 Quercus macrocarpa Michx. trees (entire-leaved, deciduous angiosperms), and 23 Metasequoia glyptostroboides Hu & W.C. Cheng trees (needle-leaved, deciduous gymnosperms). The trees were selected to cover a large range of sizes (Table 1, from 10.9 to 122.2 cm stem diameter at breast height (DBH)). Since all species are deciduous, we were able to study their total woody surface area during the leaf-off period (Figure 1). Of particular interest was M. glyptostroboides, which was selected since we wanted to study the structure of an urban-grown, needle-leaved gymnosperm, that could be scanned (alive) in a leaf-off condition; it is difficult to get complete, non-occluded scans of the stems and branches of needle-leaved evergreen species [68].

Table 1.
Summary statistics resulting from different measurements of tree size and structural complexity. DBH: Diameter at Breast Height (cm); WSA: Woody Surface Area (m2); CSA: Crown Surface Area (m2); CV: Coefficient of Variation; Db: Box-Dimension; SD: Standard Deviation (m); Min: Minimum (m); Max: Maximum (m).

Figure 1.
Leaf-off images of (A) a G. triacanthos tree, (B) a Q. macrocarpa tree, (C) a M. Glyptostroboides tree. All trees have been flagged with a pink-color tape.
Laser scanning of the G. triacanthos and Q. macrocarpa trees was accomplished, with leaves-on, in July and August 2019. The M. glyptostroboides trees were scanned, with leaves-on, in August 2020. The leaf-on tree point clouds allowed the estimation of the crown surface area of the trees (see specific methods below). The same trees were also laser-scanned in leaf-off condition, in January, February, and March 2020, in order to estimate their woody surface area (see specific methods below). Before re-scanning the study trees, we confirmed that they were not pruned by Michigan State University arborists between July 2019 and August 2020. Therefore, pruning did not impose any bias in the estimation of the woody surface area and crown surface area of the study trees, during the study period. Of course, past pruning events could have affected the tree structure observed.
2.2. Terrestrial Laser Scanning and Point Cloud Processing
All trees were scanned with the FARO Focus3D X 330 terrestrial laser scanner (FARO Technologies Inc., Lake Mary, FL, USA), which operates with a laser light of 1550 nm wavelength, typical beam divergence 0.19 mrad, and range of 0.6–330 m. Each individual tree was scanned with high resolution from a minimum of four different directions and distances in order to minimize occlusion effects, and five reference target-spheres were placed around each focal tree to spatially reference all scans and create a single point cloud for each tree following the field scanning protocols suggested by Wilkes et al. [70]. The first two scans of each tree were conducted in opposite directions from distances that allowed the top of the tree to be clearly visible. The other two scans were conducted in opposite directions (perpendicularly to the first two scans) from a closer distance to the focal tree to better capture its branching architecture and get closer views of the main stem. For large trees with complex crowns two or three additional scans were conducted below the tree crown to capture more dense point clouds of the branches. All laser scans were conducted when there was little or no wind.
Spatial co-registration and noise-filtering of all scans was automatically performed using the software SCENE 2019.2 (FARO Technologies Inc., Lake Mary, FL, USA, 2019.2). Using the same software, each tree was manually separated from the point cloud of the urban site background. This process was judged as an accurate alternative to an automatic segmentation process [48].
2.3. Tree Reconstruction from Quantitative Structure Models
Quantitative Structure Models (QSMs) [71,72,73,74] describe the three-dimensional architecture of trees by fitting cylinders to a tree’s point cloud. QSMs preserve branch and stem topology and provide information about the size, the location, the hierarchy, and the orientation of the branching network. They are currently considered to be the most robust method to model tree volume and tree-architecture [75].
Quantitative structure models were generated from the leaf-off point clouds of the trees, with the algorithm TreeQSM v.2.3.0 [76] (see example in Figure 2). There are two main steps for the tree reconstruction from a single point cloud based on this algorithm. The first step is the point cloud segmentation into stem and branches based on cover sets, and the second step includes the reconstruction of the volume and the surface area of the segments with cylinders [45,77]. TreeQSM generated multiple QSMs for each tree point cloud based on different values for the minimum and maximum size of the cover sets and it finally determined the optimal QSM for each study tree [71]. Based on the optimal QSM parameters the algorithm produced 30 additional QSMs for each study tree, which allowed for quantification of the variation of the modeled tree variables, due to the inherent stochastic component of TreeQSM [71].
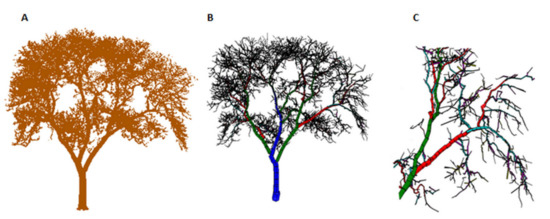
Figure 2.
(A) The leaf-off point cloud of the G. triacanthos tree from Figure 1 (artificially colored with brown color). (B) The QSM of the same tree. (C) A close-up picture of the generated QSM, composed of many cylinders fitted to the point cloud data. The colors denote the different branching orders, i.e., the main stem is colored blue, the first-order branches are colored green, the second-order branches are colored red, etc. Four facets have been used to visualize the QSM cylinders.
The definition of the main stem of a tree according to TreeQSM is based on three criteria: (1) the main stem extends near the top of a tree, (2) it goes almost straight up, and (3) it is not too curved which means that the ratio of the stem length to the stem base-tip distance, must be the minimum among all candidate main stems (Raumonen, P. personal communication, 2 June 2020). After the main stem has been determined, the first-order branches (i.e., branches attached to the main stem) are defined based on the following criteria: they are the farthest-reaching candidates, with the ratio of the branch length over the branch base-tip distance to be less than 1.2, and the branch base-tip distance to be over 75% of the maximum. The branch length/distance ratio will iteratively increase if no candidates with a ratio equal to 1.2 exist. The second-order branches are attached to the first-order branches, and they include the candidates with the longest branch base-tip distance. Branches of higher order are defined following the same rules attached to the second, third, fourth order, etc. (Raumonen, P. personal communication, 2 June 2020). Figure 2B,C shows a color-coded example of a result of this procedure.
2.4. Tree Woody Surface Area Computation
From the optimal QSMs of the leaf-off scans of the urban trees, their total woody surface area (WSA, m2) was computed as the total surface area of the cylinders that were fitted to the point cloud of each tree (Figure 2). Note: total “woody” surface area in this study is technically the surface area outside of the bark tissues. Next, the total WSA of each tree was separated between the main stem woody component and the branches woody component. The branch WSA was further analyzed by branch order (there was a maximum of eleven branching orders across all species combined), by branch-base diameter classes of 1 cm size from the diameter of the cylinder at the base of a branch (there were 48 classes across all species combined), and by branch-base height classes of 1 m size, based on the height from the base of a tree to the base cylinder of a branch (there were 25 classes across all species combined; described in detail in the Results Section).
2.5. Computation of Other Tree Structural Metrics
We wanted to study how WSA related to other published metrics of tree architectural complexity. Smith et al. [78] examined a metric called the “path fraction”, which is the mean length of all “paths” through the branching network, from the stem base to all branch tips, divided by the maximum path length. Path lengths are Euclidean metrics of tree structure and they can be calculated from a QSM based on the lengths of the interconnected cylinders whose topological hierarchy is preserved in a QSM. However, we did not simply use the QSM for each tree to compute Smith et al.’s path fraction, but instead we looked at various statistics from the distribution of path lengths, to take advantage of the rich data provided. This included the quantiles of the path lengths (25th, 50th, and 75th percentiles), as well as minimum, maximum, mean, and standard deviation of path lengths.
We computed the box-dimension (Db) metric [27], as a direct measure of above-ground structural complexity, calculated directly from the leaf-off point cloud of each tree. Db has the advantage of not having to apply a QSM to the data, it uses only the original tree point cloud. The Db metric takes into account the number of boxes that are needed to encapsulate all points of a laser-scanned tree, and how the number of boxes varies with the ratio of the box size to the original box size, which is defined as the smallest box that encapsulates the whole tree [15]. The smallest box encapsulating the entire tree point cloud is the so-called “upper cut-off”, as it represents the largest box applied to the tree for counting the number of consecutive boxes needed. Consecutive boxes always have half the edge length of the previous box so that eight of them fit exactly in the initial box. The smallest box-size among all boxes is the so-called “lower cut-off”, and it was defined to be 10 cm in this study (Figure 3A). It is a very liberal estimate of the maximum distance between two neighboring laser points at any given location in the tree. The “lower cut-off” must ensure that no virtual box is considered empty only because it fits in the “unsampled” space that was not reached by any laser beam of the laser scans. This “unsampled” space may be the result of the diverging beams emitted from the scanner leaving unscanned areas at greater distances to the scanner or simply due to occlusion effects in the tree.
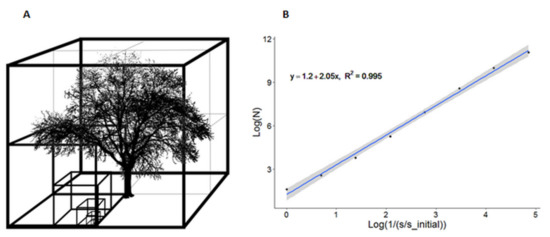
Figure 3.
(A) Illustration of the virtual boxes of different sizes that capture the leaf-off point cloud of a G. tiacanthos tree. (B) The log-log plot for the quantification of the box-dimension metric for the same tree. The regression line slope is the box-dimension of the tree, i.e., Db = 2.05. N is the number of boxes required to capture all points of the tree point cloud, s is the size of the length of each box, and s_initial is the size of the length of the initial box that encapsulates the whole tree. The 95% confidence interval has been plotted around the regression line.
Db is equal to the slope of the least-squares line when the logarithm of the number of boxes is regressed against the logarithm of the inverse of the size of a box relative to the size of the initial box [15,27] (Figure 3B). Db, which is unitless, takes values between one and three. Values smaller than one are only possible if the “lower cut-off” has not been properly chosen (i.e., mean distance between neighboring points is greater than the edge-length of the smallest box). Values of three (or greater) are not possible in reality, since it would imply that a tree is a solid cube. Db values close to but smaller than three imply trees with greater crown complexity and “space-filling character”, whereas, a perfectly cylindrical stem without branches would have Db equal to one [27]. Both the path fraction [78] and the Db [27] metrics are meant to capture the fractal-like nature of trees [42,43,44], which should explain a portion of the variation in their WSA.
Finally, the crown surface area of the study trees was computed as the convex hull from the leaf-on laser points of a tree’s crown using Heron’s formula to quantify the triangles that create the surface of this hull [24]. In this study, it refers to the photosynthetically-active surface area of a tree [15,16].
2.6. Statistical Analyses
All statistical analyses for this study were done with custom coding and available packages written in the R software language [79]. Regression analysis was used to relate the total WSA, and the branch to stem WSA, with the metrics of crown complexity and tree architecture (see Section 2.5). Correlation strengths were quantified with the Pearson correlation coefficient (r) and the statistical significance of the relationships was assessed at α = 5% level.
The total WSA of the trees was modeled as a power function of the metrics described in Section 2.5 in order to explore the relationship between WSA and these metrics. The power function form was selected since it had a better fit to the data compared to the linear model form and since power functions better describe the multiplicative processes of tree allometry (e.g., WSA allometry), and they are scale-invariant [80]. The species was added in the candidate models as a random, grouping variable that influences the exponents of the predictor variables.
The mixed-effects model is of the form:
where WSA is the total woody surface area (m2) of the trees, b is the normalization constant, Db is the box-dimension (unitless), L is one of the path length metrics in meters that were described previously, c is the scaling exponent parameter of the box-dimension (fixed effect), d is the scaling exponent parameter of the path length metrics (fixed effect), and Sc and Sd are the species random effects added to the candidate models to modify the c and d parameters, respectively, and they have three levels (i.e., G. triacanthos, Q. macrocarpa, and M. glyptostroboides). The error term () has a multiplicative structure, which is additive on a log-log scale. Assumptions of variance homoscedasticity and error normality were checked by plotting the model residuals against the fitted values, and the Q-Q plots and the histograms of the model residuals. The “nlme” function of the linear and nonlinear mixed effects models (“nlme”) R package [81] was used to fit the models. The best models were selected considering both the coefficient of determination (adjusted R2) and the Akaike information criterion (AIC).
A one-way analysis of variance (ANOVA) test, with unequal variances, was used to evaluate differences in the mean value of the branch to stem WSA ratio across the three species combined (i.e., G. triacanthos, Q. macrocarpa, and M. glyptostroboides). A one-way ANOVA test was also used to evaluate differences in mean WSA of branches per branch order, per branch-base diameter class, and per branch-base height class, across and within the above-mentioned species. For these tests, the WSA of all branches belonging to different classes for every study tree was considered. In all ANOVA tests, the normality of the data in each group was checked with Q-Q plots, and significant differences in group means were assessed at α = 5%. Finally, the coefficient of variation was used to quantify the uncertainty in estimating total WSA from the consecutive QSM reconstructions of the same point cloud of a tree.
3. Results
3.1. Estimated Total and Component Woody Surface Areas
Basic tree measurements and surface areas computed for the study trees are shown in Table 1, along with other tree statistics (discussed later). The data show that the study trees varied widely in their surface areas and other metrics of complexity.
Branches comprised the greatest portion of WSA of the urban trees studied. The branch to the main stem woody surface area (BMS) ratio ranged between 4.3 and 38.6 with the mean value of 16.3 across all study trees combined. ANOVA showed that the mean BMS differed significantly among the three species, i.e., M. glyptostroboides (MEGL), G. triacanthos (GLTR), and Q. macrocarpa (QUMA) (p < 0.001). G. triacanthos had the highest mean BMS value compared to the trees of the other two species: Mean BMSGLTR = 24.1, mean BMSQUMA = 13.4, and mean BMSMEGL = 12.1. Furthermore, a strong positive relationship was found between the BMS ratio and the Db metric of the trees (Pearson’s r = 0.6, p < 0.001).
The median branch order was five across all study tree species combined (range 1 to 11, Table 1), with M. glyptostroboides showing fewer branch orders than the two angiosperm species (median 4, range 1 to 9). ANOVA showed that the branch woody surface area (BWSA) significantly differed among the different branch orders across all study tree species combined and within each species (p < 0.001). BWSA was mainly accumulated in lower branch orders and the distribution of surface area was positively skewed (Figure 4). Second- and third-order branches supplied the greatest amount of BWSA across all study tree species combined, and for Q. macrocarpa trees (Figure 4A,C). BWSA came mainly from second-, third- and fourth-branch orders in G. triacanthos trees (Figure 4B), and from lower order (first, second and third) in M. glyptostroboides trees (Figure 4D).
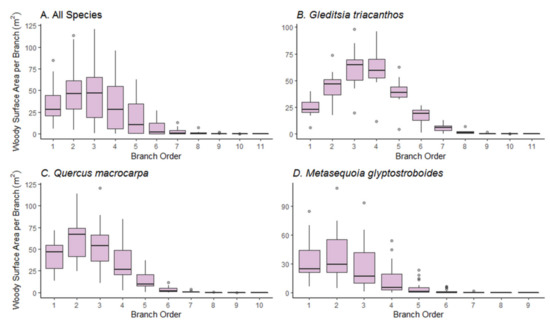
Figure 4.
Box-plots of branch woody surface area per branch order across (A) all species combined, (B) for G. triacanthos trees, (C) Q. macrocarpa trees, and (D) M. glyptostroboides trees.
Examination of BWSA by branch basal diameter (Figure 5) indicated that the BWSA followed a positive skewness, but with a somewhat bimodal distribution (except for the M. glyptostroboides trees). Medium-sized branches (between 4 and 11 cm base diameter approximately) and large branches (more than 35 cm base diameter approximately) accumulated much of the BWSA, while small branches and twigs (less than 4 cm base diameter), though numerous, accumulated a relatively small portion of the BWSA (Figure 5). ANOVA confirmed that the BWSA differed statistically among the different branch-base diameter classes across all species combined and within each species (p < 0.001).
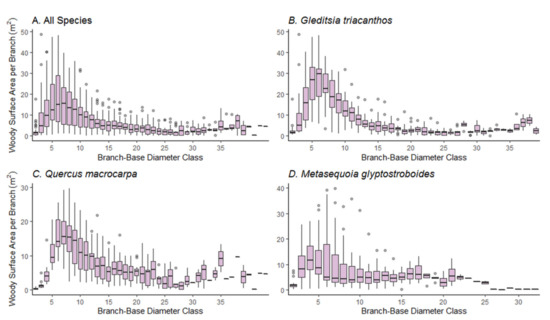
Figure 5.
Box-plots of branch woody surface area per branch-base diameter class across (A) all species combined, (B) for G. triacanthos trees, (C) Q. macrocarpa trees, and (D) M. glyptostroboides trees. The size of each class is 1 cm.
Some large trees showed very large branches, with a basal diameter greater than 35 cm (Figure 5). These “branches” were actually large forks in the stem, common to large, open-grown, urban trees (See Figure 1), which the TreeQSM algorithm defined as branches. At a major fork, the QSM determines the longest, straightest stem to the top of the tree as main stem (see details in the Methods Section above), and calls the others branches.
Since the topology of the trees is captured by the QSM, we were also able to examine how the surface area was distributed vertically in the trees (Figure 6). The BWSA differed statistically (as assessed with ANOVA) among the different branch-base height classes across all study tree species combined and within each species (p < 0.001). Graphical analysis (Figure 6) shows a parabolic distribution of relative BWSA for all study tree species combined peaking near the midpoint of the crown (0.5 on the y axis in Figure 6A). Relative BWSA peaked higher up in the tree for G. triacanthos trees (Figure 6B), about the midpoint for Q. macrocarpa trees (Figure 6C), and below the midpoint for M. glyptostroboides trees (Figure 6D).
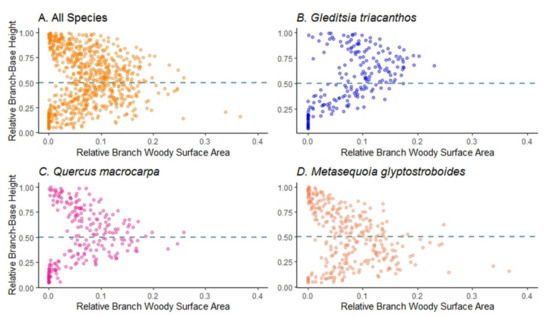
Figure 6.
Relative vertical distribution (branch base height divided by total tree height) of branch woody surface area (proportion of total branch area) for (A) all study trees, (B) G. triacanthos trees, (C) Q. macrocarpa trees, and (D) M. glyptostroboides trees. The horizontal dashed line is halfway up the tree.
3.2. Uncertainty Analysis of the Estimated Woody Surface Areas
The coefficient of variation of the WSA of the trees indicated that the uncertainty due to the consecutive QSM reconstructions of the same point cloud of a tree was on average 2.4% of the mean WSA per tree across all study tree species combined, and G. triacanthos trees had the highest uncertainty (on average 2.7% of the mean WSA per tree, Table 1). The distribution of the coefficient of variation of the WSA of the trees was positively skewed across all study tree species combined and within each species and bimodal for the G. triacanthos and M. glyptostroboides species (Figure 7A–D).
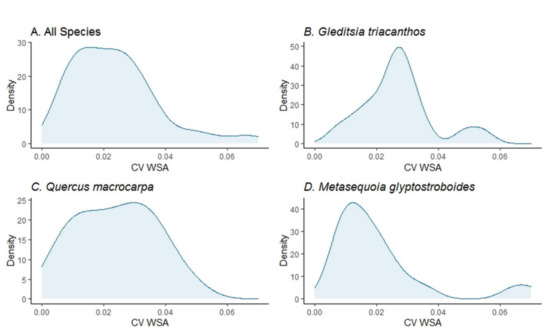
Figure 7.
Density plots of the coefficient of variation of the woody surface area (CV WSA) for (A) all study trees, (B) G. triacanthos trees, (C) Q. macrocarpa trees, and (D) M. glyptostroboides trees.
3.3. Relationships between Woody Surface Area and Metrics of Tree Architecture and Structural Complexity
Significant, positive relationships were found between the WSA of the urban trees, and the Db metric, and the different metrics that account for the length of all paths from the tree base to each branch tip (Table 2, Figure 8A–H). The strongest positive relationship was found between the WSA of the trees and the 25th percentile of path lengths (Pearson’s r = 0.87, p < 0.001, Figure 8F). However, the relationships between the WSA and the 25th percentile of path lengths, the mean path length, and the 50th percentile of path lengths, were not very different (Figure 8). The best and most parsimonious predictors of WSA (Equation (1)) were the combination of the Db metric and the 25th percentile of path lengths with species effects (Table 2). The correlation between the Db metric and the other predictor variables in each model of WSA (Table 2) was not statistically significant (i.e., p > 5%).

Table 2.
Woody surface area models with the highest adjusted R2 and lowest AIC values among all candidate models fitted to the data. Tree woody surface area (WSA) was modeled as a power function of different predictor-combinations (Equation (1)), including box-dimension (Db) and various statistics of path length (L), i.e., mean and the 25th, 50th, and 75th percentiles of path lengths. The character “|spp” denotes that species was added as a random effect, modifying the exponent of each predictor variable in the model. The best model by each statistic is highlighted in bold.
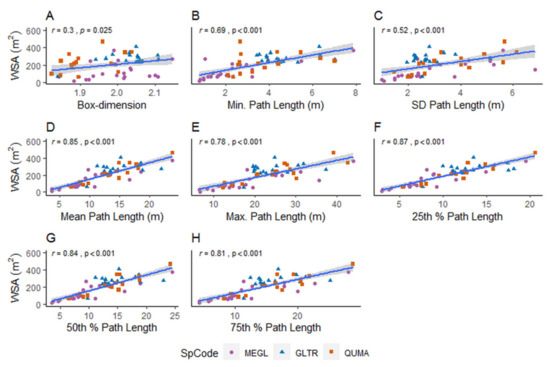
Figure 8.
Relationships between the woody surface area of the study trees (WSA in m2) and (A) the box-dimension metric, (B–H) different path length metrics with 95% confidence interval around the regression lines. The SpCode refers to the three species codes, i.e., M. glyptostroboides (MEGL), G. triacanthos (GLTR), and Q. macrocarpa (QUMA). The three species are represented with different symbols and colors.
The tree WSA was positively correlated with the crown surface area across all study tree species combined, and within each species (Figure 9A–D, p < 0.001).
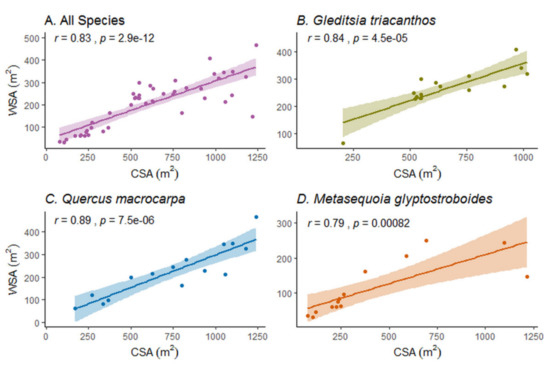
Figure 9.
Relationships of the woody surface area (WSA in m2) with the crown surface area (CSA in m2) of (A) all study trees, (B) G. triacanthos trees, (C) Q. macrocarpa trees, and (D) M. glyptostroboides trees. The data points of the three species are represented with different colors. The 95% confidence interval has been plotted around the regression lines.
4. Discussion
4.1. Advances in Urban Tree Surface Area Measurement
In this study, we used active remote sensing (TLS) to produce detailed WSA data for urban trees. Measuring the total surface area of the woody parts of trees has been challenging in the past with the only direct method via destructive sampling, which is particularly challenging and undesirable for large trees in urban areas. This study provided the first comprehensive measurements of the total above-ground WSA of urban trees with TLS, including the relative surface area of branch versus stem WSA and complete vertical characterizations of BWSAs for branches of different size and order. TLS has become an important tool used to quantify the three-dimensional structure of trees [35,75] and more accurate measurements of tree surface area may be the most important new advance in tree measurements associated with this technology. Data from mobile laser scanning (MLS) could also be used to study the WSA of trees covering larger spatial scales if occlusion effects in the point clouds are not significant. According to Dorji et al. [82], MLS data can be used to study the structural complexity of trees based on fractal analysis and quantified by the Db metric.
With any new measurement system come new sources of uncertainty. Our field procedure was designed to minimize occlusion effects in the tree point clouds by scanning the study trees from multiple directions and distances (see Section 2.2). This reduced the estimation uncertainty due to cylinder size and cylinder fitting errors in the generated QSMs [45]. The uncertainty in the estimates due to the consecutive QSM reconstructions of the same point cloud of a tree, comprised only a small portion of the estimated WSA across all study trees combined. This was on average 2.4% of the mean WSA per tree across all species combined (Table 1), while very few trees had a coefficient of variation of their WSA larger than 5% (Figure 7A–D). Therefore, the consecutive QSM reconstructions of a tree provide precise WSA estimates. This does not mean that the QSMs do not introduce bias, such as systematically over- or under- estimating surface areas of different parts of the trees, when identifying them from the point clouds.
Some large study trees had large branches with the max QSM base-diameter greater than 35 cm. Diameter overestimation of large branches (i.e., larger than 40 cm) is usually quite small in the QSMs generated by the TreeQSM algorithm (Raumonen, P. personal communication, 4 March 2021), but parts of forked stems can also be interpreted as branches. In other studies where branches were destructively sampled, an underestimation of 6% in QSM base-diameter was found for branches, with the actual base-diameter greater than 60 cm, while a diameter underestimation of 8% was observed for branches with diameters between 20 and 60 cm [83,84]. Therefore, we are confident in the general accuracy of the BWSA values produced in this study.
4.2. Relationships of the Woody Surface Area of Trees Explained by Major Theories of Tree Structure (WBE Model and Pipe Model Theory)
It has been suggested that the variation in branch area is related to the diameter of a branch and its position in the crown [29,32]. It was found here that medium and large-sized branches (based on their basal-diameter), of lower branching orders, accumulated the largest portion of the total BWSA. This pattern can be interpreted in the light of the pipe model theory [41] and the WBE model [42], which connect the tree structure with tree physiology. Both theories assume a fractal branching architecture whose vascular structure is an assemblage of tubes that taper from base to tip. Therefore, larger, lower-order branches accumulate more conducting and non-conducting tubes over their length, resulting in greater cumulative volume that scales with WSA [85]. Similarly, Weiskittel and McGuire [29], found that on average 82% of the total branch surface area in Douglas-fir (Pseudotsuga menziesii) trees was allocated into primary branches (those attached to the main stem). However, Meir et al. [34] found that small branches significantly contributed to the WSA of trees growing in a tropical rainforest.
According to the models produced in this study, much of the variation in the non-photosynthetic surface areas of urban trees can be explained by a combination of fractal-structural complexity (quantified by the Db metric), and “hydraulic” size (quantified by the Euclidean metric of the 25th percentile of the path lengths; see Smith et al. [78]), which are constrained by the genetics of tree species.
Smith et al. [78] defined the path fraction metric as the ratio of the mean path length to the maximum path length from the tree base to each branch tip, in order to quantify to what extent a real branch network differs from an ideally fractal branch network, such as that described by the WBE theory. In this study, the path fraction was not significantly related to the WSA of the trees, but as expected, significant relationships were found between the WSA and various statistics from the distribution of path lengths. This suggests that the absolute mean, variation, and distribution of path lengths may better help characterize the surface area complexity than the mean relative path length (a.k.a. the path fraction of Smith et al. [78]). Weiskittel and Maguire [29] found that the WSA of Douglas-fir (Pseudotsuga menziesii) trees increased with crown length, which agrees with the positive relationship that was found in this analysis between the total WSA of the urban trees and the 25th percentile of the path lengths, which is the frequency of the short-path lengths that affects crown length.
The WSA of the study urban trees was found to increase with their fractal-like architecture, as quantified by the Db metric [15]. According to the WBE model [42], this pattern could imply efficient respiration rates and sufficient supply for energy demanding units, e.g., leaves, chloroplasts [86], since the inherent fractal character of trees allows them to maximize the scaling of their external surface areas for gas exchange with the atmosphere, while minimizing the internal vascular distances for transferring and allocating the available resources to different organs and tissues [85,86,87].
An important issue to consider, when analyzing the relationships between surface areas and metrics of crown fractal complexity, is whether the observed patterns are confounded with tree size (e.g., DBH, total tree height, etc.). The Db metric is reported to be scale and tree-size independent [15,48], and therefore, we can use it to compare trees of different sizes [15]. Further analysis showed that the relationship between the total woody volume of the study urban trees computed from QSMs and the Db metric was not statistically significant (p > 5%), suggesting that both smaller- and larger-volume trees can be structurally complex. This could mean that architectural changes that occur through the ontogeny of trees, e.g., development of higher order branches and altered stem to branch relationships [48], might explain more complex structures in larger trees, more than their size, per se.
4.3. Anatomical and Physiological Implications of Surface Area Allocation Patterns
The surface area distribution found for these urban trees and the theories described in the previous sections have implications for understanding the anatomical structure and physiological function of urban trees, and trees in general. This study enabled not only the computation of the total WSA of trees, but also the analysis of its distribution into different components (stem and branches).
As expected, the branch-to-stem surface area ratio of the trees was found to increase with their structural complexity (as captured by the Db metric), underscoring the contribution of branching to crown complexity [15]. This ratio was found to significantly differ among the studied species, so, in this sense, it describes the resource allocation “decision” of different species to invest in increasing branch versus stem surface areas, as a functional response to urban environments. The squat form of urban trees (i.e., a wide tree crown with a short trunk) gives them mechanical stability against wind loads in cities [88], and reflects the tendency of trees to allocate less resources to growing a taller main stem as the crowding conditions decrease [88,89]. Mäkelä [90] found that “branchiness” of Scots pine (Pinus sylvestris) trees (described as the ratio of total branch cross-sectional area to stem surface area), increased as stand density decreased. Therefore, this pattern appears to hold for trees growing in both rural and urban areas. As such, the branch to stem surface area ratio could be an important component of the plant “structural economics spectrum”, which explains species-structural diversity in terms of tree architectural traits along a spectrum balancing light interception, carbon allocation, and mechanical stability [91].
The WSA of trees relates to their respiration rates and captures broad maintenance costs [17,18,19,20,21] and crown surface area refers to the photosynthetically active surface of trees and their energy income [15,16]. Therefore, the strong and positive relationship that was observed between WSA and CSA (across all study tree species combined and within each species) implies that as the respiration rate of a tree increases, its production efficiency should also increase in order to maintain sustainable growth. Otherwise, trees should lose vigor.
For trees in natural forests and plantations, the distribution of branches and foliage is heavily influenced by shading or sheltering from neighboring trees [88], but particularly the need to maintain a positive carbon balance in the leaves. Weiskittel and McGuire [29] showed that branch surface area peaked a bit below the middle of the crowns of Douglas-fir (Pseudotsuga menziesii) trees, since smaller branches near the top had considerably less surface area, while large, lower branches, with greater surface area, tended to dieback over time, due to a reduction in sustaining leaves on branches near the base of the crown. Xu and Harrington [92] found that sub-dominant trees in a plantation of Loblolly pine (Pinus taeda) distributed most of their foliage at the top third of their crowns. These patterns might be expected for trees of species which are less tolerant of shade. Niinemets and Valladares [93] produced numerical tolerance indices ranging from 1 to 5 (1 = very intolerant to 5 = very tolerant) ranking Pinus taeda = 1.99 and Pseudotsuga menziesii = 2.78.
The three urban tree species studied here showed a branch surface area vertical distribution inversely corresponding to Niinemets and Valladare’s [93] shade tolerance indices, with Gleditsia triacanthos = 1.61, Quercus macrocarpa = 2.71, and Metasequoia glyptostroboides = 3.00, showing patterns of branch area peaking in the upper-mid, middle, and lower-mid crowns, respectively (Figure 6). This result was somewhat surprising, since these trees were open-grown and not shaded by other trees. This suggests that self-shading of leaves and branches could be an important element of the branching architecture of open-grown trees [94] along with inherent shade tolerance [95], but also suggests that a mechanism other than maintaining positive carbon balance in leaves might be at play.
Another physiological explanation of this pattern of branch woody surface distribution could be a need to counterbalance optimizing light energy capture with the need to minimize the surface area for heat gain due to incoming solar radiation, and water loss through transpiration. It is well known that warm temperatures and heat islands in cities [96,97,98] cause increased rates of leaf transpiration [12]. Niinemets and Valladare’s [93] also published drought tolerance indices for the study species (drought tolerance for Gleditsia triacanthos = 4.98, Quercus macrocarpa = 3.85, and Metasequoia glyptostroboides = 2.38), showing that the more drought-tolerant the species, the more it concentrated the branch surface area towards the upper crown (see Figure 6).
Niinemets and Valladare [93] showed, over many species, that inherent traits of shade and drought tolerance of species were often negatively correlated, so the above pattern was expected. However, this study suggests that, at least for the case of open-grown, urban trees, building a branching architecture that optimizes drought tolerance may be a good explanation for branch surface area distribution. It may be that hydraulic limitations are not only an important force limiting the size and hydraulic architecture of tall trees [99,100], but also for the branching architecture of any tree whose physiological water stress exceeds their photosynthetic capacity. These findings have important implications for the management of urban forests, particularly the selection of species for urban plantings, given expected, continued increases in global temperatures and urbanization.
While surface area data have long been available for leaves [101,102,103,104,105,106,107,108], TLS, in combination with QSMs, can now be used to quantify the surface area of the “woody skeleton” of trees, which plays a vital role in gas exchange with the atmosphere. Tree respiration rates are closely related to their WSA [18,19,20] since respiration of non-photosynthetic tissues mainly occurs in the cambial sheath and the living annual growing rings around the dead heartwood [17]. Nonetheless, Sprugel [109] suggested that a forest stand with high bole WSA does not necessarily have high rates of respiration, so there is still a need to scale up from tree to stand to forest-level process modeling. Respiration still contributes a significant portion of uncertainty related to the carbon budget and offset potential of urban forests [8]. The type of data that was produced in this study could form the basis to develop new process models that describe the carbon balance and growth of urban forests under a changing climate, which has been an important focus of forest process modeling for decades [90,110].
5. Conclusions
In this study, we demonstrated the use of TLS technology to produce detailed data that quantify the total above-ground WSA of urban trees (first study objective) and we found that the study trees varied widely in their WSA. Furthermore, based on TLS data we studied the allocation patterns of WSA to different components of the woody skeleton of trees, i.e., stem and branches of different order, base-diameter, and base-height classes (second study objective), and we found that the urban trees allocated their WSA mainly to branches, while branch order, branch-base diameter, and branch-base height influenced the observed allocation pattern. The vertical allocation pattern of branch surface area was inversely related to the shade tolerance of the species.
Measuring the WSA of trees with TLS is a non-destructive method that allows explicitly accounting for the above-ground structural-fractal complexity of trees, and it does not rely on any biological assumptions for tree architecture [35], in comparison with previous methods that approximated branch and stem geometry or estimated WSAs from allometric equations [13,19,29,31,32,36,37].
This study showed that WSA is a function of the above-ground fractal-structural complexity of trees, and their “hydraulic” size quantified by different Euclidean metrics of path lengths from the tree base to each branch tip (third study objective). The observed positive relationship between the crown surface area and the woody surface area of the trees (third study objective) implies a physiological mechanism for maintaining a positive carbon balance at tree scale. In general, the type of data produced in this study describes tree surface allometry, and it can be used to develop new or inform existing process models that quantify the growth and productivity of urban forests.
Author Contributions
G.A. and D.W.M. conceived the ideas and designed the methodology for the study; G.A., D.W.M. and D.S. analyzed the data; G.A., D.W.M. and D.S. led the writing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported with funds from a joint venture agreement between Michigan State University and the United States Department of Agriculture Forest Service, Forest Inventory and Analysis Program, Northern Research Station. Part of D.W. MacFarlane’s time was paid for with funds from Michigan AgBioResearch, the USDA National Institute of Food and Agriculture. Part of G. Arseniou’s time was supported by a Bouyoukos Fellowship. Part of D. Seidel’s time was supported by the German Research Foundation (DFG) [SE2383/7-1].
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We want to acknowledge the Michigan State University Campus Arboretum (Frank W. Telewski, and Jeffrey Wilson) and the Michigan State University Department of Infrastructure, Planning and Facilities (Jerry Wahl) who permitted and assisted with the data collection.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Heisler, G.M. Energy Savings with Trees. J. Arboric. 1986, 12, 113–125. [Google Scholar]
- McPherson, E.G.; Nowak, J.D.; Rowan, A.R. (Eds.) Chicago’s Urban. Forest Ecosystem: Results of the Chicago Urban. Forest Climate Project; Gen. Tech. Rep.NE-186; U.S. Department of Agriculture, Forest Service, Northeastern Forest Experiment Station: Radnor, PA, USA, 1994; p. 201.
- McPherson, E.G. Atmospheric carbon dioxide reduction by Sacramento’s urban forest. J. Arboric. 1998, 24, 215–223. [Google Scholar]
- Nowak, D.J.; Crane, D.E. Carbon storage and sequestration by urban trees in the USA. Environ. Pollut. 2002, 116, 381–389. [Google Scholar] [CrossRef]
- MacFarlane, D.W. Potential availability of urban wood biomass in Michigan: Implications for energy production, carbon sequestration and sustainable forest management in the USA. Biomass Bioenergy 2009, 33, 628–634. [Google Scholar] [CrossRef]
- Pretzsch, H.; Biber, P.; Uhl, E.; Dahlhausen, J.; Rötzer, T.; Caldentey, J.; Koike, T.; van Con, T.; Chavanne, A.; Seifert, T.; et al. Crown size and growing space requirement of common tree species in urban centres, parks, and forests. Urban. For. Urban. Green. 2015, 14, 466–479. [Google Scholar] [CrossRef] [Green Version]
- Casalegno, S.; Anderson, K.; Hancock, S.; Gaston, K.J. Improving models of urban greenspace: From vegetation surface cover to volumetric survey, using waveform laser scanning. Methods Ecol. Evol. 2017, 8, 1443–1452. [Google Scholar] [CrossRef] [Green Version]
- Tigges, J.; Tobia Lakes, T. High resolution remote sensing for reducing uncertainties in urban forest carbon offset life cycle assessments. Carbon Balance Manag. 2017, 12, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Calfapietra, C.; Peñuelas, J.; Niinemets, Ü. Urban plant physiology: Adaptation-mitigation strategies under permanent stress. Trends Plant. Sci. 2015, 20, 72–75. [Google Scholar] [CrossRef]
- Arseniou, G.; MacFarlane, D.W. Fractal dimension of tree crowns explains species functional-trait responses to urban environments at different scales. Ecol. Appl. 2021, 31, e2297. [Google Scholar] [CrossRef]
- Lambers, H.; Chapin, F.S.; Pons, T.L. Plant Physiological Ecology, 2nd ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Pallardy, S.G. Physiology of Woody Plants, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Whittaker, R.H.; Woodwell, G.M. Surface area relations of woody plants and forest communities. Am. J. Bot. 1967, 54, 931–939. [Google Scholar] [CrossRef]
- Lehnebach, R.; Beyer, R.; Letort, V.; Heuret, P. The pipe model theory half a century on: A review. Ann. Bot. 2018, 121, 773–795. [Google Scholar] [CrossRef] [PubMed]
- Seidel, D.; Annighöfer, P.; Stiers, M.; Zemp, C.D.; Burkardt, K.; Ehbrecht, M.; Willim, K.; Kreft, H.; Hölscher, D.; Ammer, C. How a measure of tree structural complexity relates to architectural benefit-to-cost ratio, light availability, and growth of trees. Ecol. Evol. 2019, 9, 7134–7142. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Jia, W.; Wang, Q.; Huang, X. Deriving Individual -Tree Biomass from Effective Crown Data Generated by Terrestrial Laser Scanning. Remote Sens. 2019, 11, 2793. [Google Scholar] [CrossRef] [Green Version]
- Kinerson, R.S. Relationships between Plant Surface Area and Respiration in Loblolly Pine. J. Appl. Ecol. 1975, 12, 965. [Google Scholar] [CrossRef]
- Kramer, P.J.; Kozlowski, T.T. Physiology of Woody Plants; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Yoneda, T. Surface area of woody organs of an evergreen broadleaf forest tree in Japan and Southeast Asia. J. Plant. Res. 1993, 106, 229–237. [Google Scholar] [CrossRef]
- Bosc, A.; De Grandcourt, A.; Loustau, D. Variability of stem and branch maintenance respiration in a Pinus pinaster tree. Tree Physiol. 2003, 23, 227–236. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.H.; Nakane, K.; Lee, J.T.; Bang, H.S.; Na, Y.E. Stem/branch maintenance respiration of Japanese red pine stand. For. Ecol. Manag. 2007, 243, 283–290. [Google Scholar] [CrossRef] [Green Version]
- MacFarlane, D.W.; Luo, A. Quantifying tree and forest bark structure with a bark-fissure index. Can. J. For. Res. 2009, 39, 1859–1870. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial Laser Scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Metz, J.; Seidel, D.; Schall, P.; Scheffer, D.; Schulze, E.-D.; Ammer, C. Crown modeling by terrestrial laser scanning as an approach to assess the effect of aboveground intra- and interspecific competition on tree growth. For. Ecol. Manag. 2013, 310, 275–288. [Google Scholar] [CrossRef]
- MacFarlane, D.W.; Kuyah, S.; Mulia, R.; Dietz, J.; Muthuri, C.; Noordwijk, M.V. Evaluating a non-destructive method for calibrating tree biomass equations derived from tree branching architecture. Trees 2014, 28, 807–817. [Google Scholar] [CrossRef]
- Eloy, C.; Fournier, M.; Lacointe, A.; Moulia, B. Wind loads and competition for light sculpt trees into self-similar structures. Nat. Commun. 2017, 8, 1014. [Google Scholar] [CrossRef]
- Seidel, D. A holistic approach to determine tree structural complexity based on laser scanning data and fractal analysis. Ecol. Evol. 2018, 8, 128–134. [Google Scholar] [CrossRef]
- Dorji, Y.; Annighöfer, P.; Ammer, C.; Seidel, D. Response of beech (Fagus sylvatica L.) trees to competition—New insights from using fractal analysis. Remote Sens. 2019, 11, 2656. [Google Scholar] [CrossRef] [Green Version]
- Weiskittel, A.R.; Maguire, D.A. Branch surface area and its vertical distribution in coastal Douglas-fir. Trees 2006, 20, 657–667. [Google Scholar] [CrossRef]
- Kucharik, C.J.; Norman, J.M.; Gower, S.T. Measurements of branch area and adjusting leaf area index indirect measurements. Agric. For. Meteorol. 1998, 91, 69–88. [Google Scholar] [CrossRef]
- Halldin, S. Leaf and Bark Area Distribution in a Pine Forest. In The Forest-Atmosphere Interaction; Hutchison, B.A., Hicks, B.B., Eds.; Springer: Dordrecht, The Netherlands, 1985. [Google Scholar] [CrossRef]
- Baldwin, B.C.; Peterson, K.D.; Burkhart, H.E.; Amateis, R.L.; Doughterty, P.M. Equations for estimating loblolly pine branch and foliage weight and surface area distributions. Can. J. For. Res. 1997, 27, 918–927. [Google Scholar] [CrossRef]
- Damesin, C.; Ceschia, E.; Le Goff, N.; Ottorini, J.M.; Dufrêne, E. Stem and branch respiration of beech: From tree measurements to estimations at the stand level. New Phytol. 2002, 153, 159–172. [Google Scholar] [CrossRef]
- Meir, P.; Shenkin, A.; Disney, M.; Rowland, L.; Malhi, Y.; Herold, M.; da Costa, A.C.L. Plant Structure-Function Relationships and Woody Tissue Respiration: Upscaling to Forests from Laser-Derived Measurements. In Plant Respiration: Metabolic Fluxes and Carbon Balance, Advances in Photosynthesis and Respiration 43; Tcherkez, G., Ghashghaie, J., Eds.; Springer International Publishing AG: New York, NY, USA, 2017; pp. 92–105. [Google Scholar]
- Malhi, Y.; Jackson, T.; Bentley, L.P.; Lau, A.; Shenkin, A.; Herold, M.; Calders, K.; Bartholomeus, H.; Disney, M.I. New perspectives on the ecology of tree structure and tree communities through terrestrial laser scanning. Interface Focus 2018, 8, 20170052. [Google Scholar] [CrossRef] [Green Version]
- Yoneda, T.; Tamin, R.; Ogino, K. Dynamics of Aboveground Big Woody Organs in a Foothill Dipterocarp Forest, West Sumatra, Indonesia. Ecol. Res. 1990, 5, 111–130. [Google Scholar] [CrossRef]
- Jennings, D.T.; Diamond, J.B.; Watt, B.A. Population densities of spiders (Araneae) and spruce budworms (Lepidptera tortricidae) on foliage of balsam fir and red spruce in east-central Maine. J. Arachnol. 1990, 18, 181–193. [Google Scholar]
- Zou, J.; Yan, G.; Zhu, L.; Zhang, W. Woody-to-total area ratio determination with a multispectral canopy imager. Tree Physiol. 2009, 29, 1069–1080. [Google Scholar] [CrossRef] [Green Version]
- Inoue, A.; Nishizono, T. Conservation rule of stem surface area: A hypothesis. Eur. J. For. Res. 2015, 134, 599–608. [Google Scholar] [CrossRef]
- Halley, J.M.; Hartley, S.; Kallimanis, A.S.; Kunin, W.E.; Lennon, J.J.; Sgardelis, S.P. Uses and abuses of fractal methodology in ecology. Ecol. Lett. 2004, 7, 254–271. [Google Scholar] [CrossRef]
- Shinozaki, K.; Yoda, K.; Hozumi, K.; Kira, T. A quantitative analysis of plant form-the pipe model theory. I & II. Jpn. J. Ecol. 1964, 14, 133–139. [Google Scholar]
- West, G.B.; Brown, J.H.; Enquist, B. A General Model for the Origin of Allometric Scaling Laws in Biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef]
- Van Noordwijk, M.; Mulia, R. Functional branch analysis as tool for fractal scaling above and belowground trees for their additive and non-additive properties. Ecol. Model. 2002, 149, 41–51. [Google Scholar] [CrossRef]
- Mäkelä, A.; Valentine, H.T. Crown ratio influences allometric scaling in trees. Ecology 2006, 87, 2967–2972. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.S.; Avitabile, V.; Disney, M.; Armston, J.D.; et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman: New York, NY, USA, 1977. [Google Scholar]
- Seidel, D.; Ehbrecht, M.; Dorji, Y.; Jambay, J.; Ammer, C.; Annighöfer, P. Identifying architectural characteristics that determine tree structural complexity. Trees 2019, 33, 911–919. [Google Scholar] [CrossRef]
- Ma, L.; Zheng, G.; Eitel, J.U.H.; Magney, T.S.; Moskal, L.M. Determining woody-to-total area ratio using terrestrial laser scanning (TLS). Agric. For. Meteorol. 2016, 228–229, 217–228. [Google Scholar] [CrossRef] [Green Version]
- Hopkinson, C.; Chasmer, L.; Young-Pow, C.; Treitz, P. Assessing Forest metrics with a ground-based scanning lidar. Can. J. For. Res. 2004, 34, 573–583. [Google Scholar] [CrossRef] [Green Version]
- Maas, H.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
- Moskal, L.M.; Zheng, G. Retrieving Forest Inventory Variables with Terrestrial Laser Scanning (TLS) in Urban Heterogeneous Forest. Remote Sens. 2012, 4, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Vonderach, C.; Vogtle, T.; Adler, P.; Norra, S. Terrestrial laser scanning for estimating urban tree volume and carbon content. Int. J. Remote Sens. 2012, 33, 6652–6667. [Google Scholar] [CrossRef]
- Olschofsky, K.; Mues, V.; Köhl, M. Operational assessment of aboveground tree volume and biomass by terrestrial laser scanning. Comput. Electron. Agric. 2016, 127, 699–707. [Google Scholar] [CrossRef] [Green Version]
- Danson, F.M.; Hetherington, D.; Morsdorf, F.; Koetz, B.; Allgower, B. Forest canopy gap fraction from terrestrial laser scanning. IEEE Geosci. Remote Sens. Lett. 2007, 4, 157–160. [Google Scholar] [CrossRef] [Green Version]
- Strahler, A.H.; Jupp, D.L.; Woodcock, C.E.; Schaaf, C.B.; Yao, T.; Zhao, F.; Yang, X.; Lovell, J.; Culvenor, D.; Newnham, G.; et al. Retrieval of forest structural parameters using a ground-based lidar instrument (Echidna (R)). Can. J. Remote Sens. 2008, 34, 426–440. [Google Scholar] [CrossRef] [Green Version]
- Hosoi, F.; Omasa, K. Estimating Vertical Leaf Area Density Profiles of Tree Canopies Using Three-Dimensional Portable LIDAR Imaging. In Proceedings of the ISPRS Workshop Laser-Scanning, Paris, France, 1–2 September 2009; Volume 9. Part 3/W8. [Google Scholar]
- Polo, J.R.R.; Sanz, R.; Llorens, J.; Arnó, J.; Escolà, A.; Ribes-Dasi, M.; Masip, J.; Camp, F.; Gràcia, F.; Solanelles, F.; et al. A tractor-mounted scanning LIDAR for the non-destructive measurement of vegetative volume and surface area of tree-row plantations: A comparison with conventional destructive measurements. Biosyst. Eng. 2009, 102, 128–134. [Google Scholar] [CrossRef] [Green Version]
- Antonarakis, A.; Richards, K.S.; Brasington, J.; Müller, E. Determining leaf area index and leafy tree roughness using terrestrial laser scanning. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- Moorthy, I.; Millera, J.R.; Antonio Jimenez Bernic, J.; Zarco-Tejadac, P.; Hub, B.; Chend, J. Field characterization of olive (Olea europaea L.) tree crown architecture using terrestrial laser scanning data. Agric. For. Meteorol. 2011, 151, 204–214. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.L.; Fournier, R.A.; Côté, J.F.; Verstraete, M.M. Estimating leaf area distribution in savanna trees from terrestrial LiDAR measurements. Agric. For. Meteorol. 2011, 151, 1252–1266. [Google Scholar] [CrossRef]
- Jung, S.-E.; Kwak, D.-A.; Park, T.; Lee, W.-K.; Yoo, S. Estimating Crown Variables of Individual Trees Using Airborne and Terrestrial Laser Scanners. Remote Sens. 2011, 3, 2346–2363. [Google Scholar] [CrossRef] [Green Version]
- Béland, M.; Widlowski, J.L.; Fournier, R.A. A model for deriving voxel-level tree leaf area density estimates from ground-based LiDAR. Environ. Model. Softw. 2014, 51, 184–189. [Google Scholar] [CrossRef]
- Li, Y.; Guo, Q.; Su, Y.; Tao, S.; Zhao, K.; Xu, G. Retrieving the gap fraction, element clumping index, and leaf area index of individual trees using single-scan data from a terrestrial laser scanner. ISPRS J. Photogramm. Remote Sens. 2017, 130, 308–316. [Google Scholar] [CrossRef]
- Hu, R.; Bournez, E.; Cheng, S.; Jiang, H.; Nerry, F.; Landes, T.; Saudreau, M.; Kastendeuch, P.; Najjar, G.; Colin, J.; et al. Estimating the leaf area of an individual tree in urban areas using terrestrial laser scanner and path length distribution model. ISPRS J. Photogramm. Remote Sens. 2018, 144, 357–368. [Google Scholar] [CrossRef] [Green Version]
- Vicari, M.B.; Pisek, J.; Disney, M. New estimates of leaf angle distribution from terrestrial LiDAR: Comparison with measured and modeled estimates from nine broadleaf tree species. Agric. For. Meteorol. 2019, 264, 322–333. [Google Scholar] [CrossRef]
- Kankare, V.; Holocaine, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual tree biomass estimation using terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Stovall, A.E.; Vorster, A.G.; Anderson, R.S.; Evangelista, P.H.; Shugart, H.H. Non-destructive aboveground biomass estimation of coniferous trees using terrestrial LiDAR. Remote Sens. Environ. 2017, 200, 31–42. [Google Scholar] [CrossRef]
- Tanhuanpää, T.; Kankare, V.; Setälä, H.; Yli-Pelkonen, V.; Vastaranta, M.; Niemi, M.T.; Raisio, J.; Holopainen, M. Assessing above-ground biomass of open-grown urban trees: A comparison between existing models and a volume-based approach. Urban. For. Urban. Green. 2017, 21, 239–246. [Google Scholar] [CrossRef] [Green Version]
- Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; Tanago, J.G.; Bartholomeus, H.; Brede, B.; Herold, M. Data acquisition considerations for Terrestrial Laser Scanning of forest plots. Remote Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef] [Green Version]
- Kaasalainen, S.; Krooks, A.; Liski, J.; Raumonen, P.; Kaartinen, H.; Kaasalainen, M.; Puttonen, E.; Anttila, K.; Mäkipää, R. Change Detection of Tree Biomass with Terrestrial Laser Scanning and Quantitative Structure Modelling. Remote Sens. 2014, 6, 3906–3922. [Google Scholar] [CrossRef] [Green Version]
- Hackenberg, J.; Spiecker, H.; Calders, K.; Disney, M.; Raumonen, P. SimpleTree—An Efficient Open Source Tool to Build Tree Models from TLS Clouds. Forests 2015, 6, 4245–4294. [Google Scholar] [CrossRef]
- Bournez, E.; Landes, T.; Saudreau, M.; Kastendeuch, P.; Najjar, G.; Bournez, E.; Landes, T.; Saudreau, M.; Kastendeuch, P.; Najjar, G. From TLS Point Clouds to 3D Models of Trees: A Comparison of Existing Algorithms For 3D Tree Reconstruction. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 113–120. [Google Scholar] [CrossRef] [Green Version]
- Disney, M.I.; Vicari, M.B.; Burt, A.; Calders, K.; Lewis, S.L.; Raumonen, P.; Wilkes, P. Weighing trees with lasers: Advances, challenges and opportunities. Interface Focus 2018, 8, 20170048. [Google Scholar] [CrossRef] [Green Version]
- TreeQSM. Quantitative Structure Models of Single Trees from Laser Scanner Data. Version 2.3.0. Copyright (C) 2013–2017 Pasi Raumonen. Available online: https://zenodo.org/record/844626#.Xvz_nW1KjIU (accessed on 7 July 2021).
- Raumonen, P.; Casella, E.; Calders, K.; Murphy, S.; Åkerblom, M.; Kaasalainen, M. Massive-scale tree modelling from TLS data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, II-3/W4, 189–196. [Google Scholar] [CrossRef] [Green Version]
- Smith, D.D.; Sperry, J.S.; Enquist, B.; Savage, V.M.; McCulloh, K.A.; Bentley, L.P. Deviation from symmetrically self-similar branching in trees predicts altered hydraulics, mechanics, light interception and metabolic scaling. New Phytol. 2014, 201, 217–229. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015; Available online: https://www.R-project.org/ (accessed on 9 August 2021).
- Sileshi, G.W. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. Linear and Nonlinear Mixed Effects Models, R package version 3.1-152; 2021. Available online: https://CRAN.R-project.org/package=nlme (accessed on 9 August 2021).
- Dorji, Y.; Schuldt, B.; Neudam, L.; Dorji, R.; Middleby, K.; Isasa, E.; Körber, K.; Ammer, C.; Annighöfer, P.; Seidel, D. Three-dimensional quantification of tree architecture from mobile laser scanning and geometry analysis. Trees 2021, 1–14. [Google Scholar] [CrossRef]
- Lau, A.; Bentley, L.P.; Martius, C.; Shenkin, A.; Bartholomeus, H.; Raumonen, P.; Malhi, Y.; Jackson, T.; Herold, M. Quantifying branch architecture of tropical trees using terrestrial LiDAR and 3D modelling. Trees 2018, 32, 1219–1231. [Google Scholar] [CrossRef] [Green Version]
- Lau, A.; Martius, C.; Bartholumeus, H.; Shenkin, A.; Jackson, T.; Malhi, Y.; Herold, M.; Bentley, L.P. Estimating architecture-based metabolic scaling exponents of tropical trees using terrestrial LiDAR and 3D modelling. For. Ecol. Manag. 2019, 439, 132–145. [Google Scholar] [CrossRef]
- Enquist, B.J. Universal scaling in tree and vascular plant allometry: Toward a general quantitative theory linking plant form and function from cells to ecosystems. Tree Physiol. 2002, 22, 1045–1064. [Google Scholar] [CrossRef] [Green Version]
- Price, C.A.; Enquist, B.J. Scaling of mass and morphology in plants with minimal branching: An extension of the WBE model. Funct. Ecol. 2006, 20, 11–20. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. The fourth dimension of life: Fractal geometry and allometric scaling of organisms. Science 1999, 284, 1677–1679. [Google Scholar] [CrossRef] [Green Version]
- MacFarlane, D.W.; Kane, B. Neighbour effects on tree architecture: Functional trade-offs balancing crown competitiveness with wind resistance. Funct. Ecol. 2017, 31, 1624–1636. [Google Scholar] [CrossRef] [Green Version]
- Weiner, J. Allocation, plasticity and allometry in plants. Perspect. Plant. Ecol. Evol. Syst. 2004, 6, 207–215. [Google Scholar] [CrossRef]
- Mäkelä, A. A carbon balance model of growth and self-pruning in trees based on structural relationships. For. Sci. 1997, 43, 7–24. [Google Scholar]
- Verbeeck, H.; Bauters, M.; Jackson, T.; Shenkin, A.; Disney, M.; Calders, K. Time for a Plant Structural Economics Spectrum. Front. For. Glob. Chang. 2019, 2. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Harrington, T.B. Foliage biomass distribution of loblolly pine as affected by tree dominance, crown size, and stand characteristics. Can. J. For. Res. 1998, 28, 887–892. [Google Scholar] [CrossRef]
- Niinemets, Ü.; Valladares, F. Tolerance to Shade, Drought, and Waterlogging of Temperate Northern Hemisphere Trees and Shrubs. Ecol. Monogr. 2006, 76, 521–547. [Google Scholar] [CrossRef]
- Duursma, R.A.; Mäkelä, A.; Reid, D.E.; Jokela, E.J.; Porté, A.J.; Roberts, S.D. Self-shading affects allometric scaling in trees. Funct. Ecol. 2010, 24, 723–730. [Google Scholar] [CrossRef]
- Zeide, B.; Pfeifer, P. A Method for Estimation of Fractal Dimension of Tree Crowns. For. Sci. 1991, 37, 1253–1265. [Google Scholar]
- Gregg, J.W.; Jones, C.; Dawson, T.E. Urbanization effects on tree growth in the vicinity of New York City. Nat. Cell Biol. 2003, 424, 183–187. [Google Scholar] [CrossRef] [PubMed]
- Bowler, D.E.; Buyung-Ali, L.; Knight, T.M.; Pullin, A.S. Urban greening to cool towns and cities: A systematic review of the empirical evidence. Landsc. Urban. Plan. 2010, 97, 147–155. [Google Scholar] [CrossRef]
- Kostić, S.; Čukanović, J.; Orlović, S.; Ljubojević, M.; MladenoviĆ, E. Allometric Relations of Sycamore Maple (Acer pseudoplatanus) and its Red Leaf Cultivar (A. pseudoplatanus“Atropurpureum”) in Street and Park Habitats of Novi Sad (Serbia, Europe). J. For. 2019, 117, 114–127. [Google Scholar] [CrossRef]
- Ryan, M.G.; Yoder, B.J. Hydraulic limits to tree height and tree growth. Bioscience 1997, 47, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Ryan, M.G.; Phillips, N.; Bond, B.J. The hydraulic limitation hypothesis revisited. Plant. Cell Environ. 2006, 29, 67–381. [Google Scholar] [CrossRef]
- Lindsey, P.A.; Bassuk, N.L. A nondestructive image analysis technique for estimating whole-tree leaf area. Hort. Technol. 1992, 2, 66–72. [Google Scholar] [CrossRef] [Green Version]
- Nowak, D.J. Estimating leaf area and leaf biomass of open-grown deciduous urban trees. For. Sci. 1996, 42, 504–507. [Google Scholar]
- Cutini, A.; Matteucci, G.; Mugnozza, G.S. Estimation of leaf area index with the Li-Cor LAI 2000 in deciduous forests. For. Ecol. Manag. 1998, 105, 55–65. [Google Scholar] [CrossRef]
- Reich, P.B. Body size, geometry, longevity and metabolism: Do plant leaves behave like animal bodies? Trends Ecol. Evol. 2001, 16, 674–680. [Google Scholar] [CrossRef]
- Peper, P.J.; McPherson, E.G. Evaluation of four methods for estimating leaf area of isolated trees. Urban. For. Urban. Green. 2003, 2, 019–029. [Google Scholar] [CrossRef]
- McPherson, E.G.; Van Doorn, N.S.; Peper, P.J. Urban Tree Database; Forest Service Research Data Archive: Fort Collins, CO, USA, 2016. [CrossRef]
- Dettman, G.T.; MacFarlane, D.W. Trans-species predictors of tree leaf mass. Ecol. Appl. 2018, 29, e01817. [Google Scholar] [CrossRef] [Green Version]
- Chianucci, F.; Ferrara, C.; Pollastrini, M.; Corona, P. Development of digital photographic approaches to assess leaf traits in broadleaf tree species. Ecol. Indic. 2019, 106, 105547. [Google Scholar] [CrossRef]
- Sprugel, D.G. Components of woody-tissue respiration in young Abies amabilis (Dougl.) Forbes trees. Trees 1990, 4, 88–98. [Google Scholar] [CrossRef]
- Valentine, H.; Amateis, R.L.; Burkhart, H.E.; Gregoire, T.G.; Hollinger, D.Y.; MacFarlane, D.W. Projecting the growth of Loblolly pine in a changing atmosphere. South. J. Appl. For. 1999, 23, 212–216. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).