Space-Time Sea Surface pCO2 Estimation in the North Atlantic Based on CatBoost
Abstract
:1. Introduction
2. Materials and Methods
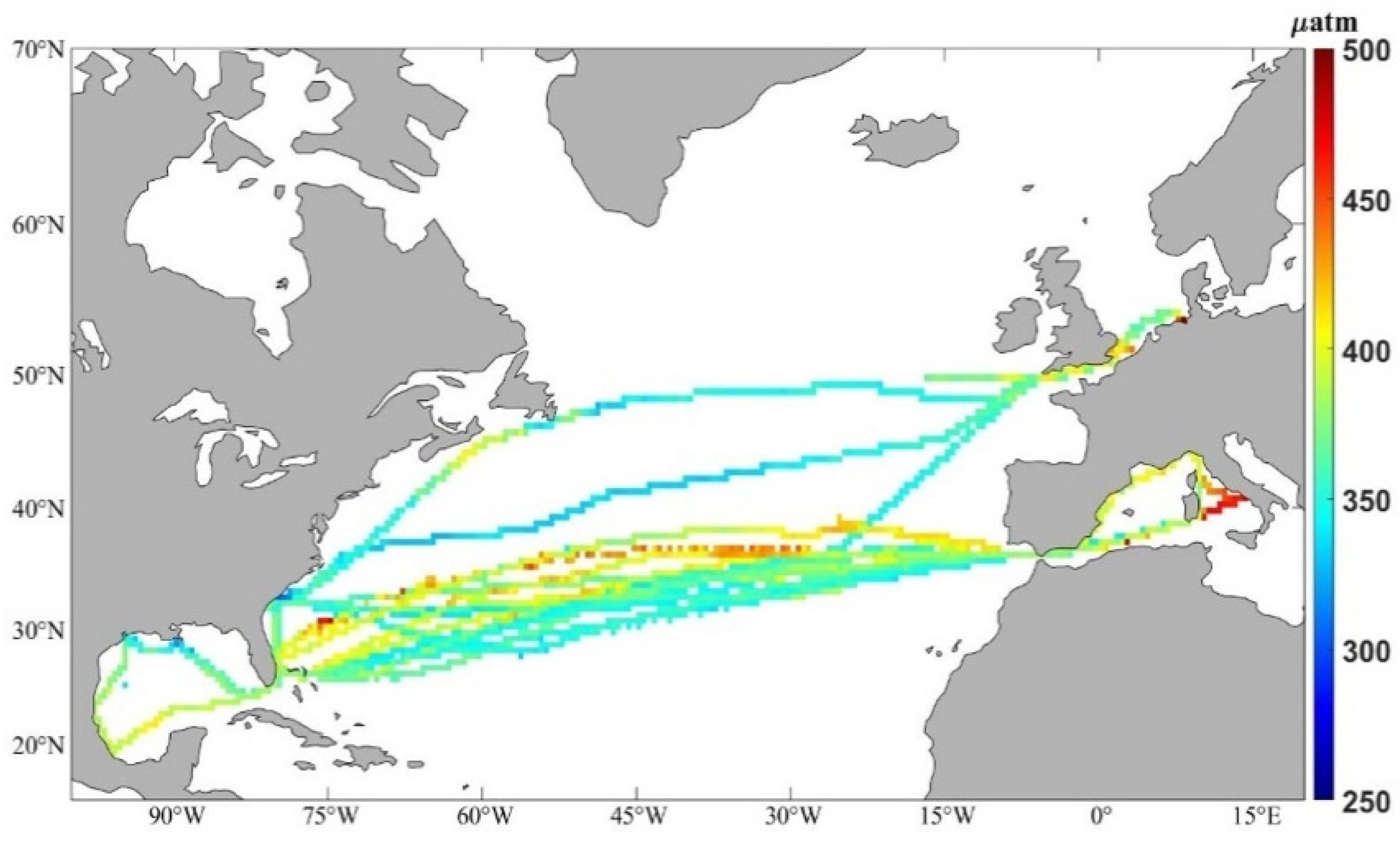
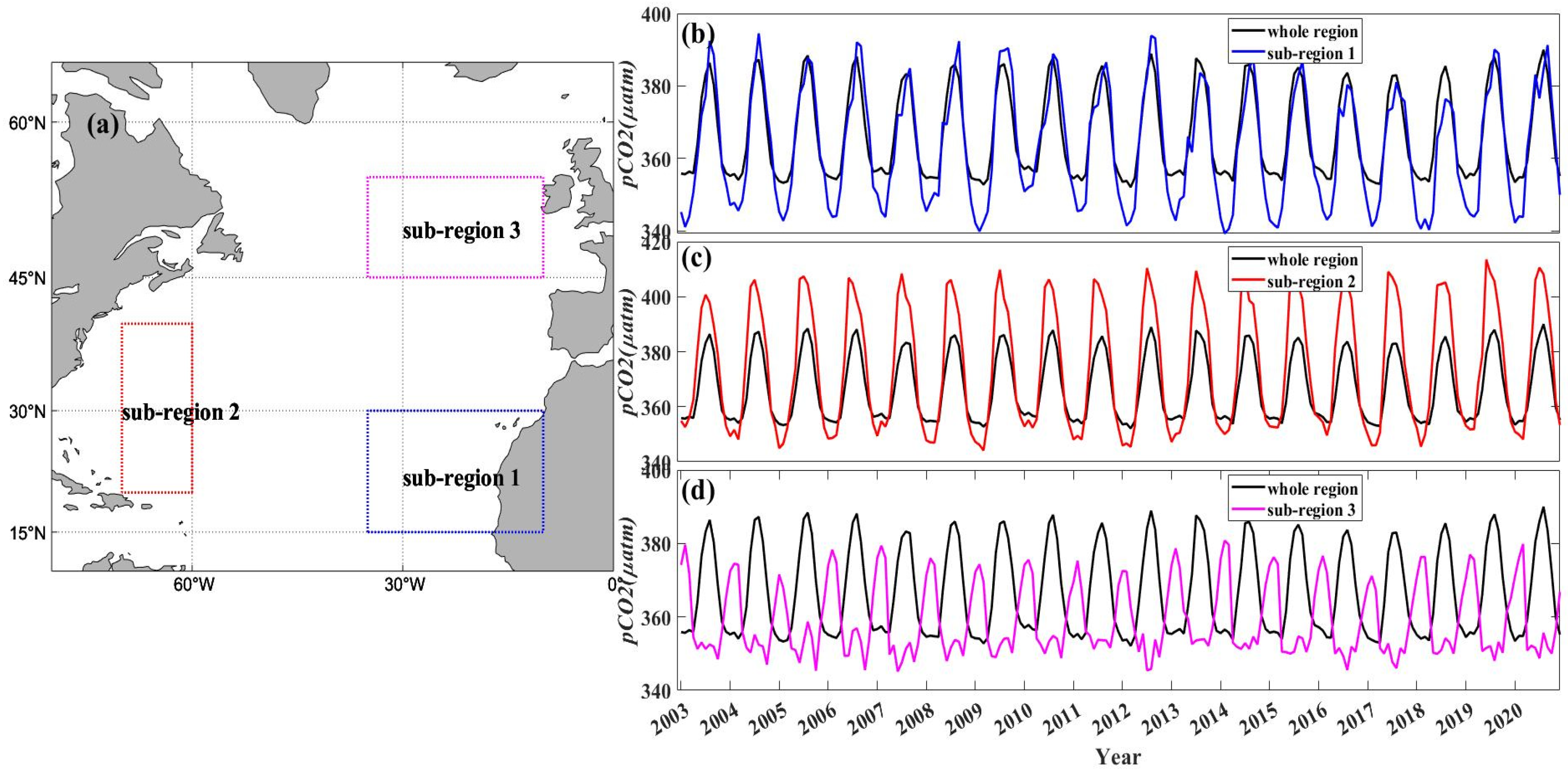
2.1. Study Region
2.2. Data Sources
2.3. Methods
3. Results
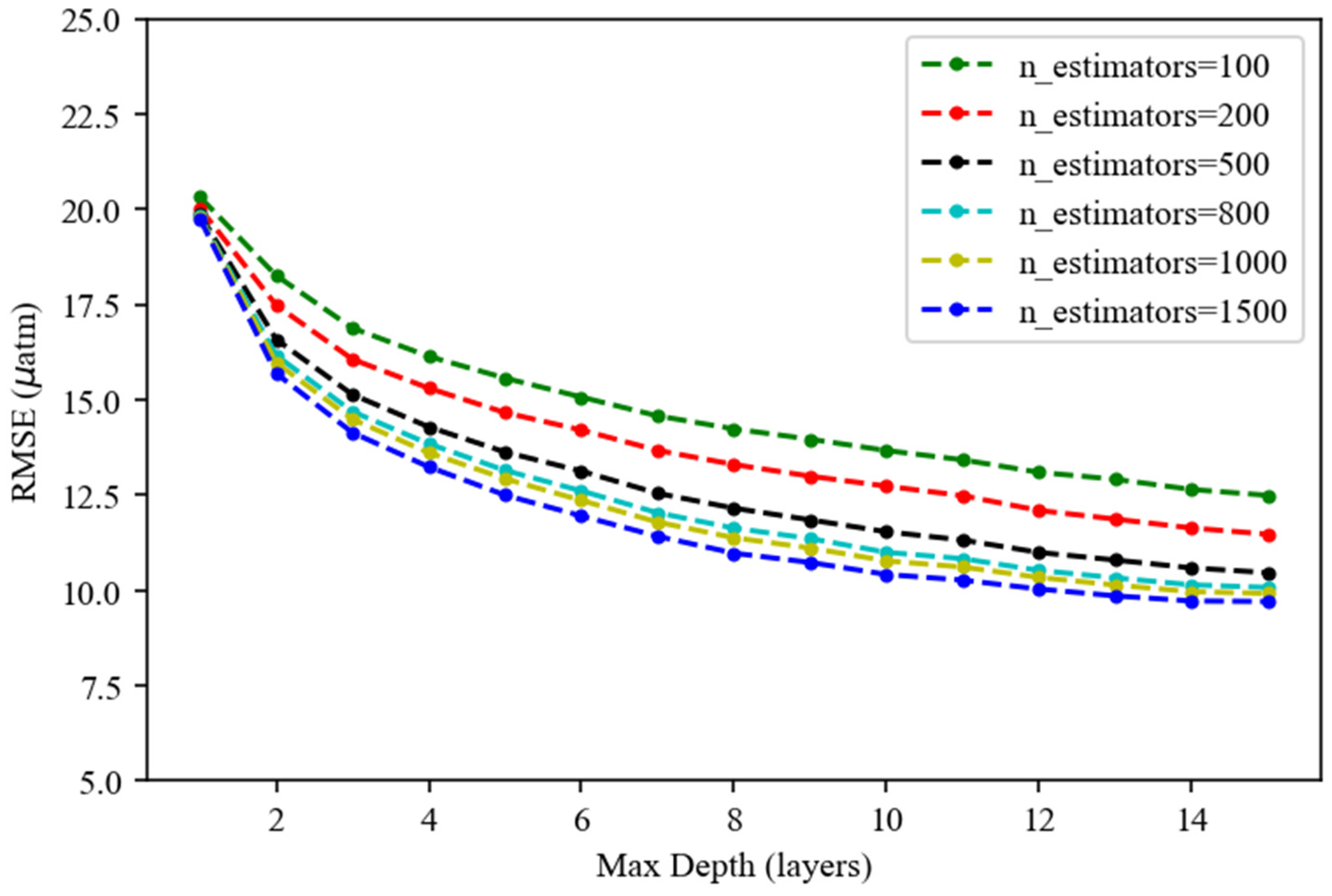
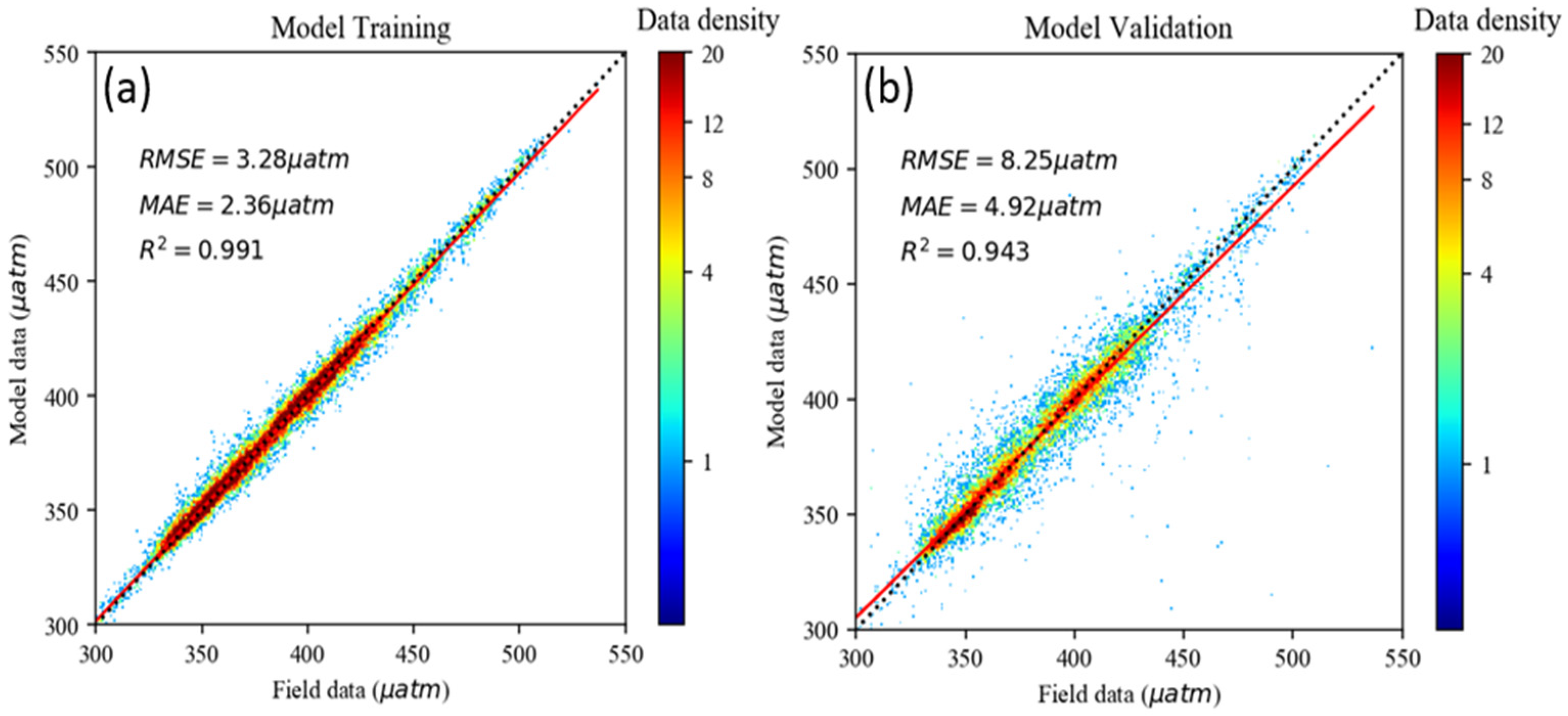
3.1. CatBoost Model Performance
3.2. Independent Validation
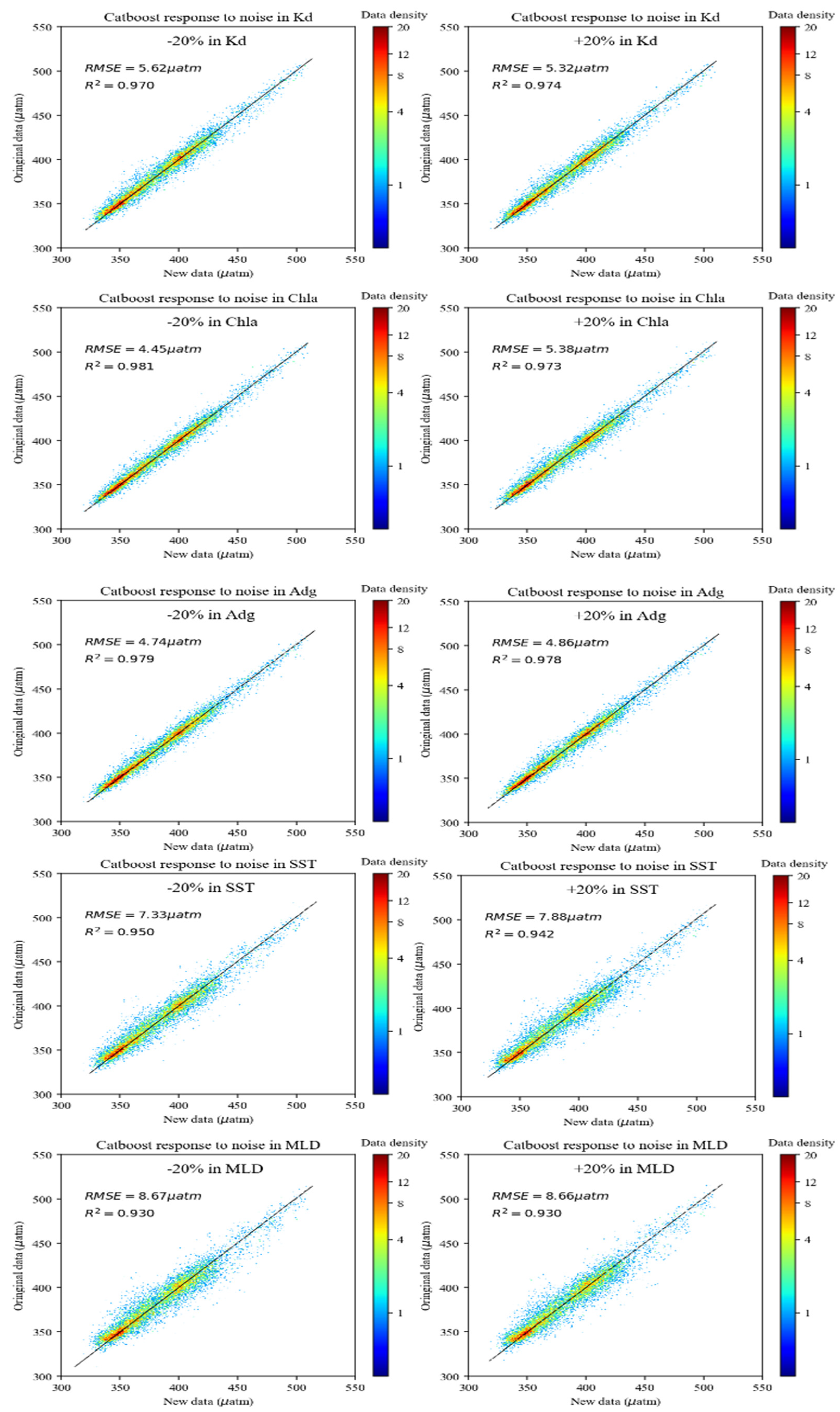
3.3. Model Sensitivity
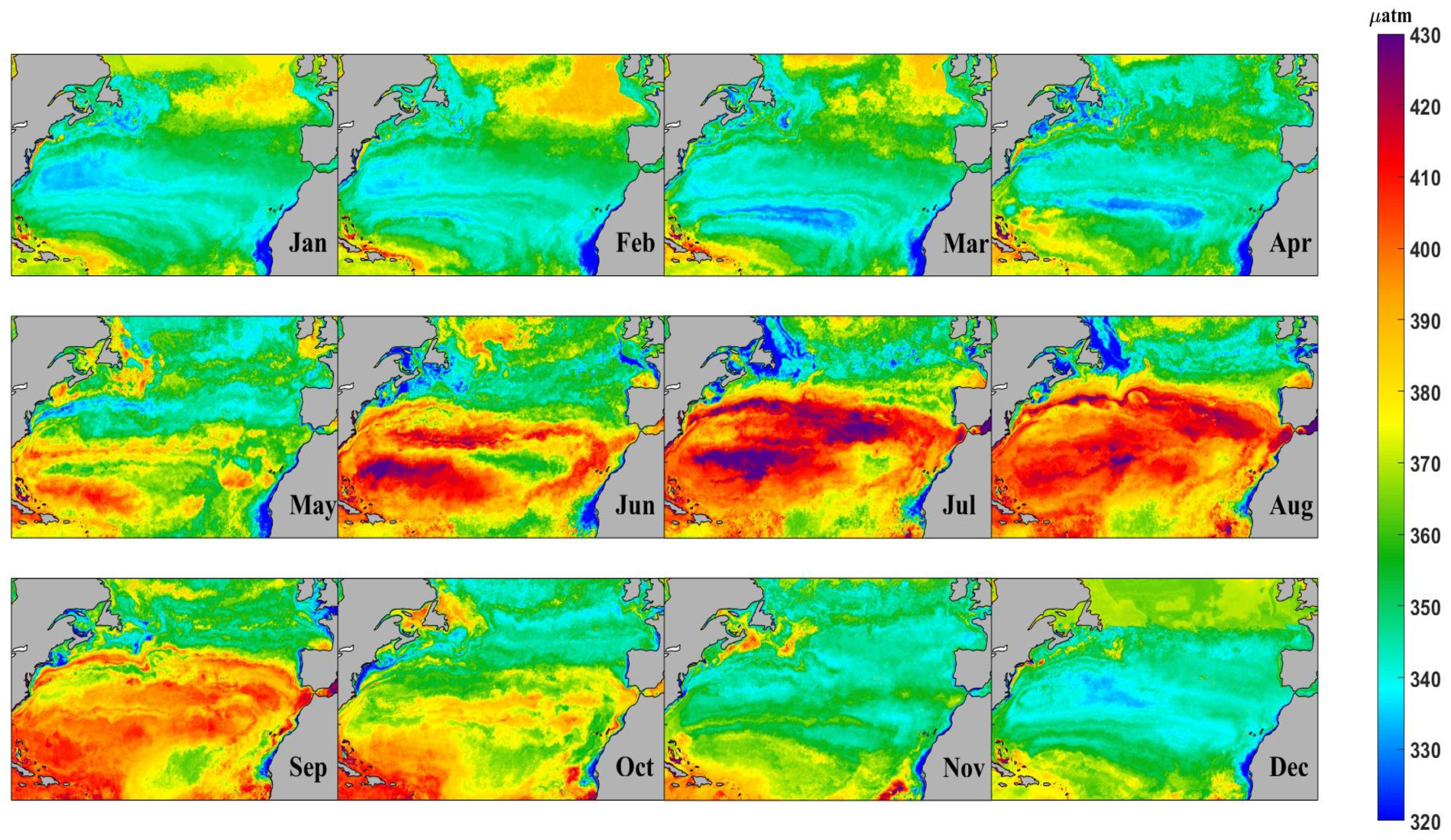
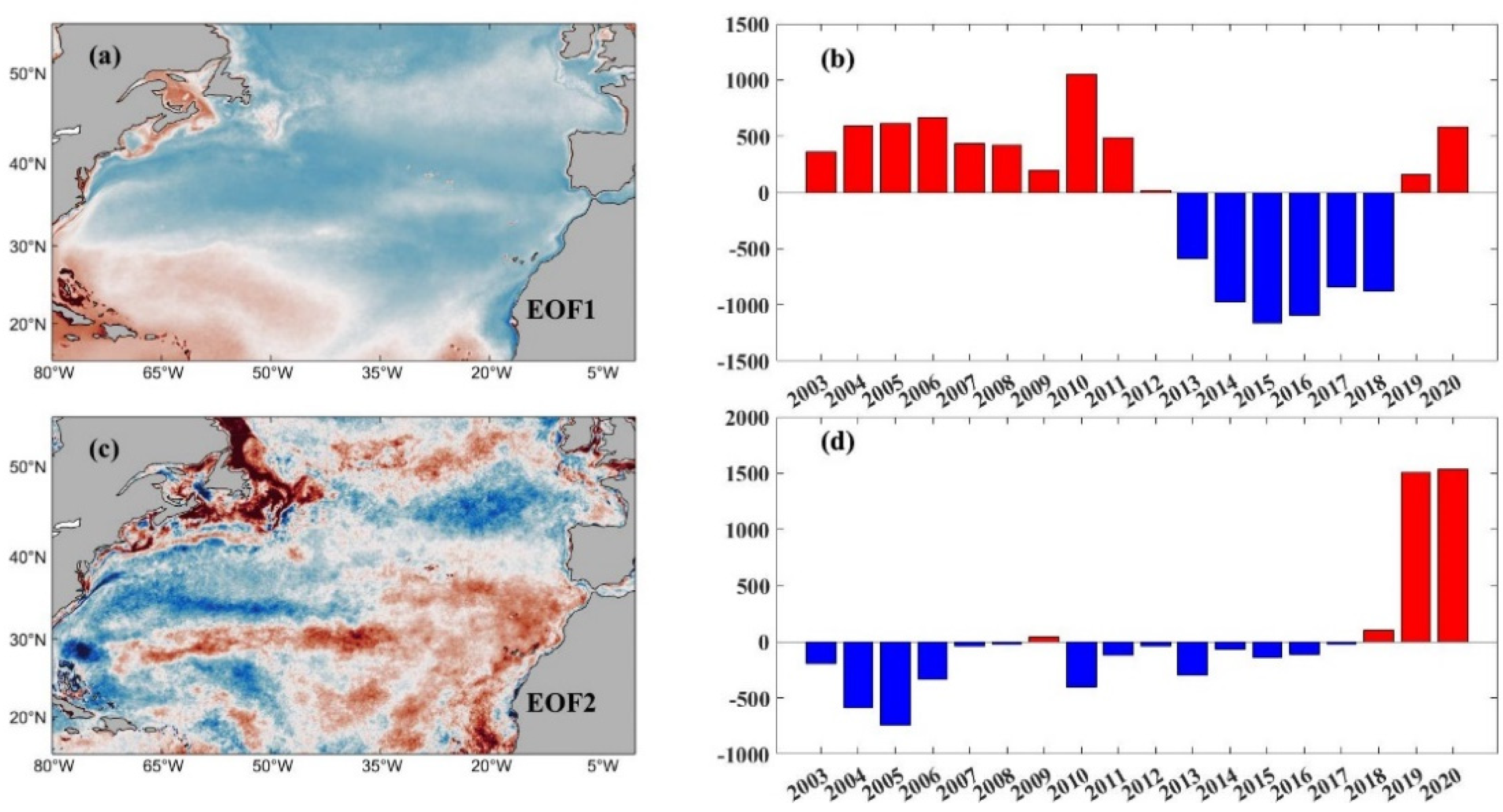
3.4. Seasonal and Interannual Variations of Surface pCO2
4. Discussion
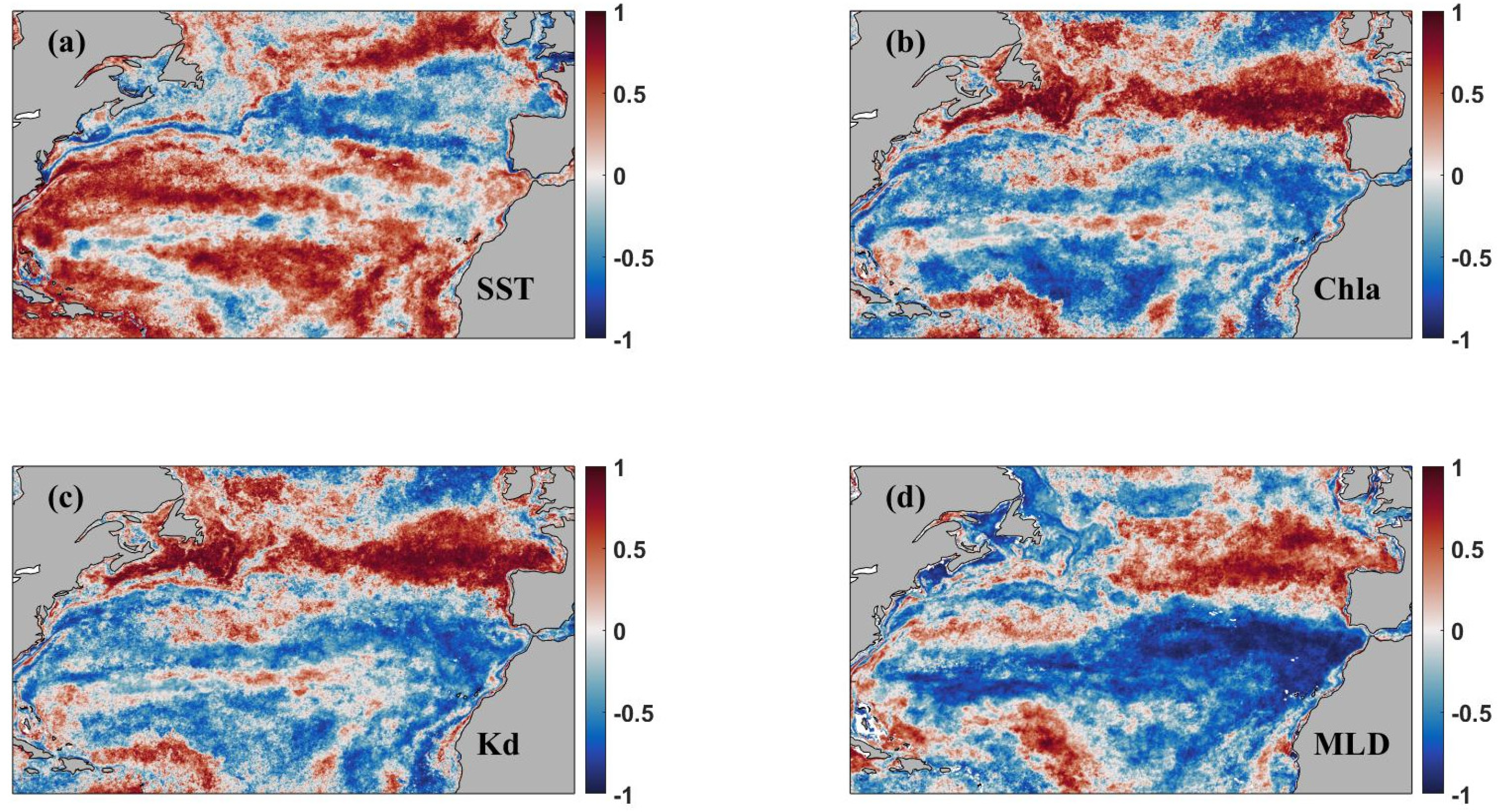
4.1. Comparison between Surface pCO2 and Different Environmental Variables
4.2. Advantages and Limitations of the CatBoost
5. Conclusions
- The interannual variation of sea surface pCO2 in the North Atlantic is relatively stable, and the quarterly variation is more pronounced especially in mid-latitudes. Since various parts of the North Atlantic are affected by different ocean currents and dominated by complex climate patterns, different regions show different trends. In general, the average sea surface pCO2 in low latitude regions is the highest, while the average sea surface pCO2 in high latitude regions is slightly higher than that in mid-latitude regions; while at the same latitude, the sea surface pCO2 in mid-high latitude areas is roughly similar. However, in low latitudes, the pCO2 in the eastern Atlantic Ocean is obviously lower than that in the western.
- The main impact factors of surface pCO2 in the North Atlantic are SST and SSS. In addition, biological activities also play a role in affecting pCO2 variations in some regions. The impact factors are different in each sub-region, on account of complex climate patterns.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Menon, S.; Denman, K.L.; Brasseur, G.; Chidthaisong, A.; Ciais, P.; Cox, P.M.; Dickinson, R.E.; Hauglustaine, D.; Heinze, C.; Holland, E.; et al. Climate Change 2007: The Physical Science Basis, Couplings Between Changes in the Climate System and Biogeochemistry; Cambridge University Press: London, OH, USA, 2007. [Google Scholar]
- Cai, W.J. Estuarine and Coastal Ocean Carbon Paradox: CO2 Sinks or Sites of Terrestrial Carbon Incineration? Annu. Rev. Mar. Sci. 2011, 3, 123–145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, W.J.; Dai, M. Letters, Air-sea exchange of carbon dioxide in ocean margins: A province-based synthesis. Geophys. Res. Lett. 2006, 33, 347–366. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Cai, W.J.; Benitez-Nelson, C.; Wang, Y. Sea surface pCO2-SST relationships across a cold-core cyclonic eddy: Implications for understanding regional variability and air-sea gas exchange. Geophys. Res. Lett. 2007, 341, 265–278. [Google Scholar]
- Sun, Q.; Tang, D.; Wang, S. Remote-sensing observations relevant to ocean acidification. Int. J. Remote Sens. 2012, 33, 7542–7558. [Google Scholar] [CrossRef] [Green Version]
- Doney, S.; Balch, W.; Fabry, V.; Feely, R. Ocean Acidification: A Critical Emerging Problem for the Ocean Sciences. Oceanography 2009, 22, 16–25. [Google Scholar] [CrossRef] [Green Version]
- Orr, J.C.; Fabry, V.J.; Aumont, O.; Bopp, L.; Doney, S.; Feely, R.A.; Gnanadesikan, A.; Gruber, N.; Ishida, A.; Joos, F.; et al. Anthropogenic ocean acidification over the twenty-first century and its impact on calcifying organisms. Nat. Cell Biol. 2005, 437, 681–686. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Cai, W.J.; He, X.; Zhai, W.; Pan, D.; Dai, M.; Yu, P. A mechanistic semi-analytical method for remotely sensing sea surface pCO2 in river-dominated coastal oceans: A case study from the East China Sea. J. Geophys. Res. Ocean. 2015, 120, 2331–2349. [Google Scholar] [CrossRef]
- Chen, S.; Hu, C.; Barnes, B.B.; Wanninkhof, R.; Cai, W.-J.; Barbero, L.; Pierrot, D. A machine learning approach to estimate surface ocean pCO2 from satellite measurements. Remote. Sens. Environ. 2019, 228, 203–226. [Google Scholar] [CrossRef]
- Chen, S.; Hu, C.; Cai, W.-J.; Yang, B. Estimating surface pCO2 in the northern Gulf of Mexico: Which remote sensing model to use? Cont. Shelf Res. 2017, 151, 94–110. [Google Scholar] [CrossRef]
- Le, C.; Gao, Y.; Cai, W.-J.; Lehrter, J.C.; Bai, Y.; Jiang, Z.-P. Estimating summer sea surface pCO2 on a river-dominated continental shelf using a satellite-based semi-mechanistic model. Remote Sens. Environ. 2019, 225, 115–126. [Google Scholar] [CrossRef]
- Fennel, K.; Wilkin, J.; Previdi, M.; Najjar, R. Denitrification effects on air-sea CO2flux in the coastal ocean: Simulations for the northwest North Atlantic. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Ikawa, H.; Faloona, I.; Kochendorfer, K.T.; Paw, U.K.T.; Oechel, W.C. Air–sea exchange of CO2 at a Northern California coastal site along the California Current upwelling system. Biogeosciences 2013, 10, 4419–4432. [Google Scholar] [CrossRef]
- Xue, L.; Cai, W.-J.; Hu, X.; Sabine, C.; Jones, S.; Sutton, A.; Jiang, L.-Q.; Reimer, J.J. Sea surface carbon dioxide at the Georgia time series site (2006–2007): Air–sea flux and controlling processes. Prog. Oceanogr. 2016, 140, 14–26. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Hu, C.; Byrne, R.H.; Robbins, L.L.; Yang, B. Remote estimation of surface pCO2 on the West Florida Shelf. Cont. Shelf Res. 2016, 128, 10–25. [Google Scholar] [CrossRef] [Green Version]
- Lohrenz, S.; Cai, W.-J.; Chakraborty, S.; Huang, W.-J.; Guo, X.; He, R.; Xue, Z.; Fennel, K.; Howden, S.; Tian, H. Satellite estimation of coastal pCO2 and air-sea flux of carbon dioxide in the northern Gulf of Mexico. Remote Sens. Environ. 2018, 207, 71–83. [Google Scholar] [CrossRef]
- Marrec, P.; Cariou, T.; Macé, E.; Morin, P.; Salt, L.A.; Vernet, M.; Taylor, B.; Paxman, K.; Bozec, Y. Dynamics of air–sea CO2 fluxes in the northwestern European shelf based on voluntary observing ship and satellite observations. Biogeosciences 2015, 12, 5371–5391. [Google Scholar] [CrossRef] [Green Version]
- Moussa, H.; Benallal, M.A.; Goyet, C.; Lefevre, N. Satellite-derived CO2 fugacity in surface seawater of the tropical Atlantic Ocean using a feedforward neural network. Int. J. Remote Sens. 2016, 37, 580–598. [Google Scholar] [CrossRef]
- Fay, A.R.; McKinley, G.A. Correlations of surface ocean pCO2 to satellite chlorophyll on monthly to interannual timescales. Glob. Biogeochem. Cycles 2017, 31, 436–455. [Google Scholar] [CrossRef]
- Zhu, Y.; Shang, S.; Zhai, W.-D.; Dai, M. Satellite-derived surface water pCO2 and air–sea CO2 fluxes in the northern South China Sea in summer. Prog. Nat. Sci. 2009, 19, 775–779. [Google Scholar] [CrossRef]
- Lee, K.; Tong, L.T.; Millero, F.J.; Sabine, C.L.; Dickson, A.G.; Goyet, C.; Park, G.H.; Wanninkhof, R.; Feely, R.A.; Key, R.M. Global relationships of total alkalinity with salinity and temperature in surface waters of the world’s oceans. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Byrne, R.H.; Wanninkhof, R. Subannual variability of total alkalinity distributions in the northeastern Gulf of Mexico. J. Geophys. Res. Ocean. 2015, 120, 3805–3816. [Google Scholar] [CrossRef] [Green Version]
- Pierrot, D.; Wallace, D.; Lewis, E. MS Excel Program Developed for CO2 System Calculations; Carbon Dioxide Information Analysis Center: Oak Ridge, TN, USA, 2006. [Google Scholar]
- Bates, N.R.; Takahashi, T.; Chipman, D.W.; Knap, A.H. Variability of pCO2 on diel to seasonal timescales in the Sargasso Sea near Bermuda. J. Geophys. Res. Ocean. 1998, 103, 15567–15585. [Google Scholar] [CrossRef]
- Turk, D.; Book, J.; McGillis, W. pCO2 and CO2 exchange during high bora winds in the Northern Adriatic. J. Mar. Syst. 2013, 117–118, 65–71. [Google Scholar] [CrossRef]
- Bates, N.R.; Merlivat, L. The influence of short-term wind variability on air-sea CO2 exchange. Geophys. Res. Lett. 2001, 28, 3281–3284. [Google Scholar] [CrossRef]
- Sarma, V.V.S.S.; Saino, T.; Sasaoka, K.; Nojiri, Y.; Ono, T.; Ishii, M.; Inoue, H.Y.; Matsumoto, K. Basin-scale pCO2 distribution using satellite sea surface temperature, Chla, and climatological salinity in the North Pacific in spring and summer. Glob. Biogeochem. Cycles 2006, 20. [Google Scholar] [CrossRef]
- Stephens, M.P.; Olson, D.B.; Samuels, G.; Fine, R.A.; Takahashi, T. Sea-air flux of CO2 in the North Pacific using shipboard and satellite data. J. Geophys. Res. Space Phys. 1995, 100, 13571–13583. [Google Scholar] [CrossRef]
- Jamet, C.; Moulin, C.; Lefevre, N. Estimation of the oceanic pCO2 in the North Atlantic from VOS lines in-situ measurements: Parameters needed to generate seasonally mean maps. Ann. Geophys. 2007, 25, 2247–2257. [Google Scholar] [CrossRef] [Green Version]
- Olsen, A.; Triñanes, J.A.; Wanninkhof, R. Sea–air flux of CO2 in the Caribbean Sea estimated using in situ and remote sensing data. Remote. Sens. Environ. 2004, 89, 309–325. [Google Scholar] [CrossRef]
- Ono, T.; Saino, T.; Kurita, N.; Sasaki, K. Basin-scale extrapolation of shipboard pCO2 data using satellite SST and Chla. Int. J. Remote Sens. 2004, 25, 3803–3815. [Google Scholar] [CrossRef]
- Rangama, Y.; Boutin, J.; Etcheto, J.; Merlivat, L.; Takahashi, T.; Delille, B.; Frankignoulle, M.; Bakker, D. Variability of the net air–sea CO2 flux inferred from shipboard and satellite measurements in the Southern Ocean south of Tasmania and New Zealand. J. Geophys. Res. Space Phys. 2005, 110, 110. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Xu, S.; Gao, Z.; Chen, H.; Zhang, Y.; Zhan, J.; Wei, L. Estimation of monthly air-sea CO2 flux in the southern Atlantic and Indian Ocean using in-situ and remotely sensed data. Remote Sens. Environ. 2011, 115, 1935–1941. [Google Scholar] [CrossRef]
- Sarma, V. Monthly variability in surface pCO2 and net air-sea CO2 flux in the Arabian Sea. J. Geophys. Res. Ocean. 2003, 108. [Google Scholar] [CrossRef]
- Mémery, L.; Lévy, M.; Vérant, S.; Merlivat, L. The relevant time scales in estimating the air–sea CO2 exchange in a mid-latitude region. Deep. Sea Res. Part I Top. Stud. Oceanogr. 2002, 49, 2067–2092. [Google Scholar] [CrossRef]
- Friedrich, T.; Oschlies, A. Neural network-based estimates of North Atlantic surface pCO2 from satellite data: A methodological study. J. Geophys. Res. Space Phys. 2009, 114, 114. [Google Scholar] [CrossRef] [Green Version]
- Landschuetzer, P.; Gruber, N.; Bakker, D.C.E.; Schuster, J.; Zeng, J. A neural network-based estimate of the seasonal to inter-annual variability of the Atlantic Ocean carbon sink. Biogeosciences 2013, 10, 7793–7815. [Google Scholar] [CrossRef] [Green Version]
- Nakaoka, S.I.; Telszewski, M.; Nojiri, Y.; Yasunaka, S.; Miyazaki, C.; Mukai, H.; Usui, N. Estimating temporal and spatial variation of ocean surface pCO2 in the North Pacific using a self-organizing map neural network technique. Biogeosciences 2013, 10, 6093–6106. [Google Scholar] [CrossRef] [Green Version]
- Telszewski, M.; Chazottes, A.; Schuster, U.; Watson, A.J.; Moulin, C.; Bakker, D.C.E.; González-Dávila, M.; Johannessen, T.; Körtzinger, A.; Lüger, H.; et al. Estimating the monthly pCO2 distribution in the North Atlantic using a self-organizing neural network. Biogeosciences 2009, 6, 1405–1421. [Google Scholar] [CrossRef] [Green Version]
- Lohrenz, S.E.; Cai, W.J. Satellite ocean color assessment of air-sea fluxes of CO2 in a river-dominated coastal margin. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Hales, B.; Strutton, P.; Saraceno, M.; Letelier, R.; Takahashi, T.; Feely, R.; Sabine, C.; Chavez, F. Satellite-based prediction of pCO2 in coastal waters of the eastern North Pacific. Prog. Oceanogr. 2012, 103, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adva. Neural Inf. Process. Syst. 2018, 6637–6647. [Google Scholar]
- Huang, G.; Wu, L.; Ma, X.; Zhang, W.; Fan, J.; Yu, X.; Zeng, W.; Zhou, H. Evaluation of CatBoost method for prediction of reference evapotranspiration in humid regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Z.; Zheng, J. CatBoost: A new approach for estimating daily reference crop evapotranspiration in arid and semi-arid regions of Northern China. J. Hydrol. 2020, 588, 125087. [Google Scholar] [CrossRef]
- Li, S.; Song, K.; Wang, S.; Liu, G.; Wen, Z.; Shang, Y.; Lyu, L.; Chen, F.; Xu, S.; Tao, H.; et al. Quantification of chlorophyll-a in typical lakes across China using Sentinel-2 MSI imagery with machine learning algorithm. Sci. Total Environ. 2021, 778, 146271. [Google Scholar] [CrossRef]
- Marshall, J.; Kushnir, Y.; Battisti, D.; Chang, P.; Czaja, A.; Dickson, R.R.; Hurrell, J.W.; McCartney, M.; Saravanan, R.; Visbeck, M. North Atlantic climate variability: Phenomena, impacts and mechanisms. Int. J. Clim. 2001, 21, 1863–1898. [Google Scholar] [CrossRef]
- Petit, J.R.; Jouzel, J.; Raynaud, D.; Barkov, N.I.; Barnola, J.-M.; Basile-Doelsch, I.; Bender, M.L.; Chappellaz, J.; Davis, M.L.; Delaygue, G.; et al. Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature 1999, 399, 429–436. [Google Scholar] [CrossRef] [Green Version]
- Bates, N.R. Interannual variability of the oceanic CO2 sink in the subtropical gyre of the North Atlantic Ocean over the last 2 decades. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef]
- Olsen, A.; Bellerby, R.G.; Johannessen, T.; Omar, A.M.; Skjelvan, I. Interannual variability in the wintertime air–sea flux of carbon dioxide in the northern North Atlantic, 1981–2001. Deep Sea Res. Part I Oceanogr. Res. Pap. 2003, 50, 1323–1338. [Google Scholar] [CrossRef] [Green Version]
- Lüger, H.; Wanninkhof, R.; Wallace, D.W.R.; Körtzinger, A. CO2 fluxes in the subtropical and subarctic North Atlantic based on measurements from a volunteer observing ship. J. Geophys. Res. Space Phys. 2006, 111, 1116. [Google Scholar] [CrossRef] [Green Version]
- Corbière, A.; Metzl, N.; Reverdin, G.; Brunet, C.; Takahashi, T. Interannual and decadal variability of the oceanic carbon sink in the North Atlantic subpolar gyre. Tellus Ser. B Chem. Phys. Meteorol. 2007, 59, 168–178. [Google Scholar] [CrossRef]
- Canadell, J.G.; Le Quéré, C.; Raupach, M.R.; Field, C.B.; Buitenhuis, E.; Ciais, P.; Conway, T.J.; Gillett, N.P.; Houghton, R.A.; Marland, G. Contributions to accelerating atmospheric CO2 growth from economic activity, carbon intensity, and efficiency of natural sinks. Proc. Natl. Acad. Sci. USA 2007, 104, 18866–18870. [Google Scholar] [CrossRef] [Green Version]
- Jo, Y.H.; Dai, M.; Zhai, W.; Yan, X.H.; Shang, S. On the variations of sea surface pCO2 in the northern South China Sea: A remote sensing based neural network approach. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; Volume 103. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H. Xgboost: Extreme gradient boosting. R Package Version 2015, 1, 1–4. [Google Scholar]
- Barnes, B.B.; Hu, C. Cross-Sensor Continuity of Satellite-Derived Water Clarity in the Gulf of Mexico: Insights Into Temporal Aliasing and Implications for Long-Term Water Clarity Assessment. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1761–1772. [Google Scholar] [CrossRef]
- Hu, C.; Muller-Karger, F.; Murch, B.; Myhre, D.; Taylor, J.; Luerssen, R.; Moses, C.; Zhang, C.; Gramer, L.; Hendee, J. Building an Automated Integrated Observing System to Detect Sea Surface Temperature Anomaly Events in the Florida Keys. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2071–2084. [Google Scholar] [CrossRef]
- Bailey, S.W.; Werdell, P.J. A multi-sensor approach for the on-orbit validation of ocean color satellite data products. Remote Sens. Environ. 2006, 102, 12–23. [Google Scholar] [CrossRef]
- Gregg, W.W.; Casey, N.W. Global and regional evaluation of the SeaWiFS chlorophyll data set. Remote Sens. Environ. 2004, 93, 463–479. [Google Scholar] [CrossRef]
- Melin, F.; Zibordi, G.; Berthon, J.F. Assessment of satellite ocean color products at a coastal site. Remote Sens. Environ. 2007, 110, 192–215. [Google Scholar] [CrossRef]
- Zhao, J.; Barnes, B.; Melo, N.; English, D.; Lapointe, B.; Muller-Karger, F.; Schaeffer, B.; Hu, C. Assessment of satellite-derived diffuse attenuation coefficients and euphotic depths in south Florida coastal waters. Remote Sens. Environ. 2013, 131, 38–50. [Google Scholar] [CrossRef]
- Lüger, H.; Wallace, D.W.; Körtzinger, A.; Nojiri, Y. The pCO2 variability in the midlatitude North Atlantic Ocean during a full annual cycle. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef] [Green Version]



| Products | Time Scale | Resources | Date |
|---|---|---|---|
| Chla | 8 days | NASA Modis/Aqua Level-3 data | January 2003–December 2020 |
| SST | 8 days | NASA Modis/Aqua Level-3 data | January 2003–December 2020 |
| Adg | 8 days | NASA Modis/Aqua Level-3 data | January 2003–December 2020 |
| Kd | 8 days | NASA Modis/Aqua Level-3 data | January 2003–December 2020 |
| MLD | 8 days | HYCOM model | January 2003–December 2020 |
| Algorithm | R2 | ||
|---|---|---|---|
| Linear Regression | 28.35 | 0.31 | 21.95 |
| k-Nearest Neighbor | 15.46 | 0.80 | 10.07 |
| Neural Network | 19.28 | 0.68 | 13.73 |
| Regression Tree | 13.07 | 0.86 | 6.03 |
| Support Vector Machine (Gaussian kernel function) | 18.35 | 0.71 | 12.28 |
| Support Vector Machine (Linear kernel function) | 29.10 | 0.31 | 21.45 |
| Random Forest | 9.75 | 0.92 | 5.57 |
| Bagging Regression | 9.69 | 0.92 | 5.59 |
| Adaboost | 19.44 | 0.68 | 14.91 |
| Gradient Boosting Regression Tree | 16.87 | 0.76 | 12.22 |
| XGBoost | 9.75 | 0.92 | 6.16 |
| Catboost | 8.25 | 0.94 | 4.92 |
| CRUISE ID | R2 | ||
|---|---|---|---|
| BMBE20100302 | 0.91 | 5.01 | 3.11 |
| BMBE20100326 | 0.89 | 7.03 | 3.25 |
| BMBE20101014 | 0.84 | 4.96 | 2.93 |
| BMBE20101202 | 0.96 | 4.42 | 2.88 |
| BMBE20110726 | 0.94 | 5.63 | 3.60 |
| BMBE20110809 | 0.91 | 5.72 | 3.27 |
| BMBE20110927 | 0.94 | 5.25 | 3.47 |
| BMBE20111119 | 0.80 | 3.51 | 2.39 |
| BMBE20120418 | 0.54 | 16.46 | 8.83 |
| BMBE20120703 | 0.78 | 5.00 | 3.22 |
| BMBE20120913 | 0.88 | 4.35 | 2.96 |
| BMBE20121220 | 0.91 | 3.69 | 2.32 |
| BMBE20130207 | 0.91 | 5.57 | 3.55 |
| BMBE20130220 | 0.90 | 4.18 | 2.70 |
| BMBE20130329 | 0.83 | 5.78 | 3.84 |
| BMBE20130515 | 0.74 | 4.46 | 3.01 |
| BMBE20130528 | 0.85 | 5.33 | 3.27 |
| BMBE20130702 | 0.89 | 10.81 | 4.02 |
| BMBE20130716 | 0.97 | 5.50 | 3.57 |
| BMBE20130903 | 0.87 | 4.62 | 3.14 |
| Cases | R2 | |
|---|---|---|
| +20% in Kd | 5.32 | 0.97 |
| −20% in Kd | 5.62 | 0.97 |
| +20% in Chla | 5.38 | 0.97 |
| −20% in Chla | 4.45 | 0.98 |
| +20% in Adg | 4.86 | 0.98 |
| −20% in Adg | 4.74 | 0.98 |
| +20% in SST | 7.88 | 0.94 |
| −20% in SST | 7.33 | 0.95 |
| +20% in MLD | 8.66 | 0.93 |
| −20% in MLD | 8.67 | 0.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; He, J.; Chen, Y.; Zhao, B. Space-Time Sea Surface pCO2 Estimation in the North Atlantic Based on CatBoost. Remote Sens. 2021, 13, 2805. https://doi.org/10.3390/rs13142805
Sun H, He J, Chen Y, Zhao B. Space-Time Sea Surface pCO2 Estimation in the North Atlantic Based on CatBoost. Remote Sensing. 2021; 13(14):2805. https://doi.org/10.3390/rs13142805
Chicago/Turabian StyleSun, Hongwei, Junyu He, Yihui Chen, and Boyu Zhao. 2021. "Space-Time Sea Surface pCO2 Estimation in the North Atlantic Based on CatBoost" Remote Sensing 13, no. 14: 2805. https://doi.org/10.3390/rs13142805
APA StyleSun, H., He, J., Chen, Y., & Zhao, B. (2021). Space-Time Sea Surface pCO2 Estimation in the North Atlantic Based on CatBoost. Remote Sensing, 13(14), 2805. https://doi.org/10.3390/rs13142805







