8-Day and Daily Maximum and Minimum Air Temperature Estimation via Machine Learning Method on a Climate Zone to Global Scale
Abstract
1. Introduction
- The first type is the index-base method such as Temperature-Vegetation Index (TVX) first proposed by Nemani and running [14], which assumes that dense vegetation canopy temperature approximates Ta [15,16]. This method is easily applied with no auxiliary data. It is widely used in the estimation of regional near-surface Ta [5,16,17]. However, the TVX method is based on dense vegetation canopy temperature and the negative relationship between the Normalized Difference Vegetation Index (NDVI) and LST. Accordingly, its application is limited and conditional. For example, Vancutsem et al. [17] showed that the TVX method did not adapt to different ecosystems over Africa due to the non-significant relationship between Ts and NDVI in their study.
- The second category is the physically-based method based on surface energy balance. For example, Sun et al. [18] and Zhu et al. [19] proposed surface energy balance theory-based methodologies to build a quantitative relationship between LST and Ta. However physically-based models are complex and these methods require large amounts of information that are usually unavailable from remote sensing observations (e.g., wind speed) [12,20]. The complexity and difficulty for application limited its extensive applications in previous studies.
- The final class of methods estimates Ta from the local statistical relationship between Ta and other variables, e.g., LST, NDVI, retrieved by remote sensing. Statistical methods are the most commonly used methods [21,22,23], including regression method [21], hierarchical Bayesian model [24], and machine learning (ML) methods, such as random forest (RF) method, support vector machine (SVM) method, deep belief network (DBN) method, and neural networks (NN) method [10,25,26,27,28,29]. In general, these statistical methods perform well within the spatial and time frame in which they were developed, but the accuracy might decrease when extended in time and space [16].
2. Materials and Method
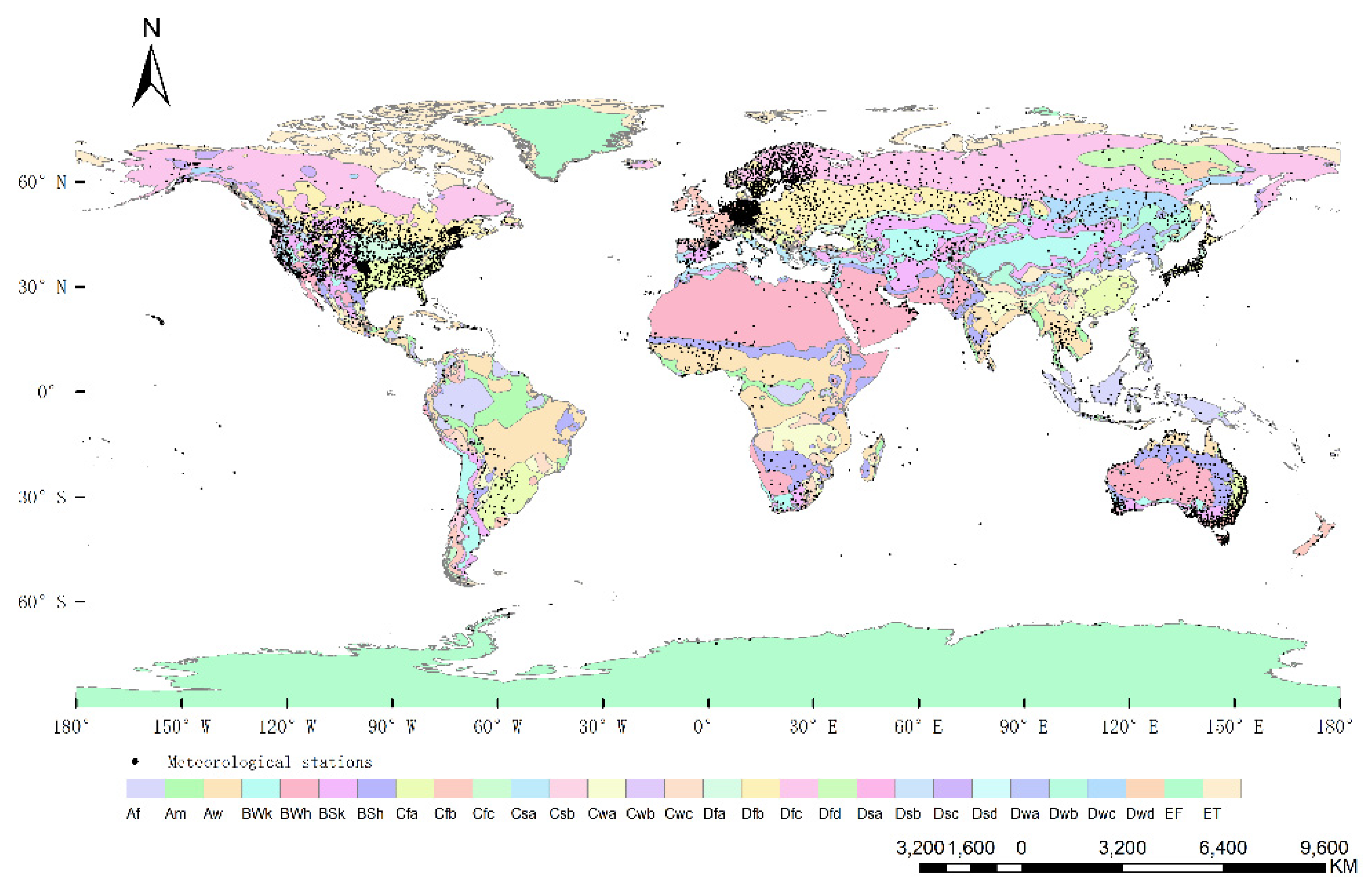
2.1. Study Area
2.2. Data Collection and Processing
2.2.1. Meteorological Observation Data
2.2.2. Satellite-Derived Observation Data
2.2.3. Auxiliary Data
2.2.4. Data Processing
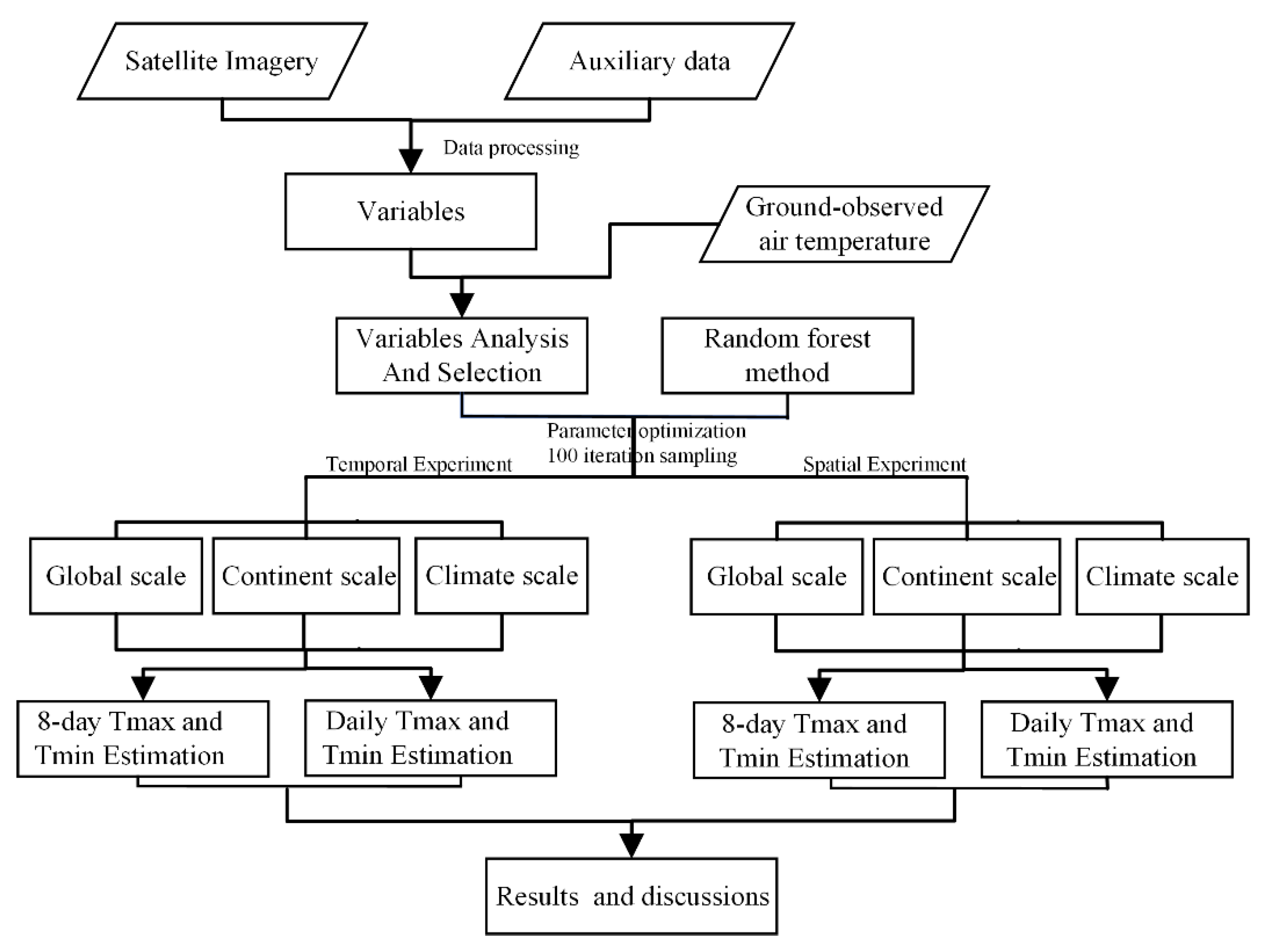
2.3. Method
2.3.1. Variable Selection Based on Physical Relationship between Ta and LST
2.3.2. Ta Estimation Based on the RF Method
2.3.3. Model Evaluation and Validation
3. Results and Discussion
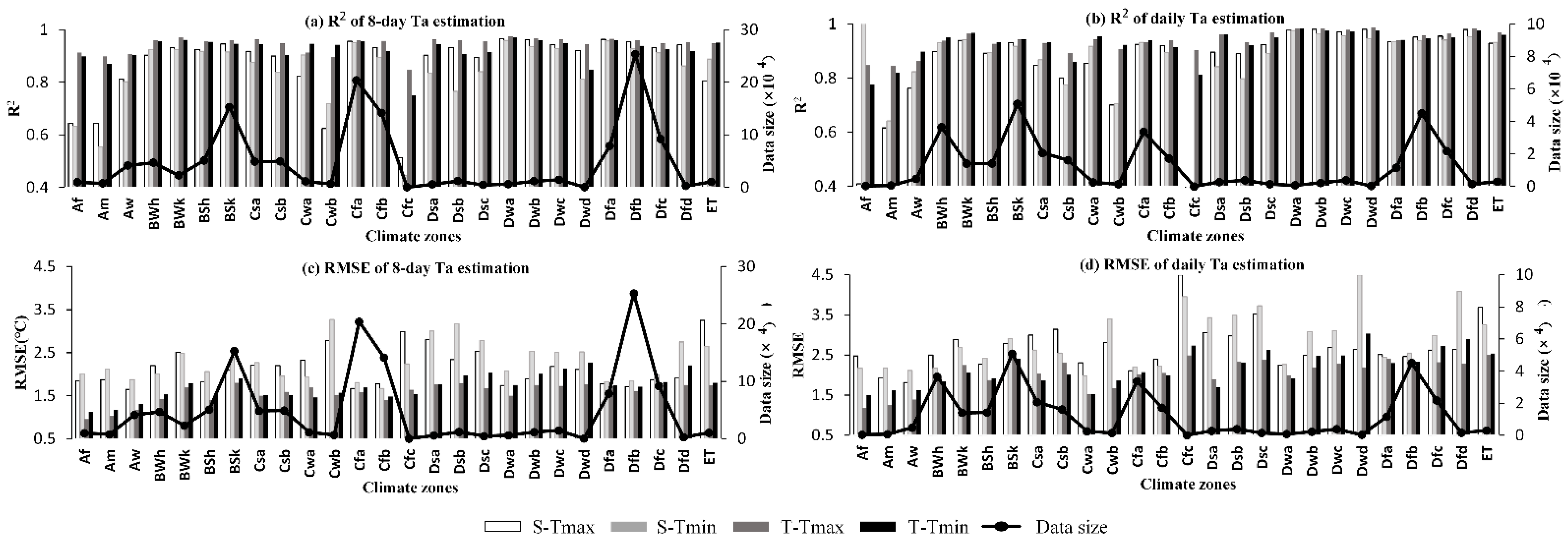
3.1. Model Performance When Trained and Validated on Global, Continental and Climate Zone Scales
3.2. Model Performance When Trained and Cross-Validated on Global, Continental and Climate Zone Scales
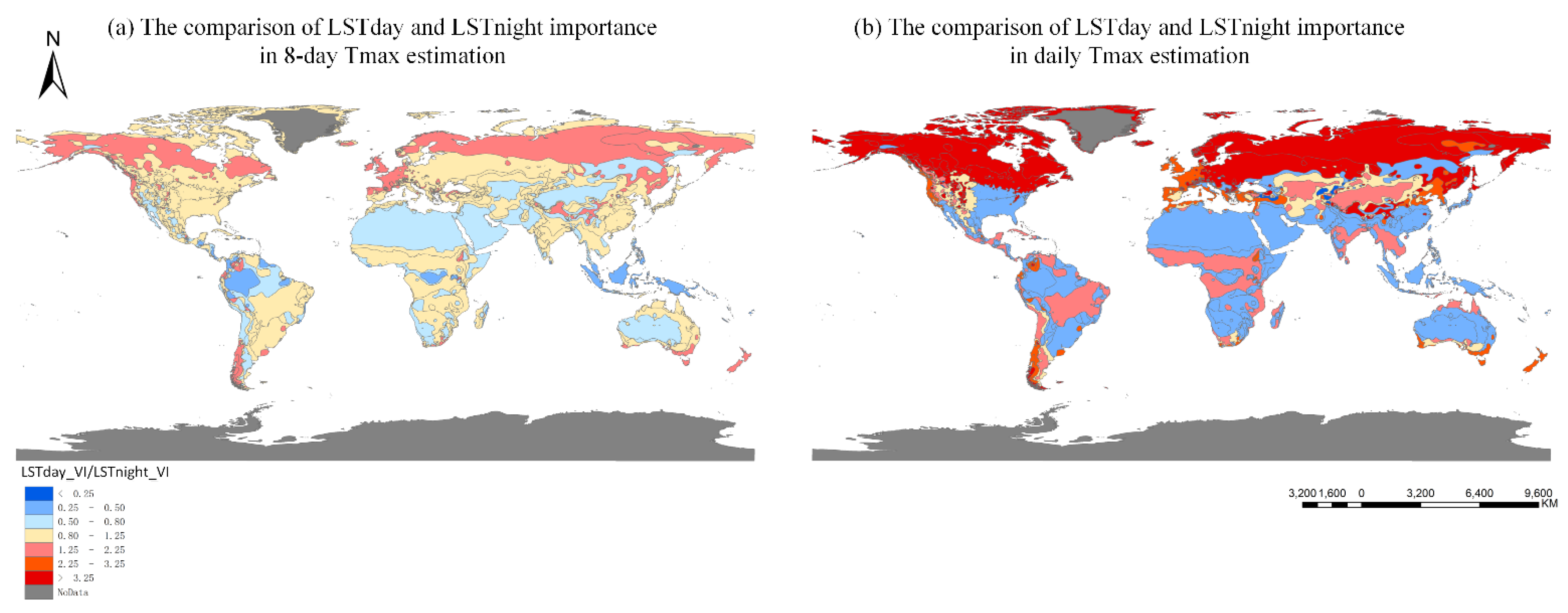
3.3. Spatial Patterns of Model Performance
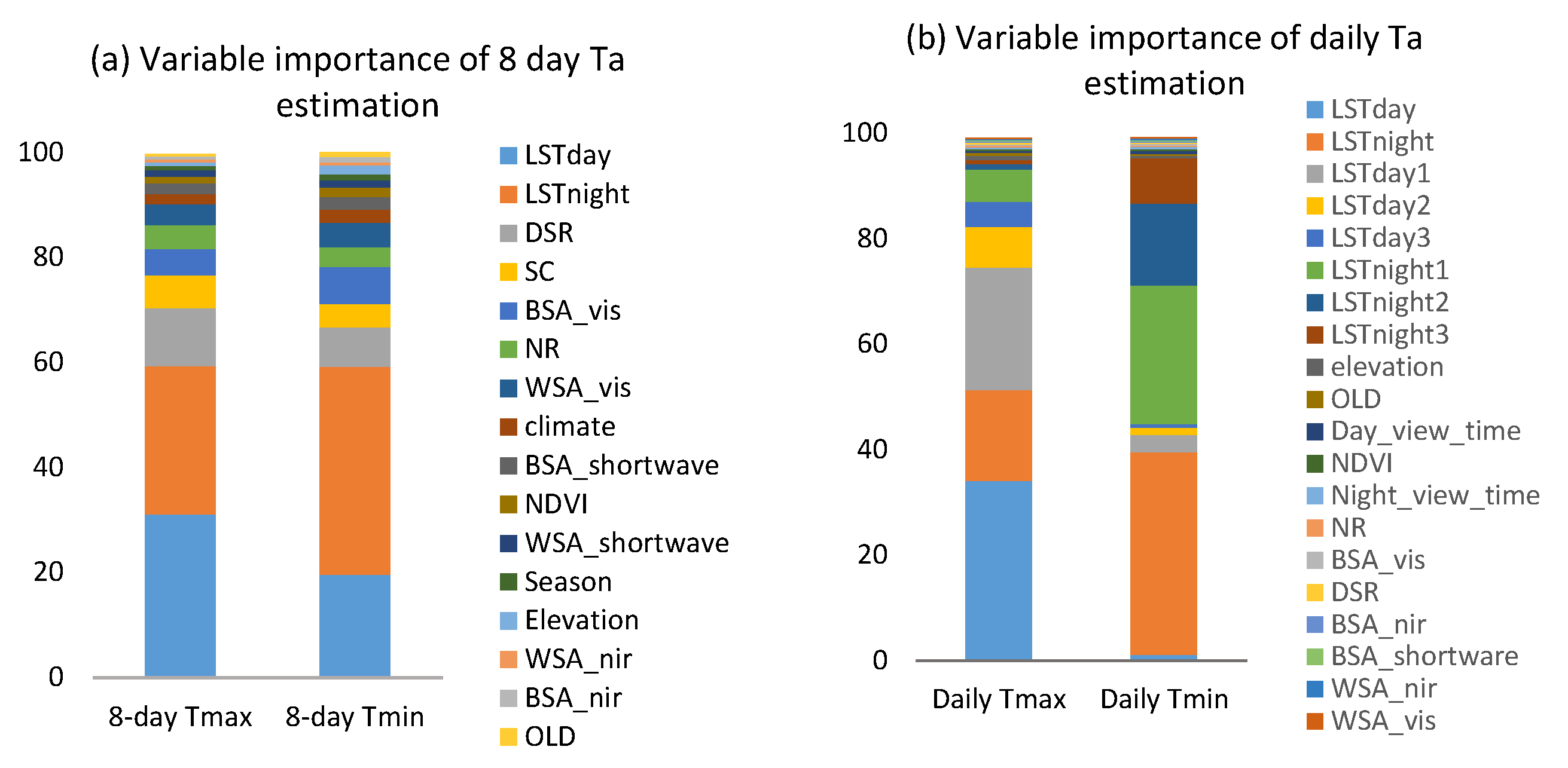
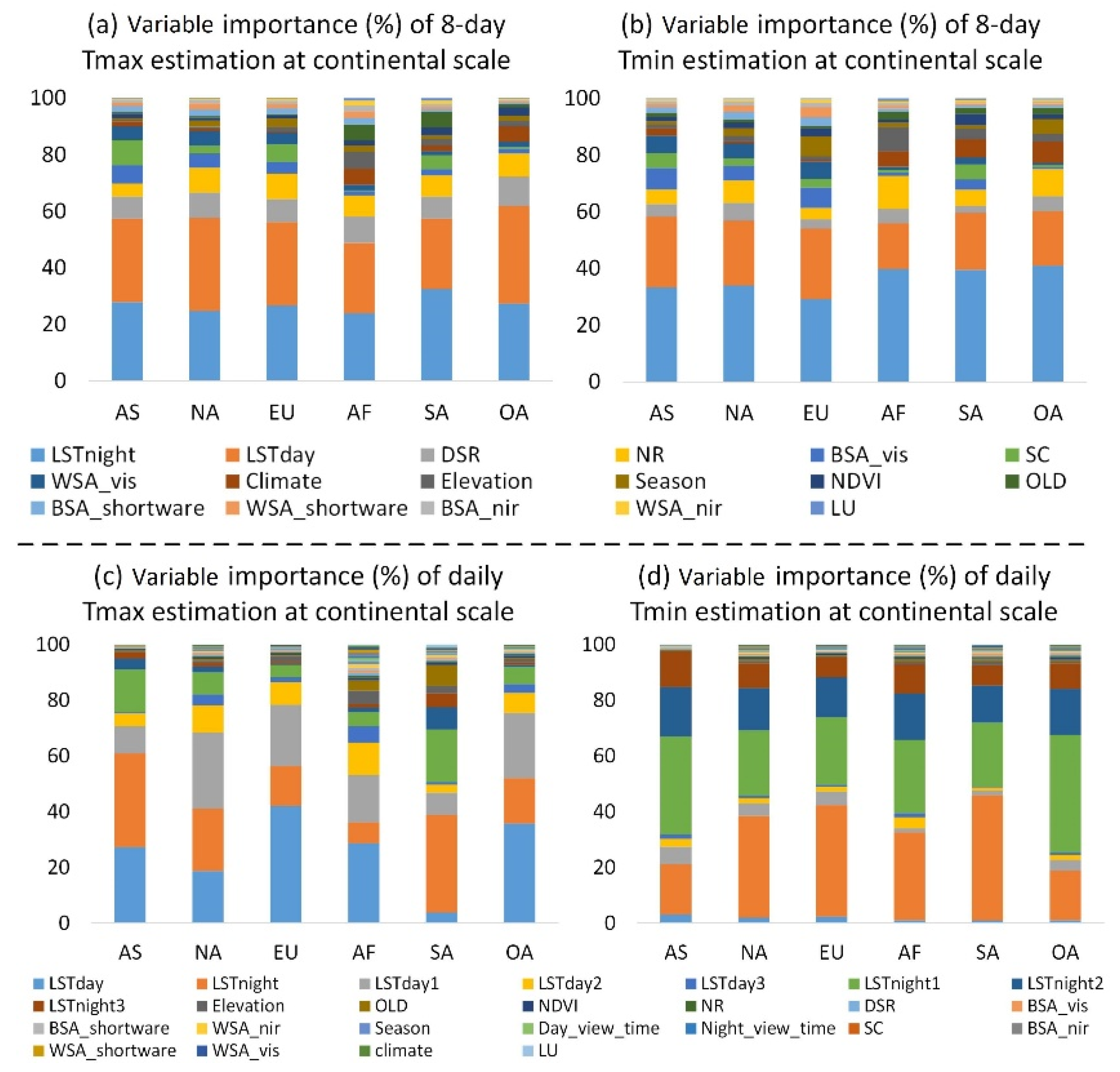
3.4. Variable Importance Analysis
3.5. Limitations and Future Studies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Montgomery, R.A.; Rice, K.E.; Stefanski, A.; Rich, R.L.; Reich, P.B. Phenological responses of temperate and boreal trees to warming depend on ambient spring temperatures, leaf habit, and geographic range. Proc. Natl. Acad. Sci. USA 2020, 117, 10397–10405. [Google Scholar] [CrossRef]
- Allen, R. Penman–Monteith equation. In Encyclopedia of Soils in the Environment; Hillel, D., Ed.; Elsevier: Oxford, UK, 2005; pp. 180–188. [Google Scholar]
- Zeng, L.; Wardlow, B.D.; Wang, R.; Shan, J.; Tadesse, T.; Hayes, M.J.; Li, D. A hybrid approach for detecting corn and soybean phenology with time-series MODIS data. Remote Sens. Environ. 2016, 181, 237–250. [Google Scholar] [CrossRef]
- Zeng, L.; Brian, W.; Tsegaye, T.; Shan, J.; Michael, H.; Li, D.; Xiang, D. Estimation of daily air temperature based on modis land surface temperature products over the corn belt in the US. Remote Sens. 2015, 7, 951–970. [Google Scholar] [CrossRef]
- Zhu, W.; Lű, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface tempera-ture products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Meyer, H.; Schmidt, J.; Detsch, F.; Nauss, T. Hourly gridded air temperatures of South Africa derived from MSG SEVIRI. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 261–267. [Google Scholar] [CrossRef]
- Rao, Y.; Liang, S.; Wang, D.; Yu, Y.; Song, Z.; Zhou, Y.; Shen, M.; Xu, B. Estimating daily average surface air temperature using satellite land surface temperature and top-of-atmosphere radiation products over the Tibetan Plateau. Remote Sens. Environ. 2019, 234, 111462. [Google Scholar] [CrossRef]
- Hooker, J.; Duveiller, G.; Cescatti, A. A global dataset of air temperature derived from satellite remote sensing and weather stations. Sci. Data 2018, 5, 180246. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Lű, A.; Jia, S.; Yan, J.; Mahmood, R. Retrievals of all-weather daytime air temperature from MODIS products. Remote Sens. Environ. 2017, 189, 152–163. [Google Scholar] [CrossRef]
- Shen, H.; Jiang, Y.; Li, T.; Cheng, Q.; Zeng, C.; Zhang, L. Deep learning-based air temperature mapping by fusing remote sensing, station, simulation and socioeconomic data. Remote Sens. Environ. 2020, 240, 111692. [Google Scholar] [CrossRef]
- Lin, S.; Moore, N.J.; Messina, J.P.; Devisser, M.H.; Wu, J. Evaluation of estimating daily maximum and minimum air tem-perature with MODIS data in east Africa. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 140. [Google Scholar] [CrossRef]
- Benali, A.; Carvalho, A.C.; Nunes, J.; Carvalhais, N.; Santos, A. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Chen, X.; Su, Z.; Ma, Y.; Middleton, E.M. Optimization of a remote sensing energy balance method over different canopy applied at global scale. Agric. For. Meteorol. 2019, 279, 107633. [Google Scholar] [CrossRef]
- Nemani, R.R.; Running, S.W. Estimation of Regional Surface Resistance to Evapotranspiration from NDVI and Thermal-IR AVHRR Data. J. Appl. Meteorol. 1989, 28, 276–284. [Google Scholar] [CrossRef]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Rgaard, A.N.; Fensholt, R.; Eklundh, L. Estimation of diurnal air temperature using MSG SEVIRI data in West Africa. Remote Sens. Environ. 2007, 110, 262–274. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, J.; Zhang, R.; Gillies, R.; Xue, Y.; Bo, Y. Air temperature retrieval from remote sensing data based on ther-modynamics. Theor. Appl. Climatol. 2005, 80, 37–48. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, C.; Zhang, G.; Zhang, H.; Hua, J. Preliminary verification of instantaneous air temperature estimation for clear sky conditions based on SEBAL. Theor. Appl. Clim. 2017, 129, 71–81. [Google Scholar] [CrossRef]
- Mostovoy, G.V.; King, R.L.; Reddy, K.R.; Kakani, V.G.; Filippova, M.G. Statistical Estimation of Daily Maximum and Minimum Air Temperatures from MODIS LST Data over the State of Mississippi. GIScience Remote Sens. 2006, 43, 78–110. [Google Scholar] [CrossRef]
- Phan, T.; Degener, J.; Kappas, M. Comparison of multiple linear regression, cubist regression, and random forest algo-rithms to estimate daily air surface temperature from dynamic combinations of MODIS LST Data. Remote Sens. 2017, 9, 398. [Google Scholar]
- Kloog, I.; Nordio, F.; Coull, B.A.; Schwartz, J. Predicting spatiotemporal mean air temperature using MODIS satellite sur-face temperature measurements across the Northeastern USA. Remote Sens. Environ. 2014, 150, 132–139. [Google Scholar] [CrossRef]
- Yang, Y.Z.; Cai, W.H.; Yang, J. Evaluation of MODIS land surface temperature data to estimate near-surface air temperature in Northeast China. Remote Sens. 2017, 9, 410. [Google Scholar] [CrossRef]
- Lu, N.; Liang, S.; Huang, G.; Qin, J.; Yao, L.; Wang, D.; Yang, K. Hierarchical Bayesian space-time estimation of monthly maximum and minimum surface air temperature. Remote Sens. Environ. 2018, 211, 48–58. [Google Scholar] [CrossRef]
- Meyer, H.; Katurji, M.; Appelhans, T.; Ller, M.U.; Nauss, T.; Roudier, P.; Zawar-Reza, P. Mapping daily air temperature for Antarctica based on MODIS LST. Remote Sens. 2016, 8, 732. [Google Scholar] [CrossRef]
- dos Santos, R.S. Estimating spatio-temporal air temperature in London (UK) using machine learning and earth observation satellite data. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102066. [Google Scholar] [CrossRef]
- Ho, H.C.; Knudby, A.; Sirovyak, P.; Xu, Y.; Hodul, M.; Henderson, S.B. Mapping maximum urban air temperature on hot summer days. Remote Sens. Environ. 2014, 154, 38–45. [Google Scholar] [CrossRef]
- Yoo, C.; Im, J.; Park, S.; Quackenbush, L.J. Estimation of daily maximum and minimum air temperatures in urban landscapes using MODIS time series satellite data. ISPRS J. Photogramm. 2018, 137, 149–162. [Google Scholar] [CrossRef]
- Jang, J.-D.; Viau, A.A.; Anctil, F. Neural network estimation of air temperatures from AVHRR data. Int. J. Remote Sens. 2004, 25, 4541–4554. [Google Scholar] [CrossRef]
- Oyler, J.W.; Ballantyne, A.; Jencso, K.; Sweet, M.; Running, S.W. Creating a topoclimatic daily air temperature dataset for the conterminous United States using homogenized station data and remotely sensed land skin temperature. Int. J. Clim. 2015, 35, 2258–2279. [Google Scholar] [CrossRef]
- Shen, S.; Leptoukh, G.G. Estimation of surface air temperature over central and eastern Eurasia from MODIS land surface temperature. Environ. Res. Lett. 2011, 6, 45206. [Google Scholar] [CrossRef]
- Janatian, N.; Sadeghi, M.; Sanaeinejad, S.H.; Bakhshian, E.; Farid, A.; Hasheminia, S.M.; Ghazanfari, S. A statistical framework for estimating air temperature using MODIS land surface temperature data. Int. J. Clim. 2017, 37, 1181–1194. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, G.; Wang, Y.; Li, Y. Impacts of Land Cover and Seasonal Variation on Maximum Air Temperature Estima-tion Using MODIS Imagery. Remote Sens. 2017, 9, 233. [Google Scholar] [CrossRef]
- Marzban, F.; Meteorologie, F.U.B.I.F.; Conrad, T.; Marzban, P.; Sodoudi, S. Estimation of the Near-Surface Air Temperature during the Day and Nighttime from MODIS in Berlin, Germany. Int. J. Adv. Remote Sens. GIS 2018, 7, 2478–2517. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, Y.; Yu, Y.; Sun, W. Empirical models for estimating daily maximum, minimum and mean air tempera-tures with MODIS land surface temperatures. Int. J. Remote Sens. 2011, 32, 9415–9440. [Google Scholar] [CrossRef]
- Didari, S.; Zand-Parsa, S. Enhancing estimation accuracy of daily maximum, minimum, and mean air temperature using spatio-temporal ground-based and remote-sensing data in southern Iran. Int. J. Remote Sens. 2018, 39, 6316–6339. [Google Scholar] [CrossRef]
- Mira, M.; Ninyerola, M.; Batalla, M.; Pesquer, L.; Pons, X. Improving mean minimum and maximum month-to-month air temperature surfaces using satellite-derived land surface temperature. Remote Sens. 2017, 9, 1313. [Google Scholar] [CrossRef]
- Lee, M.H.; Yu, J.H.; Yun, H.; Cheon, E. Development of daily maximum air temperature estimation algorithm for the Korean peninsula using modis data. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 2555–2558. [Google Scholar]
- Phan, T.; Kappas, M.; Degener, J. Estimating daily maximum and minimum land air surface temperature using modis land surface temperature data and ground truth data in Northern Vietnam. Remote Sens. 2016, 8, 1002. [Google Scholar]
- Phan, T.N.; Kappas, M.; Nguyen, K.T.; Tran, T.P.; Tran, Q.V.; Emam, A.R. Evaluation of MODIS land surface temperature products for daily air surface temperature estimation in northwest Vietnam. Int. J. Remote Sens. 2019, 40, 5544–5562. [Google Scholar] [CrossRef]
- Schwingshackl, C.; Hirschi, M.; Seneviratne, S.I. Quantifying spatiotemporal variations of soil moisture control on surface energy balance and near-surface air temperature. J. Clim. 2017, 30, 7105–7124. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- GHCN Dataset from NOAA. Available online: https://www.ncdc.noaa.gov/ (accessed on 15 May 2021).
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—a new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, J.; Hou, Y.; He, Y. Estimation of air temperature from MODIS data in east China. Int. J. Remote Sens. 2009, 30, 6261–6275. [Google Scholar] [CrossRef]
- Xu, Y.; Qin, Z.; Shen, Y. Study on the estimation of near-surface air temperature from MODIS data by statistical methods. Int. J. Remote Sens. 2012, 33, 7629–7643. [Google Scholar] [CrossRef]
- Sohrabinia, M.; Zawar-Reza, P.; Rack, W. Spatio-temporal analysis of the relationship between LST from MODIS and air temperature in New Zealand. Theor. Appl. Clim. 2015, 119, 567–583. [Google Scholar] [CrossRef]
- Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An intercomparison of the Surface Energy Balance Algorithm for Land (SEBAL) and the Two-Source Energy Balance (TSEB) modeling schemes. Remote Sens. Environ. 2007, 108, 369–384. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S. An intercomparison of regional latent heat flux estimation using remote sensing data. Int. J. Remote Sens. 2003, 24, 2221–2236. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, W.; Huang, Y.; Sun, W.; Han, P.; Yu, L.; Sun, F. Empirical estimation of near-surface air temperature in China from MODIS LST Data by considering physiographic features. Remote Sens. 2016, 8, 629. [Google Scholar] [CrossRef]
- Roerink, G.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth Part B Hydrol. Oceans Atmos. 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Malbéteau, Y.; Parkes, S.; Aragon, B.; Rosas, J.; McCabe, M.F. Capturing the diurnal cycle of land surface temperature using an unmanned aerial vehicle. Remote Sens. 2018, 10, 1407. [Google Scholar] [CrossRef]
- Kattel, D.B.; Yao, T.; Ullah, K.; Rana, A.S. Seasonal near-surface air temperature dependence on elevation and geographical coordinates for Pakistan. Theor. Appl. Climatol. 2019, 138, 1591–1613. [Google Scholar] [CrossRef]
- Wild, M.; Folini, D.; Hakuba, M.Z.; Schär, C.; Seneviratne, S.I.; Kato, S.; Rutan, D.; Ammann, C.; Wood, E.F.; König-Langlo, G. The energy balance over land and oceans: An assessment based on direct observations and CMIP5 climate models. Clim. Dyn. 2014, 44, 3393–3429. [Google Scholar] [CrossRef]
- Li, L.; Zha, Y. Mapping relative humidity, average and extreme temperature in hot summer over China. Sci. Total Environ. 2018, 615, 875–881. [Google Scholar] [CrossRef]
- Zeng, L.; Hu, S.; Xiang, D.; Zhang, X.; Li, D.; Li, L.; Zhang, T. Multilayer soil moisture mapping at a regional scale from multisource data via a machine learning method. Remote Sens. 2019, 11, 284. [Google Scholar] [CrossRef]
- Chen, F.; Liu, Y.; Liu, Q.; Qin, F. A statistical method based on remote sensing for the estimation of air temperature in China. Int. J. Clim. 2014, 35, 2131–2143. [Google Scholar] [CrossRef]
- Moser, G.; De Martino, M.; Serpico, S.B. Estimation of Air Surface Temperature from Remote Sensing Images and Pixelwise Modeling of the Estimation Uncertainty Through Support Vector Machines. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 332–349. [Google Scholar] [CrossRef]
- Khesali, E.; Mobasheri, M. A method in near-surface estimation of air temperature (NEAT) in times following the satellite passing time using MODIS images. Adv. Space Res. 2020, 65, 2339–2347. [Google Scholar] [CrossRef]
- Mutiibwa, D.; Strachan, S.; Albright, T. Land Surface Temperature and Surface Air Temperature in Complex Terrain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4762–4774. [Google Scholar] [CrossRef]
- Emamifar, S.; Rahimikhoob, A.; Noroozi, A.A. Daily mean air temperature estimation from MODIS land surface temper-ature products based on M5 model tree. Int. J. Climatol. 2013, 33, 3174–3181. [Google Scholar] [CrossRef]
- Pleim, J.E. A simple, efficient solution of flux–Profile relationships in the atmospheric surface layer. J. Appl. Meteorol. Clim. 2006, 45, 341–347. [Google Scholar] [CrossRef]
- Hughes, M.; Hall, A.; Fovell, R.G. Dynamical controls on the diurnal cycle of temperature in complex topography. Clim. Dyn. 2007, 29, 277–292. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Q.; Batkhishig, O.; Ouyang, Z. Relationship between evapotranspiration and land surface temperature under energy- and water-limited conditions in dry and cold climates. Adv. Meteorol. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Peón, J.; Recondo, C.; Calleja, J.F. Improvements in the estimation of daily minimum air temperature in peninsular Spain using MODIS land surface temperature. Int. J. Remote Sens. 2014, 35, 5148–5166. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F.; Zhang, G.; Ma, Y.; Yang, K.; Ye, M. Daily air temperature estimation on glacier surfaces in the Tibetan Plateau using MODIS LST data. J. Glaciol. 2018, 64, 132–147. [Google Scholar] [CrossRef]
- Ackerman, S.; Strabala, K.I.; Menzel, W.P.; Frey, R.A.; Moeller, C.C.; Gumley, L.E. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. Space Phys. 1998, 103, 32141–32157. [Google Scholar] [CrossRef]
- Jin, M.S.; Dickinson, R.E. Land surface skin temperature climatology: Benefitting from the strengths of satellite observations. Environ. Res. Lett. 2010, 5, 44004. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z. Radiance-based validation of the V5 MODIS land-surface temperature product. Int. J. Remote Sens. 2008, 29, 5373–5395. [Google Scholar] [CrossRef]




| Abbreviation | Data Description | Data Source | Estimation |
|---|---|---|---|
| LSTday | Daytime LST | MODIS LST products | 8-day and daily Tmax and Tmin |
| LSTnight | Nighttime LST | MODIS LST products | 8-day and daily Tmax and Tmin |
| LSTday1 | Daytime LST observed on 1 day before estimation | MODIS LST products | daily Tmax and Tmin |
| LSTday2 | Daytime LST observed on 2 days before estimation | MODIS LST products | daily Tmax and Tmin |
| LSTday3 | Daytime LST observed on 3 days before estimation | MODIS LST products | daily Tmax and Tmin |
| LSTnight1 | Nighttime LST observed on 1 day before estimation | MODIS LST products | daily Tmax and Tmin |
| LSTnight2 | Nighttime LST observed on 2 days before estimation | MODIS LST products | daily Tmax and Tmin |
| LSTnight3 | Nighttime LST observed on 3 days before estimation | MODIS LST products | daily Tmax and Tmin |
| Elevation | Elevation | SRTM global elevation data | 8-day and daily Tmax and Tmin |
| NR | Net radiation | NASA Langley Research Center | 8-day and daily Tmax and Tmin |
| DSR | Downward Shortwave Radiation | GLASS Downward Shortwave Radiation product | 8-day and daily Tmax and Tmin |
| SC | Snow cover | MODIS snow cover product | 8-day and daily Tmax and Tmin |
| OLD | Distance from the ocean | Calculated from Haversine formulation | 8-day and daily Tmax and Tmin |
| LU | Land-use type | MODIS Land cover product | 8-day and daily Tmax and Tmin |
| Season | Day of year for daily estimation; Sequence number of 8-day within the year (1–46) | 8-day and daily Tmax and Tmin | |
| NDVI | Normalized difference vegetation index | MODIS surface reflectance product for daily estimation and vegetation indices products for 8-day estimation | 8-day and daily Tmax and Tmin |
| Climate | Climate zone | Köppen-Geiger climate classification | 8-day and daily Tmax and Tmin |
| WSA_vis | White-sky Albedo in Visible albedo | GLASS Albedo Product | 8-day and daily Tmax and Tmin |
| BSA_vis | Black-sky albedo in Near-Infrared band | GLASS Albedo Product | 8-day and daily Tmax and Tmin |
| WSA_shortwave | White-sky albedo in shortwave band | GLASS Albedo Product | 8-day and daily Tmax and Tmin |
| BSA_shortwave | Black-sky albedo in shortwave band | GLASS Albedo Product | 8-day and daily Tmax and Tmin |
| WSA_nir | White-sky albedo in Near-Infrared band | GLASS Albedo Product | 8-day and daily Tmax and Tmin |
| BSA_nir | Black-sky albedo in Visible band | GLASS Albedo Product | 8-day and daily Tmax and Tmin |
| Day_view_ time | Local solar time of daytime LST observation | MODIS LST products | 8-day and daily Tmax and Tmin |
| Night_view_ time | Local solar time of nighttime LST observation | MODIS LST products | 8-day and daily Tmax and Tmin |
| 8-Day Tmax | 8-Day Tmin | Daily Tmax | Daily Tmin | |||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| S | 0.96 | 1.84 | 0.94 | 1.96 | 0.95 | 2.55 | 0.95 | 2.55 |
| T | 0.97 | 1.65 | 0.96 | 1.75 | 0.96 | 2.31 | 0.96 | 2.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, L.; Hu, Y.; Wang, R.; Zhang, X.; Peng, G.; Huang, Z.; Zhou, G.; Xiang, D.; Meng, R.; Wu, W.; et al. 8-Day and Daily Maximum and Minimum Air Temperature Estimation via Machine Learning Method on a Climate Zone to Global Scale. Remote Sens. 2021, 13, 2355. https://doi.org/10.3390/rs13122355
Zeng L, Hu Y, Wang R, Zhang X, Peng G, Huang Z, Zhou G, Xiang D, Meng R, Wu W, et al. 8-Day and Daily Maximum and Minimum Air Temperature Estimation via Machine Learning Method on a Climate Zone to Global Scale. Remote Sensing. 2021; 13(12):2355. https://doi.org/10.3390/rs13122355
Chicago/Turabian StyleZeng, Linglin, Yuchao Hu, Rui Wang, Xiang Zhang, Guozhang Peng, Zhenyu Huang, Guoqing Zhou, Daxiang Xiang, Ran Meng, Weixiong Wu, and et al. 2021. "8-Day and Daily Maximum and Minimum Air Temperature Estimation via Machine Learning Method on a Climate Zone to Global Scale" Remote Sensing 13, no. 12: 2355. https://doi.org/10.3390/rs13122355
APA StyleZeng, L., Hu, Y., Wang, R., Zhang, X., Peng, G., Huang, Z., Zhou, G., Xiang, D., Meng, R., Wu, W., & Hu, S. (2021). 8-Day and Daily Maximum and Minimum Air Temperature Estimation via Machine Learning Method on a Climate Zone to Global Scale. Remote Sensing, 13(12), 2355. https://doi.org/10.3390/rs13122355









