Abstract
This article highlights the industry experience of the development and practical implementation of a short-term photovoltaic forecasting system based on machine learning methods for a real industry-scale photovoltaic power plant implemented in a Russian power system using remote data acquisition. One of the goals of the study is to improve photovoltaic power plants generation forecasting accuracy based on open-source meteorological data, which is provided in regular weather forecasts. In order to improve the robustness of the system in terms of the forecasting accuracy, we apply newly derived feature introduction, a factor obtained as a result of feature engineering procedure, characterizing the relationship between photovoltaic power plant energy production and solar irradiation on a horizontal surface, thus taking into account the impacts of atmospheric and electrical nature. The article scrutinizes the application of different machine learning algorithms, including Random Forest regressor, Gradient Boosting Regressor, Linear Regression and Decision Trees regression, to the remotely obtained data. As a result of the application of the aforementioned approaches together with hyperparameters, tuning and pipelining of the algorithms, the optimal structure, parameters and the application sphere of different regressors were identified for various testing samples. The mathematical model developed within the framework of the study gave us the opportunity to provide robust photovoltaic energy forecasting results with mean accuracy over 92% for mostly-sunny sample days and over 83% for mostly cloudy days with different types of precipitation.
1. Introduction
Modern regional electric power systems (EPS) are characterized by an increasing share of renewable energy sources (RES). In most of the developed countries, state-supporting mechanisms are implemented for RES development, including fixed tariffs that determine the price per kilowatt/hour, mark-ups, green certificates and other mechanisms. In Russia, the competitive tendering mechanism for the supply contract for the wholesale market has become most widespread, in which the owners of power generation facilities operating on the basis of RES receive a monthly guaranteed payment for capacity. By an order of the Government of the Russian Federation, target indicators of the installed capacity of such generation in the total structure of generating capacities were determined to be 5,871 MW until 2024. At the beginning of 2018, its installed capacity excluding hydroelectric power plants in the UES of Russia amounted to 1.59 GW and in the world, 941.0 GW, and the assessment of the technically affordable energy potential of RES in Russia from various sources is estimated to be from 5–25 billion tons of oil equivalent per year, that is, an estimated 55% of the annual energy consumption.
The task of RES power generation implementation is directly related to the task of electric energy generation forecasting, since the lack of renewable energy sources’ reliable forecasts entails the need to constantly maintain a full reserve of active power in the power system [1] (in the amount of available capacity of RES), which actually means the need for an extra regulation response from thermal generation and its operation in uneconomical modes and/or regulation of the power grid congestion, which in turn causes the problem of switched on power generation excess capacities not only at the regional level, but also on a national scale. The problems of energy production forecasting at power generation facilities using various types of RES are associated with the problem of the stochastic nature of their operation modes. Such a task is multifactorial with a large number of poorly formalized and linguistic data, since it is based on meteorological and climatological data, the generalized nature of which also has a strong influence on the result of energy production forecasting [2].
The need to predict the RES generation is fixed at the state level, according to order No. 91 dated 11 February, 2019 “On approval of requirements for energy consumption forecasting and the formation of electric energy and active power balances for a calendar year and particular periods within a year”, “… The volume of electric energy production in the forecasted energy balance of the power system should be determined for wind and solar power plants - on the basis of monthly data on the average long-term value of electrical energy production by these power plants for the last three years, and in the absence of these data (including the power plants under construction), in accordance with the proposals of the owners on the formation of a consolidated forecasted balance …”. At the same time, in the dispatch centers in Russia, the task of photovoltaic power plant (PVPP) generation forecasting has not been fully addressed yet. Currently, in the short-term planning of power system operation modes in order to compensate for the stochastic decrease in power output by RES-based generation facilities [3], the volume of EPS active power reserves is increased by the total capacity declared by the owners of RES-based power generation facilities.
In order to increase the efficiency of power system operation modes’ short-term planning, in terms of power system constraints monitoring and allocating active power reserves, it is necessary to create tools for PVPP generation forecasting for short-term (one day ahead) forecasting. PVPP owners are also interested in developing forecasting tools. Under existing conditions, this will allow not only solving the problems of selecting the composition of the switched-on power generation equipment, but also ensuring effective planning of the main power generation equipment maintenance.
The above emphasizes the relevance of the study and the need to harmonize the process of introducing PVPPs into the power systems, and also reveals a number of fundamentally new problems and tasks requiring the development of new approaches to their solution from the point of view of information-analytical and mathematical principles of raw data processing and analysis [4], especially in the case of using open-source weather data, extracted from weather prediction models of the local hydrological and meteorological data providers.
Except for the poor formalization and linguistic representation of open-source weather data, the problem of weather forecasting is greatly associated with the total coverage of the area by measurements of meteorological stations and posts [5]. Evidently, sparsely populated areas have an insufficient number of available weather data acquisition points, which makes the open-source weather forecasts less reliable, making the problem of RES-based power generation forecasting more challenging.
In [6], a review of various approaches to electrical energy generation forecasting as well as an analysis of the influence of the forecasting accuracy on the power system control efficiency are described. In [7], a detailed review of existing approaches to solar power plants’ electrical energy output forecasting is provided.
On the one hand, due to the chaotic nature of weather variations, traditional forecasting methods may not provide the required level of forecasting accuracy. Moreover, the initial dataset may be subjected to various distortions caused by the peculiar features of such power plants’ operation modes. For example, in [8], the influence of dust on solar panels’ efficiency is analyzed, and in [9], the effect of snow deposits.
In addition, uneven distortions in the collected data may be caused by partial shadowing of solar panels, as shown in [10]. On the other hand, today a large number of different sensors are available, including satellite data. An example of the application of open satellite data to predict the available power of a solar power plant is given in [11].
The use of new types of data allows us to improve traditional forecasting approaches. For example, in [12], the application of the analog ensemble method for the prediction of the solar power plant energy output was described, and in [13], its modification was analyzed for open-source meteorological data. The application of numerical weather prediction (NWP) algorithms for the evaluation of the magnitude of solar irradiation is described in [14]. The implementation of the network of weather monitoring systems allows one to increase the accuracy of such forecasting, an example of which is presented in [15].
The collection of retrospective data and the development of machine learning methods allow us to identify new hidden relationships between parameters and increase the accuracy of electrical energy generation forecasting. M. Abuella and B. Chowdhury [16] describe the use of multiple linear regression for predicting the solar power plant electrical energy output based on advanced meteorological data. The use of linear regression for solving a similar problem is also described in [17]. Along with linear regression, traditional methods of working with time sequences can be used [18].
The rapid development of machine-learning technologies opens up new possibilities for the improvement of forecasting technologies. A new extreme machine learning algorithm proposed in [19] was successfully applied to solve the problem described in [20].
Along with machine-learning technologies, various algorithms for identifying model parameters are used. With the help of such models, the forecast of generated electrical energy is further carried out. In [21], a comparison of various sky models from the point of view of solar irradiation forecasting is provided. In [22,23], various models of solar panels were investigated from the point of electrical energy production.
Despite the great relevance and interest in solar energy forecasting, proved by a large number of regular publications, today, there are a few software packages that provide this functionality. One of the most popular tools for modeling and analyzing the operation of solar panels is the HOMER software package, a system for modeling combined PV systems that allows one to determine the optimal power system configuration.
In scientific literature, you can find many examples of the application of this software package for solving specific applied problems, for example, to optimize the joint operation of a PV plant with a biofuel installation [24]. You can also find examples of HOMER application to analyze the operation of solar power plants located in different geographical positions, for example, in Georgia [25], the island of Saint Martin [26], Indonesia [27], and India [28]. A detailed analysis of existing software systems and their capabilities is given in [29].
Unfortunately, most of these software systems are not applicable to Russian conditions mostly due to the lack of available meters throughout the territory of the country. More importantly, nowadays Russia is actively in the process of implementing new solar power plants, and the main problem is the availability of initial and retrospective data for developing a forecasting model.
In this regard, there is a need to develop a specialized software package adapted to Russian realities and allowing forecasting of solar irradiation at the installation site of solar panels with subsequent day-ahead forecasting of electrical energy production.
In the presented study, the authors provided a possible solution to the problem of solar power plants generation forecasting, based on the generalized open-source weather data, lacking the necessary features, characterizing specific meteorological events and conditions. A forecast is obtained by implementing a multi-stage procedure of machine learning algorithms applied to get the forecast, which is sufficiently reliable for power system control and short-term operational planning.
The rest of the article is organized as follows. The second part considers solar power generation specific features in terms of the technological and exogenous factors, which influence the solar power generation forecast. The third part addresses the detailed problem formulation and initial multi-source dataset characteristics, containing solar geometry calculated values, power plant measurements and open-source weather data.
The authors compared multiple machine-learning algorithms and provided the algorithms’ hyperparameters optimization to find the best composition of the algorithms and their parameters for sunny and cloudy days. Finally, a step-by-step procedure was introduced for better cloudy days forecasting, and the practical implementation results were discussed.
2. Solar Power Forecasting Peculiar Features
PVPP is a complicated technical system, containing electrical equipment of direct (DC) and alternating current (AC) with its own automated control systems, relay protection systems, switchgear equipment, etc. Powerful PV plants with an installed capacity above 1 MW typically work in conjunction with interconnected bulk power systems, providing electrical energy in-feed in peak and half-peak hours.
Being a part of the bulk power system incurs technical and operational rules and constraints, which are imposed by the adjacent power system and are to be strictly followed. From a technical point of view, power network topology, power system frequency and voltage level play a crucial role in PV plant electrical energy output. This means that the operation mode of the PV power plant is influenced not just by external meteorological factors, but by external and internal technological conditions, driven by the power system operation mode and the PV power plant itself.
2.1. PV Power Plant Internal Technological Factors
2.1.1. Photovoltaic Panel: Specific Features
The main PVPP element is a photovoltaic (PV) panel. The generated output of the PV panel is determined by various factors, including the power plant configuration, solar irradiation and ambient temperature.
2.1.2. Electrical Circuits of PV Power Plant
There are various topologies for connecting solar panels, and the specific power plant configuration is typically determined at the design stage. Generally, the string configuration is most often used, where several panels are sequentially connected into a string with a voltage of 12–240 V DC. Each string has a DC/DC with MPPT trackers. Several strings are connected in parallel to a DC/AC inverter providing pulse width modulation (PWM) with power output to the AC side [30].
Among the factors that influence PV generation, there are hardly-formalized heterogeneous parameters, which are given in Table 1.

Table 1.
Sources of uncertainty at the level of PV power plant.
2.2. PV Power Plant External Factors
2.2.1. Solar Irradiation
The key stage in PV plant energy output forecasting is to determine the main energy characteristic, namely, solar irradiance, which depends on many stochastic factors. The total energy flux density of solar irradiation at the surface of the earth incident on the tilted surface of the solar panel is the sum of direct, diffused and reflected irradiation. Each of these components is a difficult-to-predict parameter, depending on both atmospheric and climatic phenomena [31].
2.2.2. External Factors: Meteorological Data
The initial dataset for PV plant energy output forecasting is composed of different data sources:
- PV plant technical data, including power output history
- Meteorological actual data retrospective
- Meteorological forecasting data retrospective
- Irradiance retrospective data acquired from PV plant
As long as the data is collected from multiple sources and some features are typically not available for weather forecasts, data uncertainty may occur. For example, cloudiness in weather forecasts is typically provided in percentage [%]. Figure 1 provides a typical case of 2 days (16.10.2017 and 17.10.2017), illustrating a possible variation of the solar irradiation based on practically similar cloudiness data. In Figure 1, the red line corresponds to the cloudiness, while the blue bar chart illustrates solar irradiation for 2 sequential days, measured by the pyranometer.
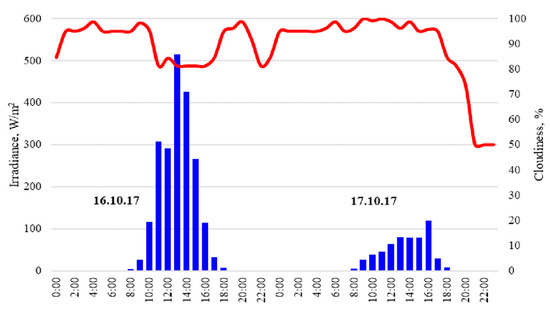
Figure 1.
Actual solar irradiance variation in similar cloudiness conditions.
Another important point is the quality of meteorological data. Up-to-date NWP models are based on actual meteorological data, provided by weather stations, spread all over the territory that is being considered. That means that the greater the redundancy of the meteorological measurements, the greater the accuracy of the weather forecast. The formulated principle imposes a computational challenge for under-populated territories with poorly developed weather stations [32].
2.3. Forecasting Problem Specification and Goals of the Study
As it was discussed, the problems with solar power plant energy output forecasting deals are:
- (1)
- PV plant is an integrated technological system, composed of non-linear electric circuit components, industrial automation and control systems, operating the functional state of AC and DC electrical installations
- (2)
- The availability of the primary energy source is highly stochastic. Different prediction time horizons correspond to different prediction models as well as different initial data that can be used to improve the prediction accuracy
- (3)
- The PV power plant forecasting problem deals with multi-source heterogeneous data. Power output measurements are typically considered together with local weather station measurements, which are extracted from data storage facilities of the automated control system of the PV power plant
So, while pursuing the goal of PV energy forecasting accuracy improvement, the following tasks have been solved:
- Investigation and justification of various mathematical approaches for day-ahead energy forecasting problems;
- Development of the PV energy forecasting software tool, dealing with heterogeneous multi-source data, acquired from local measurement systems and open-source weather data;
- Commitment to PV output forecasting accuracy of not less than 80%, which corresponds to the standard 20% admissible deviation from power system operation plan [33]
3. Problem Statement and Available Data
The development of RES in the world’s energy systems is one of the main factors that raises requirements for the collection and analysis of their data, in particular, introducing special additional requirements for sensors and collection and data read-out systems [34,35].
Earth-observing systems have progressed over the past decades in terms of image quality and image frequency [36]. Every satellite and drone system has its own limitations, namely, the number of satellites, weather and daylight for optical systems; vegetation for SAR systems; etc., but despite the limitations, this progress has led the remote sensing industry to this data volume, and the stated repetitive images frequency could provide a full daily scope of the earth surfaces using high-resolution images [37]. Nowadays, data from optical, infrared, radio, and microwave remote-sensing devices have revolutionized the meteorology and climatology, as they provide potentially global coverage and therefore improve access to areas that have a limited number of weather stations (areas with rare data) or not covered by routine observations at all. The remote sensing data supports traditional observations and is widely used in NWP, enhancing and improving weather forecasting, etc. [38], and the remote sensing science has become an essential and versatile tool for natural resource managers and researchers in government agencies, environmental institutions and industry [39].
Despite the great potential of modern methods and tools for remote sensing, unfortunately, the costs of their application are not justified in all production industries. Today, RES generation facilities are in most cases private facilities, which are financed from the owners’ funds. Not every owner of RES generation is financially able to use satellite earth observation systems to make forecasts.
In this case, generation owners carry out generation forecasting based on open meteorological data, which often, due to data quality, leads to errors and, as a consequence, problems with the generating facility participation in the energy market. Such data have the following disadvantages:
- open meteorological data delivered by the meteorological provider for the current day are averaged actual data received from a meteorological station and/or a meteorological desk away from the solar power plant, which leads to an error in determining the solar insulation flux density forecast.
- the use of current measurements obtained from meteorological sensors installed on the PVPP to reduce errors in the forecasting task is impossible without the complex statistical algorithms and the numerical models for forecasting weather conditions, which in turn represent a “substitution” of functions and services delivered by the meteorological provider;
- the data composition delivered by the meteorological provider is limited by the parameters of air temperature, wind speed and direction, and cloudiness quantitative and/or qualitative characteristics; even in the case of a numerical model for forecasting weather conditions, the data from the local meteorological station will not be enough for correction, since the cloud characteristics auto-monitoring function at local meteorological desks is usually not implemented.
All of the above problems form the goal of this study: increasing the PVPP generation forecasting accuracy based on open meteorological data.
In the current study, the PV forecasting problem refers to day-ahead active power forecasting (electrical energy) generated by a particular real grid-scale PV power plant based on the retrospective data [40].
3.1. Problem Formulation
Assuming the following initial dataset:
 where is the predicted parameter; is a feature, corresponding to the parameter; is the number of observations in the sample; and is the number of features. All the data is aligned in time.
where is the predicted parameter; is a feature, corresponding to the parameter; is the number of observations in the sample; and is the number of features. All the data is aligned in time.

The goal is to build a mathematical model that will determine the value of the new parameters according to the corresponding features with a given threshold accuracy. In other words, the task is to build a model , which, having received the input , would predict the answer .
3.2. Initial Data Sample Description
In the given problem formulation, the initial dataset includes 16 features, stored in a single database for the period from September 26, 2017 to February 5, 2019. The data was acquired from a real operating PV power plant, located in the south of the Russian Federation. Among the features, we used calculated parameters, measured data, as well as the open-source weather data, acquired from weather providers:
- Time, date: 29.09.2017–05.02.2019
- Coordinates: Latitude 46.398642, Longitude 48.515582
- Calculated parameters:
- solar declination angle, [deg.], range [−23.45, 23.45];
- sunrise time, [hour], range [4.97, 8.58];
- sunset time, [hour], range [16.87, 20.61];
- solar zenith angle cosine, range [0, 0.92];
- solar altitude angle, [deg.], range [0, 66.03];
- solar constant, 1367 [Wh/m2];
- solar irradiation at the top of the atmosphere, [Wh/m2], range [0, 1213.47];
- Measured data:
- PV power plant hourly actual generation, [kWh], range [0, 12 919.2];
- solar irradiation, [Wh/m2], range [0, 982.70]
- External source data (NWP data from open-source weather provider):
- cloudiness, [p.u.], range [0, 1], step 0.125;
- ambient temperature, [°C], range [−17, 42];
- humidity, [%], range [7, 100];
- wind speed, [m/s], range [0, 15]
The complete dataset contained 11 892 pcs. of samples. The pre-processing stage of the forecasting algorithm presupposed removal of the night-hours samples in order to make the PV power generation dataset more stationary. After night-hour removal, the total amount of the samples was obtained to be equal to 6038 pcs. As far as the data was not sufficient for a 2-year period, it was finally decided to take into account the complete year data from 26 September 2017 to 21 October as a training set and a period from 22 October 2018 to 5 February 2019 as a testing set. Initial consideration of a complete year helped the model to understand the variations of the weather conditions of separate months. In further calculations, this trained model was used for hyperparameters tuning of machine learning algorithms, addressed in the present article.
Solar radiation at the PVPPs is typically measured by the horizontally mounted pyranometers. For the certification of pyranometers, the ISO 9060 standard is used. High-precision instruments were used at the PV plant under consideration, corresponding to the ISO spectrally flat class A. The technical specifications are shown in Table 2.

Table 2.
Remote-sensing device technical specifications.
All the data were stored in a database with 1 h time resolution, conditioned by the external weather data time resolution constraints. The influencing parameters of the PV output forecasting problem are obtained using the correlation heat map, which is provided in Figure 2.
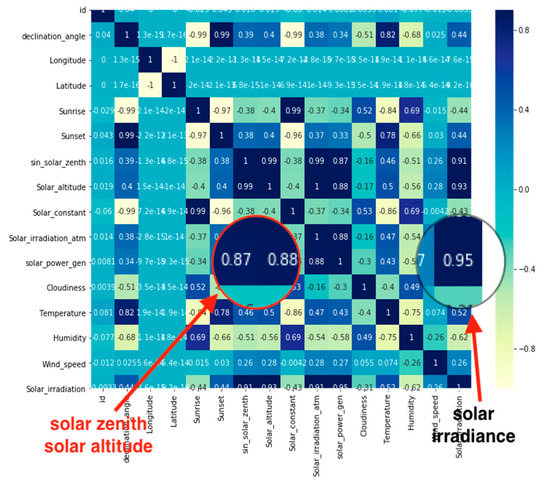
Figure 2.
The correlation matrix of the parameters/features.
As one can see from Figure 2, solar zenith angle and solar altitude angle are the major parameters after solar irradiance in the prediction of the PV energy output. It is known from practice that cloudiness is also one of the important parameters.
4. Mathematical Models Description
For the given problem formulation, the following mathematical models were used and tested: random forest regressor; gradient boosting regressor; decision trees regressor; and linear regression.
4.1. Random Forest
Random forest is an algorithm that provides fittings of many decision trees for different sub-samples of the initial dataset at the stage of training and can be generally described by the following procedure [41]:
For each n = 1, …, N (N-the number of tree in the forest):
- generate a sub-sample using bootstrap procedure
- build a decision tree for subsample
The resulting regressor is given as follows:
where N is a number of decision trees; is a decision tree.
4.2. Gradient Boosting
For the given study, Gradient boosting is implemented via the Adaptive Boosting Algorithm (AdaBoost). The regressor of the Gradient Boosting algorithm is given as follows [41]:
where is a basic function, a decision tree, typically treated as a weak learner of the algorithm.
In the course of the algorithm, each added tree is aimed at minimizing the loss function L, generated at the previous step, Fm−1. Gradient boosting solves the minimization problem by using the negative gradient of the loss function:
where is a step length, which is calculated in the course of the line search procedure.
In order to increase the accuracy of the regression problem solution, hyperparameter tuning was applied to the initial model. As a result, the hyperparameters with the most influence were estimated to be equal to: Learning rat = 0.01; Min_samples_leaf = 2; Max_feature = ‘auto’; Max_depth = 35; Alpha = 0.9; Min_samples_split = 25; n_estimators = 2000; and subsample = 0.7.
The optimal value of max_depth was experimentally found to be 35. If max_depth value is increased, overfitting of the model takes place; when data noise is taken into account, this results in degradation of the performance of the model. The optimal value of the learning rate was stated to be 0.01. A value below 0.01 also causes an overfitting effect and leads to dramatic degradation of forecasting accuracy.
4.3. Decision Trees
The Decision Tree approach is implemented via an optimized version of the CART algorithm, which is implemented by the following procedure [41]:
- partitioning of the sample space according to the training and label vectors () and , respectively;
Let the data in node m of the decision tree be referred to as Q. For each potential data split consisting of a feature j and the marginal value , partition the data into and subsets:
The impurity at node m of the Decision Tree is estimated based on the impurity function, and the decision tree parameters are selected in accordance with impurity minimization criteria.
Within the scope of the regression problem, determination of locations for future splits is carried out by estimating minimal Mean Squared Error and Mean Absolute Error:
where is the training data in node m of the Decision Tree.
Decision Tree model hyperparameters optimization lead to the following results: Max_depth = 16; Min_samples_split = 16; Min_samples_leaf = 15; Max_features = ‘auto’; Random_state = ‘16’.
Model parameters were experimentally verified for the given training sample. Max_depth was optimized to increase model fitting, but not to overfit the data sample.
4.4. Linear Regression
The Linear regression model is considered as a basic simple regressor in order to correspond to the algorithm complexity with its computational efficiency. The linear model under consideration is described by the following equation [41]:
where are regression coefficients, and is regression error.
The linear regression model is based on the ordinary least squares model (‘OLS’). Linear regression models trained along with Polynomial Featuring demonstrated better performance, so this model is also taken into consideration.
The obtained results are moderately fitted when the power is “2”. When the power is “3”, the data set is overfitted.
4.5. Quality Metrics of the Models
The algorithm we used to test the accuracy of the prediction model is r2_score; it is also known as the coefficient of determination. The r2_score (i.e. coefficient of determination) is the subtraction of the residual sum of squares of the predicted and actual values divided with the total sum of squares.
where is the actual value of the PV power plant output, kWh; and is the predicted value of PV power plant output, kWh.
Summary and results of the application of the proposed algorithms to a particular sample day forecasting with and without hyperparameter tuning and pipelining are provided in Figure 3, Figure 4, Figure 5 and Figure 6 and Table 3, Table 4, Table 5 and Table 6.
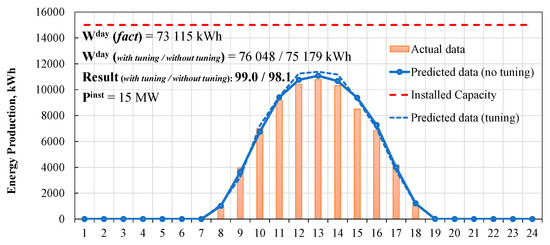
Figure 3.
One-day forecasting example with Random Forest regressor.
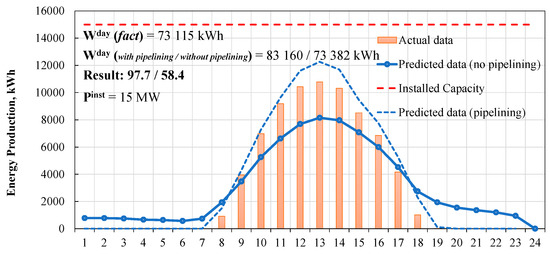
Figure 4.
One-day forecasting example with Linear Regression.
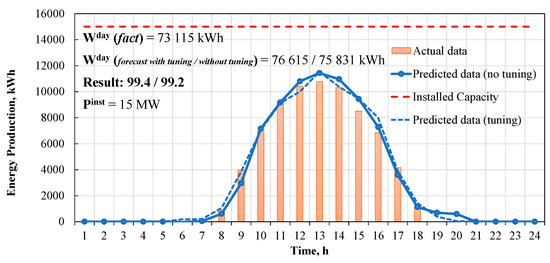
Figure 5.
One-day forecasting example with Gradient Boosting regressor.
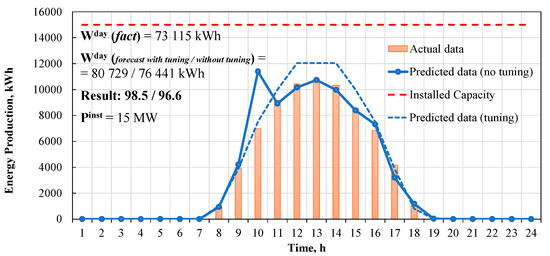
Figure 6.
One-day forecasting example with Decision Tree regressor.

Table 3.
Sample day-1 analysis: Random Forest.

Table 4.
Sample day-1 analysis: linear regression.

Table 5.
Sample day-1 analysis: gradient boosting.

Table 6.
Sample day-1 analysis: decision trees.
A particular sample day, depicted in Figure 3, Figure 4, Figure 5 and Figure 6, corresponds to early October, representing the median between summer and winter solstice in terms of the sunrise and sunset time. The forecasting procedure for stable weather days scores above 90% for all the tested algorithms, which corresponds to the state-of-the-art practice.
5. Prediction for Bad Weather Conditions
It is known that the weakest points of PV energy output forecasting are bad weather days predictions. The bad weather data is caused as a result of uneven cloud cover, moisture or also the snow and rain that degrade the solar panels’ efficiency. For a given location, all these issues take place from September to December. The box plot diagrams of the prediction accuracy are provided in Figure 7. The accuracy of the forecasting for the given months typically equals to 60–70%, which does not meet the requirements and needs to be addressed.
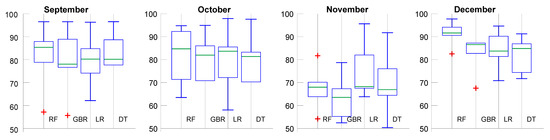
Figure 7.
Accuracy box plots for proposed machine-learning models (1-year period).
The problem of extremely uncertain weather conditions is considered on the basis of a winter day with sporadic clouds.
For the scenario, provided in Figure 8, the cloudiness and, correspondingly, PV power plant energy output along with solar irradiation are completely uncertain. The clouds are scattered all over the region of PV power plant geographical location. The sudden and unique movements of the clouds are conditioned by the high wind speeds (more than 17 m/s), which produce transient variations of PV power plant electrical energy production and result in noisy data occurrence.
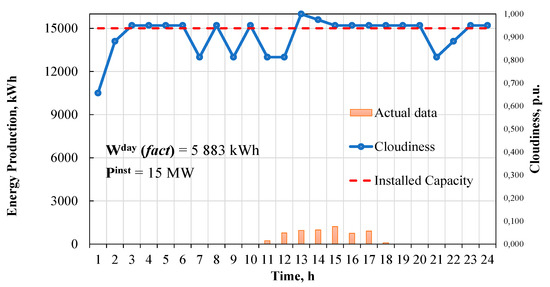
Figure 8.
PV power plant energy output plotted versus weather conditions.
In order to make the machine able to predict “bad weather” days, the following points are to be taken into account:
- In order to predict the PV energy output in sudden cloud motion conditions, the machine learning algorithm is required to be trained along with the noisy data.
- The noisy data is generally considered when the machine is trained with overfitted data, which leads to the consideration of the smallest variations in the cloudiness.
For the first time, the proposed models were tested without hyper parameters tuning in order to check whether the models work with the same efficiency even when subjected to the different situations and uncertain conditions.
The prediction gives a clear perspective of how uncertain a data set could be and how many calculation efforts the machine has to involve to predict the PV power plant energy output values. As a result, the Linear Regressor along with Decision Trees regressor did not produce an adequate solution of the PV energy output prediction problem due to high uncertainty and noise in the dataset.
Gradient Boosting Regressor along with Random Forest regressor without hyper parameters tuning resulted in the average score of 20%, which cannot be considered as a viable result for power system operation modes planning. After hyper parameters tuning, the machine is taking a lot of time (i.e. 50 seconds) to fit the noisy data with a learning rate of “0.0089” and a decision tree depth of “35”.
After running a series of calculation experiments with “bad weather” days, one can conclude that in order to eliminate data uncertainty and model overfitting, the model requires a different feature (or structure) except hyper parameters tuning for “bad” weather conditions.
6. Bad Weather Days Predictor
After scrutinizing the prediction results, we have concluded that uncertainty mostly comes from data values, which have very low PV energy output compared to other peak data points. Coming back to feature correlation analysis, we assumed that uncertain data values can be predicted by firstly predicting the solar irradiance, which is also proportional to the PV plant power output.
By predicting the horizontal solar irradiance, the following sources of uncertainty are eliminated:
- solar irradiance diffusion and reflection;
- electrical circuits of the PV power plant; and
- the state of solar panels (shadow, degradation, etc.).
So, the bad weather days prediction methodology takes the following steps:
- Predict the factor using a regressor model (K).
- Predict the solar irradiation using a regressor model (I).
- Obtain the cloudiness variance for the period (V):
- If , take
- If , take
- If , take
- If , take
- If or or , (K).
- After checking and obtaining the factor, multiply the factor with the predicted solar irradiation PSI. The multiplied value is the solar power generation predicted value:
The flowchart of the presented algorithms is given in Figure 9.
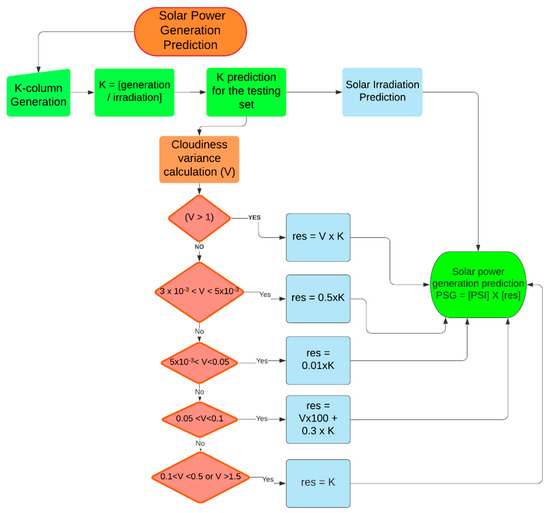
Figure 9.
Flow-chart of the K-factor algorithm.
The next important feature of the algorithm is using separate training sets based on month separation. Pre-processing the training set with different month selection is carried out separately for “Jan to Sept” dataset and “Oct to Dec" dataset.
From January to September, heavy snowfall is not likely to occur for a given geographical location, which gives the opportunity to assume the reduction of noisy values in the data set. From October to December, snowfall and foggy conditions are present in the given region of the given data, resulting in noisy data occurrence. Thus, the model is trained separately with noisy conditions and non-noisy ones, resulting in improvement of the confusion matrix. The total r2_score of the proposed algorithm is estimated to be around 80%.
From October to December, snowfall and foggy conditions are present in the given region of the given data, resulting in the occurrence of noisy data. Therefore, the model is trained separately with noisy conditions and non-noisy ones, resulting in an improvement of the confusion matrix. The total r2_score of the proposed algorithm is estimated to be around 80%. Normal weather days can be predicted with higher accuracy and without requiring the factor-based algorithm. The authors used Linear Regression with Polynomial Featuring for good weather days forecasting. After making a large number of observations of different results, we analyzed that the Gradient Boosting Regressor without hyperparameter tuning outperforms all other models. The algorithms used in the K-factor model, depending on the weather conditions, are listed in Table 7.

Table 7.
PV energy output prediction algorithms.
The short-term PVPP forecasting system developed within the framework of the study was implemented by LLC “Prosoft systems”, an industrial automation and metering systems producer, as a program unit of “Energosphera” software package, providing smart metering systems management [42]. The satellite snapshot of the PVPP under consideration is given in Figure 10. At the moment, the forecasting system is being piloted at a real PV power generation facility, located in Astrahan city in the Russian Federation.

Figure 10.
PV power plant satellite snapshot (Google Maps®).
Meteorological data is acquired in a 1-h time resolution from the external weather provider and includes cloud coverage, ambient air temperature, humidity, wind direction, and wind speed. Examples of day-ahead forecasts, generated by “Short-term Forecast of Solar Power Station Generation” program unit, which uses the developed approach, are presented in Figure 11 for the following types of weather conditions: clear, cloudy, and overcast, respectively.
Figure 11.
Energosphera: Photovoltaic power plant output forecasting.
The mean forecasting error reduced to the installed capacity of the PVPP for the time period starting from 1 October, 2017 to 31 December, 2017 was estimated to be 4.6%, which is comparable with the forecasts of global practice.
7. Conclusions
The PV power plant forecasting problem deals with multi-source heterogeneous data as far as the initial dataset is composed of the measurements, which are acquired from PV power plant metering systems, and external source weather forecasting data.
The problem was addressed by applying four different mathematical models: Random Forest regressor, Gradient Boosting Regressor, Linear Regression, and Decision Trees regression. Based on computational experiments with hyper parameters optimization and pipelining of the algorithms, the optimal structure and settings of the PV plant energy output forecasting system were identified together with the application restrictions for each of the algorithms.
During computational experiments, it was found that parameters tuning allows improvement of the algorithm performance for all non-ensemble algorithms: for linear regression from 55% to 94%, and for decision trees from 88 to 91%, while the accuracy of ensemble algorithms, such as gradient boosting on decision trees and random forest, did not change significantly.
Within the scope of the study, it was proven that the application of the universal model, applied either for good or bad weather days, may result in significant degradation of the short-term forecasting accuracy, hence, in order to improve the predictive properties of the system, several models are to be developed for various weather conditions. Moreover, it was found that good weather days when the meteorological data is assumed to be noise-free are accurately predicted by using any of the presented mathematical models with an accuracy rate of 90% and higher.
Due to the lack of features in the dataset, bad weather days are characterized by high uncertainty, which may decrease the predicting properties of the system.
To overcome the bad weather forecasting issue, the structure of the algorithm was improved by introducing a novel two-stage forecasting procedure and extracting a new feature from the raw dataset by applying feature engineering approaches. The proposed procedure is composed of the stage of solar irradiation forecasting, followed by the stage of generation factor prediction, which describes the relationship between solar irradiance and PV power plant hourly energy output. A resulting factor scaled down to the variance of the cloudiness provides a significant improvement of forecasting system robustness and prediction accuracy.
The newly introduced algorithm together with proper training sets formulation, resulted in mean 83% forecasting accuracy for bad weather days instead of 20% for Gradient Boosting Regressor and Random Forest regressor without hyper parameters tuning, demonstrating dramatic improvement of the model performance without model overfitting. Summarizing the performance of K-factor algorithm in comparison with the machine learning algorithms addressed in this paper, after taking the mean of five cross-validations with 6038 samples, the K-factor algorithm improves the performance of the addressed machine learning approaches in the following way:
- 92% accuracy of K-factor model instead of 78% accuracy of Random Forest regressor:
- 85% accuracy of K-factor model instead of 83% accuracy of Linear regressor:
- 89% accuracy of K-factor model instead of 73% accuracy of Gradient Boosting regressor;
- 81% accuracy of K-factor model instead of 56% accuracy of Decision Trees regressor.
The results obtained for K-factor model meet the requirements of the transmission and distribution power system operators in terms of 20% admissible deviations of the power system operation plan.
Based on the exhaustive calculations, it was decided to use Linear regression for good weather days forecasting and a factor-based prediction model using Gradient Boosting Regressor for bad weather days in order to sustain robustness and eliminate overfitting.
The presented system of short-term PV energy output forecasting is universal and can be used at any existing PV generation facilities as a part of the Energosfera 8.0 software package (LLC, Prosoft-Systems LLC). Currently, Prosoft-Systems together with the research team of Ural Federal University is developing a system, providing online correction of the short-term forecasts, based on the current measurements of solar irradiation and cloud motion. It is expected that the system will allow the owners of solar power plants to participate in intra-day trading procedures at the wholesale electricity and capacity market.
With the development of generating capacities based on RES, the uncertainty degree in planning the power system operating modes increases significantly. Today, reliable tools are required to predict the generation of power plants using, in particular, solar energy obtained by remote sensing [43]. For short time periods from 1 to 6 h, the generation forecast can be significantly improved by using the current data obtained by direct (proximate) observation (remote sensing) methods. When combining numerical weather forecasting systems with real-time data, forecast deviations caused by inaccuracies in numerical weather forecasting models can be corrected several hours ahead.
Author Contributions
Conceptualization, A.I.K. and S.A.E.; data curation, S.A.E., V.A.T., T.P.C. and D.N.B.; formal analysis, V.A.T. and T.P.C.; funding acquisition, A.I.K.; investigation, S.A.E., H.R., T.P.C. and D.N.B.; methodology, A.I.K., S.A.E. and H.R.; project administration, A.I.K. and H.R.; resources, V.A.T. and D.N.B.; software, A.I.K., S.A.E. and V.A.T.; supervision, A.I.K. and H.R.; validation, V.A.T., T.P.C. and D.N.B.; visualization, T.P.C.; writing–original draft, A.I.K. and H.R.; writing–review & editing, S.A.E. and D.N.B. All authors have read and agreed to the published version of the manuscript.
Funding
No funding was received for this study.
Acknowledgments
The authors are thankful to the anonymous Referees for their insightful suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gigoni, L.; Betti, A.; Crisostomi, E.; Franco, A.; Tucci, M.; Bizzarri, F.; Mucci, D. Day-Ahead Hourly Forecasting of Power Generation from Photovoltaic Plants. IEEE Trans. Sustain. Energy 2018, 9, 831–842. [Google Scholar] [CrossRef]
- Sangrody, H.; Sarailoo, M.; Zhou, N.; Tran, N.; Motalleb, M.; Foruzan, E. Weather forecasting error in solar energy forecasting. IET Renew. Power Gener. 2017, 11, 1274–1280. [Google Scholar] [CrossRef]
- Conte, F.; Massucco, S.; Schiapparelli, G.; Silvestro, F. Day-Ahead and Intra-Day Planning of Integrated BESS-PV Systems Providing Frequency Regulation. IEEE Trans. Sustain. Energy 2020, 11, 1797–1806. [Google Scholar] [CrossRef]
- Huang, C.; Wang, L.; Lai, L.L. Data-Driven Short-Term Solar Irradiance Forecasting Based on Information of Neighboring Sites. IEEE Trans. Ind. Electron. 2019, 66, 9918–9927. [Google Scholar] [CrossRef]
- Vincent, E. Larson. Chapter 12—Forecasting Solar Irradiance with Numerical Weather Prediction Models. In Solar Energy Forecasting and Resource Assessment; Academic Press: Cambridge, MA, USA, 2013; pp. 299–318. [Google Scholar]
- Orwig, K.D.; Ahlstrom, M.L.; Banunarayanan, V.; Sharp, J.; Wilczak, J.M.; Freedman, J.; Haupt, S.E.; Cline, J.; Bartholomy, O.; Hamann, H.F.; et al. Recent Trends in Variable Generation Forecasting and Its Value to the Power System. IEEE Trans. Sustain. Energy 2015, 6, 924–933. [Google Scholar] [CrossRef]
- Glassley, W.; Jan, K.; Van Dam, C.C.; Shiu, H.; Huang, J.; Braun, G.; Holland, R. California Renewable Energy Forecasting, Resource Data and Mapping; Publication Number: CEC-500-2014-026; California Energy Commission: Sacramento, CA, USA, 2012; pp. 1–135. [Google Scholar]
- Maghami, M.R.; Hizam, H.; Gomes, C.; Radzi, M.A.; Rezadad, M.I.; Hajighorbani, S. Power loss due to soiling on solar panel: A review. Renew. Sustain. Energy Rev. 2016, 59, 1307–1316. [Google Scholar] [CrossRef]
- Andrews, R.W.; Pollard, A.; Pearce, J.M. The effects of snowfall on solar photovoltaic performance. Sol. Energy 2013, 92, 84–97. [Google Scholar] [CrossRef]
- Woyte, A.; Nijs, J.; Belmans, R. Partial shadowing of photovoltaic arrays with different system configurations: Literature review and field test results. Sol. Energy 2003, 74, 217–233. [Google Scholar] [CrossRef]
- Jang, H.S.; Bae, K.Y.; Park, H.; Sung, D.K. Solar Power Prediction Based on Satellite Images and Support Vector Machine. IEEE Trans. Sustain. Energy 2016, 7, 1255–1263. [Google Scholar] [CrossRef]
- Alessandrini, S.; Monache, L.D.; Sperati, S.; Cervone, G. Analog ensemble for short-term probabilistic solar power forecast. Appl. Energy 2015, 157, 95–110. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Lu, S.; Hamann, H.F.; Hodge, B.-M.; Lehman, B. A Solar Time Based Analog Ensemble Method for Regional Solar Power Forecasting. IEEE Trans. Sustain. Energy 2019, 10, 268–279. [Google Scholar] [CrossRef]
- Kakimoto, M.; Endoh, Y.; Shin, H.; Ikeda, R.; Kusaka, H. Probabilistic Solar Irradiance Forecasting by Conditioning Joint Probability Method and Its Application to Electric Power Trading. IEEE Trans. Sustain. Energy 2019, 10, 983–993. [Google Scholar] [CrossRef]
- Andrade, J.R.; Bessa, R.J. Improving Renewable Energy Forecasting With a Grid of Numerical Weather Predictions. IEEE Trans. Sustain. Energy 2017, 8, 1571–1580. [Google Scholar] [CrossRef]
- Abuella, M.; Chowdhury, B. Solar power probabilistic forecasting by using multiple linear regression analysis. SoutheastCon 2015, 1–5. [Google Scholar] [CrossRef]
- Hong, T.; Wang, P.; Willis, H.L. A Naïve multiple linear regression benchmark for short term load forecasting. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Prema, V.; Rao, K.U. Development of statistical time series models for solar power prediction. Renew. Energy 2015, 83, 100–109. [Google Scholar] [CrossRef]
- Liang, N.; Huang, G.; Saratchandran, P.; Sundararajan, N. A Fast and Accurate Online Sequential Learning Algorithm for Feedforward Networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef]
- Golestaneh, F.; Pinson, P.; Gooi, H.B. Very Short-Term Nonparametric Probabilistic Forecasting of Renewable Energy Generation—With Application to Solar Energy. IEEE Trans. Power Syst. 2016, 31, 3850–3863. [Google Scholar] [CrossRef]
- Shukla, K.N.; Rangnekar, S.; Sudhakar, K. Comparative study of isotropic and anisotropic sky models to estimate solar radiation incident on tilted surface: A case study for Bhopal, India. Energy Rep. 2015, 1, 96–103. [Google Scholar] [CrossRef]
- Kittisontirak, S.; Dawan, P.; Atiwongsangthong, N.; Titiroongruang, W.; Chinnavornrungsee, P.; Hongsingthong, A.; Sriprapha, K.; Manosukritkul, P. A novel power output model for photovoltaic system. iEECON 2017, 1–3. [Google Scholar] [CrossRef]
- Huang, C.-J.; Huang, M.-T.; Chen, C.-C. A Novel Output Model for Photovoltaic Systems. Int. J. Smart Grid Clean Energy 2013, 2, 139–147. [Google Scholar] [CrossRef]
- Gautam, J.; Ahmed, M.I.; Kumar, P. Optimization and Comparative Analysis of Solar-Biomass Hybrid Power Generation System Using Homer. In Proceedings of the 2018 International Conference on Intelligent Circuits and Systems (ICICS), Phagwara, India, 19–20 April 2018; pp. 397–400. [Google Scholar]
- Ghose, S.; Shahat, A.E.; Haddad, R.J. Wind-solar hybrid power system cost analysis using HOMER for Statesboro, Georgia. SoutheastCon 2017, 1–3. [Google Scholar] [CrossRef]
- Mahmud, N.; Hassan, A.; Rahman, M.S. Modelling and cost analysis of hybrid energy system for St. Martin Island using HOMER. In Proceedings of the 2013 International Conference on Informatics, Electronics and Vision (ICIEV), Dhaka, Bangladesh, 17–18 May 2013; pp. 1–6. [Google Scholar]
- Rajani, A.; Darussalam, R.; Pramana, R.I.; Santosa, A. Simulation of PV-Biogas Integration on Hybrid Power Plant using HOMER: Study Case of Superior Livestock Breeding Center and Forage of Animal Feed (BBPTU-HPT) Baturraden. In Proceedings of the 2018 International Conference on Sustainable Energy Engineering and Application (ICSEEA), Tangerang, Indonesia, 1–2 November 2018; pp. 69–74. [Google Scholar]
- Vendoti, S.; Muralidhar, M.; Kiranmayi, R. HOMER Based Optimization of Solar-Wind-Diesel Hybrid System for Electrification in a Rural Village. In Proceedings of the 2018 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 4–6 January 2018; pp. 1–6. [Google Scholar]
- Wijeratne, P.; Yang, R.J.; Too, E.; Wakefield, R. Design and development of distributed solar PV systems: Do the current tools work? Sustain. Cities Soc. 2019, 45, 553–578. [Google Scholar] [CrossRef]
- Pannase, V.R.; Nanavala, H.B. A review of PV technology power generation, PV material, performance and its applications. In Proceedings of the 2017 International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 19–20 January 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Javed, A.; Shabir, H.; Ali, H.; Darwade, R.; Gite, B. Predicting Solar Irradiance Using Machine Learning Techniques. In Proceedings of the 2019 International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 1458–1462. [Google Scholar]
- Schönhuber, M.; Cuervo, F. About the Impact of NWP Models’ Temporal Resolution on Rain Attenuation Forecasts. In Proceedings of the 2019 URSI Asia-Pacific Radio Science Conference (AP-RASC), New Delhi, India, 9–15 March 2019; pp. 1–3. [Google Scholar]
- Ministry of Power and Energy of Russian Federation. On implementation of the requirements for power systems and electrical installation reliability security. In Guidelines on Power Systems Stability, 3rd ed.; Ministry of Energy of Russian Federatio: Moscow, Russia, 20 August 2018. (In Russian) [Google Scholar]
- Lukaitis, V.Y. Autonomous Power Generation Facilities, Hybrid Structures Comprising Renewable Energy Sources; Lukaitis, V.Y., Glushkov, S.Y., Eds.; Interindustry Scientific and Production Company Energospectechnic (ISPC Energospectechnic): Moscow, Russia, 2019; Volume 2, Issue 2. [Google Scholar] [CrossRef]
- Chen, W.; Liu, Y.; Wang, N. A Novel Grouping Aggregation Algorithm for Online Analytical Processing. In Proceedings of the 2012 National Conference on Information Technology and Computer Science, China, 16–18 November 2012. [Google Scholar] [CrossRef]
- Chu, Y.; Cao, G.; Hayat, H. Change Detection of Remote Sensing Image Based on Deep Neural Networks. In Proceedings of the 2016 2nd International Conference on Artificial Intelligence and Industrial Engineering (AIIE 2016), Nanjing, China, 20–21 November 2016. [Google Scholar] [CrossRef]
- Kussul, N.; Skakun, S.V.; Lavreniuk, M.; Shelestov, A.Y. Deep Learning Classification of Land Cover and Crop Types Using Remote Sensing Data. IEEE Geosci. Remote Sens. Lett. 2017. [Google Scholar] [CrossRef]
- Kuleshov, Y. Use of Remote Sensing Data for Climate Monitoring in WMO Regions II and V (Asia and the South-West Pacific). Australian Bureau of Meteorology, 1 June 2017. Available online: https://www.wmo.int/pages/prog/wcp/ccl/opace/opace2/documents/TT-URSDCM_Use_Remote_Sensing_DataClimateMonitoringRAII-V.pdf (accessed on 30 August 2020).
- K, R.E.; Townsend, P.A.; Gross, J.E.; Cohen, W.B.; Bolstad, P.; Wang, Y.Q.; Adams, P. Remote sensing change detection tools for natural resource managers: Understanding concepts and tradeoffs in the design of landscape monitoring projects. Remote Sens. Environ. 2009, 113, 1382–1396. [Google Scholar] [CrossRef]
- Eroshenko, S.; Khalyasmaa, A.; Snegirev, D. Machine learning techniques for short-term solar power stations operational mode planning. E3S Web Conf. 2018, 51, 5. [Google Scholar] [CrossRef]
- Machine learning in Python: Web-portal. Available online: https://scikit-learn.org/ (accessed on 30 August 2020).
- Prosoft-System, Engineering Company. Available online: https://www.prosoftsystems.ru/en/news/energosfera-8_0-software-package-expands-the-scope-of-capabilities (accessed on 30 August 2020).
- Edenhofer, O.; Pichs-Madruga, R.; Sokona, Y. Special Report on Renewable Energy Sources and Climate Change Mitigation; IPCC: Geneva, Switzerland, 2011; p. 1075. ISBN 978-92-9169-131-9. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).