Next Article in Journal
Industry Experience of Developing Day-Ahead Photovoltaic Plant Forecasting System Based on Machine Learning
Next Article in Special Issue
Water Quality Anomalies following the 2017 Hurricanes in Southwestern Puerto Rico: Absorption of Colored Detrital and Dissolved Material
Previous Article in Journal
Optimization of Optical Image Geometric Modeling, Application to Topography Extraction and Topographic Change Measurements Using PlanetScope and SkySat Imagery
Previous Article in Special Issue
Improved Method to Suppress Azimuth Ambiguity for Current Velocity Measurement in Coastal Waters Based on ATI-SAR Systems
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 20
10.3390/rs12203419
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Role of Mean Sea Level Annual Cycle on Extreme Water Levels Along European Coastline

by
Tomás Fernández-Montblanc
1,2,*,
Jesús Gómez-Enri
3 and
Paolo Ciavola
2
1
Department of Earth Sciences, University of Cádiz, Avda. República Saharaui s/n, 11510 Puerto Real, Cádiz, Spain
2
Department of Physics and Earth Sciences, Universitá Degli Studi di Ferrara, Via Saragat, 1, 44122 Ferrara, Italy
3
Department of Applied Physics, University of Cádiz, Avda. República Saharaui s/n, 11510 Puerto Real, Cádiz, Spain
*
Author to whom correspondence should be addressed.
Remote Sens. 2020, 12(20), 3419; https://doi.org/10.3390/rs12203419
Submission received: 10 September 2020 / Revised: 9 October 2020 / Accepted: 12 October 2020 / Published: 18 October 2020
(This article belongs to the Special Issue Coastal Waters Monitoring Using Remote Sensing Technology)
Browse Figures
Versions Notes

Abstract

:
The knowledge of extreme total water levels (ETWLs) and the derived impact, coastal flooding and erosion, is crucial to face the present and future challenges exacerbated in European densely populated coastal areas. Based on 24 years (1993–2016) of multimission radar altimetry, this paper investigates the contribution of each water level component: tide, surge and annual cycle of monthly mean sea level (MMSL) to the ETWLs. It focuses on the contribution of the annual variation of MMSL in the coastal flooding extreme events registered in a European database. In microtidal areas (Black, Baltic and Mediterranean Sea), the MMSL contribution is mostly larger than tide, and it can be at the same order of magnitude of the surge. In meso and macrotidal areas, the MMSL contribution is <20% of the total water level, but larger (>30%) in the North Sea. No correlation was observed between the average annual cycle of monthly mean sea level (AMMSL) and coastal flooding extreme events (CFEEs) along the European coastal line. Positive correlations of the component variance of MMSL with the relative frequency of CFEEs extend to the Central Mediterranean (r = 0.59), North Sea (r = 0.60) and Baltic Sea (r = 0.75). In the case of positive MMSL anomalies, the correlation expands to the Bay of Biscay and northern North Atlantic (at >90% of statistical significance). The understanding of the spatial and temporal patterns of a combination of all the components of the ETWLs shall improve the preparedness and coastal adaptation measures to reduce the impact of coastal flooding.

Graphical Abstract

1. Introduction

Coastal areas, prone to be flooded in the case of extreme water levels, are mainly low-elevation territories. In addition, the increase in subsidence rates by anthropogenic actions such as sediment supply reduction by rivers, soil compaction by changes in land use [1], as well as extraction of groundwater [2] or natural gas [3] can exacerbate the vulnerability of coastal areas. Marine flooding threatens coastal areas, causing human casualities and large socio-economic impacts [4]. This is more critical in densely populated zones with a restricted or inadequate adaptive capacity [5].
The European coastline is a densely populated area. In 2011, almost 205 million people (>40% of the European population) lived in coastal regions (<50 km from the sea), and on average, in each country with a coastal border, 36% of the population lived within 5 km from the sea [6]. Moreover, there is a large historical record of marine flooding along the European coast [7,8,9], either for the North Sea [10]; Bay of Biscay [11]; North Atlantic, Mediterranean Sea or Adriatic sea among other locations [12]. Protection measures have been taken in the last few decades, increasing preparedness for extreme water level impact along the European coast. These actions have reduced the impact and consequences of coastal flooding generated by extreme events (hereafter, CFEEs) along the European coast. Indeed, despite an increase in the exposure in coastal areas, there is a significant decreasing trend in flood fatalities and economic losses for the period 1950–2016 [13]. An outstanding example is the North Sea floods of 1953 and 2013 (storm Xavier), very similar in magnitude but with very different impacts on infrastructures and population. A considerable decline of the damage was observed in the latter [14]. However, the extreme water level is expected to increase in the next century, by the contribution of the mean sea level rise [15,16], and changes in extreme storm surge and wave characteristics [17]. On the other hand, remarkable growth in coastal risk is also expected, associated with socio-economic coastal development [18]. Therefore, there is a continuous necessity for the monitoring and improvement of the forecasting and knowledge of extreme sea-level events and the driven impact on coastal areas to face the present and future challenges.
Traditionally, Extreme Total Water Level (ETWL, henceforth) has been analysed as the sum of tidal level and non-tidal residual. The non-tidal residual includes the so-called surge or meteorological contribution (inverse barometer effect and wind setup), and the non-linear interaction between surges and tides [19,20]. The non-tidal residual can also contain the wave set-up contribution in coastal areas [21], resonance in enclosed basin [22] or contribution of the river runoff in estuaries during extreme discharges [23,24].
ETWLs are dominated by high-frequency signals (tides, surges, waves set-up and run-up), but low-frequency contributions, such as the annual cycle of sea surface height variation and associated anomalies need to be considered too. The annual cycles of the Monthly Mean Sea Level (MMSL, hereinafter) can induce sea-level variations, ranging from few centimetres to up to 0.3 m in some regions (i.e., the Gulf of Carpentaria between Australia and New Guinea) [25]. Several processes and their seasonal variability drive the annual cycle of sea surface height. Thus, the water mass addition/removal from the oceans is a major forcing of the global ocean mean sea level (MSL) variation [26], interannual variability is critical over shelf seas [27], while seasonal variability can dominate in shallower regions [28]. Freshwater runoff contributes also to the annual cycle of MSL [29], and might become dominant near the coast [30]. The effect of river discharge is limited to the areas influenced by the river mouth [31,32]. In the open ocean the annual cycle of MSL is controlled by changes in the density of the water column through the so-called steric component, dominating the sea level variability at annual timescales in the North Atlantic and in the Mediterranean Sea [33]. The steric contribution is mainly driven by the thermal expansion/contraction of the water column (thermos-steric component) associated with changes in temperature of the upper layer of the ocean; the haline expansion/contraction due to salinity changes (halo-steric component) becomes less important [34]. Although the relevance of density changes in sea surface height variability is proportional to the water column depth and can be predominant in the open ocean, it can affect by remote contribution shallower areas [35].
Tide gauges have been used for years for extreme value analysis [36,37]. Some limitations (spatial and temporal coverage) are inherent to in situ measurements [38]. Tide gauge data are also influenced by isostatic adjustment and topographic effect in many locations, hampering the interpretation of sea-level records [39].
Satellite altimetry provides homogeneous and accurate sea level measurements over the open ocean. Apart from data assimilation in the forecast system (e.g., [40]), these measurements have been used for many applications including the contribution of the MMSL seasonal cycle to the extreme water levels [41]. Altimetry observations are available around the world ocean, but the accuracy decreases in coastal zones by land and calm water contamination in the radar footprint and the bad characterisation of some of the range/geophysical corrections [42]. The use of radar altimetry to capture peaks of ETWLs during CFEEs can be limited by its low temporal resolution. Recent studies over Europe [43] show that if two or more satellites (multimission gridded products) are available, more than 90% of the ETWLs events might be captured.
The combination of low-frequency signals (the annual cycle of the sea level variation) with shorter timescale phenomena, such as surges or tides, can contribute to an increase in the ETWLs during CFEEs [44]. Thus, a better characterisation of the high/low-frequency signals can improve our knowledge of the flood risk in coastal areas [45,46]. The main aim of this work was to analyse the contribution of the seasonal cycle of the MMSL (derived from multimission radar altimetry) to the ETWLs during the period 1993–2016. We also analysed the high-frequency signals (surges and tides) contribution to the ETWLs. The combined effect of these signals might result in large flooding with associated impacts on coastal areas. This study focused on the comparison of ETWLs detected with satellite altimetry with a coastal extreme storm impact database at a pan-European scale. The paper is structured as follows; Section 2 describes the methodological approach and dataset used. Section 3 gives the obtained results in terms of ETWLs and its comparison with the storm impact database; in Section 4, the results are discussed and compared with previous studies. Finally, the main conclusions are summarised in Section 5.

2. Datasets and Methodology

2.1. Sea Level Datatasets

The altimeter dataset used was the GLOBAL OCEAN ALONG-TRACK L3 SEA SURFACE HEIGHTS REPROCESSED from CMEMS (Copernicus Marine Environment Monitoring Service) [47]. This product was derived by the DUACS (Data Unification and Altimeter Combination System) multimission altimeter data processing system [48] to provide a consistent, cross-calibrated and homogeneous data for all the altimeter missions: Topex-Poseidon; Topex-Poseidon (interleaved orbit); Jason-1; Jason-1 (interleaved orbit); Jason-1 (geodetic orbit); OSTM/Jason-2; OSTM/Jason-2 (interleaved); Jason-3; Sentinel-3A; ERS-1; ERS-2; Envisat; Envisat (extended phase); Geosat Follow On; CryoSat-2; SARAL; SARAL-DP; HY-2A; HY-2A (geodetic orbit).
The along-track product obtained from CMEMS was the reprocessed Sea Level Anomaly (SLA). Instead of using the fully 1 Hz posting rate (~7 km spatial resolution), we used the filtered and subsampled SLA included in the along-track products of CMEMS. It reduces the residual noise and small scale signals with a posting rate of 0.5 Hz (about 14 km distance between successive measurements), and temporal resolution ranging between 10 and 35 days depending on satellite mission (see [49] for more details). Along-track SLA (referenced to a mean sea surface), includes a set of corrections in order to reduce instrumental noise, range (ionospheric, dry and wet tropospheric effects, and sea state bias correction), and geophysical corrections (tides, inverse barometer and high frequency (<20 days) wind and pressure effects). The inverse barometer and high-frequency wind signal of the atmospheric forcing were removed through the so-called Dynamic Atmospheric Correction (DAC) produced by CLS (Collecte Localisation Satellites) using the Mog2D model [50]. The ocean tide was removed using the FES2014 model (including S1 and S2 components) [51].

2.2. Storm Impact Database

The CFEEs were analysed using the historic and recent coastal flooding extreme events along the European coastline. The database used integrates different systematic coastal flooding and coastal impact databases available at pan-European scale:
  • Pan-European HANZE database [8] from 1870 to 2016: 1564 flooding events were recorded including river floods and flash floods. A total of 77 events classified as coastal and compound events (river and coastal contributions to the floodings) were selected.
  • Coastal floodings in the United Kingdom [7] from 1915 to 2016: 329 events.
  • The RISC-KIT storm impact database for European coastlines [9] from 1806 to 2016: with 298 events.
Information on the impact (if available), location and time of 532 events were recorded in the analysed time period (1993–2016). The database contains records in specific locations and can include more than one event separated by time.
The geographical location of the events was normalised and referred to the European Union statistical regions NUTS3 (Nomenclature of Territorial Units for Statistics Level 3) version 2010.

2.3. Methods

We obtained the total water level (TWL) as the contribution of three components (Equation (1)):
TWL = MMSL + SSL + TIDE
where MMSL is monthly mean sea level; SSL includes the sea surface variations induced by the meteorological forcing. It includes the contribution of wind and pressure effect on the water level (the so-called surge); and TIDE is the contribution of astronomical tide. The study area focused on the pan-European area covering 32°W–42°E longitude, and 27–74°N latitude (Figure 1). The area of interest was divided in 1° × 1° tiles and time series were obtained by grouping the along-track SLA data inside each tile.
The events where TWL exceeds the 95th percentile of the TWL have been considered as the extreme total water levels (ETWLs).

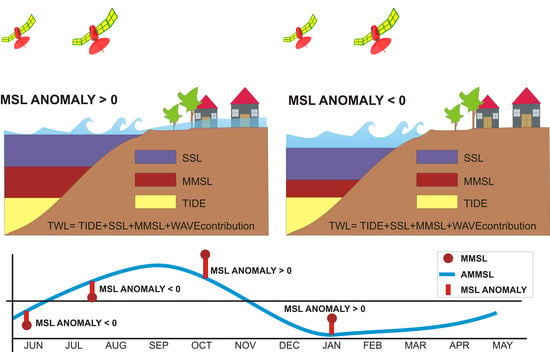
2.3.1. MMSL, AMMSL and MSL Anomalies

As mentioned, the study area was divided into regular grids of 1° × 1°. Then, monthly means were constructed with the along-track filtered SLA data inside the grids for the time period analysed; finally, the time series were linearly detrended to obtain the monthly Mean Sea Level (MMSL), which includes the steric and mass components. The MMSL was computed as the monthly mean for each year. The standard deviation (σ) of MMSL for each month representing the interannual variability was also obtained. The average monthly mean sea level (AMMSL), the so-called climatology or average annual cycle, was calculated as the interannual average of the monthly mean sea level for the whole period. Finally, the MSL anomalies (deviation in MSL respect to the mean annual cycle) were estimated subtracting the month value of the AMMSL time average (1993–2016) to the MMSL for the corresponding month following (Equation (2)):
MSL anomalies = MMSL − AMMSL

2.3.2. SSL

The meteorological component was computed following (Equation (3)):
SSL = SLADAC − MMSL
where SLADAC is the monthly mean of the SLA uncorrected by DAC; that is restoring the inverse barometer and high frequency (<20 days) wind and pressure effects removed during the product delivery. The DAC product is available at regular grids (0.5° × 0.5°), and 6 hours of temporal resolution. They were interpolated in time and space to match the altimeter dataset, and subtracted to the along-track SLA. Then, the monthly means were computed and the time series were also detrended (SLADAC).

2.3.3. TIDE

The ocean tide was calculated using the t_tide package [52] including nodal corrections, and using the amplitudes and phases of 30 tidal components of the FES2014 model (see [51] for further details). The amplitude and phase are provided in a regular grid of 0.0625° × 0.0625° and were interpolated in space to match the altimeter dataset.
The amplitude of the TWL is highly dependent on the phase lag between the surges and the tides. In addition to this, the co-occurrence of surges and spring tides might have a major impact on the floods hitting the coastal area. We analysed the relevance of AMMSL with respect to the neap-spring tidal range calculated from M2 and S2 tidal constituents ([M2-S2 M2+S2]). It is calculated according to Equation (4)
Relevance = 100 · AMMSL [ M 2 − S 2   M 2 + S 2 ]

2.3.4. Correlation of Seasonal MSL with Storm Impact Database

The relationship between the spatio-temporal pattern of MMSL, SSL and TIDE, and the areas affected by coastal flooding registered in the storm impact database was analysed along the European coastline. According to the methodology outlined in the previous section, the MMSL, SSL and TIDE contribution was calculated and assigned for each measurement in the altimetry dataset located in the 1° × 1° tiles closest to the coastline of each region avoiding measurements affected by land contamination.
Afterward, the linear correlation coefficient was calculated between the average monthly fraction of each component variance in ETWLs in the oceanographic region and the relative monthly frequency of the number of CFEEs registered in the storm impacts database at each oceanographic region. The variance of each component is expressed as a fraction of the ETWLs.
Similarly, it was calculated the correlation coefficient between AMMSL and monthly frequency of the storm impact registered on each region.
The relationship of MSL anomalies in the closest 1° × 1° and the storm event registered in the database was assessed through a t-test (alpha = 0.05) to evaluate the hypothesis that positive MSL anomalies are correlated with the storm event recorder. If the CFEEs and MSL anomalies are independent, mean value of MSL anomalies corresponding to the CFEEs should be zero, whereas a positive correlation will produce a mean value of MSL anomalies > 0.

3. Results

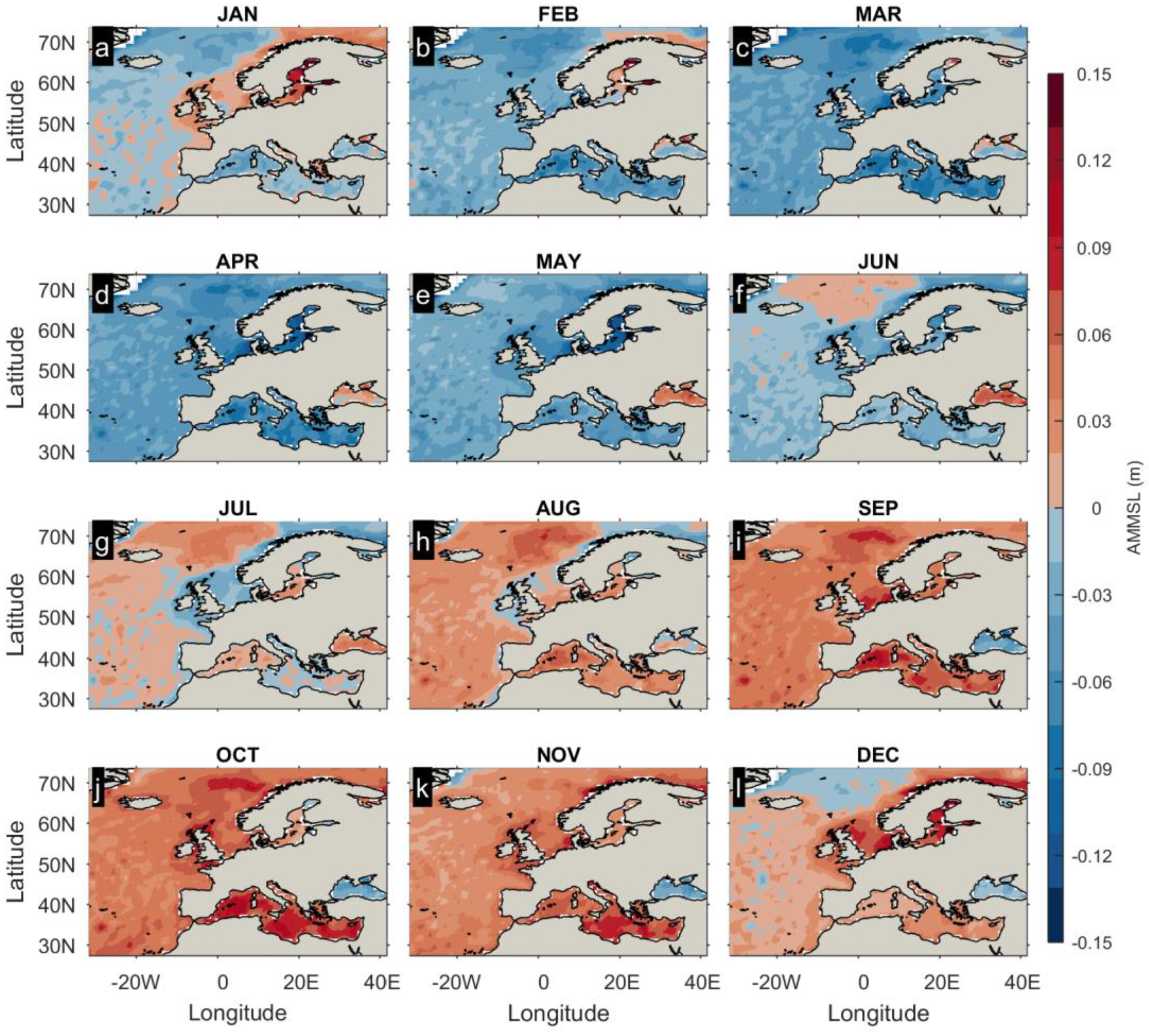
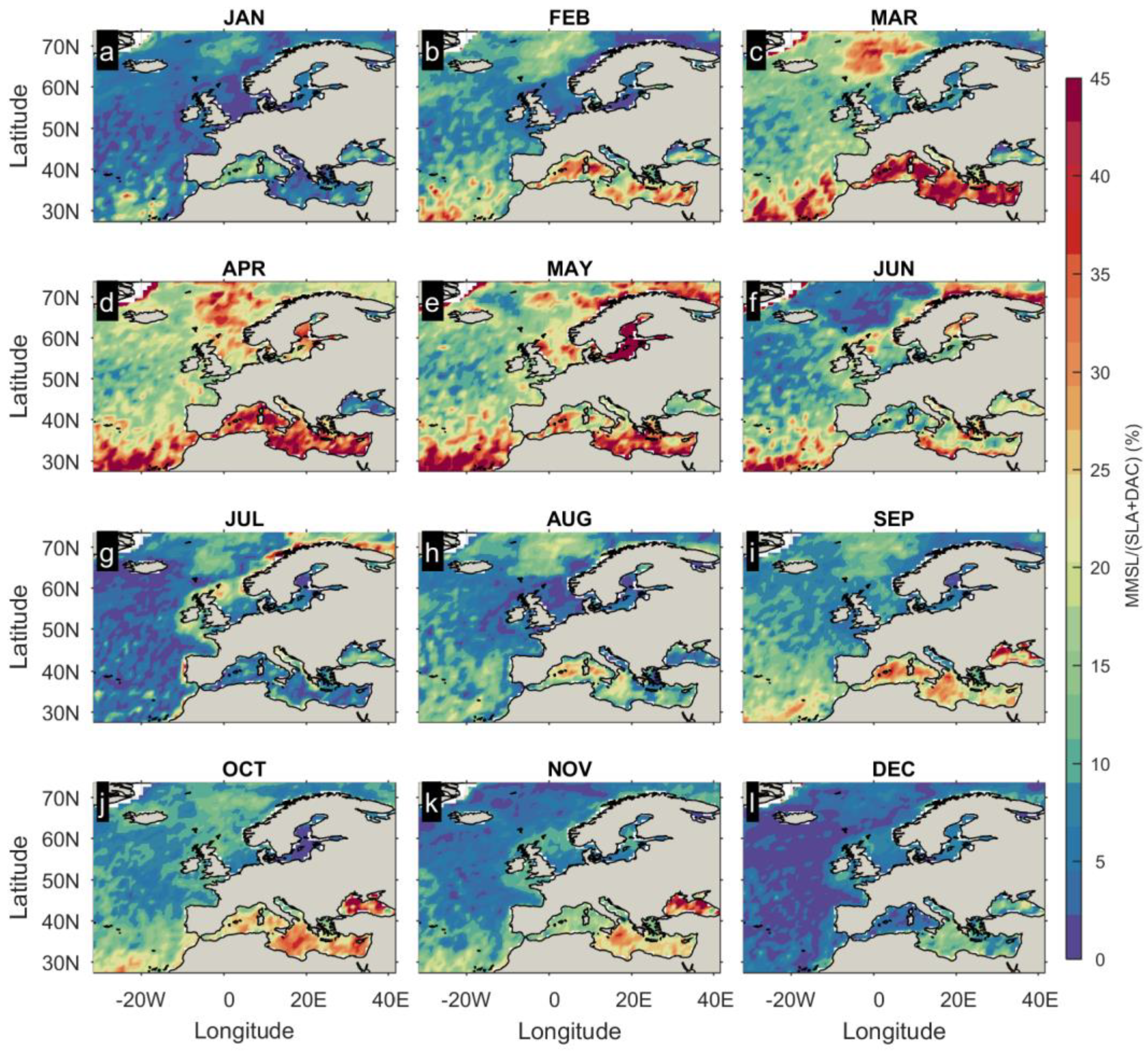
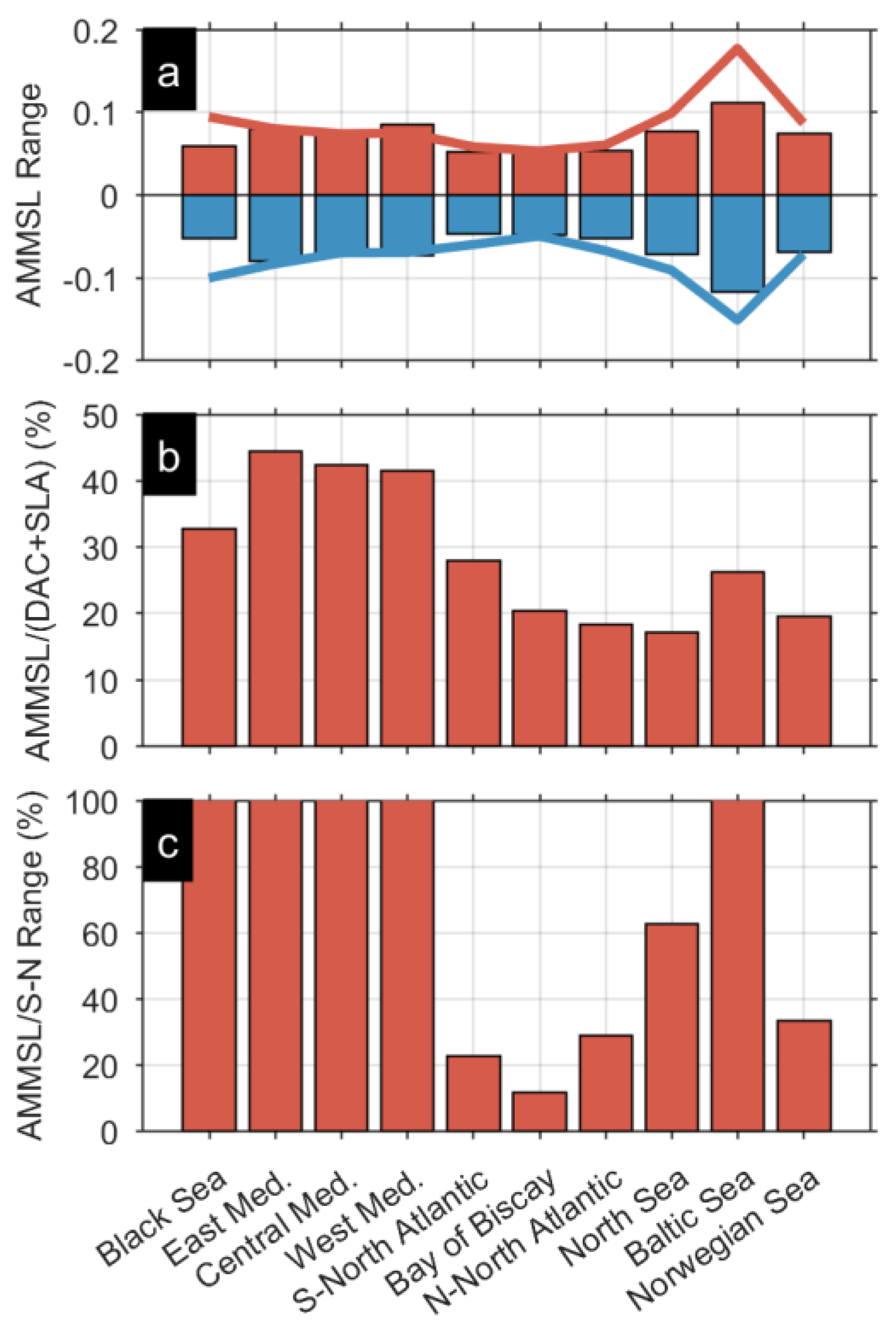
3.1. Characterization of the AMMSL and MMSL

The characterisation of AMMSL and MMSL was conducted using the full spatial coverage of the dataset in order to analyse the study area including deep ocean and areas closest to the European coast. The AMMSL is shown in Figure 2. The average annual cycle is not uniform in time and magnitude in the study area. The Mediterranean Sea and the Atlantic areas show minimum in late winter/early spring (−0.12 in the Mediterranean Sea and −0.05 m in the Atlantic) with the maximum of the annual cycle in late summer/early autumn (0.12 m in the Mediterranean and up to 0.07 m along the continental shelf in the N-North Atlantic). Some exceptions are observed in the coastal zones of the United Kingdom. The Bay of Biscay and the North Sea show a similar pattern with the minimum in spring and maximum of AMMSL in late summer/early autumn. In the North Sea, the North-Eastern coast and the German Bight present values > 0.10 m, where positive anomalies extend from September up to January. In the case of the Black Sea, the minimum/maximum (±0.10 m) is given in autumn/spring. Finally, the Baltic Sea shows the minimum/maximum (±0.12 m) in spring/autumn-early winter. Intensifications of positive AMMSL (>0.12 m) are observed in the gulfs of Bothnia and Finland during December and January. The Norwegian Sea is characterised by variations around ±0.06 m with minimum/maximum in late autumn/late spring, and intensification of positive AMMSL (0.08 m) in coastal areas.
Figure 3 illustrates the standard deviation (σ) of the annual cycle for the analysed period as an indicator of the interannual variability of the MMSL. The values are small (σ < 0.03 m) all around the year and oceanographic regions. Some exceptions with bigger standard deviations are observed in the Baltic, Black and North Seas, especially during autumn/winter seasons. In the North Sea, σ is > 0.15 m in the German Bight. The largest σ (up to >0.18 m in February) are in areas located in the head of the Gulf of Bothnia, Finland and the Eastern coast of the Baltic Sea. The deeper ocean of South/North Atlantic shows σ slightly larger (>0.04 m) with respect to the mean value.
The contribution of the AMMSL to the annual cycle obtained with the monthly maximum SLA uncorrected by meteorological forcing (SLADAC) was also analysed. We estimated the percentage of this contribution (Figure 4). The steric and mass components account for almost 45% of the uncorrected seasonal cycle in late autumn/spring in most of the oceanographic regions with the exception of the Black Sea, North Sea, Bay of Biscay and the deeper ocean of South/North Atlantic. Contributions of about 30–35% are observed in the Mediterranean Sea and Black Sea in late summer/autumn.
Regarding the relevance of the AMMSL with respect to the neap-spring tidal range calculated ([M2-S2 M2 + S2]), the results (not shown here) indicate that the AMMSL is more important than the neap-spring range in microtidal areas (Mediterranean Sea (excepting Central Med.), Black Sea and Baltic Sea). In mesotidal (S-North Atlantic and Norwegian Sea) and some macrotidal (Bay of Biscay, N-North Atlantic and Eastern coast of the North Sea) areas the contribution is smaller than 10%.
Figure 5 gives the characterisation by oceanographic region of the monthly AMMSL, its magnitude relative to SLADAC and to the range of neap-spring tide. The average range of the AMMSL during the annual cycle and its standard deviation are shown in Figure 5a. The largest seasonal range and variability was observed in the Baltic Sea (> ±0.10 m), followed by the Mediterranean Sea, and the Norwegian Sea. The weakest variation in the AMMSL was found in the Black Sea, S-North Atlantic, Bay of Biscay and N-North Atlantic. The weight of the AMMSL with respect to the non-tidal residual (SLADAC) (Figure 5b) is, on average, below 50% in all the oceanographic regions ranging from ~40% (Mediterranean Sea) to ~20% in the Bay of Biscay, N-North Atlantic, North Sea and Norwegian Sea. The average ratio of AMMSL and spring-neap range (Figure 5c) points out the major importance of AMMSL in microtidal areas: Black Sea, Mediterranean Sea and Baltic Sea. This ratio is still high in the North Sea (>60%) and below 10% in the Bay of Biscay.
The ETWLs are analysed in detail in the coastal area using a subset of the initial data. This subset covers only data contained in the closest 1° × 1° tile to the coast. Figure 6 shows the contribution in terms of the variance of the three components (MMSL, SSL and TIDE) to these extremes. For a more comprehensive visualization, the fraction of components’ variance was plotted as ternary plots: SSL is 100% in the bottom left vertex, MMSL is 100% in the upper vertex and TIDE is 100% in the bottom right; the opposite edge of each vertex gives 0% of the corresponding components’ fraction. In the Black Sea (Figure 6a), the main component in the ETWLs is the SSL, with the MMSL contribution ranging from 0 to 50%; the TIDE fraction is < 10%. The Mediterranean Sea (Figure 6b–d) shows the larger variability in the contribution of the components, particularly in the West Med. In the East Med. (Figure 6b), ETWLs are characterised by 10–40% of MMSL contribution, 60–90% for SSL, and a smaller relevance of TIDE (<20%). In the Central Med. (Figure 6c), which includes the Adriatic Sea, TIDE is the main component (70–90%), the MMSL contribution is limited to <15%, and SSL is below 30%. In West Med. (Figure 6d) the TIDE contribution ranges from 40 to 60%, MMSL and SSL around 10–30% in the case of the higher ETWLs (red dots), whereas intermediate ETWLs (orange dots) present a wider contribution of MMSL. S-North Atlantic (Figure 6e) is characterised by 70–80% (TIDE), 20–30% (SSL), and about 10% (MMSL). The Bay of Biscay (f) is the oceanographic region where MMSL shows the minor contribution (<5%), so the extreme values are most of the time a combination of SSL (0–20%), and TIDE (80–100%). In N-North Atlantic (Figure 6g) and North Sea (Figure 6h), the MMSL contribution to ETWLs is limited to <10% and <20% respectively. TIDE and SSL contribute to 20% and 80%, respectively in the N-North Atlantic. The North Sea shows scattered values for TIDE (20–95%) and SSL (0–80%) components. The Baltic Sea is the oceanographic region with the larger contribution of MMSL (20–50%), and minor contribution of SSL 50–80%. ETWLs in the Norwegian Sea are characterised by 80–95% (TIDE), 10–20% (SSL) and <10% (MMSL).

3.2. Correlation of AMMSL and MMSL with Storm Impact Database

The relationship between the spatial pattern of AMMSL and the areas affected by coastal floodings registered in the storm impact database is illustrated in Figure 7. The East Med., S-North Atlantic and Norwegian Sea do not have any records in the storm database. The only record in the Black Sea is on the west coast, with the CFEEs mainly registered from December to March (Figure 7a–c,l). The higher frequency of storms is recorded in February (AMMSL < 0.03 m). Central and West Med. are characterised by a peak occurrence of CFEEs during November and December in the Adriatic, Liguria and Catalonia coasts (Figure 7k,l) running into positive AMMSL ([0.03–0.09 m]). The S-North Atlantic is represented only by the southern coast of Portugal, where CFEEs are mainly registered on January-February (Figure 7a,b) during negative AMMSL ([−0.05–−0.03 m]). In the Bay of Biscay, the higher percentage of CFEEs occur during February-March, when the seasonal cycle shows negative AMMSL (−0.05 m). In the N-North Atlantic, most of the CFEEs take place from December to February (Figure 7a,b,l, respectively), corresponding to AMMSL around 0.07 m, 0.05 m and −0.03 m respectively. On the coast of the North Sea, the CFEEs occur mostly in January (Figure 7a) during positive AMMSL (0.07 m), except on the south-eastern English coast. In German Bight, a higher frequency of the CFEEs occur in December, when AMMSL peaks up to 0.11 m. In the Baltic Sea, most CFEEs are observed during January and December in the western coast (Figure 7a,l) running into positive monthly AMMSL (0.06 m). Likewise, the largest frequency in the Gulf of Finland occurs during January concurring with maximum AMMSL (>0.15 m).
The monthly average of the fraction of each component (SSL, TIDE and MMSL) variance in the ETWLs and the monthly frequency of the extreme events are illustrated in Figure 8. The correlation coefficient between each component and the relative monthly frequency of CFEEs is shown in Table 1. In the Black Sea and Baltic Sea, the main contributors to the ETWLs are SSL and MMSL. The CFEEs are observed from December to February coinciding with an important contribution of the MMSL (Figure 8a–i). The correlations are not significant in the Black Sea and significant (SSL and MMSL) in the Baltic Sea (Table 1). The contribution pattern of the three components is homogeneous in the Mediterranean (Figure 8b–d). Extreme events are observed from October to January (Central and West Med.). Correlations (Table 1) are significant for TIDE (Central and West Med) and MMSL (Central Med.). The remaining oceanographic areas show a major contribution of TIDE to the extremes. In the N-North Atlantic, North Sea and Norwegian Sea, the contribution of SSL is up to 30%. Significant correlations are observed in N-North Atlantic (SSL and TIDE), and North Sea (SSL, TIDE, and MMSL) (Table 1) where tidal contribution diminishes, increasing MMSL and SSL.
Figure 9 provides the temporal variability of the monthly AMMSL averaged along the coastline (closest 1° × 1° tile) over each oceanographic region; the relative monthly frequency of CFEEs registered at each region is also shown. Table 2 gives the correlation coefficient between them. According to the results, no significant correlations were found between the AMMSL in coastal areas and CFEEs.

3.3. Correlation of Monthly MSL Anomalies with Storm Impact Database

The potential impact on coastal flooding extreme events derived from changes in the MMSL with respect to the AMMSL, that is the monthly MSL anomalies, was analysed. Figure 10 shows the annual variation of MSL anomalies (ordinate axis) along the European coastline (abscissa axis). Each column represents the data corresponding to the closest 1° × 1° tile to the coast and its location along the coastline is indicated by the ISO country code to identify the coastal region. Each row represents a monthly MSL anomaly for the analysed period. The CFEEs registered in the database are presented as black dots according to the temporal and spatial location of the event. There is a clear correlation between the dates of the CFEEs and positive anomalies of the MSL with the exception of West Med. (Figure 10d) and N-North Atlantic (Figure 10g). This is confirmed by the fact that the frequency curve of MSL anomalies spatially averaged (black curves in Figure 10) and anomalies during CFEEs registered (red curves) are different in the upper tail, indicating a larger number of events during the largest positive anomalies. In the Black Sea (Figure 10a) there were six events with four/two of them during positive/negative MSL anomalies. Similarly, in the Central Med. (Figure 10c) the events that occurred during positive anomalies (51) are almost twice those registered during negative anomalies (32). MSL anomalies are especially large (>0.12 m) in the Adriatic (Central Med.) where there is a most exhaustive record of CFEEs. S-North Atlantic (Figure 10e) and Bay of Biscay (Figure 10e) are under-represented in the storm database, but the storms coincide in time with positive anomalies.
In N-North Atlantic (Figure 10g) larger anomalies than ±0.1 m are registered in the English Channel and Irish Sea, but the same number of CFEEs are observed under positive/negative anomalies (40). In the North Sea (Figure 10h) the CFEEs are registered on the west and southwestern coast (GBR and BEL) with lower MSL anomalies than in the German Bight (>0.15 m). The Baltic Sea (Figure 10i) shows strong anomalies (most of them >0.15 m) in the Gulfs of Bothnia and Finland, giving the clearest correlation of positive anomalies and CFEEs recorded in the database.
Table 3 summarises the role of MSL anomalies in each oceanographic region through the results of a t-test (alpha = 0.05). The mean value of MSL anomalies is >0 in Central Med., S-North Atlantic, North Sea and Baltic Sea, indicating a positive correlation (>95% of statistical significance). This positive correlation extends to the Bay of Biscay and N-North Atlantic with >90% of statistical significance.

4. Discussion

Recently, some studies based on tide gauges have analysed the ETWL component during extreme flooding events at the regional–local scale and its relative impact on coastal areas [53,54]. Our study, based on 24 years of satellite altimetry observations, focused on the contribution of the annual variation of MMSL to the ETWL, over the oceanographic regions around Europe. In some of these regions the annual cycle of the MMSL is markedly important as a driving contributor to the ETWLs.

4.1. Time–Space Variations of Seasonal MSL and Interannual Variability

In general, the AMMSL is in agreement with previous studies based on tide gauges and satellite altimeter data. The range of variation of the satellite-derived AMMSL is similar to the range observed by [55] in the Black Sea using tide gauge data, by [56] in the Mediterranean Sea (altimeter observations), and by [35] in the Gulf of Cadiz (tide gauges and altimeter data). We observe slightly larger values with respect to the observations made by [57] in the South and West coast of the Iberian peninsula (derived from tide gauges). The range and spatial pattern of amplification in the continental shelf in the Bay of Biscay are in line with the values reported by [58]. Further north, our results show the spatial pattern of the amplitude of the AMMSL annual cycle, increasing towards the northeastern coast in the German Bight in line with [59] (from altimeter observations).
The amplitude intensification observed from the Danish Straits to the head of the Gulfs of Finland and Bothnia was also noted by [60] using tidal gauge observations. This was also reported by [61] on the Polish coast. Finally, we found a good level of agreement between our results and those obtained by [62] in the Norwegian Sea.
The regional variations originate from different mechanisms. In the Black Sea, the AMMSL seasonal variations are dominated by freshwater balance [63]. In the Mediterranean Sea, the seasonal AMMSL is dominated by steric contribution being not negligible the mass induced by sea-level variation ([64]). The thermosteric effect is also dominant in the S-North Atlantic and South and West coast of the Iberian peninsula [35], Bay of Biscay and the N-North Atlantic. In the North Sea, the seasonal changes are mainly driven by wind, and the contribution of precipitation is not negligible during the autumn season [46]. The local steric contribution is smaller due to the shallow waters; however, long-term AMMSL variability could reflect the steric changes remotely forced [65]. In the Baltic Sea, the seasonal variation of AMMSL is primarily controlled by the direction of the prevailing wind and its role in the water exchange with the North Sea [60,66]. Moreover, seasonal variability is also influenced by river runoff and temperature [67,68].
The interannual variability of MMSL is stronger in the areas with larger amplitudes in the seasonal cycle (German Bight and Baltic Sea) (Figure 3). The variability in the North Sea is larger from December to March (Figure 3) as a result of the stronger atmospheric and meteorological forcing, as noted previously by [46]. The spatial pattern of the intensity of the MSL anomalies in coastal areas of N-North Atlantic and North Sea are in agreement with the results presented in [69]. In the Baltic Sea, the large interannual variation expands to most of the months (excluding July and August). This could be related to the domination of semi-annual variability during some periods [39]. In spite of the meteorological forcing, the sea ice cover (maximum in February and March) could contribute to the increase in interannual variability [66], along with river run-off, with maximum average and deviation values occurring from April to May [39].

4.2. Correlation of Monthly MSL Anomalies with Storm Impact Database

The assessment of the seasonal MMSL with respect to the monthly maximum SLADAC indicates a relevant contribution of MSL during winter and autumn, especially in semi-enclosed basins (Black Sea, Mediterranean Sea and Baltic Sea). Moreover, in those areas, the seasonal variation of AMMSL exceeds the neap-spring tidal range. Beyond these microtidal areas, the seasonal variation of AMMSL is also significant in the south and eastern coast of the North Sea. Those areas are characterised by the large contribution of the MMSL to the ETWLs in winter and particularly in autumn, during the seasonal peaks of MMSL. Indeed, the large correlation between the annual cycle of MMSL and the CFEEs is observed in Central Med., Baltic region and North Sea. The smaller correlation observed in the West Med. is linked to the earlier drops of MMSL after September. It is also relevant that the largest correlations between the CFEEs registered in the database and seasonally MMSL variations occur in areas with the largest interannual variability (Figure 7 and Figure 10), with the exception of the Central Med. In fact, the correlation of MSL anomalies and CFEEs extend to all regions with the exception of Black Sea and West Med. (Figure 10, Table 3), revealing the potential impact on flood risk derived from changes in the sea-level annual cycle as it was pointed out in previous works (e.g., [45,70]).
Some examples of the contribution of each component during extreme events recorded in the database and captured in the altimetry dataset are plotted in Figure 11. In the analysis, we used the closest satellite track in time and space to the location of the CFEEs. The stronger contribution of the MMSL to the ETWLs (similar in magnitude to the SSL) is observed in the Baltic Sea (Figure 11e), during the storm peak on 07-01-2005. This was also observed during storm Xaver in the North Sea and Halloween storm in the Adriatic Sea (Figure 11a,d respectively) but with a weaker MMSL contribution to the TWL peak. Similarly to the previous areas, the upper tail of the MMSL histogram indicates a higher probability of large contribution, in opposition to the histogram of MMSL in West Med and S-North Atlantic. In fact, the MMSL decreases up to 0.07 m in the West Med (Figure 11c,d) during the storm occurred on 16 December 1997 and drops in the S-North Atlantic event (Figure 11c) where the histogram reveals tidal component as the main contributor to the ETWLs.

4.3. Limitations and Future Research

According to the results, there is an important contribution of MMSL to the ETWLs. The contribution of MMSL to the ETWLs were calculated and correlated with the storm event impact database in terms of the annual cycle and MSL anomalies. The relative contribution of the MMSL to the extremes is strongly dependent on the concomitance between the storm peak in sea level and the availability of satellite altimeter data. During storms driven by atmospheric perturbations characterised by shorter temporal–spatial scales, the probability of altimeter data availability is reduced. Thus, the extreme events analysed in the Adriatic Sea West Med. (Figure 11a), and Baltic Sea (Figure 11e) underestimated the peak of ETWLs (see Table 4) because the satellite pass was not at the right time. This might be also observed in meso and macrotidal areas (i.e., North Sea) (Table 4) where ETWLs are controlled by tide and surge phase lag. The above-mentioned limitations could bias the final contribution of each component and overestimate the MMSL contribution which is well captured in the altimetry observation.
In addition to this, the availability of accurate altimetry data near the coast might be affected by land/calm water contamination, degraded range and geophysical corrections, producing inaccurate estimations of the sea level in coastal areas [71]. The screening rejects the closest data to the shore, but even though all the components analysed (SSL, TIDE and MMSL), are prone to suffer modifications by several processes (i.e., tide–surge interaction, river discharge, resonance) in the nearshore area changing the final absolute and relative contribution of each component to the TWLs in the coastal area. This limitation could be partially overcome using dedicated coastal altimetry datasets (e.g., X-TRACK, ALES) produced using specific processing techniques to get more accurate estimates of sea level in coastal areas [72,73].
Additionally, as a result of the altimetry limitation in the coastal zone, the wave contribution to the ETWLs is neglected in this study, even though it could be an important component (e.g., [74,75,76]). This fact could explain part of the differences noted in Table 4, and leads to the overestimation of the MMSL to the ETWLs.
The knowledge of past and present contributions of each individual component to the ETWLs could contribute by reducing the uncertainty of ETWLs forecast, improving the preparedness and reducing damage in the case of coastal flooding. Indeed, very often, large-scale models—especially those with a high resolution on the coast devoted to the ETWL prognosis (e.g., [80,81])—use a 2D barotropic approach neglecting steric effect and mass component sea level variation. The integration of MMSL anomalies from coastal altimetry data assimilation or prognosis through linear regression models (i.e., [69]) could improve the model performance. In light of the achieved results, this could be especially relevant in sensitive areas such as the Baltic Sea, North Sea, and Central Med.
Changes in the magnitude of ETWLs according to climate change scenarios were assessed considering stationary sea level rise (i.e., [82]) omitting the seasonal cycle or monthly MSL anomalies. However, changes in phase and amplitude of the annual cycle or monthly MSL anomalies driven by changes in atmospheric and/or hydrological patterns could modify the extreme water-level projections. Therefore, including seasonality variations of MMSL would contribute by reducing the uncertainty in ETWLs projections improving the rationality of the coastal adaptation measures.

5. Summary and Conclusions

This paper investigates the role of the main sea level components (TIDE, SSL and MMSL) in regard to the ETWL observations along the European seas. Based on 24 years of satellite altimetry, this study evaluates their relative contribution, as well as the correlation of the annual variation of MMSL and MSL anomalies with the extreme events registered in a coastal flooding database along the European coastline.
The largest seasonal range of the AMMSL is observed in the Baltic Sea (±0.11 m), West Med. ([−0.07, 0.09 m]), and the North Sea ([−0.07, 0.08 m]). The smaller MMSL variations are in the Atlantic and Bay of Biscay ([−0.05, 0.06m]). The interannual variability of the MMSL is stronger in the Baltic Sea, Black Sea, North Sea, and Norwegian Sea. The contribution of each component to the ETWLs is subject to important seasonal variations. In microtidal areas (Black Sea, Baltic and Mediterranean Sea) the MMSL contribution is larger than the TIDE most of the time, and its contribution can be at the same order of magnitude of the SSL. In meso and macrotidal areas, the MMSL contribution is <20%, but slightly larger (>30%) in the North Sea.
The comparative analysis of the altimetry data and the storm impact database indicates a non-significant correlation between the AMMSL and the monthly frequency of the CFEEs, since the maximum values of the average annual cycle mostly run on September-October along the European coastline when the low-pressure systems driving SSL are less frequent and intense. However, the average monthly fraction of component variance of MMSL presents significant values of positive correlation with the relative frequency of CFEEs in the Central Med (r = 0.59), North Sea (r = 0.60) and Baltic Sea (r = 0.75). The positive MSL anomalies are correlated with the CFEEs recorded in the database at >90% of the statistical significance in the aforementioned areas, as well as in the Bay of Biscay and N-North Atlantic.
The present contribution demonstrated that there is not a link between the AMMSL and CFEEs along the European coastline. This is caused by the antiphase of the SSL and the AMMSL in most of the oceanographic regions. However, the relationship of MSL anomalies and flooding extreme events indicates a significant and positive correlation between them along the coastline of the Central Med., S-North Atlantic, North Sea and Baltic Sea. In most of these regions, the positive correlation is observed in most of the low-lying areas prone to be flooded. In general, these regions show the largest interannual variability where MSL anomalies are mainly driven by atmospheric and meteorological forcing (North Sea), prevailing wind and the water exchange with another catchment (Baltic Sea, Adriatic Sea). Therefore, the role of MMSL should be considered either for the comprehensive analysis of the past extreme event, or future projection of coastal flooding extreme event.
Satellite altimeter observations provide a valuable and consistent sea-level dataset to analyse the contribution of TIDE, SSL and MMSL to the ETWLs. However, the accuracy of altimeter data close to the coast might be limited. The wave contribution to the ETWLs and the use of accurate sea-level data in the coastal fringe must be taken into consideration in future works. The understanding of every single component of the ETWLs and its spatial and temporal patterns shall improve the preparedness and coastal adaptation measures to reduce the impact of coastal flooding.

Author Contributions

Conceptualization, T.F.-M., J.G.-E., and P.C.; Data curation, T.F.-M.; Formal analysis, T.F.-M.; Funding acquisition, P.C.; Investigation, T.F.-M.; Methodology, T.F.-M. and J.G.-E.; Supervision, J.G.-E. and P.C.; Visualization, T.F.-M., and J.G.-E.; Writing–original draft, T.F.-M.; Writing–review & editing, T.F.-M., J.G.-E., P.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by EU from the EU-H2020 program under grant agreement number 700099 (ANYWHERE: EnhANcing emergency management and response to extreme WeatHER and climate Events). This work was partially funded by the Spanish Project: Circulation and transport processes in the estuaries of the Gulf of Cadiz: Current situation and projections of future climate change scenarios (TRUCO) (Ref.: RTI2018-100865-B-C22), and by the Coastal Environmental Observatory of the Southwest (OCASO)-Interreg POCTEC EU Project.

Acknowledgments

We thank LEGOS (Laboratoire d’Ètudes en Géophysique et Océanographie Spatiales), and Aviso+ by the DAC data distribution with support from CNES (Centre National D’Etudes Spatiales) (https://www.aviso.altimetry.fr/).

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Tessler, Z.D.; Vörösmarty, C.J.; Grossberg, M.; Gladkova, I.; Aizenman, H.; Syvitski, J.P.M.; Foufoula-Georgiou, E. Profiling risk and sustainability in coastal deltas of the world. Science 2015, 349, 638–643. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Antonellini, M.; Giambastiani, B.M.S.; Greggio, N.; Bonzi, L.; Calabrese, L.; Luciani, P.; Perini, L.; Severi, P. Processes governing natural land subsidence in the shallow coastal aquifer of the Ravenna coast, Italy. Catena 2019, 172, 76–86. [Google Scholar] [CrossRef]
  3. Taramelli, A.; Di Matteo, L.; Ciavola, P.; Guadagnano, F.; Tolomei, C. Temporal evolution of patterns and processes related to subsidence of the coastal area surrounding the Bevano River mouth (Northern Adriatic)—Italy. Ocean Coast. Manag. 2015, 108, 74–88. [Google Scholar] [CrossRef]
  4. Haigh, I.D.; Wadey, M.P.; Wahl, T.; Ozsoy, O.; Nicholls, R.J.; Brown, J.M.; Horsburgh, K.; Gouldby, B. Spatial and temporal analysis of extreme sea level and storm surge events around the coastline of the UK. Sci. Data 2016, 3, 160107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  5. Nicholls, R.J.; Cazenave, A. Sea-level rise and its impact on coastal zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef]
  6. Collet, I.; Engelbert, A. Archive: Coastal Regions—Population Statistics—Statistics Explained. 2013. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Archive:Coastal_regions_-_population_statistics (accessed on 21 February 2019).
  7. Haigh, I.D.; Ozsoy, O.; Wadey, M.P.; Nicholls, R.J.; Gallop, S.L.; Wahl, T.; Brown, J.M. An improved database of coastal flooding in the United Kingdom from 1915 to 2016. Sci. Data 2017, 4. [Google Scholar] [CrossRef] [Green Version]
  8. Paprotny, D.; Morales-Nápoles, O.; Jonkman, S.N. HANZE: A pan-European database of exposure to natural hazards and damaging historical floods since 1870. Earth Syst. Sci. Data 2018, 10, 565–581. [Google Scholar] [CrossRef] [Green Version]
  9. Ciavola, P.; Harley, M.D.; den Heijer, C. The RISC-KIT storm impact database: A new tool in support of DRR. Coast. Eng. 2018, 134, 24–32. [Google Scholar] [CrossRef]
  10. Lamb, H.; Frydendahl, K. Historic Storms of the North. Sea, British Isles and Northwest Europe; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
  11. Bertin, X.; Li, K.; Roland, A.; Zhang, Y.J.; François Breilh, J.; Chaumillon, E. A modeling-based analysis of the flooding associated with Xynthia, central Bay of Biscay. Coast. Eng. 2014, 94, 80–89. [Google Scholar] [CrossRef]
  12. Garnier, E.; Ciavola, P.; Spencer, T.; Ferreira, O.; Armaroli, C.; McIvor, A. Historical analysis of storm events: Case studies in France, England, Portugal and Italy. Coast. Eng. 2018, 134, 10–23. [Google Scholar] [CrossRef] [Green Version]
  13. Paprotny, D.; Sebastian, A.; Morales-Nápoles, O.; Jonkman, S.N. Trends in flood losses in Europe over the past 150 years. Nat. Commun. 2018. [Google Scholar] [CrossRef] [PubMed]
  14. Wadey, M.P.; Haigh, I.D.; Nicholls, R.J.; Brown, J.M.; Horsburgh, K.; Carroll, B.; Gallop, S.L.; Mason, T.; Bradshaw, E. A comparison of the 31 January–1 February 1953 and 5–6 December 2013 coastal flood events around the UK. Front. Mar. Sci. 2015, 2. [Google Scholar] [CrossRef] [Green Version]
  15. Jevrejeva, S.; Jackson, L.P.; Riva, R.E.M.; Grinsted, A.; Moore, J.C. Coastal sea level rise with warming above 2 °C. Proc. Natl. Acad. Sci. USA 2016, 113, 13342–13347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  16. Howard, T.; Palmer, M.D.; Bricheno, L.M. Contributions to 21st century projections of extreme sea-level change around the UK. Environ. Res. Commun. 2019, 1, 095002. [Google Scholar] [CrossRef]
  17. Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Feyen, L. Extreme sea levels on the rise along Europe’s coasts. Earth’s Future 2017, 5, 304–323. [Google Scholar] [CrossRef]
  18. Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Bianchi, A.; Dottori, F.; Feyen, L. Climatic and socioeconomic controls of future coastal flood risk in Europe. Nat. Clim. Chang. 2018, 8, 776–780. [Google Scholar] [CrossRef]
  19. Wankang, Y.; Baoshu, Y.; Xingru, F.; Dezhou, Y.; Guandong, G.; Haiying, C. The effect of nonlinear factors on tide-surge interaction: A case study of Typhoon Rammasun in Tieshan Bay, China. Estuar. Coast. Shelf Sci. 2019, 219, 420–428. [Google Scholar] [CrossRef]
  20. Horsburgh, K.J.; Wilson, C. Tide-surge interaction and its role in the distribution of surge residuals in the North Sea C8—C08003. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
  21. Dietrich, J.C.; Bunya, S.; Westerink, J.J.; Ebersole, B.A.; Smith, J.M.; Atkinson, J.H.; Jensen, R.; Resio, D.T.; Luettich, R.A.; Dawson, C.; et al. A High-Resolution Coupled Riverine Flow, Tide, Wind, Wind Wave, and Storm Surge Model for Southern Louisiana and Mississippi. Part II: Synoptic Description and Analysis of Hurricanes Katrina and Rita. Mon. Weather Rev. 2010, 138, 378–404. [Google Scholar] [CrossRef] [Green Version]
  22. Bertin, X.; Bruneau, N.; Breilh, J.-F.; Fortunato, A.B.; Karpytchev, M. Importance of wave age and resonance in storm surges: The case Xynthia, Bay of Biscay. Ocean. Model. 2012, 42, 16–30. [Google Scholar] [CrossRef]
  23. Bevacqua, E.; Maraun, D.; Vousdoukas, M.I.; Voukouvalas, E.; Vrac, M.; Mentaschi, L.; Widmann, M. Higher potential compound flood risk in Northern Europe under anthropogenic climate change. Sci. Adv. 2019, 9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Paprotny, D.; Vousdoukas, M.I.; Morales-Nápoles, O.; Jonkman, S.N.; Feyen, L. Pan-European hydrodynamic models and their ability to identify compound floods. Nat. Hazards. 2020, 101, 933–957. [Google Scholar] [CrossRef] [Green Version]
  25. Vinogradov, S.V.; Ponte, R.M.; Heimbach, P.; Wunsch, C. The mean seasonal cycle in sea level estimated from a data-constrained general circulation model. J. Geophys. Res. 2008, 113, C03032. [Google Scholar] [CrossRef]
  26. Jordà, G.; Gomis, D. On the interpretation of the steric and mass components of sea level variability: The case of the Mediterranean basin. J. Geophys. Res. Ocean. 2013, 118, 953–963. [Google Scholar] [CrossRef] [Green Version]
  27. Wu, Q.; Zhang, X.; Church, J.A.; Hu, J. Variability and change of sea level and its components in the Indo-Pacific region during the altimetry era. J. Geophys. Res. Ocean. 2017, 122, 1862–1881. [Google Scholar] [CrossRef]
  28. Kleinherenbrink, M.; Riva, R.; Frederikse, T.; Merrifield, M.; Wada, Y. Trends and interannual variability of mass and steric sea level in the Tropical Asian Seas. J. Geophys. Res. Ocean. 2017, 122, 6254–6276. [Google Scholar] [CrossRef]
  29. Tsimplis, M.N.; Woodworth, P.L. The global distribution of the seasonal sea level cycle calculated from coastal tide gauge data. J. Geophys. Res. 1994, 99, 16031–16039. [Google Scholar] [CrossRef]
  30. Woodworth, P.L.; Melet, A.; Marcos, M.; Ray, R.D.; Wöppelmann, G.; Sasaki, Y.N.; Cirano, M.; Hibbert, A.; Huthnance, J.M.; Monserrat, S.; et al. Forcing Factors Affecting Sea Level Changes at the Coast. Surv. Geophys. 2019, 40, 1351–1397. [Google Scholar] [CrossRef] [Green Version]
  31. Gómez-Enri, J.; Aboitiz, A.; Tejedor, B.; Villares, P. Seasonal and interannual variability in the Gulf of Cadiz: Validation of gridded altimeter products. Estuar. Coast. Shelf Sci. 2012, 96, 114–121. [Google Scholar] [CrossRef]
  32. Laiz, I.; Ferrer, L.; Plomaritis, T.A.; Charria, G. Effect of river runoff on sea level from in-situ measurements and numerical models in the Bay of Biscay. Deep. Res. Part. II Top. Stud. Oceanogr. 2014, 106, 49–67. [Google Scholar] [CrossRef] [Green Version]
  33. Laiz, I.; Gómez-Enri, J.; Tejedor, B.; Aboitiz, A.; Villares, P. Seasonal sea level variations in the Gulf of Cadiz continental shelf from in-situ measurements and satellite altimetry. Cont. Shelf Res. 2013, 53, 77–88. [Google Scholar] [CrossRef]
  34. Antonov, J.I.; Levitus, S.; Boyer, T.P. Steric sea level variations during 1957-1994: Importance of salinity. J. Geophys. Res. C Ocean. 2002, 107. [Google Scholar] [CrossRef]
  35. Laiz, I.; Tejedor, B.; Gómez-Enri, J.; Aboitiz, A.; Villares, P. Contributions to the sea level seasonal cycle within the Gulf of Cadiz (Southwestern Iberian Peninsula). J. Mar. Syst. 2016, 159, 55–66. [Google Scholar] [CrossRef]
  36. Ceres, R.L.; Forest, C.E.; Keller, K. Understanding the detectability of potential changes to the 100-year peak storm surge. Clim. Chang. 2017, 145, 221–235. [Google Scholar] [CrossRef]
  37. Menéndez, M.; Woodworth, P.L. Changes in extreme high water levels based on a quasi-global tide-gauge data set. J. Geophys. Res. Ocean. 2010, 115, C10011. [Google Scholar] [CrossRef] [Green Version]
  38. Cid, A.; Castanedo, S.; Abascal, A.J.; Menéndez, M.; Medina, R. A high resolution hindcast of the meteorological sea level component for Southern Europe: The GOS dataset. Clim. Dyn. 2014, 43, 2167–2184. [Google Scholar] [CrossRef]
  39. Stramska, M.; Kowalewska-Kalkowska, H.; Świrgoń, M. Seasonal variability in the Baltic Sea level. Oceanologia 2013, 55, 787–807. [Google Scholar] [CrossRef]
  40. De Biasio, F.; Bajo, M.; Vignudelli, S.; Umgiesser, G.; Zecchetto, S. ESA DUE eSurge-Venice project. Eur. J. Remote Sens. 2017, 50, 428–441. [Google Scholar] [CrossRef] [Green Version]
  41. Woodworth, P.L.; Menéndez, M. Changes in the mesoscale variability and in extreme sea levels over two decades as observed by satellite altimetry. J. Geophys. Res. Ocean. 2015, 120, 64–77. [Google Scholar] [CrossRef] [Green Version]
  42. Cipollini, P.; Calafat, F.M.; Jevrejeva, S.; Melet, A.; Prandi, P. Monitoring Sea Level in the Coastal Zone with Satellite Altimetry and Tide Gauges. Surv. Geophys. 2017, 38, 33–57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  43. Andersen, O.B.; Cheng, Y.; Deng, X.; Steward, M.; Gharineiat, Z. Using satellite altimetry and tide gauges for storm surge warning. In IAHS-AISH Proceedings and Reports; Copernicus GmbH: Göttingen, Germany, 2014; Volume 365, pp. 28–34. [Google Scholar]
  44. Passaro, M.; Cipollini, P.; Benveniste, J. Annual sea level variability of the coastal ocean: The Baltic Sea-North Sea transition zone. J. Geophys. Res. Ocean. 2015, 120, 3061–3078. [Google Scholar] [CrossRef] [Green Version]
  45. Calafat, F.M.; Wahl, T.; Lindsten, F.; Williams, J.; Frajka-Williams, E. Coherent modulation of the sea-level annual cycle in the United States by Atlantic Rossby waves. Nat. Commun. 2018, 9, 1–13. [Google Scholar] [CrossRef] [Green Version]
  46. Dangendorf, S.; Wahl, T.; Mudersbach, C.; Jensen, J. The Seasonal Mean Sea Level Cycle in the Southeastern North Sea. J. Coast. Res. 2013, 165, 1915–1920. [Google Scholar] [CrossRef]
  47. Copernicus—Marine Environment Monitoring Service. Available online: https://marine.copernicus.eu/ (accessed on 1 October 2018).
  48. Duacs | Altimetry Data for Sea Level Studies & Applications. Available online: https://duacs.cls.fr/ (accessed on 13 January 2018).
  49. CMEMS. QUID forSea Level TAC DUACS Products; Available online: https://resources.marine.copernicus.eu/documents/QUID/CMEMS-SL-QUID-008-032-051.pdf (accessed on 21 February 2019).
  50. Carrère, L.; Lyard, F. Modeling the barotropic response of the global ocean to atmospheric wind and pressure forcing—Comparisons with observations. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef] [Green Version]
  51. Carrere, L.; Lyard, F.; Cancet, M.; Guillot, A.; Dupuy, S.; Carrère, L.F.; Lyard, M.; Cancet, A.; Guillot, N. Picot, 2015: FES2014: A New Tidal Model Onthe Global Ocean with Enhanced Accuracy in Shallow Seas and in the Arctic Region, OSTST2015. 2014. Available online: http://meetings.aviso.altimetry.fr/fileadmin/user_upload/tx_ausyclssemi (accessed on 1 January 2019).
  52. Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
  53. Dangendorf, S.; Arns, A.; Pinto, J.G.; Ludwig, P.; Jensen, J. The exceptional influence of storm ‘Xaver’ on design water levels in the German Bight. Environ. Res. Lett. 2016, 11, 054001. [Google Scholar] [CrossRef]
  54. Serafin, K.A.; Ruggiero, P.; Stockdon, H.F. The relative contribution of waves, tides, and nontidal residuals to extreme total water levels on U.S. West Coast sandy beaches. Geophys. Res. Lett. 2017, 44, 1839–1847. [Google Scholar] [CrossRef]
  55. Avsar, N.B.; Jin, S.; Kutoglu, H.; Gurbuz, G. Sea level change along the Black Sea coast from satellite altimetry, tide gauge and GPS observations. Geod. Geodyn. 2016, 7, 50–55. [Google Scholar] [CrossRef] [Green Version]
  56. Criado-Aldeanueva, F.; Del Río Vera, J.; García-Lafuente, J. Steric and mass-induced Mediterranean sea level trends from 14 years of altimetry data. Glob. Planet. Chang. 2008, 60, 563–575. [Google Scholar] [CrossRef]
  57. Marcos, M.; Tsimplis, M.N. Forcing of coastal sea level rise patterns in the North Atlantic and the Mediterranean Sea. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
  58. Legeais, J.F.; Ablain, M.; Zawadzki, L.; Zuo, H.; Johannessen, J.A.; Scharffenberg, M.G.; Fenoglio-Marc, L.; Joana Fernandes, M.; Baltazar Andersen, O.; Rudenko, S.; et al. An improved and homogeneous altimeter sea level record from the ESA Climate Change Initiative. Earth Syst. Sci. Data 2018, 10, 281–301. [Google Scholar] [CrossRef] [Green Version]
  59. Ruiz Etcheverry, L.A.; Saraceno, M.; Piola, A.R.; Valladeau, G.; Möller, O.O. A comparison of the annual cycle of sea level in coastal areas from gridded satellite altimetry and tide gauges. Cont. Shelf Res. 2015, 92, 87–97. [Google Scholar] [CrossRef]
  60. Medvedev, I.P. Seasonal fluctuations of the Baltic Sea level. Russ. Meteorol. Hydrol. 2014, 39, 814–822. [Google Scholar] [CrossRef]
  61. Pajak, K.; Kowalczyk, K. A comparison of seasonal variations of sea level in the southern Baltic Sea from altimetry and tide gauge data. Adv. Sp. Res. 2019, 63, 1768–1780. [Google Scholar] [CrossRef]
  62. Mork, K.A.; Skagseth, Ø. Annual Sea Surface Height Variability in the Nordic Seas. In The Nordic Seas: An Integrated Perspective: Oceanography, Climatology, Biogeochemistry, and Modeling; American Geophysical Union: Washintong, DC, USA, 2005; pp. 51–64. [Google Scholar]
  63. Stanev, E.V.; Le Traon, P.-Y.; Peneva, E.L. Sea level variations and their dependency on meteorological and hydrological forcing: Analysis of altimeter and surface data for the Black Sea. J. Geophys. Res. Ocean. 2000, 105, 17203–17216. [Google Scholar] [CrossRef] [Green Version]
  64. García-García, D.; Chao, B.F.; Boy, J.P. Steric and mass-induced sea level variations in the Mediterranean Sea revisited. J. Geophys. Res. Ocean. 2010, 115, C12016. [Google Scholar] [CrossRef] [Green Version]
  65. Dangendorf, S.; Calafat, F.M.; Arns, A.; Wahl, T.; Haigh, I.D.; Jensen, J. Mean sea level variability in the North Sea: Processes and implications. J. Geophys. Res. Ocean. 2014, 119, 6820–6841. [Google Scholar] [CrossRef] [Green Version]
  66. Barbosa, S.M.; Donner, R.V. Long-term changes in the seasonality of Baltic sea level. Tellus A Dyn. Meteorol. Oceanogr. 2016, 68, 30540. [Google Scholar] [CrossRef]
  67. Hünicke, B.; Zorita, E. Influence of temperature and precipitation on decadal Baltic Sea level variations in the 20th century. Tellus, Ser. A Dyn. Meteorol. Oceanogr. 2006, 58, 141–153. [Google Scholar] [CrossRef] [Green Version]
  68. Lisitzin, E. Sea Level Changes; Elsevier Oceanography Series: Amsterdam, The Netherlands, 1974; ISBN 0444411577. [Google Scholar]
  69. Sterlini, P.; de Vries, H.; Katsman, C. Sea surface height variability in the North East Atlantic from satellite altimetry. Clim. Dyn. 2016, 47, 1285–1302. [Google Scholar] [CrossRef] [Green Version]
  70. Dangendorf, S.; Wahl, T.; Hein, H.; Jensen, J.; Mai, S.; Mudersbach, C. Mean Sea Level Variability and Influence of the North Atlantic Oscillation on Long-Term Trends in the German Bight. Water 2012, 4, 170–195. [Google Scholar] [CrossRef]
  71. Benveniste, J.; Cazenave, A.; Vignudelli, S.; Fenoglio-Marc, L.; Shah, R.; Almar, R.; Andersen, O.B.; Birol, F.; Bonnefond, P.; Bouffard, J.; et al. Requirements for a coastal hazards observing system. Front. Mar. Sci. 2019. [Google Scholar] [CrossRef] [Green Version]
  72. Passaro, M.; Rose, S.K.; Andersen, O.B.; Boergens, E.; Calafat, F.M.; Dettmering, D.; Benveniste, J. ALES+: Adapting a homogenous ocean retracker for satellite altimetry to sea ice leads, coastal and inland waters. Remote Sens. Environ. 2018, 211, 456–471. [Google Scholar] [CrossRef] [Green Version]
  73. Birol, F.; Fuller, N.; Lyard, F.; Cancet, M.; Niño, F.; Delebecque, C.; Fleury, S.; Toublanc, F.; Melet, A.; Saraceno, M.; et al. Coastal applications from nadir altimetry: Example of the X-TRACK regional products. Adv. Sp. Res. 2017, 59, 936–953. [Google Scholar] [CrossRef]
  74. Marcos, M.; Rohmer, J.; Vousdoukas, M.I.; Mentaschi, L.; Le Cozannet, G.; Amores, A. Increased Extreme Coastal Water Levels Due to the Combined Action of Storm Surges and Wind Waves. Geophys. Res. Lett. 2019, 46, 4356–4364. [Google Scholar] [CrossRef] [Green Version]
  75. Melet, A.; Meyssignac, B.; Almar, R.; Le Cozannet, G. Under-estimated wave contribution to coastal sea-level rise. Nat. Clim. Chang. 2018, 8, 234–239. [Google Scholar] [CrossRef]
  76. Serafin, K.A.; Ruggiero, P. Simulating extreme total water levels using a time-dependent, extreme value approach. J. Geophys. Res. C Ocean. 2014, 119, 6305–6329. [Google Scholar] [CrossRef] [Green Version]
  77. Harley, M.D.; Valentini, A.; Armaroli, C.; Perini, L.; Calabrese, L.; Ciavola, P. Can an early-warning system help minimize the impacts of coastal storms? A case study of the 2012 Halloween storm, northern Italy. Nat. Hazards Earth Syst. Sci. 2016, 16, 209–222. [Google Scholar] [CrossRef] [Green Version]
  78. RiscKit Storm Database. Available online: http://risckit.cloudapp.net/risckit/#/ (accessed on 16 November 2019).
  79. Wolski, T.; Wiśniewski, B.; Giza, A.; Kowalewska-Kalkowska, H.; Boman, H.; Grabbi-Kaiv, S.; Hammarklint, T.; Holfort, J.; Lydeikaite, Z. Extreme sea levels at selected stations on the Baltic Sea coast. Oceanologia 2014, 2, 259–290. [Google Scholar] [CrossRef] [Green Version]
  80. Fernández-Montblanc, T.; Vousdoukas, M.I.; Ciavola, P.; Voukouvalas, E.; Mentaschi, L.; Breyiannis, G.; Feyen, L.; Salamon, P. Towards robust pan-European storm surge forecasting. Ocean Model. 2019, 133, 129–144. [Google Scholar] [CrossRef]
  81. Muis, S.; Verlaan, M.; Winsemius, H.C.; Aerts, J.C.J.H.; Ward, P.J. A global reanalysis of storm surges and extreme sea levels. Nat. Commun. 2016, 7, 11969. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  82. Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Jevrejeva, S.; Jackson, L.P.; Feyen, L. Global probabilistic projections of extreme sea levels show intensification of coastal flood hazard. Nat. Commun. 2018, 9, 2360. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Remotesensing 12 03419 g001 550
Figure 1. Study area with the 10 oceanographic regions defined for the analysis. The colour scale indicates the number of altimetry observations in each 1° × 1° latitude and longitude cell for the period: 1993–2016.
Figure 1. Study area with the 10 oceanographic regions defined for the analysis. The colour scale indicates the number of altimetry observations in each 1° × 1° latitude and longitude cell for the period: 1993–2016.
Remotesensing 12 03419 g001
Remotesensing 12 03419 g002 550
Figure 2. Seasonality of the annual cycle ((a–l) January–December) of the average monthly mean sea level (AMMSL) in the study area from 1993 to 2016. Warm/cold colour indicates positive/negative values.
Figure 2. Seasonality of the annual cycle ((a–l) January–December) of the average monthly mean sea level (AMMSL) in the study area from 1993 to 2016. Warm/cold colour indicates positive/negative values.
Remotesensing 12 03419 g002
Remotesensing 12 03419 g003 550
Figure 3. Seasonality of the standard deviation (σ) of monthly mean sea level (MMSL) ((a–l) January–December).
Figure 3. Seasonality of the standard deviation (σ) of monthly mean sea level (MMSL) ((a–l) January–December).
Remotesensing 12 03419 g003
Remotesensing 12 03419 g004 550
Figure 4. Seasonality of the annual contribution of the seasonal cycle of the MSL to the uncorrected monthly maximum MSL (Sea Level Anomaly (SLA) + Dynamic Atmospheric Correction (DAC)) ((a–l) January–December).
Figure 4. Seasonality of the annual contribution of the seasonal cycle of the MSL to the uncorrected monthly maximum MSL (Sea Level Anomaly (SLA) + Dynamic Atmospheric Correction (DAC)) ((a–l) January–December).
Remotesensing 12 03419 g004
Remotesensing 12 03419 g005 550
Figure 5. (a) Oceanographic region average of range of AMMSL (red/blue lines show the spatially averaged standard deviation of the interannual MMSL positive/negative values, respectively). (b) Oceanographic region average of the relative value (%) of AMMSL with respect to the SSL monthly maxima (SLADAC). (c) Oceanographic region average of the relevance (%) of mean AMMSL with respect to the neap-spring tidal range following Equation (3). (Exceedance of 100% were represented as 100% in order to facilitate the intercomparison with other regions).
Figure 5. (a) Oceanographic region average of range of AMMSL (red/blue lines show the spatially averaged standard deviation of the interannual MMSL positive/negative values, respectively). (b) Oceanographic region average of the relative value (%) of AMMSL with respect to the SSL monthly maxima (SLADAC). (c) Oceanographic region average of the relevance (%) of mean AMMSL with respect to the neap-spring tidal range following Equation (3). (Exceedance of 100% were represented as 100% in order to facilitate the intercomparison with other regions).
Remotesensing 12 03419 g005
Remotesensing 12 03419 g006 550
Figure 6. Fraction of components’ variance in the extreme total water level (>95th percentile) along the coastline (closest 1° × 1° tile) of each oceanographic region (a–j) considering TIDE, SSL and MMSL. Warm/cold colour indicates bigger/smaller extreme total water levels (ETWLs).
Figure 6. Fraction of components’ variance in the extreme total water level (>95th percentile) along the coastline (closest 1° × 1° tile) of each oceanographic region (a–j) considering TIDE, SSL and MMSL. Warm/cold colour indicates bigger/smaller extreme total water levels (ETWLs).
Remotesensing 12 03419 g006
Remotesensing 12 03419 g007 550
Figure 7. Spatial pattern of the relationship between the CFEEs and the AMMSL ((a–l) January–December). The dots indicate the position of the coastal storms and the colour intensity refers to their relative monthly frequency in the affected NUTS3 region.
Figure 7. Spatial pattern of the relationship between the CFEEs and the AMMSL ((a–l) January–December). The dots indicate the position of the coastal storms and the colour intensity refers to their relative monthly frequency in the affected NUTS3 region.
Remotesensing 12 03419 g007
Remotesensing 12 03419 g008 550
Figure 8. Average monthly fraction of each components’ variance in the ETWL along the coastline (closest 1° × 1° tile) of each oceanographic region (a–j). The monthly relative frequency of storm impacts at each area (blue polygon) is also shown.
Figure 8. Average monthly fraction of each components’ variance in the ETWL along the coastline (closest 1° × 1° tile) of each oceanographic region (a–j). The monthly relative frequency of storm impacts at each area (blue polygon) is also shown.
Remotesensing 12 03419 g008
Remotesensing 12 03419 g009 550
Figure 9. AMMSL along the coastline (closest 1° × 1° tile) averaged by oceanographic regions and monthly frequency of storm impact registered on each region (larger dot size indicate higher frequency).
Figure 9. AMMSL along the coastline (closest 1° × 1° tile) averaged by oceanographic regions and monthly frequency of storm impact registered on each region (larger dot size indicate higher frequency).
Remotesensing 12 03419 g009
Remotesensing 12 03419 g010 550
Figure 10. Monthly MSL anomalies along the European coastline (warm/cold colours indicate positive/negative MSL values) for each oceanographic region (a–j). The ratio of positive/negative anomalies for the CFEEs is also indicated. The ordinate axis represents the time and the abscissa axis represents the spatial variation along the coast indicated by ISO country code labels. Black dots indicate the date and position of extreme events registered in the database. The red line represents the relative frequency distribution of the monthly anomalies corresponding to the extreme events registered in the database and black line represents the spatially average of monthly anomalies distribution in the region.
Figure 10. Monthly MSL anomalies along the European coastline (warm/cold colours indicate positive/negative MSL values) for each oceanographic region (a–j). The ratio of positive/negative anomalies for the CFEEs is also indicated. The ordinate axis represents the time and the abscissa axis represents the spatial variation along the coast indicated by ISO country code labels. Black dots indicate the date and position of extreme events registered in the database. The red line represents the relative frequency distribution of the monthly anomalies corresponding to the extreme events registered in the database and black line represents the spatially average of monthly anomalies distribution in the region.
Remotesensing 12 03419 g010
Remotesensing 12 03419 g011 550
Figure 11. Extreme events registered in the storm impact database and captured by altimetry dataset. Curves represent the histogram of each sea level component (TIDE, SSL and MMSL) in the area and vertical lines mark the magnitude of each component at the peak of the extreme event.
Figure 11. Extreme events registered in the storm impact database and captured by altimetry dataset. Curves represent the histogram of each sea level component (TIDE, SSL and MMSL) in the area and vertical lines mark the magnitude of each component at the peak of the extreme event.
Remotesensing 12 03419 g011
Table
Table 1. Rank correlation coefficient between the average monthly fraction of components’ variance of SSL, TIDE and MMSL along the coastline (closest 1° × 1° tile) of each oceanographic region and the relative monthly frequency of the storm events database. p-value is given in brackets.
Table 1. Rank correlation coefficient between the average monthly fraction of components’ variance of SSL, TIDE and MMSL along the coastline (closest 1° × 1° tile) of each oceanographic region and the relative monthly frequency of the storm events database. p-value is given in brackets.
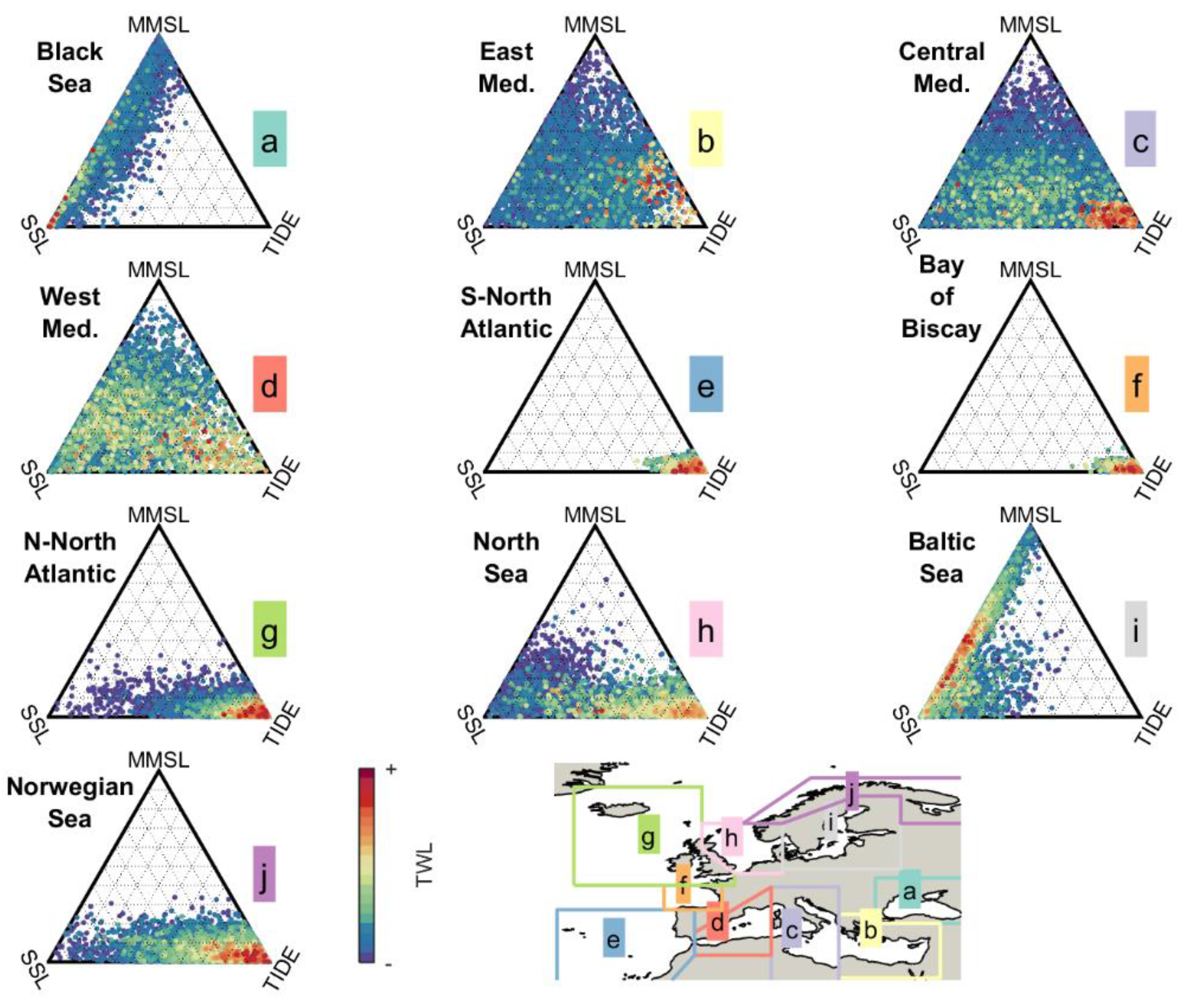
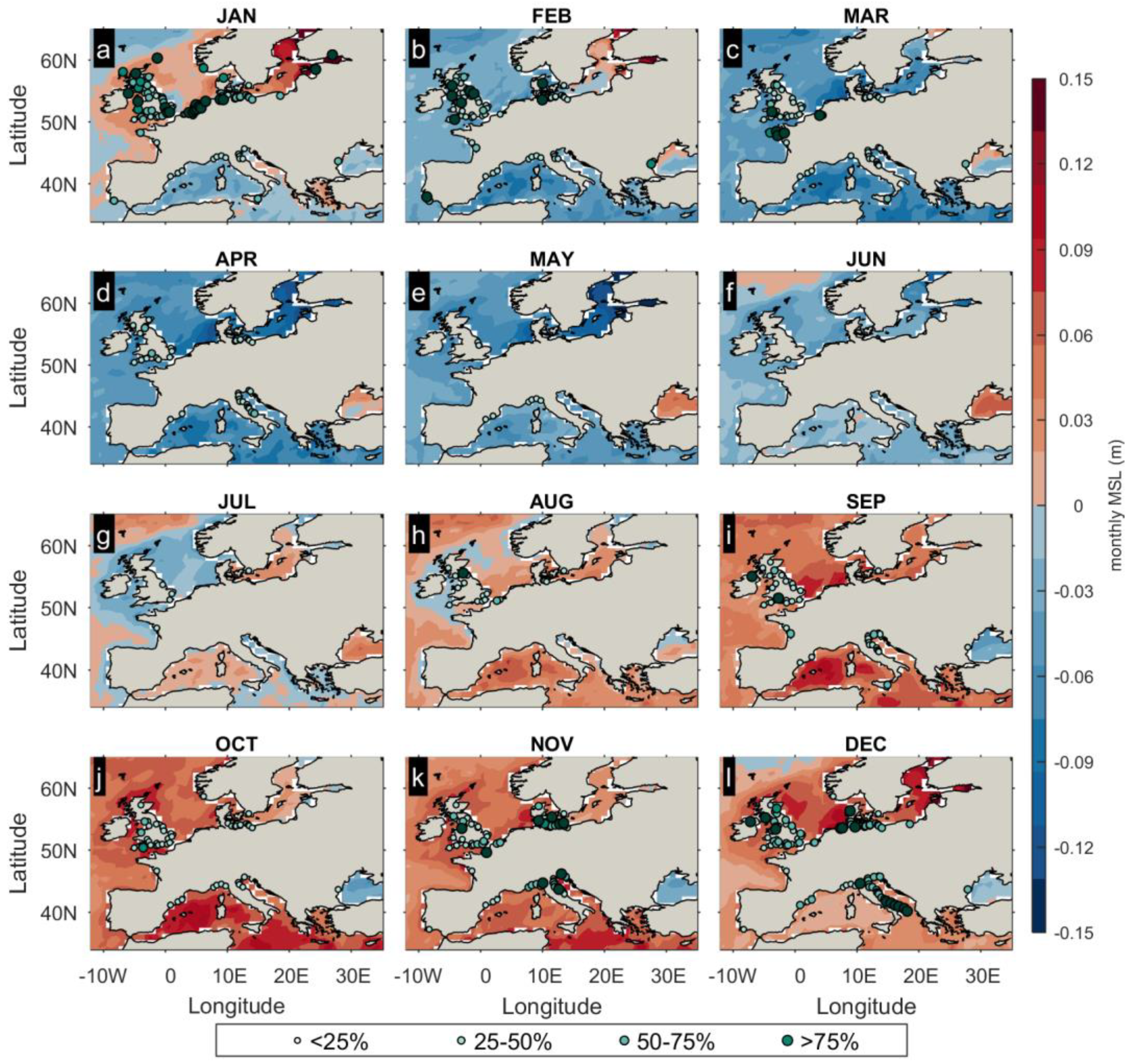
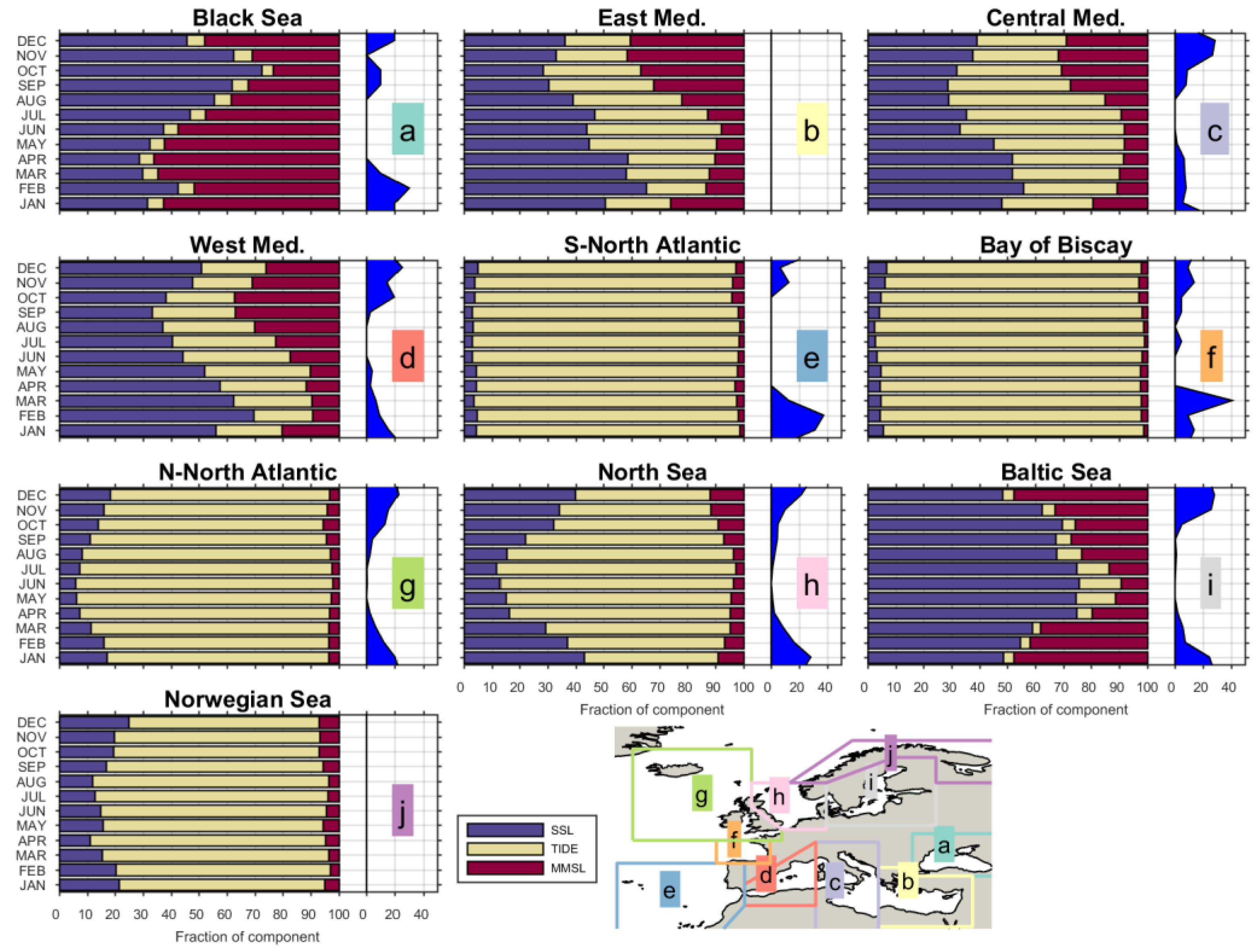
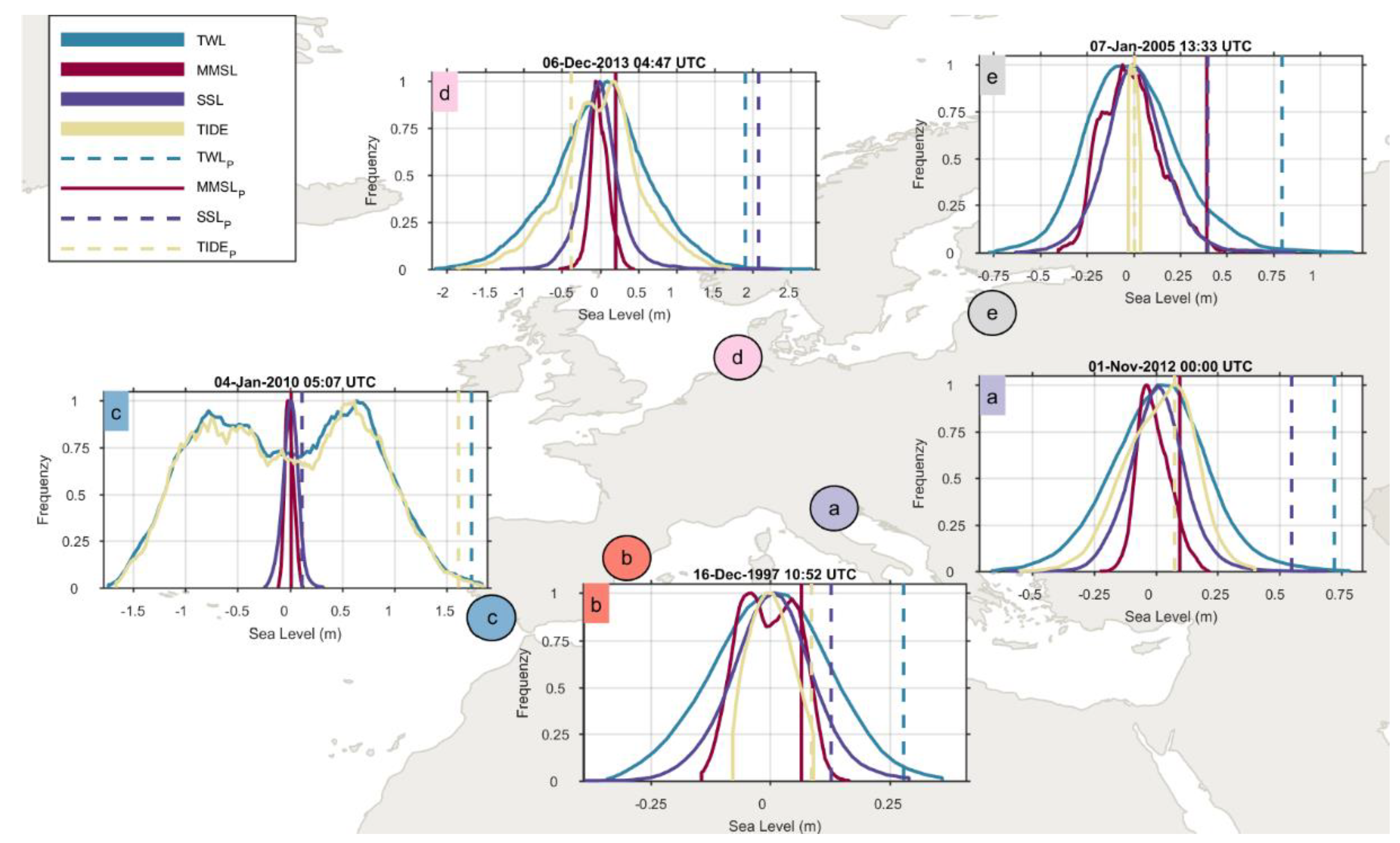
RegionBlack SeaCentral Med.West Med.S-North AtlanticBay of BiscayN-North AtlanticNorthSeaBalticSea
SSL−0.06 (0.86)0.03 (0.94)0.18 (0.57)0.52 (0.08)0.37 (0.24)0.97 (3 × 10−7)0.90 (6 × 10−5)−0.79 (2 × 10−3)
TIDE0.14 (0.66)−0.73 (7 × 10−3)−0.78 (3 × 10−3)−0.16 (0.63)−0.32 (0.32)−0.94 (4 × 10−6)−0.88 (2 × 10−4)−0.54 (0.07)
MMSL0.05 (0.87)0.73 (7 × 10−3)0.29 (0.36)−0.21 (0.52)0.12 (0.70)0.45 (0.14)0.67 (0.02)0.77 (4 × 10−3)
Table
Table 2. Rank correlation coefficient between the annual cycle ofregionally averaged AMMSL and relative monthly frequency of storm event in the database.
Table 2. Rank correlation coefficient between the annual cycle ofregionally averaged AMMSL and relative monthly frequency of storm event in the database.
RegionBlack SeaEast Med.Central Med.West Med.S-North AtlanticBay of BiscayN-North AtlanticNorth SeaBaltic SeaNorwegian Sea
Corr. coefficient−0.1-0.280.32−0.22−0.140.300.020.10-
p-value0.75-0.380.310.490.670.350.950.76-
Table
Table 3. Results of the t-test (p-value in bracket) to check the hypothesis that the MSL anomaly data comes from a population with a mean greater than zero at the 0.05% significance level. A t-test = 1 indicates that the hypothesis is accepted.
Table 3. Results of the t-test (p-value in bracket) to check the hypothesis that the MSL anomaly data comes from a population with a mean greater than zero at the 0.05% significance level. A t-test = 1 indicates that the hypothesis is accepted.
RegionBlack SeaCentral Med.West Med.S-North AtlanticBay of BiscayN-North AtlanticNorth SeaBaltic Sea
t-test (0.05)0 (0.28)1 (3 × 10−4)0 (0. 86)1 (3 × 10−3)0 (0.08)0 (0.07)1 (4 × 10−2)1 (3 × 10−7)
Mean MSL anomaly0.030.02−0.010.040.040.020.030.07
Table
Table 4. Comparison of total water levels (TWLs) peaks captured by altimetry and measured from tide gauges. The data source providing the tide gauge information is indicated in brackets.
Table 4. Comparison of total water levels (TWLs) peaks captured by altimetry and measured from tide gauges. The data source providing the tide gauge information is indicated in brackets.
Central
Med. [77])		West
Med. [78]		S-North Atlantic [78]North Sea ([53])Baltic Sea ([79])
TWLp.0.72 m (1.16 m)0.28 m (0.46 m)1.74 m (1.6 m)1.9 m (~4.67 m)0.8 m (2.22 m)
SSLp.0.55 m (0.81 m)0.13 m0.12 m2.08 m (2.67 m)0.4 m
TIDEp0.08 m (0.23 m)0.09 m1.61 m−0.38 m (~1.5 m)0.01 m
MMSLp0.1 m (~0.12 m)0.07 m0.01 m0.21 m (0.50 m)0.39
DATEp01.11.2012 00:00
(31-10-2012 23:30)		16.12.1997 10:5204.01.2010
05:07		06.12.2013 04:47
(06.12.2013 02:00)		07.01.2019 13:33
(09.01.2009 06:00)
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Fernández-Montblanc, T.; Gómez-Enri, J.; Ciavola, P. The Role of Mean Sea Level Annual Cycle on Extreme Water Levels Along European Coastline. Remote Sens. 2020, 12, 3419. https://doi.org/10.3390/rs12203419

AMA Style

Fernández-Montblanc T, Gómez-Enri J, Ciavola P. The Role of Mean Sea Level Annual Cycle on Extreme Water Levels Along European Coastline. Remote Sensing. 2020; 12(20):3419. https://doi.org/10.3390/rs12203419

Chicago/Turabian Style

Fernández-Montblanc, Tomás, Jesús Gómez-Enri, and Paolo Ciavola. 2020. "The Role of Mean Sea Level Annual Cycle on Extreme Water Levels Along European Coastline" Remote Sensing 12, no. 20: 3419. https://doi.org/10.3390/rs12203419

APA Style

Fernández-Montblanc, T., Gómez-Enri, J., & Ciavola, P. (2020). The Role of Mean Sea Level Annual Cycle on Extreme Water Levels Along European Coastline. Remote Sensing, 12(20), 3419. https://doi.org/10.3390/rs12203419

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop