Abstract
The use of individual tree detection methods to support forest management inventories has been a research topic for over two decades, but a formal assessment of these methods to produce stand-level and region-level predictions of forest attributes and measures of error is lacking. We employed model-based estimation methods in conjunction with the semi-individual tree crown approach (s-ITC) to produce predictions and measures of error for tree volume (VOL), basal area (BA), stem density (DEN), and quadratic mean diameter (QMD) at the scale of forest stands and the entire study region. We compared the s-ITC approach against the area-based approach (ABA) for predictions of region-level and stand-level attributes via model-based root mean squared errors (RMSEs). The study was conducted at the Panther Creek watershed in Oregon, USA using a set of 78 field plots and aerial lidar information. For region-level attributes, s-ITC RMSEs demonstrated changes between −31% and 17% relative to ABA models. At the stand level, median s-ITC RMSEs generally increased, with changes between −29% and 414% relative to ABA models, but demonstrated important reductions in stands where segmentation provided large increases in sample size and was less prone to extrapolation than ABA models. The ABA demonstrated smaller RMSEs in stands without sampled population units for all variables. Our findings motivate further research into niche applications where s-ITC models may consistently outperform ABA models.
1. Introduction
Interest in leveraging tree segmentation for supporting forest management planning is an active area of research in remote sensing and forest management literature. Forest managers are increasingly attracted to benefits of tree segmentation methods, including opportunities for species prediction [1,2] as a proxy for tree height for use in allometric models [3] and a widening scope of other potential attributes such as presence of wildlife habitat [4] and tree mortality [5,6]. A common use-case for tree segmentation methods is the prediction of forest inventory attributes at the scale of detected tree crowns that can be used to construct maps of forest inventory attributes at very fine scales [3,7]. These crown-level predictions can provide a basis for forest inventory predictions at scales larger than detected tree crowns by aggregating individual predictions to the stand-level. Individual tree detection methods can serve as an alternative to the more operationally common area-based approach (ABA) [8], and this study compares the suitability of one such tree segmentation method for producing stand-level predictions against the ABA.
Approaches for generating predictions of forest inventory attributes that leverage tree segmentation methods are myriad and can be classified into two distinct categories: individual tree crown (ITC) and semi-individual tree crown (s-ITC) [9,10]. In most manifestations, the ITC approach makes the explicit assumption that a detected segment in the auxiliary data represents a physical tree, and a tree matching method is employed to attach auxiliary information to a measured tree in the sample [11] p. 114. The population, therefore, is a set of trees from which a sample is selected. The s-ITC approach, in contrast, makes no such assumption, and a detected segment in the auxiliary data represents none, one, or several trees. The s-ITC approach detects tree segments, i.e., polygons, in the auxiliary data in a process similar to the ITC approach but does not involve linking detected trees to measured trees. Rather, all trees within a detected segment are used to produce a response variable for that segment, and modeling and prediction methods are carried out on these segments. The population for the s-ITC approach is the set of these segments, which are population units composed of a varying number of trees.
The s-ITC approach may be attractive for forest managers who desire predictions at the scale of detected tree segments. The s-ITC approach is therefore an alternative in areas with complex and multi-layered forest structures where ITC methods tend to have larger omission errors. However, forest managers may be interested in aggregations of segment-level predictions, such as predictions at the scale of forest stands or at the scale of an entire study region. In these cases, prediction methods that use the ITC approach tend to be negatively biased due to omission error in the tree detection and matching process [12,13]. Therefore, correction factors are needed to adjust aggregations of ITC predictions, as in the case of stand-level or region-level predictions. For the s-ITC approach, bias from omission does not exist if a compact tessellation of detected segments is made (i.e., the segmentation method does not leave gaps) of the study area that include all trees. The s-ITC approach is still able to provide predictions at the resolution of these segments, but the interpretation is that one segment is equivalent to one tree lost.
In contrast, the more operationally common area-based approach (ABA) combines fixed radius plots with coincident remote sensing data in a modeling procedure to produce forest inventory predictions for a set of regular grid cells cast across the study area, which are treated as the population of interest. The ABA is advantageous in that it does not require the measurement of tree positions because only the position of the plot is required for georeferencing remote sensing auxiliary information. However, in many implementations, the predictions are constrained to the resolution of the regular grid and can preclude prediction of attributes at finer scales.
Importantly, the ABA has been used with explicit consideration of predictions for parameters of interest, such as the total or the mean volume of timber in a forest stand, compartment, or county using small area estimation (SAE) methods [14,15,16,17]. Model-based SAE methods provide several benefits for forest management inventories. First, the use of linear mixed models affords the aggregation of individual unit-level predictions, such as pixels or tree segments, to larger scales such as forest stands or study regions. Second, model-based mean squared error estimators can be used to produce assessments of uncertainty for these aggregated predictions for both sampled and unsampled stands under the assumed model. For forest inventories that require stand-level predictions and assessments of their stand-specific uncertainties, these two aspects of model-based SAE methods are attractive.
Model-based mean squared error estimators are frequently used to compare the reliability of predictions between competing methodologies, e.g., [18,19,20], such as the ABA and the s-ITC approach. These estimators can serve as an alternative to cross validation assessments, such as those used in [21], a recent study that investigated the ITC approach and the ABA. Cross validation assessments are restricted only to those stands that contain field plots and are typically constructed for the entire sample, offering only one “global” assessment of uncertainty for all predictions [22] p. 242. Forest managers may be interested in measures of uncertainty for predictions of particular stands, i.e., a “local” assessment of uncertainty, as well as for unsampled stands. Model-based mean squared error estimators offer these measures assuming that model assumptions and their parameter estimates hold for the entire population and are an attractive alternative for forest managers.
The question remains whether, between models based on the s-ITC approach and models based on the ABA, which of the two approaches provides more reliable stand-level and region-level forest inventory predictions. A model-based SAE analysis can provide insight into the reliability of forest inventory predictions at these scales for these two alternative approaches. While model-based SAE analyses have been conducted under the ABA, a similar assessment of using the s-ITC approach is needed and can have implications for forest management planning, where the reliability of predictions at the stand- and the region-levels can be of high importance. We employ model-based SAE methods—specifically the unit-level model, which is a special case of the linear mixed effects model [23] (pp. 78–81)—to produce predictions of four forest inventory variables, including stem volume (VOL), basal area (BA), stem density (DEN), and quadratic mean diameter (QMD), for two different population types: 1) a population of detected segments produced in the manner of s-ITC, and 2) a population of grid cells produced in the manner of the ABA. Particularly, we focus on the relative performances of these inventory models at the scale of forest management stands and at the scale of the entire study region using model-based mean squared error estimates.
2. Materials
2.1. Study Area
The study was conducted in the Panther Creek watershed located in northwestern Oregon, USA. The area is composed of approximately 2580 hectares of forest with elevations ranging from 100 m to 700 m and an annual precipitation of 1500 mm. The forest types range from planted stands of Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco) to natural stands of mixed species, including western hemlock (Tsuga heterophylla (Raf.) Sarg), western red cedar (Thuja plicata Donn ex D. Don), red alder (Alnus rubra Bong.), grand fir (Abies grandis (Douglas ex D. Don) Lindley), and other minor species. Various forest management actions have been conducted in the area, and a patchwork of management is apparent, including variable retention harvest, thinning, and recent reforestation.
Forest stands and other areas were delineated using visual photographic interpretation methods using optical aerial images. A total of 144 delineations were produced, of which 14 were removed in a later interpretation phase that revealed they were either non-forested (e.g., lakes, residential areas, etc.) or recently harvested near the time of the field data collection date. The remaining 129 forest stands compose what is referred to as the study region. Figure 1 displays the Panther Creek watershed with the forest stand delineations.
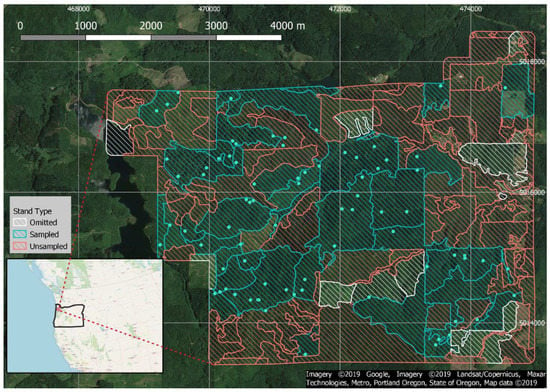
Figure 1.
Vicinity map of the Panther Creek watershed situated in the northwest of Oregon, USA. Forest stands are colored according to omitted, sampled and unsampled. Field plots are indicated in blue. Universal Transverse Mercator (UTM) Zone 10 N coordinates are given at the margins of the figure, with UTM grid lines demarcated in gray.
2.2. Field Data
A field campaign conducted between July 2009 and May 2010 produced a set of 78 field plots with a fixed radius of 16 m (approximately 0.08 ha in area) as part of a larger program not explicitly implemented for the objectives of this study. The field sample collected from the Panther Creek watershed contains a mixture of field plots from a probability-based sample selection mechanism and a non-random sampling design. Stand species compositions were visually assessed using color infrared photos to identify three groups: conifer, mixed conifer in association with hardwoods, and riparian zones. The conifer stands were identified and divided into nine strata based on 90th percentile lidar height. The mixed group and the riparian group each formed separate strata.
For the conifer group, two sampling procedures were performed, including a design-based sample and a non-random sampling design intended for model-based estimation. For the design-based sampling procedure, one stand in each of the nine conifer strata was selected using probability proportional to size. Within each selected stand, three plot centers were randomly positioned. For the non-random sample, one additional plot was selected within each of the nine stands by selecting a grid cell that represented median conditions in terms of number of first returns and 90th percentile lidar height. For the mixed group and the riparian group, all stands were selected for sampling, and two plots were randomly positioned in each stand. The remaining 36 plots were part of a separate non-random sampling program intended to sample various soil structures in the study area and were not dependent on forest conditions or structures [24]. The distribution of stands by the stand-specific sample size is given in Table 1. It is evident that a range of stand-specific sample sizes were available, which can have implications for stand-level model-based inferences (see Section 5.3). In total, 35 stands were sampled, 16 were part of the design-based sample, and 19 were part of the non-random sampling design.

Table 1.
Distribution of the number of stands by stand-specific sample size. A given column indicates the number of stands that contain the number of field plots indicated in the top row. For example, the first column indicates there are 94 stands with 0 field plots.
Field crews located the pre-allocated field plot centers using sub-meter grade GPS units and installed plot centers at the GPS measured positions. These GPS measured positions were assessed against an existing cadastral survey and were found to be within 0.25 m [24]. All trees within the plot radius that had a diameter greater than 0.5 cm and exceeded 1.37 m in height were measured. The diameters at 1.37 m up the stem and the total tree heights were measured. Each tree position was recorded relative to the established plot center by measuring its horizontal distance to the nearest 0.1 m and azimuth. For all trees, predictions of cubic stem volume were predicted using the National Volume Estimator Library [25]. For the purposes of this study, the predicted cubic volume, including top and stump, for each tree in the ground data tree list are treated as known quantities.
2.3. Lidar Data Acquisition and Processing
The aerial lidar acquisition for this study was collected 15 July 2010 during leaf on conditions using a Leica ALS60 sensor mounted on a Cessna Caravan 208B. The aircraft was flown at approximately 900 m above ground level with a scan angle of ±14° from nadir. The average pulse density for the acquisition is 20.01 pulses per square meter. The raw lidar acquisition was normalized for terrain elevation by filtering ground and non-ground points by applying the ground-filtering algorithm developed in [26]. These ground points were used to form an intermediate digital terrain model (DTM). Empty cells of this DTM were interpolated using a nearest neighbor interpolation algorithm to produce the final DTM, by which the elevation underneath each lidar point was subtracted to produce a normalized point cloud of the study area.
3. Methods
3.1. Constructing Population Units
3.1.1. Grid Cells
For the ABA, the population units are a set of grid cells that cover the entire study area, such that the grid cell size equals the size of the field plots (0.08 hectares). For each grid cell (i.e., pixel) in the population, a vector of lidar predictors was produced. Names and descriptions of lidar predictors are provided in Appendix B Table A2. All grid cells were assigned to the stand that intersected with their geometric center. Grid cells and field plots were considered to represent the same population type for the purposes of this study. VOL (), BA (), DEN (), and QMD () were computed at this scale using the entire plot-level tree lists. Table 2 provides a glossary of terms used in the remainder of the sections.

Table 2.
Glossary of frequently used terms in this study.
3.1.2. Segments
For the s-ITC approach, the population is a set of segments derived from a canopy height model. To produce a population of segments, we utilized a combination of a variable window local maxima filter [27] and a Voronoi tessellation. For the entire study area, an intermediate canopy height model was produced at a resolution of 0.33 m, where each pixel of the canopy height model represented the lidar return of maximum height. A median filter with a 3 pixel × 3 pixel kernel was passed over the intermediate canopy height model to produce the final canopy height model. Local maxima of this canopy height model were found using a two-stage filter. A fixed window local maxima filter was passed over the canopy height model such that a distance of at least 2 m must exist between detected maxima. This provided a set of candidate maxima for a variable window local maxima filter that was passed over the canopy height model in a second phase. For each candidate maximum, an allometric equation defined a search window such that only the highest maximum in the search window was retained as a final local maximum. We used the allometric equation defined in [27] that relates the height of a given pixel to the search window width:
where and are fixed coefficients, is the value of the canopy height model at position and is the search window width in meters at position . We modified the coefficients provided by [27] to provide window widths consistent with the observed tree crown radii in the canopy height model using visual inspection such that and .
The variable window local maxima output was a set of points in the study area. We used a Voronoi tessellation over these points to provide the final set of segments for analysis (Figure 2). This procedure is similar to that of the segmentation procedure proposed by [7] but does not constrain the individual segment extents based on low values in the canopy height model. This was considered appropriate as we desired a compact tessellation of the study area (i.e., a division leaving no gaps) that would eliminate the possibility of omitting trees from the sample (see Section 5.2).
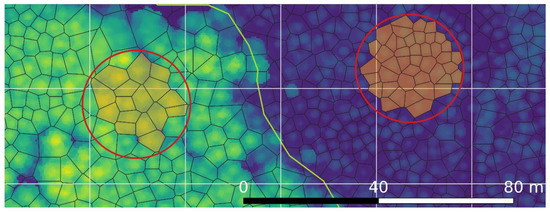
Figure 2.
Canopy height model (blue to green background) displayed underneath delineated segments (black lines) and grid cells (white lines). Two example field plots are shown (red circles) with included segments shaded in orange. The green line in the center represents a stand delineation.
For each segment, a vector of lidar predictors was derived by clipping the study-area-level point cloud by the polygon of each segment. In total, a set of 30 predictors were computed for each segment (Appendix B). In the same manner as the grid cells, segments were assigned to the stand that intersected with their geometric center. Each segment that was entirely within the plot radius plus the addition of a small constant of 0.5 m was considered a sample segment. For each sample segment, VOL, BA, DEN, and QMD were calculated using those trees contained inside the segment. Mean values and standard deviations of VOL, BA, DEN, and QMD for the field plots and the segments from their respective samples are given in Table 3. Differences between the means and the standard deviations across field plots and segments are apparent. This can be a result of fewer segments included in the sample when segments are large, i.e., in stands with larger crown widths. The segments express a wider range of values, including segments with no trees (i.e., a minimum of zero).

Table 3.
Sample means, standard deviations, and ranges for forest inventory attributes for the sample of field plots and the sample of segments. Note: for the mean and the standard deviations, a weighted mean was calculated for each plot using segment and plot areas as weights, respectively, and means and standard deviations of these scaled observations are reported in the table.
3.2. Unit-Level Model
For both the ABA and the s-ITC approaches, we employed the unit-level model, which provides predictions of grid cells and segments, respectively, while accommodating potential stand-level random effects via linear mixed models. Linear mixed models anticipate potential differences between stands that are accommodated by the specification of stand-level random effects. Predictions for individual population units are aggregated to the scale of individual stands or the study region to produce predictions and mean squared errors at these two scales. This enables comparison of the uncertainties of ABA and s-ITC at these scales. Please refer to Appendix A Table A1 for a summary of the major notation we use in the following subsections.
For both approaches, we defined the general linear mixed effects model:
where is a vector of per-unit area values where denotes the th observation in the th stand, represents the total number of forest stands, and represents the number of population units in the th stand. For example, if we consider VOL attribute, is a vector of observations of stem volume per hectare for a grid cell or a segment. is a design matrix of lidar covariates and a column of ones to accommodate an intercept. is a vector of regression coefficients. is an matrix that assigns population units to forest stands. For example, the elements of the th column of takes a value of 1 if the th element of that column is in stand and 0 otherwise. is a vector of random effects such that .is a vector of model errors that explain deviations from the stand-level random effect such that . Additionally, is independent of . This defines the basic unit-level model (e.g., [19,23]).
Because there is a mismatch in population units between a model developed using circular field plots and the population units upon which predictions are made, i.e., grid cells, we use the general term “ABA model” when referring to Equation (2) if a set of field plots was used to construct the model and “s-ITC model” when referring to Equation (2) if a set of segments was used to construct the model. Additionally, Equation (2) is defined for the entire population but in some instances it is necessary to refer only to portions of matrices and vectors that corresponded to sample units. To do so, we use the sub-index to refer to a matrix or vector that has rows corresponding to unobserved population units removed.
Specific structures were assumed for the variance–covariance matrices and . Here, we adopt particular model assumptions that specify further the general treatment of Rao and Molina [23] Ch. 7. The random effects were assumed independent and identically distributed such that . Additionally, we incorporated the possibility for heteroskedasticity on the residuals with a general variance function model (e.g., [28] p. 206):
where is a variance function covariate that represents the most correlated predictor, is the residual variance, and is a constant that accounts for heteroskedasticity. It will be convenient to use the relationship for later formulae, where is a unit-specific variance weight. We incorporated the possibility for spatial correlations between population units in the same area using a spherical correlation function:
where is the Euclidean distance in meters between the population units indexed by and computed using the centroid of the population unit geometry. Model errors were assumed to be independent across different areas, thus the resulting models had block diagonal variance–covariance structures. The variance–covariance matrix can be constructed using Equations (3) and (4):
where
and is an operator that constructs a block-diagonal matrix using the matrices indicated in the expression. The block-diagonality implies that segments or grid cells within stands may be correlated, while segments or grid cells in different stands are uncorrelated. The indices and refer to the row and the column, respectively.
3.3. Target Parameters
We considered target parameters that were linear combinations of the model coefficients and the error vectors and [20] (p. 98). For example, a target parameter may represent a mean of a forest attribute for a stand or a study-region mean (i.e., a mean of all population units in the study region). Let represent a generic target parameter for a set of population units indexed by . In all cases, the parameter can be expressed as a linear combination of the model components:
Such a generic formulation affords the construction of different target parameters for specific cases common to forest inventories, e.g., stand-level or region-level means, by constructing different vectors , , and . We considered target parameters at the stand-level for all stands in the study area and target parameters for the entire study region. First, we considered stand-level means. This implies:
where refers to the size of a population unit indexed by and , i.e., the size of a population unit in , is the number of population units in the th stand, and is the sum of population unit areas in stand . Therefore is a weighted mean of the unit-level predictor vectors in the th area. Note that, in the case of stand-level-mean prediction, is a vector of zeroes except for the th position that contains a one. We use the notation when referring to a stand-level parameter. Additionally, we reserve the notation to refer to the number of sample segments or field plots within stand . Second, a study-region mean was constructed by letting:
and
which are the weighted means of the predictor vectors and a vector of area proportions for each stand in the study region, respectively, where is the sum of the areas of all stands. We use the notation when referring to the study-region-level parameter.
For both parameter types, the term is the weighted mean of the errors of a set of population units. For large , i.e., for large numbers of grid cells or segments, this term becomes negligible and is typically disregarded for models with independent errors [20] p. 98. Thus, in the case of independent errors, we considered target parameters of the form:
3.4. Predictions for Target Parameters
Predictions for the target parameters were obtained using the empirical best linear unbiased predictor (EBLUP). We reserve the notation to refer to a prediction of made with the EBLUP. First, we obtained an estimate of the variance parameters via restricted maximum likelihood (REML) using the R package nlme [29]. Estimation of the variance parameters provided a basis for the estimated variance–covariance matrix because depends only on . An estimate of the regression coefficient vector was obtained:
A prediction for the target area parameter could be made using the EBLUP:
where the predicted area-level random effect vector is:
Note that, for unsampled stands, , and we obtained the synthetic predictor .
3.5. Model Selection
For some general attribute and population unit type , we sought the selection of a model that satisfied linearity between predictors and the response, whose Pearson’s standardized residuals expressed homoscedasticity. Models were selected using a three-phase procedure. In the first phase, the objective was to select variables for the fixed part of the model, thereby attaining a preliminary estimate of the slope coefficients . From an initial pool of thirty predictor variables, the five best candidate models for a given level of predictors plus an intercept were found via adjusted by an exhaustive search implemented by the leaps package in R [30]. This resulted in a set of 25 candidate models, five for each level of . Denote the models from this first phase as . The models in were plotted by their adjusted values and number of predictors, and parsimony was determined by finding the number of predictors at which adjusted began to level off. Models around this region were explored further via graphical inspection of residual plots. Those models that exhibited linearity moved to the second phase and composed the set of models denoted as . In the second phase, heteroscedasticity was introduced by applying variance weights using the variance function described in Equation (3) using 0, 0.5, and 1 as values for . The models in were refit with this variance function. The standardized residuals were inspected, and those models where the residual variance stabilized moved to the third phase and composed the set . Models in this set had spatial correlation structures Equation (4) added. We inspected empirical semi-variograms for each model. Models that exhibited patterns of spatial correlation in the empirical semi-variogram retained their spatial structure, and models that did not had the spatial structure removed. If more than one model remained, the model with the largest adjusted was selected as the final model. In total, eight models were selected as final models, two (one s-ITC model and one ABA model) for each of the four attributes.
3.6. Mean Squared Error Estimators
The mean squared error estimator for the predicted target parameter is a function of the estimated variance component vector and can be expressed as the sum of three components, assuming the sampling fraction, , for all areas is negligible:
The first term quantifies uncertainty caused by the random-effect variance, i.e., as if the variance components are known:
The second term quantifies uncertainty in the estimate of the coefficient vector :
where and . The third term quantifies the uncertainty of the random effect variance estimate, which is not accommodated by that treats the variance components as known:
where is the inverse Fisher information matrix (see [23] p. 180). Equations (13)–(15), as well as other relevant details are described in [23] (pp. 108–109).
In addition to the mean squared error estimator, we also produced the root mean squared error estimator:
An approximate 95% confidence interval:
Estimates of the coefficient of variation:
and the relative change, expressed as a percentage, between s-ITC and ABA root mean squared errors:
Positive values of indicate a larger s-ITC root mean squared error relative to the ABA root mean squared error in the area indexed by . A of −50%, for example, indicates that the RMSE for the s-ITC model is half as large as that of the ABA model.
4. Results
4.1. Selected Models
The standardized residuals of the eight models are displayed in Figure 3, and their parameter estimates are presented in Table 4. Figure 3 indicates some minor heteroscedasticity remaining in the DEN and the BA models for predictions exceeding 25 and 500 , even after the inclusion of the variance function, but otherwise the ABA and the s-ITC models appeared to have homoscedastic and symmetrically distributed residuals. ABA models appeared to have smaller residual variance than s-ITC for all attributes, i.e., their spread covered a smaller interval. Across population types, a number of differences in model parameter estimates were apparent, as reported in Table 4. For all inventory attributes, s-ITC models had consistently larger random effect variance estimates, i.e., , than the respective ABA models. Most notably, the ABA models for VOL and BA had near-zero estimates for . The variance function model term was consistent for VOL and BA but was not required (i.e., ) for the QMD model in the ABA case to correct heteroscedasticity. For the DEN ABA model, non-zero values of did not fully correct the heteroscedasticity beyond what was achieved with . None of the model residuals demonstrated strong spatial correlation after the inspection of empirical semi-variograms, thus we treated the errors of the unit-level observations as independent.
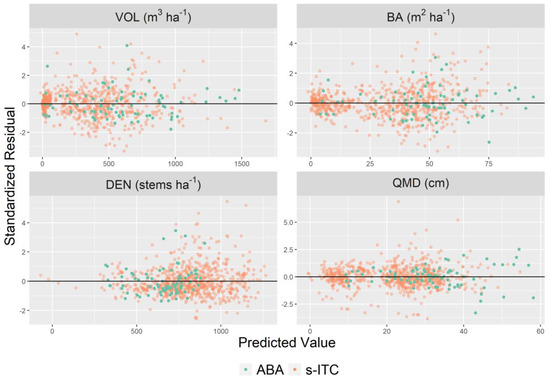
Figure 3.
Pearson’s standardized residuals of ABA (green) and s-ITC models (orange) for the four forest attributes.

Table 4.
Selected predictors and parameter estimates for the s-ITC approach and the ABA.
4.2. Estimation for the Study Region
For the entire study region, we produced predictions of the target parameters using the respective ABA and s-ITC models by aggregating unit-level predictions (Section 3.3). Table 5 displays the predictions along with their and . Some moderate differences existed among predictions generated with ABA and s-ITC models, most notably for VOL. The error components and were negligible for all models. When many stands were aggregated to produce an estimate for the study region, the mean of the random effects approached zero as the number of sample areas increased as a result of the assumption . Therefore, and , which consider the uncertainty imparted by the random effects and the estimate of the random effect variance, respectively, both became negligible. This left as the remaining source of error. and were comparable between population types, with ABA models outperforming s-ITC models for BA and DEN, while s-ITC models outperformed for QMD. Both models performed comparably for VOL.

Table 5.
Predictions of forest attributes and error components at the scale of the study region. Note that, for all models, and were < 0.01 and are not included in this table.
4.3. Estimation for Stands
For each stand, we produced a prediction of the stand-level target parameter using the respective ABA and s-ITC models. This result conveys the level of coherence between the two alternative approaches and can highlight important differences in the models where they exist. Figure 4 displays these stand-level predictions and whether that stand was sampled. Between ABA and s-ITC models, a high level of agreement, i.e., the points in the figure clustered around the diagonal line, was apparent for VOL, BA, and QMD. For VOL, small differences existed at point predictions exceeding 500 , with the s-ITC model producing larger predictions than the ABA model. The differences were larger for unsampled stands than sampled stands. For BA, differences existed at the extreme small end of the predicted values, i.e.,, with the ABA model producing larger predictions than the s-ITC model. This same pattern existed for QMD occurring at predicted values . The differences between ABA and s-ITC models were most apparent for DEN. The grid cell model appeared to saturate at a level of 900 stems per hectare, with marked differences in the upper range of segment predictions. The confidence intervals for ABA, indicated by the vertical bars, and the confidence intervals for s-ITC reflected the uncertainty of each stand-level prediction. For VOL and BA, the confidence intervals were wider for the s-ITC models than for the ABA models. For DEN and QMD, the confidence intervals were relatively consistent between ABA and s-ITC models, i.e., they were approximately the same width.
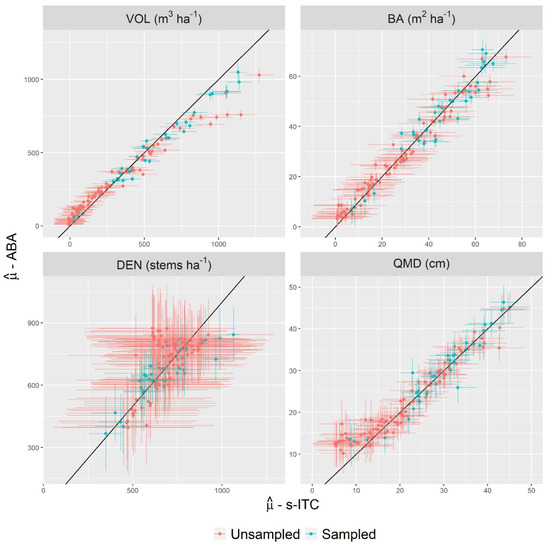
Figure 4.
Predictions of area-level parameters for VOL, BA, DEN, and QMD for s-ITC models and ABA models. Whether or not the stand had at least one field plot is indicated by the color of the point. The confidence intervals are shown as horizontal bars for s-ITC and vertical bars for ABA.
For all stand-level target parameter predictions, we produced the model-based mean squared error estimates of sampled and unsampled stands and coefficients of variation in Table 6. With the exception of DEN, the ABA models had median and that were less than those of the s-ITC models for both sampled and unsampled stands. For models where the estimated random effect variance was near zero, this implied that no substantial error was introduced from the random effect component. This was the case for ABA VOL and BA models, and the difference between the measures of error between sampled and unsampled stands was accordingly negligible.

Table 6.
Medians of estimated mean squared errors for stands partitioned by sampled (S) and unsampled (U) stands.
Figure 5 indicates the relative decrease in as it related to an increase in the number of sampled units when going from an ABA model to an s-ITC model. This increase in sample size was expressed as the ratio of the number of segments to the number of field plots for a given stand. Points that fell below the horizontal black line indicated stands where the s-ITC model achieved a smaller than the respective ABA model. This tended to occur in stands where the number of segments was much larger than the number of field plots. We refer to this increase in stand-specific sample size as “segment induced replication.” When segment induced replication was large, the decrease in relative to the ABA model tended to be large. This effect was most clear for DEN and QMD models, with more erratic behavior for the VOL and the BA models. When segment induced replication was small, tended to increase from ABA to s-ITC models for all variables. This effect was most extreme for VOL and BA models.
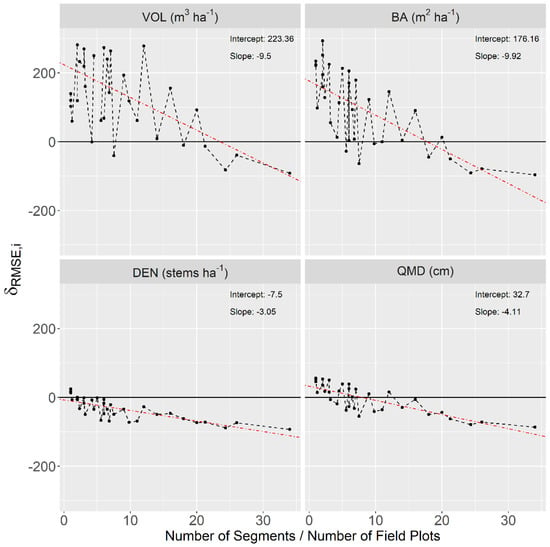
Figure 5.
The ratio of the stand-specific sample size of segments to field plots plotted against , for VOL, BA, DEN, and QMD in sampled stands. A simple linear regression (red) was fit to each attribute to demonstrate the trend, with slopes and intercepts reported for each attribute.
Figure 6 displays the error components, , and for sampled stands, ranked by the ratio of segments to field plots in ascending order. For models where the random effect variance was large, such as VOL, BA, and QMD s-ITC models, the relative share of was a very large portion of the total mean squared error for many of the sampled stands, i.e., in many cases, it accounted for the majority of the mean squared error in a specific stand. For models where this was not the case, such as DEN s-ITC model as well as DEN, BA, and VOL ABA models, the relative share of was small. For most stands, all s-ITC models with the exception of DEN appeared to have a smaller value of than the respective ABA model, with a notably smaller share of the total mean squared error estimate. The ordering within each pane of the figure, from least (top) to greatest (bottom) segment induced replication, demonstrated the impact of segment induced replication on the individual error components as well as the overall mean squared error estimate. While segment induced replication appeared to reduce all three components in most cases, the impact was most clear for for all s-ITC models with large random effect variance estimates. The term was largest for the ABA QMD and the DEN models and the s-ITC DEN model. This term did appear to be mitigated by increase in sample size for the s-ITC model but much less so for the case of the ABA model. Note that, for specific stand-level predictions, the and the error components were sizeable, unlike predictions made for the study region, because they did not benefit from aggregating predicted random effects (Section 4.2).
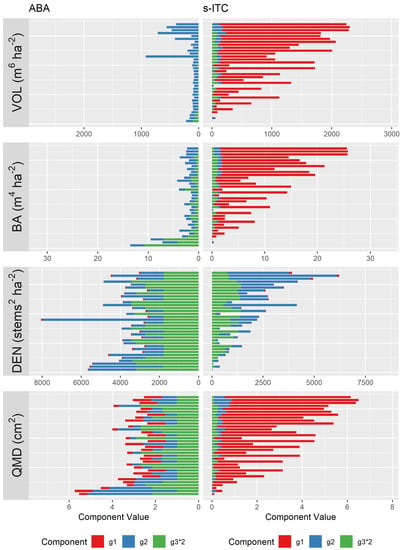
Figure 6.
Error components for segment and cell models for VOL, BA, DEN, and QMD in sampled stands. Component rows are ranked by the ratio of the number of segments to the number of field plots (as in Figure 5) in ascending order.
Figure 7 and Figure 8 display the error components and plotted against the stand-specific sample size , i.e., the number of field plots or number of segments, and the area-level prediction , respectively. The ABA models for all attributes tended to have smaller error components and, for models with small random effect variance estimates, such as VOL and BA models, these error components were uniformly small across all available sample sizes. In contrast, the s-ITC models, which tended to have larger random effect variances, required much larger sample sizes to achieve the same level for the component. For the component, it was apparent for VOL, BA, and QMD that predictions that tended to be far from the mean generally exhibited larger values for , especially for upper and smaller tails of the BA models and the upper tail of the VOL models. Some extreme values for were apparent for ABA VOL, BA, and QMD models in particular. Note that the distinct patterns for VOL, BA, and QMD in Figure 8 were the result of a fewer number of coefficients in these models and the form of the expression (Equation (15)).
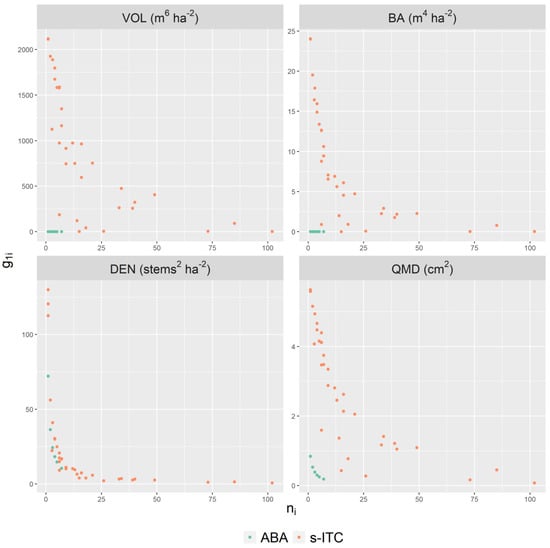
Figure 7.
The error component for all sampled stands in the study area plotted against the stand-specific sample size . Note that for unsampled stands, not displayed in this figure, was equal to the respective random effect variance estimate (Table 4).
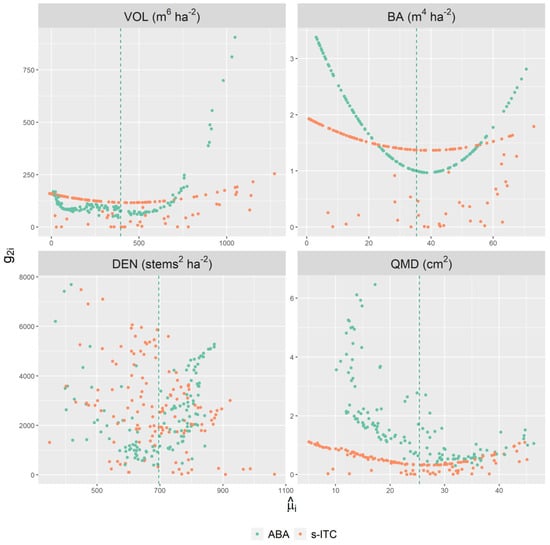
Figure 8.
The error component for all stands in the study area plotted against the stand-level prediction . The prediction of the study region mean, , is shown for the ABA as a dashed vertical line as a reference.
5. Discussion
5.1. Contribution of Error Components
We observed a mixture of results between s-ITC and ABA models. For the estimation at the scale of the study region, the two approaches provided similar RMSEs. For the stand-level estimation, the ABA provided predictions with lower RMSEs for unsampled stands (Table 6), while the s-ITC models were able to provide lower RMSEs in some sampled stands (Figure 5). Inspecting the behavior of the error components for individual stands can provide insight into the differences between these two approaches and their RMSEs. We identified changes in stand-specific and global sample sizes between the two approaches as important contributors to these differences by examining the stand-level error components , , and in turn. For the interested reader, please refer to [23] (pp. 176–179) for technical descriptions of the error components for the simpler case of homoscedastic unit-level models.
We observed that s-ITC models benefited from an increase in stand-specific sample size relative to the ABA models, and that this increase reduced the impact of the error component (Figure 7). For VOL and BA models, for ABA models was near zero and approximately equal for any given level of . While it was possible for to reduce to a level similar to that of the ABA models, it required much larger increases in sample size relative to the ABA in the realm of a 50-fold increase for the DEN model and a 75-fold increase for VOL, BA, and QMD models. The source of this increased sample size came primarily from the particular segmentation method used. For the variable window locam maxima (VWLM) and Voronoi method, shorter values of the canopy height model implied larger numbers of detected treetops in a given vicinity, which in turn increased the number of polygons produced from the tessellation. The degree to which this segment induced replication reduced is also a function of fixed plot radius, as this limits the number of segments included in the sample as plot radius declines. In our study, the plot radius was 16 m, which is typically regarded as a large plot size for forest management inventories.
The error component could be considered a source of uncertainty that involved the reliability of the estimate of the regression coefficients and the particular predictors used to make a prediction for a given stand. If the predictors in the stand were largely different than the predictors used to fit the model, for example, in a forest stand with extremely tall trees, then could be expected to be large. Generally speaking, this implies that predictions for stand-level means that tend to be far from the global mean tend to have larger values of , which can be observed in Figure 8. The patterns for observed in Figure 8 demonstrate some advantages of the s-ITC method not observed for the component. Namely, the ABA models require a larger degree of extrapolation, shown by the extremely large values for ABA VOL, BA, and QMD models. This is an intuitive result, because the s-ITC models have access to a much larger global sample size as a result of the segment induced replication and, additionally, a sample that contains a much wider range of predictor values compared to that of the ABA models.
The error term accounted for the uncertainty of the estimate of the model parameters, , themselves. For the unit-level model with block-diagonal covariance structure, this term is known to be [31], i.e., the error component declines with an increase in the number of sampled areas. However, in our case, the number of sampled areas was moderate (), and several models demonstrated large values of , specifically the QMD and the DEN ABA models and the DEN s-ITC models. Such a result is intuitive. Models that have a large random effect variance are at risk of larger , all else being equal, because the random effect variance itself is a large source of uncertainty. Additionally, larger stand-specific sample sizes, as in the case of the s-ITC models, may lead to a reduction in (see [23]).
5.2. Peculiarities of a Segment Population
A number of features of a population of segments distinguish it from a population of regular grid cells used in the area-based approach. Most apparent is that the average size of segments are much smaller than that of grid cells (Figure 2). This change in size may make observations of segments more prone to measurement error of observed variables within each population unit. To calculate forest attributes of a segment requires knowledge of the position of each tree within the larger fixed-area plot. As segment size declines, the probability of mis-assigning a tree to one segment increases if measurement error of tree positions is present. In our study, we treated the tree positions as known, but further research could propagate this additional source of error into estimates of . For operational applications, it should be stressed that the required measurement of tree positions presents an increase in the cost of field data collection campaigns, which is not strictly required for the ABA.
Sampling a segment population via fixed radius plots implies a spatial structure of sample observations that are tightly clustered, which presents an opportunity to estimate potential spatial correlation parameters. In an early phase of the analysis, we did not observe strong patterns in empirical semi-variograms for the s-ITC or the ABA that indicated any residual spatial correlation. While many pairwise distances are available at close ranges for s-ITC, e.g., those pairs that exist in the same fixed radius plot, relatively few exist outside of this range. A lack of pairwise observations at close- and mid-range distances often precludes reliable estimation of spatial correlation parameters. A failure to observe spatial correlation patterns in the available data should not be conflated with a lack of its presence in the actual state, and the decision to ignore a possible spatial correlation can lead to a risk of underestimating the mean squared error of stand-level predictions, as discussed for the ABA in [16]. Assessing the impact of ignoring a potential spatial correlation requires specialized datasets not typically found in operational forest inventories [32] or simulation studies [16], and we leave such a question for the case of s-ITC for further research.
When constructing target parameters for both ABA and s-ITC models, a geometric mismatch occurs (e.g., Figure 2) between stands as they are delineated, as they are constructed from a set of cells assigned to that stand and as they are constructed from a set of segments assigned to that stand. We observed mean absolute deviations of 0.12 (0.7%) hectares and 0.3 (1.7%) hectares between segment and cell populations, respectively, as they differed from the stand boundaries, and we expected the impact on stand-level and study region predictions to be minor. These differences were not accounted for in the presented mean squared error estimators but may lead to discrepancies in the estimate of stand-level means. For the s-ITC, the impact of this geometric mismatch would be smaller than that of the ABA given the observed mean absolute deviations, which is one potential advantage of the method. If stand-level predictions are desired for the area-as-delineated, setting to the delineated area during the construction of is one potential alternative, which is equivalent to rescaling the mean prediction to the desired area. Further corrections such as splitting population units by stand boundaries, tightly related to resolution dependence [33], may introduce bias for unit-level predictions and beget further research before serious consideration can be given.
The segmentation method we employed used a Voronoi tessellation of a set of tree height positions that were detected from a canopy height model. This is a deviation from previous s-ITC studies that used segmentation methods based on watershed segmentation [9,10] and is a simpler method compared to other state-of-the-art tree segmentation methods, e.g., [34,35,36]. While the Voronoi tessellation is simple, it guaranteed that we were able to construct the correct target parameter (e.g., the mean volume of a forest stand) by summing the response variables of the individual Voronoi segments weighted by their area (Equation (5)). Methods that produce segments by constraining the shape of the crown observed in the auxiliary data risk the omission of trees in the actual state if, for example, trees exist outside of the identified segments. If an analyst constructs a target parameter from these types of segments, there is a risk that the target parameter will not reflect the actual state. Stand-level predictions from segments of this type are therefore at risk of bias for the “true” target parameter that includes all trees.
While the Voronoi tessellation in tandem with the VWLM detection method is appropriate for the purposes of assessing stand- and region-level predictions, we did not examine the impact of different segmentation configurations or methods. However, we view our analysis as an important step in accommodating these diverse methods under a formal assessment of uncertainty at different scales. Further research could explicitly address the impact of the quality of the segmentation on segment-, stand-, and region-level predictions and compare different methods while maintaining explicit consideration for the “true” target parameter mentioned previously. We acknowledge developments in stochastic geometry, as examined in [37], as a potential source of existing methodology for solutions that may facilitate such an analysis.
5.3. Implications for Forest Management Inventories
As lidar-assisted forest inventories continue to support forest management decisions, explicit consideration of the uncertainty at the resolution where decisions are made is needed. For many forest management organizations, this decision making process is done at the stand level [38] (pp. 13–14). At the same time, the interest and the technology around tree segmentation has seen marked increase in recent years [39,40], yet studies that examine the appropriateness of segmentation methods to support stand-level decision making are rare.
Several studies have investigated small area models and their measures of error for some forest attributes in the context of the ABA. One study [19] investigated unit-level models for predicting VOL in southeastern Norway. Importantly, this study obtained random effect standard deviation estimates, i.e., , in the range of 30 to 38 , depending on whether or not heteroskedasticity was considered. Similarly, [41] obtained a estimate of 2.39 for a study area in southwestern Oregon. Both of these estimates are larger than our estimate, which was negligible (Table 4). The impact that estimates of may have on the mean squared error estimates of stand-level predictions, especially for unsampled stands (Table 6), suggesting that careful consideration should be given for the estimate of this parameter. Recent studies have investigated the estimation of under different sampling scenarios using simulated data [16,42,43] and suggest that small stand-specific sample sizes may introduce a negative bias in the estimation of stand-specific, model-based mean squared errors under the unit-level model. Our study area had sample sizes that widely varied from stand to stand (Table 1), and in this situation, the possibility of negative bias is not as clear. In any case, the sensitivity of estimates of discussed in the previously cited studies warrants further research under different sampling designs, field plot configurations, and estimation methodologies.
Small area models and the behavior of their mean squared error estimates can provide an indication where one inventory system may provide more reliable predictions than an alternative system, i.e., predictions with smaller or . Our results indicated that neither the ABA nor the s-ITC approaches provided clear advantages across all four attributes in both region-level and stand-level estimation cases. Still, a number of important implications are supported by our findings. First, for the case of stand-level predictions in unsampled stands, the ABA demonstrated more reliable performance for all four attributes (Table 6). This suggests the ABA is more suitable for forest inventories where there is a large number of unsampled stands relative to sampled stands or where management decisions need to be made for unsampled stands. Moreover, the ABA does not strictly require the measurement of tree positions, which is necessary for the s-ITC approach. However, for the case of sampled stands, the s-ITC approach demonstrated reductions in for all four attributes, which is driven by segment induced replication (Figure 5). This suggests that forest inventories that contain primarily smaller trees, which beget large increases in sample size relative to the ABA, may benefit from this phenomenon. Additionally for VOL, BA, and QMD models in particular, the s-ITC models also demonstrated lower levels of extrapolation at extreme prediction ranges (Figure 8), a phenomenon that has been noted for s-ITC in previous literature [44]. These two situations are niches where s-ITC models may be able to support reductions in relative to their ABA counterparts.
S-ITC also comes with a number of other benefits, such as an increase in the spatial resolution of unit-level predictions, increased interpretability of population units, and the ability to predict unit-level attributes such as maximum diameter or dominant species for elements whose size is closer to actual trees. While these benefits of s-ITC may be attractive for operational forest inventory systems, we present here a possible analysis that could be conducted when considering the implementation of s-ITC in support of stand-level forest inventory reporting. The methodology can be applied in many situations with similar configurations for the lidar acquisition and field data and can accommodate the comparison of s-ITC and ABA in other regions and forest types. Importantly, the estimate of the stand-specific mean squared errors, which play a large part in determining the reliability of s-ITC or ABA for stand-level reporting, can be conducted using only stands where field plots exist, greatly reducing the computational effort required to compare the two approaches in an initial screening phase. We recognize that s-ITC is one of many possible methodologies to conduct forest inventory assessments using tree segmentation [3,45] and view the incorporation of these other methods into SAE methodology as a basis for further research.
6. Conclusions
We observed a mixture of results when comparing the performance of models using the s-ITC approach and the ABA using model-based mean squared error estimators. For predictions made at the scale of the study region, s-ITC and ABA models achieved similar levels of error for all four attributes. For stand-level predictions in unsampled stands, the ABA was more reliable for all attributes, driven by smaller random effect variance estimates. In sampled stands, the s-ITC approach was able to leverage an increase in sample size to achieve smaller errors for all attributes in some stands and exhibited a smaller risk of extrapolation for VOL, BA, and QMD. This study contributes a formal assessment of the error properties of s-ITC predictions at the scale of forest stands and the study region, which can directly inform forest management planning at these scales.
Author Contributions
Writing—original draft preparation, conceptualization, formal analysis, B.F.; methodology, B.F. and F.M.; writing—review and editing F.M. and H.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the United States Forest Service, grant number 17-JV-11261989-018.
Acknowledgments
We would like to thank the Bureau of Land Management for data acquisition and Jim Flewelling for assistance in its use.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Glossary of major notation for target parameters and the unit-level model.
Table A1.
Glossary of major notation for target parameters and the unit-level model.
| Target Parameters and Their Components | |||
| Notation | Description | Notation | Description |
| for stand). | th population unit in the th area in hectares. | ||
| th area in hectares. | The sum of the areas of all population units in the entire study region in hectares. | ||
| Models and Their Components | |||
| Notation | Description | Notation | Description |
| A vector of observable quantities of the response variable for all population units. | A vector of residuals. | ||
| A design matrix of lidar covariates and an intercept for all population units. | A vector of regression coefficients. | ||
| A matrix that assigns population units to areas. | The variance-covariance matrix of . | ||
| A vector of realized random effects. | The variance-covariance matrix of . | ||
| The residual variance. | The random-effect variance. | ||
| . | , i.e., the number of field plots (ABA) or the number of segments (s-ITC) | ||
| Results Assessment Measures | |||
| Notation | Description | Notation | Description |
| The model-based root mean squared error for the predicted target parameter. | The relative change between s-ITC and ABA model-based root mean squared errors. | ||
| The approximate confidence interval for the predicted target parameter. | The estimated coefficient of variation of the predicted target parameter. | ||
Appendix B

Table A2.
Descriptions of lidar predictors considered for ABA and s-ITC models.
Table A2.
Descriptions of lidar predictors considered for ABA and s-ITC models.
| Predictor Name | Description |
|---|---|
| p_1, p_10, p_20, p_25, p_30, p_40, p_50, p_60, p_70, p_75, p_80, p_90, p_95, p_99 | The percentile of the z-dimension indicated by the trailing number. For example, p_95 describes the elevation at which 95% of the lidar points fall below. |
| max_z | The maximum z value. |
| min_z | The minimum z value. |
| mean_z | The mean z value. |
| stddev_z | The standard deviation of the z values. |
| var_z | The variance of the z values. |
| mean_z_sq | The square of the mean z value. |
| vol_cov | The product of the mean z value and the pct_r_1_above_2 metric. |
| pct_all_above_2 | The proportion of all returns above 2 m. |
| pct_all_above_mean | The proportion of all returns above the mean z value. |
| pct_r_1_above_2 | The proportion of first returns above 2 m. |
| pct_r_1_above_mean | The proportion of all returns above 2 m. |
| r_1, r_2, r_3, r_4 | The number of returns indicated by the trailing number. For example, r_1 indicates the number of first returns. |
| area | The area of the population unit (only included for s-ITC models) |
References
- Nevalainen, O.; Honkavaara, E.; Tuominen, S.; Viljanen, N.; Hakala, T.; Yu, X.; Hyyppä, J.; Saari, H.; Pölönen, I.; Imai, N.; et al. Individual tree detection and classification with UAV-based photogrammetric point clouds and hyperspectral imaging. Remote Sens. 2017, 9, 185. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, T.; Skidmore, A.K.; Heurich, M. Important LiDAR metrics for discriminating forest tree species in Central Europe. ISPRS J. Photogramm. Remote Sens. 2018, 137, 163–174. [Google Scholar] [CrossRef]
- Xu, Q.; Man, A.; Fredrickson, M.; Hou, Z.; Pitkänen, J.; Wing, B.; Ramirez, C.; Li, B.; Greenberg, J.A. Quantification of uncertainty in aboveground biomass estimates derived from small-footprint airborne LiDAR. Remote Sens. Environ. 2018, 216, 514–528. [Google Scholar] [CrossRef]
- Jeronimo, S.M.; Kane, V.R.; Churchill, D.J.; McGaughey, R.J.; Franklin, J.F. Applying LiDAR individual tree detection to management of structurally diverse forest landscapes. J. For. 2018, 116, 336–346. [Google Scholar] [CrossRef]
- Kim, Y.; Yang, Z.; Cohen, W.B.; Pflugmacher, D.; Lauver, C.L.; Vankat, J.L. Distinguishing between live and dead standing tree biomass on the North Rim of Grand Canyon National Park, USA using small-footprint lidar data. Remote Sens. Environ. 2009, 113, 2499–2510. [Google Scholar] [CrossRef]
- Wing, B.M.; Ritchie, M.W.; Boston, K.; Cohen, W.B.; Olsen, M.J. Individual snag detection using neighborhood attribute filtered airborne lidar data. Remote Sens. Environ. 2015, 163, 165–179. [Google Scholar] [CrossRef]
- Silva, C.A.; Hudak, A.T.; Vierling, L.A.; Loudermilk, E.L.; O’Brien, J.J.; Hiers, J.K.; Jack, S.B.; Gonzalez-Benecke, C.; Lee, H.; Falkowski, M.J.; et al. Imputation of individual Longleaf Pine (Pinus palustris Mill.) Tree attributes from field and LiDAR data. Can. J. Remote Sens. 2016, 42, 554–573. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Breidenbach, J.; Næsset, E.; Lien, V.; Gobakken, T.; Solberg, S. Prediction of species specific forest inventory attributes using a nonparametric semi-individual tree crown approach based on fused airborne laser scanning and multispectral data. Remote Sens. Environ. 2010, 114, 911–924. [Google Scholar] [CrossRef]
- Rahlf, J.; Breidenbach, J.; Solberg, S.; Astrup, R. Forest parameter prediction using an image-based point cloud: A comparison of semi-ITC with ABA. Forests 2015, 6, 4059–4071. [Google Scholar] [CrossRef]
- Breidenbach, J.; Astrup, R. The semi-individual tree crown approach. In Forestry Applications of Airborne Laser Scanning; Springer: Dordrecht, The Netherland, 2014; pp. 113–133. [Google Scholar]
- Hyyppa, J. Detecting and estimating attributes for single trees using laser scanner. Photogramm. J. Finl. 1999, 16, 27–42. [Google Scholar]
- Peuhkurinen, J.; Mehtätalo, L.; Maltamo, M. Comparing individual tree detection and the area-based statistical approach for the retrieval of forest stand characteristics using airborne laser scanning in Scots pine stands. Can. J. For. Res. 2011, 41, 583–598. [Google Scholar] [CrossRef]
- Breidenbach, J.; Astrup, R. Small area estimation of forest attributes in the Norwegian National Forest Inventory. Eur. J. Forest. Res. 2012, 131, 1255–1267. [Google Scholar] [CrossRef]
- Goerndt, M.E.; Monleon, V.J.; Temesgen, H. Small-area estimation of county-level forest attributes using ground data and remote sensed auxiliary information. For. Sci. 2013, 59, 536–548. [Google Scholar] [CrossRef]
- Magnussen, S.; Breidenbach, J. Model-dependent forest stand-level inference with and without estimates of stand-effects. Forestry (London) 2017, 90, 675–685. [Google Scholar] [CrossRef]
- Mauro, F.; Molina, I.; García-Abril, A.; Valbuena, R.; Ayuga-Téllez, E. Remote sensing estimates and measures of uncertainty for forest variables at different aggregation levels. Environmetrics 2016, 27, 225–238. [Google Scholar] [CrossRef]
- Hou, Z.; Mehtätalo, L.; McRoberts, R.E.; Stahl, G.; Tokola, T.; Rana, P.; Siipilehto, J.; Xu, Q. Remote sensing-assisted data assimilation and simultaneous inference for forest inventory. Remote Sens. Environ. 2019, 234, 111431. [Google Scholar] [CrossRef]
- Breidenbach, J.; Magnussen, S.; Rahlf, J.; Astrup, R. Unit-level and area-level small area estimation under heteroscedasticity using digital aerial photogrammetry data. Remote Sens. Environ. 2018, 212, 199–211. [Google Scholar] [CrossRef]
- Ubaidillah, A.; Notodiputro, K.A.; Kurnia, A.; Mangku, I.W. Multivariate Fay-Herriot models for small area estimation with application to household consumption per capita expenditure in Indonesia. J. Appl. Stat. 2019, 46, 2845–2861. [Google Scholar] [CrossRef]
- Leite, R.V.; do Amaral, C.H.; Pires, R.d.P.; Silva, C.A.; Soares, C.P.B.; Macedo, R.P.; da Silva, A.A.L.; Broadbent, E.N.; Mohan, M.; Leite, H.G. Estimating Stem Volume in Eucalyptus Plantations Using Airborne LiDAR: A Comparison of Area-and Individual Tree-Based Approaches. Remote Sens. 2020, 12, 1513. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd, ed.; Springer Science & Business Media: Berlin, Germany, 2009; ISBN 978-0-387-84858-7. [Google Scholar]
- Rao, J.N.K.; Molina, I. Small-Area Estimation, 2nd ed.; Wiley Series in Survey Methodology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Flewelling, J.W.; McFadden, G. LiDAR data and cooperative research at Panther Creek, Oregon. In Proceedings of the SilviLaser 2011, 11th International Conference on LiDAR Applications for Assessing Forest Ecosystems, Tasmania, Australia, 16–20 October 2011. [Google Scholar]
- Wang, Y. Volume Estimator Library Equations 2019. Available online: https://www.fs.fed.us/forestmanagement/products/measurement/volume/nvel/index.php (accessed on 4 August 2020).
- Zhang, K.; Chen, S.-C.; Whitman, D.; Shyu, M.-L.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne LIDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Estimating plot-level tree heights with lidar: Local filtering with a canopy-height based variable window size. Comput. Electron. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D. Mixed-Effects Models in S and S-PLUS; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. Nlme: Linear and Nonlinear Mixed Effects Models. R Package Version 3.1-141. 2019. Available online: https://cran.r-project.org/web/packages/nlme/index.html (accessed on 4 August 2020).
- Lumley, T.; Lumley, M.T. Package ‘Leaps.’ Regression Subset Selection. Thomas Lumley Based on Fortran Code by Alan Miller, 2013. Available online: http://CRAN.R-project.org/package=leaps (accessed on 18 March 2018).
- Prasad, N.N.; Rao, J.N. The estimation of the mean squared error of small-area estimators. J. Am. Stat. Assoc. 1990, 85, 163–171. [Google Scholar] [CrossRef]
- Mauro, F.; Monleon, V.J.; Temesgen, H.; Ruiz, L.A. Analysis of spatial correlation in predictive models of forest variables that use LiDAR auxiliary information. Can. J. For. Res. 2017, 47, 788–799. [Google Scholar] [CrossRef]
- Packalen, P.; Strunk, J.; Packalen, T.; Maltamo, M.; Mehtätalo, L. Resolution dependence in an area-based approach to forest inventory with airborne laser scanning. Remote Sens. Environ. 2019, 224, 192–201. [Google Scholar] [CrossRef]
- Tang, S.; Dong, P.; Buckles, B.P. Three-dimensional surface reconstruction of tree canopy from lidar point clouds using a region-based level set method. Int. J. Remote Sens. 2013, 34, 1373–1385. [Google Scholar] [CrossRef]
- Strîmbu, V.F.; Strîmbu, B.M. A graph-based segmentation algorithm for tree crown extraction using airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2015, 104, 30–43. [Google Scholar] [CrossRef]
- Yan, W.; Guan, H.; Cao, L.; Yu, Y.; Li, C.; Lu, J. A self-adaptive mean shift tree-segmentation method Using UAV LiDAR data. Remote Sens. 2020, 12, 515. [Google Scholar] [CrossRef]
- Kansanen, K.; Vauhkonen, J.; Lähivaara, T.; Mehtätalo, L. Stand density estimators based on individual tree detection and stochastic geometry. Can. J. For. Res. 2016, 46, 1359–1366. [Google Scholar] [CrossRef]
- Kangas, A.; Kangas, J.; Kurttila, M. Decision Support for Forest Management; Springer: Dordrecht, The Netherland, 2008. [Google Scholar]
- Wang, Y.; Hyyppä, J.; Liang, X.; Kaartinen, H.; Yu, X.; Lindberg, E.; Holmgren, J.; Qin, Y.; Mallet, C.; Ferraz, A.; et al. International Benchmarking of the Individual Tree Detection Methods for Modeling 3-D Canopy Structure for Silviculture and Forest Ecology Using Airborne Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5011–5027. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in automatic individual tree crown detection and delineation—Evolution of LiDAR data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef]
- Mauro, F.; Monleon, V.J.; Temesgen, H.; Ford, K.R. Analysis of area level and unit level models for small area estimation in forest inventories assisted with LiDAR auxiliary information. PLoS ONE 2017, 12, e0189401. [Google Scholar] [CrossRef] [PubMed]
- Magnussen, S.; Breidenbach, J. Retrieval of among-stand variances from one observation per stand. J. For. Sci. 2020, 66, 133–149. [Google Scholar] [CrossRef]
- Magnussen, S.; Breidenbach, J.; Mauro, F. The challenge of estimating a residual spatial autocorrelation from forest inventory data. Can. J. For. Res. 2017, 47, 1557–1566. [Google Scholar] [CrossRef]
- Breidenbach, J.; Næsset, E.; Gobakken, T. Improving k-nearest neighbor predictions in forest inventories by combining high and low density airborne laser scanning data. Remote Sens. Environ. 2012, 117, 358–365. [Google Scholar] [CrossRef]
- Kansanen, K.; Vauhkonen, J.; Lähivaara, T.; Seppänen, A.; Maltamo, M.; Mehtätalo, L. Estimating forest stand density and structure using Bayesian individual tree detection, stochastic geometry, and distribution matching. ISPRS J. Photogramm. Remote Sens. 2019, 152, 66–78. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).