Abstract
Many satellite soil moisture products are today globally available in near real-time. These observations are of paramount importance for enhancing the understanding of the hydrological cycle and particularly useful for flood forecasting purposes. In recent decades, several studies assimilated satellite soil moisture observations into rainfall-runoff models to improve their flood forecasting skills. The rationale is that a better representation of the catchment states leads to a better stream flow estimation. By exploiting the strong physical connection between the soil moisture dynamic and rainfall, some recent studies demonstrated that satellite soil moisture observations can be also used for enhancing the quality of rainfall observations. Given that the quality of the rainfall is one of the main drivers of the hydrological model uncertainty, this begs the question—to what extent updating soil moisture states leads to better flood forecasting skills than correcting rainfall forcing? In this study, we try to answer this question by using rainfall-runoff observations from 10 catchments throughout the Mediterranean area and a continuous rainfall-runoff model—MISDc—forced with reanalysis- and satellite-based rainfall observations. Satellite soil moisture retrievals from the Advanced SCATterometer (ASCAT) are either assimilated into MISDc model via the Ensemble Kalman filter to update model states or, alternatively, used to correct rainfall observations derived from a reanalysis and a satellite-based product through the integration with soil moisture-based rainfall estimates. 4–9 years (depending on the catchment) of stream flow observations are organized into calibration and validation periods to test the two different schemes. Results show that the rainfall correction is favourable if the target is the predictions of high flows while for low flows there is a small advantage of the state correction scheme with respect to the rainfall correction. The improvements for high flows are particularly large when the quality of the rainfall is relatively poor with important implications for large-scale flood forecasting in the Mediterranean area.
1. Introduction
The value of soil moisture observations for hydrological modelling is unquestionable. Soil moisture influences the partitioning of rainfall into evapotranspiration, infiltration and runoff, hence it is an important factor for determining the magnitude of flood events (e.g., [1,2]). Continuous hydrological models simulate the spatio-temporal evolution of soil moisture for single or multiple soil layers and use this information for predicting the occurrence and the magnitude of floods. A rainfall event occurring in wet and dry conditions shows large differences in terms of hydrologic response, determining the triggering or not of a potentially catastrophic flood event. Therefore, soil moisture observations represent a crucial information for improving hydrological predictions both for small [3,4] and large [5,6,7] river basins.
Measurements of soil moisture can be obtained from both in situ and satellite sensors (see [8] and [9] for two recent reviews), however, in situ observations have been rarely ingested into hydrological models [4,10,11] because their relatively scarce availability in many parts of the world. On the contrary, in recent years, it has been observed a proliferation of studies using coarser satellite soil moisture products for improving model flood forecasting skills [1,3,12,13,14,15,16,17,18]. These studies have demonstrated a general positive impact of satellite soil moisture observations with improvements that have ranged from minor [3,11] to significant [14,16,18] or no improvements. Thanks to the recent availability of high resolution soil moisture observations from Sentinel-1—and its synergy with the soil moisture observations derived from the Soil Moisture Active and Passive (SMAP, [19]) mission [20]—there is high chance that the number of hydrological assimilation studies (involving also smaller catchments) will further increase in the near future (e.g., [21]).
Thanks to the close connection between rainfall and soil moisture, coarse resolution satellite observations were also recently employed by some authors for correcting rainfall [22,23,24,25,26,27]. Corrected rainfall observations (through soil moisture) were then used for forcing hydrological models to explore whether this correction is more beneficial than the classical state update for improving flood forecasting skills [28,29,30].
Satellite soil moisture observations can therefore be ingested in hydrological models through two possible approaches: via state update through classical data assimilation (i.e., variational and sequential techniques) and via rainfall correction (or a combination of both as in [4,28]). In this respect, Crow, W.T. et al. [28] demonstrated the potential of a dual data assimilation (i.e., state correction plus rainfall correction) through a synthetic experiment by using the Ensemble Kalman Filter (EnKF, [31]). The authors highlighted however, that such dual (and simultaneous) use of soil moisture retrievals can conceivably lead to correlation between forecasting and observations errors within the EnKF, and, consequently, to sub-optimal filter performance.
Chen, F. et al. [29] applied the same approach of [28] to 13 basins in the central United States by using the real-time version of the Tropical Rainfall Measuring Mission Multi-satellite Precipitation Analysis (TMPA 3B42RT, [32]) as rainfall forcing and ASCAT [33] and SMOS [34] soil moisture observations for rainfall/state correction. In particular, for rainfall correction, they used the Soil Moisture Analysis Rainfall Tool (SMART, [22]) whereas the state correction was performed through the EnKF. The authors showed that the state correction is overall better than rainfall correction but the latter is able to improve stream flow simulations during high-flow periods better than the state correction. [30] tested the same concept to four large basins in Australia by only changing the hydrological model (i.e., PDM, Probability Distributed Model) and by including the AMSR-E (Advanced Microwave Scanning Radiometer—Earth Observing System) soil moisture product together with SMOS and ASCAT. They confirmed the previous results obtained by [33], also highlighting some of the limitations.
In this study, we further investigate the state/rainfall correction approaches and try to address the following research questions:
- To what extent updating soil moisture states leads to better flood predictions than the correction of the rainfall?
- How much these improvements are affected by the underlying accuracy of the original rainfall product used for forcing the hydrological model?
- What is the impact of the basin size and the climate conditions on the results?
Here, MISDc [35] hydrological model is used for stream flow simulations and the EnKF for correcting the model states within the first of the two approaches (approach SM-corr from here onward). The rainfall correction of a satellite-(TMPA 3B42RT) and a reanalysis-based (ERA-Interim, [36]) product is performed by their integration with rainfall estimates obtained thought the inversion of ASCAT soil moisture observations via SM2RAIN [24]. The corrected rainfall products are then used as alternative to the states correction to force MISDc within the second of the two approaches (approach P-corr from here onward). Daily stream flow observations from 10 basins (4–9 years of data) throughout the Mediterranean area are used as benchmark to address the above research questions. The application of the two schemes to a reanalysis and a satellite-based rainfall product aims to simulate a scenario of ground data scarcity as happens in many regions of the world [37].
With respect to previous studies, three important novelties are introduced: (1) a different rainfall correction algorithm (i.e., the integration of the rainfall observations is carried out with SM2RAIN), (2) a different study area—the Mediterranean area, and) the use of both satellite- and a reanalysis rainfall products which—given the different accuracy of the products—allows to test the two different schemes (i.e., the SM-corr and P-corr) as a function of the underlying rainfall quality.
The paper is organized as follows. Section 2 contains the description of the study area and the datasets used to carry out the analysis. Section 3 provides a description of the hydrological model, the data assimilation and the rainfall correction schemes as well as the performance metrics used for evaluating the results. Results and discussion are contained in Section 4 and final remarks are presented in the Conclusion section.
2. Material
2.1. Study Area
The study is carried out over the Mediterranean where flood and flash flood events cause significant economic and social losses. Mediterranean is characterized by varied and contrasting topography including the Alpine Mountains in the Italian and Balkan peninsulas, Northern Spain, and Southern France. Due to the topographic complexity, the climate includes hot-dry summers and humid-cold winters. A clear contrast exists between the more-rainy northern part of the study region (Southern Europe) and the drier southern area (North Africa, Iberian Peninsula) and between the western sides (rainsides) of the Iberian, Italian and Balkan peninsulas and their eastern sides (rainshadows). The mean annual precipitation averaged over the study area is equal to 593 ± 203 mm/year, characterized by a strong spatial variability which ranges from 20–40 mm/year in North Africa to 1500–2000 mm/year over the Alps. A significant seasonal variability exists, with the late autumn and early winter months (September to November) being the wettest where floods usually occur.
Table 1 summarizes the main characteristics of the selected study catchments, with area ranging from nearly 450 km2 for the Kolpa river basin in Slovenia to about 5000 km2 for the Tevere River basin in central Italy, mean basin elevation ranges from 197 m a.s.l. (lowland basin) to 1362 m a.s.l. (mountainous basin). Given the different climatic and physiographic conditions that characterize the selected catchments, they can be considered a representative sample of the catchments located in the Mediterranean (Figure 1).

Table 1.
Main characteristics of the investigated catchments. Cfb: temperate warm summer, Dfb: Cold Warm summer; Csa: Temperate dry and hot summer; Csb: Temperate dry and warm summer according to the Köppen classication.
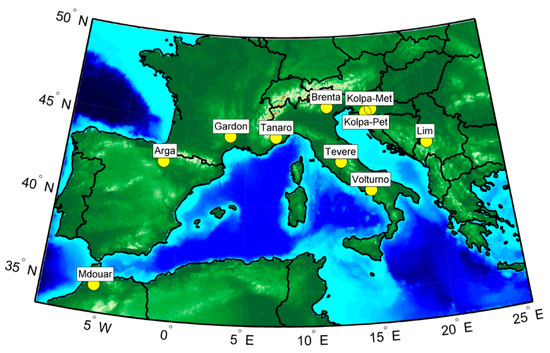
Figure 1.
Location of the investigated catchments in the Mediterranean area.
2.2. Datasets
2.2.1. Soil Moisture Observations
In this study, we used the soil moisture observations derived from the Advanced SCATterometer (ASCAT) onboard the Metop-A and -B satellites [33]. The version of the product is the “H111” which is obtained from the combination of Metop-A and -B satellites and distributed within the “EUMETSAT Satellite Application Facility on Support to Operational Hydrology and Water Management (H-SAF, http://hsaf.meteoam.it/)”. H111 is globally available since 2007 with a spatial sampling of 12.5 km and a nearly daily temporal resolution. ASCAT observations were selected because they (1) cover the periods where discharge observations are available, (2) are available in near-real time and (3) are characterized by a relatively good performance in the Mediterranean (e.g., [38,39]). Only for the purpose of characterizing the ASCAT error (see Section 3.2.1) we used the satellite soil moisture observations derived from passive product of the European Space Agency (ESA) Climate Change Initiative (CCI) (http://www.esa-soilmoisture-cci.org/) which is available from 1978 until 2016 with a spatial sampling of 0.25° and a daily temporal sampling [40]. The choice of this dataset—CCIpas—is driven by its independence with respect to ASCAT observations and its full availability during the period of analysis. Both the ASCAT and CCIpas products are spatially resampled over the catchment boundaries to provide watershed-scale average of soil moisture.
2.2.2. Rainfall and Temperature Data
As ground-based rainfall and temperature products, we used the European daily high-resolution gridded data sets of precipitation and air temperature E-OBS [41], developed as part of the EU-FP6 ENSEMBLES project. The rainfall and temperature provided by E-OBS are available for the period 1950 up to now. Given the relatively high density of the rain gauges and thermometers used by this product, E-OBS dataset can be considered as a high-quality meteorological dataset [42]. Rainfall observations derived from E-OBS will be referred for simplicity as EOBS from here onward and will be used for MISDc parameter calibration and for benchmarking non-gauge rainfall observations and stream flow simulations (via MISDc).
As satellite-based rainfall datasets, we used two products. The first product is the real-time version of the Tropical Rainfall Measuring Mission Multi-Satellite Precipitation Analysis (TMPA 3B42RT) which is available from 1997 onward with 3-hourly temporal resolution and a spatial resolution of 0.25° for the 50° north-south latitude band. The retrieval algorithm takes advantages of multiple sensors, by blending polar microwave satellite sensors with geostationary infrared data (e.g., [32]) and does not contain ground-based rain gauge observations. For simplicity, the satellite-based rainfall product is referred to as 3B42RT hereinafter. The second product is the European SM2RAIN-ASCAT dataset currently available from 2007 to 2015, with a spatial/temporal sampling of 0.25 degree/1-day (data of this product are accessible at [43]). Rainfall estimates derived from SM2RAIN-ASCAT are obtained by inverting the soil moisture observations derived from the H111 dataset (see Section 2.2.1) through SM2RAIN [24]. SM2RAIN is an algorithm for estimating rainfall accumulations from soil moisture observations. The method has demonstrated to provide accumulated rainfall estimates with an accuracy comparable (and higher depending on the regions) to state-of-the-art satellite rainfall products [24,26,44]. For further details on the method and its application, the reader is referred to [24].
In addition to satellite-based rainfall products, we used a reanalysis product derived from the ERA-Interim atmospheric ocean and land reanalysis, ERA-Interim ([36], http://www.ecmwf.int) of the European Centre for Medium-Range Weather Forecasts (ECMWF). ERA-Interim precipitation (ERA from here onward) is available from 1 January 1979 to now. In this study, daily precipitation values are obtained from the temporal aggregation of ERA-Interim 12-hourly-precipitation accumulation estimates. ERA-Interim pixels falling inside the catchment boundaries are selected from the bi-linearly interpolated 0.25° grid obtained directly from the ECMWF API.
As for soil moisture observations, rainfall and temperature data obtained from the foregoing products are averaged at the watershed scale for all the study catchments.
2.2.3. Stream Flow Data
Daily stream flow data are available for all the study catchments as described in Table 1. The discharge dataset ranges from 4 to 9 years depending on the catchment with a mean length of nearly 6 years and were collected from local authorities and from the Global Runoff Data Center (GRDC, http://www.bafg.de/GRDC/EN/01_GRDC/grdc_node.html) for the stream flow data of two Kolpa and Lim catchments.
3. Methods
In this study, the hydrological simulations are obtained through a modified version of the MISDc hydrological model [35,45]. Two data assimilation strategies are used to ingest satellite soil moisture observations into MISDc. The first one is the classical EnKF where the model states are updated by weighing the relative accuracy of ASCAT soil moisture observations with the model predictions by using a Montecarlo based approach. The second one, already used in [4,25], is based on a simple static integration scheme.
3.1. MISDc
MISDc—“Modello Idrologico Semi-Distribuito in continuo”—is a continuous rainfall-runoff model developed by [35] for the operational forecasting of flood events in the Tevere River Basin (central Italy). In this paper, a two-layers version of the model is used. With respect to the previous version, it includes a snow module and a different infiltration equation. The model uses as input daily rainfall and air temperature data and simulates the temporal evolution of two independent soil water states W1 and W2. Water is extracted from the first layer by evapotranspiration which is calculated by a linear function between the potential evaporation (estimated via the Blaney and Criddle relation modified by [45,46] and the soil saturation. A non-linear relation proposed by [47] calculates percolation from the surface to the root zone layer. The rainfall excess is calculated by a power law relationship as a function of the first layer soil saturation while base flow is a non-linear function of the soil moisture content of the third layer [48].
Three different components contribute to generate runoff: the surface runoff, the saturation excess from the surface and the deep layer and the sub-surface runoff component. The first two are summed and routed to the outlet by the Geomorphological Instantaneous Unit Hydro-graph (GIUH) while the subsurface runoff is transferred to the outlet section by a linear reservoir approach. For both routing schemes, the lag time is evaluated by the relationship proposed by [49]. Full details on model equations are already given in [35] and, hence, are not repeated here.
The 10 model parameters of the model are shown in Table 2 along with the assumed range of variability.

Table 2.
List of the calibrated parameter of MISDc model.
3.2. Soil Moisture Data Assimilation
3.2.1. Pre-Processing of Soil Moisture Observations and Error Estimation
Satellite soil moisture observations are representative of a shallow soil layer of 2–3 cm while the model first layer water capacity is 150 mm (which roughly corresponds to 300 mm by assuming a reasonable range of porosity between 0.45 and 0.5). Therefore, prior to use them for the hydrological data assimilation they require a pre-processing step to address the depth mismatch with the model state [13,14,16]. For this purpose, the recursive formulation of the Exponential filter [50,51] was used to obtain the so-called Soil Water Index (SWI) based on a single parameter, T, named characteristic time length. T was optimized by maximizing the correlation between SWI obtained from ASCAT (SWIASCAT) and the model state of the first model layer (W1). Before the assimilation, the satellite soil moisture observations were bias corrected to the model climatology by the quantile mapping approach [52]. A 2nd order polynomial function was used for mapping SWI data to the model, thus obtaining SWI*ASCAT. The same processing steps applied to ASCAT were applied to the CCIpas to obtain SWI*CCIpas. This was done for obtaining the same climatology and dynamic range of W1 and reduce the impact caused by the different vertical representativeness when used within the Triple Collocation (TC, [53]) analysis (see below).
Given the relatively poor presence of ground monitoring stations of soil moisture, the estimation of the satellite soil moisture error variance needed for data assimilation is not an easy task. In this respect, TC has demonstrated to be a reliable technique [54] to estimate the error variance of three independent soil moisture datasets provided that they are characterized by zero cross correlation errors. Here, we follow the approach of [29] and applied TC to soil moisture observations derived from the triplets built among SWI*ASCAT, SWI*CCIpas and W1 to calculate the SWI*ASCAT error variance (). In practice, the three datasets are decomposed into the corresponding climatology anomalies time series by subtracting the long-term 31-day moving average from the raw time series. This guarantees the estimation of only random error sources and a more accurate observation error variance estimate [55]. The application of TC is only performed for the calculation of the scaled error variance of SWI*ASCAT which is then used within the SM-corr approach.
The calibration of the parameters involved in the pre-processing steps (T and the coefficients of the quantile mapping) along with the estimation of the ASCAT error variance were carried out during the calibration period in order to maintain a rigorous separation with the validation period and guarantees a more objective evaluation of the different methodologies (see Section 3.5).
3.2.2. The Ensemble Kalman Filter
In hydrological data assimilation, EnKF (and its variations) have been largely used because of their computational efficiency and flexibility. The EnKF is based upon Monte Carlo method and the Kalman filter formulation to approximate the true probability distribution of the model state, conditioned on a series of observations of the model states. The EnKF was introduced as an alternative to the traditional Extended Kalman filter which has been shown to be problematic because of the strongly nonlinear dynamics of hydrological models.
Being Y(tk) the vector of system states at time step tk, Y(t) = [W1(tk), W2(tk)]T obtained via a generic model and Zk the observation vector at time tk, then, the optimal updating of Yk, can be expressed as:
where and refer to the forecast and analysis states for the ith ensemble member, respectively, Hk is the observation operator that maps the model states to the observations, vk is a synthetically generated error added to the observation Zk and represents the uncertainties of the observation process that is assumed to be a mean-zero Gaussian random variable with variance Rk. Gk is the Kalman gain:
where is 2 × 2 covariance matrix of forecast error obtained from the N-member ensemble of background predictions:
Given the preprocessing applied to the satellite SM products (see Section 3.2.1), the observation operator in Equation (2) reduces to H = [1 0]T while the observation error covariance matrix, Rk, reduces to since only pre-processed soil moisture derived from ASCAT is assimilated. The single deterministic EnKF prediction (i.e., the “analysis”) is calculated by averaging model state predictions, , and the consequent stream flow at each time step across the N members of the ensemble. In Equation (3), denotes the mean of . The covariance matrix of the forecast error was obtained by perturbing rainfall and temperature data along with the model soil moisture predictions (see next section).
3.2.3. Filter Calibration
In this study, we adopted a multiplicative model error [56] for perturbing rainfall observations (assuming no autocorrelation in the rainfall error) and an additive perturbation for temperature [13] and soil moisture predictions. These perturbations aimed to represent the main sources of model error, coming from the forcing data, the model parameters and the model structure. Rainfall was perturbed by a log-normally distributed, unit mean, spatially homogeneous and temporally uncorrelated multiplicative random noise with standard deviation equal to , whereas for temperature and soil moisture a zero-mean normally distributed additive error was chosen with standard deviations equal to and , respectively. was chosen equal to 1 °C while = 10−3. was made variable between 10−5 and 2 by assuming that the main error of the model is associated to the uncertainty in the precipitation forcing. The optimal value was selected by picking the one that, by running the filter during the calibration period, minimizes the root mean square error (RMSE) between simulated (ensemble-averaged) and observed discharge time series and ensures that innovations (the second term in square brackets in Equation (1)) have zero mean and are serially uncorrelated [57]. Note that, given the model non-linearity, the satisfaction of the latter criterion was very difficult to obtain and thus was not always guaranteed. In addition, the model error calibration based on the minimization of the RMSE as done here, assumes that the error in stream flow observations is negligible. However, if significant errors are present in observed stream flow, this procedure may be sub-optimal and the filter inflated by these errors. Alternative procedures that guarantee a more optimal filter performance are also possible [56] but are beyond to scope of the paper and are not treated here. The ensemble size was set to 50 members, more numerous ensembles were also tested but did not provide significant changes therefore N = 50 was finally set to speed up the calculations.
3.3. Rainfall Correction
3.3.1. Pre-Processing of Rainfall Observations
Prior to run the model with satellite-based rainfall estimates we bias-corrected SM2RAIN-ASCAT, ERA and 3B42RT with E-OBS rainfall observations. The main reason of the bias correction of satellite-based rainfall estimates is that—due to the indirect nature of the measurement—they are potentially affected by significant biases that can seriously impact the quality of the hydrological simulations [58]. For that, we used the same quantile mapping approach used for soil moisture bias correction [52] with a 2nd order polynomial function (different orders were preliminary tested and the 2nd order was found to perform the best). The bias corrected products will be referred to PSM2RAIN-ASC for SM2RAIN-ASCAT, PERA for ERA-Interim and P3B42RT for 3B42RT from here onward. To maintain a consistent notation, the original EOBS rainfall product will be also denoted as PEOBS in the following. As for the pre-processing of soil moisture the bias correction calibration parameters were determined during the calibration period (see Section 3.5) and then used in validation.
3.3.2. Rainfall Integration
The merging between PSM2RAIN-ASC and the specific rainfall product (i.e., P3B42RT or PERA) was carried out by a simple Newtonian nudging scheme [4]:
where t is time, PCOR is the corrected rainfall product (PERA+ SM2RAIN-ASC or P3B42RT+SM2RAIN-ASC), P* is P3B42RT or PERA. K is a static weighting parameter estimated during the calibration period by minimizing the RMSE between simulated stream flow time series and observations. K gives the relative weight of PSM2RAIN-ASC with respect to the satellite (reanalysis) rainfall product. K equal to 1 means that the error in satellite (reanalysis) rainfall is much lower than PSM2RAIN-ASC and no correction is performed while K equal to 0 means that PSM2RAIN-ASC error is much lower than satellite (reanalysis) rainfall, thus only PSM2RAIN-ASC is used. To maintain a similar methodology approach with the one used in Section 3.2.3, K was calibrated by minimizing the RMSE between simulated and observed discharge time series during the calibration period. The calibrated K for each basin were then used in validation. Being calibrated based on the RMSE between simulated and observed stream flow time series, the determination of K is subjected to the same limitations described in Section 3.2.3 (i.e., it can be inflated by errors contained in observed stream flow).
3.4. Performance Metrics
The hydrological performance of the different simulations was assessed through three different metrics specifically targeted for floods. The first metric—to evaluate the prediction of high flows—is the Nash–Sutcliffe efficiency (NSE, [59]) adapted to high-flow conditions (ANSE, [60]):
The second metric—specifically designed for low flows—is the NSE calculated on logarithmic discharges:
In Equations (5) and (6) the sum is carried over the length Nt of the observed, , and simulated , discharges vectors. The term in Equation (6), was arbitrarily chosen as a small fraction of the inter-annual mean discharge (e.g., ) and was introduced to avoid problems with nil observed or simulated discharges.
The third metric, the Kling-Gupta efficiency [61] was adopted for assessing the simulation performance for a wider range of flow conditions (but with a tendency to privilege high flow given that it was introduced for flood assessment). The KGE is a performance indicator based on the equal weighting of three sub-components: linear correlation (r), bias ratio (β = μsim/μobs), and variability (δ = CVsim/CVobs), between and . KGE is defined as follows:
being μ and CV the mean and the coefficient of variation. ANSE, NSlogQ and KGE vary between −∞ and 1 with values equal to one denoting perfect agreement between stream flow observations and simulations.
3.5. Method Implementation
The implementation of the two schemes (i.e., SM-corr and P-corr) was carried out by organizing the datasets in two sub-periods; the first sub-period was used for model parameters calibration and for the calibration of the parameters associated to the data assimilation/integration schemes. In particular, about 50–60% of discharge observations—depending on the basin—were assigned to the calibration period by guaranteeing a minimum time period of two years (see Table 1). The remainder of the period was used for validation.
The calibration of the model parameters was carried out by maximizing the KGE index between observed and simulated discharge time series obtained by forcing MISDc model with PEOBS rainfall and temperature (see Figure 2a) through a standard gradient-based automatic optimization algorithm [62]. The calibrated parameters were then used within all the simulations involving P3B42RT and PERA. As denoted in Section 3.2.1, Section 3.3.1 and Section 3.2.3, during calibration, we determined the (1) optimal rainfall bias correction parameters, (2) the parameter K related to the rainfall integration, (3) the data assimilation parameters (i.e., the characteristic time length T and the parameters associated to the bias correction of soil moisture), (4) the satellite soil moisture observation error (σ*SWI) and (5) the forecast model error. The calibrated integration/assimilation parameters were then used during the validation periods for obtaining discharge simulations for SM-corr and P-corr for a total of six different runs (Figure 2b). That is, the two off-line simulations obtained by forcing the model with PERA (OLM) and P3B42RT (OLS), the two data assimilation experiments where ASCAT soil moisture observations were assimilated into MISDc forced with PERA (DAM) and P3B42RT (DAS) and the two integration experiments where corrected rainfall PSM2RAIN-ASC + ERA (RCM) and PSM2RAIN-ASC + 3B42RT (RCS) were used to force MISDc. As a baseline for comparing the performance of satellite and reanalysis rainfall products, also the runs in which MISDc was forced with PEOBS were considered (OLG in Figure 2b).
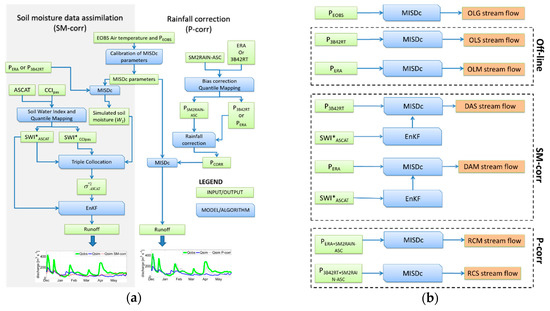
Figure 2.
(a) Flowchart illustrating the main implementation steps of the soil moisture data assimilation (SM-corr, left) and the rainfall correction (P-corr, right) methods. (b) Simulation runs used in the study.
4. Results and Discussion
4.1. MISDc Model Calibration and Validation Forced with Ground-Based Data
The calibrated parameters of MISDc (obtained by forcing the model with PEOBS) provide a median KGE efficiency index equal to 0.692 (i.e., always above 0.6 except for Volturno, see Table 1). In this respect, MISDc performance can be considered relatively good and between the intermediate (0.75 > KGE > 0.5) and good (KGE > 0.75) level as identified in [63]. This ensures the reliability of the model for stream flow simulations. Based on Table 1 (and Table 3) it can be observed that cold and more humid catchments generally perform better than warm and drier ones.

Table 3.
Kling-Gupta performance index obtained during calibration by forcing the model with PEOBS (CALIBRATION in dark grey) and during the validation period (VALIDATION in light grey and blue) for (1) MISDc model forced with PEOBS (OLG in white), (2) MISDc model forced with PERA and P3B42RT (OLM, OLS), (3) the state correction scheme (DAM, DAS) and (4) the rainfall correction scheme (RCM, RCS). Numbers in bold refer to the best score obtained in validation among OLG, OLM, DAM, RCM, OLS, DAS and RCS.
4.2. Satellite Soil Moisture Pre-Processing and Filter Calibration
Figure 3a shows the parameter T that maximises the correlation coefficient between the modelled soil moisture of the first layer W1 and the SWI*ASCAT for all the analysed catchments for PERA and P3B42RT. T is lower than 20 days for most of the catchments except Arga and Volturno where it reaches a value of about 60 days. These results are consistent with the range of values found in previous studies (e.g., [13,16,30,64]). There is not a specific pattern that is possible to identify for the study catchments because T variations are not only related to the specific catchment hydrology but also to the model and the satellite observation quality
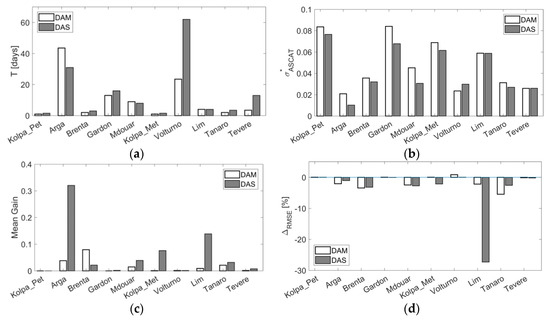
Figure 3.
Characteristic time length T (a), SWI*ASCAT error standard deviation (b), mean Kalman Gain G (c), and % improvement in RMSE between simulated and observed stream flow (d) obtained during the calibration period within the SM-corr approach by using P3B42RT (DAS) and PERA (DAM) for forcing MISDc model.
Figure 3b shows the observation error variances of SWI*ASCAT obtained by considering the triplets among SWI*ASCAT, SWICCIpas and the soil moisture simulated by MISDc model forced with PERA (P3B42RT). The error variances found with the two triplets maintain a similar comparative relationship among basins showing smaller values for drier and warm catchments (Tevere, Arga, Mdouar) and larger values for more cold and humid (mountainous) catchments (Kolpa@Petrina, Gardon, Lim). The relatively better performance of ASCAT in semi-arid environments is consistent with the results of [64,65].
Figure 3c,d plot the mean Kalman gain, G, for the first model layer and the RMSE changes obtained after the assimilation of SWI*ASCAT during the calibration period. The reduction in RMSE is relatively low and less than the 10% found by [29] with some catchments characterized by no-improvements.
4.3. Rainfall Correction Calibration
Figure 4a summarises the values of the parameter K obtained during the calibration period for all the investigated catchments while Figure 4b shows the reduction in RMSE between observed and simulated stream flow after integrating PERA and P3B42RT with PSM2RAIN-ASC through Equation (4). It can be seen that K is significantly higher for RCM (mean K = 0.77) with respect to RCS (mean K = 0.42) suggesting a higher quality of PERA with respect to P3B42RT. It can be also seen that lower K values (i.e., which means that PSM2RAIN-ASC is weighed more with respect to the counterpart product in Equation (4) provide a larger decrease in RMSE and this reduction is generally larger for RCS with respect to RCM.
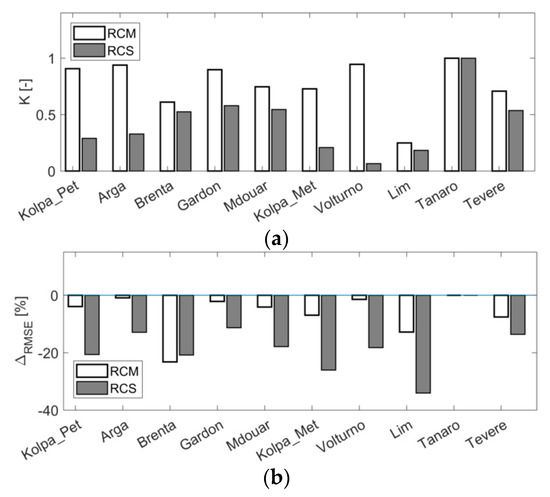
Figure 4.
Values of the calibrated gain parameter K for PERA and the P3B42RT obtained during the calibration period (a) and % reduction in RMSE between observed and simulated stream flow during the calibration period (b). K close to zero indicates that more weight is assigned to PSM2RAIN-ASCAT dataset according to Equation (4).
4.4. Rainfall Evaluation
Given the relatively high density of rain gauges used in EOBS dataset, PEOBS can be considered a good reference for evaluating the performance of P3B42RT and PERA (and their associated integrated products) over the study catchments. Figure 5 shows the scatter plots of the correlations between P3B42RT, PERA, PERA+SM2RAIN-ASC, P3B42RT+SM2RAIN-ASC and PEOBS for each catchment in Table 1 during the validation period.
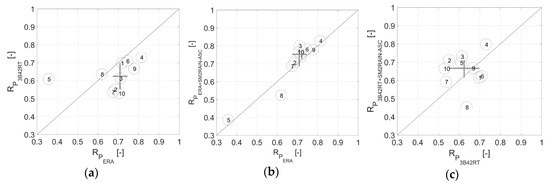
Figure 5.
(a) comparison of correlations R between PERA and P3B42RT obtained with PEOBS for all study catchments during the validation period; (b) same as panel (a) but between PERA and PERA+SM2RAIN-ASC; (c) same as panel (a) but between P3B42RT and P3B42RT+SM2RAIN-ASC. The points where the lines cross refer to the medians while the line edges represent the 25th and the 75th percentiles.
Panel a compares the correlation between PERA and P3B42RT. It can be seen that PERA performs relatively better than P3B42RT for almost all catchments thus confirming the previous results in terms of K obtained in calibration. Similar results were also found by [44] who observed a higher quality of ERA-Interim in Europe with respect to 3B42RT. The only exception is the Mdouar catchment. Here the reanalysis product performs relatively worse than the satellite-based one. A possible reason of the lower performance is related to the type of precipitation that characterizes this area (stratiform vs. convective precipitation) as also found in [66,67,68].
The integration between PSM2RAIN-ASC and PERA (P3B42RT)—which is based on minimization of the RMSE between observed and simulated stream flow during the calibration period—indirectly leads to increased rainfall quality both during the calibration (not shown) and the validation periods (Figure 5b,c). In Figure 5b,c, the Lim catchment (#8), is the only catchment where the integration provides a significant deterioration of the correlation. A slight deterioration is also observed for Kolpa@Petrina (#1) and Kolpa@Metilka (#6) when integrating P3B42RT and PSM2RAIN-ASC. However, these deteriorations (including the one of Lim catchments) are significantly lower when the rainfall products are compared in terms of RMSE (not shown). Possible reasons of the deteriorations are related to ASCAT error that, in this catchment is relatively higher (see Figure 3) and to the SM2RAIN limitations when the soil is close to saturation (see below).
4.5. Stream Flow Evaluation
Table 3 shows the performance obtained during the validation period for the off-line (OLM, OLS), SM-corr (DAM, DAS) and P-corr (RCM, RCS) runs along with the stream flow simulations obtained by forcing the model with PEOBS during the validation period (i.e., OLG run).
OLG performs relatively well for 5 out of 10 catchments (Kolpa@Petrina, Kolpa@Metilka, Gardon, Mdouar, Lim) with median KGE equal to 0.481. For the others catchments stream flow simulations are poor with the Tanaro basin providing the worst result. The performance for OLM and OLS are in general lower than OLG with median KGE equal to 0.399 and 0.289, respectively (i.e., below the intermediate level of 0.5). For OLM, the simulation for Mdouar provides KGE lower than zero due to the poor quality of PERA precipitation in this basin (as seen in Section 4.4). The topographic complexity of the study area along with the strong non-stationary performance of satellite-based rainfall products over time caused by the season and by the variable number of satellite microwave passes used for the retrieval of precipitation [42,69,70] are the main causes of the low scores obtained in the stream flow simulations with P3B42RT [71]. In practice, the satellite precipitation error has both (1) a direct effect on stream flow estimates by determining under(over) estimations due to the erroneous instantaneous precipitation and (2) an indirect effect on the state estimation that propagates in time for several days/months causing additional stream flow errors. The low scores of the stream flow estimates derived from satellite-based rainfall observations are in line with those found in many other studies in literature [30,37,71,72]. In the latter, it was who found that reanalysis-based rainfall products generally outperform satellite-based ones in hydrological modelling.
SM-corr (DAM and DAS) has generally a small positive impact on stream flow simulations in terms of KGE, with an increase in median KGE from 0.399 to 0.416 (about 4%) for DAM and from 0.289 to 0.317 for DAS (10%). The catchments that benefit more from the SM-corr scheme are Brenta, Tanaro and Tevere for DAM and Arga, Mdouar and Tevere for DAS (although for some of them KGE remains very low). One main reason for the small or no improvements observed for some catchments (e.g., Kolpa@Metilka, Kolpa@Petrina and Gardon) can be due to the specific runoff generation mechanism/model structure/data assimilation configuration. In this respect, we found that the correction of the model state in the root-zone layer for these catchments is always very small, meaning that the model is characterized by a weak coupling between the first and the second layer. Therefore, if the runoff generation mechanism is mainly associated to the root zone, then the assimilation of surface observations has a negligible impact on stream flow simulations. Similar results were also found in [11,13,15]. Other possible reasons are directly related to the ASCAT quality itself and to the different pre-processing steps that characterize the state correction scheme [16,30]. In this respect, the application of TC, the rescaling procedure and the filter calibration were applied to the calibration period and it is not guaranteed that they are optimal also in a different period (e.g., Lim catchment). This is particularly true for the satellite soil moisture error variance and for the bias which are characterized by a non-stationary behaviour over time [73]. Moreover, the introduction of auto correlated errors in the observation error derived from the application of the Exponential Filter [30] is another reason of a potential sub-optimal performance.
For P-corr, the increase in median KGE is from 0.399 to 0.456 (14%) for RCM and from 0.317 to 0.494 (71%) for RCS indicating that the precipitation correction has a remarkable impact on the stream flow simulations. In particular, RCS provides median KGE larger than the performance obtained in OLG (i.e., the model forced with PEOBS) and those obtained with RCM. Here, KGE is equal 0.494 for OLS and 0.481 for OLG with Volturno and Tevere being the best among OLG, OLS, DAS, DAM. In a recent study by [72] it was found that gauge-based and reanalysis products generally outperform satellite based products for flood simulations [72]. We found that the correction of 3B42RT with SM2RAIN rainfall estimates performs better than simulations using gauge-based observations (i.e., EOBS). This encouraging result demonstrates the potentiality to improve operational stream flow forecasting by using remotely sensed surface soil moisture.
With respect to the results obtained with OLM, both RCM and RCS are able to increase KGE scores in drier and warm catchments (e.g., Arga, Volturno, Lim and Tevere) while in more humid and cold basins we observed deteriorations or no improvement (Kolpa@Petrina, Kolpa@Metilka Tanaro and Brenta). One reason for the deterioration is the problem of saturation associated to the SM2RAIN rainfall estimates. In practice, when surface soil moisture reaches the saturation (which occurs mode frequently in more humid climates) SM2RAIN can no longer reliably inverts soil moisture to precipitation [24] and can provides significant underestimation of the rainfall events. Similar issues were found in [11] by correcting rainfall from 3B42RT via the SMART algorithm. Another possible reason for the deteriorations is related to the static nature of the integration scheme combined with the variable performance in time of satellite-based and reanalysis products. For the latter, the variable performance in time of precipitation depends on its underlying nature (stratiform or convective, [74] with potential underestimation of total precipitation for convection dominated conditions (which occur during summer/earlier autumn in the Mediterranean area, [75]). In practice, both for satellite- and reanalysis-based products it is not guarantee that K values found during the calibration period are optimal also during the validation period. In this respect, more optimal and dynamic (as a function of the current retrieval error) integration strategies will likely lead to better results.
To analyse the impact of the SM-corr and P-corr schemes on low and high flows we plotted the box plots of ANSE and NSlnQ indexes in Figure 6. For ANSE, both the SM-corr and P-corr schemes improve the model performance obtained in the off-line simulations with a clear advantage of the P-corr scheme. In median, the enhancements obtained for RCM and RCS are larger with respect to DAM and DAS and allow to obtain ANSE values close to the ones obtained in OLG (note that as for the KGE results presented in Table 3 some catchments—not shown—have ANSE values larger than the ones obtained in OLG). For low flow conditions, the performance of the model is generally lower and cannot be observed a clear advantage of one technique with respect to the other. However, in median, DAM and DAS provide a slightly better performance (note that for DAM, these scores are above those obtained in OLG). These results are consistent with those found by [11] where the rainfall correction scheme improved better high flows with respect to state correction. They are less consistent with the results of [30] who showed a higher positive impact on the stream flow prediction of the state correction with respect to the forcing correction scheme both for high and low flows (for the latter the improvements were higher though). The smaller increments obtained in the DAM and DAS cases are in line with those found in [28] and lower with respect to the ones in [11] where the state correction scheme implemented via EnKF benefited from the correction of the ensemble perturbation bias.
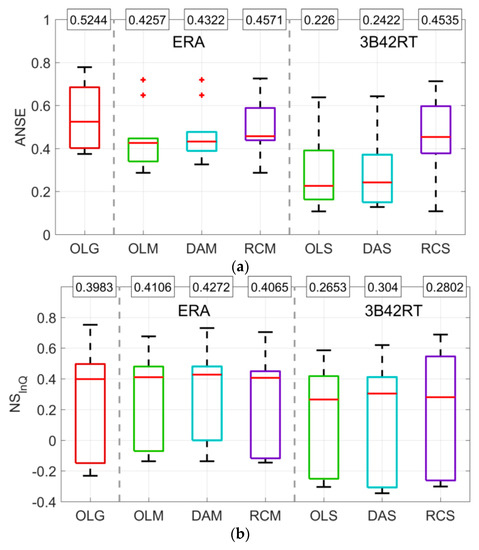
Figure 6.
Summary of the results in terms of ANSE (Nash–Sutcliffe efficiency for high-flow conditions) and NSlnQ (NS adapted for low flow conditions) for all the investigated basins during the validation period. Red box plots refer to the results obtained by forcing MISDc with PEOBS datasets; the number in the square boxes represent the median values. Results are shown for the off-line simulations (OLM, OLS), for the SM-corr scheme (DAM, DAS) and for the P-corr scheme (RCM, RCS).
Figure 7 shows the stream flow simulations for the OLM, DAM and RCM (first column) and OLS, DAS and RCS (second column) during the calibration (white background) and validation periods (grey background) for two representative catchments (Kolpa@Petrina and Tevere). In each panel, the upper plot shows the comparison in terms of stream flow whereas the bottom one displays the RMSE variation in time between simulate and observed stream flow smoothed time series (a moving mean of 60 days was chosen for sake of visualization). It can be seen that for Kolpa@Petrina catchment both the SM-corr and P-corr schemes fail to improve stream flow simulations with negligible effect on the time series. Some improvements can be seen between OLS and RCS until January 2011 but strong deteriorations occur from January 2012 onward with severe underestimation of the flow peaks during winter 2012 likely due to the issues of saturation discussed before (K for RCS is very small in this catchment and the integrated rainfall largely consists of PSM2RAIN-ASC rainfall estimates). This assumption is supported by the detrimental effect of the integration on the precipitation for this catchment as plotted in Figure 5c.
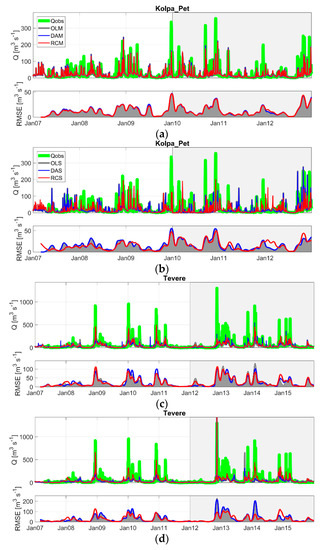
Figure 7.
Stream flow simulations in the calibration and validation period for Kolpa-Pet (panels a,b) and Tevere (panel c,d) catchments. For each catchment, the results for OLM, OLS, DAM, DAS, RCM and RCS are shown. In each panel, the upper plot shows the comparison in terms of stream flow while the bottom one shows the smoothed time series of the RMSE (by using a moving windows of 60 days for sake of visualization) between observed (Qobs) and the three simulated stream flow. The white background refers to the calibration period and the grey background to the validation.
For Tevere, we can see a more marked effect of the SM-corr and P-corr schemes with better skills for DAM for low flow conditions with respect to RCM and vice versa for high flows. The advantage of the P-corr scheme is more remarkable when the satellite precipitation product is considered. Here, RCS outperforms DAS both during the validation and the calibration period for high flow conditions, while it shows some deteriorations in terms of low flows. RCS presents also deteriorations which are particularly relevant during January 2015 (also present for RCM simulation in panel c). The climate (more humid for Kolpa@Petrina) and the hydrologic differences between the two catchments (Kolpa@Petrina is characterized by a higher baseflow component with respect to Tevere) might explain the different benefit of the state and rainfall correction schemes on the simulations.
5. Conclusions
The current availability of different satellite soil moisture products, together with the well-known importance of soil moisture observations for flood prediction, asks for the development of optimal approaches to be implemented for the full exploitation of such products. In this study, we compared two approaches for exploiting satellite soil moisture retrievals derived from the scatterometer ASCAT, namely, the state-correction scheme implemented through classical data assimilation via the EnKF and the rainfall correction scheme through the integration of satellite (and reanalysis) rainfall observations with SM2RAIN rainfall estimates. The experiments were conducted in the Mediterranean on 10 catchments of different size and different climatic conditions. A rigorous separation between calibration and validation was adopted in order to remove possible interferences of the calibration steps necessary for the selection of the parameters associated with the two schemes. Ground-based observations of discharge and rainfall were used for model calibration and for benchmarking the different simulation runs. A satellite- and reanalysis based rainfall product (i.e., 3B42RT and ERA-interim) were used to simulate a scenario of ground data scarcity as happens in many developing countries. For these two products, we performed the state and the rainfall correction schemes.
Based on the obtained results, the following main conclusions can be drawn:
- The gauge-based rainfall dataset (EOBS) performs satisfactorily well over the Mediterranean area with median ANSE and KGE values close to 0.5 (in validation) for the investigated catchments while PERA and P3B42RT provide poorer stream flow predictions.
- The soil moisture correction produces an overall slight improvement in terms of median KGE and ANSE scores (4.25% and 1.5% for ERA-Interim and 9.6% and 7.6% for 3B42RT, respectively) whereas the rainfall correction provides a much larger impact with an increase in KGE and ANSE values equal to 14.81 and 7.3% for ERA and 71.8 and 100% for 3B42RT, respectively. In summary, the impact of the rainfall correction for flood simulation is much larger than the soil moisture correction and is consistently higher when the quality of the non-corrected rainfall forcing is poor. Conversely, for low flows, the soil moisture correction schemes provide slight better results but these improvements are limited.
- After the rainfall correction, the simulation run using the satellite-based product (i.e., 3B42RT) shows KGE scores larger than those obtained by using ground-based observations (EOBS). This is an encouraging result that demonstrates the potentiality to improve operational stream flow forecasting by using remotely sensed surface soil moisture.
- The climate, the specific catchment hydrology/model configuration/data assimilation set up and the pre-processing steps associated with the two schemes exert a remarkable effect on the results that complicates the answer to weather is preferable correcting rainfall or updating the model states.
These results, which go in the same direction of few previous studies found in literature, can be very useful for advancing the understanding of the optimal use of satellite products for hydrology since they involve an area (i.e., the Mediterranean) which is very sensitive to climate change and that was not tested yet. Being subjected to many assumptions and limited in what concern the choice of the catchments, the analysis periods and the type of satellite soil moisture product (i.e., ASCAT), there is a moderate risk that these results can be case specific therefore the comparison of the two approaches over other regions, and by using other soil moisture and precipitation products is recommended and will be the object of future investigations.
Acknowledgments
The study was primarily supported by the ESA WACMOS-MED project (contract ESA/AO/1-8173/15/I-SBo) and partly by EUMETSAT Satellite Application Facility in Support of Operational Hydrology and Water Management (H-SAF) project and the Italian Civil Protection Department. The authors wish to thank Umbria Region, the Italian Civil Protection Department and Simone Gabellani (CIMA foundation) for providing stream flow data in Italy, Yves Tramblay (IRD) for the stream flow data in Morocco, Javier Loizu (Public University of Navarre) for the stream flow data of Arga catchment, Isabelle Braud (IRSTEA) for the stream flow data of Gardon catchment, and the Global Runoff Data Centre (GRDC) for the stream flow data of Kolpa and Lim catchments.
Author Contributions
Christian Massari led the manuscript, made the elaborations and wrote part of the paper. Stefania Camici, Luca Ciabatta and Luca Brocca prepared the data and helped the writing of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Beck, H.E.; de Jeu, R.A.; Schellekens, J.; van Dijk, A.I.; Bruijnzeel, L.A. Improving curve number based storm runoff estimates using soil moisture proxies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 2, 250–259. [Google Scholar] [CrossRef]
- Koster, R.D.; Mahanama, S.P.; Livneh, B.; Lettenmaier, D.P.; Reichle, R.H. Skill in stream flow forecasts derived from large-scale estimates of soil moisture and snow. Nat. Geosci. 2010, 3, 613–616. [Google Scholar] [CrossRef]
- Matgen, P.; Fenicia, F.; Heitz, S.; Plaza, D.; de Keyser, R.; Pauwels, V.R.; Wagner, W.; Savenije, H. Can ASCAT-derived soil wetness indices reduce predictive uncertainty in well-gauged areas? A comparison with in situ observed soil moisture in an assimilation application. Adv. Water Resour. 2012, 44, 49–65. [Google Scholar] [CrossRef]
- Massari, C.; Brocca, L.; Moramarco, T.; Tramblay, Y.; Lescot, J.F.D. Potential of soil moisture observations in flood modelling: Estimating initial conditions and correcting rainfall. Adv. Water Resour. 2014, 74, 44–53. [Google Scholar] [CrossRef]
- Crow, W.T.; Zhan, X. Continental-scale evaluation of remotely sensed soil moisture products. IEEE Geosci. Remote Sens. Lett. 2007, 4, 451–455. [Google Scholar] [CrossRef]
- Renzullo, L.J.; Van Dijk, A.I.; Perraud, J.M.; Collins, D.; Henderson, B.; Jin, H.; Smith, A.B.; McJannet, D.L. Continental satellite soil moisture data assimilation improves root-zone moisture analysis for water resources assessment. J. Hydrol. 2014, 519, 2747–2762. [Google Scholar] [CrossRef]
- López López, P.; Wanders, N.; Schellekens, J.; Renzullo, L.J.; Sutanudjaja, E.H.; Bierkens, M.F.P. Improved large-scale hydrological modelling through the assimilation of stream flow and downscaled satellite soil moisture observations. Hydrol. Earth Syst. Sci. 2016, 20, 3059–3076. [Google Scholar] [CrossRef]
- Romano, N. Soil moisture at local scale: Measurements and simulations. J. Hydrol. 2014, 516, 6–20. [Google Scholar] [CrossRef]
- Mohanty, B.P.; Cosh, M.H.; Lakshmi, V.; Montzka, C. Soil moisture remote sensing: State-of-the-science. Vadose Zone J. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Singh, V.P. Assimilation of observed soil moisture data in storm rainfall-runoff modeling. J. Hydrol. Eng. 2009, 14, 153–165. [Google Scholar] [CrossRef]
- Chen, F.; Crow, W.T.; Starks, P.J.; Moriasi, D.N. Improving hydrologic predictions of a catchment model via assimilation of surface soil moisture. Adv. Water Resour. 2011, 34, 526–536. [Google Scholar] [CrossRef]
- Crow, W.T.; Bindlish, R.; Jackson, T.J. The added value of spaceborne passive microwave soil moisture retrievals for forecasting rainfall-runoff partitioning. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W.; Hasenauer, S.; Hahn, S. Assimilation of surface-and root-zone ASCAT soil moisture products into rainfall–runoff modeling. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2542–2555. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Su, C.H.; Crow, W.T.; Robertson, D.E.; Leahy, C. Improving operational flood ensemble prediction by the assimilation of satellite soil moisture: Comparison between lumped and semi-distributed schemes. Hydrol. Earth Syst. Sci. 2015, 19, 1659–1676. [Google Scholar] [CrossRef]
- Lievens, H.; Tomer, S.K.; Al Bitar, A.; De Lannoy, G.J.; Drusch, M.; Dumedah, G.; Franssen, H.J.; Kerr, Y.H.; Martens, B.; Pan, M.; et al. SMOS soil moisture assimilation for improved hydrologic simulation in the Murray Darling Basin, Australia. Remote Sens. Environ. 2015, 168, 146–162. [Google Scholar] [CrossRef]
- Massari, C.; Brocca, L.; Tarpanelli, A.; Moramarco, T. Data assimilation of satellite soil moisture into rainfall-runoff modelling: A complex recipe? Remote Sens. 2015, 7, 11403–11433. [Google Scholar] [CrossRef]
- Cenci, L.; Laiolo, P.; Gabellani, S.; Campo, L.; Silvestro, F.; Delogu, F.; Boni, G.; Rudari, R. Assimilation of H-SAF soil moisture products for flash flood early warning systems. Case study: Mediterranean catchments. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5634–5646. [Google Scholar] [CrossRef]
- Laiolo, P.; Gabellani, S.; Campo, L.; Silvestro, F.; Delogu, F.; Rudari, R.; Pulvirenti, L.; Boni, G.; Fascetti, F.; Pierdicca, N.; et al. Impact of different satellite soil moisture products on the predictions of a continuous distributed hydrological model. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 131–145. [Google Scholar] [CrossRef]
- Brown, M.E.; Escobar, V.; Moran, S.; Entekhabi, D.; O’Neill, P.E.; Njoku, E.G.; Doorn, B.; Entin, J.K. NASA’s soil moisture active passive (SMAP) mission and opportunities for applications users. Bull. Am. Meteorol. Soc. 2013, 94, 1125–1128. [Google Scholar] [CrossRef]
- Lievens, H.; Reichle, R.H.; Liu, Q.; De Lannoy, G.J.M.; Dunbar, R.S.; Kim, S.B.; Das, N.N.; Cosh, M.; Walker, J.P.; Wagner, W. Joint Sentinel-1 and SMAP data assimilation to improve soil moisture estimates. Geophys. Res. Lett. 2017, 44, 6145–6153. [Google Scholar] [CrossRef]
- Cenci, L.; Pulvirenti, L.; Boni, G.; Chini, M.; Matgen, P.; Gabellani, S.; Campo, L.; Silvestro, F.; Versace, C.; Campanella, P.; et al. Satellite soil moisture assimilation: Preliminary assessment of the Sentinel 1 potentialities. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3098–3101. [Google Scholar]
- Crow, W.T.; van Den Berg, M.J.; Huffman, G.J.; Pellarin, T. Correcting rainfall using satellite-based surface soil moisture retrievals: The Soil Moisture Analysis Rainfall Tool (SMART). Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Pellarin, T.; Louvet, S.; Gruhier, C.; Quantin, G.; Legout, C. A simple and effective method for correcting soil moisture and precipitation estimates using AMSR-E measurements. Remote Sens. Environ. 2013, 136, 28–36. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W.; Wagner, W.; Levizzani, V. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data. J. Geophys. Res. Atmos. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]
- Ciabatta, L.; Brocca, L.; Massari, C.; Moramarco, T.; Puca, S.; Rinollo, A.; Gabellani, S.; Wagner, W. Integration of satellite soil moisture and rainfall observations over the Italian territory. J. Hydrometeorol. 2015, 16, 1341–1355. [Google Scholar] [CrossRef]
- Koster, R.D.; Brocca, L.; Crow, W.T.; Burgin, M.S.; De Lannoy, G.J. Precipitation estimation using L-band and C-band soil moisture retrievals. Water Resour. Res. 2016, 52, 7213–7225. [Google Scholar] [CrossRef]
- Román-Cascón, C.; Pellarin, T.; Gibon, F.; Brocca, L.; Cosme, E.; Crow, W.; Fernández-Prieto, D.; Kerr, Y.H.; Massari, C. Correcting satellite-based precipitation products through SMOS soil moisture data assimilation in two land-surface models of different complexity: API and SURFEX. Remote Sens. Environ. 2017, 200, 295–310. [Google Scholar] [CrossRef]
- Crow, W.T.; Ryu, D. A new data assimilation approach for improving runoff prediction using remotely-sensed soil moisture retrievals. Hydrol. Earth Syst. Sci. 2009, 13, 1–16. [Google Scholar] [CrossRef]
- Chen, F.; Crow, W.T.; Ryu, D. Dual forcing and state correction via soil moisture assimilation for improved rainfall–runoff modeling. J. Hydrometeorol. 2014, 15, 1832–1848. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Crow, W.T.; Su, C.H.; Robertson, D.R. Dual assimilation of satellite soil moisture to improve stream flow prediction in data-scarce catchments. Water Resour. Res. 2016, 52, 5357–5375. [Google Scholar] [CrossRef]
- Evensen, G. Data Assimilation: The Ensemble Kalman Filter; Springer: Berlin, Germany, 2009. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; de Rosnay, P.; Jann, A.; Schneider, S.; et al. The ASCAT soil moisture product: A review of its specifications, validation results, and emerging applications. Meteorol. Z. 2013, 22, 5–33. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T. Distributed rainfall-runoff modelling for flood frequency estimation and flood forecasting. Hydrol. Process. 2011, 25, 2801–2813. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Brocca, L.; Hasenauer, S.; Lacava, T.; Melone, F.; Moramarco, T.; Wagner, W.; Dorigo, W.; Matgen, P.; Martínez-Fernández, J.; Llorens, P.; et al. Soil moisture estimation through ASCAT and AMSR-E sensors: An intercomparison and validation study across Europe. Remote Sens. Environ. 2011, 115, 3390–3408. [Google Scholar] [CrossRef]
- Paulik, C.; Dorigo, W.; Wagner, W.; Kidd, R. Validation of the ASCAT Soil Water Index using in situ data from the International Soil Moisture Network. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 1–8. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI soil moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Haylock, M.R.; Hofstra, N.; Klein Tank, A.M.G.; Klok, E.J.; Jones, P.D.; New, M. A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. J. Geophys. Res. Atmos. 2008, 113, 1–12. [Google Scholar] [CrossRef]
- Stampoulis, D.; Anagnostou, E.N. Evaluation of Global Satellite Rainfall Products over Continental Europe. J. Hydrometeorol. 2012, 13, 588–603. [Google Scholar] [CrossRef]
- SM2RAIN-ASCAT (1 January 2007–31 December 2015) European Rainfall Dataset (0.25 Degree/Daily). Available online: http://dx.doi.org/10.13140/RG.2.1.4068.6481/1 (accessed on 13 February 2018).
- Massari, C.; Crow, W.; Brocca, L. An assessment of the performance of global rainfall estimates without ground-based observations. Hydrol. Earth Syst. Sci. 2017, 21, 4347–4361. [Google Scholar] [CrossRef]
- Masseroni, D.; Cislaghi, A.; Camici, S.; Massari, C.; Brocca, L. A reliable rainfall–runoff model for flood forecasting: Review and application to a semi-urbanized watershed at high flood risk in Italy. Hydrol. Res. 2017, 48, 726–740. [Google Scholar] [CrossRef]
- Doorenbos, J.; Pruitt, W.O. Background and Development of Methods to Predict Reference Crop Evapotranspiration (ETo). In Crop Water Requirements. FAO Irrigation and Drainage Paper No. 24; FAO: Rome, Italy, 1977; Appendix II; pp. 108–119. [Google Scholar]
- Famiglietti, J.S.; Wood, E.F. Multiscale modeling of spatially variable water and energy balance processes. Water Resour. Res. 1994, 30, 3061–3078. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Clark, E.A.; Wood, A.W.; Hamlet, A.F.; Lettenmaier, D.P. Twentieth-century drought in the conterminous United States. J. Hydrometeorol. 2005, 6, 985–1001. [Google Scholar] [CrossRef]
- Melone, F.; Corradini, C.; Singh, V.P. Lag prediction in ungauged basins: An investigation through actual data of the upper Tevere River valley. Hydrol. Processes 2002, 16, 1085–1094. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A method for estimating soil moisture from ERS scatterometer and soil data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Albergel, C.; Rüdiger, C.; Pellarin, T.; Calvet, J.C.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B.; Martin, E. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. 2008, 12, 1323–1337. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31, L19501. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. Oceans 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Gruber, A.; Su, C.H.; Zwieback, S.; Crow, W.; Dorigo, W.; Wagner, W. Recent advances in (soil moisture) triple collocation analysis. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 200–211. [Google Scholar] [CrossRef]
- Draper, C.; Mahfouf, J.F.; Calvet, J.C.; Martin, E.; Wagner, W. Assimilation of ASCAT near-surface soil moisture into the SIM hydrological model over France. Hydrol. Earth Syst. Sci. 2011, 15, 3829. [Google Scholar] [CrossRef]
- Tian, Y.; Huffman, G.J.; Adler, R.F.; Tang, L.; Sapiano, M.; Maggioni, V.; Wu, H. Modeling errors in daily precipitation measurements: Additive or multiplicative? Geophys. Res. Lett. 2013, 40, 2060–2065. [Google Scholar] [CrossRef]
- Crow, W.T.; Van Loon, E. Impact of Incorrect Model Error Assumptions on the Sequential Assimilation of Remotely Sensed Surface Soil Moisture. J. Hydrometeorol. 2006, 7, 421–432. [Google Scholar] [CrossRef]
- Maggioni, V.; Massari, C. On the performance of satellite precipitation products in riverine flood modeling: A review. J. Hydrol. 2018, 558, 214–224. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Hoffmann, L.; El Idrissi, A.; Pfister, L.; Hingray, B.; Guex, F.; Musy, A.; Humbert, J.; Drogue, G.; Leviandier, T. Development of regionalized hydrological models in an area with short hydrological observation series. River Res. Appl. 2004, 20, 243–254. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Bober, W. Introduction to Numerical and Analytical Methods with MATLAB® for Engineers and Scientists; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Thiemig, V. The Development of Pan-African Flood Forecasting and the Exploration of Satellite Based Precipitation Estimates. Ph.D. Thesis, Utrecht University, Utrecht, The Netherlands, 2014. [Google Scholar]
- Loizu, J.; Massari, C.; Álvarez-Mozos, J.; Tarpanelli, A.; Brocca, L.; Casalí, J. On the assimilation set-up of ASCAT soil moisture data for improving stream flow catchment simulation. Adv. Water Resour. 2018, 111, 86–104. [Google Scholar] [CrossRef]
- Fascetti, F.; Pierdicca, N.; Pulvirenti, L.; Crapolicchio, R.; Muñoz-Sabater, J. A comparison of ASCAT and SMOS soil moisture retrievals over Europe and Northern Africa from 2010 to 2013. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 135–142. [Google Scholar] [CrossRef]
- Scholze, M.; Buchwitz, M.; Dorigo, W.; Guanter, L.; Quegan, S. Reviews and syntheses: Systematic Earth observations for use in terrestrial carbon cycle data assimilation systems. Biogeosci. Discuss. 2017, 14, 3401–3429. [Google Scholar] [CrossRef]
- Peña Arancibia, J.L.; van Dijk, A.I.J.M.; Renzullo, L.J.; Mulligan, M. Evaluation of precipitation estimation accuracy in reanalyses, satellite products, and an ensemble method for regions in Australia and Sout and East Asia. J. Hydrometeorol. 2013, 14, 1323–1333. [Google Scholar] [CrossRef]
- Xie, P.; Joyce, R.J. Integrating information from satellite observations and numerical models for improved global precipitation analyses. In Remote Sensing of the Terrestrial Water Cycle, Geophysical Monograph Series; Lakshmi, V., Alsdorf, D., Anderson, M., Biancamaria, S., Cosh, M., Entin, J., Huffman, G., Kustas, W., van Oevelen, P., Painter, T., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014; Chapter 3. [Google Scholar]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Ciabatta, L.; Marra, A.C.; Panegrossi, G.; Casella, D.; Sanò, P.; Dietrich, S.; Massari, C.; Brocca, L. Daily precipitation estimation through different microwave sensors: Verification study over Italy. J. Hydrol. 2017, 545, 436–450. [Google Scholar] [CrossRef]
- Ciabatta, L.; Brocca, L.; Massari, C.; Moramarco, T.; Gabellani, S.; Puca, S.; Wagner, W. Rainfall-runoff modelling by using SM2RAIN-derived and state-of-the-art satellite rainfall products over Italy. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 163–173. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-hourly 0.25 global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589. [Google Scholar] [CrossRef]
- Su, C.-H.; Ryu, D. Multi-scale analysis of bias correction of soil moisture. Hydrol. Earth Syst. Sci. 2015, 19, 17–31. [Google Scholar] [CrossRef]
- De Leeuw, J.; Methven, J.; Blackburn, M. Evaluation of ERA-Interim reanalysis precipitation products using England and Wales observations. Q. J. R. Meteorol. Soc. 2015, 141, 798–806. [Google Scholar] [CrossRef]
- Rebora, N.; Molini, L.; Casella, E.; Comellas, A.; Fiori, E.; Pignone, F.; Siccardi, F.; Silvestro, F.; Tanelli, S.; Parodi, A. Extreme rainfall in the mediterranean: What can we learn from observations? J. Hydrometeorol. 2013, 14, 906–922. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).