Abstract
Global Positioning System (GPS) has been used in many aerial and terrestrial high precision positioning applications. Multipath affects positioning and navigation performance. This paper proposes a convolutional neural network based carrier-phase multipath detection method. The method is based on the fact that the features of multipath characteristics in multipath contaminated data can be learned and identified by a convolutional neural network. The proposed method is validated with simulated and real GPS data and compared with existing multipath mitigation methods in position domain. The results show the proposed method can detect about 80% multipath errors (i.e., recall) in both simulated and real data. The impact of the proposed method on positioning accuracy improvement is demonstrated with two datasets, 18–30% improvement is obtained by down-weighting the detected multipath measurements. The focus of this paper is on the development and test of the proposed convolutional neural network based multipath detection algorithm.
1. Introduction
Global Positioning System (GPS) has been intensively used in high precision positioning applications such as attitude determination of unmanned aerial vehicles e.g., [1] and other autonomous vehicles e.g., [2]. GPS positioning is based on the pseudorange and carrier phase measurements from multiple satellites to a GPS receiver. With a temporary or permanent reference station and a rover station, carrier phase based relative GPS biases and errors such as satellite clock and orbit offsets, ionospheric and tropospheric biases can be eliminated or greatly mitigated with differencing techniques at a short baseline between the rover and reference stations. As a result, GPS positioning can achieve centimetre level accuracy. However, positioning accuracy, availability, and continuity can be affected by signal multipath in some difficult environments because multipath errors cannot be removed or mitigated with differencing techniques [3]. The research question of this paper is: can machine learning methods be used to detect Global Navigation Satellite System (GNSS) multipath errors in high-precision positioning? To answer this question, the following two sub-sections briefly introduce GPS multipath error and mitigation as well as relevant machine learning algorithms used to detect GPS multipath errors. The architecture of the proposed model is presented in Section 2. Model validation methodologies and the relevant assessment criteria are given in Section 3. Section 4 describes how the training and validation data are collected. Section 5 explains how the parameters in the proposed models are determined. After presenting the results of simulated and real data in Section 6, a conclusion is reached in the last section.
1.1. Introduction of GPS Multipath Error and Its Mitigation
Multipath effect is caused when direct signals are received with reflected signals at an antenna as shown in Figure 1. In theory, the maximum magnitude of carrier phase multipath error is a quarter of the signal wavelength. It affects positioning accuracy and availability (due to incorrect or failed ambiguity resolution) in high precision GPS positioning applications. Many methods have been developed to detect and mitigate GPS multipath errors. Phan et al. [4,5] propose using Support Vector Machine (SVM) to estimate multipath errors with inputs of satellite elevation and azimuth by taking advantage of sidereal repeatability of GPS multipath signals. There are many other GPS multipath mitigation techniques based on the sidereal repeatability of GPS multipath signals [6,7,8,9]. Wavelet decomposition is also widely used to mitigate multipath errors [10,11,12]. These methods can only be applied to static antennas (such as at permanent International GNSS Service (IGS) stations) in unchanged environments, where the multipath repeats every sidereal day.
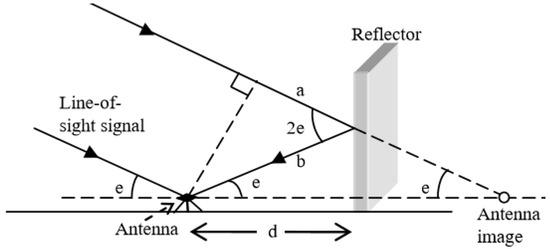
Figure 1.
Geometry of multipath signals, a reflector, and an antenna (adapted from [13]).
Multipath errors can be mitigated using stochastic models based on Carrier-to-Noise Ratio (CNR) or Signal-to-Noise Ratio (SNR) [13,14]. Simple stochastic models are based on the satellite elevation angle (E) [13,15]. For example, assuming the variance of the carrier phase error to be:
Some improved stochastic models are based on Carrier-to-Noise Ratio (CNR) or Signal-to-Noise Ratio (SNR). e.g., SIMGA-ε model [15] uses CNR to estimate carrier phase variances using the equation:
where Ci denotes a factor consisting of the carrier loop noise bandwidth and a conversion term from cycle2 to millimetres2, which includes the Li wavelength. CNR is the measured CNR from the GPS data. Some receiver and antenna designs can mitigate multipath effects. Special hardware designs such as vision correlator [16] and Multipath Estimating Delay-Lock-Loop [17] have been used by some receiver manufacturers to mitigate multipath error. Lau and Cross [18] use multiple closely spaced antennas to model multipath error based on the multipath phase differences of antenna pairs.
Most of the research above is based on static GPS data; this is because it is difficult to precisely assess the carrier phase multipath errors of kinematic data. We present a new convolutional neural network based multipath detection method for both static and kinematic data. With the development of a rotating arm rig by the authors, the multipath error of kinematic data can be assessed in the measurement domain and used to validate the detection method. In addition, a stochastic model based on the detection result is used so that the performance of the new method in the position domain can be compared with a simple elevation model and SIGMA-ε model. The proposed methods can be used in carrier phase based kinematic positioning, including Real-Time Kinematic (RTK) applications for improving kinematic positioning performance in difficult environments.
1.2. Introduction of Relevant Machine Learning Algorithms
Mathematically, convolution is defined as an operation applying one function repeatedly across the output of another function. In the context of a neural network, it means to apply repeatedly a ‘filter’ across a time series or an image. Convolutional Neural Networks (CNN) are being widely deployed in many applications, like image recognition, video analysis, and for time series processing like music, speech recognition [19,20]. Inspired by the cell structures of biological visual neuroscience, a typical CNN is composed of convolutional layers, subsampling (pooling) layers, and fully connected layers. A convolutional filter (kernel) within convolutional layers can provide a compressed representation of input data, and it can be computed using methods such as Sparse Auto-Encoder (SAE) and Principle Component Analysis (PCA). SAE is used in the proposed method because of its higher efficiency in reducing the dimension of data [21]. An SAE neural network is an unsupervised learning algorithm that applies backpropagation and sparsity constraint [21,22,23]. As demonstrated in Figure 2, a typical auto-encoder neural network has identical input and desired output values. The backpropagation algorithm is performed to minimize the reconstruction error (i.e., to make the output values equal to the input values). Apart from backpropagation, a sparsity constraint is applied to the network in SAE to make activations of neurons inactive (i.e., close to zero). With convolution filters computed using SAE, convolutional layers can extract features from input data. In the convolution layer, the activations of each filter are computed throughout the network:
where is the convolution filters (it is equivalent to a weight matrix) computed from SAE (e.g., in Figure 2 is composed of three filters with a length of 4 for each filter); ∗ is the convolution operator; represents the activation of unit in layer (For = 1, is the input data), if there is a high degree of fitting between input data and a single filter in , it will result in a high activation in convolved features; is the bias term (computed in SAE) in layer ; the sigmoid function is defined as:
The sigmoid function is used as activation function in a neural network because of the nonlinearity of sigmoid function. The derivative of the sigmoid function can be expressed by itself, i.e., , so that the derivative of the error function with respect to network inputs can be computed in a backpropagation algorithm (based on a gradient descent method). The convolved features are subsampled by a specific factor in the subsampling layer. The role of a subsampling layer is used to reduce the variance of convolved data so that the value of a particular feature over a region of an input layer can be computed and merged together. More detailed information about SAE and CNN can be found in [21,23,24].
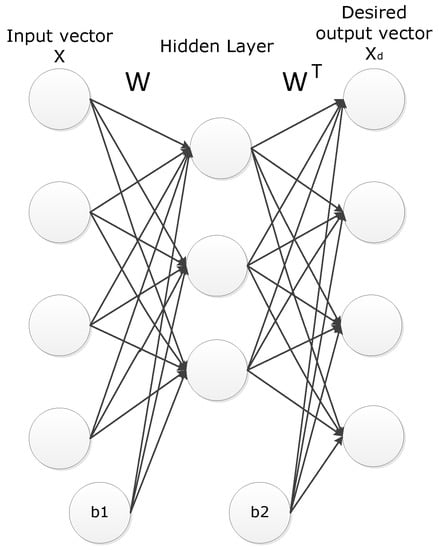
Figure 2.
A sparse auto-encoder network with a sparse representation on the hidden layer.
Two types of classifiers, softmax and random forest, are used and compared in this work. A softmax classifier is widely used in the output layer of neural networks because it can provide normalized probabilities for multiple classes and it is easy for implementation. Mathematically, the softmax function is given by:
where d is the input features, is the classes of output labels, and is the number of classes, and denotes all the parameters of the probability model. The logistic function is a special case of softmax function for binary classification (i.e., K = 2).
Softmax classifier in the output layer of CNN that can be replaced with a random forest. Random forest is a learning model for classification. A random forest is composed of many randomly generated decision trees. An individual decision tree is a tool used to divide data with hyperplanes. All trees in forests are independent. They randomly select features at each node to split data. After training, a new instance that enters the forest can be assigned into a leaf node, then all trees can ‘vote’ data for a class by their leaf distributions, and the forest makes the final decision based on the most voted class (when it is used for classification). More details of random forest can be referred to [25]. Random forest is used in this research because of its stable and superior performance over other classifiers [26] and its high robustness to outliers [27].
2. Proposed Convolutional Neural Network Based Multipath Detection Method
A new machine learning based multipath detection method is proposed and the details and complete algorithm are described in this section. The proposed method uses CNN with SAE for feature extraction and random forest/softmax for classification. CNN is used for feature extraction in the proposed method because CNN can tolerate pattern shift and deformation [28]. The proposed method doesn’t rely on the sidereal repeatability of multipath errors.
CNR and Pseudorange multipath (MP) for each frequency are used separately to extract multipath features via CNN. MP is linear combinations of the pseudorange and carrier phase observations [29], which is given by:
where (in metres) represents MP for Frequency , is the code measurement for frequency , and are the carrier phase measurements for frequencies and , respectively, and is the ratio between squared frequencies of and . The extracted features are combined together with a doubled input dimension (the reason to combine the features of CNR and MP is explained in Section 5) to train a classifier. After the training, the classifier can detect whether the data is multipath contaminated or not.
The input data structure of the proposed method is shown in Table 1. For each type of signal from satellite k, its input data CNR and MP in the same column have the same timestamp. We denote n as the length of input time window and the observation n is the latest observation. The proposed method needs current and n − 1 previous successive observations to detect the multipath in the latest observation. As a real-time detection system, there is a response time between the epoch at the observation starts to suffer from multipath error and the epoch of detection of multipath. As a result, shortening the time window of input data (i.e., decreasing n) can reduce the detection response time, and vice versa. However, decreasing n would increase difficulty in feature extraction because of less information in the input data (due to reduced feature dimension) and convolution cannot be performed when n is less than 3. The value of n is set to 16 in this work, and the determination of n is presented in Section 5.

Table 1.
Input time-series data structure; PRN denotes Pseudo Random Number.
To extract a multipath/direct-signal only feature in CNR and MP from the input data, the following steps are taken:
- Pre-process each in the time window (i.e. Table 1) to by:
- Scale the and to [0.1] using the following two equations:where and are scaled and from Table 1, respectively; is the sigmoid function defined in Equation (4). and are the upper and lower bounds of CNR in all measurements (not just in the time window). This step as data pre-processing (scaling all the input data to [0, 1]) is compulsory because sigmoid function, i.e., Equation (4), is used when training SAE in Step 3. The sigmoid function has an output range of [0, 1]. As described in Section 1, an SAE neural network has identical input and output values, so the input values of SAE need to be restricted to [0, 1] as well. The values of and are set as 60 and 30 in this research because this range covers most of the observed CNR in the direct-signal only and multipath contaminated data. An example plot of CNR in 24 h is shown in Figure 3. Unlike CNR, MP is not bounded, the logarithmic function is used in Equation (9) to scale to the range within activation range of sigmoid function, and then sigmoid function is used to make sure is within [0, 1]. can assure that has a consistent positive or negative sign with .
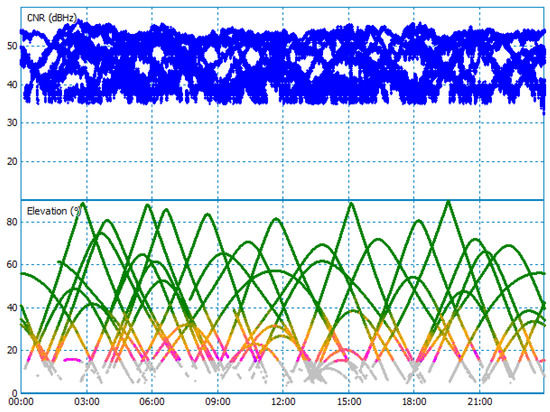 Figure 3. An example of CNR of all GPS satellites with satellite elevation angles in 24 h.
Figure 3. An example of CNR of all GPS satellites with satellite elevation angles in 24 h. - If the detector is untrained, convolution filters are trained for MP and CNR by SAE, respectively. The training is implemented in minFunc, developed by Schmidt [30]. After tuning, the parameters for convolution filters used in this work are: the number of filters = 4, the length of each filter = 5, which proved to give best performance (more detail is presented in Section 5).
- Using Equations (3) and (4) to compute the feature activations of each filter throughout the network in the convolution layer.
- In the pooling layer, the feature maps are subsampled to reduce data resolution. The determination of subsampling factor is presented in Section 5.
The process of steps 3 to 5 is illustrated in Figure 4. In the figure, the number of convolution filters is 4, convolving a single filter with a length of m over a scaled input time series with a length of n giving feature activation with a length of n − m + 1.
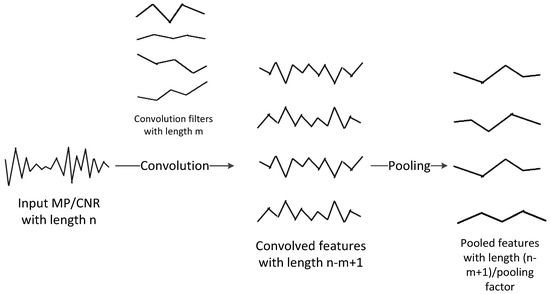
Figure 4.
Feature extraction with CNN.
Two classifiers, softmax and random forest, are compared in this work to select a suitable classifier and optimise the performance of the proposed method. The convolved and pooled feature maps of CNR and MP are combined together and then fed into classifiers as input data. For random forest, a Matlab script randomForest [31] is used in the implementation with 100 trees and each tree will grow to its maximum depth. Two types of data are used to validate the proposed method: the simulated data collected from a Spirent GS8000 GNSS signal simulator (San Jose, CA, USA) in a simulated urban canyon environment and real data collected in low multipath and severe multipath environments. Two types of labels are used for real and simulated data: direct-signal only measurement and multipath measurement. The details of data labelling are described in the following section.
3. Validation Methodologies of the Proposed Method
The proposed method learns multipath/direct-signal only features from training datasets; then, test datasets can be used to validate the trained detector. Note that the trained detector does not learn any multipath features from test datasets. Except for data used in parameter tuning (detail is presented in Section 5), all the other training and test datasets are collected in different satellite geometries with different multipath errors in observations. The proposed method has been validated with simulated and real data. The aim of testing with simulated data is to validate the proposed method in a well-controlled environment, where all the multipath/direct-only signals can be manually defined and clearly labelled. Real data is used to train and test detectors so that the feasibility of the proposed method can be examined in practice. Recall, rate of false detection, and accuracy are used to assess the performance of the trained detector, and their definitions are shown in Table 2. Recall is a metric used in machine learning to evaluate how many ‘true positive’ samples (i.e., multipath contaminated measurements in this research) can be detected by a classifier. A high recall means a classifier is sensitive to ‘true positive’ samples. The rate of false detection is the number of incorrect multipath detections as a percentage of the total number of multipath detections. Accuracy is the number of correct detections (for both multipath and direct-signal only) samples as a percentage of all samples.

Table 2.
Definition of recall, rate of false detection, and accuracy.
Training and testing with simulated data and real data are independent (i.e., no cross-validation between simulated and real data is performed) because their labels are determined with different methods (labelling of simulated data is explained in Section 4). A criterion is used to label multipath measurement on the real data based on double-differenced carrier phase residual error: if the double-differenced carrier phase residual error of a measurement at an epoch exceeds 99% (three-sigma) of measurement errors in a low multipath environment (i.e., three times of standard deviation (S.D.) of the double-differenced carrier phase errors), then that measurement is labelled as a multipath measurement. Because the proposed method process MP and CNR separately in feature extraction and ‘true’ carrier phase residuals are used to label multipath measurements, the orthogonality between CNR and MP with carrier phase has no effect on multipath detection. Multipath at the reference receiver is negligible. Real multipath errors may be small and they cannot be distinguished from noise in practice; they are labelled as a direct-signal only class. Therefore, real data will have a higher rate of false detection than simulated data. The S.D. of un-differenced random carrier phase errors are 1 mm (L1) and 1.2 mm (L2) for GPS determined in [32].
Detection results can be further validated in position domain by down-weighting the detected multipath measurements. However, developing linear or nonlinear down-weighting methods is not the main focus of this paper due to its complexity. The impact of the proposed method on positioning accuracy improvement is demonstrated by down-weighting the detected multipath measurements with a simple linear method based on the output of random forest:
where is the weight multiplier of a measurement in the weight matrix, is the total number of trees in random forest, and is the number of trees in random forest that votes for multipath class.
The work described in this paper is multidisciplinary research. In order to further help readers who may not be familiar with both multipath errors in GPS measurements and machine learning theory, a summary of key objectives and features of the paper and the proposed method is given below:
- The proposed method aims to detect multipath errors in carrier phase measurements (not signals). The multipath errors in measurements are the output of processed signals from receiver hardware. Therefore, the multipath errors to be detected in carrier-phase measurements are the results of the combination of antenna architecture and receiver signal processing architecture (including correlator design). Characteristics of multipath errors in carrier phase measurements of combinations of antennas and receivers are very similar. Factors affecting the phases and magnitudes of carrier phase multipath errors can be found in [3].
- The proposed method aims to detect multipath errors. The definition of multipath errors is described in Section 1.1 and [3]. Non-line-of-sight only measurements are not multipath contaminated measurements; therefore, the non-line-of-sight only problem is outside the scope of this investigation.
- The proposed method doesn’t rely on the repeated multipath characteristics in sidereal days, and doesn’t need multipath pattern/signature to build up in the previous consecutive measurement epochs in real-time implementation of the multipath detection. A machine learning classifier can learn the characteristics of multipath errors in carrier phase measurements from CNR and MP data in the training datasets as described in Section 2.
4. Data Description
Four tests are performed to test the proposed method with simulated and real data, and the information and names of datasets are shown in Table 3. Tests 1, 2, and 3 train and validate the proposed method with simulated kinematic data (SIMTU, SIMTR, and SIMTE), real static data (STU, STR1/2, and STE), and real kinematic data (KTU, KTR1/2, and KTE1), respectively. Test 4 further validates the trained detectors with the training and test data (KTE2) collected in two different multipath environments (near a wall on the rooftop and near a building). Test 5 compares the performance of the proposed method with those of two existing multipath mitigation methods (simple elevation based model and SIGMA-ε model). More details about data collection of tuning, training, and test datasets are described in the following section.

Table 3.
List of tests with tuning, training, and test datasets.
4.1. Description of Data Simulation and Collection
Three models are used for the multipath propagation on the Spirent GS8000 GNSS simulator. Rician fading and Rayleigh fading are used to model direct and multipath signals [33,34]. An urban canyon environment, as shown in Figure 5, is created to test the proposed method. There are four category masks in the simulated environment. Category A is a visibility mask to represent obstructions such as high-rise buildings. Category B represents normal signal arriving at these segments with no reflections (data from Category B is labelled as direct-signal only data). Category C simulates signals with their reflected signals arriving at these segments (data from Category C is labelled as multipath contaminated data).
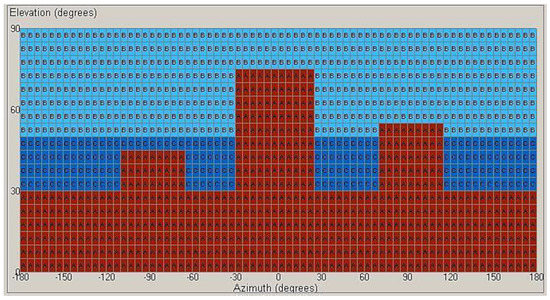
Figure 5.
A simulated urban canyon environment in the Spirent GPS signal simulation.
Datasets listed in Table 4 were conducted using the Spirent GNSS simulator, using Land Mobile mode. A moving antenna is simulated, and the antenna constantly performs circular movement with a radius of 2 meters and a speed of 1m/s, from a position with International Terrestrial Reference Frame 08 (ITRF08) coordinates of 29°48′10.6682″N, 121°33′24.2892″E, and 1.0m H. In Test 1, Dataset SIMTR is used for training the detector and Dataset SIMTU are used for parameter tuning. The tuned and trained detector is then validated with Dataset SIMTE. The proportion of direct-signal only and multipath signals are intentionally balanced (the redundant data are randomly screened out) in the training and test datasets so that the performance of the detector is unbiased for two classes. A Javad Triumph-VS receiver (San Jose, CA, USA) was used to collect simulated signals. The data were then processed by the detector to detect the multipath signals at each epoch, and assess the recall and rate of false detection.

Table 4.
List of data collected with a GNSS simulator; GDOP denotes Geometric Dilution of Precision.
4.2. Description of Real Data Collection
All the static and kinematic datasets listed in Table 5 and Table 6 were collected at the University of Nottingham Ningbo China (UNNC) using Javad Triumph VS receivers. All the data shown in Table 5 were collected with static antennas. Dataset STR1 was collected on the South Pillar on the roof of the Science and Engineering Building (SEB) at UNNC with a clear open environment shown in Figure 6a. Datasets STR2, STU, and STE were collected in a multipath environment (near a wall) shown in Figure 6b. Dataset STU is only used for parameter tuning of the detector. The reference station of Datasets STR1, STR2, STU, and STE is set on the North Pillar at SEB.

Table 5.
Details of the collection of the real static data.

Table 6.
Details of the collection of the real kinematic datasets.

Figure 6.
Images show the environments for the collection of (a) Dataset STR1; (b) Datasets STR2; STU, STE; (c) Dataset KTR1; (d) Datasets KTR2, KTU, KTE1; (e) Dataset KTE2; and (f) Dataset KTE3.
A rotating arm rig was used to collect real kinematic data. The rig has four parts, as shown in Figure 7: a base, a cabinet, a rotating arm, and two platforms. The base with a motor and a battery is at the bottom of the center. Above the base, there is a cabinet to place GPS receivers, and an antenna can be installed on the top of the cabinet. The total length of two arms (i.e., diameter of the circular trajectory) is 4 m. At the end of the rotor arm, there are two platforms. The rectangular platform is used to host an antenna and the circular one is used to hold equivalent weight to balance the arms. A rotating rig can provide a fixed trajectory (surveyed by total station) so that the ‘true’ carrier phase residuals can be calculated. In addition, when the rig is placed next to a wall, the rotation of the rig can simulate the transition between low and high multipath environments. Multipath errors change from time to time and place to place during a sidereal day; therefore, the phases and magnitudes of multipath errors in a rotation of the rotating arm rig are not repetitive (each rotation is treated separately).

Figure 7.
The rotating arm rig for testing of the proposed method with real multipath data.
All the data shown in Table 6 were collected with a kinematic antenna. Datasets KTR1 and KTR2 were collected with the rotating arm rig in a clear open environment as shown in Figure 6c and a multipath environment shown in Figure 6d, respectively. Datasets KTU and KTE1 were collected with the rotating arm rig near a wall. Dataset KTU is only used for parameter tuning of the proposed multipath detector. After tuning and training, the detector is then validated by test sets KTE1 and KTE2. Dataset KTE1 is used to test the performance of the trained multipath detector in a changing multipath environment (i.e., more multipath signals when the rover antenna moves close to a wall when comparing with rover away from the wall). The first 20 min of KTE1 is used in Test 5 to demonstrate the detection results in position domain because there are always more than five available satellites during that period, so that the effect of satellite geometry on positioning quality can be reduced when down-weighting the detected multipath measurements. The reference station of Dataset KTR1 is set on the centre of the rotation arm rig. The reference station of Datasets KTR2, KTU, and KTE1 is set on the North Pillar at SEB. ‘True’ double-differenced carrier phase residuals can be computed from the fixed solution after ambiguity resolution using the least-squares ambiguity decorrelation adjustment (LAMBDA) method [35]. Calculating the true trajectories of rover movement is compulsory for the determination of ‘true’ double-differenced carrier phase residuals. Total stations were used to measure the length of rotation radius and the inclination of the rotation plane. The phase centre variation of antenna is much smaller than phase multipath errors and it is neglected in kinematic applications. The reference station on the North Pillar is in a low multipath environment that is shown in a 24-h test presented in [36] with true carrier phase residuals. The position of the centre of the rotation arm rig is determined by static GPS surveying with similar satellite geometry when collecting Datasets KTR2, KTU, and KTE1. Dataset KTE2 further validates the detector (trained with Datasets KTR1 and KTR2) in real scenarios. Dataset KTE2 was collected on the UNNC campus near a building (shown in Figure 6e) with a moving antenna passing through five pegs with the known position determined by total stations and static GPS surveying. When antenna moves to a peg, only the first epoch was used for validation. There are 24 such epochs available in Dataset KTE2.
5. Tuning of Parameters and Comparison between Classifiers
Similar to other machine learning approaches [20,21] and filtering approaches [37], parameter tuning is an essential step. GPS L1 C/A data in Datasets SIMTU, STU, and KTU are used to tune a parameter (length of input time window) in the proposed method. Accuracy (its definition can be found in Table 2) is the criterion for parameter tuning. Figure 8 illustrates the detection accuracy of using MP, CNR and their combination when changing the length of input time windows. All the data in Figure 8 show that the combination of MP and CNR improves accuracy when compared with using MP or CNR alone. As shown in Figure 8a, increasing the length of input time window improves the accuracy on simulated data at the expense of increased detection response. Figure 8b,c show that, when the length of input time window exceeds 20 s on real static and kinematic data, the detection accuracy stops increasing. As a result, the length of input time window is set to 16 s to optimise the detection performance on real data with the shortest response time.
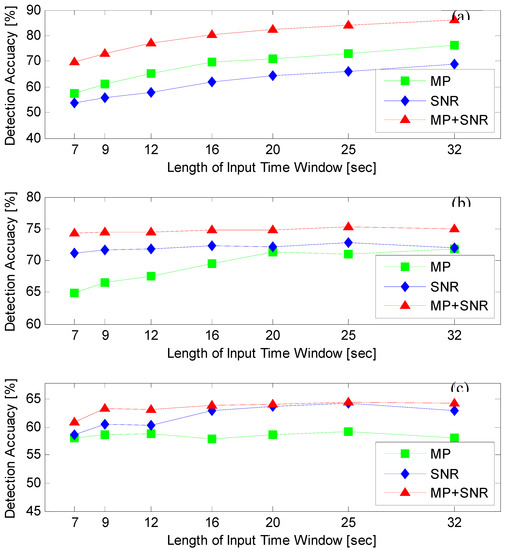
Figure 8.
Detection results using feature of MP, SNR and their combination when changing the length of input time window with Dataset SIMTU (a); STU (b); and KTU (c).
Other parameters (the number of filters, length of each filter, and subsampling factor) are tuned with the same real datasets (SIMTU, STU, and KTU) to optimise detection performance in real scenarios. Table 7 shows the detection results on tuning Dataset KTU using different number of filters with different lengths. From the table, it can be seen that changing these two parameters have slight effects on accuracy. Parameters with the best performance in tuning (i.e., a filter patch composed of four filters with a length of 5 for each filter) are used in this research.

Table 7.
Detection results of changing the number of filters and length of each filter with Dataset KTU.
Figure 9 shows the detection results using different subsampling factors with Datasets STU and KTU. The results show that accuracy gradually decreases for kinematic data with the increase of subsampling factor. This is due to correspondingly reduced resolution of feature maps after convolution operation. The value of subsampling factor is set to 2 in this study to save on computation burden of a classifier without compromising on detection accuracy.
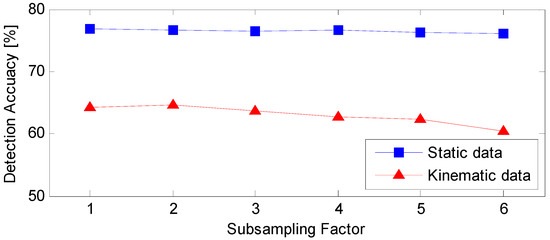
Figure 9.
Detection results when changing the subsampling factor of the pooling layer with Dataset STU (blue squares) and KTU (red triangles).
With tuned parameters in CNN, the performances of two classifiers, softmax and random forest, on GPS L1 C/A data in Datasets SIMTU, SIMTE, STU, STE, KTU, and KTE are presented in Table 8. The results show that the random forest classifier performs better than a softmax classifier in kinematic data by 1% to 10%, especially for the simulated data. However, the softmax classifier slightly outperforms random forest in static data by about 2%. This is because the softmax classifier is based on probability theory so that it performs better in static data with more predictable multipath errors. Uncertainty is involved (e.g., rapid changing of environment) in kinematic data, and decision tree based random forest outperforms because it is a highly robust classifier [27]. Therefore, the proposed method uses a softmax classifier for static data and random forest classifier for kinematic data.

Table 8.
Performance of softmax and random forest classifiers on simulated and real data.
6. Test Results
Table 9 shows the detection results (recall, rate of false detection, and accuracy) of Tests 1, 2, 3, and 4. The results of Test 1 show that the trained detector can achieve a recall of 77–87% (i.e., detect about 80% multipath measurements) with a rate of false detection of about 16% in Test 1. The detection accuracy is about 80%. Unlike simulated data, available GPS L2C and L5 data in the real kinematic datasets are not sufficient for training. Only one GPS IIF satellite (i.e., with L5 signal) and two GPS satellites with L2C signal are available in kinematic Dataset KTR2. Therefore, L5 data and L2C and L5 data are not processed in Tests 3 and 4. In Tests 2 and 3, the results show that the trained detector can achieve accuracy of about 70%. Comparing with simulated data, the real data have higher rates of false detection (over 30%). This is because a real multipath signal may have small magnitudes of multipath errors labelled as direct-signal only; they are sometimes comparable to the carrier phase measurement noise. An example of this is shown in Figure 10, where red dots represent ‘true’ residuals of measurements detected as multipath, and blue dots represent those detected as direct-signal only. Squared boxes in Figure 10 show typical multipath signals with small magnitudes of multipath errors. Results of Test 4 in Table 9 show that the trained detector can still detect multipath errors with degraded recall of about 70% when the test dataset and training dataset are collected in different environments (near a wall on rooftop and near a building). The moving trajectories and positions of pegs are shown in Figure 11.

Table 9.
Results of Tests 1, 2, 3, and 4.
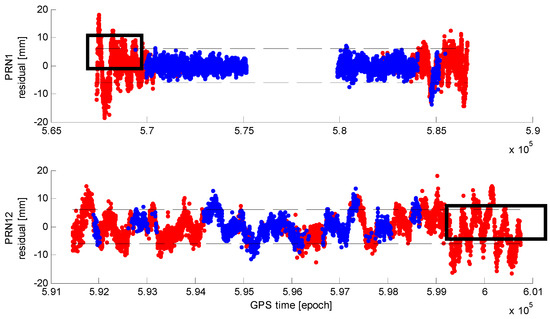
Figure 10.
‘True’ double-differenced carrier phase residuals of detected multipath measuremetns (red dots) and direct-signal only measurements (blue dots) in Dataset KTR1 (GPS L1 C/A data). Red dots in the squared areas represent mulitpath errors with small magnitudes.
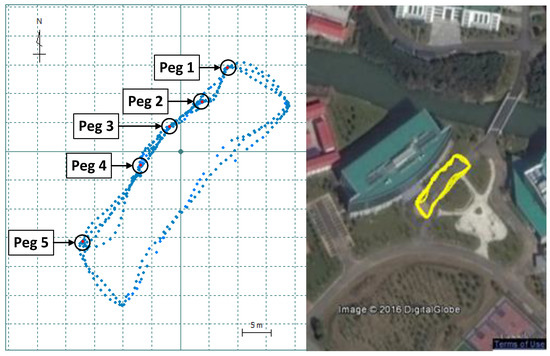
Figure 11.
The moving trajectory of antenna and positions of pegs in Dataset KTR2.
Table 10 and Table 11 show the Root Mean Square (RMS) positioning errors in horizontal and height components and 3D of the positioning solutions using simple elevation model, SIGMA-ε model, and new model based on down-weighting the detected multipath measurements (with Equation (10)). The improvements of percentage are relative to the standard least squares solution (i.e., without a stochastic model).

Table 10.
RMS errors in horizontal and height components and their percentage improvement (when comparing with the results of other stochastic models) of the tested stochastic models based on the proposed method in Dataset KTE1.

Table 11.
RMS errors in horizontal and height components and their percentage improvement (when comparing with the results of other stochastic models) of the tested stochastic models based on the proposed method in Dataset KTE3.
The results in Table 10 show that SIGMA-ε model and the proposed method outperform the standard least squares method and simple elevation model. However, Table 11 shows that the performance of the simple elevation model in Dataset KTE3 is better than that in Dataset KTE1. This is because errors (excluding multipath error caused by walls) in Dataset KTE1 collected on the rooftop are less elevation dependent compared with errors in KTE1 collected on the ground with some trees nearby (see Figure 6). The positioning errors in Table 10 (KTE1) are generally larger than those in Table 11 (KTE3) as the environment of data collection of KTE3 is more difficult than that of KTE1 (as shown in Figure 6). The deterioration for SIGMA-ε and the proposed models are probably due to the weakened satellite geometry. Generally, all the multipath mitigation methods have better positioning accuracies when compared with the standard least squares method. The improved positioning accuracy validates the proposed multipath detection method in position domain. Although the results of the proposed method show the best positioning accuracy when compared with the other two stochastic models in the two datasets, the proposed method does not significantly outperform the SIGMA-ε model in Dataset KTE1 and the simple elevation model in Dataset KTE3, respectively.
7. Conclusions
In this study, a convolutional neural network (CNN) based multipath detection method has been proposed to detect multipath in kinematic GPS positioning. The proposed method has been validated with simulated and real GPS data. The proposed method uses a CNN with a Sparse Auto-Encoder (SAE) for feature extraction. The performance of two classifiers, softmax and random forest, are compared. The results show that the softmax classifier performs better on static data and the random forest classifier performs better on kinematic data. This is because uncertainty is involved (e.g., rapid changing of environment) in kinematic multipath data, decision tree based random forest outperforms because of its high robustness. The trained detector can detect multipath contaminated measurement in real time based on the data from the current epoch and its previous successive observations. The test results with kinematic simulated data show that the proposed method can detect direct and multipath signals with accuracies of about 80%. Real kinematic data collected using a rotating arm rig (but no repetitive multipath errors) and real static data show that the method works well for GPS L1 C/A and L2 P(Y) signals with accuracies of about 70%. Real data collected near a building show that the well trained detector has an accuracy of about 60% when the training and test data are collected in two different multipath environments (close to a wall on a rooftop and near a building). In addition, the proposed method is validated in the position domain with an improvement of 18–30% in positioning accuracy using a simple linear down-weighting method, and the method outperforms a simple elevation model and SIGMA-ε model in both datasets. As a result, the tests with simulated and real data show that a multipath pattern can be detected by the proposed method, and machine learning is a feasible and promising way for detecting large GPS multipath errors. The proposed methods can be used in carrier phase based kinematic positioning, including Real-Time Kinematic (RTK) applications for improving kinematic positioning performance in difficult environments. Future work can further study the treatment of the detected multipath measurement and its effects on positioning accuracy. In addition, improving and applying the proposed methods to other GNSS (GLONASS, Galileo, and Beidou) and multi-GNSS data and high frequency (more than 1Hz) data are suggested for further research work.
Author Contributions
Conceptualization, Y.Q. and L.L.; Methodology, Y.Q. and L.L.; Software, Y.Q. and C.Z.; Validation, Y.Q., L.L. and G.W.R.; Formal Analysis, Y.Q., L.L., G.W.R. and X.M.; Investigation, Y.Q. and C.Z.; Resources, L.L.; Data Curation, Y.Q. and L.L.; Writing-Original Draft Preparation, Y.Q.; Writing-Review & Editing, L.L., G.W.R., X.M. and C.Z.; Visualization, Y.Q. and C.Z.; Supervision, L.L., G.W.R. and X.M.; Project Administration, L.L.; Funding Acquisition, L.L.
Funding
This work was carried out at the International Doctoral Innovation Centre (IDIC). The authors acknowledge the financial support from the Ningbo Education Bureau, the Ningbo Science and Technology Bureau, China’s Ministry of Science and Technology and the University of Nottingham. This research was partially funded by Engineering and Physical Sciences Research Council (EPSRC) grant number [EP/L015463/1]. The cost of building the rotating arm rig was funded by Lawrence Lau’s internal research grants (01.03.02.01.2033).
Acknowledgments
The authors would like to thank Huib de Ligt for his help in experimental setup.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lau, L.; Cross, P.; Steen, M. Flight Tests of Error-Bounded Heading and Pitch Determination with Two GPS Receivers. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 388–404. [Google Scholar] [CrossRef]
- Bhatt, D.; Aggarwal, P.; Devabhaktuni, V.; Bhattacharya, P. A novel hybrid fusion algorithm to bridge the period of GPS outages using low-cost INS. Expert Syst. Appl. 2014, 41, 2166–2173. [Google Scholar] [CrossRef]
- Lau, L.; Cross, P. Development and testing of a new ray-tracing approach to GNSS carrier-phase multipath modelling. J. Geodesy 2007, 81, 713–732. [Google Scholar] [CrossRef]
- Phan, Q.H.; Tan, S.L.; McLoughlin, I. GPS multipath mitigation: A nonlinear regression approach. GPS Solut. 2013, 17, 371–380. [Google Scholar] [CrossRef]
- Phan, Q.H.; Tan, S.L.; McLoughlin, I.; Vu, D.L. A unified framework for GPS code and carrier-phase multipath mitigation using support vector regression. Adv. Artif. Neural Syst. 2013. [Google Scholar] [CrossRef]
- Axelrad, P.; Larson, K.; Jones, B. Use of the correct satellite repeat period to characterize and reduce site-specific multipath errors. In Proceedings of the ION GNSS 2005, Long Beach, CA, USA, 13–16 September 2005; pp. 2638–2648. [Google Scholar]
- Larson, K.M.; Bilich, A.; Axelrad, P. Improving the precision of high-rate GPS. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Reuveni, Y.; Kedar, S.; Owen, S.E.; Moore, A.W.; Webb, F.H. Improving sub-daily strain estimates using GPS measurements. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Lau, L. Comparison of measurement and position domain multipath filtering techniques with the repeatable GPS orbits for static antennas. Surv. Rev. 2012, 44, 9–16. [Google Scholar] [CrossRef]
- Zhang, Y.; Bartone, C. Real-time multipath mitigation with WaveSmooth™ technique using wavelets. In Proceedings of the ION GNSS 2004, Long Beach, CA, USA, 21–24 September 2004; pp. 1181–1194. [Google Scholar]
- Elhabiby, M.; El-Ghazouly, A.; El-Sheimy, N. A new waveletbased multipath mitigation technique. In Proceedings of the ION GNSS 2008, Savannah, GA, USA, 16–19 September 2008; pp. 625–631. [Google Scholar]
- Lau, L. Wavelet packets based denoising method for measurement domain repeat-time multipath filtering in GPS static high-precision positioning applications. GPS Solut. 2017, 21, 461–474. [Google Scholar] [CrossRef]
- Lau, L.; Cross, P. A new signal-to-noise-ratio based stochastic model for GNSS high-precision carrier phase data processing algorithms in the presence of multipath errors. In Proceedings of the ION GNSS 2006, Fort Worth, TX, USA, 26–29 September 2006. [Google Scholar]
- Comp, C.J.; Axelrad, P. Adaptive SNR-based carrier phase multipath mitigation technique. Aerosp. Electron. Syst. IEEE Trans. 1998, 34, 264–276. [Google Scholar] [CrossRef]
- Hartinger, H.; Brunner, F.K. Variances of GPS phase observations: The SIGMA-e model. GPS Solut. 1999, 2, 35–43. [Google Scholar] [CrossRef]
- Fenton, P.C.; Jones, J. The theory and performance of NovAtel Inc.’s vision correlator. In Proceedings of the ION GNSS 2005, Long Beach, CA, USA, 13–16 September 2005; pp. 2178–2186. [Google Scholar]
- Townsend, B.; Van Nee, D.J.R.; Fenton, P.; Van Dierendonck, K. Performance evaluation of the multipath estimating delay lock loop. Navig. J. Inst. Navig. 1995, 42, 503–514. [Google Scholar] [CrossRef]
- Lau, L.; Cross, P. Prospects for phase multipath mitigation using antenna arrays for very high precision real-time kinematic applications in the presence of new GNSS signals. In Proceedings of the European Navigation Conference GNSS 2006, Manchester, UK, 8–10 May 2006. [Google Scholar]
- LeCun, Y.; Bengio, Y. Convolutional Networks for Images, Speech, and Time-Series. In The Handbook of Brain Theory and Neural Networks; Arbib, M.A., Ed.; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Abdel-Hamid, O.; Mohamed, A.; Jiang, H.; Deng, L.; Penn, G.; Yu, D. Convolutional neural networks for speech recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1533–1545. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Stinchcombe, M.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Lemme, A.; Reinhart, F.; Steil, J.J. Efficient online learning of a non-negative sparse autoencoder. In Proceedings of the European Symposium on Artificial Neural Networks, Bruges, Belgium, 28–30 April 2010; pp. 1–6. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Fernandez-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Gunduz, N.; Fokoue, E. Robust classification of high dimension low sample size data. arXiv, 2015; arXiv:1501.00592. [Google Scholar]
- Kim, H.; Lee, J.; Yang, H. Robust real-time face detection using hybrid neural networks. In Computational Intelligence and Bioinformatics, Proceedings of the International Conference on Intelligent Computing, ICIC 2006, Kunming, China, 16–19 August 2006; Huang, D.S., Li, K., Irwin, G.W., Eds.; Springer: Berlin/Heidelberg, Germany; pp. 721–730.
- Estey, L.H.; Meertens, C.M. TEQC: The multi-purpose toolkit for GPS/GLONASS data. GPS Solut. 1999, 3, 42–49. [Google Scholar] [CrossRef]
- Schmidt, M. minFunc: Unconstrained Differentiable Multivariate Optimization in Matlab. Available online: http://www.cs.ubc.ca/~schmidtm/Software/minFunc.html (accessed on 28 June 2014).
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Cai, C.; He, C.; Santerre, R.; Pan, L.; Cui, X.; Zhu, J. A comparative analysis of measurement noise and multipath for four constellations: GPS, BeiDou, GLONASS and Galileo. Surv. Rev. 2015, 48, 1–9. [Google Scholar] [CrossRef]
- Boulton, P.; Read, A.; MacGougan, G.; Klukas, R.; Cannon, E.; Lachapelle, G. Proposed models and methodologies for Verification Testing of AGPS-equipped cellular mobile phones in the laboratory. In Proceedings of the 15th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2002), Portland, OR, USA, 24–27 September 2002; pp. 200–212. [Google Scholar]
- Spirent Communications. SimGEM Software User Manual, Issue:4-02SR02; Spirent Communications: Crawley, UK, 2012. [Google Scholar]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Quan, Y.; Lau, L.; Roberts, G.W.; Meng, X. Measurement signal quality assessment on all available and new signals of multi-GNSS (GPS, GLONASS, Galileo, BDS, and QZSS) with real data. J. Navig. 2015, 69, 313–334. [Google Scholar] [CrossRef]
- Lau, L.; Cross, P. Phase Multipath Mitigation Techniques for High Precision Positioning in All Conditions and Environments. J. Navig. 2007, 60, 457–482. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).