Adaptive Hybrid MPPT for Photovoltaic Systems: Performance Enhancement Under Dynamic Conditions

Abstract

Optimizing energy conversion in photovoltaic (PV) systems is crucial for maximizing energy conversion efficiency and ensuring reliable operation. Achieving this requires that the PV array consistently operates at the Global Maximum Power Point (GMPP). Conventional Maximum Power Point Tracking (MPPT) algorithms, such as Perturb and Observe (P&O) and Incremental Conductance (INC), perform effectively under uniform irradiance but fail to track the GMPP under partial shading conditions (PSCs), resulting in energy losses and degraded system efficiency. To overcome this limitation, this paper proposes a hybrid MPPT method that integrates the Crayfish Optimization Algorithm (COA), a bio-inspired metaheuristic, with the P&O technique. The proposed approach combines the global exploration ability of COA with the fast convergence of P&O to ensure accurate and stable GMPP identification. The algorithm is validated under multiple irradiance patterns and benchmarked against established MPPT methods, including voltage-source and current-source region detection, Improved Variable Step Perturb and Observe and Global Scanning (VSPO&GS), and a hybrid Particle Swarm Optimization (PSO)-P&O method. Simulation studies performed in MATLAB/Simulink demonstrate that the proposed technique achieves higher accuracy, faster convergence, and enhanced robustness under PSCs. Results show that the proposed method reliably identifies the global peak, limits steady-state oscillations to below 1%, restricts maximum overshoot to 0.5%, and achieves the fastest settling time, stabilizing at the new power point significantly faster following major step changes, thereby enhancing overall PV system performance.

1. Introduction

Fossil fuels, including natural gas, coal, oil, and petroleum products, are non-renewable energy sources formed through the decomposition of ancient biomass over millions of years. In contrast, renewable energy sources are sustainable and have a lower environmental impact. With the increasing global demand for energy, significant research efforts are directed toward the development of inexhaustible alternatives to overcome the limitations of fossil fuels. Renewable sources such as geothermal, hydroelectric, biomass, wind, solar, and tidal power provide low-emission solutions with a reduced environmental footprint [1].

Photovoltaic (PV) technology is considered a promising renewable energy source for sustainable energy development owing to its availability during daylight hours and relatively low maintenance requirements. Although the initial cost of solar electricity generation remains higher than that of conventional sources, improving the efficiency of PV modules remains a key research challenge. The power output of PV systems depends strongly on solar irradiance and ambient temperature, which vary dynamically throughout the day. Consequently, numerous studies have focused on enhancing the maximum power point tracking (MPPT) performance of PV modules. MPPT is an essential component in PV system design, as it ensures the extraction of maximum power under varying operating conditions. Owing to the nonlinear nature of solar cell current–voltage (I–V) characteristics, the development of an efficient MPPT techniques is crucial to maximize output power while maintaining high system efficiency [2].

The partial shading effect in photovoltaic (PV) arrays occurs due to non-uniform solar irradiance on the cells, typically caused by trees, clouds, or building shadows. These variations generate multiple peaks in the PV curve. Although bypass diodes are used to mitigate excessive heating in shaded cells, under non-uniform conditions, they cause multiple peaks in the PV characteristics, unlike the single peak observed under uniform irradiance. As a result, the PV array may operate at a local maximum instead of the global maximum, reducing efficiency. Therefore, tracking the Global Maximum Power Point (GMPP) remains one of the major challenges in PV systems. Conventional Maximum Power Point Tracking (MPPT) algorithms are designed for uniform irradiance scenarios and fail to identify the GMPP under partial shading [3,4,5,6].

MPPT algorithms can be classified into four main categories: classical, optimization-based, intelligent, and hybrid techniques. These approaches differ in terms of accuracy, implementation cost, efficiency, and tracking speed under both steady-state and transient conditions. A comprehensive review of MPPT methods under various atmospheric conditions is presented in [7,8]. Numerous algorithms have been developed within these categories and reported in the literature, each offering distinct strengths and limitations. Classical algorithms, such as Perturb and Observe (P&O) [9], Incremental Conductance (INC) [10], and Hill Climbing (HC) [11], are widely adopted due to their simplicity, low implementation cost, and acceptable efficiency under uniform irradiance conditions. However, their performance degrades significantly under rapid environmental variations and partial shading conditions (PSCs), leading to oscillations around the maximum power point (MPP) and reduced tracking accuracy. To overcome these drawbacks, several modifications have been proposed. For instance, the authors of [12] proposed the VSPO&GS method, integrating variable-step P&O for rapid local tracking with global scanning to evaluate all peaks of the P–V curve. By adaptively adjusting step size and incorporating a restart mechanism, the algorithm ensures accurate GMPP detection and reliable re-tracking under dynamic partial shading conditions. In [13], the Voltage-Source and Current-Source Region (VSR–CSR) detection method was proposed for GMPP tracking. By analyzing I–V curve slopes and current values, the method distinguishes VSR from CSR, identifies peaks under partial shading, mitigates local convergence errors, and adaptively updates the reference voltage to ensure stable tracking.

Optimization-based techniques, including metaheuristic and soft computing approaches, have been developed to overcome the limitations of conventional methods by employing global search strategies capable of identifying the true maximum power point (MPP) under complex operating conditions. Metaheuristic algorithms [14] are generally classified into three categories: swarm intelligence (SI), evolutionary algorithms, and soft computing (SC) approaches. SI methods are inspired by collective behaviors in nature, such as Particle Swarm Optimization (PSO) [15], Ant Colony Optimization (ACO) [16], and the Cuckoo Search algorithm [17], whereas evolutionary algorithms emulate the process of natural evolution, exemplified by the Genetic Algorithm (GA) [18], which operates through selection, crossover, and mutation based on the survival of the fittest principle, with each individual in the population representing a candidate solution [19]. Recent metaheuristic methods, such as the Emperor Penguin Optimizer (EPO) [20] and the Whale Optimization Algorithm (WAO) [21], have been introduced to enhance photovoltaic (PV) system performance under partial shading conditions. The primary strength of these algorithms lies in their strong global search capability, which enables them to avoid convergence to local maxima under non-uniform irradiance. Moreover, they generally achieve faster convergence toward the global MPP compared to conventional techniques, and their adaptability improves their effectiveness in dynamic environments with varying irradiance and temperature. However, despite their superior accuracy and efficiency, metaheuristic algorithms are computationally intensive and require careful parameter tuning, which increases both implementation cost and complexity.

Intelligent techniques, such as artificial neural networks (ANNs) [22,23] and fuzzy logic (FL) [24], have been extensively investigated to enhance maximum power point tracking (MPPT) performance under partial shading conditions. ANNs are capable of learning the nonlinear relationships between input variables (e.g., irradiance, temperature, and voltage) and the corresponding optimal operating point, thereby enabling fast and accurate tracking once properly trained. However, their effectiveness strongly depends on the availability and quality of training data, and they often demand considerable computational resources, which restricts real-time implementation in low-cost controllers, processors, and embedded systems with limited capacity. Similarly, fuzzy logic controllers exhibit strong adaptability to uncertain and nonlinear environments, making them highly suitable for dynamic and real-time PV systems. Their rule-based framework facilitates effective handling of PSCs without requiring an exact mathematical model, which provides a practical advantage in complex and unpredictable operating conditions. Nevertheless, fuzzy systems necessitate careful design of rules and membership functions, and their performance may deteriorate under previously unseen operating conditions or rapidly varying irradiance profiles. Moreover, adaptive neuro-fuzzy inference systems (ANFIS) [25] have been employed for MPPT, integrating the learning capability of neural networks with the linguistic reasoning of fuzzy logic to enhance accuracy and adaptability, though at the cost of increased design complexity and computational overhead. Overall, intelligent MPPT techniques provide significant improvements in accuracy, adaptability, robustness, and tracking speed compared to conventional methods, but challenges such as data dependency, computational burden, memory requirements, implementation complexity, and overall cost remain critical barriers to large-scale deployment and widespread commercial adoption across different application domains.

No single maximum power point tracking (MPPT) algorithm can be considered universally optimal, as each technique exhibits specific limitations that may be mitigated through hybridization. The hybrid concept addresses these drawbacks by combining different methods rather than relying on a single approach. Conventional algorithms such as Perturb and Observe (P&O), Incremental Conductance (INC), and Hill Climbing (HC) are simple and cost-effective but often suffer from oscillations around the maximum power point (MPP) and reduced accuracy under partial shading conditions (PSCs). In contrast, computationally intelligent algorithms offer faster response and higher accuracy in tracking the global MPP; however, they require substantial computational resources, extensive training datasets, and costly sensors, which limit real-time implementation in low-cost systems. To overcome these challenges, hybrid approaches have been introduced by integrating classical algorithms with intelligent or metaheuristic methods. For instance, the P&O–ANN hybrid [26] improves the tracking speed of ANN while retaining the simplicity of P&O, thereby achieving faster convergence, reduced steady-state oscillations, and enhanced accuracy in dynamic irradiance conditions. The authors of [27] proposed a hybrid PSO–P&O algorithm that combines the simplicity of P&O with the global search capability of PSO. P&O enables rapid tracking and condition detection under uniform irradiance, and under partial shading, it first converges to the nearest LMPP, after which PSO searches efficiently for the GMPP, improving accuracy, convergence, and stability. Similarly, the Fuzzy Logic–Genetic Algorithm (FL–GA) approach [28] exploits the adaptability of fuzzy logic and the global search ability of GA, achieving higher accuracy under PSCs. Overall, hybrid MPPT strategies enhance PV array performance by improving reliability, increasing tracking accuracy, reducing steady-state oscillations, and achieving faster convergence with higher efficiency, particularly under dynamic atmospheric conditions. In addition, hybrid algorithms such as SSA–P&O [29] enhance PV performance by combining the global search capability of the Salp Swarm Algorithm with the local refinement of the perturb and observe method, ensuring stable tracking under partial shading conditions. SSA uses spiral evolution and Levy flights to explore the search space, while a Gaussian operator adaptively adjusts step sizes to accelerate convergence and fine-tune near the MPP. The P&O stage then performs local adjustments with a small, fixed step size to minimize power oscillations. This combination of global exploration and local refinement allows SSA–P&O to achieve high tracking precision, rapid convergence, and robustness under varying irradiance conditions.

Unlike optimization techniques such as PSO that regulate search behavior through velocity updates and personal global best memory feedback, the proposed strategy, the COA algorithm, operates through biologically inspired behavioral transitions driven by temperature-dependent state shifts. In COA, the search agents transition adaptively between summer resort exploration, competition-based exploitation, and foraging stages when optimal temperature and food size conditions are satisfied. This natural switching mechanism reduces dependence on external tuning parameters that PSO typically requires to balance global exploration and convergence speed. Furthermore, COA exhibits a superior ability to escape local optima under partial shading that is not achieved through inertia adjustment or acceleration coefficients, but through probabilistic competition and cave access decision logic when the temperature exceeds 30 °C. This process triggers agent redistribution and promotes global repositioning across the search, improving the ability to reach the GMPP. The biologically modeled reaction of COA to dynamic operating conditions allows continuous path reformation when the PV power curve shifts, enhancing tracking reliability and efficiency. These points have been integrated to clearly differentiate the proposed COA–P&O hybrid from PSO-based hybrid algorithms, emphasizing that the innovation lies not only in the hybrid structure but in the adaptive regulated optimization strategy that strengthens global tracking performance [30].

This paper presents a hybrid MPPT algorithm developed to enhance the performance of photovoltaic (PV) systems under PSCs, with comparative evaluation against conventional and advanced methods, including voltage-source and current-source region detection, Improved Variable Step Perturb and Observe and Global Scanning (VSPO&GS), and a hybrid particle swarm optimization–P&O approach. The proposed method overcomes the limitations of existing algorithms by delivering higher accuracy and reliability in tracking the global maximum power point (GMPP) under varying shading scenarios. The remainder of the paper is organized as follows: Section 2 analyzes the concept of MPPT under partial shading effect; Section 3 explains in detail the proposed MPPT technique concept. System modeling, including parameter definition, simulation case studies, verification, and results analysis, is presented in Section 4, and Section 5 concludes the work.

2. MPPT Concepts for PV Arrays Under Partial Shading

A photovoltaic (PV) array consists of multiple modules connected in series and parallel, as shown in Figure 1. The performance of the array depends on uniform solar irradiance, but environmental factors such as clouds, dust, or shadows often create partial shading conditions (PSCs). Under PSCs, shaded cells generate lower current, while unshaded cells produce higher current. Since all series-connected modules must conduct the same current, shaded cells are driven into reverse bias, absorbing energy instead of delivering it. This absorbed energy is released as heat, creating hotspots that increase thermal stress and may cause permanent degradation or failure. In severe cases, shaded cells can form open circuits that reduce system reliability. To address this problem, bypass diodes are integrated across modules. They provide an alternate current path during shading, limit reverse voltage, and prevent hotspot formation. As a result, bypass diodes protect shaded cells and improve the long-term stability of PV arrays.

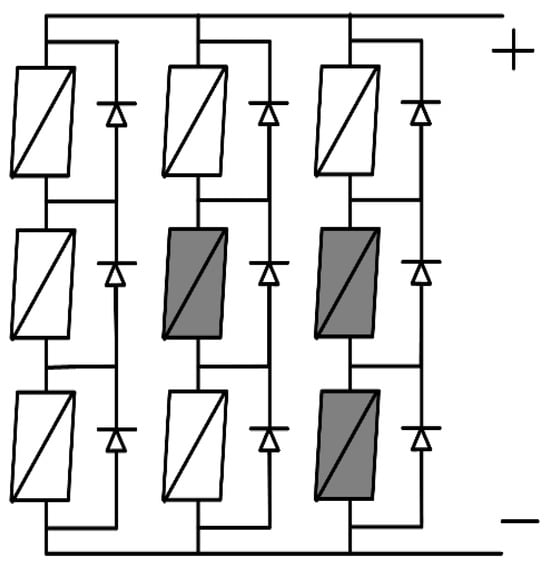
Figure 1. PV array with bypass diodes under partial shading conditions.

The maximum power point tracking (MPPT) algorithm operates as an intermediate control mechanism between the photovoltaic (PV) array and the DC–DC converter. Figure 2 illustrates the block diagram of the MPPT scheme. Its principal objective is to guarantee that the PV array consistently operates at the maximum power point (MPP), thereby enabling the highest possible energy extraction under dynamically varying atmospheric conditions. The algorithm achieves this objective by continuously monitoring the instantaneous voltage and current characteristics of the PV array, computing the corresponding output power, and determining the operating point at which maximum power is realized. Once the optimal reference point is identified, the MPPT generates a control signal to modulate the duty cycle of the DC–DC converter, thereby regulating the PV array voltage to align with the optimum operating voltage. This mechanism control process ensures rapid and stable adaptation to environmental variations, including irradiance fluctuations, temperature changes, and partial shading effects. Furthermore, the incorporation of MPPT algorithms minimizes energy losses, improves conversion efficiency, and enhances the long-term stability of PV systems. Consequently, MPPT techniques constitute a fundamental component of modern renewable energy systems, as they provide higher reliability, superior dynamic performance, and improved utilization of available solar resources in practical applications.

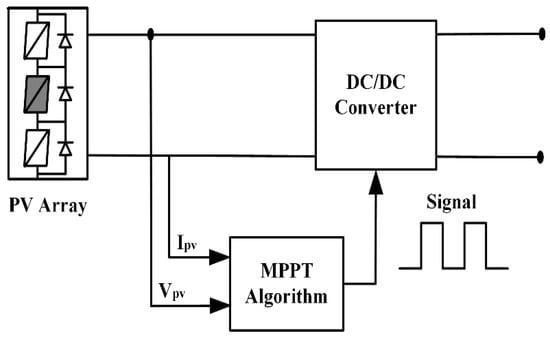
Figure 2. Block diagram of the MPPT algorithm.

3. Concept of the Proposed MPPT Technique

The PV system model consists of a PV array connected to the load through a DC–DC converter. The schematic diagram of the proposed configuration is shown in Figure 3. The system comprises several key components, each with a distinct role in ensuring optimal operation. The function of each component is discussed in detail to highlight its contribution to the overall performance and efficiency of the standalone PV system.

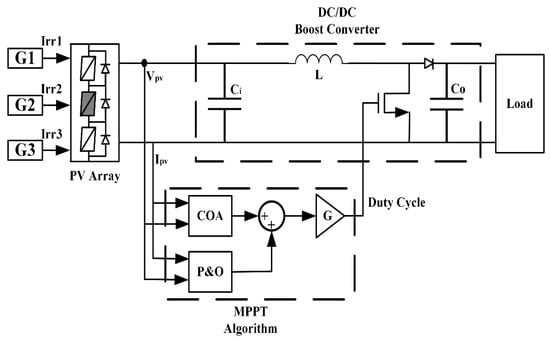
Figure 3. Schematic diagram of the proposed standalone photovoltaic (PV) system model.

The PV array serves as the primary energy source, converting solar irradiance into electrical power. The output power of the PV module is directly influenced by the incident solar irradiance, and the array specification parameters are presented in Table 1. As further illustrated in Figure 3, the PV array consists of three series-connected modules, providing a clear representation of the complete array topology used in the study. A critical component of the system is the Maximum Power Point Tracking (MPPT) algorithm, which continuously adjusts the operating point of the PV array to maintain it at or near the Maximum Power Point (MPP). The PV array’s power varies with voltage and current, forming a characteristic power–voltage (P–V) curve. MPPT regulates the duty cycle of the converter’s switching element to maximize energy extraction under varying environmental conditions, including partial shading, which can create local maxima in the P–V curve. Efficient tracking of the Global Maximum Power Point (GMPP) ensures high energy yield and rapid response to irradiance changes, improving the overall efficiency of the system.

Table 1. Specifications of the Photovoltaic (PV) Module.

Parameter	Value
Maximum power	83.28 W
Open circuit voltage (Vo.c)	12.64 V
$\mathrm{Short} \mathrm{circuit} \mathrm{current} {(\mathrm{I}}_{\mathrm{s}.\mathrm{c}})$	8.62 A
$\mathrm{Optimum} \mathrm{current}{(\mathrm{I}}_{\mathrm{m}\mathrm{p}})$	8.06 A
$\mathrm{Optimum} \mathrm{voltage}{(\mathrm{V}}_{\mathrm{m}\mathrm{p}})$	10.32 V
$\mathrm{Temp}. \mathrm{coefficient} \mathrm{of} {\mathrm{V}}_{\mathrm{o}.\mathrm{c}}$	0.06%/deg.c
$\mathrm{Temp}. \mathrm{coefficient} \mathrm{of} {\mathrm{I}}_{\mathrm{s}.\mathrm{c}}$	−0.339%/deg.c

The DC–DC converter regulates the voltage from the PV array to match load requirements by rapidly switching between on and off states. Its operation depends on the MPPT algorithm, which calculates the optimal duty cycle to generate a pulse-width modulation (PWM) signal controlling the switch element. This enables the boost converter to track the MPP effectively, ensuring efficient energy transfer. The converter parameters are defined as follows: the input capacitor C_i = 100 µF, the output capacitor C_o = 600 µF, and the inductor L = 3 mH. Finally, the load is modeled to represent the electrical demand of the system.

The operational concept of the proposed hybrid MPPT algorithm, which combines the global exploration capability of the Crayfish Optimization model with the simplicity and rapid response of the Perturb and Observe (P&O) method, is presented in this section. As shown in the system model figure, the hybrid strategy is designed to overcome the limitations of conventional techniques and to ensure reliable tracking of the global maximum power point (GMPP) under uniform and partially shaded conditions. A detailed step-by-step description of its working strategy is illustrated as follows:

3.1. Crayfish Optimization Algorithm: Concept and Operation

In recent years, numerous meta-heuristic algorithms have been proposed to enhance photovoltaic (PV) system performance under partial shading conditions. Among these, the Crayfish Optimization Algorithm (COA) has been introduced as an effective technique for Global Maximum Power Point Tracking (GMPPT). In [31], the authors demonstrated the superior performance of COA compared with several well-known meta-heuristic algorithms, including Grey Wolf Optimization (GWO) [32], Sine Cosine Algorithm (SCA) [33], and Genetic Algorithm (GA) [19]. Beyond PV applications, COA has also been applied to various optimization problems, such as clustering for vehicular routing [34] and neural network tuning [35]. COA is a bio-inspired optimization algorithm modeled after the behavioral patterns of crayfish in nature, influenced by temperature. The algorithm operates in three stages: summer resort, competition, and foraging, where temperature regulates crayfish behavior and feeding activity, thereby guiding the optimization process.

When the temperature is excessively high, crayfish enter either the competition or summer resort stage, depending on a random variable determining the probability of interaction. If the variable is less than 0.5, crayfish enter the summer resort stage without competition; if greater or equal to 0.5, they enter with competition to access the cave. Within a suitable temperature range, crayfish transition to the foraging stage. Food size determines behavior: when excessively large, claws tear it apart; when appropriate, food is consumed alternately using the second and third walking feet. These behaviors, foraging, summer resorting, and competition, form the biological basis of the Crayfish Optimization Algorithm (COA), where exploitation is modeled through foraging and competition, and exploration through summer resort behavior.

The sequence of operations in the Crayfish Optimization Algorithm (COA) consists of a structured series of computational steps designed for efficient and effective optimization of the search process. The first step involves initializing the population parameters, performed using Equation (1) according to the algorithm’s predefined rules and initial conditions.

$${\mathrm{X}}_{\mathrm{i}\mathrm{k}}={\mathrm{l}\mathrm{b}}_{\mathrm{k}}+\left({\mathrm{u}\mathrm{b}}_{\mathrm{k}}-{\mathrm{l}\mathrm{b}}_{\mathrm{k}}\right)\times rand$$

(1)

where X_ik is the position of the i-th individual in the k-th dimension, lb_k is the lower bound of the k-th population, and ub_k is the upper bound of the k-th.

The second step is to define the temperature, which determines the stage of the Crayfish Optimization Algorithm (COA), since crayfish behavior is directly influenced by temperature variations. Temperature also affects the feeding rate of crayfish, with the optimal feeding range lying between 15 °C and 30 °C, while 25 °C represents the most favorable condition. Temperature is mathematically expressed in Equation (2).

$$temp=rand\times 15+20$$

(2)

When the temperature exceeds 30 °C, crayfish move toward cooler areas by seeking protective shaded caves and entering the summer resort stage for resting, feeding, sheltering, and environmental exploration efficiently. The fitness of the selected cave position, denoted as X_shade, is defined in Equation (3).

$${\mathrm{X}}_{\mathrm{shade}}=\left({\mathrm{X}}_G+{\mathrm{X}}_L\right)/2$$

(3)

where X_G is the best position determined so far by the number of iterations, and X_L is the optimal position of the current population.

When the temperature exceeds 30 °C, crayfish may either enter the cave directly or compete for access, depending on a probabilistic random event that simulates natural variability in behavior. If the random value is less than 0.5, it indicates that no other crayfish are simultaneously attempting to occupy the cave, and the crayfish immediately enter the summer resort stage (exploration stage), as defined in Equation (4), promoting wide-ranging search of the solution space. Conversely, if the random value is greater than or equal to 0.5, crayfish compete with one another to access the cave, representing the competition stage (exploitation stage), as expressed in Equation (5), which enhances solution refinement and convergence.

$${{\mathrm{X}}_{\mathrm{i}\mathrm{k}}}^{t+1}={{\mathrm{X}}_{\mathrm{i}\mathrm{k}}}^t+\left(2-\left({\displaystyle \frac{t}{T}}\right)\right)\times rand\times \left({\mathrm{X}}_{\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{d}\mathrm{e}}-{{\mathrm{X}}_{\mathrm{i}\mathrm{k}}}^t\right)$$

(4)

where t is the current iteration number, t+1 is the next generation of iteration number, and T is the maximum number of iterations.

$${{\mathrm{X}}_{\mathrm{i}\mathrm{k}}}^{t+1}={{\mathrm{X}}_{\mathrm{i}\mathrm{k}}}^t-{{\mathrm{X}}_{(\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\left(\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\times \left(\mathrm{N}-1\right)\right)+1)\mathrm{k}}}^t+{\mathrm{X}}_{\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{d}\mathrm{e}}$$

(5)

In this context, N denotes the population size, specifying the number of candidate solutions considered during optimization. When the temperature drops below 30 °C, the environment becomes favorable for crayfish feeding, initiating the foraging stage of the Crayfish Optimization Algorithm (COA). During this stage, each crayfish moves systematically toward the food source, guided by optimization rules that mimic natural foraging behavior. Once the crayfish reaches the food source, food size is evaluated to determine the next action. This evaluation is mathematically expressed in Equation (6), where food size acts as a decisive parameter influencing whether crayfish directly consume the food or shred it into smaller pieces, simulating the balance between exploration and exploitation within the optimization framework.

$$Q={\mathrm{C}}_3\times rand\times \left({\displaystyle \frac{{\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}}_{\mathrm{i}}}{{\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}}_{\mathrm{f}\mathrm{o}\mathrm{o}\mathrm{d}}}}\right)$$

(6)

where Q is the food size, C₃ is the food factor, which refers to the largest food and has a constant value of 3, fitness_i is the fitness value of the i-th crayfish, and fitness_food is the fitness value of the food.

When the food size exceeds a threshold of 2, the crayfish employs its claws to shred the food into smaller pieces, as described in Equation (7), and then alternately uses its second and third walking feet to eat it, as expressed in Equation (8). Conversely, when the food size is less than or equal to 2, the crayfish directly approaches the food and eats it without shredding, as formulated in Equation (9).

$$X_{food}=exp\left(-{\displaystyle \frac{1}{Q}}\right)\times X_{food}$$

(7)

$${X_{ik}}^{t+1}={X_{ik}}^t+X_{food}\times p\times (\mathit{cos}\left(2\pi \times rand\right)-\mathit{sin}\left(2\pi \times rand\right))$$

(8)

where X_food is the optimal solution, and p is the food intake.

$${X_{ik}}^{t+1}={{(X}_{ik}}^t-X_{food})\times p+p\times rand\times {X_{ik}}^t$$

(9)

The objective function in the Crayfish Optimization Algorithm (COA) is defined to minimize the error between the model’s output power in the current and previous iterations, thereby ensuring maximum energy extraction and system efficiency. Each crayfish, representing a candidate solution, is evaluated based on its position in the search space by calculating the duty cycle and considering environmental and system constraints. The corresponding fitness value is the measured output power obtained from the system, and the duty cycle that yields the highest power is considered the best position. The positions of new candidates are updated according to their fitness values, which are re-evaluated in each iteration to enhance convergence reliability. When the relative error of power between the best individual of the current iteration and that of the previous iteration falls below a predefined threshold, the corresponding duty cycle is selected as the final value, ensuring operation at the maximum power point (MPP). The system continues operating with this duty cycle until shading conditions change, which changes the MPP location on the PV curve, resulting in a relative error exceeding the threshold. In such cases, the COA reactivates to re-estimate the duty cycle and re-track the MPP dynamically for continuous optimal performance. The flowchart of the Crayfish Optimization Algorithm sequence of operation can be clearly and systematically explained in Figure 4, illustrating all key computational steps.

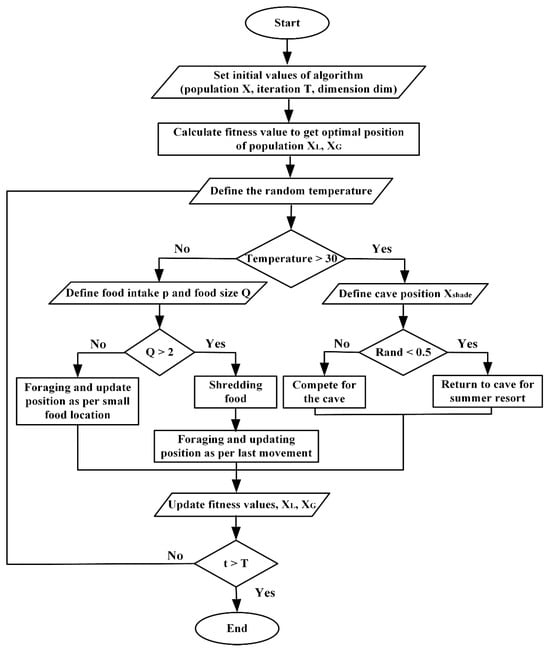
Figure 4. Flowchart of the crayfish optimization algorithm.

3.2. Perturb and Observe Method for Maximum Power Point Tracking

The perturb and observe (P&O) method is an effective Maximum Power Point Tracking (MPPT) technique, particularly under uniform irradiance conditions. It is one of the most widely studied MPPT methods due to its simple structure, ease of implementation, and low cost, making it highly suitable for a wide range of photovoltaic applications and practical energy harvesting scenarios, including small- and large-scale PV systems, residential and commercial installations, and microgrid integration. In this method, the power output of the PV array is calculated from the measured voltage and current values. The instantaneous power and voltage are compared with their previous values to determine the necessary perturbation. By incrementally adjusting the reference voltage and observing the resulting change in output power, the P&O algorithm identifies the appropriate direction to track the maximum power point. Changes in the reference voltage directly influence the PV system’s output power, and the perturbation direction is selected based on the observed power variation. The operational principle of the P&O MPPT algorithm is clearly illustrated in the flowchart shown in Figure 5.

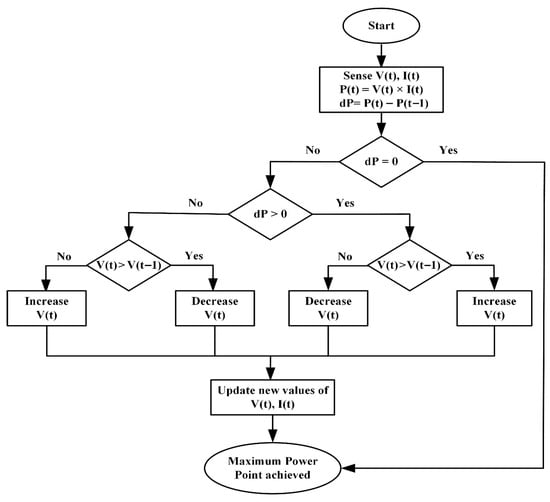
Figure 5. Flowchart of the P&O method.

3.3. Conceptual Framework and Structure of the Proposed Hybrid Algorithm

To track the Maximum Power Point (MPP) under uniform irradiation, several conventional techniques can be employed. However, under partial shading conditions, these methods fail to identify the Global Maximum Power Point (GMPP) and instead converge to local peaks. In recent years, various optimization and intelligent algorithms have been developed to overcome this limitation, each with distinct advantages and drawbacks for GMPP tracking. The hybrid approach provides an effective solution by combining the strengths of individual techniques, thereby enhancing the output power performance of the PV system. The proposed hybrid algorithm introduces a novel MPPT technique that combines the Crayfish Optimization Algorithm (COA) with the Perturb and Observe (P&O) method. The performance of this hybrid technique is evaluated under multiple simulation scenarios, including both steady-state and transient conditions, for standalone or grid-connected PV systems, as detailed in the Simulation and Results section. The implementation structure, incorporating the COA and P&O blocks, is illustrated in Figure 3 and is suitable for varying irradiance conditions on the PV array. The algorithm’s output signal is obtained by averaging the duty cycles from COA and P&O, with a gain of 0.5, to interface effectively with the DC–DC boost converter for accurate GMPP tracking, whereby the output of each algorithm was assessed individually, and a weighting process was applied to evaluate their performance contributions. An equal weight (average) was then selected to ensure balanced representation among the compared methods. The results obtained from the case studies validate the methodology effectiveness of the proposed hybrid COA-P&O algorithm and confirm that the adopted weighting approach supports fair and consistent performance evaluation.

4. Modeling and Simulation of the PV System with Defined Parameters

To evaluate the performance of the photovoltaic (PV) system, the proposed hybrid Crayfish–Perturb and Observe (COA–P&O) algorithm is assessed under both uniform and partial shading conditions. Several case study scenarios are implemented and compared against recently established MPPT techniques, including voltage-source and current-source region detection [13], Improved Variable Step P&O with Global Scanning (VSPO&GS) [12], and the hybrid PSO–P&O method [27]. The performance evaluation focuses on key criteria such as tracking accuracy, convergence speed, and oscillation around the maximum power point (MPP). To maximize the output power of the PV array, oscillation losses near the MPP must be minimized while the accuracy of tracking the global MPP (GMPP) is improved, thereby enhancing overall system efficiency. Simulation and analysis are carried out in the MATLAB/Simulink (version 2021b) environment using visualization tools such as the Simulation Data Inspector, scopes, and dashboard blocks for result generation and comparison. The performance evaluation at the end of each scenario highlights which algorithms successfully track the GMPP under changing irradiance levels and which fail, thereby demonstrating the strengths and limitations of each method and their impact on overall system efficiency.

The parameters of the selected Maximum Power Point Tracking (MPPT) techniques employed in this study are summarized as follows to ensure clarity and completeness. For the Perturb and Observe (P&O) algorithm, which is widely utilized due to its simplicity and low implementation cost, the parameters are defined as: initial duty cycle D_initial = 0.4, minimum duty cycle D_min = 0.1, maximum duty cycle D_max = 0.75, and duty cycle perturbation step ΔD = 0.02. Variable-step method adjusts the perturbation step based on the observed changes in output power, where the step is set proportionally to the power difference, |dP| = P_k − P_k⁻¹, typically using a step = 0.001 × |dP|. The Particle Swarm Optimization (PSO) technique, which leverages swarm intelligence to enhance global search capability and improve convergence speed, is configured with the following parameters: inertia weight W = 0.4, cognitive learning factor C₁ = 2, social learning factor C₂ = 2, and a maximum of 300 iterations. Finally, the Crayfish Optimization Algorithm (COA), a bio-inspired metaheuristic designed to exploit the exploratory behavior of crayfish for improved tracking accuracy under both uniform irradiance and partial shading conditions, is parameterized with a population size of 20, a maximum of 200 iterations, and a threshold temperature of 30 °C. Collectively, these configurations provide a detailed reference for the setup, comparison, and tuning of each MPPT technique considered in the simulations and performance analyses conducted in this study.

To justify the selection of the Crayfish Optimization Algorithm (COA) parameters, a convergence-based analysis was performed to examine the influence of population size and maximum iteration count on tracking performance and computational efficiency. Different population sizes were considered to evaluate their impact on search diversity and convergence speed, where smaller populations provided faster initial convergence but increased the risk of incomplete global exploration under partial shading conditions, while larger populations enhanced search coverage at the expense of higher computational burden and longer settling time. The population size of 20 was therefore selected as it provides sufficient diversity for reliable global exploration while maintaining efficient convergence. In parallel, the maximum number of iterations was chosen based on observed convergence behavior toward the global maximum power point (GMPP), where the algorithm consistently reached a stable duty cycle well before 200 iterations under the tested operating conditions. Increasing the iteration count beyond this value resulted in no significant enhancement in convergence quality while significantly increasing computational effort, without noticeable improvement in tracking accuracy. Consequently, the selected configuration of a population size of 20 and a maximum of 200 iterations ensures reliable GMPP convergence with balanced exploration capability, convergence stability, and computational efficiency, making it suitable for MPPT operation under partial shading conditions.

4.1. Case Study I: Standalone PV System

4.1.1. Case Study I: Standalone PV System Under Uniform Irradiation Conditions and Constant Temperature

In the uniform irradiance case, the three photovoltaic (PV) groups are subjected to identical irradiance levels, which vary over time at 1000, 750, 500, and 1000 W/m², as summarized in Table 2, which lists the corresponding global MPP values for each interval, while the temperature is maintained constant at 25 °C. The P–V characteristics for these conditions are shown in Figure 6, where a single peak is observed at each level, enabling straightforward tracking of the MPP. The irradiance pattern applied across the PV array is presented in Figure 7, while the corresponding duty cycle response under uniform conditions is illustrated in Figure 8. In this configuration, the incident irradiance on the upper, middle, and lower PV groups is denoted as Irr1, Irr2, and Irr3, respectively, as illustrated in the system model with details shown in Figure 3.

Table 2. Global MPP Values Under Uniform Irradiance (Case I).

	Time (s)	0–3	3–6	6–9	9–12
Irradiance (W/m2)
Irr1		1000	750	500	1000
Irr2		1000	750	500	1000
Irr3		1000	750	500	1000
Global MPP		249.84	188.37	125.53	249.84

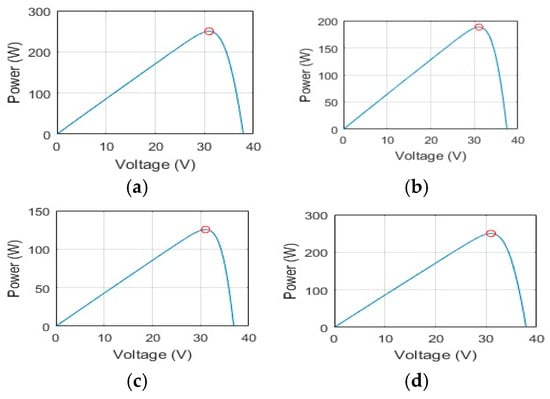
Figure 6. P–V curves under uniform irradiance at time intervals: (a) 0–3 s, (b) 3–6 s, (c) 6–9 s, and (d) 9–12 s (Case I).

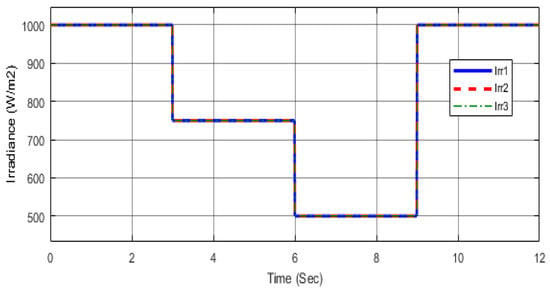
Figure 7. Time-varying irradiance pattern (Case I).

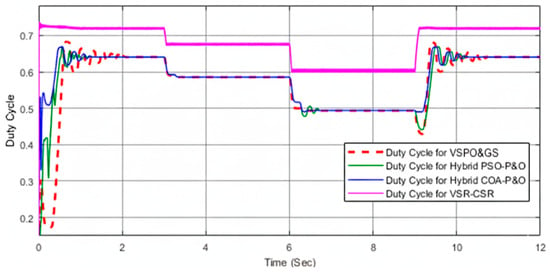
Figure 8. Generated duty cycle using VSR–CSR, VSPO&GS, PSO–P&O, and COA–P&O under uniform irradiance (Case I).

Case I analyzes uniform solar irradiance incident on the photovoltaic (PV) modules. Under this operating condition, the P–V characteristic curve exhibits a single distinctive peak corresponding to the global MPP, as illustrated clearly in Figure 6. Since the irradiance variation is relatively smooth, stable, and regular over time, all four employed algorithms, namely VSR–CSR detection, Improved Variable Step P&O with Global Scanning (VSPO&GS), the hybrid PSO–P&O, and the proposed COA–P&O, were able to successfully and consistently track the MPP, as shown in Figure 9. In particular, the proposed COA–P&O method demonstrated slightly faster convergence to the GMPP with enhanced overall tracking accuracy, stability, and robustness, especially during the final interval starting at 9 s, when the irradiance pattern changed according to the specified reference values presented in Table 2 for reliable performance validation. Moreover, compared with the other evaluated algorithms, the proposed method achieved superior efficiency by reaching the global peak points with fast response for the irradiance around 250 W, adaptability, and reliability, highlighting its practical effectiveness for real energy systems.

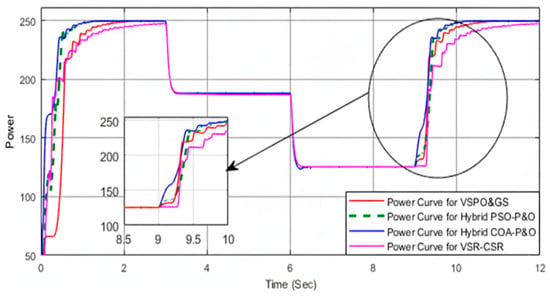
Figure 9. Output power response of VSR–CSR, VSPO&GS, PSO–P&O, and COA–P&O under uniform irradiance (Case I).

4.1.2. Case Study I: Standalone PV System Under Uniform Irradiation Conditions and Variant Temperatures

In the uniform irradiance scenario with varying temperature, the three photovoltaic (PV) groups operate under the same temperature profile, changing sequentially to 25, 40, 55, and back to 25 °C. These conditions and their corresponding global MPP values are summarized in Table 3, while irradiance remains constant at 1000 W/m². The resulting P–V characteristics are depicted in Figure 10, where a single peak is observed at each temperature level, allowing straightforward MPP tracking. The temperature pattern applied to the PV array is shown in Figure 11, and the corresponding duty cycle behavior under these conditions is illustrated in Figure 12. In this configuration, the temperatures of the upper, middle, and lower PV groups are represented as T1, T2, and T3, respectively, as explained in the system model in Figure 3.

Table 3. Global MPP Values Under Uniform Irradiance, and Variant Temperatures (Case I).

	Time (s)	0–3	3–6	6–9	9–12
Temperature (°C)
T1		25	40	55	25
T2		25	40	55	25
T3		25	40	55	25
Global MPP		249.84	234.75	219.42	249.84

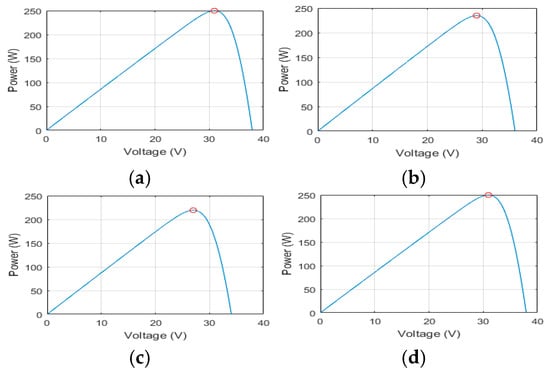
Figure 10. P–V curves under uniform irradiance, and variant temperatures at time intervals: (a) 0–3 s, (b) 3–6 s, (c) 6–9 s, and (d) 9–12 s (Case I).

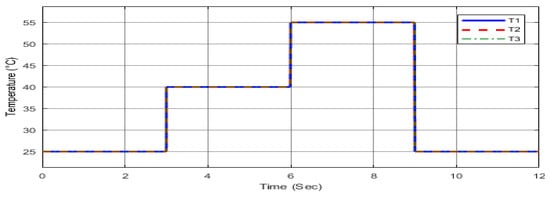
Figure 11. Time-varying temperature pattern (Case I).

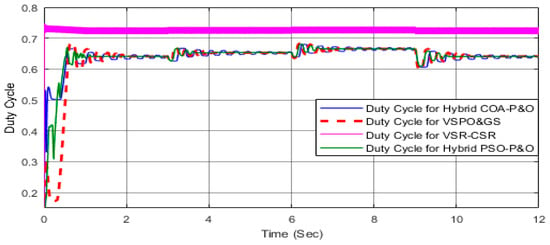
Figure 12. Generated duty cycle using VSR–CSR, VSPO&GS, PSO–P&O, and COA–P&O under uniform irradiance, and variant temperatures (Case I).

Case I investigates the performance of the photovoltaic (PV) system under uniform irradiance with varying temperature levels. Under these conditions, the P–V curve exhibits a single peak at the global MPP, as illustrated in Figure 10. All four MPPT strategies, VSR-CSR, Improved Variable Step P&O with Global Scanning (VSPO&GS), hybrid PSO-P&O, and the proposed COA-P&O, successfully track the MPP, as shown in Figure 13. However, the proposed COA-P&O demonstrates faster convergence, improved accuracy, and stronger robustness, particularly during the final temperature transition occurring at 9 s according to the values listed in Table 3. Additionally, when compared to the other methods, the proposed algorithm maintains superior tracking efficiency, rapidly reaching the global peak and ensuring adaptability and high reliability across temperature variations. These results validate the practical effectiveness of COA P&O for real PV energy conversion systems.

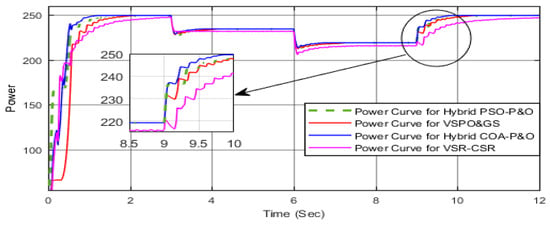
Figure 13. Output power response of VSR–CSR, VSPO&GS, PSO–P&O, and COA–P&O under uniform irradiance, and variant temperatures (Case I).

4.2. Case Study II: Standalone PV System Under Partial Shading Conditions

The irradiance of the three photovoltaic (PV) groups is set to follow varying patterns, as illustrated in Figure 14. The upper, middle, and lower PV groups are assumed to receive irradiance values corresponding to those listed in Table 4, which also presents the global maximum power point (GMPP) for each period. The P–V curves for each irradiance level, shown in Figure 15, exhibit multiple peaks, clearly highlighting the effects of partial shading under non-uniform conditions and the resulting complex power distribution among the PV modules. The corresponding duty cycle variations for these conditions are illustrated in Figure 16, providing insight into the dynamic behavior and control response of the system, as demonstrated in the system model shown in Figure 3.

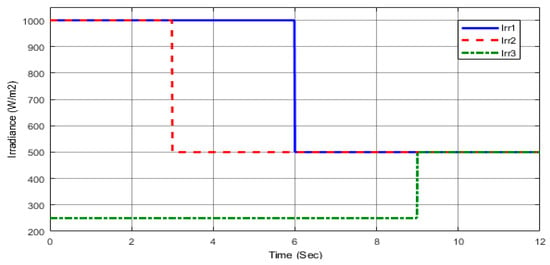
Figure 14. Time-varying irradiance pattern (Case II).

Table 4. Global MPP Values Under Partial Shading (Case II).

	Time (s)	0–3	3–6	6–9	9–12
Irradiance (W/m2)
Irr1		1000		500
Irr2		1000	500
Irr3		250			500
Global MPP		160.87	87.84	80.85	125.53

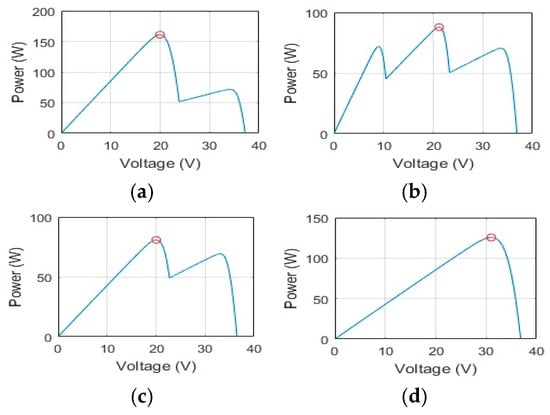
Figure 15. P–V curves under partial shading at time intervals: (a) 0–3 s, (b) 3–6 s, (c) 6–9 s, and (d) 9–12 s (Case II).

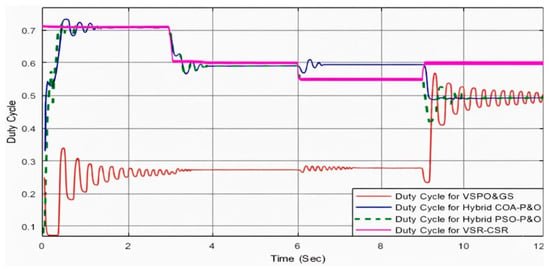
Figure 16. Generated duty cycle using VSR–CSR, VSPO&GS, PSO–P&O, and COA–P&O under partial shading (Case II).

Case II represents a realistic scenario of partial shading, where multiple peaks exist, but only one corresponds to the global maximum power point (GMPP), as shown in Figure 14. It is evident from the power curve in Figure 17, particularly in the third interval beginning at 6 s, that the proposed Hybrid COA–P&O algorithm successfully reaches the global maximum power point (GMPP) from approximately 87 W within 0.3 s, exhibiting very low overshoot and minimal oscillations. The VSR–CSR method exhibits slightly higher oscillations and a longer settling time, reaching approximately 77 W within about 0.5 s, while both the hybrid PSO–P&O and the VSPO&GS methods respond more slowly and stabilize at a lower power level of below 70 W at this period. Furthermore, in the final interval at 9 s, when the irradiance increases to approximately 125 W, the COA–P&O again effectively tracks the global peak with low overshoot and negligible oscillations, confirming its superior accuracy. In summary, the Hybrid COA–P&O algorithm achieves an optimal balance between fast convergence and low steady-state ripple, resulting in improved long-term energy capture. Although other algorithms may momentarily reach slightly higher instantaneous values, the COA–P&O’s reduced oscillations around MPP to minimize energy loss and enhance overall performance.

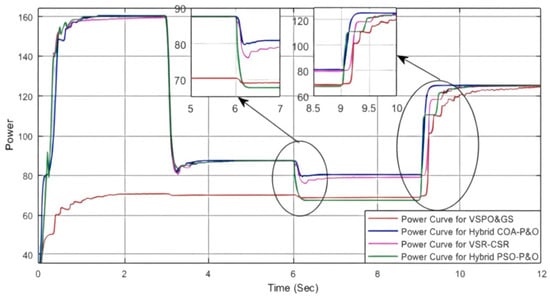
Figure 17. Output power response of VSR–CSR, VSPO&GS, PSO–P&O, and COA–P&O under partial shading (Case II).

4.3. Case Study III: Grid-Connected PV System Under Partial Shading Conditions

The PV system model consists of a PV array connected to the grid through a DC–DC converter, inverter, LC filter, and transformer. The schematic of the proposed configuration is illustrated in Figure 18. Each component plays a distinct role in ensuring optimal operation, and their functions are discussed to highlight their contributions to the overall performance and efficiency of the grid-connected PV system.

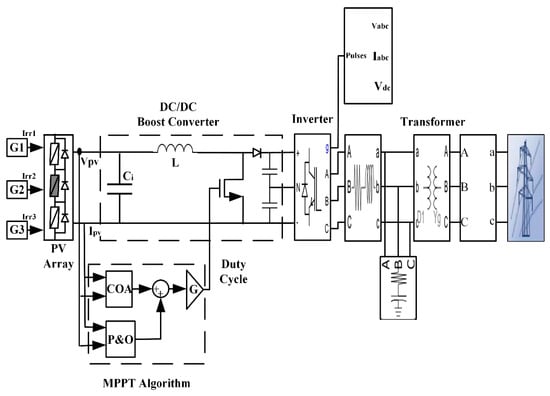
Figure 18. Schematic diagram of the proposed grid-connected photovoltaic (PV) system model.

The photovoltaic (PV) system consists of a PV array, MPPT algorithm, power converter, inverter, filter, and transformer, forming a complete grid-connected energy conversion system for efficient, reliable, and sustainable renewable power generation. The PV array comprises panels exposed to three irradiance levels (Irr1, Irr2, and Irr3) and converts sunlight into electrical energy, with the output determined primarily by the array’s voltage and current characteristics under varying environmental conditions such as temperature, shading, and irradiance fluctuations throughout the day. The MPPT algorithm continuously receives the PV voltage and current as inputs and generates a duty cycle to control the converter, ensuring operation at the maximum power point (MPP) even under partially shaded, non-uniform, or dynamically changing conditions, thereby optimizing overall energy extraction. A boost converter steps up the DC voltage from the PV array, with its output precisely regulated to track the MPP and provide stable DC voltage to the inverter for subsequent AC conversion. The inverter then converts this boosted DC into AC voltage using a three-level bridge circuit with pulse-width modulation (PWM) control, where the switching pulses depend on the inverter DC voltage as well as the grid voltage and current measurements for accurate synchronization. A filter is employed to smooth voltage and current fluctuations, reduce total harmonic distortion, and minimize ripples, thereby ensuring high-quality and stable AC output suitable for grid connection and long-term system reliability. Finally, a 100-kVA step-up transformer with a 260 V/25 kV ratio raises the voltage to grid level, enabling efficient synchronization with the network and reliable, continuous power injection into the utility grid under varying operational conditions.

The irradiance of the first photovoltaic (PV) group is varied according to a time-dependent pattern, while the other two groups are maintained at fixed levels, as shown in Figure 19. The upper, middle, and lower PV groups receive irradiance values listed in Table 5, which define GMPP for each interval under the specified condition. The corresponding P–V curves in Figure 20 exhibit multiple peaks, indicating the presence of several local maxima caused by partial shading and non-uniform irradiance across the PV array. The duty cycle behavior under these conditions, which determines the switching operation of the converter, is shown in Figure 21 to illustrate the dynamic system response. Figure 20, Figure 21 and Figure 22, representing the irradiance pattern, duty cycle, and corresponding output power, respectively, are plotted starting from the first interval at t = 2 s to highlight the system response after the initial dynamic transition required to reach the GMPP.

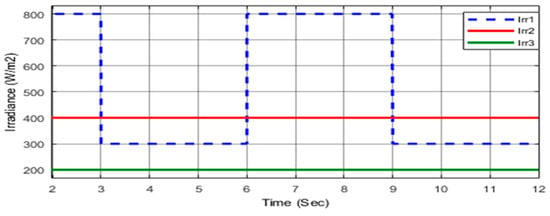
Figure 19. Time-varying irradiance pattern (Case III).

Table 5. Global MPP Values Under Partial Shading (Case III).

	Time (s)	0–3	3–6	6–9	9–12
Irradiance (W/m2)
Irr1		800	300	800	300
Irr2		400
Irr3		200
Global MPP		66.35	49.34	66.35	49.34

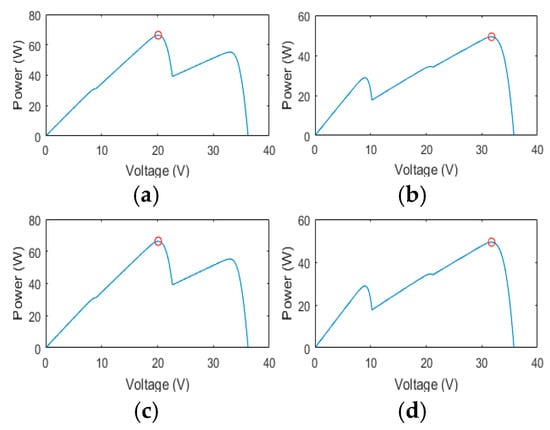
Figure 20. P–V curves under partial shading at time intervals: (a) 0–3 s, (b) 3–6 s, (c) 6–9 s, and (d) 9–12 s (Case III).

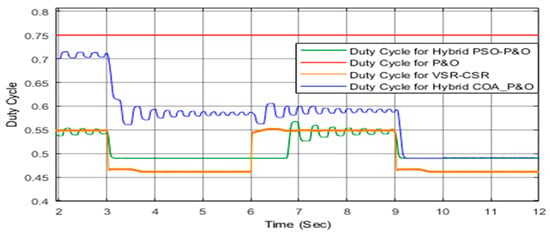
Figure 21. Generated duty cycle using VSR–CSR, VSPO&GS, PSO–P&O, and COA–P&O under partial shading (Case III).

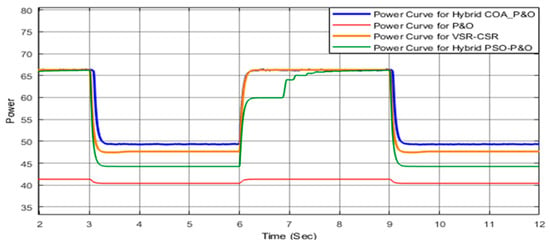
Figure 22. Output power response of VSR–CSR, VSPO&GS, PSO–P&O, and COA–P&O under partial shading (Case III).

Case III represents a partial shading scenario, which is a realistic condition reflecting the dynamic and non-uniform variations in sunlight incident on solar panels due to passing clouds, moving shadows, and other environmental factors. Under this condition, the P–V characteristic curve exhibits multiple peaks, including several local maxima, with only one point corresponding to the global maximum, as shown in Figure 19. As illustrated in the power curve in Figure 22, the second and fourth intervals, starting at 3 s and 9 s, respectively, demonstrate that the proposed Hybrid COA–P&O algorithm effectively responds to irradiance changes and achieves stability within approximately 0.2 s. It accurately tracks the global maximum power point at around 49 W with minimal overshoot. This superior performance is attributed to the COA initialization, which provides an excellent starting point for the P&O fine-tuning stage, resulting in a faster transient response and minimal oscillation distortion. The corresponding GMPP values for each interval are provided in Table 5 for reference and detailed comparison, clearly highlighting the effectiveness and practical applicability of the proposed approach under realistic partial shading conditions.

A detailed comparative analysis highlights the key distinctions between the proposed COA–P&O algorithm and widely adopted hybrid MPPT techniques such as PSO–P&O, particularly in terms of algorithmic mechanisms, exploration–exploitation balance, computational structure, and convergence behavior. The proposed method leverages COA’s temperature-adaptive behavioral transitions, which inherently regulate the shift between exploration and exploitation. In addition, the probabilistic competition and cave-selection mechanism strengthen global search robustness under partial shading, while the structured integration with P&O facilitates rapid and stable local refinement near the GMPP. Comparative justification further shows that COA exhibits lower parameter sensitivity and a biologically driven adaptation framework that avoids the reliance on inertia weight and acceleration coefficients characteristic of PSO-based methods. The quantitative results reported in the reference tables, supported by the zoomed boxes in illustrations for each case study, confirm the superior accuracy and reliability of the COA–P&O algorithm in consistently reaching the true GMPP across all tested shading scenarios, demonstrating clear performance advantages over the benchmarked techniques.

5. Conclusions

Tracking the global maximum power point (GMPP) is essential to maximize the output power of photovoltaic (PV) systems. Various MPPT techniques have been developed to achieve this objective, including conventional algorithms such as Perturb and Observe (P&O) and Incremental Conductance (INC). However, under partial shading conditions, these conventional methods fail to accurately track the global MPP, resulting in significant power losses and reduced overall energy generation. This paper proposes a hybrid MPPT technique based on the Crayfish Optimization Algorithm (COA) combined with P&O and compares its performance with voltage-source and current-source region detection, Improved Variable Step P&O with Global Scanning (VSPO&GS), and a hybrid PSO–P&O method under both steady-state and transient conditions. Detailed case studies are conducted to evaluate the proposed approach for both stand-alone and grid-connected PV systems under varying irradiance profiles, atmospheric conditions, and dynamic environmental changes. The results demonstrate superior performance, including faster response to irradiance variations, higher tracking accuracy, improved robustness, and reduced oscillations compared with established MPPT techniques. The proposed method provides enhanced tracking performance under environmental disturbances, thereby significantly improving the overall efficiency, reliability, and stability of PV systems. In summary, this research presents a robust framework for enhancing energy efficiency and operational stability in photovoltaic (PV) systems and grid integration. The proposed Hybrid COA–P&O method establishes a solid foundation for future advancements in renewable energy optimization. Future work will involve experimental validation of the COA–P&O algorithm under real world environmental conditions and its implementation in large-scale, grid-connected PV systems with the goal of optimizing performance, improving tracking accuracy, and enhancing grid stability.