Abstract
With the establishment of a competitive electricity retail market, how to optimize the retail electricity price mechanism has become the core of all kinds of retail companies to explore. Aiming at the pricing problem of time-of-use electricity price, this paper proposes a pricing strategy based on the master–slave game model. Firstly, considering the user’s electricity utility and satisfaction factors, the comprehensive benefit function of the electricity selling company with electricity price as the decision variable and the user’s comprehensive benefit function with electricity consumption as the decision variable are established, respectively. Then, a master–slave game model is established with the electricity selling company as the leader and the user as the follower, and the reverse induction method is used to solve the model. Finally, considering the influencing factors of user response ability, different electricity price types and user types are set up for simulation. The results show that the revenue of electricity retailers can be increased by up to 170,000 yuan, and the average electricity price of users can be reduced by up to 8 yuan. It is verified that the model can effectively achieve a win-win situation for both sides and promote peak shaving and valley filling. At the same time, it is proved that the role of the model is positively related to electricity price flexibility and user response capability.
1. Introduction
1.1. Background
On 15 March 2015, the Central Committee of the Communist Party of China and the State Council issued a programmatic document on the reform of the electric power system, “Several Opinions on Further Deepening the Reform of the Electric Power System (Zhongfa No. 9), “marking the implementation of the pilot reform of the electricity sales side, and the introduction of electricity sales companies as new market players into the electricity market [1]. Since then, the electricity sales companies have gradually carried out business in Guangdong, Shanxi, Shandong, and other provinces to participate in the electricity retail market transactions.
With the gradual deepening of China’s electricity market reform and the establishment of a competitive electricity retail market, how to construct a reasonable retail electricity price mechanism and design an optimized retail electricity price package has become the core of exploration by various retail electricity companies [2]. Electricity retail packages are usually characterized by a variety of electricity billing methods. In the domestic electricity market, electricity retailers can sign retail package contracts with market users for price difference sharing or time-of-use pricing. For non-market users, the electricity pricing mechanism combining block pricing and time-of-use pricing (TOU) is generally implemented [3].
In recent years, China’s provinces have successively launched rich power retail packages on retail platforms, including various time-of-use electricity price packages. As a main way of price-based demand response, time-of-use electricity price reflects the power supply cost in each period by formulating different electricity prices in different periods. It not only helps to guide users to purchase electricity decisions but also achieves the effect of peak shaving and valley filling to a certain extent [4,5], and can broaden the profit channels of electricity retailers.
Therefore, it can be seen that exploring the time-of-use pricing mechanism is a hot issue in the field of electricity market research, and it is also a major focus of retail market construction.
1.2. Literature Review
Aiming at the optimization problem of time-of-use electricity price mechanism, there are a lot of studies at home and abroad. This paper combs from the following two aspects: (1) research on time-of-use electricity price pricing model and its application field; (2) optimization method of time-of-use electricity price pricing strategy based on master–slave game model.
Time-of-use electricity price plays an important role in optimizing resource allocation, promoting energy consumption, reducing operating costs, and optimizing load curves. Based on the background of smart grid, the literature [6] developed a new energy management system based on time-of-use electricity price for household users, which effectively improved the energy utilization rate. However, the research user type is single, which fails to fully reflect the universality of the time-of-use electricity price mechanism. In Reference [7], the optimal operation model of microgrid alliance, shared energy storage and active distribution network is established. Through the cyclic iteration among the three participants, the final operation scheme and dynamic time-of-use price of the distribution network are formulated to effectively promote the consumption of renewable energy, but the real-time feedback of users is not considered, and the response potential of users is not fully explored. In Reference [8], the time-of-use electricity price is combined with the optimal operation problem of the smart microgrid, and the time-of-use electricity price is implemented under the conditions of renewable energy and incentive-based demand response to reduce the operating cost of the smart microgrid. However, from the perspective of grid operation, the interests of users are not taken into account. Reference [9] describes the user’s demand response behavior through reinforcement learning and optimizes the user’s load curve under the time-of-use electricity price mechanism but does not take into account the user’s benefit. At the same time, most of the above literature ignores the user-side benefits, fails to reflect the win-win principle, and does not fully mobilize the user-side demand response potential.
There are also many scholars at home and abroad who study time-of-use electricity price optimization and take into account the improvement of user demand response ability and the improvement of user efficiency. In Reference [10], a time-of-use pricing model considering the uncertainty of wind power is proposed. The optimal solution set is obtained by using NSGA-II multi-objective optimization algorithm with the target of peak-valley difference in equivalent net load and user dissatisfaction. At the same time, it ensures the user’s electricity comfort and the role of peak shaving and valley filling but ignores the interests of electricity sellers. Considering the characteristics of new energy grid connection and demand-side load flexibility, Reference [11] studied the dynamic period division of time-of-use electricity price mechanism and explored the potential of demand-side response but did not further study the relationship between demand-side response capability and user benefits. Reference [12] constructed a time-of-use electricity price optimization model based on the historical load data of power users and provided different electricity retail prices for users with different load characteristics, but did not study specific electricity price optimization methods for various users. The literature [13] considers the user’s independent choice behavior and optimizes the peak-valley time-of-use price with the goal of maximizing the daily profit of the electricity selling company. However, the objective function is single, and the user’s interests are not taken into account. There is no research on the optimization of 24 h time-of-use price; in Reference [14], the benefits of users, power grid, and the whole society under the peak-valley time-of-use electricity price mechanism are analyzed. Taking the benefit of all parties as the constraint condition and the minimum load peak-valley difference as the objective function, the peak-valley time-of-use electricity price optimization model is established, but it lacks the benefit analysis of the market subject of the electricity retailer. References [15,16] used the price quota curve to reflect the relationship between electricity price and users’ electricity consumption, and optimized the time-of-use electricity price with the goal of maximizing the purchase and sale revenue of electricity retailers, but did not consider the impact of electricity price changes on users’ interests.
Although the above literature has conducted in-depth discussions on the optimization of time-of-use electricity prices, in the electricity retail market, sellers and users directly interact, and the above research has not focused on the interaction mechanism of these two major market players. It neither fully considers the interest game relationship between sellers and users nor recognizes that the interaction between the two parties is a dynamic process. In this process, by effectively mobilizing the demand response ability of users, both sellers and users are likely to achieve greater economic benefits.
As an important model in game theory, the master–slave game model has been widely used in the field of electricity price formulation in recent years. Many scholars at home and abroad have studied the pricing strategy optimization problem in the electricity market through this model. In Reference [17], the game theory method is applied to the time-of-use pricing mechanism of energy, and the game pricing process for renewable energy is mainly studied, but the game model between electricity retailers and users is not constructed. Reference [18] established the AI pricing model, described the pricing problem of generative AI as a game between two companies, and studied the benefit space between competitors under the AI pricing model, but did not include users in the game model; in the literature [19,20], the sum of the user’s purchase cost and the satisfaction cost is used to represent the user’s expenditure, and the power supplier is set to maximize the profit and the power user is set to minimize the expenditure. The time-of-use electricity price pricing strategy model based on the master–slave game is established. Reference [21] established a master–slave game model under the dual objectives of maximizing the revenue of electricity retailers and maximizing the comprehensive satisfaction of multiple users. However, References [19,20,21] did not consider the user’s electricity utility as the user’s income into the user’s benefit function. Reference [22] considers the electricity purchase and sale business and interruptible load business of the electricity retailer and optimizes the terminal price on the premise of achieving a win-win situation but does not consider the dynamic pricing problem. Considering the self-elasticity and cross-elasticity of the four seasons in one year, Reference [23] constructed a seasonal time-of-use electricity price optimization model, which effectively reduced the peak-valley difference and mobilized the potential of user demand response, but did not consider the benefits of electricity retailers and users, and the objective function was single. At the same time, the above research only considers the user’s electricity consumption expenditure, does not consider the user’s income, and does not consider that the impact of the model on the benefits of both parties will be restricted by many factors, such as electricity price flexibility and user type will affect the user’s response ability, thus limiting the role of the model.
1.3. Contribution and Construction
In view of the above problems, this paper introduces electricity utility and electricity satisfaction, constructs the comprehensive benefit function of electricity retailers and users, and uses the master–slave game to simulate the interaction between the two parties. Both parties aim at maximizing benefits. As the leader, the electricity retailer first publishes the price, and as the follower, the user responds by changing the electricity consumption. Finally, a time-of-use electricity price pricing strategy model based on the master–slave game is established, and the inverse induction method is used to solve the problem. The results of the example show that the model can effectively optimize the electricity selling price of the electricity selling company and the load curve of the user and can achieve a win-win benefit for both parties. The main contributions of this paper are summarized as follows:
- (1)
- The master–slave game model is introduced into the time-of-use electricity price pricing strategy, and the user response ability is mobilized in the game process to achieve a win-win situation for both parties;
- (2)
- The user benefit function is studied, and the user’s electricity utility is introduced as the user’s income, and the user’s electricity purchase cost and satisfaction cost are taken as the user’s expenditure;
- (3)
- Three different electricity price mechanisms, fixed electricity price, peak-valley time-of-use electricity price, and 24 h time-of-use electricity price, are set up to study the impact of different electricity price flexibility on the benefits of both parties under the game model;
- (4)
- Three different types of users, including residential users, industrial users and commercial users, are set up to study the impact of different user response capabilities on the benefits of both parties under the game model.
The rest of this paper is organized as follows: in Section 2, the comprehensive benefit function of both the electricity retailer and the user is analyzed and established. In Section 3, the time-of-use electricity price pricing strategy based on the master–slave game model is constructed. Section 4 analyzes the solution process of the game model. Section 5 verifies the effectiveness of the method through an example and analyzes that the benefits of both parties are restricted by the flexibility of electricity price and the user’s response ability under the game model. Finally, the conclusion of this paper is put forward in Section 6.
2. Analysis of Electricity Sales Company and User Benefit
When formulating the price of electricity sales considering the demand response of users, the electricity sales company should not only maximize its own electricity sales revenue but also encourage users to participate in demand response and also enable users to obtain certain benefits through demand response. Therefore, before formulating the price of electricity sales, it is necessary to analyze the benefits of both electricity sales companies and electricity users.
2.1. User Electricity Efficiency
For users participating in demand response, their electricity load can be divided into two parts: fixed load and elastic load. Fixed load mainly refers to the rigid demand load for industrial production, residential lighting, and other purposes, and does not have the ability to participate in demand response. Elastic load has a certain sensitivity to electricity price, which can be used to participate in demand response. Users can flexibly formulate the electricity consumption plan of elastic load according to the electricity price, so as to reduce the cost of electricity consumption and improve the efficiency of electricity consumption.
The user’s income mainly comes from the utility of electricity, and the cost includes the cost of purchasing electricity and the cost of user satisfaction.
- (1)
- Electricity utility for users
The user’s electricity utility refers to the value obtained by the user through the consumption of electricity. This chapter references [24], in the form of a quadratic function of the user’s electricity utility, as shown in the following formula:
where represents for the user’s electricity utility during the period ; , are the relevant parameters of the electricity utility function during the period , which are related to the user type and the power consumption time, and are all greater than 0; represents for the actual power consumption in the period after the user participates in the demand response.
The response of the user load to the electricity price is limited, and the constraints on the user’s electricity consumption are as follows:
where , are, respectively, the lower limit of electricity consumption and the upper limit of electricity consumption during the period, after the user participates in the demand response.
- (2)
- Electricity satisfaction cost
If there is a deviation between the user’s actual power consumption and the demand value, it will cause a decline in user satisfaction. In general, the greater the difference between the actual power consumption and the demand value of the user, the greater the degree of decline in the user’s electricity satisfaction. The deviation function of the user’s actual power consumption and demand value is used to represent the user’s electricity satisfaction cost, as shown in the following formula:
where represents for the user’s electricity satisfaction cost in the period ; represents for the electricity satisfaction cost coefficient in the period (); represents for the user’s nominal demand for electricity during the period .
- (3)
- Electricity purchasing cost
After users participate in demand response, their actual electricity consumption will change, and the cost of purchasing electricity will also change. The user’s electricity purchase cost during the period is as follows:
where represents for the electricity selling price of the electricity selling company during the period .
In summary, the user’s electricity efficiency is equal to the electricity utility minus the electricity satisfaction cost and the electricity purchase cost, as shown in the following formula:
2.2. The Revenue of the Electricity Sales Company
After adopting the demand response, the revenue of the electricity sales company mainly comes from the sales revenue, and the cost includes the cost of purchasing electricity and the cost of user satisfaction.
- (1)
- Sales income
It is assumed that the electricity-selling company provides two types of electricity-selling contracts, fixed price and time-of-use price, to users participating in demand response. The time-of-use price is divided into section price and hourly price. The proportion of users who sign three types of electricity price contracts is , and , and is satisfied.
Fixed electricity price refers to the electricity selling company according to the user’s demand response behavior, to develop electricity prices in each period to maintain the same price. The electricity selling price, , of this type of electricity selling contract during the period is expressed as follows:
Sectional electricity price refers to the time-of-use electricity price segmented by peak-valley, and the price in each segment is different. The electricity selling price, , of this type of electricity selling contract during the period is expressed as follows:
where , , are, respectively, the electricity selling price in each segment of the peak, flat, and valley after the electricity-selling company considers the user’s demand response.
Hourly electricity price refers to the time-of-use electricity price segmented by hours, and the price is different within each hour. The electricity selling price, , of this type of electricity selling contract during the period is expressed as follows:
In the formula, represents for the hourly electricity selling price formulated by the electricity selling company after considering the user demand response.
The total electricity sales revenue, , of the electricity sales company during the period is as follows:
In addition, in order to ensure the electricity sales revenue of the electricity selling company, the price of electricity sold by the electricity selling company in each period is set to be higher than the marginal cost of electricity purchase in this period:
where represents for the marginal cost of purchasing electricity for the electricity selling company during the period .
- (2)
- Electricity purchasing cost
After the electricity sales company releases the demand response to the user, the adjustment of the user’s load changes the electricity purchase quantity of the electricity sales company, which may affect the price change in the electricity wholesale market. In general, the proportion of the user load of the electricity sales company agent to the total load is small, and the impact of the adjustment of these user loads on the wholesale price is also very small. Therefore, this paper assumes that the adjustment of user load will not cause the change in wholesale electricity price, that is, the marginal cost of purchasing electricity in each period of time is fixed.
The electricity purchase cost of the electricity selling company during the period is as follows:
- (3)
- User satisfaction cost
If the user is not satisfied with the power supply service of the electricity sales company and chooses another electricity sales company, it will cause the market share of the electricity sales company to decline and affect its electricity purchase and sale income. Assuming that the customer satisfaction cost of the electricity selling company is equal to the user’s electricity satisfaction cost, the customer satisfaction cost, , of the electricity selling company during the period is as follows:
In summary, the electricity sales company’s electricity purchase and sale benefits, , are equal to the electricity sales revenue minus the electricity purchase cost and user satisfaction cost, as shown in the following formula:
3. Construction of Pricing Strategy Model Based on Master–Slave Game
Game theory is mainly used to formulate two or more decision makers with competition and incentive relationships, and to study how each subject maximizes its benefits by optimizing its own decisions. Different from other optimization theories, the decision making of each subject in the game model will affect the decision making of other subjects, and it is also affected by the decision making of other subjects. In the field of power systems, game theory was originally applied to the electricity market, especially the game between market players such as power generation companies and power sales companies [25]. With the increasing importance of demand response in smart grid, the application of game theory on the demand side has been paid more and more attention.
The master–slave game model was proposed by Stackelberg in 1934. Its main idea is to divide the two sides of the game into the leader and the follower according to the status or decision order. The leader first makes a decision, and then the follower makes a decision according to the leader’s decision. In the electricity selling pricing strategy considering user demand response proposed in this chapter, the electricity selling company is in a dominant position, and the user is in a disadvantageous position. Therefore, it can be regarded as a main–follower game model. Both parties aim at maximizing their own benefits. The electricity selling company, as the leader, first releases the electricity selling price, and the user, as the follower, responds to the electricity price and adjusts its own electricity consumption.
3.1. Master–Slave Game Process
The process of the game between the electricity selling company and the user is shown in Figure 1, as follows:
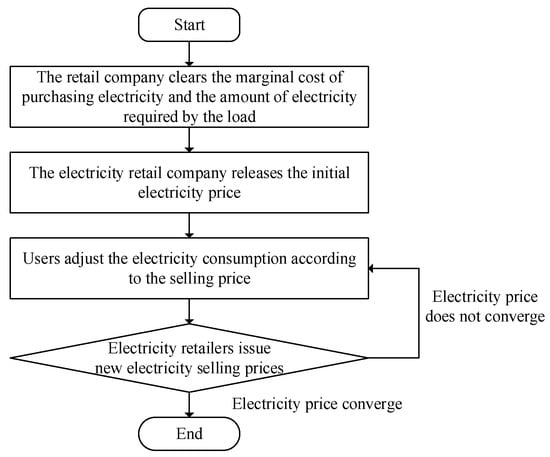
Figure 1.
Game process between power selling companies and users.
- (1)
- The electricity selling company determines its electricity purchase strategy and marginal cost of electricity purchase, as well as the nominal load demand of users;
- (2)
- As the leader, the electricity selling company formulates and publishes the electricity selling price of each period, , to the user;
- (3)
- As a follower, the user responds to the electricity sales price issued by the electricity sales company, formulates the optimal electricity consumption strategy, , and feeds it back to the electricity sales company;
- (4)
- According to the user’s feedback and its own benefit function, the electricity selling company adjusts the electricity selling price, , in each period;
- (5)
- Repeat step (3) to step (5) until the two sides no longer adjust their strategies to increase efficiency, and the game is balanced.
3.2. Game Models’ Construction
The electricity selling company takes the electricity selling price as the optimization variable, and its strategy space, , is as follows:
In the formula: is a set of -dimensional real matrices.
As the leader, the strategic goal of the electricity retailer is to maximize the benefits of purchasing and selling electricity on the basis of meeting the needs of users. The optimization model of the electricity sales company is as follows:
The user adjusts the electricity consumption according to the electricity selling price issued by the electricity selling company. The strategy space, , is as follows:
As a follower, the user’s strategic goal is to maximize the benefits of electricity consumption on the basis of comprehensive consideration of electricity utility, satisfaction, and cost. The user’s optimization model is as follows:
In the process of game between the electricity selling company and the user, the user determines the electricity consumption strategy according to the electricity selling pricing strategy of the electricity selling company, so the user’s electricity consumption is determined by the electricity selling price, and can be used as the function of . If and only if the conditions in Equation (18) are satisfied, the decision of the electricity selling company and the user is the optimal selling price and the optimal electricity consumption. Neither side can increase the benefit by changing its own decision, and the Nash equilibrium state of the game between the electricity selling company and the user is realized.
In the formula: represents for the Nash equilibrium point in the master–slave game model, and the optimal selling price of the electricity selling company and the optimal electricity consumption of the user.
4. Game Model Solution
The master–slave game model between electricity retailers and users established in this paper is a two-stage game model, which can be solved by backward induction [26,27]. Firstly, starting from the follower’s benefit maximization, the optimal response function is derived according to the user’s electricity benefit function. Then, after the electricity sales company obtains the user’s response function, it is substituted into its own electricity purchase and sale benefit function to solve the optimal electricity sales pricing strategy, that is, the game reaches equilibrium.
The conditions for the existence of a unique equilibrium solution of the game are as follows: (1) the strategy space of both sides is a bounded convex set; (2) the user has a unique optimal electricity consumption strategy for each pricing strategy of the electricity selling company; (3) the electricity selling company has a unique optimal pricing strategy for each user’s electricity consumption strategy. It can be seen from Equation (18) that the first condition is satisfied. The game model will be solved below. Firstly, the optimal power consumption strategy of the user to the electricity retailer is determined, and then the optimal pricing strategy of the electricity retailer is solved back. At the same time, it is proved that the game model satisfies the latter two conditions, and there is a unique equilibrium solution.
- (1)
- The user’s optimal power consumption strategy
In order to solve the user’s optimal electricity consumption, assuming that the electricity price of each period, , is known, the first-order partial derivative of the user’s electricity benefit function with respect to electricity consumption is obtained:
When the first-order partial derivative is equal to 0, the maximum power consumption benefit of the user is obtained. At this time, the power consumption of the user in each period, , is as follows:
Then, the second-order partial derivative of the user’s electricity efficiency, , with respect to electricity consumption, , is obtained:
and are greater than 0, so all the diagonal elements of the Hessian matrix of the user benefit function are less than 0, the remaining non-diagonal elements are 0, and the Hessian matrix is a negative definite matrix. Therefore, the electricity consumption obtained by setting the first-order partial derivative to 0 is the only optimal solution of the user benefit function, and the second condition is satisfied.
- (2)
- The optimal pricing strategy of electricity selling companies
Through the user’s optimal electricity consumption to optimize the electricity company’s pricing strategy, the user’s optimal response function (20) is substituted into the electricity company’s electricity purchase and sale benefit function, , and the following results are obtained:
The second-order partial derivative of the electricity purchase and sale benefit function of the electricity selling company with respect to the electricity price, , is obtained:
It can be seen that the Hessian matrix of the electricity sales company’s electricity purchase and sale benefit function, , is also that all diagonal elements are less than 0, and the remaining non-diagonal elements are all 0, which is a negative definite matrix. Therefore, the electricity sales company’s electricity purchase and sale benefit function, , has a unique optimal solution, and the third condition is satisfied. Based on the above, it is proved that there is a unique equilibrium solution to the time-of-use price pricing model of electricity selling companies based on master–slave game established in this chapter, which can be solved by reverse induction method.
From Equation (20), we can obtain the following:
It can be seen from Equation (24) that is a decreasing function of , so the constraint conditions in Equation (15) can be modified as follows:
Through the mathematical analysis of the master–slave game model between the electricity selling company and the user, the model is transformed into the following pricing optimization model:
5. Example Analysis
5.1. Parameter Setting
In this paper, is taken as the optimization cycle, and the spot price of a certain day in a certain area is taken as the marginal purchase cost of the electricity retailer. As shown in Figure 2, the peak-to-valley period division of the electricity retailer when selling electricity at the section price is shown in Table 1. This paper studies the influence of electricity price type and user type on the demand response pricing strategy of electricity retailers.
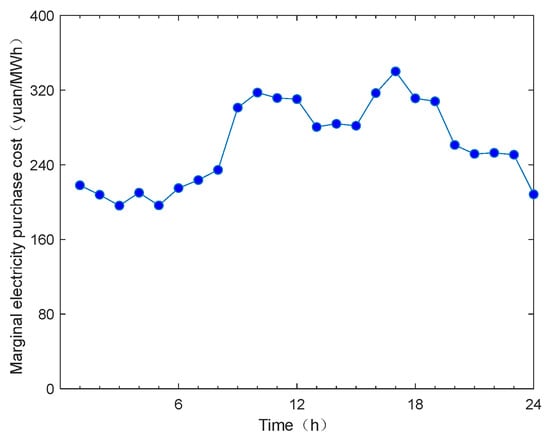
Figure 2.
Marginal electricity purchase cost of electricity selling companies in each period.

Table 1.
Peak-valley time division.
5.2. Analysis of Result
5.2.1. The Influence of Electricity Price Type
The example in this section assumes that the electricity retailers provide users with two types of retail packages: fixed electricity price and time-of-use electricity price. The time-of-use electricity price package includes peak-to-valley electricity price and 24 h electricity price to analyze the impact of the type of retail package price on the pricing strategy of the electricity retailers.
It is assumed that the users participating in the demand response are the same type of users, and their electricity utility coefficient , , and electricity satisfaction coefficient are 360, 0.005, and 0.1, respectively. The nominal demand electricity consumption and the maximum and minimum electricity consumption in each period are shown in Figure 3.
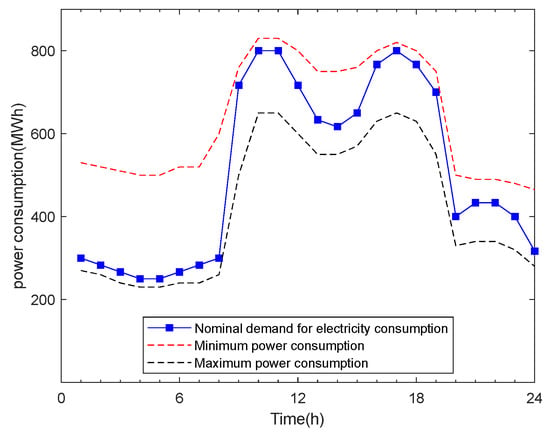
Figure 3.
The nominal demand power consumption and the maximum and minimum power consumption of users.
Figure 4 and Figure 5 are the optimal electricity price curve and the optimal electricity consumption curve of the electricity selling company and the user in each period of time under different electricity price types. From Figure 4, it can be seen that compared with the fixed price, the electricity selling company increases the selling price in the peak period and reduces the selling price in the valley period to a large extent by using the peak-valley price and the hourly price. On the whole, the curve change trend of section price and hourly price is similar to the marginal cost curve of electricity purchase of electricity selling companies, and it also reflects the change trend of user load and spot price to a certain extent, which is more in line with the market situation. Therefore, the time-of-use electricity price mechanism including peak-valley electricity price and hourly electricity price is more reasonable than the fixed electricity price. It can be seen from Figure 4 that the user’s electricity consumption curve is more stable under the implementation of section electricity price and hourly electricity price. This is due to the fact that during the trough period when the user’s electricity consumption is low, the electricity price of the section price and the hourly price is low, and the user will appropriately use more electricity to increase the efficiency of electricity consumption, or transfer the electricity consumption plan during the peak period to these periods to complete; during the peak period of electricity consumption, the electricity price of the section price and the hourly price is higher, and the user will appropriately reduce the electricity consumption during the period or use other lower price energy to replace the electricity and adjust the electricity consumption plan according to the electricity sales price in other periods, to minimize the cost of electricity purchase, thereby increasing the efficiency of electricity consumption. Compared with the section electricity price, the hourly electricity price is more flexible, more convenient for users to arrange the power consumption plan reasonably, and the power consumption curve is more gentle.
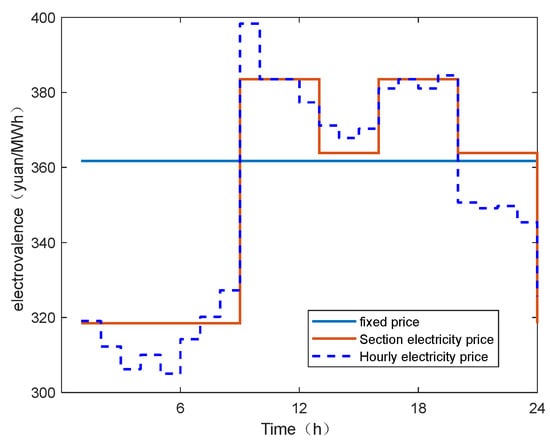
Figure 4.
Electricity selling prices of electricity selling companies under different types of electricity prices.
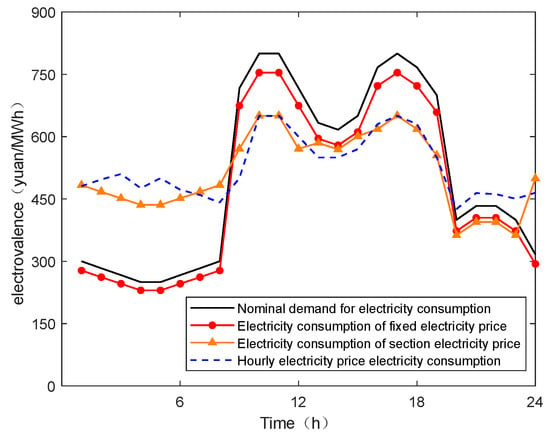
Figure 5.
User electricity consumption under different electricity price types.
Table 2 is the comparison between the benefit results and the peak-valley difference in electricity consumption under different electricity price types. With the adoption of fixed price to section price and then to hourly price by electricity selling companies, the average price gradually decreases, and the electricity consumption of users gradually increases. This is due to the fact that when the electricity selling company adopts the fixed electricity price with the same all-day electricity price, it has to set a relatively high price to cope with the high purchase cost during the peak load period. As the electricity price mechanism becomes more flexible, the average selling price decreases, which reduces the user’s electricity cost, improves its willingness to use electricity, and increases the electricity consumption. Although the average electricity price is reduced, the power consumption of users during the peak period is reduced, the total power purchase cost of the power retailer during the peak load period is reduced, and the power consumption of users is increased, so the power sales revenue of the power retailer is also improved. In addition, compared with the fixed electricity price, the section electricity price and the hourly electricity price improve the user’s electricity consumption behavior and reduce the peak-valley difference in electricity consumption. Therefore, the use of time-of-use electricity price mechanism including section electricity price and hourly electricity price can not only increase the benefits of both electricity retailers and users but also improve the stability of the power system and increase social benefits by improving the load curve.

Table 2.
Benefit results and peak-valley difference under different electricity price types.
5.2.2. The Impact of User Type
The electricity flexibility and demand response ability of different types of users are often different. In this example, we assume that the electricity selling company represents three types of users: residential, commercial, and industrial, to analyze the impact of user types on the pricing strategy of the electricity selling company.
The price demand elasticity matrix can accurately reflect the relationship between user-side electricity consumption and electricity price. It is defined as the ratio of the change rate of user electricity consumption to the change rate of electricity price. The expression is as follows:
where is the electric load response at the moment, , after the load response, is the electric load at the moment, , before the load response; is the electricity price change after the load response, is the electricity price before the load response.
Under the peak-valley three-stage segmented electricity price mechanism, the price demand elasticity matrix is as follows:
In this section, according to the parameter setting of 5.2.1, considering the self-elasticity coefficient (the sensitivity of users to their own electricity price changes in a certain time period), the sensitivity analysis of electricity price is carried out for three types of users in different time periods.
According to the analysis results of Figure 6, industrial users have the greatest sensitivity to electricity prices in each period, followed by residential users, and commercial users have the least price sensitivity. According to the different demand response capabilities, the maximum and minimum power consumption of each type of user is set, as shown in Table 3.
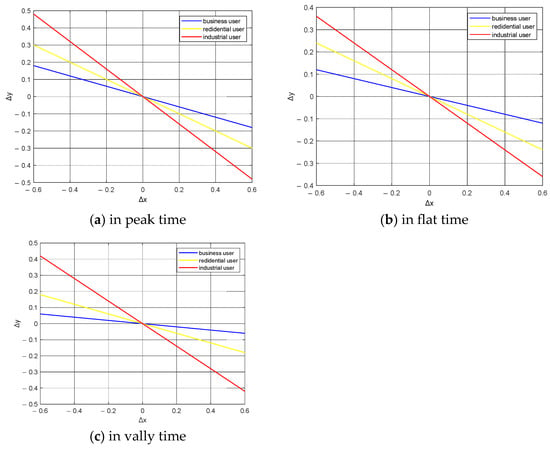
Figure 6.
Price sensitivity analysis of various types of users in different periods.

Table 3.
Maximum and minimum electricity consumption of each type of user.
Figure 7 shows the optimal electricity selling price curve of various types of users under the time-of-use electricity price. It can be seen that the pricing flexibility of electricity retailers is related to the demand response ability of users. For industrial users with strong demand response ability, their electricity prices are the highest in the peak period, the lowest in the valley period, and the peak-valley price difference is also the largest, while the commercial users with the weakest demand response ability have the smallest peak-valley price difference.
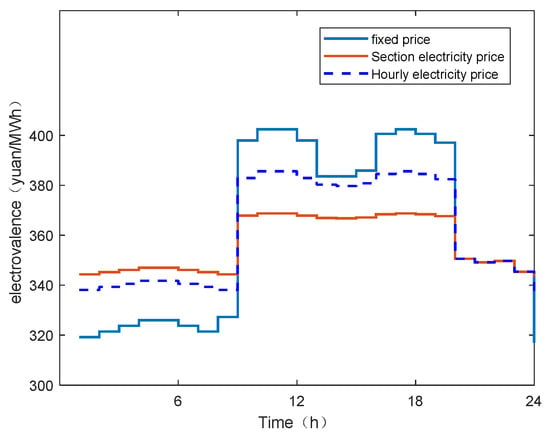
Figure 7.
Time-of-use electricity price under different types of users.
Figure 8 is the optimal electricity consumption curve of residential, commercial, and industrial users under time-of-use electricity price. It can be seen that residential users have a certain sensitivity to electricity prices. They will reduce some electricity consumption during peak load periods with higher electricity prices and appropriately increase electricity consumption during low load periods with lower electricity prices; due to the office needs of commercial users, most of their electricity demand is a rigid demand, and the demand response ability is weak. Therefore, the change in electricity consumption in peak and valley periods is not obvious. The electricity consumption curve of industrial users is more gentle than that of other types of users. This is because the electricity consumption of industrial users is mainly used for production and is more sensitive to electricity prices. Industrial users will adjust their production plans according to the electricity prices of each period, reduce production during the period of high electricity prices, and use as much electricity as possible during the period of low electricity prices, thereby reducing the average electricity cost.
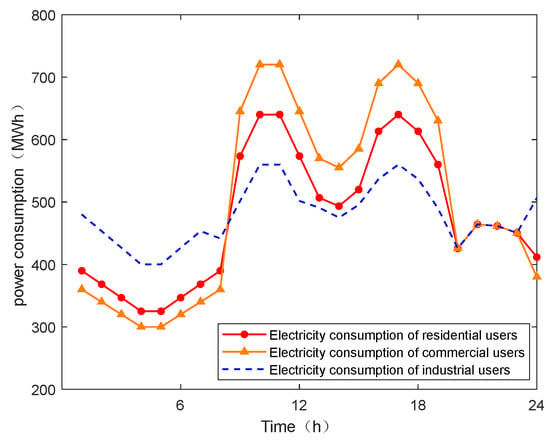
Figure 8.
Electricity consumption under different types of users.
Table 4 compares the total electricity consumption, average electricity price, electricity sales revenue, and peak-valley difference in electricity consumption under various types of users. It can be seen that after the implementation of demand response, the average electricity price of industrial users with the most flexible electricity consumption is the lowest, the total electricity consumption is the highest, and the electricity sales revenue brought to the electricity retailers is also the highest. The peak-valley difference and standard deviation of its electricity consumption are also the smallest, indicating that the demand response ability of industrial users is the strongest, and the effect of improving the benefits of both electricity retailers and users is the largest.

Table 4.
Benefit results and peak-valley difference under different user types.
6. Conclusions
In this paper, considering the factors such as the user’s electricity utility and electricity satisfaction, the interaction between the two sides in the context of demand response is described as a game problem, and the optimization model of the time-of-use pricing strategy of the electricity selling company is established. The validity of the model is verified by an example analysis, and the following conclusions are obtained:
- (1)
- Considering the utility and satisfaction of users, the comprehensive benefit function of electricity retailers and users is established. With the goal of maximizing the benefits of both parties, an optimization model of time-of-use electricity price pricing strategy based on master–slave game is established. The application of this model can mobilize the demand response ability of users, effectively optimize the pricing of electricity retailers and the load curve of users, and achieve a win-win situation for both parties;
- (2)
- Compared with the fixed price package, the average electricity price of the users is reduced by 5.4 yuan and 8.09 yuan, respectively, by using the time-of-use price package including the peak-to-valley section electricity price and the 24 electricity price. The electricity sales revenue of the company increased by 16.58 million yuan and 17.25 million yuan, respectively, and the peak-valley difference in user load decreased by 236.58 MWh and 315.39 MWh, respectively. It shows that under the game model, the benefits of both sides are affected by the flexibility of electricity price, and the benefits of power selling companies and users are better under the hourly price;
- (3)
- The demand response effect of users is related to the flexibility of users’ electricity consumption. Compared with the response effect of commercial users, the average electricity price of residents and industrial users is reduced by 2.1 yuan and 5.94 yuan, respectively, after participating in the game. The electricity sales revenue of the company increased by 7.02 million yuan and 12.07 million yuan, respectively, and the peak-valley difference in user load decreased by 104.79 MWh and 283.14 MWh, respectively. It shows that industrial users have the highest flexibility in electricity consumption, and the benefit improvement effect is the best after participating in the game.
7. Future Work
This study proposes a time-of-use electricity price optimization strategy based on the master–slave game model and verifies its effectiveness in improving the revenue and user satisfaction of electricity retailers. The research results show that the model can effectively promote peak shaving and valley filling and achieve a win-win situation between sellers and users. However, there are still some limitations in this study. Future research can be carried out from the following aspects:
- (1)
- The uncertainty of renewable energy is incorporated into the master–slave game model to study its impact on the optimization strategy of time-of-use electricity price;
- (2)
- The collaborative pricing strategy of multi-regional electricity market is studied, and the optimization mechanism of cross-regional electricity trading is explored.
Author Contributions
Formal analysis, J.L. and X.C.; investigation, W.Z.; methodology, G.H. and B.X.; project administration, J.L. and X.C.; resources, W.Z. and J.L.; software, B.X. and G.H.; supervision, J.L. and X.C.; validation, X.L. and J.Z.; visualization, J.L.; writing—original draft, X.L. and J.Z.; writing—review and editing, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number 72174151, Hubei Electric Power Technical Service Project (SGDLJY00JSJS2310034) and Hebei Science and Technology Project (SGHEJY00NYJS2400121).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Jiangping Liu, Wei Zhang, Guang Hu and Bolun Xu were employed by the company Hubei Power Exchange Center. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zhang, S. Success Criteria and Driving Forces of Power System Reform—Discussion Based on Article 9. Energy 2015, 92–96. [Google Scholar]
- Yu, X. Research on the Optimization Model of Electricity Purchase and Sale Transaction of Electricity Selling Companies in the Electricity Market Environment; North China Electric Power University: Beijing, China, 2018. [Google Scholar]
- Yuan, H.; Dong, X.; Liu, Q.; Jin, L.; Zhang, W.; Yang, Z. Design of power retail side market framework under the unified national power market system. Grid Technol. 2022, 46, 4852–4862. [Google Scholar] [CrossRef]
- Tan, X.; Chen, Y.; Li, Y.; Jing, J.; Jiang, N.; Wang, Z.; Shen, Y. Research on time-of-use price optimization considering load development and user behavior. China Electr. Power 2018, 51, 136–144. [Google Scholar] [CrossRef]
- Jerzy, A.; Józef, L.; Agnieszka, W. Seasonal variability of price elasticity of demand of households using zonal tariffs and its impact on hourly load of the power system. Energy 2020, 196, 117175. [Google Scholar] [CrossRef]
- Alsokhiry, F.; Siano, P.; Annuk, A.; Mohamed, M.A. A Novel Time-of-Use Pricing Based Energy Management System for Smart Home Appliances: Cost-Effective Method. Sustainability 2022, 14, 14556. [Google Scholar] [CrossRef]
- Liang, G.; Wang, Y.; Sun, B.; Zhang, Z. An optimization method for the distributed collaborative operation of multilateral entities considering dynamic time-of-use electricity price in active distribution network. Energies 2024, 17, 359. [Google Scholar] [CrossRef]
- Nikzad, M.; Samimi, A. Integration of optimal time-of-use pricing in stochastic programming for energy and reserve management in smart micro-grids. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 1449–1466. [Google Scholar] [CrossRef]
- Fraija, A.; Agbossou, K.; Henao, N.; Kelouwani, S.; Fournier, M.; Hosseini, S.S. A discount-based time-of-use electricity pricing strategy for demand response with minimum information using reinforcement learning. IEEE Access 2022, 10, 54018–54028. [Google Scholar] [CrossRef]
- Zhang, G.; Yan, Y.; Zhang, K.; Li, P.; Li, M.; He, Q.; Chao, H. Time-of-use pricing model considering wind power uncertainty. CSEE J. Power Energy Syst. 2020, 8, 1039–1047. [Google Scholar] [CrossRef]
- Cao, J.; He, Y.; Zhou, J.; He, L.; Long, C.; Wang, Y. Research on dynamic time-of-use price optimization of different time scales based on demand side response. J. Electr. Power Sci. Technol. 2024, 39, 242–250+268. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, J.; Wen, F.; Dong, Z. A model of customizing electricity retail prices based on load profile clustering analysis. IEEE Trans. Smart Grid 2019, 10, 3374–3386. [Google Scholar] [CrossRef]
- Lu, E.; Bie, P.; Wang, H.; Chen, Q.; Li, W.; Gu, W. Power system automation. Autom. Electr. Power Syst. 2020, 44, 177–184. [Google Scholar] [CrossRef]
- Kong, Q.; Fu, Q.; Lin, T.; Zhang, Y. Peak-valley time-of-use electricity price optimization model based on cost-benefit analysis. Power Syst. Prot. Control 2018, 46, 60–67. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, L.; Zhang, F.; Jin, D. Decision-making and risk assessment of electricity purchase and sale business. Power Syst. Autom. 2018, 47–54, 143. [Google Scholar] [CrossRef]
- Nojavan, S.; Zare, K.; Mohammadi-Ivatloo, B. Application of fuel cell and electrolyzer as hydrogen energy storage system in energy management of electricity energy retailer in the presence of the renewable energy sources and plug-in electric vehicles. Energy Convers. Manag. 2017, 136, 404–417. [Google Scholar] [CrossRef]
- Amiri-Pebdani, S.; Alinaghian, M.; Safarzadeh, S. Time-Of-Use pricing in an energy sustainable supply chain with government interventions: A game theory approach. Energy 2022, 255, 124380. [Google Scholar] [CrossRef]
- Mahmood, R. Pricing and competition for generative ai. Adv. Neural Inf. Process. Syst. 2024, 37, 75727–75748. [Google Scholar]
- Yang, P.; Tang, G.; Nehorai, A. A game-theoretic approach for optimal time-of-use electricitypricing. IEEE Trans. Power Syst. 2013, 28, 884–892. [Google Scholar] [CrossRef]
- Hu, P.; Ai, X.; Zhang, S.; Pan, X. Research on master-slave game modeling and simulation of time-of-use electricity price based on demand response. Grid Technol. 2020, 2, 585–592. [Google Scholar] [CrossRef]
- Pan, H.; Gao, H.; Yang, Y.; Ma, W.; Zhao, Y.; Liu, J. Multi-retail package design and multi-level market power purchase strategy based on master-slave game. Chin. J. Electr. Eng. 2022, 42, 4785–4800. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, L.; Tu, W.; Yuan, Z.; Gou, X. Research on the marketing strategy of electricity selling companies for users’ interruptible load-based on game theory to depict the interaction between electricity selling companies and users. Price Theory Pract. 2020, 133–136+179. [Google Scholar] [CrossRef]
- Xue, W.; Zhao, X.; Li, Y.; Mu, Y.; Tan, H.; Jia, Y.; Wang, X.; Zhao, H.; Zhao, Y. Research on the optimal design of seasonal time-of-use tariff based on the price elasticity of electricity demand. Energies 2023, 16, 1625. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, G.; Ma, K. Demand response based on Stackelberg game in smart grid. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013. [Google Scholar]
- Liu, X.; Gao, B.; Li, Y. A review of the application of game theory on the power demand side. Grid Technol. 2018, 8, 2704–2711. [Google Scholar] [CrossRef]
- Yu, M.; Hong, S.H. A Real-Time Demand-Response Algorithm for Smart Grids: A Stackelberg Game Approach. IEEE Trans. Smart Grid 2017, 7, 879–888. [Google Scholar] [CrossRef]
- Jia, L.; Tong, L. Dynamic Pricing and Distributed Energy Management for Demand Response. IEEE Trans. Smart Grid 2017, 7, 1128–1136. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).