A Step Toward Sustainable Cities: Recognizing the Transportation Modes of Urban Residents Based on Mobile Phone Location Data

Abstract

Urban residents’ transportation modes play a pivotal role in shaping transportation planning and policies for sustainable cities. Mining refined transportation modes from mobile phone location (MPL) data is a key spatiotemporal big data application for sustainable city planning and traffic management. However, key challenges persist: low recognition accuracy due to insufficient consideration of travel features of transportation modes, the positioning uncertainty of MPL data, and ineffective evaluation due to lacking validation datasets. To address these limitations, we propose an analytical framework for transportation mode recognition. First, precise moving segments are constructed through road network matching and linear interpolation, resolving the positioning uncertainty issues of MPL data. Then, we propose a comprehensive feature parameter system for transportation mode recognition and construct a transportation mode recognition model based on eXtreme Gradient Boosting (XGBoost). Finally, using synchronously collected GPS data and travel logs, we validated the framework’s recognition results, demonstrating its ability to improve the accuracy of transportation mode recognition.

1. Introduction

The imbalance between transportation supply and demand is the main cause of traffic problems such as congestion and long commuting times. Owing to the high travel demand caused by rapid economic growth, road traffic in many large cities is under tremendous pressure [1,2], particularly in China. Investigations into the transportation modes of urban residents have shown that obtaining information about their transportation modes at different times and locations can inform urban transportation planning. This information helps planning departments develop more reasonable and sustainable strategies, thereby contributing to the development of sustainable cities. The transportation mode refers to the means of transportation used by individuals traveling from the origin to the destination for a certain purpose. Common modes of transport within a city include bus, car, bicycle, walking, and rail transit (subway and light rail); additionally, ferries are used in a few cities. Accurate acquisition of urban residents’ transportation mode information is important for solving traffic problems. Traditional methods include household surveys [3], questionnaire surveys [4] and computer-assisted telephone surveys [5]. However, their results can be easily affected by the subjective cognition of the respondents. Furthermore, the questionnaire recovery rate and data quality are relatively low, and the acquisition cost is high. In recent years, with the rapid development of computers, information and communication, global positioning systems and other technologies, recognizing residents’ transportation modes by using mobile phone GPS data or MPL data has become possible. Many researchers [6,7,8] have reported that the use of MPL data to extract urban residents’ transportation modes has the advantages of good timeliness, speed, convenience, and wide population coverage. The extraction of urban residents’ transportation modes based on MPL data has attracted the attention of many researchers in the fields of transportation and geographic information science, and a series of research results have been obtained [6,9,10].

To date, many studies have focused on the development of methods for recognizing urban residents’ transportation modes based on MPL data. The main recognition methods include rule-based recognition methods [11,12,13], probability-based recognition methods [14,15], map navigation inference-based recognition methods [16,17], and machine learning-based recognition methods [18,19,20,21]. For the rule-based recognition method, some studies adopt it to distinguish different transportation modes by using expert experience to formulate recognition rules [11,12,13]. For example, Qu et al. [11] constructed fuzzy recognition rules for different transportation modes while considering the actual traffic status and land use information of base stations to distinguish cars, public transportation and walking. While this method is fast and convenient, the recognition rules are strongly affected by subjective factors, and the results have weak generalizability. For the probability-based recognition method, many studies use it to determine transportation modes by constructing a membership function or probability function for each transportation mode [14,15]. For example, Poonawala et al. [15] used a hidden Markov model (HMM) to distinguish and visualize road trips and track trips by combining Singapore’s MPL data, passenger card data and traffic network data. However, this method often has difficulty distinguishing users’ transportation modes under complex traffic conditions, leading to confusion among various transportation modes. For the map navigation inference-based recognition method, many studies infer users’ transportation modes through the information provided by navigation maps such as the navigation path and navigation time [16,17]. For example, Peng et al. [16] combined the navigation time features with MPL data to recognize transportation modes by calculating the trajectory matching degree and time correlation of different transportation modes. While this method can comprehensively consider actual traffic conditions with the help of the navigation database of the third-party platform, it relies heavily on the API interfaces of navigation platforms and incurs a large computational cost. For the machine learning-based recognition methods, the use of machine learning for transportation mode recognition has been a long-standing focus of attention for researchers both domestically and internationally [20,21]. Many research results have been generated based on this method [18,19]. In the field of transportation mode recognition, random forest (RF) method is one of the most commonly used methods, and the accuracy of transportation mode recognition based on RF method is high. For example, Arash [22] adopted multiple supervised learning algorithms to recognize transportation modes, such as K-nearest neighbors (KNNs), support vector machines (SVMs) and RF, among which the RF model demonstrated superior performance. Kimberley et al. [23] developed three distinct transportation mode recognition models based on MPL data, ultimately finding that the hybrid model integrating rule-based heuristics (RBH) with RF exhibited superior performance.

Despite the above achievements, several weaknesses remain in previous studies. First, previous studies tended to focus on the spatiotemporal differences in different transportation modes, with travel duration, travel speed and travel distance as the selected travel features, whereas the relevant geographical environment, traffic environment and navigation data have not been sufficiently considered. This can easily lead to confusion among different transportation modes in complex traffic environments and reduce recognition accuracy. Second, existing studies have not given enough attention to the positioning uncertainty issues of MPL data, which refers to the large spatial positioning error and sparse temporal sampling of MPL data. Although the use of MPL data to recognize residents’ transportation modes has advantages such as convenience and speed, the positioning uncertainty issues in MPL data can easily lead to low accuracy of transportation mode recognition results. Third, owing to the lack of corresponding verification datasets for most current recognition methods, it is impossible to accurately and effectively evaluate the recognition accuracy of urban residents’ transportation modes based on MPL data. In response to the above shortcomings, we explore a new framework for recognizing urban residents’ transportation mode based on MPL data. Before recognizing the transportation mode of the user on the travel route, we first address the positioning uncertainty issues of MPL data. To this end, we use noise records optimization method, road network matching method and trajectory interpolation method to improve the spatial accuracy and temporal sampling density of MPL data. To recognize the transportation mode of the user on the travel route, we construct a feature parameter system for residents’ transportation mode recognition based on the MPL data that is more complete and more scientific than the systems used in previous research. This feature parameter system not only accounts for the spatiotemporal features of different transportation modes, but also fully considers geographical environment features and navigation features, enhancing the model’s recognition ability in complex traffic environments. In addition, when collecting MPL data, we synchronously collect users’ GPS data and travel logs, recording the actual transportation modes used by users while they travel. We constructed a validation dataset to effectively evaluate the accuracy of the recognition model constructed in this study. We pose two core specific research questions:

(1)

How can we effectively integrate geographical environment information with real-time traffic conditions to reduce confusion among different transportation modes in complex traffic environments and improve the accuracy of residents’ transportation mode recognition based on MPL data?

(2)

Can an integrated preprocessing, trajectory interpolation, and map-matching framework, designed to compensate for the inherent positioning uncertainties of MPL data, effectively improve the accuracy of transportation mode recognition?

The rest of this article is organized as follows: Section 2 describes the dataset used in this study. Section 3 introduces the methods used in this study. Section 4 analyzes the overall recognition accuracy of the model and the role and influence of different feature parameters on the transportation mode recognition of MPL data through comparative experiments. Section 5 presents a multifaceted discussion. Section 6 concludes the paper.

2. Data and Study Area

2.1. Spatiotemporal Trajectory Data

Our research objective is to recognize urban residents’ modes of transportation based on MPL data. Compared with that of MPL data, the spatial accuracy of the GPS data is greater. The GPS data collected synchronously with the MPL data are used as the reference standard to evaluate the accuracy of the road network matching results. To evaluate the accuracy of our transportation mode recognition model, the travel logs collected synchronously with the MPL data were used as real labels to verify the recognition results. Therefore, three spatiotemporal trajectory datasets were synchronously collected in this study: MPL data, GPS data, and travel log data.

To ensure synchronous collection of the three spatiotemporal trajectory datasets, we conducted a series of data collection work. We recruited 120 volunteers to perform 4 days of data collection work in Nanjing city. Volunteers were free to schedule any four days in November 2019, but were asked to include working days and rest days. The volunteers came from diverse backgrounds, including teachers, students, logistical staff of universities, and residents living near universities. During the data collection, we provided each volunteer with a mobile phone that involved SIM card from a large operator in Nanjing and a GPS record collection app. These smartphones featured the same brand and model to reduce potential positioning bias caused by differences in device conditions. All the volunteers used the smartphones we provided to collect individual MPL data and GPS data, and allowed us to apply to the abovementioned operator for the use of their individual MPL data. All the volunteers signed an informed consent form with our research team and a data output authorization form with the abovementioned operator. In addition, formal ethical approval was obtained prior to data collection. Subsequent to the acquisition, all user identifiers within the individual trajectory dataset were subjected to an anonymization process, and stringent protocols for data storage and usage restrictions were implemented.

MPL data are a byproduct of base station positioning and are stored in the database server of mobile operators. The MPL dataset used in this study was the dataset of volunteers’ individual MPL trajectories, which was obtained from the abovementioned operator. The MPL dataset was generated by a mobile communication network using Cell-ID positioning technology. The operating principle of Cell-ID positioning technology uses the geographical coordinates of the cell tower providing service to a mobile phone at a given time as an approximation of the user’s location. Modern smartphones are usually equipped with embedded GPS receivers, which are convenient for collecting and storing GPS data. In this study, the cell phones used to collect MPL data were also used as the GPS receivers and GPS data memory. Volunteers’ individual GPS data are collected via the GPS record collection app developed by our research team. Existing studies have shown that the average positioning accuracy of GPS data collected by smart phones is about 10 m, and the best positioning accuracy can reach 3–5 m [24]. To further enhance the positioning accuracy of GPS data, we processed the GPS data via manual correction and Gaussian filtering [25]. After deviation correction, GPS positioning accuracy can reach 2–3 m. Travel logs, which are synchronized with the collection process of MPL data and GPS data, are recorded by volunteers we recruited. Specifically, we distribute forms to volunteers, who manually record their travel date, travel paths and transportation modes they take throughout the entire data collection process. All transportation modes recorded in the travel logs are real labels, which are used to evaluate the accuracy of the recognition results of our transportation mode recognition model.

Table 1, Table 2 and Table 3 show samples of MPL data, GPS data, and travel log data of a volunteer on a certain day. As shown in Table 1, each record in this MPL dataset contains the user ID, recording date, starting time, ending time, geographic coordinates (longitude/latitude in the WGS84 coordinate reference system) of the cell tower connected to the mobile terminal, corresponding planar coordinates (X-coordinate/Y-coordinate in the Beijing 1954 3-degree Gauss–Krüger CM 117E projected coordinate system), and service radius of the base station (meters). As shown in Table 2, each record in this GPS dataset contains the user ID, recording date, recording time, geographic coordinates (longitude/latitude in the WGS84 coordinate reference system) of the mobile terminal, and corresponding planar coordinates (X-coordinate/Y-coordinate in the Beijing 1954 3-degree Gauss–Krüger CM 117E projected coordinate system). As shown in Table 3, each record in this travel log dataset contains the user ID, recording date, departure time, departure location, arrival time, arrival location and transportation mode.

Table 1. Sample of MPL data for a volunteer.

User ID	Date	Starting Time	Ending Time	Longitude	Latitude	X-Coordinate	Y-Coordinate	Radius (m)
***ebe	15 November 2019	7:29:25	7:32:20	118.*****	32.*****	680***.***	355****.***	300
***ebe	15 November 2019	7:32:23	7:35:34	118.*****	32.*****	680***.***	355****.***	250
……
***ebe	15 November 2019	18:23:28	18:25:29	118.*****	32.*****	680***.***	355****.***	350
***ebe	15 November 2019	18:25:32	19:25:39	118.*****	32.*****	680***.***	355****.***	350

Note: The symbols ‘***’, ‘*****’, ‘***.***’ and ‘****.***’ indicate anonymized data (such as IDs, geographic coordinates, and planar coordinates), to protect the original data privacy.

Table 2. Sample of GPS data for a volunteer.

User ID	Date	Time	Longitude	Latitude	X-Coordinate	Y-Coordinate
***ebe	15 November 2019	7:29:17	118.*****	32.*****	678***.***	355****.***
***ebe	15 November 2019	7:29:18	118.*****	32.*****	678***.***	355****.***
……
***ebe	15 November 2019	19:19:16	118.*****	32.*****	680***.***	355****.***
***ebe	15 November 2019	19:19:18	118.*****	32.*****	680***.***	355****.***

Note: The symbols ‘***’, ‘*****’, ‘***.***’ and ‘****.***’ indicate anonymized data (such as IDs, geographic coordinates, and planar coordinates), to protect the original data privacy.

Table 3. Sample of a volunteer travel log.

User ID	Date	Departure Location	Departure Time	Arrival Location	Arrival Time	Travel Paths	Transportation Mode
***ebe	15 November 2019	Nanjing Normal University	7:33:45	Xuanwu Lake	8:30:54	Wenyuan Road → Xianyin North Road → Zhigu Avenue → Xuanwu Avenue → Longpan Road	Bus
***ebe	15 November 2019	Xuanwu Lake	9:40:44	Old Gate East	10:10:31	Xuanwu Gate Road → Central Road → Gulou Underground Interchange → Zhongshan Road → Zhongshan South Road → Zhonghua Road → Madao Street	Car
…	…	…	…	…	…	…	…
***ebe	15 November 2019	Longpanhui Shopping Center	18:45:20	Nanjing Normal University	19:16:14	Xiangfang Village Road → Inner Ring East Line → Jiuhua Mountain Tunnel → Xianyin North Road	Car

Note: The symbol ‘***’ denote anonymized ID, to protect the original data privacy.

We consider the MPL trajectory, GPS trajectory, and travel log of the same volunteer on the same day as a set of trajectory data. Due to user error, equipment failure and other reasons, not all the data could be used for experimental analysis. Only if these three kinds of data are collected concurrently, fully recorded, and have matching timestamps, can they be considered valid data. Otherwise, they will be considered invalid. Based on relevant literature [26] and considering the differing time sampling intervals between the MPL, GPS, and travel log data, a time alignment tolerance of ±10 s is used. Through synchronous data collection and filtering, we ultimately obtained 432 valid sets of trajectory data (including 432 MPL trajectories, 432 GPS trajectories and 432 travel logs). Among these, 103 datasets were collected on weekdays and 329 on rest days, resulting in a weekday-to-rest-day ratio of approximately 1:3. The proportions of staff composition, age and gender distribution are as follows: from the perspective of staff composition, student volunteers constitute the highest proportion, reaching 49.8%; followed by surrounding residents at 22.2%; logistical staff volunteers account for 15.5%; and teacher volunteers account for 12.5%. In terms of age, volunteers aged 14–18 years accounted for 7.9%, while those aged 18–30 years constituted the largest proportion, reaching 47.9%; volunteers aged 30–55 years accounted for 35.4%, and those aged 50–60 years accounted for 12.5%. In terms of gender, male volunteers account for approximately 40%, whereas female volunteers account for approximately 60%. Travel log updates are event-driven. On average, each log contains 4 entries, with the number of entries per log ranging from 2 to 7. Figure 1 displays the general statistical characteristics of the trajectory data. GPS trajectory data exhibit certain concentrations in both the number of records and the duration of recording. Specifically, 87.7% of the GPS trajectories have fewer than 10,000 records, and a very small number of trajectories reach 20,000 records (Figure 1a). Additionally, 91.2% of the GPS trajectories have a total duration of less than 10 h, with an average duration of 5.03 h and a median duration of 3.23 h (Figure 1b). The time interval between adjacent records is measured as the duration between two consecutive records in a trajectory, that is, the sampling frequency of the data. MPL trajectories have relatively short time intervals between adjacent records, ranging from a few seconds to 3 min, with an average of 7.6 s and a median of 3 s (Figure 1c). The continuous connection time of base stations is generally short, with 80% of base stations having a continuous connection time of less than 30 s. The average and median connection times are 39.45 s and 10 s, respectively, with the average being greater than the median, suggesting the presence of some longer connection durations (Figure 1d).

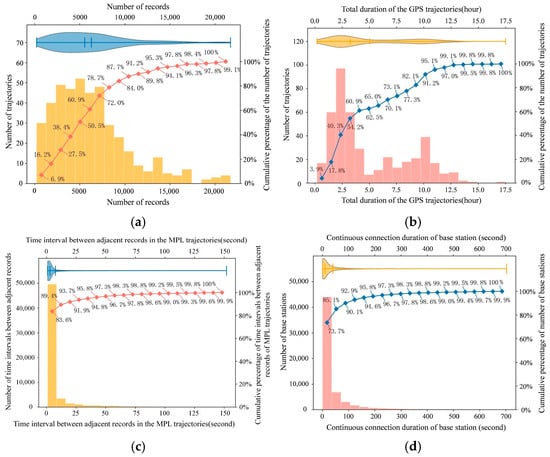
Figure 1. Statistical characterization of trajectory data: (a) number of records per trajectory in the GPS data; (b) total duration of the GPS trajectories; (c) time interval between adjacent records in the MPL trajectories; (d) continuous connection duration of the base station (i.e., the difference between the end connection time and the start connection time of the same base station positioning record).

2.2. Study Area

To capture the diverse geographical environments of Nanjing and enhance the representativeness of our sample, volunteers were recruited from multiple administrative districts throughout the city. As shown in Figure 2, our data collection area covers 9 administrative districts in Nanjing city, including Xuanwu, Qinhuai, Gulou, Jianye, Pukou, Qixia, Yuhuatai, Jiangning and Liuhe. Among them, Xuanwu, Qinhuai, Gulou, Jianye and Yuhuatai are the most concentrated urban areas. The other administrative regions are located mainly in rural areas.

Figure 2. Area range for collecting spatiotemporal trajectory data.

3. Methodologies

All methods were conducted in accordance with relevant national guidelines and regulations. This study was approved by Review Committee of School of Geography and Tourism, Anhui Normal University. We have signed written informed consent forms with the 120 volunteers participating in this study, all of whom have agreed to the use of their personal trajectory data in this study. For adolescent participants aged 14–18, we strictly adhered to ethical guidelines to safeguard their rights. Before the study, both the adolescents and their parents were invited to jointly sign informed consent forms. We provide a detailed explanation of the study’s purpose, procedures, risks, and confidentiality measures to ensure that both the adolescents and their parents fully understand.

3.1. Definition and Framework

In this section, we first clarify some terms used in this article. We then briefly introduce the analytical framework of our study.

3.1.1. Definition

This section introduces some basic concepts in the research and defines the relevant variables, as shown in Figure 3.

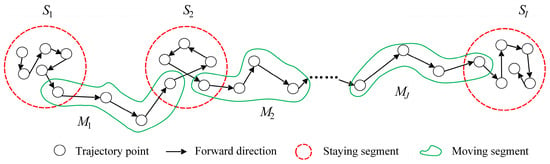
Figure 3. Schematic diagram of an MPL trajectory.

• Mobile phone location trajectory (MT)

One mobile phone location trajectory (MT) is a position sequence that forms all mobile phone location records of a user during a day sorted by time, which is expressed as:

$$MT=\{p_1,p_2,p_3,\dots ,p_n\}$$

(1)

where p denotes the MPL trajectory point (i.e., a record in the MPL data) and n is the total number of trajectory points in an MPL trajectory.

2.

Staying segment (S)

The staying segment (S) is composed of a combination of consecutive staying trajectory points extracted from the MT. The staying trajectory point refers to the continuous MPL records generated when the mobile terminal does not move at a certain location or moves within a small range. The i-th staying segment S_i can be expressed as:

$${\mathrm{S}}_i=\{p_1^{S_i},p_2^{S_i},\dots ,p_k^{S_i}\},k\le n,i\le I$$

(2)

where $p_k^{S_i}$ is the k-th trajectory point in $S_i$, k is the total number of trajectory points in $S_i$, n is the total number of trajectory points in the MT, and I is the total number of staying segments in the MT.

3.

Moving segment (M)

The moving segment (M) is composed of a combination of continuous moving trajectory points extracted from the MT. The moving trajectory point refers to the continuous MPL records generated when the mobile terminal clearly moves in space. The j-th moving segment $M_j$ can be expressed as:

$$M_j=\{p_1^{M_j},p_2^{M_j},\dots ,p_m^{M_j}\},m\le n,j\le J$$

(3)

where $p_m^{M_j}$ is the m-th trajectory point in $M_j$, m is the total number of trajectory points in $M_j$, n is the total number of trajectory points in the MT, and J is the total number of moving segments in the MT.

3.1.2. Framework

As shown in Figure 4, the overall analysis framework of this study is divided into three stages.

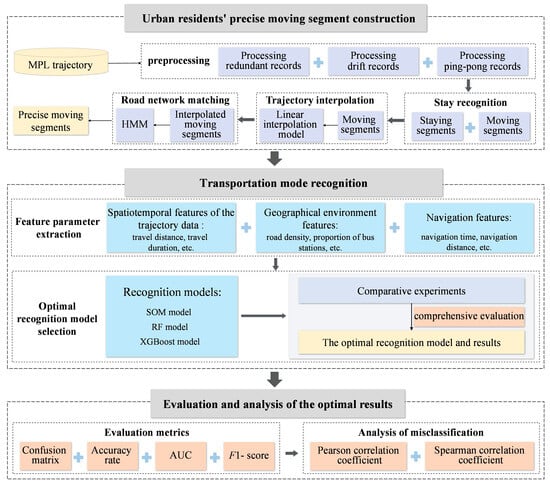
Figure 4. Analytical framework of this study.

The first stage constructs the urban residents’ precise moving segment. This stage consists of four parts: preprocessing, stop analysis, trajectory interpolation and road network matching. For preprocessing, we eliminate and correct the redundant, drift and ping-pong records in the MPL data to carry out noise record cleaning. For stop analysis, we extract the moving segments and staying segments from the MPL trajectories. Our research objective is to recognize urban residents’ modes of transportation during each moving segment. For this purpose, we further performed trajectory interpolation and road network matching on the moving segment. The moving segment after interpolation and road network matching processing is the precision moving segment.

In the second stage, the transportation mode of urban residents is recognized based on three models. This stage consists of two parts: feature parameter extraction and the optimal recognition model selection. For feature parameter extraction, we analyze the travel features of different transportation modes and examine the differences between different transportation modes. Then we improve the parameter system for recognizing transportation modes based on MPL data in three aspects: spatiotemporal features of the trajectory data (e.g., travel distance and travel duration), geographical environment features (e.g., road density and the proportion of bus stations), and navigation features (e.g., navigation time and navigation distance). For the optimal recognition model selection, this study constructs three distinct datasets and input them, respectively, into three models: a Self-Organizing Map (SOM), RF, and XGBoost, resulting in nine comparison groups (nine models in total). Through comparative experiments with these nine models and a comprehensive evaluation of multiple performance metrics, the optimal transportation mode recognition model was ultimately determined.

In the third stage, we evaluate and analyze the optimal results. This stage consists of two parts: evaluation metrics and analysis of misclassification. Using evaluation metrics, we quantify the impact of trajectory interpolation and feature parameters on transportation mode recognition. These metrics used to evaluate the optimal results include the confusion matrix, accuracy rate, AUC, and F1-score, among others. In addition, to diagnose the causes of misclassification, we quantify feature similarity using Pearson and Spearman correlation coefficients of feature parameters between Misclassified Class and Correct Classification Class.

3.2. Urban Residents’ Precise Moving Segment Construction

Before recognizing the transportation modes of urban residents, we constructed precise moving segments for each individual. To achieve this objective, we first preprocessed each trajectory in the MPL dataset to address noise-related issues. Specifically, duplicate records were removed, while drift and ping-pong records were refined using the noise record optimization method proposed by [25].

As illustrated in Figure 3, an MPL trajectory typically comprises multiple staying and moving segments, each of moving segments may involve distinct modes of transportation. Therefore, we need to extract the moving segments from the MPL trajectories. That is, stop analysis is performed based on MPL data. The commonly used methods for stop analysis based on MPL data include the DBSCAN [16], TSC-MAD [27], SMoT [28], and SMUoT algorithms [29]. Ren [30] compared these algorithms and reported that the SMUoT algorithm achieved the highest accuracy. Therefore, we use the SMUoT algorithm to perform stop analysis.

Although the utilization of MPL data for recognizing residents’ transportation modes offers notable advantages in terms of convenience and efficiency, existing studies have predominantly neglected the positioning uncertainty issues inherent in MPL data. This omission can substantially undermine the accuracy of transportation mode recognition outcomes. Although the MPL data have been preprocessed, the time sampling remains sparse, and positioning uncertainty continues to present a significant challenge. Therefore, we further performed trajectory interpolation on the extracted moving segments. In contemporary research, commonly used interpolation models for sparse trajectory data include linear interpolation model [31], nearest-neighbor interpolation model [32], and cubic spline interpolation model [33]. Among these, the linear interpolation model has emerged as the most widely adopted approach for MPL data, owing to its high computational efficiency, strong adaptability to diverse datasets, and robustness against outliers and noise. Consequently, we employed the linear interpolation model to interpolate the moving segments.

To further enhance the spatial accuracy of MPL data and mitigate its positioning uncertainty issues, we perform road network matching on the interpolated moving segments. Current mainstream map matching algorithms can be classified into four primary types: geometric matching, topological matching, probabilistic-statistical matching, and advanced matching algorithms [34]. Different methods demonstrate varying adaptation requirements based on data characteristics (such as sampling frequency and error distribution patterns) and specific application scenarios. Among advanced matching algorithms, the Hidden Markov Model (HMM) demonstrates outstanding computational efficiency, storage efficiency, and broad applicability [34], making it particularly effective for addressing errors in large-scale datasets within complex road networks. Specifically for low-frequency sampling data like MPL datasets, this model efficiently compensates for spatial information loss caused by sparse sampling, significantly improving matching accuracy while maintaining algorithmic efficiency. Therefore, we employed the HMM method for road network matching.

After the above processing, we obtained the precise moving segments. We employ the HMM method to match the road network with synchronously collected GPS data. The corrected GPS trajectories are then utilized as the validation dataset to assess the accuracy of the precise moving segments. We separately calculated the Time Window Based Hausdorff Distance [25] between the raw moving segments, precise moving segments, and corrected GPS trajectories. This calculation was performed to evaluate the accuracy of the precision moving segments by analyzing the changes in this metric before and after interpolation.

3.3. Transportation Mode Recognition Models for Urban Residents

After trajectory interpolation, we obtain the precise moving segment of the user on the travel route. To recognize the transportation mode of the user on the travel route, we construct a feature parameter system for residents’ transportation mode recognition based on the MPL data, which are more complete and more scientific than the systems used in previous research. Based on this system, this paper constructs an urban residents’ transportation mode recognition model.

3.3.1. Feature Parameter Extraction

The literature consistently identifies that common transportation modes for urban residents include walking, bicycles, electric bicycles, buses, cars, and subways [35,36]. The transportation modes recognized in this study comprise prevalent travel modalities utilized by urban residents.

As stated in the Introduction, it is necessary to combine the spatiotemporal features of residents’ travel trajectories with the relevant geographical environments and navigation conditions to improve the recognition accuracy of transportation modes. Therefore, we introduce relevant geographical environment feature parameters and navigation feature parameters to further improve the feature parameter system for residents’ transportation mode recognition based on the MPL data. Using the interpolated MPL trajectories, relevant geographical environment data, and navigation data provided by the map service platform, we extracted three major feature parameter categories: spatiotemporal feature parameters, geographical environment feature parameters, and navigation feature parameters. As shown in Table 4, we constructed a total of 35 feature parameters. We have briefly described these parameters and their sources (Supplementary Table S1).

Table 4. Summary of feature parameters.

Category	Variable	Variable	Variable
Spatiotemporal feature parameters	Travel distance	Travel duration	Average speed
	Maximum speed	Minimum speed	Velocity range
	Velocity variance	DMER: duration of morning and evening rush hours experienced during the travel process.
Geographical environment feature parameters	Road density: ratio of the total length of roads in a certain area to the area of that area.	RPCB: ratio of the number of trajectory points close to bus stations to the total number of trajectory points in the raw moving segment or precise moving segment.	RPCS: ratio of the number of trajectory points close to subway stations to the total number of trajectory points in the raw moving segment or the precise moving segment.
	RPCC: ratio of the number of trajectory points close to cycleways to the total number of trajectory points in the raw moving segment or the precise moving segment.	DONBu: distance from the origin to the nearest bus station.	DDNBu: distance from the destination to the nearest bus station.
	DONP: distance from the origin to the nearest parking lot.	DDNP: distance from the destination to the nearest parking lot.	DONS: distance from the origin to the nearest subway station.
	DDNS: distance from the destination to the nearest subway station.	DONBi: distance from the origin to the nearest bicycle parking.	DDNBi: distance from the destination to the nearest bicycle parking.
	AHD_O: average Hausdorff distance to open spaces such as green spaces, parks, etc.	AHD_R: average Hausdorff distance to a residential area.	AHD_B: average Hausdorff distance to business center.
Navigation feature parameters	NTC: navigation time of cars between the origin and destination.	NDC: navigation distance of cars between the origin and destination.	NTBu: navigation time of buses between the origin and destination.
	NDBu: navigation distance of buses between the origin and destination.	NTW: navigation time for walking between the origin and destination.	NDW: navigation distance for walking between the origin and destination.
	NTBi: navigation time of bicycles between the origin and destination.	NDBi: navigation distance of bicycles between the origin and destination.	NTE: navigation time of electric bicycles between the origin and destination.
	NDE: navigation distance of electric bicycles between the origin and destination.	NTS: navigation time of subways between the origin and destination.	NDS: navigation distance of subways between the origin and destination.

3.3.2. Transportation Mode Recognition Model

In this study, we construct three transportation mode recognition models, namely SOM, RF and XGBoost, and select the optimal model by comparing the accuracy rate.

(1)

SOM model

Transportation mode recognition based on machine learning algorithms is mainly divided into supervised learning algorithms and unsupervised learning algorithms. Compared with supervised learning algorithms, the principal advantage of unsupervised learning algorithms lies in their independence from labeled data, as they perform category partitioning solely based on the intrinsic characteristics of the data itself. In unsupervised learning algorithms, the SOM model is a classical unsupervised learning algorithm [37]. With the advantages of the network topology and the competitive learning mechanism, this model has been widely applied in many research fields such as high-latitude feature visualization, recognition and classification of spatiotemporal patterns [38,39]. Therefore, this study takes it as one of the comparison models for transportation mode recognition.

The core principle of SOM model involves establishing a topological organization through competitive learning, where neurons iteratively adjust network weights via competitive processes. The model’s key topological preservation property automatically learns and captures feature correlations, and accomplishes dimensionality reduction [40]. A neighborhood function simultaneously preserves the topological properties of the input space and regulates weight adjustments within the neighborhood radius. Through iterative refinement of the winning neuron’s topological neighborhood, high-dimensional structural features are transformed into low-dimensional discrete representations. This process achieves topology-preserving vector quantization, resulting in clusters as computational outcomes.

Before training the SOM network, each feature parameter needs to be normalized. The initial learning rate η₀ of the SOM is set to 0.5, and the initial maximum neighborhood radius is set to 5. The learning rate decreasing function η is as follows:

$${\eta }_i=R_{\max }-{\displaystyle \frac{(i+1)\times (R_{\max }-R_{\min })}{n_{iter}}}$$

(4)

where $R_{\max }$ is the maximum winning radius set; $R_{\min }$ is the minimum winning radius set; $n_{iter}$ is the number of iterations; and i is the current number of iterations.

In addition, the decay function of the winning radius during the SOM training process adopts a Gaussian function. When η decays to 0.01, the initial weights of the competitive layer neurons are randomly given as real numbers between 0 and 1.

(2)

RF model

For the supervised machine learning algorithm, we consider RF model as one of the comparison models for transportation mode recognition [22,23]. As mentioned in the introduction, this algorithm demonstrates established efficacy in transportation mode recognition.

RF is an ensemble learning algorithm that leverages the combined predictive power of multiple decision trees. Its robustness stems from the synergistic use of Bootstrap Aggregating (Bagging) and random feature selection. The Bagging method trains each tree on a random subset of the training data, drawn with replacement. Furthermore, during the growth of each tree, the optimal split at any node is determined from a randomly selected subset of features. This approach ensures that even highly correlated features do not dominate the model, as individual trees will selectively use them [41]. Applicable to both regression and classification tasks, RF for classification determines the final output through majority voting across all constituent trees.

(3)

XGBoost model

In recent years, the XGBoost model has attracted considerable attention due to its efficiency, versatility, portability, and superior predictive accuracy. It has yielded significant research achievements across diverse applications, including environmental monitoring [42], transportation systems [43], geological hazard assessment [44], and medical diagnostics [45]. Consequently, this study adopts XGBoost as one of the comparative models for transportation mode recognition.

XGBoost is characterized as an efficient machine learning algorithm grounded in the gradient boosting framework [46]. It significantly improves both predictive accuracy and computational efficiency through the use of parallel computing, regularization techniques, and optimized tree pruning. The methodology is based on two fundamental principles: additive training and optimization of the function space. Specifically, XGBoost formulates and directly optimizes an objective function that integrates both a loss function and regularization components. This objective function is approximated using a second-order Taylor expansion, while the learning of tree structures is guided by a gain maximization criterion to determine the optimal feature-split combinations that maximize information gain. During this process, the gain maximization criterion tends to select one of the most representative features for splitting, thereby naturally avoiding the interference caused by collinearity within the model [47]. Through iterative training cycles, the algorithm aggregates weighted outputs from all decision trees. In the context of multi-class classification tasks, these ensemble outputs are converted into probability distributions via the Softmax function, ultimately resulting in the final predictive model.

3.3.3. Evaluation Index of Recognition Results

To evaluate the transportation mode recognition results, we take the transportation modes in the volunteers’ travel logs recorded synchronously (as shown in Table 3) as the ground truth results for comparative analysis. We use the accuracy rate Acc, the F1-score, and the area under curve AUC to evaluate the recognition results. Among them, AUC is the area under the receiver operating characteristic (ROC) curve, which is used to detect the overall discriminative ability of the model. The calculation methods of the Acc and F1-score indicators are as follows:

$$\mathit{Acc}\hspace{0.17em}=\hspace{0.17em}{\displaystyle \frac{n_{cor}}{N}}$$

(5)

$$F1\hspace{0.17em}=\hspace{0.17em}{\displaystyle \frac{2\times \overline{Pre}\times \overline{Rec}}{\overline{Pre}+\overline{Rec}}}$$

(6)

where $n_{cor}$ is the number of samples in which the transportation mode has been correctly recognized; N is the total number of samples; $\overline{\mathit{Pre}}$ and $\overline{\mathit{Rec}}$ are average precision ratio and average recall rate, respectively. $\overline{\mathit{Pre}}$ and $\overline{\mathit{Rec}}$ are calculated as follows:

$$\overline{\mathit{Pre}}\hspace{0.17em}=\hspace{0.17em}{\displaystyle \frac{{\displaystyle \sum _{i=1}^{n}Pr{e}_i}}{n}}$$

(7)

$$\overline{Rec}={\displaystyle \frac{{\displaystyle \sum _{i=1}^{n}Re{c}_i}}{n}}$$

(8)

where $Pr{e}_i$ and $Re{c}_i$ are the precision ratio and recall rate, respectively, of the recognition of the i-th type of transportation mode; n is the total number of types of transportation modes recorded in the travel log. $Pr{e}_i$ and $Re{c}_i$ are calculated as follows:

$$Pr{e}_i={\displaystyle \frac{N_{T{P}_i}}{N_{T{P}_i}+N_{F{P}_i}}}$$

(9)

$$Re{c}_i={\displaystyle \frac{N_{T{P}_i}}{N_{T{P}_i}+N_{F{N}_i}}}$$

(10)

where $N_{T{P}_i}$ is the number of correctly recognized samples for the i-th type of transportation mode; $N_{F{P}_i}$ is the number of samples recognized from other types of transportation modes as the i-th type of transportation mode; and $N_{F{N}_i}$ is the number of samples recognized from the i-th type of transportation mode as other transportation modes.

4. Analysis Results

4.1. Precision Evaluation of the Precise Moving Segment

To evaluate the precision of the precise moving segment, we utilize GPS trajectory data, which has been synchronously collected and bias-corrected, as the reference benchmark. Specifically, we apply the HMM algorithm to perform road network matching on GPS trajectory data, thereby achieving bias correction of the GPS data. We computed the Time Window-Based Hausdorff Distance (TW_H) [25] between both the raw and precise moving segments with the synchronously collected GPS trajectories, using the variation in TW_H before and after interpolation to evaluate the precision of the precise moving segments. The larger the TW_H, the greater the distance between the moving segment and the synchronously collected GPS trajectory, indicating lower precision of the moving segment.

Figure 5 shows box plots of the TW_H values between the raw moving segments (pre-interpolation) and the synchronously collected GPS trajectories, and between the precise moving segments (post-interpolation) and the synchronously collected GPS trajectories, respectively. The results indicate that as the time window is incrementally expanded from 5 s to 30 s, the TW_H values between the precise moving segments and the GPS trajectories remain consistently lower than those between the raw moving segments and the GPS trajectories. This suggests that the construction of the precise moving segment in this study can enhance the spatial accuracy of the MPL trajectory. Within a shorter time window, for instance, 5 s, the median of TW_H values between precise moving segments and GPS trajectories decreased by 210 m compared to the median of TW_H values between the raw moving segments and GPS trajectories. This demonstrates particularly notable accuracy enhancement effects. Furthermore, we computed the average TW_H distribution before and after interpolation across time windows. The average TW_H between raw moving segments and GPS trajectories ranged from 1.27 km to 1.29 km. Following interpolation, this metric between precise moving segments and GPS trajectories decreased to 0.88–1.16 km, yielding precision enhancement rates of 8.66% to 31.25%. Collectively, linear interpolation improved moving segment accuracy, establishing a reliable data foundation for downstream applications like transportation mode recognition. Overall, the construction of precise moving segments has improved the spatial accuracy of MPL trajectories, establishing a reliable data foundation for subsequent transportation mode recognition.

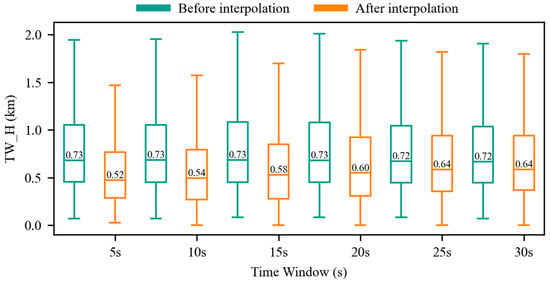
Figure 5. Boxplots of TW_H values comparing raw moving segments (pre-interpolation) and precise moving segments (post-interpolation) with the synchronously collected GPS trajectories.

4.2. Comparison of the Construction and Predictive Performance of Each Model

Following processing (including preprocessing, stop analysis, trajectory interpolation, and road network matching) of 432 MPL trajectories, 1831 precise moving segments were derived. To comprehensively evaluate the accuracy of the transportation mode recognition results in this study, as well as the effects of the precision of residents’ travel trajectories, geographical environment features, and navigation features on transportation mode recognition, we construct three datasets (D1, D2 and D3) for transportation mode recognition models and conducted comparative experiment. The specific settings are shown in Table 5. In particular, D1 and D3 use precise moving segments as samples, while D2 use raw moving segments. D1 extract the eight spatiotemporal feature parameters (Table 4) from its samples, whereas D2 and D3 both extract 35 feature parameters from their respective samples. Datasets D1, D2, and D3 have an identical sample size of 1831. Each of the three datasets was subjected to the SOM, RF, and XGBoost models, respectively, generating a total of nine comparison groups (nine models in total).

Table 5. Specific setting of the three datasets for transportation mode recognition models.

Dataset	Moving Segments Used	Feature Parameters Used
D1	Precise moving segments	Only 8 spatiotemporal feature parameters of the precise moving segment
D2	Raw moving segments	All 35 feature parameters of the raw moving segment
D3	Precise moving segments	All 35 feature parameters of the precise moving segment

The dataset was randomly split into a training set (75%) and a test set (25%) for each model. Hyperparameter optimization was employed for the nine models using grid search coupled with 5-fold cross-validation on the training set. The best-performing hyperparameters were used to construct the final travel mode recognition models. These models were subsequently evaluated on the test set, and their predictive performances are presented in Table 6. Figure 6 presents the ROC curves of the nine models on the test set. The optimal hyperparameters and corresponding predictive performance for all nine models are summarized as follows: ① Model 1 (D1 + SOM) achieved the best fit with a learning rate (η) of 0.01 and a neighborhood radius (γ) of 2.5. On the test set, it attained an AUC of 0.781, an accuracy (Acc) of 63.2%, and an F1-score of 0.633. ② Model 2 (D2 + SOM) performed best with η = 0.01 and γ = 2, yielding an AUC of 0.845, an Acc of 70.0%, and an F1-score of 0.702. ③ Model 3 (D3 + SOM) found its optimal performance with η = 0.01 and γ = 2, resulting in an AUC of 0.86, an Acc of 74.5%, and an F1-score of 0.736. ④ Model 4 (D1 + RF) achieved optimal performance with 500 decision trees (ntree), obtaining an AUC of 0.87, an Acc of 76.8%, and an F1-score of 0.765. ⑤ Model 5 (D2 + RF) performed best with ntree = 500, achieving an AUC of 0.905, an Acc of 84.0%, and an F1-score of 0.84. ⑥ Model 6 (D3 + RF) reached its optimal configuration with ntree = 300, which produced an AUC of 0.908, an Acc of 89.8%, and an F1-score of 0.902. ⑦ Model 7 (D1 + XGBoost) was optimized with a maximum tree depth (max_depth) of 7300 boosting rounds (n_estimators), and a learning rate (α) of 0.1. It demonstrated strong performance with an AUC of 0.929, an Acc of 81.5%, and an F1-score of 0.814. ⑧ Model 8 (D2 + XGBoost) achieved the best fit with max_depth = 2, n_estimators = 150, and α = 0.01, attaining an AUC of 0.948, an Acc of 86.0%, and an F1-score of 0.869. ⑨ Model 9 (D3 + XGBoost) performed best with max_depth = 5, n_estimators = 150, and α = 0.1, achieving superior results with an AUC of 0.966, an Acc of 91.8%, and an F1-score of 0.92.

Table 6. The evaluation results of different models.

Model Number	Comparison Groups	AUC	Acc	F1-Score
Model 1	D1 + SOM	0.781	63.2%	0.633
Model 2	D2 + SOM	0.845	70.0%	0.702
Model 3	D3 + SOM	0.860	74.5%	0.736
Model 4	D1 + RF	0.870	76.8%	0.765
Model 5	D2 + RF	0.905	84.0%	0.840
Model 6	D3 + RF	0.908	89.8%	0.902
Model 7	D1 + XGBoost	0.929	81.5%	0.814
Model 8	D2 + XGBoost	0.948	86.0%	0.869
Model 9	D3 + XGBoost	0.966	91.8%	0.920

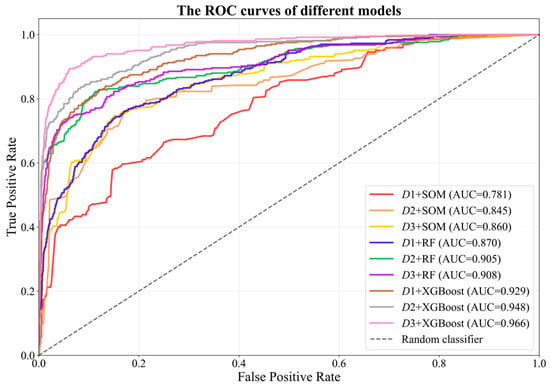
Figure 6. ROC curves of each model under test set.

Table 6 illustrates the recognition performance of three distinct datasets under the SOM, RF, and XGBoost models. Using identical datasets enables cross-model performance comparison. The results reveal that SOM achieves the lowest performance, RF exhibits moderate performance, and XGBoost attains the highest performance. Specifically, XGBoost consistently demonstrated superior performance across all datasets. In D1, it outperformed SOM and RF in accuracy by 18.3% and 4.7%, and in F1-score with respective margins of 0.181 and 0.049. This trend continued in D2, with accuracy advantages of 16.0% and 2.0%, and F1-score advantages of 0.167 and 0.029 over SOM and RF. Similarly, in D3, it led SOM and RF by 17.3% and 2.0% in accuracy, and by 0.184 and 0.018 in F1-score. These comparisons demonstrate the superior performance of XGBoost in transportation mode recognition, with its accuracy reaching 91.8% in D3. Figure 6 also indicates that Model 9 achieves the highest prediction performance (AUC = 0.966). In summary, the Model 9 (D3 + XGBoost) is the optimal transportation mode recognition model. To compare the statistical significance of model performance, we conducted 5 repeated 10-fold cross-validations on the training set, yielding 50 performance observations (Acc and AUC) for each model. Subsequent analysis of these results was performed using the Mann–Whitney U test. The results indicated that Model 9 significantly outperforms all other models, with p-values < 0.05 in the significance tests for both Acc and AUC when compared to the other models (Table 7). This conclusion is further supported by the independent test set, where the XGBoost-based model achieved the highest accuracy (91.8%) and the highest AUC (0.966). To gain deeper insights into the stability of this estimation, we performed 10,000 Bootstrap resamplings on the test set and calculated the 95% confidence interval, which was [90.2%, 92.5%]. The narrow range of this interval indicates high confidence in our estimation that the accuracy of Model 9 exceeds 90%.

Table 7. The evaluation results of different models via five repeated 10-fold cross-validations on the training set.

Model Number	Comparison Groups	Acc	p Value (Acc)	AUC	p Value (AUC)
Model 1	D1 + SOM	62.8% ± 2.3%	<0.001	0.796 ± 0.013	<0.001
Model 2	D2 + SOM	71.2% ± 1.8%	<0.001	0.851 ± 0.01	<0.001
Model 3	D3 + SOM	75.6% ± 2.5%	<0.001	0.868 ± 0.018	<0.001
Model 4	D1 + RF	76.9% ± 1.8%	<0.001	0.886 ± 0.01	<0.001
Model 5	D2 + RF	85.7% ± 1.9%	0.002	0.894 ± 0.007	0.007
Model 6	D3 + RF	90.8% ± 2.2%	0.035	0.915 ± 0.011	0.002
Model 7	D1 + XGBoost	83.7% ± 1.5%	0.001	0.937 ± 0.011	0.018
Model 8	D2 + XGBoost	88.3% ± 1.1%	0.015	0.951 ± 0.008	0.046
Model 9	D3 + XGBoost	91.9% ± 0.9%	− (Baseline)	0.969 ± 0.006	− (Baseline)

When applying identical models, the results reflect performance variations across datasets (Table 6). Overall, D2 outperforms D1, while D3 exceeds both (Table 6). Specifically, With SOM, D3’s accuracy is 11.3% higher than D1 and 4.5% higher than D2. For RF, D3 shows 13.0% and 5.8% improvements over D1 and D2. Using XGBoost, D3 achieves 10.3% and 5.8% gains over D1 and D2. The experiments demonstrate that constructing a comprehensive feature parameter system outperforms trajectory interpolation alone in enhancing recognition accuracy for urban residents’ transportation modes using MPL data. Moreover, simultaneously combining both approaches achieves the optimal recognition performance. All these results demonstrate that the following analytical framework optimizes recognition performance for MPL data: First, addressing positioning uncertainty through spatiotemporal interpolation of travel trajectories. Second, constructing a comprehensive feature parameter system incorporating spatiotemporal features of the trajectory data, geographical environment features, and navigation features. Finally, employing the XGBoost machine learning model to develop the transportation mode recognition model.

4.3. Influence of the Precision of Residents’ Travel Trajectories on Recognition Results

Based on the aforementioned findings, which demonstrate the superior performance of the XGBoost model, a further analysis was conducted to elucidate the contribution of precise movement segments and comprehensive feature parameters to transportation mode recognition within this model. Specifically, the results from the three datasets using the XGBoost model were analyzed and evaluated. Figure 7 shows the confusion matrix of the recognition results for Model 7 (D1 + XGBoost), Model 8 (D2 + XGBoost) and Model 9 (D3 + XGBoost). Based on these results, we further explore the role and impact of the precision of residents’ travel trajectories, geographical environment features, and navigation features on transportation mode recognition.

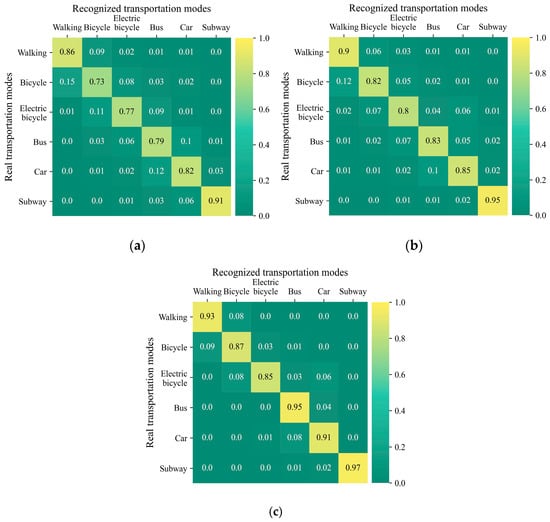
Figure 7. (a) Confusion matrix diagram of the Model 7 recognition results; (b) confusion matrix diagram of the Model 8 recognition results; (c) confusion matrix diagram of the Model 9 recognition results.

Figure 7b,c show the confusion matrix of the recognition results for Model 8 and Model 9, revealing the impact of the precision of the residents’ travel trajectories on the accuracy of transportation mode recognition. The results show that when the same set of residents’ travel feature parameters is used, road network matching and precise interpolation of the MPL trajectory can effectively improve the recognition accuracy of each transportation mode. In particular, the most substantial improvement in recognition accuracy is observed for buses and cars, with increases of 12% and 6%, respectively. The recognition accuracy increased by 5% for both bicycles and electric bicycles. The recognition accuracy of walking and subway is improved slightly, reaching 3% and 2%. Moreover, the confusion matrices of the two sets of results indicate that in the absence of road network matching and precise interpolation, almost all transportation modes are misclassified. Walking can be misclassified as bicycle, electric bicycle, bus, or car. Even between walking and car, which represent two transportation modes with substantial differences in their characteristics, instances of misclassification can still occur. Once precise moving segments are constructed, the misclassification between transportation modes with pronounced differences is reduced. However, there are more misclassifications between transportation modes with similar travel features, such as walking misclassified as bicycle and bicycle misclassified as walking and electric bicycle. After performing road network matching and precise interpolation on the MPL trajectory, the model’s ability to distinguish transportation modes with distinct travel characteristics can be improved. However, it is still difficult to fully distinguish similar transportation modes (such as walking, bicycle, electric bicycle, and between bus and car).

The results of Acc and F1-score for Model 8 and Model 9 presented in Table 6 indicate that with road network matching and interpolation processing, all the indicators improved by approximately 6%. This further indicates that the construction of precise moving segments is beneficial for improving the recognition accuracy of the urban residents’ transportation mode based on MPL data.

4.4. Influence of Geographical Environment Features and Navigation Features on Recognition Results

A comparative analysis of the overall recognition results reveals that Model 9 achieved superior performance relative to Model 7. As summarized in Table 6, Model 9 exhibited an approximate 10% gain in both Accuracy and F1-score, suggesting that the added geographical environment and navigation features contributed to the enhanced model performance. Figure 7a,c present the confusion matrices of Model 7 and Model 9 for the recognition results of each transportation mode, further revealing the impacts of geographical environment characteristics and navigation characteristics on the accuracy of transportation mode recognition. The results show that the model’s recognition accuracy for each transportation mode improved with the addition of geographical environment feature parameters and navigation feature parameters. The increase in bus recognition accuracy of 16% is the largest observed, whereas the recognition accuracies of bicycles and cars increased by 14% and 9%, respectively. The improvements in recognition accuracy for electric bicycles, subway and walking are relatively small at 8%, 6% and 7%, respectively. Furthermore, the research results indicate that the model can better distinguish similar transportation modes better after the addition of geographical environment feature parameters and navigation feature parameters. For example, in the absence of geographical environment feature parameters and navigation feature parameters, buses may be misclassified as bicycles, electric bicycles, or cars. In particular, 10% of the bus samples are misclassified as cars, whereas after adding these feature parameters, only 4% of the bus samples are misclassified as cars, and there are no misclassifications as other modes. Similarly, buses, electric bicycles, bicycles and walking all present similar situations, indicating that adding geographical environment features and navigation features is beneficial for improving the model’s ability to distinguish similar transportation modes. A detailed class-wise analysis in Figure 7c reveals varying recognition accuracy across modes. The subway mode achieved the highest accuracy (97%), with misclassifications confined solely to cars and buses. This was followed by the bus mode (95%), which was only mistaken for cars. Walking and car modes attained accuracies of 93% and 91%, respectively, and were confused only with their respective similar modes. In contrast, the bicycle (87%) and electric bicycle (85%) modes achieved lower accuracy due to their confusion with a broader set of alternatives, such as walking, buses, and each other.

In summary, the proposed comprehensive feature parameter system considerably enhances the recognition accuracy for individual transportation modes and effectively reduces misclassification between similar modes, such as bicycles and electric bicycles. Distinguishing between these two modes is notoriously challenging when relying solely on spatiotemporal feature parameters. Our framework addresses this challenge by integrating navigation feature with refined spatiotemporal dynamics, which collectively reveal systematic differences in travel behavior and kinematic potential. First and most critically, navigation feature parameters provide powerful indirect evidence for discrimination. For each moving segment, we synchronously obtained the navigation time and navigation distance for both modes. The actual travel time and distance of an authentic electric bicycle trip will closely match the navigation-calculated values for an electric bicycle (NTE and NDE) while deviating from those for a conventional bicycle (NTBi and NDBi) to a large extent. As shown in Figure 8, the gain-based feature importance analysis confirms that NDBi, NTE, and NTBi are among the most critical features, indicating that the model successfully learns the complex matching relationship between the observed trajectory and the navigation predictions for each mode. Secondly, refined spatiotemporal features capture the micro-level kinematic differences between the two modes. Despite similar trajectory shapes, electric bicycle systematically achieves higher average and maximum speeds due to power assistance. Furthermore, the assisted propulsion results in more stable power output, leading to a lower velocity variance during acceleration or uphill climbing compared to human-powered bicycles, which exhibit greater speed fluctuations. These features effectively complement and reinforce the evidence provided by the navigation parameters. Figure 8 also confirms that maximum speed and average speed are key discriminative features. Finally, geographical environment feature parameters—such as the distance from the trip origin/destination to bicycle parking points (DONBi/DDNBi) and the proximity of trajectory points to dedicated bicycle lanes (RPCC)—provide additional contextual information, further enhancing the robustness of the classification.

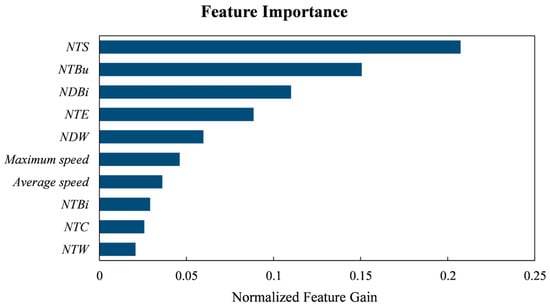
Figure 8. The top 10 most important features of Model 9.

4.5. Analysis of Misclassification

In Figure 7c, we can observe the misclassification between different modes. We find that 8% of the walking samples are misclassified as bicycles, and 9% of the bicycle samples are misclassified as walking. Additionally, the electric bicycles are misclassified mainly as bicycles or cars, with misclassification rates of 8% and 6%, respectively. The misclassification rate between cars and buses is 8%. Walking can be misclassified as bicycle, a bicycle misclassified as walking, an electric bicycle misclassified as a bicycle, an electric bicycle misclassified as a car, and a car misclassified as a bus, making these the five most common types of misclassified samples. Therefore, this study conducted an in-depth exploration of the reasons for misclassification in these five modes.

To explore the reasons for the generation of these five most common types of misclassified samples, we set up five groups of misclassification contrast sets, as shown in Table 8. The first group in Table 8 includes Class A and Class A′. The samples that are actually walking but misclassified as bicycles are defined as Class A, whereas the samples that are actually bicycles and correctly recognized as bicycles are defined as Class A′. The second group consists of Class B and Class B′. The samples that are actually bicycles but misclassified as walking are defined as Class B, whereas the samples that are actually walking and correctly recognized as walking are defined as Class B′. The third group is composed of Class C and Class C′. The samples that are actually electric bicycles but misclassified as bicycles are defined as Class C, whereas the samples that are actually bicycles and correctly recognized as bicycles are defined as Class C′. Class D and Class D′ belong to the fourth group. The samples that are actually electric bicycles but misclassified as cars are defined as Class D, whereas the samples that are actually cars and correctly recognized as cars are defined as Class D′. The fifth group comprises Class E and Class E′. The samples that are actually cars but misclassified as bus are defined as Class E, while the samples that are actually bus and correctly recognized as buses are defined as Class E′. We performed a comprehensive analysis of the 35 feature parameters (Table 4) for misclassified samples and the corresponding 35 feature parameters for correctly classified samples among the five groups of misclassification contrast sets. We quantified the similarity between them by using the Pearson correlation coefficient and Spearman correlation coefficient.

Table 8. Five groups of misclassification contrast sets.

Misclassified Class	True Class	Recognized Class	Correct Classification Class	True Class	Recognized Class
Class A	Walking	Bicycle	Class A′	Bicycle	Bicycle
Class B	Bicycle	Walking	Class B′	Walking	Walking
Class C	Electric bicycle	Bicycle	Class C′	Bicycle	Bicycle
Class D	Electric bicycle	Car	Class D′	Car	Car
Class E	Car	Bus	Class E′	Bus	Bus

As shown in Figure 9a, the navigation feature parameters (such as NDS, NTS, and NTE) and some geographical environment feature parameters (such as Road density, RPCS, and DONBu) are not strongly correlated between Class A and Class A′. However, Average speed, RPCC, and DONBi are highly correlated. Combined with actual travel habits, this misclassification is most likely caused by the fact that walking and bicycles often share non-motorized vehicle lanes and other transportation facilities. As shown in Figure 9b, the spatiotemporal feature parameters such as Average speed, Minimum speed, and Travel distance, are highly correlated between Class B and Class B′. Combined with the actual travel habits, it can be seen that this misclassification is very likely because the elderly and female cyclists ride at a slower speed, resulting in the spatiotemporal characteristics of cycling being similar to those of walking. As shown in Figure 9c, the parameters such as Travel distance, Minimum speed, NTBi, and NDBi exhibit clear correlations between Class C and Class C′. The misclassification of this group may be because of the short distance travel and slow travel caused by the different models and speed limits of electric vehicles. In this scenario, the travel characteristics are often similar to those of bicycles, so it is easy to misclassify them. As shown in Figure 9d, the parameters such as Maximum speed, Velocity range, and AHD_B are markedly correlated between Class D and Class D′. Combined with the actual situation, it can be seen that the misclassification of this group may be due to the similarity in maximum speed between certain electric bicycles and cars, as well as the habit of some users traveling to commercial areas by using electric bicycles. As shown in Figure 9e, parameters such as Minimum speed and Velocity range demonstrate a notable correlation between Class E and Class E′. Considering the actual situation, we find that this may be due to the similarity in speed characteristics between cars and buses under traffic congestion conditions, leading to misclassification. In general, misclassified samples are often the result of special circumstances such as congestion and elderly travel, which cause travel characteristics to exhibit strong similarities with other categories, leading to misclassification.

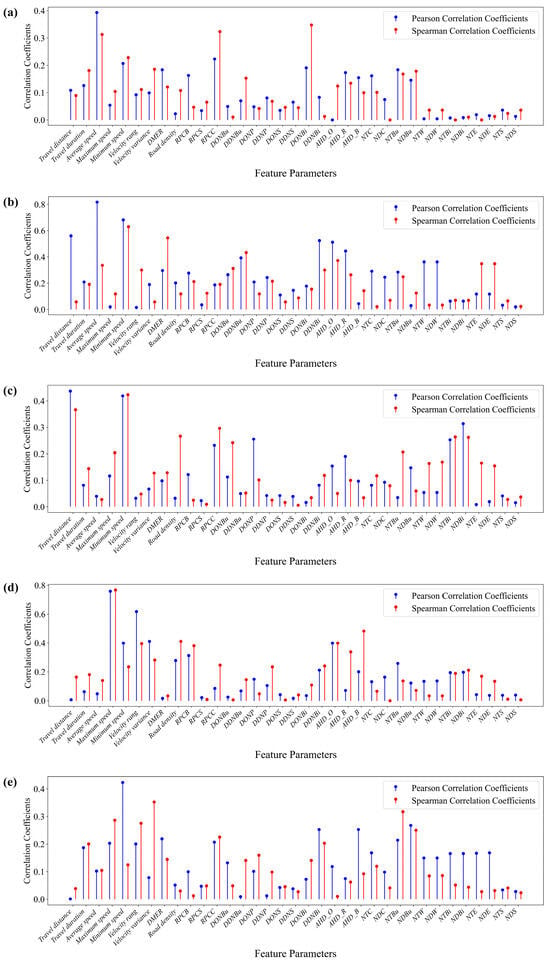
Figure 9. Pearson coefficient and Spearman coefficient between 35 feature parameters of misclassified samples and 35 feature parameters of correctly classified samples in the five groups of sample sets: (a) correlation coefficients of feature parameters between Class A and Class A′; (b) correlation coefficients of feature parameters between Class B and Class B′; (c) correlation coefficients of feature parameters between Class C and Class C′; (d) correlation coefficients of feature parameters between Class D and Class D′; (e) correlation coefficients of feature parameters between Class E and Class E′.

5. Discussion

5.1. Main Findings

The results demonstrate the multiple benefits of our method for further applications.

First, the precise moving segments we have constructed can effectively improve the expression density and quality of residents’ travel trajectories. We utilized synchronously collected and corrected GPS data as the validation dataset. It was observed that as the time window was incrementally expanded from 5 s to 30 s, the TW_H between the precise moving segments and the GPS trajectories remained consistently lower than that between the raw moving segments and the GPS trajectories, yielding precision enhancement rates of 8.66% to 31.25%. The construction of precise moving segments has improved the spatial accuracy of MPL trajectories, establishing a reliable data foundation for subsequent transportation mode recognition.

Second, the construction of precise moving segments based on MPL data can improve the recognition accuracy of the model for each transportation mode and reduce misclassification between different transportation modes. In particular, the most marked gains were observed for buses and cars, with accuracy increases of 12% and 6%, respectively. The recognition accuracy of both bicycles and electric bicycles has increased by 5%, while the recognition accuracy of walking and subway is improved slightly, reaching 3% and 2% (Figure 7).

Third, we improve and expand the feature parameter system for transportation mode recognition based on MPL data, enhancing the model’s recognition ability in complex traffic environments. As shown in Table 4, we fully consider the spatiotemporal features of the trajectory itself and extract a total of 35 feature parameters by integrating the relevant geographical environment features and navigation features. The results show that the added feature parameters can improve the model’s ability to recognize similar patterns. The increase in bus recognition accuracy of 16% is the most substantial, whereas the recognition accuracies of bicycles and cars increased by 14% and 9%, respectively. The improvements in recognition accuracy for electric bicycles, subway, and walking are relatively small at 8%, 6% and 7%, respectively (Figure 7).

Fourth, we construct a transportation mode recognition method based on XGBoost. This model employs a comprehensive feature parameter system to efficiently and accurately classify diverse transportation modes. Its enhanced adaptability to diverse regional datasets offers a cost-effective method for collecting travel mode data from urban residents. The experimental results show that the AUC, accuracy and F1-score of the model reach 0.966, 0.918, and 0.92, respectively. The model shows excellent overall performance and can effectively recognize the transportation modes of urban residents (Table 6).

5.2. Transferable Applications

Although this study used Nanjing as an example to conduct research on the recognition of urban residents’ transportation modes and did not conduct comparative analysis in other cities, the proposed model is not limited by geography and has good transferability and universality.

First, Nanjing is a city with a high degree of urbanization, complex transportation environment, and rich geographical elements. It boasts all common modes of transport, including walking, bicycles, electric bicycles, buses, cars, and subways. Furthermore, it is an extremely typical and widely representative example of a modern city. Therefore, the model constructed in this study is not limited to Nanjing, and its universality has application value in other cities as well.

Second, this study extracted 35 feature parameters from three aspects, namely, spatiotemporal features, geographical environment features, and navigation features, such as travel duration, travel distance, and other common parameters. Given that these parameters are all derived from the basic attributes of daily travel and are not limited by regional specificity, the high accuracy and strong robustness of the model are further enhanced in complex traffic environments. In future research, we will focus on the transferability of this model and conduct systematic comparative analysis in other cities to further explore the transferability and adaptability of the model in different periods and scales, providing strong support for urban transportation planning and research.

5.3. Model Robustness

To verify the robustness of the proposed XGBoost model, this study conducts validation from multiple perspectives. As detailed in Section 4.2, we performed five repetitions of 10-fold cross-validation on the training set to assess the statistical significance of model performance. Table 7 presents the results of these repeated cross-validations for different models. The analytical results consistently demonstrate that Model 9 exhibits high robustness.

First, after hyperparameter optimization for all models, Model 9 achieved the best performance on the independent test set in terms of final performance, with its AUC, accuracy, and F1-score all higher than those of the other models (see Table 6). Regarding model stability, the results of the ten-fold cross-validation provide more robust evidence. As shown in Table 7, Model 9 not only has the highest mean AUC value (0.969) but also the smallest degree of dispersion (0.006). The same trend was observed for accuracy. The Mann–Whitney U test conducted between Model 9 and the other models yielded significant p-values (p < 0.05), confirming that the performance advantage of Model 9 is not accidental.

Second, through five repeated 10-fold cross-validations, the optimal Model 9 achieved an average accuracy of 91.9% (±0.9%). The low standard deviation demonstrates that the model performance is insensitive to data partitioning. The model’s accuracy of 91.8% on the independent test set closely aligns with this result, effectively ruling out the possibility of overfitting.

Third, Model 9 demonstrated strong stability in response to data variations. Model 9 was built using precise moving segments generated via interpolation, while Model 8 utilized raw movement segments. A comparison between Model 8 and Model 9 can reflect the impact of data quality on model performance. The results show that the average accuracy of the ten-fold cross-validation after interpolation increased by 3.6% compared to that before interpolation (from 88.3% to 91.9%). The significance test of the ten-fold cross-validation yielded a p-value < 0.05. These experimental results indicate that the model can effectively adapt to the changes in data distribution caused by interpolation, and even leverage the more refined post-interpolation data to improve prediction accuracy. It exhibits strong tolerance to such data perturbations, demonstrating excellent robustness.

5.4. Future Work

We would like to note several limitations of this research. First, this study does not account for the correlations in residents’ transportation mode choices in their daily travel behaviors. Specifically, residents’ transportation mode choices exhibit certain regularities on weekdays versus weekends, as well as strong interdependencies among multiple trips made on the same day. Incorporating such regularities and correlations into the modeling process is likely to enhance the model’s performance and robustness. In future research, we aim to collect long-term MPL data to observe patterns in residents’ daily travel behavior and the associated correlations in transportation mode choices. Building on this, we will further investigate the influence of such daily travel patterns and correlations on transportation mode prediction. Second, in the transportation mode recognition model for urban residents based on XGBoost, the accuracy of road network matching is relatively low when facing complex road environments such as elevated roads and tunnels. In future research, we will conduct in-depth studies by combining road network types and travel speeds to improve the accuracy of road network matching. Third, the current study adopts a simple linear interpolation scheme for trajectory processing, which disregards both real-world travel speeds and the topological complexity of the road network. In future research, we will develop an interpolation algorithm for MPL trajectories based on speed increments, considering road network constraints, enhancing the spatiotemporal positioning precision of interpolated trajectory points. Nevertheless, we believe that the present work is an important effort to solve the problem of positioning uncertainty in MPL data, improve the practicality of the use of MPL data in urban residents’ transportation mode recognition, and extend the feature parameter system of transportation mode recognition based on MPL data.

6. Conclusions

Obtaining accurate transportation modes of urban residents serves as a cornerstone for building sustainable cities, providing essential foundation for urban planning, transportation governance, and sustainability evaluation. This is especially critical under the dual challenges of escalating traffic congestion and the pressing need for low-carbon development. With the emergence of the internet and the widespread popularity of smartphones, MPL data have become an important data source for recognizing urban residents’ transportation modes. Currently, the positioning uncertainty of MPL data and the selection of travel features are the key issues in urban residents’ transportation mode recognition based on MPL data. Although many studies have addressed these issues, problems such as insufficient consideration of travel features of transportation modes, low accuracy of MPL data, and lack of effective evaluation of recognition results still exist. In this study, we consider the self-localization features of MPL data and the behavioral features of urban residents’ travel choices, proposing a set of methods for recognizing urban residents’ transportation modes to solve the issues faced by the existing methods. Firstly, we construct the urban residents’ precise moving segments to address the positioning uncertainty issues of MPL data. This stage aims to improve the spatiotemporal density and quality of residents’ travel trajectories, providing basic data for subsequent transportation mode recognition. Secondly, we construct a comprehensive feature parameter system for recognizing urban residents’ transportation modes from three aspects, which addresses the problem of insufficient consideration of the relevant geographical environment features and navigation features in existing methods. Thirdly, we construct a transportation mode recognition model based on XGBoost, comparing it with the classic unsupervised learning algorithm SOM and the optimal recognition model RF in existing studies. The results demonstrate that samples processed with trajectory interpolation and containing comprehensive feature parameters achieve optimal performance in the XGBoost-based transportation mode recognition model. Furthermore, using real labels derived from synchronously collected travel logs that document transportation modes, we validated the recognition results, thereby mitigating the limitation of insufficient evaluation in existing studies.

The contributions of this study are twofold: theoretical and methodological. Theoretically, we advance the feature system for transportation mode recognition by integrating geographical context and real-time navigation parameters, thereby constructing a comprehensive set of influencing factors spanning three dimensions: spatiotemporal features, geographical environment features, and navigation features. This approach addresses a critical gap in existing research—specifically, the frequent oversight of geographical constraints and real-time traffic conditions—and thereby mitigates the misclassification of travel modes in complex urban environments. Methodologically, we propose a multi-step analytical framework. First, it resolves the inherent positioning uncertainty in MPL data via a hybrid technique combining road network matching and trajectory interpolation. Subsequently, a comprehensive set of feature indicators is established through systematic synthesis of key factors influencing travel behavior. Finally, a recognition model is constructed and trained using the XGBoost algorithm. This integrated framework effectively overcomes core limitations of traditional methods, including positional inaccuracy and inadequate feature representation, leading to great improvements in the accuracy and reliability of traffic mode recognition. Furthermore, this method not only improves the accuracy of transportation mode recognition, but also provides critical data and decision-making foundation for building low-carbon, efficient, and sustainable cities. It assists urban planners in optimizing transportation infrastructure and promoting green travel, thereby promoting the development of urban transportation towards a more environmentally friendly and resource-conserving direction.