Abstract
Reliable water vapor permeability (WVP) testing is crucial for sustainable construction, enabling accurate assessment of bio-mineral materials like hemp concrete, which reduce the environmental impact through renewable sourcing and improved energy efficiency. However, most studies testing or conditioning porous building materials in environmental chambers overlook the influence of chamber occupancy on airflow and humidity evacuation. While the usual practice is to collect anemometric velocity results in selected locations, few investigations apply computational fluid dynamics (CFD) to analyze the entire flow field, and humidity-field assessment is practically absent. This study addresses this gap by using CFD to examine how sample arrangement affects airflow and relative humidity (RH) in a climatic chamber containing sixteen hemp concrete specimens in dry- and wet-cup setups, aiding the reliable characterization of hygroscopic eco-composites. Three arrangements were modeled in ANSYS Fluent (2024 R1) using turbulence and species transport. Results show that unoptimized wet-cup placements cause RH deviations exceeding ISO’s ±5% tolerance, potentially biasing permeability data and undermining comparability across laboratories. A balanced wet–dry layout maintained RH within limits, improving testing reproducibility. Velocity maps reveal strong gradients above exposed sample surfaces, suggesting that standard anemometric protocols may require refinement. The presented approach highlights chamber loading as a hidden factor influencing WVP results and provides a transferable CFD-based framework to enhance testing accuracy, support sustainable material qualification, and accelerate the standardization of green-building methodologies.
1. Introduction
In the pursuit of sustainable construction practices amid escalating environmental concerns, bio-based materials such as hemp concrete have emerged as promising alternatives to traditional cementitious composites, offering significant advantages, including reduced carbon emissions through renewable hemp fiber sourcing, enhanced thermal insulation for energy-efficient buildings, improved indoor air quality via natural moisture regulation, and overall contributions to circular economy principles by utilizing agricultural by-products [1,2]. However, the inherent complexity of these materials—characterized by a heterogeneous porous structure and the incorporation of organic bio-components like hemp shives—introduces challenges in accurately assessing their hygrothermal properties, such as water vapor permeability (WVP), which are critical for ensuring long-term durability and performance in real-world applications. Conventional testing protocols, including the standardized ISO cup method [3], often assume idealized homogeneous conditions within environmental chambers, yet fail to account for the variability induced by multi-sample interactions, potentially leading to biased results and hindering the widespread adoption of these eco-friendly innovations; thus, there is an urgent need to refine and optimize such methodologies to enhance reliability and support the transition toward greener built environments.
Climatic chambers are widely used for conditioning and testing building materials under controlled environmental conditions. In water vapor permeability (WVP) studies—particularly those following the widely adopted ISO 12572 standard [3]—samples are exposed to fixed temperature (23 °C) and relative humidity (RH = 50%) conditions over an extended period to stabilize their mass before measurement. General guidelines recommend that the chamber volume should be 3–5 times greater than the volume of the conditioned product [4]. On the contrary, statistical requirements favor testing larger sample sets. Inhomogeneous structures of composites with bio-additives, such as hempcrete, call for increased thickness of tested samples, and tight laboratory schedules may further incentivize maximizing chamber occupancy. As a result, we believe that the occurrence of spatial arrangements which obstruct airflow and compromise the uniformity of environmental conditions is not rare and deserves more attention.
These concerns become more pronounced during actual WVP measurements. Unlike conditioning, which involves only the samples, the cup method requires each sample to be attached to a vessel that also contains a chemical agent—either a desiccant (dry cup) or a saturated salt solution (wet cup)—actively driving moisture absorption or emission. The combined volume of samples and vessels significantly reduces available circulation space, while active vapor exchange introduces localized humidity gradients. Limited space combined with additional sources and sinks of water vapor led us to the hypothesis of the occurrence of local zones with poor air exchange, exhibiting RH values significantly different from the indication of the chamber’s sensor. This study aims to investigate this issue with the use of CFD simulation, determining the magnitude of potential RH nonuniformities and how they translate to systematic errors in WVP calculations for the tested material, i.e., the hemp–lime concrete.
Accurate water vapor permeability (WVP) testing is essential for evaluating how construction materials manage moisture, directly influencing structural durability, biological stability, indoor air quality, and occupant comfort [2]. Recent studies show that hemp concrete can replace conventional materials such as drywall, OSB, and EPS [2,5] in residential construction while maintaining satisfactory hygrothermal performance. Other investigations highlight that hemp–lime composites effectively buffer moisture, reduce vapor gradients, and contribute to healthier indoor environments [6]. Porous hemp-based boards also provide excellent sound-dampening properties and can be rendered fire-retardant through suitable treatments [6].
Approaches to ensuring the biological stability of such materials vary: they can be treated with antifungal agents [7], or conversely, fungal growth can be intentionally harnessed to improve mechanical integrity [8]. Research on mycelium-based composites (MBCs) demonstrates that fungal mycelium can be deliberately cultivated on lignocellulosic substrates—including hemp fibers and hurds—to serve as a natural binding phase rather than a contaminant. In these systems, the mycelium colonizes the hemp matrix and forms a cohesive hyphal network that binds the particles into lightweight, mechanically stable panels after drying or heat treatment [8].
In this broader context, ensuring reliable and reproducible WVP data becomes critical. Underestimating or inconsistently measuring humidity transfer can lead to errors in predicting moisture accumulation, fungal development, or the long-term degradation of breathable bio-based walls and insulation systems.
In our work, this context justifies why we emphasize the variability and potential error sources in WVP measurements—not merely as a laboratory curiosity but as a direct link to sustainable building outcomes. If local relative humidity (RH) above a sample–vessel assembly is higher than the chamber setpoint (as our CFD results show), then the WVP calculation will be systematically biased, leading to biased modeling of the hygrothermal performance of porous building materials.
The ISO 12572 standard [3] defines strict limits for measurement parameters during WVP testing: temperature variation must remain within ±1 %, RH within ± 5 %, and air velocity above the cup between 0.02 and 0.3 m/s. For highly permeable materials, Annex G [3] recommends airflow velocities above 2 m/s to avoid surface-layer correction factors. Nevertheless, the exact method of velocity measurement is not specified, and the RH is typically assumed to be in accordance with the indication of the chamber control system.
Recently, many experimental studies were devoted to verify and improve the procedures of water vapor permeability testing in hemp concretes. Seng et al. [9] examined the effects of airflow velocity, sample thickness, and incorporation of water vapor interface resistances in the calculations, showing that each of these factors caused up to a 10% difference in measured WVPs for tested scenarios, and their cumulative effect may reach even 30%. Colinart and Glouannec [10,11] and Pietrak et al. [2,12] investigated the effects of various desiccants and cup’s inner relative humidity, emphasizing that it should actually be measured rather than assumed based on tables published in the ISO 12572 standard. Finally, Colinart and Magniont [13] presented the results of a round-robin study, where the same hemp concrete was tested by six independent laboratories using a unified experimental protocol. Authors [13] present interesting considerations regarding the influence of air velocity and the type of desiccant on the measurement results and achieved stabilities of water vapor flux through the sample.
Despite the widespread use of climatic chambers, few studies have analyzed the uniformity of internal conditions—particularly relative humidity (RH)—and their influence on test results. As noted by Ramezani et al. [14], only limited research has examined chamber performance through numerical or experimental methods, with most studies focusing on chamber behavior in isolation, without accounting for internal obstructions or moisture-active components. Some studies, e.g., Vololonirina and Perrin [15], used CFD to derive velocity fields in chambers loaded with WVP test vessels, without considering moisture transport, emission, or removal.
It may appear that ensuring sufficient airflow velocity above the samples is adequate to maintain proper mass exchange and prevent large local deviations from the target RH of 50%. However, even when average airspeed is acceptable, regions of elevated or reduced RH can still form above the samples—particularly if localized circulation zones develop that exchange moisture with their surroundings to a limited extent. Our study surpasses previous numerical efforts by incorporating moisture transport effects, enabling a more refined and realistic analysis of internal chamber behavior. It verifies three vessel arrangement scenarios, revealing that two configurations led to the formation of stagnation zones and localized RH levels exceeding ISO limits, while only one arrangement maintained compliant conditions throughout the chamber. Although it focuses on a specific chamber model and measurement geometry, the findings highlight the critical influence of the internal layout on test reliability. The simulations not only demonstrate the magnitude of the issue but show that finding a compliant arrangement that functions even under crowded conditions is possible. Our work highlights the value of CFD analysis in optimizing experimental setup, and signals that the problem at hand may require further research and improvement of used standards.
2. Material and Methods
2.1. Physical Characteristics of the Modeled System
The investigation concerned the KBK-200W environmental chamber manufactured by Wamed (Poland). Its technical specifications, as provided by the manufacturer, are summarized in Table 1. It should be noted that the investigated device had undergone certain modifications due to the unavailability of original replacement parts. For instance, the stock fans were replaced with two 45 W models from EBM-PAPST [16]. Despite these changes, the overall performance of the chamber remained close to the original.

Table 1.
Specifications of the modeled climatic chamber as given by the manufacturer.
The chamber has a typical construction, featuring a front door sealed with a rubber gasket and a loading space measuring 550 × 1030 × 360 mm (W × H × D). Its internal environment is regulated by both heating and cooling systems, allowing it to maintain temperatures between 5 °C and 70 °C. Relative humidity is controlled using a humidification loop and a condenser loop.
A photograph of the device loaded with samples is available in [2]. The present study was motivated by a planned water vapor permeability (WVP) test involving the simultaneous conditioning of 16 hemp–lime concrete samples—eight in the dry-cup configuration and eight in the wet-cup configuration. Figure 1a,b illustrate the modeled geometry, including the interior of the climatic chamber and the sample–vessel assemblies, while Figure 1c provides the dimensions of a single assembly. The chamber manufacturer provides only one internal humidity sensor, located upstream of one of the fans (i.e., near the edge of the upper air outlet shown in Figure 1a). During WVP testing, the vessels with mounted samples are placed on four wire shelves; however, these shelves were omitted from the simulation model for simplicity.
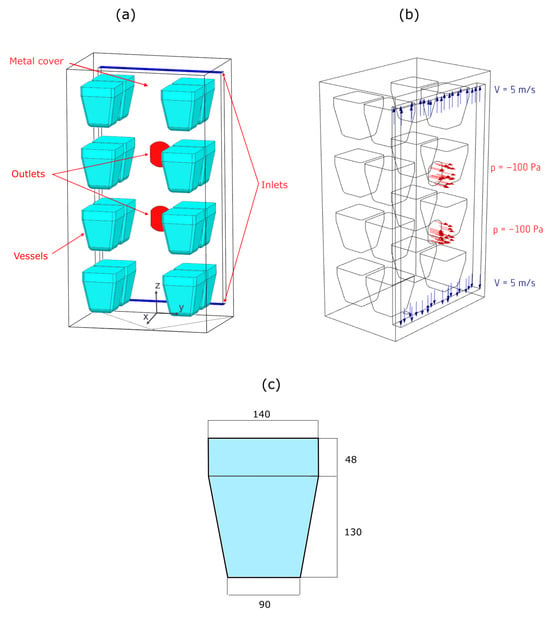
Figure 1.
Schematic of the climate chamber interior with sample/vessel assemblies (a), applied velocity and pressure boundary conditions (b), and the geometry of the sample/vessel assembly (c).
The sample compartment is cuboid in shape with a pyramid-shaped bottom to allow condensate drainage. The rear wall of the chamber is covered by an additional metal panel, behind which the air-conditioning components are housed. These include the following:
- Two spiral heaters,
- Two 45 W axial fans (each located behind a central opening),
- Two radiator assemblies connected to Peltier modules,
- Inlets and outlets for the condenser, and
- Inlets and outlets for the humidification loop.
The symmetrical arrangement of these components with respect to both vertical and horizontal symmetry planes of the rear wall results in symmetric flow conditions at the air supply and extraction openings, as depicted in Figure 1b. This figure illustrates the adopted approach to modeling air circulation within the sample compartment. In our main simulations, the elements enclosed behind the rear metal cover were not modeled explicitly; instead, their influence was represented using appropriate boundary conditions at the supply and extraction openings.
2.2. Modeling Details
2.2.1. Boundary Conditions
From the perspective of the sample compartment, the upper and lower openings in the metal cover acted as air inlets, while the two central openings served as outlets (Figure 1b). Accordingly, the final simulations defined these boundaries as velocity inlets (top and bottom) and pressure outlets (central openings), respectively. The assigned values—5 m/s inlet velocity and –100 Pa outlet pressure relative to the chamber’s operating pressure—were derived from the characteristics of the two axial fans installed behind the metal cover.
To determine boundary conditions that realistically reproduced the influence of the fans, preliminary simulations were carried out in which the airflow behind the metal cover was included, and fan-type boundary conditions were applied at the surfaces of two central openings (outlets). The fan boundary condition requires the specification of a pressure jump value. Based on technical data [16], the fans had a power rating of 45 W, a volumetric flow rate of 340 m3/h, dimensions of 138 × 57 mm, and a rotational speed of 2800 RPM. A fan efficiency of 0.8 was assumed. The pressure rise generated by each is [17]
where is the pressure rise, P is the rotor power, is the volumetric flow rate (here expressed in dm3/s), and is the fan efficiency. For , , and , we obtain
The results of the preliminary simulations were analyzed to obtain the velocity and pressure profiles shown in Figure 2. They indicate that the velocity profile at the inlet boundaries may be approximated with a constant value of 5 m/s, and the pressure immediately upstream of the fans (at the outlet boundaries) is −100 Pa relative to the chamber’s operating pressure, which justifies the inlet and outlet settings shown in Figure 1b used in the main analyses.
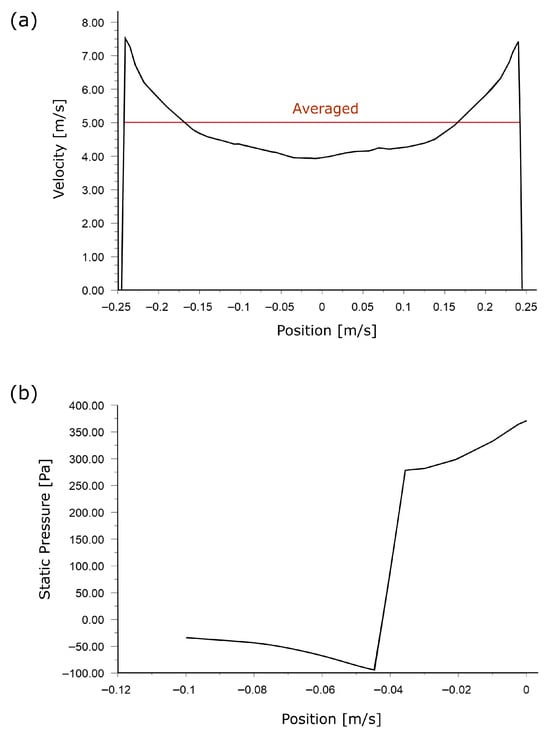
Figure 2.
Velocity profile at the sample compartment inlet resulting from fan operation (a) and pressure change for air flowing through the fan (b), where the red solid line marks the averaged velocity.
The boundary parameters used in the main analyses were as follows: at the velocity inlet, the turbulence intensity and turbulence length scale were set to 5% (a conservative assumption for low-speed internal flows) and 0.04 m (corresponding to the shorter edge of the inlet), respectively. An entry temperature of 23 °C was also specified, consistent with the target chamber conditions.
To maintain 50% relative humidity (RH) in the chamber, we set the water vapor mass fraction at the inlet from the saturation vapor pressure. Following ISO 13788 [18], the saturation vapor pressure at temperature T is
For = 23 °C,
The water vapor partial pressure at RH is
With RH =50%,
Assuming ideal gas behavior, the mole fraction of water vapor in the chamber is
where is the chamber operating pressure. Taking ,
The mixture molar mass is
with and . Numerically,
The inlet mass fraction of water vapor is then
so that
This mass fraction was prescribed at the inlet surface in ANSYS Fluent. Additionally, water vapor mass fluxes g were imposed at the top surfaces of the sample/vessel assemblies based on previously measured average values for hemp concrete [12]:
In terms of heat transfer, null heat flux was assumed at both assembly and chamber walls. This is due to the fact that the environmental chamber walls are thermally insulated to ensure minimal external influence, and the measured temperature differences between assembly interiors and sample compartments are negligible (see, e.g., [12]).
2.2.2. Operating Conditions
In the Operating Conditions panel, the chamber reference pressure and temperature were set to 1 bar and 23 °C, respectively. Because the water–air mixture composition varies across the domain, the local density changes. For such cases, it is recommended to define the Specified Operating Density, i.e., a reference density used to reduce round-off errors in body-force calculations [19].
The body force per unit volume is
where is the local density, is the operating (reference) density, and g is the gravitational acceleration.
By default, the solver sets to the domain-average density, which may be unstable if density depends on the evolving solution. We therefore prescribe a constant value from the ideal gas relation
with , (23 °C), universal gas constant , and mixture molar mass (from Equation (5)).
Numerically,
2.2.3. Models
The governing equations were solved using the finite volume method (FVM) in a transient, pressure-based RANS framework [20], using the ANSYS Fluent (2024 R1) software [19]. Continuity, momentum, turbulence (realizable k–), and water vapor transport equations were included, while the energy equation was disabled due to the nearly isothermal chamber conditions. The Species Transport model, suitable for molecularly mixed gases, has been applied in similar chamber studies [14]. Alternative humidity models (Multiphase and Multiphase with Wet Steam) were rejected: the former target flows with distinct phases and possible phase change, which is unnecessary here since condensation or evaporation is not expected at 50% RH; the latter is intended for saturated steam applications and does not allow direct RH specification.
The gas mixture consisted of air and water vapor, with the latter defined as the primary species. Species concentrations were governed by convection, diffusion, and prescribed source terms, while reactions were neglected. The diffusive mass flux was evaluated for each species as follows [14]:
where is the diffusive mass flux of species i (units ), is the mixture density (), is the molecular mass diffusivity of species i in the mixture (), is the turbulent viscosity (), is the turbulent Schmidt number (–), is the thermal–diffusion (Soret) coefficient with units of , is the mass fraction (–), T is temperature (K), and ∇ is the gradient operator.
Heat transfer was neglected due to the minimal temperature gradients and the dominance of forced convection. As such, the energy equation was not solved, and temperature was treated as constant throughout the domain. Due to that, the thermal part of Equation (10) was inactive.
The pressure-based solver was run in transient mode with gravity enabled. Turbulence was modeled using the realizable k– model with Standard Wall Treatment [19], also used in [14]. The resulting values were close to 30, satisfying the wall-function requirement ().
2.2.4. Materials
The thermophysical properties of water and air were taken from the Ansys Fluent materials database. Density was modeled using the incompressible ideal gas formulation, which evaluates the local density from the ideal gas law. In this approach, density varies with the local mixture composition (through the molar mass) and temperature (here, assumed constant), while the effect of spatial pressure variations is neglected by using a constant value equal to the operating pressure. Mass diffusity was calculated according to the kinetic theory and viscosity according to the mass-weighted mixing law [21].
2.2.5. Discretization and Solution Methods
The computational mesh was prepared in Fluent Meshing (2024 R1). A total of 1,795,216 polyhedral elements were generated, with a maximum cell size of 5 mm. Such elements offer a low aspect ratio and robustness to various flow directions. The mesh is shown in Figure 3, including a close-up of the vessel/sample assembly surface. The interior of the vessel/sample assemblies was not meshed.
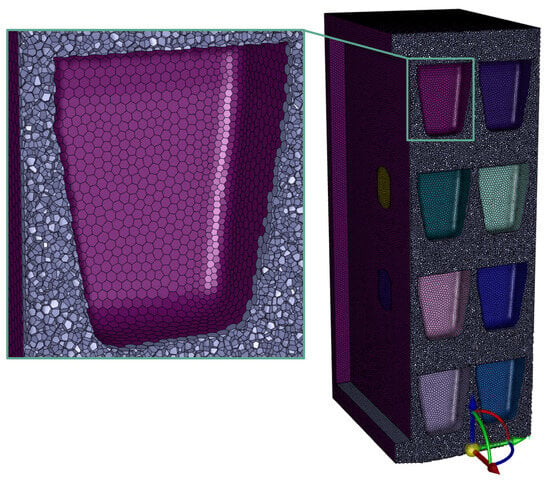
Figure 3.
Computational mesh generated in Fluent Meshing.
The results presented in Table 2 and Table 3 confirm that the obtained solutions are independent of both the applied time step and the computational mesh. Reducing the time step from 0.04 s to 0.01 s resulted in a negligible change in the average relative humidity () and velocity (), below 0.15%. Similarly, increasing the cell count from 1.38 to 2.41 million produced variations smaller than 0.2%. These differences are within the expected numerical uncertainty range, demonstrating that the adopted discretization parameters ensure stable and converged results for the analyzed flow and humidity fields. Consequently, the middle tested values—a time step of 0.02 s and a mesh of 1,795,216 elements—were selected for the final simulations as a trade-off between accuracy and computational efficiency.

Table 2.
Time-step independence verification for average relative humidity () and velocity () at s.

Table 3.
Mesh independence verification for average relative humidity () and velocity () at s.
In the Solution Methods panel, the pressure–velocity coupling was set to Coupled. Pressure discretization used the Body Force Weighted scheme [19], while momentum, turbulence, and water vapor mass fraction equations employed the Second Order Upwind scheme for improved accuracy. For the transient formulation, the Second Order Implicit time-stepping method was applied. With characteristic flow velocity of 5 m/s and a time step of 0.02 s, the Courant number was equal to 20, which is within the recommended range [19], providing a balance between stability and convergence speed [19].
Simulations were initialized with zero velocity and a water vapor mass fraction of 0.00878 (Equation (6)). A maximum of 20 iterations per time step was allowed, with residuals converging below . The computation was stopped after 500 steps (10 s of simulated time), at which point velocity, temperature, and relative humidity fields had stabilized. Each case required approximately 20 h of computation on a workstation with an Intel® CoreTM i7-6820HQ (4 cores), 32 GB RAM, and NVIDIA® Quadro® M2000M GPU.
3. Results and Discussion
3.1. Introduction
The investigation assumed that the chamber was loaded with 16 sample vessel assemblies, half configured as dry cups and the other half as wet cups, representing a typical testing scenario. Because the assemblies either emit or absorb moisture, their spatial arrangement can significantly influence local relative humidity (RH) despite forced air circulation. Two initial layouts were assumed to maximize internal uniformity by distributing an equal number of wet and dry samples on each shelf (Figure 4a,b). However, these “common sense” layouts did not bring satisfactory homogenization results. A third layout (Figure 4c), identified through analysis of the velocity field, yielded the most uniform RH distribution across the domain. Interestingly, this configuration would not appear optimal at first glance.
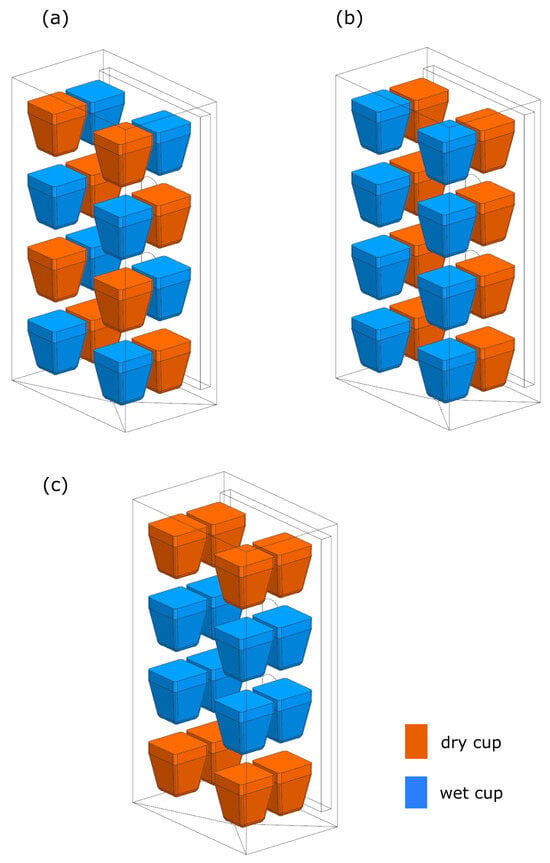
Figure 4.
Tested cup arrangements.
3.2. Velocity
Figure 5a compares the average domain velocities for the three tested configurations. The differences are negligible at all time instants. In each case, the velocity stabilizes after approximately 10 s of flow time at around 2.25 m/s, regardless of the layout. Owing to these minimal differences, and to focus on the most relevant results (in our opinion, the local RH distributions), we chose to present detailed velocity field diagrams only for the baseline case, in which the humidity sources and sinks associated with the testing vessels were disabled. This configuration accurately illustrates the flow pattern determined solely by the chamber geometry and boundary conditions, as the fields change only insignificantly when the sources and sinks on the sample surfaces are enabled.
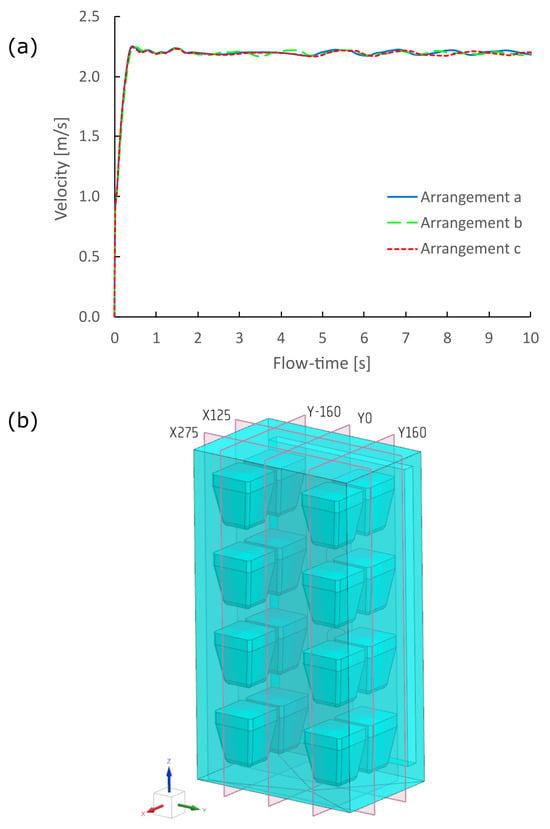
Figure 5.
Evolution of the average velocity within the domain (a), and the definition of characteristic cross-section planes for results display (b).
Figure 5b defines the characteristic planes used to present the detailed results of the velocity field, while Figure 6 shows the corresponding field distributions. The planes X125, X275, Y160, and Y–160 were selected so that they intersect at representative central points above the sample–cup assemblies, enabling a clear comparison of local flow and RH conditions. The plane Y0 passes vertically through the center of the chamber. The results in Figure 6 indicate that assemblies placed on the middle shelves satisfy the velocity criterion of exceeding 2 m/s, with air speeds above the specimen reaching 4–5 m/s. On the upper shelf, the front-row assemblies reach approximately 3–4 m/s, while the back row remains relatively stagnant, with velocities above 1 m/s only over limited surface areas. Air circulation over the bottom-shelf assemblies is weakest—mostly below 1 m/s, particularly in the back row.
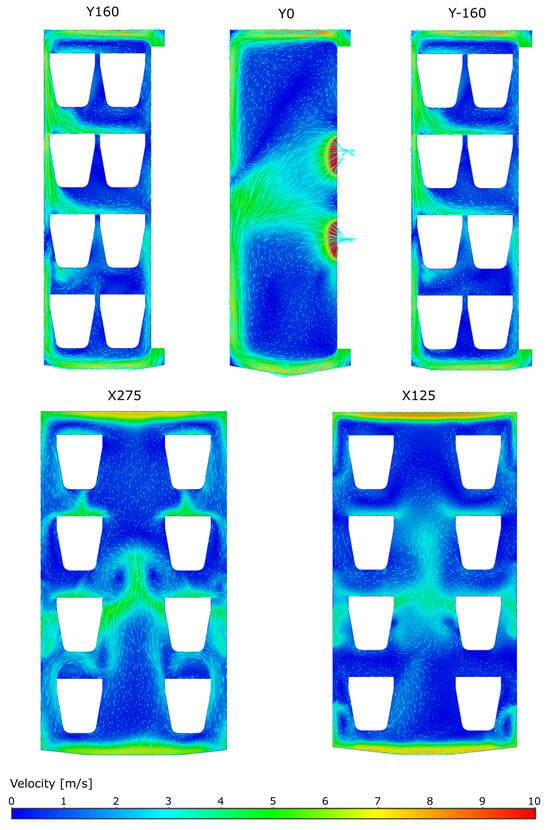
Figure 6.
Velocity fields at the characteristic planes.
Although the geometry of the sample compartment, together with the positions of the inlets, outlets, and obstacles formed by the assemblies, exhibits a degree of symmetry with respect to the central horizontal plane, the gravitational force acts downward, which explains the occurrence of the most stagnant conditions in the lower region of the chamber—particularly above the lowermost layer of sample–vessel assemblies.
A detailed examination of the velocity fields reveals that measurements taken above the samples are highly sensitive to the precise placement of the anemometer due to strong local velocity gradients. For instance, nearly stagnant conditions may occur immediately adjacent to the sample surface, while just a few centimeters higher, the flow already exceeds the 2 m/s threshold. The standard [3] does not specify the distance above the sample at which the anemometer probe should be positioned; it only requires that the indicated velocity be at least 2 m/s. This leaves considerable room for inconsistency. Our analysis suggests that this measurement distance should be standardized to ensure reproducibility and comparability of results. It also highlights the value of CFD simulations as a complementary tool for verifying experimental measurements.
3.3. Relative Humidity
The RH distributions for all test vessel arrangements defined in Figure 4 are presented in Figure 7, Figure 8 and Figure 9 using characteristic planes indicated in Figure 5b (excluding plane Y0, which does not intersect any assembly and hence is nonessential for the RH analysis). The results show that placing wet cups on either the top or bottom shelf produces localized regions of elevated RH above the samples (Figure 7 and Figure 8). As shown in Figure 6, both the lower and upper shelves were characterized by large stagnant zones, resulting in poor evacuation of water vapor emitted from the surfaces of the wet sample–vessel assemblies. The CFD simulations allowed these effects to be quantified, revealing that local RH values above such assemblies can reach up to 90%, substantially exceeding the ISO tolerance of 5%.
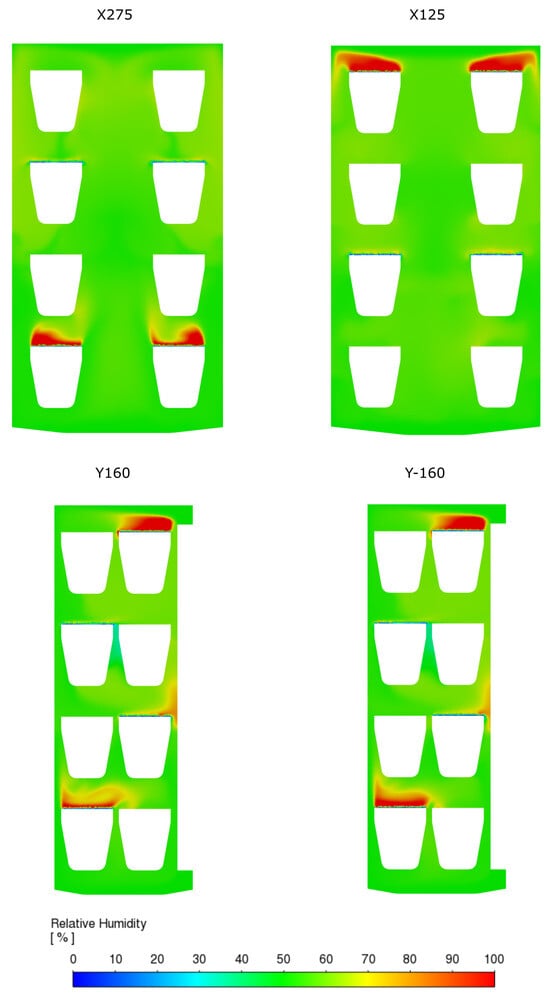
Figure 7.
Simulated RH fields for arrangement a.
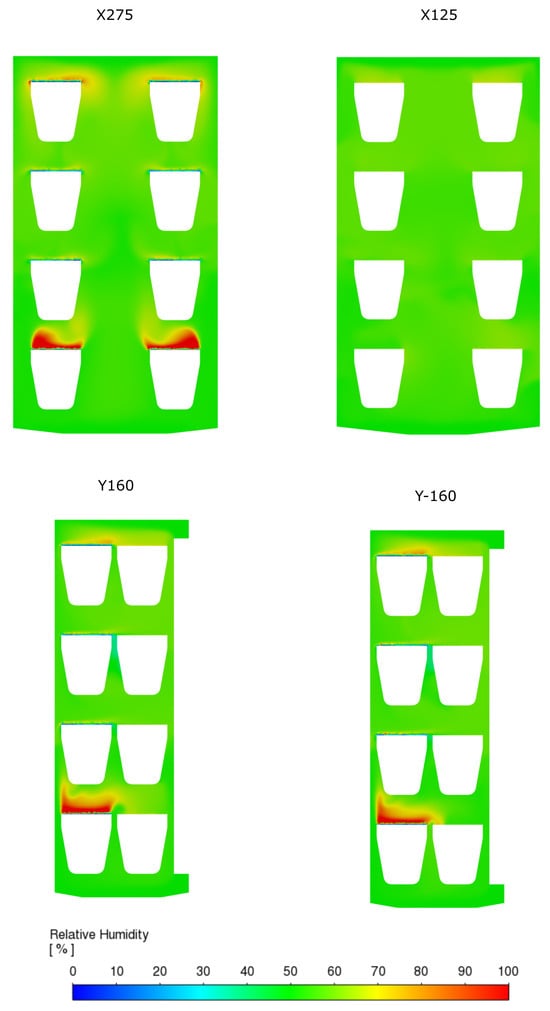
Figure 8.
Simulated RH fields for arrangement b.
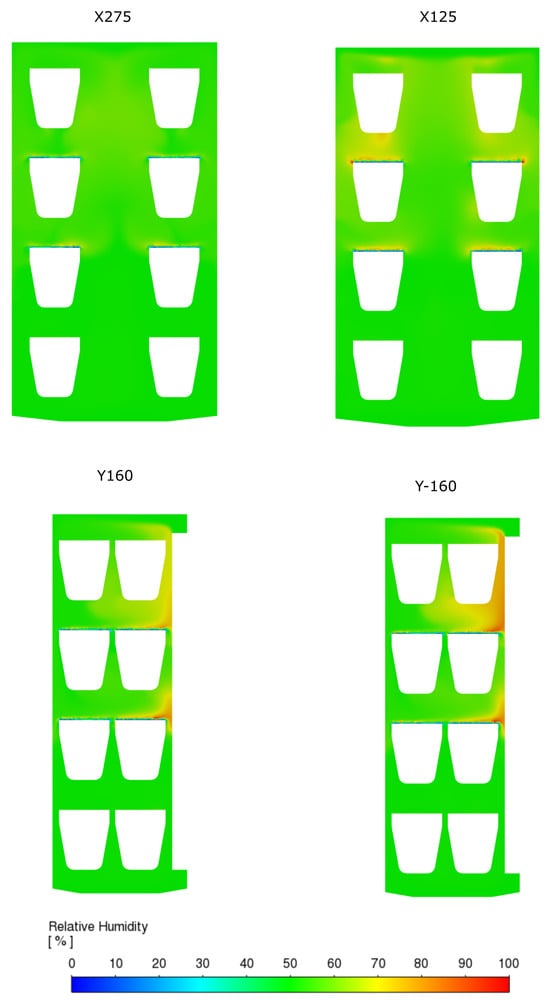
Figure 9.
Simulated RH fields for arrangement c.
Interestingly, the humidity sinks formed by dry sample/vessel assemblies did not cause significant RH deviations from the target value of 50%, even when located in low-velocity regions. The greater RH-disturbing effect of wet cups compared to dry ones can be attributed to differences in water vapor fluxes. The flux emitted by wet assemblies is approximately 1.7 times higher than that absorbed by dry assemblies (see Equation (7)).
These observations led us to arrangement c, in which the moisture-emitting vessels were placed on the two middle shelves (characterized by the best air exchange), while the top and bottom shelves were reserved for the moisture-absorbing vessels. In this configuration, zones of elevated RH were substantially smaller, with lower average deviations. Although localized areas above the moist samples still reached 70–80% RH, their spatial extent was clearly reduced compared to cases a and b. As before, the dry samples located in low-velocity zones did not present significant issues, owing to the lower moisture flux at their surfaces.
Figure 10, showing the evolution of average RH in the domain, serves as a concise summary of these findings. The average RH for arrangement c (54.5%) falls within the ISO tolerance, whereas arrangements a and b exceed it, with respective values of 57.3% and 56.4%.
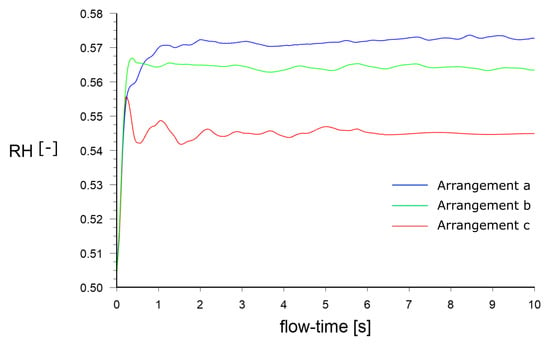
Figure 10.
Change in avergage RH within the domain for tested cup arrangements.
3.4. Discussion
The observed influence of sample arrangement can be interpreted through the interaction between chamber geometry, airflow distribution, and moisture transport. In all configurations, the placement of vessels alters the available cross-section for air passage, thereby shaping local velocity fields and the efficiency of humidity evacuation. Regions directly exposed to the main air stream experience higher flow velocities along the upper surfaces of the samples, which promotes effective removal of moisture from wet-cup specimens and faster drying of adjacent dry-cup samples. Conversely, areas that are shielded by neighboring vessels or located away from the principal circulation paths tend to form recirculation zones or near-stagnant pockets, where moisture accumulates and relative humidity rises above the average chamber value. These patterns are highly dependent on the geometric proportions of the chamber and on the positioning and strength of the air inlet, outlet, and fan. Consequently, both the layout of the test vessels and the internal flow design jointly determine how well the chamber maintains uniform hygric conditions, highlighting the need to consider geometry-induced air-exchange limitations when comparing results between laboratories or chamber designs.
It should be emphasized that undetected local RH elevations above the sample–vessel assemblies can lead to significant systematic errors in the determination of WVP. The standard [3] assumes that the relative humidity above the sample surface is equal to the nominal setpoint value (typically 50%), which is then used directly in the WVP calculation. In reality, as demonstrated by our simulations, local deviations can be substantial. For instance, using the results reported in [12], it can be shown that for wet cups, a 4% error in the supplied RH value translates to an average error of approximately 6.5% in the calculated WVP of hemp concrete. Specifically, when the actual RH above the sample is 4% higher than the assumed chamber value, the resulting WVP is on average underestimated by about 6.5%. The same study shows that the calculated WVP decreases by about 60% when the supplied RH difference between the dry cup interior and its exterior is increased by 25%. These estimations fully justify the importance of verifying local humidity conditions during testing and, where possible, applying CFD-supported optimizations to minimize systematic bias.
3.5. Limitations and Recommendations
Although the model was verified through grid and time-step independence studies, a full experimental validation was not performed. Nevertheless, several observations support the physical reliability of the obtained results. The simulated mean velocity (approximately 2.25 m/s) agrees with values measured during our previous water vapor permeability tests [2], while the poor evacuation of humidity in the bottom region of the chamber—confirmed both by local RH checks and the present simulations—further substantiates the model’s credibility. The realizable k– turbulence model with Standard Wall Treatment was employed, which, although known to smooth fine-scale turbulence and near-wall effects, has been successfully applied in similar chamber studies [14]. The energy equation was disabled, as the chamber was well insulated and temperature gradients between cup interiors and chamber space were negligible, ensuring near-isothermal conditions. Overall, we believe that the simulations accurately signal an overlooked aspect of building material testing. Future work should include targeted experimental validation of local velocity and humidity fields to further consolidate these findings.
Although the present simulations were carried out for a specific environmental chamber geometry and for hemp concrete specimens tested using the ISO cup method, the observed phenomena are expected to be broadly relevant to other hygroscopic materials and testing protocols conducted in high-load chambers. The insights gained here extend beyond hemp concrete testing. Any test configuration involving a mixture of wet and dry samples in a confined, mechanically ventilated space is susceptible to similar deviations from target conditions. In such cases, a deliberate placement strategy—favoring positioning of high-emission sources in regions of good air exchange—can help maintain compliance with standard tolerances and minimize measurement bias. Therefore, the methodology outlined in this work can be readily adapted as a diagnostic tool for optimizing environmental chamber layouts in diverse material testing applications.
Bearing in mind all limitations listed above, the following further limitations should be noted:
- Geometric simplification. The modeled geometry did not include the wire shelves supporting the test assemblies. Their presence would likely alter the results by introducing additional flow turbulence.
- Assembly shape. The analyzed case involved relatively tall sample/cup assemblies which may be seen as non-representative; however, example designs in the ISO standard [3] also exhibit comparable height-to-width ratios, and the modeled geometry reflects real designs used by the authors [2].
- Control system assumptions. The simulation assumed a fixed behavior of the humidification system, i.e., the air inlets continuously supplied air at 50% RH. Combined with moisture emissions from the cups exceeding absorption, this resulted in an average RH higher than the 50% target. In reality, a control system would periodically switch off the humidifier or employ the Peltier cooler to condensate water in order to maintain a 50% reading at the sensor location. Although such control logic could be implemented in ANSYS Fluent in a dynamic simulation, we deliberately chose a simpler problem setup to ensure a robust and easily reproducible methodology. This simplification adequately illustrates when excessive humidity is properly evacuated from wet cups, while avoiding the complexities of simulating dynamic control effects.
- Sample configuration. The ISO standard [3] specifies only the required total exposed surface area, allowing fewer samples if each has a larger surface. Such designs, however, may lead to horizontal rather than vertical flow obstructions. In any case, CFD analysis of the type presented here can support the optimal configuration of samples, balancing chamber throughput with methodological rigor.
Future studies should explore a wider range of chamber designs and geometries, as well as the influence of measurement assembly size and shape. This study demonstrated that the sample layout can be manually adjusted to significantly improve the uniformity of RH conditions within the chamber. Nevertheless, it should be noted that modern computational tools offer dedicated optimization modules that could be employed to obtain even more refined configurations. Apart from the numerical modeling, we recommend to use additional humidity sensors within environmental chambers for improved accuracy of sustainable materials testing.
4. Conclusions
- Local deviations from target humidity conditions in highly loaded environmental chambers present a real risk, potentially causing systematic errors in water vapor permeability measurements.
- Reliable determination of water vapor permeability (WVP) is crucial for accurately predicting moisture accumulation, mold development, and the long-term degradation of breathable bio-based walls and insulation systems. Since the durability and hygrothermal performance of such materials depend strongly on their ability to regulate vapor transport, even small measurement inconsistencies can lead to substantial errors in modeling and design.
- Even under high chamber load, a configuration ensuring good homogenization of the RH field was identified using the diagnostic methodology proposed.
- The degree of RH deviation above a sample from the target value is related to the absolute magnitude of the sample’s humidity source or sink.
- Velocity fields in the crowded chamber exhibited steep gradients; therefore, velocity measurement distance from the sample surface should be codified for reproducibility.
- For robust results, researchers should consider installing additional humidity sensors above the exposed surfaces instead of relying on the indications of the device sensor.
Author Contributions
K.P.: writing—original draft, writing—review and editing, methodology, formal analysis, supervision; K.K.: investigation, software, methodology, formal analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be made available on request.
Acknowledgments
The authors thank Łukasz Cieślikiewicz for valuable explanations regarding the details of the environmental chamber operation and gratefully acknowledge Sustainability (MDPI) for providing a full waiver of the article processing charge (APC) for this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CFD | Computational Fluid Dynamics |
| EPS | Expanded Polystyrene Board |
| MBC | Mycelium-Based Composite |
| OSB | Oriented Strand Board |
| RANS | Reynolds-Averaged Navier Stokes |
| RH | Relative Humidity |
| WVP | Water Vapor Permeability |
References
- Sinka, M.; Van den Heede, P.; De Belie, N.; Bajare, D.; Sahmenko, G.; Korjakins, A. Comparative life cycle assessment of magnesium binders as an alternative for hemp concrete. Resour. Conserv. Recycl. 2018, 133, 288–299. [Google Scholar] [CrossRef]
- Pietrak, K.; Krakowiak, M.; Cieślikiewicz, Ł.; Brzyski, P.; Łapka, P. Magnesium–hemp concrete is less vapor-permeable than lime–hemp concrete while the cup method is still problematic. Build. Environ. 2025, 280, 113112. [Google Scholar] [CrossRef]
- ISO 12572:2016; Hygrothermal Performance of Building Materials and Products—Determination of Water Vapour Transmission Properties—Cup Method. International Organization for Standardization: Geneva, Switzerland, 2016.
- TESTEX Textile. Complete Guide to Environmental Test Chambers/Temperature–Humidity Chambers. Available online: https://www.testextextile.com/complete-guide-to-environmental-test-chambers-temperature-humidity-chambers/ (accessed on 4 April 2024).
- Palani, H.; Tang, M.; Zhang, R.; Desjarlais, A. Assessing the hygrothermal performance of bio-based materials in building wall systems. Constr. Build. Mater. 2025, 492, 142907. [Google Scholar] [CrossRef]
- Raja, P.; Murugan, V.; Ravichandran, S.; Behera, L.; Mensah, R.A.; Mani, S.; Kasi, A.; Balasubramanian, K.B.N.; Sas, G.; Vahabi, H.; et al. A review of sustainable bio-based insulation materials for energy-efficient buildings. Macromol. Mater. Eng. 2023, 308, 2300086. [Google Scholar] [CrossRef]
- Obuka, V.; Sinka, M.; Nikolajeva, V.; Kostjukova, S.; Ozola-Davidane, R.; Klavins, M. Microbiological stability of bio-based building materials. J. Ecol. Eng. 2021, 22, 296–313. [Google Scholar] [CrossRef]
- Motamedi, S.; Rousse, D.R.; Promis, G. A review of mycelium bio-composites as energy-efficient sustainable building materials. Energies 2025, 18, 4225. [Google Scholar] [CrossRef]
- Seng, B.; Magniont, C.; Lorente, S. Characterization of a precast hemp concrete block. Part II: Hygric properties. J. Build. Eng. 2019, 24, 100579. [Google Scholar] [CrossRef]
- Colinart, T.; Glouannec, P. On the importance of desiccant during the determination of water vapor permeability of permeable insulation material. E3S Web Conf. 2020, 172, 14003. [Google Scholar] [CrossRef]
- Colinart, T.; Glouannec, P. Accuracy of water vapor permeability of building materials reassessed by measuring cup’s inner relative humidity. Build. Environ. 2022, 217, 109038. [Google Scholar] [CrossRef]
- Pietrak, K.; Krakowiak, M.; Łapka, P. Experimental verification of conditions within the cups in the cup method of water vapor permeability measurement. J. Phys. Conf. Ser. 2023, 2423, 012009. [Google Scholar] [CrossRef]
- Colinart, T.; Magniont, C. RILEM TC 275-HDB: Results of round-robin testing for the vapor permeability of hemp concrete. Mater. Struct. 2025, 58, 117. [Google Scholar] [CrossRef]
- Ramezani, B.; Tadeu, A.; Jesus, T.; Brett, M.; Mendes, J. Evaluation of the thermofluidic performance of climatic chambers: Numerical and experimental studies. Fluids 2021, 6, 433. [Google Scholar] [CrossRef]
- Vololonirina, O.; Perrin, B. Inquiries into the measurement of vapour permeability of permeable materials. Constr. Build. Mater. 2016, 102, 338–348. [Google Scholar] [CrossRef]
- SOS Electronic. A2S130-AA03-01 Axial Fan. Available online: https://www.soselectronic.com/pl/products/ebm-papst/a2s130-aa03-01-155029 (accessed on 8 April 2025).
- DesignBuilder Software Ltd. Calculating Fan Pressure Rise. Available online: https://designbuilder.co.uk/helpv7.0/Content/CalculatingFanPressureRise.htm (accessed on 28 April 2024).
- ISO 13788:2003; Hygrothermal Performance of Building Components and Building Elements—Internal Surface Temperature to Avoid Critical Surface Humidity and Interstitial Condensation—Calculation Methods. International Organization for Standardization: Geneva, Switzerland, 2003.
- Pawłucki, M.; Kryś, M. CFD dla Inżynierów; Helion SA: Gliwice, Poland, 2020. [Google Scholar]
- Durbin, P.A.; Reif, B.A. Statistical Theory and Modeling for Turbulent Flow, 2nd ed.; John Wiley & Sons, Ltd.: London, UK, 2010. [Google Scholar]
- ANSYS, Inc. Workshop 03—Multi-Species Flow and Postprocessing. 2014. Available online: https://courses.ansys.com (accessed on 24 April 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).