Banana Yield Prediction Using Random Forest, Integrating Phenology Data, Soil Properties, Spectral Technology, and UAV Imagery in the Ecuadorian Littoral Region

Abstract

Accurate banana yield prediction is essential for optimizing agricultural management and ensuring food security in tropical regions, yet traditional estimation methods remain labor-intensive and error prone. This study developed a predictive model for banana yield in Buena Fé, Ecuador, using Random Forest integrated with phenological data, soil properties, spectral technology, and UAV imagery. Data were collected from a 75.2 ha banana farm divided into 26 lots, combining multispectral drone imagery, soil physicochemical analyses, and banana agronomic measurements (height, diameter, bunch weight). A rigorous variable selection process identified six key predictors: NDVI, plant height, plant diameter, soil nitrogen, porosity, and slope. Three machine learning algorithms were compared through 5-fold cross-validation with systematic hyperparameter optimization. Random Forest demonstrated superior performance, with R² = 0.956 and RMSE=1164.9 kg ha⁻¹, representing only CV = 2.79% of mean production. NDVI emerged as the most influential predictor (importance = 0.212), followed by slope (0.184) and plant structural variables. Local sensitivity analysis revealed distinct response patterns between low- and high-production scenarios, with plant diameter showing the greatest impact (+74.9 boxes ha⁻¹) under limiting conditions, while NDVI dominated (−140.4 boxes ha⁻¹) under optimal conditions. The model provides a robust tool for precision agriculture applications in tropical banana production systems.

1. Introduction

Bananas (Musa AAA) are one of the most important crops worldwide, both for their nutritional value and economic impact [1], and they are among the main globally exported commodities [2]. However, banana production faces significant challenges, such as climate variability, soil degradation, and the need to optimize resources to maintain sustainability and competitiveness of the sector [3]. In this context, accurate crop yield prediction becomes an essential tool for informed decision-making in agricultural management.

Traditionally, in some Latin American regions, yield estimation has been based on empirical methods and manual observations, which are laborious, costly, and prone to errors [4,5]. Nevertheless, the advancement of technologies such as remote sensing, Unmanned Aerial Vehicles (UAVs), and supervised machine learning has opened new possibilities to improve precision and efficiency in agricultural yield prediction [6,7]. These technologies allow for the capture and analysis of high spatial and temporal resolution data, integrating key variables such as crop phenology, soil physicochemical properties, and spectral reflectance, which are directly related to plant growth and development [8].

Banana phenology, which includes critical stages such as flowering and fruit filling, is a fundamental indicator for predicting yield [9]. On the other hand, soil physicochemical parameters, such as pH, organic matter, and nutrient availability, directly influence crop productivity [10]. Spectral technology, through multispectral and hyperspectral sensors, allows for the monitoring of plant health status and vigor through vegetation indices, such as the NDVI (Normalized Difference Vegetation Index), which are correlated with biomass and productive potential [8]. Additionally, UAVs offer a versatile platform for capturing high-resolution images, facilitating spatial and temporal analysis of large crop extensions.

The use of Random Forest techniques, multiple linear regression, and neural networks allows for the integration of these heterogeneous and complex variables to generate robust predictive models [11,12]. These models not only improve precision in yield estimation but also identify patterns and non-linear relationships between variables, resulting in a powerful tool for precision agriculture [13].

This study aims to develop a predictive model for banana yield in the central tropical region of Ecuador, using Random Forest (RF) and integrating data from productive phenology, soil physicochemical properties, and UAV-derived imagery. The expected outcomes are intended to support the optimization of crop management, enhance productivity, and promote sustainable agricultural practices in one of the world’s most important banana-producing regions. The hypothesis proposed is that models integrating spectral, agronomic, and edaphological variables can predict banana yield more accurately. This formulation provides a clear scientific framework linking data-driven modeling with precision agriculture applications.

2. Materials and Methods

2.1. Study Area

The work was conducted on a banana farm located in Buena Fe city (WGS84: lat −0.818409; long −79.479516), Los Ríos province, which is located in the central-north of Ecuador’s coastal region. Los Ríos province is Ecuador’s main banana yield province [14]. It has the following geophysical characteristics: altitude of 103 m.a.s.l., with a tropical rainy climate of 22.6 °C and 2257.85 mm of precipitation on average [15]. The study farm has an area of 75.2 ha (Figure 1) and is divided into 26 administrative plots that were further subdivided according to vegetation conditions, ensuring homogeneity for analysis. All data were collected during April 2024, corresponding to the final month of the agronomic cycle of the established Williams banana plantation, whose complete cycle spans approximately one year.

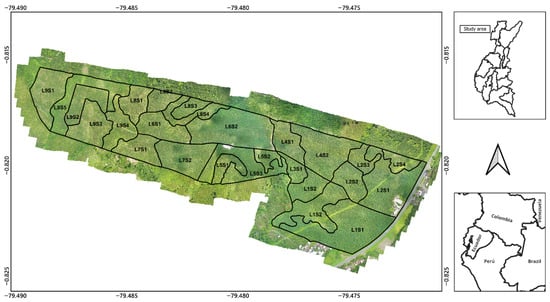
Figure 1. Orthophotomosaic of the study farm, with delimitation of banana yield plots (L1S1–L9S5). The insets show the geographic location of the site within Los Ríos province–Ecuador–South America.

2.2. Spectral Data and UAV Images

The acquisition of multispectral and RGB data was performed using a DJI Mavic 3M drone (DJI, Shenzhen, China) equipped with an integrated four-spectral-band system (Green: 560, Red: 650, Red Edge: 730, NIR: 860) and a wide-angle sensor with a 4/3 CMOS sensor with 20 megapixels. The drone was calibrated in 2024 using the DJI Fly V 1.19.0 software. The system operated at 80 m altitude, generating a spatial resolution of 6.4 cm/pixel for multispectral bands and 1.4 cm/pixel for RGB, following the relationship GSD = (height × pixel size)/focal distance [16]. Georeferencing employed a D-RTK 2 Mobile Station, achieving an absolute precision of ±10 cm (horizontal) and ±18 cm (vertical).

Operational parameters and quality control: flights were executed between 10:00 and 14:00 (local time) under 65% ± 5% cloud cover, wind of 1.1 m/s, and average irradiance of 750 ± 100 W/m². Double grid routes were implemented with 80% frontal and lateral overlap, guaranteeing metric, angular precision, and spectral quality; drone speed was constant at 5 m/s. These parameters are optimized for homogeneous coverage in banana crops [17]. The Mavic 3M has a solar light spectral sensor that compensated incident irradiance in real time, but radiometric calibration was also performed following ASTM E2590-22 protocols using a Micasense panel with 50% reflectance certified by NIST [18], with pre/post-flight readings at a perpendicular angle ±5° with respect to solar incidence [19].

Multispectral and visible image processing was performed using Pix4D Mapper software [20]. Images captured by the drone (both multispectral and RGB) were imported to the software along with metadata files and GNSS/RTK records to ensure centimetric georeferencing. The WGS 84/UTM zone 17S geodetic reference system was configured, corresponding to the study area.

For initial calibration and image alignment, advanced feature detection and matching algorithms were employed, identifying homologous points between images to estimate relative positions and internal camera parameters (autocalibration). Maximum resolution and precision processing parameters were chosen to optimize the results. In the second stage, a dense point cloud was generated through stereo correlation, from which both the Digital Surface Model (DSM/DTM) and image orthorectification were derived. For this phase, the highest density and quality parameters were selected due to the importance of three-dimensional models and geometric correction in orthomosaics [21]. Subsequently, corrected images were merged for orthomosaic creation. For multispectral images, manual radiometric calibration was performed using reference panels and irradiance metadata collected in the field, thus guaranteeing radiometric homogeneity of the products. As a result, radiometrically homogeneous RGB and multispectral orthomosaics were obtained and exported in TIF format.

Using the multispectral orthomosaic, NDVI (1) [22] was generated, performed in QGIS software using the raster calculator [23]. To determine the exact NDVI value within each plot, the OTSU model (2) [24] was used. OTSU is an automatic thresholding method that maximizes interclass variance to separate pixels [25]. This allowed for the fractionation of the image and generation of banana and soil masks, which guaranteed effective NDVI values of bananas in each plot. Finally, the Digital Terrain Model (DTM) was used to determine the degree of slope.

$$NDVI=(\rho \_NIR-\rho \_Red)/ (\rho \_NIR+\rho \_Red)$$

(1)

where $\rho \_NIR$ represents vegetation reflectance in the near infrared (860 nm) and $\rho \_Red$ represents the reflectance of red (650 nm).

$${\sigma }_b^2\left(t\right)={\omega }^0\left(t\right)· {\omega }^1\left(t\right)· {\left[ {\mu }^0\left(t\right)-{\mu }^1\left(t\right)\right]}^2$$

(2)

where $t$ is the optimal threshold value of intensity levels; ${\omega }^0\left(t\right)$ represents the cumulative probability of the background class; ${\omega }^1\left(t\right)$ is the cumulative probability of the object class; ${\mu }^0\left(t\right)$ calculates the mean intensity of the background; and, ${\mu }^1\left(t\right)$ determines the mean intensity of the object.

2.3. Soil Data

Physical and chemical soil properties were evaluated in 26 composite samples, one for each plot of the banana plantation (Figure 1), from subsamples taken in zigzag at a depth of 0–20 cm. Current soil moisture ($\sigma$) was determined using the gravimetric method: drying samples in an oven at 105 °C to constant weight (3), where “$m\_w$” is the weight of the wet sample and “$m\_d$” is the weight after drying. Bulk density (g/cm³) was obtained using a cylinder of known volume to extract an undisturbed sample, which was dried at 105 °C, and calculated as the relationship between dry weight and cylinder volume. From this value, total porosity ($\theta$) (4) was estimated, where “Pb” is bulk density and “Ps” is the real soil density (2.65 g/cm³). Finally, total nitrogen (mg/kg) was determined using the Kjeldahl method, which involves digestion with sulfuric acid, distillation, and titration, according to procedures described by Pansu and Gautheyrou (2006) [26].

$$\sigma (\%)= (m\_w-m\_d)/m\_d \times 100$$

(3)

$$\theta (\%)=(1-Pb/Ps)\times 100$$

(4)

2.4. Agronomic Data

In each plot, 10 banana plants (Musa AAA) of the Williams variety from the Cavendish subgroup originating in Southeast Asia were selected through simple random sampling, ensuring representativeness of productive conditions. To avoid spatial dependence of measurements, plants were located at a minimum distance of nine meters from each other, following methodological recommendations applied in banana agronomic studies and perennial crops [27,28]. This separation reduces the effect of spatial autocorrelation, ensuring that observations capture natural variability within the plot and do not depend solely on specific microenvironmental conditions.

Each selected plant was identified with a unique code and marked in the field to facilitate data collection of phenological variables (height, diameter) in addition to yield data derived from the bunch at harvest time. The choice of 10 plants per plot follows protocols used in banana yield and phenology research, where sampling between 8 and 12 plants per experimental unit is sufficient to capture agronomic variability without compromising the statistical precision of the analyses [29,30]. The agronomic data collection was carried out during April, coinciding with the end of the winter season in Ecuador’s coastal region. At this time, the evaluated plants were between 12 and 14 weeks post-flowering, corresponding to the fruit-filling stage [31], just prior to harvest. This stage was selected due to its strong correlation with final yield, as reported in previous studies on banana crops under tropical conditions.

Plant height was measured from the base of the pseudostem to the base of the peduncle, where the emerged bell is born, using a laser rangefinder, recording observations of inclination or damage; diameter was determined at 1.0 m above ground with a caliper, avoiding loose sheaths and excessive pressure [32]; and finally, plant weight was obtained by taking cut subsamples and weighing them on a platform scale [27].

Bunch weight was defined as the total fresh weight of the harvested bunch, excluding the long peduncle. For its determination, each bunch was suspended on a platform scale, recording the total weight in kg [33]; additionally, the specific weight of hands destined for export is obtained. The number of hands was obtained by direct counting at harvest time, considering only commercial hands of the bunch and excluding the “false hand” according to the farm’s yields and market standards [34]. The ratio was calculated from the relationship between bunch weight and number of hands to determine the number of boxes that the bunch can fill [35]. Yield was estimated from the average weight of bunches per plant, expressed in kilograms, and scaled per hectare and the proportion of plants effectively harvested (5) [36]. Alternatively, when an area sampled with total harvest was available, yield was calculated by dividing the sum of bunch weights by the area in hectares:

$$Yield\hspace{0.17em}\left(kg {ha}^{-1}\right)={\displaystyle \frac{{\sum }_{i}BunchWeigh{t}_i}{A\hspace{0.17em}\left(ha\right)}}$$

(5)

2.5. Model Development

To develop the predictive model, six moments were considered.

2.5.1. Data Preprocessing

In this step, categorical variable conversion (slope) and normalization of numerical variables proceeded: NDVI, plant height (m), plant diameter (cm), moisture (%), porosity (%), density (g/cm³), nitrogen (mg/kg), plant weight (lb), bunch weight (lb), number of hands, ratio, and yield (kg ha⁻¹), using the MinMaxScaler technique [37], which is a normalization method that adjusts each numerical variable so that its values are within a range between 0 and 1 [38]. This allows large-scale models to acquire knowledge more effectively, maintaining data essence without assuming a normal distribution [39].

2.5.2. Predictor Variable Selection

Selection was carried out in two complementary stages. First, pairwise correlations between all candidate variables were evaluated; redundant predictors above the widely used threshold of r > 0.8 were removed [40], retaining those of greater agronomic relevance. On the resulting subset, the Variance Inflation Factor (VIF) was computed [3]; variables with a VIF > 5, considered indicative of problematic multicollinearity [41], were excluded to avoid coefficient instability and inflated standard errors. This two-step procedure delivered a parsimonious set of predictors with high agronomic significance and minimal statistical redundancy.

2.5.3. Modeling

For the predictive model, three algorithms were employed: Ridge Regression (RR), Random Forest (RF), and Gradient Boosting (GB), with the objective of estimating banana yield. For each algorithm, a systematic hyperparameter search was performed through 5-fold cross-validation (GridSearchCV) [42], directly optimizing the RMSE (Root Mean Squared Error) metric through the negative scoring function (neg_root_mean_squared_error) [43,44] to guarantee selection of configurations with a lower prediction error. For model fitting, a systematic hyperparameter search with 5-fold cross-validation was employed, directly optimizing RMSE for each algorithm. In the case of RR [11], the degree of regularization was calibrated to balance bias and variance; in RF, combinations that control ensemble complexity were explored, including number of trees, maximum depth of each tree, and minimum criterion for node division [45]; and in GB, both the number of estimators and learning rate and depth of individual trees were adjusted, seeking to capture non-linear relationships without overfitting [43]. The best model of each family was selected based on its average performance in cross-validation and then evaluated on an independent test set through R² and RMSE to compare their predictive capacity and generalization.

2.5.4. Hyperparameter Tuning for Random Forest Model

By selecting RF as the optimal and robust model, training was performed through 5-fold cross-validation (as explained previously) of similar size in each interaction; four blocks are used to train the model, and one remaining block is used to assess its performance (80–20). This technique allows for the measurement of each model’s generalization capacity against unseen data and avoidance of overfitting risk [46]. Key hyperparameters were n_estimators [12], max_depth [47], and min_samples_split [48]. Ranges were selected according to best practices in agricultural modeling: moderate trees (100–300) for precision–efficiency balance [49], restricted depth (3–7) to control complexity [50], and minimum division (2–4 samples) to prevent overfitting [51]. This approach follows established protocols in crop yield prediction [46,52].

2.5.5. Python Code Implementation to Deploy the Model

The entire analysis flow, from initial data processing to final predictive model implementation, was developed in Python 3.13 [53] using a set of specialized scientific libraries. In the preprocessing stage, “pandas” [54] was used for table management and transformation, “numpy” [54,55] was used for numerical operations, and “scikit-learn” [13,56] was used for missing value imputation with “MinMaxScaler” for Min–Max normalization. Variable selection relied on pandas for paired correlation calculation and “statsmodels” to obtain the Variance Inflation Factor (VIF). In the modeling and fitting phase, “scikit-learn” estimators were used: “Ridge”, “RandomForestRegressor”, and “GradientBoostingRegressor”; a systematic hyperparameter search was performed with “GridSearchCV” under a cross-validation scheme. For evaluation, “r²_score” and “mean_squared_error” functions were employed to obtain the RMSE. Finally, visualization and result diagnosis used “matplotlib” for plotting relationships, residuals, and variable importances.

2.5.6. Evaluation in Probable Scenarios

To evaluate the practical utility of the developed RF predictive model, two contrasting base scenarios were generated, one of low yield and another of high yield, defined through specific values of selected predictor variables (NDVI, plant height, diameter, soil nitrogen, porosity, and slope). These scenarios were created with the purpose of representing typical conditions observed in the field, providing clear reference points for interpreting model predictions. Subsequently, a local sensitivity analysis was performed for each scenario, evaluating how estimated yield varied with individual changes of ±10% in each of the continuous variables. This technique allowed for the identification of which predictors have a greater influence on estimated yield and determination of the degree of stability or local sensitivity of the model to realistic variations in input values. Finally, obtained predictions were converted from kg ha⁻¹ to operational units (boxes per hectare), considering the export box weight of 18.14 kg. This conversion allows for the interpretation of results from a more practical perspective oriented to decision-making in crop management and logistics (Figure 2).

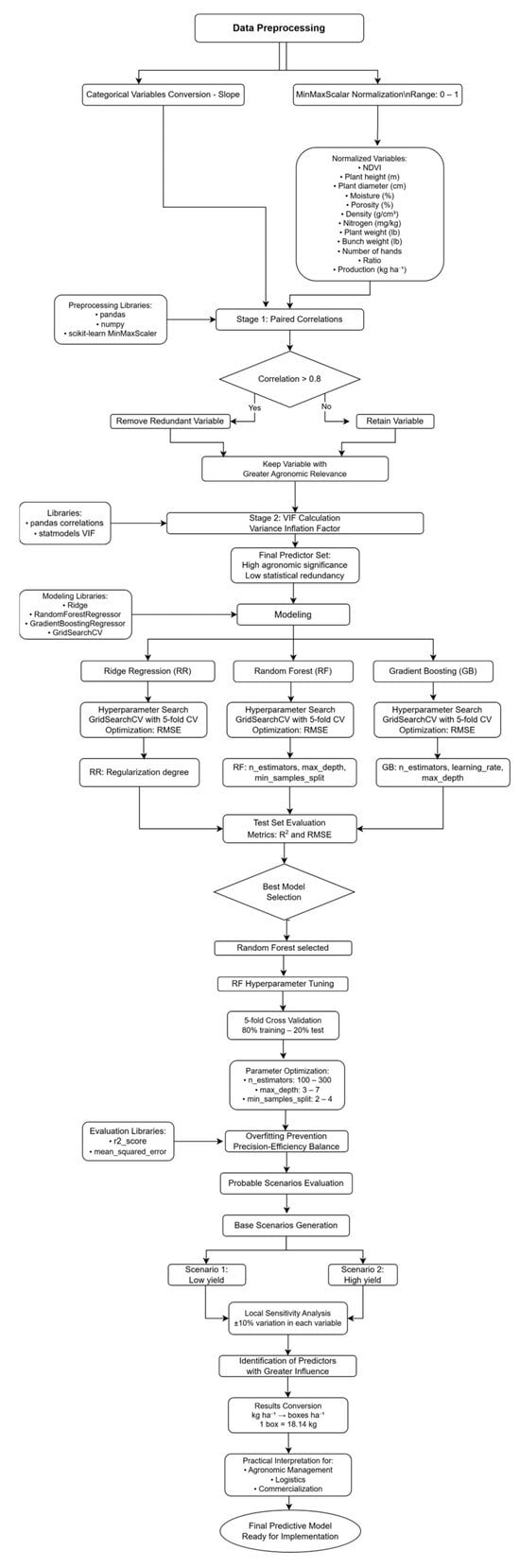
Figure 2. Algorithm for predictive modeling using machine learning. The process includes (1) data preprocessing; (2) variable selection through correlation analysis and VIP projection; (3) training and optimization of multiple algorithms (RR, RF, GB); (4) selection of the best model (Random Forest); and (5) sensitivity analysis and applicability in agronomic scenarios for practical management.

3. Results

From field-collected data and subsequent processing, experimental datasets were formed that allowed for the analysis of the main spectral, soil, agronomic, and yield variables (Figure 3).

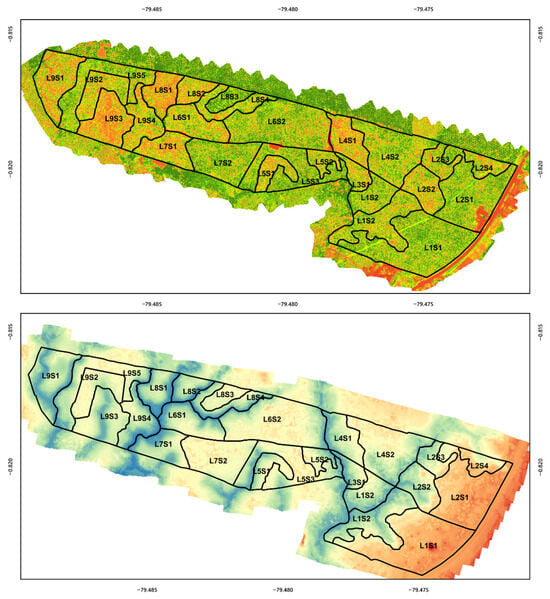
Figure 3. (top) The NDVI map (Normalized Difference Vegetation Index), obtained from multispectral images, which allows for the identification of the variability in plant vegetative vigor. (bottom) The Digital Terrain Model (DTM), which represents the topographic variation of the farm.

3.1. Results of Variables

As a first result, a parsimonious subset of primary predictors with strong agronomic relevance and low statistical redundancy was identified and selected (Table 1). NDVI emerged as the main predictor due to its high correlation with yield (r = 0.92) and low VIF (1.88), followed by plant height (r = 0.85, VIF = 2.35) as an early indicator of vegetative vigor. Plant diameter, although initially presenting multicollinearity (high VIF), was conserved after correcting this redundancy (adjusted VIF = 1.2) due to its recognized agronomic importance. Among the soil variables, nitrogen content (r = 0.82, VIF = 3.21) and soil porosity (r = 0.78, adjusted VIF = 1.8) were maintained as key predictors, and finally, slope category transformed to ordinal was included for its influence on drainage and stability (VIF = 1.05). Redundant or problematic variables were excluded to avoid information leakage and overfitting: plant weight due to strong multicollinearity with plant diameter (r = 0.97), moisture and density due to redundancy with porosity, and variables directly related to the predictor variable (bunch weight, number of hands). This process guaranteed a balanced input set for modeling, with informative predictors and minimization of distorting effects due to multicollinearity.

Table 1. Evaluation of predictor variables for banana yield model.

Variable	Type	Included	VIF	Main Decision/Reason
NDVI	Spectral	yes	1.88	Principal predictor; high correlation with yield
Plant height (m)	Agronomic	yes	2.35	Early indicator of vegetative vigor
Diameter (cm)	Agronomic	yes	28.76	Conserved for agronomic relevance (corrected VIF: 1.2)
Nitrogen (mg/kg)	Soil	yes	3.21	Key nutrient for crop development
Porosity (%)	Soil	yes	6.99	Conserved as physical soil indicator (corrected VIF: 1.8)
Slope	Topographic	yes	1.05	Transformed to ordinal; affects drainage and stability
Plant weight (pounds)	Agronomic	no	31.25	Excluded due to multicollinearity with diameter (r = 0.97)
Moisture (%)	Soil	no	7.12	Excluded due to multicollinearity with porosity (r = 0.83)
Density (g/cm3)	Soil	no	15.43	Excluded due to redundancy with porosity (r = −0.92)
Bunch weight (pounds)	yield	no	-	Excluded due to data leakage (yield component)
Number of hands	yield	no	22.47	Excluded for being component of label variable
Ratio	Calculated	no	18.92	Excluded due to ambiguous definition and multicollinearity

3.2. Modeling Results

In the comparison of the three models Ridge Regression, Random Forest, and Gradient Boosting (Table 2), hyperparameters were tuned through cross-validation to minimize prediction error. RF showed the best performance, with R² = 0.956 and RMSE of 1164.9 kg ha⁻¹, suggesting slight superiority in stability and capacity to capture complex relationships under noise. GB presented close performance (R² = 0.953, RMSE = 1190.2 kg ha⁻¹), while Ridge Regression, although not modeling non-linearities with the same flexibility, offered comparable results (R² = 0.950, RMSE = 1223 kg ha⁻¹) and served as a reference for its regularized linear form. Although differences between the models were small, these results support RF selection when robustness and stability are prioritized, maintaining other approaches as comparison points or as potential components in ensembles to improve generalization.

Table 2. Trained model evaluation table.

Model	Best Hyperparameters	R2	RMSE (kg ha−1)
Ridge Regression	α = 0.1	0.950	1223.4
Random Forest	max_depth = 7, min_samples_split = 2, n_estimators = 150	0.956	1164.9
Gradient Boosting	learning_rate = 0.1, max_depth = 3, n_estimators = 150	0.953	1190.2

The best estimator by grid search was an RF with the following hyperparameters: 150 trees (n_estimators = 150), maximum depth of 7 (max_depth = 7), minimum node division with at least 2 samples (min_samples_split = 2), and leaves that can contain a single observation (min_samples_leaf = 1). Bootstrap sampling was enabled (Bootstrap = True), and at each division, all available variables were considered (max_features = 1.0). The division criterion used was squared error (criterion = ‘squared_error’), and internal out-of-bag evaluation was not employed (oob_score = False). Random seed was fixed at 42 (random_state = 42) to guarantee reproducibility. The rest of the parameters were maintained at their default values: no post hoc pruning was applied, the number of leaf nodes was not restricted, and a minimum improvement in impurity was not used for division.

The optimized RF model achieved exceptional predictive performance on the independent test set, with a coefficient of determination R² = 0.956, indicating the model’s capacity to explain 95% of the observed variability in banana yield. The absolute error, quantified through Root Mean Squared Error (RMSE), was 1164.91 kg ha⁻¹, a value representing only 2.79% of the mean yield observed in the test data (41,747.05 kg ha⁻¹), evidencing high relative precision according to international agronomic standards (CV < 5%). Residual analysis confirmed model robustness, showing insignificant bias (residual mean = 29.80 kg ha⁻¹, equivalent to 0.07% of mean yield) and homoscedasticity in error distribution (residual standard deviation = 1164.53 kg ha⁻¹), validating the absence of systematic error patterns in the predictions.

Figure 4 represents the variable importances of the RF model according to the mean decrease in impurity method. The values next to each bar are normalized importance scores; a longer bar indicates that the variable contributes more to prediction error reduction. NDVI is the most influential predictor (0.212), followed by slope (0.184), plant height (0.177), and plant diameter (0.167). The soil variables nitrogen (0.137) and porosity (0.123) have a smaller but still relevant contribution.

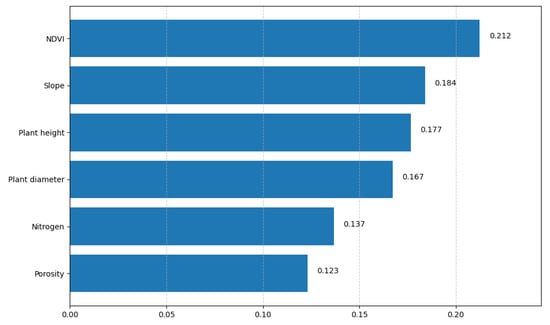
Figure 4. The figure shows variable importances according to the RF model trained for banana yield prediction; the X axis represents variable importance, and the Y axis represents variables.

Regarding residuals versus model predictions (Figure 5), the horizontal axis corresponds to estimated yield (kg ha⁻¹), and the vertical axis corresponds to residual $y\_obs-y\_pred$; each point represents an observation from the test set (plots) and is labeled with its case identifier, allowing individual tracking of plots with peculiar errors. Positive residuals (above the dashed line at zero) indicate model underestimations (actual yield was greater than predicted), while negative residuals reflect overestimations.

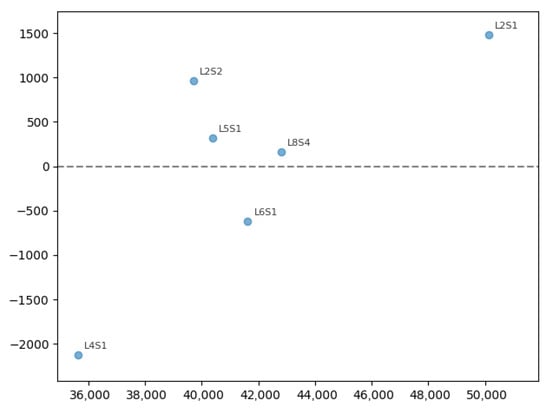
Figure 5. Residuals vs. predictions from the model. Each point is labeled with its plot case; the dashed line indicates zero residual, the X axis represents yield kg ha⁻¹, and the Y axis represents residuals. Positive residuals represent underestimations, and negative ones represent overestimations.

Plot L4S1 presents a negative residual of −2200 kg ha⁻¹, that is, the model overestimated the yield for that sample, while plot L2S1 shows a positive residual (+1500 kg ha⁻¹), corresponding to an underestimation. Other cases, like L2S2, L5S1, and L8S4, exhibit moderate and slight deviations, and L6S1 exhibits a punctual overestimation. General dispersion does not suggest a clear systematic pattern of heteroscedasticity, although there is variability in error magnitude along the prediction range. The overall MAE of 944.52 kg ha⁻¹ indicates that, on average, the predictions deviate by approximately 2.3% from the observed values (relative to a mean production of 41,747 kg ha⁻¹). Identification of these individual cases allows the subsequent analysis to investigate whether they respond to atypical agronomic conditions, measurement errors, or model limitations in certain subgroups.

The relationship between observed and predicted yield by the RF model on the test set is presented. The inset reports the fit metrics, which are a high coefficient of determination (R² = 0.95) and an RMSE of 1164.9 kg ha⁻¹; the identity line (red dashed) represents the perfect prediction situation; while the best fit line (blue) was obtained by regression between observed and predicted values. Its estimated slope is 0.81, with a 95% confidence interval (0.65–0.98), and the intercept is 7709, with a confidence interval (880–14,538) kg ha⁻¹. The shaded band around the fit line indicates the 95% confidence interval, reflecting uncertainty in the estimated trend. Additionally, it indicates that 92% of points are within ±2124 kg ha⁻¹ of the prediction, giving an idea of individual error dispersion with respect to the fitted line (Figure 6). Data points cluster reasonably close to the diagonal, with some evident deviations at the extremes of the yield range.

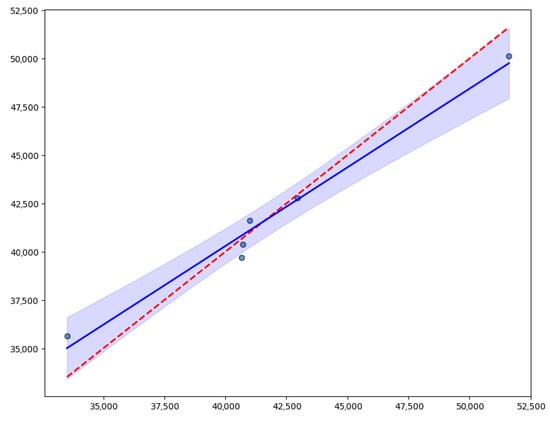
Figure 6. Relationship between observed and predicted yield by the Random Forest model. The X axis shows measured yield (kg ha⁻¹), the Y axis shows the estimated yield, the dashed line is identity (perfect prediction), and the solid line is the best fit line.

3.3. Sensitivity Analysis

Two representative scenarios were generated to evaluate the estimated banana crop yield through the Random Forest model: one of low yield (NDVI = 0.65, height = 2.5 m, diameter = 16.0 cm, nitrogen = 30 mg/kg, porosity = 33%, slope category = 3) and another of high yield (NDVI = 0.85, height = 3.0 m, diameter = 18.0 cm, nitrogen = 45 mg/kg, porosity = 40%, slope category = 1). To this scenario, the yield value of boxes ha^-1 is added, which is achieved by dividing the estimated yield by the export weight of the banana box, which is 18.14 kg. The low-yield scenario prediction was 35,942.7 kg ha⁻¹, equivalent to 1981.4 boxes ha-1, while the high-yield scenario reached an estimate of 45,791.7 kg ha⁻¹, equivalent to 2524.4 boxes ha^-1 (Table 3).

Table 3. Scenarios represent typical conditions of low and high banana crop yield; evaluation of model predictive performance.

Yield	NDVI	Height (m)	Diameter (cm)	Nitrogen (%)	Porosity (%)	Slope	Yield (kg ha−1)	Boxes ha−1
Baja	0.70	2.5	16.0	20	30	3	35,988.5	1983.9
Alta	0.85	4.0	25	55	45	1	50,571.7	2787.9

A local sensitivity simulation of ±10% was performed on each individual predictor in both scenarios; underestimated and overestimated results “delta” (Δ) can be observed, indicating absolute change with respect to the base scenario (Table 4). The most notable results are, in the low-yield scenario, increasing plant diameter by 10% resulted in the most significant increase in estimated yield (+1358.8 kg ha⁻¹, equivalent to +74.9 boxes ha^-1), followed by an increase in plant height (+991.6 kg ha⁻¹, equivalent to +54.7 boxes ha^-1) and NDVI (+979.1 kg ha⁻¹, equivalent to +54.0 boxes ha^-1). NDVI reduction by 10% generated the greatest decrease (−351.2 kg ha⁻¹, equivalent to −19.4 boxes/ha). In this same scenario, variations in nitrogen did not cause changes in predicted yield (delta = 0 kg ha⁻¹). In the high-yield scenario, NDVI reduction by 10% produced the greatest decrease in yield (−2546.1 kg ha⁻¹, equivalent to −140.4 boxes ha^-1), followed by nitrogen reduction (−1315.2 kg ha⁻¹, equivalent to −72.5 boxes ha^-1) and porosity reduction (−436.6 kg ha⁻¹, equivalent to −24.1 boxes ha^-1). Height and diameter variables showed no sensitivity in the high-yield scenario, maintaining constant values regardless of applied variations. The slope variable, being a nominal variable, was considered in this analysis due to its categorical nature.

Table 4. Sensitivity analysis (±10%) on base scenarios; delta (Δ) response values.

Yield	Modified Variable	Change (%)	Yield (kg ha−1)	Δ Yield (kg ha−1)	Boxes ha−1	Δ Boxes ha−1
Low	NDVI	−10%	35,637.30	−351.19	1964.57	−19.36
Low	NDVI	+10%	36,967.59	+979.09	2037.90	+53.97
Low	Height	−10%	35,988.49	0.00	1983.93	0.00
Low	Height	+10%	36,980.12	+991.63	2038.60	+54.67
Low	Diameter	−10%	35,988.49	0.00	1983.93	0.00
Low	Diameter	+10%	37,347.32	+1358.83	2058.84	+74.91
Low	Nitrogen	−10%	35,988.49	0.00	1983.93	0.00
Low	Nitrogen	+10%	35,988.49	0.00	1983.93	0.00
Low	Porosity	−10%	35,988.49	0.00	1983.93	0.00
Low	Porosity	+10%	36,920.10	+268.67	1998.74	+14.81
High	NDVI	−10%	48,025.58	2647.50	−2546.10	−140.36
High	NDVI	+10%	50,571.68	2787.85	0.00	0.00
High	Height	−10%	50,571.68	2787.85	0.00	0.00
High	Height	+10%	50,571.68	2787.85	0.00	0.00
High	Diameter	−10%	50,571.68	2787.85	0.00	0.00
High	Diameter	+10%	50,571.68	2787.85	0.00	0.00
High	Nitrogen	−10%	49,256.46	2715.35	−1315.20	−72.50
High	Nitrogen	+10%	50,571.68	2787.85	0.00	0.00
High	Porosity	−10%	50,135.07	2763.79	−436.61	−24.07
High	Porosity	+10%	50,571.68	2787.85	0.00	0.00

4. Discussion

The identification of a parsimonious subset of early predictors, characterized by high agronomic relevance and low statistical redundancy, constitutes a key methodological advance in agricultural modeling. The variable selection process, based on statistical criteria (correlation, VIF) and agronomic criteria, is consistent with established protocols in precision agriculture. Our results demonstrate that NDVI emerges as the main predictor due to its strong correlation with yield (R² = 0.92) and minimal multicollinearity risk (VIF = 1.88). This premise aligns with [57,58], who highlight that NDVI integrates early physiological responses to water stress and nutritional deficit in bananas, surpassing in situ indicators in predictive capacity [59].

The inclusion of plant height (r = 0.85, VIF = 2.35) as an indicator of vegetative vigor reinforces its diagnostic role in the banana vegetative cycle, a critical period where it explains >75% of yield variance according to Burke et al. 2020 [60]. Stem diameter (VIF = 1.2), a variable related to yield and vigor [61], is justified by its causal relationship with fruit filling (r = 0.89), coinciding with recommendations to prioritize morphological variables over correctable redundancies [62].

Among the soil variables, nitrogen (r = 0.82) and porosity (r = 0.78) showed determinant influence, supporting critical thresholds reported by Richter et al. 2020 [63] in tropical soils (>35 mg/kg and 35–40%, respectively) [64]. The ordinal transformation of slope (VIF = 1.05) efficiently captured its non-linear impact on soil drainage, where slopes > 5° reduce yields by 12–18% according to tropical topographies [65] and also reduce runoff [66].

Our cross-validated experiment confirms that the three algorithms reach almost asymptotic predictive performance (R² ≥ 0.950, RMSE ≤ 1 223 kg ha⁻¹). Nevertheless, the 2–5% lower RMSE achieved by RF relative to GB and RR is consistent with recent evidence from high-dimensional, noisy agronomic datasets.

Benchmarking studies on Sentinel-2-derived features for winter-wheat yield mapping have reported RF R² values of 0.93 vs. 0.91 for GB, coupled with a 14% reduction in RMSE under strong spatial heterogeneity [67]. A similar pattern was observed across Sudano-Sahelian rice plots, where RF outperformed RR (R² 0.88 vs. 0.83) and GB (R² 0.88 vs. 0.86) in the presence of smallholder-induced noise [68]. Morellos et al. 2023 [69] systematically tested biomass predictors and found RF exhibits the lowest cross-validated RMSE coefficient of variation (8.7%), corroborating our finding of superior stability. In spring-wheat trials under variable N management, Wang et al. 2020 [70] reported RF RMSE = 1.12 t ha⁻¹ versus 1.17 t ha⁻¹ for GB and 1.25 t ha⁻¹ for Ridge, paralleling the 25–58 kg ha⁻¹ gap we observed. Finally, Padarian et al. 2019 [71] demonstrated that RF’s bagging mechanism attenuates the impact of noisy covariates, yielding ~4% and ~7% lower RMSE than GB and Ridge, respectively, in continental-scale wheat yield prediction.

The marginal yet consistent superiority of RF can be attributed to two complementary properties. First, its ensemble of de-correlated trees reduces variance without substantially increasing bias, which is particularly advantageous when the signal-to-noise ratio is modest [69]. Second, RF’s out-of-bag error provides an unbiased internal validation that lessens the risk of overfitting when hyperparameter grids are wide, a circumstance not fully replicated by the single hold-out or k-fold strategies used in GB and RR [71]. GB, although capable of capturing slightly more complex interactions through sequential optimization, displayed higher sensitivity to hyperparameter tuning and, therefore, larger dispersion in RMSE across folds—an effect previously noted by [68]. RR, acting as a linear baseline, confirmed that the yield–predictor relationships depart appreciably from linearity; nevertheless, its regularized coefficients remain valuable as an interpretable benchmark and as a potential diversity term in future stacking ensembles.

Despite RF being the superior model, the XGBoost-based approach has proven to be comparable with state-of-the-art deep learning approaches, supporting the choice of ensemble methods as robust alternatives to more complex techniques [72]. The RMSE of 1190.2 kg ha⁻¹ obtained with GB represents a minimal difference compared to RF (25.3 kg ha⁻¹), suggesting that both algorithms similarly capture yield variability in bananas. The optimized hyperparameters for GB (learning_rate = 0.1, max_depth = 3, n_estimators = 150) indicate a conservative configuration that prevents overfitting, a critical aspect in agricultural data where generalization is fundamental for practical applications.

Hyperparameters optimized through grid search (n_estimators = 150, max_depth = 7, min_samples_split = 2) resulted in a balanced configuration that prevents both overfitting and underfitting. The selection of 150 trees is consistent with recent studies suggesting that values between 100 and 300 estimators provide the best compromise between precision and computational efficiency in agricultural applications [73]. The maximum depth of seven levels indicates that relationships captured by the model are moderately complex, which is appropriate for agricultural systems where interactions between variables can be significant, but not excessively deep. The use of all available variables at each division (max_features = 1.0) and bootstrap sampling (Bootstrap = True) maximizes diversity among ensemble trees, contributing to the observed predictive robustness. The conservative configuration of min_samples_split = 2 and min_samples_leaf = 1 allows the model to capture detailed patterns without compromising generalization [45], a crucial aspect for practical application in precision agriculture.

Robust model validation through residual analysis revealed exceptional characteristics of precision and absence of systematic bias. The minimal bias observed (residual mean = 29.80 kg ha⁻¹, equivalent to 0.07% of mean yield) indicates that the model does not present systematic trends of overestimation or underestimation, a fundamental aspect for reliability in practical applications. This characteristic is consistent with RF theoretical properties, which tends to produce unbiased predictions due to its ensemble structure [72].

The local sensitivity analysis implemented in this study represents a valuable and necessary methodology for the interpretation and validation of machine learning models in agricultural prediction [74], although its specific application in this context remains relatively unexplored in specialized literature. Sensitivity analysis is a qualitative research methodology of a model and its parameters that helps identify parameters affecting model output, distinguishing between local and global sensitivity analyses [74].

The results obtained reveal distinctive behavioral patterns between low- and high-yield scenarios that provide crucial insights for model interpretability. In the low-yield scenario, the predominance of plant diameter (+74.9 boxes ha⁻¹) as the most influential variable suggests that crop morphological characteristics exert primary control over yield when yield conditions are limiting. This finding is consistent with agricultural literature that establishes the importance of plant structural variables in yield determination under stress [75].

Contrarily, in the high-yield scenario, NDVI emerges as the variable with greatest impact (−140.4 boxes ha⁻¹ with 10% reduction), indicating that, when growth conditions are optimal, plant vigor and photosynthetic activity indicators become the main yield determinants. This transition in variable importance hierarchy between scenarios suggests the existence of non-linear response thresholds that machine learning models capture effectively. Tree-based models, such as RF and GB, capture non-linear yield patterns [76], which explains the models’ capacity to detect these contextual differences. The absence of sensitivity of certain variables in each scenario (nitrogen in low yield; altitude and diameter in high yield) reveals the models’ functional specialization according to yield conditions [77].

From a methodological perspective, sensitivity analysis is on the path to becoming an integral part of mathematical modeling [78], and the results of this study demonstrate its practical utility for optimizing agricultural management strategies. The ±10% variation applied provides a realistic reference framework for evaluating model robustness against natural fluctuations in crop conditions, thus contributing to prediction reliability in real field scenarios.

The use of machine learning models makes it possible to optimize the application of fertilizers and water, reducing diffuse pollution and emissions of nitrogen oxides, a potent greenhouse gas [13]. This study, therefore, provides a strategy for advancing agricultural sustainability in the context of precision agriculture and sustainability.

The use of multispectral images and the NDVI vegetation index has proven effective for assessing the physiological status of crops without the need for destructive sampling, aligning with the results presented in [6], where this technology applied in agriculture reduces the carbon footprint associated with conventional monitoring. The inclusion of variables such as porosity and nitrogen in the model promotes more responsible soil management, preventing its degradation and enhancing its long-term ecological functionality, as proposed in [10].

Predictive models enable more efficient agricultural planning, reducing post-harvest losses and optimizing logistics, which translates into economic savings for producers, especially in small-scale systems [79]. In addition, the use of open-source platforms and low-cost sensors democratizes access to precision agriculture technologies, which is essential for digital inclusion in agriculture in Ecuador and other developing countries around the world [80].

The FAO technical paper projects that a +1.2 °C rise in annual average temperature and more intense rainfall events in Ecuador’s banana belt will shorten the crop cycle, reduce bunch weight, and increase black-Sigatoka pressure. Our experimental site in Buena Fe already experiences the warm end of the country’s banana climate envelope (22.6 °C mean vs. 21 °C national average), suggesting that even a modest regional warming (+0.5–1 °C) could push the orchard toward the temperature threshold identified by FAO [81] for accelerated phenology. Conversely, the 2258 mm annual precipitation recorded on-farm is only 35% of the 6000 mm extreme quoted for Quevedo, indicating that the plantation is currently water secure; nevertheless, the FAO warning of more erratic rainfall implies that the observed 0 mm readings in several dekads (Figure 2) may become longer or more frequent. Because we obtained high yield-prediction accuracy with NDVI as the dominant predictor, the model implicitly captures canopy-level responses to these micro-climatic fluctuations; therefore, incorporating the FAO-recommended high-resolution weather time series into future RF runs should further tighten RMSE and provide the early-warning tool the FAO calls for without waiting for visible stress symptoms. Overall, this study corroborates the FAO conclusion: traditional coastal banana zones such as Buena Fe remain productive, but their climatic buffer is narrowing, and spectral-based monitoring is a viable, low-cost adaptation to maintain yield stability under forthcoming climate shifts.

5. Conclusions

This study demonstrates that integrating spectral indices (NDVI), crop structural variables, soil properties, and a Random Forest model enables the estimation of banana yield with high accuracy and robustness. The relative importance of NDVI compared to soil physical properties validates the prioritization of remote sensing as a rapid, scalable, and cost-effective tool for early yield prediction in banana crops. Consequently, the proposed approach not only supports decision-making in banana management (fertilization, irrigation, and protection) but also contributes to Sustainable Development Goals (SDGs) 2, 12, and 13 by enhancing productivity, reducing food losses, and lowering emissions associated with excessive input use. These findings lay the groundwork for a more sustainable, equitable, and resilient tropical agriculture. Furthermore, they open avenues for future research exploring algorithms adapted to diverse tropical cropping systems (e.g., XGBoost, neural networks) or operational precision agriculture platforms based on high-resolution temporal series.