A Passenger Flow-Based Resilience Measurement Model for Sustainable Operation of the Metro Station

Abstract

Metro stations serve as critical hubs for passenger gathering and scattering. Under disturbing scenarios, a station’s ability to respond to disturbances, named resilience, fundamentally governs the operational stability, sustainability and emergency performance of the metro network. Existing metro network resilience studies typically treated stations merely as topological nodes, making it impossible to account for the internal passenger flow organization and facility capacities of the station. The resilience of the station itself cannot be characterized and quantified. This study focuses on the metro station’s resilience. From the perspective of sustainable operation, considering the passenger flow management of the station, the station’s resilience is defined as the ability of the station to maintain its basic service capabilities and minimize the number of delayed passengers within the station during disturbances. A passenger delay coefficient is introduced to quantify variations in passenger delay volumes within the station. The total number of passengers entering and leaving a station is used to quantify its service capacity. A resilience measurement model for the station is constructed by coupling the passenger delay coefficient and the service capacity. A case study of a transfer station experiencing a sudden passenger surge is conducted for model validation, considering passenger flow control measures and train capacity constraints. The results demonstrate that the model measures the station’s resilience across varying passenger flow management strategies effectively. This study provides a quantitative tool for measuring metro station resilience, enabling emergency responses, operational optimization and policy formulation that support the sustainable and stable operation of metro stations and networks.

1. Introduction

Metro stations function as primary hubs for passenger gathering and scattering in the metro system. Once metro stations are confronted with operational disturbances, unexpected passenger surges, natural hazards or security incidents, metro systems experience immediate operational impacts that may escalate to passenger safety risks [1,2,3]. Therefore, the ability of metro stations to respond to disturbances, named resilience, is important for ensuring operational safety, stability and sustainability [4,5] of the metro system. Current research predominantly examines metro network resilience, while stations are typically simplified and represented as topological nodes [6]. However, this nodal representation makes it impossible to reflect the influence of internal passenger flow organization and facility capacity of stations on network resilience. The resilience of station operations remains understudied, with limited methodologies available for their quantitative measurement and precise characterization.

This study takes metro station resilience as the primary research focus. From the perspective of sustainable operation, taking passenger flow management into account, station resilience is defined as the ability to maintain basic service capabilities and reduce the number of delayed passengers within the station when disturbances occur. A passenger delay coefficient represents changes in the number of delayed passengers within the station. The service capacity of the station is operationalized through the total number of passengers entering and leaving the station. The resilience measurement model for the station is constructed by coupling the passenger delay coefficient and the station’s service capacity. The contributions of this study are as follows. (i) Establishing a novel definition of metro station resilience from the perspective of sustainable operation of the metro station. (ii) Developing passenger flow-based resilience measurement metrics. (iii) Formulating a measurement model that couples passenger flow dynamics with service capacity.

Section 2 provides a comprehensive review of existing research. Section 3 offers a detailed introduction to the definition, measurement metrics, and measurement model of station resilience. Section 4 verifies the proposed model by simulating a sudden surge in passenger numbers at a transfer station. Section 5 summarizes the research results, discusses the study’s limitations and proposes directions for future research.

2. Literature Review

Holling [7] pioneered the resilience concept in ecological systems, characterizing it as a system’s ability to recover its original equilibrium state following disturbances. This conceptual framework was subsequently adapted to metro systems, giving rise to the notion of metro system resilience. The current research paradigm predominantly examines resilience at the metro network level, and existing definitions of metro network resilience emphasize the ability of metro networks to recover to a specific state after being affected by disturbances. Ma et al. [8], Xu et al. [9] and Xing et al. [10] conceptualized resilience as the ability to resist and absorb disturbances and recover to a normal state. Chopra et al. [11] defined metro network resilience as the ability to maintain structure and function in the face of disruption. Xu et al. [12] proposed a comprehensive resilience framework incorporating four dimensions: preparedness for, resistance to, recovery from, and adaptation to stochastic failures, deliberate attacks and various contingencies. Zhang et al. [13] and Diab et al. [14] defined metro network resilience as “the connection level after node failures and the ability to quickly recover to an acceptable connection level through appropriate repair measures.”

In terms of measuring the resilience of metro networks, total passenger flow [15], origin-destination (OD) travel volume [16] and passenger travel time [17] are most commonly selected as resilience metrics. Zhang et al. [18] utilized additional passenger waiting time and station capacity to assess the resilience of metro networks during significant fluctuations in passenger flow or sudden disruptions by considering factors such as passenger flow, train operations and passenger behavior. Martello et al. [19] proposed a general framework for assessing metro network resilience, incorporating the exposure of interest, system sensitivity and topology. Ma et al. [15] formulated multidimensional resilience metrics that synthesize passenger flow variations, timetable adjustments and route choice behaviors for comprehensive network resilience assessment. Chen et al. [20] assessed the resilience of a metro system under random and malicious disturbances using passenger trip frequency and travel time. The resilience triangle paradigm [21] dominates current measurement models, quantifying resilience through simulated performance degradation profiles under various attack scenarios. For example, D’ Lima et al. [22] applied a mean-reverting random model to analyze the propagation of shocks, employing the London Underground as an example. Cong et al. [23] developed a multi-agent simulation system to estimate the impact of unexpected disruptions on passenger travel behavior in metro networks. Some researchers employ optimization methods to assess the recovery ability of metro networks under specific disturbance scenarios [24,25,26].

In terms of research into the importance of metro stations for the resilience of metro networks, Kopsidas and Kepaptsoglou [27] developed topologically based metrics to pinpoint stations requiring operational continuity during network-wide disruptions. Saadat et al. [28] evaluated the efficiency and vulnerability of the metro network based on its topological features and identified critical stations and rail segments in Washington, DC’s metro network during disruptions. Subsequent research by Saadat et al. [29] used the criticality of stations to determine the order in which metro network stations should be restored in the event of disruption. Lu et al. [30] employed an improved cascade failure model to analyze cascading failures in the Shanghai metro network, finding that once a large volume of passengers floods into stations near a failed station, it accelerates the spread of cascading failures. Yang et al. [31] integrated smart card data, multi-agent simulation and the minimum–maximum normalization method to identify critical metro stations. Ma et al. [8] proposed a resilience assessment model for metro networks targeting passenger travel services, identifying transfer stations as potential weak links in the metro network. Xu et al. [32] implemented a multidimensional resilience framework on the Hong Kong metro network, demonstrating that station density enhances network robustness when surrounding stations face lower common risks. However, stations are simplified and represented as nodes in these studies. These nodal representations fundamentally overlook intra-station passenger flow dynamics and facility capacity constraints, resulting in inadequate metro station resilience characterization.

Currently, there is limited research focusing specifically on metro station resilience. Zhang et al. [33] developed a multidimensional indicator system incorporating four dimensions (external environment, entrance configuration, socioeconomic context and post-disaster response) for station resilience evaluation, with indicator quantification achieved through the InfoWorks ICM model. Jiao et al. [34] proposed a cloud-based station resilience assessment model accounting for station structural configurations, emergency protocols and resource deployment strategies. To assess the ability of metro stations to respond to public health risks, Lu et al. [35] simulated and analyzed three passenger scheduling strategies using AnyLogic. Liu et al. [36] and Xu et al. [37] integrated station infrastructure characteristics into queueing-theoretic models of passenger flows, quantifying station resilience based on the accumulated loss of passenger travel time. Zhang et al. [38,39] and Qiu et al. [40] utilized deep learning methods [41,42] to predict and analyze the impact of passenger flow on the service efficiency of metro stations. Additionally, some researchers have focused on designing emergency response plans for metro stations [43]. For example, Zhou et al. [44] developed a bi-level optimization framework for evacuation management, simultaneously determining optimal guide deployment (quantity, initial positions) and routing strategies. The framework integrates passenger guidance requirements with multi-guide coordination mechanisms to enhance crowd evacuation efficiency in emergency scenarios. Zhang et al. [45] developed an integrated optimization model combining simulation and machine learning methods to optimize station facility planning and corresponding personnel allocation schemes.

In summary, the current research still has the following limitations. (i) Previous studies emphasize the passive restoration of metro network status rather than the active adaptation and dynamic response of metro stations to disturbances. (ii) Oversimplification of stations as topological nodes, making it impossible to consider intra-station passenger flow dynamics and facility capacity constraints, leading to inadequate operational station resilience quantification. (iii) Station resilience measurement models largely rely on cumulative losses of performance metrics, failing to capture differences between various response strategies to disturbances.

3. Methodology

This section defines the resilience of metro stations, develops resilience metrics based on an analysis of influencing factors, and proposes a model for measuring metro station resilience.

3.1. Definition and Influencing Factors of Station Resilience

As understanding of systems and their interactions with the environment has deepened, Holling [46] explained resilience as a continuous and evolving process. Building on this, Walker et al. [47] emphasized that system resilience should be considered based on the attributes that govern its functioning, primarily the behavior of system actors, especially managers. When confronted with external disturbances and internal constraints, the actions of these actors determine whether the system can avoid transitioning into an undesirable state or recover to a desirable one. Collectively, these perspectives define resilience as the ability of system actors to dynamically adapt to external disturbances. This perspective also applies to metro station systems. When disturbances occur, fixed constraints such as the capacity of station facilities and trains can affect passenger movement and distribution. Nevertheless, station managers can implement flexible strategies, such as passenger flow control and guidance or adjustments to train operation plans, according to the specific characteristics of the disturbance. These actions enable stations to evacuate passengers efficiently and maintain continuous service delivery. Considering that the ultimate goal of the metro station operation is to ensure safe and smooth passenger travel, the effects of any configuration or management adjustment are ultimately reflected in passenger flow dynamics. Building on the concepts proposed by Holling and Walker, the resilience of a metro station can be defined from the perspective of passenger service as the station’s ability to maintain its basic service capacity and minimize the number of delayed passengers within the station during a disturbance. Delayed passengers are defined as those who are unable to board a train or exit the station through the turnstiles. Service capacity refers to the number of times the station serves passengers within a given period. The basic service capacity is the station service capacity achievable when no disturbances occur. A station that can sustain a higher service capacity and minimize the number of delayed passengers demonstrates greater resilience. Conversely, a reduction in service capacity or a rise in unavoidable delays indicates diminished resilience.

This paper focuses on three primary factors influencing the resilience of metro stations: passenger flow organization, train capacity and station facilities. Passenger flow organization involves measures such as passenger flow control, directional signage, flexible evacuation routes, and so on, which help ensure the rapid and orderly departure of passengers. Train capacity can be enhanced through flexible scheduling and the deployment of backup trains to promptly relieve crowding within the station. Station facilities, through well-designed capacity redundancy, provide the physical foundation for absorbing and responding to disturbances. These three factors interact dynamically and collectively shape the resilience of metro stations.

3.2. Resilience Measurement Metrics for the Station

Based on the definition of metro station resilience and its key influencing factors, two metrics are proposed to measure station resilience: the passenger delay coefficient and station service capacity.

(1) Passenger delay coefficient

The passenger delay coefficient quantifies a station’s ability to reduce the number of delayed passengers within the station. It is defined as the proportion of delayed passengers remaining in the station during a given period, resulting from the combined effects of passenger flow management, train operations and station facilities. Therefore, the number of delayed passengers within a given period is calculated as the product of the delayed passengers from the previous period and the passenger delay coefficient. It is assumed that the number of delayed passengers within the station at period $k$ is $X\left(k\right)$, then the number of delayed passengers within the station at period $k+1$ is $X\left(k+1\right)$, as shown in Equation (1).

$$X\left(k+1\right)=A\left(k\right)·X\left(k\right),$$

(1)

where $A\left(k\right)$ is the passenger delay coefficient for the station, which consists of two components. The first component, denoted as $\alpha \left(k\right)$, represents the maximum proportion of delayed passengers who are unable to leave the station during period $k$. This value depends on train capacity, turnstile throughput, and whether passengers can board trains or exit the station in time. The second component, denoted as $\theta \left(k\right)$, represents the proportion of additional delayed passengers caused by new entries into the station during period $k$. $\theta \left(k\right)$ is influenced by the extent to which station managers can control the number of passengers entering. The passenger delay coefficient for the period $k$ is given by Equation (2).

$$A\left(k\right)=\alpha \left(k\right)+\theta \left(k\right),$$

(2)

where $\alpha \left(k\right)$ is calculated by Equation (3).

$$\alpha \left(k\right)=1-{\displaystyle \frac{C_{train}+{\displaystyle \sum _{i=1}^n{C}_{gate}^i}·k}{\left({\lambda }_1+{\lambda }_2\right)·k}},$$

(3)

where $C_{train}$ represents the remaining train capacity after passengers have alighted at the station. $C_{gate}^i$ denotes the actual throughput capacity of the $i$th exit turnstile, which is less than its theoretical maximum. ${\lambda }_1$ and ${\lambda }_2$ represent the number of delayed passengers within the station reaching the platform and exiting through the turnstiles per unit time, respectively. The value of ${\lambda }_1$ and ${\lambda }_2$ depends on the emergency response measures implemented by station managers during the disturbance, such as timely guidance and evacuation of passengers within the station. Note that $\alpha \left(k\right)$ is not always greater than zero. $\alpha \left(k\right)<0$ indicates that all delayed passengers in the station can leave and that there is sufficient remaining capacity in both the train and the turnstiles to accommodate additional passengers. $\alpha \left(k\right)=0$ indicates that the available capacity of the train and turnstiles is only sufficient to serve the existing delayed passengers within the station.

In Equation (2), $\theta \left(k\right)$ consists of two components: ${\theta }_1$, the proportion of delayed passengers who have reached the platform, and ${\theta }_2$, the proportion of delayed passengers who have not yet reached the platform. The values of ${\theta }_1$ and ${\theta }_2$ can be obtained through video surveillance data or queueing theory-based simulations [37]. $\theta \left(k\right)>0$ indicates that passengers are allowed to enter the station during period $k$, while $\theta \left(k\right)=0$ represents scenarios in which no passengers enter during period $k$. In certain emergencies, such as natural disasters, fires or malicious attacks, both entry and exit turnstiles may be used to evacuate all passengers from the station. In such cases, the value of $\theta \left(k\right)$ may be negative, indicating that entry turnstiles are also being used for outbound passenger flow.

It can be observed that when the capacities of trains and exit turnstiles are sufficient to meet passenger outflow demand, the value of $A\left(k\right)$ may become negative. In such cases, the physical interpretation of Equation (1) becomes ambiguous. To address this issue, constraints on the value of $A\left(k\right)$ are specified, as shown in Equation (4).

$$A\left(k\right)=\left\{\begin{array}{ll}\alpha \left(k\right)+\theta \left(k\right)& \alpha \left(k\right)+{\theta }_1>0 \\ {\theta }_2& \alpha \left(k\right)+{\theta }_1<0\end{array}\right.,$$

(4)

where $\alpha \left(k\right)+{\theta }_1>0$ indicates that the capacity of the trains and exit turnstiles is insufficient to meet the passenger outflow demand within the station. $\alpha \left(k\right)+{\theta }_1<0$ indicates that the train and turnstile capacities are sufficient to accommodate all passengers wishing to exit. In the case of $\alpha \left(k\right)+{\theta }_1<0$, delays occur because passengers entering are unable to reach the platform in time to board the train.

(2) Station service capacity

Previous studies have characterized station service capacity based on the number of passengers, consisting of boarding and exiting passengers, within a given period [48]. However, this approach does not accurately capture the full extent of services provided by the station, as it overlooks cases in which a single passenger uses multiple station facilities, for example, passengers enter the station through the turnstiles and board the train. To address this limitation, station service capacity is instead measured by the number of times the station serves passengers within a given period. Specifically, metro station services are categorized into three types: entering the station, boarding the train and exiting the station. The sum of the number of passengers performing these three actions within a period is used to represent the station’s service capacity. The station’s service capacity during a given period $k$ is shown in Equation (5).

$$S\left(k\right)=S_{in}^{gate}+S_{out}^{train}+S_{out}^{gate},$$

(5)

where $S_{in}^{gate}$ represents the number of passengers entering the station during the period $k$, taking passenger flow control into account. $S_{out}^{train}$ and $S_{out}^{gate}$ represent the number of passengers leaving the station via trains and turnstiles, respectively, during the period $k$.

3.3. Resilience Measurement Model for the Station

According to the definition of metro station resilience, resilience reflects a combination of the station’s service capacity and its ability to reduce passenger delays. Therefore, the product of these two components is used to quantify resilience. However, the passenger delay coefficient is a negative indicator: the smaller its value, the greater the station’s ability to reduce delays. As a result, directly using this coefficient in the resilience formula would produce a counterintuitive outcome, i.e., higher resilience values would imply lower actual resilience. To address this issue, the ability to reduce delays is redefined as the difference between 1 and the passenger delay coefficient. For a non-transfer station, the resilience of a metro station during period $k$ is defined as shown in Equation (6).

$$R\left(k\right)=\left(1-A\left(k\right)\right)·S\left(k\right),$$

(6)

For transfer stations serving multiple lines, the station is treated as a set of intermediate stations, one for each line. Passengers transferring to other lines are considered delayed passengers on the corresponding destination lines. The overall resilience of the transfer station is calculated as the average of the resilience values of these individual intermediate stations.

4. Numerical Experiments

To evaluate the practicality of the proposed model, a simulation of a sudden passenger surge at a transfer station is conducted, incorporating passenger flow control measures. The resulting resilience metrics under varying passenger entry volumes are analyzed and discussed.

4.1. Experimental Data and Procedure

By constructing a schedule-based passenger flow assignment model, the dynamic behaviors of passengers selecting trains under sudden passenger surge scenarios are simulated based on actual OD data, thereby calculating the station resilience under varying passenger flow scenarios.

(1) Data source

This study focuses on a representative metro station selected from the network of Xi’an in China. The simplified network topology is illustrated in Figure 1. The network comprises 4 lines, 89 nodes, and 91 links. Green circular nodes indicate six transfer stations, while red square nodes denote eight terminal stations. The target station, S1, serves as a transfer point between Lines 1 and 2. It is equipped with 6 entrances/exits, 16 entry turnstiles, and 34 exit turnstiles. The station is located in an area with a high density of schools and hospitals and primarily serves commuting and holiday-related passenger flows.

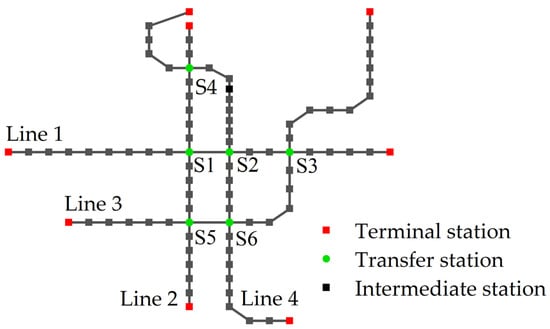
Figure 1. Topological structure of the metro network in Xi’an.

The basic passenger flow data used in the experiment is derived from OD data collected from the metro network between 07:00 and 10:00 on a typical weekday. It is assumed that the proportion of passengers traveling to various destinations remains constant after entering the station. To validate the proposed resilience measurement model, it is assumed that, at 08:00, the passenger inflow at transfer station S1 reaches seven times the normal (undisturbed) level.

(2) Simulation procedure

Based on actual OD flows, three different levels of sudden passenger surge scenarios are set: two times, four times, and seven times the original OD flow. A schedule-based passenger flow assignment model is employed to allocate the OD flows to trains accordingly to simulate passenger boarding and transfer behaviors during different periods [49], yielding the number of passengers entering the station, boarding trains, transferring between lines and exiting the station. The station resilience measurement model is calculated based on the aforementioned output passenger flow data.

A schedule-based passenger flow assignment model is employed to simulate passenger travel behavior, incorporating time-related travel costs. The specific model parameters are listed in Table 1. During flow assignment, passengers are allowed to choose the second-shortest path, and those who do so are considered to have entered the station but not yet reached the platform, thus categorized as delayed passengers within the station. It is assumed that trains in both directions arrive and depart simultaneously, and the time interval $k$ is set to 3 min based on the train departure frequency. Furthermore, to prevent the accumulation of delays, passenger flow organization measures are assumed to be implemented during each time interval, allowing all delayed passengers within the station to reach the platform or exit during that period. The parameter settings and calculation methods for the station resilience measurement model are listed in Table 2.

Table 1. Parameter settings for the schedule-based passenger flow assignment model.

Maximum Train Speed	Maximum Train Capacity	Acceleration		Train Dwell Time	Train Frequency
		Entering Station	Leaving Station
80 km/h	1440	−0.5 m/s2	0.5 m/s2	40 s	Lines 1, 2, 3, and 4 each have a frequency of 20 trains per hour.

Table 2. Parameter setting and calculation method of the station resilience measurement model.

Parameter	Parameter Value and Calculation Method
$C_{train}$	$C_{train}=C_{train}^{\max }-\left(N_{on}-N_{alight}\right)$, $\mathrm{where} C_{train}^{\max }$ $\mathrm{is} \mathrm{the} \mathrm{maximum} \mathrm{train} \mathrm{capacity}. N_{on}$ $\mathrm{is} \mathrm{the} \mathrm{volume} \mathrm{of} \mathrm{passengers} \mathrm{on} \mathrm{the} \mathrm{train}. N_{alight}$ is the volume of passengers alighting from the train.
$k$	3 min.
${\displaystyle \sum _{i=1}^n{C}_{gate}^i}·k$	The volume of passengers exiting the station.
${\lambda }_1$$, {\lambda }_2$	Followed by a Poisson distribution [37,48].
${\theta }_1$	The proportion of passengers opting for the shortest route relative to the number of delayed passengers within the station.
${\theta }_2$	The proportion of passengers opting for the second-shortest route relative to the number of delayed passengers within the station.
$S_{in}^{gate}$	The volume of passengers entering the station.
$S_{out}^{gate}$	The volume of passengers exiting the station.
$S_{out}^{train}$	The volume of boarding passengers.

4.2. Results and Discussion

The calculated results for the station’s ability to reduce the number of delayed passengers, service capacity, and resilience are analyzed and discussed.

(1) Ability to reduce the number of delayed passengers

Figure 2 illustrates the temporal variation in the station’s ability to reduce the number of delayed passengers. S1-line1 and S1-line2 refer to station S1 on Line 1 and Line 2, respectively. The labels “7 times”, “4 times”, and “2 times” indicate that the passenger inflow reached seven, four, and two times the normal (undisturbed) level, corresponding to different levels of passenger flow control measures. It can be observed that the ability to reduce the number of delayed passengers improves as the number of passengers entering decreases. This is because, with both trains and exit turnstiles operating normally on S1-line1 and S1-line2, a lower inflow results in fewer newly delayed passengers within the station, thereby reducing the overall number of delayed passengers.

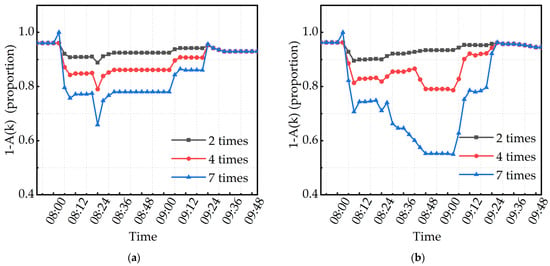
Figure 2. Temporal variation in the ability to reduce delayed passengers of S1-line1 and S1-line2 under different passenger inflow levels. (a) The ability to reduce delayed passengers of S1-line1; (b) The ability to reduce delayed passengers of S1-line2.

(2) Station service capacity

Figure 3 presents the temporal distribution of station service capacity for S1-line1 and S1-line2. As the period corresponds to the morning peak hours, both passenger inflow and outflow exhibit a single-peak distribution. Consequently, station service capacity first increases and then decreases over time, which is consistent with real-world metro operation. In comparison with Figure 2, it can be observed that as service capacity increases, the ability to reduce passenger delays declines. This indicates that the train capacity and exit turnstile capacity are sufficient to meet passenger outflow demand. However, the growing number of passengers entering leads to an accumulation of passengers who have not yet reached the platform. As a result, the number of delayed passengers in the station also increases.

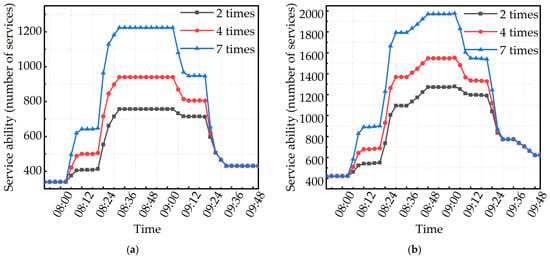
Figure 3. Temporal variation in the service capacity of S1-line1 and S1-line2 under different passenger inflow levels. (a) The service capacity of S1-line1; (b) The service capacity of S1-line2.

(3) Station resilience

Figure 4 illustrates the temporal distribution of resilience at Station S1 under varying levels of passenger inflow. It can be observed that before the disturbance (i.e., before 08:00), the station’s resilience is not zero. This is attributed to the presence of transfer passengers and those who, despite entering the station, fail to board the train in time, such as passengers who arrive shortly before a train departs and are unable to reach the platform promptly. This demonstrates that resilience remains active throughout station operations and manifests differently under distinct passenger flow control scenarios. Following the disturbance, a comparison of different inflow levels reveals that the resilience value under the four-times inflow scenario is similar to that under the seven-times scenario, yet significantly higher than that under the two-times scenario. This indicates that the four-times inflow level achieves a better balance between maintaining service capacity and minimizing passenger delays, making it a more effective passenger flow control measure, which is consistent with the conclusion proposed by Yuan et al. [50]: ‘optimal passenger flow control should balance passenger travel and minimize the number of delayed passengers within the station’.

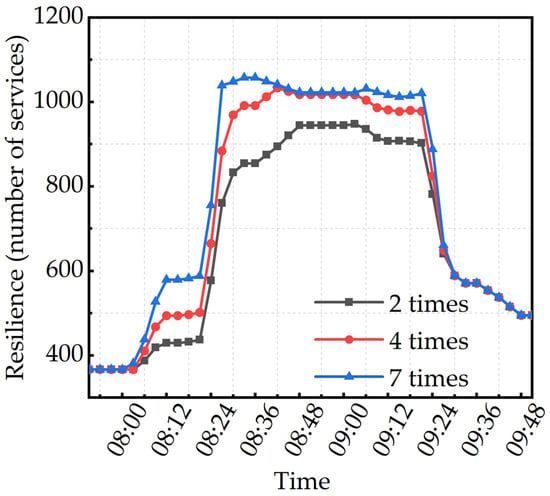
Figure 4. Temporal distribution of the resilience of Station S1 under different passenger inflow levels.

Figure 5 depicts the relationship between the average number of delayed passengers within the station for S1-line1 and S1-line2 and the resilience of Station S1. The resilience distribution boundary is defined as the upper and lower bounds of a station’s resilience under varying passenger flow control strategies. The dashed lines indicate the resilience distribution boundaries corresponding to the maximum number of delayed passengers under inflow levels of two times, four times, and seven times. A comparison of these boundary regions reveals that as the growth rate of passenger delays increases, the growth rate of resilience gradually declines. This phenomenon aligns with the negative correlation between resilience and passenger delays proposed by Liu et al. [36] and Xu et al. [37]. This phenomenon arises because, although the station’s service capacity increases with rising passenger inflow, its ability to reduce delays diminishes. The interaction between these two opposing trends results in a deceleration of resilience growth, demonstrating that the proposed station resilience measurement model is sensitive to varying disturbance scenarios.

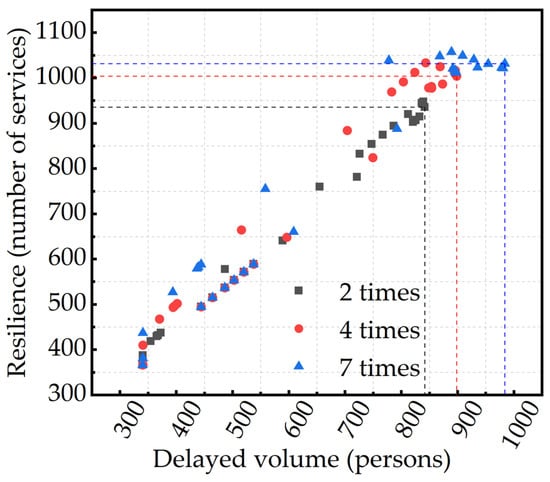
Figure 5. Relationship between the average number of passenger delays on S1-line1 and S1-line2 and the resilience of Station S1.

Figure 6 illustrates the relationship between the average passenger inflow at S1-line1 and S1-line2 and the resilience of Station S1. The dashed lines represent resilience distribution boundaries, defined by the maximum passenger inflow under the two-times, four-times, and seven-times scenarios. It can be observed that within each region, resilience increases with passenger inflow. This indicates that, despite varying flow control measures, the station can maintain service capacity while effectively reducing delays. However, a comparison of the regional boundaries reveals that the rate of increase in resilience gradually diminishes as the inflow continues to rise. A possible explanation is that the station’s service capacity approaches its upper limit due to constraints on train capacity, while its ability to reduce passenger delays continues to decline. This interaction results in a slower growth of overall resilience.

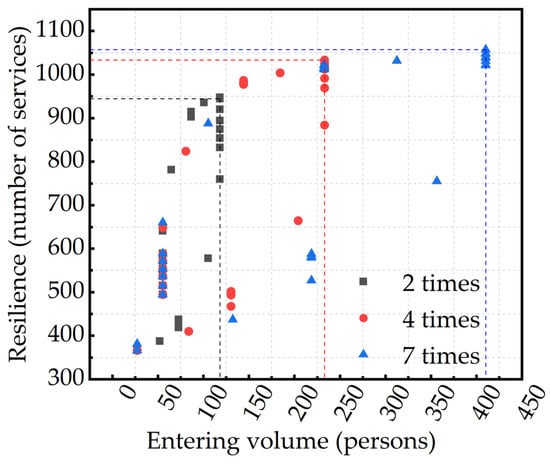
Figure 6. Relationship between the average passenger inflow on S1-line1 and S1-line2 and the resilience of Station S1.

5. Conclusions

From the perspective of the sustainable operation of the metro station, this study defines station resilience as the ability of a metro station to maintain its basic service capacity and reduce the number of passenger delays during disturbances. A passenger delay coefficient is used to represent changes in delayed passenger volume, while the total number of passengers entering and leaving the station is used to quantify service capacity. By coupling these two metrics, a station resilience measurement model is developed. The proposed model, based on passenger flow dynamics and independent of disturbance types, is suitable for measuring station resilience under various disturbance scenarios. Its output resilience values provide a quantitative basis for assisting managers in formulating strategies for passenger flow control, emergency response and resource allocation, while also laying the foundation for constructing a resilience analysis framework for the metro network, thereby enhancing its stability and sustainability of operation in the long term. The practicality of the proposed model is validated through a simulation of a sudden passenger surge at a transfer station. Experimental results demonstrate that the model can effectively measure the resilience of metro stations under different flow control strategies and identify the optimal passenger flow control measure based on the resilience outcomes.

Future research should investigate how insights into metro station resilience and its quantitative measurement can be leveraged to enhance the operational efficiency of both individual stations and the broader metro network. Potential directions include optimizing passenger flow management strategies to strengthen station-level resilience, examining the influence of station resilience on overall network stability and emergency response ability, and enhancing network-wide resilience through the coordinated optimization of resilience across multiple stations. Furthermore, the broader structural and governance factors of the socio-technical system, such as social resource allocation and multi-system coordination, could also be incorporated into the study of station resilience. These potential directions would provide valuable perspectives on metro station resilience within the context of transportation and social systems.