A Fuzzy MCDM Approach for the Evaluation of Sustainable Aviation Fuel Alternatives Under Uncertainty

Abstract

The increasing carbon footprint of civil aviation has made the use of Sustainable Aviation Fuel (SAF) a strategic necessity in line with the sector’s sustainability goals. This study evaluates the existing SAF types based on environmental, economic, technical and social criteria, determines the criteria weights with Fuzzy-Step-Wise Weight Assessment Ratio Analysis (F-SWARA) and selects the most suitable alternative through Spherical Fuzzy-Multi Objective Optimization on the basis of Ratio Analysis plus full MULTIplicative form (SF-MULTIMOORA) method. The alternative evaluation process was carried out on a Python-based online platform and sensitivity analysis was performed on five different scenarios. According to the findings, the Hydroprocessed Esters and Fatty Acids (HEFA-SPK) alternative stands out as the most suitable option in all scenarios, followed by the Fischer-Tropsch Synthetic Paraffinic Kerosene (FT-SPK) alternative. In contrast, Alcohol-to-Jet (ATJ-SPK) and Power-to-Liquid (PtL) options seem to be more variable and less stable. The study provides methodological contributions for the evaluation of SAF alternatives with fuzzy multi-criteria decision making (MCDM) methods and provides strategic implications for manufacturers and airlines in achieving the low-carbon targets of the aviation sector.

1. Introduction

Considering the rapid growth of civil aviation, its energy consumption and dependence on fossil fuels, reducing its carbon footprint becomes inevitable in terms of sustainability goals. The International Air Transport Association (IATA) is developing various strategies towards the goal of net zero carbon emissions by 2050 [1]. These strategies encompass energy efficiency, operational improvements, new aircraft technologies and the use of SAF. In line with the net zero emission target, SAF is considered one of the most effective decarbonization solutions for the aviation industry, which is among the critical areas for climate change mitigation [2].

SAFs are low-carbon-footprint alternative fuels that can replace fossil-based jet fuels and are produced from a variety of renewable sources such as biomass, waste oils, alcohols or directly from carbon dioxide. The main types of SAFs in use or under development today include [3]:

• HEFA-SPK: It is obtained from vegetable oils and animal fats by hydroprocessing. It is the most widely used type of SAF due to its compatibility with existing infrastructure and high energy density.
• FT-SPK: It is produced by chemically converting synthetic gas obtained by the gasification of biomass into liquid fuel. It provides high-purity fuel.
• ATJ-SPK: It is obtained by chemical conversion from alcohols such as ethanol or isobutanol. It has high applicability in countries with strong alcohol infrastructure.
• CHJ (Catalytic Hydrothermolysis Jet): It enables the conversion of animal fats and vegetable oils into jet fuel by hydrothermal processing.
• HFS-SIP (Hydroprocessed Fermented Sugars-Synthetic Iso-Paraffins): It is produced by hydro-processing the substances formed as a result of the fermentation of sugar-based raw materials.
• HC-HEFA: It is a special type of HEFA resistant to cold climatic conditions.
• PtL: It is a potentially carbon-neutral production method through which hydrogen obtained from water electrolysis is converted into synthetic fuel by combining with carbon dioxide.

These fuel types offer operational advantages, not only in terms of environmental sustainability but also because they are compatible with existing fuel infrastructures.

When choosing between SAF types, many different and often conflicting criteria need to be considered simultaneously, ranging from environmental impacts to economic feasibility, from technical feasibility to social acceptability. Therefore, MCDM methods provide an effective tool to systematically analyze this complex structure. MCDM methods are systematic decision support tools that help to identify the best option in cases where multiple and often conflicting criteria exist. MCDM methods enable choices to be made in such multidimensional evaluations. It offers a comprehensive and balanced perspective to decision makers, especially in multidimensional problems such as sustainability. Many different MCDM techniques such as Analytic Hierarchy Process (AHP), Analytic Network Process (ANP), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR), Measurement of Alternatives and Ranking according to Compromise Solution (MARCOS), Logarithmic Percentage Change-Driven Objective Weighting (LOPCOW) are used [2,4,5]. However, real-world problems often involve uncertainty and subjectivity. For this reason, fuzzy set theory has been widely used in modeling uncertain data since 1965. In addition to the type 1 fuzzy sets (T1FS) and type 2 fuzzy sets (T2FS) developed by Zadeh, more advanced approaches such as intuitionistic fuzzy sets (IFSs), Pythagorean fuzzy sets (PFSs), neutrosophic fuzzy sets (NFSs), unstable fuzzy sets (HFSs) and spherical fuzzy sets (SFSs) have been proposed [6,7,8]. These extensions make it possible to handle decision maker uncertainty and subjectivity more sensitively in MCDM problems.

There are many studies in the literature that directly evaluate SAF alternatives with MCDM techniques. Previous studies have analyzed SAF alternatives using different MCDM techniques. For instance, Ecer et al. (2025) combined extended forms of LOPCOW and MARCOS based on interval-valued fuzzy neutrosophic numbers (IVFNN) [2]. Chinnasamy et al. (2023) evaluated 12 SAF producers with AHP and WASPAS, focusing on technologies and feedstocks such as HEFA, ATJ, and FP [9]. Pietrowichz (2023) examined SAF life cycle emissions and emphasized the strong influence of land use change, finding miscanthus-based FT fuel to have the lowest emissions [10]. Rajamanickam et al. (2023) applied the EDAS method to rank SAF alternatives and concluded that natural gas-based FT fuels were the most suitable [11]. Cabrera and Sousa (2022) investigated production methods, technological barriers, and future potential of SAF [3].

Beyond SAF-specific studies, fuzzy MCDM approaches have been applied to other aviation-related decision problems. Ardil (2023) proposed a fuzzy combined MCDM analysis using Euclidean and linear distances, demonstrating its applicability through the case of unmanned fighter jet procurement [12]. In another work, Ardil (2023) introduced the Proximity Measure Method (PMM) for group decision making in aviation contexts [13]. Bakır et al. (2021) developed a framework integrating fuzzy PIPRECIA and fuzzy MARCOS to evaluate six regional aircraft alternatives based on 14 criteria, with operating cost identified as the most critical factor [14].

More recent contributions have emphasized sustainability and advanced fuzzy approaches in aviation. Mizrak et al. (2024) presented a sustainability plan for Istanbul Airport using entropy weighting and 2-tuple linguistic T-SF MCDM, incorporating innovative technologies such as IoT monitoring and blockchain-based reporting [15]. Mizrak and Şahin (2025) integrated AI-supported expert weighting with spherical fuzzy CRITIC–RATGOS to prioritize investments in sustainable airport energy systems, highlighting AI-based energy management and solar microgrids as top solutions [16].

A review of the literature indicates that most SAF evaluation studies rely on a limited number of criteria and do not fully cover all dimensions of sustainability. Moreover, the spherical fuzzy set approach has rarely been applied in the selection of SAF alternatives. Therefore, a comprehensive evaluation of SAF alternatives that combines F-SWARA for weighting and SF-MULTIMOORA for ranking is still lacking. Addressing this gap, our study provides a holistic assessment covering environmental, economic, social, and technical dimensions.

The main objective of this study is to evaluate SAF types with a holistic approach in terms of environmental, economic, social and technical criteria and, in this context, to determine the most appropriate fuel type by determining the criteria weights through F-SWARA method and ranking the alternatives via SF-MULTIMOORA method. This study offers the following original contributions:

• The F-SWARA and SF-MULTIMOORA methods were used together for the first time in SAF assessment.
• The study initially considered 24 criteria covering environmental, economic, social and technical dimensions; based on expert evaluations, the analysis focused on the most critical ones.
• Sensitivity analysis was performed across five different scenarios to test the reliability of the findings.
• The study not only provides a methodological contribution but also offers practical insights that could serve as a strategic roadmap for industry stakeholders.

To ensure that all sustainability dimensions are adequately reflected, the study was further supported by sensitivity analyses, in which representative criteria from each main dimension (environmental, economic, social, technical) were selected to test the robustness of the results.

The remaining sections of the paper are organized as follows: Section 2 presents the methodology and problem definition; Section 3 applies the proposed model to SAF alternatives; Section 4 discusses the findings and sensitivity analysis; and Section 5 presents the conclusions, managerial and policy implications, and future research recommendations.

2. Materials and Methods

2.1. Research Methodology

Methodology of the research consists of two main stages: criteria weighting and ranking of alternatives. In the first stage, 24 criteria identified based on the literature review were weighted by the F-SWARA method after being evaluated by the decision makers. This method is preferred as it more realistically reflects the uncertainty in expert judgments and considers the ranked comparisons of decision makers. Based on the criteria weights obtained as a result of the F-SWARA analysis, the 8 criteria with the highest importance were selected. The F-SWARA method was repeated for the selected criteria. The resulting criteria weights were used to evaluate 4 alternative SAF types in the second phase of the study. SF-MULTIMOORA method was applied for ranking the alternatives. This method combines multiple evaluation approaches (Ratio system, Reference Point approach and Spherical Fuzzy Multiplicative Method) with spherical fuzzy numbers to provide a more comprehensive and reliable decision support. Sensitivity analysis was also performed to test the stability of the model. Under this analysis, the changes in the rankings of the alternatives were evaluated by varying the weight scenarios and the stability of the results obtained was tested. This holistic methodological approach allows for a multi-dimensional assessment of sustainable fuel options from environmental, economic, social and technical aspects. Methodological workflow of the study is given in Figure 1.

2.2. Defining of SAF Types Selection Problem

This study aims to determine the most suitable option among alternative fuel types within the context of the MCDM problem. Since it is not possible to consider different criteria independently in the decision-making process, the use of multi-criteria decision-making methods is essential. These methods allow for the combined evaluation of both qualitative and quantitative data, allowing decision-makers to make a more balanced and rational choice.

In this context, the aim of the study is to systematically determine the most suitable option among alternative fuel types evaluated within the sustainability axis, in line with the established criteria. The obtained results aim to contribute to the shaping of energy policies and support the development of sustainable transportation and energy systems.

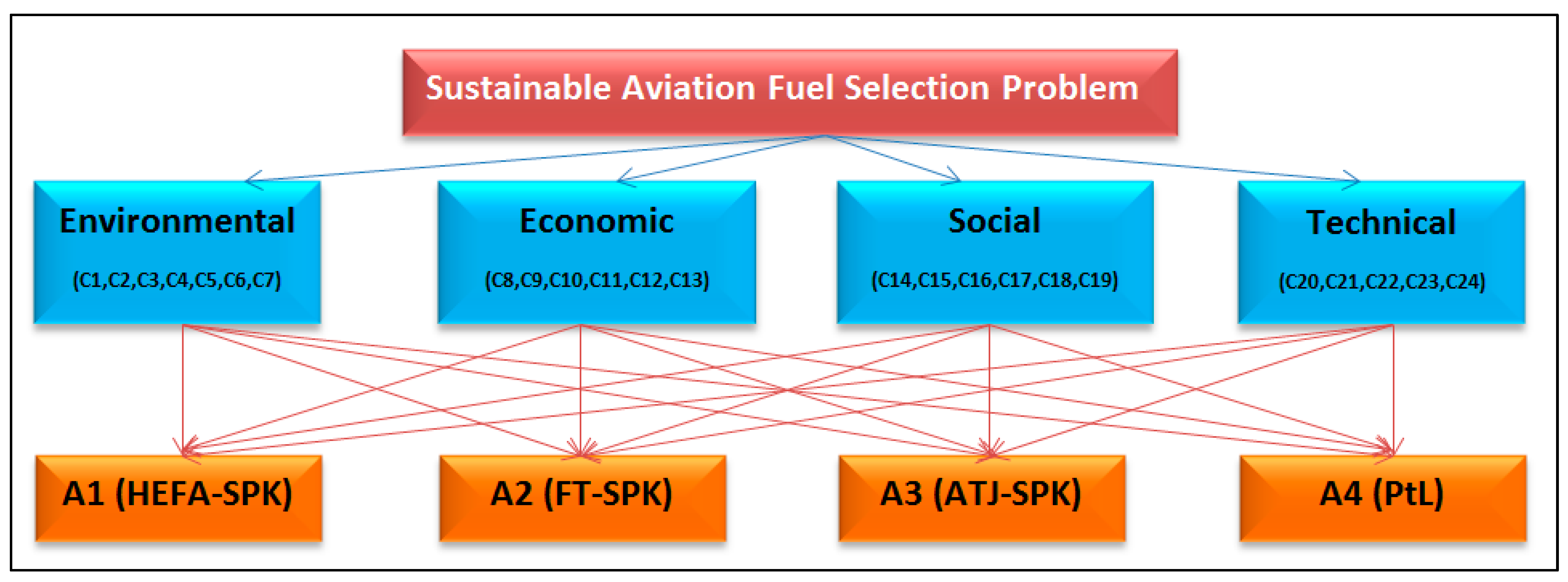
The study is conducted in two stages. The first stage is to determine the criteria for the sustainable fuel type selection problem, and the second stage is to evaluate fuel type alternatives. For both stages, the literature was reviewed, and four different fuel type selections were evaluated, considering four main criteria and 24 sub-criteria. The main criteria for fuel selection were determined as environmental, economic, social, and technical. Sub-criteria within these main criteria were considered, and the HEFA-SPK, FT-SPK, ATJ-SPK, and PtL fuel types were ranked in order of importance. The hierarchical structure of the problem is shown in Figure 2. Furthermore, the information provided by the experts involved in calculating the importance ratings among the criteria and the alternatives is shown in

Table 1. Expert Informations.

Experts	Title	Experience	Contribution to the Study	Professional Fields
Expert1	Manager	20 years	Determining criteria, alternatives and criteria weights	Airport operations and management
Expert2	Expert	18 years	Creating the decision matrix	Fuel supply chain and logistics
Expert3	Expert	15 years	Creating the decision matrix	Airline management and operations
Expert4	Expert	10 years	Creating the decision matrix	Airport ground operations and airline support services

. The next section provides detailed information about the identified criteria and alternatives.

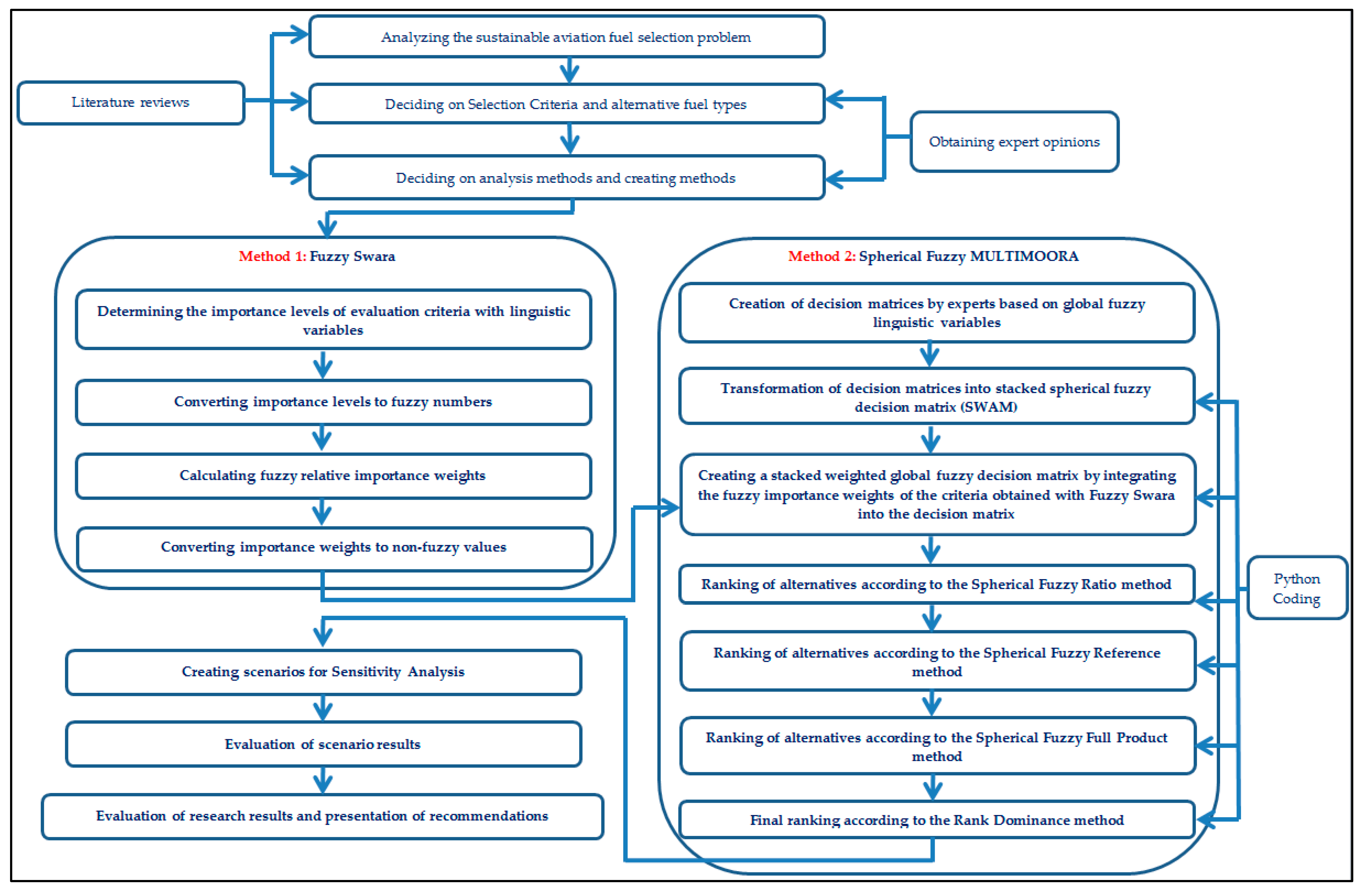
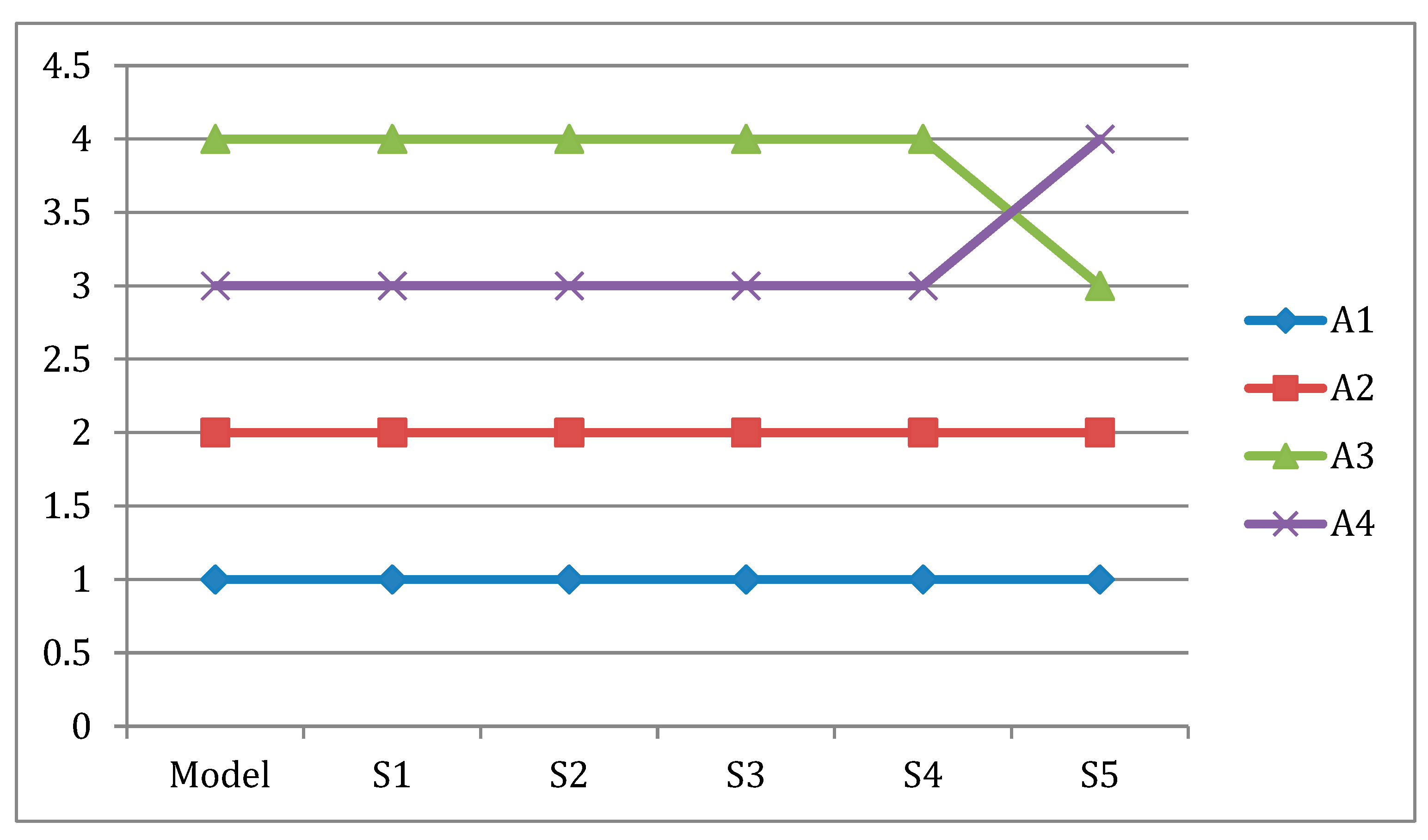
Figure 3 presents the multi-criteria decision-making process for SAF selection, which addresses uncertain and subjective assessments. The process begins with criteria selection using fuzzy numbers and fuzzy linguistic variables, taking into account expert opinions and a literature review. After weighting using the F-SWARA method, fuzzy decision matrices were created. Then, alternative fuels were ranked by applying SF-MULTIMOORA methods. In the final stage, scenarios for sensitivity analysis were created and evaluated, and the results were analyzed.

2.3. Determining SAF Selection Criteria and Alternatives

This section summarizes the criteria used in SAF selection studies in the existing literature and the alternative fuels evaluated in these selection studies. As a result of the reviewed literature, the criteria and alternative fuels to be used in this study were determined.

In their study, Ahmad et al. (2021) propose a MCDM process with stakeholder participation for the evaluation of SAF production pathways [17]. Methodologically, the weight of each criterion was determined based on the assessments of various stakeholder groups (industry representatives, policy makers, academics, etc.) using a stakeholder-based weighting approach, and then alternative production pathways were ranked using weighted scoring. The criteria assessed include 10 main elements covering the environmental, social and economic dimensions of sustainability, such as greenhouse gas emissions, total cost, energy efficiency, resource availability, political support, social acceptance and employment impact. According to the results, technologies such as waste-based gasification and biomass gasification were identified as the most sustainable fuel production pathways with the highest scores. The study reveals that integrating various stakeholder perspectives can improve decision quality. Chai and Zhou (2022) developed a new hybrid MCDM method for the evaluation of sustainable alternative aviation fuels under supply chain management [18]. The method determines the criteria weights with SWARA and then ranks the alternatives with the Combined Compromise Solution (CoCoSo) method. The criteria set consists of economic (cost, profitability), environmental (emissions, environmental impact), social (public acceptance, labor impact) and technical (technology level, energy efficiency) dimensions. According to the results of the exercise, biomass-based FT fuels stood out as the most sustainable alternative, while fossil-based options received lower scores. It is also stated that SWARA method is useful for decision makers to understand the relative importance of criteria, while CoCoSo provides consistent results in ranking. This hybrid model provides decision makers with a flexible and effective roadmap for SAF selection. In their review, Cabrera and Sousa (2022) comprehensively analyze the existing literature by examining the environmental, economic and technical aspects of SAF use in aviation [3]. Although the study does not directly use an MCDM method, the evaluation theme is structured around multiple criteria such as environmental impacts (greenhouse gas emissions, carbon footprint), technical suitability (engine compatibility, energy intensity) and economic viability (production cost, raw material availability). Among the most discussed SAF types in the literature, HEFA, FT, ATJ and PtL fuels stand out. The authors emphasize that PtL and HEFA fuels stand out in terms of environmental sustainability, but factors such as cost, policy support and infrastructure alignment are barriers to widespread use. The study reveals that political and economic regulation, as well as technical compliance, are critical for the widespread adoption of sustainable aviation fuels. Chinnasamy et al. (2023) evaluated various SAF production technologies in terms of strategic criteria and applied the WASPAS method to determine the most appropriate technology [9]. In the decision-making process, 6 alternative technologies were compared based on 9 main criteria determined by expert opinions. These criteria include technical, economic and environmental factors such as capital cost, operating cost, technology readiness level (TRL), emissions reduction, raw material availability, policy support and technological flexibility. As a result of the ranking by WASPAS method, FT Synthesis (FTS) method was determined as the most suitable SAF production technology. The study emphasizes that, to achieve sustainability goals, the selection of appropriate technology should be evaluated with holistic criteria. In a review study, Kurzawska-Pietrowicz (2023) analyzes the life cycle emissions of SAFs and, in particular, the environmental impacts of CORSIA eligible fuels [10]. The study compares LCA values for various production pathways (e.g., FT, HEFA, ATJ) and raw materials (e.g., miscanthus, jatropha, agricultural waste). The main criteria used include Total Life Cycle Emissions, Core LCA (emissions from production and distribution processes) and ILUC (emissions from Indirect Land Use Change). The findings revealed that the lowest emissions were in fuels produced from miscanthus plant and FT method. In the HEFA method, jatropha oil presented the lowest value, while for some feedstocks (e.g., maize) the LCA value was even higher than for fossil fuels. In conclusion, the type of raw material, growing conditions and especially the ILUC factor play a critical role in the environmental sustainability of SAFs. Rajamanickam et al. (2023) presented a MCDM approach for the selection of sustainable alternatives in aviation fuel supply chain management [11]. Throughout the decision-making process, TOPSIS and AHP methods were used together to evaluate alternative fuels in a multidimensional manner. The main criteria used in the analysis included sustainability-based indicators such as cost, greenhouse gas emissions, environmental impact, energy efficiency, technological maturity and public acceptance. Criteria weights were determined by AHP method and alternatives were ranked by TOPSIS method. According to the results, environmental and economic criteria were prioritized, and biofuel-based alternatives were found to offer more sustainable options. The study highlights the importance of systematic decision support methods in sustainable fuel selection. Ecer et al. (2025) applied LOPCOW and MARCOS methods by integrating them in an interval-valued fuzzy neutrosophic environment to evaluate SAF suppliers for airlines [2]. The main criteria used in the assessment include economic, environmental and technical factors such as fuel quality, lead time, cost, environmental impact, technological relevance, sustainable production capacity and political relevance. While LOPCOW method was used to determine the criteria weights, MARCOS method was used to rank alternative suppliers. The findings show that suppliers with high sustainability performance, low environmental impact and operationally reliable suppliers receive higher scores. It is also emphasized that the proposed model provides decision makers with more flexible and reliable results under uncertainty. The study highlights the importance of multidimensional assessment approaches in the SAF supply chain. AbdelAziz et al. (2025) evaluated alternative aviation fuels using MCDM methods to improve sustainable supply chain management in the aviation industry [19]. The weights of 20 criteria were determined by CRITIC method, and four fuel alternatives were ranked by Stable Preference Ordering Towards Ideal Solution (SPOTIS) method. Expert uncertainties are modeled using singular-valued neutrosophic numbers. According to the study, algae-based fuel was identified as the most sustainable alternative, while soy-based fuel scored the lowest. Among the most important criteria are production cost, capital cost and fuel price, while water consumption is the least important. Environmental and social sustainability criteria such as energy consumption, greenhouse gas emissions, environmental impact, technology maturity, public acceptance and traceability are also included. Robustness of the model was tested by sensitivity analysis, and the results were found to be consistent.

In this study, the criteria are classified under four main headings: environmental, economic, social and technical/institutional, considering the SAF literature. We have structured 24 sub-criteria that are prominent in the literature review and frequently used in MCDM studies (Table 2). Table 2 shows the common criteria for sustainable aviation fuel selection selected from the reviewed literature. Each criterion has been clearly defined in line with the information obtained from practices in the literature and sector reports.

In line with the literature, a comprehensive set of 24 criteria encompassing environmental, economic, social, and technical dimensions was initially identified. However, based on expert assessments, the analysis was conducted on the eight criteria deemed most critical. Similar approaches have been adopted in previous studies; broad pools of criteria were identified from the literature and then narrowed down based on expert judgment to focus on the most influential factors [20]. This method ensures that the analysis focuses on criteria that are both methodologically valid and have the highest practical impact.

Table 2. Importance scale used in criteria comparisons.

Main Criteria	Sub-Criteria	Abbreviation	Explanation	References
Environmental	Carbon Emissions Reduction	C1	Reducing CO2 and other greenhouse gases emitted by aviation operations.	[9,11,18,19]
Environmental	Energy Consumption and Efficiency	C2	Total energy consumed by airport operations and how efficiently it is used.	[3,17,18,19]
Environmental	Waste Management and Recycling	C3	Processes for waste separation, recycling, and hazardous material disposal.	[10,17,18]
Environmental	Water Consumption and Management	C4	Total fresh water consumption and treatment/reuse practices.	[11,19,21]
Environmental	Noise Pollution Management	C5	Reduction in aircraft and ground operations noise impacting surroundings.	[11]
Environmental	Conservation of Natural Resources	C6	Efforts to preserve natural resources used in airport construction and operation.	[17,18]
Environmental	Ecological Effects (Air, Soil, Biodiversity)	C7	Impact of operations on surrounding ecosystems and biodiversity.	[11]
Economic	Investment Cost	C8	Initial capital cost required for sustainable infrastructure and technologies.	[2,3,9,17,18]
Economic	Operational and Maintenance Costs	C9	Recurring costs related to running and maintaining sustainability systems.	[17,18,19]
Economic	Return on Investment (ROI) and Payback Period	C10	Time required to recover investment through operational savings.	[19,21]
Economic	Economic Feasibility	C11	Overall financial viability of sustainability practices.	[11,18]
Economic	Energy Cost Savings	C12	Monetary savings resulting from energy efficiency initiatives.	[11,19]
Economic	Contribution to Local Economy	C13	Impacts on employment and regional economic development.	[18,19]
Social	Passenger Satisfaction	C14	Passengers’ perception of comfort, convenience, and service quality.	[19]
Social	Employee Satisfaction and Occupational Safety	C15	Working conditions and safety standards for airport staff.	[11]
Social	Social Acceptance and Responsibility	C16	Extent to which communities support airport sustainability initiatives.	[18,19]
Social	Accessibility (Disabled-Friendly Infrastructure)	C17	Availability of inclusive design and services for all passengers.	[21]
Social	Employment Impact	C18	Effect of sustainability practices on job creation.	[18]
Social	Stakeholder Engagement	C19	Involvement of stakeholders in sustainability planning.	[2]
Technical	Sustainability Certifications (e.g., ISO 14001, LEED)	C20	Recognition by external bodies for meeting sustainability standards.	[11,18]
Technical	Sustainability Reporting	C21	Regular publication of sustainability performance and initiatives.	[2,9]
Technical	Technological Infrastructure Readiness	C22	Level of integration and modernity of supporting technologies.	[9,11]
Technical	Digital Monitoring and Tracking Systems	C23	Use of digital tools to monitor sustainability indicators.	[3,18]
Technical	Policy and Strategy Integration	C24	Alignment of sustainability practices with national/institutional goals.	[2,18]

Table 2. Importance scale used in criteria comparisons.

Main Criteria	Sub-Criteria	Abbreviation	Explanation	References
Environmental	Carbon Emissions Reduction	C1	Reducing CO2 and other greenhouse gases emitted by aviation operations.	[9,11,18,19]
Environmental	Energy Consumption and Efficiency	C2	Total energy consumed by airport operations and how efficiently it is used.	[3,17,18,19]
Environmental	Waste Management and Recycling	C3	Processes for waste separation, recycling, and hazardous material disposal.	[10,17,18]
Environmental	Water Consumption and Management	C4	Total fresh water consumption and treatment/reuse practices.	[11,19,21]
Environmental	Noise Pollution Management	C5	Reduction in aircraft and ground operations noise impacting surroundings.	[11]
Environmental	Conservation of Natural Resources	C6	Efforts to preserve natural resources used in airport construction and operation.	[17,18]
Environmental	Ecological Effects (Air, Soil, Biodiversity)	C7	Impact of operations on surrounding ecosystems and biodiversity.	[11]
Economic	Investment Cost	C8	Initial capital cost required for sustainable infrastructure and technologies.	[2,3,9,17,18]
Economic	Operational and Maintenance Costs	C9	Recurring costs related to running and maintaining sustainability systems.	[17,18,19]
Economic	Return on Investment (ROI) and Payback Period	C10	Time required to recover investment through operational savings.	[19,21]
Economic	Economic Feasibility	C11	Overall financial viability of sustainability practices.	[11,18]
Economic	Energy Cost Savings	C12	Monetary savings resulting from energy efficiency initiatives.	[11,19]
Economic	Contribution to Local Economy	C13	Impacts on employment and regional economic development.	[18,19]
Social	Passenger Satisfaction	C14	Passengers’ perception of comfort, convenience, and service quality.	[19]
Social	Employee Satisfaction and Occupational Safety	C15	Working conditions and safety standards for airport staff.	[11]
Social	Social Acceptance and Responsibility	C16	Extent to which communities support airport sustainability initiatives.	[18,19]
Social	Accessibility (Disabled-Friendly Infrastructure)	C17	Availability of inclusive design and services for all passengers.	[21]
Social	Employment Impact	C18	Effect of sustainability practices on job creation.	[18]
Social	Stakeholder Engagement	C19	Involvement of stakeholders in sustainability planning.	[2]
Technical	Sustainability Certifications (e.g., ISO 14001, LEED)	C20	Recognition by external bodies for meeting sustainability standards.	[11,18]
Technical	Sustainability Reporting	C21	Regular publication of sustainability performance and initiatives.	[2,9]
Technical	Technological Infrastructure Readiness	C22	Level of integration and modernity of supporting technologies.	[9,11]
Technical	Digital Monitoring and Tracking Systems	C23	Use of digital tools to monitor sustainability indicators.	[3,18]
Technical	Policy and Strategy Integration	C24	Alignment of sustainability practices with national/institutional goals.	[2,18]

The SAF alternatives to be evaluated under this study were determined by considering the production routes that are frequently encountered in the literature and that stand out in terms of various criteria. Numerous studies in the literature provide comprehensive assessments of different types of SAFs from environmental, economic, technical and social dimensions. Ahmad et al. (2021) evaluated seven different SAF production routes (HEFA, FT-BtL, ATJ, PtL, FP, Hydrothermal Liquefaction (HTL), Aqueous Phase Reforming (APR) with multi-stakeholder participation [17]. The HEFA production pathway stands out in terms of technology maturity and cost-effectiveness, while the PtL option stands out for its carbon neutrality potential. Chai and Zhou (2022) analyzed sustainable alternative jet fuels such as HEFA, FT-SPK, ATJ-SPK, HRJ and DME-Jet using multi-criteria decision making. While HEFA was found advantageous in terms of environmental impacts, FT-SPK was noted for its technical maturity and ATJ for its economic viability [18]. Rajamanickam et al. (2023) compared alternative fuels such as HEFA, FT-SPK, ATJ-SPK, HRJ and DME-Jet in this study conducted within the framework of supply chain management [11]. Based on environmental and economic criteria, HEFA-SPK was the most suitable option. In their literature review, Kurzawska-Pietrowicz (2023) [10] compared the life cycle emissions of SAF types such as HEFA, FT-SPK, ATJ-SPK and SIP. In particular, miscanthus-based FT-SPK fuel was found to be the most environmentally advantageous option with negative carbon emissions, while jatropha-based HEFA stood out for its low land use impact. Chinnasamy et al. (2023) evaluated fuel production technologies such as HEFA, FT-SPK, ATJ-SPK, HTL, FP and APR in this analysis using the WASPAS method [9]. Based on the overall scoring, HEFA-SPK was identified as the most suitable alternative in terms of technology maturity, low emission potential and economic viability. In a study centered on the production of HEFA-SPK from canola oil, Antony et al. (2024) modeled potential production facilities in Canada using spatial analysis [22]. Canola was evaluated as a suitable and sustainable source for HEFA production due to its widespread agricultural production and high oil yield. Ullah et al. (2023) produced sustainable aviation fuel by catalytic hydrothermolysis method from oil obtained via carinata plant [23]. This resource, which does not compete with food production and can also produce diesel as a by-product, stands out as an alternative that can be grown on marginal soils, especially with low emissions. AbdelAziz (2025) evaluated the supply chain performance of SAF types such as FT-SPK, HEFA-SPK, ATJ-SPK, SIP and DSHC [19]. FT-SPK was found to be environmentally strong, while HEFA and ATJ-SPK were identified as alternatives preferred due to the prevalence of their production technologies and their cost-effectiveness. Ecer et al. (2025) evaluated SAF types obtained from various biomass sources (camelina, jatropha, used cooking oil, municipal waste, etc.) in this study [2]. The technical, environmental and economic performances of the fuels were compared and the HEFA-SPK types, especially those produced from waste-based sources such as used cooking oil (UCO) and jatropha, stood out in terms of suitability.

Table 3. Alternatives.

Alternative	Abbreviation	Raw Materials	Production	Advantage
HEFA-SPK	A1	Vegetable oils (e.g., jatropha, canola, carinata), animal fats, UCO.	Oils are hydroprocessed; glycerin is separated, long-chain hydrocarbons are cut, and converted into jet fuel.	It is the most widely used type of SAF today. It is compatible with existing infrastructures (drop-in) and has a high energy density.
FT-SPK	A2	Biomass (e.g., miscanthus, forest/residual waste), coal or natural gas	Biomass is gasified → synthetic gas (syngas) is obtained → liquid fuel is synthesized by the FT reaction.	It produces high purity fuel, carbon content can be controlled.
ATJ-SPK	A3	Alcohols of biological origin such as ethanol and isobutanol.	Alcohol molecules are converted into jet fuel through dehydration, oligomerization, and hydrotreating.	Since bioethanol infrastructure is widespread, its applicability is high in some countries.
PtL	A4	Carbon dioxide (CO2) and water (H2O), renewable electricity.	Water electrolysis is performed with renewable energy → hydrogen is produced → synthetic liquid fuel (e-kerosene) is obtained by combining it with CO2.	It is the only method with carbon neutral potential (direct use of CO2).

shows the alternative fuels to be evaluated in the study selected from the literature reviewed.

In addition, the reliability of the data sources was ensured by combining peer-reviewed academic studies, internationally recognized reports (e.g., IATA, ICAO, ASTM), and expert evaluations from industry professionals with more than ten years of experience in aviation operations [24,25]. This integration of multiple sources strengthens the validity and credibility of the criteria used in the analysis.

In addition to the advantages discussed above, it should be noted that some of these alternatives (e.g., HEFA-SPK, FT-SPK, ATJ-SPK, SIP) are certified for use when blended with conventional jet fuels at specific ratios under ASTM D7566. This certification ensures compliance with international safety and performance standards and increases the practical applicability and acceptance of these fuels in the aviation industry [26,27].

2.4. Fuzzy Sets

Classical set theory operates on a binary principle: an element either fully belongs to a set (membership = 1) or not at all (membership = 0). Fuzzy Set Theory, introduced by Lotfi A. Zadeh in 1965, revolutionized this concept by allowing partial membership [6]. This is crucial for modeling real-world concepts that are inherently vague or qualitative, such as “hot weather”, “tall person”, or “high speed”.

In a fuzzy set, each element is assigned a membership value between 0 and 1, indicating its degree of belonging to the set. A value of 0.9 indicates that the element is very strongly associated with the set, while a value of 0.1 indicates that it is very weakly associated. All variables used in the study are included in Appendix A.

Formal Definition:

A fuzzy set μ defined in the universe X is characterized by a membership function ${\mathrm{\mu }}_{\mathrm{Ã}}$($x$) that maps each element in X to a real number in the interval [0, 1].

$$Ã=\left\{\right( x, {\mathrm{\mu }}_{\mathrm{Ã}}\left(x\right)) | x \in X\}$$

where ${\mathrm{\mu }}_{\mathrm{Ã}}$($x$): X → [0, 1].

Membership functions are defined in various ways in the literature, depending on the problem definition. The most commonly used membership functions are triangular and trapezoidal membership functions [28]. The membership function of the triangular fuzzy set à ($l$, $m$, $u$) is defined as in Equation (1) and shown as in Figure 4.

$${\mathrm{\mu }}_{\mathrm{Ã}}(x)=\left\{\begin{array}{c}0, x<1;\\ \\ {\displaystyle \frac{x-l}{m-l}} l\le x \le m;\\ \\ {\displaystyle \frac{u-x}{u-m}} m\le x \le u;\\ \\ 0, x>u.\end{array}\right.$$

(1)

The basic operations for two triangular fuzzy sets ${Ã}_1$($l_1, m_1, u_1$) ve ${Ã}_2$($l_2, m_2, u_2$) are defined over their membership functions as follows:

$${\tilde{\mathrm{A}}}_1\oplus {\tilde{\mathrm{A}}}_2= (l_1, m_1,u_1) + (l_2, m_2,u_2) = ({l_1+ l}_2, m_1+ m_2,u_1+ u_2)$$

(2)

$${\tilde{\mathrm{A}}}_1(-){\tilde{\mathrm{A}}}_2=(l_1, m_1,u_1)-(l_2, m_2,u_2)=({l_1-u}_2, m_1-m_2,u_1+l_2)$$

(3)

$${\tilde{\mathrm{A}}}_1⨂{\tilde{\mathrm{A}}}_2=(l_1, m_1,u_1) \ast (l_2, m_2,u_2)=({l_1\ast l}_2, m_1\ast m_2,u_1\ast u_2)$$

(4)

$${\tilde{\mathrm{A}}}_1/{\tilde{\mathrm{A}}}_2=(l_1, m_1,u_1)/(l_2, m_2,u_2)=({l_1/u}_2, m_1/m_2,u_1/l_2)$$

(5)

$$k\ast {\tilde{\mathrm{A}}}_1=\ast (l_1, m_1,u_1)=({k\ast l}_1, {k\ast m}_1,k\ast u_2)$$

(6)

$${{\tilde{\mathrm{A}}}_1}^{-1}={(l_1, m_1, u_1)\mathrm{ }}^{-1}=({1/u}_1, 1/m_1,1/l_1)$$

(7)

2.5. Fuzzy SWARA

In this study, the F-SWARA method was preferred for determining the criterion weights, as it directly reflects expert opinions and provides a systematic weighting process. In the literature, various fuzzy and hybrid MCDM methods have also been successfully applied for weighting criteria and ranking alternatives under uncertainty [29]. For example, Nguyen et al. integrated the SF-AHP with the WASPAS-F method in a global fuzzy environment to evaluate government strategies against the COVID-19 pandemic [30]. Such approaches demonstrate the flexibility of fuzzy extensions in more sensitively capturing decision-maker uncertainty. Considering the scope of our study, the F-SWARA method was adopted as a practical way to systematically incorporate expert evaluations. The main steps of the F-SWARA method are summarized as follows [31]:

Step 1: Evaluation criteria $j$ are ranked by decision makers based on their level of importance.

Step 2: By using the linguistic variables specified in

Table 4. Linguistic Variables.

Linguistic Variables	Fuzzy Number (l, m, u)
Equally Important (EI)	(1, 1, 1)	(1, 1, 1)
Moderately less important (MI)	(2/3, 1, 3/2)	(0.67, 1, 1.50)
Less Important (LI)	(2/5, 1/2, 2/3)	(0.40, 0.50, 0.67)
Very Less Important (VI)	(2/7, 1/3, 2/5)	(0.29, 0.33, 0.40)
Much Less Important (MuI)	(2/9, 1/4, 2/7)	(0.22, 0.25, 0.29)

, the “relative importance levels” are calculated by comparing the $j$ criterion with the $j-1$ criterion with a higher level of importance than itself. This value is expressed as ${\tilde{S}}_j={\tilde{S}}_j^l, {\tilde{S}}_j^m, {\tilde{S}}_j^u$.

Step 3: The ${\tilde{k}}_j$ value for all criteria is calculated using Equation (8).

In this formula,

$$\left\{{\tilde{k}}_j=\left\{\begin{array}{cc}\hfill 1,& j=1\hfill \\ \hfill {\tilde{S}}_j+1,& j>1\hfill \end{array}\right.\right. {\tilde{k}}_j=({\tilde{k}}_j^l, {\tilde{k}}_j^m, {\tilde{k}}_j^u)$$

(8)

Step 4: The ${\tilde{q}}_j$ value for all criteria is calculated using Equation (9).

In this formula,

$$\left\{{\tilde{q}}_i=\left\{\begin{array}{cc}\hfill 1,& j=1\hfill \\ \hfill {\displaystyle \frac{{\tilde{q}}_{j-1}}{{\tilde{k}}_j}},& j>1\hfill \end{array}\right.\right. {\tilde{q}}_j=({\tilde{q}}_j^l, {\tilde{q}}_j^m, {\tilde{q}}_j^u)$$

(9)

Step 5: The ${\tilde{w}}_j$ value for all criteria is calculated using Equation (10).

$${\tilde{w}}_j={\displaystyle \frac{{\tilde{q}}_j}{\sum _{k=1}^n{\tilde{q}}_k}} {\tilde{w}}_j=({\tilde{w}}_j^l, {\tilde{w}}_j^m, {\tilde{w}}_j^u)$$

(10)

Step 6: The fuzzy relative importance weight values obtained for all criteria are converted into normal/non-fuzzy values using Equation (11).

$$w_j={\displaystyle \frac{w_j^u + (4\ast w_j^m) + w_j^l}{6}}$$

(11)

2.6. Spherical Fuzzy Sets

Spherical Fuzzy Sets (SFS) represent a significant extension of traditional fuzzy sets and other models like Pythagorean and picture fuzzy sets. Developed by Kutlu Gündoğdu and Cengiz Kahraman, SFS are designed to handle situations where decision-makers or systems need to express not just a degree of membership but also independent degrees of non-membership and hesitancy (uncertainty) simultaneously [32].

The unique and powerful constraint of a Spherical Fuzzy Set is that the squared sum of membership, non-membership, and hesitancy parameters for any element must be less than or equal to 1. This defines a spherical volume of possible values, which is the origin of the name.

Formal Definition

A Spherical Fuzzy Set ${\tilde{\mathrm{A}}}_{\mathrm{S}}$ of the universe of discourse X is given by:

$${\tilde{\mathrm{A}}}_{\mathrm{S}}= \{⟨x, ({\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}(x), {\mathrm{v}}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}(x), {\mathrm{\pi }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}(x) (x))⟩ | x \in X\}$$

where

${\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}$ (x): X → [0, 1] is the membership function of x.

${\mathrm{v}}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}$ (x): X → [0, 1] is the non-membership function of x.

${\mathrm{\pi }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}$ (x): X → [0, 1] is the hesitancy function of x.

These functions must satisfy the following condition for all x ∈ X:

$$0 \le {{\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2\left(x\right) + {{\mathrm{v}}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2\left(x\right) + {{\mathrm{\pi }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2\left(x\right) \le 1$$

Operations with spherical fuzzy sets are defined as follows: (λ is a positive scalar).

$${\tilde{\mathrm{A}}}_{\mathrm{S}}\oplus {\tilde{\mathrm{B}}}_{\mathrm{S}}=\left\{{\left[{{\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2+{{\mathrm{\mu }}_{{\tilde{\mathrm{B}}}_{\mathrm{S}}}}^2-{{\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2{{\mathrm{\mu }}_{{\tilde{\mathrm{B}}}_{\mathrm{S}}}}^2\right]}^{1/2}, {\mathrm{v}}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}{\mathrm{v}}_{{\tilde{\mathrm{B}}}_{\mathrm{S}}}, {\left[\left(1-{{\mathrm{\mu }}_{{\tilde{\mathrm{B}}}_{\mathrm{S}}}}^2\right){{\mathrm{\pi }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2+\left(1-{{\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2\right){{\mathrm{\pi }}_{{\tilde{\mathrm{B}}}_{\mathrm{S}}}}^2-{{\mathrm{\pi }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2{{\mathrm{\pi }}_{{\tilde{\mathrm{B}}}_{\mathrm{S}}}}^2\right]}^{1/2} \right\}$$

(12)

$${\tilde{\mathrm{A}}}_{\mathrm{S}}⨂{\tilde{\mathrm{B}}}_{\mathrm{S}}=\left\{{\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}{\mathrm{\mu }}_{{\tilde{\mathrm{B}}}_{\mathrm{S}}}, {\left[{{\mathrm{v}}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2+{{\mathrm{v}}_{{\tilde{\mathrm{B}}}_{\mathrm{S}}}}^2-{{\mathrm{v}}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2{{\mathrm{v}}_{{\tilde{\mathrm{B}}}_{\mathrm{S}}}}^2\right]}^{1/2}, {\left[\left(1-{{\mathrm{v}}_{{\tilde{\mathrm{B}}}_{\mathrm{S}}}}^2\right){{\mathrm{\pi }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2+\left(1-{{\mathrm{v}}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2\right){{\mathrm{\pi }}_{{\tilde{\mathrm{B}}}_{\mathrm{S}}}}^2-{{\mathrm{\pi }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2{{\mathrm{\pi }}_{{\tilde{\mathrm{B}}}_{\mathrm{S}}}}^2\right]}^{1/2} \right\}$$

(13)

$$\mathrm{\lambda }. {\tilde{\mathrm{A}}}_{\mathrm{S}}=\left\{{\left[1-{\left(1-{{\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2\right)}^{\lambda }\right]}^{1/2}, {{\mathrm{v}}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^{\lambda }, {\left[{\left(1-{{\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2\right)}^{\lambda }-{\left(1-{{\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2-{{\mathrm{\pi }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2\right)}^{\lambda }\right]}^{1/2} \right\}$$

(14)

$${{\tilde{\mathrm{A}}}_{\mathrm{S}}\mathrm{ }}^{\lambda }=\left\{{{\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^{\lambda }, {\left[1-{\left(1-{{\mathrm{v}}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2\right)}^{\lambda }\right]}^{1/2}, {\left[{\left(1-{{\mathrm{v}}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2\right)}^{\lambda }-{\left(1-{{\mathrm{v}}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2-{{\mathrm{\pi }}_{{\tilde{\mathrm{A}}}_{\mathrm{S}}}}^2\right)}^{\lambda }\right]}^{1/2} \right\}$$

(15)

2.7. SF-MULTIMOORA

SF-MULTIMOORA method was proposed by Gündoğdu and basically includes the Spherical ratio method, Spherical reference point method and Spherical full multiplicative form method [33]. The first four steps of these methods are the same. The SF-MULTIMOORA method, with its multifaceted evaluation structure, allows for a balanced analysis of both advantages and disadvantages. The use of spherical fuzzy numbers covers a wider range of decision maker uncertainties. The reason why SF-MULTIMOORA is preferred in this study is that spherical fuzzy sets can reflect uncertainty and hesitations more precisely than classical fuzzy sets and thus provide higher reliability in the evaluation of alternatives.

The method, which evaluates the data in a spherical fuzzy environment, expresses the $X=\left\{x_1, x_2,\dots x_m\right\} (m\ge 2)$ $m$ number of alternatives in a matrix structure and the number of criteria in the $C=\left\{C_1, C_2, \dots C_n\right\}$ finite number. In the evaluation of alternatives, the value of each alternative given according to the criterion is expressed as $C_j\left(X_i\right)$ (i = 1, 2, …, m ve j = 1, 2, …, n) and is shown as spherically fuzzy as $C_j\left(X_i\right)$ = (${\mu }_{ij}, v_{ij}, {\pi }_{ij}$). $w=\left\{w_1, w_2, \dots w_n\right\}$ also refers to the weight vector of the decision makers, which must take a value between $0\le w_j\le 1$ and satisfy the equality of ${\sum }_{j=1}^n{w}_j=1$.

Step 1. Formation of decision matrices involving the evaluation of alternatives based on scales by decision makers using scales.

The linguistic expressions used in the evaluation while creating the decision matrices are given in

Table 5. Spherical Fuzzy 9-Point Linguistic Scale.

Linguistic Terms	($\mu , \mathit{v}$, π)	Linguistic Terms	($\mu , \mathit{v}$, π)
Extremely High Importance	(0.9; 0.1; 0.1)	Medium Low Importance	(0.4; 0.6; 0.4)
Very High Importance	(0.8; 0.2; 0.2)	Low Importance	(0.3; 0.7; 0.3)
High Importance	(0.7; 0.3; 0.3)	Very Low Importance	(0.2; 0.8; 0.2)
Medium High Importance	(0.6; 0.4; 0.4)	Extremely Low Importance	(0.1; 0.9; 0.1)
Medium Importance	(0.5; 0.5; 0.5)

. Of the linguistic expressions in the table, the linguistic expression with the higher value for the benefit criterion and the linguistic expression with the lower value for the cost criterion are used.

Step 2. Aggregation of spherical fuzzy importance weight data assigned to criteria by decision makers using Equation (16).

$$\begin{array}{cc}{\mathrm{SWAM}}_w({\tilde{\mathrm{A}}}_{\mathrm{S}1},& \dots , {\tilde{\mathrm{A}}}_{\mathrm{Sn}}) =w_1{\tilde{\mathrm{A}}}_{\mathrm{S}1}+{ w}_2{\tilde{\mathrm{A}}}_{\mathrm{S}2}+\dots +w_{\mathrm{n}}{\tilde{\mathrm{A}}}_{\mathrm{Sn}}\\ & =\left\{{\left[1\text{-}{\Pi }_{\mathrm{i}=1}^{\mathrm{n}}{(1\text{-}{\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{{\mathrm{S}}_{\mathrm{i}}}}^2)}^{w_i}\right]}^{1/2}, {\Pi }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{v}}_{{\tilde{\mathrm{A}}}_{{\mathrm{S}}_{\mathrm{i}}}}^{w_i}, {\left[{\Pi }_{\mathrm{i}=1}^{\mathrm{n}}{(1{\text{-}\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{{\mathrm{S}}_{\mathrm{i}}}}^2)}^{w_i}\text{-}{\Pi }_{\mathrm{i}=1}^{\mathrm{n}}{(1\text{-}{\mathrm{\mu }}_{{\tilde{\mathrm{A}}}_{{\mathrm{S}}_{\mathrm{i}}}}^2\text{-})}^{w_i}\right]}^{1/2} \right\}\end{array}$$

(16)

Step 3. The different decision matrices created by the decision makers are converted into an agglomerated global fuzzy decision matrix using the agglomerative operator presented in Equation (16). The structure of the created decision matrix is shown in Equation (17). $D={\left(C_j\left(X_i\right)\right)}_{mxn}$ is spherical fuzzy decision matrix. Structure of the decision matrix is given in Equation (17).

$$\begin{array}{c}D={\left(C_j\left(X_i\right)\right)}_{mxn}\\ =\left(\begin{array}{c}\left({\mu }_{11}, v_{11}, {\pi }_{11}\right) \left({\mu }_{12}, v_{12}, {\pi }_{12}\right)\dots \left({\mu }_{1n}, v_{1n}, {\pi }_{1n}\right) \left({\mu }_{21}, v_{21}, {\pi }_{21}\right) \left({\mu }_{22}, v_{22}, {\pi }_{22}\right)\dots \\ \left({\mu }_{2n}, v_{2n}, {\pi }_{2n}\right) \dots \left({\mu }_{m1}, v_{m1}, {\pi }_{m1}\right) \left({\mu }_{m2}, v_{m2}, {\pi }_{m2}\right)\dots ({\mu }_{mn}, v_{mn}, {\pi }_{mn}) \end{array}\right)\end{array}$$

(17)

In the decision-making, all criteria are treated as benefit criteria to ensure consistency in evaluation, regardless of whether they are originally cost or benefit in nature. Decision makers assign higher linguistic terms to alternatives that perform better with respect to each criterion. For cost criteria, where lower values are more desirable, alternatives with low costs are evaluated more favorably and are therefore assigned higher linguistic ratings [33].

Step 4. Construction of an aggregated weighted spherical fuzzy decision matrix. The criterion weights obtained in Step 2 and the decision matrix values obtained in Step 3 are transformed into an aggregated weighted spherical fuzzy decision matrix using Equation (13). It is shown by the equation below.

$$D={\left(C_j\left(X_{iw}\right)\right)}_{mxn}=\left(\begin{array}{c}\left({\mu }_{11w}, v_{11w}, {\pi }_{11w}\right) \left({\mu }_{12w}, v_{12w}, {\pi }_{12w}\right)\dots \left({\mu }_{1nw}, v_{1nw}, {\pi }_{1nw}\right) \left({\mu }_{21w}, v_{21w}, {\pi }_{21w}\right) \left({\mu }_{22w}, v_{22w}, {\pi }_{22w}\right)\dots \\ \left({\mu }_{2nw}, v_{2nw}, {\pi }_{2nw}\right) \dots \left({\mu }_{m1w}, v_{m1w}, {\pi }_{m1w}\right) \left({\mu }_{m2w}, v_{m2w}, {\pi }_{m2w}\right)\dots ({\mu }_{mnw}, v_{mnw}, {\pi }_{mnw}) \end{array}\right)$$

(18)

The aggregated weighted spherical fuzzy decision matrix created by the first four steps above will be the starting point for all three methods to be used.

2.7.1. Spherical Fuzzy Ratio Method

Step 1. In this step, the values ${Ỹ}_i^{+}$ are obtained by using the aggregated weighted spherical fuzzy decision matrix Equation (19).

$${Ỹ}_i^{+}=\left({\left[{1-{\Pi }_{j=1}^n(1-{\mu }_{A_{S_j}}^2)}^{1/n}\right]}^{1/2}, {\Pi }_{j=1}^n{v}_{A_{S_j}}^{1/n}, {\left[{{\Pi }_{j=1}^n(1-{\mu }_{A_{S_j}}^2)}^{1/n}-{{\Pi }_{j=1}^n(1-{\mu }_{A_{S_j}}^2-{\pi }_{A_{S_j}}^2)}^{1/n}\right]}^{1/2}\right)$$

(19)

Step 2. The resulting values are then defuzzied using Equation (20) below.

$$y_i^{+}=Score\left({Ỹ}_i^{+}\right)={(2{\mu }_{{Ỹ}_i^{+}}-{\displaystyle \frac{{\pi }_{{Ỹ}_i^{+}}}{2}})}^2-{\left(v_{{Ỹ}_i^{+}}-{\displaystyle \frac{{\pi }_{{Ỹ}_i^{+}}}{2}}\right)}^2$$

(20)

Step 3. The alternatives will be ranked by their defuzzied $y_i^{+}$ values and the one with the highest value will be determined as the best alternative.

2.7.2. Spherical Fuzzy Reference Method

Step 1. In this step, the reference points are identified using the aggregated weighted spherical fuzzy decision matrix Equation (21). Reference points are obtained by determining the highest score function from the spherical fuzzy data used in the evaluation of alternatives based on each criterion.

$$\begin{array}{c}{X}_j^{*}=\left\{C_j, \begin{array}{c}max\\ i\end{array}<Score \left(C_j\left(X_{iw}\right)\right)>|j=1, 2, \dots , n\right\}\\ \hspace{1em}\mathrm{or}\\ X_j^{\ast }=\left\{〈C_1,\mathrm{ }({\mu }_1, v_1, {\pi }_1)〉, \dots , 〈C_n,\mathrm{ }({\mu }_n, v_n, {\pi }_n)〉\right\}\end{array}$$

(21)

Step 2. The distance of all alternatives to the reference point is calculated by Equation (22).

$$d\left(X_{ij},X_j^{*}\right)={\displaystyle \frac{1}{2}}\left(\left|{{\mu }_{x_{ij}}}^2-{{\mu }_{x_j^{*}}}^2\right|+\left|{v_{x_{ij}}}^2-{v_{x_j^{*}}}^2\right|+\left|{{\pi }_{x_{ij}}}^2-{{\pi }_{x_j^{*}}}^2\right|\right)$$

(22)

Step 3. Equation (23) is used to calculate the deviation values of the alternatives from the reference point. The best alternative will be the one with the lowest deviation.

$${min}_i\left\{{max}_{j}d(X_{ij},X_j^{*}) \right\}$$

(23)

2.7.3. Spherical Fuzzy Full Multiplicative Form Method

Step 1. In this step, the aggregated weighted spherical fuzzy decision matrix values ${Ã}_i$ are calculated using Equation (24).

$${Ã}_i=\left({\Pi }_{j=1}^m{\mu }_{{Ã}_{ij}}, {\left[1-{\Pi }_{j=1}^m(1-v_{{Ã}_{ij}}^2)\right]}^{1/2},{\left[{\Pi }_{j=1}^m\left(1-v_{{Ã}_{ij}}^2\right)-{\Pi }_{j=1}^m\left(1-v_{{Ã}_{ij}}^2\right)-{\pi }_{{Ã}_{ij}}^2\right]}^{1/2}\right)$$

(24)

Step 2. Using Equation (25), the ${Ã}_i$ values are defuzzied.

$$a_i=Skor\left({Ã}_i\right)={(2{\mu }_{{Ã}_{ij}}-{\displaystyle \frac{{\pi }_{{Ã}_i}}{2}})}^2-{(v_{{Ã}_i}-{\displaystyle \frac{{\pi }_{{Ã}_i}}{2}})}^2$$

(25)

Step 3. The alternatives are ranked by defuzzied values. The best alternative will be determined as the one with the highest value.

2.7.4. Rank Dominance Method

Rank dominance theory was first used by Breuers and Zavadskas in 2010 [34]. It is based on the axiom that an ordinal scale of a certain ordinal type can be replaced by an ordinal scale of another type. According to this method, the more dominant alternatives will be determined by evaluating the results of the three different methods included in SF-MULTIMOORA method.

3. Results and Discussion

3.1. Finding Selection Criteria Weights

In this study, F-SWARA method was applied as a first step to evaluate sustainable aviation fuels in a multi-criteria decision-making process. Microsoft Excel 2016 software was used for method calculations. F-SWARA application steps are as follows:

Step 1: The criteria identified through the literature review were evaluated by considering previous studies and expert assessments. Accordingly, the importance of each criterion was determined, and the criteria were ranked by their level of importance.

Step 2: The relative importance levels between the criteria were calculated using the linguistic variables specified in Table 3.

Steps 3, 4, 5: $k_j, q_j, w_j$ values were calculated for all criteria.

Step 6: The fuzzy relative importance weight values obtained for all criteria were converted into non-fuzzy values.

Table 6. FSWARA calculation values applied to SAF selection criteria.

Criteria	Importance Ranking	Relationship with Previous Criteria	l_Value	m_Value	u_Value	${\mathit{w}}_{\mathit{j}}^{\mathit{l}}$	${\mathit{w}}_{\mathit{j}}^{\mathit{m}}$	${\mathit{w}}_{\mathit{j}}^{\mathit{u}}$	${\mathit{w}}_{\mathit{j}}$
C1	1	-	0	0	0	0.258	0.285	0.319	0.2862786264
C2	2	VI	0.29	0.33	0.4	0.200	0.214	0.228	0.2142491658
C10	3	MuI	0.22	0.25	0.29	0.164	0.172	0.177	0.1711121944
C11	4	VI	0.29	0.33	0.4	0.127	0.129	0.126	0.1281851086
C3	5	LI	0.4	0.5	0.67	0.091	0.086	0.076	0.0850370203
C5	6	MI	0.67	1	1.5	0.054	0.043	0.030	0.0427528704
C4	7	EI	1	1	1	0.027	0.021	0.015	0.0213764352
C7	8	MuI	0.22	0.33	0.4	0.022	0.016	0.011	0.0162847694
C20	9	LI	0.4	0.5	0.67	0.016	0.011	0.006	0.0109111100
C8	10	MuI	0.22	0.33	0.4	0.013	0.008	0.005	0.0083430641
C9	11	VI	0.29	0.33	0.4	0.010	0.006	0.003	0.0062947036
C6	12	LI	0.4	0.5	0.67	0.007	0.004	0.002	0.0042393713
C12	13	MI	0.67	1	1.5	0.004	0.002	0.001	0.0022056497
C14	14	EI	1	1	1	0.002	0.001	0.000	0.0011028248
C15	15	LI	0.4	0.5	0.67	0.002	0.001	0.000	0.0007479035
C13	16	MI	0.67	1	1.5	0.001	0.000	0.000	0.0003954346
C21	17	MI	0.67	1	1.5	0.001	0.000	0.000	0.0002113653
C16	18	MI	0.67	1	1.5	0.000	0.000	0.000	0.0001141687
C17	19	EI	1	1	1	0.000	0.000	0.000	0.0000570843
C23	20	LI	0.4	0.5	0.67	0.000	0.000	0.000	0.0000392862
C18	21	VI	0.29	0.33	0.4	0.000	0.000	0.000	0.0000299701
C19	22	MI	0.67	1	1.5	0.000	0.000	0.000	0.0000164425
C22	23	MI	0.67	1	1.5	0.000	0.000	0.000	0.0000091047
C24	24	LI	0.4	0.5	0.67	0.000	0.000	0.000	0.0000063251
								Total	1.000

shows the FSWARA calculations.

Carefully examining Table 6, it is observed that the sum of w_j values is 1. The fact that the sum of the criteria weights is one indicates that the calculations are correct. According to the table, the three most important criteria are “reduction of carbon emissions”, “energy consumption and efficiency” and “waste management and recycling”, while the three least important criteria are “stakeholder engagement”, “preparation for technological infrastructure” and “policy and strategy integration”. For sustainable aviation fuels, companies’ choices are largely influenced by environmental and economic criteria, while social and technical criteria are considered less important.

Based on the results obtained through the F-SWARA method, the 8 criteria with the highest weights were selected as the prominent elements in the decision-making process. These 8 criteria were re-weighted by the Fuzzy SWARA method to be used in the evaluation of alternatives in the second stage of the study (

Table 7. Criterion weights for the top 8 criteria with high weight scores using F-SWARA.

Criteria	Weights	Description
C1	0.296408	Environmental
C2	0.221889	Environmental
C10	0.177246	Economic
C11	0.132815	Economic
C3	0.088158	Environmental
C5	0.044380	Environmental
C4	0.022190	Environmental
C7	0.016913	Environmental

). In this way, decision makers’ priorities are accurately reflected even within a narrowed set of criteria.

Although the eight criteria derived through the F-SWARA method did not initially include the social and technological dimensions, under the sensitivity analysis the two sub-criteria with the highest weights from each main criterion group (environmental, economic, social, technical/institutional) were selected, resulting in a total of eight representative criteria. This approach ensured that all dimensions of sustainability were represented, strengthened the robustness of the model, and confirmed that the results remained consistent across different perspectives.

3.2. Finding the Rank Order of the Alternatives

In this part of the study, alternative fuel types were evaluated by SF-MULTIMOORA method based on eight criteria, which were firstly determined and re-weighted by F-SWARA method. SF-MULTIMOORA algorithm was used for ranking the alternatives with the help of online python compiler (Figure 5).

The SF-MULTIMOORA algorithm combines three basic approaches to provide decision makers with a comprehensive analysis. This algorithm, developed on Python 2025, provides final ranking with evaluation based on normalized values. Operation of the algorithm is summarized in Figure 6. The basic functions used in the process are explained below.

• Decision matrix and weights are determined.
• A Spherical Fuzzy Set class is created, and the accuracy of the membership degrees is checked.
• SWAM (Spherical Weighted Arithmetic Mean) is calculated.
• The score function is defined and compares the decision alternatives.
• It is ranked by three different methods using Ratio, Reference Point, and FMF (geometric score) methods.
• Final scoring is performed with SF-MULTIMOORA.
• Finally, the results are shown.

According to the Spherical Fuzzy 9-Point Linguistic Scale in Table 5, a decision matrix was created in line with the opinions 3 of the experts in

Table 8. Decision matrix of the first 8 criteria with high weight scores of Expert1.

	C1	C2	C10	C11	C3	C5	C4	C7
A1	(0.8, 0.2, 0.2)	(0.7, 0.3, 0.3)	(0.8, 0.2, 0.2)	(0.9, 0.1, 0.1)	(0.7, 0.3, 0.3)	(0.7, 0.3, 0.3)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)
A2	(0.9, 0.1, 0.1)	(0.5, 0.5, 0.5)	(0.7, 0.3, 0.3)	(0.7, 0.3, 0.3)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)	(0.6, 0.4, 0.4)	(0.7, 0.3, 0.3)
A3	(0.7, 0.3, 0.3)	(0.6, 0.4, 0.4)	(0.6, 0.4, 0.4)	(0.3, 0.7, 0.3)	(0.7, 0.3, 0.3)	(0.4, 0.6, 0.4)	(0.7, 0.3, 0.3)	(0.5, 0.5, 0.5)
A4	(0.9, 0.1, 0.1)	(0.2, 0.8, 0.2)	(0.1, 0.9, 0.1)	(0.1, 0.9, 0.1)	(0.8, 0.2, 0.2)	(0.1, 0.9, 0.1)	(0.2, 0.8, 0.2)	(0.8, 0.2, 0.2)

,

Table 9. Decision matrix of the first 8 criteria with high weight scores of Expert2.

	C1	C2	C10	C11	C3	C5	C4	C7
A1	(0.8, 0.2, 0.2)	(0.7, 0.3, 0.3)	(0.8, 0.2, 0.2)	(0.9, 0.1, 0.1)	(0.7, 0.3, 0.3)	(0.7, 0.3, 0.3)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)
A2	(0.9, 0.1, 0.1)	(0.5, 0.5, 0.5)	(0.7, 0.3, 0.3)	(0.7, 0.3, 0.3)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)	(0.6, 0.4, 0.4)	(0.7, 0.3, 0.3)
A3	(0.7, 0.3, 0.3)	(0.6, 0.4, 0.4)	(0.6, 0.4, 0.4)	(0.3, 0.7, 0.3)	(0.7, 0.3, 0.3)	(0.4, 0.6, 0.4)	(0.7, 0.3, 0.3)	(0.5, 0.5, 0.5)
A4	(0.9, 0.1, 0.1)	(0.2, 0.8, 0.2)	(0.1, 0.9, 0.1)	(0.1, 0.9, 0.1)	(0.8, 0.2, 0.2)	(0.1, 0.9, 0.1)	(0.2, 0.8, 0.2)	(0.8, 0.2, 0.2)

and

Table 10. Decision matrix of the first 8 criteria with high weight scores of Expert3.

	C1	C2	C10	C11	C3	C5	C4	C7
A1	(0.8, 0.2, 0.2)	(0.6, 0.4, 0.4)	(0.7, 0.3, 0.3)	(0.9, 0.1, 0.1)	(0.7, 0.3, 0.3)	(0.6, 0.4, 0.4)	(0.4, 0.6, 0.4)	(0.6, 0.4, 0.4)
A2	(0.9, 0.1, 0.1)	(0.5, 0.5, 0.5)	(0.6, 0.4, 0.4)	(0.7, 0.3, 0.3)	(0.6, 0.4, 0.4)	(0.6, 0.4, 0.4)	(0.7, 0.3, 0.3)	(0.7, 0.3, 0.3)
A3	(0.7, 0.3, 0.3)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)	(0.4, 0.6, 0.4)	(0.6, 0.4, 0.4)	(0.5, 0.5, 0.5)	(0.5, 0.5, 0.5)	(0.4, 0.6, 0.4)
A4	(0.9, 0.1, 0.1)	(0.3, 0.7, 0.3)	(0.1, 0.9, 0.1)	(0.1, 0.9, 0.1)	(0.7, 0.3, 0.3)	(0.1, 0.9, 0.1)	(0.3, 0.7, 0.3)	(0.7, 0.3, 0.3)

. In the F-SWARA method, the calculated weights of the first 8 criteria with high weights out of 24 criteria were used (Table 7).

Figure 7 shows the functions used in python. Codes were generated based on these functions. The diagram highlights the concept of a Spherical Fuzzy Class, a term rooted in fuzzy logic and decision-making theory. In the context of spherical fuzzy sets, the aggregated matrix is used to consolidate the spherical fuzzy values.

• SphericalFuzzy (Class)

This class represents the spherical fuzzy values used for each criterion. membership: It shows how well an alternative meets a criterion. non-membership: It shows how unsuitable it is. hesitancy: It is a degree of indecision, i.e., uncertainty due to lack of information.

2.

Decision matrices and weights are embedded into the code.

3.

SWAM is used to evaluate alternatives based on spherical fuzzy sets. Each criterion is assigned a weight reflecting its importance, and the overall score of each alternative is calculated by taking the weighted average of its performance across all criteria.

4.

After applying Equation (16), the aggregated matrix of the model is shown in

Table 11. Aggregated matrix.

	C1	C2	C10	C11	C3	C5	C4	C7
A1	(0.772, 0.232, 0.229)	(0.671, 0.333, 0.330)	(0.772, 0.232, 0.229)	(0.875, 0.131, 0.126)	(0.739, 0.266, 0.262)	(0.671, 0.333, 0.330)	(0.470, 0.474, 0.464)	(0.537, 0.467, 0.464)
A2	(0.875, 0.131, 0.126)	(0.537, 0.467, 0.464)	(0.671, 0.333, 0.330)	(0.700, 0.300, 0.300)	(0.537, 0.467, 0.464)	(0.537, 0.467, 0.464)	(0.638, 0.366, 0.363)	(0.671, 0.333, 0.330)
A3	(0.671, 0.333, 0.330)	(0.570, 0.434, 0.431)	(0.570, 0.434, 0.431)	(0.371, 0.373, 0.363)	(0.671, 0.333, 0.330)	(0.470, 0.474, 0.464)	(0.561, 0.403, 0.391)	(0.470, 0.474, 0.464)
A4	(0.875, 0.131, 0.126)	(0.338, 0.340, 0.330)	(0.142, 0.143, 0.126)	(0.142, 0.143, 0.126)	(0.739, 0.266, 0.262)	(0.142, 0.143, 0.126)	(0.271, 0.273, 0.262)	(0.739, 0.266, 0.262)

.

5.

Rankings are determined according to the Ratio Reference Point, Full Multiplicative Form, and MULTIMOORA steps.

6.

print(…) commands: At the end of the code, all calculated scores and rankings are printed on the screen.

As a result of the algorithm steps applied, the following results were obtained. According to this result, the order from the largest value to the smallest value is A1, A2, A4 and A3 by the Ratio method. According to the reference method, A1, A2, A4 and A3 are ranked as the most important alternative with the smallest value. According to the FMF method, the order of values from the largest to the smallest is A1, A2, A3 and A4. The overall score is in the form of SF-MULTIMOORA ranking. As a result of the three different analysis approaches applied (Ratio System, Reference Point Approach, FMF), alternative A1 was found to be in the leading position in all of them. This shows that A1 has a balanced and strong profile in terms of both environmental and economic criteria for sustainable aviation fuel selection. On the other hand, alternative A3 received generally low scores, suggesting that its poor performance in some criteria negatively affected its overall ranking. The ranks are shown in

Table 12. Rankings for all techniques.

Model	Ratio	Reference	FMF	Final Rank
A1	1	1	1	1
A2	2	2	2	2
A3	4	4	3	4
A4	3	3	4	3

.

3.3. Sensitivity Analysis

Sensitivity analysis of the algorithm was performed with varying criteria weights and selections. These analyses aim to test the flexibility of the decision-making process and the robustness of the algorithm to varying weight structures. In the sensitivity analysis, especially when the effect of criterion C1 is tested, the fact that there is no significant change in the alternative ranking shows the stability of the decision-making structure. Especially in MCDM methods, it is used to understand how results are affected when criteria weights or alternative values change. In this study, 5 scenarios were identified. The ways in which the scenarios were created are given in

Table 13. Scenarios created for sensitivity analysis.

Scenarios	Explanation
S1:	Increasing the weight of the most important criterion by 25%
S2:	Increasing the weight of the most important criterion by 50%
S3:	Increasing environmental criteria by 20%
S4:	Increasing economic criteria by 20%
S5:	Choosing 2 sub-criteria from each main criterion

below.

Under the sensitivity analysis scenario, two sub-criteria with the highest weights were selected from each main criteria group (environmental, economic, social, technical/institutional), resulting in a total of 8 representative criteria (

Table 14. With F-SWARA, the weights of the first two criteria of each main criterion with high weight scores.

Criteria	Weights	Description
C1	0.301399	Environmental
C2	0.225683	Environmental
C10	0.180308	Economic
C11	0.135143	Economic
C14	0.067572	Social
C15	0.044876	Social
C20	0.029878	Technical
C21	0.015142	Technical

). Since the S5 scenario was created by taking the two most important criteria from each main criteria, the aggregated matrix was calculated as given in

Table 15. Aggregated Matrix for Scenario 5.

	C1	C2	C10	C11	C3	C5	C4	C7
A1	(0.772, 0.232, 0.229)	(0.338, 0.340, 0.330)	(0.772, 0.232, 0.229)	(0.875, 0.131, 0.126)	(0.739, 0.266, 0.262)	(0.671, 0.333, 0.330)	(0.470, 0.474, 0.464)	(0.537, 0.467, 0.464)
A2	(0.875, 0.131, 0.126)	(0.570, 0.434, 0.431)	(0.671, 0.333, 0.330)	(0.700, 0.300, 0.300)	(0.537, 0.467, 0.464)	(0.537, 0.467, 0.464)	(0.638, 0.366, 0.363)	(0.671, 0.333, 0.330)
A3	(0.671, 0.333, 0.330)	(0.537, 0.467, 0.464)	(0.570, 0.434, 0.431)	(0.371, 0.373, 0.363)	(0.671, 0.333, 0.330)	(0.470, 0.474, 0.464)	(0.561, 0.403, 0.391)	(0.470, 0.474, 0.464)
A4	(0.875, 0.131, 0.126)	(0.739, 0.266, 0.262)	(0.142, 0.143, 0.126)	(0.142, 0.143, 0.126)	(0.739, 0.266, 0.262)	(0.142, 0.143, 0.126)	(0.271, 0.273, 0.262)	(0.739, 0.266, 0.262)

. Through the 3 of experts created based on these criteria, the same alternatives were re-evaluated via the SF-MULTIMOORA method.

Figure 8 shows the ranking changes in the four SAF alternatives (A1–A4) under the base model and five different scenarios. When SF-MULTIMOORA results are compared by scenarios, the base model and scenarios S1, S2, S3 and S4 give the same result, while in S5 the first two rankings are the same and only a change is observed in the order of the last two alternatives. In the light of these results, it was determined that the study was resistant to change.

Figure 9 presents the performance rankings of four models (A1 to A4) based on three methods: Ratio, Reference, and FMF, along with a calculated Final Rank. These evaluations are shown for a main scenario and five different scenarios (S1 to S5). A1 consistently ranks first across all criteria and scenarios, making it the most successful model overall. A2 typically holds the second position, though its performance slightly varies in scenarios S3 and S5. A3 and A4 generally rank lower, with A3 occasionally outperforming A4 depending on changes in FMF scores. The Final Rank appears to be determined by summing the individual rankings from the three alternatives, where a lower total indicates a better final position. This ranking method highlights the consistency and superiority of A1, while also revealing how small changes in one criterion can affect the overall standing of other models.

According to the results of the sensitivity analysis, A1 (HEFA-SPK) and A2 (FT-SPK) exhibited a highly stable performance in all scenarios, maintaining their 1st and 2nd place positions, respectively. In contrast, A3 (ATJ-SPK) and A4 (PtL) showed variation in ranking with scenarios. A4, which initially ranked the 3rd, maintained this position until the S4 scenario, but was overtaken by A3 in the S5 scenario and dropped to the 4th place. The rise in A3 is directly related to scenarios where the weighting of criteria such as carbon neutrality, environmental impact and use of renewable energy is increased. These findings reveal the robustness of A1 and A2 to the overall set of criteria, and the sensitivity of A3 and A4 to criteria priorities. In conclusion, the sensitivity analysis shows that the relative preferences among SAF alternatives may vary depending on the scenario, but some alternatives stand out as stable choices under all conditions.

4. Discussion

The results obtained with the F-SWARA method applied in the criteria weighting process revealed that environmental factors were the most effective criteria group in the evaluation of sustainable aviation fuels. This is closely linked to the fact that the aviation sector is under increasing environmental pressures and there are strong global commitments to reduce carbon emissions. In particular, factors such as reducing the carbon footprint, energy efficiency and protection of natural resources were among the priority criteria for decision makers.

Environmental criteria are followed by the economic dimension in terms of weight. Economic criteria such as return on investment, production costs and infrastructure compatibility play an important role in the decision-making process, especially for practitioners and investors. The commercialization potential and economic viability of SAF technologies are critical to the widespread adoption of sustainable transformation.

Although the weights of the technical and social criteria groups were lower than those of the environmental and economic criteria, they were considered as important complementary elements in the decision-making process. Technical criteria included the energy density of the fuel, compatibility with existing systems and maturity of the production technology, while social criteria encompassed social acceptance, employment impact and non-competition with food production.

The results show that priorities in the evaluation of SAF types are shaped by the focus on environmental sustainability. However, an assessment without considering factors such as economic and technical relevance will be insufficient to produce viable strategies. Adopting a holistic approach therefore plays a balancing role in the decision-making process.

As a result of the evaluation through the SF-MULTIMOORA method, the HEFA-SPK (A1) alternative consistently ranked first in all scenarios. This is due to the multifaceted advantages of the HEFA-SPK. First, HEFA-SPK is the most widely used sustainable aviation fuel today and is fully compatible with existing jet engines and airport infrastructure. Moreover, the fact that it can be produced with a variety of waste-based feedstocks such as vegetable oils, animal fats and used cooking oils makes it attractive in terms of both environmental sustainability and economic viability. The fact that the production process is less complex and the initial investment costs are relatively low compared to other alternatives contributes to the preference of this type in practice.

The FT-SPK (A2) alternative was consistently ranked second in all scenarios. This type of fuel is environmentally strong in that it can provide negative carbon emissions, especially when using biomass sources such as miscanthus. Moreover, capacity of the Fischer-Tropsch synthesis to produce high purity fuel is a major technical advantage. However, the investment and operating costs of this production method are higher compared to HEFA-SPK. Therefore, despite its technical superiority, the FT-SPK was disadvantaged in cost criteria, causing it to lag behind the HEFA-SPK.

While the ATJ-SPK (A3) alternative ranked fourth in the first four scenarios, it move up to third place in the S5 scenarios. This variability can be explained by the fact that ATJ-SPK is particularly advantageous in terms of economic viability but performs relatively poorly on environmental and technical criteria. Although this fuel, derived from alcohol-based sources, can take advantage of the bioethanol infrastructure prevalent in some countries, it lags behind other alternatives in terms of carbon emissions, energy intensity and technological maturity. The ATJ-SPK (A3) alternative ranked third in the main model and in the first four scenarios, while it dropped to fourth place only in the fifth scenario. This variability can be explained by the fact that ATJ-SPK is particularly advantageous in terms of economic viability but performs relatively poorly on environmental and technical criteria. Although this fuel, derived from alcohol-based sources, can benefit from the widespread bioethanol infrastructure in some countries, it lags behind other alternatives in terms of carbon emissions, energy intensity, and technological maturity.

The PtL (A4) alternative ranked last in the first four scenarios but moved up one place to third in the fifth scenarios. However, it dropped back to fourth place in the fifth scenario, indicating a sensitivity to changes in the weighting of evaluation criteria. PtL is a synthetic fuel produced directly by synthesizing CO2 and water with renewable electricity and is highly valuable for its carbon neutrality potential. However, because the technology is not widespread on a commercial scale and because of the high cost of the production process, it remains lower in the ranking when the weight of environmental criteria is reduced. The PtL (A4) alternative ranked third in the main model and in the first four scenarios, while it dropped to fourth place only in the fifth scenario. This indicates that PtL maintained its advantage in scenarios where environmental criteria were prioritized. PtL is a synthetic fuel produced directly by synthesizing CO₂ and water with renewable electricity and is highly valuable due to its carbon neutrality potential. However, since the technology has not yet been widely commercialized and the production process is costly, its ranking declined in scenarios where the weight of environmental criteria was reduced.

As a result, the HEFA-SPK alternative stands out as the most suitable SAF type with a balanced performance in terms of environmental, economic, technical and social criteria. FT-SPK is a strong option from an environmental and technical point of view but remains in second place due to its cost disadvantage. PtL, with its carbon neutrality potential, is particularly prominent in environmental terms and ranked third in the main model and the first four scenarios, while it dropped to fourth place only in the fifth scenario. ATJ-SPK, on the other hand, offered some economic advantages but remained the least preferred option due to its relatively weak performance in environmental and technical criteria. These findings reveal that decision makers should evaluate various alternatives based on their criteria priorities and emphasize the importance of holistic evaluation of SAF technologies.

5. Conclusions and Future Work

The civil aviation sector is one of the fastest growing areas of transportation on a global scale and has become important in terms of environmental sustainability due to increasing energy demand and fossil fuel use. In this context, SAF is considered as a strategic solution for reducing environmental impacts and enabling energy transition. First, the criteria weights were determined using the F-SWARA method and ranked using the SF-MULTIMOORA method. SF-MULTIMOORA was implemented through Online Python Compiler and sensitivity analysis was performed over five different scenarios.

According to the results obtained, HEFA-SPK fuel was identified as the most suitable alternative in the main model and in all scenarios, scoring the highest with A1 code. ATJ-SPK fuel received the lowest score in the main model with code A3. In the sensitivity analysis, HEFA-SPK fuel with code A1 and FT-SPK with code A2 remained constant in the first two rows, while PtL fuel moved to the last row in the last scenarios. These findings have important strategic implications for producers and investors. The consistent performance of HEFA-SPK fuel suggests that this type should be encouraged and the production infrastructure should be shaped accordingly. Although HEFA-SPK and FT-SPK stand out as low-risk and high-potential options for investment decisions, more detailed feasibility and risk analyses are recommended for fuel types such as ATJ-SPK and PtL.

This study fills the methodological gap in the literature, providing a holistic and systematic approach to the evaluation of SAF alternatives, while contributing to the achievement of sustainability goals of the aviation industry. The study is important in terms of the use of programming language in CRM methods.

The robustness of the findings is reinforced by the fact that the evaluation criteria were derived from peer-reviewed studies, international standards (e.g., ASTM D7566, ICAO guidance), and expert judgments from senior professionals in the aviation sector. This multi-source approach ensures that the analysis is grounded in both academic and practical evidence, thereby increasing the reliability of the results.

This study is considered to be the first in the literature to integrate the F-SWARA and SF-MULTIMOORA methods in the evaluation of SAF alternatives in a global fuzzy environment. This originality stems from combining an innovative fuzzy decision-making framework with a comprehensive sustainability perspective, which has not been addressed in previous studies.

This study has some limitations. These include criteria weights and alternative ratings being based on limited literature and expert opinion. The practical example is based on four alternatives; it can be expanded with various raw material types and production methods. Differences between countries could not be considered in the technical, economic and environmental data of SAFs. In future studies, it is recommended to collect data with larger sample groups and to evaluate using various fuzzy MCDM methods in order to overcome these limitations.