Abstract
Hospitals are an important piece of infrastructure for global emergency management, and their evacuation efficiency is crucial during large-scale disasters or public health crises. Traditional evacuation methods mainly focus on proximity and often overlook dynamic pedestrian density and channel capacity, leading to local congestion and increased risk. This study introduces a dynamic optimization evacuation path planning framework based on flow space theory to address the overall inefficiency in hospital evacuation. We model the hospital space as a dynamic network flow, analyze evacuation time through walking and queuing time, and apply a density–velocity correction model to adjust path allocation in real time. Using the MassMotion 11.0 platform to compare the evacuation of simulated hospital models before and after path optimization, the results showed that the average evacuation time was reduced by 10.58%, the waiting time in high-density areas was shortened, and the overall efficiency was improved. Empirical exercises show that path optimization can shorten evacuation time, demonstrating that spatial optimization strategies enhance hospital resilience. These results confirm the practical value of the flow space theory in emergency management for dealing with disasters. The flow space theory enriches the theoretical system of evacuation planning and contributes to a more in-depth study of people’s evacuation behaviors and the optimization of evacuation strategies.
1. Introduction
Personnel evacuation constitutes a critical issue in architectural safety design and emergency management. In specialized facilities such as hospitals, evacuation complexity becomes significantly greater than in conventional structures due to heterogeneous population compositions and marked behavioral variances [1]. Traditional evacuation route optimization methods, primarily focused on the shortest-path algorithms and proximity-based heuristics, frequently induce localized path congestion during implementation, thereby prolonging evacuation durations [2]. However, these approaches often overlook sustainability principles (e.g., energy efficiency, resource allocation, and equitable access for vulnerable populations), crucial for aligning evacuation planning with SDGs (Sustainable Development Goals), especially SDG11 (Sustainable Cities) and SDG3 (Health Equity). Consequently, developing efficient and safety-compliant evacuation routing strategies in complex architectural environments has emerged as both a focal research priority and persistent technical challenge [3].
Space of Flows Theory offers a dynamic and holistic research perspective for addressing evacuation challenges. The operational efficiency of evacuation systems originates from the unobstructed circulation of critical elements such as population dynamics and information flows within a flow space framework. The theoretical framework of the space of flows was put forward by the Spanish sociologist Manuel Castells. The space of flows refers to a new form of space composed of various flows (such as information, capital, people, goods, etc.) based on information technology and network infrastructure. It breaks through the limitations of traditional geographical space and emphasizes the fluidity and network characteristics of space. This theoretical framework conceptualizes human movement as dynamic fluid systems, integrating corridor capacity limits, population density distributions, and flow velocity parameters to optimize evacuation routes, effectively reducing congestion risks and improving evacuation efficiency.
This study constructs a hospital evacuation route optimization model by integrating Space of Flows Theory with network flow modeling and uses the MassMotion platform for simulation verification. The model analyzes changes in evacuation duration before and after optimization, with walking time and queuing time as evaluation parameters. Validation conducted through MassMotion simulations has confirmed the practical effectiveness of the optimized plan. The evacuation simulations have become more viable as they enable safer evacuations [4,5]. Results demonstrate that Space of Flows Theory dynamically adjusts crowd distribution, reduces congestion in high-density areas, and significantly improves evacuation efficiency, providing essential theoretical and technical support for emergency evacuation design in complex healthcare environments.
2. Research Status
The rapid advancement of urbanization and continuous expansion of building scales have significantly heightened safety concerns in high-density public spaces [6]. Concurrently, the accelerated development of information technology has driven transformative changes in hospital functional networks and material workflows, necessitating innovative designs in spatial organization, area allocation, and flexibility, as illustrated in Figure 1, to meet evolving socioeconomic demands [7]. Effective partitioning and organization of localized functional units, along with optimized spatial configurations, are critical for improving operational efficiency in healthcare facilities [8]. In specialized environments such as hospitals, evacuation challenges are markedly intensified due to heterogeneous population compositions including patients, medical staff, and visitors, dynamic occupancy patterns, and varying mobility capacities. Emergency evacuations during critical events like fires or earthquakes directly determine life safety outcomes [9,10]. Consequently, the design of efficient evacuation routes that ensure rapid and secure egress has become a pivotal research focus at the intersection of architectural design and safety management.

Figure 1.
Exhibition inside a modern general hospital; interior decoration renderings were generated using Revit rendering. (a) Corridor decoration rendering. (b) Lobby decoration rendering.
Traditional evacuation route optimization methods predominantly rely on the shortest-path principle, where evacuation routes are determined by calculating the minimal-distance paths through corridors or exits [11]. However, this approach fails to account for dynamic variations in crowd density, walking velocities, and path capacity constraints, frequently inducing localized corridor congestion during evacuation processes. Such congestion prolongs evacuation durations and elevates safety risks. Ran Ye et al. combined field experiments with computational modeling to analyze pedestrian evacuation dynamics and congestion mitigation strategies at building exits [4]. Using PeTrack software, they tracked movement trajectories of eight volunteers to study behavioral patterns during emergency evacuations. Their findings revealed divergent velocity vector decompositions under varying exit configurations, elucidating lateral evacuation pressure, exit bottleneck phenomena, and the “faster-is-slower” effect. This study has certain limitations. The experiment did not take into account the complex behavioral characteristics of pedestrians. The scenario setting is single, and special evacuation situations have not been covered, which affects the universality and accuracy of the research results [4]. In complex architectural structures, rational allocation of evacuation routes proves critical for operational efficiency. Al Bochi, A. (2023) [12] comprehensively evaluated current research on evacuating mobility-impaired individuals in built environments. The study cataloged existing strategies, assistive technologies, and specialized equipment while analyzing their limitations, with particular emphasis on evacuation challenges and solutions for populations with visual impairments or other accessibility requirements. Theoretically, this study fails to adequately consider special scenarios and extreme situations and lacks integration [12]. Collectively, prior studies demonstrate some key limitations:
- (i)
- Over-reliance on static shortest-path algorithms neglects dynamic crowd density fluctuations;
- (ii)
- Hospital-specific complexities (e.g., heterogeneous mobility of patients) are insufficiently addressed.
This study bridges these gaps by proposing a flow space-driven framework that dynamically optimizes routes while embedding health equity and resource efficiency.
In recent years, Space of Flows Theory has gained increasing attention as a dynamic optimization strategy in evacuation research [13]. Distinct from traditional place-based spatial paradigms, this theory emphasizes human connectivity, communication, and interaction rather than mere physical spatial occupation [14]. The evolution of information and communication technologies has fundamentally transformed social interactions, economic activities, and structural organization, collectively reshaping spatial cognition [15]. By conceptualizing crowd movement as a dynamic fluid process governed by density, flow rate, and velocity parameters, Space of Flows Theory enables more flexible and effective evacuation solutions than conventional approaches.
Despite its demonstrated potential, integrating this theory with modern computational models and simulation tools to quantitatively assess evacuation efficiency improvements remains an open research challenge. Wang, J. H. et al. (2019) [16] used MassMotion to establish a simulation model based on social forces based on experimental properties. After setting a buffer zone, the evacuation efficiency significantly improved at high expected speeds, and the evacuation time shortened with the increase in buffer zone length [16]. Zhu, Y. (2022) [17] improved the traditional Dijkstra algorithm for route planning and upgraded the evacuation model from 2D to 3D. At the same time, the Lasso regression method is used to take into account the road factors in pedestrian speed, and the location of shelters is selected and optimized through calculation results. Then, based on the improved 3D Dijkstra algorithm, the optimal evacuation route method for different flood disaster risk levels is proposed [17]. Zhu, Q. K. et al. (2024) developed PyroSim-based fire spread models for aging university buildings, analyzing smoke visibility, temperature at 2 m elevation, and CO concentration variations across fire scenarios, while Pathfinder simulations calculated safe evacuation durations [18]. Khalili, S. M. et al. (2024) investigated evacuation plan optimization through traffic flow rerouting and shelter location selection, aiming to develop enhanced decision-support tools [19]. Zhang, Z. W. (2025) established a congestion prediction model for Chinese academic libraries by integrating Fire Dynamics Simulator (FDS), agent-based modeling (ABM), and machine learning (ML) techniques [20].
This study investigates hospital evacuation route optimization through the integration of Space of Flows Theory with network flow modeling, validated via MassMotion simulations [21], thereby providing novel theoretical frameworks and technical methodologies for evacuation system design.
3. Research Methods
3.1. Theoretical Framework of Flow Space for Evacuation Routes
3.1.1. Concept and Connotation of Flow Space Theory
Flow Space Theory constitutes a theoretical framework that integrates the dynamic flow characteristics of human crowds with the physical properties of spatial environments, primarily focusing on the analysis of movement behaviors and flow distribution within confined spaces. This theory abstracts evacuation scenarios into continuous flow spaces, simulating crowd movement patterns and behavioral regularities through the examination of dynamic interactions among parameters including spatial capacity, flow rate, density, and velocity. The core tenet of Flow Space Theory lies in its dual focus; while addressing individual locomotion, it conceptualizes crowds as cohesive fluid entities, employing principles analogous to fluid dynamics to analyze their spatiotemporal evolution.
3.1.2. Optimizing Evacuation Routes Using Flow Space Theory
Traditional evacuation route selection methods predominantly rely on static shortest-path algorithms, which fail to account for dynamic crowd flow characteristics and density-dependent velocity variations. This oversight frequently induces severe congestion along specific pathways, thereby prolonging evacuation durations. To address these limitations, we propose a route adjustment methodology that optimizes path selection to reduce evacuation time through systematic flow redistribution [22]. In the process of optimizing the evacuation routes, taking into account the evacuation needs of people in different areas and ensuring that vulnerable groups can be evacuated quickly and safely is helpful for achieving health equity (SDG 3). At the same time, improving the evacuation efficiency and reducing the occupation of urban emergency resources are in line with the concept of sustainable cities (SDG 11). Flow Space Theory demonstrates superior efficacy by dynamically analyzing interdependencies among density, flow velocity, and capacity constraints. This approach enables balanced crowd flow distribution while preventing localized bottlenecks through real-time adaptive routing. The theory’s principal advantage lies in its global optimization perspective, which not only minimizes queuing delays but also enhances both evacuation efficiency and safety metrics. Such capabilities prove particularly valuable in complex architectural configurations featuring multi-exit layouts and interconnected passageways.
3.1.3. Network Flow Model Optimization and Computation Based on Flow Space Theory
Ye, S. (2024) regards the tourism corridor as a system consisting of multiple tourism nodes and transportation roads, where transportation roads serve as the basic carrier for tourist flow, while tourism nodes play a role in attracting and dispersing tourist flow [23]. Applying this conceptual framework to evacuation research, complex evacuation problems can be abstracted into network flow models via flow space theory optimization. Evacuation zones are divided into multiple nodes and paths, with flow volume, capacity, and density–velocity relationships defined according to pedestrian movement characteristics. Building upon this, the network flow model focuses on flow allocation across paths, establishing a mathematical representation of evacuation dynamics through flow conservation equations and capacity constraints.
Rungta, M. et al. (2012) [24] developed a bi-objective dynamic network flow model. Its core lies in the Minimum Time Least Path (MTLP) model, which achieves evacuation via minimal paths within the shortest duration. To address large-scale multi-objective challenges, the study implemented a three-phase MTLP solution, introducing a virtual “super-sink” node to consolidate path flows [24]. Integrated with flow space theory, the model transcends shortest-path optimization by balancing flow distribution to reduce congestion, thereby decreasing queuing time and enhancing systemic evacuation efficiency. This methodology provides a computational foundation for analyzing and optimizing complex evacuation scenarios.
3.2. Comparative Calculation of Evacuation Time Using the Network Flow Model
Evaluating evacuation time is the most direct and effective method to verify evacuation efficiency. By measuring the time required for personnel to safely transfer from a location to a safe area, the efficiency of the evacuation process can be intuitively assessed [25]. The core of calculating evacuation time using network flow models lies in abstracting evacuation scenarios into flow networks composed of nodes and paths. By defining parameters such as flow volume, capacity, and velocity, the model simulates personnel movement across different paths. The model first calculates flow distribution based on flow conservation and path capacity constraints, then dynamically adjusts walking speeds using density–velocity relationships, and finally aggregates walking and queuing times across all paths to determine total evacuation duration. Assessing evacuation time requires considering more complex factors and conducting refined calculations to ensure accuracy [26].
Siam, M. R. K. (2025) [27] conducted empirical analysis on the expected evacuation logistics of households and the ETE components of wildfire evacuation. In the study, evacuation time was decomposed and analyzed; evacuation time was divided into expected evacuation preparation and travel time [27]. Separating evacuation time into walking and queuing times allows detailed analysis of temporal consumption during different evacuation phases, identifying key optimization targets. Walking time refers to normal movement duration in corridors or stairways, primarily influenced by speed and path length, while queuing time denotes waiting periods caused by capacity limitations or exit congestion.
Even when considering density–velocity relationships, queuing time calculation remains essential. Density–velocity correlations mainly reflect walking states in corridors or exit paths, whereas queuing time represents dynamic waiting phenomena typically occurring at channel entrances or exits due to capacity constraints or flow imbalances. These two temporal dimensions complement each other, jointly determining total evacuation duration.
3.3. Validation of Theoretical Optimization and Network Model Calculations Using Simulation Software
By utilizing MassMotion simulation software, the practical effectiveness of Space of Flows Theory in optimizing evacuation routes can be directly validated [28]. A geometric model of the building, as illustrated in Figure 2, is imported into the software, and evacuation paths optimized through Space of Flows Theory are implemented by setting dynamic navigation meshes and crowd behavior parameters such as walking speed and exit capacity. Simulations are conducted to observe evacuation processes under both traditional path schemes and Space of Flows-optimized scenarios. During simulation, the software dynamically calculates key metrics including crowd flow patterns, corridor congestion levels, and total evacuation time. Comparative analysis of the two schemes demonstrates the practical value of Space of Flows Theory in reducing queuing time, alleviating pressure in high-density zones, and improving overall evacuation efficiency. These results provide robust data support and empirical validation for the theoretical application.

Figure 2.
Building geometry model created using Revit 2017 (Revit is a three-dimensional modeling software widely used in the field of architectural design, which is developed by Autodesk, San Rafael, CA, USA).
4. Model Construction
The extensive application of network flow theory across various disciplines has demonstrated its capability to address numerous practical problems through network flow modeling. The hospital personnel evacuation issue examined in this study can likewise be systematically analyzed within a network flow framework. The primary objective of this research is to conduct a rigorous analysis of the fundamental characteristics inherent to hospital evacuation scenarios, thereby abstracting the operational complexities of real-world hospital evacuations into a formal network flow model. This theoretical formalization provides a robust foundation for subsequent system design optimization.
4.1. Fundamental Concepts of the Network Flow Model
The network flow model serves as a powerful analytical tool for studying and optimizing evacuation problems, with extensive applications spanning traffic flow, logistics, communications, and other domains. This modeling framework operates by abstracting practical problems into directed graphs, where defined parameters systematically characterize flow distribution and dynamic variations across network architectures.
4.1.1. Parameter Definition
The parameter definitions of network flow models form the foundational basis for model construction. In the model, nodes represent critical evacuation points such as wards, corridors, stairwells, and exits, typically denoting personnel’s initial positions, path intersections, or destinations. Edges represent connections between nodes, including corridors, stairs, and elevators, where edge capacity refers to the maximum pedestrian flow a passage can accommodate per unit time, determined by factors like corridor width or stair capacity. Source nodes represent evacuation starting points, while sink nodes denote target exits or assembly areas [29]. In network flow digraph studies, strict conventions govern the symbolic representation of parameters. To facilitate subsequent theoretical analysis and algorithmic implementation, this study standardizes the notation of relevant parameters.
1. Evacuate directed graph : represents the set of nodes, represents the set of edges.
(1) Each node also has the following attributes:
Node numbering: Nodes are categorized into source nodes and sink nodes. When a node is a source node, it is denoted as ; when a node is a sink node, it is denoted as
Node capacity: represents the capacity of a node.
represents the capacity of the source node, represents the capacity of the sink node.
(2) Each edge has the following attributes:
Edge numbering: Edges are formed by connecting nodes and are represented as . Edges can also be simply denoted as .
Edge capacity: represents the capacity of the edge; the unit of measurement is persons per second.
Edge flow: represents the flow on the edge; the unit of measurement is persons per second.
Edge length: represents the length of the edge, which corresponds to the actual distance between nodes; the unit of measurement is meters.
Edge width: represents the width of the edge, which corresponds to the actual width of corridors or door frames; the unit of measurement is meters.
Edge area: ; the unit of measurement is square meters, calculated using the formula:
2. Evacuation Time
Total Evacuation Time (): The time from when the first person begins evacuating until the last person completes evacuation.
Walking Time (): The time individuals spend moving along the network paths.
Queueing Time (): The time individuals spend waiting due to capacity constraints at corridors or exits.
Flow Speed: The speed at which individuals pass through a given edge, which is influenced by edge capacity and population density.
4.1.2. Conventional Evacuation Methods
Based on the hospital building layout plan (Figure 3), and following the above modeling strategy, we constructed the corresponding network flow directed graph (Figure 4). The architectural layout comprises 2 fire exits and 57 functional zones, each serving distinct purposes such as offices, wards, locker rooms, and restrooms. The simulated population numbers were obtained through on-site investigations of similar hospitals. We recorded the number of people at different times of a tertiary hospital in Urumqi for five consecutive days. The recorded results are shown in Table 1. Analysis reveals that in large cities, the occupancy rate of tertiary hospitals ranges from 80% to 95%. During peak visiting hours, the number of family members is almost equal to that of patients.
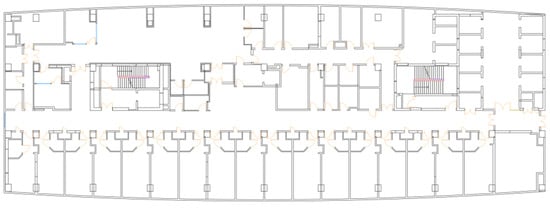
Figure 3.
Hospital architectural layout plan. (The yellow ones are room doors, and the red ones are evacuation stairs).
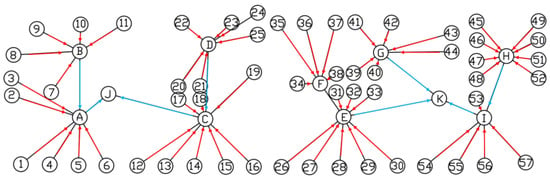
Figure 4.
Network flow model directed graph, numbers represent the source points, and letters represent the sink points, orange represents the edge and direction from the source point to the sink point, while red represents the edge and direction from the sink point to the sink point.

Table 1.
Personnel fluctuation record table.
Meanwhile, the numbers of patients of different types were also recorded, and the results are presented in Table 2. The conditions of patients of different types will have an impact on the evacuation speed.

Table 2.
Number of patients by type and symptom descriptions.
The simulation experiment was set in an extreme environment; that is, with an occupancy rate of 100% and during the peak visiting period. Patients were arranged in corresponding wards. For example, ordinary patients were placed in general wards, and critically ill patients were in intensive care units. Considering that in case of an emergency, there may be patients who are receiving treatment and are unable to evacuate independently, since the evacuation conditions for such patients are the same as those for critically ill patients, these patients undergoing treatment were also regarded as critically ill patients and arranged in the corresponding treatment rooms.
As shown in Figure 4, each room is designated as a source node, with evacuees initially moving to corridor sink nodes, then progressing toward stairwell sink nodes or subsequent sink nodes. The directional flow toward stairwells defines the edge orientations in the network flow digraph. All nodal and edge parameters are documented in Appendix A (Standard Evacuation Time Calculation Table).
4.2. Calculation of Evacuation Time
The incorporation of queuing time into network flow models constitutes a critical refinement for enhancing evacuation time calculation precision. This methodological advancement not only improves behavioral fidelity in crowd dynamics simulations but also enables more authentic representation of pedestrian movement patterns during evacuation route optimization. The optimization objective focuses on mitigating queuing delays through strategic path selection, necessitating simultaneous consideration of both walking time and queuing time parameters within the modeling framework. The subsequent discussion details the technical implementation.
1. Decomposition of Evacuation Time
In the formula, represents the time from when the first person begins evacuating until the last person completes the evacuation. represents the time spent by individuals moving along the network paths and represents the time individuals need to wait due to channel or exit capacity limitations.
2. Walking Time
Walking time refers to the duration required for individuals to travel from their initial positions to final exits via evacuation routes. This temporal metric is primarily determined by path length, pedestrian walking speed, and path unobstructedness.
(1) Calculation of Walking Time for a Single Path
represents the actual walking duration from origin to destination. Under idealized, congestion-free conditions, can be defined as the theoretical flow time—the time required for an individual to reach the destination at a constant speed without obstructions or delays.
represents the walking time, is the path length, and is the walking speed, which is typically described as 1.4 m/s in standard specifications [30]. In the absence of congestion, equals .
(2) Considering the impact of flow distribution on walking time in the network flow model.
However, in the network flow model, the impact of flow on walking time needs to be considered. The flow represents the flow on the path , referring to the number of people passing through that path. The larger the flow, the more likely it is to cause congestion in the passage, which in turn affects walking speed.
In the equation, represents the length of the edge and represents the walking speed; represents the function between flow and capacity, indicating the impact of flow on walking speed. represents the evacuation speed of the crowd under the influence of density, taking into account the functional relationship between flow and capacity.
According to Fire safety engineering Part 9: Guidance on evaluation of behavior and movement of people, GB/T31593.9-2015 [30], the movement time during evacuation is influenced by multiple factors, including the physical conditions of evacuees, occupant density, and the spread of fire smoke. For detailed guidelines on the impact of personnel physical conditions and crowd density on movement time, as well as calculations for horizontal and vertical movement speeds, refer to Annex H (Informative) of the standard.
—the density of people on edge , measured in people per square meter; —the evacuation speed of normal and healthy people (take 1.4 for horizontal evacuation); —harmonic factor (take 0.266).
According to Fire safety engineering Part 9: Guidance on evaluation of behavior and movement of people, GB/T31593.9-2015 H.3 [30], it is stated that the evacuation speed of a normal and healthy person is 1.4. However, in the simulation of a hospital environment, the impact of diseases on the evacuation speed needs to be considered. According to Fire safety engineering Part 9: Guidance on evaluation of behavior and movement of people, GB/T31593.9-2015 H.5.4, the influence of limited mobility on the walking speed is mentioned. We can refer to GB/T31593.9-2015 H.5.4 to find the corresponding walking speed for the objects of the simulation experiment. The speed of patients with mobility is set as 1, the speed of patients who need assistance is 0.78, and the speed of severely ill patients is 1.3. In the subsequent simulation calculations, we will set different speeds for patients with different disease types in different rooms.
The calculation of personnel density is as follows:
is the total number of people on edge and is the area of edge .
In the standard, personnel density can only be calculated between 0.54 and 3.8 people per square meter. When the personnel density exceeds 3.8 people per square meter, queuing occurs, and we need to use to calculate the total evacuation time . When D > 3.8 people/m2, set = = 1.4 m/s to obtain the walking time .
3. Queuing Time
The queuing time is primarily determined by passage capacity, flow rate, and whether the flow rate exceeds the passage capacity. For each passage or node, the calculation of queueing time can be derived based on the relationship between flow rate and capacity.
(1) Basic queueing time calculation:
represents the queueing time on edge ; represents the number of people queuing on edge , i.e., the flow of people exceeding the capacity; and represents the capacity of edge .
The number of people in the queue refers to the number of individuals who are delayed on the path and waiting to pass when the flow exceeds the channel capacity. The queueing number can be calculated as the difference between the flow and the capacity:
(2) Derivation of Queueing Time
In the case without queuing, when the flow does not exceed the channel capacity , i.e., , there is no queuing phenomenon. In this case, the queueing time is 0.
In the case of queuing, when the flow exceeds the channel capacity , a portion of the people will need to queue. In this case, the formula for calculating the queueing time is
represents the number of people passing through the channel per unit of time exceeding the channel capacity; is the capacity of the channel, representing the number of people that can pass through the channel per unit of time.
Flow calculation:
—the width of edge ; —the personnel density on edge ; —the evacuation speed of personnel on edge .
According to the standard Fire safety engineering Part 9: Guidance on evaluation of behavior and movement of people, GB/T31593.9-2015 [30], when 3.8 people/m2, congestion occurs and the flow speed becomes 0. Therefore, the maximum allowable personnel density for pedestrian flow is 3.8 people/m2.
Capacity calculation:
—maximum person density, which does not represent the maximum value but rather the optimal person density. It is set to 0.25 by the standard. When 0.25, the flow speed will change according to the person density; —evacuation speed. The standard stipulates that the unobstructed evacuation speed is 1.4 m/s.
4. Calculation of Evacuation Time
The evacuation time for each edge is calculated by summing its walking time and queuing time. Subsequently, the edge requiring the longest evacuation time at each sink node is designated as the final evacuation route. The total evacuation duration is derived by summing these critical-path evacuation times.
n represents the number of sink points (or destination points)
Therefore, this process can be conceptualized as a longest-path identification strategy, enabling the calculation of total evacuation duration from initiation to completion for rational evacuation planning, thereby ensuring all individuals exit safely within minimal time.
When dividing evacuation zones into two sections, it is critical to note that the evacuation duration of the slowest subzone determines the total evacuation time.
As documented in Appendix A (Conventional Evacuation Time Calculation Table), analyses demonstrate that under idealized evacuation conditions using traditional proximity principles, the total evacuation duration is 57.935 s. While this duration may seem brief, each second critically impacts life safety during emergencies.
Notably, the computational model reveals an emergent issue: excessive personnel density in the right section of the simulated environment. This indicates prolonged egress times for occupants in this area due to queuing delays caused by upstream congestion, inevitably extending total evacuation duration. Such density-driven bottlenecks constitute essential considerations in evacuation plan design.
5. Optimize the Evacuation Time of the Route
5.1. Optimization Strategy for Evacuation Routes Based on Flows Space Theory
The evacuation route optimization method proposed in this study is grounded in Space of Flows Theory, aiming to scientifically regulate crowd flow allocation to alleviate queuing time caused by path capacity constraints. Throughout the evacuation process, personnel density and path capacity are two core influencing factors. When flow exceeds path capacity, queuing phenomena emerge, significantly extending total evacuation duration. Space of Flows Theory uniquely abstracts evacuation environments into fluid contexts and synergizes with network flow modeling to transform complex route optimization into flow allocation problems, enabling dynamic path adjustment. By modifying routes to reduce queuing time, total evacuation time decreases. This redistribution strategy not only minimizes congestion but also promotes equitable resource utilization—ensuring remote or socioeconomically disadvantaged sections of the hospital receive comparable evacuation efficiency, a critical step toward inclusive disaster preparedness.
Utilizing Space of Flows Theory, we optimized evacuation routes to dynamically guide evacuees toward distant exits while avoiding congestion zones (as shown in Figure 5). Simulations revealed point (18, E) exhibited the longest queuing time. To mitigate this, we redefined sink nodes (34, E), (35, E), (36, F) as (34, C), (35, D), and (36, D), forming new evacuation paths (34, C), (35, D), and (36, D). While this adjustment cannot directly shorten path length at (18, E), it effectively reduces personnel density along the route, thereby decreasing queuing time.
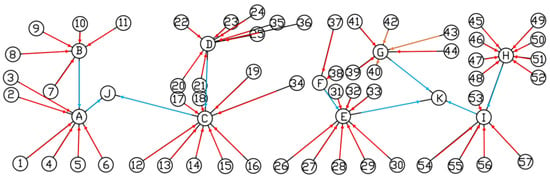
Figure 5.
Optimized network flow model directed graph, numbers represent the source points, and letters represent the sink points, orange represents the edge and direction from the source point to the sink point, while red represents the edge and direction from the sink point to the sink point.
5.2. Optimized Evacuation Time
Simulation results and detailed analyses are provided in Appendix B (Post-Optimization Evacuation Duration Calculation Table). The data explicitly demonstrates that the original sink node E exhibited the highest personnel density, which critically influenced evacuation route selection. The congestion at the sink node E is mainly due to the narrowness of the connected passageways, and since the sink node E is a necessary node for the evacuation of most source nodes, it fails to meet the flow requirements for personnel evacuation. This situation is caused by the limitations of the building’s structural design. Under the E sink configuration, the required evacuation duration was 57.935 s, representing the total evacuation time. Through model optimization, personnel from source nodes 34, 35, and 36 were redirected to sink nodes C and D. While this adjustment did not alter the evacuation duration at sink E, it effectively reduced the overall evacuation time.
Specifically, the optimized evacuation duration decreased to 48.397 s, achieving a 9.538 s reduction compared to the baseline. This outcome indicates that despite the high density and prolonged evacuation time at sink nodes E, the optimized evacuation framework balances temporal efficiency and spatial equity by redirecting traffic flows from congested areas to underused exits, aiding mobility-impaired individuals and reducing reliance on high-risk corridors. Consequently, the model optimization not only enhanced temporal efficiency but also provided actionable insights for evacuation route planning.
6. Simulation
6.1. Simulation Software
MassMotion is a specialized simulation tool designed for modeling and analyzing evacuation processes in complex architecture environments. The software employs advanced algorithms and human factors engineering principles to simulate realistic crowd dynamics and predict evacuation efficiency and safety metrics across emergency scenarios. MassMotion has extensive applications in evacuation planning and analysis for facilities including, but not limited to, hospitals, commercial centers, public transit hubs, and educational institutions. Its core functionality enables safety analysts, architectural designers, and emergency management professionals to evaluate and optimize evacuation routes through dynamic pedestrian behavior simulation within built environments.
6.2. Simulation Settings
In MassMotion, conducting crowd flow simulations involves a systematic workflow of modeling, parameter configuration, and simulation execution to accurately replicate evacuation scenarios and perform performance analysis. The initial step requires importing the building’s geometric model through BIM files, as illustrated in Figure 6, to ensure comprehensive representation of spatial layouts. Subsequent spatial attribute assignments include setting actual corridor widths to define passage capacities, specifying exit flow rates to determine maximum throughput, and adding obstacles to reflect physical constraints.
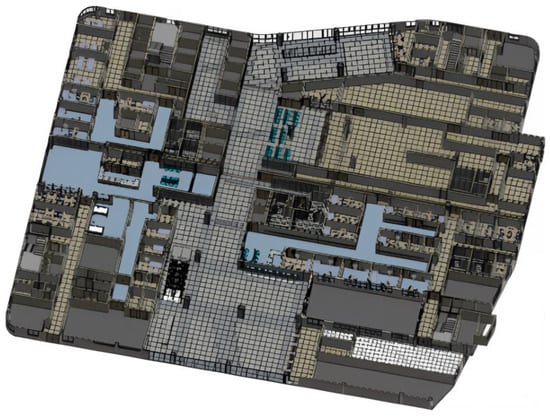
Figure 6.
The BIM architectural geometric model rendered using Revit (Revit is a three-dimensional modeling software widely used in the field of architectural design, which is developed by Autodesk).
Navigation mesh generation constitutes a critical phase, delineating pedestrian walkable areas and movement paths within the structure. During parameterization, crowd attributes such as initial positions and evacuation priorities are defined.
By executing simulations, MassMotion dynamically calculates pedestrian trajectories, evacuation durations, and density evolution, as illustrated in Figure 7. These data are utilized to analyze corridor/exit congestion levels and critical evacuation paths, providing empirical foundations for optimizing evacuation strategies.

Figure 7.
Simulated evacuation process using MassMotion software and display of real-time data.
6.3. Simulation Result
6.3.1. Simulation of Conventional Evacuation Methods
The simulation generates an evacuation time diagram based on the conventional proximity principle, recording the time when the last individual exits the floor as the total evacuation duration, while also producing a maximum personnel density diagram (Figure 8 and Figure 9). These results align with the computational outcomes of the network flow model, demonstrating elevated density values in queuing segments within the personnel density distribution.
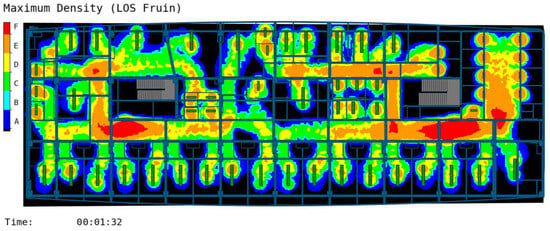
Figure 8.
Maximum density map of personnel simulated by MassMotion for routine evacuation. (A–F represent personnel density levels, from low to high).
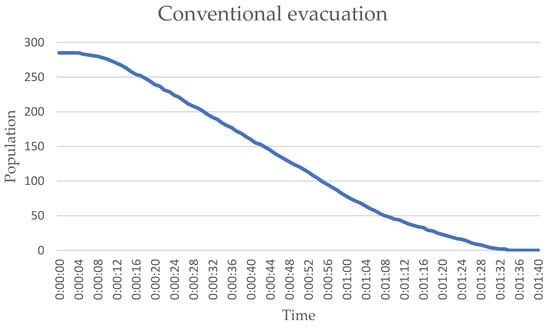
Figure 9.
Conventional evacuation simulation personnel-counting diagram by MassMotion.
6.3.2. Simulation After Optimization of Flow Space Theory
The application of Space of Flows Theory optimizes evacuation routes by redirecting pedestrian flows away from high-density zones and rationally allocating crowds to alternative exits or evacuation pathways, thereby enhancing overall evacuation efficiency and reducing evacuation duration.
Based on prior operational protocols, adjustments to evacuation exits in specific rooms resulted in variations in evacuation times and maximum density metrics. Detailed changes are illustrated in Figure 10 and Figure 11.
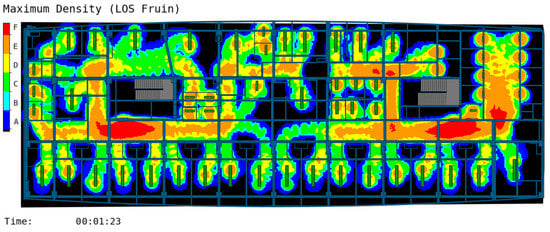
Figure 10.
Optimization of evacuation simulation personnel maximum density map using MassMotion simulation. (A–F represent personnel density levels, from low to high).
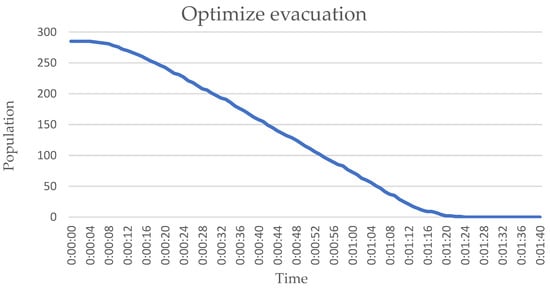
Figure 11.
Optimized evacuation simulation personnel-counting diagram by MassMotion.
6.4. Comparison of Simulation Results
The conventional simulation method yielded an evacuation duration of 82 s, encompassing the entire process from initial evacuation instruction reception to safe egress. This duration accounts for time spent locating nearest exits, navigating crowded corridors/stairwells/elevators, and potential emergency-induced delays. Post-optimization evacuation duration decreased to 73 s, demonstrating that refined evacuation strategies and procedures can effectively reduce evacuation time. The streamlined population distribution further improves the long-term operational sustainability of hospital infrastructure and reduces the overload of emergency systems, which is the key to maintaining functional continuity in repeated disasters.
As illustrated in Figure 12, maximum personnel density metrics also improved in the same spatial domain. This indicates that optimized evacuation protocols not only shorten evacuation duration but also enhance concurrent evacuation throughput—a critical advancement for life safety preservation and casualty mitigation during emergencies. Although spatial optimization can effectively alleviate congestion, it is interconnected with factors such as communication systems and evacuation signage. Only by comprehensively considering these factors and conducting overall optimization can the best evacuation results be achieved.

Figure 12.
Comparison of maximum density maps of personnel within a specific area; compare (a) optimized personnel density map and (b) conventional personnel density map to obtain the change in maximum personnel density. (The areas marked in red are regions with significant changes).
7. Empirical Study on Evacuation Simulation
7.1. Design of Evacuation Simulation
To further verify the practical effectiveness of the flow space theory optimization model and explore the impact of emergency training on evacuation efficiency, this study organized three field evacuation simulation experiments in a tertiary hospital in Urumqi (structurally similar to the simulation scenario in the paper). The experiments covered a standard floor of the inpatient department, with participants including patients (including 27 mobility-impaired individuals, 16 patients requiring assistance, and 2 critically ill patients), medical staff, and family members, totaling 85 people. The three simulations adopted different strategies, and a comparative analysis was conducted on the differences in evacuation time and influencing factors:
Drill 1: Evacuation using the traditional the shortest-path principle (benchmark scenario);
Drill 2: Application of flow space optimized paths (based on the model in Section 5.1);
Drill 3: Addition of an earthquake scenario, requiring execution of a 12 s earthquake-proof action before evacuation.
7.2. Analysis of Evacuation Simulation Results
As shown in the recorded results in Table 3, chaos occurred at the scene during the first simulation. When the evacuation notice was delivered, many people needed 2–5 s to react before starting to evacuate, and congestion appeared at the sink node according to the shortest-path principle. In the second simulation, it was clearly felt that people immediately began to evacuate when the evacuation notice was conveyed, and the optimized path alleviated the congestion in the channels. The third simulation modeled evacuation in an earthquake scenario, requiring a 12 s earthquake-proof action first. The results showed that after two training sessions, the evacuation became more skillful, and with the reflection during the earthquake-evasion time, the evacuation approach became clearer.

Table 3.
Table of evacuation simulation results analysis.
7.3. Implications for Emergency Management
In terms of enhancing emergency response efficiency, dynamic path optimization serves as the fundamental support. Relying on the theory of flow space, it can effectively overcome the limitations of static path design by regulating personnel flow, especially in scenarios with dense crowds and a large number of vulnerable groups. Emergency training is a key complement; regular full-process simulation drills (it is recommended that hospitals carry out at least one drill per quarter) have been proven to significantly reduce “human delays” such as decision-making hesitation and coordination chaos. The focus should be on strengthening the zonal guidance capabilities of medical staff and the autonomous risk-avoidance awareness of patients. Meanwhile, the necessity of scenario-based simulation cannot be ignored. Diverse disaster scenarios such as fires and earthquakes must be incorporated to test the robustness of emergency plans, and special procedures should be formulated for special links like the “shelter–evacuation” interface to ensure the integrity and efficiency of the response chain.
This experiment only covered horizontal evacuation scenarios on a single floor and did not involve vertical evacuation situations such as stair usage after elevator outages. Additionally, in the experiment, speed changes caused by psychological factors like panic were still simulated using assumed parameters. Future research should incorporate physiological data such as eye-tracking and heart rate monitoring to achieve more realistic human behavior modeling.
8. Conclusions
This study systematically investigates the optimization of hospital evacuation routes through an integrated methodology combining Space of Flows Theory with network flow modeling. The findings reveal that traditional shortest-path-based evacuation approaches frequently induce localized congestion, thereby prolonging evacuation durations. By implementing Space of Flows Theory, dynamic adjustments to crowd distribution and route selection effectively balance flow allocation, reduce waiting times in high-density zones, and significantly enhance systemic evacuation efficiency.
A network flow model was developed to quantify the impacts of walking time and queuing time on total evacuation duration, while a global optimization perspective informed the formulation of a dynamic crowd flow allocation strategy. However, there is still room for improvement in the network flow mathematical model. For example, the pedestrian density should be a dynamic parameter, and accordingly, the speed should also change dynamically. Additionally, too few factors affecting pedestrian evacuation speed have been considered. Factors such as panic psychology and the damage of disasters to buildings should also be taken into account. Although the simulation using MassMotion has been quite similar to the reality, the functions of MassMotion are not yet comprehensive. For example, it cannot reflect the uncertainties of people during evacuation and the influence of the environment on evacuation, among other aspects. Validation through MassMotion simulations confirmed the practical efficacy of this theoretical framework, demonstrating a 9 s reduction in evacuation duration and more uniform personnel density distributions. Evacuation drills were conducted in similar hospitals, and a comparison of the drill results showed that the path optimization based on flow space theory indeed played a role in alleviating congestion. These results robustly validate the application value of Space of Flows Theory in emergency evacuation scenarios.
By integrating dynamic traffic optimization design principles, supports the paradigm of ‘efficient emergency response’, ensuring that hospitals can quickly evacuate personnel during disasters while minimizing long-term environmental and socio-economic damage. This framework provides policy makers with actionable insights to coordinate emergency response efficiency with sustainable development goals, particularly in disaster-prone areas facing escalating climate risks.
However, this study mainly focuses on optimizing the evacuation routes for a specific floor of a certain type of hospital. The applicability of the research results for hospitals with different layouts still needs to be further verified. There are still aspects that can be improved in the mathematical model and verification method of this study. In future research, the incorporation of more factors of human behavior and the establishment of a more complete dynamic path capacity model are recommended.
Author Contributions
Conception and methodology, Y.W.; writing—editing and data curation, J.X.; Guidance and supervision, X.H. All authors have read and agreed to the published version of the manuscript.
Funding
Natural Science Foundation of Xinjiang Uygur Autonomous (Grant No. 2023D01C188); National Natural Science Foundation of China (Grant No. 52368051); Tanachi Talent Program of Xinjiang Uygur Autonomous; the Excellent Graduate Innovation Project of Xinjiang University (Grant No. XJ2025G063); the Excellent Graduate Innovation Project of Xinjiang University (Grant No. XJDX2025YJS218); Postgraduate Education and Teaching Reform Project of Xinjiang University (Grant No. XJDX2024YJG72); Teaching Case Library Construction Project for Professional Degree Postgraduates of Xinjiang University (Grant No. XJDX2025YALK07); and Research and Development of Key Construction Technologies for the Bazhou People’s Hospital Project Industry–University–Research Cooperation Agreement: 202409140034.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this research are available from the corresponding author upon reasonable request.
Conflicts of Interest
Author Yilai Wu was employed by the company CCCC Second Highway Engineering Co., Ltd. Author Xuekelaiti Haiyirete was employed by the company Xinjiang Xindewang Construction Project Management Consulting Co., Ltd. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A. (Standard Evacuation Time Calculation Table)
| Node Starting Point | Node Endpoint | Edge Label | People | Edge Width | Edge Lengths | Edge Area | Occupant Density | Edge Flow | Edge Capacity | Flow Rate | Walking Time | Queuing Time | Evacuation Time at the Edge | Path Evacuation Time |
| 1 | A | (1, A) | 2 | 1.3 | 8.146 | 10.590 | 0.189 | 0.182 | 0.455 | 0.741 | 10.996 | 10.996 | ||
| 2 | A | (2, A) | 0 | 1.0 | 7.617 | 7.617 | 0.000 | 0.000 | 0.350 | |||||
| 3 | A | (3, A) | 0 | 1.0 | 8.614 | 8.614 | 0.000 | 0.000 | 0.350 | |||||
| 4 | A | (4, A) | 4 | 1.3 | 5.548 | 7.212 | 0.555 | 0.615 | 0.455 | 0.852 | 6.508 | 0.351 | ||
| 5 | A | (5, A) | 4 | 1.3 | 4.463 | 5.802 | 0.689 | 0.732 | 0.455 | 0.817 | 5.465 | 0.609 | ||
| 6 | A | (6, A) | 4 | 1.3 | 5.417 | 7.042 | 0.568 | 0.627 | 0.455 | 0.849 | 6.381 | 0.378 | ||
| 7 | B | (7, B) | 2 | 1.2 | 4.702 | 5.642 | 0.354 | 0.501 | 0.420 | 1.177 | 3.993 | 0.192 | ||
| 8 | B | (8, B) | 0 | 1.2 | 6.942 | 8.330 | 0.000 | 0.000 | 0.420 | |||||
| 9 | B | (9, B) | 0 | 1.2 | 4.524 | 5.429 | 0.000 | 0.000 | 0.420 | |||||
| 10 | B | (10, B) | 2 | 1.2 | 1.640 | 1.968 | 1.016 | 1.157 | 0.420 | 0.949 | 1.729 | 1.754 | ||
| 11 | B | (11, B) | 4 | 2.7 | 5.048 | 13.630 | 0.293 | 0.950 | 0.945 | 1.199 | 4.212 | |||
| B | A | (B, A) | 8 | 1.5 | 6.882 | 10.323 | 0.775 | 1.200 | 0.525 | 1.032 | 6.669 | 1.285 | 7.954 | |
| A | J | (A, J) | 22 | 1.5 | 2.992 | 4.488 | 4.902 | 10.294 | 0.525 | 1.400 | 2.137 | 18.608 | 20.745 | 39.695 |
| 12 | C | (12, C) | 4 | 1.3 | 9.128 | 11.866 | 0.337 | 0.399 | 0.455 | 0.910 | 10.027 | 10.027 | ||
| 13 | C | (13, C) | 4 | 1.3 | 6.334 | 8.234 | 0.486 | 0.550 | 0.455 | 0.871 | 7.274 | 0.209 | ||
| 14 | C | (14, C) | 6 | 1.3 | 4.525 | 5.883 | 1.020 | 0.966 | 0.455 | 0.729 | 6.210 | 1.124 | ||
| 15 | C | (15, C) | 6 | 1.3 | 5.018 | 6.523 | 0.920 | 0.903 | 0.455 | 0.755 | 6.643 | 0.985 | ||
| 16 | C | (16, C) | 6 | 1.3 | 7.149 | 9.294 | 0.646 | 0.695 | 0.455 | 0.828 | 8.631 | 0.528 | ||
| 17 | C | (17, C) | 0 | 1.0 | 2.473 | 2.473 | 0.000 | 0.000 | 0.350 | |||||
| 18 | C | (18, C) | 2 | 1.3 | 0.783 | 1.018 | 1.965 | 1.585 | 0.455 | 0.621 | 1.262 | 2.484 | ||
| 19 | C | (19, C) | 0 | 1.0 | 7.106 | 7.106 | 0.000 | 0.000 | 0.350 | |||||
| 20 | D | (20, D) | 0 | 1.0 | 4.971 | 4.971 | 0.000 | 0.000 | 0.350 | |||||
| 21 | D | (21, D) | 2 | 1.0 | 3.751 | 3.751 | 0.533 | 0.595 | 0.350 | 1.116 | 3.362 | 0.700 | ||
| 22 | D | (22, D) | 4 | 2.7 | 2.604 | 7.031 | 0.569 | 1.695 | 0.945 | 1.103 | 2.360 | 0.793 | ||
| 23 | D | (23, D) | 2 | 2.7 | 2.287 | 6.175 | 0.324 | 1.039 | 0.945 | 1.188 | 1.925 | 0.099 | ||
| 24 | D | (24, D) | 0 | 1.0 | 5.895 | 5.895 | 0.000 | 0.000 | 0.350 | |||||
| 25 | D | (25, D) | 0 | 1.0 | 4.766 | 4.766 | 0.000 | 0.000 | 0.350 | |||||
| D | C | (D, C) | 8 | 1.5 | 8.085 | 12.128 | 0.660 | 1.061 | 0.525 | 1.072 | 7.543 | 1.020 | 8.563 | |
| C | J | (C, J) | 36 | 2.6 | 11.506 | 29.916 | 1.203 | 2.305 | 0.910 | 0.737 | 15.621 | 1.532 | 17.154 | 35.744 |
| 26 | E | (26, E) | 6 | 1.3 | 8.760 | 11.388 | 0.527 | 0.589 | 0.455 | 0.860 | 10.188 | |||
| 27 | E | (27, E) | 6 | 1.3 | 6.218 | 8.083 | 0.742 | 0.774 | 0.455 | 0.803 | 7.748 | 0.702 | ||
| 28 | E | (28, E) | 6 | 1.3 | 4.872 | 6.334 | 0.947 | 0.921 | 0.455 | 0.748 | 6.513 | 1.025 | ||
| 29 | E | (29, E) | 6 | 1.3 | 5.537 | 7.198 | 0.834 | 0.843 | 0.455 | 0.778 | 7.114 | 0.854 | ||
| 30 | E | (30, E) | 4 | 1.3 | 7.809 | 10.152 | 0.394 | 0.459 | 0.455 | 0.895 | 8.723 | 0.008 | ||
| 31 | E | (31, E) | 0 | 1.0 | 1.455 | 1.455 | 0.000 | 0.000 | 0.350 | |||||
| 32 | E | (32, E) | 0 | 1.0 | 1.673 | 1.673 | 0.000 | 0.000 | 0.350 | |||||
| 33 | E | (33, E) | 0 | 1.0 | 3.338 | 3.338 | 0.000 | 0.000 | 0.350 | |||||
| 34 | F | (34, F) | 3 | 1.0 | 1.085 | 1.085 | 2.765 | 1.024 | 0.350 | 0.370 | 2.930 | 1.926 | ||
| 35 | F | (35, F) | 3 | 1.0 | 7.940 | 7.940 | 0.378 | 0.476 | 0.350 | 1.259 | 6.305 | 0.359 | ||
| 36 | F | (36, F) | 3 | 1.0 | 6.413 | 6.413 | 0.468 | 0.573 | 0.350 | 1.226 | 5.232 | 0.638 | ||
| 37 | F | (37, F) | 3 | 1.0 | 6.461 | 6.461 | 0.464 | 0.570 | 0.350 | 1.227 | 5.265 | 0.628 | ||
| 38 | F | (38, F) | 3 | 1.0 | 0.551 | 0.551 | 5.445 | 7.623 | 0.350 | 1.400 | 0.394 | 20.779 | 21.172 | |
| F | E | (F, E) | 15 | 1.0 | 3.488 | 3.488 | 4.300 | 6.021 | 0.350 | 1.400 | 2.491 | 16.202 | 18.693 | |
| E | K | (E, K) | 43 | 2.6 | 11.114 | 28.896 | 1.488 | 2.664 | 0.910 | 0.688 | 16.143 | 1.927 | 18.070 | 57.935 |
| 39 | G | (39, G) | 3 | 1.0 | 2.618 | 2.618 | 1.146 | 1.115 | 0.350 | 0.973 | 2.690 | 2.186 | ||
| 40 | G | (40, G) | 0 | 1.0 | 0.864 | 0.864 | 0.000 | 0.000 | 0.350 | |||||
| 41 | G | (41, G) | 3 | 1.0 | 3.360 | 3.360 | 0.893 | 0.953 | 0.350 | 1.068 | 3.148 | 1.723 | ||
| 42 | G | (42, G) | 0 | 1.5 | 2.269 | 3.404 | 0.000 | 0.000 | 0.525 | |||||
| 43 | G | (43, G) | 3 | 1.0 | 7.886 | 7.886 | 0.380 | 0.479 | 0.350 | 1.258 | 6.267 | 0.368 | 6.635 | |
| 44 | G | (44, G) | 3 | 1.0 | 7.535 | 7.535 | 0.398 | 0.498 | 0.350 | 1.252 | 6.020 | 0.424 | ||
| G | K | (G, K) | 12 | 1.5 | 8.000 | 12.000 | 1.000 | 1.541 | 0.525 | 1.028 | 7.785 | 1.936 | 9.721 | 16.356 |
| 45 | H | (45, K) | 3 | 1.1 | 4.163 | 4.579 | 0.655 | 0.833 | 0.385 | 1.156 | 3.601 | 1.164 | ||
| 46 | H | (46, K) | 3 | 1.1 | 2.519 | 2.771 | 1.083 | 1.187 | 0.385 | 0.997 | 2.527 | 2.084 | ||
| 47 | H | (47, K) | 3 | 1.1 | 2.087 | 2.296 | 1.307 | 1.313 | 0.385 | 0.913 | 2.285 | 2.410 | ||
| 48 | H | (48, K) | 3 | 1.1 | 3.076 | 3.384 | 0.887 | 1.043 | 0.385 | 1.070 | 2.875 | 1.710 | ||
| 49 | H | (49, K) | 3 | 1.1 | 4.407 | 4.848 | 0.619 | 0.796 | 0.385 | 1.170 | 3.768 | 1.068 | ||
| 50 | H | (50, K) | 3 | 1.1 | 2.814 | 3.095 | 0.969 | 1.108 | 0.385 | 1.039 | 2.708 | 1.877 | ||
| 51 | H | (51, K) | 3 | 1.1 | 2.366 | 2.603 | 1.153 | 1.231 | 0.385 | 0.971 | 2.437 | 2.197 | ||
| 52 | H | (52, K) | 3 | 1.1 | 3.252 | 3.577 | 0.839 | 1.003 | 0.385 | 1.088 | 2.990 | 1.606 | ||
| 53 | I | (53, I) | 0 | 1.5 | 0.761 | 1.142 | 0.000 | 0.000 | 0.525 | |||||
| 54 | I | (54, I) | 4 | 1.3 | 8.312 | 10.806 | 0.370 | 0.434 | 0.455 | 0.902 | 9.220 | 9.220 | ||
| 55 | I | (55, I) | 4 | 1.3 | 5.614 | 7.298 | 0.548 | 0.609 | 0.455 | 0.854 | 6.572 | 0.338 | ||
| 56 | I | (56, I) | 4 | 1.3 | 4.432 | 5.762 | 0.694 | 0.736 | 0.455 | 0.815 | 5.436 | 0.617 | ||
| 57 | I | (57, I) | 2 | 1.3 | 6.234 | 8.104 | 0.247 | 0.420 | 0.455 | 1.308 | 4.766 | |||
| H | I | (H, I) | 14 | 2.1 | 6.835 | 14.354 | 0.975 | 2.124 | 0.735 | 1.037 | 6.593 | 1.889 | 8.482 | |
| I | K | (I, K) | 38 | 1.5 | 4.598 | 6.897 | 5.510 | 11.570 | 0.525 | 1.400 | 3.284 | 21.039 | 24.323 | 42.025 |
Appendix B. (Optimized Evacuation Time Calculation Table)
| Node Starting Point | Node Endpoint | Edge Label | People | Edge Width | Edge Lengths | Edge Area | Occupant Density | Edge Flow | Edge Capacity | Flow Rate | Walking Time | Queuing Time | Evacuation Time at the Edge | Path Evacuation Time |
| 1 | A | (1, A) | 2 | 1.3 | 8.146 | 10.590 | 0.189 | 0.182 | 0.455 | 0.741 | 10.996 | 10.996 | ||
| 2 | A | (2, A) | 0 | 1.0 | 7.617 | 7.617 | 0.000 | 0.000 | 0.350 | |||||
| 3 | A | (3, A) | 0 | 1.0 | 8.614 | 8.614 | 0.000 | 0.000 | 0.350 | |||||
| 4 | A | (4, A) | 4 | 1.3 | 5.548 | 7.212 | 0.555 | 0.615 | 0.455 | 0.852 | 6.508 | 0.351 | ||
| 5 | A | (5, A) | 4 | 1.3 | 4.463 | 5.802 | 0.689 | 0.732 | 0.455 | 0.817 | 5.465 | 0.609 | ||
| 6 | A | (6, A) | 4 | 1.3 | 5.417 | 7.042 | 0.568 | 0.627 | 0.455 | 0.849 | 6.381 | 0.378 | ||
| 7 | B | (7, B) | 2 | 1.2 | 4.702 | 5.642 | 0.354 | 0.501 | 0.420 | 1.177 | 3.993 | 0.192 | ||
| 8 | B | (8, B) | 0 | 1.2 | 6.942 | 8.330 | 0.000 | 0.000 | 0.420 | |||||
| 9 | B | (9, B) | 0 | 1.2 | 4.524 | 5.429 | 0.000 | 0.000 | 0.420 | |||||
| 10 | B | (10, B) | 2 | 1.2 | 1.640 | 1.968 | 1.016 | 1.157 | 0.420 | 0.949 | 1.729 | 1.754 | ||
| 11 | B | (11, B) | 4 | 2.7 | 5.048 | 13.630 | 0.293 | 0.950 | 0.945 | 1.199 | 4.212 | |||
| B | A | (B, A) | 8 | 1.5 | 6.882 | 10.323 | 0.775 | 1.200 | 0.525 | 1.032 | 6.669 | 1.285 | 7.954 | |
| A | J | (A, J) | 22 | 1.5 | 2.992 | 4.488 | 4.902 | 10.294 | 0.525 | 1.400 | 2.137 | 18.608 | 20.745 | 39.695 |
| 12 | C | (12, C) | 4 | 1.3 | 9.128 | 11.866 | 0.337 | 0.399 | 0.455 | 0.910 | 10.027 | 10.027 | ||
| 13 | C | (13, C) | 4 | 1.3 | 6.334 | 8.234 | 0.486 | 0.550 | 0.455 | 0.871 | 7.274 | 0.209 | ||
| 14 | C | (14, C) | 6 | 1.3 | 4.525 | 5.883 | 1.020 | 0.966 | 0.455 | 0.729 | 6.210 | 1.124 | ||
| 15 | C | (15, C) | 6 | 1.3 | 5.018 | 6.523 | 0.920 | 0.903 | 0.455 | 0.755 | 6.643 | 0.985 | ||
| 16 | C | (16, C) | 6 | 1.3 | 7.149 | 9.294 | 0.646 | 0.695 | 0.455 | 0.828 | 8.631 | 0.528 | ||
| 17 | C | (17, C) | 0 | 1.0 | 2.473 | 2.473 | 0.000 | 0.000 | 0.350 | |||||
| 18 | C | (18, C) | 2 | 1.3 | 0.783 | 1.018 | 1.965 | 1.585 | 0.455 | 0.621 | 1.262 | 2.484 | ||
| 19 | C | (19, C) | 0 | 1.0 | 7.106 | 7.106 | 0.000 | 0.000 | 0.350 | |||||
| 34 | C | (34, C) | 3 | 1.0 | 11.260 | 11.260 | 0.266 | 0.347 | 0.350 | 1.301 | 8.656 | |||
| 20 | D | (20, D) | 0 | 1.0 | 4.971 | 4.971 | 0.000 | 0.000 | 0.350 | |||||
| 21 | D | (21, D) | 2 | 1.0 | 3.751 | 3.751 | 0.533 | 0.595 | 0.350 | 1.116 | 3.362 | 0.700 | ||
| 22 | D | (22, D) | 4 | 2.7 | 2.604 | 7.031 | 0.569 | 1.695 | 0.945 | 1.103 | 2.360 | 0.793 | ||
| 23 | D | (23, D) | 2 | 2.7 | 2.287 | 6.175 | 0.324 | 1.039 | 0.945 | 1.188 | 1.925 | 0.099 | ||
| 24 | D | (24, D) | 0 | 1.0 | 5.895 | 5.895 | 0.000 | 0.000 | 0.350 | |||||
| 25 | D | (25, D) | 0 | 1.0 | 4.766 | 4.766 | 0.000 | 0.000 | 0.350 | |||||
| 35 | D | (35, D) | 3 | 1.0 | 7.760 | 7.760 | 0.387 | 0.486 | 0.350 | 1.256 | 6.178 | 0.387 | ||
| 36 | D | (36, D) | 3 | 1.0 | 11.300 | 11.300 | 0.265 | 0.345 | 0.350 | 1.301 | 8.685 | |||
| D | C | (D, C) | 14 | 1.5 | 8.085 | 12.128 | 1.154 | 1.611 | 0.525 | 0.931 | 8.689 | 2.069 | 10.758 | |
| C | J | (C, J) | 45 | 2.6 | 11.506 | 29.916 | 1.504 | 2.389 | 0.910 | 0.611 | 18.835 | 1.626 | 20.460 | 31.218 |
| 26 | E | (26, E) | 6 | 1.3 | 8.760 | 11.388 | 0.527 | 0.589 | 0.455 | 0.860 | 10.188 | 10.188 | ||
| 27 | E | (27, E) | 6 | 1.3 | 6.218 | 8.083 | 0.742 | 0.774 | 0.455 | 0.803 | 7.748 | 0.702 | ||
| 28 | E | (28, E) | 6 | 1.3 | 4.872 | 6.334 | 0.947 | 0.921 | 0.455 | 0.748 | 6.513 | 1.025 | ||
| 29 | E | (29, E) | 6 | 1.3 | 5.537 | 7.198 | 0.834 | 0.843 | 0.455 | 0.778 | 7.114 | 0.854 | ||
| 30 | E | (30, E) | 4 | 1.3 | 7.809 | 10.152 | 0.394 | 0.459 | 0.455 | 0.895 | 8.723 | 0.008 | ||
| 31 | E | (31, E) | 0 | 1.0 | 1.455 | 1.455 | 0.000 | 0.000 | 0.350 | |||||
| 32 | E | (32, E) | 0 | 1.0 | 1.673 | 1.673 | 0.000 | 0.000 | 0.350 | |||||
| 33 | E | (33, E) | 0 | 1.0 | 3.338 | 3.338 | 0.000 | 0.000 | 0.350 | |||||
| 36 | F | (36, F) | 3 | 1.0 | 6.413 | 6.413 | 0.468 | 0.573 | 0.350 | 1.226 | 5.232 | 0.638 | ||
| 37 | F | (37, F) | 3 | 1.0 | 6.461 | 6.461 | 0.464 | 0.570 | 0.350 | 1.227 | 5.265 | 0.628 | ||
| 38 | F | (38, F) | 3 | 1.0 | 0.551 | 0.551 | 5.445 | 7.623 | 0.350 | 1.400 | 0.394 | 20.779 | 21.172 | |
| F | E | (F, E) | 9 | 1.0 | 3.488 | 3.488 | 2.580 | 1.133 | 0.350 | 0.439 | 7.943 | 2.237 | ||
| E | K | (E, K) | 37 | 2.6 | 11.114 | 28.896 | 1.280 | 2.409 | 0.910 | 0.724 | 15.360 | 1.647 | 17.007 | 48.367 |
| 39 | G | (39, G) | 3 | 1.0 | 2.618 | 2.618 | 1.146 | 1.115 | 0.350 | 0.973 | 2.690 | 2.186 | ||
| 40 | G | (40, G) | 0 | 1.0 | 0.864 | 0.864 | 0.000 | 0.000 | 0.350 | |||||
| 41 | G | (41, G) | 3 | 1.0 | 3.360 | 3.360 | 0.893 | 0.953 | 0.350 | 1.068 | 3.148 | 1.723 | ||
| 42 | G | (42, G) | 0 | 1.5 | 2.269 | 3.404 | 0.000 | 0.000 | 0.525 | |||||
| 43 | G | (43, G) | 3 | 1.0 | 7.886 | 7.886 | 0.380 | 0.479 | 0.350 | 1.258 | 6.267 | 0.368 | 6.635 | |
| 44 | G | (44, G) | 3 | 1.0 | 7.535 | 7.535 | 0.398 | 0.498 | 0.350 | 1.252 | 6.020 | 0.424 | ||
| G | K | (G, K) | 12 | 1.5 | 8.000 | 12.000 | 1.000 | 1.541 | 0.525 | 1.028 | 7.785 | 1.936 | 9.721 | 16.356 |
| 45 | H | (45, K) | 3 | 1.1 | 4.163 | 4.579 | 0.655 | 0.833 | 0.385 | 1.156 | 3.601 | 1.164 | ||
| 46 | H | (46, K) | 3 | 1.1 | 2.519 | 2.771 | 1.083 | 1.187 | 0.385 | 0.997 | 2.527 | 2.084 | ||
| 47 | H | (47, K) | 3 | 1.1 | 2.087 | 2.296 | 1.307 | 1.313 | 0.385 | 0.913 | 2.285 | 2.410 | ||
| 48 | H | (48, K) | 3 | 1.1 | 3.076 | 3.384 | 0.887 | 1.043 | 0.385 | 1.070 | 2.875 | 1.710 | ||
| 49 | H | (49, K) | 3 | 1.1 | 4.407 | 4.848 | 0.619 | 0.796 | 0.385 | 1.170 | 3.768 | 1.068 | 4.836 | |
| 50 | H | (50, K) | 3 | 1.1 | 2.814 | 3.095 | 0.969 | 1.108 | 0.385 | 1.039 | 2.708 | 1.877 | ||
| 51 | H | (51, K) | 3 | 1.1 | 2.366 | 2.603 | 1.153 | 1.231 | 0.385 | 0.971 | 2.437 | 2.197 | ||
| 52 | H | (52, K) | 3 | 1.1 | 3.252 | 3.577 | 0.839 | 1.003 | 0.385 | 1.088 | 2.990 | 1.606 | ||
| 53 | I | (53, I) | 0 | 1.5 | 0.761 | 1.142 | 0.000 | 0.000 | 0.525 | |||||
| 54 | I | (54, I) | 4 | 1.3 | 8.312 | 10.806 | 0.370 | 0.434 | 0.455 | 0.902 | 9.220 | 9.220 | ||
| 55 | I | (55, I) | 4 | 1.3 | 5.614 | 7.298 | 0.548 | 0.609 | 0.455 | 0.854 | 6.572 | 0.338 | ||
| 56 | I | (56, I) | 4 | 1.3 | 4.432 | 5.762 | 0.694 | 0.736 | 0.455 | 0.815 | 5.436 | 0.617 | ||
| 57 | I | (57, I) | 2 | 1.3 | 6.234 | 8.104 | 0.247 | 0.420 | 0.455 | 1.308 | 4.766 | |||
| H | I | (H, I) | 14 | 2.1 | 6.835 | 14.354 | 0.975 | 2.124 | 0.735 | 1.037 | 6.593 | 1.889 | ||
| I | K | (I, K) | 38 | 1.5 | 4.598 | 6.897 | 5.510 | 11.570 | 0.525 | 1.400 | 3.284 | 21.039 | 24.323 | 38.379 |
References
- Wheeler-McAnally, R. The John Sealy Hospital Fire Evacuation. Crit. Care Nurse 2024, 44, 64–70. [Google Scholar] [CrossRef]
- Wang, H.; Liu, H.; Li, W.H. Crowd evacuation path planning and simulation method based on deep reinforcement learning and repulsive force field. Appl. Intell. 2025, 55, 297. [Google Scholar] [CrossRef]
- Zhu, J.; Dang, P.; Zhang, J.; Cao, Y.; Wu, J.; Li, W.; Hu, Y.; You, J. The impact of spatial scale on layout learning and individual evacuation behavior in indoor fires: Single-scale learning perspectives. Int. J. Geogr. Inf. Sci. 2024, 38, 77–99. [Google Scholar] [CrossRef]
- Ye, R.; Li, J.C.; Lu, H.C.; Wang, Y.; Pan, Y.; Wang, J. A study on the arch mechanism of pedestrian evacuation and congestion alleviation strategies at building exits. J. Build. Eng. 2024, 88, 109159. [Google Scholar] [CrossRef]
- Abir, I.M.; Ibrahim, A.M.; Toha, S.F. A review on the hospital evacuation simulation models. Int. J. Disaster Risk Reduct. 2022, 77, 103083. [Google Scholar] [CrossRef]
- Shi, Y.L.; Yang, J.Y.; Keith, M.; Song, K.; Li, Y.; Guan, C. Spatial Accessibility Patterns to Public Hospitals in Shanghai: An Improved Gravity Model. Prof. Geogr. 2022, 74, 265–289. [Google Scholar] [CrossRef]
- Saltos, D.N.; Kristensen, S.R. How economic policies which drive competition amongst hospitals impacts quality of care: The case of the English NHS (A systematic review). Am. J. Surg. 2025, 244, 116237. [Google Scholar] [CrossRef]
- Xu, J.; Peng, Y.; Ye, C.; Gao, S.; Cheng, M. Hospital Flow Simulation and Space Layout Planning Based on Low-Trust Social Force Model. IEEE Access 2024, 12, 90135–90144. [Google Scholar] [CrossRef]
- Zayas, V.; Mokha, A.; Low, S. Constructing Hospitals for Functionality after Earthquakes: Saves Lives and Costs! Buildings 2023, 13, 2741. [Google Scholar] [CrossRef]
- Shimoto, M.; Cho, K.; Kurata, M.; Hitomi, M.; Kato, Y.; Aida, S.; Sugiyama, O.; Maki, N.; Ohtsuru, S. Hospital Evacuation Implications After the 2016 Kumamoto Earthquake. Disaster Med. Public Health Prep. 2023, 16, 2680–2682. [Google Scholar] [CrossRef]
- Kodur, V.; Jha, A.; Lajnef, N. Critical Egress Parameters Governing Assisted Evacuation in Hospital Buildings. Fire 2024, 7, 85. [Google Scholar] [CrossRef]
- Al Bochi, A.; Roberts, B.W.; Sajid, W.; Ghulam, Z.; Weiler, M.; Sharma, Y.; Marquez-Chin, C.; Pong, S.; Vette, A.H.; Dutta, T. Evacuation Solutions for Individuals with Functional Limitations in the Indoor Built Environment: A Scoping Review. Buildings 2023, 13, 2779. [Google Scholar] [CrossRef]
- Weber, L.; Mohn, S.B.; Vecchio, F.; Fili, A. Beyond deportation: Researching the control of outward mobility using a space of flows logic. Glob. Netw. 2020, 20, 65–84. [Google Scholar] [CrossRef]
- Li, J.W.; Qian, J.; Liu, Y.L. A Novel Analysis Method of Geographical Centrality Based on Space of Flows. ISPRS Int. J. Geo-Inf. 2015, 6, 153. [Google Scholar] [CrossRef]
- Berglund, E. Forest, flows and identities in finland’s information society. Cult. Stud. 2008, 22, 412–430. [Google Scholar] [CrossRef]
- Wang, J.H.; Jin, B.W.; Li, J.; Chen, F.; Wang, Z.; Sun, J. Method for guiding crowd evacuation at exit: The buffer zone. Saf. Sci. 2019, 118, 88–95. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, H.; Wang, Z.; Li, Q.; Dou, Z.; Xie, W.; Zhang, Z.; Wang, R.; Nie, W. Optimal Evacuation Route Planning of Urban Personnel at Different Risk Levels of Flood Disasters Based on the Improved 3D Dijkstra’s Algorithm. Sustainability 2022, 14, 10250. [Google Scholar] [CrossRef]
- Zhu, Q.K.; Li, J.W.; Du, Y.F. Simulation Study of Personnel Evacuation in Fire Scenarios of Old School Buildings. J. Syst. Simul. 2024, 36, 2043–2053. [Google Scholar] [CrossRef]
- Khalili, S.M.; Mojtahedi, M.; Steinmetz-Weiss, C.; Sanderson, D. A Systematic Literature Review on Transit-Based Evacuation Planning in Emergency Logistics Management: Optimisation and Modelling Approaches. Buildings 2024, 14, 176. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Ling, W.; Yang, Z.; Wei, X.; Wang, H. A congestion prediction model for optimizing emergency evacuation design of university libraries in China. J. Build. Eng. 2025, 99, 111537. [Google Scholar] [CrossRef]
- Enshan, C.; van de Spek, S.; van der Hoeven, F.; Triggianese, M. Evaluate user satisfaction for urban design of railway station areas: An assessment framework using agent-based simulation. Environ. Impact Assess. Rev. 2025, 110, 107685. [Google Scholar] [CrossRef]
- Wang, L.; Jin, J.G. Utilizing and optimizing non-disrupted lines for evacuating passengers in Urban rail transit networks during disruptions. Transp. B Transp. Dyn. 2025, 13, 2440588. [Google Scholar] [CrossRef]
- Ye, S.; Li, Z.Q.; Xi, J.C. A Model for Estimating the Tourism Carrying Capacity of a Tourism Corridor: A Case Study of the Qinghai–Tibet Plateau. Sustainability 2024, 16, 5466. [Google Scholar] [CrossRef]
- Rungta, M.; Lim, G.J.; Baharnemati, M. Optimal egress time calculation and path generation for large evacuation networks. Ann. Oper. Res. 2012, 201, 403–421. [Google Scholar] [CrossRef]
- Pan, Z.; Wei, Q.; Torp, O.; Lau, A. Influence of Evacuation Walkway Design Parameters on Passenger Evacuation Time along Elevated Rail Transit Lines Using a Multi-Agent Simulation. Sustainability 2019, 11, 6049. [Google Scholar] [CrossRef]
- Lovreglio, R.; Kuligowski, E. A pre-evacuation study using data from evacuation drills and false alarm evacuations in a university library. Fire Saf. J. 2022, 131, 103595. [Google Scholar] [CrossRef]
- Siam, M.R.K.; Staes, B.M.; Lindell, M.K.; Wang, H. Lessons Learned From the 2018 Attica Wildfire: Households’ Expectations of Evacuation Logistics and Evacuation Time Estimate Components. Fire Technol. 2025, 61, 795–827. [Google Scholar] [CrossRef]
- Guo, W.H.; He, Y.W. Optimized Wayfinding Signage Positioning in Hospital Built Environment through Medical Data and Flows Simulations. Buildings 2022, 12, 1426. [Google Scholar] [CrossRef]
- Chen, S.; Lin, Y. Search for All Minimal Paths in a General Large Flow Network. IEEE Trans. Reliab. 2012, 61, 949–956. [Google Scholar] [CrossRef]
- GB/T31593.9-2015; Fire Safety Engineering Part 9: Guidance on Evaluation of Behaviour and Movement. Standards Press of China: Beijing, China, 2015.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).