Abstract
Water management has evolved significantly, but sustainability remains a critical challenge. Ancient Roman aqueducts, despite their engineering marvel, operated with constant flow, leading to substantial water waste. Later, rooftop reservoir systems continued this inefficiency, as excess water would overflow. Only recently have demand-driven networks shown potential for reducing waste, though substantial water leaks continue to undermine these efforts. Achieving true sustainability in water distribution requires minimizing leaks through the use of models that adopt accurate water demand scenarios and identifying an optimal peak factor (PF). In fact, water distribution networks (WDNs) are commonly designed, analyzed, and calibrated using deterministic demand scenarios based on average annual consumption and scaled by a chosen PF. However, for efficient design and management, it is essential to associate a probabilistic value with the consumption data used in the analyses. This study introduces a novel methodology for estimating PFs with a specific return period at the District Meter Area (DMA) scale, utilizing extreme value statistical analysis. The generalized Pareto distribution (GPD) models were applied to provide more reliable PF estimates. The proposed methodology was validated using hourly residential consumption data from a DMA located in Southern Italy, demonstrating its effectiveness in improving the accuracy of WDN design.
1. Introduction
In an era where climate change and population growth are placing increasing strain on water distribution systems (WDSs), optimizing water use becomes essential. Minimizing leaks and waste through the use of efficient technologies, infrastructure maintenance, and public awareness not only helps preserve a precious resource but also reduces environmental impact and ensures equitable water access for future generations. Responsible and mindful water use is therefore crucial for sustainability and for addressing the challenges related to water scarcity. In this context, the shift from roof tank-based WDSs to demand-driven networks has resulted in a tangible reduction in water waste, as highlighted by industry reports. It was indeed revealed in an interview with a water utility manager that on average, a household served by the former system in an Italian city consumes around 5200 m3 of water per year, while the same household, when served by a demand-driven system, reduces its annual consumption to less than 2300 m3 (Figure 1).
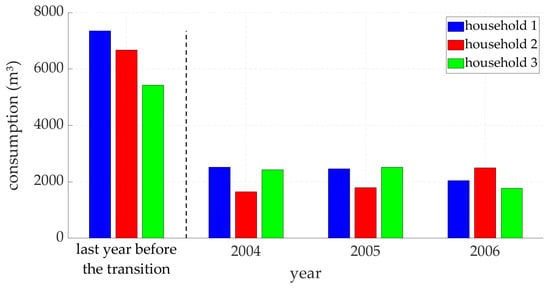
Figure 1.
The reduction in water consumption due to the transition from the roof tank-based system to the demand-driven system, which occurred between 2000 and 2003 in all three households. The first group of bars in the graph represents the consumption data prior to this transition.
Further improvements in system performance are still possible, especially through more efficient monitoring and management strategies.
Traditionally, deterministic assumptions have formed the basis for the design and management of WDNs. Conventional designs often operate under the assumption that one or more model input variables are known with precision. However, deterministic assumptions can significantly diverge from real-world conditions due to the uncertainty that governs water demand patterns. One variable that has historically been treated as constant is the water demand scenario. This scenario is obtained by appropriately scaling the annual average consumption scenario with a peak factor (PF) [1,2], depending on the size and socio-economic characteristics of the area covered by the WDN. This choice is cautionary, since peak water demand implies one of the most challenging operational conditions for an urban WDN. Understanding this factor and its impact on maximum water demand leads to estimating appropriate peak design factors for a more economical and efficient design of water and wastewater supply systems. The value of the PF is not unequivocally fixed but assumes different values depending on either the empirical factor evaluated for the specific area or the chosen literature formula.
There are many formulas in the literature that allow the PF to be estimated as a function of the number of users, and each of them is deduced based on precise temporal and spatial aggregations. The literature proposes many different methodologies for estimating the PF, mainly differentiated by the spatial scale to which they refer. Among the techniques proposed is the top-down deterministic approach (TDA), which analyzes the total water consumption of the WDN [3,4,5]. Although these studies may refer to situations in which leaks are reduced to values considered physiological, the presence of this unexpected consumption may lead to an underestimation of the recorded peaks. In contrast to the TDA, with the development of smart metering systems, it has become easier to devise bottom-up approaches (BUAs). BUAs do not have the problem of underestimation of the PF due to the presence of water leaks, as they are based on the measurement of consumption by individual flow meters. An example of a BUA is the proposal, by Buchberger et al. [6], of a statistically based probability model that would evaluate peak water demand for single and multi-family dwellings. The limitation of this work is inherent in the fact of having measured only short periods for each user, not being able to claim to have grasped the actual maximum peak that occurred. More recently, Gargano et al. [7] have proposed a probabilistic approach which demonstrates the reliability of the log-normal and Gumbel distributions in representing the daily peak water demand.
The problem with BUAs in the literature is related to the spatial and temporal extension of the sample. In agreement with what has been found in recent bibliographic reviews on the existing water consumption datasets [8,9], there are no accessible datasets of water consumption with samples measured for at least one year. In addition, leaving aside the temporal extension of the sampling, most of the peak studies are usually with reference to small samples of households or to residential areas with a minimum of 5000–10,000 residents. Less attention is given to the case of a DMA, where the peak phenomenon is often more important if compared with the average flow requirements.
Another key consideration in PF analysis is related to the fact that the PFs are used with the aim of considering the critical conditions for the system. For this reason, it is not useful to consider PFs that occur ordinarily, while it is important to analyze an actual extreme PF unexpectedly occurring in water consumption scenarios. In this paper, we want to present a methodology for performing a statistical analysis aimed at estimating the extreme PFs suitable for a DMA starting from hourly measurements collected by a smart metering system. For this purpose, the analysis of the extremes is followed according to the Peaks-Over-Threshold (POT) methodology. The POT methodology has been studied in very different fields, such as hydrology, climatology, wave theory, air pollution, and finance. In the field of water consumption, as far as the authors know, this methodology has already been applied only by Vonk et al. [10] but for other purposes.
To validate the proposed methodology, we propose a case study of the DMA of Soccavo, located in Naples (Italy). The DMA is equipped with a smart metering system that provided water consumption measurements performed with a one-hour time aggregation on more than 3000 households for four years. The analysis was performed at different spatial scales, with the aim of showing the evolution of the PF in statistical terms as the number of households grows.
2. Materials and Methods
The PF is defined as the ratio of the maximum flow measured at that temporal scale against the daily average flow. The conventional methods for estimating the PF are based on empirical deterministic expressions, derived from a combination of field measurements and engineering judgment. While existing PF expressions have performed well, they lack a firm theoretical basis. In addition to the poor theoretical basis, the empirical formulations are also strongly affected by the limited amount of available data.
These observations raise the following question: is it possible that due to short sampling, a fundamental phenomenon for the estimation of the effective PFs is neglected? In fact, estimating the characteristic quantities of a WDS over short and ordinary periods can underestimate the effect of sociological events. Confirmations of this statement are provided by the studies recently carried out by Buchberger et al. [6], which point out that residential water use tends to be greater on weekends than on weekdays, and much more by Vonk et al. [10], who mention the importance of holidays in estimating PFs. In applying the methodology to a case study (Section 3), the authors will show the importance of considering this sociological factor.
Furthermore, regardless of why a PF occurs, a distinction needs to be made between ordinary PFs that occur daily and extreme PFs. The functionality of the system is undermined by the latter; therefore, it is these values that the authors intend to focus on in this work. Dividing extreme events from ordinary events is a common practice in time series analysis. The set of PFs is a time series, so extreme value analysis methodology can be applied to these data.
In the literature of extreme values, there are two models that can be used, the block maxima method (BM) and the Peak-Over-Threshold (POT) method [11]. The BM method belongs to the classical extreme value theory and allows for selecting only the maximum observation of a reasonably large chunk of the time series (usually, it is considered a year). Considering the already mentioned scarcity of available datasets and their reduced temporal extension, it becomes impossible to think of applying this methodology for the study of a time series of water consumption. Furthermore, a necessary condition for statistical analyses is that the sample analyzed is stationary and ergodic, but the time series of consumption rarely allows for stationarity and ergodicity due to the rapid variation in the sociological characteristics of users. Neglecting such an aspect leads to incorrect information that does not allow us to obtain a reliable forecast on water consumption and, consequently, on PFs. For this reason, collecting many years of water consumption measurements increases the number of annual maxima useful for BM-type analyses, but irreparably compromises their reliability. The optimal sample is therefore short enough to guarantee stationarity and ergodicity but long enough to allow for the detection of extreme phenomena.
With a sample equipped with these characteristics, the POT method is instead optimal for studying PF time series because it considers all the data that exceed a prescribed high threshold regardless of the number of years recorded. This allows for more data to be retrieved in a single year, increasing sample size. The POT method involves the use of a threshold that isolates the values considered extremes with respect to the rest of the data and defines a probabilistic model for the tail of all these values over threshold. It is shown that for sufficiently high thresholds u, the distribution of extreme values, approximates a general Pareto distribution (GPD) with a shape parameter and a scale parameter . The GPD parameters allow one to derive a design PF and assign it a return period in years.
For the correct use of the POT method, it is essential to ensure that each POT is statistically independent of the other ones, since the independence criterion is a prerequisite to any statistical frequency analysis. Added to this are two other requirements that must be met to apply this methodology: the number of annual occurrences must be Poisson-distributed, and the GPD must have an optimal fit with the selected POTs. The main difficulty of this methodology is represented by the choice of a suitable threshold that makes it possible to respect the three aforementioned conditions. The following paragraphs will illustrate the entire procedure proposed, which allows for the evaluation of the PFs expected at a given return period, starting from consumption measurements.
Extreme Value Statistics Applied to Peak Factors
The procedure followed involves retaining only those PFs that exceed the considered threshold value. For each threshold, a set of POTs is collected, which can be related to two consecutive consumption measures. However, according to the theory of partial duration series (PDS), consecutive peaks are indicative of a single phenomenon, such as a sociological event (e.g., a meal), requiring the selection of the highest peak in the consecutive series to represent the event while maintaining independence between the selected POTs.
The choice of the optimal threshold is crucial and delicate, ensuring the composition of a suitable sample of POTs, as subsequent analyses will rely on it. A high threshold reduces the number of selected events to increase independence, while a lower threshold yields more events but may violate theoretical requirements. The key goal of threshold selection is therefore to choose the smallest threshold value producing extreme values following the limit exceedance model (GPD family). Numerous methods for threshold selection have been proposed in the literature, recently reviewed by Pan et al. [12], but currently, no method seems to be preferred over others. Whichever methodology is chosen, it is essential to verify the conditions validating the statistical analysis.
The first necessary condition is independence of the data series, assessed using Kendall’s test to check the independence of the POT series [13]. This test analyzes the ordering of the POTs and identifies any dependence between them based on the comparison of all the pairs that can be combined. Due to the way the sample is composed, raising the threshold tends to make the test verified.
After verifying independence, subsequent checks validate the selected threshold with reference to the expected probability distribution for the sample of available peaks. Remembering that sampling for peaks above the threshold defines a sample of values whose probabilistic distribution is identified in the GPD, this distribution must be valid for the set of peaks extracted at the chosen threshold. To ensure that the chosen threshold is adequate, it is therefore necessary to verify that the GPD hypotheses are satisfied. For this purpose, an efficient procedure seems to be testing the goodness of fit of the GPD. According to Claps and Laio [14], the problem with this analysis is finding appropriate tests when the parameters of the distribution are unknown and their estimate is based on the sample of exceedances. In this case, the classical goodness of fit tests depend on the distribution adopted. A specific test based on Cramer–von Mises and Anderson–Darling statistics has been proposed by Choulakian and Stephens [15] for the GPD. In this test, the measure of the mean square displacement between the empirical and hypothetical cumulated distribution functions is compared to the acceptance limits of the test for different significance levels. A positive response to this comparison indicates that the dataset collected with a specific threshold is compatible with being a random sample from a given distribution. A sample that satisfies these two conditions can be used for GPD fitting.
The proposed methodology aims to evaluate PFs with an associated return period in years. For this purpose, it is required to obtain the generalized extreme value (GEV) distribution parameters from the GPD parameters and to make it possible, the peaks must follow a Poisson process. To this aim, the test proposed by Cunnane [16] is used. The test is based on the identification of an acceptance limit of the value assumed by the dispersion index of the sample, defined as the ratio of the variance to the mean of the number of annual occurrences. Ensured that the distribution of independent PFs tests the Poisson hypothesis, it is therefore possible to link the cumulative distribution function of the PFs’ F(p) according to the GPD to that of the annual maxima G(p) via
where represents the average number of PFs verified annually and p is the PF value.
According to Lang et al. [17], when one parameter is not sufficient to describe the whole complexity of the distribution, the binomial and negative binomial distributions are valid alternatives to the Poisson distribution. In these cases, Eastoe et al. [18] demonstrated that relationships analogous to Equation (1) can be derived which non-significantly overestimate the variance of the estimate, as proven by Bhunya et al. [19].
All thresholds that simultaneously verify the three above conditions are suitable for POT analysis. The optimal choice falls on the minimum valid threshold in order to have the largest possible sample available.
After determining the optimal threshold, it is possible to estimate the parameters of the GPD, also known as the Pareto–Pickands distribution [20]. Given a location parameter , a shape parameter , and a scale parameter , which in the case of modeling POT models will be dependent on the choice of the threshold u, independent observations of threshold exceedance are assumed to be GP-distributed with , and . Leaving the complete definition of GPD to the literature articles [11,21], the cumulated distribution function of the GPD is given by
Once this estimation procedure is completed, we can evaluate the suitability of the chosen threshold using a graphical method. Although graphical methods are commonly used due to their superior estimation speed compared to more complex techniques [22], they should not be solely relied upon due to their subjective nature. Therefore, in this study, graphical methods are employed solely to confirm the quality of the estimate obtained through the automated method outlined earlier based on specific criteria. By representing the estimated parameters as a function of the threshold u graphically, we aim to verify their stability [11], a technique known as a parameter stability plot or threshold stability plot [23]. In this case, the threshold is well chosen if it refers to a trait in which the GPD parameters both remain stable for small changes in the threshold.
Subsequently, a comparison between the empirical cumulated distribution function (cdf) and the cdf obtained with the estimated GPD parameters serves as an additional test of the result quality.
Once the parameters of the GPD are estimated for the assigned optimal threshold, the distribution of the annual maxima is obtained by substituting Equation (2) in Equation (1). This substitution yields a GEV enabling the estimation of the peak factor (PF) for a given return period in years (T) using the inverse of the CDF of the PFs, denoted as . Specifically, it is as follows:
Substituting Equation (3) in Equation (2) allows us to estimate the following:
The formulated relationship between the peak factor and return period is associated with specific spatial aggregation, reflecting the number of monitored users upon which the PFs of the time series used for analysis were estimated. This procedure can be applied to homogeneous samples of varying sizes. By collecting data for each spatial aggregation, we can derive a law describing the decrease in the PF with aggregation. The points describing this decrease can be interpolated with a function whose parameters are specific to the return period with which it is estimated. By regularizing the curves relating to the various return periods with a procedure of minimization of the quadratic differences between the PFs and the curves, a family of curves is obtained. This family of regularized curves uniquely defines a peak value for an assigned spatial aggregation to a specific return period.
3. Application
3.1. The Analyzed DMA
The measurements collected by the “ABC Napoli” water company in a District Meter Area (DMA) of Naples were utilized to validate the proposed methodology. A project centered on the Soccavo DMA made it possible to collect 7 years of measurements on 4865 smart meters.
Consumption data are recorded on an hourly basis, offering a favorable compromise for companies. In fact, this temporal aggregation allows for maintaining an accurate estimate of the measure in a DMA [24] without excessively increasing the data to be transferred, stored, and analyzed [25,26].
The smart meter system deployed in the Soccavo DMA is set up so that if an error is detected in the data transmission of a flow meter, the system records zero consumption for that flow meter for the entire day. This feature enables the unique identification of flow meters retaining information content daily. Consequently, system performance is impacted, leading to the exclusion of certain years of data.
To validate the proposed extreme PF estimation methodology, measurements from 3866 residential flow meters spanning from 2016 to 2018 were examined. A subset of this dataset was previously utilized by Del Giudice et al. [27] for different PF analyses. Considering the system’s operation, a minimum of 1000 hourly measurements were collected daily throughout the specified period for this study.
3.2. Sample Preparation
The proposed methodology aims to identify the statistical parameters that characterize the extreme PFs for each spatial aggregation. The different spatial aggregations can be obtained from the complete dataset, aggregating the required number of flow meters each time by choosing the most appropriate ones for the purpose from the complete sample. Since the aim is to obtain the maximum PFs recorded in a specific hour from each spatial aggregation, the choice must be made to guarantee the maximum PF for each aggregation.
The flow meters that in a single day recorded non-zero measurements in the analyzed period range from 28% (1087 flow meters) to 80% (3072 flow meters), with an average of 60% (about 2400 flow meters). Figure 2 shows that the daily efficiency of the smart metering system (obtained as the ratio between the non-zero daily measurements and the 3866 residential meters analyzed) is highly variable, with a decreasing trend in measurements collected in the last year analyzed. To avoid that the eventual switching off of some flow meters essential for PF estimation permanently influence the analysis, maximum aggregations of 1000 flow meters are considered, that is, the minimum number always recorded by the system in the four years considered.
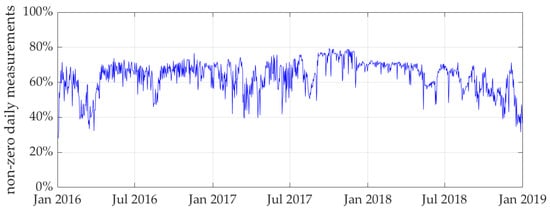
Figure 2.
The daily efficiency of the residential smart metering system during the study period.
For the proposed application, the data have not been subjected to signal cleaning of any outliers. The reason for preserving outliers is that we are specifically interested in peaks; removing extreme values purely on statistical grounds is likely to distort the analysis.
For example, it has been observed that the maximum annual PF occurs on Christmas day, in which recorded consumption is extremely different from average consumption due to a different composition and number of users inside homes. An analysis based on the average data measured on the flow meters can lead to the identification of an outlier, which is erroneously eliminated leading to an underestimation of the PF.
Starting from the complete hourly consumption dataset of the 3866 residential flow meters, for each spatial aggregation, the hourly PF is calculated following a very simple procedure aimed at identifying the maximum possible value obtainable for that number of users. In particular, the steps followed for each hour of each day are as follows:
- The hourly PF of a single meter is calculated aswhere is the hourly consumption of the flow meters i = 1, …, 3866 in hour j = 1, …, 35,064 on the considered day and is the average annual hourly consumption of the flow meter i.
- The counters are sorted according to decreasing .
- To calculate the maximum PFj measurable in hour j from N = 1, …, 990 m, the first N flow meters ordered in step 2 are considered. The hourly PFj for the spatial aggregation N is evaluated as
It must be specified that this procedure assumes complete reliability if all flow meters are simultaneously recorded for the entire analyzed period, whereas it has already been clarified that the sample used for the application is incomplete. This lack can lead to an estimation error in the peak value obtained, which increases as the efficiency of the smart metering system decreases. The steps followed to identify the maximum hourly recordable PF are a procedure designed to maximize the information available, with reliability linked to the quality of the system of remote transmission.
While the incompleteness of the signal is a limitation of the analysis, the presence of measurements performed directly on the flow meter is a rare advantage. In fact, the direct measurement on the flow meter allows only the actual water consumption of the user to be measured, without the risk of registering any water losses in the WDN. This advantage significantly improves peak estimation compared to analyses performed on the total inflow measurement.
Overall, the dataset used is of great value, making up for the lack of complete data with the rare length of the time series measured in the absence of water losses.
3.3. Extreme Value Statistics on the Soccavo DMA
The analysis of the PFs on every single spatial aggregation is presented below for the case of 600 aggregated flow meters. An analogous procedure was applied to all other possible combinations.
Following the steps of the proposed procedure, the hourly PFs relating to the aggregation considered were calculated for all the data recorded from January 2016 to December 2018. Subsequently the POTs were identified for each single possible threshold according to the characteristics required by the PDS theory. The POTs identified using this procedure for the aggregation of 600 users are shown in red in Figure 3. Looking at the graph, it can be clearly seen how the POTs are distinct from the rest of the time series, which instead contains the maximum daily PFs recorded on ordinary days. This distinction clarifies how the proposal of this work, aimed at identifying the probability of an extreme event, differs from the rest of the works proposed regarding PFs.
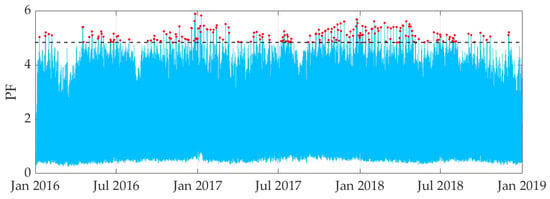
Figure 3.
A time series of the PFs obtained for 600 aggregate meters (light blue). For the optimal threshold identified by the dotted line, the selected POTs are circled in red.
The choice of the optimal threshold is linked to the validity of the conditions necessary for the applicability of the theory of extreme values.
The first test carried out is the Kendall test, which allows for verifying the set of thresholds for which the independence of the resulting POTs is ensured. This test eliminates lower thresholds, creating a lower bound for the suitable threshold. In this example, the lowest threshold that allows for guaranteeing the independence of the POT series according to the test is 4.08. However, as can be seen in Figure 4, with this threshold, PFs which relate to ordinary consumption conditions (blue dots) are considered.
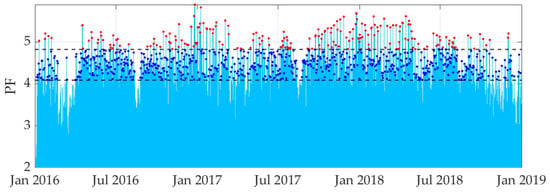
Figure 4.
An extract from the historical series of PFs obtained for a total of 600 m (light blue). The sample of POTs selected by the minimum threshold (identified by the lowest dotted line) that satisfies the Kendall test is shown in blue; the one that satisfies the entire set of required conditions is shown in red and delimited by the highest dotted line.
Among all the thresholds above this limit imposed by the Kendall test, it was therefore appropriate to identify the minimum threshold for which the GDP hypotheses are verified. The Cramer–von Mises test consents to verify that the dataset is compatible with being a random sampling from a GPD. Since it is established that W2 is the statistic used to measure the discrepancy between an empirical cumulative distribution function (ecdf) and a cdf, a threshold can be selected if the W2 value assumed by the series at that threshold falls below the limit imposed by the test. The first acceptable threshold in this case is equal to 4.82; the first value that verifies the test is in the acceptable zone.
This identified threshold is also deemed suitable according to the graphical method, as both estimators are located in a stable area (Figure 5).
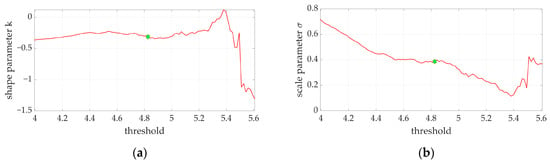
Figure 5.
Parameter stability plots. (a) Shape parameter stability plot; (b) scale parameter stability plot. The green symbol represents the parameter conditions corresponding to the selected threshold. The presence of a stable neighborhood in both cases confirms the solution is optimal, validated by graphical methods.
At this point in the procedure, it is possible to estimate the GDP parameters corresponding to the identified optimal threshold and to verify the quality of the fitting using a probability chart (Figure 6). The quality of the fitting also appears accurate in the tails of the distribution, guaranteeing a reliable estimate.
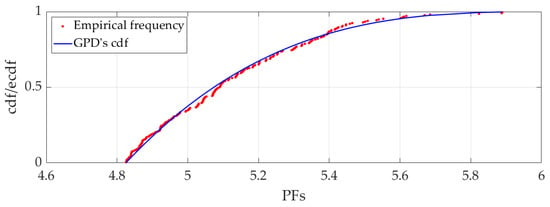
Figure 6.
Probability chart: comparison between the empirical frequency and the cdf.
Ensuring that the estimate made is reliable, after verifying that the distribution of annual POTs is such as to guarantee the transition to GEV distribution, it is possible to assign a return period in years to the peak values using Equation (4).
By conducting the complete procedure on all spatial aggregations, it is possible to identify the evolution of expected peaks with a given return period as the aggregation varies. Figure 7 illustrates the trend of PFs expected at return periods of 2, 5, 10, 20, 50, and 100 years across different spatial aggregations performed in steps of 10 units.
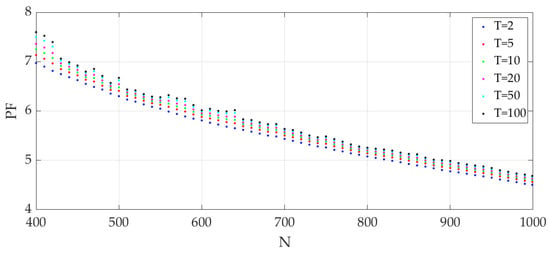
Figure 7.
Descending trend in PFs with increasing spatial aggregation for different return periods.
The points represented exactly follow the trend of a curve for return periods comparable to the one measured (return periods equal to 2 and 5 years), while a slight uncertainty is observed for longer times. Nonetheless, it is possible to identify the presence of a scaling law in any case. Thus, we can fit the estimated PFs with a power curve, which exhibits an excellent level of fitting for each T (the coefficient of determination R2 remains consistently above 0.99, ranging from 0.9986 for T = 2 years to 0.9903 for T = 100 years), as demonstrated by the example presented in Figure 8 for the return period of 2 years. The function that evaluates the PF at a certain T (in years) for an aggregation of N flow meters is
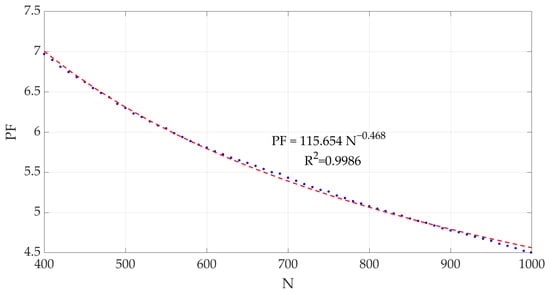
Figure 8.
Interpolation of the expected PF value with T = 2 years (blue points) with a power curve (red line).
Each curve (one for each T) is defined by the two parameters and . These parameters also exhibit a scaling law with spatial aggregation, as shown in Figure 9. In particular, the two parameters of Equation (7) follow a natural logarithmic trend with the associated return period T. Equations (8) and (9) represent the scaling law of the considered parameters. Table 1 summarizes the values assumed by the parameters that define Equation (8) and its analogs, used to represent Figure 9.
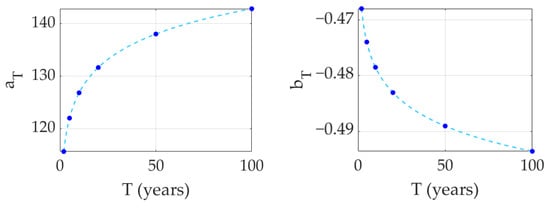
Figure 9.
Scaling laws of parameters constituting Equation (7). The blue dots represent the a and b estimated at the relative return period T; the dotted lines represent the scaling laws of the single parameters (Equations (8) and (9)).

Table 1.
Scaling law parameters governing Equations (8) and (9).
The regression of the curves defined by Equation (7) using the regularized quantile method on the parameters a and b (constituting Equations (8) and (9)) allows for the unique identification of the probability curves of the PFs at different return periods T (Figure 10).
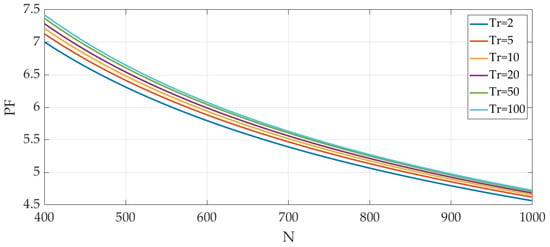
Figure 10.
Scaling law of peak factors for different return periods T.
4. Conclusions
This paper presents a methodology for analyzing extremes applied to water consumption. As an adaptation of formulas traditionally employed in other fields, the proposed approach allows for the estimation of peak factors at the scale of a DMA, assigning them a return period. From a multi-year time series of peak factors, extreme events can be identified by selecting an appropriate threshold. This threshold ensures that the resulting series of values above can be considered an independent sequence of extreme values. The identified peaks are then statistically analyzed to establish scaling laws for the peak factor as a function of the number of aggregated households within a DMA and the desired return period. This linkage between a probabilistic level and resulting dimensioning enhances the reliability of the entire process, contributing to an improvement in current procedures. The resulting analysis is more precautionary yet accurate and adaptable to the specific case under examination, leading to more sustainable water resource management. In particular, the ability to monitor and accurately reproduce the actual PFs of the network, identifying their sociological characteristics and accounting for them to enable a more effective response in the WDN, reduces water waste and optimizes the use of an increasingly valuable resource. An appropriate peak factor ensures effective pressure management by preventing excessive pressure, which leads to water leaks and wastage, while avoiding insufficient pressure, which could result in service interruptions for end users. In this regard, the proposed methodology contributes to ensuring more efficient and sustainable water management, a key goal in an era of increasing global water emergencies.
The proposed methodology was tested on a real DMA in Southern Italy equipped with a smart meter system. The results of the measurement campaign highlighted issues related to data incompleteness, and the lack of simultaneity in DMA measurements suggested a solution based on maximizing the available information. The proposed solution offers guidance on how to extract information from smart systems, which often contain gaps, in order to leverage the information provided by the current state of technological advancement. The increasing availability of smart metering systems in the coming years will provide larger datasets with better yields and longer temporal durations, advancements that will facilitate the validation of the empirically identified scaling laws to represent and reproduce the phenomenon.
Author Contributions
Conceptualization, M.M. and R.G.; Methodology, M.M. and R.G.; Software, M.M.; Validation, M.M. and R.G.; Resources, R.G.; Writing—review & editing, M.M.; Supervision, R.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from the water company Acqua Bene Comune Napoli.
Acknowledgments
The authors thank Acqua Bene Comune for having supplied demand data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mays, L.W. Water Distribution Systems Handbook, 1st ed.; McGraw Hill: New York, NY, USA, 2000; ISBN 9780071776776. [Google Scholar]
- McDonald, H.S.; Clinton, T.A. Water Demand Projections—City of Oxnard; Granicus: Denver, CO, USA, 2015; Volume 2.2. [Google Scholar]
- Adamowski, J.; Karapataki, C. Comparison of Multivariate Regression and Artificial Neural Networks for Peak Urban Water-Demand Forecasting: Evaluation of Different ANN Learning Algorithms. J. Hydrol. Eng. 2010, 15, 729–743. [Google Scholar] [CrossRef]
- Tricarico, C.; de Marinis, G.; Gargano, R.; Leopardi, A. Peak Residential Water Demand. Proc. Inst. Civ. Eng. Water Manag. 2007, 160, 115–121. [Google Scholar] [CrossRef]
- Balacco, G.; Gioia, A.; Iacobellis, V.; Piccinni, A.F. At-Site Assessment of a Regional Design Criterium for Water-Demand Peak Factor Evaluation. Water 2019, 11, 24. [Google Scholar] [CrossRef]
- Buchberger, S.; Omaghomi, T.; Wolfe, T.; Hewit, J.; Cole, D. Peak Water Demand Study. Probability Estimates for Efficient Fixtures in Single and Multi-Family Residential Buildings; IAPMO: Ontario, CA, USA, 2017. [Google Scholar]
- Gargano, R.; Tricarico, C.; Granata, F.; Santopietro, S.; de Marinis, G. Probabilistic Models for the Peak Residential Water Demand. Water 2017, 9, 417. [Google Scholar] [CrossRef]
- Mazzoni, F.; Alvisi, S.; Blokker, M.; Buchberger, S.G.; Castelletti, A.; Cominola, A.; Gross, M.-P.; Jacobs, H.E.; Mayer, P.; Steffelbauer, D.B.; et al. Investigating the Characteristics of Residential End Uses of Water: A Worldwide Review. Water Res. 2023, 230, 119500. [Google Scholar] [CrossRef]
- Di Mauro, A.; Cominola, A.; Castelletti, A.; Di Nardo, A. Urban Water Consumption at Multiple Spatial and Temporal Scales. A Review of Existing Datasets. Water 2021, 13, 36. [Google Scholar] [CrossRef]
- Vonk, E.; Cirkel, D.G.; Blokker, M. Estimating Peak Daily Water Demand under Different Climate Change and Vacation Scenarios. Water 2019, 11, 1874. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: Berlin/Heidelberg, Germany, 2001; ISBN 1852334592. [Google Scholar]
- Pan, X.; Rahman, A.; Haddad, K.; Ouarda, T.B.M.J. Peaks-over-Threshold Model in Flood Frequency Analysis: A Scoping Review. Stoch. Environ. Res. Risk Assess. 2022, 36, 2419–2435. [Google Scholar] [CrossRef]
- Ferguson, T.S.; Genest, C.; Hallin, M. Kendall’s Tau for Serial Dependence. Can. J. Stat. 2000, 28, 587–604. [Google Scholar] [CrossRef]
- Claps, P.; Laio, F. Can Continuous Streamflow Data Support Flood Frequency Analysis? An Alternative to the Partial Duration Series Approach. Water Resour. Res. 2003, 39, 1–11. [Google Scholar] [CrossRef]
- Choulakian, V.; Stephens, M.A. Goodness-of-Fit Tests for the Generalized Pareto Distribution. Technometrics 2001, 43, 478–484. [Google Scholar] [CrossRef]
- Cunnane, C. A Note on the Poisson Assumption in Partial Duration Series Models. Water Resour. Res. 1979, 15, 489–494. [Google Scholar] [CrossRef]
- Lang, M.; Ouarda, T.B.M.J.; Bobée, B. Towards Operational Guidelines for Over-Threshold Modeling. J. Hydrol. 1999, 225, 103–117. [Google Scholar] [CrossRef]
- Eastoe, E.F.; Tawn, J.A. Statistical Models for Overdispersion in the Frequency of Peaks over Threshold Data for a Flow Series. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Bhunya, P.K.; Berndtsson, R.; Jain, S.K.; Kumar, R. Flood Analysis Using Negative Binomial and Generalized Pareto Models in Partial Duration Series (PDS). J. Hydrol. 2013, 497, 121–132. [Google Scholar] [CrossRef]
- Pickands, J.I. Statistical Inference Using Extreme Order Statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar]
- Naess, A. Applied Extreme Value Statistics Including the Acer Method; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Solari, S.; Eguen, M.; José Polo, M.; Losada, M.A. Peaks Over Threshold (POT): A Methodology for Automatic Threshold Estimation Using Goodness of Fit p-Value. Water Resour. Res. 2017, 53, 2833–2849. [Google Scholar] [CrossRef]
- Scarrott, C.; MacDonald, A. A Review of Extreme Value Threshold Estimation and Uncertainty Quantification. Revstat Stat. J. 2012, 10, 33–60. [Google Scholar]
- Creaco, E.; Signori, P.; Papiri, S.; Ciaponi, C. Peak Demand Assessment and Hydraulic Analysis in WDN Design. J. Water Resour. Plan. Manag. 2018, 144, 1–9. [Google Scholar] [CrossRef]
- Cominola, A.; Giuliani, M.; Castelletti, A.; Rosenberg, D.E.; Abdallah, A.M. Implications of Data Sampling Resolution on Water Use Simulation, End-Use Disaggregation, and Demand Management. Environ. Model. Softw. 2018, 102, 199–212. [Google Scholar] [CrossRef]
- Oracle. Smart Metering for Water Utilitie—White Paper; Oracle: Santa Clara, CA, USA, 2009. [Google Scholar]
- Padulano, R.; Del Giudice, G. A Nonparametric Framework for Water Consumption Data Cleansing: An Application to a Smart Water Network in Naples (Italy). J. Hydroinform. 2020, 22, 666–680. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).