Uncertainty in Determination of the Soil-Water Characteristic Curve Based on the van Genuchten Model

Abstract

The van Genuchten (1980) (VG) model is one of the most popular and widely used equations to achieve the best fitting of experimental data of the soil-water characteristic curve (SWCC) test. As the best-fitted SWCC is determined from regression analysis, there are various possible solutions for the best-fitted curve (or the determined fitting parameters). The residual error, which is obtained from regression analyses, can be considered as an index indicating the incapability of the SWCC equation in representing the measured SWCC experimental data. As a result, there is always uncertainty associated with determined SWCC from the regression analysis. The residual error from the regression analysis can be used for the quantification of the uncertainty of determined SWCC. In this paper, Taylor’s expansion is adopted, and only the first-order term is considered for the VG model. Subsequently, the variances of the fitting parameters in the VG model are estimated from the residual error. Consequently, the uncertainty of SWCC using the VG model is quantified by using the upper and lower bounds with a 95% confidence level. The artificial soil, composed of mixed sand and kaolin, was prepared for the SWCC measurement. This paper shows that the proposed method can be used to quantify the uncertainty of SWCC from different specimens (a total of 12 specimens).

1. Introduction

The soil-water characteristic curve (SWCC) is considered key for the implementation of the principles of unsaturated soil mechanics because it can be used for the estimation of the hydraulic conductivity function, the shear function, and the tensile strength function for the unsaturated soil (Zhai and Rahardjo [1] and Zhai et al. [2,3,4]). Various mathematical forms have been proposed for the representation of the SWCC by different researchers such as Brooks and Corey [5], Gardner [6], van Genuchten [7], Fredlund and Xing [8], Leong and Rahardjo [9], etc. Among SWCC equations, both the van Genuchten [7] model (VG model) and Fredlund and Xing’s [8] model (FX model) are the most popular and widely used by the engineers for the representation of the SWCC. Zhai and Rahardjo [10] explained the methodology in the estimation of the variability of the determined SWCC based on the FX model. Almessiere et al. [11] synthesized new hard–soft nanocomposites vis an in situ sol–gel route. Turchenko et al. [12] created indium-substituted strontium hexaferrites via the conventional solid-phase reaction and found linear dependence of the unit cell parameters. Tanbn et al. [13] proposed formulae estimating the van Genuchten model fitting parameters for unsaturated clean sand soils by using Genetic Programming. Rahimia et al. [14] proposed a matrix of unsaturated permeability estimation models including SWCC equations and relative permeability to estimate the unsaturated permeability function. It seems that the uncertainty in the determined SWCC using the VG model has been rarely reported. It is necessary to have mathematical equations to quantify the uncertainty of the SWCC based on the VG model because the VG model is also widely used by engineers. If the SWCC is expressed in the form of the degree of saturation, then the VG model can be illustrated in Equation (1) as follows:

$$\frac{S-S_{\mathrm{r}}}{1-S_r}=\frac{1}{{\left[1+{\left(a_v\psi \right)}^{n_v}\right]}^{m_v}},$$

(1)

where a_v, n_v, and m_v are fitting parameters in the VG model; ψ is the soil suction; S is the degree of saturation; and S_r is a rough estimation of the residual saturation.

The works from Kool et al. [15], Mishra and Parker [16] and Zhai and Rahardjo [10] indicated that the uncertainty in the fitting parameters can be estimated from the variance of the fitting parameter. Fang et al. [17] gathered the VG model parameters of the SWCC’s data in the Loess Plateau area, and used trend analysis and one-variable linear regression methods to investigate the regional distribution law of the VG model parameter and created the calculated method for the unsaturated permeability coefficient. The variances of the fitting parameters can be estimated by using the first-order error method based on Taylor’s expansion. In this paper, a similar methodology is adopted for the estimation of the uncertainty of the fitting parameters (a_v, n_v, and m_v) in the VG model. By adopting the first-order term and ignoring the high-order terms, degree of saturation can be expressed based on Taylor’s expansion as follows:

$$S\approx S\left(\hat{x}\right)+\frac{\partial S}{\partial x}\left(x-\hat{x}\right),$$

(2)

where x and $\hat{x}$ are the unknown variable and the observed value of the variable, S($\hat{x}$) is the function that defines the relationship between the degree of saturation and the unknown variable x, and S is the computed degree of saturation.

The correlation between the variance of f(x) and the variable x can be obtained as follows:

$$Var\left[f(x)\right]={{\displaystyle \sum \left[\frac{\partial f\left(x\right)}{\partial x}\right]}}^T\frac{\partial f\left(x\right)}{\partial x}E\left[{(x-\widehat{x})}^2\right]={{\displaystyle \sum \left[\frac{\partial f\left(x\right)}{\partial x}\right]}}^T\frac{\partial f\left(x\right)}{\partial x}Var(x),$$

(3)

where E is the statistical expectation.

As a result, the variance of x can be obtained from variance of f(x) as follows:

$$Var\left[x\right]=\frac{Var\left[f\left(x\right)\right]}{{{\displaystyle \sum \left[\frac{\partial f\left(x\right)}{\partial x}\right]}}^T\frac{\partial f\left(x\right)}{\partial x}}.$$

(4)

If the total number of the measured data points is M, then the degree of freedom for the variance of the unknown parameters is M-3 because there are three fitting parameters in the VG model in total. Therefore, the variances of S, a_v, n_v, and m_v can be obtained from Equations (5)–(8):

$$Var\left[S\right]=\frac{SSE}{M-3},$$

(5)

$$Var\left[a_v\right]=\frac{SSE}{\left(M-3\right)\left[{\displaystyle \sum _{i=1}^M{\left(\frac{\partial S\left({\psi }_i\right)}{\partial a_v}\right)}^2}\right]},$$

(6)

$$Var\left[n_v\right]=\frac{SSE}{\left(M-3\right)\left[{\displaystyle \sum _{i=1}^M{\left(\frac{\partial S\left({\psi }_i\right)}{\partial n_v}\right)}^2}\right]},$$

(7)

and

$$Var\left[m_v\right]=\frac{SSE}{\left(M-3\right)\left[{\displaystyle \sum _{i=1}^M{\left(\frac{\partial S\left({\psi }_i\right)}{\partial m_v}\right)}^2}\right]},$$

(8)

where SSE is the sum of squared error from the best-fitting procedure and M is the total number of measured data points.

Differentiating Equation (1) to a_v, n_v, and m_v gives Equations (9)–(11) as follows:

$$\frac{\partial S}{\partial a_v}=\frac{-m_v{n}_v{\left(a_v\psi \right)}^{n_v}}{a_v{\left[1+{\left(a_v\psi \right)}^{n_v}\right]}^{m_v+1}}\left(1-S_r\right),$$

(9)

$$\frac{\partial S}{\partial n_v}=\frac{-m_v{\left(a_v\psi \right)}^{n_v}\ln \left(a_v\psi \right)}{{\left[1+{\left(a_v\psi \right)}^{n_v}\right]}^{m_v+1}}\left(1-S_r\right),$$

(10)

and

$$\frac{\partial S}{\partial m_v}=\frac{-\ln \left[1+{\left(a_v\psi \right)}^{n_v}\right]}{{\left[1+{\left(a_v\psi \right)}^{n_v}\right]}^{m_v}}\left(1-S_r\right).$$

(11)

As a result, the variances of a_v, n_v, and m_v in the VG model can be obtained by substituting Equations (9), (10), and (11) into Equations (6), (7), and (8), respectively.

Kool and Parker [18] explained that the uncertainty of the unknown parameter could be approximately estimated by using t-statistics with two tailed confidence limits and α significance level. Both the lower and upper limits of x can be obtained as $\widehat{x}-t_{\frac{\alpha }{2}}\sqrt{Var(x)}$ and $\widehat{x}+t_{\frac{\alpha }{2}}\sqrt{Var(x)}$, respectively.

Therefore, both the maximum and minimum values of the fitting parameters in the VG model can be obtained as follows:

$$\{\begin{array}{l}{a}_{v\max }=a_v+t_{\frac{\alpha }{2}}\sqrt{Var(a_v)}\\ a_{v\min }=a_v-t_{\frac{\alpha }{2}}\sqrt{Var(a_v)}\end{array},$$

(12)

$$\{\begin{array}{l}{n}_{v\max }=n_v+t_{\frac{\alpha }{2}}\sqrt{Var(n_v)}\\ n_{v\min }=n_v-t_{\frac{\alpha }{2}}\sqrt{Var(n_v)}\end{array},$$

(13)

and

$$\{\begin{array}{l}{m}_{v\max }=m_v+t_{\frac{\alpha }{2}}\sqrt{Var(m_v)}\\ m_{v\min }=m_v-t_{\frac{\alpha }{2}}\sqrt{Var(m_v)}\end{array},$$

(14)

where a_vmax, n_vmax, and m_vmax are the maximum values of those fitting parameters, while a_vmin, n_vmin, and m_vmin are the minimum values.

Different combinations of those fitting parameters give different SWCCs. It is observed that the value of aψ controls the determined S. Therefore, two conditions should be considered in the determination of the maximum and minimum values of S.

When aψ < 1, the maximum S, which defines the upper bound of the determined SWCC, and the minimum S, which defines the lower bound of the determined SWCC, can be obtained from Equations (15) and (16), respectively:

$$S_{upper}=S_r+\frac{(1-S_r)}{{\left[1+{\left(a_{v\min }\psi \right)}^{n_{v\max }}\right]}^{m_{v\min }}}$$

(15)

and

$$S_{lower}=S_r+\frac{(1-S_r)}{{\left[1+{\left(a_{v\max }\psi \right)}^{n_{v\min }}\right]}^{m_{v\mathrm{m}}{}_{\mathrm{a}\mathrm{x}}}}.$$

(16)

When aψ > 1, both the maximum and minimum S can be obtained from Equations (17) and (18), respectively:

$$S_{upper}=S_r+\frac{(1-S_r)}{{\left[1+{\left(a_{v\min }\psi \right)}^{n_{v\min }}\right]}^{m_{v\min }}}$$

(17)

and

$$S_{lower}=S_r+\frac{(1-S_r)}{{\left[1+{\left(a_{v\max }\psi \right)}^{n_{v\max }}\right]}^{m_{v\max }}}$$

(18)

As a result, the uncertainty of the SWCC based on the VG model can be quantified by using the upper and lower bounds of the SWCC, which can be computed by using Equations (15)–(18).

2. Materials and Methods

As specimens with clean sand easily collapse when fully saturated, kaolin, which is a cohesive material, was mixed with sand to prepare the soil specimen. Zhai [19] mixed graded sand (73%) with coarse kaolin L2 (27%) and prepared 12 nos of specimens with the same initial conditions (same initial water content and same initial void ratio) by using static compaction equipment. To ensure all the specimens were tested under the same conditions, all the specimens were placed on one pressure plate. Both the grain size distribution data for the graded sand and the coarse kaolin are illustrated in Figure 1. The electrical static compaction machine and the specimens prepared for the SWCC measurement are shown in Figure 2a and Figure 2b, respectively.

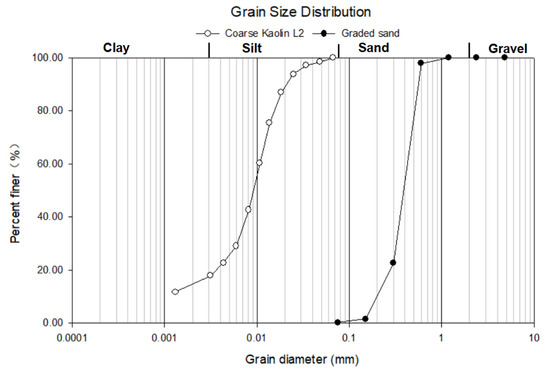
Figure 1. Illustration of grain-size distribution data for graded sand and coarse kaolin.

Figure 2. Illustration of static compaction machine and 12 nos of specimen prepared for the SWCC measurement. (a) Electrical static compaction machine. (b) Specimens.

3. Results

The measured SWCC data for the 12 nos of specimens are illustrated in Table 1. The experimental data of the compacted sand–kaolin mixture are used in this paper. The standard deviation of measured degree of saturation, average value, and the coefficient of variation of the measured degree of saturation corresponding to different suctions are illustrated in Table 2. The best-fitted upper and lower bounds of the SWCCs for those 12 nos of specimens are illustrated in Figure 3. The fitting parameters for the SWCC of each specimen are illustrated in Table 3.

Table 1. Measured SWCC data for the compacted sand with kaolin (from Zhai, [19]).

Suction (kPa)	Measured Degree of Saturation, S
	S1 1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12
0.10	1	1	1	1	1	1	1	1	1	1	1	1
11.17	0.856	0.864	0.864	0.853	0.861	0.865	0.857	0.853	0.863	0.890	0.887	0.874
31.17	0.766	0.758	0.751	0.743	0.745	0.744	0.738	0.741	0.741	0.772	0.774	0.755
51.17	0.664	0.649	0.642	0.638	0.640	0.634	0.633	0.635	0.634	0.657	0.659	0.646
71.17	0.575	0.563	0.558	0.556	0.559	0.557	0.554	0.557	0.555	0.569	0.571	0.563
91.17	0.521	0.512	0.510	0.507	0.508	0.509	0.508	0.512	0.509	0.519	0.519	0.513
191.17	0.348	0.346	0.348	0.344	0.345	0.347	0.349	0.348	0.348	0.347	0.349	0.345
291.17	0.266	0.268	0.267	0.267	0.267	0.268	0.267	0.269	0.270	0.269	0.269	0.269
391.17	0.230	0.230	0.230	0.229	0.229	0.229	0.232	0.232	0.231	0.231	0.232	0.233
471.17	0.204	0.205	0.204	0.204	0.203	0.205	0.206	0.207	0.208	0.205	0.205	0.204

¹ S1 to S12 denotes specimens 1 to 12.

Table 2. Uncertainty of measured degree of saturation of compacted sand with kaolin at different suction levels.

Suction (kPa)	Variance	Average	Coefficient of Variation
0.10	0	1	0
11.17	1.49 × 10−4	0.866	0.014
31.17	1.6 × 10−4	0.752	0.017
51.17	1.16 × 10−4	0.644	0.017
71.17	4.74 × 10−5	0.561	0.012
91.17	2.35 × 10−5	0.512	0.009
191.17	2.73 × 10−6	0.347	0.005
291.17	1.45 × 10−6	0.268	0.005
391.17	1.88 × 10−6	0.231	0.006
471.17	2 × 10−6	0.205	0.007

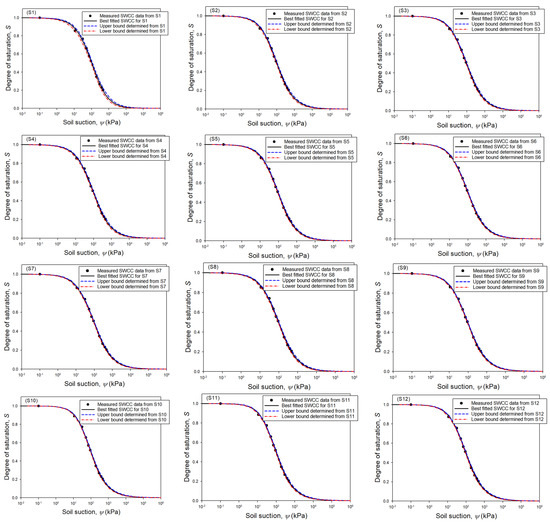
Figure 3. Illustration of the best-fitted SWCC, upper bound, and lower bound for the compacted sand with kaolin.

Table 3. Best-fitting parameters in the VG model of SWCCs for the different specimens.

S/N	av	nv	mv	S/N	av	nv	mv
S1	0.008	0.885	1.121	S7	0.012	0.896	0.909
S2	0.013	0.948	0.867	S8	0.011	0.872	0.985
S3	0.013	0.941	0.887	S9	0.014	0.934	0.826
S4	0.011	0.887	0.967	S10	0.018	1.107	0.655
S5	0.012	0.919	0.902	S11	0.017	1.085	0.682
S6	0.014	0.94	0.837	S12	0.016	1.003	0.757

The standard deviation (S2) and the coefficient of variation (CoV) are defined by Equations (19) and (20), respectively:

$$S^2=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}}{n-1}}$$

(19)

and

$$CoV=\frac{S}{\overline{x}},$$

(20)

where x_i is the observed value, $\overline{x}$ is the average value of the data in the sample, and n is the total number of the sample.

4. Discussion

Both Figure 3 and Table 3 indicate that results from the 12 sets of specimens differ from each other. In other words, the experimental data from any set of specimens cannot perfectly represent the SWCC from other specimens. As a result, using the best-fitted SWCC together with the upper and lower bounds, as proposed in this study, can show better performance than the conventional single curve in the representation of the soil-water characteristic of soil. Figure 3 indicates that the band defined by the upper and lower bounds can cover most of measured data for the entire suction range. Table 2 indicates that high CoV of measured degree of saturation occurs within the range of 11.17 to 71.17 kPa, which is within the transition zone, according to Vanapalli et al. [20]. If the measured data from 12 nos of specimens are used for the best fitting, then the best-fitted, upper, and lower bounds of the SWCC can be obtained, as illustrated in Figure 4.

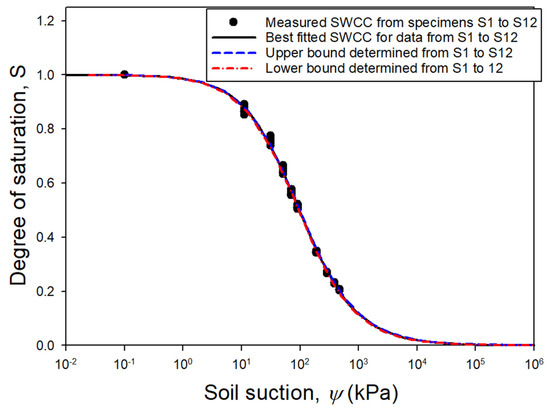
Figure 4. Illustration of best-fitted, upper, and lower bounds of the SWCC based on data from 12 nos of specimens.

Figure 4 shows that the upper and lower bounds almost superimpose the best-fitted SWCC. Some of the experimental data are out of the band defined by both the upper and lower bounds. It is interesting to observe that the band defined in Figure 4 (12 sets of experimental data) is narrower than that defined in Figure 3 (1 set of experimental data). As the experimental data for each specimen are relatively consistent, the residual error does not increase much with an increase in the number of specimens. However, the variance of fitting parameters decreases significantly with an increase in the number of specimens. Consequently, this makes the band of the upper and lower bounds obtained from a large sample size narrower than that from a small sample size. It is known that hydraulic conductivity and the shear strength of unsaturated soil is commonly estimated from the SWCC. The uncertainty in representation of the SWCC using the VG model can be quantified by using the proposed equations in this paper. As a result, the uncertainty in the estimated hydraulic conductivity and the shear strength of unsaturated soil can also be quantified. By using the proposed method, the uncertainty in the computed factor of safety for the unsaturated soil slope can also be evaluated.

5. Conclusions

First, the variance of fitting parameters (a_v, n_v, and m_v) in the VG model was determined based on Taylor’s expansion. Subsequently, both the maximum and minimum values of those fitting parameters were determined by adopting the student t distribution function. Consequently, both the upper and lower bounds of the SWCC were determined through different combinations of those fitting parameters. The uncertainty of the SWCC based on the VG model was quantified well by using those upper and lower bounds of the SWCC. The best-fitted SWCC together with the upper and lower bounds defined by using the method proposed in this study show better performance than the conventional single curve (best-fitted SWCC) in the representation of the soil-water characteristics of soil. Both upper and lower bounds proposed in this study are helpful for the estimation of the variability in the estimated hydraulic conductivity and the shear strength of unsaturated soil. This method can be used to evaluate the uncertainty in the computed factor of safety for the unsaturated soil slope.