A Hybrid DNN Model for Travel Time Estimation from Spatio-Temporal Features

Abstract

Due to recent advances in the Vehicular Internet of Things (VIoT), a large volume of traffic trajectory data has been generated. The trajectory data is highly unstructured and pre-processing it is a very cumbersome task, due to the complexity of the traffic data. However, the accuracy of traffic flow learning models depends on the quantity and quality of preprocessed data. Hence, there is a significant gap between the size and quality of benchmarked traffic datasets and the respective learning models. Additionally, generating a custom traffic dataset with required feature points in a constrained environment is very difficult. This research aims to harness the power of the deep learning hybrid model with datasets that have fewer feature points. Therefore, a hybrid deep learning model that extracts the optimal feature points from the existing dataset using a stacked autoencoder is presented. Handcrafted feature points are fed into the hybrid deep neural network to predict the travel path and travel time between two geographic points. The chengdu1 and chengdu2 standard reference datasets are used to realize our hypothesis of the evolution of a hybrid deep neural network with minimal feature points. The hybrid model includes the graph neural networks (GNN) and the residual networks (ResNet) preceded by the stacked autoencoder (SAE). This hybrid model simultaneously learns the temporal and spatial characteristics of the traffic data. Temporal feature points are optimally reduced using Stacked Autoencoder to improve the accuracy of the deep neural network. The proposed GNN + Resnet model performance was compared to models in the literature using root mean square error (RMSE) loss, mean absolute error (MAE) and mean absolute percentile error (MAPE). The proposed model was found to perform better by improving the travel time prediction loss on chengdu1 and chengdu2 datasets. An in-depth comprehension of the proposed GNN + Resnet model for predicting travel time during peak and off-peak periods is also presented. The model’s RMSE loss was improved up to 22.59% for peak hours traffic data and up to 11.05% for off-peak hours traffic data in the chengdu1 dataset.

1. Introduction

Many developing countries, such as India, make an important contribution to the development of public road infrastructure. In India, public transportation systems are used to reduce traffic congestion, leading to access to various places within connected cities. However, many show reluctance to use public transport and prefer to go with their own vehicle. This is understandable as transportation systems can easily be affected by weather conditions, traffic lights, traffic changes, rush hours and highway events. Road traffic congestion often causes delays in established times as well as inconsistencies in the estimation of travel times. In many cases, the time difference between the estimated and actual arrival time can be half an hour or more. This is not just about traveler plans but also about economic growth. As a result, there is an increased demand for technological solutions to address problems.

There are a variety of factors that drive the estimation of travel time using different learning models, and these models depend on the selection of optimal paths. Many factors, such as passenger boarding time, trip cancellations, road blockages, road maintenance, etc., are immeasurable and cannot be considered in the estimation of travel time. Travel time is defined as the sum of the free-flow travel time and the delay caused by traffic jams. The delays in traffic jams that occur during the journey are important factors for estimating the journey time. Travel delays are divided into unexpected delays and systematic delays. Unexpected delays are rare and very difficult to measure and predict. Systematic delay is the delay caused by traffic congestion along a road section. These systematic delays are frequent, measurable and vary with the time of day and can be used to estimate travel time between two geographic locations. This can be predicted by looking at the traffic flow patterns between two nodes that occurred on the previous trip, while the previous trip was made by the same vehicle or by another vehicle.

During peak and off-peak hours of the day, the actual travel time varies with high variance, mainly due to time spent in rush hour traffic jams. Among the mainstream technologies, Advanced Vehicle Location Systems (AVLS) are used to monitor the current latitude and longitude positions of vehicles, aided by a GPS system located in each vehicle. The trajectory information collected by the GPS can be used to signal major delays and the information is then processed to provide better route options. Many transportation companies are in the process of deploying smart systems to communicate information such as vehicle arrival times and travel times to the public via web/mobile apps or smart devices.

Recently, researchers have begun collecting trajectory data to develop learning models to understand traffic patterns, resulting in travel time estimates and optimal path prediction. Probe vehicles were used in the traffic research to collect floating car (FCD) data, including timestamped geolocations. These probe vehicles communicate with each other to collect trajectory data as the vehicles travel in the city. With the advent of vehicles and devices with GPS, vehicle and commuter trajectory data is readily available in large quantities. However, it is very difficult to understand the patterns in the raw and sparse data source with a very low penetration rate, i.e., the ratio of the probe vehicles to the total number of vehicles in the road segment. Other problems when using the FCD are the mapping of vehicle geolocation data to road maps. The trajectory of the probe vehicles does not reflect the actual start and end of the paths and their links. The data patterns in the vehicle trajectory will then overlap. Due to the problems mentioned above, there is a large gap between the raw and sparse data source that generates the trajectory of vehicles and its use in estimating travel time. An advanced preprocessing technique is required before the data is entered into the learning models. Almost all learning models in existence to date have focused on features, such as vehicle speed and vehicle direction information as well as geospatial location and timestamps for many research vehicles. Even these methods have not given due importance to the introduction of preprocessing models for extracting functions. Therefore, a learning model is needed for cases where minimal trajectory data is available.

Many traditional methods, such as vector autoregressive (VAR), historical (HA), and autoregressive integrated moving average (ARIMA) models, process temporal or spatial data but not both. On the other hand, hand-crafted feature models failed to capture the spatial relationships inherent in traffic data.

By interpreting the traffic as a diagram, the model can capture the spatial connections between traffic points. Research interest is growing in time series based Deep Learning (DL) models, such as the spatio-temporal-residual networks (ST-ResNet) model and the convolutional neural networks (CNN) based model, graph neural networks (GNN) and their applicability for traffic data analysis are widely used.

GNN was introduced as a tool for synchronous and global extraction and learning of propagation patterns in graphs. By combining these two components, the researchers simultaneously estimate traffic flows by combining the data collected at the node and graph level. If a vehicle chooses a particular connection, the propagation model can be described using GNN. GNN also helps to understand vehicle models during both peak and off-peak hours. The propagation module in GNN is based on static relations between vertices on a longer time axis and requires a large amount of trajectory data to predict travel time.

This research aims to overcome the need for large amounts of temporal trajectory data from multiple vehicle nodes, thereby reducing the limitations of trajectory data collection. By using Stacked Autoencoder to reduce the dimensionality of temporal data, the complexity of the data acquisition process is reduced.

The contributions in this research work are as follows:

• Stacked autoencoder is used to reduce the dimensionality of a temporary feature map;
• Graph neural network uses spatial characteristics (connection graph) to understand the strength of connections (spatial characteristics at the node level);
• Graph convolved feature map is inserted into ResNet and consists of 26 fully connected layers with skip connection;
• The hybridization of GNN + ResNet is obtained to simultaneously learn the spatial and temporal characteristics.

The proposed hybrid model based on GNN + ResNet is implemented on the Chengdu dataset to learn the spatial and temporal characteristics of vehicle nodes. The learned model estimates the time and path for the given source and destination points in Google Maps. We used the ResNet model on the GNN layers and pre-training intuition dictates that the initial layers do not need to be recycled every epoch. Only added or changed layers need to be formed. Therefore, the layers are frozen while the models are pre-formed.

The remainder of the manuscript is organized as follows: Section 2 provides the detailed analysis of existing work and datasets. Section 3 describes methodologies for constructing a hybrid deep neural model for traffic flow prediction. Section 4 demonstrates the design of the deep neural model using the chengdu1 and chengdu2 datasets and compares the work to existing work. Section 5 concludes the proposed model with open research questions.

2. Related Works

The framework for intelligent transport system (ITS) services in urban cities is gradually expanding, but the amount of traffic infrastructure is very limited. As a result, travel time estimation (TTE) has become a critical and important issue for enabling ITS in all cities. Nowadays, people expect a good accuracy of the TTE module when using city features or street maps. Accurate travel time estimation can benefit ITS services with optimal route design, vehicle allocation and reduction of traffic congestion. However, the TTE estimate is difficult to solve due to the complex road structure and the dynamic space-time relationships that exist between the different road structures at different times of the day.

In urban traffic situations, big trajectory data is very often available in a minimally processed form. Predicting travel time from raw trajectory data of high attribute elements is very tedious. However, in most cases, the model becomes outdated due to the complexity of minutiae in traffic data. The work of [1,2] attempted to derive a framework for travel time estimation, but did not consider the availability of preprocessed spatio-temporal feature points. The work of [3] proposed a spatio-temporal autoregressive mobility model to predict urban traffic flow.

Some time series models [4,5,6,7,8,9,10] have become popular for implementing the TTE module. These time series models exploit the highly unstructured and limited available data and reveal the variety of trajectory data and its verifiable source. Although these traditional time series models are simple, natural and computationally light, they cannot accommodate complex and dynamic spatial and temporal characteristics, limiting improvements in accuracy.

In time series models, autoregression-based moving average models and their variants are often used for traffic forecasting [4,6,11,12,13,14,15]. Similarly, many machine learning models are often designed for fully curated small to medium sized traffic trajectory datasets. Moreover, when the temporal data is frequently used by the learning models, the geographical dependence of the traffic information is ignored or little considered. The machine learning models in [6,16,17] do not support large-scale spatio-temporal datasets that are highly dynamic and have a larger number of feature variables. Here too, the process of cleaning the raw data leads to high computational costs.

Feature-based techniques [18,19,20,21,22,23,24,25,26,27,28] incorporate the TTE module using a regression-based prediction model with feature variables handcrafted from the data of traffic. Unlike ML models, Gaussian process models initiate traffic data features using subspace sampling techniques but do not contain spatio-temporal connections. However, although Gaussian-based techniques are powerful and feasible to predict traffic flow estimation at peak hours, they require high computational load.

In recent years, researchers have turned to deep learning models and then to hybrid deep learning models. Deep neural networks can achieve significant performance gains by leveraging higher computing power with large-scale feature maps generated from raw traffic path data. Even when feature maps are dynamic with complex bindings, deep learning models outperform traditional learning methods as developed in [11,12,13]. The encoder-based work in [29,30,31,32,33,34,35,36,37] has done a detailed study on the autoencoder model to better predict traffic flow. Autoencoder is used by many researchers to denoise feature points in large datasets. DL models in [38,39,40,41,42,43] used a comprehensive learning model for the prediction of traffic flows for special events, demonstrating that RNN has a good effect in estimating travel time. The convolutional neural networks (CNN) models in [44,45,46] proposed a DNN-based traffic flow model to predict the historical value of the traffic flow and used CNN to extract the characteristics of the local traffic flow.

The methods based on dynamic feedback in [20,47,48] proposed an in-depth study of a recurrent convolutional neural network (eRCNN) structure with error feedback for prediction of continuous traffic flow. For an even better traffic prediction by examining the speed of continuous traffic, the work in [48] also proposed a recurrent convolutional neural network (eRCNN) with error feedback, exploiting the possibility of rational integration of both RNN and CNN to study the logical time series models that can conform according to traffic conditions.

A number of research works have used convolutional neural networks (CNNs) to extract spatial connections from two-layered geospatial traffic data [49,50,51]. Since it is very difficult to represent the traffic network using 2D grids, few studies in [30,52,53] have attempted to convert the structure of the traffic network into images, which are then used to map spatial similarities between different locations. However, space–time relationships are not reflected in transforming geographic images into different matrices and in learning landmarks using CNN. Because traffic information is space–time, constantly changing with time and space, and presents complicated dynamic space-time situations, CNNs with different learning and optimization techniques are unable to understand the patterns in urban traffic data. Traffic Information on spatial planning over time is also influenced by external variables, such as climatic conditions, occasions or characteristics of the road.

Many researchers are studying hybrid deep learning models that would combine several basic linear models to capture the geographic locations and temporal interactions of traffic data. Many of the related works [51,54,55,56,57] consider relationships within spatial and temporal data independently of each other and do not consider their combined relationships. As a result, spatial and temporal relationships are not fully exploited to improve accuracy in learning the dynamics of urban traffic data. To address these limitations in hybrid learning models, the researchers sought to integrate geographic and temporal data into a proximity, or tensor, graphical model. For example, ref. [49] obtained a constrained space–time network by interconnecting and coupling all available nodes on temporal instances n − 1, n and n + 1. The relationships between each node and its spatio-temporal neighbors are directly recorded by the topological architecture of the constrained spatio-temporal network. Among the many CNN-based models, only a few have attempted to demonstrate the power of CNN-based learning models. The work of [28] developed a deep learning-based automatic encoder model for traffic flow prediction that captures both local trends and long-term dependencies on traffic patterns. In [58], a CNN-based multitasking deep learning model has been proposed that considers both spatial and temporal characteristics to learn the traffic flows of different nodes.

To combine spatio-temporal properties with semantic data, a multi-view deep learning model to predict taxi requests has been proposed in [59], using long short-term memory (LSTM) to learn temporal properties and CNN to learn spatial properties locally in independent transport nodes. This joint spatio-temporal model failed to learn the dependencies present in the taxi multi-node trajectory data. These models ignore the topological structure of the transport network, which makes it impossible to train a fine-grained spatio-temporal representation. Models capture high-level spatial and temporal dynamics by stacking multiple layers but ignore the impact of low-level information at different scales on high-level information.

The work proposed in [60] presented an improvised CNN to extract individual image-level features for COVID-19 classification. The relation aware representations are extracted using GCN. The image level features extracted from CNN and GCN are fused using Deep Feature Fusion.

The work in [61] infers that the single view classification is not sufficient for object recognition tasks in complex environments. A multi-view representation of the image leads to efficient classification models. Fusing of convolutional feature maps at different depths is proposed in the literature, which reiterates the necessity of hybrid fusion models for classification tasks.

A comprehensive evaluation of multi-modal feature maps is presented in [62], whereas a learning model was developed for a binary classification problem based on gesture movement. The work inferred that multi-view representation gives better results when compared to single-view representation of data.

A comparative study of a car crash dataset is simulated in [63], whereas it is clearly inferred that the frequent pattern in the traffic data leads to new knowledge discovery.

The nonlinear crash worthiness of the small electric vehicle travelling at different velocities is depicted in [64], which explains a cardinal relationship between the trajectory of the vehicle and deacceleration of the vehicle. The research impresses that the traffic trajectory data is highly correlated with the crash analysis of electric vehicles.

In general, deep learning models accumulate essential learning blocks or levels to frame an in-depth project, and the entire network is trained end-to-end. With the advancement of graph convolutional networks (GCN), deep learning techniques in the light of space–time graphs are becoming more effective for predicting traffic flows. GCN is the advancement of normal convolution maps, which can deal with learning spatial representation in non-Euclidean designs. The convolution of the original graph was presented in [54], which was characterized in the spectral region. In view of this work, ref. [57] extended the configuration approach for the convolution component in graph networks to reduce the complexity of using graph convolutions. The graph convolutional network (GCN) [51] extends the convolution operation to extend graph-structured information that is better suited for addressing the structure of the traffic network. Many spatial GCNNs have been proposed in the literature [4,47] to address this challenge. Most GCN models encountered a problem that was too smooth, making it difficult to deepen graph networks [55]. In addition to GCN, Recurrent Neural Network (RNN) [22,24] and its variants, LSTM [25] or Gated Recurrent Unit (GRU) GRU [26], are also used to model time dependence. Table 1 presents a summary of the main strategies used to model the spatio-temporal characteristics of traffic data, with an overview of the performance measures used by the models.

Table 1. Summary of the different models in literatures with their performance metrics and loss functions.

Ref. No.	Model	Dataset	Performance Measures
			RMSE	MAE	MAPE	Loss Function
[4]	GCNN	METR-LA	7.24	3.47	9.57	N.A.
[49]	STGNN-TTE	Chengdu1	88.03	60.71	0.2606	Average Loss
		Chengdu2	121.14	63.38	0.2568
		Porto	52.35	39.25	0.1474
[50]	Graph Phased LSTM	Xi’an	6.814	4.921	0.295	Optimal loss
		Beijing	12.558	9.956	0.665
[51]	Caltrans PeMS	GE_GAN	18.40	13.11	4.11	Discriminator
[52]	Beijing	TTPNet	NA	118.59	11.42	first-order proximity
[53]	AE-LSTM	PeMS	28.23	20.16	0.072
[54]	GERNN	SCATS	8.827	6.327	NA	True traffic
[55]	Convolutional Residual Neural Network	Madrid City Council	NA	39.65	19.08	MSE
[56]	UrbanPy	TaxiBj	8.030	1.790	0.531	KL-divergence
		Happy Valley	8.332	1.732	0.508
[57]	Moroccan	Extreme Learning Machine (ELM)	2.8779	1.9666	14.3785	Symmetric
[58]	Combined Deep Learning Prediction (cdlp)	Jiangxi Road	11.42	7.84	21.84	CDLP
		South Fuzhou	6.52	3.26	5.12
[59]	Hybrid	Q-Traffic	NA	NA	9.22	N.A.
[60]	Spatial-Temporal Transformer Network	PeMS-Bay	4.50	1.95	4.58	Mean Absolute loss
		PeMSD7 (M)	6.17	3.12	7.89
[61]	ARIMA Model	Chengdu	12.44	5.32	154.64	N.A.

There is room for improvement in performance metrics that measure the accuracy of the traffic flow forecast prediction. In this article, we propose to introduce a hybrid deep neural model optimized to improve the accuracy of the travel time estimation module using Stacked AutoEncoder (SAE) and Graph Neural Network (GNN).

3. Methodology

Smart cities can effectively improve the quality of urban life. However, as the population increases, there is a greater demand for transportation vehicles. In the development of smart cities, estimating travel time is a challenging and important task due to the increase in the number of vehicles in smart cities and the traffic monitoring system.

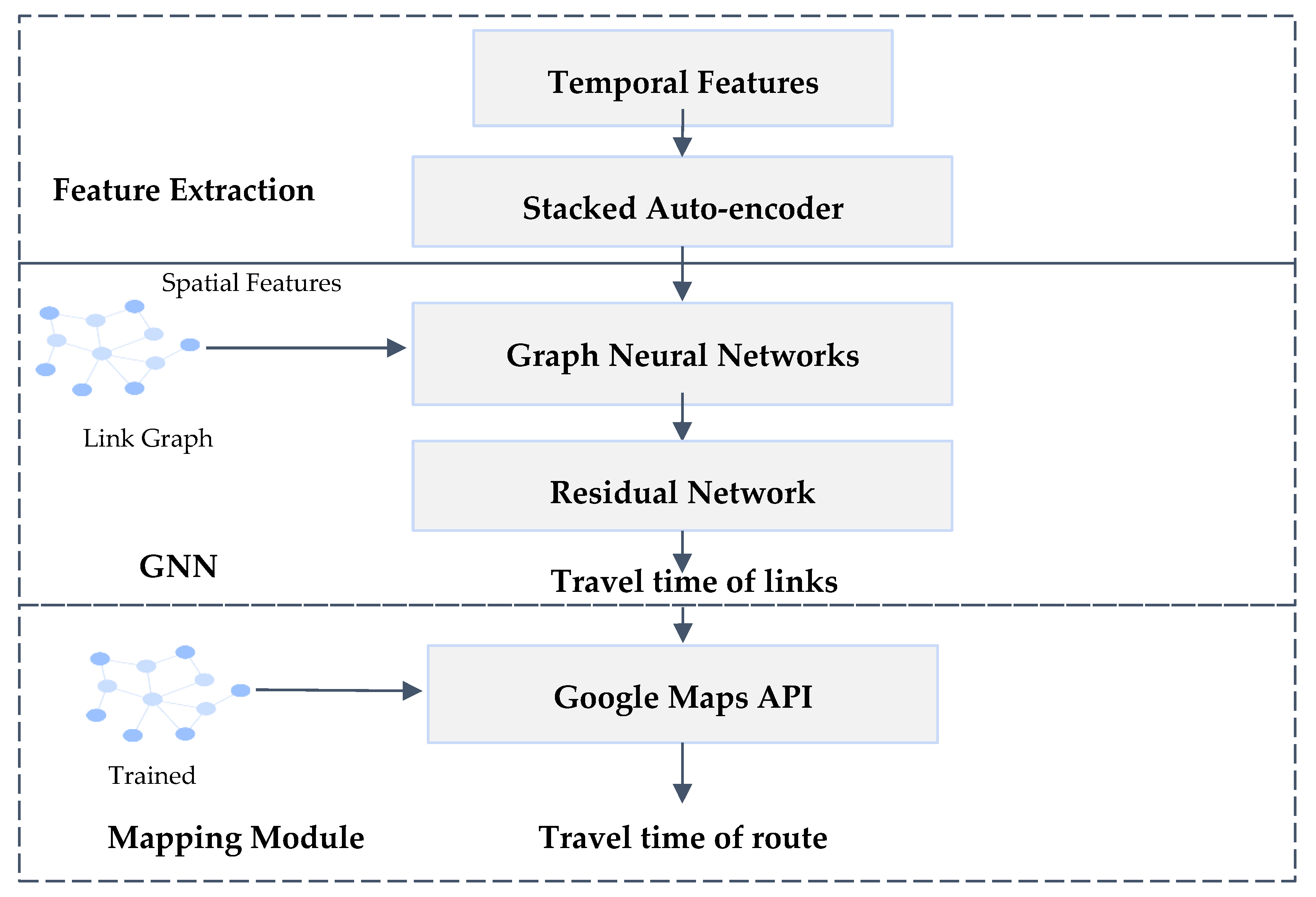
The methodology proposed in this work, as shown in Figure 1, aims to design a hybrid deep learning framework that simultaneously learns both spatio-temporal characteristics of traffic data using stacked autoencoder, residual networks and graph neural networks. The temporal attributes of the traffic data are extracted using a stacked autoencoder. The four GNN layers extract the map of the spatial characteristics from the trajectory data of the vehicle node in the traffic data. Then, the GNN layers are linked to the remaining 26 blocks to generate the links corresponding to the travel time and path of the vehicle nodes in the data set. Skipping connections in the rest block allows the model to inherit activations from multiple levels. This reduces the number of training periods and training samples compared to traditional fully connected levels.

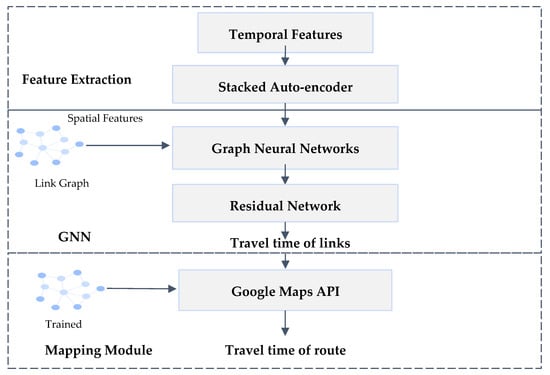
Figure 1. Proposed Hybrid Deep Learning Pipeline that learns spatio-temporal features for travel time prediction.

The temporal feature maps generated by the stacked autoencoder are concatenated with the GNN to prepare feature maps of the spatio-temporal traffic data. The fused feature maps contain node distance and travel time between the nodes. These feature maps in the form of graph adjacency matrices are used to predict traffic flow by estimating the travel time.

In the proposed work, we use the Chengdu city dataset, which contains the trajectories of 14,000 taxi trips in the period from 3 August 2014 to 23 August 2014. Although the travel data collection period is minimal, the number of nodes/vehicle drivers used for the dataset is large compared to other reference datasets. This helps to understand traffic behavior in crowded traffic environments. Trajectory data consists of spatial and temporal features used to simultaneously generate feature maps using autoencoder and GNN.

Time attributes are the time taken by 50 individual taxis to travel on a particular link. They are represented by ‘Data1’, ‘Data2’, ………, ‘Data49’, ‘Data50’. The time characteristics are the time taken by the taxis to travel from one location to another. Spatial data consists of information about road networks and their physical connectivity with attribute names such as ‘Link’, ‘Node_Start’, ‘Longitude_Start’, ‘Latitude_Start’, ‘Node_End’, ‘Longitude_End’, ‘Latitude_End’, ‘Length’. Each record represents an edge, whose start and end nodes are given, respectively, by the ‘Node_Start’ and ‘Node_End’ columns. The summary of the dataset is shown in Table 2.

Table 2. Summary of Chengdu dataset.

Distribution	Weekday Peak	Weekday Off-Peak	Weekend Peak	Weekend Off-Peak
No. of points (roads)	5943
Spatial distribution (start) (Lat, Long)	(103.9299735, 30.56811912)	(103.9299735, 30.56811912)	(103.9299735, 30.56811912)	(103.9299735, 30.56811912)
Spatial distribution (end)(Lat, Long)	(103.9299735, 30.56811912)	(103.9299735, 30.56811912)	(103.9299735, 30.56811912)	(103.9299735, 30.56811912)
Avg moving time (s)	63.7096	46.4763	61.3718	46.5097
Max moving time(s)	337.9256	250.6087	293.6739	253.8487
Min moving time (s)	4.9793	3.3162	12.8908	2.8709
Median (s)	53.4519	37.6102	51.4952	37.675

Vehicle node travel time is collected in 20 days in different time periods in Chengdu city. Time data is divided into four categories, such as peak hours on weekdays and weekends, off-peak hours on weekdays and weekends. Each secondary data set is 1 GB, which equates to a total of 4 GB of space-time data. Typically, any deep learning model requires a large amount of traffic data to learn and evolve. However, the large volume of enroute traffic data is redundant in nature. While training a deep neural network with 50 temporal capabilities from a 4 GB dataset is an advantage, as the availability of non-redundant trajectory data is a major challenge. Therefore, we propose a stacked autoencoder to analyze the 50 temporal characteristics and the unique characteristic map to reduce the size of the temporal features. Temporary redundant data is identified and deleted using the automatic stacked encryption network.

3.1. Dimensionality Reduction Using Stacked Autoencoder

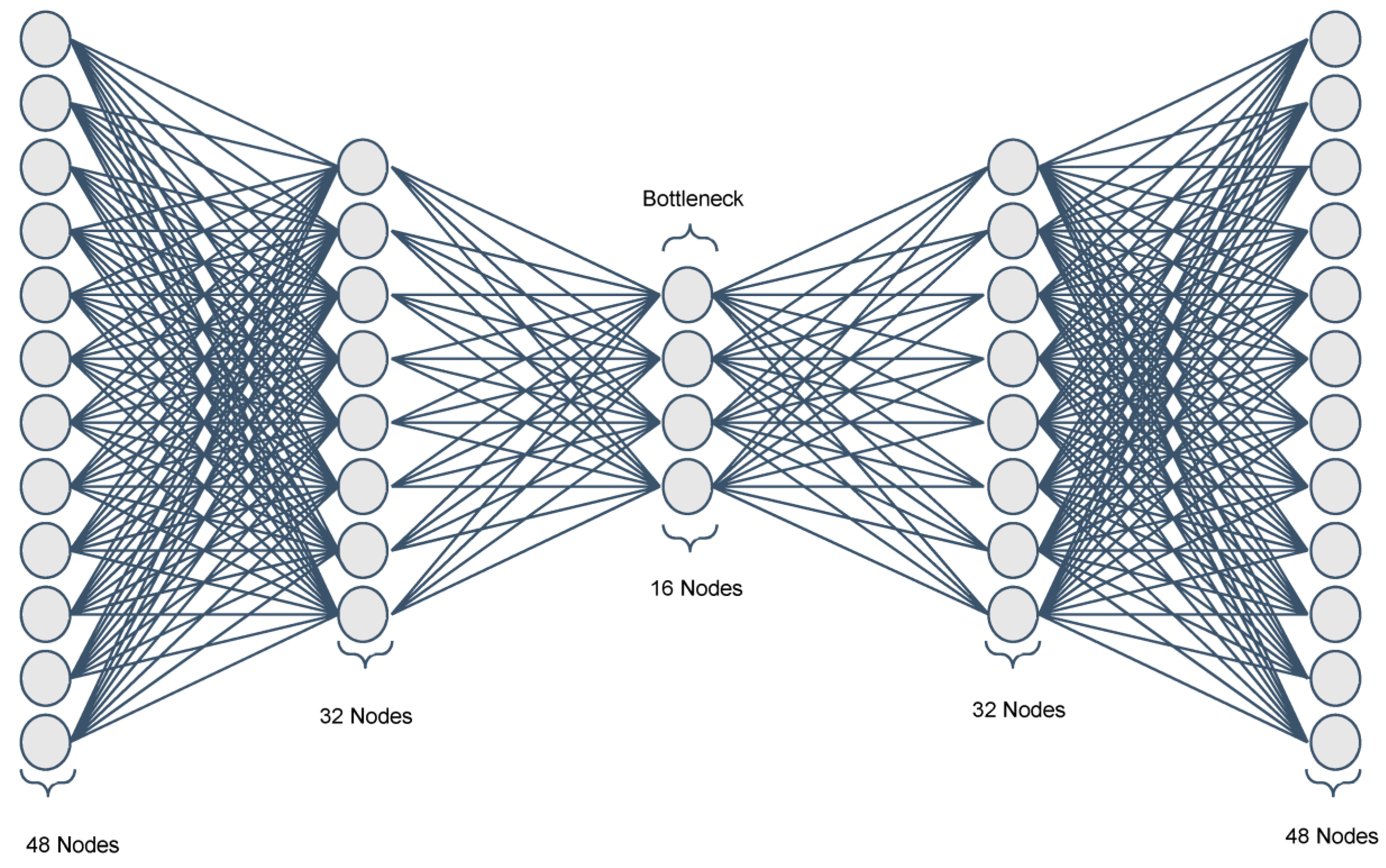
Overfitting occurs when a model learns too well on a set of training data but does not perform well with unseen real data. An autoencoder is an unsupervised learning network that uses backpropagation to generate an output feature map that is very similar to an input feature map by removing redundant features in the original dataset. In order to quantitatively reduce the amount of redundant traffic data, a stacked autoencoder feature selection approach is used in this work. The purpose of the autoencoder is to learn temporal characteristics by training the encoding layers of the network to capture the most important aspects of the input sequence in a low-dimensional representation. A stacked autoencoder, as shown in Figure 2, is a neural network composed of multiple layers of sparse autoencoders, with the output of each hidden layer connected to the input of the next hidden layer. The bottleneck layer represents features after lossless compression has been performed on the input feature map. For some datasets, such as vehicle trajectory data, there is a complex relationship between features. A single sparse autoencoder is not enough to reduce the dimensionality of feature maps and complex temporal features. Despite the compelling reasons to represent the map of the complex temporal characteristics of the trajectory, we used a stacked autoencoder with two layers in the encoding, a bottleneck layer and two layers in the decoding process. Trainable encoder and decoder sets constitute the autocoder training process, which can be modeled using Equations (1) and (2). In this proposed work, the stacked auto coding network is designed with six dense layers and one bottleneck layer stacked sequentially with the ReLU activation function and hyperparameters, such as learning rate adjusted to 0.01 for a batch size 1 with the Adam optimizer, as shown in Figure 3.

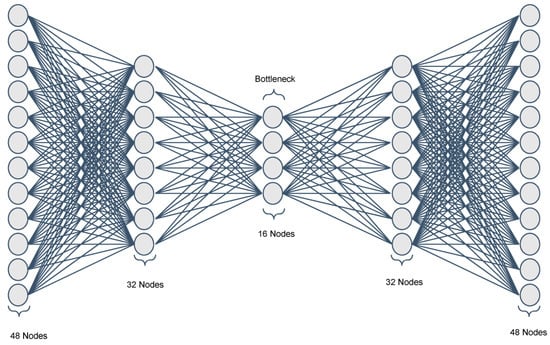
Figure 2. Trainable dense layers of the stacked autoencoder.

Figure 3. Stacked autoencoder with six dense layers for training temporal trajectory data.

Given an original input sequence data X = {x₁, x₂, …, x_k}, where xi ∈ Rd. The characteristic sequence T = {t₁, t₂, …, t_k}, where ti ∈ Rl of the original data is obtained using Equation (1). The output of the encoder is used as the input of the decoder. The decoder reconstructs the original data to Y = {y₁, y₂, …, y_k}, where yi ∈ Rd by using the characteristic sequence T. The purpose of decoding is to verify whether the extracted features are valid and represent the original input sequence before and after the encoding process. Once the stacked layers in the autoencoder complete the training, the encoder is used to extract the characteristics of the original data to represent the dimensionally reduced feature map of the temporal data. The bottleneck layer has a reduced number of nodes

t_i = f(w_t·x_i + b_t)

(1)

y_i = g(w_y·t_i + b_y)

(2)

where f(·) is the sigmoid activation function for encoding layers and g(·) is the sigmoid activation function for the decoding layers. W_t is the encoder’s weight matrix, and b_t is the bias vector, W_y the decoder’s weight matrix, and b_y the bias vector. The reconstruction error in the decoding layers is calculated using Equation (3), where the difference between the reconstructed data sequence Y and the original data sequence X is infinitesimally small (of 10⁻⁵ order), which signifies that the characteristic sequence T is valid. For the Chengdu dataset, the stacked autoencoder (SAE) with 16 hidden layers is sufficient to reconstruct the characteristic sequence, which implies that the 50 temporal features in the original temporal feature space can be represented using 16 temporal features, thereby reducing the dimensionality of the temporal feature space.

$$\mathrm{L} (\mathrm{X}, \mathrm{Y})=\frac{1}{2}{{\displaystyle \sum }}_{i=1}^n|x_i-y_i{|}^2$$

(3)

After dimensional reduction using the stacked autoencoder, we fuse the non-redundant 16 temporal features along with 9 spatial features. The fused feature map is fed into the graph neural network, which consists of graph convolutions and residual blocks to predict the travel time between two given nodes.

3.2. Graph Neural Network (GNN)

Almost everyone is using social media in his/her day-to-day life. In other words, everyone is using graph data structures in Facebook graph API’s recommendation systems, web analytics, etc. Graphs are also an excellent tool for understanding social relationships. The reason is that all are dynamic in nature and graphs [62] have gave the best performance in handling such data. A graph is a data structure made up of nodes (vertices) and edges that are joined to represent information that has no clear beginning or conclusion. When plotted in 2D (or even nD) space, all the nodes occupy a position in space, commonly grouped according to related properties. Every node has a set of spatial and temporal features defining the traffic data. More complex problems can be solved using graphs by reducing them into simpler forms by transforming them into representations from various perspectives. Each edge connects two nodes together and shows the interaction or relationship between them. The messages and their effects on edge and node states are learnt using graph neural networks, which are used in a message forwarding method. So, GNN has been taken into consideration as an appealing modeling technique for travel time prediction.

These GNNs can represent information from their location at negligent depths and can capture graph dependencies with the message passing between graph nodes. Road networks can now be naturally created as a graph structure, considering the traffic network as a temporary space graph where the nodes are in the streets, the edges are measured between the pairs of nodes, and each node has a medium speed of traffic within the window as dynamic input features. Predicting traffic speed, volume or traffic congestion on road networks is critical to a smart transport system. In the case of travel time estimation, this could be time of the day, the position (latitude and longitude) corresponding to that node. However, graphically generated data is ubiquitous in that it can be distributed by node classification, graph classification, graph visibility, link prediction, and graph compilation with the help of GNNs.

In the GNN, the nearby nodes will be transmitting messages among themselves. Since the structure will not be changing, setting a bias of the area where it will be easier for the nodes to only rely on close by nodes, which only needs a single step of message transmission. The method will then allow the GNN to use a road network connection adequately. Due to the training of the model, the intersections can be easily predicted for delays that are predictable due to the peak hours which will not change randomly, or specifically on some dates, which can also be noted by the model. This very feature gives our model potential. Therefore, a super component which contains a varying amount of length and complexity, i.e., simple two-point routes to a large set of lines which consists of numerous amounts of nodes, can be processed by our GNN with ease.

A GNN takes a graph G (V,E) as input.

• The feature matrix of the graph is represented by X with dimension N × F⁰ where N is the number of nodes and F⁰ is the number of input features for each node.

The hidden layers in the GNN are represented in the form $Z_i=f\left(z^{i-1},A\right)$ where, $Z^{0 }=x$, and f is the propagation factor. Each hidden layer $z_i$ has a feature matrix $N\times f^i$. Each row $N$ in the feature matrix corresponds to the nodes’ feature at level i. The propagation rule at Equation (4) decides whether the features at each hidden layer are to be accumulated for the feature map generation for the successive layers.

f (Zⁱ, A) = σ(AZⁱWⁱ)

(4)

where Wⁱ is the weight matrix that corresponds to layer i and σ is a non-linear activation function ReLU. The weight matrix has dimensions Fⁱ × Fⁱ⁺¹, which means that the size of the weight matrix’s first dimension influences the number of features at the following i + 1 layers.

In the dataset, we have source and destination points; these points act as nodes and the connection between them is the edge. So, using these points, we can generate a graph with corresponding nodes and edges. For this purpose, we use the deep graph library (DGL) to generate a graph structure from our dataset. DGL represents a directed graph as a DGL graph object. We can construct a graph by specifying the number of nodes in the graph as well as the list of source and destination nodes. Nodes in the graph have consecutive IDs starting from 0, which are given as Node_Start in our dataset; similarly, we have Node_End for the destination node. The connection between the different nodes and the complexity of the linkages are shown in Figure 4. The spatial dispersion of the datapoints shows the complexity of the road network; the connecting edges show the availability of paths between the nodes.

Figure 4. A graph shows the spatial disparity of the nodes and their connectivity.

An overall architecture is shown in Figure 5. We have used 4 GCN layers, 26 fully connected layers. The GCN layer performs graph convolution on the graph generated earlier and then gives the edge feature. This output will be given to the residual network architecture for predicting the time between two nodes.

Figure 5. Proposed GNN model for extracting edge level and node level feature maps.

3.3. Residual Network

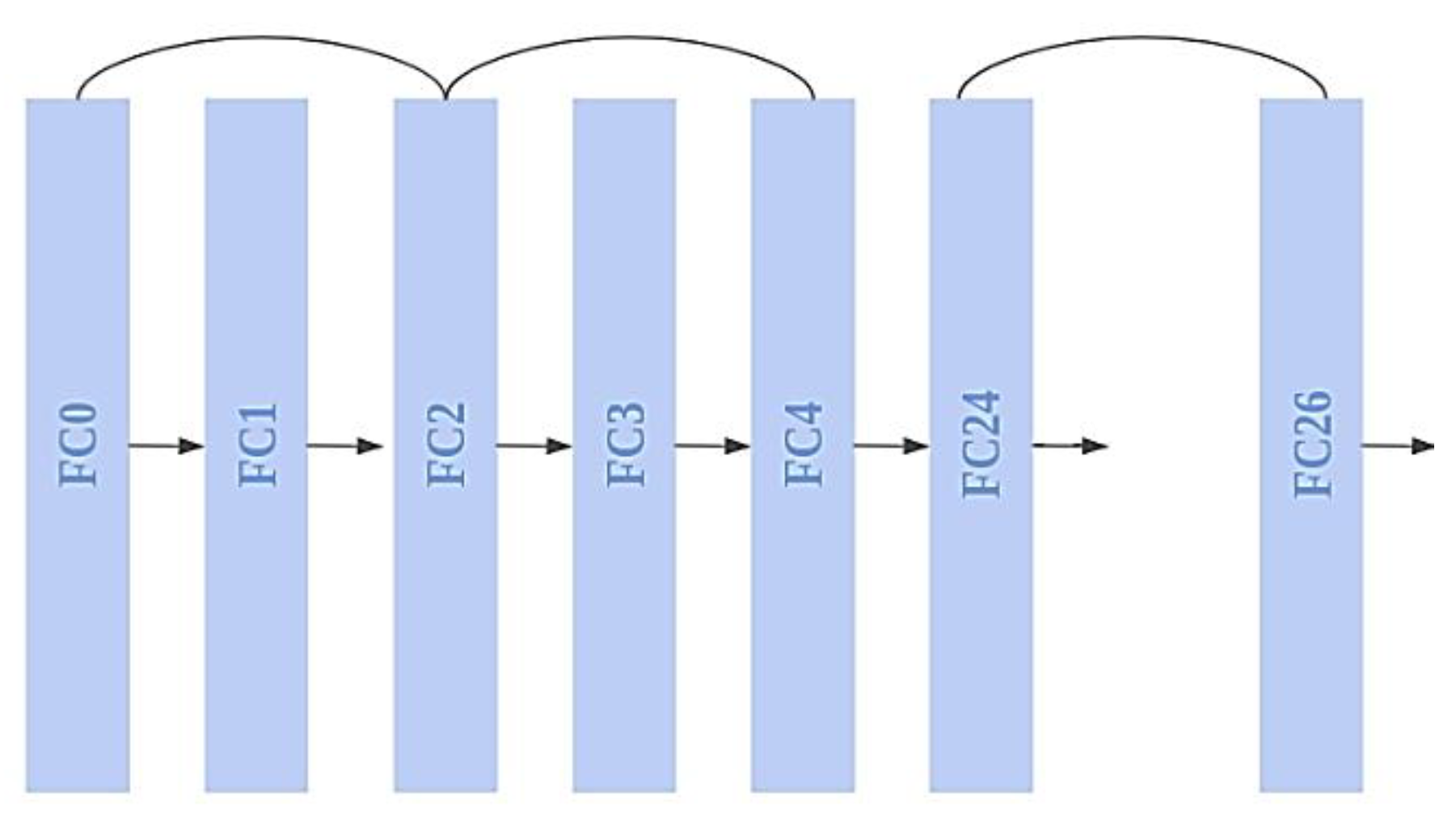
After data processed through GNN, the output (i.e., produced node classification, graph classification, graph visibility, link prediction) is passed through the residual network architecture to predict the travel time for every edge in the network, as shown in Figure 6.

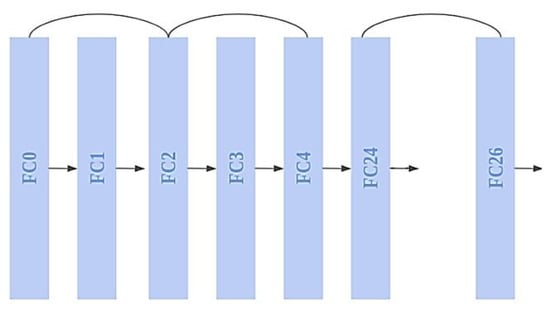
Figure 6. ResNet Model: 26-FC layers with skip connections.

Instead of allowing layers to learn the underlying mapping, we let the network fit the residual mapping. So, rather than starting with Q(x), let the network fit.

F(x): = Q(x) − x which gives Q(x): = F(x) + x.

(5)

The benefit of including this type of skip connection is that if any layer degrades architecture performance, it will be skipped by regularization. As a result, very deep neural networks can be trained without the issues caused by vanishing/exploding gradients.

By enabling different shortcut channels for the gradient to flow through, the skip connections strategy in ResNet overcomes the problem of disappearing gradient in deep CNNs. In addition, if any layer is detrimental to the architecture’s performance, regularization will skip it. The model is a hybrid of graph convolution (GCN) layers and residual blocks layer forming ResNet architecture. The GCN layers are 4 in number, and they extract information from the graph structure using spatial and temporal features. These GCN layers are then connected to residual blocks, which are 26 in number. The skip connections in the residual block helps the model to learn on previous and present activations, thus it requires a smaller number of training epochs compared to the conventional fully connected layers.

The input to the model is the graph network and the model learns the graph features and trains on the edge features. After the final epoch, we get the duration for traveling edges. Hence, we receive a trained graph with output on the edge. The activation function used for the model is ReLU activation and for the training optimizer function is Adam optimizer. The loss function used during training is root mean square error (RMSE).

The output layer generates the predicted values of travel time for each node instead of a classification. To predict the travel time of each edge, we used fully connected layers at the end of residual network architecture instead of the soft-max layer. These predicted travel times for each edge are provided to the succeeding layers to generate the maps and routes.

The predicted travel times of each edge in the graph are given to Google API as input to produce the least time and the shortest route between the two nodes. A road network is constructed by considering the two nodes with edges corresponding to the route. After constructing the road network, the time for the routes that are in the network are calculated.

4. Experimental Analysis

The dataset consisting of latitude and longitude as temporal features, we have proposed a stacked autoencoder and sparse autoencoder to extract the feature vectors. Stacked autoencoder is trained for 150 epochs and we obtained the subset of 16 temporal features. We found that there are 16 features that contain all the information as available in the original 50 temporal features. The autoencoder represents the input at the output; it means input and output are same. So, when this input and output are the same we cut down the autoencoder from the bottleneck layer.

Using the spatial features, the graph is obtained from the dataset by using ‘Node_Start’ and ‘Node_End’ Features, then the obtained graph is the skeleton of the graph; node features such as ‘Latitude’ and ‘Longitude’ are fed into the nodes, and the edge features such as ‘Length’, ‘Data1’, ‘Data2’……‘Data16’ are fed into the edges. This makes a graph with all the features in its nodes and edges.

The GNN will check the neighboring nodes around a center node, along with a specified filter and parameterized size, which is being fed back to it as we run multiple epochs on it which provides us with required weights. The model first determines the nodes by the graph labeling method provided as the center-based methods and then selects the sequence of the fixed node length. Second, to address the issue of random nodes, a fixed size is created for each node. Finally, a local graph is usually made according to graph labeling procedures so that nodes in the same structural field are assigned the same positions, followed by learning to represent with existing feature maps. However, the layout of the nodes is determined by the labeling method provided and is usually based solely on the structure of the graph.

In graphs that correspond to the edge character information, the filter weight parameters are usually set to certain boundary features in the node area. For the use of end-to-end attributes, the edge-conditioned convolution (ECC) function is designed by lending a view of a flexible filter network. For the model, we create a graph. We specifically use the spatial convolutional network, a sub part of GNN. Since we require spatial features to be studied in order for the model to understand the abstract concepts of the links that have been made and as a result help us with predicting the time travel estimate, we access all the parameters that have been generated and then we get our input layer.

For our case, we have a total of 41 parameters that we need to provide to produce the hidden layers. For the hidden layers, we firstly start with a few convolutional layers, starting with input features and one by one connecting the input list with the layer. Then, we add few more hidden layers of fully connected layers in a linear pattern. Next, we apply a ReLU function on the model to overcome the vanishing gradient problem, allowing the model to have a relatively quicker learning. As mentioned above, where we applied our idea overall, we applied multiple layers for more proper prediction. In this regard, we define a loss function for our model. After feeding the model with any loss function and running Adam optimizer, weight parameters are trained.

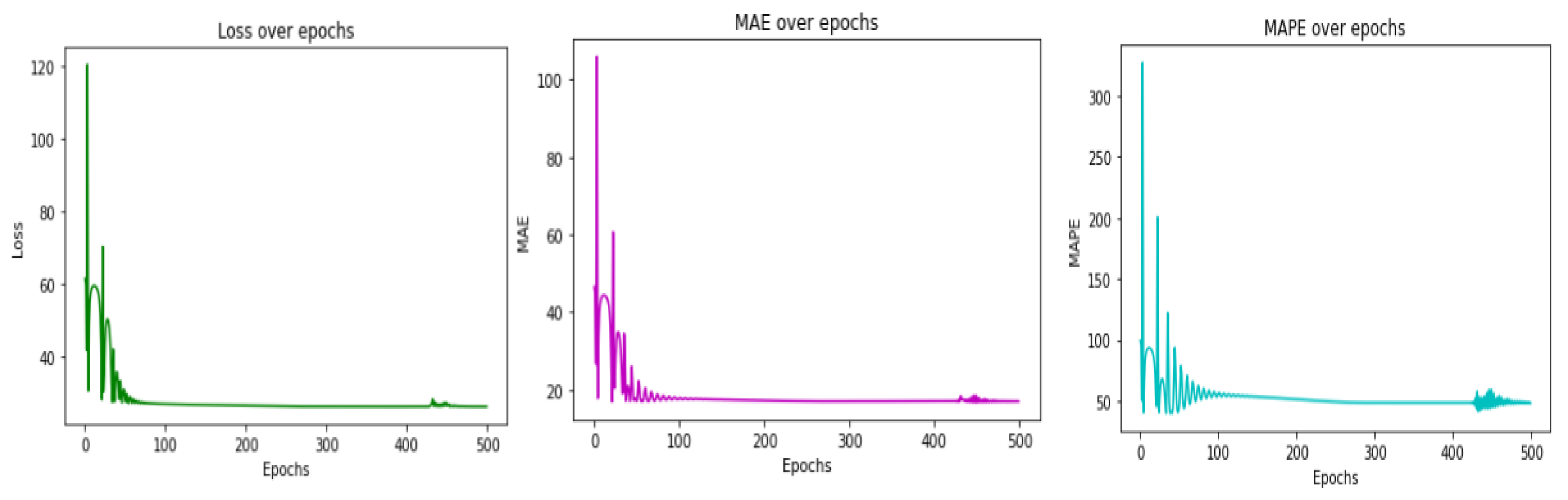
Initially, we are provided with interconnected nodes that will be representing the Chengdu dataset. These nodes will be presented for the model. The temporal features are needed to predict the travel time from one node to another node. In order to tackle this problem, we will be using the stacked autoencoder to reduce the number of features from 50 to 16, to optimize the training time and reduce the computational costs. Hence, the complex road network structures can be learnt since the feature size has been reduced, as shown in Figure 7. The specific features are properly chosen via autoencoders, so no drastic changes even after reducing the number of features which decides in predicting the output. The model is made with the help of graph convolutional network GCN. The required number of layers were accordingly added. The spatial convolutional network (SCN), which is a sub part of GCN, is mainly used because we need a method similar to CNN where we can apply convolution, Relu function and pooling on fixed as well as on arbitrary center node, thus helping with graph classification and link prediction; thus, predicting the time travel estimation between specified links. It has been a powerful tool for analyzing graph data. The graph model or ‘g’ is the result after we put it through the graph generation function provided by the Python deep graph library (‘dgl’). We have been provided with 1902 nodes, and we obtain 5943 edges or links in the result. The graph contains the 16 features we provided after applying the autoencoders, and it stores it in a scheme. Finally, in the result, we will have a predicted time for every possible connected link as per the inputs provided to us. There are some redundant losses that are minimized during the course of epochs. Figure 7 provides the training loss up to 500 epochs. We implemented our proposed framework using PyTorch 1.8 and ran all the models on NVIDIA Tesla V 100 GPU.

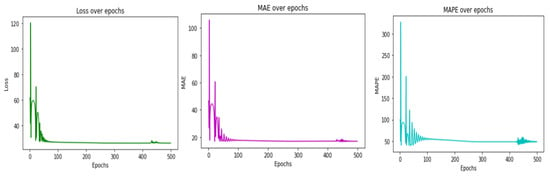
Figure 7. RMSE loss, MAE and MAPE curves for the proposed GNN + Resnet Model.

The performance of the model is measured using the RMSE loss, mean average error (MAE) and mean average percentile error (MAPE) by using the equations below.

$$\mathrm{MAE}=\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n\left|y_i-\widehat{y_i}\right|$$

(6)

$$\mathrm{MAPE}=\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n\frac{\left|y_i-\widehat{y_i}\right|}{y_i}$$

(7)

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{\left|y_i-\widehat{y_i}\right|}^2}$$

(8)

where $y$ and $\widehat{y }$ are observation and prediction values, respectively.

As shown in Table 3, our proposed model outperforms existing models for both the chengdu1 and chengdu2 datasets for all the evaluation metrics.

Table 3. Performance comparisons of the proposed GNN + ResNet model.

Model	Chengdu1			Chengdu2
	RMSE	MAE	MAPE	RMSE	MAE	MAPE
ARIMA	147.32	91.69	0.5621	192.48	102.44	0.5485
TEMP	116.38	77.5	0.3903	155.34	81.19	0.4057
LightGBM	107.89	71.97	0.3518	142.56	74.1	0.3316
MlpTTE	96.17	66.58	0.2963	128.52	68.31	0.2839
RnnTTE	95.29	65.74	0.2915	128.79	68.43	0.2841
DeepTTE	93.68	64.03	0.2864	127.24	67.39	0.2807
STGCN	94.37	65.02	0.2787	127.89	67.58	0.272
DRCNN	96.78	66.34	0.2817	130.11	69.57	0.2786
Graph Wavenet	92.65	63.57	0.2725	126.58	67.1	0.2701
STGCN TTE	88.03	60.71	0.2606	121.14	63.38	0.2568
GNN ResNet (ours)	88.79	57.48	0.2616	121.24	61.65	0.2628

The existing model’s performance is poor, especially compared to those which are using handcrafted machine learning methods, due to less discrimination of the ability to grasp complex and dynamic changes in spatio-temporal characteristics for travel-time estimation. Clearly, GNN-ResNet50 has shown better performance than all existing methods over metrics (RMSE, MAE and MAPE). Table 4 shows that our proposed GNN-ResNet50 model outperformed, for predicting the travel time, all other hand-crafted machine learning and benchmark deep learning models on chengdu1 and chengdu2 datasets. These improvements are bagged because we are using the stacked autoencoder to extract the feature as vectors and graphs generated from spatial and temporal features to predict the travel time for every node by using combined GNN and ResNet models. Optimal routes are estimated by using the Google map API.

Table 4. Performance of our proposed model GNN ResNet with other graph-based models for estimating the travel times of each link on two datasets.

Model	Chengdu1			Chengdu2
Spatio-Temporal GCN	RMSE	MAE	MAPE	RMSE	MAE	MAPE
STGCN	33.87	18.79	0.5301	52.33	21.13	0.5345
DRCNN	35.75	19.42	0.5457	54.21	21.88	0.5519
Graph Wavenet	33.12	18.23	0.5264	51.08	20.76	0.533
Spatio-Temporal GNN TTE	31.28	17.57	0.5152	49.77	20.01	0.5217
GNN + ResNet (ours)	31.06	17.23	0.5028	49.63	18.43	0.5314

We evaluated our proposed GNN + ResNet model with other Ggraph based deep learning models on predicting the travel time for each node. It is found that our proposed GNN + Resnet model outperformed travel time prediction on chengdu1 and chengdu2 datasets as given in Table 4.

We tested our GNN + ResNet model in various temporal circumstances, compared with other baseline models, and presented the comparisons in Table 5 for chengdu1 dataset and in Table 6 for chengdu2 dataset. The proposed GNN + Resnet model exhibits more reliable performance in different temporal scenarios, such as rush and non-rush hours. To verify the performance of the model in various temporal circumstances, the chengdu1 and chengdu2 datasets are partitioned into rush hours and non-rush hours by considering the time periods and traffic condition. The results show that traffic flows are more unpredictable in rush hours due to traffic congestion. The model improved in percentage in RMSE, MAE and MAPE with 13.13%, 22.59%, 1.72% on the chengdu1 dataset and at least a 1.32%, 2.90%, and 2.91% percentage improvement on the chengdu2 dataset. For the non-rush hours, our model exhibits improvements in RMSE, MAE and MAPE with 11.05%, 4.63% and 17% on the chengdu1 dataset and at least 2.36%, 1.54% and 6.42% on the chengdu2 dataset.

Table 5. Performance comparison of proposed GNN + residual network under different temporal scenarios on chengdu1 dataset.

Model	Chengdu1
	Rush Hours			Non-Rush Hours
	RMSE	MAE	MAPE	RMSE	MAE	MAPE
ARIMA	132.58	93.46	0.5731	120.41	88.93	0.551
Empirical	110.41	79.41	0.4022	102.33	75.44	0.3896
Light Gradient Boosting Machine	101.34	74.67	0.3582	93.48	70.1	0.3476
Multiple Layer Perceptron	90.84	67.01	0.2991	86.95	61.36	0.2931
Recurrent Neural Network TTE	89.49	66.16	0.2967	84.09	60.14	0.2884
Deep Convolution TTE	87.24	64.93	0.2889	83.05	59.51	0.2851
Spatio Temporal Graph Convolutional TTE	88.27	65.35	0.2810	83.56	59.43	0.2726
Deep Regions with Convolution Neural Network	90.57	66.72	0.2883	86.83	61.05	0.2785
Deep Spatial-Temporal Graph	86.49	64.10	0.2789	82.19	59.36	0.2692
Spatio Temporal Graph Neural Network	82.65	61.45	0.2662	77.34	56.55	0.2581
GNN + ResNet (ours)	71.79	46.99	0.2616	68.79	53.93	0.2142

Table 6. Performance of GNN + ResNet model with other graph based models under different temporal scenarios on chengdu2 dataset.

Model	Chengdu2
	Rush Hours			Non-Rush Hours
	RMSE	MAE	MAPE	RMSE	MAE	MAPE
ARIMA	175.84	105.74	0.5733	158.32	100.65	0.5387
Empirical	144.66	83.52	0.4341	136.55	80.02	0.3982
Light Gradient Boosting Machine	131.94	76.63	0.3589	125.84	72.38	0.3224
Multiple Layer Perceptron	122.67	69.16	0.2908	117.15	68.02	0.2806
Recurrent Neural Network TTE	122.12	69.21	0.2911	117.47	68.18	0.281
Deep Convolution TTE	121.56	68.63	0.2885	117.1	67.07	0.2793
Spatio Temporal Graph Convolutional TTE	121.35	68.41	0.2798	116.27	67.19	0.2703
Deep Regions with Convolution Neural Network	125.22	70.14	0.2823	120.17	69.08	0.2759
Deep Spatial-Temporal Graph	120.62	68.16	0.2759	115.86	65.91	0.2684
Spatio Temporal Graph Neural Network	114.25	64.45	0.2611	110.83	62.77	0.2551
GNN + ResNet (ours)	112.74	66.32	0.2535	108.21	63.74	0.2387

To evaluate and verify the effective learning of model parameters on spatio-temporal data, we conducted the experiment on a variant of GNN, i.e., on FCN and the results are given in Table 7. FCN consist of 4 GCN layers, 26 fully connected layers and 6 dense layers used to predict the travel time for each node. The proposed GNN + ResNet model consists of 4 GCN layers, 26 fully connected layers with skip connections. While training deep neural nets, the performance of the model drops with the increase in depth of the architecture. This is known as the degradation problem. To avoid the degradation problem, skip connections are used in which the activations from the previous layers are given as input such that the past activations are not degraded during training.

Table 7. Performance comparison of GNN + Resnet with FCN for travel time estimation.

Model	Chengdu1			Chengdu2
	RMSE	MAE	MAPE	RMSE	MAE	MAPE
FCN	92.31	72.3	0.3221	112.21	63.74	0.2387
GNN ResNet (ours)	88.79	57.48	0.2616	26.26	16.98	0.48

We observed that our proposed GNN-ResNet model exhibits better performance than our FCN model, as given in Table 7, i.e., the combination of feature representation and distinct feature representation can improve the learning of spatio-temporal representation.

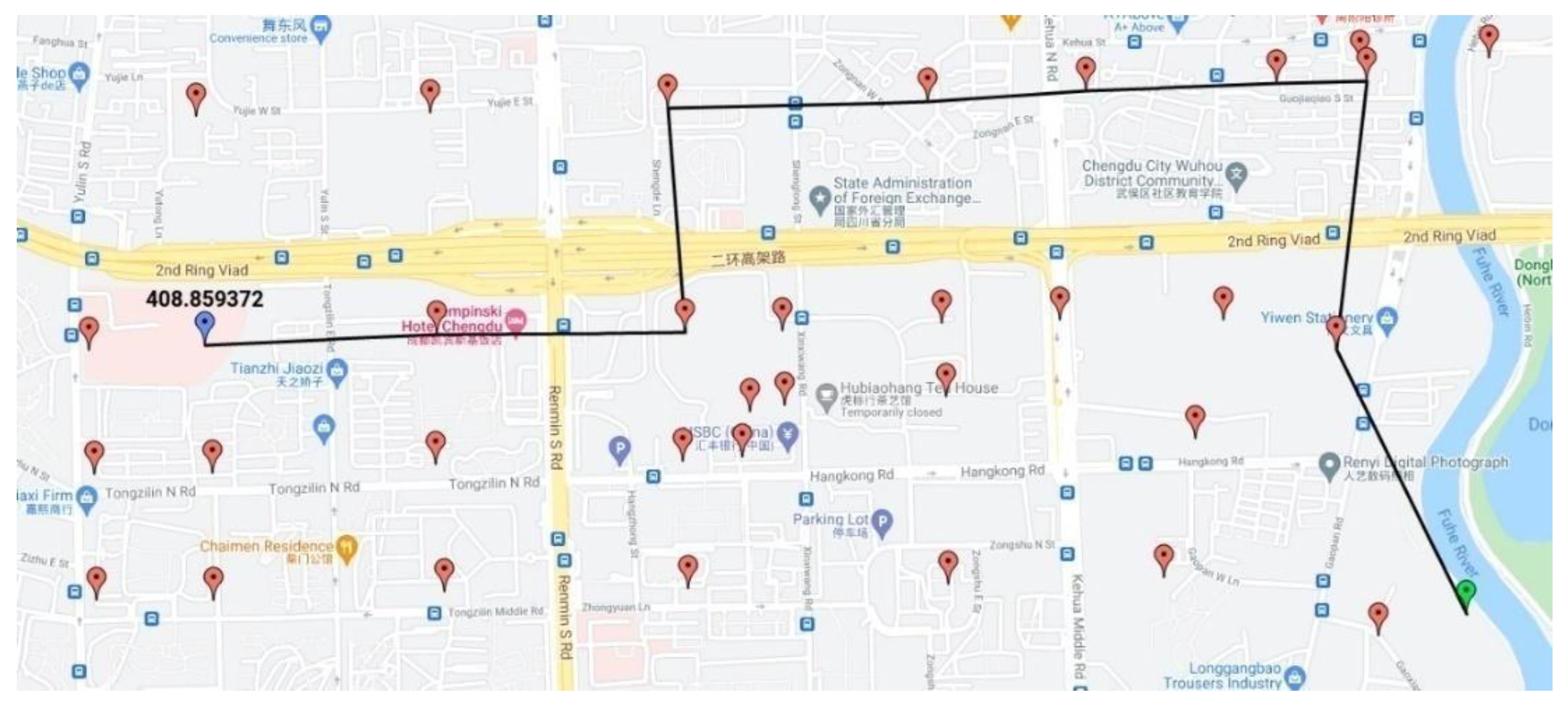
The output of the proposed framework takes the spatial and temporal data, and all produced 1902 nodes are plotted on the Google map, and the user can select source and destination nodes. For the output, the user can see the different source and destination locations and their optimal path. The output in Google Maps shows the optimal path between the two selected nodes and the estimated time to reach the destination (Blue marker) from the source (Green marker), as shown in Figure 8, Figure 9 and Figure 10, respectively.

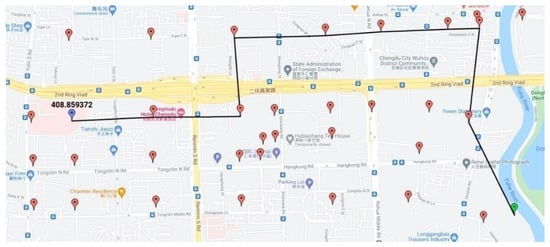
Figure 8. Results in Google Map using our GNN + Resnet model with estimated travel time (in seconds) for distant points.

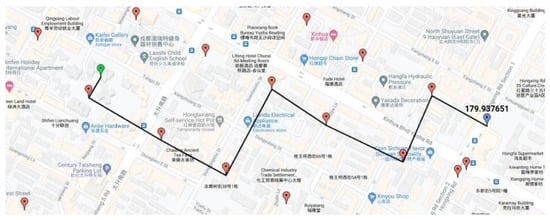
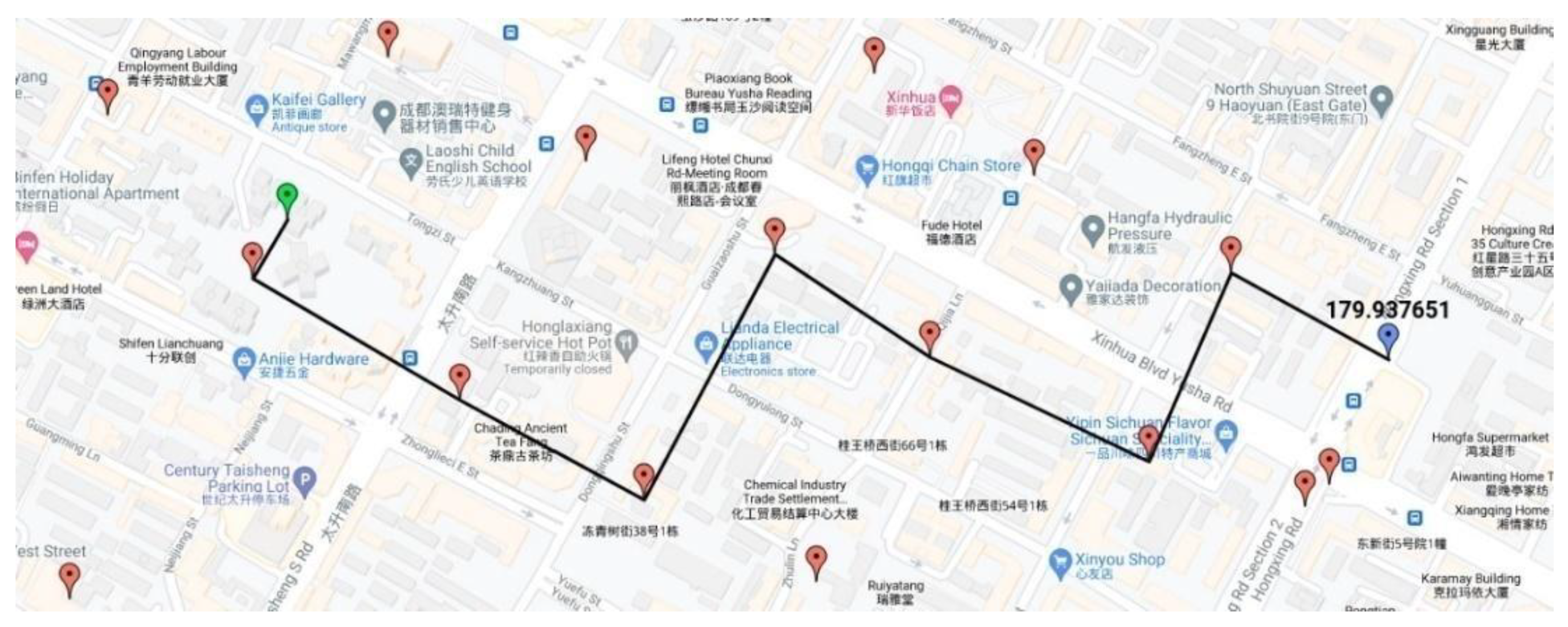
Figure 9. Results in Google Map using our GNN + Resnet model with estimated travel time (in seconds) for a nearer points.

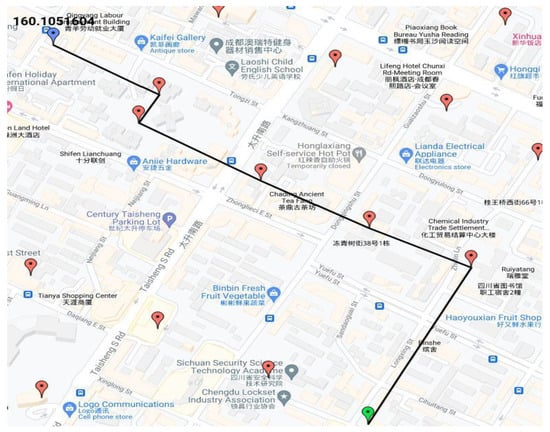
Figure 10. Results in Google Map using our GNN + Resnet model with estimated travel time (in seconds) for very nearer points.

5. Conclusions

We have proposed a graph-based hybrid deep learning model named GNN-ResNet50 for predicting travel time. We used the Chengdu dataset. More redundant data from the Chengdu dataset was eliminated by using the stacked autoencoder; these features are classified with the rapid development of GNNs and residual network architecture to predict traffic flow using spatial-temporal correlation. In this paper, we first summarized several well-known existing methods, which serve as the basis for developing a general framework for traffic forecasting using spatial-temporal dependencies; then, we implemented two architectures, the first using only the fully connected layer to predict travel time; and finally we introduced skip connections in the architecture to get a residual network architecture, which resulted in less training time compared to the fully connected architecture. The results of the proposed model are significantly better when compared with state-of-the-art approaches, such as STGNN-TTE. This research work can be directed toward analyzing the road traffic network in an unconstrained environment, where the flow of traffic is highly non-linear, by considering factors such as driver behavior, travel speed, experience of the driver, etc. The work can be further extended to include different weather conditions, such as rain and fog and nighttime conditions, which will surely influence arriving at the results presented here. The results presented hereunder are derived based on Chengdu dataset1 and Chengdu dataset2. Finally, open research issues were presented based on experimental results on selected benchmark datasets for future development in this research field.