A Review on Rain Signal Attenuation Modeling, Analysis and Validation Techniques: Advances, Challenges and Future Direction

Abstract

Radio waves are attenuated by atmospheric phenomena such as snow, rain, dust, clouds, and ice, which absorb radio signals. Signal attenuation becomes more severe at extremely high frequencies, usually above 10 GHz. In typical equatorial and tropical locations, rain attenuation is more prevalent. Some established research works have attempted to provide state-of-the-art reviews on modeling and analysis of rain attenuation in the context of extremely high frequencies. However, the existing review works conducted over three decades (1990 to 2022), have not adequately provided comprehensive taxonomies for each method of rain attenuation modeling to expose the trends and possible future research directions. Also, taxonomies of the methods of model validation and regional developmental efforts on rain attenuation modeling have not been explicitly highlighted in the literature. To address these gaps, this paper conducted an extensive literature survey on rain attenuation modeling, methods of analyses, and model validation techniques, leveraging the ITU-R regional categorizations. Specifically, taxonomies in different rain attenuation modeling and analysis areas are extensively discussed. Key findings from the detailed survey have shown that many open research questions, challenges, and applications could open up new research frontiers, leading to novel findings in rain attenuation. Finally, this study is expected to be reference material for the design and analysis of rain attenuation.

1. Introduction

The increasing demand for high data rate and capacity, and the inability of previous generations to meet these demands, have motivated the research and development of the 5G communication network [1,2]. The 5G wireless network has promised to provide a multi-Gigabit-per-second (Gbps) data rate with extremely low latency and better quality of service (QoS) that would support critical services. These services comprise, but are not limited to, the provision of e-health, especially in rural areas [3,4,5], equitable and inclusive education [6,7,8], smart farming [9,10], and bridging of the digital divide [11,12,13].

Millimeter wave (mmWave) communication within the frequency range 30–300 GHz has been proven to be the candidate band for 5G communication networks and beyond due to the scarcity of spectrum frequency below 5 GHz (sub-6 GHz) [14,15,16,17,18]. The mmWave band offers the security of communication transmissions and supports the large bandwidth required to provide higher data rates for fronthaul, backhaul and short building-to-building links [2,19,20,21,22]. However, the major drawback of the millimeter wave signal is its inability to travel over a long distance due to its susceptibility to attenuation by various atmospheric phenomena such as rain, foliage, and other atmospheric absorption [23,24,25,26,27,28,29,30].

Rain, among all other atmospheric phenomena, is the major source of microwave and millimeter wave signal attenuation through absorption and scattering in terrestrial and satellite communication links. When the operating frequency exceeds 10 GHz, the attenuation effect becomes very severe, particularly in the tropics, with tendencies of heavy and thunderous rain droplets and depths [31,32,33,34]. Rainfall is a complex meteorological phenomenon due to its inhomogeneous behavior in terms of duration, frequency of occurrence, and location. The inhomogeneous nature makes it highly unpredictable and challenging when estimating its effect on link design. However, if the rainfall rate variation throughout the entire signal path is known, the rain attenuation can be estimated from the integration of the specific attenuation and path length [35,36]. Conventionally, rain rates are measured using rain gauges, disdrometers, and weather radars. The data obtained from such measuring instruments are usually used to develop models that help in predicting and, in some cases, mitigating the effect of rain attenuation on the links.

Several researchers over the years have developed novel models and methods, in some instances modifying existing ones for estimating rain rates across various frequencies and climatic locations [37,38,39,40,41,42,43]; notably, the ITU-R has also developed a couple of models [44,45]. It is worthy to note that some of the climatic variables such as wind speed, rainfall intensity, frequency, polarization, path length, temperature, humidity, etc., have impending effects on rain attenuation. These thus expose the limit of validity of most of the aforementioned models as these models attempt to evaluate the relationship between rain rate and path length to obtain rain attenuation [46].

This paper aims to conduct a systematic review of rain attenuation models. The different prediction and mitigation models are broached, including the taxonomies in different areas of rain attenuation modeling and analysis, noting research gaps and recommending further directions of research. The noteworthy contributions of this review paper are outlined as follows:

▪

An extensive, systematic review of rain attenuation models for the past 30 years (1990–2022) is provided.

▪

A panoramic view of rain attenuation models and an exhaustive review of studies that have utilized these models is presented, including a taxonomy that followed the work of [47].

▪

A comprehensive analysis of the total and specific attenuation based on various atmospheric conditions and other impairments, including the radome, is discussed.

▪

An exhaustive review of rain attenuation prediction using machine learning models is presented, including a proposed taxonomy of these models.

▪

An in-depth analysis and review of fade mitigation techniques is presented.

▪

Critical open research issues and future research directions are identified for rain attenuation and elaborated.

The structure of the paper is as follows: The “Review of Previous Rain Attenuation Models” Section 2 reviews prior review works on rain attenuation models. The “Background on Rain Attenuation” Section 3 summarizes the theory of rain attenuation, rain attenuation factors, and the various ways to obtain rain rate data, as well as the survey of rain attenuation across regions. The “Rain Attenuation Models” Section 4 discusses and reviews the various existing rain attenuation models. Furthermore, signal attenuation due to various atmospheric impairments and total propagation attenuation is examined in the “Total Attenuation” Section 5. Similarly, the specific attenuation scenarios are presented in the “Specific Attenuation” Section 6. The “Review of Different Methods of Model Validation” Section 7 summarizes the various model validation techniques, including the properties of the existing rain attenuation models. The various machine learning-based models are presented and reviewed in the “Machine Learning-Based Rain Attenuation Prediction Models” Section 8. The various fade mitigation techniques, including the weaknesses of the ITU-R model for short distances, are discussed and reviewed in the “Fade Mitigation Techniques For 5G” Section 9. The “Further Research Direction” Section 10 provides a clear path for further research in rain attenuation. Finally, a concise conclusion is drawn in the “Conclusion” Section 11.

2. Review of Previous Rain Attenuation Models

This section presents a systematic review of previous works on rain attenuation, covering the last three decades, 1990 to 2022, with a binocular focus on review articles only. The academic databases employed for this review include IEEE Explore, MDPI, ACM Digital Library, Springer, Science Direct, and Google Scholar. These databases are comprised of reliable and good quality peer-reviewed publications such as review articles, research articles, and conference papers. The search term “rain attenuation review” was used to query these databases to obtain relevant literature review articles published between 1990 and 2022, from which 16,668 review publications were obtained across all the selected databases, all written in the English language which had been chosen as one of the inclusion criteria. To avoid duplicates, papers found on a generic database such as Google Scholar were traced back to their respective publishing journal and counted under that journal, rather than being counted under Google Scholar. Figure 1 shows the article selection process used to screen the pool of articles to further reduce the search results. Table 1 summarizes the number of articles obtained from the different databases consulted, including the percentage in descending order in terms of relevance to the subject of interest. Table 2 presents an overview of previous rain attenuation model reviews which includes their objectives and findings. Table 3 provides a summary of the comparison between the current survey and the existing ones.

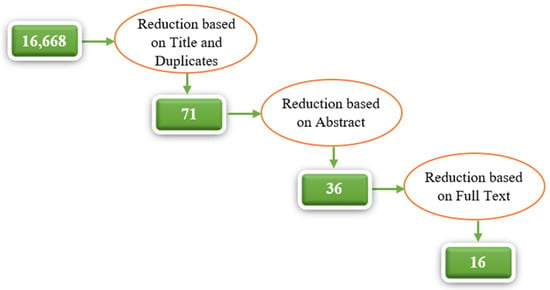
Figure 1. Articles Selection Process.

Table 1. Search Databases and Number of Articles.

S/N	Article Sources	URL	No. of Articles	Percentage (%)
1	Google Scholar	https://scholar.google.com/	6	37.50
2	IEEE Explore	https://ieeexplore.ieee.org/	5	31.25
3	MDPI	https://www.mdpi.com/	4	25.00
4	Springer	https://www.springer.com/gp	1	6.25
5	ACM Digital Library	https://dl.acm.org/	0	0.00
		Total =	16	100

Table 2. Summary of Previous Rain Attenuation Review Publications.

Ref.	Title of Publication	Objectives	Findings	Year
[48]	Development of rain-attenuation and rain-rate maps for satellite system design in the Ku and Ka bands in Colombia	To present the review of some of the most important rain-rate and rain-attenuation measurement campaigns.	The average deviation between models and measurements is approximately 30%, and no model is suitable for all climate zones of the world.	2004
[49]	Review of Rain Attenuation Studies in Tropical and Equatorial Regions in Brazil	To provide a review of rain attenuation research works based on measurements performed in tropical and equatorial regions of Brazil.	Based on the reviews, it was found that the available models are only suitable for temperate climates and not suitable for tropical and equatorial climates.	2005
[50]	Effect of Rain on Millimeter-Wave Propagation—A Review	To review the impact of rain on millimeter wave propagation.	The study briefly reviewed the Mie theory, various drop size distributions based on the point rain rate, cross-polarization, statistical models, rain attenuation models, and frequency and path length scaling for rain attenuation statistics.	2007
[51]	Variability of millimeter wave rain attenuation and rain rate prediction: A survey	To review the literature on rain attenuation and rain rate prediction methods proposed by researchers around the globe to evaluate the performance under varying meteorological and topographical conditions with a focus on the reports made in the Indian subcontinent.	Among the contending models, Garcia-Lopez’s model is suitable for predicting rain attenuation in the northern region of India due to its simplicity and less complexity.	2007
[52]	Analysis and parameterization of methodologies for the conversion of rain-rate cumulative distributions from various integration times to one minute	Review the main models used for converting rain statistics from various integration times to one minute.	Only conversion models with a maximum of two parameters are suitable for worldwide application, of which the Lavergnat-Gole model is recommended as the best for any integration times and climate regions.	2009
[53]	A Review on Rain Attenuation of Radio Waves	To understand rain attenuation occurrences, how they can be measured, and review all measurement methods developed so far.	Rain attenuation is mostly calculated using empirical formulations relating the rain rate with specific attenuation. This method is significant only when the frequency exceeds 5–10 GHz, and also, rain drop-based modeling is most accurate in terms of exactness.	2012
[54]	Review of Rain Attenuation Studies in Tropical and Equatorial Regions in Malaysia: An Overview	To review all previous research work related to rain-induced attenuation for microwave propagation in Malaysia’s tropical climate.	Rain rate value and the regression factor for the raindrop size distribution vary in Malaysia based on the region for measuring the rain attenuation.	2013
[55]	Precipitation and other propagation impairments effects microwave and millimeter wave bands: a mini survey	To review and discuss rain attenuation models developed worldwide using various measurement campaigns for microwave and millimeter wave frequencies.	The ITU-R model, when compared to other prediction models, either under- or over-estimates, especially for tropical region measurement sites.	2019
[32]	Atmospheric Impairments and Mitigation Techniques for High-Frequency Earth-Space Communication System in Heavy Rain Region: A Brief Review	To briefly review previous works on the atmospheric effects, particularly rain and clouds, on high-frequency satellite communication.	The study presented research works to distinguish scintillation from rain attenuation. Then discussed and reviewed different rain attenuation models and their characteristics in heavy rain regions. Also presented were cloud and water vapor attenuation models and then discussed the different propagation impairment mitigation techniques.	2019
[56]	Earth-to-Earth Microwave Rain Attenuation Measurements: A Survey on the Recent Literature	Research challenges and future trends are to conduct a systematic review of rainfall measurement using earth-to-earth microwave signal attenuation from backhaul cellular microwave links and experimental setup.	Microwave path attenuation is a promising and reliable method for estimating the rain rate. Also, factors such as the wet antenna effects and jitters caused by wind on antennas may lead to significant errors too.	2020
[57]	Experimental Studies of Slant-Path Rain Attenuation Over Tropical and Equatorial Regions: A Brief Review	Review and summarize the performance of various rain attenuation models validated against satellite signal measurement in tropical and equatorial regions.	Among the 33 models reviewed, none was suitable for all locations and percentage-exceedance levels. Still, the ITU-R and DAH models are suitable for low rain rates compared to other models.	2021
[58]	An overview of rain attenuation research in Bangladesh	To review rain attenuation research works, global research trends, and research scope in Bangladesh.	Rain attenuation models that can be used for tropical and subtropical regions cannot be directly used over Bangladesh without appropriate testing and verification.	2021
[59]	Scaling of Rain Attenuation Models: A Survey	To develop a rain attenuation scaling technique taxonomy and review research work according to the taxonomy and perform a comparative study on these techniques.	The study reviewed more than 17 rain attenuation scaling models. SAM model can estimate the spatial distribution when the rain rate and radio link are distributed uniformly. However, a more sophisticated spatial rainfall distribution is required.
[47]	A Survey of Rain Attenuation Prediction Models for Terrestrial Links—Current Research Challenges and State-of-the-Art	To conduct a comprehensive review of the different rain attenuation prediction models for terrestrial links	This study reviewed 18 rain attenuation models based on the survey. It found that no rain prediction model can solely satisfy all the geographic locations and climatic variations over time.
[60]	A Survey of Rain Fade Models for Earth–Space Telecommunication Links—Taxonomy, Methods, and Comparative Study	To review different slant path rain attenuation prediction models based on different aspects such as rain regions, rain structure, rainfall rate, elevation angle.	This study reviewed more than 23 rain attenuation models for satellite links, and it found that models work well for locations where they are developed and might not function well for other locations.
[61]	Rain Attenuation Prediction Models in Microwave and Millimeter Bands for Satellite Communication System: A Review	To review the rain rate integration time, rain height, and rain attenuation models for microwave and millimeter bands satellite systems.	The study reviewed three classes of rain rate integration time conversion methods and then reviewed six rain attenuation prediction models for satellite-to-earth communication.

Table 3. Summary of Comparison between the Current and Existing Surveys.

Ref.	Empirical Models	Statistical Models	Optimization-Based Models	Physical Models	Fade Slope Models	Mitigation Models	Machine-Learning Models
[48]	✓	✓	×	✓	×	×	×
[49]	✓	✓	×	×	×	×	×
[50]	✓	✓	×	✓	×	×	×
[51]	✓	✓	×	×	×	×	×
[52]	✓	✓	×	✓	×	×	×
[53]	×	✓	×	×	×	×	×
[54]	✓	✓	×	×	×	×	×
[55]	✓	✓	×	✓	×	×	×
[32]	×	✓	×	×	×	✓	×
[56]	×	✓	×	×	×	×	×
[57]	✓	✓	×	✓	×	×	×
[58]	×	×	×	×	×	×	×
[59]	×	✓	×	×	×	×	×
[47]	✓	✓	✓	✓	✓	×	×
[60]	✓	✓	×	✓	✓	×	✓
[61]	✓	✓	×	✓	×	×	×
Current Survey	✓	✓	✓	✓	✓	✓	✓

From Table 3, it can be seen that most review works focused more on empirical and statistical models without considering mitigation models as well as machine learning-based models for rain attenuation. Also, most of the review work that included the rain attenuation prediction models did not consider the rain fade mitigation techniques and vice versa. From the overall systematic review, it can be seen that there is very little review work done on rain attenuation that shows the trend of work done in the research area and proffers further direction. Hence, this paper aims to extensively review and analyze the different existing prediction and mitigation models for rain attenuation, including machine learning-based models, as well as provide further directions to bridge these existing gaps

3. Background on Rain Attenuation

This section provides a preliminary discussion on rain attenuation, which includes the theory behind rain attenuation, rain attenuation factors, rain data gathering methods, and spatial interpolation methods for estimating rain rate.

3.1. Theory of Rain Attenuation

In general, electromagnetic waves transport photons, which carry energy $E=h\nu$ where h is Planck’s constant and $\nu$ is the frequency of the emitted electromagnetic wave. Absorption and dispersion occur as the wave travels through matter. Absorption is the capacity of an atom and molecule to retain the energy conveyed by the photons. In the case of dispersion, the retained energy of the photons is re-emitted out, taking various paths with varying concentrations. The spatially dispersed waves are responsible for scattering [56]. These activities caused electromagnetic signals to be attenuated by rain. In this regard, the energy of the molecules can be expressed as Equation (1):

$$E_M=E_E(\wedge )+E_v\left(v\right)+E_R\left(j\right)+E_T$$

(1)

where $E_M$ is the energy of the molecule, $E_E(\wedge )$ is the electron energy of the molecule, $E_v\left(v\right)$ is the vibrational energy of the atom around the equilibrium position of the molecule, $E_R\left(j\right)$ is the rotational energy corresponding to the rotation of the molecule about its symmetry axis, and $E_T$ is the translational motion energy of the molecule. The difference in energy between a molecule’s initial and excited states is said to be equal to the absorbed energy of the photon when the molecule changes its quantum level. Figure 2 illustrates that raindrops can cause electromagnetic signals to be absorbed, scattered, diffracted, and depolarized.

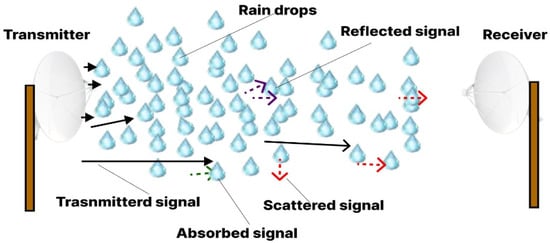
Figure 2. Impact of Rain on Electromagnetic Wave Propagation [62].

As the frequency increases, the wavelength becomes smaller. When the wavelength of the rain is a few mm less than the frequency, the attenuation increases. The Average Raindrop Size (ARS) has a diameter of 1.67 mm while 10–100 GHz signals have wavelengths of 30–3 mm. A raindrop has an average diameter of 0.1–5 mm. In the case of Rayleigh scattering by raindrops, known as the scattering function as given in Equation (2), the droplet size is substantially less than the wavelength, which is satisfied for frequencies up to 3 GHz. The function specifically applies to the raindrop scattering properties and is affected by the radius of the raindrop, the shape of the raindrop, the complex permittivity, and the frequency of the transmitted signal.

$$f=\frac{{\xi }_d-1}{{\xi }_d+2}\times \frac{{\pi }^2}{{\mathsf{\lambda }}^2} D^3$$

(2)

where ${\xi }_d$ is the complex permittivity of the droplet, $D$ is the raindrop size, and $\lambda$ is the wavelength. Mie’s approximation for the scattering function is given as Equation (3):

$$f=\frac{j{\lambda }^3}{{\pi }^3{D}^2}{\left[{{\displaystyle \sum }}_{n=1}^{\infty }\left(2n+1\right)\left(M_c\right)\right]}^{*}$$

(3)

where $j$ is the imaginary unit and $M_c=x_n+y_n$ is the Mie’s coefficients which are constituted of Bessel functions of order $n$. The vertical and horizontal polarization for the specific rain attenuation can be expressed as Equation (4):

$${\gamma }_{h,v}=8.686·{10}^3·\frac{2\pi }{k}·lm{\displaystyle \int }{f}_{h,v}\left(D\right)·N\left(D,R_r\right)dD$$

(4)

where $k$ is the propagation constant, $D$ is the raindrop size, and $N\left(D, R\right)$ is the raindrop size distribution which can be calculated using Equation (5) as:

$$N\left(D,R_r\right)=8000·e^{-4.1·D/R_r^{0.21}}$$

(5)

where $R_r$ denotes the rain rate in mm/h.

3.2. Rain Attenuation Factors

3.2.1. Path Length

The path length is critical in determining Rain Attenuation $A$ which can be estimated by multiplying the effective propagation path length ($L_p$) and specific rain attenuation $(\gamma$) as shown in Equation (6) [2]. Figure 3 depicts a conventional experimental setup to measure rain attenuation, which consists of transmitter and receiver stations separated by a distance or path length $L_p$

$$A=\gamma L_p$$

(6)

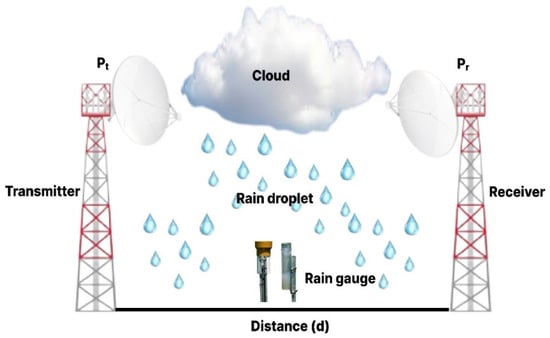
Figure 3. A Conventional Experimental Setup to Estimate Rain Attenuation [56].

Specific attenuation is calculated using a 1-min cumulative distribution rain rate expressed in decibels per kilometer (dB/km). The path length, typically determined at one end, can be estimated by multiplying the path adjustment factor by the real distance. However, it can be determined from Equation (6) with respect to the point rain rate [62]. According to [47], many models compute the effective propagation path length by employing a compensatory factor known as the path reduction factor or path adjustment factor.

3.2.2. Frequency and Polarization

The specific attenuation, $\mathbf{\gamma }$ (dB/km), expressed in terms of the rain rate, frequency, and polarization, can be easily estimated using the power-law relationship as shown in Equation (7):

$$\mathbf{\gamma }=\mathit{a}{\mathit{R}}_{\mathit{p}}^{\mathit{b}}$$

(7)

where ${\mathit{R}}_{\mathit{p}}$ denotes rainfall rate exceeded at p% of the time, $\mathit{a}$ and $\mathit{b}$ are the functions of frequency that depends on the polarization, which can be empirical values and can be obtained experimentally [21,63]. The ITU-R P.838-3 [44] includes a look-up table for values of $\mathit{a}$ and $\mathit{b}$ for frequencies ranging from 1 to 100 GHz in vertical and horizontal polarization.

3.3. Different Sources and Procedures of Rain Rate Data Collection

Due to the dependence of rain attenuation on rain data, available procedures for rain data collection are defined in this section. These methods range from available databases, experimental, synthetic, and data-logged methods, to prediction techniques based on interpolation methods.

3.3.1. Rain Data from Databases

The ITU-R Study Group 3 databanks (DBSG3) [64] rain database is one of the most extensively utilized databases as it contains an extensive set of measurement data of attenuation due to various weather conditions. Furthermore, several weather databases from European institutions, such as the European Center for Medium-Range Weather Forecasts, are available and are alternative sources of rain rate data. Unfortunately, the centers do not give information or have rain attenuation equipment for tropical locations. It has therefore been established that those tropical countries need models that could assist in developing their databases for rain data which could be used to prepare the corresponding rain attenuation databases. Other databanks hold weather data that are local to their location; for example, in Nigeria there is the Nigerian Meteorological Agency (NiMet) that can provide recent weather data that can be used by researchers to easily develop and evaluate models as well as estimate the effect of these weather conditions on communication.

3.3.2. Synthetic and Data-Logged Method of Rain Rate Estimation

A mathematical method that can be used to generate rain attenuation time series accurately, known as the Synthetic Storm Technique (SST), converts a rain rate time series at a specific location into a rain attenuation time series [65]. This technique is used in place of the logged data technique to save time and cost.

3.3.3. Experimental Setup

The best way to obtain the rain rate is by measurement through weather instruments and facilities, for instance, a disdrometer or a rain gauge, at a reduced integrating time. A disdrometer is a device that detects raindrop size distributions (DSD). In some instances, the terminal velocity of falling hydrometeors can also be used to distinguish between various kinds of precipitation such as raindrops, snowflakes, graupel, or hail over time [66,67]. Figure 4 depicts a typical setup for rain rate measurement using a disdrometer.

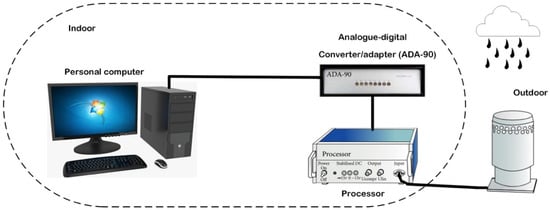
Figure 4. Measurement System for a Disdrometer [68].

Many studies have employed various kinds of disdrometers, such as the JW RD80 disdrometer [69], or optical disdrometers which use image or laser technology [70,71], to obtain rainfall data used in predicting the rain attenuation within a particular region. However, they are subject to wind and evaporation errors.

The amount of rainfall within a particular location over a period of time can be measured accurately using a meteorological instrument known as a rain gauge. Rain gauges are frequently utilized because of their ease of use and dependability, thus lowering installation and maintenance costs. They also provide reliable in-place observations [66]. However, due to their sparse distribution, rain gauges are inadequate for estimating area rainfall, especially in areas with many spatial variabilities, like mountain ranges. The tipping bucket rain gauge is a popular rain gauge in which each tip correlates to a specific amount of rainfall [72]. Figure 5 shows a tipping bucket rain gauge.

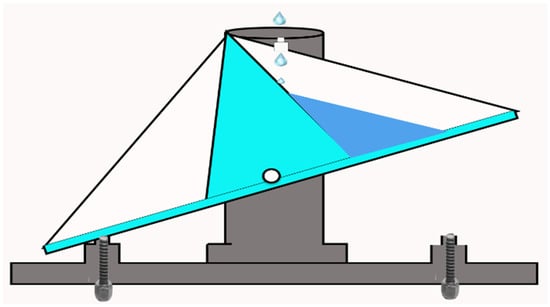
Figure 5. Tipping Bucket Rain Gauge [73].

Atmospheric parameters—air pressure, humidity, temperature, wind direction, and speed, as well as precipitation—can be measured using instruments and equipment housed in a facility known as a weather station. Information obtained can be employed to study and forecast weather and climate. A weather radar is a remote sensing device used by hydrological and meteorological communities to estimate area precipitation with high spatial and temporal precision [74]. To measure the rain rate in some instances, the rain cell’s radar information can be used by sending out an electromagnetic signal that interacts with the raindrops at the atmospheric level, which would reflect the intercepted power towards the radar—backscattering. According to [75], using radar to compute the rain rate primarily involves three steps: (1) Calibrating the radar, which influences the accuracy of the rain rates as a miscalibration can lead to bias in the rain rate results. (2) Quality control, which is the scrutinization of the radar data to reduce the effects of non-meteorological scatters both on the ground and in the atmosphere such as aircraft, etc. (3) Rain rate estimation using the calibrated reflectivity values, which describes the size, shape, state, and concentration of the hydrometeor as well as the azimuth, distance, polarization, intensity, phase, etc., which can be used to then compute the rain rate. Most research did not utilize a weather radar, but rather used either a disdrometer or a rain gauge and, in most cases, used the combination of both to get rainfall data.

3.3.4. Spatial Interpolation Method for Rain Rate Prediction

The use of spatial distribution methods for rain rate prediction is critical due to the impossibility of measuring rain rates everywhere in a given location. When experimental methods cannot accurately calculate rain rates, the spatial distribution method is employed to ensure accuracy. Some mathematical models have been developed to improve the accuracy of this method. One such model is called the Inverse Distance Weighting (IDW) method, and the expression for the determination of the rain rate at a location up to 30 km is as shown in Equation (8):

$$R_r={{\displaystyle \sum }}_{i=1}^N{w}_i{R}_i$$

(8)

where $R_r$is the rain rate, $N$ is the number of rain gauges, $R_i$ is the weighted sum of the rain gauges’ readings, and $w_i$ is the weight of each rain gauge reading. The MultiEXCELL method can be used in a situation where local rain data are available. Several kinds of literature have used this method to obtain rain rates. The calculation and estimation of rain attenuation based on the three factors have been discussed in this section. The four different data collection methods were also presented and discussed, as well as the spatial interpolation methods of rain rate prediction used to ensure accuracy, based on mathematical models, in locations where an experimental setup cannot accurately measure the rain rate.

3.4. Survey across Regions

Rain as a natural event is defined using different rate intensity thresholds. The most generally used term in the literature is based on the interval when the rain rate exceeds 0.2 mm/h. Based on an approach that seeks to exploit the inhomogeneous nature of tropical rain distribution, called Site Diversity, a rainfall event can either be convective (CV), stratiform (ST), or storm-wind [76].

A CV rain event is an intense rainstorm within a small geographical area for a short duration. ST, on the other hand, is a mild shower that lasts longer and is more widespread. Storm-wind rain is a rainstorm characterized by intense clouds and severe aftereffects in some local locations for brief periods [77,78]. Hence, since all the rain types are defined within the distance domain called rain cells, any two links located at different places (or cells) will experience different levels of attenuation while receiving signals from the same source [79]. CV and ST are more prevalent in the tropics and in temperate regions, respectively [80].

Rainfall is a crucial climatic component in a tropical environment like Nigeria where it can severely influence both earth-space and satellite communication links operating at frequencies exceeding 10 GHz, thus making it a critical design factor for wireless communication systems. This impairment is termed rain attenuation and is found to vary directly with both the raindrop size and the rain rate [81]. The two existing approaches for estimating rain attenuation both use measured rainfall rate statistics, namely, (1) empirical methods where attenuation due to rain is estimated using real measured rain data from databases across various tropical areas, and (2) physical methods which deal with the physical characteristics involved in the estimation of attenuation process [54,82]. However, the resource implications for an empirical approach to be adopted, particularly in the tropics, have rendered it less realistic, significantly impacting the availability of the much-needed rain measurement data to build appropriate physical models for the design of abundant wireless channels [83].

Over the years, the ITU-R sector has been able to develop, through research efforts, a unified global model that can be used to estimate the attenuation due to rain for both LOS and NLOS environments corresponding to the major global divide that has divided the world into temperate and tropical regions. The new ITU-R 530-16 results from ongoing work and developments to solve performance problems associated with prior models. However, measured rain data from the equatorial and tropical areas have not been employed to validate this model [84]. Table 4 shows the summary of different work carried out across regions based on the ITU, including the model proposed, findings, and site locations.

Table 4. Summary of Rain Attenuation across Regions.

ITU Region	Country	Ref.	Model	Remarks	Location
Asia Region 3	India	[85]	Millimeter-Wave Propagation model (MPM), ITU-R frequency scaling model	Data on radiometric measurements were presented in this study for atmospheric attenuation at a tropical location, demonstrating that water vapor, as well as rain rate, is an important cause of attenuation at Ka-band frequencies.	Kolkata/Tropical location
		[86]	Salonen model	The obtained cumulative distribution of liquid water content deviates from ITU-R. The ITU-R model eventually overestimates cloud attenuation at a frequency below 50 GHz and underestimates at a frequency above 70 GHz.	Kolkata/Tropical location, India
		[87]	Raindrop size distribution in five different locations in India was assumed to be lognormal distribution.	The dependency of the DSD on climatic conditions leads to attenuation disparity and indifferent location between ITR-R and DSD models.	Shillong (SHL), Ahmedabad (AHM), Trivandrum (TVM) for three years each, Kharagpur (KGP), and Hassan (HAS) for 2 years each
	Malaysia	[88]	The ITU-R model was evaluated against the frequency diversity model. Also, a higher fade margin is used from 12 dB to 16 dB.	The developed model can minimize signal attenuation in heavy rainfall areas. Furthermore, the model is suitable for higher fade margins.	Southeast Asia
		[62]	The Abdul Rahman model, ITU-R model, modified Silva Mello model, modified Moupfouma model, and Lin model were compared for a horizontal variation of rainfall.	The results showed that all models estimated attenuation at 1 and 11 dB for both 6 and 28 GHz.	Johor Bahru, Malaysia
		[89]	The method for converting rainfall data is suitable for satellite applications. The study utilized three prediction models.	The predicted results were good compared to direct observations and other tropical conditions.	4-year data were collected at UTM, Skudai Campus, Malaysia
Asia Region 3		[90]	77 locations are used to determine the best fade margin for 5 GHz. ITU-R P.837-7, ITU-R P.530-17, and synthetic techniques were employed to get 1-min data and long-term rain attenuation.	The fade margin for 26 GHz is obtained to be 6.50 to 10 dB for 99.99 link network availability. However, at 28 GHz, the fade margin was determined to be 7 to 11 dB.	Peninsular Malaysia
		[91]	At 26 GHz, and distances of 0.3 and 1.3 km, the path reduction factor was compared using the ITU-R P-530-17, Abdulrahman, Lin, and da Silva Mello models.	The results obtained have shown that all the models accurately predicted the attenuation due to rain at 1.3 km.	Johor Bahru city in Malaysia
	China	[92]	Numerical Method	In the Ka-band, rain attenuation and rain attenuation ratios outperform the ITU-R model in China.	58 locations in China
		[93]	The cumulative lognormal and Gamma distributions of rain rates were compared to half-empirical conversion coefficients for China.	The study derives 1-min cumulative distributions from piecewise regression to a Gamma distribution through half-empirical conversion coefficients. It further compares the two distributions and concludes that Gamma outperformed the datasets.	Hourly rain rates from 333 rain gauge stations in China were taken in 1991 to study the point rain rate cumulative distributions
	Korea	[94]	The study evaluated the performance of each of the following models: Abdulrahman, ITU-R P.530-16, Mello, Moupfouma models, Lin and differential equation.	The research proposed new prediction models based on the correlation between the theoretical and effective specific attenuation validated by employing two links at 38 and 75 GHz. The study also presented a 1-min rainfall rate derivation from higher integration time.	South Korea
Africa Region 1	Tanzania	[95]	40-year data for 22 locations spread across the entire country were used in the study. Hybridization of Chebil and refined Moupfouma-Martin methods using data collected for 40 years across 22 locations.	The contour map of the rain rate and attenuation for Ka and Ku bands was developed using the Kriging interpolation technique at 0.1 and 0.01%. The maps indicated a higher rain rate in certain zones than the ITU estimates.	Tanzania’s locations include the Central Area, Lake Victoria basin, Northern Coast including the Unguja and Pemba Islands, Northern Highland, Southern Coast, South Highland, South-western, and Western Area
	Rwanda	[96]	A backpropagation neural network (BPNN) was used for dynamic rain fading. Markov model was used to determine storms’ frequency of occurrence, and rain spikes for different rainstorms were analyzed using queueing theory.	The results have shown that the maximum rain rate in Rwanda ranges from 150 mm/hr and above with an 11.42% probability of occurrence. In addition, rain size diameter is critical in rain mitigation strategy development.	Butare (2.6078° S, 29.7368° E)
Africa Region 1	Kenya	[97]	The specific attenuation for both polarizations and the frequency ranging from 1 to 100 GHz was predicted using two years of experimental data. The ITU-R is a standard for rain attenuation.	According to the report, the western part of Kenya is more vulnerable to rain-induced network failures than the rest of the country. It also demonstrates that the horizontally polarized radio wave is weaker than its vertical counterpart.	Muranga, Kamusinga, Mukumu, Kebabii, and Habasweni, Kenya
	South Africa	[98]	ITU-R	Findings from this research can be applied to network planning in South Africa for wireless networks such as microwave and millimeter broadband. The study demonstrates that rainfall attenuates terrestrial and satellite LOS connectivity in the SHF and EHF bands.	Data were collected at one-minute intervals over 2 years at 139.7 m above sea level by the Department of Electrical and Electronics and Computer Engineering of the University of KwaZulu-Natal
		[99]	ITU-R, Kriging Interpolation method. One-minute rain rate and rain attenuation contour maps models were developed for the selected locations.	The study provides useful results for terrestrial and satellite system designers to determine the appropriate EIRP and receiver point characteristics over the desired coverage area.	Eastern Cape, Free State, Gauteng, Kwazulu-Natal, Limpopo, Mpumalanga, Northwest, Northern Cape, Western Cape
		[69]	A rain rate model has been developed suitable for 10 locations in South Africa, compared to the model proposed by ITU using a power-law regression model.	The research was carried out at three different frequencies: 12, 30, and 60 GHz for 30-sec, 1-min, and 5-min rain rates. The developed model provided detailed information on the specific attenuation for both micro- and millimeter-wave frequencies in South Africa.	The study locations are Upington, Polokwane, Mossel Bay, Mafikeng, Irin, East London, Durban, Cape Town, Bloemfontein, and Bethlehem
	Botswana	[100]	The Mie scattering approach was utilized to predict specific rain attenuation, and many distributions, such as log-normal, were employed to forecast attenuation.	The results reveal that the extinction coefficients are more temperature dependent at lower frequencies for the lognormal distribution. Furthermore, at lower microwave frequencies, the absorption coefficient is high but declines exponentially with rain temperature.	4 diverse locations in Botswana
	Nigeria	[33]	A 12-year experimental rainfall dataset was employed to develop a realistic predictive model for rain rate intensity levels was performed.	Results showed that horizontal polarization has a 12% higher rain attenuation than vertical polarization.	Lokaja, Kogi State, Nigeria
		[34]	Empirical attenuation model based on prognosis for earth-space communication frequency in a tropical savanna climate region.	The results indicated a consistent increase in the attenuation as the signal frequency increased where free space is more prevalent. The results also demonstrated that the effect of clouds and gases on signals is less when compared to rain.	Lokaja, Kogi State, Nigeria
Africa Region 1	Ghana	[101]	The Moupfouma and ITU-R models for Kumasi were evaluated against the local 1-min measured. The inverse-distance weighting method and Arc GIS software were used to develop geographical maps.	The results from this study were employed to choose a best-suited estimation model for the 22 weather stations in Ghana. After that, the ITU-R model estimated the attenuation due to rain.	Kumasi, Ghana
North America Region 2	USA	[102]	Two ITU-R—P.530 and P.838—standards were used to calculate the losses in 5 GHz with 99.9% link availability at 24 GHz, 28 GHz, and 38 GHz.	Attenuation is proportional to the rainfall rate, frequency, and polarization.	Palo Alto, California
Europe Region 2	Greece	[103]	Power-law rain estimation model, global rain attenuation prediction models	The research proposed a rain estimation model for the S-band based on observations in a specialized and precise experimental setup, revealing that rain attenuation is non-negligible at frequencies above 6 GHz.	Ioannina, northwestern Greece
		[104]	ITU-R P.618-9, ITU-R P.838-3, and ITU-R P.838-3, respectively, for Attenuation, Specific Attenuation, and Rain Height.	Six-year point rain data collected by the National Hellenic Meteorological Service (NHMS) was employed to derive statistics for 0.001%-time of the average year, which were then used to create precise maps of rain rate and attenuation to aid in the design of Greece’s satellite communications systems.	12 locations were used in the study: Agrinio, Alexandroupoli, Hellinikon, Heraklion, Ioannina, Lamia, Larisa, Limnos, Milos, Pyrgos, Serres, and Chios
	UK	[105]	Tropical rain measuring mission satellite to determine the rain rate distribution in the tropics.	The results have shown how the rain rate over 5 km was converted into 1 km square with the help of a correction factor. Finally, the results were compared with ITU-R DBSG3 and Ref. ITU-R P. 837-7.	42 sites were used in the studies

4. Rain Attenuation Models

In this section, the different existing rain attenuation models classified under five categories are presented and discussed as well as a brief review of previous research on rain attenuation in 5G using these models.

4.1. Empirical Models

This section discusses some of the empirical models and reviews relevant work on rain attenuation for 5G using these models. An empirical model is based on experimental data observations that can be described mathematically. Eight empirical models are used for the rain attenuation model, and a review of the rain attenuation modeling using these models is presented in Table 5.

4.1.1. Garcia Model

This model [106] is one of the modified versions of the Lin model that is best suited for temperate European locations and can be represented mathematically expressed as shown in Equation (9):

$$A=a{R}_r^b{L}_p\frac{1}{0.5+\left[\frac{L\left(3R_r-3.9L_p+255\right)}{2636}\right]}, \mathrm{for} R_r > 10 \mathrm{mm}/\mathrm{h}, L_p > 5 \mathrm{km}$$

(9)

where $A$ denotes rain attenuation (dB), $R_r$ denotes rain rate (mm/h) averaged on a given time interval of 1 min, $L_p$ is the path length in km, and $a$ and $b$ are functions of frequency.

4.1.2. Crane Model

This model [37] predicts high attenuation in low rainfall locations and offers global rain distribution. It can be expressed mathematically as shown in Equation (10):

$$A=a{R}_p^b\left[\frac{e^{u\alpha d}-1}{u\alpha }-\frac{b^{\alpha }{e}^{c\alpha d}}{c\alpha }+\frac{b^{\alpha }{e}^{c\alpha D}}{c\alpha }\right],\hspace{1em}d\le D\le 22.5\mathrm{km}$$

(10)

where $A$ denotes rain attenuation (dB), $R_p$ denotes rain rate (mm/h) exceeded at %p of the time, and $a$ and $b$ are functions of frequency. Other remaining coefficients are empirical constants of the model, expressed in Equations (11)–(14):

$$u=\frac{\ln \left[b{e}^{cd}\right]}{d},$$

(11)

$$b=2.3R_p^{-0.17},$$

(12)

$$c=0.026-0.03\ln R_p$$

(13)

$$d=3.8-0.6\ln R_p$$

(14)

4.1.3. Mello Model

This model [40] was developed by utilizing a complete rainfall rate distribution as input to predict the rain attenuation cumulative distribution due to the inaccurate prediction of the ITU-R model, where two regions having different rainfall rate conditions would have similar values of rain attenuation $A_p$, and can be expressed mathematically as shown in Equation (15):

$$A_p=a{\left[1.763R_r{}^{0.753+0.197/L_p}\right]}^b\frac{L_p }{1+L_p /119R_r{}^{-0.244}}$$

(15)

where $A_p$ denotes rain attenuation exceeded at p% of the time, $R_r$ denotes rainfall rate in mm/h, $L_p$ is the path length, while $a$ and $b$ are functions of frequency.

4.1.4. Moupfouma Model

In this model [39], $L_T$ is the distance between ground stations, that is, the actual propagation path length; its equivalent propagation path length $L_{eq}$can be determined using an adjustment factor that ensures the uniformity of the rain on the entire propagation path and can be represented mathematically as shown in Equation (16):

$$A_p=a{R}_p^b\times L_{eq}\left(R_p, L_T\right)$$

(16)

where $A_p$ is the rain attenuation expressed in dB exceeded at p% of the time. The specific attenuation in terms of the rain rate expressed in dB/km is $a{R}_p^b$, $R_p$ is the rain rate exceeded p% of the time, and $L_{eq}$ is the equivalent path length for which the rain propagation is assumed to be uniform.

4.1.5. Peric Model

According to [47], this dynamic model has no real network–environment test and application. Rather, it is based on the cumulative distribution function for a particular area of interest, the number of rain occurrences that exceed the rain intensity threshold, the rain advection vector intensity, and the rain advection vector azimuth.

4.1.6. Abdulrahman Model

Using a variety of non-linear regression approaches, this model [107] investigates the correlation between path adjustment factors and different physical path lengths. The rain attenuation, based on this model, can be expressed mathematically as shown in Equation (17):

$$A_p=\mu \left[S\left(R_p\right)\right]$$

(17)

where:

$$\mu =\left[\frac{R_p}{\alpha +b\left(1-r_p\right)}\right]$$

(18)

$A_p$ is the rain attenuation (dB) exceeded at p% of the time, $R_p$ denotes rain rate (mm/h) exceeded at p% of the time, and $S\left(R_p\right)$ is the slope which can be expressed in Equation (19):

$$S\left(R_p\right)=\beta R_p^{\alpha -1}$$

(19)

where:

$$\beta =k\left[\alpha +b\left(1-r_p\right)\right]L_e$$

(20)

4.1.7. Da Silva Model

This model [108] was primarily developed to estimate the rain attenuation in earth–space and terrestrial links. The model utilized a complete rainfall rate distribution as input and can be applied for terrestrial and slant links. A more general prediction method that includes slant links but is more suitable for terrestrial links can be represented mathematically as shown in Equation (21):

$$A_p=a{\left[\left(R_e\left(R_p,L_p, \theta \right)\right)\right]}^b.\frac{L_p}{1+L_{p}cos\theta /L_o}$$

(21)

where $A_p$ denotes rain attenuation exceeded at p% of time, $R_p$ denotes rain rate (mm/h) exceeded at p% of time, $a$ and $b$ are functions of frequency, $R_e$ denotes the approximate effective rain rate and can each be expressed mathematically as shown in Equation (22):

$$R_e=1.74R_r{}^{0.786+0.197/L_{p}cos\theta }$$

(22)

For slant links, $L_p=(h_r-h_a)/\sin \theta$. However, for terrestrial links, $\theta =0$ and $L_o=d_c$, which denotes cell diameter expressed as shown in Equation (23):

$$d_c=119R_r{}^{-0.33}$$

(23)

4.1.8. Budalal Model

This model [43] is best suited for short-range outdoor links in a 5G network with frequencies above 25 GHz. It can be expressed mathematically as shown in Equations (24) and (25):

$$I_{f\gamma }=\left[\frac{1}{1.77L_p{}^{0.77}{R}_p^{-0.05}}\right], \mathrm{for}f \le 40 \mathrm{GHz}, L_p < 1 \mathrm{km}$$

(24)

$$I_{f\gamma }={\left[\frac{1}{0.477L_p{}^{0.633}{R}_p^{0.073}{f}^{0.123}}\right]}^2, \mathrm{for} f > 40 \mathrm{GHz}, L_p < 1 \mathrm{km}$$

(25)

where $L_p$ is the path length, $R_p$ denotes rain rate (mm/h) exceeded at p% of time, $f$ is the frequency in GHz, and $I_{f\gamma }$ is the proposed Increment Factor.

Table 5 presents the summary of works that have utilized these empirical models including the methodology adopted, method of validation, and findings.

Table 5. Summary of Rain Attenuation Using Empirical Models.

Ref.	Objective of Research	Methodology Adopted	Method of Validation	Result Obtained	Year
[43]	To investigate and modify the ITU-R P.530-17 rain attenuation prediction model for terrestrial line-of-sight at short-distance for 26 and 38 GHz at mm-wave frequencies in Malaysia.	Two links operating at 26 and 38 GHz were used to collect weather data employing a Casella rain gauge for 1 year with a 1-min integration time and path length of 300 m.	The study validated the proposed model by employing two links operating at 25 GHz with a path length of 223 m in Japan and 75 GHz with a path length of 100 m in Korea.	The results reveal that all estimations are close to the suggested prediction model.	2020
[2]	To compare five different prediction models to find the optimal rain attenuation model for 5G in Malaysia.	The research utilized a 1-year precipitation data collected from a tipping bucket rain gauge over a link of 0.2 km path length operating at 6 and 28 GHz.	The rain attenuation was calculated from the product of the specific attenuation and the path length at a rain rate of 0.01% as shown below: $A_p=\gamma L_{eq}$	Results revealed that the modified Mello model estimated a lower value for the attenuation for low and high operating frequencies.	2020
[20]	To investigate the effect of rain on short-range fixed links, that is, building-to-building transmission.	Data utilized for this research were obtained using a PWS100 high-performance disdrometer at 25.84 and 77.52 GHz.	The ITU-R and DSD models were employed to predict the attenuation due to rain expressed mathematically as: $\gamma =a{R}^b$ $\gamma =4.343\times {10}^3{{\displaystyle \int }}_0^{\infty }{\delta }_{ext}\left(D\right)N\left(D\right)dD$	The results showed that the ITU-R model overestimates the attenuation for lower rain rates, whereas for higher rain rates it estimates lower attenuation than the DSD model.	2019
[21]	To investigate the effect of precipitation and wet antennas on millimeter-wave transmission links operating at 28 GHz and 38 GHz Line of Sight (LOS).	The study used a 700 m path length millimeter wave link operating at 28 and 38 GHz in central Beijing. A disdrometer and rain gauge was employed to measure rainfall and the received signal level was gathered every 15 s.	A power law equation was used to calculate the expected signal attenuation (theoretical) and then compared with the measured signal attenuation (practical): $A=a{R}^b$	Results showed that the measured signal attenuation was 1–1.5 dB greater than expected for 28 GHz, 1.6–2.5 dB greater than expected for 38 GHz due to the wet antenna, and a signal loss of 4.2 dB was recorded over the 700 m link.	2019
[62]	To investigate the effect of rain using real-world observations on mm-wave propagation at 26 GHz frequency.	The study used a microwave 5G radio link technology with a 1.3 km path length to collect measurements logged daily. Then, every year, MATLAB was utilized to process and analyze data.	Two ITU-R models—P.530-16 and P.838-3—were employed to measure the effect of rain on the propagation of electromagnetic signals.	Results showed that the specific attenuation at 0.01% was 26.2 dB/km at 120 mm/hr. The rain rate and the estimated rain attenuation across 1.3 km was 34 dB.	2018
[109]	Improve rain attenuation estimates for 5G wireless networks operating in heavy rain zones at 28 GHz and 38 GHz.	The study used 3-year raindrop size distribution data gathered in Kuala Lumpur, Malaysia, utilizing a “Joss-type” RD69 disdrometer, which comprised 100,512 rainy data with a 1-min integration time.	Gamma and normalized models were used to evaluate the performance and can respectively be expressed mathematically as: $N\left(D\right)=N_o{D}^{\mu }{e}^{-\left(\wedge D\right)}$ $N\left(D\right)=N_{w}f\left(\mu \right){(\frac{D}{D_m})}^{\mu }{e}^{\left[-\left(4+\mu \right)\frac{D}{D_m}\right]}$	The results demonstrated that the locally determined power laws appear to be the most accurate link between specific attenuation and rainfall intensity.	2017
[94]	To compare six alternative models to find the best rain attenuation model for higher microwave bands in Icheon, South Korea.	The study used 3-year rainfall data gathered via line-of-sight terrestrial links at 38 and 75 GHz, with path lengths of 3.2 and 0.1 km, respectively, and an average sampling rate of 1 min.	The relative error margin, ${\epsilon }_p$, was employed to evaluate the models and can be expressed mathematically as: ${\epsilon }_p=\frac{R_{pred}\left(P\right)-R_{meas}\left(P\right)}{R_{meas}\left(P\right)}\times 100\%$	The analytical results showed that the ITU-R P. 530-16 model predicted accurately for both 38 and 75 GHz, whereas the Abdulrahman model predicted accurately for just 38 GHz.	2017
[19]	To investigate the impact of rain on short-range radio networks operating at the 35 GHz mmWave frequency.	The measurement was experimentally obtained from a 35 GHz radio link with a path length of 230 m to measure rain-specific attenuation and rain rate distribution.	Experiments of rain attenuation at 103 GHz with a path length of 390 m at different rainfall rates were conducted to validate the rain rate distribution.	Results after comparison showed that Wellbul distribution for raindrops is following the experiments.	2006

Table 5. Summary of Rain Attenuation Using Empirical Models.

Ref.	Objective of Research	Methodology Adopted	Method of Validation	Result Obtained	Year
[43]	To investigate and modify the ITU-R P.530-17 rain attenuation prediction model for terrestrial line-of-sight at short-distance for 26 and 38 GHz at mm-wave frequencies in Malaysia.	Two links operating at 26 and 38 GHz were used to collect weather data employing a Casella rain gauge for 1 year with a 1-min integration time and path length of 300 m.	The study validated the proposed model by employing two links operating at 25 GHz with a path length of 223 m in Japan and 75 GHz with a path length of 100 m in Korea.	The results reveal that all estimations are close to the suggested prediction model.	2020
[2]	To compare five different prediction models to find the optimal rain attenuation model for 5G in Malaysia.	The research utilized a 1-year precipitation data collected from a tipping bucket rain gauge over a link of 0.2 km path length operating at 6 and 28 GHz.	The rain attenuation was calculated from the product of the specific attenuation and the path length at a rain rate of 0.01% as shown below: $A_p=\gamma L_{eq}$	Results revealed that the modified Mello model estimated a lower value for the attenuation for low and high operating frequencies.	2020
[20]	To investigate the effect of rain on short-range fixed links, that is, building-to-building transmission.	Data utilized for this research were obtained using a PWS100 high-performance disdrometer at 25.84 and 77.52 GHz.	The ITU-R and DSD models were employed to predict the attenuation due to rain expressed mathematically as: $\gamma =a{R}^b$ $\gamma =4.343\times {10}^3{{\displaystyle \int }}_0^{\infty }{\delta }_{ext}\left(D\right)N\left(D\right)dD$	The results showed that the ITU-R model overestimates the attenuation for lower rain rates, whereas for higher rain rates it estimates lower attenuation than the DSD model.	2019
[21]	To investigate the effect of precipitation and wet antennas on millimeter-wave transmission links operating at 28 GHz and 38 GHz Line of Sight (LOS).	The study used a 700 m path length millimeter wave link operating at 28 and 38 GHz in central Beijing. A disdrometer and rain gauge was employed to measure rainfall and the received signal level was gathered every 15 s.	A power law equation was used to calculate the expected signal attenuation (theoretical) and then compared with the measured signal attenuation (practical): $A=a{R}^b$	Results showed that the measured signal attenuation was 1–1.5 dB greater than expected for 28 GHz, 1.6–2.5 dB greater than expected for 38 GHz due to the wet antenna, and a signal loss of 4.2 dB was recorded over the 700 m link.	2019
[62]	To investigate the effect of rain using real-world observations on mm-wave propagation at 26 GHz frequency.	The study used a microwave 5G radio link technology with a 1.3 km path length to collect measurements logged daily. Then, every year, MATLAB was utilized to process and analyze data.	Two ITU-R models—P.530-16 and P.838-3—were employed to measure the effect of rain on the propagation of electromagnetic signals.	Results showed that the specific attenuation at 0.01% was 26.2 dB/km at 120 mm/hr. The rain rate and the estimated rain attenuation across 1.3 km was 34 dB.	2018
[109]	Improve rain attenuation estimates for 5G wireless networks operating in heavy rain zones at 28 GHz and 38 GHz.	The study used 3-year raindrop size distribution data gathered in Kuala Lumpur, Malaysia, utilizing a “Joss-type” RD69 disdrometer, which comprised 100,512 rainy data with a 1-min integration time.	Gamma and normalized models were used to evaluate the performance and can respectively be expressed mathematically as: $N\left(D\right)=N_o{D}^{\mu }{e}^{-\left(\wedge D\right)}$ $N\left(D\right)=N_{w}f\left(\mu \right){(\frac{D}{D_m})}^{\mu }{e}^{\left[-\left(4+\mu \right)\frac{D}{D_m}\right]}$	The results demonstrated that the locally determined power laws appear to be the most accurate link between specific attenuation and rainfall intensity.	2017
[94]	To compare six alternative models to find the best rain attenuation model for higher microwave bands in Icheon, South Korea.	The study used 3-year rainfall data gathered via line-of-sight terrestrial links at 38 and 75 GHz, with path lengths of 3.2 and 0.1 km, respectively, and an average sampling rate of 1 min.	The relative error margin, ${\epsilon }_p$, was employed to evaluate the models and can be expressed mathematically as: ${\epsilon }_p=\frac{R_{pred}\left(P\right)-R_{meas}\left(P\right)}{R_{meas}\left(P\right)}\times 100\%$	The analytical results showed that the ITU-R P. 530-16 model predicted accurately for both 38 and 75 GHz, whereas the Abdulrahman model predicted accurately for just 38 GHz.	2017
[19]	To investigate the impact of rain on short-range radio networks operating at the 35 GHz mmWave frequency.	The measurement was experimentally obtained from a 35 GHz radio link with a path length of 230 m to measure rain-specific attenuation and rain rate distribution.	Experiments of rain attenuation at 103 GHz with a path length of 390 m at different rainfall rates were conducted to validate the rain rate distribution.	Results after comparison showed that Wellbul distribution for raindrops is following the experiments.	2006

4.2. Statistical Models

This section introduces and discusses the various prediction models in the statistical model category and reviews previous works based on these models on rain attenuation for the 5G network. A statistical model, as opposed to an empirical model, is based on statistical meteorological data analysis, and results are derived by regression analysis. Two statistical models are considered: the ITU-R model and the Singh model.

4.2.1. ITU-R Model

This model can estimate rain attenuation for frequencies ranging from 1 to 100 GHz with path lengths up to 60 km. It is based on the distance factor that depends on the rain-rate $R_r$, link length, frequency, and the coefficient of the specific attenuation $\gamma$ [47,110]. The International Telecommunication Union’s Radiocommunication Sector (ITU-R) issued some recommendations that have become the most generally used globally in estimating rain attenuation [63]. The ITU model is based on a parameter of 0.01% of the annual rain rate. Rain attenuation is caused by the overall rainfall crossing the propagation path, typically described as the integration of the specific attenuation along the path. The model gives $99.99\%$ fade depth attenuation as expressed in Equation (26):

$$A_p=a{R}_r^{b}dr \left(\mathrm{dB}\right)$$

(26)

where $R_r$ is the rain rate measured in mm/h and defined as $99.99\%$ of the rain rate for a specific location, $a{R}^b$ is measured in $\mathrm{dB}/\mathrm{km}$ and gives the specific attenuation, $L_p$ is the length of the link measured in km, $a$ and $b$ are functions of frequency at 20$°C$, while path adjustment factor $r$ is expressed as in Equation (27):

$$r=\frac{1}{1+L_p/L_{eq}}$$

(27)

where $L_{eq}$ gives the effective path length and is mathematically expressed as shown in Equation (28):

$$L_{eq}=35e^{-0.015R_r} \left(\mathrm{km}\right)$$

(28)

The model has become a worldwide baseline for evaluating research findings, though not without flaws, such as focusing on the effect of rain while ignoring the effects of other meteorological elements such as snowflakes or hail [84]. The model has further been reported to indicate a poor correlation with experimental data, especially in the tropics [111]. Furthermore, its use outside its prescribed limited frequency and rain rate ranges could inflict up to a whopping $10\%$ error [112]. It also features more complex computations involving high-frequency asymptotic expansion because of the inhomogeneous nature of tropical raindrop-size distributions [113,114,115]. Lastly, for wider applications, the model depends on extrapolation in respect of computations for rain spheres and rain rates, which could be a potent source of error in the tropics [116]. Because of the above limitations of the ITU-R P618-9, the latest modification—ITU-R P530-16—features the inclusion of location-tuning parameters [84]. The path reduction factor can be expressed as given in Equation (29):

$$r=\frac{1}{0.477\left(L_p^{0.633}\right)R_p^{0.073a}{f}^{0.123}-10.579\left[1-\exp \left(-0.024L_p\right)\right]}$$

(29)

The equations of interpolation for various percentages of time ranging from 0.001 to 1% are expressed in Equations (30)–(34):

$$\frac{A_p}{A_{0.01}}=C_1{P}^{-\left|C_2+C_3.{\log }_{10}P\right|}$$

(30)

$$C_1=\left({0.07}^{C_0}\right)\left[{0.12}^{\left(1-C_0\right)}\right]$$

(31)

$$C_2=0.855C_0+0.546\left(1-C_0\right)$$

(32)

$$C_3=0.139C_0+0.043\left(1-C_0\right)$$

(33)

$$C_0=\{\begin{array}{l}0.12+0.4\left|{\log }_{10}{\left(\frac{f}{10}\right)}^{0.8}\right| f\ge 10 \mathrm{GHz}\\ 0.12 f<10 \mathrm{GHz}\end{array}$$

(34)

where $R_p$denotes the rain rate (mm/h) exceeded at p% of the time, $r$ denotes the path adjustment factor exceeded at the same percentage of the time, $L_p$ denotes the radio path length (km), C_n denotes the interpolation constant where n = 1,2,3, while $a$ and $b$ are functions of frequency obtained from [44]. The latest modification to the ITU-R model line, the ITU-R 530-16, has been reported to have shown significant improvement in handling attenuation, even though point accuracy is still far-fetched, and there is a need for more sustained efforts on a more realistic estimation of attenuation in the tropical and equatorial regions.

4.2.2. Singh Model

For the frequency range of 1 GHz to 100 GHz, the Singh model adopts the analytical method of ITU to determine specific attenuation, depending on the polarization type, vertical or horizontal. However, for most of the computational system requirements, the Singh model is simpler than the ITU model as it tries to do away with the requirement of determining the frequency-dependent regression coefficients, $a$ and $b$. Due to the intricacy of the other prediction models, this is a simple mathematical model that has only square and cubic equations that are solely reliant on the frequency and rain rates. As a result, calculating the attenuation induced by higher frequencies at any given frequency and rain rate is relatively simple [63]. The mathematical representation of this model is given in Equation (35):

$$\gamma =w{f}^3+x{f}^2+yf+z$$

(35)

where $\gamma$ denotes the specific attenuation (dB/km), $f$ denotes the frequency, and the coefficients $w, x, y, z$for horizontal polarization in terms of the rain rate $R_r$ are given in Equations (36)–(39):

$$w_h=1.422\times {10}^{-9}{R}_r^2+2.03\times {10}^{-7}{R}_r-1.21$$

(36)

$$x_h=1.963\times {10}^{-7}{R}_r^2+8.618\times {10}^{-7}{R}_r+0.0019$$

(37)

$$y_h=2.114\times {10}^{-6}{R}_r^2+0.01R_r-0.036$$

(38)

$$z_h=3\times {10}^{-5}{R}_r^2-0.040R_r –0.031$$

(39)

and Equations (40)–(43) are for vertical polarization:

$$w_v=-5.520\times {10}^{-12}{R}_r^3+3.26\times {10}^{-9}{R}_r^2-1.21R_r\times {10}^{-7}-6\times {10}^{-6}$$

(40)

$$x_v=8\times {10}^{-10}{R}_r^3-4.552\times {10}^{-7}{R}_r^2-3.03R_r\times 10{ }^{-5}+0.001$$

(41)

$$y_v=-5.71\times {10}^{-9}{R}_r^3+6\times {10}^{-7}{R}_r^2+8.707R_r\times {10}^{-3}-0.018$$

(42)

$$z_v=-1.073\times {10}^{-7}{R}_r^3+1.068\times {10}^{-4}{R}_r^2-0.0598R_r+0.0442$$

(43)

Table 6 presents the summary of works that utilized these statistical models including the methodology adopted, method of validation, and results obtained.

Table 6. Summary of Rain Attenuation Using Statistical Models.

Ref.	Objective of Research	Methodology Adopted	Method of Validation	Result Obtained	Year
[117]	To study rain attenuation for mmWave 5G applications utilizing long-term statistics across short-range fixed networks.	This study utilized 3 different experimental links to collect precipitation data. The first two links have a path length of 36 m operating at 25.84 and 77.54 GHz, while the third link has a path length of 200 m operating at 77.125 GHz.	The ITU-R and DSD models were employed to predict the attenuation due to rain expressed mathematically as: $\gamma =a{R}^b$ $\gamma =4.343\times {10}^3{{\displaystyle \int }}_0^{\infty }{\delta }_{ext}\left(D\right)N\left(D\right)dD$	The investigation revealed that the DSD required more than rainfall rates to estimate attenuation effectively, but the ITU-R P.530-18 performs better with a limited distance factor.	2022
[72]	To extensively provide analysis on the 1-min rain rate and attenuation forecast for 5G communication links by evaluating rainfall data at 26 GHz and 38 GHz propagation frequencies.	The study used a tipping bucket rain gauge connected to a data logger to collect 2-year rainfall data at the Bosso campus of the Federal University of Technology in Minna.	ITU-R P530-17 model was used to evaluate the rain rate at 0.01% and can be represented mathematically as: $A_p=\gamma L_{eq}$	Results showed that attenuation is directly proportional to both frequency and pathlengths; therefore, there would be a high-value attenuation for a path length above 1 km. Hence, there is a need to increase the output power above the computed attenuation value.	2021
[118]	To study the effectiveness of several ITU models in predicting rain rates and attenuation in Malaysia’s tropical climate with the worst month parameter estimation.	The study used three datasets from various times and locations in Malaysia that were collected over a Line-of-Sight scenario at 26 GHz and 1.3 km.	The work measured the performance of ITU models. The study utilized the absolute error at 0.01% and Root Mean Square Error (RMSE) model validation techniques.	Results showed that ITU-R 837-1 is more appropriate than other ITU-R models in predicting climate properties based on the absolute error and the computed RSME. ITU method 2 outperforms other ITU models.	2021
[91]	To evaluate the path adjustment factor of the ITU-R, Abdul-Rahman, Lin, and Mello models for rain attenuation estimation.	Two Ericsson links at 26 GHz and different distances of 1.3 km and 0.3 km were employed to collect data for two years at a sample period of one second.	The rain attenuation was calculated from the product of the specific attenuation and the path length at a rain rate of 0.01%, as shown below: $A_p=\gamma L_{eq}$	At a path length of 0.3 km, none of the models successfully predicted rain attenuation; however, at 1.3 km, all models accurately estimated the rain attenuation.	2020
[119]	To evaluate the statistics of the attenuation due to rain for 5G in heavy rain zones of equatorial Malaysia.	The research utilized 3-year data collected between the years 1992–1994 in Kuala Lumpur, Malaysia, with a 1-min sampling interval.	ITU-R model and the synthetic storm technique (SST) were employed to estimate the attenuation due to rain based on varying path lengths, frequency, and monsoon impacts.	The results showed that for 0.2 km, the estimated attenuation was less than 5 dB, implying that the shorter the distance between the base stations, the smaller the influence of rain attenuation, therefore improving the link’s performance.	2020
[71]	To study rain attenuation and its relationship to operational frequency and Drop Size Distribution (DSD).	A laser-based disdrometer was employed to collect rain data for 1 year over two radio links of 325 m operating at 73 and 83 GHz.	The work evaluates the accuracy of the prediction model. The measured data obtained from both links were compared to an ITU-R model.	Results showed that the SC EXCELL and Lin models accurately estimate short links irrespective of the frequency.	2020
[22]	To study the influence of the attenuation due to rain attenuation on both direct LOS and indirect NLOS side links for short-distance building-to-building transmission.	The study collected weather and channel data over two mmWave bands using a high-performance PWS100 disdrometer and a custom-made channel sounder, respectively, between 25.84 and 77.52 GHz.	The work utilized the rain rate, and the attenuation due to rain from both links was compared to an ITU-R model and the DSD model using Mie scattering.	The results show that the indirect NLOS side link experiences a greater amount of attenuation than the direct LOS link.	2020
[120]	To investigate the effect of rainfall intensity on radio propagation at 21.8 and 73.5 GHz in the K and E bands, respectively.	Two E-band links at 73.5 GHz with distances of 1.8 and 0.3 km and one K-band 21.8 GHz link at a distance of 1.8 km were utilized to obtain data at a sample interval of 15 min.	The empirical CDF for the highest rain attenuation was evaluated against the 1-min estimated rain attenuation CDF and also with some other prediction models.	The results obtained at a rain rate of 140mm/hr and time percentages of 0.03% and 0.01% showed that the E-band has 10 dB attenuation more than the K-band.	2020
[110]	To determine which rain attenuation models, ITU-R P.530-17 and Mello and Ghiani’s model, provide the accurate estimation for 5G networks in the tropical environment of Malaysia.	The research employed two experimental millimeter-wave links running at 26 and 38 GHz, with a path length of 301 m between antennas, as well as a data gathering system and a sample period of 1 s.	$\mathrm{The} \mathrm{work} \mathrm{validates} \mathrm{the} \mathrm{models}. \mathrm{The} \mathrm{relative} \mathrm{error} \mathrm{figure} {\epsilon }_p$ was employed, which is mathematically represented as: ${\epsilon }_p=\frac{R_{est}\left(P\right)-R_{meas}\left(P\right)}{R_{meas}\left(P\right)}\times 100\%$	The results showed that the ITU-R model gave the closest estimation to the measured attenuation; hence, it is best suited for tropical environments.	2019
[121]	To study the impact of the attenuation due to rain on 26 GHz mm-wave signal in a wet tropical location.	The study utilized a 5G microwave link operating at a 26.2 GHz frequency band as a test-bed with a path length of 1.3 km to continuously collect measurements for one year for a sampling interval of 1 min.	The linear regression method was used to calculate the rain rate of the worst month and the statistics of the rain attenuation: $Q=Q_{1}p+\beta$	The results showed that the ITU-R model inaccurately estimated the rain rate and attenuation up to a percentage value of 143% and 159%, respectively, for the study area.	2019
[122]	To investigate the rain attenuation cumulative distribution and rainfall rate in Ukraine.	The study utilized rainfall data collected for a time interval of 5 min with a 15 dB/km attenuation threshold for a 1 km horizontal channel operating at frequencies 28, 38, 60, and 94 GHz.	Radio-physical MPM model was used to determine the warm and worst months of the year.	The results showed that reliable communication at zenith-range and average angles of view is attainable for all studied frequency ranges with a 99.99% probability for a 1-year estimation term.	2019
[123]	To investigate various uplink and downlink frequency bands, the overall atmospheric absorption caused by dry air (oxygen) and water vapor on the earth-space path.	This study utilized 7-year meteorological data gathered from Atmospheric Infrared Sounder (AIRS) satellites between the years 2002 and 2009.	The Rec. ITU-RP 676 model was utilized to validate the results.	The results showed that there was 99.9% availability in C and Ku bands in West Africa with low fading between 0.04–0.09 dB and 0.01–1 dB, respectively.	2018
[84]	To validate a new ITU-R rain attenuation prediction model over Malaysia’s equatorial region.	The study utilized radar and rain gauge data obtained from MMD and DIDM over six different links in six distinct locations.	The proposed model was compared with four other rain attenuation models in terms of the RMS, standard deviation, and mean error.	Results showed that the new ITU-R model was able to address the problem of underestimation faced by the existing ITU-R model.	2019
[70]	To estimate the rain-specific attenuation of horizontally and vertically polarized millimeter waves using T-matrix calculations.	A 2-dimensional video disdrometer (DVD) was used in this research to collect 1-year rainfall data across terrestrial links operating at 38 GHz in Peninsular Malaysia.	The power-law fit relationship was used to compare the estimated values from the 2-DVD dataset with values from the ITU-R P.838-3: $\gamma =a{R}_r^b$	The results showed that the power-law fit excellently corresponds with the local-laws fit. However, there are numerous inconsistencies with the ITU-R recommendation.	2017
[94]	To study how local environment propagation affects the slant path attenuation for both Ku and Ka bands.	This research utilized 3-year rainfall data collected using two experimental setups operating at dual-band frequencies of 12.25 and 20.73 GHz and 6 and 19.8 GHz, respectively.	Two ITU-R models were employed for analysis with experimentally derived coefficient sets.	The results demonstrated the importance of the regression coefficients for specific attenuation based on ITU-R recommendations.	2017
[124]	To investigate rain attenuation estimation in both millimeter and microwave bands in Ethiopia for terrestrial radio networks.	The study utilized two-year rain intensity data collected from Ethiopia’s national meteorological agency with a 15-min integration time for various year percentages.	The ITU-R model was also employed to estimate the rainfall attenuation for ten different sites around the country over terrestrial radio links.	According to the findings, Bahirdar and Dubti are expected to receive the most and least amount of rain attenuation, respectively.	2015
[125]	To study 1-min rain rate information collected over two years in Akure, Nigeria.	An electronic weather station and a self-emptying tipping spoon were employed to obtain measurements and gather rain data which were then stored using a data logger.	The work validates the result, the prediction error, RMSE, SC-RMSE, as well as the Spearman’s rank correlation were employed.	Findings revealed that no single model would provide a decent fit while outperforming all others.	2014
[126]	To highlight the disparity between recorded attenuation due to rain for tropical Malaysia as well as ITU-R projections.	Four links were employed, each operating at a different frequency, 14.6, 21.95, 26, and 38 GHz, with a path length of 300 m and a 1-min integration period.	The rain attenuation estimation of the ITU-R was evaluated against the measured rain attenuation CDF.	Results showed that the path length is proportional to the deviation, and the ITU-R prediction model was underestimated for tropical regions.	2013
[81]	To analyze one-minute rain data collected in South Africa from January to December 2009.	The study measured 1-min rain data using a JD RD-80 disdrometer for a total period of 1 year to obtain 729 rain rate samples.	The chi-squared statistics, as well as the root, mean square tests, were employed to validate the results accurately.	The results showed that the gamma model performed the best for the different classes of rain taken under consideration.	2011
[127]	To propose a modified ITU-R rain attenuation model in tropical climates, particularly for Malaysia.	The research utilized 3 years of rain rate and rain attenuation data obtained from satellite Super-C where frequency, cumulative rain rate, and elevation angle were the major parameters.	Comparison between the proposed model and the existing ITU-R model in terms of rain prediction errors such as RMS and percentage error.	Results showed that the proposed model performed better than the existing ITU-R model; hence, it is suitable for a tropical climate such as Malaysia.	2011

4.3. Fade-Slope Model

This section discusses the different models in the fade-slope models category and reviews previous works on rain attenuation for 5G networks using these models. The fade slope represents the variation in the attenuation due to rain in terms of the attenuation level, sample time, and environmental conditions such as drop size distribution and rain type. To establish the fade mitigation measures, a fade slope is necessary. The two fade-slope models discussed here are the Andrade model and the Chebil model.

4.3.1. Andrade Model

The fade-slope variance [128] is proportional to the attenuation and can be expressed mathematically as shown in Equation (44):

$$f\left(f_s|A\right)=\frac{1.38}{\sqrt{\mathrm{K}·A}{\left[1+f_s^2/\mathrm{K}·A\right]}^{6.7}}$$

(44)

where $f_s$ is the fade slope, $A$ denotes the rain attenuation, and $\mathrm{K}$ is the constant of proportionality. The next level attenuation $A\left(t_i+t_p\right)$ can be estimated from the current attenuation value $A\left(t_i\right)$ and fade slope $f_s$ randomly by the predictor using Equation (45):

$$A\left(t_i+t_p\right)=A\left(t_i\right)+f_s{t}_p$$

(45)

where $t_p$ denotes the prediction time; $t_p=10$ can be considered the minimum prediction time or the time of experimental sampling data.

4.3.2. Chebil Model

This model [129] can be expressed mathematically as given in Equation (46):

$$\mathrm{P}=\frac{1}{{\sigma }_{f_s}\sqrt{2\pi }}\exp \left(0.5{\left(\frac{f_s}{{\sigma }_{f_s}}\right)}^2\right)$$

(46)

where $\mathrm{P}$ is the conditional distribution of the fade slope, $f_s$ is the fade slope, and ${\sigma }_{f_s}$ is the fade-slope standard deviation expressed in Equation (47):

$${\sigma }_{f_s}=0.00012A^3-0.003A^2+0.027A-0.0016$$

(47)

where $A$ is the rain attenuation.

Table 7 presents the summary of research works that have used these fade-slope models including the methodology adopted, methods of validation, and results obtained.

Table 7. Summary of Rain Attenuation Using Fade-Slope Models.

Ref.	Objective of Research	Methodology Adopted	Method of Validation	Result Obtained	Year
[130]	To investigates the propagation of the mm-waves at the 38 GHz link based on real measurement data in Malaysia.	The study used 1-year rainfall data gathered over a 38 GHz line-of-sight link with a path length of 300 m and a sample interval of 1 min.	The distributions of the attenuation due to rain was evaluated against the modified ITU-R distance-factor model at different time percentages to validate the accuracy of the model.	The results showed excellent correspondence between the modified model’s estimation and the measured rain fade in Malaysia as well as other available data from various locations.	2022
[90]	To examine the impact of attenuation due to rain for 5G in Malaysia and propose an optimal rain fade margin.	A tipping bucket rain gauge and RD-69 disdrometer were used to obtain three separate datasets for various periods.	$\mathrm{The} \mathrm{prediction} \mathrm{model} \mathrm{error}, {\epsilon }_p$, was used to validate the models and is represented mathematically as: ${\epsilon }_p=\frac{R_{est}\left(P\right) - R_{meas}\left(P\right)}{R_{meas}\left(P\right)}\times 100\%$	The results showed the optimum attenuation margin for 5G should range from 6.5 to 10 dB for a 26 GHz link and 7 to 11 dB at the 28 GHz link.	2021
[129]	To study the properties of the measured rain fade slope distribution for different attenuation levels.	Three experimental microwave links were employed for this study at 300 m.	To validate the model, the chi-square goodness-of-fit test was employed: $X_c^2={{\displaystyle \sum }}_{i=1}^N\frac{{\left(O_i-E_i\right)}^2}{E_i}$	The results showed that the ITU-R model evaluated against relevant measured distributions could not be generalized for all cases.	2020
[131]	To study and evaluate fade slope for rainstorms with speeds greater than 40 mm/h at various rain type boundaries.	The study used 2-year rain-rate data from Durban, South Africa, using a RD-80 disdrometer and a 30-s sampling time.	The rate of change of attenuation, R, and the attenuation threshold, T, have a power-law relationship, which is given by: $R=u{T}^v$	The results revealed that the fade slope is related to the attenuation threshold and is affected by the type of rain.	2019
[21]	To study the effect of rain intensity on signal-level measurements for mm-wave radio links across short distances and quantify the fading bias to achieve a more accurate estimate of the rain rate over the link.	LOS scenarios were measured using backhaul networks during rainy days in Beijing, China. The reading was compared to local rain measurements from a disdrometer and a rain gauge.	At 25 GHz, a wet test revealed up to 4 dB loss due to the thickness of the water coating on the antenna. After the rain ended (one hour later), the attenuation was still higher due to the wet residue on the antenna.	It was concluded that if the received signal was monitored for longer, the fading pattern could be quantified.	2019
[132]	To research the impact of heavy rain on link performance to accurately estimate the attenuation using dynamic rain fade measures to sustain link connectivity.	The study utilized 17-year rainfall data collected using two different types of measurement tools, JW RD-80 disdrometer and rain gauge with three different sampling times.	The work aims to determine which dynamic fade mitigation to employ; the backpropagation neural network (BPNN) model was utilized to anticipate the condition of the link. The model was validated using rainfall events of variable magnitudes from several rainfall regimes.	The backpropagation neural network (BPNN) model predicted rain attenuation and outperformed other models in the decision-making process between rain fade mitigation approaches.	2018

4.4. Physical Models

The physical models and a review of previous works on rain attenuation that utilized these models for 5G networks are discussed in this section. The physical models were developed based on the correspondence between the formation of the rain attenuation model formulation and the physical structure of rain events. There are three physical models, which include:

4.4.1. Crane Two-Component (T-C) Model

The model was proposed primarily for Western Europe and the United States; however, it has difficulty estimating rainfall features such as the frequency of occurrence and mean rainfall for weak and powerful rain cells. This rain attenuation prediction model presents separate procedures for heavy and mild rain statistics to account for the contributions of areas with heavy rainstorms (also known as volume cells) and larger areas of lesser rain intensity enclosing the showers (also known as debris), as for a stratiform rain event associated with Europe and America [133]. For a particular propagation path, the model adopts the existence of either a sole volume cell, debris, or both. It is targeted at calculating the probability that a certain attenuation level is surpassed, whose value might be produced by either component of the rain process (volume cell or debris). These probabilities are calculated independently and summed up to produce the desired estimate. At its simplest, the model involves the following steps: (a) propagation path determination for the global climate; (b) establishment of a mathematical link between the anticipated path length in volume cell and debris regions; (c) determinination of the expected amount of attenuation; (d) calculation of the required rain rate to produce rain attenuation; and (e) calculation of the probability that the given attenuation is set in step (c) above, given by the expression in Equation (48):

$$P\left(\gamma \right)=P_c\left(1+\frac{L_c}{W_c}\right)e^{R_D/R_c}+P_D\left(1+\frac{L_D}{W_D^{″}}\right)\eta \left(\frac{\ln R_r^{″}-\ln R_d}{{\sigma }_D}\right)$$

(48)

where $P\left(\gamma \right)$ is the desired probability that the specific attenuation is exceeded, $P_c$ is the probability of a cell, $P_D$ denotes the probability of debris, $\eta$ is the normal distribution function, ${\sigma }_D$ is the standard deviation of the natural logarithm of the rain rate, $W_c$ and $W_D$ are the length scale (in kilometers) for the cell and debris, respectively, $L_c$ and $L_D$ are the cell and debris respective path lengths, and $R_D$ and $R_c$ are the rain rates for debris and cell, respectively.

The model has been reported to work for both satellite and terrestrial links. However, it has exhibited relative difficulty in determining some parameters, such as the probabilities of occurrence and average rainfall for both volume cells and debris.

4.4.2. Ghiani Model

This model [41] is based on MultiEXCELL-derived rain attenuation statistics and is a correction-based path reduction factor model for terrestrial networks. It can be expressed mathematically as shown in Equation (49):

$$A=\underset{L}{{\displaystyle \int }}\gamma R_r\left(l\right)dl=\underset{L}{{\displaystyle \int }}a{R}_r{\left(l\right)}^{b}dl$$

(49)

Calculating the rain attenuation $A$ assuming the rain rate $R_r$ is constant throughout the transmission link in terms of the path reduction factor $r$ given by Equation (50):

$$A=a{R}_r{}^b{L}_{p}r$$

(50)

Deriving the path reduction factor $r$ for the rain maps generated by the MultiEXCELL model:

$$r=A/a{R}_r{}^b{L}_p$$

(51)

It was also noted that the average path reduction factor (PF) trends followed an exponential function expressed in Equation (52):

$$r_{av}=x\left(f,L_p\right)e^{-y\left(f,L_p\right)R}+z\left(f,L_p\right)$$

(52)

where the symbols $x$, $y$, and $z$ are regression coefficients of the path length and frequency. By neglecting the effect of frequency, the rain attenuation $A$ can be expressed in Equation (53):

$$A=a{R}_r{}^b{L}_p\left[x\left(L_p\right)e^{-y\left(L_p\right)R}+z\left(L_p\right)\right]$$

(53)

where the coefficients $x$, $y$, and $z$ can be expressed as Equations (54)–(56), respectively:

$$x=-0.8743e^{-0.1111R_r}+0.9061$$

(54)

$$y=-0.0931e^{-0.0183R_r}+0.1002$$

(55)

$$z=-0.6613e^{-0.178R_r}+0.3965$$

(56)

4.4.3. Capsoni Model

This model [134] is made up of multiple rain cell formations known as kernels, in which the rainfall intensity varies with distance from the center in terms of the peak intensity as expressed in Equation (57):

$$R_f=R_{pk}{e}^{-{\rho }_d/{\rho }_{do}}$$

(57)

where $R_f$ is the rainfall, ${\rho }_d$ is the distance from the center, ${\rho }_{do}$ is the conditional average radius, and $R_{pk}$ is the peak intensity; the cumulative probability of attenuation $P\left(A\right)$ can be expressed mathematically in Equation (58):

$$P\left(A\right)={{\displaystyle \int }}_{R_e}^{\infty }x·[0.5I{n}^2(R_{pk}/R_e)+\frac{1}{4\pi {\overline{\rho }}_o}In\left(R_{pk}/R_e)]·[-P\left(R_{pk}\right)\prime \prime \prime \right]d\left(In{R}_{pk}\right)$$

(58)

where $R_e$ is the effective rain rate and $x=e^{-{\rho }_d/{\rho }_{do}}$.

The rain distribution can be computed using the Equation (59):

$$P\left(R_f\right)=P_{o}I{n}^n\left(\frac{R_f{}^{*}}{R_f}\right)$$

(59)

This model does not provide attenuation. However, it can be easily estimated through a synthetic rain rate employing an appropriate estimation model. The COST 205, 1985 database was used to validate the model. EXCELL has been widely used to investigate the performance of telecommunications links. However, two drawbacks associated with it are, on the one hand, the choice of exponential distribution of rain rate, which is not observed in nature, and on the other hand, the overestimation of $R_e$. The enhanced EXCELL is said to work for both stratiform and convective rain. Table 8 presents a summary of work that has utilized these physical models including the methodology adopted, the methods of validation, and the results obtained.

Table 8. Summary of Rain Attenuation Using Physical Models.

Ref.	Objective of Research	Methodology Adopted	Method of Validation	Result Obtained	Year
[135]	To study the effect of the propagation properties of THz waves in falling snow and a snow layer.	Theoretical investigation between 100–400 GHz band between 0–20 °C.	Mie scattering theory is employed to fit the measured data.	Results showed THz wave suffers higher signal loss in snow than in the rain under an identical fall rate.	2019
[41]	To develop a model for predicting rain attenuation affecting terrestrial links based on a physical approach.	The research considered and utilized experimental data collected worldwide.	The relative error margin ${\epsilon }_p$ was used to validate the models and can be expressed mathematically as: ${\epsilon }_p=\frac{R_{pred}\left(P\right)-R_{meas}\left(P\right)}{R_{meas}\left(P\right)}\times 100\%$	Results obtained after analysis showed that the model able to predict the MultiEXCELL-derived rain attenuation statistics with very satisfactory accuracy but requires more validation.	2017
[136]	To provide 1-min rainfall rates for use in estimating the effect of rain on the propagation of radio waves through the earth-space in Malaysia.	The study used rainfall data from two TRMM satellite datasets and estimated thunderstorm ratio over 57 locations in Malaysia.	The percentage error metric was used to validate the results with several ground data sources from NOAA, GPCC, and NASA.	For Malaysia, the correlation coefficient was 0.79–0.89, and the average bias error between TRMM and GPCC was ±50 mm.	2013

4.5. Optimization-Based Models

The optimization-based models emphasize the use of the optimization process in the formulation of input parameters for additional factors affecting rain attenuation, such as the minimum error value. This section presents and discusses three different models in the optimization-based models category as well as provides a review of previous work done using these models.

4.5.1. Pinto Model

This model is an improved variant of the ITU-R P.530-17 rain attenuation prediction model, which is likewise based on the distance correction factor $r$ as used in the ITU-R model, as well as the effective rainfall rate distribution ($R_e$) [137]. This model can be represented mathematically as shown in Equation (60):

$$A_p=a{\left[x_1{R}_p{}^{\left(x_2+x_3/L_p\right)}\right]}^b{L}_p·\frac{1}{x_4{d}^{x_5}{R}_p{}^{x_6}{f}^{x_7}+x_8\left(x-e^{x_9{L}_p}\right)}$$

(60)

where $A_p$ is the rain attenuation at %p of time, $R_p$ denotes the rain rate at %p of time, $L_p$ denotes the path length, and $a$ and $b$ are functions of frequency.

The model employs the quasi-Newton approach and particle swarm optimization (PSO) to reduce the RMSE. The quasi-Newton multiple nonlinear regression (QNMRN) and Gaussian RMSE (GRMSE) algorithms are used to generate the coefficients $x_1, x_2,\dots ,x_9$ which are then fine-tuned using the PSO method.

4.5.2. Livieratos Model

This regression method relies on Supervised Machine Learning (SML) that leverages Gaussian process (GP) compatible kernel functions derived using the ITU Study Group Databank [42]. Cross-validation was employed to evaluate the performance of the model based on four kernel functions; however, the rain attenuation algorithm must be trained in a specific area of interest to predict rain attenuation in a certain geography, weather, or carrier frequency.

4.5.3. Develi Model

This model [38] was tested utilizing the Differential Evolution Approach (DEA) optimization technique at 97 GHz on a terrestrial link in the United Kingdom (UK). The model was used to show the nonlinear relationship between the inputs (rainfall rate and percentage of time) and outputs (rainfall rate and percentage of time) (rain attenuation) given in Equation (61):

$$A\left(t\right)={{\displaystyle \sum }}_{h=0}^H{a}_h{x}^h\left(t\right)+{{\displaystyle \sum }}_{n=1}^N{b}_n{R}_r^n\left(t\right)$$

(61)

where $A$ denotes the rain attenuation, $R_r$denotes the rainfall rate, $x\left(t\right)$ denotes the time percentage, and the sum of the parameters $H$ and $N$ determines the number of the input terms in the model while the parameters $a_0\dots a_k$ and $b_0\dots b_n$ are the model parameters. Equation (61) can be rewritten in closed form as shown in Equation (62):

$$A\left(t\right)=f\left(x\left(t\right),y\left(t\right),a_0,a_1,\dots ,a_K, b_1,b_2,\dots ,b_N\right)$$

(62)

where the function $f(·)$ denotes the nonlinear relationship between $A\left(t\right)$, $R_r\left(t\right),$ and $x\left(t\right)$. The mean absolute model error ($E$) can be defined as Equation (63):

$$E=\frac{1}{M}{{\displaystyle \sum }}_{k=1}^M\left|m_k\left(t\right)-A_k\left(t\right)\right|$$

(63)

where $M$ denotes the amount of information in the measurement set. Substituting Equation (62) into Equation (63) gives Equation (64):

$$E=\frac{1}{M}{{\displaystyle \sum }}_{k=1}^M\left|m_k\left(t\right)-f\left(x\left(t\right),y\left(t\right),a_0,a_1,\dots ,a_K, b_1,b_2,\dots ,b_N\right)\right|$$

(64)

The cost function for this equation is the mean absolute error, which is employed to derive the optimized error using the DEA algorithm. The mutation operation is crucial to the DE algorithm. The mutant vector can be written as shown in Equation (65):

$${\varsigma }^{M,i}={\varsigma }^{n,opt}+P_m\left({\varsigma }^{n,p_1}-{\varsigma }^{n,p_2}\right),\hspace{1em}i\ne p_1 \mathrm{and} i\ne p_2$$

(65)

where $n$ denotes the generation index, $P_m$ denotes the mutation variable, $p_1$, $p_2$ and $i$ are three arbitrarily chosen individual indexes, and the $M$ and $opt$ refer to the gene pool and the optimal entity in the population, respectively. Different works that have utilized these optimization-based models have been reviewed and presented in Table 9 including the methodology adopted, the various method of validation used, as well as the results obtained.

Table 9. Summary of Rain Attenuation Using Optimization-Based Models.

Ref.	Objective of Research	Methodology Adopted	Method of Validation	Result Obtained	Year
[42]	To develop a novel rain attenuation prediction model using Supervised Machine Learning (SML) and the Gaussian process (GP) for regression.	The study used experimental data retrieved from the ITU-R databank, which includes 89 experimental links located in various countries with operational frequencies ranging from 7 to 137 GHz at 0.5 to 58 km.	A 5-fold Cross-validation approach was employed to evaluate the model. However, the RMS was calculated to compare the model to other models: ${\rho }_v=\sqrt{{\mu }_v^2+{\sigma }_v^2}$	The model outperformed the four prediction models under consideration, including the ITU-R, Silva-Melo, Moupfouma, and Lin models.	2019
[138]	To estimate rain rate using measured rain attenuation for Tokyo Tech mmwave model network.	The study utilized a fixed wireless access link with an antenna having a high gain of 29 dBi, where rain rate data was recorded every 5 seconds.	The rain attenuation is calculated using the estimated clear-weather level.	From the measurement and estimation, it was shown that the error between them was between 0.1–0.3 dB.	2010

Table 10 presents and classifies the various rain attenuation prediction models in terms of their input parameters or functions such as path length, frequency, rain rate, etc.

Table 10. Input Parameters of the Existing Terrestrial Rain Attenuation Models.

Model Category	Models	References	Parameters
			Path Length	Frequency	Rain Rate	Polarization	Rain Rate Exceeded	Effective Path Length	Effective Rainfall Rate	Time Series
Empirical Models	Garcia	[106]	✓	✓	✓	✓	×	×	×	×
	Crane	[37]	✓	✓	✓	✓	✓	×	×	×
	Mello	[40]	✓	✓	✓	✓	✓	✓	✓	×
	Moupfouma	[39]	✓	✓	✓	✓	✓	✓	×	×
	Perić	[139]	✓	✓	✓	✓	×	×	×	×
	Abdulrahman	[107]	✓	✓	✓	✓	✓	✓	×	×
	Da Silva	[108]	✓	✓	✓	✓	✓	✓	✓	×
	Budalal	[43]	✓	✓	✓	✓	✓	×	✓	×
Statistical Models	ITU-R	[140]	✓	✓	✓	✓	✓	✓	×	×
	Singh	[63]	×	✓	✓	✓	×	×	×	×
Fade-Slope Models	Andrade	[128]	✓	✓	✓	✓	×	×	×	✓
	Chebil	[129]	✓	✓	✓	✓	×	×	×	✓
Physical Models	Crane T-C	[133]	✓	✓	✓	✓	×	×	×	×
	Ghiani	[41]	✓	✓	✓	✓	×	✓	×	×
	Capsino	[134]	✓	✓	✓	✓	×	×	×	×
Optimization-Based Models	Pinto	[137]	✓	✓	✓	✓	✓	×	✓	×
	Livieratos	[42]	✓	✓	✓	✓	✓	×	×	×
	Develi	[38]	×	×	✓	×	×	×	×	✓

This section has reviewed the various existing models used in modeling rain attenuation. Eventually, it grouped them into five categories: empirical, statistical, physical, fade-slope, and optimization-based models, which can be employed to estimate attenuation due to rain in tropical locations. According to the reviews, it can be concluded that none of the prediction models can be considered a complete model sufficient to accurately meet all demands for various infrastructure setup characteristics, geographic regions, or climate variations. From the taxonomy table, it can be seen that most of the models took into consideration the path length, frequency, and polarization, except the Develi model, which only considered the rain rate and time-series parameters.

5. Total Attenuation

This section examines signal attenuation due to the cloud, rainfall, atmospheric gases, and the total propagation attenuation loss, as well as providing a summary of these models and their input parameters.

5.1. Propagation through Cloud

Cloud liquid water content is another atmospheric element, apart from rain, that absorbs and scatters electromagnetic signals, especially for frequencies above 10 GHz, propagating from the sender to the receiver, causing attenuation of the signal. The impact of a cloud on signals is less than that of rain since the attenuation is determined by the cloud’s properties, such as its width, depth, and thermal readings (temperature), unlike rain which takes into consideration the communicating system’s parameters [141]. According to [142], cloud attenuation can be measured or quantified using the liquid water content and can be mathematically expressed as shown in Equation (66):

$$A_{cl}={\gamma }_c\frac{L_{wc}}{sin\theta }$$

(66)

where $L_{wc}$ is the liquid water content, $\theta$ is the angle of elevation, and ${\gamma }_c$cloud-specific attenuation coefficient, which can be expressed mathematically as shown in Equation (67):

$${\gamma }_c=\frac{0.819f}{\epsilon ″\left[1-{\left(\raisebox{1ex}{$2+\epsilon \prime $}\!\left/ \!\raisebox{-1ex}{$\epsilon ″$}\right.\right)}^2\right]}$$

(67)

where $\epsilon$ is the complex dielectric permittivity of water contents within the cloud.

$${\epsilon }^{\prime }=\frac{{\epsilon }_0-{\epsilon }_1}{1+{\left(\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$f{r}_{pri}$}\right.\right)}^2}+\frac{{\epsilon }_1-{\epsilon }_2}{{\left(\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$f{r}_{sec}$}\right.\right)}^2}+{\epsilon }_2$$

(68)

$${\epsilon }^{″}=\frac{f\left({\epsilon }_0-{\epsilon }_1\right)}{f{r}_{pri}\left[1+{\left(\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$f{r}_{pri}$}\right.\right)}^2\right]}+\frac{f\left({\epsilon }_1-{\epsilon }_2\right)}{f{r}_{sec}\left[1+{\left(\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$f{r}_{sec}$}\right.\right)}^2\right]}$$

(69)

$${\epsilon }_0=77.6+103.3\left(\frac{300}{T_k}-1\right)$$

(70)

$$f{r}_{pri}=20.09-142\left(\frac{300}{T}-1\right)+294{\left(\frac{300}{T}-1\right)}^2$$

(71)

$$f{r}_{sec}=590-1500\left(\frac{300}{T}-1\right)$$

(72)

where $f{r}_{pri}$ and $f{r}_{sec}$ denote the principal and secondary relaxation frequencies, respectively, $T$ is the temperature, and the values of ${\epsilon }_1$ and ${\epsilon }_2$ are 5.48 and 3.51, respectively.

5.2. Propagation through Rain

Rain, one of the main dynamic natural occurrences, reduces the power of transmitted electromagnetic signals due to absorption and dispersion depending on the rainfall rate and the physical structure, such as the width, height, and number of droplets that the signal passes through [34,142]. The universal power-law model used to describe the rain attenuation and specific attenuation are provided in Equations (6) and (7). The relationship between the path length ($L_p$) and the path reduction factor ($r$) is also provided in Equation (29). The power-law parameters $a$ and $b$ can be derived using the following Equations (73) and (74):

$$\log a={{\displaystyle \sum }}_{j-1}^4\left(x_j{e}^{-{\left(\frac{\log f_c-y_j}{z_j}\right)}^2}\right)+m_k\log f+z_k$$

(73)

$$\log b={{\displaystyle \sum }}_{j=1}^5\left(x_i{e}^{-{\left(\frac{\log f_c-y_i}{z_i}\right)}^2}\right)+m_n\log f+z_n$$

(74)

The rain rate $R_r$ can be derived in terms of the total depth of water droplets caused by rain (mm) and the total time of rainfall (hrs.) as expressed in Equation (75):

$$R_r=\frac{\mathrm{Total} \mathrm{depth} \mathrm{of} \mathrm{rainfall}}{\mathrm{Entire} \mathrm{rainfall} \mathrm{duration}}$$

(75)

5.3. Propagation through Atmospheric Gases

Numerous gases, including oxygen and water vapor, are present in the atmosphere. These gases have varying heights, loftiness, and breadths, resulting in varying degrees of multipath attenuation of electromagnetic signals [34]. The attenuation caused by oxygen can be distinguished from all other atmospheric impairments. Its impact is consistent across all regions and it is not dependent on any meteorological parameters, unlike the attenuation due to water vapor which absorbs and scatters the signal and is based on meteorological properties such as temperature, water vapor content, and height above sea level [143]. According to [144], the attenuation caused by water vapor (for $f\le 350 \mathrm{GHz}$) and oxygen (dry air) can be calculated, respectively, as shown in Equations (76) and (77):

$$A_{wv}=\left[\begin{array}{c}3.27\times {10}^{-2}{r}_t+1.67\times {10}^{-3}\frac{\rho r_t^7}{r_p}+7.7\times {10}^{-4}{f}^{0.5}+\frac{3.79}{{\left(f-22.235\right)}^2+9.8r_p^2{r}_t}+\dots \\ \frac{3.79}{{\left(f-183.31\right)}^2+11.85r_p^2{r}_t}+\frac{4.0l{r}_t}{{\left(f-325.153\right)}^2+10.44r_p^2{r}_t}\end{array}\right]f^2\rho r_p{r}_t\times {10}^{-4}$$

(76)

$$A_{ox}=\left[\frac{7.27r_t}{f^2+0.351r_p^2{r}_t^2}+\frac{7.5}{{\left(f-57\right)}^2+2.44r_p^2{r}_t^5}\right]f^2{r}_p^2{r}_t^t\times {10}^{-3}\hspace{1em}\mathrm{for} f\le 57 \mathrm{GHz}$$

(77)

where $A_{wv}$ denotes the attenuation caused by water vapor, $f$ denotes the frequency (GHz), $r_p=p/1013$, $r_t=288/\left(273+T\right)$, $p$ is pressure, $T$ is temperature, and $A_{ox}$is the attenuation caused by oxygen. The total attenuation due to atmospheric gases for both uplink and downlink transmission can be expressed as shown in Equation (78):

$$A_{gs}=\left[\frac{h_{ox}{A}_{ox}+h_{wv}{A}_{wv}}{sin\theta }\right]$$

(78)

where $h_{ox}$ and $h_{wv}$ are the equivalent height for oxygen (dry air) and water vapor, respectively, and $\theta$ denotes the angle of elevation.

5.4. Propagation through Radome

A radome, coined from the two words radar and dome, is a weatherproof enclosure constructed of structural plastic to protect the surface of an antenna, such as a microwave or radar antenna, from external environmental disturbances like wind, rain, ice, sand, and ultraviolet rays, and also to conceal the electronic equipment of the antenna from the public [145,146]. The radome can attenuate the receiving and transmitting signals, especially when wet; hence, it should be constructed using low-permittivity materials, shaped to achieve good transparency for the desired frequency, and hydrophobic-coated to avoid additional attenuation due to the wet radome surface [147,148]. Attenuation due to radome occurs by reflection and absorption based on the signal frequency as well as the thermal reading (temperature) and width of the water slab [149]. A simple model was utilized by [150] to calculate the overall radome attenuation through a two-layer structure and expressed as in Equation (79)

$$A_{rad}=-10\log {\left[\frac{T_1{T}_2{T}_3{e}^{-j\left({\tau }_r+{\tau }_w\right)}}{1+{\mathsf{\Gamma }}_1{\mathsf{\Gamma }}_2{e}^{-j2{\tau }_r}+{\mathsf{\Gamma }}_2{\mathsf{\Gamma }}_3{e}^{-j2{\tau }_w}+{\mathsf{\Gamma }}_1{\mathsf{\Gamma }}_3{e}^{-j2({\tau }_r+{\tau }_w)}}\right]}^2$$

(79)

where ${\tau }_r$ and ${\tau }_w$ denote the electrical thickness of the radome and water layers, respectively, expressed as given in Equations (80) and (81):

$${\tau }_r=k_o\sqrt{{\epsilon }_r{d}_r}$$

(80)

$${\tau }_w=k_o\sqrt{{\epsilon }_w{d}_w}$$

(81)

where $k_o$ denotes the free-space wavenumber, ${\epsilon }_r$ denotes the complex relative dielectric constants of the radome material, ${\epsilon }_w$ denotes the complex relative dielectric constants of the water at the X band, while $d_r$ and $d_w$ denote the physical thickness of the radome and water layer, respectively.

$T_{1,2,3}$ and ${\mathsf{\Gamma }}_{1,2,3}$ denote the respective transmission and reflection coefficients for the electric field at the (1) air–radome, (2) radome–water, and (3) water–air interfaces, and expressed as shown in Equations (82)–(85):

$${\mathsf{\Gamma }}_1=\frac{1-\sqrt{{\epsilon }_r}}{1+\sqrt{{\epsilon }_r}}$$

(82)

$${\mathsf{\Gamma }}_2=\frac{\sqrt{{\epsilon }_r}-\sqrt{{\epsilon }_w}}{\sqrt{{\epsilon }_r}+\sqrt{{\epsilon }_w}}$$

(83)

$${\mathsf{\Gamma }}_3=\frac{\sqrt{{\epsilon }_w}-1}{\sqrt{{\epsilon }_w}+1}$$

(84)

$$T_{1,2,3}=1+{\mathsf{\Gamma }}_{1,2,3}$$

(85)

The thickness of water, according to [149], can be related to the rainfall rate using Gibble’s Equation (86):

$$t_w={\left(\frac{3{\mu }_kðR_r}{2g}\right)}^{1/3}$$

(86)

where $t_w$ is the thickness of the water layer, ${\mu }_k$ denotes the kinematic viscosity of water (kg/m/s), $ð$ denotes the radius of the radome, $R_r$ denotes the rainfall rate, and $g$ denotes the gravitational acceleration.

5.5. Total Propagation Attenuation Loss

The total attenuation is a critical parameter to consider as it provides the necessary information for effectively designing communication links such as Earth–satellite and terrestrial communication links. The total attenuation, as defined by [45], is the sum of the individual attenuation parameters, including attenuation caused when the signal propagates through free space, clouds, rain, atmospheric gases, radome, etc. Hence, the total attenuation can be mathematically expressed as shown in Equation (87):

$$T_{att}=A_{nL}+A_{fs}+A_{cl}+A+A_{gs}+A_{rad}$$

(87)

where $A_{nL}$ is the attenuation loss due to non-line of sight, $A_{fs}$ denotes the free space attenuation as expressed in [151], $A_{cl}$ denotes the attenuation due to cloud Equation (66), $A$ attenuation due to rain Equation (6), $A_{gs}$attenuation due to atmospheric gases (dry air and water vapor) Equation (78), and $A_{rad}$ attenuation due to radome Equation (79).

Table 11 presents the various input parameters of the different atmospheric impairments models as well as radome for total attenuation.

Table 11. Input Parameters of the Atmospheric Impairments Models for Total Attenuation.

Atmospheric Impairments	References	Parameter
		Frequency	Distance	Temperature	Dielectric Constant	Pressure	Thickness	Polarization	Equivalent Height	Angle of Elevation	Rain Rate	Wavelength	Gain
Free Space	[152]	✓	✓	×	×	×	×	×	✓	×	×	✓	✓
Rain	[34]	✓	✓	×	×	×	×	✓	×	×	✓	✓	✓
Cloud	[142]	✓	×	✓	✓	×	✓	×	✓	✓	×	×	×
Atmospheric Gases	[144]	✓	×	✓	×	✓	×	×	✓	✓	×	×	×
Radomes	[150]	×	×	×	✓	×	✓	×	×	×	✓	×	×

5.6. Review of Total Attenuation Models

This section reviews various signal propagation models used to calculate attenuation as signals travel through various media, including free space, clouds, rain, radomes, and atmospheric gases (water vapor and dry air). These are summarized in Table 12, Table 13 and Table 14 for propagation through the cloud, atmospheric gases, and radome, respectively.

Table 12. Summary of Attenuation through the Cloud.

Ref.	Freq.	Location	Method of Validation	General Comments/Findings	Year
[153]	20–200 GHz	14 locations in Europe (not specified)	The average error coupled with the RMS was used to validate the model’s accuracy.	The results show a very good prediction performance with an overall RMS of the approximation error of 3.4%, slightly dependent on the frequency between 60 and 170 GHz.	2014
[154]	32 GHz	Cebreros, Spain	The cloud-specific attenuation contribution was modeled with a stochastic process well defined in both amplitude and time domains.	The time variations of the simulated stochastic process can simulate the behavior of a real cloud attenuation contribution in a good manner, even in the time domain.	2019
[155]	30–300 GHz	Northern (Sodankyla, Finland) and Southern (Trapani, Italy) Europe	The average error coupled with the RMS was used to validate the model’s (SMOC) accuracy.	High-resolution three-dimensional cloud fields were developed using this model. Results showed that, when taking into account all sites, the average RMS of the error on the CCDF of the cloud liquid water content is equivalent to 0.09 mm, which demonstrated good agreement with the other estimation made using other data.	2014
[156]	60 GHz and above	Durban and Cape Town in South Africa	This study utilized two separate sites and evaluated the coefficient of the specific attenuation against the water droplets at various temperatures as a function of the frequency.	Results based on several notable cloud characteristics revealed that specific attenuation coefficients and cloud attenuation increase with frequency, demonstrating the influence of the LWC on signals.	2021
[157]	18.9 GHz	Nanyang Technological University (NTU), Singapore	The various models were validated using the yearly (2014 and 2015) cloud-induced attenuation CCDF.	The ITU-R model underestimates the cloud attenuation in tropical regions, according to the results of the yearly CCDF, which indicated that at 0.01%-time percentage, the attenuation due to cloud could range up to 4.2 dB in tropical regions.	2017

Table 13. Summary of Attenuation through Atmospheric Gases.

Ref.	Freq.	Location	Method of Validation	General Comments/Findings	Year
[158]	20–100 GHz	24 sites worldwide	The average error coupled with the RMS was used to validate the prediction accuracy following ITU-R standard P.311-15.	Results indicated that the model’s prediction accuracy improves significantly for the current recommendation and is less dependent on the operational frequency (20–100 GHz range) and the considered site.	2016
[159]	1–350 GHz	24 sites worldwide	The average and root mean square of the error figure were used to validate the prediction accuracy following ITU-R standard P.311-15.	The proposed method outperforms the other methods listed in ITU-R Annex 2 (P.676-10) Rec., according to the results of an evaluation against a large sample of radiosonde data.	2017
[160]	10–350 GHz	24 sites worldwide	The proposed model was evaluated against the RAOBS data sample for predicting the path oxygen attenuation in terms of the average estimation error as well as the RMS.	The obtained results demonstrated a very excellent level of accuracy in terms of overall prediction error and performance stability, which turns out to be slightly frequency-dependent and almost site-independent.	2017
[79]	1–350 GHz	Spino d’Adda, Italy	The mean and root mean square values of the prediction error calculated every 5 s were used to validate the model’s accuracy.	Results indicated that version 11 of ITU-R P.676 significantly underestimates the attenuation due to gases, while the previous version is accurate enough to be used to estimate the tropospheric attenuation.	2019
[123]	4–40 GHz	Nigeria, West Africa	The gaseous attenuation for West Africa was estimated and validated using the ITU-R P 676 model.	Results showed that C and Ku bands have low signal fade, whereas the Ka and V bands have higher signal fade for both oxygen and water vapor. Additionally, the western section of West Africa showed a larger increase in attenuation due to gas than the southern part of West Africa.	2018

Table 14. Summary of Attenuation through Radome.

Ref.	Freq.	Methodology Adopted	Method of Validation	General Comments/Findings	Year
[161]	150–300 GHz	The research used a Stepped Frequency Radar (SFR) and a Frequency Modulated Continuous Wave (FMCW) Radar to collect measurements.	The measured results were compared to the Fresnel theory of transmission and reflection for multilayer structures in the study.	The obtained results were in good agreement with the theoretical model that explains the signal loss caused by layers of water on a radome. The results also revealed a significant correlation between consistent water layer thickness and signal reduction.	2016
[149]	8–12 GHz (X-band)	An antenna was employed in the study as a time-domain reflectometer and probe.	A laboratory that measures the reflectance produced by radome panels at the X band was designed to evaluate the designed system.	The results revealed that when absorption is negligible, the novel instrument for characterizing the influence of a radome in dry and wet conditions can be used to provide reliable results.	2018
[146]	1–14 GHz	The proposed multi-layer radome design methodology is based on multiple structures, a-sandwich, which was not employed in typical radomes with multilayers.	A radome with multilayers and ultra-wideband features operating between 1 to 14 GHz was proposed, constructed, and assessed to validate the proposed design methodology.	The results demonstrated a strong correspondence between the calculated and measured results with less than 0.1 dB absolute error for all scanning angles.	2020
[147]	8–12 GHz (X-band)	The study used ARPA Piemonte polarimetric X-band radar (ARX) data and two validation procedures.	The first method estimated two-way wet radome losses using an empirical model based on self-consistency, whereas the other method evaluated the radar accumulations against the rainfall gauge measurements with and without radome adjustment.	Results obtained based on the rainfall comparisons showed that the self-consistency method is an efficient real-time correction of the effects introduced by a wet radome.	2013

6. Specific Attenuation

This section presents and discusses the specific attenuation models calculation based on rainfall, atmospheric gases (oxygen and water vapor), and clouds.

6.1. Specific Attenuation Model Due to Rainfall

As described earlier, Equations (6), (7), (29), and (73)–(75) provide detailed relationships of specific attenuation (dB/km) due to rainfall across terrestrial communication channels and also the relationship between the specific attenuation and rainfall rate, frequency, and polarization characteristics.

6.2. Specific Attenuation Model Due to Atmospheric Gases

The specific attenuation due to atmospheric gases, according to [144], can be precisely calculated as the sum of the individual spectral lines from oxygen and water vapor at any value of pressure, temperature, and humidity along with a few additional parameters as shown in Equation (88):

$$\gamma ={\gamma }_o+{\gamma }_w=0.1820f\left(N_{ox}^{″}\left(f\right)+N_{wv}^{″}\left(f\right)\right)$$

(88)

where ${\gamma }_o$ and ${\gamma }_w$ denote the specific attenuation (dB/km) for oxygen and water vapor, respectively, $f$ denotes the frequency (GHz) while $N_{ox}^{″}\left(f\right)$ and $N_{wv}^{″}\left(f\right)$ are the imaginary parts of the frequency-dependent complex refractivity expressed as in Equations (89) and (90):

$$N_{ox}^{″}\left(f\right)={{\displaystyle \sum }}_{i\left(ox\right)}{S}_i{F}_i+N_D^{″}\left(f\right)$$

(89)

$$N_{wv}^{″}\left(f\right)={{\displaystyle \sum }}_{i\left(wv\right)}{S}_i{F}_i$$

(90)

where $S_i$ denotes the strength of the $i$th oxygen or water vapor line, $F_i$ denotes the oxygen or water vapor line shape factor, and $N_D^{″}\left(f\right)$ denotes the dry continuum due to pressure-induced nitrogen absorption and the Debye spectrum as given by Equation (91). That is,

$$N_D^{″}\left(f\right)=fp{\phi }^2\left[\frac{6.14\times {10}^{-5}}{\partial \left[1+{\left[\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$\partial $}\right.\right]}^2\right]}+\frac{1.4\times {10}^{-12}p{\phi }^{1.5}}{1+1.9\times {10}^{-5}{f}^{1.5}}\right]$$

(91)

where $\partial$ denotes the width parameter for the Debye spectrum expressed in Equation (92):

$$\partial =5.6\times {10}^{-4}\left(p+e\right){\phi }^{0.8}$$

(92)

The line strength $S_i$ can be obtained for both dry air and water vapor using the following Equations (93) and (94):

$$S_i=a_1\times {10}^{-7}p{\phi }^3{e}^{a_2\left(1-\phi \right)}\hspace{1em}\mathrm{For} \mathrm{dry} \mathrm{air} \left(\mathrm{oxygen}\right)$$

(93)

$$S_i=b_1\times {10}^{-1}e{\phi }^{3.5}{e}^{b_2\left(1-\phi \right)}\hspace{1em}\mathrm{For} \mathrm{water} \mathrm{vapor}$$

(94)

where $\mathrm{T}$ is the temperature in Kelvin, $\phi =300/\mathrm{T}$, $p$ denotes the oxygen pressure ($\mathrm{hPa}$), and $e$ is the water vapor partial pressure ($\mathrm{hPa}$). Hence, the total barometric pressure can be expressed in Equation (95):

$$p_{tot }=p+e$$

(95)

6.3. Specific Attenuation Due to Clouds

It has been shown in [162] that the Rayleigh Scattering Approximation is accurate for frequencies up to 200 GHz for clouds or fog that contain predominantly small droplets of diameter less than 0.01 cm and the specific attenuation due to the cloud can be expressed in Equation (96):

$${\gamma }_c\left(f,T\right)=K_l\left(f,T\right)M$$

(96)

where ${\gamma }_c$ denotes the specific attenuation within the cloud (dB/km), $f$ denotes the frequency, $T$ denotes the cloud liquid water temperature (Kelvin), $M$ denotes the liquid water density in the cloud or fog (g/m³), and $K_l$ denotes the cloud liquid water-specific attenuation coefficient, which can be represented mathematically as Equation (97):

$$K_l=\frac{{\gamma }_c}{M}$$

(97)

Table 15 presents the various input parameters of the different atmospheric impairments models for specific attenuation.

Table 15. Input Parameters of the Atmospheric Impairment for Specific Attenuation.

Atmospheric Impairment	References	Parameters
		Frequency	Distance	Temperature	Pressure	Polarization	Drop Size Distribution	Rain Rate	Dielectric Permittivity	Effective Path Length	Density
Rain	[44]	✓	✓	×	×	✓	✓	✓	×	✓	×
Dry Air and Water Vapor	[144]	✓	✓	✓	✓	×	×	×	×	×	×
Cloud or Fog	[162]	✓	×	✓	×	×	×	×	✓	×	✓

6.4. Review of Total Attenuation Models

This section reviews various signal propagation models used to calculate specific attenuation as signals travel through various media, such as clouds, rain, and atmospheric gases (water vapor and dry air). Table 16 presents the summary of specific models.

Table 16. Summary of Specific Attenuation Models.

Ref.	Objective of Research	Methodology Adopted	Frequency	Method of Validation	Year
[112]	To establish a repository of k and α values for the frequencies up to 1000 GHz.	Logarithmic regression was applied to Mie’s scattering calculations, Laws and Parsons, and Marshall–Palmer DSD on widespread and convective rain.	1–1000 GHz	Comparison with direct measurement values.	1978
[163]	To establish a relationship between the regression coefficients of attenuation (a and b) and frequency.	The study employed the power law to estimate the relationship between the regression coefficients and the frequency analytically with a rain rate range of 5–100 mm/h.	1–400 GHz	The work validates the model; the ITU-R database was utilized. However, to compare the model to other models, their absolute and relative errors were calculated and compared.	2001
[54]	To review works done in attenuation and investigate prediction models.	The study utilized the reduction factor and frequency scaling to predict total attenuation.	15 GHz, 23 GHz, 26 GHz and 38 GHz	The ITU-R database is used to validate.	2013
[164]	To propose a novel methodology using standard equipment for the calibration in real-time of the power-law parameters.	Real measurements logged by CMNs and a standard rain gauge were employed to calibrate the parameters of the power law.	10–100 GHz	Calibrated power-law parametric values were validated using the ITU-R values.	2016
[42]	To develop an enhanced rain attenuation prediction model with a universal perspective.	The study employed supervised machine learning (SML) to formulate enhanced models.	30–300 GHz	$\mathrm{The} R^2$ measure is used to express the efficacy of the regression.	2019

The power law has been used to calculate rain attenuation since the 1940s and is still being used to estimate the attenuation by network designers and operators. The ITU-R standard has provided a simplified technical standard that guides the establishment of the power-law based correlation between the attenuation due to rain and the rainfall rate (P.838-3). More recently, the power law was explored for monitoring rainfall occasioned by the availability of attenuation data collected from the Commercial Microwave Networks (CMNs) backhaul infrastructure. This advancement has paved the way for opportunistic surveillance instruments that require little or no additional hardware or cost. Also, more recently, supervised machine learning (SML) is gaining traction in the quest for calibrating the power-law parameters.

7. Review of Different Methods of Model Validation

This section presents a review of different model validation methods and summarizes model validation techniques.

In the literature, when new mathematical models are developed, there is usually a means to validate the model. For rain attenuation, the models are subjected to different validation tests to determine their ability to predict rain attenuation. According to the ITU-R, there are standard procedures for testing the validity of mathematical models developed for rain attenuation predictions. As a result, it is necessary to analyze some of these models to determine the current and future developments in this area. Some of the works of literature in this field were noted in [165]. In this context, this study has executively selected four model validation methodologies based on the recommendation of the ITU-R [166] which are available in the literature. The methodologies are (I) an input-to-output correlation or coefficient of determination, (II) Root Mean Square Error (RMSE) and RMS functions, (III) goodness-of-fit function, and (IV) Chi-square models.

The coefficient of determination function is defined as the total variations in a proposed model or, in some cases, multiple regression models. Mathematically, it is defined in Equation (98):

$$R^2=\frac{\mathrm{Explained} \mathrm{Variation}}{\mathrm{Total} \mathrm{Variation}}$$

(98)

Root Mean Square Error (RMSE) is utilized to measure the difference in numerical estimation and can be expressed mathematically as given in Equation (99):

$$\mathrm{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^N{\left(O_i-P_i\right)}^2}{N}}$$

(99)

Another variant of the RMSE function is the Spread-Corrected RMSE (SC-RMSE) as expressed in Equation (100):

$$\mathrm{SC}\_\mathrm{RMSE}=\sqrt{\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{\left|{\epsilon }_p{}^{\prime }\right|}^2}$$

(100)

where:

$${\epsilon }_p{}^{\prime }=\left|{\epsilon }_p\right|-{\sigma }_p$$

(101)

The goodness-of-fit function $\epsilon {\left(p\right)}_T$ can be used to test how well the developed model observed data fits the predicted data and this can be expressed in Equation (102):

$$\epsilon {\left(P\right)}_T=\frac{A_{p,predicted}-A_{p,measured}}{A_{p,measured}}\times 100 [\%]$$

(102)

In some cases, this is called the Pearson goodness-of-fit function, and the expression for this is defined in Equation (103):

$$X^2={{\displaystyle \sum }}_j\frac{{\left(O_j-E_j\right)}^2}{E_j}$$

(103)

where $O_j$ is the observed count in cell $j$ and $E_j$ is the expected count in the cell $j$ when $0.001\%<p<1\%$.

Chi-square can also be used to validate developed models and can be expressed mathematically as defined in Equation (104). The Chi-square statistics were employed to evaluate the method’s performance.

$$X^2={{\displaystyle \sum }}_{i=1}^N\frac{{(A_{p,predicted}-A_{p,measured})}^2}{A_{p,predicted,i}}$$

(104)

The difference between the predicted rain rate value and the measured rain rate value is given by relative error (${\epsilon }_p$) expressed in Equation (105):

$${\epsilon }_p={ℛ}_p-{ℛ}_m$$

(105)

where ${ℛ}_p$: is the predicted value and ${ℛ}_m$ is the measured rain rate estimated for $0.001\%<p<1\%$. The maximum error and the mean error can be expressed mathematically as shown in Equations (106) and (107), respectively:

$$\mathrm{Maximum} \mathrm{error}=\max \left({\epsilon }_p\right)$$

(106)

$$\mathrm{Mean} \mathrm{error} \mathrm{E}=\frac{1}{n}{{\displaystyle \sum }}_i^n{\epsilon }_p$$

(107)

Rank Correlation, $\rho$

This measures the strength of the relationship of related data. It does not assume measurement for statistical dependence between the measured and predicted; hence, it is non-parametric. Mathematically, it can be expressed as shown in Equation (108):

$$\rho =\frac{{{\displaystyle \sum }}_p({ℛ}_p-\overline{{ℛ}_p})\left({ℛ}_m-\overline{{ℛ}_m}\right)}{\sqrt{{{\displaystyle \sum }}_p{\left({ℛ}_p-\overline{{ℛ}_p}\right)}^2{{\displaystyle \sum }}_p{\left({ℛ}_m-\overline{{ℛ}_m}\right)}^3}}\hspace{1em}-1<\rho <1$$

(108)

where $\overline{{ℛ}_p }\& \overline{{ℛ}_m}$ are mean measured and predicted rain rates for $0.001\%<p<1\%$.

Table 17 presents the properties of the various existing rain attenuation models based on the thresholds for each parameter considered when developing the models including the predicted rain attenuation value range.

Table 17. Properties of the Existing Rain Attenuation Prediction Models.

Model Category	Models	References	Path Length (km)	Frequency (GHz)	Percentage of Time (%)	Rain Rate (mm/h)	Rain Rate (min)	Attenuation (dB)	Number of Years
Empirical Models	Garcia	[106]	12–58	10.8–36	0.0001–0.1	140	1	10–60	2
	Crane	[37]	0–22.5	11–36.5	0.001–2	140	5	10–60	24
	Mello	[40]	0.5–58	–	0.001–0.1	140	–	–	–
	Moupfouma	[39]	0.1 and 3.2	38	0.001–0.1	33	1	15.65–64.54	3
	Perić	[139]	2–4	80	0.001–0.1	30 & 45	–	15–30	2
	Abdulrahman	[107]	0.1 and 3.2	38	0.001–0.1	0–100	1	6.03–40.66	3
	Da Silva	[108]	0.5–58	7–137	0.001–0.1	140	–	–	81
	Budalal	[43]	0.3	25–75	0.001–10	–	1	10–50	1
Statistical Models	ITU-R	[140]	0.1 and 3.2	75	0.001–0.1	0–100	1	3.22–15.71	3
	Singh	[63]	–	10–100	–	10–300	–	5–60	–
Fade-Slope Models	Andrade	[128]	12.8–43	14.52–14.55	–	–	–	1–30	1–2
	Chebil	[129]	0.3	15–38	–	–	2	1–15	16 months
Physical Models	Crane T-C	[133]	1.3–58	7–82	0.001–0.1	140	–	1–30	–
	Ghiani	[41]	1–20	10–50	0.001–0.1	54	1	0–15	1–10
	Capsino	[134]	–	12–18	–	4	–	–	59
Optimization-Based Models	Pinto	[137]	0.5–58	1–100	0.001–0.1	–	–	0–70	–
	Livieratos	[42]	0.5–58	7–137	0.001–0.1	4.5–230	–	0–50	–
	Develi	[38]	6.526	97	0.1–1	1.3–6.86	–	7.85–24.79	1

From Table 17, it can be seen that rain attenuation increases with increasing rainfall rates. Furthermore, as the time percentage increases, the rain attenuation values decrease. For example, at p = 1%, the attenuation value can be as low as 1.01 dB, whereas the attenuation can be as high as 40.48 dB at 0.001% [94]. However, according to ITU recommendations, a low value for the standard deviation and root mean square (RMS) for the majority of time percentages indicate that the proposed model is highly accurate [167].

Table 18 presents a summary of some works that have successfully utilized any of the aforementioned model validation techniques to evaluate the performance of their respective proposed models.

Table 18. Summary of Model Validation Techniques.

Ref.	Validation Technique	Comments/Findings	Year
[165]	Percentage error and RMS	Four rain attenuation models were compared in terms of the percentage error and root mean square to evaluate the performance over six operational point-to-point microwave links.	2014
[71]	Mean Error and Mean RMS	It has been established that the enhanced synthetic storm technique shows better accuracy and reliability for rain attenuation prediction EHF on a statistical basis (direct) and event basis (frequency scaling).	2020
[41]	Mean Error and Mean RMS	The proposed model was tested against the Brazilian model and the ITU-R model. There is a need to include the dataset in the ITU-R DBSG3 database for optimal or superior accuracy of the rain attenuation.	2017
[168]	Mean Error and Mean RMS	This work proposed a novel model based on an exponential profile of the rain cell because the rain attenuation model consistently increases with both time percentage, rain rate, and elevation angle. Eventually the new model outperforms the previous models in terms of prediction and anomalous behavior.	2018
[39]	RMS	The proposed model can predict when rain attenuation would be exceeded on both SHF and EHF radio waves.	2009
[137]	RMS	Non-linear regression is used to derive a model for rain attenuation. The result was based on experiments in both temperate and tropical regions. Also, model finetuning was carried out using PSO.	2019
[94]	The goodness of fits and Pearson goodness of fits	Different matrices were used to evaluate the performance of the permanent models. Furthermore, ITU-R P.530-16 and Abdulrahman models outperform at 38 GHz. However, ITU-R P.530-16 yields a better estimate at 75 GHz with a lower error probability.	2017
[134]	Chi-square	The proposed rain, site diversity, and rain scattering predictions were developed, and the model was tested on data collected in Europe using a satellite SIRIO and OTS. The results were excellent, and the efficacy of the statistical method was developed.	1987

From Table 18, it is clear from the method of validation that root mean square (RMS) is the method that most of the researchers are using to test the accuracy of the developed models. Some methods that have not been given attention are the Kolmogorov–Smirnov and the Anderson–Darling tests.

8. Machine Learning-Based Rain Attenuation Prediction Models

This section presents the reviews of machine-learning-based rain attenuation prediction models that have been proposed to date (August 2022) and a taxonomy. Also, a brief review of the issues with aerial communication is provided. Table 19 summarizes the machine learning-based rain attenuation models.

Table 19. Summary of Machine Learning-Based Models.

Ref.	Objectives	Methodology Adopted	Method of Validation	Comments/Findings	Year
[169]	To predict rain attenuation for multiple frequencies using a machine learning-based estimation approach and to compare with other models.	The study utilized a radiometer and laser precipitation monitor to obtain data for frequencies 22.234, 22.5, 23.034, 23.834, 25, 26.234, 28, and 30 GHz.	Minimum Mean Squared Error (MMSE) and Root Mean Square (RMS) were used to compare the proposed machine, the learning-based adaptive spline model, to the power-law model.	Results showed that the estimation values obtained by the proposed model are more accurate than those obtained by the power-law model.	2021
[170]	To propose a novel deep learning architecture that predicts future rain fade using satellite and radar imagery data as well as link power measurement.	The study chose 7 collocated locations for Echostar 19 and 24 and utilized data from the 4th quarter of 2018 to the 1st quarter of 2021.	The proposed model was compared with other machine learning-based approaches and evaluated in terms of accuracy, precision, recall, and f1-score for both long- and short-term prediction.	Results showed that the proposed model outperforms the other models in terms of accuracy, recall, precision, and f1-score, especially for long-term prediction.	2021
[171]	To accurately predict rain attenuation using Backpropagation Neural Network (BPNN) technique.	The study utilized data from three terrestrial microwave links operating at 23 and 38 GHz frequencies.	The proposed model was validated using 38 GHz fade slope data as well as a chi-square fitness test.	Results showed that the BPNN model is efficient for the prediction of rain attenuation in Nigeria.	2021
[172]	To compare various models and perform real-time prediction of rain attenuation data for the Earth–Space communication link (ESCL).	The study utilized 12-year data obtained from the South Africa Weather Service, where the data was split into two for training and testing the proposed network.	Comparison between the ANN rain-induced attenuation with existing models such as ITU-R and Moupfouma models were used to validate the performance of the model.	The result showed that the ANN-based model produced more accurate results with minimum errors than the ITU-R and Moupfouma models.	2020
[173]	To design a new model for calculating the specific attenuation due to rain at various rain rates using machine learning techniques	The study gathered data from the ITU-R model for defined values of a and b at different frequencies, which was used for the training of the model using Python.	A comparison between the proposed model and the ITU-R model was conducted.	Results showed that the accuracy obtained in the proposed model was approximately 97%.	2020
[96]	To predict rain rate and attenuation using a trained backpropagation neural network (BPNN) in the sub-tropical region of Durban, South Africa.	This study utilized a JWD RD-80 disdrometer to collect 4-year training and 1.5-year validation data for a sampling time of 30 s.	The performance of the trained BPNN was evaluated using the mean square error and TANSIG transfer function and validated using the 1.5-year data, then compared with the ITU-R model.	Results showed a relatively small margin of error between predicted rain attenuation exceeded at 0.01% of an average year.	2019
[174]	To show how ANN can be employed for rain attenuation prediction and to compare rain attenuation estimated by ANN with that of the ITU model in specific locations in Nigeria.	The study utilized 7-year data from 6 locations to train the ANN object, created using a feed-forward backpropagation neural network learning algorithm.	To test the prediction performance of the trained ANN, 3-year data were fed into it. Then to evaluate the ANN, a comparison with the ITU-R model was carried out in terms of the mean squared error.	Results showed that the predicted values of the ANN almost correspond with the calculated value of the ITU-R model with a mean squared error of less than 1 dB.	2019
[175]	To investigate rain attenuation models that used simple ANNs with a single hidden layer and propose a method for expanding databases.	The study utilized a stepwise methodology comprising 6 steps for the method of expanding databases, such as data selection, data validation, etc.	The physical consistency test was used to validate the results obtained.	Results showed that a simple ANN-based model could perform better than existing models if trained properly using a large database.	2019
[176]	To present an improved rain attenuation prediction in satellite communication using ANN models in four provinces of South Africa.	The study utilized 5-min integration time data obtained from the South Africa Weather Services based on 68.5E Intelsat 20 (IS-20) satellite footprint and a downlink frequency of 12.75 GHz.	A comparison was carried out between the ANN models, ITU-R model, and the SAM model in terms of Root Mean Square Error (RMSE) and Mean Square Error (MSE).	Results showed that the ANN models were able to estimate rain attenuation for all the selected locations accurately and outperformed both the ITU-R and SAM models.	2019
[42]	To develop a novel rain attenuation prediction model using Supervised Machine Learning (SML) and the Gaussian process (GP) for regression.	The study used experimental data retrieved from the ITU-R databank, which includes 89 experimental links located in various countries with operational frequencies ranging from 7 to 137 GHz at 0.5 to 58 km.	A 5-fold Cross-validation approach was employed to evaluate the model. However, the RMS was calculated to compare the model to other models: ${\rho }_v=\sqrt{{\mu }_v^2+{\sigma }_v^2}$	The model outperformed the four prediction models under consideration, including the ITU-R, Silva-Melo, Moupfouma, and Lin models.	2019
[177]	To utilize Feedforward Backpropagation Neural Network as a technique for predicting rain attenuation in satellite links at higher frequency in South Africa.	The study utilized 5-min integration time rainfall data obtained from four provinces by the South Africa Weather Services (SAWS) over ten years.	Root Mean Squared Error (RSME) and Correlation Coefficient were used to evaluate the performance of the proposed model against three existing prediction models.	Results showed that the ANN model produced accurate results in all four provinces with minimum error and best correlation coefficient.	2019
[178]	To predict rain attenuation using the ANN model and perform a comparison with the ITU-R model.	The study utilized a Percival disdrometer to measure and record rain rate data at a 1-min integration time at 25 GHz.	A comparison between the ANN model and the ITU-R model was conducted.	Results showed the ANN model performed better than the ITU-R model.	2017
[179]	To develop a neural network-based rain attenuation prediction model (BPNN) that can predict the rain rate in advance.	The study utilized 4-year data obtained using JW RD-80 Disdrometer measurements with a sampling time of 30 s which was used to train and test the model.	The accuracy of the model was evaluated in terms of the Root Mean Square Error (RMSE) and the Mean Square Error (MSE) for different rainfall events.	Error analysis results produced a low value, confirming that the proposed BPNN model can be trained and used for rain attenuation prediction.	2017
[180]	To propose new machine learning methods using KNN and ANN for predicting short-term rain attenuation for ground wireless communications.	The study utilized time-series of rainfall radar maps data obtained from the JMA webpage to train the KNN and ANN objects.	Comparisons between the actual rain rate and the predicted rain rate, between ANN and KNN in terms of the total attenuation without distance, and finally between ANN and KNN in terms of moderate rainfall.	Results showed that the ANN method became less accurate than the KNN method after the comparison without distance, but both methods performed better than those proposed in the literature.	2015
[181]	To propose two novel rain attenuation prediction models based on BPNN and LS-SVM algorithms for 60 GHz millimeter wave.	The study randomly selected samples from experimental results used previously in research to establish a relationship between the rain intensity and rain attenuation, excluding other parameters.	A comparison between these proposed models and the ITU-R model was conducted in terms of accuracy and stability.	Results showed that BPNN outperforms the ITU-R model in terms of accuracy and stability, but the LS-SVM is a mode ideal model for rain attenuation prediction for 60 GHz frequency.	2013
[182]	To develop a method of short-term prediction of rain attenuation using an ANN with a self-adaptation technique to varying parameters.	This study utilized Ku band data obtained from 3 different locations in India for the testing and validation of the model.	To evaluate the performance of the model, a comparison between the proposed model and other short-term prediction models was carried out.	Results showed that the accuracy decreases with prediction interval but remains within an acceptable range.	2012
[183]	To develop an ANN method based on the extinction cross-section data for rain attenuation prediction in microwave and millimeter wave frequencies.	The study utilized extension cross section data obtained from Modified Prupacher-and-Pitter (MPP) using the Finite Element Method for frequencies ranging between 1–100 GHz.	The mean square error and correlation coefficient were used to evaluate the performance of the developed model.	Results showed that the ANN produces accurate results for estimating the extension cross-section of a raindrop, making it a suitable tool for predicting rain attenuation.	2008
[184]	To propose a new and better rain attenuation model known as EPNet-evolved artificial neural networks (EPANN).	The study utilized data obtained from the ITU-R (CCIR) databank, which contains earth-space rain attenuation measurement data which was used to train and test the proposed model.	A comparison between the proposed ANN and ITU-R models was conducted in terms of the prediction error.	Results showed that the proposed model is suitable for predicting rain attenuation and performs better than ANN and ITU-R models.	2001

Findings from Table 19 indicate that machine learning models are simple and can accurately predict rain attenuation. However, it can also be seen that the performance of most of the machine learning-based models developed was evaluated against a statistical model, the ITU-R model of which the ML-based model performs better.

Table 20 presents the various machine learning-based models considered in the literature.

Table 20. Machine Learning-Based Models Considered in the Literature.

References	BPNN	SL-ANN	FFBNN	KNN	EPANN	LS-SVM	Linear Spline Regression	CNN	LSTM	FFDTD	CFBP	AANN	EBP	SML
[184]	×	×	×	×	✓	×	×	×	×	×	×	×	×	×
[183]	×	✓	×	×	×	×	×	×	×	×	×	×	×	×
[182]	×	×	×	×	×	×	×	×	×	×	×	✓	×	×
[181]	✓	×	×	×	×	✓	×	×	×	×	×	×	×	×
[180]	×	×	×	✓	×	×	×	×	×	×	×	×	×	×
[179]	✓	×	×	×	×	×	×	×	×	×	×	×	×	×
[178]	×	✓	×	×	×	×	×	×	×	×	×	×	×	×
[42]	×	×	×	×	×	×	×	×	×	×	×	×	×	✓
[177]	×	×	✓	×	×	×	×	×	×	×	×	×	×	×
[176]	×	×	✓	×	×	×	×	×	×	✓	✓	×	✓	×
[175]	×	✓	×	×	×	×	×	×	×	×	×	×	×	×
[174]	✓	×	✓	×	×	×	×	×	×	×	×	×	×	×
[96]	✓	×	×	×	×	×	×	×	×	×	×	×	×	×
[173]	×	×	×	×	×	×	×	×	×	×	×	×	×	✓
[172]	×	×	✓	×	×	×	×	×	×	×	✓	×	×	×
[171]	✓	×	×	×	×	×	×	×	×	×	×	×	×	×
[170]	×	×	×	×	×	×	×	✓	×	×	×	×	×	×
[169]	×	×	×	×	×	×	✓	×	×	×	×	×	×	×

From Table 20, it can be seen that only a few ML-based rain attenuation models have been developed and evaluated; hence, there are still gaps to fill this research area. Figure 6 shows the taxonomy of the machine learning-based rain attenuation models considered in the literature.

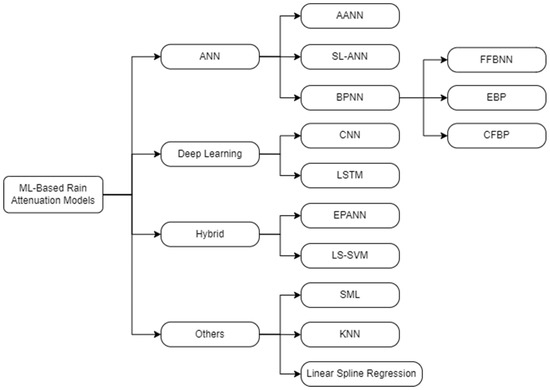
Figure 6. Taxonomy of the Machine Learning-Based Rain Attenuation Models.

Aerial Communication

Unmanned Aerial Vehicles (UAVs), popularly known as drones, are self-contained and can fly autonomously or be controlled by base stations. These autonomous node applications offer intriguing new approaches to completing a mission, whether related to military or civilian operations such as remote sensing, managing wildlife, traffic monitoring, etc. [185]. UAV communication has become an integral part of the development of the 5G and beyond network; however, one of the major application challenges faced by 5G and beyond UAV communication is weather and climate change. In [186], aerial channel models, precisely the air-to-ground channel models for different meteorological conditions such as rain, fog, and snow were investigated within a frequency range from 2–900 GHz based on the specific attenuation models for the different meteorology conditions. The results showed that rain and snow are very severe for mm-wave and THz bands, respectively. The effect of rain on the deployment of a UAV as an aerial base station in Malaysia was studied in [187] where the antenna height of the user, attenuation due to rain, and high-frequency penetration loss were considered for both the outdoor-to-outdoor and outdoor-to-indoor path loss models. The study utilized two algorithms known as Particle Swarm Optimization (PSO) and Gradient Descent. The results obtained indicated that the PSO algorithm requires less iteration to converge compared to the GO algorithm and that the effect of rain attenuation increases for higher frequency which results in a corresponding need for the UAV to increase its transmit power by a factor of 4 and 15 for outdoor-to-outdoor and outdoor-to-indoor, respectively.

9. Fade Mitigation Techniques for 5G

Fade mitigation techniques (FMTs) are adaptive communication systems employed to correct in real time the effect of attenuation on slant path [188]. Fading has three major effects: rapid fluctuations in signal strength over short distances or intervals, alterations in signal frequency, and multiple signals arriving at different times. Signals are spread out in time when they are put together at the antenna. This can result in signal smearing and interference between received bits.

Due to high rainfall in tropical climates, a signal is attenuated, and this signal attenuation can be decreased utilizing FMT. To regulate FMT approaches in real-time, there is the need to first understand the dynamic and statistical features of attenuation due to rain, which is the major source of channel or path loss, especially when the frequency exceeds 10 GHz [189]. Several methods to mitigate attenuation at the physical layer are classified as Power Control, Adaptive Waveform, Diversity, and Layer 2. The power control, adaptive waveforms, and Layer 2 techniques benefit from the system’s idle excess resources, whereas the diversity technique uses a re-route method. With the sharing of idle resources, the main aim is to make up for the fading of the link to sustain or optimize the performance. The diversity technique, on the other hand, can preserve the performance of the link by altering the geometry of the link or the frequency band [190].

9.1. Types of Fading

The different types of fading, as shown in Figure 7, are given considering the various channel impairments and positions of the transmitter and receiver.

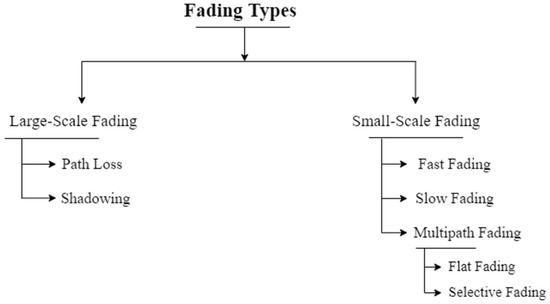
Figure 7. Different Types of Fading.

9.1.1. Large-Scale Fading

Path loss produced by the impacts of the signal traveling over broad areas is referred to as large-scale fading. The presence of noticeable topographical characteristics such as mountains/hills, trees/forests, billboards, clumps of buildings, etc., between the transmitter and receiver affects this phenomenon [191]. Path loss and shadowing effects are included in large-scale fading.

A.

Path Loss

As signals propagate through the medium over a long distance, the signal strength decreases with an increase in the distance. This is referred to as path loss or attenuation [151]. The amplitude of signals spreads as they propagate through the medium and, if not compensated for, the signal would become unintelligible at the receiving end. This loss is independent of the communicating parameters such as the transmitter, the type of medium, or the receiver, although it can be mitigated by increasing the area of the receiver’s capture [191].

B.

Shadowing

This refers to signal power loss caused by obstructions in the propagation route. Shadowing effects can be used to reduce signal loss in various ways. One of the most effective is LOS propagation. The EM wave frequency also affects shadowing losses. EM waves can pass through different surfaces but lose power, i.e., signal attenuation. The type of surface and the frequency of the signal determine the amount of loss. In general, as the frequency increases, the penetration power of a signal decreases.

9.1.2. Small-Scale Fading

Small-scale fading describes the substantial variations in the phase and amplitude of a signal that can occur due to minor variations in the spatial separation between a transmitter and receiver [191]. Small-scale fading occurs when the intermediate components in the signal’s path change. Multipath propagation, motion between sender and destination, surrounding object speed, and signal transmission bandwidth are all physical elements that cause small-scale fading. Small-scale fading in the radio propagation channel is influenced by the physical causes highlighted below:

• Multipath propagation

This is one of the elements that contribute to radio signal deterioration. Because of the irregularity in the atmosphere, the Point Radio Refractive Gradient (PRRG) varies with height, time of day, and season [192]. As a result of this phenomenon, radio waves arrive at the receiving antenna via two or more routes. Because of this inter-symbol interference, the time the signal takes to reach the destination becomes lengthened. Effects of multipath include constructive interference, destructive interference, and signal phase shifting.

2.

Speed of the mobile

The effect of the various doppler shifts on multipath components is random frequency modulation between the base station and the mobile. Doppler shift is positive when receiving mobile travels toward the base station, and it is negative otherwise [192,193].

3.

Speed of surrounding objects

The effect of objects being in motion in the radio channel is a Doppler shift based on varying times on the multipath components. However, if the neighboring objects move faster than the mobile, this effect precedes fading [193].

4.

Transmission bandwidth of the signal

If the bandwidth of the transmitted signal exceeds the “bandwidth” of the multipath channel—which is measured by the coherence bandwidth—distortion will occur on the receiving signal, although fading would not occur over a small distance. However, if the bandwidth of the transmitted signal is lower than the bandwidth of the multipath channel bandwidth, there would not be a distortion of the received signal, but its signal power changes frequently. The coherence bandwidth, related to the channel’s unique multipath structure, is used to quantify the channel’s bandwidth. Coherence bandwidth is defined as the estimate of the maximum frequency for which the signal is in relation to the amplitude [192].

The types of small-scale fading include the following:

A.

Frequency selective fading: The signal is transmitted and received via multiple propagation paths, each with relative delay and amplitude variation. Multipath propagation occurs when different regions of the transmitted signal spectrum are attenuated differentially, resulting in frequency selective fading. The channel spectral response is not flat in this case, but exhibits dip or fade in response to reflections canceling particular frequencies at the receiver.

B.

Frequency non-selective fading: Frequency non-selective fading, also known as flat fading, occurs when all signal component frequencies experience nearly the same amount of fading. Such fading occurs when the transmitted signal’s bandwidth is less than the channel’s coherence bandwidth. If the symbol period of the signal is greater than the RMS delay spread of the channel, then the fading is flat.

C.

Slow fading: Slow fading can occur as a result of occurrences such as shadowing, which occurs when a significant object, for example, a mountain/hill or a billboard, obstructs the path of the signal between the source and destination. It occurs over time and alters the received signal mean value. It is mostly concerned with moving away from the source and observing the estimated decrease in the intensity of the signal.

D.

Fast fading: In this case, the signal suffers from frequency dispersion due to Doppler spreading, which causes distortion. Fast fading is based on the speed of the mobile and the bandwidth of the transmitted signal. Due to the rapid changes in the channel, which is more than the signal period, the channel alters in one period.

9.2. Power Control Technique (PCT)

The PCT-fed mitigation concept is divided into four: (i) Up-Link Power Control (ULPC), (ii) End-End Power Control (EEPC), (iii) Down-Link Power Control (DLPC), and (iv) Onboard Beam Size (OBBS). However, in case the rain fade lasts a long time and is expensive, then the power control strategy demands high power capacity because the satellite transmitter that provides coverage to a diverse set of customers in various geographical regions must continuously operate at, or close to, the maximum power to mitigate the attenuation experienced by just one of the ground stations [190].

9.3. Adaptive Waveform

The primary idea that regulates adaptive transmission is to maintain a constant Eb/No by adjusting transmission parameters such as power level, symbol rate, modulation order, coding rate/scheme, or any combination of these parameters [194]. Adaptive Waveform is classified into three stages, which are: (i) Adaptive Coding (AC), (ii) Adaptive Modulation (AM), and (iii) Data Rate Reduction (DRR) techniques [195,196,197].

9.4. Diversity Reception Techniques

The diversity reception technique compensates for fading channel impairments and is typically achieved, for example, by using two or more receiving antennas. The diversity technique is employed to mitigate or compensate for fades experienced by the receiver. Base stations and mobile receivers can both use diverse approaches. These strategies aim to reroute signals within the network to mitigate network disruptions caused by atmospheric perturbation. Diversity is of three types: site diversity (SD), satellite diversity (SatD), and frequency diversity (FD) [188]. These procedures are quite costly since the related equipment must be redundant. Some of these techniques are applied [88] where a frequency diversity model has been used to reduce signal attenuation in heavy rainfall zones. The FD is used to overcome the rain fade in microwave point-to-point links as discussed in [198]. Figure 8 depicts the site diversity technique which consists of linking two or more ground stations that are receiving the same signal so that if the signal is attenuated in one area, another ground station can compensate for it.

Figure 8. Illustration of Site Diversity Scheme.

9.5. Frequency Variation Correction Factor

Frequency variation performance can be defined in terms of the outage percentage of time [88]. The variation correction factor $\left(I\right)$ [189,193] can be expressed mathematically as shown in Equation (109):

$$I=\frac{P_{ND}\left(A\right)}{P_{WD}\left(A\right)}$$

(109)

where $P_{ND}\left(A\right)$ denotes the outage percentage of an exact fade margin with no variation, and $P_{wD}\left(A\right)$ denotes the outage percentage with the same fade margin in the variation frequency.

From Equation (109), the correction factor depends on the outage level at the required attenuation, frequency separation, and diversity frequency. The specific attenuation for the frequency is considered the starting point of the correction factor development [189]. A diversity correction factor model was proposed in [199] with a frequency separation of 5 GHz based on the fading margin required for system design. The result showed a significant improvement within the frequencies ranging from 5 to 15 GHz, with no improvement above 15 GHz. However, a model for any frequency separation and path length for microwave communications is required.

9.6. Mitigation Techniques at Layer 2

At the layer 2 levels, FMTs do not try to mitigate a fade occurrence but instead rely on message re-transmission. At layer 2, two distinct approaches are possible: Automatic Repeat Request (ARQ) and Time Diversity (TD).

9.6.1. Automatic Repeat Request (ARQ)

ARQ is a data transmission error-control system that uses acknowledgments (or negative acknowledgments) and timeouts to achieve reliable data transmission across an unstable communication link. ARQ protocols are classified into three types: (i) Stop and Wait ARQ, (ii) Selective Repeat ARQ, and (iii) Go-Back-N ARQ [200]. ARQ has a higher spectral efficiency than repetition coding since it requires several transmissions only when the first transmission happens in a severe fading state. However, the ARQ requires a feedback channel because of the increased reliability requirements, which increases latency.

9.6.2. Time Diversity

In time diversity, signals of the same information are broadcast over the same channel but within a time interval $\mathsf{\Delta }t$ that exceeds the coherence time of the channel. The multiple signals would be transmitted with a distinct fading condition, hence the diversity. Before the transmission, a redundant error compensating code is inserted into the signal, which is then spread over time using bit-interleaving. As a result, erroneous bursts are avoided, simplifying error correction. This technique employs a propagation mid-term estimation model to determine the best time to re-broadcast the signal without the need to repeat the request [193,201].

Different types of fading mitigation techniques were identified and explained. It can be seen that their principles of operations are different; however, they complement one another. In some cases, hybridization is inevitable to improve availability/reliability, capacity improvement, and limit interference when there is the need to mitigate high impairments. Given these, Table 21 highlights some recent literature in these regards.

Table 21. Summary of Fade Mitigation Techniques.

Ref.	Objective of Study	Methodology Adopted	Result Obtained	Year
[197]	To develop an adaptive coding-modulation scheme based on a neuro-fuzzy system to achieve the required BER performance and channel data.	The study used MATLAB to simulate and analyze the neuro-fuzzy inference system to choose the optimal modulation-coding rate pair.	The results indicated that a system with a low-order QAM scheme and a low-convolutional coding rate is efficient at sustaining the availability of the link in severe tropical regions.	2022
[202]	Using the Macroscopic Diversity Scheme, the work mitigates rain attenuation for mmWave (30–300 GHz) and THz frequency (above 300 GHz).	The study used the DSD model to estimate the attenuation due to rain, and then employed the macroscopic diversity technique to mitigate it.	The study concluded by utilizing macroscopic diversity. If a signal from a hub is attenuated by rain, a handover process takes place for another hub that is not affected by rain to take over the service.	2021
[203]	An adaptive per-link power control strategy based on a proportional-integral-derivative (PID) controller was used to reduce attenuation due to rain for a wireless communication link.	The study used three separate stations, each with MICAz as both the transmitter and receiver, to investigate the relationship between power transmitted and link quality.	Compared to other controller systems, the PID controller provides an optimal response for adaptive power control due to its shorter rising and setting time.	2019
[204]	To reduce attenuation due to rain for a wireless fixed link in Port Harcourt using the Adaptive Power Control (APC) technique.	The study utilized 5-year (2012–2016) rainfall readings for modeling, and mitigating rain attenuation analyzed using MATLAB software.	Results after analysis showed that 2014 was the worst year for rainfall with the highest attenuation, which was successfully mitigated by the ATPC technique.	2018
[205]	To mitigate rain attenuation for 12.255 GHz earth-to-satellite link using time diversity technique in Malaysia.	The research utilized 2-year data collected using a 2.4 m-size SUPERBIRD-C satellite transmitting at a frequency of 12.255 GHz.	The results showed that the gain recorded at 0.1% outage exceeded 6 dB, while at 0.01% outage the gain exceeded 8 dB for a time delay of 10 min.	2018
[189]	To develop an estimation model employing the frequency diversity correction for FMT between 50 and 90 GHz.	The study employed the ITU-R model to estimate the attenuation due to rain based on the calculated rainfall rate in the South-East Asia tropical region.	The results indicated that the improvement does not vary for frequencies up to 70 GHz but changes for frequencies above 70 GHz.	2017
[206]	To evaluate the influence of rain on lower and higher operating frequencies and to design a fade mitigation technique known as a switching circuit.	The study used a tipping bucket rain gauge to collect 1-year rainfall data utilizing an experimental link where the transmitter and receiver operate in two frequency bands, 5.8 GHz and 26 GHz.	Results showed a negligible impact of rainfall for the 5.8 GHz link, whereas the effect is much stronger for 26 GHz, hence switching to the lower band during heavy rain.	2015
[199]	To propose and develop a prediction model to reduce rain fade between 5 and 40 GHz, known as the frequency diversity improvement factor.	The study employed the ITU-R model to estimate the attenuation due to rain using measured rain rates in Malaysia.	Results showed that rapid improvement was observed within the frequency separation range of 5–15 GHz, but no improvement was observed for separation above 15 GHz.	2015

9.7. Weakness of ITU-R Model for Rain Attenuation Research for 5G Networks and Beyond

The ITU-R model does not correctly predict rain attenuation over a short distance for 5G network or beyond. As a result, the impacts of rain over short distances cannot be accurately estimated using the conventional models that rely on the ITU-R model. The inadequacy of the ITU-R model to accurately estimate the attenuation due to rain along paths less than 2 km was shown in [71]. One such study in the literature showed the evaluation of the ITU-R model in rain attenuation prediction in the 33–45 dB range [207]. The research was done in Budapest for a path length of 2.3 km at 72.56 GHz. The authors demonstrated that the ITU-R model overestimated the attenuation when evaluated against the measured attenuation. A comparable analysis predicted 26 and 38 GHz availability as 98.6% and 99.5%, respectively. An experimental investigation was conducted in Malaysia at a distance of 0.3 km between source and destination, with predictions made using the ITU-R model [43]. Further research has found that the ITU-R model has a larger prediction error for distances less than 1 km [43,71,94,208,209,210]. Table 22 presents the summary of the weakness of the ITUR-R model for short-distance applications.

Table 22. Summary of Works That Have Shown the Short-Distance Inability of the ITU-R Model.

Ref.	Location	Time	Frequency (GHz)	Distance (m)	General Comments/Findings	Year
[94]	Korea	3 yrs.	38/75	100	They developed a regression model to predict attenuation at 75 Hz, and the model was benchmarked with six existing models.	2017
[43]	Malaysia	1 yr.	26/38	300	This research utilized the effective distance to calculate the error between measured and estimated attenuation.	2020
[71]	Italy	4 months	73/83	325	The possibility of using existing models on attenuation predictions on the E band has been analyzed.	2020
[20]	United Kingdom	1 yr.	25.84/77.52	35	Effects of rain on building to building along with wet antenna effects over a short range have been analyzed.	2019
[209]	Korea	1 yr.	73/83	500	The ITU-R model was deemed unsuitable in Korea with a 100 mm/hr rain rate.	2013
[210]	Mexico	3 months	84	560	Many experiments were carried out to determine the attenuation under standard conditions	2017
[208]	Japan	10 months	120	400	In this case, the results obtained agreed with each other at a maximum rain rate (600 mm/hr).	2009
[211]	Czech Republic	5 yrs.	58	850	It has been established that the annual average and worst month of the year disagreed with attenuation obtained by the ITU-R model.	2007
[212]	Albuquerque, United States of America	1.5 yrs.	72/84	1700	Techniques for determining specific attenuation were presented since the ITU-R model inaccurately predicted attenuation in the area.	2019

10. Future Research Directions

The section discusses further research directions for rain attenuation for 5G millimeter-wave and briefly explains some of the industrial applications of the 5G technology.

10.1. Application of Machine Learning Techniques

The literature has shown that Artificial Intelligence (AI) is a very vast field that encompasses both machine learning (ML) and deep learning (DL), and also finds applications in many areas of research, some of which are engineering, management, security, medicine, science, environment, energy, and finance [213,214]. In the same way, AI-based models can be employed to accurately predict rain attenuation, as well as mitigate it, in both satellite and terrestrial communication links with minimum computations and errors [169,170,171,172]. Based on the review provided in Table 19, it can be seen that the performance of these developed AI-based models was mostly evaluated against a statistical model—the ITU-R model—and most of these models relied on temporal rain data and cannot generalize large-scale systems [170]. Also, there are still few developed AI-based models, particularly for the mitigation of rain attenuation for the 5G network and beyond. Therefore, for future directions, the following are recommended:

• More novel AI-based models that can predict and particularly mitigate rain attenuation for the 5G network and beyond should be developed that are not solely based on temporal rain data.
• An efficient and simple AI-based path length reduction model should be developed which can be used to determine the most appropriate path correction factor.
• A novel and robust AI-based model should be proposed that can serve as a benchmark for the evaluation of other newly developed AI-based models at all frequency and rain rate ranges.

10.2. Regular Accessibility to Rain Data

It is known that rain behavior is changing due to climate change and weather conditions across the globe. Therefore, it is critical to establish a periodic check of the network availability against the expected system design availability so that if the difference between the predicted and the actual system attenuation is significant, then the system can be modified for restoration to normal. In addition, if the method used for rain attenuation is dependent on a database, then there is a need to frequently update the database with the most recent rain rate data. However, one of the major challenges with this periodic checking is the cost; therefore, for future work a cost-effective and easy way to generate and collect rain data should be proposed.

10.3. Rain Attenuation Research for 5G and beyond UAV Communication Network

The Unmanned Aerial Vehicle (UAV) has been proven to be an integral part of the development of the 5G network and beyond; however, rain is one of the major meteorological conditions that affects UAV communication, especially for mm-wave. Furthermore, there is very little research on how weather and climate conditions can affect 5G and beyond UAV communication networks as it is difficult to meet QoS requirements under dynamic environments with varying locations. Further work recommends that adaptive beamforming techniques for UAV communication for both millimeter and THz bands considering the effects of various meteorological conditions should be studied and models that can accurately predict and mitigate these effects should be developed.

11. Conclusions

Rain is a significant source of attenuation for electromagnetic wave propagation, particularly when the frequency range exceeds 10 GHz. This paper conducted a systematic review of research efforts on rain attenuation models. Some of these investigations have resulted in novel findings and models. According to the study, existing rain attenuation prediction models have been classified as empirical, statistical, physical, fade-slope, and optimization-based models. It can be seen that, although the Crane and ITU-R models are the most widely used models for rain attenuation prediction, they under- or overestimate the attenuation in tropical regions. Hence, none of the existing models can accommodate all the environmental factors considered in the design of a wireless network. There is a need for more research in different environments. Also, RMS is the most widely celebrated method for testing the accuracy of the developed rain attenuation models for different environments. However, other methods that have not been given the expected attention are still available. This study also examined existing fading mitigation approaches where it was seen that the adaptive waveform techniques are the most utilized method. Machine learning-based models were also presented and from the review, it can be seen that this research area still has many gaps to fill in terms of developing a model to accurately predict, and particularly to mitigate rain attenuation. Moreover, other areas of further research that could assist global communities to achieve higher penetrations of the new technology were highlighted. If all of these are given the expected attention, there is room for further improvement in cost, reliability, and energy consumption for future communication networks. This study can serve as reference material for network designers and for new and existing researchers to enhance their skills in developing 5G and beyond 5G wireless networks.