Abstract
Competition in electricity markets leads to volatile conditions which cause persistent price fluctuations over time. This study explores the problem of electricity pricing fluctuations in the DE-LU bidding zone from October 2018 to March 2022 by applying time series analysis. The determinants of electricity price fluctuations are broken down into three groups: exogenous prices (gas, coal and CO2 prices), internal (consumption and generation) and external (net import between neighboring bidding zones) electricity flows. Based on the SARIMAX model, we tried to combine all these factors to forecast electricity prices in the single bidding zone. It was found that the SARIMAX (1, 1, 2) × (3, 1, 0, 7) model with exogenous prices, internal and external electricity flows, which has the lowest AIC and MAPE values, is the best-fitted model for the DE-LU bidding zone. Anonymous trading and unpredictable individual bidding strategies lead to persistent price volatility, which causes electricity prices to deviate from fundamental trends. To reveal the risk factors, the SARIMAX model of electricity prices needs to be supplemented with a GARCH model of the residual returns. For forecasting electricity price residual volatility in the DE-LU bidding zone, the SARIMAX model with exogenous prices, internal and external electricity flows must be accompanied with the GARCH (7, 0) model.
1. Introduction
The liberalization of the EU electricity markets reveals risks of uncertainty associated with success or failure in competition. Short-term trade, anonymity of participants and marginal pricing make it impossible to exactly determine generation units that will cover the consumer load or the unit that will meet the last MWh of electricity demanded, and, consequently, establish the market clearing price (according to European legislation, day-ahead prices can vary from −500 €/MWh to 3000 €/MWh [1]). Electricity prices have historically been dispersed over time and space. The causes of spatial dispersion of electricity prices were previously determined by Qiang et al. (2021) as geographical orientation, direction of electricity flows and structure of electricity generation [2]. Electricity prices are also dispersed over time. Changes in electricity prices are conditioned by numerous variables, and, at the same time, demonstrate their own patterns. Market participants strive to diversify their bidding strategies, while relevant authorities and market operators strive to prevent market manipulation. All this determines the increasing application of methods of time series analysis and electricity price forecasting.
Today, ENTSO-E supports forecasting of (i) the total load for day-ahead, week-ahead, month-ahead and year-ahead; (ii) the total scheduled generation for day-ahead; (iii) the day-ahead and intraday generation of wind and solar; and (iv) the day-ahead scheduled cross-border exchanges [3]. However, there is no forecasting of electricity prices, which confuses market participants in choosing bidding strategies and forces each of them to carry out such forecasting on their own.
Numerous studies deal with methods for electricity price forecasting (an overview of a variety of such methods can be found in [4,5]), where a special focus is made on time series models, including the ARIMA (Autoregressive Integrated Moving Average), SARIMA (Seasonal Autoregressive Integrated Moving Average), ARIMAX (Autoregressive Integrated Moving Average with Exogenous Factors) and SARIMAX (Seasonal Autoregressive Integrated Moving Average with Exogenous Factors) models, as well as the GARCH (Generalized Autoregressive Conditional Heteroscedastic) model. Researchers have built time series models to forecast electricity prices for different time intervals and various local markets; however, such forecasting should be carried out continuously, and forecasts need to be updated regularly based on relevant information both in the internal electricity market and in related markets.
Contreras et al. (2002) were among the first scientists to propose using an ARIMA model to forecast 24 market clearing day-ahead prices. They applied an ARIMA model to forecast prices in the electricity markets of Spain and California and found that the Spanish model needed the previous 5 h to predict hour-ahead electricity prices, as opposed to the 2 h needed by the Californian model. The ARIMA models predicted results more accurately until the markets experienced high spikes and became highly volatile [6]. Later, Conejo et al. (2005) developed a modification of ARIMA models using the wavelet transform to convert ill-behaved price series in a set of better-behaved constitutive series by taking into consideration daily and weekly error variances. They concluded that the future values of the constitutive series could be forecasted accurately using a simple ARIMA model [7]. Gao et al. (2016) developed an ARIMA model for forecasting prices in the UK electricity market for one period ahead (in the next day and next week). They warned not to overfit the model with time-domain lags and historical price data [8]. Gao et al. (2017) compared the models of ARIMA and artificial neural network, which were applied to the price forecasts for up to three steps or eight weeks ahead in the UK electricity market, and found that the ARIMA model gave a greater improvement than the last one in terms of root mean square errors [9].
Electricity consumption is cyclical, varying by months, days of the week and hours. For this reason, a wide range of research deals with the inclusion of seasonal patterns in electricity price forecasts. Thus, scientists also investigate the influence of seasonal patterns on electricity price fluctuations [10,11]. Among SARIMA models, it is worth mentioning a double seasonal ARIMA, proposed by García-Martos and Conejo, to account for weekly and daily cycles in the electricity market [12]. Jakaša et al. (2011) also used a SARIMA model to predict day-ahead prices for the German electricity market. They found 3-day-ago non-seasonal effect and week-ago seasonal effect to predict the day-ahead price [13]. Česnavičiu (2020) constructed the weighted SARIMA (1,1,1) model, adjusting it according to the percentage value defined by the exponential AR (1) forecast. It fairly approximated the actual time series and caught the peak values for the Lithuanian electricity market [14].
Changes in electricity prices over time are also determined by a continuum of fundamental factors [15,16,17], for the accounting of which ARIMAX models are used. Misiorek and Weron (2005) calibrated the ARMAX model with system load as the exogenous variable for forecasting prices in the Californian electricity market [18]. In the opinion of Karabiber and Xydis (2019), the ARIMA model needs to be extended to include seven regressors: temperature, consumption and production prognosis, wind prognosis, oil prices, natural gas prices and hydro-reservoir levels. They looked at the Danish day-ahead electricity market and found that the ARIMAX model outperformed others in terms of mean error [19]. Angamuthu et al. (2019) considered 17 variables, including 9 exogenous ones: power demand; hydro, solar, wind, coal and combined cycle power generation; and temperature, wind speed and radiation. They combined the ARIMA model with other forecasting models to improve residual errors in predicting hourly spot prices [20]. Habenet al. (2021) applied ARX and ARIMAX models and predicted electricity supply-and-demand curves to produce a probabilistic price forecast [21].
In many studies, researchers have tried to combine endogenous electricity prices with exogenous fundamental factors and seasonal patterns [22,23,24,25,26]. Cruz et al. (2011) found that accounting for the wind generation forecast in a SARIMAX model, along with the inclusion of the day of the week by means of periodic models, improves the predictive accuracy of electricity price forecasting [24]. De Marcos et al. (2019) used load/demand factors as exogenous terms in the SARIMAX model [25]. As proven by Ferre et al. (2021), SARIMAX is one of the best performance techniques, making reliable predictions for the German electricity market and having the advantage through its explanatory variables of better capturing the price volatility. The SARIMAX model built by the researchers included hourly load, wind and solar generation [26].
Despite previous electricity prices, fundamentals and seasonality, electricity prices remain extremely volatile and are subject to the influence of the individual behavior of market participants [27,28,29,30]. Therefore, a current research focus is forecasting price spikes in electricity markets. Among the studies considering this problem, it is worth mentioning the study by Chinnathambi et al. [20]. Another study in this area was carried out by Zhao et al. (2018). They assessed numerous times series models (ARMA, ARIMA, SARIMA, SARIMAX and ARIMA-GARCH) for predicting electricity prices in the MISO region (USA) and found it helpful to improve the prediction accuracy through including electricity price volatility as an exogeneous factor in the ARMAX-GARCH model [31]. A similar study was conducted by Pourghorban et al. (2019) for the Iranian electricity market [32].
Today, European electricity markets are under unprecedented pressure from primary resource prices. For example, the average Dutch TTF Natural Gas price grew by five times, API2 Rotterdam Coal and European Emission Allowance prices by two times each, while the electricity prices increased by three times in 2021 compared to 2020. As of 21 December 2021, in the DE-LU bidding zone, the maximum daily electricity price was recorded at the level of 435 €/MWh, with the maximum gas price being 180 €/MWh. The coal prices passed the peak on 5 October 2021 at a level of 236 Euro/t, and the CO2 prices did so on 8 December 2021 at a level of 87 Euro/t CO2 eq. In Q1 2022 (7 March 2022–8 March 2022), new price maximums were set at 486 €/MWh, 227 €/MWh and 403 Euro/t for electricity, gas and coal, respectively, while the maximum for CO2 prices was updated a month earlier (8 February 2022) and amounted to 97 Euro/t CO2 eq. [3,33,34,35]. All this requires taking into consideration new situations in the functioning of electricity markets and forecasting of electricity prices.
Therefore, the purpose of this work is to develop a methodological approach to forecasting electricity prices that will ensure their constant updating and reproducibility by market participants. The hypothesis of the study is that changes in electricity prices over time are determined by a combination of fundamental factors of the internal market and external related markets, and uncertainty of the behavior of electricity market participants. This study therefore provides a methodological approach to electricity price forecasting, based on time series analysis, which allows: (i) tracking the behavior of electricity prices depending on their own patterns and fundamental factors of electricity and other related markets; (ii) revealing the risks of electricity price residual volatility due to unpredictable bidding strategies of market participants.
Having investigated studies on electricity price forecasting based on time series analysis (Timeline), it can be noted that this study correlates with its key areas and can improve the understanding of the behavior of electricity prices in the market under uncertain conditions (Figure 1).
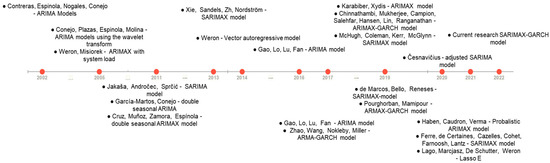
Figure 1.
Timeline of methods of time series analysis and electricity price forecasting. Source: constructed by the authors based on [4,5,6,12,13,14,18,19,20,21,22,23,24,25,26,30,31,32].
The remainder of this paper is organized as follows. Section 2 considers the materials and methods used for electricity price analysis and forecasting. Section 3 presents the detailed results of the electricity price modelling and forecasting: Section 3.1 describes the results of the data analysis to predefine the time series models; Section 3.2 focuses on the results of the construction of the time series models, based on fundamental factors of the electricity and related markets, as well as providing the forecast for the next month; Section 3.3 gives details of the time series models’ residuals and describes the construction of the time series models to forecast their volatility. Section 4 presents a discussion of key conclusions and recommendations.
2. Materials and Methods
2.1. Methodological Approach
The general design of the research is based on the methodological approach presented in the flowchart in Figure 2.
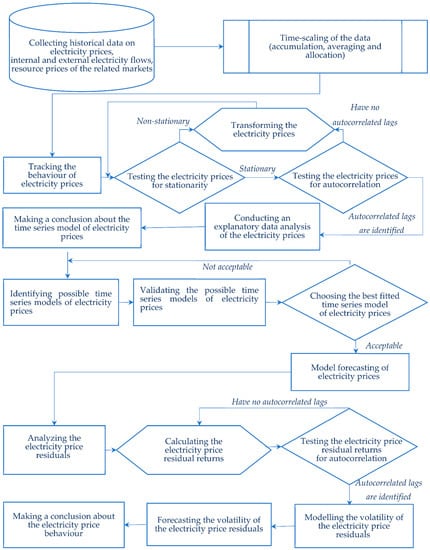
Figure 2.
Time series analysis and forecasting of the electricity prices. Source: developed by the authors based on [4,5,18,19,20,21,22,23,24,25,26,30,31,32].
2.2. Data Collection and Preparation
Time series analysis of electricity prices employs the ENTSO-E Transparency Platform database [3] for the DE-LU bidding zone. The choice of this bidding zone was due to its size and level of trade development (in 2021, its electricity consumption was approximately 20% of the EU’s total consumption [36], with 120 power generation units being in operation, and it traded with 11 neighboring bidding zones [3] on 2 highly liquid trading platforms (Epex Spot [37] and NordPool [38]). The foregoing allowed us to assume that this electricity market was highly competitive. The database comprised day-ahead hourly electricity prices from the moment of its separation from the AT bidding zone (October 2018) to March 2022. Then, the data were converted into daily electricity prices as an arithmetic mean of the hourly electricity prices for the delivery periods between 0.00 UTC (incl.) and 24.00 UTC (excl.). The destination database included 1277 points.
To further improve the quality of the time series models, we needed additional data on the current and day-ahead forecasted electricity generation and consumption flows and net external electricity flows between neighboring bidding zones, which were also accumulated from the ENTSO-E Transparency Platform [3]. Prices of the related energy markets, namely, Dutch TTF Natural Gas price (further gas price) [33], API2 Rotterdam Coal price (further coal price) [34] and European Emissions Allowance price (further CO2 price) [35] were also used as exogenous variables.
All data were collected and prepared for analysis with the help of the Power Query add-in package for Microsoft Excel (developed by Microsoft Corp. [39]).
2.3. Data Analysis
For the purpose of the analysis of electricity prices, development of their time series model and their further forecast, presented in this article, Python code was developed in the open-source Jupiter Notebook [40]. To define the best-fitted model, the Auto Arima package was applied (see Supplementary Materials).
The data analysis was carried out in 3 stages: descriptive statistics; stationarity and autocorrelation tests; exploratory data analysis.
Descriptive statistics were used as the first stage of the data analysis. In general, they help summarize and condense data, aggregate results, determine the frequency of data distribution and measure their central tendency and dispersion [41,42]. Descriptive statistics of electricity prices allow one to have a quick glance at the behavior of electricity prices and the influence of fundamental factors on them. Commonly applied measures, such as mean (µ), median (Me), standard deviation (std.dev.), variation (var), volatility (vol), and skewness (S) and kurtosis (K), were used to track the behavior of electricity prices over time.
The next stage in the analysis was testing the data for stationarity and autocorrelation. To check the data for stationarity, an augmented Dickey–Fuller test (ADF test), which presents likelihood ratio statistics for the rejection of the null hypothesis about the non-stationarity of time series, was carried out [43,44]. If the raw time series are non-stationary, they must be converted to stationary ones. For this purpose, we used price returns (the percentage change between two consequent prices) and price differences (the difference between two consequent prices). To track the influence of lagged endogenous variables, we estimated two autocorrelation functions, that is, autocorrelation function (ACF) and partial autocorrelation function (PACF), which are plotted correlograms used to tentatively identify the most likely lags for a time series model. ACF is responsive to immediate impacts (autoregressive (AR) components) and PACF is responsive to secondary impacts (moving average (MA) components) of previous data [45,46]. The second stage of the analysis enabled converting the data to stationary data and drawing a preliminary conclusion about the time series model.
The third stage involved an exploratory data analysis (EDA), which helped identify the trend, seasonal and residual components and describe the model formulation. It was visualized, plotted and manipulated without any assumptions [47,48].
In general, data analysis is a pre-processing phase of building a time series model.
2.4. Model Development and Forecasting
First, to build the model, the dataset was split into the historical and testing period. The historical period was defined as 90% of the initial data volume, i.e., until 23 November 2021 inclusive, and the testing period included 128 days, from 24 November 2021 to 31 March 2022.
The time series analysis of electricity prices involved the evolution of the models from ARIMA to SARIMAX with exogenous prices, internal and external electricity flows. The specification of the models under study is as follows:
- (1)
- ARIMA (p, d, q), developed by Box and Jenkins (1970) [49]:
- (2)
- SARIMA (p, d, q) (P, D, Q, s), first suggested by Chatfield and Prothero (1973) [50]:
- (3)
- ARIMAX (p, d, q)×, first used by Young and Whitehead (1977) [51]:
- (4)
- SARIMAX (p, d, q) (P, D, Q, s)×, developed by Holst et al. (1988) [52]:where p is the autoregressive component; q is the moving average component; d is the integration order (the number of times needed to ensure stationarity); P is the seasonal variation of the autoregressive component; Q is the seasonal variation of the moving average component; D is the seasonal integration order; s is the length of the seasonal cycle; Yt, Yt−i are the values in the current period and i periods ago, respectively; ∆d is the difference between the values in the current period and d periods ago; are error terms for the current period and j periods ago; c is the baseline constant factor; is the part of the value i periods ago relevant in explaining the current one; is the seasonal lagged value s × l periods ago; is the seasonal lagged error for s × k periods ago; is the part of the error for j periods ago relevant in explaining the current value; is the part of the seasonal lagged value l periods ago relevant in explaining the current one; is the part of the seasonal lagged error for k periods ago relevant in explaining the current value; X is the exogeneous factor; is the slope coefficient for the exogeneous factor.
The specification of the time series models was made based on maximization of the log likelihood function (LLF) and minimization of the Akaike information criterion (AIC), using the Auto Arima package in Python. The autoregressive and moving average components were selected if their p-values were less than 0.05. At the same time, external regressors were left in the model even if their p-values were more than 0.05, which allowed us to track fundamental factors affecting electricity prices. The model construction results were compared with the true testing data both through their visualization and based on the criteria of mean absolute percentage error (MAPE) [53,54].
Our final decision was to supplement the SARIMA models with 3 groups of exogenous factors: (i) exogenous prices (gas, coal and CO2 prices), (ii) internal (consumption and generation) electricity flows, and (iii) external (net import) electricity flows. At each stage, we demonstrated how the SARIMAX models evolved as additional groups of factors were included.
SARIMAX models can become a practical, widely used tool in electricity price forecasting. To prove this, we used various developed models to forecast electricity prices for April and compared the obtained values with the actual prices, which were already known at the study completion date.
Despite the variety of fundamental factors, SARIMAX models are characterized by the presence of significant residuals, which, as expected, are determined by individual bidding strategies of market participants and are correlated with such a phenomenon as volatility. Therefore, the next step was forecasting the volatility of residuals. To forecast residuals and reveal their volatility, we constructed a GARCH model, which was created by Bollerslev (1986). The model has the following specification [55]):
where is unconditional variance; are current and past conditional variances, respectively; is the squared residual of the past variance; is the numeric coefficient for the past squared residual; is the numeric coefficient for the past conditional variance.
Thus, the proposed approach is based on forecasting electricity prices under the influence of fundamental factors (SARIMAX models) and forecasting volatility (GARCH models) as a consequence of the influence of individual decisions of market participants.
To build the forecast for the next period, actual electricity price data and external regressor forecasts are updated as they become available on the ENTSO-E Transparency Platform and European power exchanges. To forecast prices within a month, a fixed valuation scheme is used, while a recursive valuation scheme is used to predict electricity prices for each subsequent month (their features are defined in [56]).
3. Results
3.1. Data Analysis of Electricity Prices
The presented statistical analysis of electricity prices was the starting point in searching for fundamental impact factors and studying their fluctuations over time (Table 1). The upheavals in the electricity market made it possible to suggest the heterogeneity of electricity prices over the period under study.

Table 1.
Descriptive statistics of electricity prices in the DE-LU bidding zone in October 2018–March 2022.
In Q4 2018, the distribution of electricity prices in the DE-LU bidding zone was close to normal (Me was higher than µ by 2.47 €/MWh), homogeneous (var = 25.3%), peaked (K = 1.5) and left-skewed (S = −0.8), with a moderate volatility level (vol = 48.5%). The interval range was the smallest, amounting to 71.32 €/MWh. The prevailing price distribution was determined by a moderate GDP growth rate (1.1% p.a.) and replacement of fossil fuel (except gas) in power generation with renewable energy sources (RES). At the same time, an increase in the prices for coal (+4% p.a.), gas (+32% p.a.) and CO2 (+170%) was observed. In 2018, electricity prices in the DE-LU bidding zone were among the lowest in the EU.
In 2019, there was a significant decrease in electricity prices in the DE-LU bidding zone; however, their distribution remained close to normal (Me was higher than µ by 1.54 €/MWh), relatively homogeneous (var = 31.5%), sharply peaked (K = 8.1) and left-skewed (S = −0.8), with a high volatility level (vol = 141.1%). The interval range µ was 125.66 €/MWh. This situation was conditioned by a decrease in electricity consumption during a mild winter, despite a stable real GDP growth rate (1.1% p.a.), a rapid increase in renewable generation and a sharp increase in international trade (the electricity exports exceeded its imports by 1.8 times). At the same time, there was a decrease in gas prices (−41% p.a.) and an increase in CO2 prices (+57% p.a.), which led to a coal-to-gas switching in power generation.
In 2020, the decline in electricity prices in the DE-LU bidding zone continued, but in addition to the existing factors (mild winter, development of renewable generation, switching power generation from coal to gas), there was a decrease in electricity consumption due to restrictions of socio-economic activity associated with the COVID-19 pandemic (the real GDP growth amounted to 4.6% p. a). Despite the pandemic, the electricity imports grew by 23%, while the exports fell by 9%. However, the distribution of electricity prices in the DE-LU bidding zone was still close to normal (Me was higher than µ by 1.12 €/MWh), peaked (K = 1.6) and left-skewed (S = −0.4), but, at the same time, heterogeneous (var = 45.7%) and highly volatile (vol = 194.4%). Frequent price spikes, but with a smoothed magnitude, were observed. The interval range was considerably higher (100.03 €/MWh) compared to 2019. The gas and CO2 prices fell in the 1st half of 2020 but recovered in the 2nd half of 2020, while the profitability of coal generation dropped below 0.
In 2021, there was a reversal of the downtrend and the distribution abruptly became abnormal (Me was lower than µ by 22.33 €/MWh, and std.dev. reached 66.93 €/MWh), while staying peaked (K = 4.2) but right-skewed (S = 1.8), heterogeneous (var = 69.1%) and with a moderate volatility level (vol = 79.1%). The economic recovery (with a real GDP growth of 2.9% p.a.) was accompanied by an increase in electricity and gas consumption, whereas the volume of international trade in electricity more than doubled. The aforementioned, together with the tense geopolitical situation, caused a sharp increase in the prices for gas (94 €/MWh in Q4 2021), coal (157 €/t in Q4 2021) and CO2 (69 €/tCO2 in Q4 2021) and, as a consequence, growth in the electricity prices (178.9 €/MWh in Q4 2021). Such price trends caused the reverse switching of electricity generation from gas to coal and an increase in the share of nuclear energy.
At the beginning of 2022, there was a softening of the upward trend for the electricity prices observed in 2021. However, this trend was reversed by the Russian invasion of Ukraine. In Q1 2022, the average electricity price accounted for 184.60 €/MWh, the distribution was abnormal (Me = 177.85), peaked (K = 4.2), right-skewed (S = 0.9), heterogeneous (var = 48.3%) and with a relatively high volatility level (vol = 79.1%). On 8 March 2022, the electricity prices hit a new all-time high of 486 €/MWh, the gas price being 246 €/MWh and the CO2 price being 68.10 €/tCO2.
In general, from October 2018 to March 2022, the distribution of the electricity prices in the DE-LU bidding zone can be considered abnormal, heterogeneous, peaked, right-skewed and highly variable. Under such conditions, tracking changes in the electricity prices is complicated due to both the action of many fundamental factors and the chaotic behavior of market participants, which requires the use of complex methods for analyzing and forecasting time series. Fundamental factors determining the changes in the prices over time can be considered the behavior of the prices in the related markets, electricity consumption and the structure of internal generation and external trade.
The electricity prices depend on the ratio and distribution of the forces of electricity demand and supply at a particular point in time, which makes them non-stationary and poorly predictable. Figure 3 shows the ACF and PACF plots, as well as the results of the ADF test for (i) daily electricity prices, (ii) electricity price returns and (iii) electricity price differences, which allows one to determine the correct time series for the analysis and forecast.
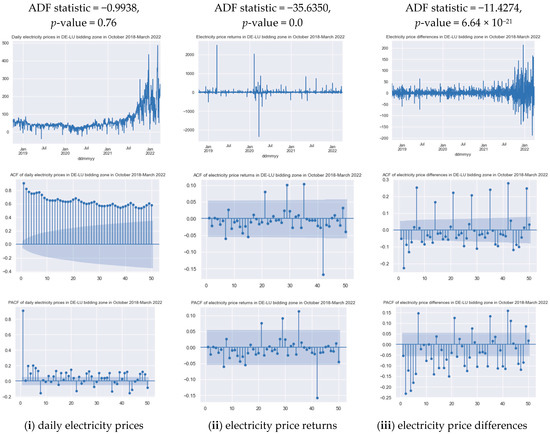
Figure 3.
Autocorrelation and stationarity of the daily electricity prices in the DE-LU bidding zone. Source: constructed by the authors based on [3].
The critical values of the ADF statistic are: for p-value = 0.01, −3.4356; p-value = 0.05, −2.8638; and p-value = 0.1, −2.5680. These results have allowed to conclude the following:
- The time series of the daily electricity prices are non-stationary. Thus, the null hypothesis has failed to be rejected. The electricity prices have a partly time-dependent structure with no constant variance over time. In this regard, they cannot be used as raw data for the analysis and forecasting;
- Whereas the time series of electricity price returns and electricity price differences are stationary, their current values are conditional and can be used for forecasting,the ACF and PACF plots for electricity price returns show no significant lags, i.e., immediate and secondary impacts of the past values of the time series on the current periods;
- The ACF and PACF plots for electricity price differences show numerous impacts, which proves the expediency of using the ARIMA model based on exact difference–stationary time series;
- The ACF plot of electricity price differences also indicates the presence of seasonality every 7 lags, which corresponds to a weekly cycle of electricity consumption and, accordingly, fluctuations in the electricity prices.
The exploratory data analysis of electricity price differences by additive components (trend, seasonal and residual) allows mathematical confirmation of the hypothesis about seasonality of price fluctuations (Figure 4).
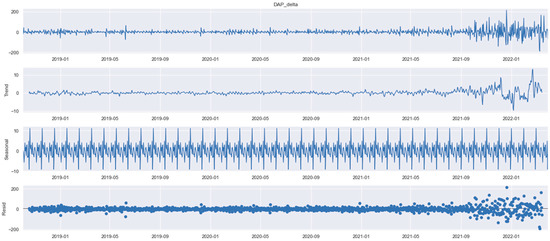
Figure 4.
EDA of electricity price differences in the DE-LU bidding zone. Source: constructed by the authors based on [3].
If we look at the difference in the electricity prices before the decomposition, no patterns or trends can be observed. Their values revert around zero until September 2021, after which they demonstrate a great deviation from zero. The trend component allows one to assume the absence of an obvious tendency until the same period, after which a quadratic trend can be admitted. There is a strong seasonal pattern reflecting fluctuations of electricity prices by delivery periods: each month, 4–5 price spikes, reflecting daily price fluctuations over the week, can be recognized. The remaining residuals are caused by other exogenous factors, which strongly affected electricity markets starting from the end of Q3 2021.
The abovementioned leads to the conclusion about the practicability of using a SARIMA model and supplementing it with exogenous fundamental factors, i.e., building a SARIMAX model.
3.2. Time Series Analysis of Electricity Prices and Their Forecasting
Appendix A presents the evolution of the models of electricity price fluctuations over time, from a simple ARIMA to complex SARIMAX models. According to the AIC values, a qualitative improvement of the models with the inclusion of seasonal parameters and external factors is observed, the values decreasing from 11,761 for the ARIMA model to 9853 for the SARIMAX model. The results of building the SARIMAX models with the following groups of X-factor differences are presented in:
- Table 2 for exogenous prices (gas, coal and CO2 prices);
 Table 2. Results of building the SARIMAX model with exogenous prices.
Table 2. Results of building the SARIMAX model with exogenous prices. - Table 3 for exogenous prices and internal (consumption and generation) electricity flows;
 Table 3. Results of building the SARIMAX model with exogenous prices and internal electricity flows.
Table 3. Results of building the SARIMAX model with exogenous prices and internal electricity flows. - Table 4 for exogenous prices, internal and external (net import) electricity flows.
 Table 4. Results of building the SARIMAX model with exogenous prices, internal and external flows.
Table 4. Results of building the SARIMAX model with exogenous prices, internal and external flows.
The visualization of the SARIMAX models for the testing period shows how they cover extreme fluctuations in the electricity prices due to changes in the market conditions (Figure 5).
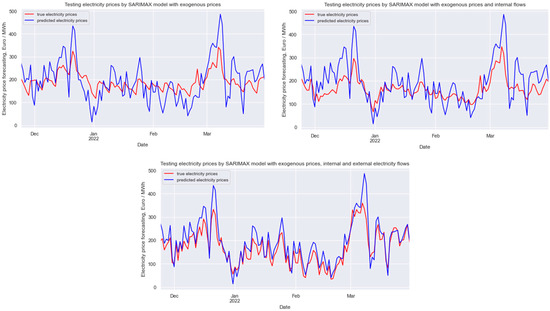
Figure 5.
Observed and forecasted electricity prices in the DE-LU bidding zone for the testing period (24 November 2021–31 March 2022). Source: constructed by the authors based on [3,33,34,35].
The modelling results are as follows.
In the SARIMAX model with exogenous prices, an immediate impact (AR components) on the change in the electricity prices is exerted by its day-ago and 2-days-ago prices: inversely proportional (coef. = −0.11) and directly proportional (coef. = 0.31), respectively. In this case, random effects (MA components) of the previous period prices have a significant impact (coef. = 0.73). We observed an immediate directly proportional impact of the week-ago electricity prices (coef. = 0.99) and secondary inversely proportional impact of the 2-weeks-ago random effects (coef. = −0.9264 and coef. = −0.13 for the first and second week ago, respectively), and a directly proportional impact of the random effects of the third week ago (coef. = 0.1321). The prices for gas (coef. = 1.62) and CO2 (coef. = 0.27) have an immediate directly proportional impact on the changes in the electricity price, while coal prices have an immediate inversely proportional impact (coef. = −0.02), but this factor is insignificant (p-value = 0.25). The standard error and MAPE of the first model accounts for 408 €/MWh and 34%, respectively. Therefore, forecasting electricity prices based on the SARIMAX model with only exogenous prices is quite risky.
In the SARIMAX model with exogenous prices and internal flows, gas prices exert an immediate positive impact (coef. = 1.93), while coal prices have a negative immediate impact and CO2 prices have an insignificant immediate positive impact (coef. = 0.06, p-value = 0.55). Oil, nuclear, hydro, solar and biofuel generation, the p-value for which exceeds a significant level, are also insignificant for pricing in this bidding area. However, coal and gas generation and consumption exert a directly proportional impact (with the coefficients of 0.008, 0.014 and 0.03, respectively); wind and nuclear power generation, and pumped storage exert an inversely proportional impact (with the coefficients of −0.011, −0.024 and −0.085, respectively). At the same time, this model shows no immediate impact of previous prices but only a secondary directly proportional impact of the 3-day random deviations that have a damping effect (with the coefficients of 0.58, 0.15 and 0.08, respectively). Furthermore, an immediate impact of the 3-week seasonal effects (with the coefficients of 0.17, 0.04 and 0.13, respectively) is observed. The standard error and MAPE of the second model are still significant and account for 272 €/MWh and 24%. Therefore, we cannot rely on the SARIMAX with exogenous prices and internal flows, and above all because its best-fitted model by Auto Arima Package is integrated in the order of 0 and the data are non-stationary.
The SARIMAX model with exogenous prices, internal and external flows comprises 23 external factors, AR and MA components, and seasonal patterns. All three price factors are statistically significant; however, as with the previous models, gas and CO2 prices exert a directly proportional impact (with the coefficients of 0.92 and 0.58, respectively), while the coal prices have an inversely proportional impact (coef. = −0.10). All types of generation, except oil, hydro and biofuel, are statistically significant. At the same time, wind and solar generation as well as pumped storage have an inversely proportional impact (with the coefficients of −0.007, −0.011 and −0.05, respectively), while coal, gas and nuclear power generation have a directly proportional impact (with the coefficients of 0.017, 0.013 and 0.028, respectively). The excess of the electricity imports over its exports in case of such bidding zones as AT, BE, CH, DK1, NL, NO2 and SE4 will cause an increase in the electricity prices in the DE-LU bidding zone, while the opposite situation of an excess of electricity exports over imports will cause a decrease. Trading with such zones as CZ, DK2, FR and PL does not affect the changes in the pricing in the DE-LU bidding zone. The day-ago and 3-weeks-ago prices have a directly proportional impact on the formation of the electricity prices (with the coefficients of 0.37, 0.13, 0.07 and 0.13, respectively), the 2-days-ago random effects have an inversely proportional impact (with the coefficients of −0.73 and −0.18, respectively). The standard error and MAPE of the third model are significantly lower than in the previous two and account for 154 €/MWh and 17%, respectively. Thus, the SARIMAX model with exogenous prices, internal and external flows can be defined as the best-fitted model of electricity prices to use for their forecasting.
With the application of SARIMAX models, prices for the next month can be forecasted (Figure 6) and compared with the actual values (Table 5).
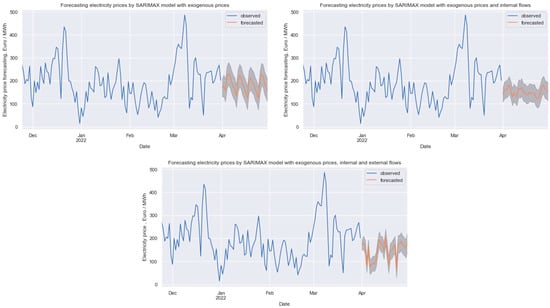
Figure 6.
Forecast of the electricity prices in the DE-LU bidding zone for the next 30 days. Source: constructed by authors based on the results of previous research.

Table 5.
Comparison of the actual and forecasted values of electricity prices in the DE-LU bidding zone for April 2022.
According to the SARIMAX model with exogenous prices, electricity prices are forecasted to decline gradually by the end of the month, with pronounced cyclical trends. Thus, the maximum price at the beginning of the month is 232 €/MWh and at the end of the month is 228 €/MWh, while the minimum price at the beginning of the month is 133 €/MWh and at the end of the month is 122 €/MWh. The forecasted average monthly price is 183 €/MWh. The lower bound of the forecast is in the range of 74–183 €/MWh, and the upper bound is in the range of 172–281 €/MWh.
When using the SARIMAX model with exogenous prices and internal flows, the forecasted price trend is not clearly defined. The forecasted prices are in the range of 122–182 €/MWh with the average monthly price being at the level of 152 €/MWh. The decrease in the forecasted values is associated with both the reduction in electricity consumption and the increase in wind and solar power generation. The lower bound of the forecast is in the range of 83–144 €/MWh, and the upper bound is in the range of 160–221 €/MWh.
The forecast, with the help of the SARIMAX model with exogenous prices, internal and external flows, indicates a wide range of electricity price fluctuations with four pronounced negative price spikes. The average monthly price is 147 €/MWh, the prices varying from 66 to 206 €/MWh. The lower bound of the forecast is in the range of 28–171 €/MWh, while the upper bound is in the range 103–240 €/MWh. Thus, the development of international trade relations will facilitate the flow of cheap surplus electricity from renewable energy sources between the neighboring bidding zones.
In April 2022, the actual electricity price in the DE-LU bidding zone was in the range of 55–238 €/MWh, with an average level of 166 €/MWh. The comparison of forecasted values with actual ones allows one to determine the average forecast error, which for the SARIMAX model with exogenous prices is 37%; the SARIMAX model with exogenous prices and internal flows is 34%; the SARIMAX model with exogenous prices, internal and external flows is 24%, and the values of the maximum error (on Easter Day, i.e., 17 April 2022) are 213%, 155% and 55%, respectively.
Thus, the first part of the hypothesis that the SARIMAX model with exogenous prices, internal and external flows reflects the influence of fundamental factors on the formation of electricity prices can be confirmed.
3.3. Residual Forecasting
The free pricing and anonymity of trade lead to electricity market participants’ using a variety of bidding strategies in the competition. This, in turn, causes unforeseen surges in the electricity prices despite the impact of the fundamental factors. In this paper, price spikes are investigated through volatility of electricity price residuals. Table 6 provides a description of the electricity price residuals of the studied SARIMAX models.

Table 6.
Quartile distribution of the electricity price residuals after the modelling.
As can be seen, although the average value of residuals for all models is less than 1 €/MWh, or 10%, the quartile distribution of the residuals shows significant differences: 269 €/MWh, or 674%, for the first model; 246 €/MWh, or 570%, for the second model; and 216 €/MWh, or 381%, for the third model. With an increase in the fundamental factors, the value of residuals decreases.
In this regard, it is reasonable to build a model for forecasting electricity price residuals using GARCH models, which, unlike SARIMAX models, involve forecasting volatility for a certain period. Figure 7 and Table 7, Table 8 and Table 9 show (i) the PACF plots, which help determine the number of time lags to build the models, (ii) the results of building the models, (iii) the visualization of the models based on the historical data, and (iv) the results of forecasting residual returns for the next 30 periods.
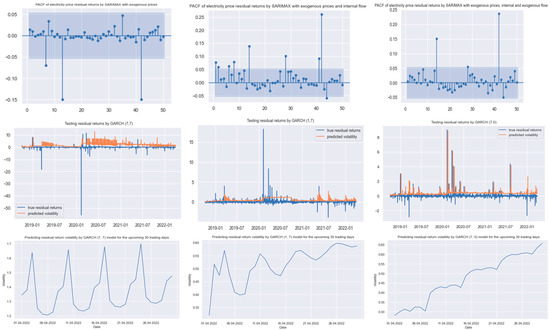
Figure 7.
Results of modelling and forecasting the volatility of the electricity price residuals. Source: constructed by the authors based on the results of previous research.

Table 7.
Results of building the GARCH models of electricity price residual returns by the SARIMAX model with exogenous prices.

Table 8.
Results of building the GARCH models of electricity price residual returns by the SARIMAX model with exogenous prices and internal flows.

Table 9.
Results of building the GARCH models of electricity price residual returns by the SARIMAX model with exogenous prices, internal and external flows.
The results of the GARCH modelling of the residual volatility indicate the following.
In case of forecasting the electricity prices by means of the SARIMAX model with exogenous prices, it is reasonable to model the residual volatility with the use of the GARCH (7, 7). The alpha and beta coefficients for up to 7 lags are insignificant and negligible. In this case, the volatility has the greatest influence on the 7th day ago (beta coef. = 0.9514), while the previous daily return is less significant (alpha coef. = 0.0482). As can be seen from the visualization of the GARCH model, the first model shows a significant volatility magnitude and leads to burst periods of random shocks. Therefore, the forecasted relative residuals of the electricity prices for the next 30 days may vary from 120% to 170%.
In the case of applying the SARIMAX model with exogenous prices and internal flows, it is reasonable to predict the volatility of the electricity price residuals using the GARCH (1, 7). According to the PACF, numerous time lags can be identified; however, based on the LLF, AIC and p-values, it is reasonable to choose only one time lag to account for the previous residual returns (alpha coef. = 0.4812). Furthermore, the volatility values are significantly affected by random shocks of the residual return volatility 7 days before (beta coef. = 0.4643), while other parameters of the second GARCH model are insignificant. The visualization of this model shows that it can simulate the price residual volatility for the recent periods, while it does not capture the earlier jumps. One of the reasons is that the original model is non-integrated. The forecast of the price residual volatility using the GARCH (1, 7) shows that prices increase cyclically as the forecasts move away from the actual values, from 32% to 59%.
In the case of using the SARIMAX model with exogenous prices, internal and external electricity flows for electricity price forecasting, it is reasonable to predict the volatility of electricity price residuals based on the GARCH (7). Although PACF shows 14 time lags, the alpha coefficient for the 14th lag is insignificant, whereas the alpha coefficient for the 7th lag equals 0.886. The visualization of this model shows that it can almost precisely capture the price residual volatility in the previous periods. Accordingly, we can conclude that there is a gradual increase in the volatility of the electricity price residuals in the forecast period with the prolongation of the forecast period from 28% to 68%.
As can be noted from the LLF and AIC values, and the number of the alpha and beta coefficients of the presented GARCH models, the more complex the SARIMAX model is for electricity price forecasting and the higher its quality, the simpler the GARCH model is for forecasting residual volatility and the higher its quality.
Thus, the application of GARCH modelling of residual volatility allows one to evaluate the risk component associated with the uncertainty of market participants’ behavior (the second part of the hypothesis).
Updating the data allows the model to be rebuilt for other periods (Appendix B) or other bidding zones.
4. Discussion and Conclusions
This study proposed a methodological approach to electricity price forecasting, which applied:
- SARIMAX modelling of the influence of fundamental factors of the internal and external related markets on the changes in electricity prices over time. These factors are considered to be: (i) exogenous prices (gas, coal and CO2 prices), (ii) internal (consumption and generation) electricity flows, and (iii) external (net import) electricity flows;
- GARCH modelling of the volatility of the electricity price residuals, which allows tracking and forecasting the risks of price distortions under the influence of individual trading strategies of electricity market participants.
In the study, the proposed methodological approach for the EU’s largest DE-LU bidding zone was tested. We established that, starting from Q3 2021, the distribution of the electricity prices becomes abnormal under the influence of external factors, especially gas, coal and CO2 prices.
The ADF test, the ACF and PACF, as well as the EDA, have proved the reasonability of using electricity price differences and building SARIMAX models for electricity price forecasting.
The SARIMAX (1, 1, 2) × (3, 1, 0, 7) model with exogenous prices, internal and external flows, which had the maximum LLF and the minimum AIC and MAPE values, was defined as the best-fitted model.
The use of SARIMAX modelling makes it possible to identify the exogenous prices, types of generation and directions of international trade in electricity that are statistically significant for electricity pricing in a particular bidding zone. For the DE-LU bidding zone, these are all exogenous prices (gas, coal and CO2 prices), conventional (coal, gas and nuclear) and intermittent RES (wind and solar) power generation, pumped storage and external electricity flows between seven neighboring bidding zones (AT, BE, CH, DK1, NL, NO2 and SE4). This model enables tracking price fluctuations over time. Thus, for April 2022, four price drops (4 April 2022, 7 April 2022, 9 April 2022 and 23 April 2022) were forecasted. The application of this model showed an average forecast error of 17% for the testing period and 24% for the forecast period.
To assess the risks associated with the uncertainty of participants’ behavior in a competitive environment, the reasonability of using GARCH modelling of the volatility of electricity price residuals has been proved. At the same time, it has been shown that the more complex the SARIMAX model is, the simpler the GARCH model of the volatility of its residuals is. Thus, in the case of the DE-LU bidding zone, to forecast the volatility of the residuals of the SARIMAX model with exogenous prices, internal and external flows, it is reasonable to use the GARCH (7) model. The paper proves that with the prolongation of the forecast period, the risks associated with price uncertainty due to individual bidding strategies of the participants increase.
Therefore, the proposed methodological approach to electricity price forecasting can be used by both market participants (to support them in making decisions about pricing strategies in the electricity market) and market operators (NEMOs and TSOs). The updating of data through the ENTSO-E Transparency Platform and platforms of related markets (e.g., EEX) makes this approach easily reproducible for other periods and other bidding zones. For each specific zone and each time interval, the models will differ.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/su14159081/s1, Auto Arima package description.
Author Contributions
Conceptualization, D.W. and T.S.; methodology, D.W., M.K. and T.S.; validation, M.K. and T.S.; formal analysis, V.K. and T.S.; project administration, I.G. and V.K.; investigation, V.K. and T.S.; data curation, M.S. and T.S.; writing—original draft preparation, V.K. and T.S.; writing—review and editing, I.G. and T.S.; visualization, T.S. and M.S.; supervision, M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://transparency.entsoe.eu/, https://finance.yahoo.com/, https://www.marketwatch.com/, https://www.eex.com/.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ACF | autocorrelation function |
| ADF test | augmented Dickey–Fuller test |
| AIC | Akaike information criterion |
| AR component | autoregressive component |
| ARCH | autoregressive conditional heteroscedastic |
| ARIMA | autoregressive integrated moving average |
| ARIMAX | autoregressive integrated moving average with exogenous factors |
| DE-LU bidding zone | German/Luxemburg bidding zone |
| EDA | exploratory data analysis |
| ENTSO-E | European Association for the Cooperation of Transmission System Operators for Electricity |
| GARCH | generalized autoregressive conditional heteroscedastic |
| LLF | log likelihood function |
| MA component | moving average component |
| NEMO | nominated electricity market operator |
| PACF | partial autocorrelation function |
| SARIMA | seasonal autoregressive integrated moving average |
| SARIMAX | seasonal autoregressive integrated moving average with exogenous factors |
| TSO | transmission system operators |
Appendix A
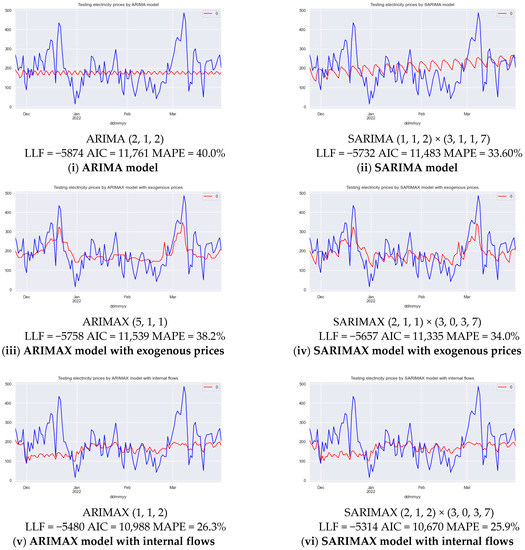
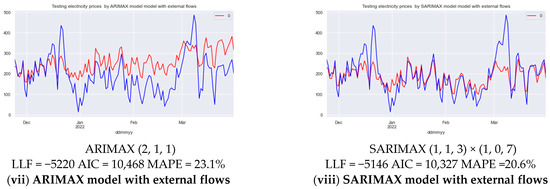
Figure A1.
Testing the electricity prices by different time series models. Source: constructed by the authors based on [3,32,33,34].
Appendix B

Table A1.
Re-fitting the SARIMAX model with exogenous prices, internal and external flows for May 2022.
Table A1.
Re-fitting the SARIMAX model with exogenous prices, internal and external flows for May 2022.
| Parameter | Coef. | Std. Err. | p-Value | Parameter | Coef. | Std. Err. | p-Value |
|---|---|---|---|---|---|---|---|
| SARIMAX (1, 1, 2) × (3, 1, 0, 7) LLF = −5199 AIC = 10,469 MAPE = 17.42% | |||||||
| Gas_price | 0.963 | 0.04 | 0 | CH_net_flows | 0.0032 | 0.011 | 0.777 |
| Coal_price | 0.1746 | 0.024 | 0 | CZ_net_flows | −0.1234 | 0.038 | 0.001 |
| CO2_price | 0.0066 | 0.115 | 0.955 | DK1_net_flows | 0.1938 | 0.01 | 0 |
| Consumption | 0.0023 | 0.001 | 0.005 | DK2_net_flows | −0.0447 | 0.024 | 0.059 |
| Coal_gen | 0.0096 | 0.002 | 0 | FR_net_flows | −0.0212 | 0.029 | 0.467 |
| Gas_gen | 0.0054 | 0.006 | 0.335 | NL_net_flows | 0.0141 | 0.01 | 0.142 |
| Oil_gen | 0.0018 | 0.111 | 0.102 | NO2_net_flows | 0.1937 | 0.013 | 0 |
| Hydro_gen | 0.0211 | 0.018 | 0.24 | SE4_net_flows | 0.3047 | 0.126 | 0.015 |
| Pumped_ stor | −0.0376 | 0.029 | 0.2 | ar.L1 | 0.3891 | 0.04 | 0 |
| Wind_gen | −0.0018 | 0.001 | 0.147 | ma.L1 | −0.8082 | 0.042 | 0 |
| Solar_gen | −0.0031 | 0.004 | 0.389 | ma.L2 | −0.0996 | 0.032 | 0.002 |
| Biofuels_gen | 0.0225 | 0.016 | 0.164 | ar.S.L7 | 0.1624 | 0.021 | 0 |
| Nuclear_gen | 0.023 | 0.013 | 0.076 | ar.S.L14 | 0.108 | 0.025 | 0 |
| AT_net_flows | 0.1573 | 0.016 | 0 | ar.S.L21 | 0.1023 | 0.024 | 0 |
| BE_net_flows | 0.0941 | 0.017 | 0 | sigma2 | 182.075 | 3.934 | 0 |
Source: constructed by the authors based on [3,32,33,34].
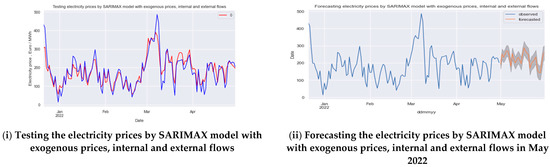
Figure A2.
Electricity price forecasting by the SARIMAX model with exogenous prices, internal and external flows in the DE-LU bidding zone for the testing and forecast periods.

Table A2.
Re-fitting the GARCH model of residual return volatility in the DE-LU bidding zone for May 2022.
Table A2.
Re-fitting the GARCH model of residual return volatility in the DE-LU bidding zone for May 2022.
| Parameter | Coef. | Std. Err. | p-Value | Parameter | Coef. | Std. Err. | p-Value |
|---|---|---|---|---|---|---|---|
| GARCH (7, 0) LLF = −739 AIC = 1497 | |||||||
| omega | 0.0907 | 2.83 × 10−2 | 1.34 × 10−3 | alpha [4] | 0 | 1.06 × 10−3 | 1 |
| alpha [1] | 2.19 × 10−4 | 2.58 × 10−4 | 0.395 | alpha [5] | 0 | 2.79 × 10−3 | 1 |
| alpha [2] | 5.17 × 10−9 | 1.58 × 10−3 | 1 | alpha [6] | 0 | 2.33 × 10−4 | 1 |
| alpha [3] | 0 | 2.93 × 10−3 | 1 | alpha [7] | 0.9998 | 0.603 | 9.75 × 10−2 |
Source: calculated by the authors based on the results of previous research.
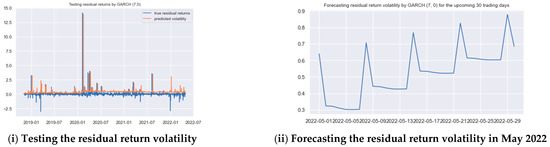
Figure A3.
Forecasting the residual return volatility in the DE-LU bidding zone for the testing and forecast periods. Source: constructed by the authors based on the results of previous research.
References
- Regulation (EU) 2015/1222 of 24 July 2015 Establishing a Guideline on Capacity Allocation and Congestion Management. EUR-LEX. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A32015R1222 (accessed on 1 May 2022).
- Chen, Q.; Balian, A.; Kyzym, M.; Salashenko, T.; Gryshova, I.; Khaustova, V. Electricity Markets Instability: Causes of Price Dispersion. Sustainability 2021, 13, 12343. [Google Scholar] [CrossRef]
- ENTSO-E Transparency Platform. Available online: https://transparency.entsoe.eu/ (accessed on 1 May 2022).
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef] [Green Version]
- Lago, J.; Marcjasz, G.; De Schutter, B.; Weron, R. Forecasting day-ahead electricity prices: A review of state-of-the-art algorithms, best practices and an open-access benchmark. Appl. Energy 2021, 293, 116983. [Google Scholar] [CrossRef]
- Contreras, J.; Espinola, R.; Nogales, F.J.; Conejo, A.J. ARIMA Models to Predict Next-Day Electricity Prices. IEEE Power Eng. Rev. 2002, 22, 57. [Google Scholar] [CrossRef]
- Conejo, A.J.; Plazas, M.A.; Espinola, R.; Molina, A.B. Day-ahead electricity price forecasting using the wavelet transform and ARIMA models. IEEE Trans. Power Syst. 2005, 20, 1035–1042. [Google Scholar] [CrossRef]
- Gao, G.; Lo, K.; Lu, J.; Fan, F. A Short-Term Electricity Price Forecasting Scheme for Power Market. World J. Eng. Technol. 2016, 4, 58–65. [Google Scholar] [CrossRef] [Green Version]
- Gao, G.; Lo, K.; Lu, J.; Fan, F. Comparison of ARIMA and ANN Models Used in Electricity Price Forecasting for Power Market. World J. Eng. Technol. 2017, 9, 120–126. [Google Scholar] [CrossRef] [Green Version]
- Mayer, K.; Trück, S. Electricity markets around the world. J. Commod. Mark. 2018, 9, 77–100. [Google Scholar] [CrossRef]
- Li, K.; Cursio, J.D.; Jiang, M.; Liang, X. The significance of calendar effects in the electricity market. Appl. Energy 2019, 235, 487–494. [Google Scholar] [CrossRef] [Green Version]
- García-Martos, C.; Conejo, A.J. Price Forecasting Techniques in Power Systems. In Wiley Encyclopedia of Electrical and Electronics Engineering; Wiley: Hoboken, NJ, USA, 2013; pp. 1–23. [Google Scholar]
- Jakaša, T.; Andročec, I.; Sprčić, P. Electricity price forecasting—ARIMA model approach. In Proceedings of the 2011 8th International Conference on the European Energy Market (EEM), Zagreb, Croatia, 25–27 May 2011; pp. 222–225. [Google Scholar]
- Česnavičius, M. Lithuanian electricity market price forecasting model based on univariate time series analysis. Energetika 2020, 66, 39–46. [Google Scholar] [CrossRef]
- Benini, M.; Marracci, M.; Pelacchi, P.; Venturini, A. Day-ahead market price volatility analysis in deregulated electricity markets. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; Volume 3, pp. 1354–1359. [Google Scholar]
- Hirth, L. What caused the drop in European electricity prices? A factor decomposition analysis. Energy J. 2018, 39, 143–157. [Google Scholar] [CrossRef] [Green Version]
- Mosquera-López, S.; Nursimulu, A. Drivers of electricity price dynamics: Comparative analysis of spot and futures markets. Energy Policy 2019, 126, 76–87. [Google Scholar] [CrossRef]
- Weron, R.; Misiorek, A. Forecasting Spot Electricity Prices with Time Series Models. In Proceedings of the International Conference “The European Electricity Market EEM-05”, Lodz, Poland, 10–12 May 2005; pp. 133–141. [Google Scholar]
- Karabiber, O.A.; Xydis, G. Electricity Price Forecasting in the Danish Day-Ahead Market Using the TBATS, ANN and ARIMA Methods. Energies 2019, 12, 928. [Google Scholar] [CrossRef] [Green Version]
- Angamuthu Chinnathambi, R.; Mukherjee, A.; Campion, M.; Salehfar, H.; Hansen, T.M.; Lin, J.; Ranganathan, P. A Multi-Stage Price Forecasting Model for Day-Ahead Electricity Markets. Forecasting 2019, 1, 26–46. [Google Scholar] [CrossRef] [Green Version]
- Haben, S.; Caudron, J.; Verma, J. Probabilistic Day-Ahead Wholesale Price Forecast: A Case Study in Great Britain. Forecasting 2021, 3, 596–632. [Google Scholar] [CrossRef]
- McHugh, C.; Coleman, S.; Kerr, D.; McGlynn, D. Forecasting Day-ahead Electricity Prices with A SARIMAX Model. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 1523–1529. [Google Scholar]
- Xie, M.; Sandels, C.; Zhu, K.; Nordström, L. A seasonal ARIMA model with exogenous variables for elspot electricity prices in Sweden. In Proceedings of the 2013 10th International Conference on the European Energy Market (EEM), Stockholm, Sweden, 27–31 May 2013; pp. 1–4. [Google Scholar]
- Cruz, A.; Muñoz, A.; Zamora, J.L.; Espínola, R. The effect of wind generation and weekday on Spanish electricity spot price forecasting. Electr. Power Syst. Res. 2011, 81, 1924–1935. [Google Scholar] [CrossRef]
- de Marcos, R.A.; Bello, A.; Reneses, J. Short-Term Electricity Price Forecasting with a Composite Fundamental-Econometric Hybrid Methodology. Energies 2019, 12, 1067. [Google Scholar] [CrossRef] [Green Version]
- Ferre, A.; de Certaines, G.; Cazelles, J.; Cohet, T.; Farnoosh, A.; Lantz, F. Short-Term Electricity Price Forecasting Models Comparative Analysis: Machine Learning vs. Econometrics; Les Cahiers de l’Economie No. 143; IFP Énergies Nouvelles, IFP School: Rueil-Malmaison, France, 2021; p. 26. [Google Scholar]
- Baatz, B.; Barrett, J.; Stickles, B. Estimating the Value of Energy Efficiency to Reduce Wholesale Energy Price Volatility; Report U1803; American Council for an Energy-Efficient Economy: Washington, DC, USA, 2018; p. 30. [Google Scholar]
- Božić, Z.; Dobromirov, D.; Arsić, J.; Radišić, M.; Ślusarczyk, B. Power Exchange Prices: Comparison of Volatility in European Markets. Energies 2020, 13, 5620. [Google Scholar] [CrossRef]
- Dong, S.; Li, H.; Wallin, F.; Avelin, A.; Zhang, Q.; Yu, Z. Volatility of electricity price in Denmark and Sweden. Energy Procedia 2019, 158, 4331–4337. [Google Scholar] [CrossRef]
- Wang, D.; Gryshova, I.; Balian, A.; Kyzym, M.; Salashenko, T.; Khaustova, V.; Davidyuk, O. Assessment of Power System Sustainability and Compromises between the Development Goals. Sustainability 2022, 14, 2236. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, C.; Nokleby, M.; Miller, C.J. Improving Short-Term Electricity Price Forecasting Using Day-Ahead LMP with ARIMA Models. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Pourghorban, M.; Mamipour, S. Day-Ahead Electricity Price Forecasting with Emphasis on Its Volatility in Iran (GARCH Combined with ARIMA Models). In Proceedings of the International Conference on Innovations in Business Administration and Economics, Tehran, Iran, 14 February 2019; Available online: https://mpra.ub.uni-muenchen.de/94826/ (accessed on 1 May 2022).
- Dutch TTF Natural Gas Calendar. Yahoo Finance. Available online: https://finance.yahoo.com/quote/TTF%3DF/history?p=TTF%3DF (accessed on 1 May 2022).
- MarketWatch. Coal (API2) CIF ARA (ARGUS-McCloskey) Continuous Contract. Available online: https://www.marketwatch.com/investing/future/mtfc00 (accessed on 1 May 2022).
- EEX EUA SPOT. European Energy Exchange AG. Available online: https://www.eex.com/en/market-data/environmental-markets/spot-market (accessed on 1 May 2022).
- Eurostat Database. Supply, Transformation and Consumption of Electricity—Monthly Data. Available online: https://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=nrg_cb_em&lang=en (accessed on 1 May 2022).
- European Power Exchange, SE. Available online: https://www.epexspot.com/en/market-data (accessed on 1 May 2022).
- Nord Pool, AS. Available online: https://www.nordpoolgroup.com/en/ (accessed on 1 May 2022).
- Power Query. Microsoft Corp. Available online: https://powerquery.microsoft.com/en-us/ (accessed on 1 May 2022).
- Jupyter. Available online: https://jupyter.org/ (accessed on 1 May 2022).
- McPherson, G. Statistics in Scientific Investigation: Its Basis, Application, and Interpretation, 1st ed.; Springer: New York, NY, USA, 1990; p. 666. [Google Scholar]
- Wildemuth, B.M. Applications of Social Research Methods to Questions in Information and Library Science, 2nd ed.; Libraries Unlimited: Santa Barbara, CA, USA, 2017; p. 433. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control, 5th ed.; Wiley and Sons Inc.: Hoboken, NJ, USA, 2015; p. 712. [Google Scholar]
- Song, Q.; Esogbue, A.O. A New Algorithm for Automated Box-Jenkins ARMA Time Series Modeling Using Residual Autocorrelation/Partial Autocorrelation Functions. Ind. Eng. Manag. Syst. 2006, 5, 116–125. [Google Scholar]
- Chatfield, C. Exploratory data analysis. Eur. J. Oper. Res. 1986, 23, 5–13. [Google Scholar] [CrossRef]
- Komorowski, M.; Marshall, D.C.; Salciccioli, J.D.; Crutain, Y. Exploratory Data Analysis. In Secondary Analysis of Electronic Health Records; Springer International Publishing: Cham, Switzerland, 2016; pp. 185–203. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970; p. 575. [Google Scholar]
- Chatfield, C.; Prothero, D.L. Box-Jenkins seasonal forecasting: Problems in a case-study. J. R. Stat. Soc. Ser. A Gen. 1973, 136, 295–336. [Google Scholar] [CrossRef]
- Young, P.; Whitehead, P. A recursive approach to time series analysis for multivariable systems. Int. J. Control 1977, 25, 457–482. [Google Scholar] [CrossRef]
- Holst, J.; Ekelund, J.; Persson, A. Load Forecasting in Power Networks. Belastningsprognosering i Kraftnaet, Technical Report; Lund Institute of Technology: Lund, Sweden, 1988; p. 91. [Google Scholar]
- Chen, B.; Zhu, Y.; Hu, J.; Principe, J.C. System Identification Under Information Divergence Criteria. In System Parameter Identification: Information Criteria and Algorithms, 1st ed.; Newnes: Oxford, UK, 2013; pp. 167–204. [Google Scholar]
- McKenzie, J. Mean absolute percentage error and bias in economic forecasting. Econ. Lett. 2011, 113, 259–262. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized Autoregressive Conditional Heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef] [Green Version]
- Rossi, B. Density Forecasts in Economics and Policymaking. Els Opuscles del CREI. Nr. 37. 2014. Available online: http://www.crei.cat/wp-content/uploads/opuscles/140929110100_ENG_ang_37.pdf (accessed on 30 June 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).