Abstract
With automated vehicles (AVs), reversible lanes could be a sustainable transportation solution once there is vehicle-to-infrastructure connectivity informing AVs about the lane configuration changes. This paper introduced the reversible lane network design problem (RL-NDP), formulated in mixed-integer non-linear mathematical programming—both the traffic assignment and the reversible lane decisions were embedded. The model was applied on an hourly basis in the case study of the city of Delft, the Netherlands. Reversible lanes are examined under no traffic equilibrium (former paths are maintained); user-equilibrium (UE) assignment (AVs decide their own paths); and system-optimum (SO) traffic assignment (AVs are forced to follow SO paths). We found out that reversible lanes reduce congested roads, total travel times, and delays up to 36%, 9%, and 22%, respectively. The SO scenario was revealed to be beneficial in reducing the total travel time and congested roads in peak hours, whereas UE is equally optimal in the remaining hours. A dual-scenario mixing SO and UE throughout the day reduced congested roads, total travel times, and delay up to 40%, 8%, and 19%, respectively, yet increased 1% in travel distance. The spatial analysis suggested a substantial lane variability in the suburbs, yet a strong presence of reversible lanes in the city center.
1. Introduction
Reversible lanes are road car traffic lanes whose flow direction can be changed to accommodate an increase in demand in one of the directions. Currently, this strategy is applied to median lanes in multilane roads. Up until now, reversible lanes are of complex implementation because of the difficult adjustment for human driving and the need for investment in variable traffic signs [1]. Previous research on road safety has always revealed that reversible lanes have negative impacts on road safety. With the promise of vehicle-to-infrastructure (V2I) communication and vehicle automation, car-to-car frontal crashes in reversible lanes could be highly mitigated [2].
The new automated vehicles (AVs) paradigm unveils an increasing travel demand accruing, for instance, from the citizens that were not able to drive previously, e.g., the elderly and youth [3], but also from the ride-hailing services which somewhat complement mass transit and induce a change in behavior detrimental to public transportation [4,5]. Such increasing demand depends on the willingness towards AVs, which is promising in the next decades [6,7]. This AV disruption may compromise the sustainability of the whole traffic system, requiring innovative transportation solutions in this automated mobility transition [8].
In this sense, the AVs paradigm clearly supports the use of reversible lanes in urban environments, as long as V2I guarantees that vehicles are informed of such changes. As reversible lanes have a direct impact on road capacity, the following research questions arise: Can reversible lanes contribute to mitigating congestion in urban areas? In what terms does an enforced system-optimal perspective allied with reversible lanes implementation contribute to the traffic system? What main impacts can one expect from this strategy?
Hitherto, research on the topic of reversible lanes has focused on signalized intersections and median lane problems [9,10]. Reversible lane problems assume that there would be at least one lane in each road direction, but that assumption is no longer needed once vehicles become automated and a smart system is put in place to control the roadway layout. AVs’ driving task will be performed automatically and autonomously and, under a connected traffic control system, be informed of the road lane configuration dynamically [11]. The roadway layout would then be decided dynamically as a function of the ongoing traffic flow to achieve the maximum benefits of this strategy.
This futuristic vision leads to a novel network design problem proposed in this paper, designated as the Reversible Lane Network Design Problem (RL-NDP) for AV traffic. The RL-NDP is formulated as a macroscopic mathematical model in a mixed-integer non-linear programming (MINLP) problem. We aim at replicating the upcoming benefits of reversible lanes at a network level and testing their effects in two distinct traffic assignment mechanisms: user-equilibrium (UE) versus system-optimum (SO) traffic assignment, i.e., the selfish and unselfish behavior, respectively. The number of lanes for each road direction is optimized, while a traffic assignment equilibrium is computed for the given traffic demand (trips) and supply (road capacity).
To extract the first tentative conclusions, we use the case study city of Delft in the Netherlands, where the reversible lanes vary dynamically on an hourly base. First, we model the current traffic situation, i.e., without reversible lanes in UE conditions. Then, reversible lanes are evaluated under the following scenarios: the first days of the implementation of reversible lanes, while drivers still follow the previous driving paths (current scenario); a selfish scenario under the UE traffic assignment, replicating a situation where AVs choose their own paths; and third, a hypothetical futuristic social scenario under an SO traffic assignment that is only possible if V2I is controlling AV paths. A resulting scenario is derived from the comparative analysis of UE and SO scenarios—the minimization of congested roads and total delay are the criteria. Such a dual-scenario reflects a situation where AVs are forced to follow system-optimal paths in specific hours of the day and can decide their journey in the remaining part of the day.
The remainder of the article is organized as follows. Section 2 presents a background literature review focused on the reversible lane problem. Section 3 introduces the RL-NDP formulation as an MINLP problem. In Section 4, the application to the Delft case study is explained. Finally, Section 5 reports the main conclusions and presents some suggestions for future work.
2. Background
In general, the literature around reversible lanes has been increasing over the last two decades—with reinforced attention in the last few years. However, it is important to note that this growing trend alone hides the strong variability in the research output of the topic. In the early 2000s, the benefits of such a strategy were evident in road capacity increase and were applied in many facility types [12,13]. However, in the human-driven vehicles paradigm, traffic conflicts have been identified due to the human maladaptation to reversible lanes, which leads to low operating efficiency and a low lane utilization rate [1,14]. In practice, reversible lanes are applied as median reversible lanes in bridges [9] and freeway construction zones [15]. More recently, a few researchers have made attempts to study the impact of reversible lane operation for homogeneous traffic [15,16,17]. Reference [18] investigated the cooperative bargain for the separation of traffic flows in smart reversible lanes, focused on disseminating messages under global traffic information to make consistent movements when separating the flows.
The decision problem regarding reversible lanes is also linked to the study of the contraflow problem, usually studied regarding evacuation operations [19]. Reversible lanes in the context of AVs are therefore a form of network design problem, both at the tactical (e.g., the orientation of streets, lane allocation, and exclusive lanes) and at the operational level (e.g., scheduling problem). Typically formulated as bi-level, the upper-level decides on the lanes, changing their performance depending on the lower-level travelers’ routing decisions [20]. The formulation of such a problem transforms, therefore, two problems in a complex problem with an NP-hard solving nature [21]. Heuristics, metaheuristics, and iterative optimization methods usually deal with this complexity, yet a local optimum may be found instead of the global optimum.
Most of the existing research related to reversible lanes involves the optimization of signalized intersections, from a microscopic perspective. Reference [22] presented a methodology using genetic algorithms and micro-simulation techniques (AIMSUN) to estimate possible gains for real-time lane topological changes in a small network with eight signalized junctions, while assuming an advanced traffic information system. In [23], a single-level optimization model was developed, formulated in mixed-integer linear programming (MILP), to design median reversible lanes while accounting for the turns and signal-timing features, in an urban corridor with three signalized intersections. Reference [10] defined a bi-level problem to optimize the capacity of the signalized road network by allocating reversible lanes in the upper level, and then performed a deterministic UE assignment, solved by genetic algorithms, and applied the method to a numerical example. In [24], the focus was on signalized diamond interchanges, presenting a binary mixed-integer linear program (BMILP) that simultaneously optimizes lane markings, dynamic usage of the reversible lane, and signal timings. In [17], a novel microsimulation model was proposed to evaluate the impact of (median) reversible lanes operation on urban undivided roads in mixed traffic, which revealed a road capacity increase of 20%, on average.
Most of the literature concerning reversible lanes has been focused on emergency rescue and evacuation in metropolitan regions threatened by hurricanes and catastrophes [19,25,26,27,28]. Looking at traffic operations, [29] optimized reversible lanes within a traffic network by formulating a bi-level program, minimizing the total system cost based on flow entropy at the upper-level, and on the lower level the stochastic UE assignment; this was solved by a chaotic optimization algorithm. Reference [30] proposed a simulation-based optimization problem on a grid network, through a bi-level formulation for the time-varying lane-based capacity reversibility problem, and solved it by genetic algorithms and the VISTA simulator, which simulates traffic in UE conditions. In [31], a bi-level model that considers queueing at signalized junctions was proposed: the upper model optimizes the reversible lane assignment, which can be solved with the enumeration method or the Monte Carlo algorithm for small and large networks, respectively; the lower level is a stochastic UE model that is solved by the method of successive averages. Recently, [32] proposed a new approach of considering the influence of intersections and tested, in a numerical example, their modified algorithm, which finds critical edges to add directional node weights, on the basis of the maximal capacity path algorithm for the classical maximum flow problem. Reference [33] proposed a histogram-based estimation of a distribution algorithm to solve the optimization problem of reversible lanes as a bi-level problem, which revealed better convergence, speed, and precision than the genetic algorithms. Within the topic of AVs, [11] combined reversible lanes with AV routing and scheduling, although it was limited by not considering congestion (travel times are an input).
Most of these studies have been formulated as bi-level problems to account for both the perspective of system-optimal design and travelers’ selfish routing behavior. They are generally solved in two-parts through metaheuristics (e.g., genetic algorithms), making the search for the optimal solution hard and mostly undetermined. Our proposal for a single-level optimization model puts together both perspectives in a simpler formulation. It considers traffic congestion and tests the reversible lanes’ traffic strategy interaction with the traffic assignment problem in UE and/or SO conditions. The complexity of solving the problem is reduced, and global optimality can be guaranteed. Joining such interaction between the reversible lanes’ strategy and the traffic assignment method makes this problem highly combinatorial. Its calculation time is proportional to the network size and travel demand.
UE considers two main assumptions [34]: first, all users have identical driving behavior; second, users have full information (i.e., travel time on every possible path), meaning that they consistently make the correct decisions regarding path choice. The SO assumes that vehicles choose their paths in order to benefit the whole social system [35]. These assumptions can only be made in a scenario where vehicles will be directed to choose specific paths without the intervention of human drivers—a reality in a future with fully automated vehicles. Smart cities with a connected traffic control system with V2I being aware of the traffic situation (e.g., congested roads, accidents, and construction work) can inform and instruct vehicles to make socially desirable path choices.
3. The Reversible Lane Network Design Problem (RL-NDP)
3.1. Mathematical Formulation
The following mathematical formulation is a single-level problem, deciding on the reversible lanes while performing the traffic assignment in the same problem. It admits periodic lane reconfigurations, given a specific time-varying demand—i.e., Origin-Destination (OD) matrix for AVs for different periods of the day. We assumed that there is 100% coverage of V2I communication, and all AVs are equipped with this technology so that they are informed of the lane configuration throughout the network.
This is a network optimization problem from a macro modeling perspective. All lanes are considered potentially reversible, and at every road intersection, the model guarantees that at least one lane converges or diverges from that node.
The interaction between the reversible lanes and intersection performance was not evaluated in this paper, as signal control in a scenario with AVs might not be needed, and such performance is still mostly unknown. Also, pedestrians’ interaction with reversible lanes was not part of the main problem, though naturally there should be traffic lights managing their crossing for road safety reasons.
Sets
| : | set of nodes in the network, where is the number of nodes. |
| : | set of links of the road network where vehicles move. |
| : | set of origin–destination pairs that represent the travel demand in the network, i.e., . |
| : | set of time periods, where is the number of time periods (e.g., hours). |
Parameters
| : | demand trips from an origin node towards a destination node , of period to , . |
| : | minimum driving travel time in free-flow speed at the link , expressed in hours. |
| : | the current number of lanes at the link . |
| : | lane capacity of the link , expressed in vehicles for the period of analysis. |
| : | big number. |
Decision variables
| : | integer variable equal to the number of lanes of each road link , of period to |
| : | continuous variable that corresponds to the flow of AVs in each link and each OD pair , of period to |
Objective Function
The objective function (1) minimizes the traffic assignment function in UE conditions. The alternative objective function (2) reproduces the SO traffic assignment:
The Bureau of Public Roads (BPR) function (3) reflects the link performance functions, with and as parameters. Note that is added to allow the dynamic change from two-way to one-way roads (zero lanes in one of the directions):
Constraints
The objective functions are subject to the following constraints (4)–(13).
Constraints (4)–(6) define the traffic assignment problem. For each OD pair, AV flows are generated (4) in the origin node , absorbed (5) in the destination node , and there is flow conservation (6) in the intermediate nodes.
Constraints (7)-(11) define the reversible lanes problem. The first three constraints set the lower bound of the lane decision variables. In the intermediate nodes (7), flow is passing through, and constraints (6) already ensure that there is at least one lane converging and diverging from every node, since the flow arriving must leave that node. However, in nodes (intersections) that generate or absorb trips, there must be one lane that converges and diverges to and from that node—constraints (8) and (9). Constraint (10) sets the upper bound, i.e., the number of lanes of both road directions. Constraint (11) ensures that the sum of the lanes of both directions must correspond to the existing number of lanes on both sides of the road.
Constraints (12) and (13) set the domain of the decision variables.
3.2. Scenarios
In order to understand the benefits of reversible lanes and their traffic implications, we ran four scenarios, detailed in Table 1. Scenario O was the base scenario, and it represents the current traffic UE situation without reversible lanes. Scenario A represented the first days of implementation, showing the immediate impacts (short-term) of reversible lanes, whereby AVs could still be following their previous paths (from scenario O). In scenario B, the model optimized the reversible lane problem while performing a UE, meaning that AVs chose their path by minimizing their individual travel times (selfish behavior), i.e., a UE scenario likely to happen in the long-term if there is no centrally-managed traffic system. Scenario C optimized the reversible lane problem under a SO traffic assignment, which is only possible if the system (with V2I connectivity) gives instructions to AVs during their trips, forcing them to follow the system-optimal paths (unselfish behavior).

Table 1.
Scenario descriptions.
The pseudo-code used to run these scenarios is detailed in the following Algorithms 1–3.
| Algorithm 1 Scenario O: traffic assignment problem without the reversible lane problem | ||
| 1: 2: 3: 4: 5: 6: 7: 8: 9: | While do function Objective Function end-function Clear all decision variables end-do |
|
| Algorithm 2 Scenario A: the reversible lane problem without changing the traffic assignment | ||
| 1: 2: 3: 4: 5: 6: 7: 8: 9: | While do read variables from scenario O function Objective Function end-function Clear all decision variables end-do |
|
| Algorithm 3 Scenarios B and C: both the reversible lane and traffic assignment problems (UE and SO) | ||
| 1: 2: 3: 4: 5: 6: 7: 8: | While do function Objective Function end-function Clear all decision variables end-do |
|
4. Application to the Case Study City of Delft
4.1. Setting up the Case Study
The RL-NDP model was exemplified for the case study city of Delft, in the Netherlands. Figure 1 illustrates the network of the city, which was simplified to 46 nodes and 122 links, which represented 61 road segments, i.e., each link represents a direction. There were two types of road links, with one (1-1) or two lanes (2-2) per direction, with a free-flow speed of 50 and 70 km/h, respectively, and a lane capacity of 1441 vehicles per hour. The city center was close to node 3, while the TU Delft campus, the most significant traffic generator, was close to node 31. Major residential areas were in the southern region (e.g., node 6).
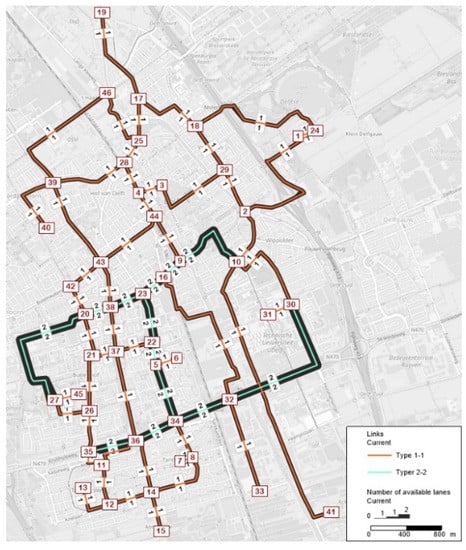
Figure 1.
Network representation of the city of Delft, the Netherlands.
The traffic demand collected by the Dutch government (MON 2007/2008) is available for transport research. The filtered dataset contained a collection of 152 trips from 29 sampled households who traveled inside the city on a working day in the year of 2008, ignoring external trips. Expansion factors were given for a typical working day, usually varying from 200 to 1300, leading to 137,832 trips by 14,640 households, yielding an average sample rate of 0.2% [36]. The final travel demand corresponded to 120,600 trips through 58 OD pairs over the day. In this case study city, the RL-NDP was exemplified on an hourly basis, meaning that reversible lanes changed every hour—see demand trips in Figure 2.
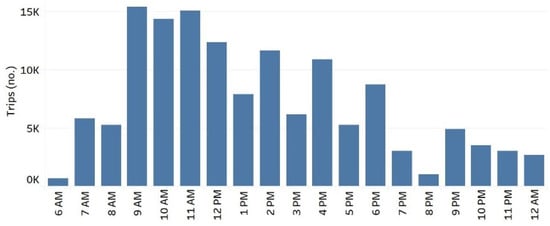
Figure 2.
Trips data of the city of Delft, the Netherlands.
Furthermore, the BPR [37] function (3) used the reference values .
4.2. Experiments
The RL-NDP model was implemented in the Mosel language and solved by Xpress 8.1 [38] in a computer with a processor of 4.2 GHz Intel Core i7-7700K and 16GB RAM. Our MINLP problem was solved by the FICO Xpress-NLP SLP solver designed for large-scale nonconvex problems that use a mixed-integer successive linear programming approach, combining branch and bound and successive linear programming. For convex NLP problems, global optimality is guaranteed, and the same applies for MINLP problems if its continuous relaxation is convex. However, the relationship between the traffic assignment problem and the reversible lane problem was not linear; hence, the global optimality could be compromised. For more information about the Xpress Solver [39], and the existent solvers for convex MINLP, the reader may consult reference [40].
Table 2 summarizes the results of the experiments, showing the value of the objective function (expressed in hours vehicles) and its computation time. Scenario O took just 3 seconds, while scenario A took 11 seconds. Since Scenario B and C held the complex non-linearity of the RL-NDP model, the calculation time rose to 11 and 53 minutes, respectively.

Table 2.
Model results: objective function.
The number of reversible lanes adapted every hour to the travel demand in order to optimize the overall traffic system performance. Figure 3 shows the percentage of roads whose lane directions were changed throughout the day. It also shows the percentage of road links that became one-way roads. On average, 19% of the road links had reversible lanes, and 9% switched from two-way to one-way direction during the day (Figure 3). Reversible lanes are optimal throughout the day, even with the current driving paths (scenario A). In the long-term, such traffic rearrangement towards UE (scenario B) would need fewer reversible lanes than towards an SO traffic assignment (scenario C).
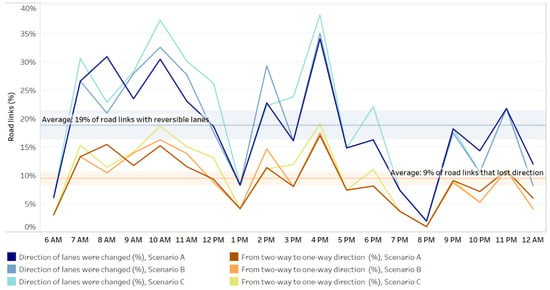
Figure 3.
Graphical analysis of the reversible lanes strategy throughout the day.
Reversible lanes were implemented hourly, so the design changed throughout the day in the network. Figure 4 illustrates the lane configuration for the period between 9am to 10 am. The roadway layout is colored according to types: roads with one lane per direction (type 1-1); roads with two lanes per direction (type 2-2) or one-way roads with two lanes (type 2-0); roads with three lanes in one direction and one lane in the opposite one (type 3-1); and one-way roads with four lanes (type 4-0).
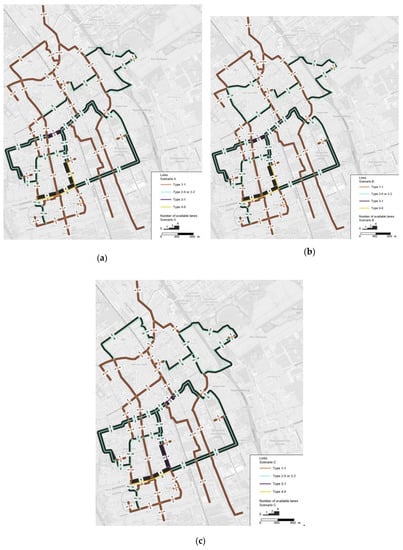
Figure 4.
Lane configuration for the period between 9h–10h am: (a) Scenario A; (b) Scenario B; (c) Scenario C.
During this period from 9 am to 10 am, reversible lanes were mostly needed in the southern region, close to residential areas, as people commuted to work. Besides this, the northern part of the network was highly varied amongst scenarios A, B, and C.
4.3. Impacts at the Traffic Level
This subsection analyses traffic performance indicators (detailed in Table 3) in every scenario; more specifically, the degree of saturation, congestion, number of congested road links, total travel distance, total travel times, and total delay.

Table 3.
Model results: traffic performance indicators.
The degree of saturation corresponds to the traffic flow divided by the road capacity at each link. Currently (scenario O), the degree of saturation is on average 71.4%, but with the strategy of implementing reversible lanes that degree reduced to an average of 50.2% in non-equilibrium traffic conditions (scenario A). In equilibrium conditions, the degree of saturation was between 51.6% and 47.9% for the UE and SO scenarios (B and C, respectively). Scenario C seems to be the best scenario in the long-term, and that happens because the minimization of the total system travel times causes a geographical dispersion of the traffic flows and, consequently, an overall reduction of the degree of saturation.
The congestion shown in Figure 5 was calculated through a weighted average of the degree of saturation using the length of each link as a weighting factor. The implementation of reversible lanes was revealed to have a positive impact in reducing congestion, dropping from 15.7% (scenario O) to 11.4% (variation of 4.3%) in SO conditions (scenario C). Surprisingly, the UE scenario had lower congestion at the network level than the SO scenario, although the UE-SO difference (scenarios B and C) was just 0.2%. This lower congestion level in UE occurs because in SO, the traffic flow dispersion reduces the degree of saturation, but it induces slightly longer trips.
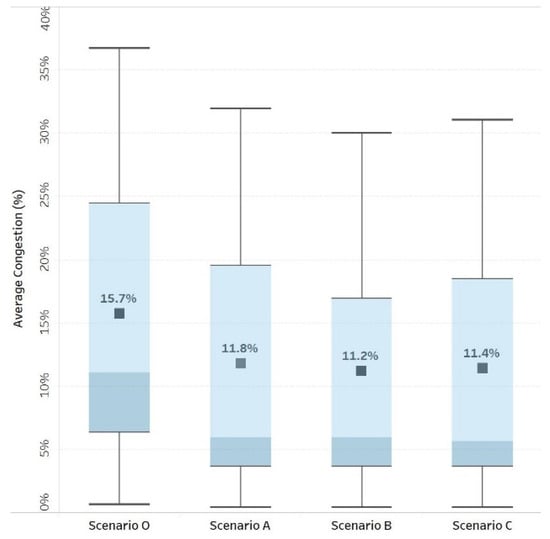
Figure 5.
Congestion at network-level.
Therefore, the congestion at the network level does not give a clear perspective of congested roads (degree of saturation equal to or higher than one). Congested roads are a major concern in urban regions, linked with queueing and delay. Figure 6 illustrates the length of congested links in every scenario. Currently (scenario O), there are 171 kilometers of congested roads in a whole day. The implementation of reversible lanes would help to reduce it to123 kilometers, with the potential of reduction to 101 kilometers in the long run with the SO assignment.
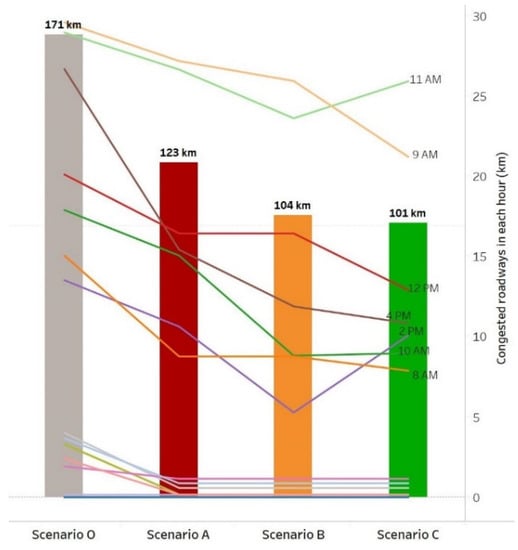
Figure 6.
Congested road links evolution.
It is not clear which strategy is the most beneficial: UE (selfish behavior in which every occupant chooses a path) or SO (centralized social behavior). For example, at 9 am, congested roads were initially 30 km and dropped to 21 km in scenario C (SO conditions). At 11 am this length dropped from 29 km to 24 km in scenario B (UE conditions)—here, SO conditions would not be as beneficial (26 km of congested roads). Therefore, traffic demand at each hour can perform differently in UE or SO conditions as far as congested links are concerned.
The comparison of the total distance traveled amongst scenarios with scenario O is shown in Figure 7. As expected, reversible lanes did not have an impact on the short-term (scenario A), because the paths were the same as in scenario O. In UE conditions (scenario B), the total distance reduced by 4k km veh. In SO conditions, AVs are forced to follow the optimal system paths, and the total distance increased by 19k km veh.
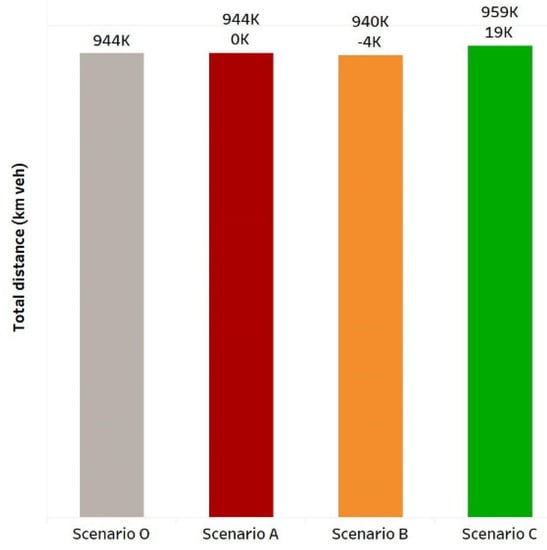
Figure 7.
Total distance variation.
Lastly, the total travel time and delay are depicted in Figure 8. Delay corresponds to the sum of the difference between the actual travel time and the minimum travel time (in free-flow conditions) in each road link. Reversible lanes already reduced travel times in the short-term (scenario A), especially in the long-term (scenario C). The SO scenario C is the most beneficial, producing lower travel times than the ones obtained in UE scenarios (A and B). There was a noticeable reduction in the total delay. In scenarios A and B (UE), the total travel time reduction was proportional to the total delay reduction. In scenario C (SO), the total travel time reduced by 2.9k h veh, and the total delay reduction was 3.2k h veh, which reflects the reduction of congested roads accompanied by longer trips performed in free-flow speed.
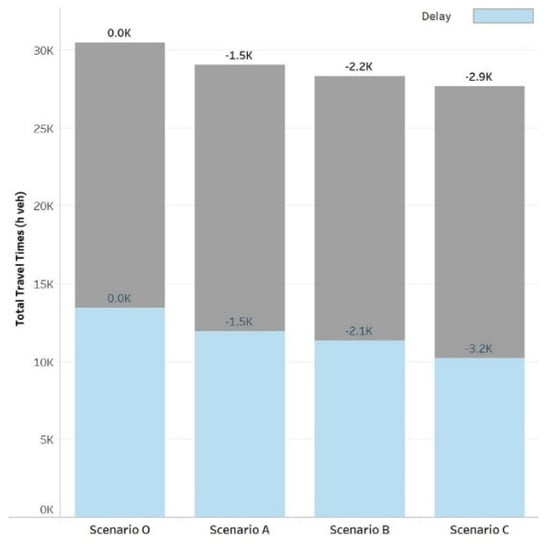
Figure 8.
Total travel time and total delay variation.
Figure 9 shows the percentage difference of each scenario relative to scenario O in every performance indicator. The comparison between the UE and the SO is depicted in black boxes. The SO was beneficial in some hours of the day (e.g., 9 am and 10 am), reducing congested roads and total delay. There were hours in which such difference is not clear (e.g., 6 am and 1 pm). Setting up an SO traffic distribution in some hours of the day while allowing AVs to decide on their own paths (UE) in the remaining part of the day—called the “dual scenario”—could be beneficial. The criteria used to create the dual scenario (summarized at the end of Figure 9) were: first, the highest reduction of congested roads (degree of saturation equal or higher than one); then, the highest reduction of total delay. In the remaining hours, the UE scenario was given preference so that AVs were free to follow their shortest paths, as the SO implies paths controlled by the centralized system.
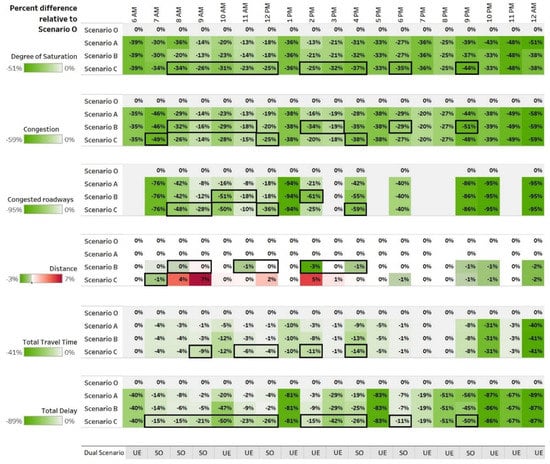
Figure 9.
Hourly analysis of the main traffic performance indicators.
Figure 10 shows the daily aggregated analysis—each hour was weighted by its travel demand. Of scenarios B and C, the best solution for the whole day would be scenario C, forcing SO traffic assignment conditions all day. Scenario B (UE conditions all day) still revealed a fair traffic performance but greatly reduced the total distance. The dual scenario revealed an intermediate performance between scenarios B and C in most of the traffic indicators—total travel times were reduced up to 8%, while the total delay was reduced by 19%. Nevertheless, the dual scenario was the one that highly reduced congested roads by 40%, still compromising the total distance, with a slight increase of 1%.
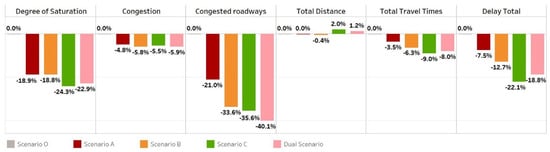
Figure 10.
Graphical comparison with current scenario O: daily analysis (hours adjusted by travel demand).
4.4. Impacts at the Spatial Level
An essential aspect of the network design is the location of these reversible lanes. The need for reversible lanes occurs in links where most of the traffic circulates in one direction rather than having a balance between the two directions. In the morning commute period, many lanes will turn to one direction, and in the afternoon, the direction will be inverted. This might indicate that those reversible lanes will be much more dynamic in the suburbs, because traffic demand is more imbalanced in those places compared to the city center. In this section, we analyze where the reversible lanes are being generated throughout the day in the case study city and their corresponding degree of saturation.
Figure 11 depicts the degree of saturation in scenario O, reflecting the current situation. The illustration shows that in the city center (close to node 3), the daily average degree of saturation is above capacity (105%–110%). Close to TU Delft (node 31) and towards the northern part of the city, roads are saturated way above 50% in both directions.
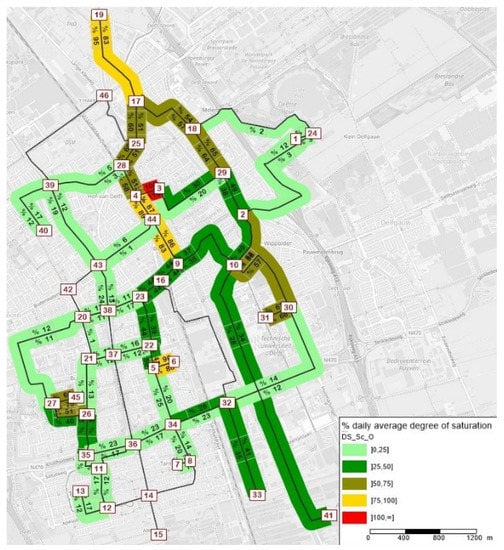
Figure 11.
Graphical representation of the average degree of saturation in scenario O.
Figure 12 shows the daily variability of reversible lanes and the degrees of saturation for scenario A—reflecting the implications of reversible lanes in the first days. Reversible lanes helped the city center (node 3) to reduce its degree of saturation (from 105%–110% to 86%–103% each way), holding a different lane layout than the initially set 47% of the day (9 hours out of 19 hours analyzed). Close to residential areas (node 27), there was an average small degree of saturation (5%), that set a different lane layout than the original one 26% (5 out of 19 hours) of the day.
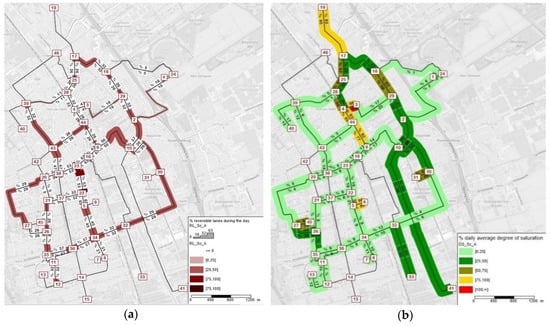
Figure 12.
Scenario A—network representation of the (a) daily lane layout variation and (b) the degree of saturation.
Similarly, Figure 13 illustrates the results for scenario B—with reversible lanes and the system is in UE equilibrium conditions (AVs follow their individual selfish paths). The results were similar to scenario A. Reversible lanes reduced congestion in the city center, for example, looking at link 4-44 the degree of saturation in the first days (scenario A) was 83%–82% each way and decreased to 68%–66% each way in the long-term (scenario B). The lane layout of link 4-44 varied 42% of the day (in scenario A this was 26%), i.e., in scenario B the lane layout was different from the original layout for 8 hours, while in scenario A this was 5 hours out of the 19 hours studied in the dataset—reflecting an increase in variability as the average degree of saturation decreases.
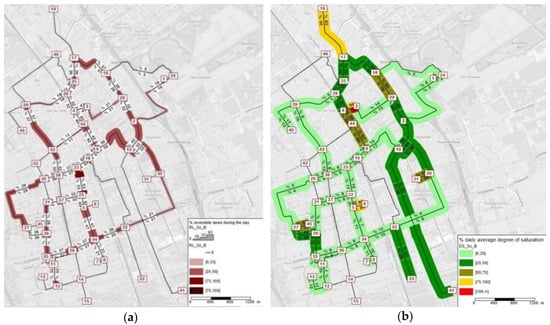
Figure 13.
Scenario B—network representation of (a) the daily lane layout variation and (b) the degree of saturation.
Figure 14 illustrates the variability of reversible lanes and the average degree of saturation for scenario C—the scenario that implied SO paths all over the day (AVs are forced to follow the paths given by the centralized system). The city center clearly saw a reduction in traffic congestion under capacity level (63%–82%), with a lane layout different from the original for 58% of the day (11 h out of 19 h), showing a higher lane layout variability.
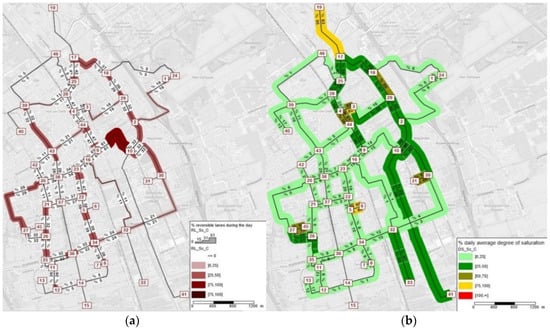
Figure 14.
Scenario C—network representation of (a) the daily lane layout variation and (b) the degree of saturation.
The dual scenario—the one where SO worked in some hours and UE in the remaining part of the day—revealed lower degrees of saturation all over the network, strongly reflecting the congestion reduction already mentioned. Still, the congestion located in the city center was not so well mitigated as in the previous scenario C (SO), though it was still better than scenario B (UE). The variability of reversible lanes decreased in the suburbs (e.g., link 27-20 and 32-16), which can be positive for road safety (see Figure 15).
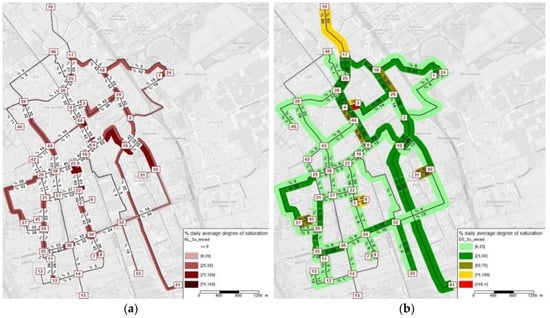
Figure 15.
Dual Scenario—network representation of (a) the daily lane layout variation and (b) the degree of saturation.
Figure 16 zooms into the city center, showing the evolution of congestion (degree of saturation) across every scenario. Reversible lanes already helped to reduce congestion in the short-term (scenario A), but congested roads only disappeared in the long-term for the scenario with SO paths (scenario C). The dual scenario revealed an intermediate performance between scenarios B and C, although presented results closer to scenario C (working in SO conditions).
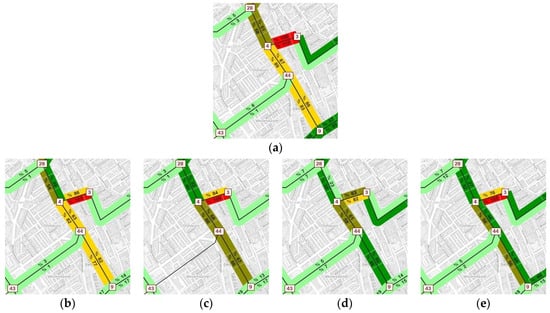
Figure 16.
Congestion in the city center (% degree of saturation) in every scenario evaluated: (a) current scenario O without reversible lanes, (b) scenario A same previous routes, (c) scenario B in user-equilibrium (UE) conditions all day, (d) scenario C in system-optimum (SO) conditions all day, and (e) dual scenario with SO in some hours of the day and UE in the remaining hours.
5. Conclusions and Future Work
In this paper, we proposed a mathematical model for solving the Reversible Lane Network Design Problem (RL-NDP) taking advantage of a future with AVs. The model optimizes the number of lanes in each road direction on an urban road network for every hour of the day, and it can be run under UE or SO traffic conditions. The mathematical model was formulated as a mixed-integer non-linear programming problem (MINLP). Our contribution was focused on studying the implementation of reversible lanes in the short- and long-term, analyzing the immediate impacts when traffic is not yet in equilibrium and the impacts when traffic rearranges itself, reaching a user-equilibrium. The paper also evaluated reversible lanes, along with a traffic control system that might (or might not) take control over AV paths and force them to follow a system optimal path—a condition only possible with V2I connectivity and a centralized routing system that instructs AVs to follow SO paths.
Four scenarios were evaluated. Scenario O corresponded to the current situation, as traffic runs under UE conditions without reversible lanes, i.e., a fixed lane layout. Three scenarios with reversible lanes were considered: scenario A, reflecting the first days of implementing reversible lanes where paths were the same as the ones experienced in scenario O; and two long-term scenarios, B and C, that considered a UE and a SO traffic assignment, respectively. A fifth scenario was derived from a comparative hourly analysis of scenarios B and C—the so-called dual scenario considered SO in some hours of the day and UE in the remaining ones, optimizing the strategy of reversible lanes on an hourly basis.
The model was applied to the network of the city of Delft, for every hour in all scenarios, and proved to be an easy tool to guide the reversible lane implementation throughout the day as a function of the travel demand and the existing road capacity. The optimal solutions were obtained within satisfactory computation times, given the combinatorial nature of the problem. The simple traffic assignment problem, scenario O, took just a few seconds, while scenario A, which corresponded to only deciding on the reversible lane problem, took 11 seconds. Scenarios B and C, the RL-NDP model, took 11 and 54 minutes, respectively.
Reversible lanes have the potential to reduce the degree of saturation, congestion, congested roads, travel times, and delay, regardless of the traffic assignment considered. However, travel distance is sensitive to the type of traffic assignment. With UE, the total distance reduced by 0.4% while in SO it increased by 2.0% at the same time that congestion was mitigated. In peak hours, the SO scenario was revealed to have a better performance in most of the traffic performance indicators. The dual scenario combining UE or SO at each hour showed a total distance increase of 1.2%. In this optimal scenario, congested roads were reduced by 40.1%, and total travel times and delay decreased by 8.0% and 18.8%, respectively.
The study of the spatial location of congestion and variability of this strategy revealed that reversible lanes naturally vary more frequently in zones where demand is imbalanced throughout the day (residential areas). In city centers, congestion can still be reduced by the use of reversible lanes, although congested roads only disappeared in the SO scenario.
Given these results, the SO scenario was confirmed to be the ideal one in the future to reduce total travel times, delay, and traffic congestion located in the city center. Notwithstanding this, the dual UE–SO scenario appeared to be the best at reducing congested roads all through the day.
With the new AV paradigm, municipalities will be mostly concerned with congested road links and their influence on air pollution and energy consumption. Therefore, a future with SO paths, which might be a reality with automated traffic and a smart traffic control system, can have a positive impact and contribute to achieving sustainability goals. The application of the RL-NDP model points to the need for investment to inform AVs of their required SO paths and make the SO traffic assignment a reality.
The RL-NDP model can be adjusted to some of the prospective benefits of the automated driving features, such as the chance to have narrower lanes or higher traffic efficiency, which will increase the overall road capacity. Since the main objective of this paper was to assess and evaluate how reversible lanes improve the overall traffic system, we considered the current lane capacity as well as the current travel demand. Yet, the model formulation allowed such changes. Certainly, an increase in lane capacity will bring added travel time savings. For example, in the BPR function considered, an increase of 40% in lane capacity means a reduction of 74% of the total travel time experienced in every road link. Still, how much AVs will affect lane capacity is uncertain; literature speculates an increase between 40% and 80% in urban roads [41,42].
Nevertheless, the RL-NDP model was formulated with the introduction of some simplifications and assumptions—for example, the time for the lane adjustment between the different periods (hours) was not considered, and mobility patterns were the same as today. Also, the model simplified the dynamic of the reversible lanes’ strategy in every intersection, ignoring the number of turns, which could generate a delay in the nodes. As future work, we may consider adding the delay in every node in a scenario with AVs at a macroscopic perspective (i.e., network level) and studying the impacts on pollution.
Author Contributions
Conceptualization, formal analysis, writing—review and editing, L.C., G.H.d.A.C. and J.P.T.; methodology, validation, visualization, data curation, investigation, writing—original draft preparation, L.C.; resources, supervision, project administration, G.H.d.A.C. and J.P.T.; software, funding acquisition, L.C. and G.H.d.A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Portuguese Foundation for Science and Technology (FCT): the first author was supported by grant number PD/BD/113760/2015 under the MIT Portugal Program in Transportation Systems; and the second author was supported by the Driving2Driverless project, grant number PTDC/ECI-TRA/31923/2017.
Acknowledgments
The authors would like to thank FICO (Xpress software provider) for establishing a research agreement with the Department of Transport & Planning at TU Delft. Also, PTV (VISUM software used in illustrations) for establishing a research agreement with the Faculty of Engineering of the University of Porto. The authors would like to thank Kees van Goeverden for supplying a filtered database of the Netherlands mobility in 2008/2009.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cao, Y.; Zuo, Z.; Xu, H. Analysis of Traffic Conflict Characteristic at Temporary Reversible Lane, Period. Polytech. Transp. Eng. 2014, 42, 73–76. [Google Scholar] [CrossRef]
- Kulmala, R.; Rämä, P.; Sihvola, N. Safety Impacts of Cooperative Systems; 21st ICTCT Workshop; ICTCT Proceedings: Riga, Latvia, 2008. [Google Scholar]
- Harper, C.D.; Hendrickson, C.T.; Mangones, S.; Samaras, C. Estimating potential increases in travel with autonomous vehicles for the non-driving, elderly and people with travel-restrictive medical conditions. Transp. Res. Part C Emerg. Technol. 2016, 72, 1–9. [Google Scholar] [CrossRef]
- Conway, M.; Salon, D.; King, D.; Coll, M.H.; Vandersmissen, M.H.; Thériault, M.; Chung, K.H.; Babar, Y.; Burtch, G.; Neuzil, P.; et al. Disruptive Transportation: The Adoption, Utilization, and Impacts of Ride-Hailing in the United States. SSRN 2017. [Google Scholar] [CrossRef]
- Sadowsky, N.; Nelson, E. The Impact of Ride-Hailing Services on Public Transportation Use: A Discontinuity Regression Analysis. Economics 2017, Department Working Paper Series. 13. [Google Scholar]
- Kelley, S.B.; Lane, B.W.; DeCicco, J.M. Pumping the brakes on robot cars: Current urban traveler willingness to consider driverless vehicles. Sustainability 2019, 11, 5042. [Google Scholar] [CrossRef]
- Nordhoff, S.; de Winter, J.; Kyriakidis, M.; van Arem, B.; Happee, R. Acceptance of Driverless Vehicles: Results from a Large Cross-National Questionnaire Study. J. Adv. Transp. 2018. [Google Scholar] [CrossRef]
- Hopkins, D.; Schwanen, T. Automated mobility transitions: Governing processes in the UK. Sustainability 2018, 10, 956. [Google Scholar] [CrossRef]
- Bede, Z.; Torok, A. Theoretical investigation of traffic equilibrium on bridges. Transp. Telecommun. 2014. [Google Scholar] [CrossRef]
- Wang, J.; Deng, W. Optimizing capacity of signalized road network with reversible lanes. Transport 2015, 33, 1–11. [Google Scholar] [CrossRef]
- Chu, K.F.; Lam, A.Y.S.; Li, V.O.K. Dynamic lane reversal routing and scheduling for connected autonomous vehicles. In Proceedings of the 2017 International Smart Cities Conference (ISC2), Wuxi, China, 14–17 September 2007. [Google Scholar] [CrossRef]
- Wolshon, B.; Lambert, L. Reversible Lane Systems: Synthesis of Practice. J. Transp. Eng. 2006, 132, 933–944. [Google Scholar] [CrossRef]
- Wolshon, B.; Lambert, L. Planning and operational practices for reversible roadways. ITE J. (Inst. Transp. Eng. 2006, 76, 38–43. [Google Scholar]
- Lambert, L.; Wolshon, B. Characterization and comparison of traffic flow on reversible roadways. J. Adv. Transp. 2010, 113–122. [Google Scholar] [CrossRef]
- Waleczek, H.; Geistefeldt, J.; Cindric-Middendorf, D.; Riegelhuth, G. Traffic Flow at a Freeway Work Zone with Reversible Median Lane. Transp. Res. Procedia 2016. [Google Scholar] [CrossRef]
- Li, X.; Chen, J.; Wang, H. Study on Flow Direction Changing Method of Reversible Lanes on Urban Arterial Roadways in China. Procedia Soc. Behav. Sci. 2013. [Google Scholar] [CrossRef]
- Kotagi, P.B.; Asaithambi, G. Microsimulation approach for evaluation of reversible lane operation on urban undivided roads in mixed traffic. Transp. A Transp. Sci. 2019. [Google Scholar] [CrossRef]
- Xiao, G.; Zhang, H.; Sun, N.; Chen, Y.; Shi, J.; Zhang, Y. Cooperative Bargain for the Autonomous Separation of Traffic Flows in Smart Reversible Lanes. Complexity 2019. [Google Scholar] [CrossRef]
- Wolshon, B. “One-Way-Out”: Contraflow Freeway Operation for Hurricane Evacuation. Nat. Hazards Rev. 2002. [Google Scholar] [CrossRef]
- Magnanti, T.L.; Wong, R.T. Network Design and Transportation Planning: Models and Algorithms. Transp. Sci. 1984, 18, 1–55. [Google Scholar] [CrossRef]
- Ben-Ayed, O.; Boyce, D.E.; Blair, C.E., III. A general bilevel linear programming formulation of the network design problem. Transp. Res. Part B Methodol. 1988, 22, 311–318. [Google Scholar] [CrossRef]
- Geraldes, R. Reconfiguração topológica da rede rodoviária como instrumento de mitigação de problemas de congestionamento não recorrente; Universidade Técnica de Lisboa, Instituto Superior Técnico: Lisbon, Portugal, 2011. [Google Scholar]
- Zhao, J.; Ma, W.; Liu, Y.; Yang, X. Integrated design and operation of urban arterials with reversible lanes. Transp. B 2014. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Yang, X. Operation of signalized diamond interchanges with frontage roads using dynamic reversible lane control. Transp. Res. Part C Emerg. Technol. 2015, 51, 196–209. [Google Scholar] [CrossRef]
- Williams, B.M.; Tagliaferri, A.P.; Meinhold, S.S.; Hummer, J.E.; Rouphail, N.M. Simulation and Analysis of Freeway Lane Reversal for Coastal Hurricane Evacuation. J. Urban Plan. Dev. 2007. [Google Scholar] [CrossRef]
- Hua, J.; Ren, G.; Cheng, Y.; Yu, C.; Ran, B. Large-scale evacuation network optimization: A bi-level control method with uncertain arterial demand. Transp. Plan. Technol. 2015, 38, 777–794. [Google Scholar] [CrossRef]
- Tuydes, H.; Ziliaskopoulos, A. Tabu-Based Heuristic Approach for Optimization of Network Evacuation Contraflow. Transp. Res. Rec. J. Transp. Res. Board 2007. [Google Scholar] [CrossRef]
- Zhang, X.; Zhong, Q.; Luo, Q. Evaluation of Transportation Network Reliability under Emergency Based on Reserve Capacity. J. Adv. Transp. 2019. [Google Scholar] [CrossRef]
- Wu, J.J.; Sun, H.J.; Gao, Z.Y.; Zhang, H.Z. Reversible lane-based traffic network optimization with an advanced traveller information system. Eng. Optim. 2009, 41, 87–97. [Google Scholar] [CrossRef]
- Karoonsoontawong, A.; Lin, D.-Y.Y. Time-varying lane-based capacity reversibility for traffic management. Comput. Civ. Infrastruct. Eng. 2011, 26, 632–646. [Google Scholar] [CrossRef]
- Lu, T.; Yang, Z.; Ma, D.; Jin, S. Bi-Level Programming Model for Dynamic Reversible Lane Assignment. IEEE Access 2018, 6, 71592–71601. [Google Scholar] [CrossRef]
- Mo, J.; Gao, M.; Liu, L. An Improved Critical-Edge Model for Finding Optimal Contraflow Links Considering the Influence of Intersections. Math. Probl. Eng. 2019. [Google Scholar] [CrossRef]
- You, R.; Chen, W.N.; Gong, Y.J.; Lin, Y.; Zhang, J. A Histogram Estimation of Distribution Algorithm for Reversible Lanes Optimization Problems. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019. [Google Scholar] [CrossRef]
- Sheffi, Y. Urban Transportation Network; Pretince Hall: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
- Newell, G.F. Traffic Flow on Transportation Networks; MIT Press: Cambridge, MA, USA, 1980. [Google Scholar]
- de Correia, G.H.; van Arem, B. Solving the User Optimum Privately Owned Automated Vehicles Assignment Problem (UO-POAVAP): A model to explore the impacts of self-driving vehicles on urban mobility. Transp. Res. Part B Methodol. 2016, 87, 64–88. [Google Scholar] [CrossRef]
- United States Bureau of Public Roads. Traffic Assignment Manual. Urban Planning Division; U.S. Department of Commerce: Washington, DC, USA, 1964. [Google Scholar]
- FICO. Getting Started with Xpress Release 8.1; Fair Isaac Corporation: San Jose, CA, USA, 2017. [Google Scholar]
- Fair Isaac Corporation. XPress Solver—Nonlinear Reference Manual. 2019. Available online: https://www.fico.com/fico-xpress-optimization/docs/latest/solver/nonlinear/HTML/GUID-4B40E940-6A38-342F-9531-A13E84FB1467.html (accessed on 7 July 2019).
- Kronqvist, J.; Bernal, D.E.; Lundell, A.; Grossmann, I.E. A review and comparison of solvers for convex MINLP. Optim. Eng. 2019, 20, 397–455. [Google Scholar] [CrossRef]
- Friedrich, B. Verkehrliche Wirkung autonomer Fahrzeuge. In Autonomes Fahren; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Meyer, J.; Becker, H.; Bösch, P.M.; Axhausen, K.W. Autonomous vehicles: The next jump in accessibilities? Res. Transp. Econ. 2017, 62, 80–91. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).