A Survey on Environmentally Friendly Vehicle Routing Problem and a Proposal of Its Classification

Abstract

The growth of environmental awareness and more robust enforcement of numerous regulations to reduce greenhouse gas (GHG) emissions have directed efforts towards addressing current environmental challenges. Considering the Vehicle Routing Problem (VRP), one of the effective strategies to control greenhouse gas emissions is to convert the fossil fuel-powered fleet into Environmentally Friendly Vehicles (EFVs). Given the multitude of constraints and assumptions defined for different types of VRPs, as well as assumptions and operational constraints specific to each type of EFV, many variants of environmentally friendly VRPs (EF-VRP) have been introduced. In this paper, studies conducted on the subject of EF-VRP are reviewed, considering all the road transport EFV types and problem variants, and classifying and discussing with a single holistic vision. The aim of this paper is twofold. First, it determines a classification of EF-VRP studies based on different types of EFVs, i.e., Alternative-Fuel Vehicles (AFVs), Electric Vehicles (EVs) and Hybrid Vehicles (HVs). Second, it presents a comprehensive survey by considering each variant of the classification, technical constraints and solution methods arising in the literature. The results of this paper show that studies on EF-VRP are relatively novel and there is still room for large improvements in several areas. So, to determine future insights, for each classification of EF-VRP studies, the paper provides the literature gaps and future research needs.

1. Introduction

The increased social and environmental awareness has created growing support for environmental regulations to control GHG emissions. This trend and the rising energy costs have led to increased attempts to address emerging environmental challenges. Generally, state-owned and private sectors are both responsible for the GHG emissions (i.e., CO₂, N₂O) and pollutants (i.e., CO, SO_x, NO_x, soot, PM₁₀, contrails, etc.) across the world as well as the associated negative consequences by various activities in construction, transportation, manufacturing, etc. [1,2]. However, the environmental efforts in these two sectors mainly affect transportation because it influences the environment in several ways by various modes including road, rail, waterborne transports, and air freight. The vehicles used in these modes are responsible for emissions of air pollutants and GHG, and the environment is also affected by the infrastructure required by the vehicles. For instance, the transportation sector in Europe accounts for 30% of CO₂ emissions, a share that rises to 40% in urban areas [3]. To address this issue, the European Union plans to achieve a 40% reduction by 2030 [4]. The Green Vehicle Routing Problem (G-VRP), which seeks to incorporate the environmental aspects of transportation into VRP, is one of the most interesting problems in the field of logistics and transportation. The goal of this problem is to earn economic benefits while also taking into account environmental considerations. It is necessary to specify the recipients of these benefits to catch their value proposition. Thus, it is necessary to define the main actors involved in logistics and transportation and analyze their business models and the interaction between them. In this context, some studies have explored the business models based on new transportation options (e.g., green vehicles adoption, etc.) and on collaborative strategies for achieving reasonable levels of sustainability and efficiency in logistics activities. Examples of the operational advantages of an integrated vision of the business models and methods can be found in Perboli and Rosano [5], Rosano et al. [6], Perboli et al. [7], and Brotcorne et al. [8].

One of the available strategies for achieving the goals of the G-VRP is to use environmentally friendly vehicles (EFVs). The sustainability benefits of alternative and green fuel resources, such as biodiesel, electricity, ethanol, hydrogen, methanol, natural gas, as a potential substitute for Internal Combustion Engine Vehicles (ICEVs) leads to the adoption of alternative fuel utilization in VRP by defining Alternative Fuel Vehicles (AFVs) as a general type of EFVs. In the relevant literature, some of the studies have been presented as Alternative-Fuel Vehicle Routing Problem (AF-VRP) and do not explicitly refer to the type of vehicle fuel. In particular, Electric Vehicles (EVs) and Hybrid Vehicles (HVs) have been considered as specialized types of AFVs and studied separately with their special characteristics. In most of the studies, EVs have been considered as an idealistic alternative to the ICEVs for freight distribution, as they are emission-free when used, and produce little noise pollution [9]. However, due to the occurrence of combustion emissions for EVs in generating electricity, the different assumptions in the time of charging and the country-specific electricity generation mix, assessing combustion emissions of EVs in different countries is an important issue (see Jochem et al. [10] and Ji et al. [11] for examples of assessments of the EVs emissions in Germany and China, respectively). According to the U.S. Department of Energy, EVs can convert around 59–62% of the received electrical energy to the power in the wheels, but for ICEVs, this ratio is as low as 17–21% [12]. However, there are still constraints on the EVs usage, including the limited availability of recharging stations, the limited driving range of EVs, and the relatively long time used for recharging of these vehicles. Another alternative that has been used in the literature is the HVs, which can consume both electricity and conventional fuel. This capability of HVs provides a solution to reduce transportation costs and emissions while avoiding the operational constraints of EVs [13]. So, two other problems in the routing of EFVs have been introduced in the literature: Electric VRP (E-VRP) and Hybrid VRP (H-VRP). As a result, the classification scheme on the EFVs routing problem (EF-VRP) can be constituted based on the problem characteristics and their application scenarios, by considering three different variants of routing problem as follows: Alternative-Fuel VRP (AF-VRP), Electric VRP (E-VRP), and Hybrid VRP (H-VRP). (Figure 1).

Figure 1. Variants of Environmentally Friendly Vehicle Routing Problem.

Despite the significant volume of works published in the field of EF-VRPs, there is no review paper focusing on EF-VRPs, considering all the different road EFVs types and problem variants, and classifying and discussing with a single holistic vision. The review papers that are somewhat related to this area are those published by Pelletier et al. [14], Juan et al. [15], Margaritis et al. [16], Crainic et al. [17], Schiffer et al. [18], and Erdelić and Carić [19]. These works have addressed the general usage of EVs in transportation and logistics and have partly mentioned the studies in the field of routing problem with AFVs, EVs, and HVs. The mentioned reviews did not present a proper classification for the EF-VRPs and did not discuss the technical characteristics of the variety of problems in this area. These points are crucial both from a modeling and solving point of view. First, technical constraints can drastically change the behavior and properties of the model. Second, a similar characteristic can arise in different settings, giving a plethora of solving methods and redefining the same characteristics or constraints with different names. Thus, the literature presents some lacks.

Therefore, this study is aimed to fulfill this gap along two axes: First, it determines a classification of EF-VRP studies based on different types of EFVs, i.e., Alternative-Fuel Vehicles (AFVs), Electric Vehicles (EVs), and Hybrid Vehicles (HVs). All of the existing problems which have applied environmentally friendly vehicles are classified under the name of Environmentally Friendly Vehicle Routing Problem (EF-VRP). Given the variety of vehicles with unique characteristics that can be considered in EF-VRPs, they are far more complex than VRP that uses a fleet of fossil-fueled vehicles. The first studies in the field of EF-VRP were those carried out by Conrad and Figliozzi [20], Erdoğan and Miller-Hooks [21], Abdallah [22], and Schneider et al. [23]. Later, and particularly in recent years, many other works in the form of journal papers, conference papers, research reports, thesis, and books have been published in this area. Second, it presents a comprehensive survey by considering each variant of the classification, technical constraints, and solution methods arising in the literature. The search conducted on the databases is based on 125 studies on EF-VRP extracted from the main relevant databases, making our study the one based on the largest database of works from the literature. As a result, the main contributions of this paper may be summarized as follows:

• A comprehensive and relevant classification for the literature devoted to Environmentally Friendly Vehicle Routing Problems (EF-VRPs) is presented.
• The survey is conducted to cover the literature related to Alternative-Fuel, Electric and Hybrid Vehicle Routing Problems.
• 125 publications are analyzed in three categories and new problem variants are discussed and classified.
• The existing research gaps are discussed, and some suggestions are provided for future works in each classification.

The remainder of the paper is organized as follows: Section 2 describes the technical constraints and assumptions used in EF-VRPs. Section 3 investigates the studies on AFV routing problems. The EVs routing problem and its variants are reviewed in Section 4. Section 5 describes the HEV routing problem and studies in this area. Section 6 reviews the solution methods for EF-VRPs, followed by conclusions and potential future research directions in Section 7.

Methodology of Survey Research

The classical VRP is one of the fundamental problems in operational research, which seeks to determine how a set of vehicles can serve a set of customers in such a way as to minimize the total cost of travel in a transportation network. The green VRP is a variant of VRP, which seeks to minimize both the economic cost and the environmental cost of vehicle routing [24]. According to Lin et al. [25], the VRPs that follow a green approach can be divided into three broad categories: Green-VRP, Pollution-Routing Problem (PRP), and VRP in Reverse Logistics (VRPRL) (Figure 2). One of the subcategories of the Green-VRP is to use EFVs (EF-VRP in Figure 2) [25].

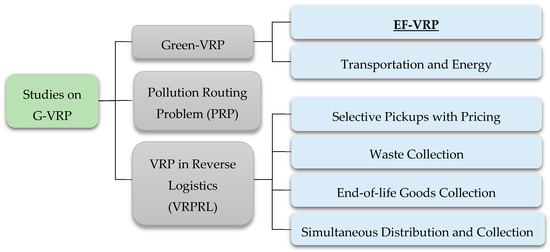
Figure 2. Classification of studies on green vehicle routing problem (G-VRP) according to Lin et al. [25].

The search for the existing works on the EF-VRP was conducted in prominent databases including Scopus, Web of Science, Science Direct, Springer Link EBSCO, Taylor & Francis Elsevier, Wiley, Springer, and IEEE Xplore. To cover a wide range of research, including books, papers, journals, and conferences, and according to the availability of certain information, data were gathered from Google Scholar, extracting from the pages with a minimum number of publications equal to 10. After filtering them by keywords (environmentally friendly vehicles, electric vehicle, hybrid vehicle routing, hybrid electric vehicle routing, plug-in hybrid electric vehicle routing, time windows, pickup and delivery, time-dependent, mixed fleet, alternative fuel vehicle routing problem, green-VRP, and green vehicle routing problem), the data sources were limited to 125 studies. Since the first study on the EF-VRP subject was published in 2011, the time span of this study was limited to the period of 2011–2020. After a manual filtering based on the analysis of the abstracts, our final database was then based on 125 studies on EF-VRP.

2. Technical Constraints and Assumptions in EF-VRPs

The unique characteristics of EFVs have limited their use in VRPs. These characteristics include maximum battery capacity and maximum travel distance without refueling (recharging or battery swapping), duration of refueling (recharging or battery swapping), location of refueling (recharging or battery swapping) stations, fuel (charge) consumption rate, etc. These technical constraints and characteristics can be addressed by a variety of creative solutions, such as establishing battery swapping stations and partial recharge or refueling stations at customer sites. In this section, some of the significant constraints and assumptions of EFVs are explained, as follows:

Fullrefueling (recharging): In this assumption, a vehicle that visits a refueling (recharging) station is fully refueled (recharged) and continues its service as long as its fuel tank (battery) can support it.

Partialrefueling (recharging): In this assumption, a vehicle can decide to only partially fill its fuel tank (recharge its battery) to spend less time at the refueling (recharging) station. Felipe et al. [24] were the first researchers to consider the partial recharging in EF-VRPs. A significant portion of recent studies on EF-VRPs have chosen to use this assumption.

Nointrarouterecharging (refueling) facility: In some studies, it is possible to refuel (recharge) vehicles only in the depot and there are no intraroute facilities for refueling (recharging) in the middle of the route. Hence, in order to cover the fuel tank or battery capacity constraints, authors cover the vehicles’ maximum driving range, and consider the refueling (recharging) process in the base location of the EFVs where the vehicles can be parked overnight and recharged.

Batteryswapping: One method to recharge a group of vehicles along a route is to establish some stations for swapping batteries. Logistics companies can benefit from this approach in several ways. The most significant benefit of the battery swapping approach is the increased recharging speed and reduced time loss. A battery swapping operation can be completed in less than 10 min, which makes it significantly faster than recharging operation [26]. Another advantage of battery swapping is that the used-up batteries can be recharged at night when electricity is charged at a discount [27].

Refueling (recharging) or battery swapping at customers sites: In this assumption, it is supposed that refueling (recharging) or battery swapping services are made available at all or some of the customers’ sites [20].

Refueling (recharging) or battery swapping at specific vertices: In this approach, refueling (recharging) or battery swapping services are not permissible at all customer sites. The assumption of having specific vertices on the network as refueling (recharging) stations was first introduced by Li-ying and Yuan-bin [28].

Simultaneousrefueling (recharging) station siting: EFVs have a shorter driving range than ICEVs. Thus, the proper placement of refueling (recharging) stations can result in a timely provision of the energy needed by vehicles to continue visiting the remaining customers. This assumption involves combining the routing problem with the location problem, and therefore, the expansion of the EF-VRP into Environmentally Friendly Location Routing Problem (EF-LRP). Given the investment needed to construct refueling (recharging or battery swapping) stations at multiple sites, many studies have focused on the goal of minimizing the number of refueling (recharging) stations in the distribution network. Yang and Sun [29] were the first to consider the problem of establishing and operating battery swapping stations to minimize the number of these facilities in a network.

Fixedrefueling (recharging) time: The time spent for refueling (recharging or battery swapping) is one of the critical factors in the use of EFVs. One assumption commonly used in the vehicle routing literature is that the refueling (recharging) time is constant across a network.

Nonlinearrefueling (recharging) process: This assumption involves considering a more realistic nonlinear relationship between the time spent on recharging (refueling) and the amount of fuel (energy) transferred to the vehicle [30]. In most of the existing E-VRP models, the battery charging level is assumed to be a linear function of charging time, but in reality, this function is nonlinear. Accordingly, the use of a practical linear estimation for nonlinear charging behavior can significantly contribute to making the problem and its solutions more realistic.

Batterylifedegradation: The investment loss due to battery degradation is too costly to be ignored. Battery life degradation can be considered as a function of three factors: temperature, State of Charge (SOC), and Depth of Discharge (DOD). In a study by Barco et al. [31], battery degradation in E-VRP was modeled alongside other assumptions of this problem. In this model, the three factors mentioned above are integrated into a degradation cost ($c_{deg}$), which is defined as follows:

$$c_{deg}=c_{bat}\left(L_{QT}+L_{Q,SOC}+L_{Q,DOD}\right),$$

(1)

where $c_{deg}$ is the initial cost of the battery and $L_{QT}$,$L_{Q,SOC}$, and $L_{Q,DOD}$ are the initial cost of the battery, the percentages of battery degradation due to temperature, SOC and DOD, respectively. Further details on battery degradation and other technical characteristics of electric vehicles are available in the study of Pelletier et al. [32].

Effectofload, travelingspeed, andambienttemperatureonfuel (charge) consumption: Speed and weight variation are essential determinants of the vehicles energy consumption while traveling [33]. Additionally, temperature affects energy consumption due to heater use and decreased battery efficiency in cold temperatures, and increased use of air conditioning in hot temperatures [34]. In the literature related to EFVs, these factors are referred to as load, speed, and ambient temperature effects. In this regard, Lin et al. [35] stated that the effect of the load on routing strategies of EFVs could not be ignored. They developed a model for the E-VRP, where the effect of the load on the battery consumption rate was considered and evaluated in a case study. According to this study, the rate of acceleration/deceleration, which is affected by traffic conditions and environmental factors, plays a significant role in vehicle energy consumption [31]. Furthermore, Rastani et al. [34] investigated the impact of ambient temperature on the fleet sizing, battery recharging, and routing decisions of EVs in logistics operations for the first time.

Refueling (recharging or battery swapping) cost: Generally, the refueling (recharging or swapping) process is a costly operation that should be optimized to minimize the total cost of a distribution network. The assumption of time-dependent charging cost was first introduced by Sassi et al. [36], who considered three different charging technologies, namely, slow charging, moderate charging, and fast charging with different costs.

Differentchargingtechnologies: Decision-making on the selection of possible charging technologies could also be an effective way to better control charging time in the E-VRP context. For customers who have narrow time windows, this issue could make them more accessible by fast charging at recharging stations, or if the time windows are long, a better economic approach could be slow charging [19]. Sassi et al. [36] and Felipe et al. [24] analyzed the effect of different charging technologies on the recharge cost for the first time.

Multipledrivingmodes (Multi-mode): A Hybrid Electric Vehicle (HEV) is powered by two power sources, it consumes both electricity and gasoline during driving. The energy consumption of an HEV on each road segment depends on the HEV driving modes. For the first time, Doppstadt et al. [37] assumed four different modes of operation: pure combustion (conventional) mode, pure electric mode, charging mode in which the battery is charged while driving with the combustion engine, and a boost mode in which combustion and electric engines are combined for the drive. Further, Zhen et al. [37] considered this conception and defined four modes including the electric motor (battery-based mode), being mainly powered by the engine (gasoline-based mode), the two being jointly driven (balance mode), or only powered by the engine (only gasoline mode).

Waitinqueuebeforetherecharging (refueling) service: The number of chargers or servers in a recharging (refueling) station is limited and the chargers or servers may be occupied and may not be available at the time of the vehicle’s arrival. Hence, the EFV may need to queue for some time before it starts recharging (refueling) its battery or fuel tank [38,39]. Recently, Keskin et al. [38,40,41] and Poonthalir and Nadarajan [39] extended the EF-VRP by considering queue formation at the recharging (refueling) stations using M/M/1 and M/G/1 queueing systems.

As a result, it should be noted that the limited driving range of EFVs, the existence of a set of refueling (recharging) stations vertices which may be visited more than once or not at all, and the possibility of the vehicles’ driving range extension due to the facilities visiting, represent the complications that were not be presented in the classical VRP or most variants thereof. Thus, heuristics and exacts solutions used for the classical VRP or related variants cannot directly be applied in solving the EF-VRPs. Not only might such heuristics and exact algorithms result in solutions that perform poorly, but these solutions may not even be feasible [21]. So, AF-VRP, E-VRP, and H-VRP can be considered as distinct classes of the VRP and particular variants of the EF-VRP because of its complexity, technical constraints, and new solution methods which have been implemented to solve them.

Vehicle types. 23 (18%), 90 (72%), and 12 (10%) studies belong to the AF-VRP, E-VRP, and H-VRP, respectively. Figure 3 shows the share of research on the EF-VRP variants. As indicated in this figure, previous works have mostly been focused on E-VRPs, and there exists a research gap on the other two variants of the problem, especially the H-VRP. Figure 4 shows the number of papers published on each variant of the problem since 2011. In the mentioned subcategories, there are multiple and technical constraints that can create different variants of the EF-VRP. The most important constraints and assumptions are described in the following subsections.

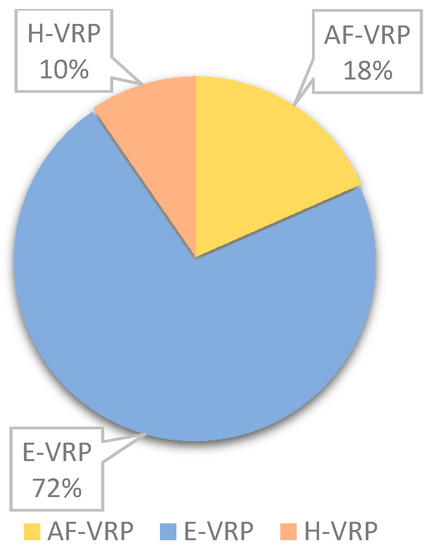
Figure 3. Contribution of research on Alternative-Fuel VRP (AF-VRP), Electric VRP (E-VRP), and Hybrid VRP (H-VRP) from all studies related to the Environmentally Friendly Vehicle Routing Problem (EF-VRP).

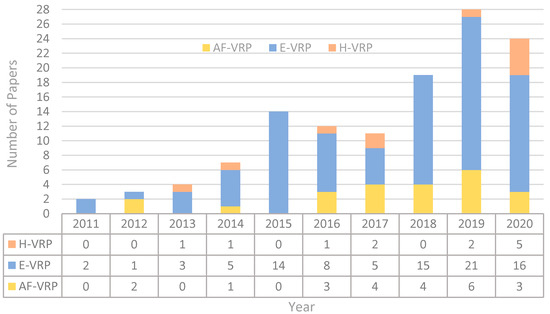
Figure 4. The number of papers published on AF-VRP, E-VRP, and H-VRP.

3. Alternative Fuel Vehicle Routing Problem

One group of EFVs is known as Alternative Fuel Vehicles (AFVs). Their primary characteristic is use of alternative and green fuel resources, such as biodiesel, electricity, ethanol, hydrogen, methanol, natural gas, which limit the maximum distance that can be traveled by them. Moreover, due to type of fuel (energy) consumed by AFVs, their refueling (recharging) stations require special equipment and cannot be established by a distributor company. So, AFVs can be considered as a general type of EFVs, while EVs and HEVs are specialized types. Although most AFV studies do not explicitly refer to the type of vehicle fuel, they do use the assumptions stated in Section 2.

In this paper, these works are also placed in the category of AF-VRP. It should be noted that many researchers have referred to this problem as Green-VRP, but the present paper uses the term Alternative Fuel Vehicle Routing Problem (AF-VRP), in order to avoid confusion with the broader definition of G-VRP.

The AF-VRP was first introduced by Erdoğan and Miller-Hooks [21]. In that work, a set of AFVs fleet located in a central depot has to serve a set of customers in a distribution network. The AFSs are placed along the paths to ensure that the AFVs can serve customers adequately. In that study, the problem had been formulated in the form of a Mixed Integer Linear Problem model, which ensures that all customers are visited only once, fuel tank level upon arrival at a node is non-negative, and conformity to the maximum tour duration constraint is guaranteed provided that each tour begins and ends at the depot. The problem was solved by two heuristic methods with an improvement technique. An example of a feasible solution for this AF-VRP is illustrated in Figure 5. In this example, there are 17 customers and 6 AFSs, and refueling operations are performed to continue the route at AFSs, and the level of vehicle tanks is refilled when the vehicles arrive at AFSs vertices. In the first tour, the AFV moves from the depot to the customer 5 considering relatively a long path and consumes considerable stored fuel. So, before arriving at the location of customer 5, it needs to refuel at AFS 2. To arrive at the depot on the first tour, the vehicle must visit another AFS one more time. Because of the short distance on the second tour, there is no need to refuel. Serving customers is provided on tours 3 and 4, similar to the first tour.

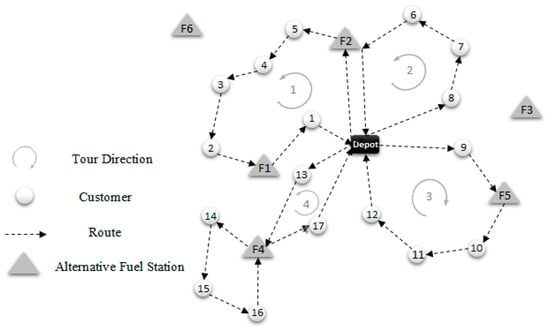
Figure 5. Example of a solution for AF-VRP.

3.1. Reviewing the Studies Conducted on AF-VRP

In addition to Erdoğan and Miller-Hooks [21], some other studies also used the AFV fleet to serve customers. By presenting a problem entitled Sustainable Vehicle Routing, Omidvar and Tavakkoli-Moghaddam [42] set the economic profit as their primary objective, and considered avoiding congestion and traffic, reducing GHG, and reducing fuel consumption in AFVs in the proposed model. Taha et al. [43] introduced a variant of the one given by Erdoğan and Miller-Hooks [21] with multiple depots. The new model of Koç and Karaoglan [44] has fewer variables and constraints, and more than one stop is not allowed for refueling each vehicle between two nodes in a transportation network. Montoya et al. [45] presented an effective two-phase heuristic method for solving the AF-VRP. Bruglieri et al. [46] introduced a new model for the AF-VRP without cloning AFSs. Yavuz and Çapar [47] presented a model that can consider several alternative-fuel vehicles by adopting different driving ranges, refueling times, and availability of refueling stations. Andelmin and Bartolini [48] modeled the AF-VRP using a multi-graph, in which there is no need to model the refueling stops en-route. Leggieri and Haouari [49] gave a nonlinear compact formulation for the time and energy consumption constraints of the AF-VRP. They used an approach to reduce the use of several variables and constraints, included a set of preprocessing conditions, and applied a reduction procedure to solve the AF-VRP. Yavuz [50] proposed an iterated beam search algorithm for the AF-VRP. Affi et al. [51] presented a Variable Neighborhood Search (VNS) algorithm for solving the AF-VRP. Madankumar and Rajendran [52] presented a basic model for the AF-VRP. The paper also investigated the scenario of considering different fuel prices at different AFSs as an extension of the proposed model. Moreover, in another model, the problem of Pickups and Deliveries in a Semiconductor Supply Chain (PDP-SSC) was provided regardless of AFVs and AFSs, to evaluate the performance of the first model, which is consistent with the PDP-SSC model. Poonthalir and Nadarajan [53] presented a bi-objective problem considering fuel consumption efficiency. Zhang et al. [54] developed Erdoğan and Miller-Hooks’s [21] work by incorporating the limited loading capacity. Hooshmand and MirHassani [55] presented an AF-VRP in a densely populated urban area, taking into account traffic constraints and minimizing CO2 emissions, under time-dependent travel speeds, limited driving range, and the limited capacity of vehicles with alternative fuels. Koyuncu and Yavuz [56] established a unified framework for mixed fleet AF-VRP, which considers three different types of refueling policies to shorten the time for refueling stops. Bruglieri et al. [57] presented a precise two-phase method called the path-based solution for solving the AF-VRP. Normasari et al. [58] presented a new variant of the AF-VRP, namely, Capacitated G-VRP (CGVRP) and solved the problem by applying a Simulated Annealing (SA) heuristic algorithm. Ashtine and Pishvaee [59] analyzed the economic and environmental impacts of different AFVs, and qualified that biodiesel can reduce GHG by 37% compared to conventional diesel based on equivalent carbon dioxide measure. They proposed two base models in which, routing optimization for each vehicle with the total pollution costs or Carbon Dioxide Equivalent (CO2eq), for a single fuel fleet or a fleet composed of different alternative and petroleum vehicles, is minimized. Poonthalir and Nadarajan [39] integrated M/M/1 queue model at the AFSs and AF-VRP and proposed an enhanced Chemical Reaction Optimization (e-CRO) algorithm with the bacterial transformation to solve it. Shao and Dessouky [60] considered Compressed Natural Gas (CNG) as one of the possible solutions for fossil fuel substitution because of its wide availability, engine compatibility, and low operations costs in routing AFVs including the choice of CNG fuel stations. Zhang et al. [61] proposed the Multi-Depot Green Vehicle Routing Problem (MDGVRP) as a new variant of AF-VRP to minimize the total carbon emissions. Nosrati and Arshadi Khamesh [62] considered the risk management by integrating the reliability concept into the AF-VRP. They modeled the problem as nonlinear and bi-objective mixed-integer programming to minimize the total cost of routing and maximize the system reliability.

Table 1 briefly presents the assumptions and constraints of the AFV. The first two columns indicate the references and their publication year. The next twelve columns pertain to the assumptions and constraints of the VRP. It should be noted that the diversity of the VRP is much more than the twelve cases mentioned, but due to the importance and usage of the assumptions raised in the EF-VRP, these constraints and assumptions have been considered. The eleven columns considered in the classification of AFV’s Related Technical Constraints and Assumptions relate to the special characteristics of AFVs. This table also features calculated percentages of usage for each characteristic. This value is equal to a percentage of papers that have considered the intended characteristic, obtained as the ratio of the number of papers containing the corresponding characteristic over the total number of papers. The last column illustrates the type of objective functions including minimization of Total Traveled Distance, Overall Costs, Emission or Energy Consumption, Total Time Duration (including traveling time, servicing time, recharging time, and waiting time), Number of Vehicle and Number of Refueling (Recharging) Stations which have been reported as Dist., Costs (including acquisition cost of the vehicles, recharging, refueling, or battery swapping cost, Station installation cost, etc.), Em., TTD, NV, and NS, respectively.

Table 1. Summary of studies conducted on AF-VRPs.

Year	Reference	VRP Constraints and Characteristics													AFV’s Related Technical Constraints and Assumptions											Objective Function
		Time Windows	Pickup and Delivery	Travel Time	Capacitated	Fleet Size	Mixed Fleet		Periodic	Stochastic	Time-Dependent	Multi-Depot	Multi-Echelon	Loading	Full Refuel (Recharge)	Partial Refuel (Recharge)	No Intra-Route Refueling (Recharging) Facility	Refueling at Customer Site	Refueling (Recharging) at Special Vertices	Fixed Refueling (Recharging) Time	Simultaneous Refueling (Recharging) Station Siting	Load, Speed Traveling or Ambient Temperature Effect	Refueling (Recharging) Cost	Nonlinear Refueling (Recharging) Process	Wait in Queue at Refueling Stations
							AFVs and Other Types	Pure AFVs
	% of Papers	9%	4%	91%	43%	4%	17%	0%	0%	9%	9%	4%	0%	0%	100%	4%	0%	17%	100%	78%	0%	13%	13%	0%	4%	#
2012	Erdoğan and Miller-Hooks (EMH) [21]			✓											✓				✓	✓						Dist.
2012	Omidvar and Tavakkoli-Moghaddam [42]	✓		✓	✓						✓				✓				✓	✓						Dist, Em, NV TTD
2014	Taha et al. [43]			✓											✓				✓	✓						Dist.
2016	Koç and Karaoglan (KK) [44]			✓	✓										✓				✓	✓						Dist
2016	Montoya et al. (MSH) [45]			✓											✓				✓	✓						Dist
2016	Bruglieri et al. [46]			✓											✓				✓	✓						Dist
2017	Yavuz and Çapar (YÇ) [47]			✓			✓								✓			✓	✓				✓			Dist., Em, Costs
2017	Andelmin and Bartolini (AB) [48]			✓											✓				✓	✓						Dist
2017	Leggieri and Haouari [49]			✓											✓				✓	✓						Dist
2017	Yavuz [50]			✓			✓								✓			✓	✓							Dist
2018	Affi et al. [51]			✓											✓				✓	✓						Dist
2018	Madankumar and Rajendran [52]	✓	✓	✓	✓										✓				✓	✓			✓			Dist, Cost
2018	Poonthalir and Nadarajan [53]			✓						✓					✓				✓	✓		✓				Dist. Em
2018	Zhang et al. [54]				✓										✓				✓							Dist.
2019	Hooshmand and MirHassani [55]			✓	✓						✓				✓				✓	✓		✓				Em
2019	Koyuncu and Yavuz [56]			✓	✓		✓								✓	✓		✓	✓				✓			Dist., Costs
2019	Bruglieri et al. [57]			✓											✓				✓	✓						Dist
2019	Normasari et al. [58]			✓	✓										✓				✓	✓						Dist
2019	Poonthalir and Nadarajan [39]			✓											✓				✓	✓					✓	Dist
2019	Ashtine and Pishvaee [59]			✓	✓										✓			✓	✓	✓		✓				Costs, Em
2020	Shao and Dessouky [60]			✓	✓	✓	✓								✓				✓	✓						TTD
2020	Zhang et al. [61]				✓							✓			✓				✓							Em
2020	Nosrati and Arshadi Khamesh [62]			✓						✓					✓				✓	✓						Costs

3.2. AF-VRP Literature Gaps and Future Research

Studying the routing problem of AFVs from two different perspectives, namely, VRP constraints and characteristics, and AFV’s related technical constraints and assumptions, will determine the research gaps of the AF-VRP literature and provide the potential future researches in this field (as shown in Table 1). For example, by considering VRP constraints, using a set of AFVs to serve the final customers can be an attractive and economical issue in a two-echelon distribution system, due to the environmental regulations in the urban environment. Moreover, a Periodic AF-VRP, in which requested demands must be satisfied over a multi-period, or considering the size of items to be distributed in loading VRP application, can be interesting to analyze for future research. In addition, in the field of AFVs’ related technical constraints and assumptions, different strategies of refueling AFVs such as partial or nonlinear refueling process, simultaneous refueling (recharging) station siting, analysis of the potential of load, traveling speed, ambient temperature effect in fuel consumption, emission reduction, and different patterns of energy consumption can be considered more for future studies to make AF-VRPs comprehensive, more applicable, and closer to real-world issues.

4. Route Planning on Electric Vehicles

Generally, the E-VRP is defined on an undirected, complete graph G = (V; A). In this problem, a set of electric vehicles serves as environmentally friendly vehicles. Figure 6 presents an example of E-VRP. In this example, there are 15 customers and 4 charging stations, and full charging in the depot and charging stations is made possible. For better understanding, the battery state of charge at the time of arriving each node is specified in the figure. In the first tour, when the EV moves from the depot to customer 10, considering the relatively long path and using half of the stored energy, it visits charging station 3 to continue the path and serve customers 11 and 12, and continues its path after the recharging process. In the second tour, considering the proximity of customers 1, 2, and 3, there is no need to recharge, and the EV returns to the depot after servicing the customers. On the third tour, after visiting customers 13 and 14, and considering the long path to customer 15, the EV returns to the charging station and fully charges itself.

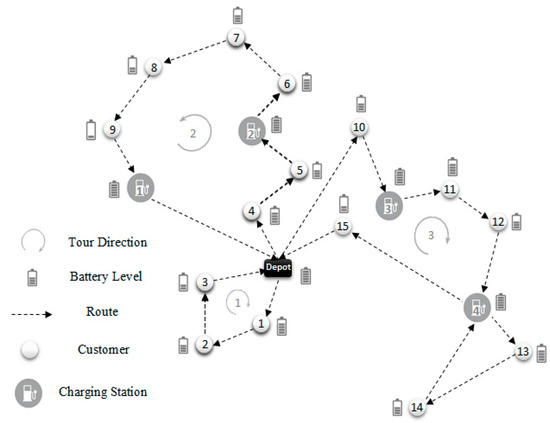
Figure 6. An example of an E-VRP solution.

4.1. Reviewing the Studies Conducted on E-VRP

The E-VRP is similar in definition to the AF-VRP. It can even be considered as a more specialized variant of the AF-VRP. However, the unique characteristics of the EVs and the specific strategies to deal with these features include battery swapping, partial recharging, recharging rate, battery life, etc., which have been considered in various studies alongside different solution methods. Since this study attempts to concentrate on the nature of the problem and application of EF-VRP, our E-VRP classification scheme is based on the technical and operational characteristics of the problem (e.g., time windows structure, vehicle heterogeneity, recharging scenarios, locating strategies, charging function) and their application scenarios, rather than the solution methods and related algorithms. Based on implementing different and integrated characteristics of VRPs, and the most frequent and essential technical constraints of EVs, E-VRP studies can be classified in eleven different variants based on the nature of these characteristics which have been used in the EF-VRP literature. These variants are: 1. E-VRP with Time Windows (E-VRP-TW), 2. E-VRP with Partial Recharging (E-VRP-PR), 3. E-VRP with Mixed Fleet (E-VRP-MF), 4. E-VRP with Battery Swapping Stations (E-VRP- BSS), 5. Electric Location- Routing Problem (E-LRP), 6. E-VRP with Nonlinear Charging function (E-VRP-NL), 7. Time-Dependent Electric Vehicle Routing Problem (TD-E-VRP), 8. Loading E-VRP (L-E-VRP), 9. Periodic E-VRP (P-E-VRP), and 10. Two-Echelon E-VRP (2E-E-VRP). Other works of literature that have applied some particular constraints and EV features have been put in one another category, namely, other related studies.

4.1.1. Electric Vehicle Routing Problem with Time Windows (E-VRP-TW)

The E-VRP-TW is an extension of the well-known VRP-TW, which has a higher complexity than the classical VRP-TW problem. The E-VRP-TW was considered earlier than other E-VRPs. In this problem, a set of EVs served customers, each with a predetermined time window. Not visiting in pre-specified intervals reduces customers’ satisfaction or, in the worst cases, even creates to solutions not usable in practice. Considering the constraints of battery capacity and recharging time of batteries challenge serving to customers in predetermined periods, and solution faces more difficulty compared to using ICEVs. The first formal publication on the E-VRP-TW was presented by Schneider et al. [23], who extended the VRP-TW. Afroditi et al. [3] extended the E-VRP, taking into account vehicle capacity constraints, time windows, and predetermined vehicle charging levels. Taking into account some factors such as rolling resistance, air resistance, gradient resistance, and energy recuperation and minimizing energy consumption in the problem, Preis et al. [63] developed the new variant of E-VRP-TW. Bruglieri et al. [64] used VNS Branching (VNSB) as a math-heuristic method for solving the problem. Considering the dependence of energy consumption of EVs on various factors such as ground gradient, weight, and speed of the vehicle, Basso et al. [65] developed a new E-VRP-TW model so that the speed of vehicles during different hours of the day was considered as a variable due to the volume of traffic. Barco et al. [31] proposed a method for transporting passengers using E-VRP-TW, in which the vehicle charging schedule was considered to minimize costs and reduce battery degradation. Kancharla and Ramadurai [66] considered significant parameters such as speed, acceleration, load, and grade, which affect the battery consumption rate, and estimated the amount of energy required by the EV engine. Zuo et al. [67] applied factors such as limited battery capacity, charging station selection, and determining the battery charging time to improve the efficiency of EVs in the logistics system. Keskin et al. [40] developed the problem considering time-dependent queueing times at the stations. Erdem and Koç [68] combined the Home Health Care Routing Problem (HHCRP) and E-VRP-TW, namely, Electric Vehicles in Home Care Routing Problem, to reduce the environmental impact of home health care operations. Zhang et al. [69] developed a model that takes into consideration visiting the charging station in the routing in reverse logistics. Keskin et al. [41] considered EVs’ possible waiting in the queue before recharging their battery due to a limited number of available chargers in E-VRP-TW. M/M/1 queueing system equations have been used to model waiting times. Recently, Keskin et al. [38] extended the previous work by considering stochastic waiting times at the recharging stations and using M/G/1 queueing system to model the waiting times. Goeke [70] extended the well-known Pickup and Delivery Problem with Time Windows (PDPTW) by applying EVs to serve the customer demand. Xiao et al. [71] introduced the energy/electricity consumption rate (ECR) per unit of traveled distance into the E-VRP-TW for the first time. Meng and Ma [72] presented a new problem by calculating more accurate cost of the logistics includes fixed, transportation, charging, and time-windows violation penalty costs and combining the two charging strategies of fast charging and battery swapping and each EV can charge its battery or replace it according to the minimum of the battery replacement time and fast charging time. In order to optimize resource allocation, and reduce energy consumption and road congestion, soft time-windows was considered in this study. Similar to the previous paper, Taş [73] considered soft time-windows constraints and proposed Electric Vehicle Routing Problem with Flexible Time Windows (E-VRP-FTW) to minimize the traveling costs, the costs of using electric vehicles and the penalty costs incurred for earliness and lateness. Löffler et al. [74] extended the E-VRP-TW by considering possibility of both full and partial recharge, in which at most one recharge per vehicle route is allowed.

4.1.2. Electric Vehicle Routing Problem with Partial Recharging (E-VRP-PR)

Considering the assumption of the partial recharge and overnight charge for EVs results in one of the operational and functional variants of the E-VRP. Conrad and Figliozzi [20] considered the possibility of a partial recharge. The remarkable point of that study was the possibility of recharging electric vehicles at customer sites. Accordingly, Felipe et al. [24], for the first time, formulated a formal problem as a variant of the E-VRP, namely, E-VRP-PR. They formulated the problem using a set of EVs in the model presented by Erdoğan and Miller-Hooks [21]. Ding et al. [75] extended the E-VRP-TW model, taking into account additional technical constraints such as the limited number of chargers in a charging station. In his proposed model, Moghaddam [76] sought to achieve the optimal number of EVs and charging stations with a limited number of EVs and the number of charging stations. Keskin and Çatay [77] combined the problem with the E-VRP-TW. Desaulniers et al. [78] presented four different variants of the E-VRP-TW-PR with different possibilities of full or partial recharging. Considering the possibility of equipping charging stations with new facilities that affect the duration of the recharge process, Keskin and Çatay [79] presented the E-VRP-TW model taking into account partial recharging by three configurations of normal, fast, and super-fast charging. A matheuristic for a similar problem with partial recharging was proposed by Bruglieri et al. [80]. To reduce the impact of the long recharging times associated with the intra-route stops, Cortés-Murcia et al. [81] proposed a routing problem that takes E-VRP-TW constraints, partial recharges, as well as the possibility of serving a customer during the recharging operation. In other words, for each visit to a recharging station, it is possible to visit one customer, namely, a satellite customer while the vehicle is in the charging process. The visit could represent any type of alternative mode (walking, bikes, drones, segways, etc.) A fuzzy optimization model is proposed by Zhang et al. [82] based on credibility theory for electric vehicle routing problem with time windows and recharging stations. In this study, the partial recharge was considered under the uncertain environment, and fuzzy numbers were used to denote the uncertainties of service time, battery energy consumption, and travel time.

4.1.3. Electric Vehicle Routing Problem with Battery Swapping Stations (E-VRP-BSS)

The concept of BSS was first considered by Yang and Sun [29] to address simultaneous decisions regarding the location of battery swapping facilities and EV routing. Goeke et al. [83] present an Adaptive VNS (AVNS) for the BSS-EV-LRP which leads to better results than TS-MCWS and SIGALNS in nearly all of the given test instances. Regardless of battery swapping facility siting decisions, Chen et al. [84] developed a new E-VRP-BSS model. This problem was studied considering customers’ time windows, BSSs, and constant battery swapping time. Hof et al. [85] proposed the development of solving methods of problems with intermediate stops, namely, Battery Swap Station Location-Routing Problem with Capacitated Electric Vehicles (BSS-EV-LRP), considering the location of battery swapping stations and EV routing, and minimizing the number of BSSs and routing of EVs. Verma [86] developed the VRP with time windows, charging stations, and battery swapping stations. Taking into account the lengthy process of recharging, as well as the costly battery swapping, he considered the possibility to conduct both processes at the stations considered in the model. Mao et al. [87] presented an E-VRP-TW problem in which two recharging options are provided at each charging station. The first one is to recharge the battery partially which is cost efficient and the second one is battery swapping whose operation time is very short compared to the travel time of the route, but the cost is higher than the former option. Recently, Raeesi et al. [88] introduced the mobile battery swapping for the first time, by considering Battery Swapping Vans (BSVs) to swap the depleted battery on an EVs with a fully charged one at a designated time and space, and provide the battery swapping service to multiple EVs.

4.1.4. Electric Vehicle Routing Problem with Mixed Fleet (E-VRP-MF)

By and large, if the assumption of identical vehicles is freed in the classical VRP, it becomes possible to use different vehicles in terms of capacity, speed, energy consumption, etc. [25]. This new assumption is called “mixed fleet” in different studies. Regarding the applied EVs in the load transportation industry, and in order to implement this assumption in the E-VRP, the two problem types have been proposed as follows:

Amixedfleetforcombiningdifferentvariantsofvehicles. This approach seeks to simultaneously use various variants of vehicles, including EVs, AFVs, ICEVs, etc., in a distribution fleet. This is because heterogeneous and different vehicles are considered to be more applied in the real world due to the different speed, price, equipment, technology, and capacity [25]. Due to the increased use of EVs in distribution systems, optimal route planning can provide cost-effective interactions among different variants of vehicles, considering different vehicles. In this regard, some studies were presented which are discussed below: Gonçalves et al. [89] investigated three different scenarios in the routing problem of vehicles with the pickups and delivery with the heterogeneous fleet of EVs and ICEVs. Sassi et al. [36] presented a new formulation for combining heterogeneous ICEVs and EVs to serve a set of customers. In two other studies, i.e., Sassi et al. [90] and Sassi et al. [91], an Iterated TS (ITS) and multi-start Iterated Local Search (ILS) were proposed for solving the problem. Goeke and Schneider [92] considered a set of similar EVs with a set of similar ICEVs for customer service provision. Murakami and Morita [93] presented a variant of the VRP for EVs and ICEVs, which can be considered as a variant of the E-VRP-MF. In this problem, the EVs were used as an aid to the transportation fleet, and not recharged. Sundar et al. [94] developed a problem to efficiently manage a group of independent vehicles (AFVs and EVs). Kopfer and Vornhusen [95] analyzed various vehicle fleets with differently sized EVs and ICEVs. Macrina et al. [96] presented a variant of the E-VRP-MF, considering the time windows and partial recharging. Villegas et al. [97] studied a problem in which a set of ICEVs and EVs are used and a set of technicians serve a set of customers in a geographical zone. The problem is a combination of Workforce Scheduling and Routing Problem (WSRP) and the E-VRP-MF problem, leading to the formation of the routing and scheduling problem of technicians with the ICEVs and EVs.

MixedfleetofpureEVs. In this approach, there are EV types with different features, such as driving range, load capacity, and acquisition cost [98]. Thus, companies are forced to have a smaller number of larger EVs. Accordingly, considering different types of EVs in a distribution system can be cost-effective and provide optimal freight distribution operations with more flexibility. Considering the distribution of urban load, Van Duin et al. [99] used a variety of different types of EVs to meet the demand for a set of customers. In this problem, the stop time for eating lunch was considered by the driver at the customer’s site. Hiermann et al. [100] presented the mixed fleet concept in E-VRP-TW by a working paper. Then, Hiermann et al. [101] combined the E-VRP-TW and the Fleet Size Mix Vehicle Routing Problem with Time Windows (FSM-VRPTW) and introduced a new E-VRP. In this study, a series of EVs were used that are different in purchasing cost, load capacity, battery capacity, power consumption rate/distance, and exclusive charging rate. In the problem of Lebeau et al. [102], EVs were used, which varied in terms of load capacity, weight, maximum battery capacity, fixed costs, and running costs of each vehicle and driver costs, and recharging is possible for EVs at the depot only. Zhao and Lu [103] combined the features of the E-VRP-TW and E-VRP-MF with some other classical VRP assumptions and applied it in a real-world E-VRP raised by a logistics company.

4.1.5. Electric Location-Routing Problem (E-LRP)

Some studies on the EVs routing focused both on deciding on the route planning of this vehicle variant, with an emphasis on the driving range and the long times of recharging process, and the siting of charging stations to utilize the necessary charging infrastructure. Accordingly, another kind of the E-VRP called E-LRP was provided, which simultaneously focused on the EVs routing and charging station siting decisions. In this regard, the following studies are examined below. Worley et al. [104] simultaneously provided a model for EVs routing with the siting of recharging stations and used the model to solve a case study related to a company in Chicago. Li-ying and Yuan-bin [28] considered the strategy of locating recharging stations in the E-VRP-TW problem. In this study, the strategy of charging stations includes selecting the type of charging station and their location. Schiffer et al. [105] investigated the competitiveness of EVs in the load logistics industry in a case study. This evaluation was based on simultaneous decisions on vehicle routing and location of charging stations. Schiffer and Walther [106] presented a problem, in which in addition to the routing decisions of the EVs, the siting decision of charging stations and partial recharging were also taken into account. Schiffer and Walther [107] present a generic problem formulation for LRP with Intra-route Facilities (LRPIF), in which the location of facilities for intermediate stops has to be determined to keep vehicles operational. Considering the uncertainty patterns in a spatial distribution, demand and time windows of customers in location-routing problem, Schiffer and Walther [108] used a robust approach to cover the assumption of uncertainty raised and decided on how to route the EV and how to establish charging stations. Paz et al. [109] presented the Multi-Depot E-LRP with Time Windows (MD-EV-LRP-TW), in which three different models formed were investigated based on the assumptions of battery switching stations, partial recharging of EVs, and the combination of these two assumptions. Zhou and Tan [110] presented a problem to manage EV routing planning and location decisions about BSSs. Schiffer et al. [111] extended the LRPIF considering different types of facilities at which either freight replenishment or energy recharging is possible or both. Gatica et al. [112] used four strategies of Random Generation, Customer Location, Great Route, and K-Means to locate charging stations and a heuristic method to route the EVs fleet. Almouhanna et al. [113] addressed LRP with a Constrained Distance (LRPCD) which is used by EVs in location and routing decisions. In this study, decisions related to opening multiple depots, allocating customers to them, simultaneously locating depots (not recharging facilities), and routing EVs with limited driving ranges are considered.

4.1.6. Electric Vehicle Routing Problem with Nonlinear Charging Function (E-VRP-NL)

The assumption of nonlinear charging of EVs is a significant hypothesis considered only in recent years and it has led to the formation of another variant of the E-VRP called E-VRP-NL. For the first time, Montoya et al. [114] considered the amount of charge as the decision variable and the concave function of charging time and partial recharging and in the E-VRP model and presented a new formula. In this problem, each recharging station has a slow, moderate, or fast charging mode that is considered in modeling battery charging functions of EVs and allows for partial recharging of EVs. Montoya [115] researched several variants of the E-VRP: green VRP (GVRP), E-VRP with partial recharging and nonlinear charging functions, and the technician routing problem with a mixed fleet of ICEVs and EVs. For each problem, effective solving procedures were proposed: multi-space sampling heuristic, iterated local search enhanced with heuristic concentration, and two-phase parallel metaheuristic based on solving a set of sub-problems and extended set-covering formulation. Montoya et al. [116] presented a problem that seeks to minimize the total travel time, including the driving time, and the vehicle recharging time. Froger et al. [30] presented two new formulations based on an arc-based tracking of the time and the SOC and classical node-based tracking for the E-VRP-NL. In both models provided, a procedure was used to prevent the repetition of charging nodes. Zuo et al. [117] considered new practical factors such as the nonlinear SOC time charging function, the charging options of multiple visits of CSs with flexible charging time, and maintaining the battery SOC above a safe level. Koç et al. [118] developed the E-VRPNL problem, taking into account the various companies able to conduct a joint investment in CSs, and presented the E-VRP with Shared Charging Stations (E-VRP-SCS). Lee [119] presented a novel branch-and-price-based approach for the EVRP with nonlinear charging functions by introducing an extended charging stations network. The application of the extended charging stations network with the column generation approach has provided the possibility of explicitly considering the nonlinear charging function without any approximations. Kancharla and Ramadurai [120] integrated the load-dependent discharging assumption in the energy estimation with E-VRP-NL. They developed a modified ALNS algorithm delivering improved performance with new removal and insertion operators specific to the proposed problem.

4.1.7. Time-Dependent Electric Vehicle Routing Problem (TD-E-VRP)

In environments with high congestion such as urban areas, failing to pay attention to urban traffic in routing leads to non-optimal solutions to the problem, because in environments with traffic congestion, the time required to traverse the road depends not only on the distance of the road but also on the starting time of travel. So, traffic congestion is an important factor that affects the use of EVs and routing decisions in city logistics [121]. The time-dependency assumption is a feature that has covered this real-world constraint in the VRP literature. In the E-VRP, two studies have focused on this issue. First, Shao et al. [122] considered travel time variable to reflect the dynamic traffic environment with some of the operational scales considered in EVs and provided the E-VRP with Charging Time and Variable Travel Time (E-VRP-CTVTT). Recently, Lu et al. [123] used the well-known time-dependency assumption in E-VRP-TW and proposed the TD-E-VRP for the first time. Zhang et al. [124] introduced time-dependent travel speeds and congestion tolls into the E-VRP-TW. In this problem, a fixed congestion toll needs to be paid when a vehicle enters a peak period.

4.1.8. Loading Electric Vehicle Routing Problem (L-E-VRP)

The size of items to be distributed is an important factor that decides whether it is possible to load them into loading space in some VRP applications. Such problems are solved through solving a variety of two- or three-dimensional bin packing problems (2BPP-3BPP) and by using separate processes to solve VRP and loading problem. Incorporation of the features and constraints of the loading problem into VRP has led to the development of new problems that simultaneously assess both issues. Two-dimensional loading capacitated vehicle routing problem and three-dimensional loading capacitated vehicle routing problem (2L-CVRP and 3L-CVRP) are among the most applicable approaches in this regard. The difference between these two is in the nature of demanded items; the basic assumption of 2L-CVRP is that items cannot be loaded on top of each other, while 3L-CVRP has no such assumption [125]. Recently, Zhu et al. [126] examined this feature in the E-VRP by defining a multi-depot capacitated electric vehicle routing problem where client demand is composed of two-dimensional weighted items. They considered the effect of items’ weight on the battery consumption and provided the possibility for the EVs to decide when and where to charge or replace the batteries in the distribution network.

4.1.9. Periodic Electric Vehicle Routing Problem (P-E-VRP)

Most of the time, customers make their demands in set of periods (days) in a planning horizon. In other words, each customer has one or more visit combinations which include one or more periods (days) [127]. Once a customer’s visit combination is selected, the customer must be satisfied in the existing day(s) in the visit combination. In this approach, route planning must be performed in each period which is affected by other periods, integrally. Kouider et al. [128] combined this concept with E-VRP and introduced the Periodic Electric Vehicle Routing Problem (P-E-VRP), in which the routing and charging are planned over a multi-period horizon. This work aimed to minimize the total cost of routing and charging over the time horizon. They did not propose any mathematical model for the problem, and just presented two constructive heuristics based on clustering technique and insertion strategy.

4.1.10. Two-Echelon Electric Vehicle Routing Problem (2E-E-VRP)

An increase in environmental, social, and regulatory concerns, as well as an increase in traffic volumes in cities, caused the public and private organizations to change their attitudes towards designing the transportation system and the freight distribution in the supply chain. The implementation of multi-echelon distribution systems, and especially the two-echelon freight distribution, is an approach to face these challenges [129]. In the two-echelon distribution system, which is a multi-echelon distribution system, the freight is delivered to the intermediate depots and then to intermediate customers [130]. The two studies presented in recent years are as follows: Breunig et al. [131] presented the Two-Echelon VRP by adding the EV fleet to serve customers and introduced the Electric Two-Echelon VRP (E2E-VRP). In this problem, EVs were used to deliver goods to customers and in the second echelon of the problem. It was also possible to recharge EVs in a set of charging stations available at the second echelon. Jie et al. [132] investigated the Two-Echelon E-VRP with BSS (2E-E-VRP-BSS), considering the limited driving range of EVs and battery swapping strategies. Vehicles at both echelons were electric, with the difference that the first-echelon vehicles had more battery capacity than the second echelon vehicles. Moreover, a cost was considered in the proposed model for battery swapping. The objective is to minimize the cost of driving EVs at both echelons, loading and unloading operations in the intermediate depots, and the cost of the battery swapping of the EVs.

4.1.11. Other Related Studies of E-VRPs

Recently, a new design, the modular EVs, was introduced. In this case, the EV charging is split into separate modules that can be loaded/unloaded at specified locations, allowing the possibility of having more charge. Using modular EVs in the VRP was raised by Aggoune-Mtalaa et al. [133] for the first time in an urban distribution of goods to demonstrate the added value of using this variant of the vehicle, and presented the Modular electric Vehicle Routing Problem (Me-VRP). Rezgui et al. [134] extended the Me-VRP which involves electric modular vehicles for goods distribution in the urban environment, by fleet size, mixed fleet, and time windows, well-known VRP concepts. Schneider et al. [135] presented the E-VRP with Recharging Facilities (E-VRP-RF) as a particular case of the VRP with Intermediate Stops (VRPIS) and developed an Adaptive VNS (AVNS) to solve the problem. Zhang et al. [136] presented an E-VRP model that sought to minimize energy consumption by EVs, in which a comprehensive approach was used to calculate the energy consumption rate of EVs. For integrating energy consumption estimation into a E-VRP, Basso et al. [137] proposed a two-stage E-VRP that integrates path finding with route planning. The energy consumption of electric trucks in Gothenburg, Sweden, has been estimated based on a comparison between numerical simulations and the actual consumption data measured on the public transport route. Pelletier et al. [138] introduced a practical transportation problem that can deal with the presence of uncertainties surrounding the energy consumption of EFVs, and solve it by a robust optimization framework and a two-phase heuristic method based on large neighborhood search. Lu and Wang [139] proposed the Dynamic Capacitated E-VRP (DC-E-VRP), in which the information of partial customers is unknown and revealed during the execution of the plan in the dynamic problem. An effective scheduling generation scheme, population initialization, two search strategies on representation and scheduling and crossover operators have been designed to solve the problem. Granada-Echeverri et al. [140] proposed the Electric Vehicle Routing Problem with Backhauls (E-VRP-B) that includes both a set of customers to whom products are to be delivered and a set of customers whose goods need to be transported back to the distribution center. Both the linehaul customers and the backhaul customers must be visited contiguously, and all routes must contain at least one linehaul customer. Reyes-Rubiano et al. [141] considered both driving range limitations and uncertainty conditions in E-VRP, which might cause route failures when the vehicle runs out of battery, and presented the Electric Vehicle Routing Problem with Stochastic Travel Times (E-VRP-ST). Kullman et al. [142,143] offered an implementation of a solution method that suffers none of the issues which are common in solving the E-VRP. The issues are inexactness, inefficiency, and lack of robustness of the solution methods. So, they used the Fixed Route Vehicle Charging Problem (FRVCP) as a subproblem in E-VRP based on the labeling algorithm of the Froger et al. [30]. The solution implementation has been provided in an open-source Python package to remove the burden of implementation for future E-VRP researchers. Kullman et al. [144] proposed a new extension of the E-VRP called E-VRP with Public-Private Recharging Strategy (E-VRP-PP), in which demand for charging stations was unclear and followed a real queue process. In this regard, the Markov decision process (MDP) was used for modeling the E-VRP-PP. They utilized the piece-wise linear charging time function to consider the public charging stations, at which waiting time may incur due to the unknown demand using the same charging station. They developed a decomposition approach to separate the routing decision from the charging decision. Table 2 determines the classification of each study on the E-VRP-TW (TW), E-VRP-PR (PR), E-VRP-BSS (BSS), E-VRP-MF (MF), E-LRP (LRP), E-VRP-NL (NL), L-E-VRP (Lo), P-E-VRP (Pe), 2E-E-VRP (2E), and Other Related Studies (ORS) and covers several classifications. This table also calculates the contribution of each variant in the E-VRP literature. Table 3 summarizes the assumptions and constraints of the E-VRPs. The first two columns indicate the references and their publication year. The next twelve columns pertain to the assumptions and constraints of the VRP. The diversity of the VRP is far more than the twelve cases mentioned; however, these characteristics are included considering the importance and usage of the assumptions made in the E-VRP. The next fourteen columns relate to the operational assumptions of the EVs. The type of the objective functions is shown in the last column. The percentage of usage for each feature is computed the in the same way as that of Table 1.

Table 2. Classification of papers based on different variants of E-VRP.

Year	Reference	Name	Variants
			TW	PR	BSS	MF	LRP	NL	TD	Lo	Pe	2E	ORS
	% of papers	#	65%	33%	14%	22%	17%	15%	4%	1%	1%	2%	12%
2011	Conrad and Figliozzi [20]	Recharging VRP (R-VRP)	TW	PR
2011	Gonçalves et al. [89]	E- VRP-MF				MF
2012	Worley et al. [104]	E-VRP					LRP
2013	Van Duin et al. [99]	EV Fleet Size and Mix VRP–TW (E-FSM-VRP-TW)	TW			MF
2014	Afroditi et al. [3]	E-VRP-TW	TW
2014	Preis et al. [63]	E-VRP-TW	TW
2014	Schneider et al. (SSG) [23]	E-VRP-TW	TW
2014	Hiermann et al. (HPH) [100]	Electric Fleet Size and Mix VRP-TW and Recharging Station (E-FSMVRPTW)	TW			MF
2014	Felipe et al. (FORT) [24]	G-VRP with Multiple Technologies and PR		PR
2014	Sassi et al. [36]	Heterogeneous E-VRP with Time Dependent Charging Costs and a MF (HE-VRP-TD-MF)	TW	PR		MF
2015	Sassi et al. [90]	VRP with MF of conventional and heterogeneous EVs (VRP- MFHEV)	TW	PR		MF
2015	Sassi et al. [91]	VRP with MF of conventional and heterogeneous EVs (VRP- HFCC)	TW	PR		MF
2015	Schneider et al. [135]	E-VRP with recharging facilities (E-VRP-RF)											ORS
2015	Bruglieri et al. [64]	E-VRP-TW	TW
2015	Lebeau et al. [102]	Fleet Size and VRP-TW for EV (FSM-VRP-TW-EV)	TW			MF
2015	Yang and Sun (YS) [29]	EVs BSS LRP (EV-BSS-LRP)			BSS		LRP
2015	Goeke et al. (GHS) [83]	EVs BSS LRP (EV-BSS-LRP)			BSS		LRP
2015	Li-ying and Yuan-bin [28]	EV Multiple CS LRP with TW (EV-MCS-LRPTW)	TW				LRP
2015	Goeke and Schneider (GS) [92]	E-VRP-TW-MF	TW			MF		NL
2015	Ding et al. [75]	Conflict-Free E-VRP with Capacitated Charging Stations and PR	TW	PR
2015	Moghaddam [76]	E-VRP-TW-PR	TW	PR
2015	Montoya et al. [114]	E-VRP with PR and NL charging function (E-VRP-NL)		PR				NL
2015	Aggoune-Mtalaa et al. [133]	Modular electric VRP (Me-VRP)	TW										ORS
2015	Murakami and Morita [93]	Electric and Fuel-engine VRP (EFVRP)				MF
2016	Keskin and Çatay (KÇ) [77]	E-VRP-TW with fast charge (E-VRP-TW-FC)	TW	PR
2016	Desaulniers et al. [78]	E-VRP-TW with Single (S) recharge per route and Full (F) recharge (E-VRP-TW-SF) E-VRP-TW with Multiple and Partial (P) recharge (E-VRP-TW-SP) E-VRP-TW with Single (S) recharge per route and Full (F) recharge (E-VRP-TW-SF) E-VRP-TW with Multiple and PR (EVRPTW-MP)	TW	PR
2016	Sundar et al. [94]	Fuel-Constrained Autonomous Vehicle Path Planning Problem (FCAVPP)				MF
2016	Schiffer et al. [105]	E-LRP	TW			MF	LRP
2016	Chen et al. [84]	E-VRP-TW-BSS	TW		BSS
2016	Hiermann et al. (HPRH) [101]	Electric Fleet Size and Mix VRP-TW and Recharging Stations (E-FSM-TW)	TW			MF
2016	Montoya (MSH 1 2 3) [115]	E-VRP-NL E-FSMFTW	TW			MF		NL
2016	Lin et al. [35]	E-VRP				MF
2016	Basso et al. [65]	E-VRP-TW	TW						TD
2017	Barco et al. [31]	E-VRP	TW
2017	Schiffer and Walther [106]	E-LRP with TW and PR (E-LRP-TW-PR)	TW	PR			LRP
2017	Montoya et al. (MGMV17) [116]	E-VRP-NL						NL
2017	Bruglieri et al. [80]	E-VRP-TW-PR	TW	PR
2017	Hof et al. (HSG) [85]	BBS-EV-LRP			BSS		LRP
2017	Shao et al. [122]	E-VRP with Charging Time and Variable Travel Time (E-VRP-CTVTT)	TW						TD
2018	Schiffer and Walther (SW) [107]	LRP with intra-route facilities (LRPIF)	TW	PR	BSS		LRP
2018	Schiffer and Walther [108]	Robust E-LRP with TW and PR (R-E-LRP-TW-PR)	TW	PR			LRP
2018	Paz et al. [109]	Multi-Depot E-LRP with TW (MD-EV-LRP-TW)	TW	PR			LRP
2018	Kancharla and Ramadurai [66]	E-VRP-TW	TW
2018	Zhang et al. [136]	E-VRP with minimizing energy consumption											ORS
2018	Verma [86]	E-VRP-TW-BSS	TW		BSS
2018	Zhou and Tan [110]	Electric Vehicle Handling Routing and BSS Location Problem (EV-HR-BSSL)			BSS		LRP
2018	Villegas et al. [97]	Technician Routing and Scheduling Problem with Conventional and Electric Vehicles (TRSP-CEV)				MF
2018	Kullman et al. [142]							NL					ORS
2018	Keskin and Çatay [79]	E-VRP-TW	TW	PR
2018	Zuo et al. [67]	E-VRP-TW	TW
2018	Gatica et al. [112]	E-LRP					LRP
2018	SSL [111]	LRPIF with multiple resources (LRPIF-MF)	TW	PR	BSS		LRP
2018	Zhang et al. [69]	E-VRP with Soft TW and Recharging Stations in the Reverse Logistics	TW	PR
2018	Kouider et al. [128]	Periodic E-VRP (P-E-VRP)		PR							Pe
2019	Kopfer and Vornhusen [95]	Energy VRPTW, Recharge Stations and Vehicle Classes (EVRPTW-R-VC)	TW			MF
2019	Froger et al. [30]	E-VRP-NL						NL
2019	Macrina et al. [96]	Green Mixed VRP with Partial Battery Recharging and TW (G-MF-VRP-PR-TW)	TW	PR		MF
2019	Jie et al. [132]	Two-Echelon E-VRP with BSS (2E-E-VRP-BSS)			BSS							2E
2019	Zuo et al. [117]	E-VRP-TW with concave nonlinear charging function (EVRPTW-CNCF).	TW					NL
2019	Koç et al. [118]	E-VRP with Shared Charging Stations (E-VRP-SCS)		PR			LRP	NL
2019	Breunig et al. [131]	Electric Two-Echelon VRP (E2E-VRP)										2E
2019	Keskin et al. [40]	E-VRP-TW with time-dependent waiting times at recharging stations	TW					NL
2019	Zhao and Lu [103]	Real World E-VRP	TW			MF
2019	Erdem and Koç [68]	E-VRP-TW with Home Care Routing Problem	TW	PR		MF
2019	Rastani et al. [34]	E-VRP-TW-PR	TW	PR
2019	Pelletier et al. [138]	E-VRP with Energy Consumption Uncertainty (E-VRP-ECU)											ORS
2019	Keskin et al. [41]	E-VRP-TW with Stochastic Waiting Times at Recharging Stations	TW					NL
2019	Cortés-Murcia et al. (Hybrid-ILS) [81]	E-VRPTW with Satellite Customers (E-VRTWsc)	TW	PR
2019	Rezgui et al. [134]	Modular electric VRP (Me-VRP)	TW			MF							ORS
2019	Basso et al. [137]	Two-stage E-VRP (2sEVRP)	TW										ORS
2019	Goeke [70]	Pickup and Delivery Problem with Time Windows and Electric Vehicles (PDPTW-EV)	TW	PR
2019	Lu and Wang [139]	Dynamic Capacitated E-VRP (DC-E-VRP)	TW										ORS
2019	Xiao et al. [71]	E-VRP-TW considering the energy/electricity consumption rate (E-VRP-TW-ECR)	TW
2019	Lu et al. [139]	Time-Dependent E-VRP (TD-E-VRP)	TW						TD
2019	Reyes-Rubiano et al. [141]	E-VRP with stochastic travel times (E-VRP-ST)											ORS
2020	Meng and Ma [72]	E-VRP-TW	TW		BSS
2020	Taş [73]	E-VRP with Flexible Time Windows (E-VRP-FTW)	TW
2020	Granada-Echeverri et al. [140]	E-VRP with Backhauls (E-VRP-B)											ORS
2020	Kullman et al. [143]	Fixed Route Vehicle Charging Problem (FRVCP)						NL					ORS
2020	Kullman et al. [144]	E-VRP with public-private recharging strategy (E-VRP-PP)						NL					ORS
2020	Lee [119]	E-VRP with nonlinear charging Time						NL
2020	Mao et al. [87]	E-VRP-TW and Multiple Recharging Options (E-VRP-TW&MC)	TW	PR	BSS
2020	Almouhanna et al. [113]	LRP with a Constrained Distance (LRPCD)					LRP
2020	Zhang et al. [82]	Fuzzy E-VRP-TW (F-E-VRP-TW)	TW	PR
2020	Zhang et al. [124]	A time-dependent E-VRP with congestion tolls and time window constraints (TD-E-VRP-CT)	TW	PR					TD
2020	Zhu et al. [126]	Two-Dimensional Multi-Depot E-VRP (2L-MDEVRP)			BSS					Lo
2020	Kancharla and Ramadurai [120]	E-VRP-NL and Load-Dependent Discharging (E-VRP-NL-LD) E-VRP-NL-LD with Capacitated Charging Stations (E-VRP-NL-LD-CCS)		PR				NL
2020	Löffler et al. [74]	E-VRP-TW with and Single recharge (E-VRP-TW-S)	TW	PR				NL
2020	Raeesi et al. [34]	E-VRP-TW and Synchronised Mobile Battery Swapping (EVRPTW-SMBS)	TW		BSS
2020	Keskin et al. [38]	E-VRP-TW and stochastic waiting times at recharging stations	TW

Table 3. Summary of studies conducted on E-VRP.

Year	Reference	VRP Constraints and Characteristics												EV’s Related Technical Constraints and Assumptions															Objective Function
		Time Windows	Pickup and Delivery	Travel Time	Capacitated	Fleet Size	Mixed Fleet		Periodic	Stochastic	Time-Dependent	Multi-Depot	Multi-Echelon	Loading	Full Recharges	Partial Recharges	No Intra-Route Recharging Facility	Charging or Swapping at Customer Site	Charging or Swapping at special vertices	Battery Swapping	Fixed Charging or Battery Swapping Time	Simultaneous Charging Station Siting	Battery Life Degradation	Load, Speed Traveling or Temperature Effect	Recharging (Swapping) Cost	Nonlinear Recharging	Different Charging Technologies	Wait in Queue at Refueling Stations
							EVs and Other Types	Pure Evs
	% of papers	65%	10%	76%	84%	36%	13%	11%	1%	9%	4%	4%	2%	1%	82%	35%	8%	7%	75%	15%	25%	14%	2%	21%	25%	19%	19%	4%	#
2011	Conrad and Figliozzi [20]	✓			✓	✓									✓	✓		✓			✓				✓				NV
2011	Gonçalves et al. [89]		✓		✓		✓								✓						✓								Costs
2012	Worley et al. [104]		✓		✓										✓				✓		✓	✓			✓				Costs, NS
2013	Van Duin et al. [99]	✓		✓	✓	✓		✓		✓							✓												Costs, NV, TTD
2014	Afroditi et al. [3]	✓			✓	✓									✓				✓		✓			✓					Dist, NV
2014	Preis et al. [63]	✓		✓	✓										✓				✓		✓			✓					Em
2014	SSG [23]	✓		✓	✓	✓									✓				✓										Dist
2014	HPH [100]	✓		✓	✓	✓		✓							✓				✓										Dist., NV
2014	FORT [24]			✓	✓										✓	✓			✓					✓	✓		✓		Costs
2014	Sassi et al. [36]	✓		✓	✓		✓								✓	✓			✓						✓		✓		Costs
2015	Sassi et al. [90]	✓		✓	✓		✓	✓							✓	✓			✓						✓		✓		Costs
2015	Sassi et al. [91]	✓		✓	✓		✓								✓	✓			✓						✓		✓		Costs
2015	Schneider et al. [135]			✓	✓	✓									✓				✓										Costs, NV
2015	Bruglieri et al. [64]	✓		✓	✓	✓									✓				✓						✓				NV, TTD
2015	Lebeau et al. [102]	✓		✓	✓	✓	✓	✓							✓		✓						✓	✓			✓		Costs
2015	YS [29]				✓													✓	✓	✓		✓							Costs, NS
2015	GHS [83]				✓										✓			✓	✓	✓		✓							Costs, NS
2015	Li-ying and Yuan-bin [28]	✓		✓	✓										✓			✓	✓			✓		✓	✓		✓		Costs
2015	GS [92]	✓		✓	✓		✓								✓				✓					✓					Dist., Costs, Em
2015	Ding et al. [75]	✓	✓	✓	✓										✓	✓			✓								✓		Dist.
2015	Moghaddam [76]	✓		✓		✓									✓	✓			✓		✓								NV, NS
2015	Montoya et al. [114]			✓											✓	✓			✓							✓	✓		TTD
2015	Aggoune-Mtalaa et al. [133]	✓	✓	✓	✓												✓							✓					Costs, Em
2015	Murakami and Morita [93]				✓	✓	✓										✓												Costs
2016	KÇ [77]	✓		✓	✓										✓	✓			✓										Dist
2016	Sundar et al. [94]				✓		✓								✓				✓										Dist
2016	Schiffer et al. [105]	✓			✓	✓	✓								✓				✓		✓	✓							Costs, Dist, NS NV, Em
2016	Desaulniers et al. [78]	✓		✓	✓										✓	✓			✓					✓	✓				Costs
2016	Chen et al. [84]	✓		✓	✓	✓													✓	✓					✓				Dist
2016	HPRH [101]	✓			✓	✓		✓							✓				✓										Costs
2016	MSH 1 2 3 [115]	✓		✓	✓	✓									✓	✓			✓						✓	✓	✓		Costs, TTD
2016	Lin et al. [35]		✓	✓	✓			✓							✓				✓						✓				Costs
2016	Basso et al. [65]	✓		✓	✓						✓				✓				✓		✓								Em, TTD
2017	Barco et al. [31]	✓	✓	✓	✓										✓				✓				✓	✓					Em
2017	Schiffer and Walther [106]	✓			✓	✓									✓	✓		✓	✓			✓		✓					Dist, NV, NS
2017	MGMV17 [116]			✓											✓	✓			✓							✓	✓		TTD
2017	Bruglieri et al. [80]	✓		✓	✓	✓									✓	✓			✓										TTD
2017	HSG [85]				✓										✓					✓		✓					✓		Costs
2017	Shao et al. [122]	✓		✓	✓						✓				✓				✓					✓	✓				Costs
2018	SW [107]	✓		✓	✓	✓										✓			✓	✓					✓				Costs, NV, NS
2018	Schiffer and Walther [108]	✓		✓	✓	✓				✓					✓	✓			✓		✓								Costs, NV, NS
2018	Paz et al. [109]	✓		✓	✓	✓						✓				✓		✓	✓	✓		✓							Dist.
2018	Verma [86]	✓		✓	✓										✓				✓	✓									Costs
2018	Kancharla and Ramadurai [66]	✓		✓											✓				✓		✓			✓					Em
2018	Zhang et al. [136]			✓											✓				✓										Em
2018	Zhou and Tan [110]				✓														✓	✓	✓	✓							Costs
2018	Villegas et al. [97]			✓			✓								✓										✓	✓			Costs
2018	Kullman et al. [142]			✓											✓				✓							✓			TTD
2018	Keskin and Çatay [79]	✓		✓	✓	✓									✓	✓									✓	✓	✓		Costs, NV
2018	Zuo et al. [67]	✓		✓	✓										✓				✓		✓								Costs
2018	Gatica et al. [112]				✓										✓						✓	✓							Dist.
2018	SSL [111]	✓		✓	✓										✓	✓			✓	✓		✓							Costs, NV, NS
2018	Zhang et al. [69]	✓		✓	✓										✓	✓		✓			✓								Costs, NV
2018	Kouider et al. [128]			✓	✓				✓							✓			✓		✓				✓				Costs
2019	Kopfer and Vornhusen [95]	✓		✓	✓		✓	✓							✓						✓								Em
2019	Froger et al. [30]			✓											✓				✓							✓			TTD
2019	Macrina et al. [96]	✓					✓								✓	✓			✓								✓		Costs
2019	Jie et al. [132]				✓								✓						✓	✓					✓				Costs
2019	Zuo et al. [117]	✓		✓	✓	✓									✓											✓			Costs, NV
2019	Koç et al. [118]			✓								✓			✓	✓						✓				✓	✓		Costs
2019	Breunig et al. [131]				✓								✓		✓				✓										Dist.
2019	Keskin et al. [40]	✓		✓	✓	✓									✓											✓		✓	Costs, Dist, Em, NV
2019	Zhao and Lu [103]	✓	✓	✓	✓			✓							✓				✓			✓			✓				Costs, NV
2019	Erdem and Koç [68]	✓		✓				✓							✓	✓			✓										TTD
2019	Rastani et al. [34]	✓		✓	✓	✓									✓	✓			✓					✓					Em
2019	Pelletier et al. [138]			✓	✓					✓							✓							✓					Costs, Em
2019	Keskin et al. [41]	✓		✓	✓	✓				✓					✓				✓							✓		✓	Costs, Em
2019	Cortés-Murcia et al. [81]	✓		✓	✓										✓	✓													RT
2019	Rezgui et al. [134]	✓		✓	✓	✓		✓							✓				✓						✓				Costs, NV, Dist.
2019	Basso et al. [137]	✓		✓	✓										✓				✓					✓					Em
2019	Goeke [70]	✓	✓	✓	✓										✓	✓			✓										Costs
2019	Lu and Wang [139]	✓			✓	✓									✓				✓										Costs
2019	Xiao et al. [71]	✓		✓	✓												✓							✓					Costs, Em
2019	Reyes-Rubiano et al. [141]			✓	✓					✓							✓												TTD
2019	Lu et al. [139]	✓		✓	✓	✓					✓				✓				✓					✓					Costs, Em
2020	Meng and Ma [72]	✓		✓	✓	✓									✓				✓	✓	✓				✓				Costs
2020	Taş [73]	✓		✓	✓	✓									✓				✓		✓								Costs, NV
2020	Granada-Echeverri et al. [140]		✓		✓										✓				✓										Costs
2020	Kullman et al. [143]			✓											✓				✓							✓			TTD
2020	Kullman et al. [144]			✓						✓					✓				✓							✓		✓	TTD
2020	Lee [119]			✓											✓											✓	✓		TTD
2020	Mao et al. [87]	✓		✓	✓	✓										✓			✓	✓	✓				✓		✓		Costs, NV
2020	Almouhanna et al. [113]				✓	✓						✓																	Costs, Dist., NV
2020	Zhang et al. [82]	✓		✓	✓					✓					✓	✓			✓		✓								Dist.
2020	Zhang et al. [124]	✓		✓	✓						✓				✓	✓			✓		✓			✓	✓				TTD, Costs
2020	Zhu et al. [126]				✓							✓		✓	✓				✓	✓									Dist.
2020	Kancharla and Ramadurai [120]			✓	✓										✓	✓			✓					✓		✓	✓		TTD
2020	Löffler et al. [74]	✓		✓	✓										✓	✓			✓		✓					✓			Costs
2020	Raeesi et al. [34]	✓		✓	✓	✓											✓			✓	✓								Costs, NV
2020	Keskin et al. [38]	✓		✓	✓	✓				✓					✓				✓							✓		✓	Costs, Em

4.2. E-VRP Literature Gaps and Future Researcch

An overview of Table 3 shows the emerging of researches area on the problem of EVs and its subcategories. Many of the applied assumptions in the VRP, along with the characteristics associated with EVs have not so far been addressed, or few were addressed. What stands out most in the issue of E-VRP is the combination of basic and classical VRP assumptions and constraints to make the E-VRP variants comprehensive, more applicable and closer to real-world issues. For example, using a set of EVs can be attractive and economical in a two-echelon distribution system, due to the environmental regulations in the urban environment, to serve the final customers in the second level. However, due to driving constraints in urban environments, the amount of charge for this type of vehicles is affected by many obstacles in the urban environment and therefore, requires well-designed and reliable planning. The assumption of time dependency and the existence of constraints associated with traffic changes in urban environments in a two-echelon system introduce the problem of E-VRP with time-dependent two-echelon systems. Moreover, in many real-world applications of distribution systems, the decision process covers more than one period, spanning several days or even several weeks. The investigation of the effect of using EVs can be attractive in planning for a scope longer than a period Cacchiani et al. [127]. A combination of other practical issues of VRP can provide various analyses of what-if scenarios, for example, depot location, fleet size and mix, departure time, customers’ demand, and their time-windows can lead to reaching more applicable and closer to real-world issues in the field of EF-VRP. Besides, from EV’s related technical constraints and assumptions perspective, investigating the effect of technologies used on different types of batteries in parameters such as recharging consumption rate, recharging time duration, the effect of vehicle speed or weight on the amount of charging, the cost of recharging, and battery degradation are among the few that are subject to limited researches and can be interesting subjects for future research.

5. Route Planning on Hybrid Electric Vehicles

Despite the significant benefits of using EVs in goods distribution, there are some limitations in this variant of vehicles that cannot be ignored. The limited number of recharging stations, considerable time spent on recharging, frequent recharging, the high cost of the battery swapping, and the limited driving range in this type of vehicles are some of the constraints [145]. Using a vehicle with two or more power sources called a Hybrid Electric Vehicle (HEV) is considered an appropriate strategy to overcome these constraints [21]. The term HEV is mostly used when referring to a vehicle the propulsion system of which is an Internal Combustion Engine (ICE) (usually uses gasoline) along with one or more electric engines, and the vehicle can use one or both sources of energy. In recent years, using HEVs has remarkably increased in the logistics and freight sector. By and large, EHVs are categorized based on electrical engine performance, vehicle charging supply, electric engine architecture, their capacity to connect to the power grid to charge the battery, the hybridization factor degree, variants of electric engines, etc. In the following, the classification of EHVs is presented.

5.1. Classification of HEVs

Considering the unique characteristics and technical specifications of different variants of HEVs, various approaches were used by researchers to classify such variants of vehicles. The HEV uses a combination of the output energy of the ICE and an electric engine that uses the energy stored in a battery. Actually, in this vehicle, the benefits of using internal combustion and electric engines are merged to achieve various goals, namely, increasing vehicle power, reducing environmental pollution, improving fuel economy, or extra auxiliary power for EVs. Such vehicles are capable of moving through using an ICE or an electric engine separately, as well as using both engines to increase power. The vehicle battery is charged via regenerative braking as well as the internal combustion engine and is not able to connect to the charging source. The Plug-in Hybrid Electric Vehicle (PHEV) is similar to the HEV. It is powered by an ICE engine and an electric engine that uses the energy stored in the battery. The difference between these two vehicles resides in the fact that PHEVs can be connected to the grid to charge their batteries. Similar to the HEVs, this energy can be provided through regenerative braking and ICE.

The present study categorizes and investigates studies on the HEVs routing on this basis. There are other classifications for HEVs in the literature, which are briefly mentioned for further information.

5.1.1. Classification Based on Electric Engine Architecture

Lukic et al. [146] believe that mechanical connections are considered a proper standard for classifying HEVs. Based on the electric engine design in using fossil or electric fuel, HEVs fall into three types of parallel hybrid, series hybrid, and parallel-series hybrid [147]. In parallel hybrid vehicles, fossil fuels provide the energy required by the conventional engine, and the energy stored in the battery provides the power required by the electric engine. Recharging the battery takes place using a generator during a typical driving process. In this vehicle type, the vehicle can independently move using either an ICE or an electric engine. On the opposite side, there are series-hybrid vehicles, in which the ICE acts as a driver of the generator, which should recharge the vehicle battery. In this category of vehicles, only the electric engine moves the vehicle. If the battery runs low, then the combustion engine automatically charges the battery. In parallel-series hybrid vehicles, the characteristic of both series-hybrid and parallel-hybrid are considered integrated, with the exception that an extra mechanical connection is used in comparison with the hybrid series vehicles and an extra generator is used compared to the hybrid parallel vehicles, i.e., the parallel-series hybrid vehicle provides ICEs and electric engines with the power, either independently or in partnership. Compared to the two hybrid vehicles mentioned above, the parallel-series hybrid is relatively complicated and more costly than the others [148]. Both HEV and PHEV vehicles can have parallel, series, or parallel-series engine models.

Other classifications for HEVs were presented in Chan’s [148] designing perspective. Moreover, Curtin et al. [147] used the term “hybrid electric vehicle” or HEV to identify the parallel vehicle type and used the ”plug-in hybrid electric vehicle” or PHEV to the series vehicle.

5.1.2. Classification Based on Hybridization Degree

To better classify HEVs, Lukic et al. [146] categorized these vehicles based on the Hybridization Factor (HF). This categorization was presented between HF = 0 (internal combustion engine vehicle (ICEV) and HF = 1 (electric vehicle (EV)) in which HF is defined as (2):

$$HF=\frac{P_{EM}}{P_{EM}+P_{ICE}}$$

(2)

where $P_{EM}$ and $P_{ICE}$ respectively represent the maximum power of the electric and the combustion engine, and considering their value, each of the hybrid electric vehicles mentioned is determined. Based on this classification, hybrid vehicles can be categorized into the four following classifications: Micro-HEVs, Mild-HEVs, Power-assisted HEVs, and Plug-In HEVs. By and large, Table 4 presents the most significant types of HEVs, and the related characteristics of each type of vehicle appearing in the literature. Despite the production of a wide range of HEVs, only a small part of this wide range has been studied in the field of logistics and transportation in order to face various transportation problems and environmental challenges. Undoubtedly, the increase in the complexity and unique characteristics of each vehicle affects the route planning problems and creates difficulties in their optimum usage in the distribution industry. Bearing this in mind, the number of constraints related to the HEVs is more than the EVs constraints, and this issue complicates the design of correct planning in this area. Accordingly, a general classification was used so far in H-VRPs, and as a result of considering other classifications, paves the way for numerous further research areas for studying this type of vehicles in the field of VRP. In the following, various types of H-VRP are investigated.

Table 4. Different classifications for Hybrid Electric Vehicles.

Type of Classification of the Hybrid Vehicle	General classification	HEV	A combination of internal combustion engine (ICE) and an electric engine power source Using the electric engine of the charge available in the battery Charging the battery using regenerative braking and ICE
		PHEV	A combination of internal combustion engine (ICE) and an electric engine power source Using the electric engine of the charge available in the battery Charging the battery using regenerative braking and ICE Chargeability through connecting to the charging source
	Types of Powertrain	Parallel-Hybrid	Providing the ICE engine power through fossil fuels Providing electric engine power through the energy stored in batteries Ability to move the vehicle through the ICE engine and electric engine Ability to charge the battery while driving The possibility of connecting the vehicle to the power grid, in which case the vehicle will be plug-in parallel (Parallel or Blended PHEVs)
		Series-Hybrid	The role of the ICE engine as a generator to provide the required engine power Movement of the vehicle by electric engine The possibility of connecting the vehicle to the power grid, in which case the vehicle will be a plug-in series called PHEVs series, or Extended Range Electric Vehicles
		Parallel-Series Hybrid	Considering integrated Parallel-Series Hybrid characteristics Movement of the vehicle by electric engine Use of an extra mechanical connection compared to the hybrid series Use of an extra generator compared to parallel-hybrid High cost and complex structure
	Hybridization Factor	Micro-HEVsHF < 0.1	Limited and automatic usage of the electric engine as a combination of the starter and alternator to provide a fast start/stop operation Preventing ICE engine activity when the vehicle stops The movement of vehicle by ICE engine The electric engine alone cannot drive the vehicle Saves fuel by 10%
		Mild-HEVsHF < 0.25	It enjoys a powerful electric propulsion system Using an electric engine to reinforce the ICE acceleration Absorbing energy through regenerative braking The energy power in batteries is more compared to Micro-HEVs. The electric engine alone cannot drive the vehicle Saves fuel by 10–20%
		Power-assist HEVS0.25 < HF < 0.5	Provides strong electric drive to support ICE The vehicle can operate as all-electric system with zero emissions ICE alone cannot guarantee vehicle propulsion Saves fuel by more than 50%
		Plug-In (HEV)HF > 0.5	Uses batteries that can be charged with conventional power grid Considerably prolongs the driving range of electric vehicle Significantly saves fuel

5.2. Hybrid Vehicle Routing Problem

The H-VRP aims at meeting the demand for a set of customers using HVs and seeks to minimize the distribution network costs. Studies on HV routing problem have considered the classification; it has been presented by the Energy Efficiency & Renewable Energy [4] in the form of two types, namely, HEV and PHEV. Figure 7 illustrates the classification of studies conducted on the HVs routing. Figure 7 indicates that the VRP presented with this type of vehicle can be divided into two general classifications: Hybrid Electric Vehicle Routing Problem (HE-VRP) and the Plug-in Hybrid Electric Vehicle Routing Problem (PHE-VRP), each of which will be elaborated in the following.

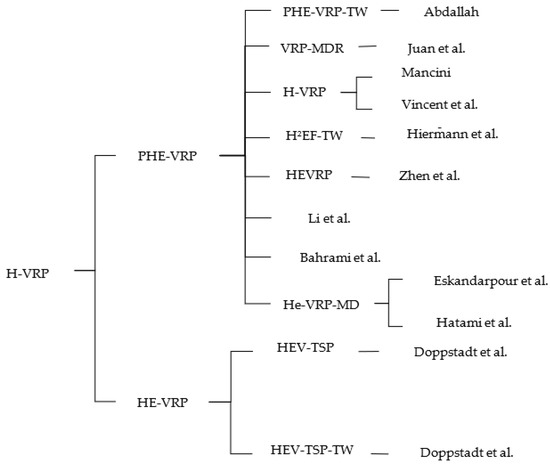
Figure 7. Classification of problems presented on the H-VRP.

5.2.1. Hybrid Electric Vehicle Routing Problem (HE-VRP)

The only problem presented is the HEV Travelling Salesman Problem (HEVTSP) as a simplified example of the VRP, which was published by Doppstadt et al. [37]. In order to cover the applied assumptions of the HEV usages, four different modes of this vehicle were considered for the problem, including: pure combustion (conventional) mode, pure electric mode (movement using the electric engine), charging mode (in which the battery is charged while driving with the combustion engine), boost mode (where combustion and electric engines are used in combination to move the vehicle). They used an innovative Tabu Search (TS) to solve the proposed problem, in which two primary stages of the initial response and recovery step were used. They generated a number of problem instances to investigate the performance of the proposed algorithm. Doppstadt et al. [149] recently developed the previous problem by adding Time-Windows constraints and presented a new solution approach. They developed a new heuristic solution approach based on parallelized VNS and generated a new set of benchmark instances to evaluate the proposed solution approach. Figure 8 presents an example of a feasible solution for HEV-TSP [37,149]. In this example, there are six customers who are served with an HEV. The HEV can benefit from four modes as mentioned above to complete its route.

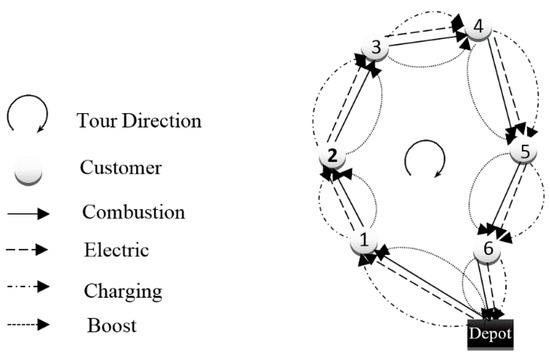
Figure 8. Example of a feasible solution for HEV-TSP provided by Doppstadt et al. [37,149].

5.2.2. Plug-In Hybrid Electric Vehicle Routing Problem (PHE-VRP)

In the current literature, some researchers studied application of PHEVs to serve customers in the VRP problem. The PHEVs have a high capacity battery that can be charged by the power grid. The high capacity of the battery of such a vehicle provides the possibility of a fully electric movement for this type of vehicles in short distances. Various studies have considered the possibility to recharge PHEVs at a charging station, customer sites or other locations, which are discussed in the following: Abdallah [22] investigated using PHEVs in his study for the first time and presented the Plug-In Hybrid Electric Vehicle Routing Problem with Time Windows (PHE-VRPTW). In the model presented in this paper, the possibility of partial recharging of PHEVs in each node of a distribution network was considered, and the refueling process of PHEVs was not considered. Juan et al. [150] developed the VRP with Multiple Driving Range (VRPMDR), in which there was a set of mixed fleets consisting of different variants of EVs and PHEVs, with different driving ranges. In that study, vehicles with different battery capacities, leading to different values of driving ranges for each vehicle, were studied in the routing process. Mancini [145] posed a problem, in which the propulsion switch of HVs between battery and fuel was possible considering preferences and at any time of driving. The problem was called the Hybrid Vehicle Routing Problem (H-VRP), in which the unit of driving cost in electric mode is far lower than other vehicle driving modes. This study has not mentioned the type of HV used; however, regarding the possibility of recharging vehicles at recharging stations, it can be categorized in the PHEV routing problem classification. Hiermann et al. [151] formulated a problem, in which three types of vehicles including ICEV, EV, and PHEV were considered to serve customers in the VRP. Vincent et al. [13] presented the H-VRP using PHEV. The model presented for this problem was inspired by the mathematical model presented by Erdoğan and Miller-Hooks [21]. Eskandarpour et al. [152] considered a heterogeneous fleet of EVs with respect to loading capacities as well as driving ranges and proposed the Heterogeneous Vehicle Routing Problem with Multiple Driving ranges and loading capacities (HeVRPMD). They considered different maximum driving ranges for each vehicle without any recharging decisions and proposed an enhanced variant of Multi-Directional Local Search (EMDLS) to solve the problem. Hatami et al. [153] solved the HeVRPMD by a Multi-Round Iterated Greedy (MRIG) metaheuristic based on a successive approximations method to solve the problem. Recently, Zhen et al. [154] proposed a new study of a PHE-VRP with mode selection. This paper has been considered as the first study in selecting PHEVs’ different modes for each road segment in VRP. In this problem, PHEV can choose the appropriate mode (battery- or gasoline-based) according to different road conditions. PHEVs can be recharged at recharging stations during the delivery tour. For efficiently solving the proposed model, they design an Improved Particle Swarm Algorithm (IPSO) in which a labeling procedure is involved. Li et al. [155] proposed a new hybrid optimization algorithm merging the memetic algorithm and the sequential variable neighborhood descent to solve PHE-VRP. Bahrami et al. [156] presented a model which is distinguished from the literature problems in considering different rates of emission for two sources of energy, and the total energy consumption minimization. In addition, the regenerative braking for the PHEV was considered for the first time. The proposed model have was solved with an exact and heuristic algorithm. Moreover, they implemented a case study for the problem

Table 5 presents a summary of the assumptions and constraints of the H-VRP. In this table, the first column indicates the publications references. The third column specifies the type of HVs that were investigated in two types of PHEV and HEV. The next eleven columns relate to the assumptions and constraints of the H-VRP. The next fifteen columns relate to the operational assumptions of the HVs. The same as Table 1 and Table 3, the last column illustrates the type of objective functions and the percentage of usage for each feature is computed.

Table 5. Summary of studies conducted on H-VRP.

Year	Reference	HV Type		VRP Constraints and Characteristics													HV’s Related Technical Constraints and Assumptions															Objective Function
		HEV	PHEV	Time Windows	Pickup and Delivery	Travel Time	Capacitated	Fleet Size	Mixed Fleet		Periodic	Stochastic	Time-Dependent	Multi-Depot	Multi-Echelon	Loading	Full Recharges	Partial Recharges	Maximum Driving Range	Charging or Swapping at Customer Site	Charging or Swapping at Special Vertices	Battery Swapping	Fixed Charging or Battery Swapping Time	Simultaneous Charging Station Siting	Battery Life Degradation	Load, Speed Traveling or Ambient Temperature Effect	Recharging (Swapping) Cost	Nonlinear Refueling (Recharging)	Different Charging Technologies	Multi-mode	Wait in Queue at Recharging Stations
									HVs and Other Types	Pure Hvs
	% of papers	17%	83%	25%	0%	33%	58%	25%	33%	33%	0%	0%	0%	0%	0%	0%	58%	17%	25%	8%	42%	0%	17%	0%	0%	0%	17%	0%	8%	25%	0%	#
2013	Abdallah [22]		✓	✓			✓										✓	✓		✓	✓						✓					Costs
2014	Juan et al. (MRH) [150]		✓				✓	✓	✓	✓									✓													Dist.
2016	Doppstadt et al. [37]	✓				✓																								✓		Costs
2017	Mancini (MH) [145]		✓														✓				✓		✓									Costs
2017	Vincent et al. [13]		✓				✓	✓									✓				✓		✓				✓					Costs
2019	HGA [151]		✓	✓		✓	✓		✓	✓							✓	✓			✓											Costs
2019	Eskandarpour et al. [152]		✓				✓		✓	✓									✓													Dist.
2020	Zhen et al. [154]		✓				✓										✓													✓		Em
2020	Doppstadt et al. [149]	✓		✓		✓																								✓		Costs
2020	Li et al. [155]		✓			✓											✓				✓											Costs
2020	Bahrami et al. [156]		✓					✓									✓												✓			Em
2020	Hatami et al. [153]		✓				✓		✓	✓									✓													Dist.

5.3. H-VRP Literature Gaps and Future Research

The existence of a variety of HVs from the standpoint of characteristics such as type (Parallel, Series, Parallel-Series, Micro, Mild, Power-assist, Plug-in HEVs, etc., as shown in Table 4), load-carrying capacity, battery capacity, technology applied in batteries, and pricing raises the question of whether a fleet of different vehicles is effective in reducing the cost of distribution. This problem is significant in H-VRPs because various levels of hybrid vehicles with different characteristics have been developed in recent years. In addition, determining the number of vehicles needed to meet customers’ demand along with other distribution costs, defining planning horizon to meet customers’ demands in multi-period, real pattern of daily traffic congestion, stochastic conditions in the distribution network, multi-depot application, multi-echelon services, and loading issues, which is related to the size of items to be distributed, are significant and practical assumptions that have not been effectively investigated in the domain mentioned above. These assumptions could be studied by interested researchers for future research in H-VRP. Investigating each of these problems can answer many questions about the benefits of using HVs and increase using these vehicles in distribution systems throughout the world, thereby reducing the environmental effect of transportation. As a recommendation for further research on H-VRP in terms of HV’s related technical constraints and assumptions, interested researchers can develop practical characteristics associated with HVs which have so far not been addressed, such as battery swapping and life degradation assumptions, simultaneous charging station siting, load, speed traveling or ambient temperature effect, nonlinear refueling (recharging), wait in queue at refueling (recharging) stations, etc.

6. EF-VRP Solution Methods

Because of the higher complexity of EF-VRPs, solution methods including exact, heuristic, and meta-heuristic algorithms designed for the classical VRP or related variants cannot directly be used in solving these problems [21]. This section provides a comprehensive review of the solution methods specifically developed for the EF-VRPs. Considering the explanations provided for each of the studies published on the EF-VRP, it is possible to include the proposed solution methods in three different classifications, namely, the exact, heuristic, and metaheuristic methods. It should be noted that some studies arrived at a mathematical model of the problem and its solution by using some solvers such as CPLEX, AMPL, Gurobi, etc. in the environment of some existing commercial software, including GAMS, LINGO, etc., and such studies are categorized in the classification of solving with using commercial software. Besides, some studies have implemented their problem in real-world case studies to reflect real world service area. Because the evaluation and analysis of the solution methods need a detailed discussion, this study just focuses on providing general insights and determining the most effective solution methods in the EF-VRP literature. So, analyzing the solution methods from different perspectives in detail can be an interesting topic to fill the gap.

In each of these studies, problem instances have commonly been used to evaluate the proposed model and solution methods. There are two approaches to problem instances. The first approach is that the instances have been generated by the authors, and a few of them are based on real-world data. Most of the instances have been adopted from artificial data and derived from the classical ones, as the Solomon [157] ones, but the problems are mainly urban delivery-related. This issue made the studies of EF-VRPs considerably out of the real-world information and problems, and not evaluating these kinds of real-world issues led to the lack of applied studies in this field. In the second approach, the existing standard benchmark problem instances, which have been presented in earlier studies, have been used to evaluate the proposed model or solution methods. In the literature, benchmark problem instances for various EF-VRP variants have been created. These instances provide a data set for a variety of solution methods that solve a particular EF-VRP variant. In this way, the performance of different algorithms and solution results can be evaluated and compared in terms of different criteria, such as Solution Quality (SQ) (i.e., total traveled distances or energy consumption), Computational or CPU Time (CT), Number of EFVs (NV) and Number of (Refueling, Recharging, or Battery Swapping) Stations (NS). Accordingly, to give an overview of solution methods of each variant of the EF-VRP, Table 6, Table 7 and Table 8 are formed, which analyze the AF-VRP, E-VRP, and H-VRP, respectively. In these tables, the references and their publication year are shown in the first two columns. The third column specifies the characteristics of the solution method and problem instances used in each study, divided into four subcategories of Number of Generated and Solved Instances, Size, Instances/Algorithm Name or Acronym, Link of Benchmark instances and Model or Solution Method Evaluation. Below the first section, the number of generated or solved instances is presented, which is equal to the number of newly generated benchmark problem instances or the number of solved problem instances in each paper. The size of instances in terms of the number of customers, the number of vehicles and the number of fuel (battery charging or swapping) stations, instance abbreviation or solving algorithm (underlined abbreviation have been adapted from authors name) and access link to the set of benchmark instances are specified in other columns. Below, the next section, model, or solution method evaluation with each set of instances or data considered in each paper is addressed. In this column, performance analysis of mathematical models or solution methods compared to other available results and methods in the literature are presented in terms of SQ, CT, NV, and NS. For example, the phrase SQ: DBCA outperformed MCWS in the first cell of this column in Table 6 related to the outperforming of DBCA rather than the MCWS in Erdoğan and Miller-Hooks [21] study in terms of Solution Quality. In addition, the best solution methods in terms of above features for solving each benchmark instances in the literature are determined in a bold description at the end of each related cell. The fourth column covers the solution methods presented in each paper, which are devoted to one or more methods. The studies marked by “ *”present new benchmark instances and are used as standard benchmarks in other studies. In the absence of an instance link, the NOI abbreviation is used, which means “Not on the Internet”. The percentage of each of the solution approaches is specified in each table.

Table 6. Summary of solution methods and instances provided in AF-VRP.

Year	Reference	Characteristics of Solution Method and Problem Instances					Solution Methods
		Number of Generated and Solved Instances	Size (Min-Max Number of Vehicles/Customers/Recharging (Swapping) Station)	Instances/Solution Method Name or Acronym	Link	Model or Solution Method Evaluation	Exact	Heuristic	Metaheuristic	Commercial Software	Case Study
	% of papers	#	#	#	#	#	17%	52%	26%	22%	4%
2012	EMH [21] *	52	4–84/20–500/2–28	Green-VRP/Modified Clarke and Wright Savings (MCWS) and Density-Based Clustering Algorithm (DBCA) (EMH)	NOI	Randomly generated small problem instances. Real World (larger problem instances) data in Colombia. SQ: DBCA outperformed MCWS.		✓			✓
2012	Omidvar and Tavakkoli-Moghaddam [42]	20	3–25/10–100/5–200	/Simulated Annealing (SA) and Genetic Algorithm (GA)	-	Randomly generated instances based on Solomon [157]. SQ: SA outperformed GA, CT: GA outperformed SA.			✓
2014	Taha et al. [43]	10 (Green –VRP)	1–3/5–10/2–3	/Formulation	-	Model evaluation based on EMH [21]’s benchmark instances.				✓
2016	KK [44]	40 (Green-VRP)	/20/2–10	/Branch-and-Cut (B&C) (KK)	-	B&C performance analysis on EMH [21]’s small instances. SQ: B&C outperformed EMH [21]’s small instances.	✓	✓
2016	MSH [45]	52 (Green-VRP)	3–73/20–500/2–28	/Multi-space Sampling Heuristic (MSH)	-	Algorithm analysis based on EMH [21]’s benchmark instances. SQ&CT&NV: MSH [45] outperformed other approaches. Fastest approach on EMH [21] benchmark instances		✓
2016	Bruglieri et al. [46]	20 (Green-VRP)	/20/3–6	/Formulation	-	Model performance analysis on EMH [21]’s small instances. SQ&CT: New model outperformed EMH [21] and KK’s [44] approaches.				✓
2017	YÇ [47] *	190	/20–80/	Mixed-Fleet Green Vehicle Routing Problem (MGVRP)/Variable Neighborhood Search (VNS) and Heuristic Pareto Optimization (YÇ)	http://myavuz.people.ua.edu	20 customer-modified instances from EMH’s [21] benchmark instances. New generated 50 and 80 customer instances.		✓	✓
2017	AB [48] *	40 (New) + 9 (Green-VRP)	6–19/47–110/3–28	AB1 & AB2/Set Partitioning Formulation (AB)	http://www.vrp-rep.org/variants/item/g-vrp.html	Two new problem instances sets based on EMH [21]. Capable to solve EMH’s [21] instances and new instances. SQ&CT&NV: The best approach from AB’s [48] instances.	✓
2017	Leggieri and Haouari [49]	40 (Green-VRP)	6–10/20/2–10	/Formulation (FRLT1, 2, 3,4)	-	Model performance analysis on EMH [21]’s small instances. SQ & CT: New approach outperformed KK [44]’s method.				✓
2017	Yavuz [50]	30 (New) + 12 (Green-VRP)	/10–80/	/Iterated Beam Search	NOI	Solution method performance analysis on YÇ [47] and EMH [21] instances.		✓
2018	Madankumar and Rajendran [52]	40 (New) + 28 (PDP-SSC)	2–5/5–7/1–2	Green Vehicle Routing Problems with Pickups and Deliveries in a Semiconductor Supply Chain (G-VRPPD-SSC)/Three new formulations	https://www.dropbox.com/l/sh/c7W2AyL7AgDjFBYGnnH5gs https://www.dropbox.com/l/sh/UnJ73CAhZhTJxIZk0UmQnn https://www.dropbox.com/l/sh/Vwi8ePIeiLuTO6791bBtiq	Randomly generated problem instances for each new model.				✓
2018	Poonthalir and Nadarajan [53]	40 (Green –VRP)	/20/3	/Particle Swarm Optimization with Greedy Mutation Operator and Time varying acceleration coefficient (TVa-PSOGMO)	-	Algorithm performance analysis on EMH’s [21] instances. Proposed algorithm works well for all the EMH’s [21] data sets.			✓
2018	Zhang et al. [54]	30	/15–150/2–8	Capacitated Green Vehicle Routing Problem (CGVRP)/two-phase heuristic and Ant Colony System (ACS) algorithm	NOI	Randomly generated benchmark instances. SQ: ACS outperformed two phase heuristics. CT: two-phase heuristics outperformed ACS.		✓	✓
2018	Affi et al. [51]	52 (Green –VRP)	3–72/20–500/3–21	/Variable Neighborhood Search (VNS)	-	VNS performance analysis on EMH’s [21] instances. SQ and CT: VNS outperformed other methods on EMH [21]’s small instances. SQ: VNS improved some BKS in EMH [21]’s large instances.			✓
2019	Hooshmand and MirHassani [55]	70	2–12/10–100/2–4	TDGVRP-AF/A hybridization ofMIP model and Greedy Randomized Adaptive Search Procedure (GRASP)	NOI	Time Dependent Green VRP with Alternative Fuel powered vehicles problem (TDGVRP-AF). Randomly generated instances in different sizes.		✓
2019	Koyuncu and Yavuz [56]	10 (Green-VRP) + 10 (MGVRP)	/20–50/2–4	/two formulations: node- and arc-duplicating. Strengthened by two label setting algorithms and improved lower bound	-	MDGVRP-Node Duplicating Formulation (MDGVRP-NDF) MDGVRP-Arc Duplicating Formulation (MDGVRP-ADF) Two-formulation analysis on EMH [21] and YÇ [47] instances. Arc duplication formulation outperformed node duplication one on these instances.	✓
2019	Bruglieri et al. [57]	40 (Green-VRP) + 40 (AB1 & AB2)	6–25/20–100/3–11	/A Path-Based exact Approach (PBA)	-	PBA performance analysis on EMH [21] and AB’s [48] instances. SQ & CT: PBA outperformed all approaches on EMH [21]’s instances. SQ: PBA outperformed MSH [45] in solving AB [48]’s instances. CT: PBA differs from AB [48]’s methods in solving AB [48]’s instances. CT: The best approach for EMH’s [21] instances.	✓	✓
2019	Normasari et al. [58]	52 (Green-VRP)	3–83/20–500/2–28	/Simulated Annealing (SA)	-	New model (Capacitated Green Vehicle Routing Problem (CGVRP)) and algorithm performance analysis based on EMH [21]’s instances. SQ: SA outperformed EMH [21] and SSG [23] solution methods. CT: SA outperformed EMH [21] and SSG [23] solution methodsSQ: The best approach for EMH’s [21] instances		✓
2019	Poonthalir and Nadarajan [39]	40 (New) + 52 (Green-VRP)	3–78/20–500/2–28	Green Vehicle Routing Problem with Queues (GVRP-Q)/enhanced Chemical Reaction Optimization (e-CRO)	NOI	New instances based on EMH’s [21] instances. Algorithm performance analysis on EMH’s [21] instances Proposed algorithm works well for all the EMH’s [21] data sets		✓
2019	Ashtine and Pishvaee [59]	10	3–78/10–15/2–28	/AF-VRP	-	Proposed models performance analysis				✓
2020	Shao and Dessouky [60]	30	3–5/8–32/3–10	VRP with Alternative Fuel Vehicles with Fixed Fueling Time (VRPAFVFFT)/combined ALNS and MIP model	NOI	Algorithm performance analysis on new randomly generated problem instances		✓
2020	Zhang et al. [61]	30	/15–150/2–8	Multi-Depot Green Vehicle Routing Problem (MDGVRP)/Two-phase heuristic Ant Colony System (TSACS)	NOI	Algorithm performance analysis on new randomly generated problem instances		✓
2020	Nosrati and Arshadi Khamesh [62]	28	/3–16/3	/Multi-Objective Simulated Annealing (MOSA)	-	Algorithm performance analysis on EMH [21]’s benchmark instances			✓

The best solution methods for solving each benchmark in the literature are highlighted in bold. The studies marked by “ *” present new benchmark instances and are used as standard benchmarks in other studies. In the absence of an instance link, the NOI abbreviation is used, which means “Not on the Internet”.

Table 7. Summary of solution methods and instances provided in E-VRP.

Year	Reference	Characteristics of Solution Method and Problem Instances					Solution Methods
		Number of Generated and Solved Instances	Size (Min-Max Number of Vehicles/Customers/Recharging (Swapping) Station)	Instances/Algorithm Name or Acronym	Link	Model or Solution Method Evaluation	Exact	Heuristic	Metaheuristic	Commercial Software	Case Study
	% of papers	#	#	#	#	#	14%	44%	34%	23%	17%
2011	Conrad and Figliozzi [20]	30 sets	5–13/40/-	/Formulation	-	Randomly generated instances based on Solomon instances				✓
2011	Gonçalves et al. [89]	-	-	/Formulation	-	Model application in a battery distributor company in Portugal.				✓	✓
2012	Worley et al. [104]	-	-	/Formulation	-	Model application in parcel delivery company in Chicago				✓	✓
2013	Van Duin et al. [99]	-	-	/Formulation	-	Model application in urban area in the inner-city Amsterdam.				✓	✓
2014	SSG [23] *	92 (New) + 76 (MDVRPI) + 52 (Green-VRP)	1–18/5–100/2–21	E-VRP-TW/ Variable Neighborhood Search with Tabu search (VNS-TS) Schneider (SSG)	http://evrptw.wiwi.uni-frankfurt.de	Two new sets of problem instances based on Solomon instances VNS-TS analysis on Multi-Depot VRP with Inter-depot Routes (MD-VRP-I) & EMH [21]’s benchmark instances SQ & CT: VNS-TS outperformed the Crevier et al. [158] approach on MD-VRP-I benchmark instances CT: VNS-TS outperformed the Tarantilis et al. [159] approach. SQ & CT: VNS-TS outperformed EMH’s [21] two approaches NV: The best approach on SSG [23]’s benchmark instances			✓
2014	HPH [100]	108	-/5–15/2–8	/Adaptive Large Neighborhood Search (ALNS) (HPH)	-	ALNS analysis on SSG [23]’s and FSMVRPTW instances. SQ & CT: HPH [100] differs from SSG [23]’s approach. SQ & CT: HPH [100] differs from BKSs of FSMVRPTW’s instances.			✓
2014	Afroditi et al. [3]	-	-	/Formulation	-	No resolution method is proposed for solving the problem	-	-	-	-	-
2014	Preis et al. [63]	160	No restriction/10–100/3	/Adapted Tabu Search	NOI	Randomly generated instances.		✓
2014	FORT [24] *	60 (New)+ 56 (E-VRPTW) + 40 (Green-VRP)	25–100/100–400/5–9	GVRP-MTPR/48 improving Algorithms (48A) and Simulated Annealing(SA) Felipe (FORT)	http://www.mat.ucm.es/_gregoriotd/GVRPen.htm	New randomly generated instances (FORT [24]) 48A & SA algorithms performance analysis on FORT [24], SSG [23], and EMH [21] instances. SQ & CT: Different results in different size of instances. SQ: 48A & SA outperformed EMH’s [21] DBCA approach. SQ: 48A & SA unable to improve SSG [23] approach.		✓	✓
2014	Sassi et al. [36]	9	26/300–550/-	/Charging Routing Heuristic (CRH)	-	Real data instances of two French fleet management companies.		✓			✓
2015	Sassi et al. [90]	29	100/100/21	/Iterated Tabu Search based on a Large NeighborhoodSearch (ITS-LNS)	-	Use three SSG [23] instances to evaluate the solution method.			✓
2015	Sassi et al. [91]	9	26/330–550/15–35	/Multi-start Iterated Local Search (Multi-start ILS)	-	Real data instances provided by a French company.			✓
2015	Schneider et al. [135]	90 (New) + 52 (Green-VRP)+ 76 (VRPIS)	-/20–500/2–28	EVRPRF/Adaptive VNS (AVNS)	NOI	AVNS analysis on EMH [21] and VRP with Intermediate Stops (VRPIS) benchmark instances. SQ&CT: AVNS outperformed SSG [23], and EMH [21] MCWS approaches. New EVRPRF instances based on CVRP benchmark instances.		✓
2015	Bruglieri et al. [64]	6	1–2/5–10/-	/VNS Branching (VNSB)	NOI	Use six SSG [23]’s instances to evaluate the VNSB.		✓
2015	Lebeau et al. [102]	21	2–10/5–25/-	/Savings Heuristic Algorithm	http://mamca.be/plebeau/FSMVRPTW-EV	Randomly generated instances based on a real case. Evaluation the effect of different classes of EVs.		✓			✓
2015	YS [29] *	68	2–38/16–480/1–14	BSS–EV– LRP/modified Sweep heuristic, Iterated Greedy, Adaptive Large Neighborhood Search (SIGALNS) & Tabu Search-modified (TS-MCWS) (YS)	NOI	New sets of instances based on CVRP benchmark instances. SIGALNS & TS-MCWS algorithms performance analysis. SQ & CT: SIGALNS outperformed TS-MCWS.		✓	✓
2015	Li-ying and Yuan-bin [28]	29	2–42/6–200/6–50	/Adaptive VNS with tabu search (AVNS/TS)	NOI	Randomly generated problem instances based on Demir et al. [160]. Pollution Routing Problem (PRP) instances.			✓
2015	Ding et al. [75]	24	2–10/5–100/1–20	/hybrid VNS-TS	NOI	New instances generated based on SSG [23]’s instances.			✓
2015	GHS [83]	30	2–10/6–480/0–2	/Adaptive VNS (AVNS) (GHS)	NOI	AVNS performance analysis on YS [29]’s benchmark instances. SQ&CT&NV&NS: GHS [83] solution method outperformed YS [29] SIGALNS approach.	✓	✓
2015	Montoya et al. [114]	20	-/2–3/10	/Formulation	www.vrp-rep.org	Randomly generated instances Comparison of various methods of charging.				✓
2015	GS [92]	180 (New) + 56 (VRP-TW)+ 56 (E-VRP-TW)	ICEV number correspond to the PRP which is gradually substituted with EVs until /10–200/	E-VRPTWMF/ALNS (GS)	http://www.logistikplanung.tu-darmstadt.de/logistikplanung_und_informationssysteme/forschung_16/publikationen_14/index.de.jsp	New sets of instances generated based on the Demir et al. [160] PRP instances. ALNS performance analysis on SSG [23] and VRPTW benchmark instances. SQ: GS [92] differs from BKS in VRPTW. NV: GS [92] was able to reach similar value. CT: GS [92] outperformed VRPTW benchmark instances. SQ & NC & CT: GS [92] outperformed HPH [100], and SSG [23] approaches on SSG [23] instances. CT&NV: The best approach on SSG [23]’s benchmark instances.			✓
2015	Moghaddam [76]	180	1–2/5/1	/Formulation	-	Random instances based on Solomon [157] to evaluate the model.				✓
2015	Aggoune-Mtalaa et al. [133]	36	10–49/100–400/-	/Genetic Algorithm	-	Model evaluation based on Solomon [157] benchmark instances.		✓
2015	Murakami and Morita [93]	18	0–5/20–40/	/Column Generation Model	-	Randomly instances generated based on Christofides and Eilon’s [161] benchmark instances.	✓
2016	KÇ [77] *	92 (New) +92 (E-VRP-TW)	1–18/5–100/2–21	E-VRP-TW-PR/ALNS (KÇ)	NOI	ALNS performance analysis on SSG [23]’s benchmark instances. ALNS performance analysis on SSG’s [23] benchmark instances with relaxed full recharging assumption SQ: KÇ’s [77] method differs from SSG’s [23] method. NV: KÇ’s [77] method differs from the SSG [23], HPH [100] & GS [92] methods. Evaluation charging strategies by SSG’s [23] benchmark instances.			✓
2016	Schiffer et al. [105]	12	30–45/144–302/4–44	/ALNS	-	Model application in urban area in a German Retail Company.			✓		✓
2016	Desaulniers et al. [78] *	168	/25–100/21	E-VRPTW-(SF, SP, MF, MP)/Branch-Price-and-Cut	https://w1.cirrelt.ca/~errico/,	Different Exact algorithms performance analysis on different variants of E-VRPTW-PR by SSG’s [23] benchmark instances.	✓
2016	Sundar et al. [94]	35	3–5/10–40/4	/Branch & Cut	-	Randomly generated instances for four formulations analysis. SQ & CT: Two arc-based outperformed two node-based.SQ & CT: Second arc-based formulation outperformed first one.	✓
2016	HPRH [101] *	724	/5–100/2–21	E-FSMFTW/ALNS, Branch & Price (BnP) to obtain optimal solutions for smaller instances, and lower bounds for larger instances (HPRH)	http://dx.doi.org/10.1016/j.ejor.2016.01.038	New benchmark instances based on SSG [23] and description of the vehicle type classes of Liu and Shen [162].	✓		✓
2016	MSH 1 2 3 [115]	144 (New)+ 52 (Green-VRP) + 92 (E-FSMFTW)	/5–100/2–21	E-VRP-NL, E-VRP-NL-PR, TRP-CEV/ILS, heuristic concentration (HC), GRASP, parallel matheuristic (PMa). (MSH 1 2 3)	NOI	Solution method performance analysis on EMH [21] and HPRH [101] benchmark instances. SQ & CT: MSH 1 2 3 [115] outperformed EMH [21], SSG [23] and FORT [24] solution methods. SQ & CT: MSH 1 2 3 [115] differ from HPRH [101] solution method		✓	✓
2016	Chen et al. [84]	36 (E-VRP-TW)	1–5/5–15/2–8	/Formulation	-	E-VRP-TW-BSS model evaluation on SSG’s [23] instances. NV: E-VRP-TW-BSS model outperformed SSG’s [23] model. SQ: E-VRP-TW-BSS differs from SSG’s [23] model.				✓
2016	Lin et al. [35]	1	4/13/2	/Formulation		Model application in Austin Texas.					✓
2016	Basso et al. [65]	17	-/15/-	/Formulation	-	Randomly generated small instances.				✓
2013	Barco et al. [31]	-	6–10/20/2–10	/Differential Evolution. (DE)	-	Simulation analysis in Airport Shuttle Service in Bogotá, Colombia.		✓			✓
2017	Schiffer and Walther [106] *	36	1–5/5–15/1–8	E-LRP-TW-PR/Formulation	NOI	New E-LRP-TW-PR benchmark small instances based on SSG [23] small instances with considering all vertices as potential charging station vertices and relaxed full recharging assumption. E-LRP-TW-PR model analysis based on SSG’s [23] small instances with considering all vertices as potential charging station vertices and relaxed full recharging assumption.				✓
2017	MGMV17 [116] *	120	-/10–320/5–38	E-VRP-NL/Iterated local search and a heuristic concentration (ILS+HS) (MGMV17)	www.vrp-rep.org	New problem instances generation for E-VRP-NL. ILS+HS performance analysis on generated instances.			✓	✓
2017	Shao et al. [122]	10	/50/20	/Genetic Algorithm (GA)	-	Performance analysis in Beijing urban area.		✓			✓
2017	Bruglieri et al. [80]	36	1–5/5–15/2–8	/VNS local Branching (VNSB) and Three-Phase Matheuristic (TPM)	-	VNSB & TPM performance analysis on SSG’s [23] instances. SC: TPM outperformed VNSB. CT: VNSB outperformed TPM.			✓
2017	HSG [85] *	34 (New)68 (BSS–EV–LRP)	5–39/50–483/1–10	BSS–EV– LRP/Adaptive VNS (AVNS) (HSG)	http://dx.doi.org/10.1016/j.trb.2016.11.009	AVNS performance analysis on YS’s [29] CVRP benchmark instances. SQ&CT&NV&NS: HSG [85] outperformed YS’s [29] SIGALNS approach. New instances generated based on SSG’s [23] benchmark instances. CT&NS: The best approach for YS’s [29] benchmark instances			✓
2018	SW [107] *	56 (New)+ 24 (New)+ 36 (E-LRP-TW-PR)+ 24 (BSS-EV-LRP) + 56 (E-VRP-TW) + 56 (E-VRP-TW-PR)	1–18/5–160/	E-LRP-TW-PR/Adaptive Large Neighborhood Search (ALNS)(SW)	http://www.om.rwthbreak/>-aachen.de/data/uploads/lrpifinst.zip	New E-LRP-TW-PR benchmark large instances based on SSG’s [23] 100 customer instances with considering all vertices as potential charging station vertices and relaxed full recharging assumption. New instances generated based on real-world instances for E-LRP-TW-PR. Algorithm analysis on Schiffer and Walther [106], SSG [23], and YS’s [29] benchmark instances. SQ&CT: SW [107] differs from BKSs of SSG [23] on average. SQ: SW [107] outperformed GHS [83] on YS [29]’s instances. SQ&CT&NV: SW [107] outperformed KÇ’s [77] BKSs. SQ: SW [107] outperformed HSG [85].			✓
2018	Schiffer and Walther [108]	120	2–4/16–200/2–14	/Adaptive Large Neighborhood Search (ALNS)	10.1016/j.omega.2017.09.003	New instances generated based on Solomon’s [157] benchmark instances.				✓
2018	Paz et al. [109]	36	1–5/5–10/0–15	MDEVLRPTW-BS, MDEVLRPTW-BSPR, MDEVLRPTW-PR/Formulation	http://academia.utp.edu.co/planeamiento/?p=3561	New instances generated based on Schiffer and Walther [106]’s E-LRP-TW-PR benchmark small instances.				✓
2018	Kancharla and Ramadurai [66]	56	4–35/100–200/21	/Adaptive Large Neighborhood Search (ALNS)	-	ALNS performance analysis on SSG [23]’s benchmark instances SQ & NV: ALNS differs from SSG [23]’s VNS-TS approach.			✓
2018	Zhang et al. [136]	55	/2–150/2–8	E-VRP with minimizing energy consumption/Ant Colony (AC) & ALNS	NOI	New randomly generated instances. ALNS & AC algorithms performance analysis. SQ&CT: AC outperformed ALNS.			✓
2018	Verma [86]	92	1–18/5–100/2–21	/local search combined with Genetic Algorithm	-	Heuristic Algorithm analysis on SSG [23]’s instances. SQ: The Heuristic algorithm outperformed SSG’s [23] VNS-TS approach. CT: The Heuristic algorithm outperformed SSG’s [23] model.		✓
2018	Zhou and Tan [110]	13	/5–60/	EV–HR–BSSL/Improved Discrete Cuckoo Search (IDCS)Real Genetic Algorithm (RGA)Modified Discrete Artificial Bee colony (MDABC)	NOI	New randomly generated instances based on Emde et al. [163]. SQ: IDCS outperformed RGA & MDABC. CT: RGA outperformed IDCS & MDABC. SQ: IDCS outperformed the Wang et al. [164] method.		✓
2018	Zuo et al. [67]	25	5/3–5/5	/Formulation	-	Model analysis by generated instances based on Solomon [157] instances.				✓
2018	Gatica et al. [112]	30	/75–150/7–151	/four solution strategies: Random Generation, Customer Location, GreatRoute, and K-Means	-	Algorithm analysis based on Taillard’s [165] benchmark instances.		✓
2018	Villegas et al. [97]	24 (New)204 (E-FSMFTW)	/5–167/1–21	TRSP-CEV/parallel matheuristic (PMa)	www.data.gouv.fr	New TRSP-CEV instances. PMa performance analysis based on HPRH’s [101] benchmark instances. SQ: Pma outperformed HPRH’s [101] ALNS approach on small instances. SQ: Pma differs from HPRH’s [101] ALNS and HGA [151] approaches on large instances. CT: Pma outperformed the HPRH [101] ALNS and HGA [151] approaches. Model application in French electricity giant ENEDIS.		✓			✓
2018	Kullman et al. [142]	90	/10–40/2–4	/Decomposition	-	New randomly generated instances based on the Villegas et al. [97] case study.		✓
2018	Keskin and Çatay [79]	92 (E-VRP-TW)60 (GVRP-MTPR)	/5–400/5–21	/combined ALNS and an exact method (Matheuristic)	-	Solution method analysis on SSG’s [23] benchmark instances. Solution method analysis on FORT’s [24] benchmark instances. SQ&CT: The matheuristic outperformed FORT [24] method. SQ&CT: The best approach for FORT [24] instances.	✓	✓
2018	SSL [111]	56 (New)24 (BSS–EV– LRP)56 (E-LRP-TW PR)	-/16–480/2–21	LRPIF-MR/hybrid of ALNS and Local Search (LS)(SSL)	http://www.om.rwth-aachen.de/data/uploads/lrpifinst.zip.	New LRPIF-MR benchmark instances by modifying Solomon [157] instances of Schiffer and Walther [106]. Algorithm performance analysis on YS’s [29] instances. Algorithm performance analysis on SSG’s [23] instances with relaxed full recharging assumption and considering all vertices as potential charging station vertices. SQ: SSL [111] outperformed SW [107]. SQ: SSL [111] outperformed HSG [85]. CT: SSL [111] differs from SW [107]. SQ: The best approach for YS [29] benchmark instances SQ&CT: The best approach for LRPIF-MR benchmark instances			✓
2018	Zhang et al. [69]	1	2/15/4	/Formulation	-	An instance problem from Solomon’s [157] benchmark instances				✓
2018	Kouider et al. [128]	50	2–7/100–200/	P-E-VRP/Clustering Heuristic (CLH) & Best Insertion Heuristic (BIH)	NOI	New P-E-VRP instances inspired by the FORT [24] data instances.SQ: BIH outperformed CLHCT:CIH outperformed BIHSQ,CT: The best approaches on P-E-VRP benchmark instances.			✓
2019	Kopfer and Vornhusen [95]	10	1–6/10/	/Formulation	-	New randomly generated instances.				✓
2019	Froger et al. [30]	120	/10–20/0–4	/arc-based MILP Path Label and Heuristic algorithm	-	Algorithms analysis on MGMV17 [116]’s benchmark instances. Arc-based formulation outperformed node-based formulations of literature. SQ: Proposed method outperformed MGMV17 [116]’s BKS of E-VRP-NL. CT: The best approaches on MGMV17 [116]’s benchmark instances.	✓	✓		✓
2019	Macrina et al. [96]	260	/5–25/	GMFVRP-PRTW/Iterated Local Search (ILS)	-	Algorithm analysis on modified SSG [23] benchmark instances.		✓
2019	Jie et al. [132]	253 (New)234 (2E-VRP)	2-/7–200/5	2E-EVRP-BSS/a Column Generation and an Adaptive Large NeighborhoodSearch (CG-ALNS)	NOI	New 2E-EVRP-BSS benchmark instances based on available 2E-VRP benchmark instances. CG-ALNS compared to Hemmelmayr et al. [166] and Breunig et al. [167] on 2E-VRP benchmark instances. SQ: CG-ALNS slightly differs from BKSs. SQ,CT&NV: The best approach on 2E-EVRP-BSS benchmark instances.	✓	✓
2019	Zuo et al. [117]	1	-0.125	EVRPTW-CNCF/Formulation	http://w.ba.neu.edu/~msolomon/problems.htm	New generated instances based on Solomon’s (1987) instances				✓
2019	Koç et al. [118]	120 (New)120 (E-VRP-NL)	/10–320/5–38	E-VRP-SCS/Heuristic algorithm based on ALNS framework	NOI	Algorithm analysis on the modified MGMV17 [116] benchmark instances SQ: Heuristic differs from the MGMV17 [116] approach. SQ & CT: The best approach on E-VRP-SCS benchmark instances.		✓
2019	Breunig et al. [131]	54	4–35/21–200/2–50	E2EVRP/large neighborhood search (LNS) metaheuristic and an exact mathematical programming Algorithm (LNS-E2E)	https://www.univie.ac.at/prolog/research/electric2EVRP and https://w1.cirrelt.ca/~vidalt/en/VRP-resources.html.	New E2EVRP benchmark instances based on available 2E-VRP benchmark instances and SSG [23] and Desaulniers et al. [78] benchmark instances. SQ, CT&NV: The best approach on E2EVRP benchmark instances.	✓		✓
2019	Keskin et al. [40]	48	1–18/5–100/2–21	E-VRP-TW with Time-Dependent Waiting Times at Recharging Stations/a matheuristic that combines ALNS with exact method	NOI	Algorithm performance analysis based on SSG [23]’s instances with considering Time-Dependent Waiting Times at Recharging Stations. SQ, CT&NV: The best approach on SSG [23]’s benchmark instances with considering Time-Dependent Waiting Times at Recharging Stations.	✓	✓
2019	Zhao and Lu [103]	40	-/100–111/3–14	Real World E-VRP/ALNS	NOI	Real world instances based on a logistics company in Wuhan, China.			✓		✓
2019	Erdem and Koç [68]	60	2–520/10–445/1–16	HHCRP/Hybrid metaheuristic	NOI	Randomly generated instances based on the Hiermann et al. [168] benchmark instance.			✓
2019	Rastani et al. [34]	65 (New)1 (Case study)	1–19/5–100/3–21	E-VRP-TW-PR with considering different temperature conditions/ALNS	NOI	Model and algorithm performance analysis based on SSG [23]’s instances with considering different temperature conditions. SQ, CT&NV: The best approach on SSG’s [23] benchmark instances with considering different temperature conditions.			✓		✓
2019	Pelletier et al. [138]	30 (New)124 (CVRP)	3–65/10–320/-	E-VRP-ECU /two phase Set Partitioning Large Neighborhood Search (LNS+SP)	NOI	Model, Robust optimization and algorithm performance analysis on new generated instances based on MGMV17′s [116] instances. Two-phase algorithm (LNS+SP) performance analysis on CVRP and Robust CVRP (RCVRP) existing benchmark instances			✓
2019	Keskin et al. [41]	36	2–4/10/5	/M/M/1 queueing system equations	-	Model analysis on SSG [23] 10-customer instances				✓
2019	Cortés-Murcia et al. [81]	92 (New)56 (E-VRP-TW-PR)	1–18/5–100/2–21	E-VRPTWsc /Hybrid Iterated Local Search (Hybrid ILS)	https://doi.org/10.1016/j.tre.2019.08.015	Hybrid-ILS performance analysis on SSG’s [23] benchmark instances with relaxed full recharging assumption. Hybrid-ILS performance analysis on SSG’s [23] benchmark instances with satellite customers assumption (E-VRPTWsc). SQ & CT & NV: Hybrid-ILS [81] outperformed KÇ [77], SW [107], and HGA [151], approaches on SSG’s [23] benchmark instances with relaxed full recharging assumption (E-VRP-TW-PR). SQ, CT&NV: The best approach on SSG’s [23] benchmark instances with relaxed full recharging assumption. SQ, CT&NV: The best approach on SSG’s [23] benchmark instances with satellite customers assumption.			✓
2019	Rezgui et al. [134]	86	2–33/5–400/	/VNS	-	Algorithm performance analysis of Solomon [157] benchmark instances.			✓
2019	Basso et al. [137]	58 (New)	/5–20/	Comparison between numerical simulations and the actual energy consumption data measured on the public transport route	https://www.electricitygoteborg.se	Randomly generated instances. Real data from Gothenburg, Sweden					✓
2019	Goeke [70]	92 (New)176 (PDP-TW)	1–22/3–50/2–21	PDPTW-EV/Granular Tabu Search (GTS)	http://www.vrp-rep.org/datasets/item/2019-0001.html.	GTS performance analysis on SSG’s [23] benchmark instances with pickup and delivery assumption. GTS performance analysis on PDPTW benchmark instances SQ, CT&NV: The best approach on SSG’s [23] benchmark instances with pickup and delivery assumption.		✓
2019	Lu and Wang [139]	60	/15–150/2–8	/Bi-Strategy Based OptimizationAlgorithm (BSOA)	-	Algorithm performance analysis on Zhang et al. [54] benchmark instances.		✓
2019	Xiao et al. [71]	56	/25–100/	/Dynamic Heuristic Solution	-	Test instances derived from Solomon [157] benchmark instances.		✓
2019	Lu et al. [139]	180 (New)180 (TD-PRP)	-/20–100/-	TD-E-VRP/Iterated VNS (IVNS)	NOI	TD-E-VRP new benchmark instances generated based on GS’s [92] E-VRP-TW instances modification. Proposed IVNS performance analysis on TD-Pollution Routing Problem (TD-PRP) instances compared with the Francesschetti et al. [169] ALNS algorithm. SQ: IVNS outperformed ALNS			✓
2019	Reyes-Rubiano et al. [141]	54	5–20/50–1200/	/Monte Carlo simulation with a multi-start Metaheuristic (simheuristic)	-	Method analysis on Uchoa et al. [170] benchmark instances Method analysis on modified on Uchoa et al. [170] benchmark instances under uncertainty conditions.		✓
2020	Meng and Ma [72]	1	2–4/25/5	/Ant Colony Algorithm	-	Model analysis on modified instance number R101 from Solomon [157] data set		✓
2020	Taş [73]	18	1–4/5–15/2–7	/Column generation	-	Evaluating benefits of flexible time windows on SSG [23] small instances Performance analysis on SSG [23] small instances	✓
2020	Granada-Echeverri et al. [140]	95 (New)95 (VRPB)	/20–150/	/Iterated Local Search (ILS) used as initial methodology	http://academia.utp.edu.co/planeamiento/sistemas-de-prueba/	Proposed analysis on VRP with Backhauls (VRPB) literature instances and newly generated Electric VRPB (E-VRPB) instances by modifying VRPB instances.				✓
2020	Kullman et al. [143]	30,000	/10–40/18	/Decomposition	-	New randomly generated instances based on the Froger et al. [30] testbed.		✓
2020	Kullman et al. [144]	102	/8–26/6–79	/Labeling algorithm open-source Python-based implementation	-	New randomly generated instances based on the Villegas et al. [97] case study.		✓
2020	Lee [119]	131	1/15–36/4–5	EVRP/Branch-and-Price	-	New randomly generated instances based on Solomon [157] and Augerat et al. [171] instances	✓
2020	Mao et al. [87]	56	/100/21	/hybridization of an improved ACO algorithm, insertion heuristic and enhanced local search (ACO-LS)	-	Problem and Algorithm analysis on SSG [23] benchmark instances		✓
2020	Almouhanna et al. [113]	16 (New)58 (New)58 (LRP)	/12–200/	LRPCD/Multi-Start Biased-Randomized Heuristic (MSBRH) and Biased-Randomized VNS (BR-VNS)	http://neos-server.org	New LRPCD instances by modifying existing LRP instances. Algorithm performance analysis on LRP benchmark instances SQ: BR-VNS outperformed MSBRH. CT: MSBRH outperformed BR-VNS. SQ, CT: The best approaches on the Almouhanna et al. [113] benchmark instances.		✓	✓	✓
2020	Zhang et al. [82]	30 (New)4 (E-VRP-TW)	/30–200/2–8	F-EVRPTW/ALNS and VNS with the fuzzy simulation method	https://doi.org/10.6084/m9.figshare.10288326	New randomly benchmark instances generated. Model evaluation by four SSG [23] instances.		✓
2020	Zhang et al. [124]	123 (New)	1–18/5–100/2–21	TD-E-VRP-CT/Adaptive Large Neighborhood Search (ALNS)	NOI	New model and ALNS performance analysis on SSG’s [23] benchmark instances with time-dependent property. SQ, CT&NV: The best approach on SSG’s [23] benchmark instances with time-dependent property.		✓
2020	Zhu et al. [126]	1 (New)36 (E-VRP-TW) 180 (2L-CVRP)	-/5–36/2–7	2L-MDEVR/Saving Heuristic Algorithm with VNS algorithm (SSH-VNS)	NOI	Algorithm performance analysis on 2L-CVRP benchmark instances. Algorithm performance analysis on SSG’s [23] small benchmark instances. A new instance generated to analyze the 2L-MDEVRP model and SSH-VNS		✓			✓
2020	Kancharla and Ramadurai [120]	120 (New) 120 (New) 120 (E-VRP-NL)	/10–320/5–38	E-VRP-NL-LD, E-VRP-NL-LD-CCS/Adaptive Large Neighborhood Search (ALNS)	NOI	Model and ALNS performance analysis on MGMV17′s [116] benchmark instances. SQ: ALNS outperformed the MGMV17 [116] and Froger et al. [30] methods on E-VRP-NL instances. New problem instances generation for E-VRP-NL-LD. New problem instances generation for E-VRP-NL-LD-CCS. SQ: The best approach on MGMV17 [116] benchmark instances. SQ: The best approach on Kancharla and Ramadurai [120] benchmark instances		✓
2020	Löffler et al. [74]	168 (E-VRPTW-(SF, SP, MF, MP))	/25–100/21	/Large Neighborhood Search (LNS) and Granular Tabu Search (GTS), called LNS × GTS	-	Different LNS × GTS algorithm performance analysis on different variants of the Desaulniers et al. [78] benchmark instances. SQ & CT: LNS × GTS outperformed the Desaulniers et al. [78] method. SQ & CT: The best approach on the Desaulniers et al. [78] benchmark instances.		✓
2020	Raeesi et al. [88]	148	/5–100/21	EVRPTW-SMBS/ two-stage hybridization of a dynamic programming and an integer programming algorithm	https://data.kent.ac.uk/105/	New instances generated by modifying SSG [23] benchmark instances.		✓
2020	Keskin et al. [38]	29	/25–100/21	/ALNS	-	ALNS performance analysis on modified E-VRP-TW-SP instances of Desaulniers et al. [78].		✓

Table 8. Summary of the solution methods and instances provided in H-VRP.

Year	Reference	Characteristics of Solution Method and Problem Instances					Solution Methods
		Number of Generated and Solved Instances	Size (Min-Max Number of Vehicles/Customers/Recharging (Swapping) Station)	Instances/Algorithm Name or Acronym	Link	Model or Solution Method Evaluation	Exact	Heuristic	Metaheuristic	Commercial Software	Case Study
	% of papers	#	#	#	#	#	8%	50%	58%	0%	16%
2013	Abdallah [22]	150	3–33/16–100/-	PHEVRPTW/Lagrangian relaxation and Tabu Search	NOI	New model and Algorithms analysis based on Solomon [157] benchmark instances.		✓
2014	MRH [150]	20	3–15/21–134/-	VRPMDR/Multi-Round Heuristic algorithm (MRH)	NOI	Algorithm analysis on modified CVRP benchmark instances by considering three classifications of vehicles: 1. ICE and PHEV vehicles, 2. medium-range EVs, and 3. short-range EVs.		✓
2016	Doppstadt et al. [37] *	36	-/8–50/-	HEV-TSP/Iterated Tabu Search & Local Search	https://data.mendeley.com/datasets/9j3tt84hyx/2	New benchmark instances based on real-world delivery. SQ: The best approach on HEV-TSP’s benchmark instances.		✓	✓		✓
2017	MH [145]	9 (New) 52 (Green-VRP)	4–78/20–500/2–28	H-VRP/Matheuristic, Method (MH)	NOI	Algorithm analysis on EMH’s [21] benchmark instances. SQ: MH [145] outperformed the EMH [21] and FORT [24] approaches, and similar SSG [23] approach in small size instances. CT: MH [145] outperformed SSG [23], differs from Felipe et al. [24] in small size instances. SQ: MH [145] outperformed the EMH [21] and FORT [24] approaches, and differs from the SSG [23] approach in large instances. CT: MH [145] differs from the SSG [23] and FORT [24] approaches in large size instances. New randomly generated benchmark instances.		✓
2017	Vincent et al. [13]	16 (New) 16 (CVRP)	3–10/29–134/	H-VRP/Simulated Annealing with a Restart Strategy (SA RS)	NOI	Algorithm performance analysis on CVRP benchmark instances Algorithm performance analysis on newly H-VRP instances			✓
2019	HGA [151]	56 (New) + 56 (E-VRPTW) + 56 (E-VRPTWPR) + 56 (E-FSMFTW)	1–18/5–100/2–21	H2E-FTW/Combination of Genetic Algorithm and Large Neighborhood Search (LNS) (HGA)	http://www.vrp-rep.org/datasets/item/2017-0029.html.	New H2E-FTW benchmark instances by adding three vehicle classes including ICEV, PHEV and EV. Algorithm performance analysis on SSG’s [23] benchmark instances. Algorithm performance analysis on SSG’s [23] benchmark instances with relaxed full recharging assumption. Algorithm performance analysis on SSG’s [23] benchmark instances with the fleet composition extension. SQ & CT: HGA [151] outperformed SSG [23], HPH [100], GS [92], and KÇ’s [77] approaches on SSG’s [23] benchmark instances for E-VRPTW. SQ & CT: HGA [151] outperformed KÇ’s [77] approach on SSG [23]’s benchmark instances with relaxed full recharging assumption (E-VRPTWPR). SQ & CT: HGA [151] outperformed HPRH [101] and Montoya Montoya’s [115] approaches on approach on SSG’s [23] benchmark instances with the fleet composition extension (E-FSMFTW). SQ: The best approach on SSG’s [23] benchmark instances. SQ&CT: The best approach on SSG’s [23] benchmark instances with the fleet composition extension			✓
2019	Eskandarpour et al. [152]	25	3–38/22–420/	/an enhanced variant of Multi-Directional Local Search (EMDLS)	-	Algorithm analysis on CVRP benchmark instances EMDLS compared to MDLS, Improved MDLS (IMDLS), non-dominated sorting genetic algorithm II (NSGAII), non-dominated sorting genetic algorithm III (NS- GAIII), and the weighting and epsilon-constraint methods.			✓
2020	Zhen et al. [154]	45	2–11/5–100/2–11	HEVRP with mode selection/Improved Particle Swarm Optimization Algorithm (IPSO)	NOI	New generated instances based on Solomon’s [157] instances.			✓
2020	Doppstadt et al. [149]	180 (New) + 36 (HEV-TSP)	/8–50/	HEV-TSP-TW/Parallel-VNS (P-VNS)	https://data.mendeley.com/datasets/9j3tt84hyx/2	New benchmark instances by adding Time Windows to the Doppstadt et al. [37] benchmark instancesSQ & CT: The best approach on HEV-TSP-TW’s benchmark instances. CT: The best approach on HEV-TSP’s benchmark instances.		✓
2020	Li et al. [155]	14	4–10/32–100/0–8	/A memetic algorithm a using a Sequential Variable Neighborhood Descent (SVND)	-	New generated instances on modified CVRP benchmark instances.			✓
2020	Bahrami et al. [156]	17	2–10/13–50/	/Branch-and-Price and a Heuristic Algorithm	-	Randomly generated instances based on VRP instances Case study on Toronto.	✓	✓			✓
2020	Hatami et al. [153]	33	3–15/21–134/	/Multi-Round Iterated Greedy (MRIG)	-	Algorithm analysis on CVRP benchmark instances Comparison of the proposed solution method MRH [150] method on VRP-MD.			✓

6.1. Most Usable EF-VRP Benchmark Instances

Recent studies on the EF-VRP have largely focused on the creation and use of standard benchmarks instances. In this section, the most usable and effective benchmark instances to solve each variant of EF-VRP instances are described.

6.1.1. AF-VRP

Green-VRP. Erdoğan and Miller-Hooks (EMH) [21] generated four sets which contain ten instances, each comprising 20 customers (which are either uniformly distributed or clustered) and between two and ten refueling facilities. The fifth set presents a case study conducted by the authors and consists of twelve instances involving between 111 and 500 customers and 21 to 28 facilities. The geographical coordinates given in the instances have to be converted to distances between vertices using the Haversine formula using an average earth radius of 4182.45 miles.

MGVRP. Yavuz and Çapar (YÇ) [47] applied 19 different data sets with different characteristics such as how the customers are distributed over space (uniformly or clustered), and the service area attributes by using adapted instances from Erdoğan and Miller-Hooks [21].

AB1 & AB2. Andelmin and Bartolini (AB) [48] introduced new instances by extracting customers from larger instances of Erdoğan and Miller-Hooks [21]. AB contains two subsets: AB1 and AB2. The AB1 instances have the same parameter values as the original ones in Erdoğan and Miller-Hooks [21] and guarantee that each customer can be served with at most a single refueling stop. The AB2 instances have the same refueling stations and customers as those initially considered in the AB1 before applying the removal. Indeed, the AB2 instances also contain customers that cannot be served with a single refueling stop.

6.1.2. E-VRP

The most commonly used benchmark problem instances presented in the E-VRP and its variants are presented by Schneider et al. [23]. These benchmark instances have been addressed in studies by SSG and first used to evaluate the proposed hybrid VNS-TS algorithm in solving the E-VRPTW. Proposed E-VRP-TW formulations aim to first optimize the number of vehicles used and then decrease the total distance of the routes.

E-VRP-TW. Schneider et al. (SSG) [23] constructed 36 small and 56 large instances based on the well-known VRPTW instances of Solomon [157] The large instances include three main problem classes where 100 customers and 21 recharging stations are clustered (C), randomly distributed (R), and both clustered and randomly distributed (RC) over a 100 × 100 grid. Each set also has two subsets, type 1 and type 2, which differ by the length of time windows and the vehicle load and battery capacities. The small instances include three subsets of 12 problems, each involving 5, 10, and 15 customers randomly drawn from the large instances.

E-VRP-TW-PR. Keskin and Çatay (KÇ) [77] relaxed the assumption of EVs full recharging on Schneider et al. [23] instances, resulting in the E-VRP-TW with partial recharging (E-VRPTW-PR) and provided new solutions for a different set derived from the ones by Schneider et al. [23].

GVRP-MTPR. Felipe et al. (FORT) [24] addressed the E-VRP with multiple charger types, and partial recharges and proposed the data set which is referred to as FORT instances and consists of two different configurations involving five and nine stations. Each configuration includes three sets of ten instances with 100, 200, and 400 customers distributed randomly. In total, the data set includes 60 instances.

E-VRPTW-(SF, SP, MF, MP). To analyze the new assumptions in E-VRP-TW such as single or multiple recharge(s) per route within the fully or partial recharges, Desaulniers et al. [78] modified the Schneider et al. [23] E-VRPTW instances and presented a set of new instances, namely, E-VRPTW-(SF, SP, MF, MP).

BSS-EV-LRP. Yang and Sun (YS) [29] modified several CVRP benchmark instances from the literature to generate BSS-EV-LRP instances. Besides, Hof et al. (HSG) [85] provided new BSS-EV-LRP meaningful instances concerning the necessity of using BSSs by modifying the Schneider et al. [23] benchmark instances.

E-LRP-TW-PR. Schiffer and Walther (SW) [106] analyzed the influence of partial recharging and simultaneous sitting in planning models for electric logistics fleets on the Schneider et al. [23] small instances. They consider all vertices as potential charging station locations. They limited the experiments to the instances with 5, 10, and 15 customers, deriving a set of 36 instances in total. Schiffer and Walther (SW) [107] did the same thing for large 56 instances with 100 customers provided by Schneider et al. [23] for the E-VRP-TW, considering all vertices as potential charging station vertices. Furthermore, Schiffer and Walther (SW) [107] created 24 new instances based on a real-world case of the ELRP-TWPR based on data that have been collected within an extensive field test with the German retail company.

E-FSMFTW. Hiermann et al. (HPRH) [101] proposed new sets of benchmark instances based on Schneider et al. [23] combined with the vehicle type definition for the Fleet Size and Mix fleet of Liu and Shen [162]. They considered three (increasing) battery capacities and customer location patterns: randomly distributed (r), clustered (c), or a mix of both (rc).

E-VRP-NL. Montoya et al. (MGMV17) [116] generated a new set of instances using real data for the EV configuration and battery charging functions. They generated 30 sets of customer locations and located the customers in a geographic space of 120 × 120 km using either a random uniform distribution, a random clustered distribution, or a mixture of both. For each of the 30 sets of locations, the customer location strategy using a uniform probability distribution was chosen.

6.1.3. H-VRP

HEV-TSP. Doppstadt et al. [37] generated a new benchmark instances problem to investigate the performance of the proposed algorithm. The instances generated were divided into three different classifications at different intervals between the depot and delivery area. In the first set, the depot was proximate to the delivery area. In the second and third sets, the distance was considered 28 and 57 km, respectively. Furthermore, for each set of instance problems, different driving speeds were considered for vehicles. In the generated instance studies, the number of customers was considered among 8, 10, 20, and 50 variables.

To the best of our knowledge, all new instances in the EF-VRP literature and their so-far best-known methods in terms of SQ, CT, NV, and NS are presented in Table 9. All of these new instances can be analyzed for more comparison by authors in future studies.

Table 9. Summarized results for the EF-VRP generated instances.

Problem Type	EF-VRP Instances Name	Presented by:	Solved by:	So-Far Best-Known Methods
AF-VRP	Green-VRP	EMH [21]	EMH [21]; SSG [23]; Felipe et al. [24] Taha et al. [43]; Schneider et al. [135]; KK [44]; MSH [45]; MSH 1 2 3 [115]; Bruglieri et al. [46]; AB [48]; Leggieri and Haouari [49]; Yavuz [50]; Affi et al. [51]; Poonthalir and Nadarajan [53]; Koyuncu and Yavuz [56]; MH [145]; Bruglieri et al. [57]; Normasari et al. [58]; Poonthalir and Nadarajan [39]; Nosrati and Arshadi Khamesh [62]; MH [145]; Yavuz [50]	SQ: Bruglieri et al. [46] CT: MSH [45]
	MGVRP	YÇ [47]	YÇ [47]; Yavuz [50]	SQ: YÇ [47] CT: Yavuz [50]
	G-VRP	AB [48]	AB [48]; Bruglieri et al. [57]	SQ: AB [48] CT: Bruglieri et al. [57]
	G-VRPPD-SSC	Madankumar and Rajendran [52]	Madankumar and Rajendran [52]	Madankumar and Rajendran [52]
	CGVRP	Zhang et al. [54]	Zhang et al. [54]	Zhang et al. [54]
	GVRP-Q	Poonthalir and Nadarajan [39]	Poonthalir and Nadarajan [39]	Poonthalir and Nadarajan [39]
	VRPAFVFFT	Shao and Dessouky [60]	Shao and Dessouky [60]	Shao and Dessouky [60]
	MDGVRP	Zhang et al. [61]	Zhang et al. [61]	Zhang et al. [61]
E-VRP	E-VRPTW	SSG [23]	SSG [23]; FORT [24]; Schneider et al. [135]; GS [92]; KÇ [77]; Chen et al. [84]; SW [107]; Kancharla and Ramadurai [66]; Verma [86]; Keskin and Çatay [79]; HGA [151]; Zhang et al. [82]; Zhu et al. [126]	SQ: HGA [151] CT: GS [92] NV: SSG [23] and GS [92]
	EVRPRF	Schneider et al. [135]	Schneider et al. [135]	Schneider et al. [135]
	E-VRPTWPR	KÇ [77]	KÇ [77]; SW [107]; HGA [151]; Cortés-Murcia et al. [81]	SQ&CT&NV: Cortés-Murcia et al. [81]
	GVRP-MTPR	FORT [24]	FORT [24]; Keskin and Çatay [79]	SQ&CT: Keskin and Çatay [79]
	E-VRPTW-(SF, SP, MF, MP)	Desaulniers et al. [78]	Desaulniers et al. [78], Löffler et al. [74]	SQ&CT: Löffler et al. [74]
	BSS-EV-LRP	YS [29]	YS [29]; GHS [83]; SW [107]; Hof et al. [85]; SSL [111]	SQ: SSL [111] CT: Hof et al. [85] NS: Hof et al. [85]
		HSG [85]	HSG [85]	HSG [85]
	E-LRPTWPR	Schiffer and Walther [106] for small instances SW [107] for large instances	Schiffer and Walther [106]; SW [107]; Schiffer et al. [111]	SQ&CT: Schiffer and Walther [106]; SW [107]
		SW [107]	SW [107]; SSL [111]	SSL [111]
	E-FSMFTW	HPRH [101]	HPRH [101]; MSH 1 2 3 [115]; Villegas et al. [97]; HGA [151]	SQ: HGA [151] CT: Villegas et al. [97]
	E-VRPNL	MSH 1 2 3 [115] MGMV17 [116]	MSH 1 2 3 [115]; MGMV17 [116]; Froger et al. [30]; Koç et al. [118]; Kancharla and Ramadurai [120]	SQ; Kancharla and Ramadurai [120] CT: Froger et al. [30]
		Lee [119]	Lee [119]	Lee [119]
	E-VRPNLPR	MSH 1 2 3 [115]	MSH 1 2 3 [115]	MSH 1 2 3 [115]
	E-VRP-NL-LD & E-VRP-NL-LD-CCS	Kancharla and Ramadurai [120]	Kancharla and Ramadurai [120]	Kancharla and Ramadurai [120]
	E-VRPTWMF	GS [92]	GS [92]	GS [92]
	MDEVLRPTW-BSPR	Paz et al. [109]	Paz et al. [109]	Paz et al. [109]
	E-VRP with minimizing energy consumption	Zhang et al. [136]	Zhang et al. [136]	Zhang et al. [136]
	EV–HR–BSSL	Zhou and Tan [110]	Zhou and Tan [110]	Zhou and Tan [110]
	TRSP-CEV	MSH 1 2 3 [115]	MSH 1 2 3 [115]; Villegas et al. [97]	SQ: Villegas et al. [97] CT: Villegas et al. [97]
	LRPIF-MR	SSL [111]	SSL [111]	SSL [111]
	GMFVRP-PRTW	Macrina et al. [96]	Macrina et al. [96]	Macrina et al. [96]
	2E-EVRP-BSS	Jie et al. [132]	Jie et al. [132]	Jie et al. [132]
	EVRPTW-CNCF	Zuo et al. [117]	Zuo et al. [117]	Zuo et al. [117]
	E-VRP-SCS	Koç et al. [118]	Koç et al. [118]	Koç et al. [118]
	E2EVRP	Breunig et al. [131]	Breunig et al. [131]	Breunig et al. [131]
	E-VRP-TW with Time-Dependent Waiting Times at Recharging Stations	Keskin et al. [40]	Keskin et al. [40]	Keskin et al. [40]
	P-E-VRP	Kouider et al. [128]	Kouider et al. [128]	Kouider et al. [128]
	E-VRPTWsc	Cortés-Murcia et al. [81]	Cortés-Murcia et al. [81]	Cortés-Murcia et al. [81]
	PDPTW-EV	Goeke [70]	Goeke [70]	Goeke [70]
	Real World E-VRP	Zhao and Lu [103]	Zhao and Lu [103]	Zhao and Lu [103]
	HHCRP	Erdem and Koç [68]	Erdem and Koç [68]	Erdem and Koç [68]
	E-VRP-ECU	Pelletier et al. [138]	Pelletier et al. [138]	Pelletier et al. [138]
	TD-E-VRP	Lu et al. [139]	Lu et al. [139]	Lu et al. [139]
	LRPCD	Almouhanna et al. [113]	Almouhanna et al. [113]	Almouhanna et al. [113]
	F-EVRPTW	Zhang et al. [82]	Zhang et al. [82]	Zhang et al. [82]
	TD-E-VRP-CT	Zhang et al. [124]	Zhang et al. [124]	Zhang et al. [124]
	EVRPTW-CNCF	Zuo et al. [117]	Zuo et al. [117]	Zuo et al. [117]
	E-VRP-NL-LD, E-VRP-NL-LD-CCS	Kancharla and Ramadurai [120]	Kancharla and Ramadurai [120]	Kancharla and Ramadurai [120]
	EVRPTW-SMBS	Raeesi et al. [88]	Raeesi et al. [88]	Raeesi et al. [88]
H-VRP	PHEVRPTW	Abdallah [22]	Abdallah [22]	Abdallah [22]
	VRPMDR	MRH [150]	MRH [150]	MRH [150]
	HEV-TSP	Doppstadt et al. [37]	Doppstadt et al. [37]; Doppstadt et al. [149]	SQ: Doppstadt et al. [37] CT: Doppstadt et al. [149]
	H-VRP	H-VRP	MH [145]	MH [145]	MH [145]
	H-VRP	Vincent et al. [13]	Vincent et al. [13]	Vincent et al. [13]
	H2E-FTW	HGA [151]	HGA [151]	HGA [151]
	HEVRP with mode selection	Zhen et al. [154]	Zhen et al. [154]	Zhen et al. [154]
	HEV-TSP-TW	Doppstadt et al. [149]	Doppstadt et al. [149]	Doppstadt et al. [149]

7. Conclusions

This study presented a comprehensive review of the literature concerning on the Environmentally Friendly Routing Problem (EF-VRP). In this research, the EFVs were categorized into three classifications of Alternative-Fuel Vehicle (AFV), Electric Vehicle (EV), and Hybrid Vehicle (HV), and were separately investigated. Reviewing the studies on the routing of each of these vehicles was conducted based on three fundamental approaches: I. The classical constraints and assumptions existing in the field of the VRP that led to the formation of different variants of these problems; II. General characteristics and operational constraints existing concerning the EFVs; III. Solution methods to solve different variants of VRP problems. This research indicated that there are numerous research problems and gaps in the field of EF-VRPs which were provided for each classification of EF-VRP studies. Investigating each of these problems can answer many questions about the benefits of using EFVs and increase using these vehicles in distribution systems throughout the world, thereby reducing the environmental side effects of transportation.

In the reviewed papers, researchers focus just on the operational part, disregarding the underlying business model. There is a need for such an integration, because it can bring new insights on both aspects. Crainic et al. [17] highlighted that there is a more general lack. Only in the past decade some papers have shown the benefits of a mix of qualitative and quantitative approaches for sustainable and green logistics (Rosano et al. [6], Perboli and Rosano [5], Perboli and Rosano [172], De Marco et al. [173], Tadei et al. [174], Brotcorne et al. [8], Perboli et al. [175], Perboli et al. [176], Fadda et al. [177], and Perboli et al. [178]). This is a big gap between the literature and practice. In fact, the lack of a link between the methods and the business solutions prevent the usage of the results coming from the academia in the industry, as witnessed by the analysis of the results of Smart City projects [179].